An acoustically controlled helical microrobot

Abstract

As a next-generation toolkit, microrobots can transform a wide range of fields, including micromanufacturing, electronics, microfluidics, tissue engineering, and medicine. While still in their infancy, acoustically actuated microrobots are becoming increasingly attractive. However, the interaction of acoustics with microstructure geometry is poorly understood, and its study is necessary for developing next-generation acoustically powered microrobots. We present an acoustically driven helical microrobot with a length of 350 μm and a diameter of 100 μm that is capable of locomotion using a fin-like double-helix microstructure. This microrobot responds to sound stimuli at ~12 to 19 kHz and mimics the spiral motion of natural microswimmers such as spirochetes. The asymmetric double helix interacts with the incident acoustic field, inducing a propulsion torque that causes the microrobot to rotate around its long axis. Moreover, our microrobot has the unique feature of its directionality being switchable by simply tuning the acoustic frequency. We demonstrate this locomotion in 2D and 3D artificial vasculatures using a single sound source.

An acoustically driven helical microrobot with a double-helix microstructure capable of corkscrew-like locomotion was developed.

INTRODUCTION

Corkscrew motions are ubiquitous among nature’s microscopic swimmers, having evolved in various strains of bacteria, spermatozoa, and other microswimmers as a means of overcoming the viscous drag that dominates at the microscale. For example, spirochete, a pathogen that causes diseases such as Lyme disease and syphilis, can swim in viscous environments like gel, blood, lymph, or connective tissue through rotation of periplasmic rotors, leading to its overall rotation and corresponding translation (1, 2). Biomimicking such a motion in artificial swimmers is extremely challenging but crucial to the development of next-generation microrobots. The pioneering work of Ghosh et al. and Zhang et al. has demonstrated helical motion using magnetic actuation (3, 4); however, such motion has yet to be successfully implemented with any other actuation method. Several other pioneering physical and chemical microscale propulsion strategies have been studied, including biohybrids (5, 6), chemical reactions (7, 8), optics (9), enzymes (10–13), electric fields (14), magnetics (15–19), and acoustics (20–25). However, poor biocompatibility, low speed and force, and poor navigation capabilities limit the potential of existing approaches, particularly for medical applications. For example, microrobots that use chemical fuels and electric fields for propulsion may not be entirely biocompatible, as these mechanisms could damage biological tissue. Recently, a promising new possibility has emerged in which enzymes are used to catalyze a reaction resulting in propulsion. However, so far, no controlled manipulation of enzyme-powered microrobots has been demonstrated. Another sophisticated strategy for microrobot propulsion is light activation of photoactive liquid-crystal elastomers; although these can be made biocompatible, light penetrates only to a depth of a few millimeters in human skin and may be absorbed or scattered by surrounding tissue, making in vivo use of this system difficult. Acoustically and magnetically powered micro/nanorobots are well suited for surgical operations, as both acoustic waves and magnetic fields can penetrate deep into the tissue of animal or human bodies and generate a broad range of forces that can result in strong propulsive forces (5, 6, 15–17, 26–29). Magnetic microrobots are well known for their precise navigation capabilities but require a complex multistep microfabrication process, including doping with magnetic materials; moreover, magnetic manipulation systems are associated with bulky and expensive apparatus. Furthermore, there are strong limitations to the rate of change of the magnetic flux to avoid harmful electromagnetic induction in a medical application.

However, acoustically actuated wireless microrobots, while still in the very early stages of development, are becoming increasingly attractive, as acoustic control can generate large propulsive forces, can penetrate deep into the tissue, cannot be affected by the opaque nature of animal or human bodies, requires a simple microrobot design, and does not entail complex manipulation systems. In the design of ultrasound-based microrobots, it is important to consider the interaction between acoustic waves and (i) material composition and (ii) the geometry of microstructures. For example, trapped microbubbles in polymeric cavities cause intense scattering, bringing about strong propulsive forces when activated by ultrasound (30, 31). Different sizes and arrangements of microbubbles lead to different motions: rotational and directional (32, 33). Although acoustically activated microbubbles can generate large propulsive force, their instability limits their practical application in vivo. Furthermore, advanced hydrophobic treatments are required to maintain microbubbles within submicrometer cavities (33). To overcome this challenge, researchers have developed bubble-free, acoustically activated micro- and nanorobots. For example, propulsion has been demonstrated through the acoustic oscillation of appendages such as artificial flagella and ciliary bands (24, 25). Wang et al. (34) demonstrated propulsion using bimetallic rods at the pressure nodes of a standing acoustic wave field. This system, however, is intrinsically dependent on the boundaries of a resonating acoustic chamber, which limits its use in vivo, and many of its mechanisms remain unknown. Nonetheless, most acoustic systems of propulsion have not been shown to propel in three-dimensional (3D) vasculature environments, which is crucial for in vivo navigation. Recently, Ren et al. (30) and Aghakhani et al. (33) have demonstrated 3D manipulation of bubble-activated acoustic microrobots; however, these microrobots require gas-filled microbubbles, can only be propelled unidirectionally when they are exposed to ultrasound, and are not able to steer without the application of an external magnetic field. Furthermore, they are difficult to manipulate in vasculature when the microrobots’ length exceeds the diameter of the vessel; thus, a microrobot design is needed that can induce bidirectional motion without physical orientation, which is necessary to avoid occluding the vessels. To introduce novel acoustic propulsion mechanisms with new functionalities, we need to investigate the ways in which sound interacts with the microarchitectures of various geometrical configurations. At present, the interaction between acoustic wave fields and complex geometrical microstructures, particularly in the context of propulsion, has almost not at all been studied.

Here, inspired by the helical geometry of spirochete bacteria, we present an acoustically driven helical microrobot (or micropropeller) that is capable of locomotion using a fin-like double-helix vane. This microrobot responds to external sound stimuli and mimics the spiral motion used by spirochetes and spirilla, which are natural microswimmers. The asymmetrical double-helix shape serves to interact with the incident acoustic field, inducing a propulsion torque that causes the microrobot to rotate around its long axis. Moreover, our microrobot has the unique feature of a propulsion direction that is switchable simply via tuning the acoustic frequency. We demonstrate this locomotion in artificial arbitrarily shaped 2D and 3D vasculatures using a single sound source. Because ultrasound is already in widespread use as an imaging modality in clinical settings, our robotic system can be seamlessly integrated into its practices; thus, our findings could contribute significantly to the development of next-generation smart microrobots for noninvasive surgical procedures.

RESULTS

Particle design

Inspired by the locomotion of helical natural microswimmers such as Spirochete bacteria (Fig. 1A), we have designed a wireless microrobot consisting of a cylindrical core and a double-helical vane that coils around the core (see Fig. 1). The double-helical vane can be seen as a superposition of two curved vanes that spiral along the surface of the cylindrical core as helicoids. When this microrobot is surrounded by a fluid like water and exposed to an acoustic field, it is propelled forward by a corkscrew-like motion, where the particle rotates around the axis of its cylindrical core and simultaneously translates along this axis. Our microrobots can be directly manufactured by a high-resolution two-photon lithography 3D printing technique [see Fig. 2 (A and B)]. The microrobots that we have manufactured for the present study have a length l = 350 μm and diameter σ = 100 μm and are made from a polymeric material (see Materials and Methods).

Fig. 1. Spirochete-inspired propulsion based on acoustic actuation.

(A) Micrograph showing the spiral morphology of Spirochete bacteria (51), which execute translation motion through rotation in viscosity-dominated fluids, reprinted with permission from (51). Copyright ª 2023 Yale Journal of Biology and Medicine. (B) An illustration of a wireless bioinspired robot that propels in response to an external sound field. (C) A concept schematic illustrates the use of such microrobots for noninvasive surgery in vasculatures.

Fig. 2. Design, fabrication, and concept of the acoustically actuated helical microrobot.

(A) The acoustic helical microrobots are mass-manufactured using the two-photon lithography technique. The bottom inset shows different designs of the microrobots featuring helical vanes with radius r_d = 1.0, 0.65, 0.43, and 0.22. (B) Micrograph illustrating the top view of the fabricated microrobots on a thin glass slide. The inset shows the detail of vane. (C) Side view of the fabricated microrobots. Schematic and fluorescent micrographs (right) illustrating the helical vane structures on the microrobot with r_d = 0.43 and 0.22. The pink and blue colors represent the two respective levorotatory double-helix vanes developed on the microrobot. (D) Image sequences demonstrate the acoustic microrobots’ translational and rotational motion in response to an acoustic stimulus at 13.5 kHz. The insets show the clockwise rotation of the microrobot, which is indicated by the orientation of the vane geometry. (E) Schematic of the experimental setup. The polydimethylsiloxane (PDMS)–based microchannel was bonded onto a glass slide adjacent to a piezo transducer, which generates the acoustic wave field. The inset illustrates the manipulation of the microrobot within a microchannel of arbitrary shape. Scale bars, 40 μm.

Propulsion mechanism

To determine the forces and torques exerted on these microrobots and thus to characterize their propulsion mechanism, we performed acoustofluidic computer simulations. They are based on the compressible Navier-Stokes equations

$$\frac{\mathrm{\partial }}{\mathrm{\partial }t}\mathrm{\rho }{u}_i+{\mathrm{\partial }}_j\mathrm{\rho }{u}_j{u}_i={\mathrm{\partial }}_j{\text{Σ}}_{ji}$$ (1)

with the momentum-stress tensor

$${\text{Σ}}_{ji}=\mathrm{\mu }({\mathrm{\partial }}_j{u}_i+{\mathrm{\partial }}_i{u}_j-\frac{2}{3}{\mathrm{\partial }}_k{u}_k{\mathrm{\delta }}_{ji})+\mathrm{\zeta }{\mathrm{\partial }}_k{u}_k{\mathrm{\delta }}_{ji}-p{\mathrm{\delta }}_{ji}$$ (2)

where t denotes time; ∂_i denotes a partial derivative with respect to the ith spatial coordinate; u_i, ρ, and p are the fluid’s velocity, mass density, and pressure fields; μ and ζ are its constant shear and bulk viscosities; g represents additional source terms; and δ is the Kronecker-delta symbol. In addition, we used the continuity equation. To simulate a microrobot, we used the same system and parameter values as in the experiments and calculated the sound propagation in the fluid and its interaction with the particle by solving this set of equations numerically. For this purpose, we used the self-developed acoustofluidics software AcoDyn, which makes use of the finite-volume method. The numerical solutions of the equations yield the time-dependent density, velocity, and pressure fields in the fluid around the particle. The total force F_i and torque T_i on the particle can be expressed in terms of the density, velocity, and pressure fields as an integral over the particle volume Ω as

$$F_i={\int }_{\text{Ω}}{\mathrm{\partial }}_j{\sum }_{ji}d\text{Ω},T_i={\int }_{\text{Ω}}{\in }_{ilk}{r}_l{\mathrm{\partial }}_j{\sum }_{jk}d\text{Ω}$$ (3)

where ε is the Levi-Civita symbol and r_i is the location of the volume element dΩ relative to the microrobot’s center. We do not consider wave propagation through the material of the particle. Therefore, Stokes’ theorem can be used to rewrite F_i as an integral over the particle surface ∂Ω as

$$F_i={\int }_{\mathrm{\partial }\text{Ω}}{n}_j{\sum }_{ji}dS,T_i={\int }_{\mathrm{\partial }\text{Ω}}{\in }_{ilk}{r}_l{n}_j{\sum }_{jk}dS$$ (4)

where n_i is the normal vector of the surface element d∂Ω = n_idS (35) with the surface differential dS. To obtain the propulsion force and torque, we time-averaged F_i and T_i locally over one wave period and determined their values for large times.

Because the structure of the microrobot has no translational invariance, a full 3D simulation was needed to investigate the microrobot’s propulsion mechanism. Furthermore, a large domain in space and time [many wave periods to reach a sufficiently converged solution (36)] needed to be covered with high resolution, especially around the particle, and with a small temporal step size (37). See note S1 for details on the simulations.

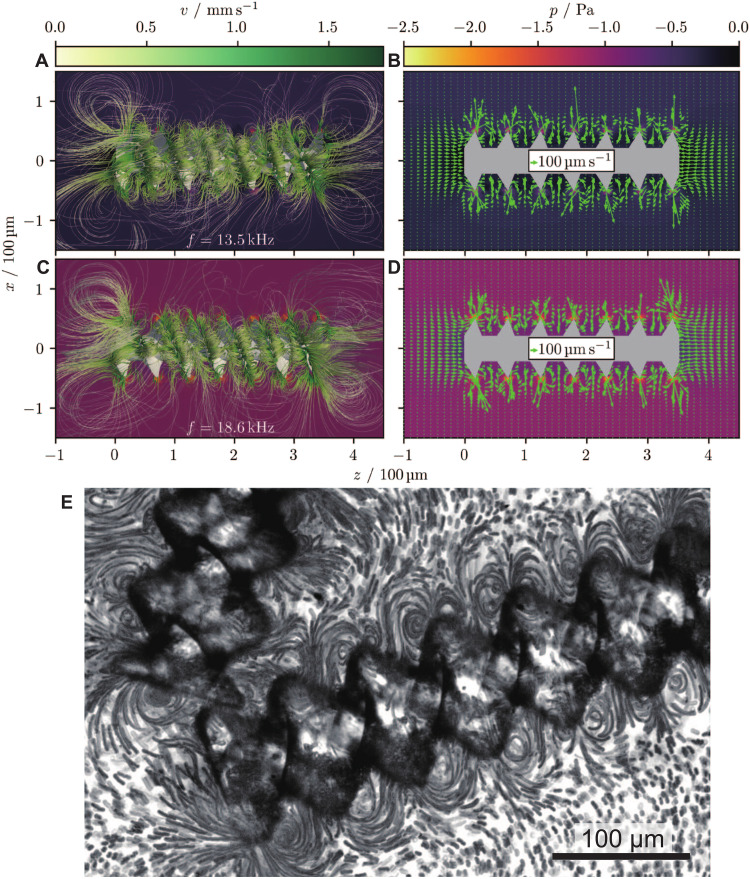
The 3D simulations unveil the propulsion experienced under sound exposure, as depicted in Fig. 3. For symmetry reasons, the propulsion torque must be generated by the interaction of the acoustic field in the fluid with the helical vanes of the microrobot. Furthermore, the torque must be parallel to the particle’s main axis. The subsequent nonreciprocal corkscrew-like motion around this axis (depicted in Fig. 2D) can be observed in all experiments. The simulation results show that the rotation of the particle is not a side effect of translational propulsion in combination with a helical particle shape. Instead, there is a significant propulsion torque that leads to the particle’s rotation directly and, in combination with the helical particle shape, can contribute to the particle’s translational propulsion. In a low Reynolds number fluid (the Reynolds number Re = ρuσ/μ, with the characteristic length scale σ = 100 μm, is Re < 0.03 ≪ 1), acoustic microstreaming may play a role in propulsion. Our simulation results show a significant acoustic microstreaming around a microrobot (see Fig. 3). The microstreaming flow velocities reach approximately 350 μm/s at 10 V_PP and 18.6 kHz, which is of the same order as the observed velocities of the microrobots in the experiments conducted at 10 V_PP (fig. S1 and movie S1).

Fig. 3. Results of acoustofluidic simulations for the flow field around the microrobot.

(A to D) The simulations correspond to a particle with length of 350 μm, outer diameter of 100 μm, helicity h_d = 1.08, and relative inner diameter r_d = 0.43. Furthermore, the sound frequency is 13.5 kHz (A and B) and 18.6 kHz (C and D). The subfigures in the left column (A and C) show 3D streamlines in the fluid around the particle, whereas in the right column (B and D) a 2D cross section of the velocity field is shown. The pressure field is shown in the background. One can see vortices that form at the tips of the microbots’ fins (see also movie S1). All quantities shown are averaged over the last simulated wave period. The simulations were performed using the fluid dynamics solver AcoDyn. (E) Micrograph of stacked images illustrates the developed acoustic streaming around the microrobot at an excitation frequency and voltage of 18.6 kHz and 10 V_PP, respectively (see also movie S1).

This suggests that the acoustic microstreaming is the main reason for the propulsion of the microrobots. Acoustic streaming has been identified as the origin of acoustic propulsion also for other microparticles (38). One might wonder why acoustic streaming has a significant effect on our microrobots despite their relatively large size. This can be explained by the special shape of our microparticles. As can be seen in Fig. 3, the acoustic streaming occurs mainly along the fin-like vanes, which determine a length scale much smaller than the microrobot itself.

We now address the connection between the translational and rotational motion of the microrobot in more detail. The fact that, in all experiments, fast translational motion could be observed together with rotation around the particle’s main axis indicates strongly that the geometrical shape of the microrobot results in a coupling between translational and angular propulsion. Intuitively, this mechanism is caused by the hydrodynamic resistance of the microrobot’s helical fin structure. To verify this hypothesis, we compared the experimental translation velocity of the microrobot with the theoretical velocity induced solely by its rotation, as predicted by the particle’s hydrodynamic resistance matrix.

In a liquid at a low Reynolds number, the hydrodynamic resistance matrix can be used to transform between a particle’s translational or angular velocity and the force or torque acting on the particle that causes these velocities

$$\overrightarrow{\mathbf{K}}=\mathrm{\mu }\mathcal{H}\overrightarrow{\mathbf{w}}$$ (5)

Here, $\overrightarrow{\mathbf{K}}={(\overrightarrow{\mathbf{F}},\overrightarrow{\mathbf{T}})}^T$ is the force-torque vector that acts on the particle, $\mathcal{H}$ is its shape-dependent 6 × 6–dimensional hydrodynamic resistance matrix, and $\overrightarrow{\mathbf{w}}={(\overrightarrow{\mathbf{v}},\overrightarrow{\mathbf{\text{ω}}})}^T$ is the particle’s translational-angular velocity vector with the translational velocity $\overrightarrow{\mathbf{v}}$ and the angular velocity $\overrightarrow{\mathbf{\text{ω}}}$. To determine $\mathcal{H}$, we used the software HydResMat (39, 40), which solves the Stokes equation using the finite element method.

Because the main rotation action of the particles in the experiments is observed around a particle’s main axis, it can be concluded that the main torque acting on the particle acts along this axis. Assuming a force-torque vector $\overrightarrow{\mathbf{K}}$, where all vector components except for T_z, which is the torque component parallel to the main axis, are zero, we can find a value for T_z such that the corresponding angular velocity ω_z matches that observed in the experiments. In this way, an approximation is gained for both the propulsion torque of the particle and the component of the translation velocity resulting purely from the particle’s rotational motion.

Using the hydrodynamic resistance of the particle, the maximum rotation speed of ω_z ≈ 1.66 Hz observed in the experiments results in a translational velocity of v_rtz ≈ 126 μm/s, which only slightly differs from the translational velocity of v_tz ≈ 111.9 μm/s that we observed in the experiments. The corresponding torque along the main axis of the particle is T_z ≈ 618 nN·μm. Repeating this comparison between the theoretically predicted rotation-induced translation velocity and the translation velocity observed in experiments for particles with slightly differing geometrical properties allows for a quantitative assertion of how significant the contribution of the particles’ rotation to its translational motion is. The “structure-dependent behavior” section below will show a strong coherency between the rotation-induced translational velocity v_rt introduced purely through hydrodynamic translational-rotational coupling and the total translational velocity v_t observed in the experiments. This indicates that the rotation about the main axis of the particle is a major contributor to its translational motion. The small discrepancy between v_rt and v_t can be explained, in part, by acoustic radiation applying a driving force to the particle directly and by drag between the particle and the channel walls in the experiments, which has not been taken into account for the calculation of $\mathcal{H}$. The evidently strong coupling between acoustically induced rotation and translation is a unique feature of our particle design.

The flow and pressure fields surrounding the microrobot can be calculated using acoustofluidic simulations. As depicted in Fig. 3, vortices are formed near the fins and at both ends of the particle. The formation of the latter has already been observed to be common in acoustically propelled microparticles (36, 37, 41). The vortices near the fins form two helicoidal vortex tubes that wind around the particle. These vortex tubes generate a tangential fluid flow along the vanes of the microrobot, which explain (at least partially) the torque generated by the microrobot (see also movie S1).

Manipulation in 2D channel

We manipulated our microrobots in two different environments: a rectangular acoustic chamber filled with water and a circular microchannel with diameter of 500 μm filled with an isopropyl alcohol solution. The acoustic chamber and microchannel were made of polydimethylsiloxane (PDMS) and, together with a piezoelectric transducer, bonded onto a glass slide (see also Fig. 2). The piezoelectric transducer, which generates the sound field driving the microrobots, is regulated by an external function generator connected to an amplifier. The entire setup was mounted on a microscope, and the experiments were recorded using high-speed and high-sensitivity cameras to analyze the mechanism behind the propulsion (see Materials and Methods for more details).

In response to an acoustic field, the microrobot advances unidirectionally along the channel at a uniform speed while rotating about its z axis. Figure 4A shows the left-to-right locomotion of the microrobot at ~100 μm/s accompanied by clockwise rotation at 1.66 s⁻¹ when the microrobot is exposed to an acoustic field with frequency f₁ = 13.5 kHz and peak-to-peak voltage of 20 V_PP. As we modulate the driving frequency of the acoustic signal, the microrobot shows a counterclockwise rotation and translational motion in the opposite direction. Figure 4B illustrates the right-to-left motion of the microrobot at ~70 μm/s and rotation at 0.9 s⁻¹ for f₂ = 18.6 kHz and 60 V_PP. Figure 4 (C and D) shows this bidirectional propulsion along a channel. Upon activation at f₁, the microrobot is translated along the microchannel at ~100 μm/s. After 13.2 s, we turned off the acoustic signal, causing the microrobot to roll back to the middle of the microchannel because of gravity. At 22.5 s, when the transducer was activated again at f₂, the microrobot was propelled in the opposite direction at ~70 μm/s. This ability to alter the directionality of the microrobot by almost 180° by simply switching the activation frequency of the acoustic signal is a unique feature that can potentially avoid occluding vessels when acoustically actuated microrobots are applied in medicine. The calculated wavelength of the acoustic wave at 13.5 and 18.6 kHz (λ = c/f, and c is 1500 m/s) is approximately 111 and 81 mm, respectively, which is almost three orders of magnitude greater than the dimensions of the microrobots.

Fig. 4. Translational motion of the microrobot in a circular microchannel.

(A) The microrobot exhibits left-to-right locomotion in response to an external acoustic wave at f₁ = 13.5 kHz and 20 V_PP. The symbol P(t) in the top schematic represents the pressure wave, while the black arrow indicates the direction of the acoustic wave field. (B) The microrobot exhibits right-to-left locomotion for f₂ = 18.6 kHz and 60 V_PP. (C) A microrobot illustrates its bidirectionality when switching from f₁ = 13.5 kHz and 20 V_PP to f₂ = 18.6 kHz and 60 V_PP. (D) The plot illustrates the speed profile of the microrobot during its bidirectional trajectory. (E) The microrobot’s left-to-right velocity v_t1 and right-to-left velocity v_t2 versus the acoustic driving voltage V_PP indicate that the microrobot propels at a speed nearly proportional to ${\mathrm{V}}_{\mathrm{PP}}^2$

. The inset shows the corresponding log-log plot. Note that the scaling of v_t2 was difficult to predict because of a lack of data points at higher voltages, as the maximum voltage is restricted by our amplifier at 60 V_PP. Scale bars, 100 μm. The direction of gravity is antiparallel to the y direction (indicated by ⨀), i.e., perpendicular to the figure plane. Each data point represents the average velocity of at least three microrobots. The error bar represents the SD.

The unidirectional and bidirectional trajectories of the microrobot are consistent both in the rectangular chamber (fig. S3 and movie S2) and in the microchannel (movie S3), indicating that its behavior is determined by the acoustic field and not significantly influenced by the channel wall. The microrobot executed cork-screw motion, i.e., rotation combined with translation in a straight trajectory in both open and closed channels. However, the excitation frequencies varied by 11% between the rectangular chamber and open channel, which could be attributed to differences between the water and ethanol solutions in which the microrobots were submerged. We also observed that the left-to-right (i.e., parallel to the sound propagation) propulsion velocity is generally ~40% greater than the right-to-left (i.e., antiparallel to the sound propagation) propulsion velocity, independent of the boundary condition. The structural changes or the shape in the helicoidal vortex tubes that wind around the vane are distinctly different between the two different excitation frequencies, as shown in Fig. 3. These changes, although intricate and delicate, have a subtle visual impact, which may not be immediately apparent (Fig. 3, A and C). However, our streaming experiments reveal a flow reversal around the microrobot when the frequency is switched (see also movie S4). We hypothesize that these subtle structural changes in the vortex tube, as well as the streaming behavior, play a crucial role in the observed variations in propulsion strength and direction.

We further measured the speed of the microrobot as a function of the intensity of the incident acoustic field, controlled by adjusting the voltage applied to the piezoelectric transducer. The propulsion velocity ν_t scales quadratically with the applied voltage V_PP, i.e., ν_t ∝ ${\mathrm{V}}_{\mathrm{PP}}^2$, as shown in Fig. 4E. This scaling relationship is expected because the acoustic pressure amplitude is proportional to V_PP and the acoustic energy density is proportional to the pressure amplitude squared (41). Numerical and experimental studies have shown that the pressure amplitude depends linearly on applied voltage for small signal power values (31).

The consistent coherency of rotational and translational velocity signifies the fact that the rotation of the microrobot contributes to translation. Approximating the torque experienced by the particle through hydrodynamic resistance, calculated from the hydrodynamic resistance matrix $\mathcal{H}$ using the observed terminal angular velocity, yields a translational velocity of ~126.0 μm/s purely through particle rotation and hydrodynamic resistance, without taking account of any other effects. This fact also indicates that particle rotation is a main contributor to the overall particle velocity. The difference between the observed translational velocity and the one calculated for rotational-translational coupling through hydrodynamic resistance can, in part, be explained by the absence of friction forces between the particle and the channel walls in the computational model.

Structure-dependent behavior of the microrobot

In this section, we investigate the parametric effects of the width and pitch of the helical vane structure on the microrobot’s propulsion. To characterize the width, we introduce as a dimensionless parameter the effective radius ratio (r_d = r/R), which describes the ratio of the radius r of the microrobot’s cylindrical core to the microrobot’s total radius R. First, we fabricated a cylindrical microstructure without any helical vanes (i.e., r_d = 1), which also served as a control in that, when subjected to acoustic stimulation, the microstructure undergoes no rotational motion and nearly no translational motion. We then designed microrobots with helical vanes with r_d values of 0.65, 0.43, and 0.22. The design and cartoon schematics of the microrobots are shown in Fig. 5A (left). As r_d decreases, the microrobots’ vanes become wider, resulting in faster rotation rates and higher translation velocities at constant activation parameters of 13.5 kHz and 20 V_PP, as shown in Fig. 5A. The micrographs shown in Fig. 5A represent the distances traveled by these different microrobots over 10 s of acoustic stimulation; the microrobot with the lowest r_d value (r_d = 0.22) traveled the farthest (see also movie S6). Figure 5B estimates the translational velocity v_t and rotational velocity ω of a microrobot as functions of r_d. Lower r_d values result in larger values of v_t and ω, which can be attributed to the larger dimensions of the vanes. We further calculated, on the basis of the microrobots’ hydrodynamic resistance matrix (see the “Propulsion mechanism” section for details), their translational velocity v_rt that corresponds to their rotational velocity ω as a function of r_d (see Fig. 5B). The result for v_rt is very similar to v_t, indicating that the microrobots’ rotation is crucial for their propulsion.

Fig. 5. The structure-dependent behavior of the microrobots.

(A) Parametric study of the effect of the effective diameter ratio (r_d = r/R) on the translation and rotation velocities of the microrobot. With decreasing r_d values, microrobots exhibit faster translation, which can be attributed to increases in their vane width and surface area. The left panel illustrates the design of microrobots with r_d = 1.0, 0.65, 0.43, and 0.22. Right: The distance traveled for each corresponding r_d value over 10 s at the constant activation parameters of 13.5 kHz and 20 V_PP; see also movie S6. Scale bar, 200 μm. (B) Plot of a microrobot’s translational velocity v_t (green), angular velocity ω (blue), and rotation-induced translational velocity v_rt (white) as functions of r_d. (C) Parametric study of the effect of the helical pitch h_d = P/(2R) on the translation and rotation velocities of the microrobot. Left: The design of microrobots with h_d = 2.16, 1.08, and 0.54. Right: The distance traveled for each corresponding h_d value over 6 s at 13.5 kHz and 20 V_PP; see also movie S7. Scale bar, 200 μm. (D) Plot of the microrobot’s translational velocity v_t (green), angular velocity ω (blue), and rotation-induced translational velocity v_rt (white) as functions of h_d.

Next, we characterized the effect of the reduced helical pitch h_d = P/(2R) on the microrobots’ propulsion, where P is the helical pitch. We fabricated microrobots that had h_d values of 2.16, 1.08, and 0.54. As h_d decreases, the number of helical turns on the microrobot’s surface increases, as demonstrated in Fig. 5C (see also movie S7). Microrobots with lower h_d values exhibited faster angular and translational propulsion velocities when exposed to acoustic stimulation; a microrobot with h_d = 0.54 was propelled the most rapidly at ~150 μm/s. Figure 5D indicates the translational velocity v_t and the rotational velocity ω attained by the microrobots as functions of h_d. As h_d decreases, both v_t and ω increase, which might be attributed to the larger number of helical turns of the vanes. We further calculated the microrobots’ translational velocity v_rt from ω as a function of h_d, which supported the importance of the microrobots’ rotation for their translational propulsion.

Manipulation in 3D channel

Microrobots that can deliver drugs directly to lesions through the vasculature are the next generation of drug carriers. To execute this task, microrobots should be able to navigate in 3D vasculatures. In this section, we study the microrobots’ propulsion and navigation behavior in response to acoustic stimulation in arbitrary 3D vasculatures. We created PDMS-based microchannels with various angles (0°, 15°, 25°, 45°, 60°, and 75°), defined as the angle of inclination of the microchannel to the horizontal plane, as shown in Fig. 6A. These PDMS-based microchannels are fabricated by molding electric wires into PDMS, which are removed after curing. Figure 6B shows a photograph of a PDMS-based microchannel. The concept of bidirectional motion when the excitation frequency is switched from f_down (downward) to f_up (upward) is shown in Fig. 6C. Figure 6D shows superimposed images of microrobots during downward motion at 15°, 25°, 45°, 60°, and 75° inclinations at excitation frequencies of f_down = 11.7 to 13.7 kHz. The microrobots executed rotation along their long axis and traveled at an almost uniform velocity (see also movie S8). When we increased the slope from 45° to 60°, no noticeable change in behavior was observed. As the microrobot is propelled through channels with larger slopes 45°, 60°, and 75°, it becomes blurry or out of focus because we kept the focus of the microscope constant. This effect is more pronounced with 75° slope at the right of Fig. 6D (bottom).

Fig. 6. Manipulation of the microrobots in a 3D artificial vasculature.

(A) A schematic illustrates the manipulation of acoustic helical microrobots in channels with different inclination angles (see also fig. S5). (B) The photograph depicts a 3D PDMS-based artificial vasculature mounted on a glass slide adjacent to a piezo transducer. The inset shows the fluorescently labeled channel with a circular cross section. (C) Concept of bidirectional motion when the excitation frequency is switched from f_down (downward) to f_up (upward). (D) Superimposed images showing downward motion (f_down = 11.7 to 13.7 kHz) of microrobots in 3D channels with angles of 0°, 15°, 25°, 45°, 60°, and 75°. (E) Examples of superimposed images showing an upward propulsion (frequency f_up = 14.5 to 15.1 kHz) of microrobots in 3D channels with angles of 15° and 45°. See also movies S8 and S9. Scale bars, 250 μm.

In addition to the downward motion, the developed microrobots also exhibited controlled upward motion in a microchannel, as shown in Fig. 6E. The microrobot changed the direction of its rotational and translational motion as the stimulation frequency (f_up = 14.5 to 15.1 kHz) was modulated in microchannels at inclinations 15° and 45°, indicating that bidirectionality of the microrobots is preserved in 3D vasculatures (movie S9). The time stamps in Fig. 6E indicate that the microrobot propelled significantly slower in a 45° slope vasculature compared to a 15° slope vasculature. Thus, a higher voltage is required to counteract gravity and sustain upward motion as the inclination angle is increased.

Because of challenges associated with repeatedly bonding the piezo transducer and the fluidic channel in the same location on the glass slide that represents a base plate in the experimental setup, slight frequency shifts have been observed across various experiments. To optimize the driving frequency of the microrobot, we swept the excitation frequency in the range of 10 to 20 kHz by an electronic function generator while maintaining a fixed voltage and estimating the microrobot’s maximum speed using a camera connected to the microscope. However, upon successful calibration of the acoustic device (a quick and real-time process), the excitation frequency remains constant throughout subsequent experiments. The 3D manipulation and bidirectionality of acoustically actuated microrobots pose a bottleneck in many situations; our observations indicate that our microrobots offer a promising solution for this issue.

DISCUSSION

This study presents biomimetic, acoustically controlled, spiral-shaped microrobots inspired by Spirochete bacteria. The microrobots respond to sound stimuli from outside the body and mimic the spiral motion of natural microswimmers to execute propulsion at low Reynolds numbers. They exhibit simultaneous rotation and translation motion, enabled by the interaction between acoustics and the double-helix microstructure. The microrobots have exhibited bidirectional capabilities, meaning that they can propel even antiparallel to the propagation direction of the sound wave using a single acoustic piezo transducer. Furthermore, we have successfully shown that our microrobots can move through both 2D and 3D channels and can travel longer distances (see also fig. S4 and movie S4).

Magnetically actuated helicoidal microrobots have been used for propulsion at low Reynolds numbers (4, 18, 42–45). Typically, these microrobots are designed by applying a magnetic metal coating, which requires magnetization to enable their response to a rotating magnetic field. Furthermore, magnetic microrobots are often restricted to a step-out frequency (typically in the hertz regime), where the magnetic torque applied is unable to keep the microrobot synchronized with the external magnetic field. This limitation cannot be resolved by increasing the magnetic flux density because electromagnetic induction must be kept at a harmless level in a medical application. In contrast, acoustically activated microrobots have different propulsion mechanics and concepts, resulting in faster propulsion. Translation velocities of acoustically actuated microrobots scale quadratically with input voltage and can reach larger values. Our microrobots’ translation velocity, as shown in fig. S6, is comparable to magnetically actuated helical robots.

Our current helical microrobots rely on the geometry of their microstructure and are composed of a single polymer material. As a result, our microrobots eliminate the need for magnetic coatings, metal deposition, or additional magnetization steps. When acoustic fields encounter obstacles, they scatter the sound field. Metal particles scatter more strongly than polymer particles. We plan to create microrobots using metal or by coating our polymer resin microstructures with various metals. We will examine how acoustic propulsion affects different helix-shaped microstructure designs and material combinations. Further research will concentrate on enhancing the microrobot’s translational motion by improving their geometry, size, and materials to achieve faster rotation-induced movement.

Advancements in microrobot technology will also aim at 3D manipulation in a complex physiological environment by incorporating other techniques. For example, magnetic materials can be coupled with microrobots to enhance their steerability. A transducer array can also shape a specific sound field, contributing to the microrobot’s steerability, which is particularly important in branched channels. In addition, future research will examine the microrobots’ steering capabilities using acoustics alone. Microstructures, when exposed to an acoustic field, can generate various types of vortex flow fields, primarily influenced by the excitation frequencies. By activating a glass capillary at different frequencies, diverse oscillation modes can be induced, resulting in the generation of distinct vortex patterns (46). This phenomenon can be leveraged to precisely control microrobot movement using only acoustic fields. Researchers aim to explore acoustic activation of microrobots to induce different acoustic streaming profiles for steering purposes (38) while also stimulating the microrobots at frequencies in the range of 10 to 20 kHz to induce propulsion.

Our research will further study acoustic microrobot propulsion, specifically in dynamic and unstructured environments, which are particularly important for physiological conditions in vivo. To enhance the efficiency and effectiveness of the propulsion process, we aim to streamline and automate the entire process by integrating reinforcement learning strategies (47). By incorporating such strategies, the microrobots can learn from their experiences and optimize their movements in response to various environmental conditions, enabling more efficient navigation. When a microrobot confronts rough terrain and experiences immobilization, a burst of high-voltage stimulation can be applied to surmount the barrier and resume propulsion. In addition, we have previously demonstrated that when microrobots are pushed toward the wall in a Poiseuille-type flow (21, 23, 48), they experience minimal drag, allowing them to effectively propel against the liquid flow. This concept can be used to encounter blood flow for in vivo conditions. Furthermore, in consideration of safety, the estimated acoustic intensity required to activate our microrobot was approximately 21.68 to 200.21 mW/cm², which is considered safe, as it remains below the Food and Drug Administration’s established maximum permitted spatial-peak temporal-average of 720 mW/cm² (see also note S2 for details) (49, 50). However, as the attenuation in various organs differs, concrete intensity tests are suggested.

At present, our microrobots can propel in artificial vasculature with bidirectional capability. When microrobots perform tasks in vivo, they may encounter a number of challenges, including head-to-tail inversion in tiny vessels. When the particles are long compared to the vessel diameter, they can cause an occlusion by reorientation or cannot be able to invert their orientation and, thus, propulsion direction at all. Because our microrobots can move bidirectionally without head-to-tail inversion by tuning the excitation frequency, we can prevent these problems. We also look forward to having our microrobots navigate through smaller blood vessels and capillaries. Microstructures with submicrometer helical characteristics can be easily fabricated with 2D photon lithography. When scaling down the microrobots, the underlying propulsion mechanism will require further study. However, as we scale the microrobots down, the dominance of the acoustic radiation and streaming forces will change. The velocity field around the particle, as calculated through our acoustofluidic simulations (see Fig. 3), as well as the motion of tracer particles around the microrobot (see Fig. 3E), strongly suggests that microstreaming plays a significant role and may even be the primary factor contributing to the propulsion of our microrobots (38). Future work will examine how the microrobots’ size affects their propulsion, which will lead to a better understanding of the propulsion mechanism in general.

The concept of the rotational and translational motion of microrobots can be further used in the development of wireless stents. For instance, we can design a stent with a similar helix structure and use acoustics to implant it into the lesion area through acoustic manipulation. Future microrobots can be more functional for more flexible and customized biomedical applications. For example, drug-containing microbubbles can be equipped with our microrobots in the process of drug delivery by using transducers with different excitation frequencies to prevent interference between their propulsion and drug-delivery functions. In addition, as our microrobot is manipulated by acoustics, integrating it with clinical ultrasound may be possible for simultaneous manipulation and monitoring of its motion. The developed microrobots can also trap and transport micro- to millimeter-sized objects, such as cells, organoids, tissue constructs, and model organisms like Caenorhabditis elegans and zebrafish embryos to desired locations using the scattered sound fields of the microrobots. Furthermore, the microrobots can be built with hollow cavities to trap and transport sperm cells for in vitro fertilization.

MATERIALS AND METHODS

Fabrication of helical microrobots

The acoustics-driven helical microrobots were directly mass-fabricated according to a standard procedure by Nanoscribe (Nanoscribe Photonic Professional GT, Nanoscribe GmbH) based on two-photon 3D laser lithography (24). This technique allowed the direct and precise printing of complex 3D micro/nanostructures at an enhanced resolution. A drop of photoresist (IP-Dip, Nanoscribe GmbH) was placed on an indium tin oxide–coated standard glass slide (25 mm by 25 mm by 1 mm), which was precisely inserted into a microscope system for laser writing through a 63× objective. The printing system could expose and cure the photoresist programmatically layer by layer, as shown in Fig. 2B. After writing, the glass slide with microrobots was carefully developed in 1-methoxy-2-propanol acetate developer for 10 min and rinsed using isopropyl alcohol (IPA) for 2 min.

Fabrication of acoustic chamber and channels

Experiments were conducted to investigate 2D and 3D manipulation in two different geometries: a PDMS-based rectangular chamber with dimensions of 20 mm by 20 mm and a circular microchannel with a diameter of 500 μm. For the rectangular chamber, a piece of glass was used as the mold, while for the circular microchannel, a wire with a diameter of 500 μm served as the mold. The fabrication process involved pouring PDMS (Dow Corning) into the assembled molds and subsequently curing it in a heater at 80°C for 2 hours. In addition, to create more complex 3D microchannels, wires with a diameter of 500 μm were used. This process resulted in the formation of microchannels with various angles, including 0°, 15°, 25°, 45°, 60°, and 75°, as depicted in Fig. 6B and fig. S5.

Manipulation of the microrobot

The PDMS-based microchannel was carefully bonded to a glass slide measuring 75 mm by 25 mm by 1 mm after surface plasma treatment. Adjacent to the PDMS channel, a piezoelectric transducer (Steiner & Martins Inc., USA), which generates the acoustic field, was also bonded. The entire setup was mounted on an inverted microscope (AxioVertAxiovert 200, Carl Zeiss, Germany) equipped with various objectives (2.5×, 5×, 10×, and 20×) for imaging the microrobots. The microscope featured high-speed (Kron Technologies Inc., Canada) and high-sensitivity (Photometrics, USA) cameras to record and characterize the propulsion of the microrobots.

The microrobots were transferred into the channel using an optical fiber. For the rectangular chamber, a solution of water was injected, while the circular channel was filled with isopropyl alcohol as the solvent. The manipulation system primarily comprised a function generator (Tektronix Inc., USA) and an amplifier (Digitum-Elektronik, Germany) to generate an adjustable acoustic wave with parameters such as wave types, voltage, and frequency. In the experiment, a continuous square wave with a voltage range of 15 to 60 V_PP (peak-to-peak) and a frequency of 10 to 20 kHz was applied.

Acoustofluidic simulations

The simulation results were obtained from acoustofluidic simulations performed using the software AcoDyn (version 2.1). For the simulation setup, a cylindrical fluid domain with a radius of 250 μm was created around a microrobot with a length of 350 μm, outer diameter of 100 μm, r_d = 0.43, and h_d = 1.08. A traveling wave was generated using a time-periodic boundary condition on the cylinder face behind the microrobot (negative z axis) and dampened using a periodic forcing zone on the opposite cylinder face (positive z axis) to prevent wave reflection. For the mantle of the cylindrical fluid domain, we used a symmetric impenetrable slippy boundary condition, whereas on the particle surface, we prescribed a non-slippy surface. The simulations were run to near convergence at 100 wave periods.

Supplementary Materials

This PDF file includes:

Figs. S1 to S7

Notes S1 and S2

Table S1

Legends for movies S1 to S9

References

Other Supplementary Material for this manuscript includes the following:

Movies S1 to S9