Abstract
Heat engines convert thermal energy into mechanical work both in the classical and quantum regimes1. However, quantum theory offers genuine non-classical forms of energy, different from heat, which so far have not been exploited in cyclic engines. Here we experimentally realize a quantum many-body engine fuelled by the energy difference between fermionic and bosonic ensembles of ultracold particles that follows from the Pauli exclusion principle2. We employ a harmonically trapped superfluid gas of 6Li atoms close to a magnetic Feshbach resonance3 that allows us to effectively change the quantum statistics from Bose–Einstein to Fermi–Dirac, by tuning the gas between a Bose–Einstein condensate of bosonic molecules and a unitary Fermi gas (and back) through a magnetic field4–10. The quantum nature of such a Pauli engine is revealed by contrasting it with an engine in the classical thermal regime and with a purely interaction-driven device. We obtain a work output of several 106 vibrational quanta per cycle with an efficiency of up to 25%. Our findings establish quantum statistics as a useful thermodynamic resource for work production.
Subject terms: Quantum physics, Thermodynamics, Ultracold gases
This study reports the creation of a model thermodynamic engine that is fuelled by the energy difference resulting from changing the statistics of a quantum gas from bosonic to fermionic.
Main
Work and heat are two fundamental forms of energy transfer in thermodynamics. Work corresponds to energy change at constant entropy, as in the case of the variation of the position of a piston, whereas heat exchange necessarily causes entropy increase1. From a microscopic point of view, work corresponds to a displacement of energy levels and heat to a modification of their level probability distribution by contact with a thermal bath, for constantly driven quantum systems11. In other cases, this distinction may not always hold12–14. Quantum heat engines realized so far convert thermal energy into mechanical work by cyclically operating between effective thermal reservoirs at different temperatures15–20 like their classical counterparts, where heating and cooling strokes redistribute the quantum state populations21. However, owing to the existence of distinct particle (Fermi or Bose) statistics, the level occupation probabilities of quantum many-body systems may strongly differ at the same temperature1. Changing the quantum statistics would thus lead to a new, purely quantum, form of energy transfer.
At ultralow temperatures, in the quantum-degenerate regime, an ensemble of indistinguishable bosonic particles will all accumulate in the ground state, whereas fermionic systems will occupy quantum states with increasing energy due to the Pauli exclusion principle2. These different quantum statistical behaviours are intimately linked to the symmetry of the many-body wavefunctions and originate from the spin-values of the particles. They also result in a profound energy difference between the two particle classes and the emergence of a degeneracy pressure in the Fermi systems. The exclusion principle plays an essential role for the stability of matter22 and the physics of stars23. A change in quantum statistics may be experimentally achieved in interacting atomic Fermi gases using Feshbach resonances3. In such systems, the crossover between a Bardeen–Cooper–Schrieffer (BCS) state of pairs of fermions to a molecular Bose–Einstein condensate (BEC) state of diatomic bosonic molecules can be realized by tuning an external magnetic field4–10.
Here, we report the experimental realization of a new many-body quantum engine (‘Pauli engine’) where the temperature variation, usually induced through coupling to a hot or cold thermal bath, is replaced by a change of quantum statistics of the system, from Bose–Einstein to Fermi–Dirac (and back). This engine cyclically converts energy stemming from the Pauli exclusion principle (‘Pauli energy’) into work. Its mechanism is of purely quantum origin, since the difference between fermions and bosons disappears in the classical high-temperature limit. We specifically employ an ultracold two-component Fermi gas of 6Li atoms confined in a combined opto-magnetic trap24 (Fig. 1), prepared close to a magnetic Feshbach resonance. Inspired by the quantum Otto motor25, we implement a cycle by adiabatically varying the trap frequency by means of the power of the laser forming the trapping potential, and hence perform work. We further adiabatically change the magnetic field through the crossover at constant trap frequency, which thus changes the quantum statistics and the associated occupation probabilities. This step leads to the exchange of Pauli energy instead of heat. We emphasize that all strokes can, in principle, be described by Hamiltonian dynamics, which preserves the entropy of the system throughout the cycle, in contrast with conventional quantum heat engines15–21. We measure atom numbers and cloud radii from in situ absorption images26, from which we determine the energy of the gas after each stroke. We employ the latter quantities to evaluate both efficiency and work output of the Pauli engine, analyse its thermodynamic performance when parameters are varied and compare it with theoretical calculations.
Fig. 1. Principles of the quantum Pauli engine.
a, Schematic of the experimental set-up. The atom cloud (purple ellipsoid) is trapped in the combined fields of a magnetic saddle potential (orange surface) and an optical dipole trap potential (blue cylinder) operating at a wavelength of 1,070 nm. The absorption pictures are taken with an imaging beam (purple arrow) in the −z direction. The scale bar on the absorption picture corresponds to 50 μm. b, Cycle of the Pauli engine. Starting with a molecular BEC that macroscopically populates the ground state of the trap at well-defined temperature T (point A), the first step, A → B, performs work W1 on the system by compressing the cloud through an increase of the radial trap frequency . This is achieved by enhancing the power of the trapping laser. The second stroke, B → C, increases the magnetic field strength from BA = 763.6 G (76.36 mT) to the resonant field BC = 832.2 G, while keeping the trap frequency constant. This leads to a change in the quantum statistics of the system as the working medium now forms a Fermi sea with an associated addition of Pauli energy , which substitutes the heat stroke. Step C → D expands the trap back to the frequency and corresponds to the second work stroke W3. Finally, the system is brought back to the initial state with bosonic quantum statistics during step D → A by reducing BC to BA, which corresponds to a change in the Pauli energy . The population distributions in the harmonic trap of the atoms with spin up (blue) and spin down (red) are indicated at each corner. c, Examples of absorption pictures at each point of the engine cycle, where the particular change in size from B → C is due to the Pauli stroke indicating that the Pauli energy increases the size of the cloud in the external potential. Scale bars, 50 μm.
It is instructive to begin with a discussion of the simple case of a one-dimensional (1D) harmonically trapped non-interacting ideal gas at zero temperature to gain physical insight into the energetic possibilities of the Pauli principle2. A fully bosonic system only populates the ground state with energy EB = Nħω/2, where N is the number of particles, ħ is the reduced Planck constant and ω is the trap frequency1. By contrast, the fermionic counterpart populates all the energy levels up to the Fermi energy EF = ħω(2N − 1)/2 and the total energy of the system is accordingly EF = ħωN2/2 (ref. 1). The resulting energy difference due to the change of quantum statistics, the Pauli energy, is therefore EP = EF − EB = ħωN(N − 1)/2. This enormous difference of total energy at zero temperature originates from the underlying quantum statistics, dictating a population probability distribution across the available quantum energy levels En according to , where the + (−) sign in the denominator is for fermions (bosons) with half-integer (integer) spin27; here, μ is the chemical potential and kB is the Boltzmann constant. For increasing temperature, both distributions reduce to the classical Boltzmann factor. Microscopically, the Pauli energy is equal to EP = ∑nΔfnEn, an expression reminiscent of that of heat for systems coupled to a bath11. Importantly, the quadratic dependence of the energy difference on the particle number between BEC and Fermi sea in the 1D case implies that the Pauli energy can be substantial for large N, far exceeding typical energy scales in comparable quantum thermal machines. The influence of the quantum statistics on work production has been theoretically discussed in refs. 28–30 and a quantum heat engine operating across a BEC phase transition has been considered in ref. 31.
We prepare an interacting, three-dimensional (3D) quantum-degenerate two-component Fermi gas of up to N = 6 × 1056 Li atoms (Fig. 1a) (for details see ref. 32), with equal population Ni = N/2 of two lowest-lying Zeeman states i. A broad Feshbach resonance centred at (ref. 33) allows us to change the nature of the many-body state: a molecular BEC of N/2 molecules is formed at magnetic field strengths below the resonance, whereas on resonance a strongly interacting Fermi sea of N 6Li atoms emerges.
For the bosonic regime, we operate at BA = 763.6 G = BB, where the molecular BEC has an interaction parameter of 1/kFa ≈ 2.3; kF denotes the magnitude of the Fermi wavevector and is the s-wave scattering length, with the background scattering length abg and the resonance width Δ (ref. 3). The temperature of the gas is about T ≈ 120 nK, corresponding to T/TF ≈ 0.3 with Fermi temperature , where is the geometric mean trap frequency, which can be experimentally controlled. The unitary regime (which saturates the unitarity bound of the scattering matrix) appears on resonance, BC = 832.2 G = BD. In this limit, the gas is dilute, but strongly interacting, and exhibits universal behaviour, which is independent of the microscopic details owing to the divergence of the scattering length, 1/kFa = 0 (refs. 10,34). Pauli blocking of occupied single-particle states here leads to Fermi–Dirac-type statistics35–38. However, it is also possible to change the magnetic field and, therefore, the interactions, without changing the statistics by staying away from the resonance. When the molecular BEC is adiabatically ramped to unitarity, the reduced temperature drops to values well below T/TF < 0.2 (ref. 39).
The experimental implementation of the Pauli cycle ABCD starts with a molecular BEC (Fig. 1b). It consists of four strokes: compression, fermionization, expansion and bosonization. We first analyse the Pauli stroke B → C during which the change of quantum statistics takes place. Contrary to an ideal gas, atoms in the experiment are not at zero temperature and further interact with a strength that depends on the magnetic field. All of these have an effect on the cloud size.
For a harmonically trapped interacting Fermi gas, total energy E and trap energy U are related by means of the generalized virial theorem , with the contact and the mass m of a 6Li atom40–42. For a resonantly interacting gas, the contact vanishes and E = 2U. Using the radial symmetry of the trap, with radial frequencies ωx ≈ ωz, the trap energy is given by , where ⟨x2⟩, ⟨y2⟩ are the mean-square sizes of the cloud in the x, y directions, determined by means of in situ absorption images. In the molecular BEC regime, the total energy additionally comprises the molecular binding energy and the residual particle–particle interaction (Methods). The binding energy does not contribute to work production and is thus omitted. To isolate the contributions to the cloud size coming from the change of statistics (Pauli energy) and from the change of the residual particle–particle repulsion with the magnetic field, we compare, in Fig. 2a, the energy difference ΔU for a Pauli stroke (where interaction strength and quantum statistics are both changed by moving to the fermionic regime) with a so-called Feshbach stroke, where we change the interaction strength but effectively remain in the bosonic regime43,44. We further contrast the quantum Pauli stroke with a similar stroke in the thermal regime, with the same magnetic field ramp, at a much higher temperature of T/TF ≈ 0.7 in Fig. 2b to stress the quantum nature of the effect. We observe that the change of quantum statistics during the Pauli stroke yields a much larger energy difference ΔU and a much faster increase with the particle number compared with the two other strokes. Hence, we may conclude that the variation ΔU is mostly due to the quantum Pauli energy EP. An increase of turn-over energy in the quantum degenerate compared with the thermal regime was also recently observed in ref. 45. We also note good agreement with the theoretical curves (solid lines) obtained using analytical formulas in the Thomas–Fermi regime for the molecular BEC35,46 and the known energy expressions for a strongly interacting Fermi gas at unitarity34,35 (Methods).
Fig. 2. Contribution of the Pauli energy.
a,b, Trap energy variation ΔU as a function of the number of atoms in a single spin state for the magnetic field change between cycle points B → C for a gas performing a Pauli stroke (bringing the gas from a molecular BEC to a unitary gas, cyan), a Feshbach stroke (always remaining in the molecular BEC regime, orange) and a thermal stroke for the same magnetic fields as in the Pauli stroke (red). Symbols represent mean values of 20 repetitions; solid lines are predictions of our model. Owing to the much increased temperature of the gas in the thermal case, trap depth and compression ratio have been chosen differently in the experimental realization to be for the Pauli and Feshbach strokes: T ≈ 120 nK, T/TF ≈ 0.3 (measured in the molecular BEC regime) and (a); and for the thermal stroke: T ≈ 1,150 nK, T/TF ≈ 0.7 (measured in the molecular BEC regime) and (the higher temperature also means that fewer atoms are lost by evaporation) (b). The insets show microscopic sketches of the quantum state of the gas, transitioning between the molecular BEC and Fermi sea, remaining in the molecular BEC, or transitioning between a gas of free molecules to a gas of free atoms, respectively. The error bars for all data points denote 1σ statistical fluctuations of 20 repetitions. c, Pressure–volume (p–V) diagram of the Pauli engine for different compression ratios (black solid and dashed lines). The blue (red) line indicates the equation of state of the Fermi gas (molecular BEC). Varying the compression ratio moves the state of the gas along each line, effectively changing the engine points B and C, whereas the Pauli strokes (bosonization and fermionization) induce transitions between the red and blue lines.
The exclusion principle not only affects the energy but also the pressure of a quantum system: the pressure of a degenerate Fermi gas is indeed non-zero at zero temperature in contrast to that of a Bose gas1. From that perspective, the Pauli engine reduces the pressure of the Fermi gas at constant entropy by converting it into a molecular BEC and exploits the fact that work done on the gas during compression is smaller than during expansion because of its different dependence on the number of atoms. The pressure of the working medium may be defined as p = −(∂E/∂V) (ref. 1), with the cloud’s volume V determined from the measured radii (Methods). The corresponding work along one branch is then given by the familiar expression −∫ pdV. The experimentally reconstructed p–V diagram is shown in Fig. 2c. As our engine does not require coupling to an external bath, it differs from any quantum machine experimentally realized so far21.
To experimentally evaluate the performance of the Pauli engine, we extract the energy change for every cycle stroke, by determining the clouds’ radii in the trap from absorption images (Methods and Fig. 3). The work output W and the efficiency η may then be computed in analogy with standard quantum engines21 as
| 1 |
where the Pauli energy replaces the heat input Q2 in the efficiency. This is the main difference from a thermally driven engine. As with all quantum engines built so far15–21, the produced work is calculated, since the coupling to a work load is experimentally challenging to realize.
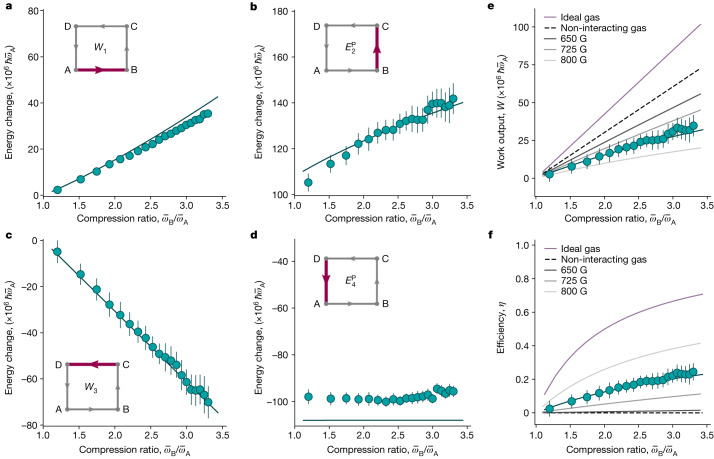
Fig. 3. Performance of the Pauli engine.
a–d, Work contributions, W1 (a) and W3 (c), and Pauli energies, (b) and (d), as a function of the compression ratio for fixed and fixed number of atoms at point A. The experimental data points (cyan dots) are the mean value of 20 repetitions and the error bars indicate their 1σ statistical uncertainty. The numerical calculations are indicated by the (cyan) solid lines. The insets show the corresponding stroke. e,f, Work output W (e) and efficiency η (f). The experimental points and the numerical simulations are in cyan. For comparison, the W and η values for a non-interacting gas are depicted as black dashed lines. They have been obtained by setting the s-wave scattering length a to zero for points A and B (this limit corresponds to a magnetic field BA far below the resonance, leading to point-like composite bosons with infinite binding energy) and using the formulas for the energy at unitarity for points C and D. Also, W and η for an ideal gas are shown as purple solid lines and mark the upper bounds of the machine. They have been obtained by using the energy of ideal gases in the degenerate regime (Bose gas for points A and B and Fermi gas for points C and D). The grey solid lines are the theoretical values obtained for different magnetic fields: BA = 800 G, 725 G and 650 G from lighter to darker (dimer–dimer interaction strength g/g0 = 2.53, 0.51 and 0.16, respectively, with g0 being the interaction strength for BA = 763.3 G).
The energy changes for individual strokes (Fig. 3a–d) allow one to obtain an intuitive understanding of the performance. The two work strokes (Fig. 3a) and (Fig. 3c) simply follow the variation of the trap frequency. The important Pauli-stroke energy change (Fig. 3b) directly reflects the growing Fermi energy in steeper potentials for constant particle numbers, pointing towards increased work output for increased compression ratio. The complementary stroke (Fig. 3d) is independent of this change because the trap frequency is fixed in the experiment. The difference of about 10% between theory and data seen in stroke (Fig. 3d) is mainly due to the evaporation of hot molecules in the relatively shallow trap.
We observe that the work output W and the efficiency η both increase with the compression ratio (Fig. 3e–f), with a total work output of up to and an efficiency above 10% for compression ratios larger than 1.5. The largest efficiency achieved in the experiment is 25%, whereas, for a very large compression ratio of about 10 (not accessible in our experiment), the theoretical efficiency for the same experimental parameters can be higher than 50%. With a cycle time of tcyc = 1.6 s, the power P = W/tcyc is finite with values of up to 10−24 J s−1. The power could be increased by driving the Pauli engine diabatically, being then fundamentally limited by quantum speed limits47. However, non-adiabatic transitions are expected to suppress the efficiency15–21. Moreover, increased atom losses would further reduce the overall performance.
In addition, we note that W increases with the number of atoms as well as with the number of consecutive cycles (Fig. 4a–c), whereas η remains constant (at about 7% for the chosen parameters to limit atom losses that lower the work output). An additional increase of W with atom number can be expected in reduced dimensions, where the degeneracies in the trap are less. The comparison between the quantum-statistics-driven Pauli cycle and the interaction-driven Feshbach cycle in Fig. 4a,b shows that the Pauli engine outperforms the Feshbach engine, whose efficiency is essentially zero. Finally, the produced work scales as W ∝ Nα with α = 1.73(18), which is close to the theoretical prediction of 1.4 (Fig. 4a), which is different from the value one finds for a non-interacting classical gas48.
Fig. 4. Comparison of the performance of quantum many-body devices.
a,b, Work output (a) and efficiency (b) as a function of the number of atoms in one spin state for a compression ratio for the Pauli engine (cyan dots) and the Feshbach cycle (orange diamonds). Small symbols denote individual realizations; large symbols indicate mean values of 20 repetitions with error bars indicating 1σ statistical fluctuations. For comparison, calculations for a non-interacting gas (black dashed line) and an ideal gas (purple solid line) are shown. Dotted lines are fits to the respective work output W ∝ Nα. The fitted exponents α are 1.73(18) and 1.58(13) for the Pauli engine and Feshbach cycle, respectively, well reproduced by our theoretical model (solid cyan and orange lines). Importantly, the efficiency of the Feshbach cycle is essentially zero. c, Accumulated work output (cyan dots) and efficiency (blue triangles) of the Pauli engine over several cycles for a compression ratio and an initial number of atoms in one spin state of about Ni = 2.5 × 105.
Thermodynamics is primarily the study of energy and its transformations. While most investigations of quantum thermodynamics have focused so far on conventional energy forms, such as work and heat21, we have shown that, by changing the quantum statistics of a system, a new form of energy transfer, which cyclically converts Pauli energy into work, can be realized. This effect, based on the Pauli exclusion principle, is intrinsically quantum. The Pauli energy associated with such a modification of quantum statistics may be very large: in solids, the energy of electrons in the conduction band corresponds to thousands of kelvin, much above the usually accessible thermal energies49. At the same time, since the operation of the Pauli engine follows, in principle, Hamiltonian dynamics owing to the absence of heat baths, it is not subjected to common friction mechanisms of quantum motors21. This could lead to energy-efficient quantum machines, including both engines and refrigerators. We further emphasize that the change of quantum statistics is a widespread phenomenon in many-body quantum systems (many bosons are actually composed of fermions). Cooper pairing plays, for instance, an essential role in superconductivity and superfluidity in condensed-matter systems50, which, unlike Feshbach resonances in cold-atom systems, do not require a tunable magnetic field. Exploring the exotic properties and the potential applications of this unconventional form of quantum energy transfer appears to be a fascinating prospect.
Methods
Set-up and sequence
We prepare a degenerate two-component fermionic 6Li gas in the two lowest-lying Zeeman substates of the electronic ground state 2S1/2 confined in an elongated quasi-harmonic trap comprising a magnetic and an optical dipole trap (ODT) operating at a wavelength of 1,070 nm; for details of the experimental set-up, see ref. 32. We cool the gas using evaporative cooling until reaching a temperature of 120 nK in a trap with geometric mean trap frequency , where typical values used for the engine performance are given in Extended Data Table 1. Evaporation takes place on the BEC side of the crossover at a magnetic field of 763.6 G. After evaporation, we hold the cloud for 150 ms to let it equilibrate. By varying the loading time of the magneto-optical trap before evaporation, we adjust the number of atoms per spin state Ni of the cloud from 1.75 × 105 up to 3.0 × 105.
Extended Data Table 1.
Experimental settings of the three types of cycles for which we vary the number of atoms

For the case in which we change the compression ratio of the Pauli engine, the power of the ODT laser PB is iterated from 50 mW up to 1 W in steps of 50 mW. We extract the values of the s-wave scattering length a from ref. 33.
The quantum Pauli cycle is implemented by alternating changes of the trap frequency through the dipole trap laser and of the interaction strength through the magnetic field close to the Feshbach resonance. Extended Data Fig. 1 illustrates the experimental sequence of a single cycle. After initial preparation of the molecular BEC, we compress the trap adiabatically, increasing the laser power of the ODT during 300 ms from PA to PB. The trap frequencies in both radial directions increase with the square root of the laser power of the ODT whereas the trap frequency along the axial direction remains irrelevant compared with the trapping frequency of the magnetic field for all the powers used in this work. The resulting geometric mean trap frequencies are given in Extended Data Table 1. After a waiting time of 150 ms with constant trap frequency, we reach cycle point B. Then, we adiabatically increase the magnetic field strength linearly from BA to BC to change the interaction strength during the stroke B → C. Changing the magnetic field strength does not substantially alter the trap frequency in the axial direction. After a waiting time of 150 ms with constant magnetic field, we reach point C. In the next step, we ramp the ODT laser power to the initial value PA, expanding the gas (C → D) in the trap. Finally, we close the cycle with a second magnetic field ramp back to BA. After running an entire cycle, we verify that the measurement point A2 is equivalent to point A. In all of the measurement series, we have BA < BC, PA < PB and, therefore, . Extended Data Table 1 summarizes the experimental parameters for the three types of cycles that we run.
Extended Data Fig. 1. Sequence of the Pauli engine cycle.

Magnetic field strength (cyan) and power of the ODT laser (orange). The imaging points during the cycle are marked with purple arrows (A denotes the first point of the cycle and A2 the last one after a full cycle).
Atom-number measurement
To determine the number of atoms from in situ absorption pictures, we image the energetically higher-lying spin state mI = 1 by standard absorption imaging on a charge-coupled device camera. This procedure is identical for all the regimes considered. Since the number of atoms of the spin state mI = 0 is the same as for mI = 1, the total number of atoms N (sum of atoms with spin up and down) is twice the number of atoms of the measured spin state Ni. Importantly, in the case of a molecular BEC, the number of molecules is half the number of total atoms. We extract the column density from the measured absorption pictures. Adding up the density pixelwise and including the camera’s pixel area and the imaging system’s magnification, we obtain the number of atoms. We include additional laser-intensity-dependent corrections51. The imaging system has a resolution of 2.2 μm. The optical absorption cross-section changes its value throughout the BEC–BCS crossover, because it depends on the optical transition frequency26 which is, in turn, a function of the magnetic field strength. We determine the absorption cross-section for a magnetic field of 763.6 G and we use this value for further magnetic field strengths. This leads to the fact that the measured number of atoms on resonance is higher than the actual number of atoms. Therefore, we determine a correction factor to compensate this imperfection in independent measurements at different magnetic field strengths (Extended Data Fig. 2). We prepare an atomic cloud of varying atom number at BA = 763.6 G. We then measure the atom number for this field at points A and B. We repeat the measurement for BC and, to exclude atom loss, we ramp the field from BB = BA adiabatically to BC and back to BB before measuring. The atom numbers for BB with and without the additional ramp to C are almost identical, from which we conclude that the number measured at BC has to be the same. The correction factor is then calculated from the difference in atom number between these two data sets.
Extended Data Fig. 2. Determination of the correction factor of the number of atoms on resonance for the Pauli engine.

Measured number of atoms of one spin state Ni in point B (red), C (orange), and return to point Breturn after reaching point C (purple) in dependence of the number of atoms of one spin state in point A. The measured number of atoms in point C cannot differ from the number of atoms in points B and Breturn, when the later are equal. Therefore, the measured number of atoms on resonance is higher than the actual number of atoms. Data points are averages of ten repetitions, uncertainties indicate one standard deviation. The inset shows the calculated deviation (orange points) for the number of atoms on resonance in dependence of . The mean value of these deviations is 15 % and is visible as a black line, their standard deviation is the grey area. The x-axis of the inset spans the same range as the main axis.
Extended Data Fig. 3 shows the measured number of atoms for one spin state Ni for the different points of the cycle of the Pauli engine as a function of the number of atoms of one spin state in point A. The correction factors for different magnetic fields are included. In this way, we independently verify that we experimentally have a constant number of atoms during the cycle from A → D through B and C. Only the last stroke D → A2 suffers from atom losses of about 10%. These losses primarily occur when the quantum statistics are changed from Fermi–Dirac to Bose–Einstein in a shallow trap. The thermodynamics of adiabatic transfers through the crossover has been theoretically studied in ref. 39. During the change of statistics, bosonic molecules are formed. We attribute the losses to an excess-energy transfer between molecules during the ramping. Owing to the relatively low trap depth (needed for a high compression ratio), even small kinetic energies are sufficient to remove molecules from the trap.
Extended Data Fig. 3. Atom-number correction in the Pauli cycle.

Corrected number of atoms of one spin state Ni in the points of the cycle A (first point of the cycle, black solid line), B (red), C (orange), D (purple), and A2 (last point of the cycle, cyan) in dependence of the corrected number of atoms of one spin state in point A. Experimental data belong to the Pauli engine in Fig. 4(a) and (c) with a compression ratio of , the number of atoms is experimentally varied. Uncertainty is the standard deviation of 20 repetitions.
The measured atom number has an uncertainty due to several mechanisms. First, the produced quantum gases feature a fluctuating number of particles due to uncontrolled technical fluctuations in, for example, cooling- and trapping-laser intensity or magnetic-field currents. But it is also due to physical statistical fluctuations, such as Poissonian fluctuations of the particle number during laser cooling or fluctuations occurring during the phase transition to a quantum fluid. These mechanisms cause fluctuations of the particle number of the produced ultracold clouds. Second, even for identical atom numbers, an additional uncertainty originates from the measurement process. We deploy resonant high-intensity absorption imaging52,53 on the transition to acquire the column-integrated density distribution. Determining the accurate atom number from the resulting images requires precise control over the imaging pulse length and power, as well as calibration of the camera counts and effective absorption cross-section. In particular, fluctuations of the laser power after transmission through the imaging system in addition to camera noise are the main origin of statistical density uncertainties and dominate the uncertainty indicated in the measured data points. A systematic uncertainty is due to limited knowledge of the absorption cross-section. It can, in principle, be determined by the transition wavelength, but its value can change owing to optical pumping, the presence of magnetic fields or polarization effects, and was, therefore, determined by comparing theoretical density distributions of a BEC with measured ones51. The correction factor for our specific system was evaluated from a χ2 fit and has a systematic uncertainty of less than 10%. The resulting statistical atom-number fluctuations dominate the uncertainty for identical experimental parameters. We quantify them by the 1σ standard deviation of typically 20 identical realizations and indicate them as bars in equations (2) and (3) as well as in Figs. 2 and 4 around the mean atom number of the respective measurement series.
Cloud-radii determination
We obtain line densities of the quantum gases by integrating the column-integrated density distributions of the two-dimensional (2D) absorption pictures n2D(x, y) = ∫ n3D(x, y, z) dz along the x and y directions separately. We fit these distributions with a 1D-integrated Thomas–Fermi profile. The Thomas–Fermi profiles are different for the interaction regimes throughout the BEC–BCS crossover. In the Thomas–Fermi limit, the in situ density distribution of a molecular BEC has the shape9
| 2 |
where is the Thomas–Fermi radius of the atomic cloud in the x direction. For a resonantly interacting Fermi gas right at , the density profile in the x direction can be written as34
| 3 |
with the rescaled Thomas–Fermi radius in the x direction. Therefore, we determine the measured cloud radii in both regimes by fitting the measured density profiles with the appropriate line shapes. The extracted radii in the x and y directions are shown in Extended Data Fig. 4. Our experimental set-up does not allow measurements of the radii Rz in the z direction. For this radial direction, however, we use the measured radius Rx in the x direction (radial) and correct the value with the corresponding ratio of the trap frequencies Rz = (ωx/ωz)Rx (refs. 46,54).
Extended Data Fig. 4. Realization of the Pauli engine.
(a)-(d) Measured radii RmBEC and at each point of the cycle as a function of the compression ratio for constant number of atoms . Radii are extracted by fits of the density profiles with equations (2) or (3). Radii are shown in x-direction (cyan circles) and y-direction (purple triangles). Experimental data are the mean value of 20 repetitions and the corresponding error bars indicate the propagation of the uncertainty of standard deviation of the measurement parameters. The insets show schematics of the cycle, where the point at which the measurement is taken is highlighted (purple). In (d), we compare the experimental values of the radii for A (first point of the cycle) in grey with the last point of the cycle A2 in the x (y) direction. The trap frequency has no influence on the first measurement point A and is constant for the different compression ratios. Therefore, this setting is only measured once with 20 repetitions. The experimental radii in A2 (last point of the cycle) are measured after running a full cycle (data points). On the right two exemplary absorption pictures at point C are shown.
Temperature measurements
We determine the temperature of the molecular BEC by means of a bimodal fit of the density profile (for more details, see ref. 32) at a magnetic field strength of 680 G. This value of B is chosen by considering the following trade-off: at lower magnetic fields, losses in the atom clouds are too high for quantitative temperature determination, whereas for higher magnetic fields, the condensate and thermal parts are not well separated, which complicates a bimodal fit.
Owing to three-body recombination losses in the range between 550 G and 750 G (ref. 55), molecule losses in the cloud are already significant at 680 G. To avoid these losses, we choose a field of 763.6 G as the start of the Pauli cycle. To determine the temperature in an independent measurement, we ramp the field to 680 G during 200 ms and determine the temperature there. However, since decreasing the magnetic field value adiabatically throughout the BEC–BCS crossover increases the temperature T of the gas39,48, the measured temperature at 680 G is an upper bound for the temperature at point A and beyond. For the work stroke between points A and B, we increase the mean trap frequency. We observe that the reduced temperature T/TF of the gas does not show significant changes during these work strokes. The temperature T does not change after ramping the trapping frequency back and forth. Because of this, we determine the temperature of the cloud, as mentioned above, with a bimodal fit for the two settings. First, we ramp the magnetic field from 763.6 G (value at point A) to 680 G to determine the temperature there. Second, we restart the sequence and run the cycle until point B. Afterwards, we change the direction of the cycle and go directly back to point A. A magnetic field sweep to 680 G allows again a temperature measurement. Extended Data Fig. 5 shows that the temperatures of the cloud after reversal to point A (cyan points) lie within the error (grey shaded area) of the initial temperature at point A (black line). We observe that an increase in temperature of less than 10% takes place for higher ratios of the mean trapping frequency, which can be neglected in the analysis (see below).
Extended Data Fig. 5. Measured temperature T for point A after ramping the magnetic field directly to 680 G (black line).

Uncertainty is the standard deviation of ten repetitions (grey area). The cloud is compressed by increasing the mean trap frequency in stroke A → B. Afterwards, inverting the cycle direction leads again to point A. There, the temperature measurement is repeated after ramping the magnetic field to 680 G (cyan data points). Error bars show the standard deviation of ten repetitions. For comparison, critical temperature (purple solid line) and Fermi temperature (orange solid line) are depicted for point A. Shaded area shows the uncertainty and is of the order of the line thickness.
The method described above holds for atomic clouds below the critical temperature. For a thermal gas, we can directly determine the temperature of the magnetic field at the cycle point. At finite temperatures, density profiles of thermal clouds can be approximated with a classical Boltzmann distribution. The temperature Tj can be calculated dependent on direction j of the cloud (ref. 46), with σj as width of a Gaussian determined by fitting the 1D density profiles with . In the case of molecular bosons, we use 2m for the mass instead of m. Hence, interactions directly influence the width of the cloud; we interpret this temperature for our experiment as an approximated temperature.
Energy calculation
The calculation of the total energy EmBEC of a molecular BEC is based on the Gross–Pitaevskii equation in the Thomas–Fermi limit for a harmonic trapping potential and for zero temperature. This energy consists of two parts, the kinetic energy Ekin and the energy in the Thomas–Fermi limit ETF, which takes into account the oscillator and interaction energies46,54
| 4 |
where RmBEC is the geometric mean radius of the cloud. The chemical potential is given by
| 5 |
where add = 0.6a is the s-wave scattering length for molecules8 and is the oscillator length. The radii and molecule numbers are extracted from the absorption pictures for the considered interaction strengths. When including the molecular energy, which gives the amount of energy needed to dissociate a molecule into two atoms, the total energy of the molecular BEC EmBEC,m is given by
| 6 |
On resonance, the scattering length diverges and the binding energy vanishes. When we tune the magnetic field to resonance, the system evolves into a strongly interacting unitary Fermi gas. Its total energy is related to that of an ideal binary Fermi gas through scaling with the universal constant
| 7 |
where is the Fermi energy10,33,34,56. This zero-temperature expression provides a good approximation for T/TF < 0.2 as supported by the energy measurements on resonance reported in refs. 56–58 (the low-T measurements are almost independent of T in the mentioned range). It should be noted that owing to the different temperature dependency of the entropy of the bosonic (Sbosons ∝ T3) and fermionic (Sfermions ∝ T) trapped gases, a decrease in the temperature is expected when performing an adiabatic sweep from the molecular BEC side to the BCS side and to unitarity. This internal temperature decrease is another indication that the operation of the Pauli engine is not driven by thermal energy. Since the condition T/TF < 0.2 is fully satisfied for points C and D in all of our experiments the zero-T formulas on resonance are highly accurate.
The obtained experimental values were contrasted with those obtained using well-known formulas for BECs46,54 in the Thomas–Fermi limit for interacting bosons adapted as previously explained for composite bosons made up of fermions of opposite spin states5,6,59. In these cases, we use the theoretically expected radius and a constant number of particles during the cycle equal to the experimental number of particles at point A. Using equations (4), (5) and in equation (6), we obtain the following energy for the molecular BEC regime at zero temperature.
| 8 |
where the first two terms are related to the energy of bosonic particles in a trap including the interaction between bosons (the molecules interact with each other by means of a contact interaction46 that can be quantified using the interaction strength8 g = 1.2πħ2a/m) and the last term is the contribution of the molecular energy of each of the pairs. For the zero-T calculations of the ground-state energy of the bosonic system, we also numerically solve the Gross–Pitaevskii equation with the bosonic interaction in terms of the dimer–dimer scattering length. Owing to the range of the experimental parameters, the Thomas–Fermi approximation holds in all our experiments in the molecular BEC regime; therefore, the numerical results are the same as those obtained when using equation (8) (refs. 46,54). Extended Data Fig. 6 shows the experimental and theoretical energies for each point of the Pauli cycle for the data set of Fig. 3 (point A denotes the first point of the cycle and point A2 the last point after a full cycle).
Extended Data Fig. 6. Realization of the Pauli engine.
Energies (a) EB, (b) EC, (c) ED, and (d) EA (first point of the cycle) and (last point of the cycle) at each point of the cycle as a function of the compression ratio for constant number of atoms Ni ≈ 2.5 × 105. Experimental data (cyan points) are the mean value of 20 repetitions and the corresponding error bars indicate the propagation of uncertainty of standard deviation of the measurement parameters. The experimental data fits well to numerical calculations (cyan solid line), except for point A2 in (d) because of atom losses. The insets show schematics of the engine with the individually points of the engine highlighted in purple. In (d) the experimental value of the energy EA is shown in grey for comparison to A2. The trap frequency has no influence in the first measurement at point A, and is constant for the different compression ratios. Therefore, EA is only measured once with 20 repetitions.
For low but non-zero temperature, the Thomas–Fermi approximation to the Gross–Pitaevskii equation reads46
| 9 |
According to Tan’s generalized virial theorem10,42,60–62, the energy for a cigar-shaped trapped Fermi gas is given by , where r and z stand for the radial and axial coordinates, respectively, and is the contact (a measure of the probability for two fermions with opposite spins being close together10). This expression is valid for any value of the scattering length a and for any temperature T. On resonance, that is, at unitarity, we have 1/kFa = 0 and a finite . Therefore the virial theorem reduces to the case presented by Thomas et al. in refs. 40,41, that is, . In the weak coupling limit for the molecular BEC side, the contact reduces to , in which case the last term of the virial expression gives the total molecular energy and the virial energy reduces to equations (8) and (9) (refs. 42,46). All of this means that the expression −ħ2/(ma2) for the molecular term holds even for T/TF ≈ 0.7 as long as the experiments are realized in the deep molecular BEC regime. For our magnetic fields, this condition is fulfilled for the Pauli engine and Feshbach cycle as well as for the thermal cycle. Furthermore, measurements of the molecular energy were presented in ref. 4 for T/TF ≈ 0.15, which show that the formula −ħ2/(ma2) holds for T/TF ≈ 0.2 in a complete B sweep from molecular BEC to unitarity.
In the high-T regime the interactions are negligible and the distributions can be approximated by Maxwell–Boltzmann distributions. When the thermal energy kBT is large enough to break all the pairs, the energy can be approximated by that of an ideal classical gas of atomic particles for both magnetic fields. In this case, the temperature in the work strokes does not change and there is no work output. When the thermal energy is below the binding energy, the energy for a magnetic field below resonance corresponds to a classical gas of molecules with mass 2m whereas the energy at the resonant field is given by a classical gas of atoms in a harmonic trap. The molecular term cancels in the total work output giving . The temperature of the gas is obtained through a Gaussian fitting of the density profile leading to , where σ is the width of the fitted density profile. Since and and the mass of the molecules is twice that of one of the atoms, we find and , that is, . The work vanishes for σA = σD and σB = σC. In our experiments, the widths do not show significant statistical differences and therefore the work output vanishes for the engine running in the high-T regime.
Let us now detail each one of the theoretical curves presented in the main text. Based on Tan’s generalized virial theorem, we calculate the theoretical trap energy of Fig. 2 by means of equation (9) without the molecular term and using the experimental temperatures at points A and B, whereas for the points C and D we use the energy for zero T at unitarity given by equation (7). The vanishing efficiency for the thermal case is expected from the classical gas argument of the previous paragraph. The cyan curves in Fig. 3 arise from numerical calculations of the Gross–Pitaevskii equation. The black dashed curves in Fig. 3e,f were also calculated by solving numerically the Gross–Pitaevskii equation and yield the same results as an ideal molecular gas of point-like bosons having an infinite binding energy, which leads to and ηnon-interacting = 0. The purple curves in Fig. 3e,f correspond to the results obtained for ideal Bose and Fermi gases in the highly degenerate regime and lead to
| 10 |
and
| 11 |
The ideal efficiency is similar to the maximum Otto efficiency25. Compared with these upper limits, we find that the experimental system shows reduced values but of the same order of magnitude. Our model allows us to predict the performance for different magnetic field values in the molecular BEC regime. The grey curves in Fig. 3e,f and the theoretical curves of Fig. 4 follow from equations (8) and (7). Since the latter calculations rely on zero-T formulas, we interpret their results as an upper bound or limit for the work output and efficiency. To show that this estimation is accurate, we need to consider two aspects. First, for the two on-resonance points (C, D), we consider the zero-T calculations to be a good approximation because of the aforementioned decay in the temperature between the molecular BEC regime and unitarity in the adiabatic sweep. Owing to the dominance of the molecular term on the molecular BEC side, the efficiency obtained when including the temperature overlaps with that obtained within the zero-T approximation. For the data of Fig. 4, the zero-T calculations give an efficiency of about 0.07(2) while the finite-T formulas give an efficiency of about 0.05(3). A null hypothesis test for the mean difference gives a P value of 0.1. Setting the usual significance of α = 0.05, the null hypothesis of equal efficiencies cannot be rejected. Therefore, we conclude that the finite-T corrections have no notable effects on the efficiency of our engine.
Figure 3e,f shows that the work output is reduced with increased initial effective repulsion of the molecular BEC, whereas the efficiency increases. This scaling of the work output is a consequence of the competition between interactions among molecules in the initial molecular BEC state and the effect of changing the quantum statistics. For stronger initial effective repulsion, the molecular BEC cloud already exhibits a relatively large energy in the trap, so that the change of quantum statistics can only contribute a comparatively smaller amount of energy during the Pauli stroke. This suggests an optimal work output for an initially non-interacting molecular BEC. It is important to mention that even though the binding energy has no consequences for the work output (the s-wave scattering length does not change during the work strokes) it still has to be provided to the system during the Pauli stroke when dissociating a molecule into two atoms; hence, it must be included in the energy-cost calculation of the engine’s efficiency. This binding energy quickly grows as the magnetic field deviates from the resonance value and the associated energy cost quickly reduces the efficiency. For the experimentally inaccessible case of a non-interacting molecular BEC, this binding energy is so large that the efficiency of the Pauli cycle is essentially zero. These considerations point toward an optimal point of operation which might, additionally, be temperature dependent.
An important result that demonstrates the non-classical drive of the Pauli engine is reproduced by both experimental findings and the theoretical model: the work output as a function of the number of particles W ∝ Nα scales with a fitted exponent α = 1.73(18), which is close to the prediction of 1.4 given by theory (Fig. 4a). The exponent of the work output with particle number is different from the 1D case mentioned in the introduction due to a modified density of states, that is, the number of available single-particle states in the potential. Although a similar exponent is expected for the Feshbach-driven stroke which remains always in the molecular BEC regime, the efficiency for this engine is close to zero. Most importantly, the exponent is larger than one, which is the expected exponent for a non-interacting, classical gas1,48,63.
Pressure and volume calculations
The pressure of the system is calculated as p = −∂E/∂V. As explained in the previous paragraph, the zero-T energy constitutes a good approximation for the system and, therefore, we calculate the pressure for T = 0. For computing the derivative at the experimentally obtained volumes, we use that, on the molecular BEC side, the theoretical volume is given by
| 12 |
whereas, on resonance, the volume has a different dependence on the number of atoms and on the geometric mean of the trap frequency, and is given by
| 13 |
(refs. 34,46,54,64). The experimental volume in both cases is computed as the volume of an ellipsoid having the radii obtained by means of equations (2) and (3). Extended Data Fig. 7 shows the corresponding values of volume V and pressure p as a function of the compression ratio. The p–V diagram in Fig. 2c is obtained using these experimental data (points) and by calculating the corresponding theoretical curves. For completeness, we also checked that the work output obtained from the area inside the p–V diagram −∫ p dV is in agreement with that shown in Fig. 3e.
Extended Data Fig. 7. Pressure and volume for the Pauli engine.

Volume V and pressure p (panel (a) and (b) respectively) for each point of the Pauli cycle: B (red), C (orange), D (purple), and A2 (last point of the cycle, cyan). The measurements corresponds to the same ones as in Fig. 3 of the main text. The data for the volume are the mean value of 20 repetitions with error bars that lie inside the point size, the error bars in the pressure indicate the propagation of uncertainty of standard deviation of the measurement parameters.
A closer analogy with a quantum Otto cycle can be drawn using generalized parameters for p and V (refs. 65,66). It will be interesting in the future to extend this concept to ensembles with changing quantum statistics and to evaluate the performance of the Pauli engine according to this description.
Online content
Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-023-06469-8.
Acknowledgements
This work was supported by the German Research Foundation (DFG) by means of the Collaborative Research Center Sonderforschungsbereich SFB/TR185 (Project 277625399) and Forschergruppe FOR 2724. It was also supported by the Okinawa Institute of Science and Technology Graduate University. J.K. was supported by the Max Planck Graduate Center with the Johannes Gutenberg-Universität Mainz. E.C. was supported by the Argentinian National Scientific and Technical Research Council (CONICET). T.F. was supported by JSPS KAKENHI grant no. JP23K03290. T.F. and T.B. are also supported by JST grant no. JPMJPF2221. We thank B. Nagler and A. Guthmann for carefully reading the manuscript.
Extended data figures and tables
Author contributions
E.L., T.B. and A.W. conceived the research. J.K. and S.B. ran the experimental apparatus. J.K. took and analysed the experimental data. E.C. contributed to the analysis. E.C., K.M., T.F. and T.B. provided the theoretical models and J.K. contributed to the modelling. All authors contributed to the interpretation of the data, writing of the manuscript and critical feedback.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Funding
Open access funding provided by Rheinland-Pfälzische Technische Universität Kaiserslautern-Landau.
Data availability
All data of the figures in the manuscript and Methods are available in a Zenodo repository 10.5281/zenodo.7886857 (ref. 67).
Code availability
The codes that support the findings of this paper are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
is available for this paper at 10.1038/s41586-023-06469-8.
References
- 1.Callen HB. Thermodynamics and an Introduction to Thermostatistics. Wiley; 1985. [Google Scholar]
- 2.Massimi M. Pauli’s Exclusion Principle: The Origin and Validation of a Scientific Principle. Cambridge Univ. Press; 1999. [Google Scholar]
- 3.Chin C, Grimm R, Julienne P, Tiesinga E. Feshbach resonances in ultracold gases. Rev. Mod. Phys. 2010;82:1225–1286. [Google Scholar]
- 4.Regal CA, Ticknor C, Bohn JL, Jin DS. Creation of ultracold molecules from a Fermi gas of atoms. Nature. 2003;424:47–50. doi: 10.1038/nature01738. [DOI] [PubMed] [Google Scholar]
- 5.Jochim S, et al. Bose–Einstein condensation of molecules. Science. 2003;302:2101–2103. doi: 10.1126/science.1093280. [DOI] [PubMed] [Google Scholar]
- 6.Zwierlein MW, et al. Observation of Bose–Einstein condensation of molecules. Phys. Rev. Lett. 2003;91:250401. doi: 10.1103/PhysRevLett.91.250401. [DOI] [PubMed] [Google Scholar]
- 7.Regal CA, Greiner M, Jin DS. Observation of resonance condensation of Fermionic atom pairs. Phys. Rev. Lett. 2004;92:040403. doi: 10.1103/PhysRevLett.92.040403. [DOI] [PubMed] [Google Scholar]
- 8.Petrov DS, Salomon C, Shlyapnikov GV. Weakly bound dimers of fermionic atoms. Phys. Rev. Lett. 2004;93:090404. doi: 10.1103/PhysRevLett.93.090404. [DOI] [PubMed] [Google Scholar]
- 9.Bartenstein M, et al. Crossover from a molecular Bose–Einstein condensate to a degenerate rermi gas. Phys. Rev. Lett. 2004;92:120401. doi: 10.1103/PhysRevLett.92.120401. [DOI] [PubMed] [Google Scholar]
- 10.Zwerger, W The BCS–BEC Crossover and the Unitary Fermi Gas (Springer, 2012)
- 11.Alicki R. The quantum open system as a model of the heat engine. J. Phys. A: Math. Gen. 1979;12:L103. [Google Scholar]
- 12.Roßnagel J, Abah O, Schmidt-Kaler F, Singer K, Lutz E. Nanoscale heat engine beyond the Carnot limit. Phys. Rev. Lett. 2014;112:030602. doi: 10.1103/PhysRevLett.112.030602. [DOI] [PubMed] [Google Scholar]
- 13.Klaers J, Faelt S, Imamoglu A, Togan E. Squeezed thermal reservoirs as a resource for a nanomechanical engine beyond the Carnot limit. Phys. Rev. X. 2017;7:031044. [Google Scholar]
- 14.Niedenzu W, Mukherjee V, Ghosh A, Kofman AG, Kurizki G. Quantum engine efficiency bound beyond the second law of thermodynamics. Nat. Commun. 2018;9:165. doi: 10.1038/s41467-017-01991-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zou Y, Jiang Y, Mei Y, Guo X, Du S. Quantum heat engine using electromagnetically induced transparency. Phys. Rev. Lett. 2017;119:050602. doi: 10.1103/PhysRevLett.119.050602. [DOI] [PubMed] [Google Scholar]
- 16.Klatzow J, et al. Experimental demonstration of quantum effects in the operation of microscopic heat engines. Phys. Rev. Lett. 2019;122:110601. doi: 10.1103/PhysRevLett.122.110601. [DOI] [PubMed] [Google Scholar]
- 17.de Assis RJ, et al. Efficiency of a quantum Otto heat engine operating under a reservoir at effective negative temperatures. Phys. Rev. Lett. 2019;122:240602. doi: 10.1103/PhysRevLett.122.240602. [DOI] [PubMed] [Google Scholar]
- 18.Peterson JPS, et al. Experimental characterization of a spin quantum heat engine. Phys. Rev. Lett. 2019;123:240601. doi: 10.1103/PhysRevLett.123.240601. [DOI] [PubMed] [Google Scholar]
- 19.Bouton Q, et al. A quantum heat engine driven by atomic collisions. Nat. Commun. 2021;12:2063. doi: 10.1038/s41467-021-22222-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim, J. et al. A photonic quantum engine driven by superradiance. Nat. Photon. 16, 707–711 (2022).
- 21.Myers NM, Abah O, Deffner S. Quantum thermodynamic devices: from theoretical proposals to experimental reality. AVS Quantum Sci. 2022;4:027101. [Google Scholar]
- 22.Lieb EH, Seiringer R. The Stability of Matter in Quantum Mechanics. Cambridge; 2010. [Google Scholar]
- 23.Philips AC. The Physics of Stars. Wiley; 1994. [Google Scholar]
- 24.Metcalf, H. J & Straten, van der, P. Laser Cooling and Trapping (Springer, 1999)
- 25.Kosloff R, Rezek Y. The quantum harmonic Otto cycle. Entropy. 2017;19:136. [Google Scholar]
- 26.Foot CJ. Atomic Physics. Oxford Univ. Press; 2005. [Google Scholar]
- 27.Pauli W. The connection between spin and statistics. Phys. Rev. 1940;58:716–722. [Google Scholar]
- 28.Myers NM, Deffner S. Bosons outperform fermions: the thermodynamic advantage of symmetry. Phys. Rev. E. 2020;101:012110. doi: 10.1103/PhysRevE.101.012110. [DOI] [PubMed] [Google Scholar]
- 29.Watanabe G, Venkatesh BP, Talkner P, Hwang M-J, del Campo A. Quantum statistical enhancement of the collective performance of multiple bosonic engines. Phys. Rev. Lett. 2020;124:210603. doi: 10.1103/PhysRevLett.124.210603. [DOI] [PubMed] [Google Scholar]
- 30.Holmes Z, Anders J, Mintert F. Enhanced energy transfer to an optomechanical piston from indistinguishable photons. Phys. Rev. Lett. 2020;124:210601. doi: 10.1103/PhysRevLett.124.210601. [DOI] [PubMed] [Google Scholar]
- 31.Myers NM, et al. Boosting engine performance with Bose–Einstein condensation. New J. Phys. 2022;24:025001. [Google Scholar]
- 32.Gänger B, Phieler J, Nagler B, Widera A. A versatile apparatus for fermionic lithium quantum gases based on an interference-filter laser system. Rev. Sci. Instrum. 2018;89:093105. doi: 10.1063/1.5045827. [DOI] [PubMed] [Google Scholar]
- 33.Zürn G, et al. Precise characterization of 6Li Feshbach resonances using trap-sideband-resolved RF spectroscopy of weakly bound molecules. Phys. Rev. Lett. 2013;110:135301. doi: 10.1103/PhysRevLett.110.135301. [DOI] [PubMed] [Google Scholar]
- 34.Giorgini S, Pitaevskii LP, Stringari S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 2008;80:1215–1274. [Google Scholar]
- 35.Inguscio M, Ketterle W, Stringari S, Roati G. Quantum Matter at Ultralow Temperatures. IOS; 2016. [Google Scholar]
- 36.Bouvrie PA, Tichy MC, Roditi I. Composite-boson approach to molecular Bose–Einstein condensates in mixtures of ultracold Fermi gases. Phys. Rev. A. 2017;95:023617. [Google Scholar]
- 37.Bouvrie PA, Cuestas E, Roditi I, Majtey AP. Entanglement between two spatially separated ultracold interacting Fermi gases. Phys. Rev. A. 2019;99:063601. [Google Scholar]
- 38.Wu Y-S. Statistical distribution for generalized ideal gas of fractional-statistics particles. Phys. Rev. Lett. 1994;73:922–925. doi: 10.1103/PhysRevLett.73.922. [DOI] [PubMed] [Google Scholar]
- 39.Chen Q, Stajic J, Levin K. Thermodynamics of interacting fermions in atomic traps. Phys. Rev. Lett. 2005;95:260405. doi: 10.1103/PhysRevLett.95.260405. [DOI] [PubMed] [Google Scholar]
- 40.Thomas JE, Kinast J, Turlapov A. Virial theorem and universality in a unitary Fermi gas. Phys. Rev. Lett. 2005;95:120402. doi: 10.1103/PhysRevLett.95.120402. [DOI] [PubMed] [Google Scholar]
- 41.Thomas JE. Energy measurement and virial theorem for confined universal Fermi gases. Phys. Rev. A. 2008;78:013630. [Google Scholar]
- 42.Tan S. Generalized virial theorem and pressure relation for a strongly correlated Fermi gas. Ann. Phys. 2008;323:2987–2990. [Google Scholar]
- 43.Li J, Fogarty T, Campbell S, Chen X, Busch T. An efficient nonlinear Feshbach engine. New J. Phys. 2018;20:015005. [Google Scholar]
- 44.Keller T, Fogarty T, Li J, Busch T. Feshbach engine in the Thomas–Fermi regime. Phys. Rev. Res. 2020;2:033335. [Google Scholar]
- 45.Simmons, E. Q. et al. Thermodynamic engine with a quantum degenerate working fluid. Preprint at https://arXiv.org/cond-mat.quant-gas/2304.00659 (2023).
- 46.Dalfovo F, Giorgini S, Pitaevskii LP, Stringari S. Theory of Bose-Einstein condensation in trapped gases. Rev. Mod. Phys. 1999;71:463–512. [Google Scholar]
- 47.Abah O, Lutz E. Energy-efficient heat engines. EPL. 2017;118:40005. [Google Scholar]
- 48.Williams JE, Nygaard N, Clark CW. Phase diagrams for an ideal gas mixture of fermionic atoms and bosonic molecules. New J. Phys. 2004;6:123–123. [Google Scholar]
- 49.Ashcroft NW, Mermin ND. Solid State Physics. Harcourt; 1976. [Google Scholar]
- 50.Leggett AJ. Quantum Liquids. Bose condensation and Cooper Pairing in Condensed-Matter Systems. Cambridge Univ. Press; 2006. [Google Scholar]
- 51.Nagler, B. Bose–Einstein condensates and degenerate Fermi gases in static and dynamic disorder potentials. PhD thesis, TU Kaiserslautern (2020).
- 52.Reinaudi G, Lahaye T, Wang Z, Guéry-Odelin D. Strong saturation absorption imaging of dense clouds of ultracold atoms. Opt. Lett. 2007;32:3143. doi: 10.1364/ol.32.003143. [DOI] [PubMed] [Google Scholar]
- 53.Horikoshi M, et al. Appropriate probe condition for absorption imaging of ultracold 6Li atoms. J. Phys. Soc. Jpn. 2017;86:104301. [Google Scholar]
- 54.Pitaevskii LP, Stringari S. Bose. Oxford Univ. Press; 2003. [Google Scholar]
- 55.Jochim, S. Bose-Einstein Condensation of Molecules. PhD thesis, Leopold-Franzens-Universität, Innsbruck (2004).
- 56.Kinast J, et al. Heat capacity of a strongly interacting Fermi gas. Science. 2005;307:1296–1299. doi: 10.1126/science.1109220. [DOI] [PubMed] [Google Scholar]
- 57.Horikoshi M, Nakajima S, Ueda M, Mukaiyama T. Measurement of universal thermodynamic functions for a unitary Fermi gas. Science. 2010;327:442. doi: 10.1126/science.1183012. [DOI] [PubMed] [Google Scholar]
- 58.Horikoshi M, Koashi M, Tajima H, Ohashi Y, Kuwata-Gonokami M. Ground-state thermodynamic quantities of homogeneous spin-1/2 fermions from the BCS region to the unitarity limit. Phys. Rev. X. 2017;7:041004. [Google Scholar]
- 59.Greiner M, Regal CA, Jin DS. Emergence of a molecular Bose–Einstein condensate from a Fermi gas. Nature. 2003;426:537–540. doi: 10.1038/nature02199. [DOI] [PubMed] [Google Scholar]
- 60.Liu X-J, Hu H, Drummond PD. Virial expansion for a strongly correlated Fermi gas. Phys. Rev. Lett. 2009;102:160401. doi: 10.1103/PhysRevLett.102.160401. [DOI] [PubMed] [Google Scholar]
- 61.Hu H, Liu X-J, Drummond PD. Static structure factor of a strongly correlated Fermi gas at large momenta. EPL. 2010;91:20005. [Google Scholar]
- 62.Hu H, Liu X-J, Drummond PD. Universal contact of strongly interacting fermions at finite temperatures. New J. Phys. 2011;13:035007. [Google Scholar]
- 63.Beau, M., Jaramillo, J. & Del Campo, A. Scaling-up quantum heat engines efficiently via shortcuts to adiabaticity. Entropy18, 168 (2016).
- 64.Kinast, J. M. Thermodynamics and Superfluidity of a Strongly Interacting Fermi Gas. PhD thesis, Duke Univ. (2006).
- 65.Romero-Rochín V. Equation of state of an interacting Bose gas confined by a harmonic trap: the role of the “harmonic” pressure. Phys. Rev. Lett. 2005;94:130601. doi: 10.1103/PhysRevLett.94.130601. [DOI] [PubMed] [Google Scholar]
- 66.Sandoval-Figueroa N, Romero-Rochín V. Thermodynamics of trapped gases: generalized mechanical variables, equation of state, and heat capacity. Phys. Rev. E. 2008;78:061129. doi: 10.1103/PhysRevE.78.061129. [DOI] [PubMed] [Google Scholar]
- 67.Koch, J. et al. A quantum engine in the BEC-BCS crossover. Zenodo10.5281/zenodo.7886857 (2022).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data of the figures in the manuscript and Methods are available in a Zenodo repository 10.5281/zenodo.7886857 (ref. 67).
The codes that support the findings of this paper are available from the corresponding author upon reasonable request.