Decoding stoichiometric protein synthesis in E. coli through translation rate parameters

Abstract

E. coli is one of the most widely used organisms for understanding the principles of cellular and molecular genetics. However, we are yet to understand the origin of several experimental observations related to the regulation of gene expression in E. coli. One of the prominent examples in this context is the proportional synthesis in multiprotein complexes where all of their obligate subunits are produced in proportion to their stoichiometry. In this work, by combining the next-generation sequencing data with the stochastic simulations of protein synthesis, we explain the origin of proportional protein synthesis in multicomponent complexes. We find that the estimated initiation rates for the translation of all subunits in those complexes are proportional to their stoichiometry. This constraint on protein synthesis kinetics enforces proportional protein synthesis without requiring any feedback mechanism. We also find that the translation initiation rates in E. coli are influenced by the coding sequence length and the enrichment of A and C nucleotides near the start codon. Thus, this study rationalizes the role of conserved and nonrandom features of genes in regulating the translation kinetics and unravels a key principle of the regulation of protein synthesis.

Why it matters

The components of multiprotein complexes in E. coli are produced in proportion to their stoichiometry in the complex. This proportional protein synthesis maximizes the utilization of ribosomes and thus ensures an efficient and balanced distribution of cellular resources. However, the origin of such a proportional protein synthesis remains unknown. In this study, using the next-generation sequencing data we compute the gene-specific translation initiation rates and codon translation rates. Using those measured rate parameters, we discover that the proportional protein synthesis in multiprotein complexes, which are coded by a single operon, is enforced by balancing the translation initiation rates. This means the translation initiation rate for each component within the multiprotein complexes is directly proportional to its stoichiometric coefficient. Thus, this study enhances our understanding of how protein synthesis is regulated at different levels.

Introduction

Proteins perform a wide range of biological functions, including genome regulation, transport of chemical species, inter- and intracellular communication, immune response, energy transduction, etc. (1,2,3,4,5). Their synthesis is tightly regulated because precise protein levels are required in a cell to perform many essential functions (6,7,8,9,10). One of the prime examples of such fine-tuned regulation is the proportional synthesis of all subunits in multiprotein complexes (6,11,12,13,14,15). The synthesis rate of obligate subunits in those complexes is proportional to their stoichiometry. Any disruption in proportional protein synthesis may result in the loss of an essential function (16,17,18). Also, a weak or no regulation of protein synthesis would require more assistance from the degradation machinery to maintain the required protein levels and stoichiometry, leading to enormous wastage of cellular resources (19). Therefore, nature favors proportional synthesis rather than producing an excess amount of unusable proteins (6,11,14,20). Proportional protein synthesis is observed across a range of organisms, including E. coli, S. cerevisiae, B. subtilis, etc. (6,12,20). However, the exact mechanism for such precise control of protein synthesis is not fully understood (6).

The cellular protein abundance is regulated by a balance between the protein synthesis and proteolysis. The synthesis of protein molecules is regulated at two stages: transcription and translation (6,21,22,23,24,25,26). An increase in mRNA copy number, which is controlled at transcription level, leads to a corresponding increase in protein production (22,23,27,28). Different feedback mechanisms modulate mRNA copy number according to physiological and cellular conditions to attain the desired protein levels (21,29,30,31). At the translation level, protein synthesis is regulated at the initiation and elongation steps, providing additional control points for fine-tuning the cellular protein abundance (6,26,32). Thus, the knowledge of rate parameters with which these two steps occur may offer a detailed insight into the regulation of protein synthesis. Specifically in bacterial multiprotein complexes where an operon encodes all of its obligate subunits. Therefore, there is no variation in the copy number of mRNAs encoding those components, if none of them are being encoded by other mRNA isomers. Thus, the proportional synthesis can be managed at the translational level (6,11,20).

In this paper, to understand the regulation of protein synthesis, we extract the translation initiation and codon translation rates in E. coli using ribosome profiling and RNA-seq data (6,33). We find that the estimated initiation rates in E. coli are influenced by coding sequence (CDS) length, mRNA structure near the start codon, and the number of A and C nucleotides in the 5′ untranslated regions (UTRs). Then, by simulating protein synthesis using the estimated translation rate parameters, we show that translation initiation is the rate-limiting step of protein synthesis and is one of the main determinants of cellular protein levels in E. coli (34,35). We also explain the origin of proportional protein synthesis in multiprotein complexes encoded by a single operon. We observe that the initiation rate of translation for all obligate subunits in these complexes is directly proportional to their stoichiometry. This constraint on protein synthesis kinetics ensures that their synthesis occurs proportionally. These findings demonstrate that proportional protein synthesis within these complexes is an inherent genetic feature, requiring no feedback mechanisms to maintain the necessary protein levels.

Methods

Calculation of initiation rate

We used a previously developed chemical-kinetic method to extract the gene-specific translation initiation rates in E. coli (26). This method is based on the following mathematical relation between the initiation rate and ribosome occupancy.

$$\alpha \left(i\right)=\frac{\rho \left(i\right)\left(L\left(i\right)-1\right)}{T\left(i\right)\left(1-\sum _{k=2}^{11}\rho \left(k,i\right)\right)}$$ (1)

In Eq. 1, α(i) is the initiation rate of the i^th transcript. L(i) is the number of codons in the coding sequence, and T(i) is the mean translation time taken by a ribosome to complete the synthesis of a single protein molecule. ρ(k,i) is the average ribosome occupancy at k^th codon of the i^th transcript and ρ(i) is the average ribosome density on the transcript. ρ(k,i) is defined as the fraction of times a ribosome’s A-site occupies a specific codon from a large number of independent configurations, and lies between 0 and 1.

A ribosome spans 10 consecutive codon positions and initiates protein synthesis by positioning its A-site at the second codon position (36). Consequently, any ribosome present at codon positions 2 to 11 (i.e., the ribosome A-site) will act as a physical barrier, hindering other ribosomes from initiating protein synthesis. Due to this steric interaction, the sum of average ribosome occupancy ρ(k,i) from codon positions 2 to 11 of the transcript will always be less than 1. Therefore, the denominator $\left(1-\sum _{k=2}^{11}\rho \left(k,i\right)\right)$ in Eq. 1 is always positive. The details of how we calculated $\rho \left(i\right),\rho \left(k,i\right)$, and $T\left(i\right)$ are explained in the subsequent subsections.

Calculation of codon translation time

We use the same chemical kinetic method to calculate the average translation time of a codon (26). This method computes the average codon translation time by using the following expression that requires ribosome profiling reads as input parameters.

$$\tau \left(i,j\right)=\frac{N\left(i,j\right)}{\sum _{j=2}^{L\left(i\right)}N\left(i,j\right)}T\left(i\right)$$ (2)

In Eq. 2, N(i,j) is the number of Ribo-seq reads that are aligned to the j^th codon position of the i^th transcript.

Estimation of N(i,j)

We calculate N(i,j) by using the ribosome profiling data reported in (33) and (6) with NCBI accession numbers GSE72899 and GSE53767, respectively. We start by trimming off the adapter sequence (CTGTAGGCACCATCAAT) from the raw ribosome profiling reads by using the software CUTADAPT 3.4 (37). Next, we filter out the low-quality reads using PRINSEQ-lite 0.20.4, since the sequenced data may contain fragments coming from rRNA molecules (26). Therefore, we also align those RNA fragments to the rRNA sequences (38) using the software BOWTIE 2.3.5.1 (39). The remaining unaligned RNA fragments are the ribosome footprints. We then determine the coordinates of those footprints using TOPHAT v2.1.1 on E. coli (strain MG1665) (40). A ribosome is an extended object that spans around 10 successive codons but translates the codon present at its A-site (26,32). Therefore, we next identify the position of the ribosome A-site on all ribosome footprints. For this, we used a fixed offset of 11 nucleotides from the 3′ end of the fragment (41,42). The total number of A-sites assigned to the j^th codon of gene i is N(i,j) (Eq. 2). Note well, to reduce the statistical uncertainty in our computation, we only selected the genes that have high RPKM (reads per kilobase per million mapped reads) values (Ribo-seq RPKM > 10 for (33) data set and RNA-seq RPKM > 45 and Ribo-seq RPKM > 25 for (6) data set). This minimizes the statistical uncertainty associated with estimating the codon translation rate.

Estimation of ρ(i) and ρ(i,j)

Accurate estimation of translation initiation rate using the chemical kinetic method requires the average ribosome density of E. coli transcripts (Eq. 1). We get the average ribosome density of a transcript using the polysome profiling data reported in (43). However, this data set contains the average ribosome density of only 732 genes. Therefore, to get the average ribosome density of remaining genes, we use the following linear relationship between the average ribosome density and translation efficiency (26).

$$\rho \left(i\right)=\xi TE\left(i\right)$$ (3)

In Eq. 3, TE(i) is the translation efficiency of the i^th transcript, which is the ratio of RPKM values of Ribo-seq with RNA-seq. ξ in Eq. 3 is a proportionality constant that was obtained by measuring the slope of the best fit line between ρ(i) and TE(i), which is 0.042 and 0.0095 (Figs. S1 and S2) for the data sets (Ribo-seq and RNA-seq) reported in (6,33) and (Ribo-seq and RNA-seq) reported in (6). The average occupancy of a codon is determined by using the formula $\rho \left(i,j\right)=\frac{N\left(i,j\right)\rho \left(i\right)\left(L\left(i\right)-1\right)}{N\left(i\right)}$, where N(i) is the number of Ribo-seq reads aligned to the i^th transcript (26). Note, to reduce the statistical uncertainty in our computation, we only selected the genes that have high RPKM values (Ribo-seq RPKM $>10$ for (33) data set and RNA-seq RPKM $>45$ and Ribo-seq RPKM $>25$ for (6) data set).

Calculation of T(i)

Calculation of average codon translation rate using Eq. 2 also requires the average time a ribosome takes to make the full-length protein. We calculate this using a scaling relation reported in (26,44). According to this relation, T(i) can be approximated as the product of average codon translation time and the number of codons in the mRNA molecule. We used the average codon translation time of 62.5 ms to calculate the T(i) for all E. coli transcripts (45,46,47).

Protein synthesis simulations

We performed protein synthesis simulations using the TASEP model (48,49,50,51,52,53). In this model, an mRNA is conceptualized as a linear open lattice, with each site representing a codon. Thus, the number of sites in this one-dimensional lattice is equal to the total number of codons in the mRNA sequence. A ribosome in this model is like an extended rod covering 10 successive codons with the location of A-site at the sixth lattice site from the 5′ end. In this model, the initiation of protein synthesis occurs as ribosome subunits assemble at the start codon of the transcript i, with a rate denoted by α(i). Then, the ribosome starts moving from 5′ to 3′ end by taking one step at a time. In each of such steps, it jumps to the following codon and extends the nascent protein by adding one amino acid subunit. The movement of the ribosome from codon position j to j + 1 takes place with rate ω(j,i), if the (j + 10) codon is not occupied by other downstream ribosomes. We simulated the TASEP model of protein synthesis by using Gillespie’s algorithm described in (54).

Results

Transcriptome-wide estimation of gene-specific initiation rates

In prokaryotes, translation initiates when 30S ribosomal subunit binds at the start codon of an mRNA, which is later joined by 50S subunit, forming the translation initiation complex (55,56,57). We calculated the rate with which this step occurs in E. coli transcripts by using a chemical kinetic method (26). This approach requires RNA-seq, Ribo-seq, and polysome profiling data to calculate the gene-specific translation initiation rates. In this study, first we use the Ribo-seq and RNA-seq data reported in (33) and (6), respectively, whereas polysome profiling data were from (43). Note, the Ribo-seq experiment in (33) and the RNA-seq experiment in (6) were performed under similar conditions. The details of how we estimated the translation initiation rates using those data sets are provided in the methods. The mean and median of the estimated initiation rates of 1708 E. coli transcripts are 0.18 and 0.14 s⁻¹, respectively (Fig. 1 A) and the numerical values of gene-specific translation initiation rates are provided in the supporting material.

Fig. 1.

Estimation of translation initiation rates in E. coli and molecular factors that may influence them. Probability distribution of the estimated E. coli initiation rates is plotted in (A). E. coli initiation rates are plotted against the CDS length, mRNA stability near the start codon, and Shine-Dalgarno (SD) similarity score in (B), (C), and (D), respectively. In (D), blue color data points are the average initiation rates at different SD similarity scores.

The accurate estimation of translation initiation rates allows to identify the molecular factors that can influence and regulate them (54). To this end, first we test how the CDS length affects the translation initiation rate in E. coli. We test this because the start and stop codons remain in proximity of each other in shorter transcripts (58,59). Therefore, ribosomes that terminate protein synthesis at the stop codon can readily diffuse to the start codon of that specific transcript. As expected, we find a statistically significant correlation between E. coli translation initiation rates and CDS length (Fig. 1 B, R = −0.20). An mRNA structure near the start codon could also influence translation initiation rate. This is because a stable mRNA structure near the start codon can make it inaccessible for translation initiation (25,60,61,62). Indeed, many gene optimization methods minimize the stability of mRNA structure near the start codon for enhancing the translation efficiency in heterologous gene expression (63,64,65,66). However, the stability of which specific portion of the 5′ UTR and coding region has the strongest influence on initiation rates remains unclear (6,67). To address this, we consider a portion of 20 nucleotides for each of the transcripts, vary its starting position from −50 to +10 nucleotide with a step size of 10 nucleotides, and measure the folding energy of each portion using the Vienna package (68). Then, for each starting point, we measure the Pearson and Spearman’s correlation between the mRNA stability and initiation rates. We repeat this procedure by varying the size of the window ranging from 20 to 130 nucleotides with a step size of 5 nucleotides. The correlation for each of the cases is provided in Table S1 (see supporting material). We find that the strongest correlation was obtained when the window size was 125 nucleotides and the starting point was 40 nucleotides upstream of the AUG codon (Fig. 1 C).

The ribosome binding site (RBS) is a sequence of around 10 nucleotides that helps to recruit ribosomes for translation initiation (69,70). The RBS is complementary to an rRNA sequence that plays a crucial role in the binding of the ribosome to an mRNA transcript. In E. coli, it is AGGAGG and is known as Shine-Dalgarno (SD) sequence (71,72). However, how strongly the SD sequence affects translation efficiency remains controversial (6,35,67,73). For example, despite the conserved nature of the SD sequence, Saito et al. (35) show it to have no effect on translation efficiency, whereas many codon optimization methods rely on optimizing RBS to enhance translation efficiency (69,70). To resolve this conundrum, first we scan 5′ UTR of a transcript and measure the similarity with SD sequence between −13 and −8 nucleotides. Similar to their study (35), we did not find any correlation between translation initiation rates calculated using the Ribo-seq data reported in (33) and SD similarity (Fig. 1 D). Taken together, these results show that the SD sequence present between −13 and −8 nucleotides may not influence translation initiation rate.

Using the variants of four different E. coli transcripts, Saito et al. have shown that an enrichment of A and C nucleotides near the start codon increases and decreases the ribosome occupancy, respectively (35). We test whether this modification in ribosome occupancy is a consequence of the changes in the translation initiation rates. To address this, we scanned the portions of mRNA molecules between −25 and +10 nucleotides to find whether the enrichment of any nucleotide in this region influences the translation initiation rate. The details of the boundaries of the mRNA portions we choose for this analysis and the correlation of the number of A, U, C, and G nucleotides in those regions with the translation initiation rate are given in the supporting material. For the A nucleotide, the strongest correlation was obtained when it was counted between the start codon and five nucleotides upstream of it. For the C nucleotide, it was the region between the start codon and 13 nucleotides upstream of it that gave the strongest correlation (Fig. 2; Table S2). One possible explanation for this is that the enrichment of A nucleotides in the 5′ UTR may tend to decrease the stability of any structure in this region, thus increasing the initiation rate. Similarly, the enrichment of C nucleotides in this region may have the opposite effect on initiation rate (35). In addition to that, the interactions between the small ribosomal subunit and A and C nucleotides in the vicinity of the start codon may also influence the formation of a ribosome-mRNA complex at the start codon, which requires further investigation. However, the number of U and G nucleotides did not show any significant correlation with translation initiation rate (Table S2). These results show that the enrichment of A and C nucleotides increase and decrease the initiation rates, respectively, and thus modulates ribosome occupancy.

Fig. 2.

Enrichment of A and C nucleotides near the start codon influences the initiation rate. Translation initiation rates are plotted against the number of A and C nucleotides between the start codon and 5 and 13 nucleotides upstream of it in (A) and (B), respectively. Blue colored points in both figures are the average initiation rates at different number of A and C nucleotides in (A) and (B), respectively.

We also calculated initiation rates using the Ribo-seq and RNA-seq data as reported in (6) and found similar results (see supporting material, Figs S3 and S4). In addition, we observed a robust correlation between the initiation rate calculated from Ribo-seq in (33) and (6), respectively, whereas, in both the cases RNA-seq data were from (6) (Fig. S5, R $=0.90$).

In summary, we have calculated gene-specific translation initiation rates for E. coli transcripts. We also show that the CDS length, mRNA structure near the start codon, and the repeats of A and C nucleotides near the start codon influence the initiation rates in E. coli transcripts.

Estimation of individual codon translation time

We calculate the translation time of all sense codons in E. coli by using a chemical kinetic method (26). The method requires ribosome profiling data to calculate the average translation time of a codon. In this study, first we use the ribosome profiling data reported in (33) and calculate the translation time of all E. coli codons. The calculated mean and median translation time of E. coli codons are provided in the supporting material. We also find a significant variation in the translation time of a codon type at different locations in the transcriptome (Fig. S6).

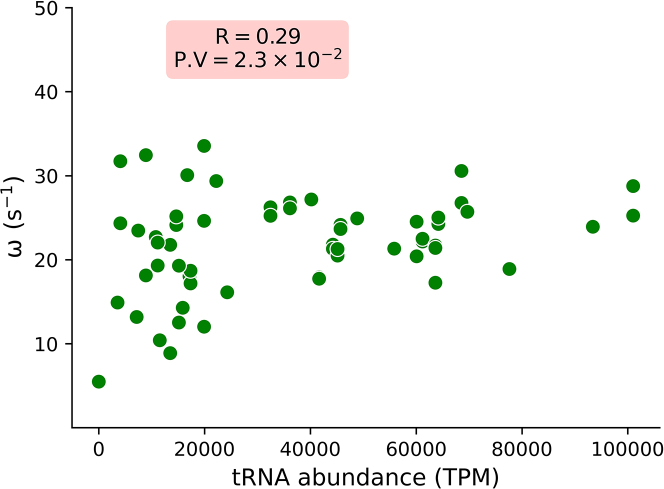
We then explore how different mRNA features influence average codon translation time. To this end, we plot the codon translation rate as a function of cognate tRNA abundance and find a statistically significant correlation between them (Fig. 3, R = 0.29). The reason for this dependence is that the amino acids can be easily delivered to ribosomes at a relatively higher cognate tRNA concentration (74,75,76,77).

Fig. 3.

The average codon translation rate at which a specific codon is translated by the ribosome is influenced by the concentration of its corresponding cognate tRNA molecule.

We also calculate the codon translation rate using the ribosome profiling data reported in (6) and find similar results (supporting material, Fig. S7). The estimated codon translation rates are provided in the supporting material.

We also test the accuracy of the estimated average codon translation times. To this end, we carry out an in silico ribosome profiling experiment. In this experiment, we simulated protein synthesis on each E. coli transcript using the computed translation rate parameters (see methods). These simulations provided multiple uncorrelated snapshots of the gene translation system, each containing information about the ribosome A-site positions across the transcript. We treated each ribosome in these snapshots as separate Ribo-seq reads. We continued capturing such snapshots until the number of in silico Ribo-seq reads matched the in vivo reads reported in (33). This process ensured that the in silico ribosome profiles have a similar level of uncertainty as the in vivo profiles. We repeated this procedure for each transcript, quantifying the Pearson correlation between the normalized in vivo and in silico ribosome density. The distribution of the transcriptome-wide Pearson correlation is shown in Fig. S8. We observed that the Pearson correlation between different transcripts ranged from 0.35 to 0.96, with a median value of 0.71. The observed correlations in each of the transcripts were comparable with those reported in previous studies (26,49). Thus, these results reinforce the accuracy and validity of the computed codon translation rates.

Translation initiation is the rate-limiting step

After the estimation of translation initiation and codon translation rates we ask what determines the rate of protein synthesis from an E. coli transcript. To understand this, first we test the accuracy of the estimated translation initiation and codon translation rates. Therefore, we perform protein synthesis simulations on all 1708 E. coli transcripts and measure the rate of protein synthesis, f(i), for each of the transcripts. In these simulations, we use translation initiation and codon translation rates computed from Ribo-seq and RNA-seq data reported in (33) and (6), respectively. See methods for details of how we simulated protein synthesis using Gillespie’s algorithm. Then, we calculate the overall protein production rate, F(i), for each E. coli protein by multiplying f(i) with mRNA copy number reported in (78). We find that the protein production rate computed from our model strongly correlates with the experimentally measured rates in (6) (Fig. 4 A, R = 0.83). This shows the high accuracy of the translation rate parameters we measured in this study. Therefore, now we can use our simulation data for understanding what determines cellular protein levels.

Fig. 4.

Translation initiation and mRNA copy number determines the cellular protein abundance. (A) Overall protein synthesis rate measured from our simulations (F) are plotted against the ones reported in experiments (6). (B) Protein synthesis rate from each E. coli transcript (f) is plotted as a function of translation initiation rate (discrete data points). The red solid line is the identity line. (C) Cellular protein abundances are plotted against the product of the mRNA copy number and initiation rate.

In yeast, the process of translation initiation serves as the primary rate-limiting step in protein synthesis (25,26,32,79,80). Therefore, we also test how strongly translation initiation affects overall protein synthesis in E. coli. We plot the protein synthesis rate as a function of translation initiation rate and find a strong correlation between them (Fig. 4 B). We also observe that the initiation rate puts an upper bound to the rate of protein synthesis, and the difference between the rate of protein synthesis and initiation rate is less than 13% in more than 70% of the total transcripts. Taken together, these observations clearly show that translation initiation is the main determinant of the rate of protein synthesis from an E. coli transcript. Then, next we plot the product of mRNA copy number and initiation rate with E. coli protein abundance reported in (81) and find a strong correlation between them (Fig. 4 C, R = 0.86). These results suggest that translation initiation rate and mRNA copy number are the two main determinants of cellular protein abundance. This means that the regulation of protein synthesis at the transcription and translational levels are managed by mRNA copy number and translation initiation rates, respectively. We find similar results when we carry out protein synthesis simulations by using the translation initiation and codon translation rates computed from the Ribo-seq and RNA-seq data reported in (6) (supporting material, Fig. S9).

Predicting translation initiation rate using mRNA sequence features

The estimated translation initiation rates in this study have shown statistically significant correlations with folding energy, CDS length, and the number of A and C nucleotides in the 5′ UTR (Figs. 1, 2, S3, and S4). To further gain deeper insights into the individual and combined impacts of these variables on translation initiation rates, we employed a random forest-based multivariable regression model. The model was trained by using the 333 transcripts for which the numerical values of all parameters that influence initiation rates were available. Utilizing 80% of the data set for training and the remaining portion for testing, we observed a consistent level of correlations between the measured and predicted initiation rates in both sets (Fig. 5, Pearson R = 0.75). In addition, we determined the relative contributions of SD score, number of A and C nucleotides, folding energy, and CDS length, accounting for 9.6, 9.1, 9.5, 37.7, and 34.1%, respectively, in the overall variation of initiation rates. This shows that it is the mRNA folding energy and the transcript length that contribute most to the variations in in vivo initiation rates in E. coli. We also found similar results when we trained the model using the initiation rates computed from the Ribo-seq and RNA-seq data reported in (6) (Fig. S10).

Fig. 5.

Machine learning model predicts translation initiation rate with a reasonable accuracy. (A) Predicted initiation rates are plotted against the ones computed using the Ribo-seq and RNA-seq data reported in (6,33). (B) The relative contribution of molecular factors influencing initiation rate is shown.

Unlike previous approaches for predicting initiation rates, which rely on variations in the UTR and coding sequence region of a specific transcript (69,82,83), typically a GFP protein, our model was trained using the in vivo initiation rate data. This key difference allows our model to account for a broader range of factors that can potentially impact translation initiation rates.

Regulation of stoichiometric levels in a complex in E. coli

Cellular systems depend on several multiprotein complexes for a range of functional requirements (84,85,86). The components of these multiprotein complexes are synthesized in proportion to their stoichiometry in the complex, known as proportional protein synthesis (6,11,12,13,14). Proportional protein synthesis minimizes the role of protein degradation in maintaining the desired protein levels (6,13). Thus, minimizing the overall wastage of cellular resources. There are two different types of mechanism that allow such a strict control of protein synthesis. The first is the hardcoded regulation where proportional protein synthesis is built-in in the gene expression system. The second one is the feedback mechanism where a controller accesses the synthesis rates of the components of multiprotein complexes and then gives the instructions to either increase or decrease their production. However, which of these two mechanism is responsible for proportional protein synthesis remains unclear.

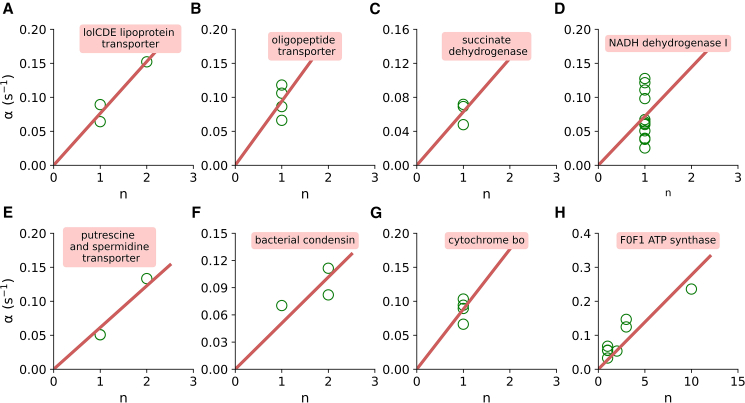
Protein synthesis at the translational level is mainly regulated by the step of translation initiation (Figs. 4 and S9). Therefore, if the proportional protein synthesis is hardcoded in the gene expression system, it must have been tuned by the translation initiation rate. First, we test this hypothesis for complexes that contain only two different subunits and are coded by the same polycistronic gene. To this end, we compare the initiation rates normalized by the stoichiometric coefficient of the protein and find that this ratio is almost equal for both components of the protein complexes (Figs. 6 and S11). This shows that proportional protein synthesis in those complexes is enforced by balancing the translation initiation rates. Next, we test the role of initiation rate in enforcing the proportional protein synthesis in complexes that have more than two components. For this, we plot the initiation rate of all components of a complex against their stoichiometry coefficient (Figs. 7 and S12). We find that, in the majority of cases, all components of a complex closely align with the line of best fit, indicating that the initiation rate of translation for each component is directly proportional to their stoichiometry. We also find significant deviations from the best fit line in NADH dehydrogenase I and oligopeptide transporter (Figs. 7 and S12). This is because stoichiometric protein synthesis is not maintained in these two complexes (Fig. S17). The deviation observed in these two complexes could be attributed to the dominant control of protein components at the degradation level and the dynamic nature of those complexes (6,13,34,87). It is worth noting that, while the majority (92% of the total stable multiprotein complexes) adhere to stoichiometric protein synthesis, these two complexes represent the remaining exception (6).

Fig. 6.

Translation initiation rate normalized by the stoichiometric coefficient of both components of a two-protein complex are plotted against each other. Note, here both components of the complex are coded by a polycistronic transcript. The solid line is the identity line. Translation initiation rates were estimated using the Ribo-seq and RNA-seq data reported in (33) and (6), respectively.

Fig. 7.

Translation initiation rate for each of the components of eight different complexes are plotted against their stoichiometric coefficient (A–H). All components of these complexes are encoded by a single polycistronic transcript. The red solid line is the best-fit line passing through the origin. Translation initiation rates were estimated using the Ribo-seq and RNA-seq data reported in (33) and (6), respectively.

Next, we consider the two-protein complexes whose components are not coded by a polycistronic transcript. For this, first we compare the normalized translation initiation rates for both components but find a significant deviation of the data points from the identity line (Figs. S13 and S14). This deviation can be caused by the differences in mRNA abundance as it also has a significant influence on cellular protein levels (Figs. 4 C and S9 C). Therefore, we further compare the normalized initiation rates by multiplying them with mRNA abundance reported in (88). We find that the normalized overall production rate of both components of the complexes are very close to the identity line (Figs. 8 and S15). We also analyze protein complexes that consist of more than two subunits of protein molecules, but are not coded on a single operon. To do this, we plot the product of the initiation rate and mRNA abundance against the stoichiometric coefficient of each transcript that codes for a protein molecule in the complex. We find that the overall production rate of these components is close to the best-fit line (Fig. S16). This suggests that probably a feedback mechanism is required to tune the desired mRNA abundance in those complexes that are coded by multiple transcripts and requires further investigation. We performed this analysis on a total of 33 out of 64 stable well-characterized complexes (6). The reasons for choosing these 33 complexes are given in the supporting material. Taken together, these results show that proportional protein synthesis is hardcoded in multiprotein complexes where all proteins are translated by a single polycistronic mRNA. However, the modulation of mRNA abundance is required to enforce the proportional synthesis in complexes whose components are translated from multiple transcripts.

Fig. 8.

The overall protein synthesis rate normalized by protein stoichiometry of the both subunits of two-component protein complexes are plotted against each other. Both subunits of these complexes are not coded by a single operon. The red solid line is the identity line. Translation initiation rates were estimated using the Ribo-seq and RNA-seq data reported in (33) and (6), respectively.

Discussion

Evolutionary selection pressure has introduced several nonrandom features to the genetic material that regulates protein synthesis kinetics and controls cellular protein levels (26,74,77,79,80,89,90). In this paper, we demonstrate how these nonrandom features affect the rate of protein synthesis by extracting the translation rate parameters using next-generation sequencing data. We find that the presence of an A nucleotide in the 5′ UTR upregulates the initiation rate, whereas it is downregulated by a stable structure near the start codon, CDS length, and the presence of C nucleotides in the 5′ UTR (Figs. 1, 2, S3, and S4). We also show that translation initiation is the step that determines the rate of protein synthesis from a single transcript, whereas cellular protein abundance is determined by the product of the translation initiation rate and mRNA copy number.

Li et al. have shown that the members of multiprotein complexes in E. coli are produced in proportion to their stoichiometry in the complex (6). However, the origin of such a proportional protein synthesis remains unknown (6,12,13,20,29). In this paper, by analyzing the estimated initiation rate, we find that the proportional protein synthesis in multiprotein complexes are enforced by balancing the translation initiation rate (Figs. 6, 7, S11, and S12). This means that the initiation rate of the translation of each of the component is proportional to their stoichiometric coefficient in the multiprotein complexes. This result suggests that stoichiometric protein synthesis is hardcoded and does not require any feedback to maintain the desired protein levels in a cell. However, multiprotein complexes whose components are not a part of the same operon may require a feedback mechanism to maintain the stoichiometric protein synthesis. Further investigations are required to understand how transcription and translational regulation of gene expression complement each other to ensure proportional protein synthesis in those complexes.

The recent findings of Lalanne et al. reveal that the proportional synthesis is not only restricted to the components of multiprotein complexes but also extends to the expression of various components within different metabolic pathways across different species (91). For example, in both B. subtilis and E. coli, the ratio of ribosomal proteins and initiation, elongation, and termination factors remains constant. This pathway-specific stoichiometry demonstrates remarkable robustness against any changes in the growth conditions, indicating that proportional protein synthesis is tightly regulated at multiple levels, including transcription, translation, and mRNA decay. By maintaining stoichiometric protein synthesis at different levels, cells adopt a multifaceted strategy that maximizes the utilization of ribosomes and thus ensures an efficient and balanced distribution of cellular resources (92). While the recent findings provide valuable insights into this complex process, there is still much to uncover about the different layers of proportional protein synthesis and the precise mechanisms that govern their coordination (20).

The mechanism of translation initiation in eukaryotes is very different than prokaryotes. In eukaryotes, a small ribosome subunit is recruited at the 5′ cap and then it starts scanning the UTR and coding region to find the canonical start codon (93,94,95,96). However, in prokaryotes, a small ribosome subunit directly binds to a region near the start codon (97,98,99,100). This difference in the mechanism of ribosome recruitment is also reflected in the portion of the mRNA transcript whose stability affects the initiation rate. In eukaryotes, it is the folding energy of the first 70 nucleotides from the 5′ end of the UTR that influences the initiation rate (26), whereas in E. coli it is the region between −40 and 85 nucleotides that affects the initiation rate, consistent with the mechanism of translation initiation (Figs. 1 C and S3 C). The average codon translation rate in E. coli is three times higher than in S. cerevisiae. Despite that, the mean and median of the estimated initiation rates are very similar those estimated in S. cerevisiae (26). This shows that protein synthesis in E. coli is more stringently limited by the translation initiation rate. This result is also consistent with a stronger correlation of protein copy number with α×mRNA abundance in E. coli compared with S. cerevisiae (26).

We show that proportional protein synthesis in multiprotein complexes is enforced by carefully balancing the translation initiation rates (Figs. 6, 7, S11, and S12). This balance results in a cellular abundance of the components of multiprotein complexes that precisely aligns with their stoichiometry within the complex. However, internal or external factors can disturb stoichiometric protein levels. In such situations, additional feedback mechanisms may be required to restore stoichiometric protein levels. For example, a faster degradation of the proteins lacking their binding partner could be one of the mechanisms to ensure the stoichiometric protein levels after such a disturbance (101). Nevertheless, further studies are needed to understand how cells cope with such disturbances in cellular protein levels. In summary, this study has given new insights into how various conserved and nonrandom features of the genetic material regulates the cellular protein level. This work will also guide future gene optimization methods by providing a better sense of how initiation rates can be optimized.

Author contributions

I.U.I. analyzed data, developed the simulation model, and performed the analysis. I.U.I. and A.K.S. designed the study and wrote the manuscript.

Editor: Sarah Rauscher.