On Support Recovery with Sparse CCA: Information Theoretic and Computational Limits

Abstract

In this paper, we consider asymptotically exact support recovery in the context of high dimensional and sparse Canonical Correlation Analysis (CCA). Our main results describe four regimes of interest based on information theoretic and computational considerations. In regimes of “low” sparsity we describe a simple, general, and computationally easy method for support recovery, whereas in a regime of “high” sparsity, it turns out that support recovery is information theoretically impossible. For the sake of information theoretic lower bounds, our results also demonstrate a non-trivial requirement on the “minimal” size of the nonzero elements of the canonical vectors that is required for asymptotically consistent support recovery. Subsequently, the regime of “moderate” sparsity is further divided into two subregimes. In the lower of the two sparsity regimes, we show that polynomial time support recovery is possible by using a sharp analysis of a co-ordinate thresholding [1] type method. In contrast, in the higher end of the moderate sparsity regime, appealing to the “Low Degree Polynomial” Conjecture [2], we provide evidence that polynomial time support recovery methods are inconsistent. Finally, we carry out numerical experiments to compare the efficacy of various methods discussed.

I. Introduction

Canonical Correlation Analysis (CCA) is a highly popular technique to perform initial dimension reduction while exploring relationships between two multivariate objects. Due to its natural interpretability and success in finding latent information, CCA has found enthusiasm across vast canvas of disciplines, which include, but are not limited to psychology and agriculture, information retrieving [3]-[5], brain-computer interface [6], neuroimaging [7], genomics [8], organizational research [9], natural language processing [10], [11], fMRI data analysis [12], computer vision [13], and speech recognition [14], [15].

Early developments in the theory and applications of CCA have now been well documented in the statistical literature, and we refer the interested reader to [16] and references therein for further details. However, the modern surge in interest for CCA, often being motivated by data from high throughput biological experiments [17]-[19], requires re-thinking several aspects of the traditional theory and methods. A natural structural constraint that has gained popularity in this regard, is that of sparsity, i.e., the phenomenon of an (unknown) collection of variables being related to each other. In order to formally introduce the framework of sparse CCA, we present our statistical setup next. We shall consider n-i.i.d. samples $(X_i,Y_i)\sim \mathbb{P}$ with $X_i\in {\mathbb{R}}^p$ and $Y_i\in {\mathbb{R}}^q$ being multivariate mean zero random variables with joint variance covariance matrix

$$\Sigma =\left[\begin{array}{cc}\hfill {\Sigma }_x\hfill & \hfill {\Sigma }_{yx}\hfill \\ \hfill {\Sigma }_{yx}\hfill & \hfill {\Sigma }_y\hfill \end{array}\right].$$ (1)

The first canonical correlation ${\Lambda }_1$ is then defined as the maximum possible correlation between two linear combinations of X and Y. This definition interprets ${\Lambda }_1$ as the optimal value of the following maximization problem:

$$\begin{gathered} \underset{u\in R^p,v\in R^q}{maximize}{u}^T{\Sigma }_{xy}v \\ \text{subject to}{u}^T{\Sigma }_{x}u=v^T{\Sigma }_{y}v=1. \end{gathered}$$ (2)

The solutions to (2) are the vectors that maximize the correlation of the projections of X and Y in those respective directions. Higher order canonical correlations can thereafter be defined in a recursive fashion (cf. [20]). In particular, for $j\ge 1$, we define the j^th canonical correlation ${\Lambda }_j$ and the corresponding directions u_j and v_j by maximizing (2) with the additional constraint

$$u^T{\Sigma }_x{u}_l=v^T{\Sigma }_y{v}_l=0,0\le l\le j-1.$$ (3)

As mentioned earlier, in many modern data examples, the sample size n is typically at most comparable to or much smaller than p or q – rendering the classical CCA inconsistent and inadequate without further structural assumptions [21]-[23]. The framework of Sparse Canonical Correlation Analysis (SCCA) (cf. [8], [24]), where the u_i’s and the v_i’s are sparse vectors, was subsequently developed to target low dimensional structures (that allows consistent estimation) when p, q are potentially larger than n. The corresponding sparse estimates of the leading canonical directions naturally perform variable selection, thereby leading to the recovery of their support (cf. [8], [19], [24], [25]). It is unknown, however, under what settings, this naïve method of support recovery, or any other method for the matter, is consistent. The support recovery of the leading canonical directions serves an important purpose of identifying groups of variables that explain the most linear dependence among high dimensional random objects (X and Y) under study – and thereby renders crucial interpretability. Asymptotically optimal support recovery is yet to be explored systematically in the context of SCCA – both theoretically, and from the computational viewpoint. In fact, despite the renewed enthusiasm for CCA, both the theoretical and applied communities have mainly focused on the estimation of the leading canonical directions, and relevant scalable algorithms – see, e.g., [22], [24], [26]-[28]. This paper explores the crucial question of support recovery in the context of SCCA. ¹

The problem of support recovery for SCCA naturally connects to a vast class of variable selection problems (cf. [29]-[33]). The problem closest in terms of complexity turns out to be the sparse PCA (SPCA) problem [34]. Support recovery in the latter problem is known to present interesting information theoretic and computational bottlenecks (cf. [30], [35]-[37]). Moreover, information theoretic and computational issues also arise in context of SCCA estimation problem (cf. [24], [26]-[28]). In view of the above, it is natural to expect that such information theoretic and computational issues exist in context of SCCA support recovery problem as well. However, the techniques used in SPCA support recovery analysis are not directly applicable to the SCCA problem, which poses additional challenges due to the presence of high dimensional nuisance parameters ${\Sigma }_x$ and ${\Sigma }_y$. The main focus of our work is therefore retrieving the complete picture of the information theoretic and computational limitations of SCCA support recovery. Before going into further details, we present a brief summary of our contributions, and defer the discussions on the main subtleties to Section III. Our methods can be implemented using the R package Support.CCA [38].

A. Summary of Main Results

We say a method successfully recovers the support if it achieves exact recovery with probability tending to one uniformly over the sparse parameter spaces defined in Section II. In the sequel, we denote the cardinality of the combined support of the u_i’s and the v_i’s by s_x and s_y, respectively. Thus s_x and s_y will be our respective sparsity parameters. Our main contributions are listed below.

1). General methodology:

In Section III-A, we construct a general algorithm called RecoverSupp, which leads to successful support recovery whenever the latter is information theoretically tractable. This also serves as the first step in creating a polynomial time procedure for recovering support in one of the difficult regimes of the problem – see e,g. Corollary 2, which shows that RecoverSupp accompanied by a co-ordinate thresholding type method recovers the support in polynomial time in a regime that requires subtle analysis. Moreover, Theorem 1 shows that the minimal signal strength required by RecoverSupp matches the information theoretic limit whenever the nuisance precision matrices ${\Sigma }_x^{-1}$ and ${\Sigma }_y^{-1}$ are sufficiently sparse.

2). Information theoretic and computational hardness as a function of sparsity:

As the sparsity level increases, we show that the CCA support recovery problem transitions from being efficiently solvable, to NP hard (conjectured), and to information theoretically impossible. According to this hardness pattern, the sparsity domain can be partitioned into the following three regimes: (i) $s_x$, $s_y\lesssim \sqrt{n}$, $(\text{ii})\sqrt{n}\lesssim s_x$, $s_y\lesssim n∕\log (p+q)$, and (iii) $s_x$, $s_y\gtrsim n∕\log (p+q)$. We describe below the distinguishing behaviours of these three regimes, which is consistent with the sparse PCA scenario.

• We show that when $s_x$, $s_y\lesssim \sqrt{n∕\log (p+q)}$ (“easy regime”), polynomial time support recovery is possible, and well-known consistent estimators of the canonical correlates (cf. [24], [28]) can be utilized to that end. When $\sqrt{n∕\log (p+q)}\lesssim s_x$, $s_y\lesssim \sqrt{n}$ (“difficult regime”), we show that a co-ordinate thresholding type algorithm (inspired by [1]) succeeds provided $p+q\asymp n$. We call the last regime “difficult” because it is unknown whether existing estimation methods like COLAR [28] or SCCA [24] have valid statistical guarantees in this regime – see Section III-A and Section III-D for more details.

• In Section III-C, we show that when $\sqrt{n}\lesssim s_x$, $s_y\lesssim n∕\log (p+q)$ (“hard regime”), support recovery is computationally hard subject to the so called “low degree polynomial conjecture” recently popularized by [39], [40], and [2]. Of course, this phenomenon is observable only when p, $q\gtrsim n$, because otherwise, the problem would be solvable by the ordinary CCA analysis (cf. [23], [41]). Our findings are consistent with the conjectured computational barrier in context of SCCA estimation problem [28].

• When $s_x$, $s_y\gtrsim n∕\log (p+q)$, we show that support recovery is information theoretically impossible (see Section III-B).

3). Information theoretic hardness as a function of minimal signal strength:

In context of support recovery, the signal strength is quantified by

$${\text{Sig}}_x=\underset{k\in [p]}{\text{min}}\underset{i\in [r]}{\max }\mid (u_i{)}_k\mid \text{and}{\text{Sig}}_y=\underset{k\in [q]}{\text{min}}\underset{i\in [r]}{\max }\mid (v_i{)}_k\mid .$$

Generally, support recovery algorithms require the signal strength to lie above some threshold. As a concrete example, the detailed analyses provided in [1], [30], and [35] are all based on the nonzero principal component elements being of the order $\pm 1∕\sqrt{\text{sparsity}}$. To the best of our knowledge, prior to our work, there was no result in the PCA/CCA literature on the information theoretic limit of the minimal signal strength. Generally, PCA studies assume that the top eigenvectors are de-localized, i.e., the principal components have elements of the order $O(1∕\sqrt{s})$ and thereby mostly considered the cases of de-localized eigenvectors. We do not make any such assumption on the canonical covariates, and thereby we believe that our study paints a more complete picture of the support recovery.

• In Section III-B, we show that ${\text{Sig}}_x\gtrsim \sqrt{\log (p-s_x)∕n}$ (or ${\text{Sig}}_y\gtrsim \sqrt{\log (q-s_y)∕n}$) is a necessary requirement for successful support recovery by U (or V).

B. Notation

For a vector $x\in {\mathbb{R}}^p$, we denote its support by $D(x)=\{i:x_i\ne 0\}$. We will overload notation, and for a matrix $A\in {\mathbb{R}}^{p\times q}$, we will denote by D(A) the indexes of the nonzero rows of A. By an abuse of notation, sometimes we will refer to D(A) as the support of A as well. When $A\in {\mathbb{R}}^{p\times q}$ and $\alpha \in {\mathbb{R}}^p$ are unknown parameters, generally, the estimator of their supports will be denoted by $\widehat{D}(A)$ and $\widehat{D}(\alpha )$, respectively. We let $\mathbb{N}$ denote the set of all positive numbers, and write $\mathbb{Z}$ for the set of all natural numbers {0, 1, 2, … ,}. For any $n\in \mathbb{N}$, We let [n] denote the set {1, … , n}. We define the projection of A onto $D\subset [p]\times [q]$ by

$${\left({𝒫}_{{}_D}\{A\}\right)}_{i,j}=\{\begin{array}{cc}{A}_{i,j}\hfill & \text{if}(i,j)\in D,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}\phantom{\}}$$ (4)

For any finite set $𝒜$, we denote its cardinality by $\mid 𝒜\mid$. Also, for any event $ℬ$, we let $1\{ℬ\}$ be the indicator of the event $ℬ$. For any $p\in \mathbb{N}$, we let ${\mathbb{S}}^{p-1}$ denote the unit sphere in ${\mathbb{R}}^p$.

We let $\Vert \cdot {\Vert }_k$ be the usual l_k norm in ${\mathbb{R}}^k$ for $k\in \mathbb{Z}$. In particular, we let $\Vert x{\Vert }_0$ denote the number of nonzero elements of a vector $x\in {\mathbb{R}}^p$. For any probability measure $\mathbb{P}$ on the Borel sigma field of ${\mathbb{R}}^p$, we let $L_2(\mathbb{P})$ to be the set of all measurable functions $f:{\mathbb{R}}^p\mapsto \mathbb{R}$ such that $\Vert f{\Vert }_{L_2(\mathbb{P})}=\sqrt{\int f^{2}d\mathbb{P}}<\infty$. The corresponding $L_2(\mathbb{P})$ inner product will be denoted by $\langle \cdot ,\cdot {\rangle }_{L_2(\mathbb{P})}$. We denote the operator norm and the Frobenius norm of a matrix $A\in {\mathbb{R}}^{p\times q}$ by $\Vert A{\Vert }_{op}$ and $\Vert A{\Vert }_F$, respectively. We let A_i* and A_j denote the i-th row and j-th column of A, respectively. For $k\in \mathbb{N}$, we define the norms $\Vert A{\Vert }_{k,\infty }={\max }_{j\in [q]}\Vert A_j{\Vert }_k$ and $\Vert A{\Vert }_{\infty ,k}={\max }_{i\in [q]}\Vert A_{i\ast }{\Vert }_k$. The maximum and minimum eigenvalues of a square matrix A will be denoted by ${\Lambda }_{max}(A)$ and ${\Lambda }_{min}(A)$, respectively. Also, we let s(A) denote the maximum number of nonzero entries in any column of A, i.e., $s(A)={\max }_{j\in [q]}\Vert A_j{\Vert }_0$.

The results in this paper are mostly asymptotic (in n) in nature and thus require some standard asymptotic notations. If a_n and b_n are two sequences of real numbers then $a_n\gg b_n$ (and $a_n\ll b_n$) implies that $a_n∕b_n\to \infty$ (and $a_n∕b_n\to 0$) as $n\to \infty$, respectively. Similarly $a_n\gtrsim b_n$ (and $a_n\lesssim b_n$) implies that ${\text{lim inf}}_{n\to \infty }{a}_n∕b_n=C$ for some $C\in (0,\infty ]$ (and ${\text{lim sup}}_{n\to \infty }{a}_n∕b_n=C$ for some $C\in [0,\infty )$). Alternatively, $a_n=o(b_n)$ will also imply $a_n\ll b_n$ and $a_n=O(b_n)$ will imply that ${\text{lim sup}}_{n\to \infty }{a}_n∕b_n=C$ for some $C\in [0,\infty )$. We write $a_n\asymp b_n$ if there are positive constants C₁ and C₂ such that $C_1{b}_n\le a_n\le C_2{b}_n$ for all $n\in \mathbb{N}$. We will write $a_n=\tilde{\Phi }(b_n)$ to indicate a_n and b_n are asymptotically of the same order up to a poly-log term. Finally, in our mathematical statements, C and c will be two different generic constants which can vary from line to line.

II. Mathematical Formalism

We denote the rank of ${\Sigma }_{xy}$ by r. It can be shown that exactly r canonical correlations are positive and the rest are zero in the model (2). We will consider the matrices $U=[u_1,\dots ,u_r]$ and $V=[v_1,\dots ,v_r]$. From (2) and (3), it is not hard to see that $U^T{\Sigma }_{x}U=I_p$ and $V^T{\Sigma }_{y}V=I_q$. The indexes of the nonzero rows of U and V, respectively, are the combined support of the u_i’s and the v_i’s. Since we are interested in the recovery of the latter, it will be useful for us to study of the properties of U and V. To that end, we often make use of the following representation connecting ${\Sigma }_{xy}$ to U and V [16]:

$${\Sigma }_{xy}={\Sigma }_{x}U\Lambda V^T{\Sigma }_y={\Sigma }_x\left(\sum _{i=1}^r{\Lambda }_i{u}_i{v}_i^T\right){\Sigma }_y.$$ (5)

To keep our results straightforward, we restrict our attention to a particular model $𝒫(r,s_x,s_y,ℬ)$ throughout, defined as follows.

Definition 1. Suppose $(X,Y)\sim \mathbb{P}$. Let $ℬ>1$ be a constant. We say $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$ if

• A1(Sub-Gaussian) X and Y are sub-Gaussian random vectors (cf. [42]), with joint covariance matrix Σ as defined in (1). Also rank$({\Sigma }_{xy})=r$.
• A2Recall the definition of the canonical correlation ${\Lambda }_i’s$ from (3). Note that by definition, $0\le {\Lambda }_r\le \cdots \le {\Lambda }_1$. For $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$, ${\Lambda }_r$ additionally satisfies ${\Lambda }_r\ge 1∕ℬ$.
• A3(Sparsity) The number of nonzero rows of U and V are s_x and s_y, respectively, that is $s_x=\mid {\cup }_{i=1}^{r}D(u_i)\mid$ and $s_y=\mid {\cup }_{i=1}^{r}D(v_i)\mid$. Here U and V are as defined in (5).
• A4
  (Bounded eigenvalue)

  $$1∕ℬ<{\Lambda }_{min}({\Sigma }_y),{\Lambda }_{min}({\Sigma }_y),{\Lambda }_{max}({\Sigma }_x),{\Lambda }_{max}({\Sigma }_y)<ℬ.$$
• A5(Positive eigen-gap) ${\Lambda }_i-{\Lambda }_{i-1}\ge {ℬ}^{-1}$ for i = 2, … , r.

Sometimes we will consider a sub-model of $𝒫(r,s_x,s_y,ℬ)$ where each $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$ is Gaussian. This model will be denoted by ${𝒫}_G(r,s_x,s_y,ℬ)$, where “G” stands for the Gaussian assumption. Some remarks on the modeling assumptions A1—A5 are in order, which we provide next.

• A1.We begin by noting that we do not require X and Y to be jointly sub-Gaussian. Moreover, the individual sub-Gaussian assumption itself is common in the $s_x$, $s_y\lesssim \sqrt{n}∕\log (p+q)$ regime in the SCCA literature (cf. [24], [28], [43]). Our proof techniques depend crucially on the sub-Gaussian assumption. We also anticipate that the results derived in this paper will change under the violation of this assumption. For the sharper analysis in the difficult regime ($\sqrt{n∕\log (p+q)}\lesssim s_x$, $s_y\lesssim \sqrt{n}$), our proof techniques require the Gaussian model ${𝒫}_G$ – which is in parallel with [1]’s treatment of the sparse PCA in the corresponding difficult regime. In general, the Gaussian spiked model assumption in sparse PCA goes back to [44], and is common in the PCA literature (cf. [30], [35]).
• A2-A4.These assumptions are standard in the analysis of canonical correlations (cf. [24], [28]).
• A5.This assumption concerns the gap between consecutive canonical correlation strengths. However, we refer to this gap as “Eigengap” because of its similarity with the Eigengap in the sparse PCA literature (cf. [1], [45]). This assumption is necessary for the estimation of the i-th canonical covariates. Indeed, if ${\lambda }_i={\lambda }_{i+1}$ then there is no hope of estimating the i-th canonical covariates because they are not identifiable, and so support recovery also becomes infeasible. This assumption can be relaxed to requiring only k many λ_i’s to be strictly larger than ${\lambda }_{i-1}’\mathrm{s}$ where k ≤ r. In this case, we can recover the support of only the first k canonical covariates.

In the following sections, we will denote the preliminary estimators of U and V by $\widehat{U}$ and $\widehat{V}$, respectively. The columns of $\widehat{U}$ and $\widehat{V}$ will be denoted by ${\widehat{u}}_{n,i}$ and ${\widehat{v}}_{n,i}(i\in [r])$, respectively. Therefore ${\widehat{u}}_{n,i}$ and ${\widehat{v}}_{n,i}$ will stand for the corresponding preliminary estimators of u_i and v_i. In case of CCA, the u_i’s and v_i’s are identifiable only up to a sign flip. Hence, they are also estimable only up to a sign flip. Finally, we denote the empirical estimates of ${\Sigma }_x$, ${\Sigma }_y$, and ${\Sigma }_{xy}$, by ${\widehat{\Sigma }}_{n,x}$, ${\widehat{\Sigma }}_{n,y}$, and ${\widehat{\Sigma }}_{n,xy}$, respectively – which will often be appended with superscripts to denote their estimation through suitable subsamples of the data ². Finally, we let $C_{ℬ}$ denote a positive constant which depends on $\mathbb{P}$ only through $ℬ$, but can vary from line to line.

III. Main Results

We divide our main results into the following parts based on both statistical and computational difficulties of different regimes. First, in Section III-A we present a general method and associated sufficient conditions for support recovery. This allows us to elicit a sequence of questions regarding necessity of the conditions and remaining gaps both from statistical and computational perspectives. Our subsequent sections are devoted to answering these very questions. In particular, in Section III-B we discuss information theoretic lower bounds followed by evidence for statistical-computational gaps in Section III-C. Finally, we close a final computational gap in asymptotic regime through sharp analysis of a special co-ordinate-thresholding type method in Section III-D.

A. A Simple and General Method:

We begin with a simple method for estimating the support, which readily establishes the result for the easy regime, and sets the directions for the investigation into other more subtle regimes. Since the estimation of D(U) and D(V) are similar, we focus only on the estimation of D(V) for the time being.

Suppose $\widehat{V}$ is a row sparse estimator of V. The nonzero indexes of $\widehat{V}$ is the most intuitive estimator of D(V). Such an $\widehat{V}$ is also easily attainable because most estimators of the canonical directions in the high dimension are sparse (cf. [24], [26], [28] among others). Although we have not yet been able to show the validity of this apparently “naïve” method, we provide numerical results in Section IV to explore its finite sample performance. However, a simple method can refine these initial estimators, to often optimally recover the support D(V). We now provide the details of this method and derive its asymptotic properties.

To that end, suppose we have at our disposal an estimating procedure for ${\Sigma }_y^{-1}$, which we generically denote by ${\widehat{\Omega }}_n$ and an estimator $\widehat{U}\in {\mathbb{R}}^{p\times r}$ of U. We split the sample in two equal parts, and compute ${\widehat{U}}^{(1)}$ and ${\widehat{\Omega }}_n^{(1)}$ from the first part of the sample, and the estimator ${\widehat{\Sigma }}_{n,xy}^{(2)}$ from the second part of the sample. Define ${\widehat{V}}^{clean}={\widehat{\Omega }}_n^{(1)}{\widehat{\Sigma }}_{n,yx}^{(2)}{\widehat{U}}^{(1)}$. Our estimator of D(V) is then given by

$$\widehat{D}(V)≔\{i\in [q]:\mid {\widehat{V}}_{ik}^{clean}\mid >\text{cut for some}k\in [r]\},$$ (6)

where cut is a pre-specified cut-off or threshold. We will discuss more on cut later. The resulting algorithm will be referred as RecoverSupp from now on. Algorithm 1 gives the algorithm for the support recovery of V, but the full version of RecoverSupp, which estimates D(U) and D(V) simultaneously, can be found in Appendix A; see Algorithm 3 there. RecoverSupp is similar in spirit to the “cleaning” step in the sparse PCA support recovery literature (cf. [1]). One thing to remember here is that ${\widehat{V}}^{clean}$ is not an estimator V. In fact, the (i, j)-th element of ${\widehat{V}}^{clean}$ is an estimator of ${\Lambda }_i(v_i{)}_j$.

Remark 1. In many applications, the rank r may be unknown. [46] (see Section 4.6.5 therein) suggests to use the screeplot of the canonical correlations to estimate r. Screeplot is also a popular tool to estimate the number of nonzero principal components in PCA analysis [1]. For CCA, the screeplot is the plot of the estimated canonical correlations versus their orders. If there is a clear gap between two successive correlations, [46] suggests taking the larger correlation as the estimator of ${\Lambda }_r$. One can use [24]’s SCCA method to estimate the canonical correlations to obtain the screeplot. There can be other ways of estimating r. For example, in their trans-eQTL study, [47] uses a resampling technique on a holdout dataset to generate observations from the null distribution of the i-th canonical correlation estimate under the hypothesis $H_0:{\Lambda }_i=0$, where $i\in [\text{min}(p,q)]$. The largest i, for which the test is rejected, is taken as the estimated rank. A similar technique has been used by [48] to select the ranks for a related method JIVE.

Algorithm 1 RecoverSupp ${\widehat{U}}^{(1)},{\widehat{\Omega }}_n^{(1)},{\widehat{\Sigma }}_{n,xy}^{(2)},\text{cut},r$): sup-port recovery of V

$$\begin{array}{cc}\hfill & \mathrm{Input}:1)\text{Preliminary estimators}{\widehat{U}}^{(1)}\text{and}{\widehat{\Omega }}_n^{(1)}\text{of}U\text{and}\hfill \\ \hfill & {\Sigma }_y^{-1},\text{respectively},\text{based on sample}{O}_1=(x_i,y_i{)}_{i=1}^{[n∕2]}.\hfill \\ \hfill & 2)\text{Estimator}{\widehat{\Sigma }}_{n,xy}^{(2)}\text{of}{\Sigma }_{xy}\text{based}\text{on}\text{sample}{O}_2=\hfill \\ \hfill & (x_i,y_i{)}_{i=[n∕2]+1}^n.\hfill \\ \hfill & 3)\text{Threshold level}\text{cut}>0\text{and rank}r\in \mathbb{N}.\hfill \\ \hfill & \mathrm{Output}:\widehat{D}(V),\text{an estimator of}D(V).\hfill \\ \hfill & 1)\mathrm{Cleaning}:{\widehat{V}}^{clean}\leftarrow {\widehat{\Omega }}_n^{(1)}{\widehat{\Sigma }}_{n,yx}^{(2)}{\widehat{U}}^{(1)}.\hfill \\ \hfill & 2)\mathrm{Threshold}:\text{Compute}\widehat{D}(V)\text{as}\text{in}(6).\hfill \\ \hfill & \mathrm{return}:\widehat{D}(V).\hfill \end{array}$$

It turns out that, albeit being so simple, RecoverSupp has desirable statistical guarantees provided ${\widehat{U}}^{(1)}$ and ${\widehat{\Omega }}_n^{(1)}$ are reasonable estimators of U and ${\Sigma }_y^{-1}$, respectively. These theoretical properties of RecoverSupp, and the hypotheses and queries generated thereof, lay out the roadmap for the rest of our paper. However, before getting into the detailed theoretical analysis of RecoverSupp, we state a l₂-consistency condition on ${\widehat{u}}_{n,i}$ and ${\widehat{v}}_{n,i}’\mathrm{s}$, where we remind the readers that we let ${\widehat{u}}_{n,i}$ and ${\widehat{v}}_{n,i}$ denote the i-th columns of $\widehat{V}$ and $\widehat{U}$, respectively. Recall also that the i-th columns of U and V are denoted by u_i and v_i, respectively.

Condition 1 (l₂ consistency ). There exists a function $Err\equiv Err:(n,p,q,s_x,s_y,ℬ)\mapsto \mathbb{R}$ so that $\mid Err\mid <1∕(2ℬ\sqrt{r})$ and the estimators ${\widehat{u}}_{n,i}$ and ${\widehat{v}}_{n,i}$ of u_i and v_i satisfy

$$\underset{i\in [r]}{\max }\underset{w\in \{\pm 1\}}{\text{min}}\mid (w{\widehat{u}}_{n,i}-u_i{)}^T{\Sigma }_x(w{\widehat{u}}_{n,i}-u_i)\mid <Er{r}^2,$$

$$\underset{i\in \left[r\right]}{\max }\underset{w\in \{\pm 1\}}{\text{min}}\mid (w{\widehat{v}}_{n,i}-v_i{)}^T{\Sigma }_y(w{\widehat{v}}_{n,i}-v_i)\mid <Er{r}^2$$

with $\mathbb{P}$ probability 1 − o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$.

We will discuss the estimators which satisfy Condition 1 later. Theorem 1 also requires the signal strength Sig_y to be at least of the order ${ϵ}_n={\xi }_n\sqrt{\log (p+q)s({\Sigma }_y^{-1})∕n}$, where the parameter ${\xi }_n$ depends on the type of ${\widehat{\Omega }}_n$ as follows:

1. ${\widehat{\Omega }}_n$ is of type A if there exists C_pre > 0 so that ${\widehat{\Omega }}_n$ satisfies $\Vert {\widehat{\Omega }}_n-{\Sigma }_y^{-1}{\Vert }_{\infty ,1}\le C_{\text{pre}}s({\Sigma }_y^{-1})\sqrt{(\log q)∕n}$ with $\mathbb{P}$ probability 1 − o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$. Here we remind the readers that $s({\Sigma }_y^{-1})={\max }_{j\in [q]}\Vert ({\Sigma }_y^{-1}{)}_j{\Vert }_0$. In this case, ${\xi }_n=C_{\text{pre}}\sqrt{s({\Sigma }_y^{-1})}$.

2. ${\widehat{\Omega }}_n$ is of type B if $\Vert {\widehat{\Omega }}_n-{\Sigma }_y^{-1}{\Vert }_{\infty ,2}\le C_{\text{pre}}\sqrt{s({\Sigma }_y^{-1})\log (q)∕n}$ with $\mathbb{P}$ probability 1 − o(1) uniformly over $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$ for some C_pre > 0. In this case, ${\xi }_n=C_{\text{pre}}\max \{\sqrt{r(\log q)∕n},1\}$.

3. ${\widehat{\Omega }}_n$ is of type C if ${\widehat{\Omega }}_n={\Sigma }_y^{-1}$. In this case, ${\xi }_n=1$.

The estimation error of ${\widehat{\Omega }}_n$ clearly decays from type A to C, with the error being zero at type C. Because $\sqrt{r(\log q)∕n}$ is generally much smaller than $s({\Sigma }_y^{-1})$, ${\xi }_n$ shrinks from Case A to Case C monotonously as well. Thus it is fair to say that ${\xi }_n$ reflects the precision of the estimator ${\widehat{\Omega }}_n$ in that ${\xi }_n$ is smaller if ${\widehat{\Omega }}_n$ is a sharper estimator. We are now ready to state Theorem 1. This theorem is proved in Appendix C.

Theorem 1. Suppose $\log (p\vee q)=o(n)$ and the estimators ${\widehat{u}}_{n,i}’s$ satisfy Condition 1. Further suppose ${\widehat{\Omega }}_n$ is of type A, B, or C, which are stated above. Let ${ϵ}_n={\xi }_n\sqrt{\log (p+q)s({\Sigma }_y^{-1})∕n}$ where ${\xi }_n$ depends on the type of ${\widehat{\Omega }}_n$ as outlined above. Then there exists a constant $C_{ℬ}^{\prime }>0$, depending only on $ℬ>0$, so that if

$$Si{g}_y>2C_{ℬ}^{\prime }{∊}_n,$$ (7)

and $cut\in [C_{ℬ}^{\prime }{ϵ}_n∕(2ℬ)$, $({\theta }_n-1)C_{ℬ}^{\prime }{ϵ}_n∕(2ℬ)]$ with ${\theta }_n=Si{g}_y∕(C_{ℬ}^{\prime }{ϵ}_n)$, then the algorithm RecoverSupp fully recovers D(V) with $\mathbb{P}$ probability 1 − o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$ (for ${\widehat{\Omega }}_n$ of type A and C), or uniformly over $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$ (for ${\widehat{\Omega }}_n$ of type B).

The assumption that log p and log q are o(n) appears in all theoretical works of CCA (cf. [24], [28]). A requirement of this type is generally unavoidable. Note that Theorem 1 implies a more precise estimator ${\widehat{\Omega }}_n$ requires smaller signal strength for full support recovery.

Main idea behind the proof of Theorem 1:

Because ${\Lambda }_i(v_i{)}_k=e_k^T{\Sigma }_y^{-1}{\Sigma }_{yx}{u}_i$, ${\widehat{V}}_{ik}^{clean}$ is an estimator of ${\Lambda }_i(v_i{)}_k$ for $i\in [q]$ and $k\in [r]$. If $k\notin D(V)$, then $(v_i{)}_k=0$ for all $i\in [r]$. Therefore, in this case, we expect ${\widehat{V}}_{ik}^{clean}$ to be small for all $i\in [q]$. We will show that whenever $k\notin D(V)$, $\mid {\widehat{V}}_{ik}^{clean}\mid$ is uniformly bounded by $C_1{ϵ}_n$ for $i\in [q]$ and $k\in [r]$ with high probability. Here $C_1>0$ is a constant. Second, when $(v_i{)}_k\ne 0$, we will show that ${\max }_{i\in [r]}\mid {\widehat{V}}_{ik}^{clean}\mid$ can not be too small. In fact, we will show that

$$\underset{i\in [r]}{\max }\mid {\widehat{V}}_{ik}^{clean}\mid >C_2\underset{i\in [r]}{\max }\mid {\Lambda }_i(v_i{)}_k\mid -C_1{ϵ}_n,k\in [r]$$ (8)

for some $C_2>0$ with high probability in this case. The lower bound in the above inequality is bounded below by $C_2{\text{Sig}}_y-C_1{ϵ}_n$. Thus, if the minimal signal strength Sig_y is bounded below by a large enough multiple of ϵ_n, then the lower bound $C_2{\text{Sig}}_y-C_1{ϵ}_n$ will be larger than the upper bound $C_1{ϵ}_n$ in the $k\notin D(V)$ case. Therefore, in this scenario, we can choose C > 0 so that

$$C_1{ϵ}_n<C{ϵ}_n<C_2{\text{Sig}}_y-C_1{ϵ}_n.$$

If we set $\text{cut}=C{ϵ}_n$, then the above inequality leads to.

$$\underset{i\notin D(V)}{\text{sup}}\mid {\widehat{V}}_{ik}^{clean}\mid <\text{cut}<\underset{i\in D(V)}{\text{inf}}\mid {\widehat{V}}_{ik}^{clean}\mid .$$

These C₁ and C₂ are behind the constant $C_{ℬ}^{\prime }$ in (7) and our choice of θ_n.

Thus the key step in the proof of Theorem 1 is analyzing the bias of ${\widehat{V}}_{ik}^{clean}$, which hinges on the following bias decomposition:

$$\begin{gathered} \mid {\widehat{V}}_{ik}^{clean}-{\Lambda }_i(v_i{)}_k\mid \le \underset{T_1(i,k)}{\underbrace{\mid e_k^T({\widehat{\Omega }}_n-{\Phi }_0){\widehat{\Sigma }}_{n,yx}{\widehat{u}}_{n,i}\mid }} \\ +\underset{T_2(i,k)}{\underbrace{\mid e_k^T{\Phi }_0({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}\mid }}+\underset{T_3(i,k)}{\underbrace{\mid e_k^T{\Phi }_0{\Sigma }_{yx}({\widehat{u}}_{n,i}-u_i)\mid }}. \end{gathered}$$ (9)

Note that the term $T_1(i,k)$ corresponds to the bias in estimating ${\Phi }_0$. Similarly, the error terms $T_2(i,k)$ and $T_3(i,k)$ incur due to the bias in estimating ${\Sigma }_{yx}$ and u_i, respectively. The main contributing term in the upper bound in (9) is $T_1(i,k)$. One can use the consistency property of ${\widehat{\Omega }}_n$ to show that $T_1(i,k)$ is of the order $O_p({ϵ}_n)$. Since ${\widehat{\Omega }}_n$ has different rates and modes of convergence in cases A, B, and C, $T_1(i,k)$ has different orders in cases A, B, and C, which explains why ϵ_n is of different order in these cases.

The term $T_2(i,k)$ is much smaller – it is of the order $(s({\Sigma }_x^{-1})\log (p+q))∕n{)}^{1∕2}$. The proof bases on the fact that the l_∞ error of estimating ${\Sigma }_{xy}$ by ${\widehat{\Sigma }}_{n,xy}$ is of the order $(\log (p+q)∕n{)}^{1∕2}$ for subgaussian X and Y. The error term $T_3(i,k)$ is exactly zero for $i\notin D(V)$, and hence does not contribute. Thus only $T_1(i,k)$ and $T_2(i,k)$ contribute to the bias of ${\widehat{V}}_{ik}^{clean}$ for $i\notin D(V)$, which is therefore bounded by $C_1{ϵ}_n$ for some C₁ > 0 with high probability in this case. The term $T_3(i,k)$ does contribute to the bias of ${\widehat{V}}_{ik}^{clean}$ for $i\in D(V)$, however, and it is of the order $\sqrt{r}{\max }_{j\in [r]}\mid (v_j{)}_k\mid \text{Err}$ in this case. Because Err is small by Condition 1, we can show that $T_3(i,k)$ is smaller than ${\max }_{i\in [r]}{\Lambda }_i\mid (v_i{)}_k\mid$, which eventually leads to the relation in (8), thus completing the proof. We have already mentioned that RecoverSupp is analogous to the cleaning step in sparse PCA. Therefore the proof of Theorem 1 has similarities with some analogous results in sparse PCA. See for example Theorem 3 of [1], which proves the consistency of a “cleaned” estimator of the joint support of the spiked principal components. However, the proof in the CCA case is a bit more involved because of the presence of ${\Sigma }_y^{-1}$, which needs to be estimated for the cleaning step. Different estimators of ${\Sigma }_y^{-1}$ can have different rates of convergence, which leads to the different types of the estimators. This ultimately leads to different requirements on the order of the threshold cut and the minimal signal strength Sig_y.

Next we will discuss the implications of Theorem 1, but before getting into that detail, we will make two important remarks.

Remark 2. Although the estimation of the high dimensional precision matrix ${\Sigma }_y^{-1}$ is potentially complicated, it is often unavoidable owing to the inherent subtlety of the CCA framework due to the presence of high dimensional nuisance parameters ${\Sigma }_x$ and ${\Sigma }_y$. [26] also used precision matrix estimator for partial recovery of the support. In case of sparse CCA, to the best of our knowledge, there does not exist an algorithm that can recover the support, partially or completely, without estimating the precision matrix. However, our requirements on ${\widehat{\Omega }}_n$ are not strict in that many common precision matrix estimators, e.g., the nodewise Lasso [49, Theorem 2.4], the thresholding estimator [50, Theorem 1 and Section 2.3], and the CLIME estimator [51, Theorem 6] exhibit the decay rate of type A and B under standard sparsity assumptions on ${\Sigma }_y^{-1}$. We will not get into the detail of the sparsity requirements on ${\Sigma }_y^{-1}$ because they are unrelated to the sparsity of U or V, and hence are irrelevant to the primary goal of the current paper.

Remark 3. In the easy regime $s_y\lesssim \sqrt{n∕(\log (p+q)}$, polynomial time estimators satisfying Condition 1 are already available, e.g., COLAR [28, Theorem 4.2] or SCCA [24, Condition C4]. Thus it is easily seen that polynomial time support recovery is possible in the easy regime provided (7) is satisfied.

The implications of Theorem 1 in context of the sparsity requirements on D(U) and D(V) for full support recovery are somewhat implicit through the assumptions and conditions. However, the restriction on the sparsity is indirectly imposed by two different sources – which we elaborate on now. To keep the interpretations simple, throughout the following discussion, we assume that (a) $r=O(n∕\log q)$, (b) p and q are of the same order, and (c) s_x and s_y are also of the same order. Note that (a) implies ${\xi }_n=O(1)$ for a type B estimator of ${\widehat{\Omega }}_n$. Since we separate the task of estimating the nuisance parameter ${\Sigma }_y^{-1}$ from the support recovery of V, we also assume that $s({\Sigma }_y^{-1})=O(1)$, which implies ${\xi }_n=O(1)$ for a type A estimator of ${\widehat{\Omega }}_n$. The assumption $s({\Sigma }_y^{-1})=O(1)$, combined with (a), reduces the minimal signal strength condition (7) in Theorem 1 to ${\text{Sig}}_y\ge C_{ℬ}\sqrt{\log (p+q)∕n}$.

In lieu of the discussion above, the first source of sparsity restriction is the minimal signal strength condition (7) on Sig_y. To see this, first note that

$$1=v_i^T{\Sigma }_y{v}_i\ge {\Lambda }_{min}({\Sigma }_y)\Vert v_i{\Vert }_2^2$$

where $i\in [r]$. Since ${\Lambda }_{min}({\Sigma }_y)\ge {ℬ}^{-1}$,

$${\Lambda }_{min}({\Sigma }_y)\Vert v_i{\Vert }_2^2\ge \Vert v_i{\Vert }_2^2∕ℬ\ge {\text{Sig}}_y^2{s}_y∕ℬ,$$

implying ${\text{Sig}}_y\le \sqrt{ℬ}{s}_y^{-1∕2}$. Therefore, implicit in Theorem 1 lies the condition

$$s_y\le \frac{C_{ℬ}^{2}n}{\log (p+q)},$$ (10)

which is enforced by the minimal signal strength requirement (7). Thus Theorem 1 does not hold for $s_y\gg n∕\log (p+q)$ even when $s({\Sigma }_y^{-1})$ and r are small. This regime requires some attention because in case of sparse PCA [30] and linear regression [29], support recovery at $s\gg n∕\log (p-s)$ ³ is proven to be information theoretically impossible. However, although a parallel result can be intuited to hold for CCA, the details of the nuances of SCCA support recovery in this regime is yet to be explored. Therefore, the sparsity requirement in (10) raises the question whether support recovery for CCA is at all possible when $s_y\gg n∕\log (p+q)$, even if ${\Sigma }_x$ and ${\Sigma }_y$ is known.

Question 1. Does there exist any decoder $\widehat{D}$ such that ${\text{sup}}_{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}\mathbb{P}(\widehat{D}(V)\ne D(V))\to 0$ when $s_y\gg n∕\log (q-s_y)$?

A related question is whether the minimal signal strength requirement (7) is necessary. To the best of our knowledge, there is no formal study on the information theoretic limit of the minimal signal strength even in context of the sparse PCA support recovery. Indeed, as we noted before, the detailed analyses of support recovery for SPCA provided in [1], [30], and [35] are all based on the nonzero principal component elements being of the order $O(1∕\sqrt{s})$. Finally, although this question is not directly related to the sparsity conditions, it indeed probes the sharpness of the results in Theorem 1.

Question 2. What is the minimum signal strength required for the recovery of D(V)?

We will discuss Question 1 and Question 2 at greater length in Section III-B. In particular, Theorem 2(A) shows that there exists C > 0 so that support recovery at $s_y\ge C{ℬ}^{-2}n∕\log (q-s_y)$ is indeed information theoretically intractable. On the other hand, in Theorem 2(B), we show that the minimal signal strength has to be of the order $ℬ\sqrt{\log (q-s_y)∕n}$ for full recovery of D(V). Thus when $p\asymp q$, (7) is indeed necessary from information theoretic perspectives.

The second source of restriction on the sparsity lies in Condition 1. Condition 1 is a l₂-consistency condition, which has sparsity requirement itself owing the inherent hardness in the estimation of U. Indeed, Theorem 3.3 of [28] entails that it is impossible to estimate the canonical directions u_i’s consistently if $s_x>Cn∕(r+\log (ep∕s_x))$ for some large C > 0. Hence, Condition 1 indirectly imposes the restriction $s_x\lesssim n∕\max \{\log (p∕s_x),r\}$. However, when $s_x\asymp s_y$, $p\asymp q$, and $r=O(1)$, the above restriction is already absorbed into the condition $s_y\lesssim n∕\log (q-s_y)$ elicited in the last paragraph. In fact, there exist consistent estimators of U whenever $s_x\lesssim n∕\max \{\log (p∕s_x),r\}$ and $s_y\lesssim n∕\max \{\log (q∕s_y),r\}$ (see [27] or Section 3 of [28]). Therefore, in the latter regime, RecoverSupp coupled with the above-mentioned estimators succeeds. In view of the above, it might be tempting to think that Condition 1 does not impose significant additional restrictions. The restriction due to Condition 1, however, is rather subtle and manifests itself through computational challenges. Note that when support recovery is information theoretically possible, the computational hardness of recovery by RecoverSupp will be at least as much as that of the estimation of U. Indeed, the estimators of U which work in the regime $s_x\asymp n∕\log (p∕s_x)$, $s_y\asymp n∕\log (q∕s_y)$ are not adaptive of the sparsity, and they require a search over exponentially many sets of size s_x and s_y. Furthermore, under $𝒫(r,s_x,s_y,ℬ)$, all polynomial time consistent estimators of U in the literature, e.g., COLAR [28, Theorem 4.2] or SCCA [24, Condition C4], require s_x, s_y to be of the order $\sqrt{n∕\log (p+q)}$. In fact, [28] indicates that estimation of U or V for sparsity of larger order is NP hard.

The above raises the question whether RecoverSupp (or any method as such) can succeed at polynomial time when $\sqrt{n∕\log (p+q)}\ll s_x$, $s_y\lesssim n∕\log (p+q)$. We turn to the landscape of sparse PCA for intuition. Indeed, in case of sparse PCA, different scenarios are observed in the regime $s\lesssim n∕\log p$, depending on whether $\sqrt{n}\ll s\lesssim n∕\log p$, or $s\lesssim \sqrt{n}$ (we recall that for SPCA we denote the sparsity of the leading principal component direction generically through s). We focus on the sub-regime $\sqrt{n}\ll s\lesssim n∕\log p$ first. In this case, both estimation and support recovery for sparse PCA are conjectured to be NP hard, which means no polynomial time method succeeds; see Section III-C for more details. The above hints that the regime $s_x$, $s_y\gg \sqrt{n}$ is NP hard for sparse CCA as well.

Question 3. Is there any polynomial time method that can recover the support D(V) when $s_x$, $s_y\gg \sqrt{n}$?

We dedicate Section III-C to answering this question. Subject to the recent advances in the low degree polynomial conjecture, we establish computational hardness of the regime $s_x$, $s_y\gg \sqrt{n}$ (up to a logarithmic factor gap) subject to $n\lesssim p$, q. Our results are consistent with [28]’s findings in the estimation case and cover a broader regime; see Remark 5 for a comparison.

When the sparsity is of the order $\sqrt{n}$ and $p\asymp n$, however, polynomial time support recovery and estimation are possible for the sparse PCA case. [1] showed that a co-ordinate thresholding type spectral algorithm works in this regime. Thus the following question is immediate.

Question 4. Is there any polynomial time method that can recover the support D(V) when $s_x$, $s_y\in [\sqrt{n∕\log (p+q)},\sqrt{n}]$?

We give an affirmative answer to Question 4 in Section III-D, which is in parallel with the observations for the sparse PCA. In fact, Corollary 2 shows that when ${\Sigma }_x$ and ${\Sigma }_y$ are known, $p+q\asymp n$, and $s_x$, $s_y\lesssim \sqrt{n}$, estimation is possible in polynomial time. Since estimation is possible, RecoverSupp suffices for polynomial time support recovery in this regime, where $\sqrt{n}$ is well below the information theoretic limit of $n∕\log (p+q)$. The main tool used in Section III-D is co-ordinate thresholding, which is originally a method for high dimensional matrix estimation [50], and apparently has nothing to do with estimation of canonical directions. However, under our setup, if the covariance matrix is consistently estimated in operator norm, by Wedin’s Sin θ Theorem [52], an SVD is enough to get a consistent estimator of U and V suitable for further precise analysis.

Remark 4. RecoverSupp uses sample splitting, which can reduce the efficiency. One can swap between the samples and compute two estimators of the supports. One can easily show that both the intersection and the union of the resulting supports enjoy the asymptotic guarantees of Theorem 1.

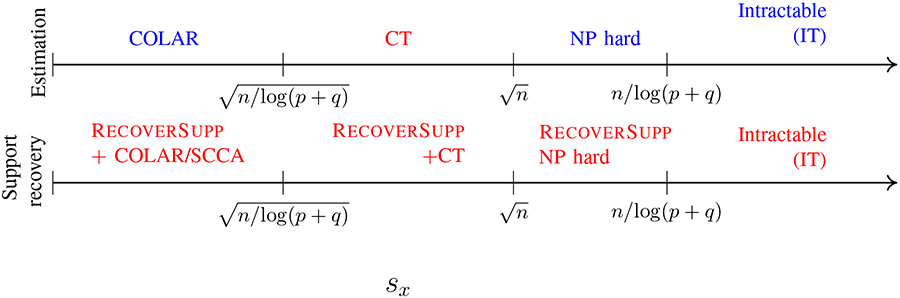
This section can be best summarized by Figure 1, which gives the information theoretic and computational landscape of sparse CCA analysis in terms of the sparsity. In other words, Figure 1 gives the phase transition plot for SCCA support recovery with respect to sparsity. It can be seen that our contributions (colored in red) complete the picture, which was initiated by [28].

Fig. 1:

Phase transition plots for SCCA estimation and support recovery problems with respect to sparsity. We have taken $s_x=s_y$ here. COLAR corresponds to the estimation method of [28]. Our contributions are colored in red. See [28] for more details on the regions colored in blue.

B. Information Theoretic Lower Bounds: Answers to Question 1 and 2

Theorem 2 establishes the information theoretic limits on the sparsity levels s_x, s_y, and the signal strengths Sig_x and Sig_y. The proof of Theorem 2 is deferred to Appendix D.

Theorem 2. Suppose $\widehat{D}(U)$ and $\widehat{D}(V)$ are estimators of D(U) and D(V), respectively. Let s_x, s_y > 1, and $p-s_x$, $q-s_y>16$. Then the following assertions hold:

1. If $s_x>16n∕\{({ℬ}^2-1)\log (p-s_x)\}$, then

   $$\underset{\widehat{D}}{\text{inf}}\underset{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}{\text{sup}}\mathbb{P}\left(\widehat{D}(U)\ne D(U)\right)>1∕2.$$
   On the other hand, if $s_y>16n∕\{({ℬ}^2-1)\log (q-s_y)\}$, then

   $$\underset{\widehat{D}}{\text{inf}}\underset{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}{\text{sup}}\mathbb{P}\left(\widehat{D}(V)\ne D(V)\right)>1∕2.$$
2. Let ${𝒫}_{Sig}(r,s_x,s_y,ℬ)$ be the class of distributions $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$ satisfying $Si{g}_x^2\le ({ℬ}^2-1)(\log (p-s_x))∕(8n)$. Then

   $$\underset{\widehat{D}}{\text{inf}}\underset{\mathbb{P}\in {𝒫}_{Sig}(r,s_x,s_y,ℬ)}{\text{sup}}\mathbb{P}\left(\widehat{D}(U)\ne D(U)\right)>1∕2.$$
   On the other hand, if $Si{g}_y^2\le ({ℬ}^2-1)(\log (q-s_y))∕(8n)$, Then

   $$\underset{\widehat{D}}{\text{inf}}\underset{\mathbb{P}\in {𝒫}_{Sig}(r,s_x,s_y,ℬ)}{\text{sup}}\mathbb{P}\left(\widehat{D}(V)\ne D(V)\right)>1∕2.$$

In both cases, the infimum is over all possible decoders $\widehat{D}(U)$ and $\widehat{D}(V)$.

First, we discuss the implications of part A of Theorem 2. This part entails that for full support recovery of V, the minimum sample size requirement is of the order $s_y\log (q-s_y)$. This requirement is consistent with the traditional lower bound on n in context of support recovery for sparse PCA [30, Theorem 3] and L₁ regression [29, Corollary 1]. However, when $r=O(1)$, the sample size requirement for estimation of V is slightly relaxed, that is, $n\gg s_y\log (q∕s_y)$ [28, Theorem 3.2]. Therefore, from information theoretic point of view, the task of full support recovery appears to be slightly harder than the task of estimation. The scenario for partial support recovery might be different and we do not pursue it here. Moreover, as mentioned earlier, in the regime $s_y\lesssim C_{ℬ}n∕\log (p+q)$, RecoverSupp works with [28]’s (see Section 3 therein) estimator of U. Thus part A of Theorem 2 implies that $n∕\log (p+q)$ is the information theoretic upper bound on the sparsity for the full support recovery of sparse CCA.

Part B of Theorem 2 implies that it is not possible to push the minimum signal strength below the level $O(\sqrt{\log (q-s_y)∕n})$. Thus the minimal signal strength requirement (7) by Theorem 1 is indeed minimal up to a factor of ${\xi }_n\sqrt{s({\Sigma }_y^{-1})}$. The last statement can be refined further. To that end, we remind the readers that for a good estimator of ${\Sigma }_y^{-1}$, i.e., a type B estimator, ${\xi }_n=O(1)$ if $r=O(n∕\log q)$. However, the latter always holds if support recovery is at all possible, because in that case $s_y\lesssim n∕\log (p+q)$, and elementary linear algebra gives $s_y\ge r$. Thus, it is fair to say that, provided a good estimator of ${\Sigma }_y^{-1}$, the requirement (7) is minimal up to a factor of $\sqrt{s({\Sigma }_y^{-1})}$. Indeed, this implies that for banded inverses with finite band-width our results are rate optimal.

It is further worth comparing this part of the result to the SPCA literature. In the SPCA support recovery literature, generally, the lower bound on the signal strength is depicted in terms of the sparsity s, and usually a signal strength of order $O(1∕\sqrt{s})$ is postulated (cf. [1], [30], [35]). Using our proof strategies, it can be easily shown that for SPCA, the analogous lower bound on the signal strength would be $\sqrt{\log (p-s)∕n}$. The latter is generally much smaller than $1∕\sqrt{s}$ and only when $s\asymp n∕\log (p)$, the requirement of $1∕\sqrt{s}$ close to the lower bound. Thus, in the regime $s\lesssim \sqrt{n∕\log p}$, the lower bound should rather be of the order $O(1∕s)$. Therefore the minimum signal strength requirement of $O(1∕\sqrt{s})$ typically assumed in SPCA literature seems larger than necessary.

Main idea behind the proof of Theorem 2:

The main device used in this proof is Fano’s inequality [53]. Note that for any $𝒞\subset 𝒫(r,s_x,s_y,ℬ)$,

$$\underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in 𝒞}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right)<\underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right).$$ (11)

Therefore it suffices to show that the left hand side in the above inequality is bounded away from 1/2 for some carefully chosen $𝒞$. If $𝒞$ is finite, we can lower bound the left hand side of (11) using Fano’s inequality [53], which yields

$$\underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in 𝒞}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right)\ge 1-\frac{\frac{{\sum }_{{\mathbb{P}}_1,{\mathbb{P}}_2\in c}KL({\mathbb{P}}_1^n\mid {\mathbb{P}}_2^n)}{\mid 𝒞{\mid }^2}+\log 2}{\log (\mid 𝒞\mid -1)},$$ (12)

Thus the main task is to choose $𝒞$ in a way so that the right hand side (RHS) of (12) is large. We will choose $𝒞$ so that X and Y are jointly Gaussian. In particular, $X\sim N_p(0,I_p)$, $Y\sim N_q(0,I_q)$, and ${\Sigma }_{xy}=\rho {\beta }_0{\alpha }^T$ where ${\beta }_0\in {\mathbb{S}}^{q-1}$ and $\rho \in (0,1)$ are fixed, and α is allowed to vary in a set $ℰ\subset {\mathbb{S}}^{p-1}$. In this model, r = 1, ρ is the canonical correlation, and α and β₀ are the left and right canonical covariates, respectively. Also, $\mathbb{P}$ varies across $𝒞$ as α varies across $ℰ$. Moreover, $\mid 𝒞\mid =\mid ℰ\mid$. Our main task boils down to choosing $ℰ$ carefully.

The idea behind choosing $ℰ$ is as follows. For any decoder, i.e., an estimator of the support, the chance of making error increases when $\mid ℰ\mid$ is large. This can also be seen noting that the right hand side of (12) increases as $\mid ℰ\mid =\mid 𝒞\mid$ increases. However, even if we prefer a larger $ℰ$, we need to ensure that the KL divergence between the distributions in the resulting $𝒞$ is small. The reason is that, for a large $ℰ$, the right hand side of (12) can be small unless the KL divergence between the corresponding distributions in $𝒞$ is small. In other words, any decoder will face a challenge detecting the true support of α when there are many distributions to choose from, and these distributions are also close to each other in KL distance.

For part A of Theorem 2, we choose $ℰ$ in the following way. Letting

$${\alpha }_0=(\underset{s_x\text{many}}{\underbrace{1∕{\sqrt{s}}_x,\dots ,1∕{\sqrt{s}}_x}},\underset{p-s_x\text{many}}{\underbrace{0,\dots ,0}}),$$

we let $ℰ$ be the class of α’s which are obtained by replacing one of the $1∕{\sqrt{s}}_x’\mathrm{s}$ in α₀ by 0, and one of the zero’s in α₀ by $1∕{\sqrt{s}}_x$. A typical α obtained this way looks like

$$\alpha =\left(\underset{s_x\text{many}}{\underbrace{1∕{\sqrt{s}}_x,\dots ,0,\dots 1∕{\sqrt{s}}_x}},\underset{p-s_x\text{many}}{\underbrace{0,\dots ,1∕\sqrt{{\mathrm{s}}_{\mathrm{x}}},\dots ,0}}\right).$$

In this case, it turns out that $\mid ℰ\mid =s_x(p-s_x)$. Under the conditions of part A of 2, we can show that the RHS of (12) is bounded below by 1/2 for this $ℰ$. The proof of part A is similar to its PCA analogue, which is Theorem 3 of [30]. The latter theorem is also based on Fano’s lemma and uses a similar construction for $ℰ$. However, there is no PCA analogue of part B. For part B of Theorem 2, we let $ℰ$ be the class of all α’s so that

$$\alpha =\left(\underset{s_x-1\text{many}}{\underbrace{b,\dots ,b}},\underset{p-s_x+1\text{many}}{\underbrace{0,\dots ,0,z,0,\dots ,0}}\right).$$

where

$$z=\sqrt{\frac{1-{\rho }^2}{4n{\rho }^2}}\log \left(\frac{p-s_x}{4}\right)$$

can take any position out of the $p-s_x+1$ positions. Clearly, $\mid ℰ\mid =p-s_x+1$. It can be shown that the RHS of (12) is bounded below by 1/2 in this case as well.

C. Computational Limits and Low Degree Polynomials: Answer to Question 3

We have so far explored the information theoretic upper and lower bounds for recovering the true support of leading canonical correlation directions. However, as indicated in the discussion preceding Question 3, the statistically optimal procedures in the regime where $\sqrt{n}\lesssim s_x$, $s_y\lesssim n∕\log (p+q)$ are computationally intensive and is of exponential complexity (as a function of p, q). In particular, [28] have already showed that when s_x and s_y belong to parts of this regime, estimation of the canonical correlates is computationally hard, subject to a computational complexity based Planted Clique Conjecture. For the case of support recovery, the SPCA has been explored in detail and the corresponding computational hardness has been established in analogous regimes – see, e.g., [1], [30], and [35] for details. A similar phenomenon of computational hardness is observed in case of SPCA spike detection problem [54]. In light of the above, it is natural to believe that the SCCA support recovery is also computationally hard in the regime $\sqrt{n}\lesssim s_x$, $s_y\lesssim n∕\log (p+q)$, and, as a result, yields a statistical-computational gap. Although several paths exist to provide evidence towards such gaps ⁴, the recent developments using “Predictions from Low Degree Polynomials” [2], [39], [40] is particularly appealing due its simplicity in exposition. In order to show computationally hardness of the SCCA support recovery problem in the $s_x$, $s_y\in (\sqrt{n},n∕\log (p+q))$ regime, we shall resort to this very style of ideas, which has so far been applied successfully to explore statistical-computational gaps under sparse PCA [36], Stochastic Block Models, and tensor PCA [40], among others. This will allow us to explore the computational hardness of the problem in the entire regime where

$$s_x+s_y\gtrsim (\sqrt{n})(\log n{)}^c,$$ (13)

compared to the somewhat partial results (see Remark 5 for detailed comparison) in earlier literature.

We divide our discussions to argue the existence of a statistical-computational gap in this regime as follows. Starting with a brief background on the statistical literature on such gaps, we first present a natural reduction of our problem to a suitable hypothesis testing problem in Section III-C1. Subsequently, in Section III-C2 we present the main idea of the “low degree polynomial conjecture” by appealing to the recent developments in [39], [40], and [2]. Finally, we present our main result for this regime in Section III-C3, thereby providing evidence of the aforementioned gap modulo the Low Degree Polynomial Conjecture presented in Conjecture 1.

1). Reduction to Testing Problem::

Denote by ${\mathbb{Q}}_n$ the distribution of a $N_{p+q}(0,I_{p+q})$ random vector. Therefore $(X,Y)\sim \mathbb{Q}$ corresponds to the case when X and Y are uncorrelated. We first show that there is any scope of support recovery in $𝒫(r,s_x,s_y,ℬ)$ only if $𝒫(r,s_x,s_y,ℬ)$ is distinguishable from $\mathbb{Q}$, i.e., the test $H_0:(X,Y)\sim \mathbb{Q}$ vs. $H_1:(X,Y)\sim \mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$ has asymptotic zero error.

To formalize the ideas, suppose we observe i.i.d random vectors $\{X_i,Y_i{\}}_{i=1}^n$ which are distributed either as $\mathbb{P}$ or $\mathbb{Q}$. We denote the n-fold product measures corresponding to $\mathbb{P}$ and $\mathbb{Q}$ by ${\mathbb{P}}_n$ and ${\mathbb{Q}}_n$, respectively. Note that if $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$, then ${\mathbb{P}}_n\in 𝒫(r,s_x,s_y,ℬ{)}^n$. We overload notation, and denote the combined sample $\{X_i{\}}_{i=1}^n$ and $\{Y_i{\}}_{i=1}^n$ by X and Y respectively. In this section, X and Y should be viewed as unordered sets. The test ${\Phi }_n:{\mathbb{R}}^{pn+qn}\mapsto \{0,1\}$ for testing the null $H_0:(\mathbf{X},\mathbf{Y})\sim {\mathbb{Q}}_n$ vs. the alternative $H_1:(\mathbf{X},\mathbf{Y})\sim {\mathbb{P}}_n$ is said to strongly distinguish ${\mathbb{P}}_n$ and ${\mathbb{Q}}_n$ if

$$\underset{n}{\text{lim}}{\mathbb{Q}}_n({\Phi }_n(\mathbf{X},\mathbf{Y})=1)+\underset{n}{\text{lim}}{\mathbb{P}}_n({\Phi }_n(\mathbf{X},\mathbf{Y})=0)=0.$$

The above implies that both the type I error and the type II error of Φ_n converges to zero as $n\to \infty$. In case of composite alternative $H_1:(\mathbf{X},\mathbf{Y})\sim {\mathbb{P}}_n\in 𝒫(r,s_x,s_y,ℬ{)}^n$, the test strongly distinguishes ${\mathbb{Q}}_n$ from $𝒫(r,s_x,s_y,ℬ{)}^n$ if

$$\begin{gathered} \underset{n\to \infty }{\text{lim}\text{inf}}\{{\mathbb{Q}}_n({\Phi }_n(\mathbf{X},\mathbf{Y})=1)\phantom{\}} \\ +\phantom{\{}\underset{{\mathbb{P}}_n\in 𝒫(r,s_x,s_y,ℬ{)}^n}{\text{sup}}{\mathbb{P}}_n({\Phi }_n(\mathbf{X},\mathbf{Y})=0)\}=0. \end{gathered}$$

Now we explain how support recovery and the testing framework are connected. Suppose there exist decoders which exactly recover D(U) and D(V) under $𝒫(r,s_x,s_y,ℬ)$ for $ℬ\ge 0$. Then the trivial test, which rejects the null if either of the estimated supports is non-empty, strongly distinguishes ${\mathbb{Q}}_n$ from $𝒫(r,s_x,s_y,ℬ{)}^n$. The above can be coined as the following lemma.

Lemma 1. Suppose there exist polynomial time decoders ${\widehat{D}}_x$ and ${\widehat{D}}_y$ of D(U) and D(V) so that

$$\begin{gathered} \underset{n\to \infty }{\text{lim}\text{inf}}\underset{{\mathbb{P}}_n\in 𝒫(r,s_x,s_y,ℬ{)}^n}{\text{sup}}{\mathbb{P}}_n({\widehat{D}}_x(\mathbf{X},\mathbf{Y})=D(U)\phantom{)} \\ and\phantom{(}{\widehat{D}}_y(\mathbf{X},\mathbf{Y})=D(V))=1 \end{gathered}$$ (14)

Further assume, ${\mathbb{Q}}_n({\widehat{D}}_x(\mathbf{X},\mathbf{Y})=\varnothing )\to 1$, and ${\mathbb{Q}}_n({\widehat{D}}_y(\mathbf{X},\mathbf{Y})=\varnothing )\to 1$. Then there exists a polynomial time test which strongly distinguishes $𝒫(r,s_x,s_y,ℬ{)}^n$ and ${\mathbb{Q}}_n$.

Thus, if a regime does not allow any polynomial time test for distinguishing ${\mathbb{Q}}_n$ from $𝒫(r,s_x,s_y,ℬ{)}^n$, there can be no polynomial time computable consistent decoder for D(U) and D(V). Therefore, it suffices to show that there is no polynomial time test which distinguishes ${\mathbb{Q}}_n$ from $𝒫(r,s_x,s_y,ℬ{)}^n$ in the regime $s_x$, $s_y\gg \sqrt{n}$. To be more explicit, we want to show that if $s_x$, $s_y\gg \sqrt{n}$, then

$$\begin{gathered} \underset{n\to \infty }{\text{lim}\text{inf}}\{{\mathbb{Q}}_n({\Phi }_n(\mathbf{X},\mathbf{Y})=1)\phantom{\}} \\ +\phantom{\{}\underset{{\mathbb{P}}_n\in 𝒫(r,s_x,s_y,ℬ{)}^n}{\text{sup}}{\mathbb{P}}_n({\Phi }_n(\mathbf{X},\mathbf{Y})=0)\}>0 \end{gathered}$$ (15)

for any Φ_n that is computable in polynomial time.

The testing problem under concern is commonly known as the CCA detection problem, owing to its alternative formulation as $H_0:{\Lambda }_1=0$ vs. $H_1:{\Lambda }_1>0$. In other words, the test tries to detect if there is any signal in the data. Note that, Lemma 1 also implies that detection is an easier problem than support recovery in that the former is always possible whenever the latter is feasible. The opposite direction may not be true, however, since detection does not reveal much information on the support.

2). Background on the Low-degree Framework:

We shall provide a brief introduction to the low-degree polynomial conjecture which forms the basis of our analyses here, and refer the interested reader to [39], [40], and [2] for in-depth discussions on the topic. We will apply this method in context of the test $H_0:(\mathbf{X},\mathbf{Y})\sim {\mathbb{Q}}_n$ vs. $H_1:(\mathbf{X},\mathbf{Y})\sim {\mathbb{P}}_n$. The low-degree method centers around the likelihood ratio ${\mathbb{L}}_n$, which takes the form $\frac{d{\mathbb{P}}_n}{d{\mathbb{Q}}_n}$ in the above framework. Our key tool here will be the Hermite polynomials, which form a basis system of $L_2({\mathbb{Q}}_n)$ [62]. Central to the low-degree approach lies the projection of ${\mathbb{L}}_n$ onto the subspace (of $L_2({\mathbb{Q}}_n)$) formed by the Hermite polynomials of degree at most $D_n\in \mathbb{N}$. The latter projection, to be denoted by ${\mathbb{L}}_n^{\le D_n}$ from now on, is important because it measures how well polynomials of degree ≤ D_n can distinguish ${\mathbb{P}}_n$ from ${\mathbb{Q}}_n$. In particular,

$$\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}≔\underset{f\text{deg}\le D_n}{\max }\frac{{\mathbb{E}}_{{\mathbb{P}}_n}[f(\mathbf{X},\mathbf{Y})]}{\sqrt{{\mathbb{E}}_{{\mathbb{Q}}_n}[f(\mathbf{X},\mathbf{Y}{)}^2]}},$$ (16)

where the maximization is over polynomials $f:{\mathbb{R}}^{n(p+q)}\mapsto \mathbb{R}$ of degree at most D_n [36].

The $L_2(\mathbb{Q})$ norm of the untruncated likelihood ratio ${\mathbb{L}}_n$ has long held an important place in the theory hypothesis testing since $\Vert {\mathbb{L}}_n{\Vert }_{L_2(\mathbb{Q})}=O(1)$ implies ${\mathbb{P}}_n$ and ${\mathbb{Q}}_n$ are asymptotically indistinguishable. While the untruncated likelihood ratio ${\mathbb{L}}_n$ is connected to the existence of any distinguishing test, degree D_n projections of ${\mathbb{L}}_n$ are connected to the existence of polynomial time distinguishing tests. The implications of the above heuristics are made precise by the following conjecture [40, Hypothesis 2.1.5].

Conjecture 1 (Informal). Suppose $t:\mathbb{N}\mapsto \mathbb{N}$. For “nice” sequences of distributions ${\mathbb{P}}_n$ and ${\mathbb{Q}}_n$, if $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}=O(1)$ as n → ∞ whenever D_n ≤ t(n)polylog(n), then there is no time-n^t(n) test ${\Phi }_n:{\mathbb{R}}^{n(p+q)}\mapsto \{0,1\}$ that strongly distinguishes ${\mathbb{P}}_n$ and ${\mathbb{Q}}_n$.

Thus Conjecture 1 implies that the degree-D_n polynomial ${\mathbb{L}}_n^{\le D_n}$ is a proxy for time-n^t(n) algorithms [2]. If we can show that $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}=O(1)$ for a D_n of the order $(\log n{)}^{1+ϵ}$ for some ϵ > 0, then the low degree Conjecture says that no polynomial time test can strongly distinguish ${\mathbb{P}}_n$ and ${\mathbb{Q}}_n$ [2, Conjecture 1.16].

Conjecture 1 is informal in the sense that we do not specify the “nice” distributions, which are defined in Section 4.2.4 of [2] (see also Conjecture 2.2.4 of [40]). Niceness requires ${\mathbb{P}}_n$ to be sufficiently symmetric, which is generally guaranteed by naturally occurring high dimensional problems like ours. The condition of “niceness” is attributed to eliminate pathological cases where the testing can be made easier by methods like Gaussian elimination. See [40] for more details.

3). Main Result:

Similar to [36], we will consider a Bayesian framework. It might not be immediately clear how a Bayesian formulation will fit into the low-degree framework, and lead to (15). However, the connection will be clear soon. We put independent Rademacher priors ${\pi }_x$ and ${\pi }_y$ on α and β. We say $\alpha \sim {\pi }_x$ if ${\alpha }_1,\dots ,{\alpha }_p$ are i.i.d., and for each $i\in [p]$,

$${\alpha }_i=\{\begin{array}{cc}1∕\sqrt{s_x}\hfill & w.p.s_x∕(2p)\hfill \\ -1∕\sqrt{s_x}\hfill & w.p.s_x∕(2p)\hfill \\ 0\hfill & w.p.1-s_x∕p.\hfill \end{array}\phantom{\}}$$ (17)

The Rademacher prior ${\pi }_y$ can be defined similarly. We will denote the product measure ${\pi }_x\times {\pi }_y$ by $\pi$. Let us define

$$\Sigma (\alpha ,\beta ,\rho )=\left[\begin{array}{cc}\hfill I_p\hfill & \hfill \rho \alpha {\beta }^T\hfill \\ \hfill \rho \beta {\alpha }^T\hfill & \hfill I_q\hfill \end{array}\right],\alpha \in {\mathbb{R}}^p,\beta \in {\mathbb{R}}^q,\rho >0.$$ (18)

When $\rho \Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<1$, $\Sigma (\alpha ,\beta ,\rho )$ is the covariance matrix corresponding to $X\sim N_p(0,I_p)$ and $Y\sim N_q(0,I_q)$ with covariance $\text{cov}(X,Y)=\rho \alpha {\beta }^T$. Hence, for $\Sigma (\alpha ,\beta ,\rho )$ to be positive definite, $\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<1∕\rho$ is a sufficient condition. The priors ${\pi }_x$ and ${\pi }_y$ put positive weight on α and β that do not lead to a positive definite $\Sigma (\alpha ,\beta ,\rho )$, and hence calls for extra care during the low-degree analysis. This subtlety is absent in the sparse PCA analogue [36].

Let us define

$${\mathbb{P}}_{\alpha ,\beta }=\{\begin{array}{cc}N(0,\Sigma (\alpha ,\beta ,1∕ℬ))\hfill & \text{when}\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\hfill \\ \mathbb{Q}\hfill & \text{o.w.}\hfill \end{array}\phantom{\}}$$ (19)

We denote the n-fold product measure corresponding to ${\mathbb{P}}_{\alpha ,\beta }$ by ${\mathbb{P}}_{n,\alpha ,\beta }$. If $(\mathbf{X},\mathbf{Y})\mid \alpha ,\beta \sim {\mathbb{P}}_{n,\alpha ,\beta }$, then the marginal density of (X, Y) is ${\mathbb{E}}_{\alpha \sim {\pi }_x,\beta \sim {\pi }_y}d{\mathbb{P}}_{n,\alpha ,\beta }$. The following lemma, which is proved in Appendix H-C, explains how the Bayesian framework is connected to (15).

Lemma 2. Suppose $ℬ>2$ and $s_x,s_y\to \infty$. Then

$$\begin{gathered} \underset{n}{\text{lim}\text{inf}}\underset{{\mathbb{P}}_n\in {𝒫}_G(r,2s_x,2s_y,ℬ{)}^n}{\text{sup}}{\mathbb{P}}_n\left({\Phi }_n(\mathbf{X},\mathbf{Y})=0\right) \\ \ge \underset{n}{\text{lim}\text{inf}}{\mathbb{E}}_{\pi }{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=0\right), \end{gathered}$$

where ${\mathbb{E}}_{\pi }$ is the shorthand for ${\mathbb{E}}_{\alpha \sim {\pi }_x,\beta \sim {\pi }_y}$.

Note that a similar result holds for $𝒫(r,s_x,s_y,ℬ)$ as well because ${𝒫}_G(r,s_x,s_y,ℬ)\subset 𝒫(r,s_x,s_y,ℬ)$. Lemma 2 implies that to show (15), it suffices to show that a polynomial time computable ${\Phi }_n$ fails to strongly distinguish the marginal distribution of X and Y from ${\mathbb{Q}}_n$. However, the latter falls within the realms of the low degree framework because the corresponding likelihood ratio takes the form

$${\mathbb{L}}_n=\frac{{\mathbb{E}}_{\alpha \sim {\pi }_x,\beta \sim {\pi }_y}d{\mathbb{P}}_{n,\alpha ,\beta }}{d{\mathbb{Q}}_n(\mathbf{X},\mathbf{Y})}.$$ (20)

Using priors on the alternative space is a common trick to convert a composite alternative to a simple alternative, which generally yields more easily to various mathematical tools.

If we can show that $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2=O(1)$ for some $D_n=O(\log n)$, then Conjecture 1 would indicate that a $n^{\tilde{\Theta }(D_n{)}_{{}_{-}}}$ time computable ${\Phi }_n$ fails to distinguish the distribution of ${\mathbb{E}}_{\alpha \sim {\pi }_x,\beta \sim {\pi }_y}d{\mathbb{P}}_{n,\alpha ,\beta }$ from ${\mathbb{Q}}_n$. Theorem 3 accomplishes the above under some additional conditions on p, q, and n, which we will discuss shortly. Theorem 3 is proved in Appendix E.

Theorem 3. Suppose $D_n\le \text{min}(\sqrt{p},\sqrt{q},n)$,

$$s_x,s_y\ge \sqrt{en{D}_n}∕ℬandp,q\ge 3en∕{ℬ}^2.$$ (21)

Then $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$ is O(1) where ${\mathbb{L}}_n$ is as defined in (20).

The following Corollary results from combining Lemma 2 with Theorem 3.

Corollary 1.Suppose

$$s_x,s_y\ge 2\sqrt{en{D}_n}∕ℬandp,q\ge 3en∕{ℬ}^2.$$ (22)

If Conjecture 1 is true, then for $D_n\le \text{min}(\sqrt{p},\sqrt{q},n)$, there is no time$\text{-}{n}^{\tilde{\Theta }(D_n)}$ test that strongly distinguishes ${𝒫}_G(r,s_x,s_y,ℬ)$ and ${\mathbb{Q}}_n$.

Corollary 1 conjectures that polynomial time algorithms can not strongly distinguish ${𝒫}_G(r,s_x,s_y,ℬ{)}^n$ and ${\mathbb{Q}}_n$ provided s_x, s_y, p, and q satisfy (22). Therefore under (22), Lemma 1 conjectures support recovery to be NP hard.

Now we discuss a bit on condition (22). The first constraint in (22) is expected because it ensures $s_x$, $s_y\gg \sqrt{n}$, which indicates that the sparsity is in the hard regime. We need to explain a bit on why the other constraint p, $q>3en∕{ℬ}^2$ is needed. If $n\gg p,q$, the sample canonical correlations are consistent, and therefore strong separation is possible in polynomial time without any restriction on the sparsity [23], [41]. Even if $p∕n\to c_1\in (0,1)$ and $q∕n\to c_2\in (0,1)$, then also strong separation is possible in model 18 provided the canonical correlation ρ is larger than some threshold depending on c₁ and c₂ [23]. The restriction p, $q>3en∕{ℬ}^2$ ensures that the problem is hard enough so that the vanilla CCA does not lead to successful detection. The constant 3e is not sharp and possibly can be improved. The necessity of the condition p, $q\gtrsim n∕{ℬ}^2$ is unknown for support recovery, however. Since support recovery is a harder problem than detection, in the hard regime, polynomial time support recovery algorithms may fail at a weaker condition on n, p, and q.

Remark 5. [Comparison with previous work:] As mentioned earlier, [28] was the first to discover the existence of computational gap in context of sparse CCA. In their seminal work, [28] established the computational hardness of CCA estimation problem at a particular subregime of $s_x$, $s_y\gg \sqrt{n}∕(ℬ\sqrt{\log (p+q)})$ provided $ℬ\to \infty$ is allowed. In view of the above, it was hinted that sparse CCA becomes computationally hard when $s_x$, $s_y\gg \sqrt{n}∕(ℬ\sqrt{\log (p+q)})$. However, when $ℬ$ is bounded, the entire regime $s_x$, $s_y\gg \sqrt{n}∕(ℬ\sqrt{\log (p+q)})$ is probably not computationally hard. In Section III-D, we show that if $p+q\asymp n$, then both polynomial time estimation and support recovery are possible if $s_x+s_y\lesssim \sqrt{n}$, at least in the known ${\Sigma }_x$ and ${\Sigma }_y$ case. The latter sparsity regime can be considerably larger than $s_x$, $s_y\lesssim \sqrt{n∕\log (p+q)}$. Together, Section III-D and the current section indicate that in the bounded $ℬ$ case, the transition of computational hardness for sparse CCA probably happens at the sparsity level $\sqrt{n}$, not $\sqrt{n∕\log (p+q)}$, which is consistent with sparse PCA. Also, the low-degree polynomial conjecture allowed us to explore almost the entire targeted regime $s_x$, $s_y\gg \sqrt{n}$, where [28], who used the planted clique conjecture, considers only a subregime of $s_x$, $s_y\gg \sqrt{n}∕(ℬ\sqrt{\log (p+q)})$.

We will end the current section with a brief outline of the proof of Theorem 3.

The main idea behind the proof of Theorem 3:

Let us denote by ${\Pi }_n^{\le D_n}$ the linear span of all $n(p+q)$-variate Hermite polynomials of degree at most D_n. For each $z\in {\mathbb{Z}}^m$ and $y\in {\mathbb{R}}^m$, we let ${\widehat{H}}_z(y)={\prod }_{i=1}^m{\widehat{h}}_{z_i}(y_i)$, where ${\widehat{h}}_{z_i}$ is the univariate normalized Hermite polynomial of degree z_i. We will discuss the Hermite polynomials in greater detail in Appendix E. Any normalized m-variate Hermite polynomial is of the form ${\widehat{H}}_z$, where $z\in {\mathbb{Z}}^m$. Then ${\Pi }_n^{\le D_n}$ is the linear span of all ${\widehat{H}}_w’\mathrm{s}$ with

$$w\in {𝒞}_l≔\left\{z\in {\mathbb{Z}}^{n(p+q)}:\sum _{i=1}^{n(p+q)}{z}_i\le D_n\right\}.$$

Since ${\mathbb{L}}_n^{\le D_n}$ is the projection of ${\mathbb{L}}_n$ on ${\Pi }_n^{\le D_n}$, it then holds that

$$\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2=\sum _{w\in {𝒞}_l}\langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^2.$$

The first step of the proof is to find out the expression of $\langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^n$. Since $w\in {\mathbb{Z}}^{n(p+q)}$, we can partition w into w = (w₁, … , w_n), where $w_i\in {\mathbb{Z}}^{p+q}$ for each i ∈ [n]. Using some algebra, we can show that

$$\langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}={\mathbb{E}}_{\pi }\left[\prod _{i\in [n]}{\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta }}\left[{\widehat{H}}_{w_i}(X_i,Y_i)\right]\right].$$

Exploiting the properties of Hermite polynomials, it can be shown that

$$\begin{gathered} {\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta }}\left[{\widehat{H}}_{w_i}(X_i,Y_i)\right] \\ =\frac{1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}}{\sqrt{{\prod }_{j=1}^{p+q}(w_i{)}_j!}} \\ \times {\phantom{\mid }{\partial }_i^{w_i}\left(\text{exp}\left\{\frac{1}{2}{t}^T\left(\Sigma (\alpha ,\beta ,1∕ℬ)-I_{p+q}\right)t\right\}\right)\mid }_{t=(0,\dots ,0)}, \end{gathered}$$

where for $z\in {\mathbb{Z}}^{p+q}$, $t\in {\mathbb{R}}^{p+q}$, and any function $f:{\mathbb{R}}^{p+q}\mapsto \mathbb{R}$, the notation ${\partial }_t^z(f(t)){\mid }_{t=(0,\dots ,0)}$ stands for the z-th order partial derivative of f with respect to t evaluated at the origin. The rest of the proof is similar to the PCA analogue in [36], but there is an extra indicator term for the CCA case. Following [36], we use the common trick of using replicas of α and β to simplify the algebra. Suppose ${\alpha }_1$, ${\alpha }_2\sim {\pi }_x$ and ${\beta }_1$, ${\beta }_2\sim {\pi }_y$ are independent. Let W be the indicator function of the event $\mid ({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\mid <{ℬ}^2$. Denote by $((1-x{)}^{-n}{)}^{\le p}$ the p-th order truncation of the Taylor series expansion of $(1-x{)}^{-n}$ at x = 0. Following some algebra, it can be shown that

$$\begin{gathered} \Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2 \\ ={\mathbb{E}}_{\pi }\left[W{\left\{{\left(1-{ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\right)}^{-n}\right\}}^{\le \lfloor D_n∕2\rfloor }\right]. \end{gathered}$$

Comparing the above with the analogous result for PCA, namely Lemma 4.2 of [36], we note that the indicator term W does not appear in the PCA analogue. The indicator term W appears in the CCA case because we had set ${\mathbb{P}}_{\alpha ,\beta }$ to be $\mathbb{Q}$ for $\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2>ℬ$ to tackle the extra restrictions on α and β in this case.

D. A Polynomial Time Algorithm for $\sqrt{n}∕\log (p+q)\ll s_x,s_y\ll \sqrt{n}$ Regime : Answer to Question 4

In this subsection, we show that in the difficult regime $s_x+s_y\in [\sqrt{n∕\log (p+q)},\sqrt{n}]$, using a soft co-ordinate thresholding (CT) type algorithm, we can estimate the canonical directions consistently when $p+q\asymp n$. CT was introduced by the seminal work of [50] for the purpose of estimating high dimensional covariance matrices. For SPCA, [1]’s CT is the only algorithm that provably recovers the full support in the difficult regime (see also [35]). In context of CCA, [26] uses CT for partial support recovery in the rank one model under what we referred to as the easy regime. However, [26]’s main goal was the estimation of the leading canonical vectors, not support recovery. As a result, [26] detects the support of the relatively large elements of the leading canonical directions, which are subsequently used to obtain consistent preliminary estimators of the leading canonical directions. Our thresholding level and theoretical analysis are different from that of [26] because the analytical tools used in the easy regime do not work in the difficult regime.

1). Methodology: Estimation via CT:

By “thresholding a matrix A co-ordinate-wise”, we will roughly mean the process of assigning the value zero to any element of A which is below a certain threshold in absolute value. Similar to [1], we will consider the soft thresholding operator, which, at threshold level t, takes the form

$$\eta (x,t)=\{\begin{array}{cc}x-t\hfill & x>t\hfill \\ 0\hfill & \mid x\mid <t\hfill \\ x+t\hfill & x<-t.\hfill \end{array}\phantom{\}}$$

It will be worth noting that the soft thresholding operator $x\mapsto \eta (x,t)$ is continuous.

Algorithm 2 Coordinate Thresholding (CT) for estimating D(V)

$$\begin{array}{cc}\hfill & \mathrm{Input}:1)\text{Sample covariance matrices}{\widehat{\Sigma }}_{n,xy}^{(1)}\text{and}{\widehat{\Sigma }}_{n,xy}^{(2)}\hfill \\ \hfill & \text{based}\text{on}\text{samples}{O}_1=(x_i,y_i{)}_{i=1}^{[n∕2]}\text{and}{O}_2=\hfill \\ \hfill & (x_i,y_i{)}_{i=[n∕2]+1}^n,\text{respectively}.\hfill \\ \hfill & 2)\text{Variances}{\Sigma }_x\text{and}{\Sigma }_y.\hfill \\ \hfill & 3)\text{Parameters}\text{Thr}\text{and}\text{cut}.\hfill \\ \hfill & 4)r,\text{i.e.},\text{rank of}{\Sigma }_{xy}\hfill \\ \hfill & \mathrm{Output}:\widehat{D}(V).\hfill \\ \hfill & 1)\mathrm{Peeling}:\text{calculate}{\tilde{\Sigma }}_{xy}={\Sigma }_x^{-1}{\widehat{\Sigma }}_{n,xy}^{(1)}{\Sigma }_y^{-1}.\hfill \\ \hfill & 2)\mathrm{Threshold}:\text{Letting}N=m+n,\text{perform soft thresh}\text{-}\hfill \\ \hfill & \text{olding}x\mapsto \eta (x;\text{Thr}∕\sqrt{N})\text{entrywise}\text{on}{\tilde{\Sigma }}_{xy}\text{to}\hfill \\ \hfill & \text{obtain thresholded}\eta ({\tilde{\Sigma }}_{xy}).\hfill \\ \hfill & 3)\mathrm{Sandwithch}:\eta ({\tilde{\Sigma }}_{xy})\mapsto {\Sigma }_x^{1∕2}\eta ({\tilde{\Sigma }}_{xy}){\Sigma }_y^{1∕2}.\hfill \\ \hfill & 4)\mathrm{SVD}:\text{Find}{\widehat{U}}_{pre},\text{the matrix of the leading}r\text{singular}\hfill \\ \hfill & \text{vector of}{\Sigma }_x^{1∕2}\eta ({\tilde{\Sigma }}_{xy}){\Sigma }_y^{1∕2}.\hfill \\ \hfill & 5)\mathrm{Premultiply}:\text{Set}{\widehat{U}}^{(1)}={\Sigma }_x^{1∕2}{\widehat{U}}_{pre}.\hfill \\ \hfill & \mathrm{return}:\text{RECOVERSUPP}({\widehat{U}}^{(1)},\text{cut},{\Sigma }_y^{-1},{\widehat{\Sigma }}_{n,xy}^{(2)},r)\text{where}\hfill \\ \hfill & \text{RECOVERSUPP}\text{is given by Algorithm}1\hfill \end{array}$$

We will also assume that the covariance matrices ${\Sigma }_x$ and ${\Sigma }_y$ are known. To understand the difficulty of unknown ${\Sigma }_x$ and ${\Sigma }_y$, we remind the readers that ${\Sigma }_{xy}={\Sigma }_{x}U\Lambda V^T{\Sigma }_y$. Because the matrices U and V are sandwiched between the matrices ${\Sigma }_x$ and ${\Sigma }_y$, their sparsity pattern does not get reflected in the sparsity pattern of ${\Sigma }_{xy}$. Therefore, if one blindly applies CT to ${\widehat{\Sigma }}_{n,xy}$, they can at best hope to recover the sparsity pattern of the outer matrices ${\Sigma }_x$ and ${\Sigma }_y$. If the supports of the matrices U and V are of main concern, CT should rather be applied on the matrix ${\tilde{\Sigma }}_{xy}={\Sigma }_x^{-1}{\widehat{\Sigma }}_{n,xy}{\Sigma }_y^{-1}$. If ${\Sigma }_x$ and ${\Sigma }_y$ are unknown, one needs to efficiently estimate ${\tilde{\Sigma }}_{xy}$ before the application of CT. Although under certain structural conditions, it is possible to find rate optimal estimators ${\widehat{\Sigma }}_{n,x}^{-1}$ and ${\widehat{\Sigma }}_{n,y}^{-1}$ of ${\Sigma }_x^{-1}$ and ${\Sigma }_y^{-1}$ at least in theory, the errors $\Vert ({\widehat{\Sigma }}_{n,x}^{-1}-{\Sigma }_x^{-1}){\widehat{\Sigma }}_{n,xy}{\Sigma }_y^{-1}{\Vert }_{op}$ and $\Vert {\Sigma }_x^{-1}{\widehat{\Sigma }}_{n,xy}({\widehat{\Sigma }}_{n,y}^{-1}-{\Sigma }_y^{-1}){\Vert }_{op}$ may still blow up due to the presence of the high dimensional matrix ${\widehat{\Sigma }}_{n,xy}$, which can be as big as $O(\sqrt{(p+q)∕n})$ in operator norm. One may be tempted to replace ${\widehat{\Sigma }}_{n,xy}$ with a sparse estimator of ${\Sigma }_{xy}$ to facilitate faster estimation, but that does not work because we explicitly require the formulation of ${\widehat{\Sigma }}_{n,xy}$ as the sum of Wishart matrices (see equation 37 in the proof). The latter representation, which is critical for the sharp analysis, may not be preserved by a CLIME [51] or nodewise Lasso estimator [49] of Σ_xy.

We remark in passing that it is possible to obtain an estimator $\widehat{A}$ so that $\mid \widehat{A}-{\tilde{\Sigma }}_{xy}{\mid }_{\infty }=o_p(1)$. Although the latter does not provide much control over the operator norm of $\widehat{A}-{\tilde{\Sigma }}_{xy}$, it is sufficient for partial support recovery, e.g., the recovery of the rows of U or V with strongest signals. (See Appendix B of [26] for example, for some results in this direction under the easy regime when r = 1.)

As indicated by the previous paragraph, we apply coordinate thresholding to the matrix ${\tilde{\Sigma }}_{xy}={\Sigma }_x^{-1}{\widehat{\Sigma }}_{n,xy}{\Sigma }_y^{-1}$, which directly targets the matrix ${\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}=U\Lambda V^T$. We call this step the peeling step because it extracts the matrix ${\tilde{\Sigma }}_{xy}$ from the sandwiched matrix ${\widehat{\Sigma }}_{n,xy}={\Sigma }_x{\tilde{\Sigma }}_{xy}{\Sigma }_y$. We then perform the entry-wise co-ordinate thresholding algorithm on the peeled form ${\tilde{\Sigma }}_{xy}$ with threshold Thr so as to obtain $\eta ({\tilde{\Sigma }}_{xy};\text{Thr}∕\sqrt{n})$. We postpone the discussion on Thr to Section III-D2. The thresholded matrix is an estimator of ${\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}$, but we need an estimator of ${\Sigma }_x^{-1∕2}{\Sigma }_{xy}{\Sigma }_y^{-1∕2}$. Therefore, we again sandwich ${\tilde{\Sigma }}_{xy}$ between ${\Sigma }_x^{1∕2}$ and ${\Sigma }_y^{1∕2}$. The motivation behind this sandwiching is that if $\Vert {\tilde{\Sigma }}_{xy}-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}={ϵ}_n$, then ${\Sigma }_x^{1∕2}{\tilde{\Sigma }}_{xy}{\Sigma }_y^{1∕2}$ is a good estimator of ${\Sigma }_x^{-1∕2}{\Sigma }_{xy}{\Sigma }_y^{-1∕2}$ in that

$$\Vert {\Sigma }_x^{1∕2}{\tilde{\Sigma }}_{xy}{\Sigma }_y^{1∕2}-{\Sigma }_x^{-1∕2}{\Sigma }_{xy}{\Sigma }_y^{-1∕2}{\Vert }_{op}\le \sqrt{\Vert {\Sigma }_x{\Vert }_{op}\Vert {\Sigma }_y{\Vert }_{op}}{ϵ}_n\le ℬ{ϵ}_n.$$

However, ${\Sigma }_x^{1∕2}U\Lambda V^T{\Sigma }_y^{1∕2}$ is an SVD of ${\Sigma }_x^{-1∕2}{\Sigma }_{xy}{\Sigma }_y^{-1∕2}$. Using Davis-Kahan sin theta theorem [52], one can show that the SVD of ${\Sigma }_x^{1∕2}{\tilde{\Sigma }}_{xy}{\Sigma }_y^{1∕2}$ produces estimators ${\widehat{U}}^{\prime }$ and ${\widehat{V}}^{\prime }$ of ${\Sigma }_x^{1∕2}U$ and ${\Sigma }_y^{1∕2}V$, where the columns of ${\widehat{U}}^{\prime }$ and ${\widehat{V}}^{\prime }$ are ϵ_n-consistent in l₂ norm for the columns of ${\Sigma }_x^{1∕2}U$ and ${\Sigma }_y^{1∕2}V$, respectively, up to a sign flip (cf. Theorem 2 of [52]). Pre-multiplying the resulting U′ by ${\Sigma }_x^{-1∕2}$ yields an estimator $\widehat{U}$ of U up to a sign flip of the columns. We do not worry about the sign flip because Condition 1 allows for the sign flips of the columns. Therefore, we feed this $\widehat{U}$ into RecoverSupp as our final step. See Algorithm 2 for more details.

Remark 6. In case of electronic health records data, it is possible to obtain large surrogate data on X and Y separately and thus might allow relaxing the known precision matrices assumption above. We do not pursue such semi-supervised setups here.

2). Analysis of the CT Algorithm:

For the asymptotic analysis of the CT algorithm, we will assume the underlying distribution to be Gaussian, i.e., $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$. This Gaussian assumption will be used to perform a crucial decomposition of sample covariance matrix, which typically holds for Gaussian random vectors. [1], who used similar devices for obtaining the sharp rate results in SPCA, also required a similar Gaussian assumption. We do not yet know how to extend these results to sub-Gaussian random vectors.

Let us consider the threshold $\text{Thr}∕\sqrt{n}$, where Thr is explicitly given in Theorem 4. Unfortunately, tuning of Thr requires the knowledge of the underlying sparsity s_x and s_y. Similar to [1], our thresholding level is different than the traditional choice of order $O(\sqrt{\log (p+q)∕n})$ in the easy regime analyzed in [50], [63] and [26]. The latter level is too large to successfully recover all the nonzero elements in the difficult regime. We threshold ${\tilde{\Sigma }}_{xy}$ at a lower level, which in its turn, complicates the analysis to a greater degree. Our main result in this direction, stated in Theorem 4, is proved in Appendix F.

Theorem 4. Suppose $(X_i,Y_i)\sim \mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$. Further suppose $s_x+s_y<\sqrt{n}$, $p\vee q=o(\log n)$, and $\log n=o(\sqrt{p}\vee \sqrt{q})$. Let K and C₁ be constants so that $K\ge 1288{ℬ}^4$ and $C_1\ge C{ℬ}^4$, where C > 0 is an absolute constant. Suppose the threshold level Thr is defined by

$$Thr=\{\begin{array}{c}\sqrt{C_1\log (p+q)}\hfill \\ if(s_x+s_y{)}^2<2^{1∕4}(p+q{)}^{3∕4}(casei)\hfill \\ {\left(K\log \left(\frac{p+q}{(s_x+s_y{)}^2}\right)\right)}^{1∕2}\hfill \\ if{2}^{1∕4}(p+q{)}^{3∕4}\le (s_x+s_y{)}^2\le (p+q)∕e\hfill \\ (caseii)\hfill \\ 0o.w.(caseiii).\hfill \end{array}\phantom{\}}$$

Suppose $c_{ℬ}$ is a constant that takes the value K, C₁, or one in case (i), (ii), and (iii), respectively. Then there exists an absolute constant C > 0 so that the following holds with probability 1 − o(1) for ${\tilde{\Sigma }}_{xy}={\Sigma }_x^{-1}{\widehat{\Sigma }}_{n,xy}{\Sigma }_y^{-1}$ :

$$\begin{gathered} \Vert \eta ({\tilde{\Sigma }}_{xy};\eta )-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le C{ℬ}^2\frac{(s_x+s_y)}{\sqrt{n}} \\ \times \max \left\{{\left(c_{ℬ}\log \left(\frac{p+q}{(s_x+s_y{)}^2}\right)\right)}^{1∕2},1\right\}. \end{gathered}$$

To disentangle the statement of Theorem 4, let us assume $p+q\asymp n$ for the time being. Then case (ii) in the theorem corresponds to $n^{3∕4}\lesssim (s_x+s_y{)}^2\le n$. Thus, CT works in the difficult regime provided $p+q\asymp n$. It should be noted that the threshold for this case is almost of the order $O(1∕\sqrt{n})$, which is much smaller than $O(\sqrt{\log (p+q)∕n})$, the traditional threshold for the easy regime. Next, observe that case (i) is an easy case because $s_x+s_y$ is much smaller than $\sqrt{n}$. Therefore, in this case, the traditional threshold of the easy regime works. Case (iii) includes the hard regime, where polynomial time support recovery is probably impossible. Because it is unlikely that CT can improve over the vanilla estimator ${\tilde{\Sigma }}_{xy}$ in this regime, a threshold of zero is set.

Remark 7. Theorem 4 requires $\log n=o(\sqrt{p}\vee \sqrt{q})$ because one of our concentration inequalities in the analysis of case (ii) needs this technical condition (see Lemma 8). The omitted regime $\log n>C(\sqrt{p}\vee \sqrt{q})$ is indeed an easier one, where special methods like CT is not even required. In fact, it is well known that subgaussian X and Y satisfy (cf. Theorem 4.7.1 of [42])

$$\Vert {\widehat{\Sigma }}_{n,xy}-{\Sigma }_{xy}{\Vert }_{op}\le C\left({\left(\frac{p+q}{n}\right)}^{1∕2}+\frac{p+q}{n}\right),$$

which is $O(\log n∕\sqrt{n})$ in the regime under concern. Including this result in the statement of Theorem 4 could unnecessarily lengthen the exposition. Therefore, we decided to exclude this regime from Theorem 4 to focus more on the $s_x+s_y\approx \sqrt{p+q}$ regime.

Remark 8. The statement of Theorem 4 is not explicit on the lower bound of the constant C₁. However, our simulation shows that the algorithm works for $C_1\ge 50{ℬ}^4$. Both threshold parameters C₁ and K in Theorem 4 depend on the unknown $ℬ>0$. The proof actually shows that $ℬ$ can be replaced by $\max \{{\Lambda }_{max}({\Sigma }_x)$, ${\Lambda }_{max}({\Sigma }_y)$, ${\Lambda }_{max}({\Sigma }_x^{-1})$, ${\Lambda }_{max}({\Sigma }_y^{-1})\}$.

Finally, Theorem 4 leads to the following corollary, which establishes that in the difficult regime, there exist estimators which satisfy Condition 1, and Algorithm 2 succeeds with probability one provided $p+q\asymp n$. This answers Question 4 in the affirmative for Gaussian distributions.

Corollary 2. Instate the conditions of Theorem 4. Then there exists $C_{ℬ}>0$ so that if

$$n\ge C_{ℬ}r(s_x+s_y{)}^2\max \left\{\log \left(\frac{p+q}{(s_x+s_y{)}^2}\right),1\right\},$$ (23)

then the ${\widehat{U}}^{(1)}$ defined in Algorithm 2 satisfies Condition 1, and ${\text{inf}}_{\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)}\mathbb{P}$(Algorithm 2 correctly recovers $D(V)){\to }_{n}1$.

We defer the proof of Corollary 2 to Appendix G. We will now present a brief outline of the proof of Theorem 4.

Main idea behind the proof of Theorem 4:

The proof hinges on the hidden variable representation of X and Y due to [64]. We discuss this representation in detail in Appendix C-2, which basically says the data matrices X and Y can be represented as

$$\mathbf{X}=\mathbf{Z}{𝒲}_1^T+{\mathbf{Z}}_1{\mathscr{H}}_1^T\text{and}\mathbf{Y}=\mathbf{Z}{𝒲}_2^T+{\mathbf{Z}}_2{\mathscr{H}}_2^T,$$

where $\mathbf{Z}\in {\mathbb{R}}^{n\times r}$, ${\mathbf{Z}}_1\in {\mathbb{R}}^{n\times p}$, and ${\mathbf{Z}}_2\in {\mathbb{R}}^{n\times q}$ are independent standard Gaussian data matrices, and ${𝒲}_1={\Sigma }_{x}U{\Lambda }^{1∕2}$, ${𝒲}_2={\Sigma }_{y}V{\Lambda }^{1∕2}$, ${\mathscr{H}}_1=({\Sigma }_x-{𝒲}_1{𝒲}_1^T{)}^{1∕2}$, and ${\mathscr{H}}_2=({\Sigma }_y-{𝒲}_2{𝒲}_2^T{)}^{1∕2}$. We will later show in Section C-2 that ${\mathscr{H}}_1$ and ${\mathscr{H}}_2$ are well defined positive definite matrices. It follows that ${\widehat{\Sigma }}_{n,xy}=X^{T}Y∕n$ has the representation

$$\begin{gathered} {\widehat{\Sigma }}_{n,xy}=\frac{1}{n}\{{𝒲}_1{\mathbf{Z}}^T\mathbf{Z}{𝒲}_2^T+{𝒲}_1{\mathbf{Z}}^T{\mathbf{Z}}_2{\mathscr{H}}_2+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T\mathbf{Z}{𝒲}_2^T\phantom{\}} \\ \phantom{\{}+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\mathscr{H}}_2\}. \end{gathered}$$

Next, we define some sets. Let $E_1={\cup }_{i=1}^{r}D(u_i)$, $F_1=[p]\setminus E_1$, $E_2={\cup }_{i=1}^{r}D(v_i)$, and $F_2=[q]\setminus E_2$. Therefore E₁ and E₂ correspond to the supports, where F₁ and F₂ correspond to their complements. Now we partition [p] × [q] into the following three sets:

$$E=E_1\times E_2,F=F_1\times F_2,$$ (24)

and

$$G=\left(F_1\times E_2\right)\cup \left(E_1\times F_2\right).$$ (25)

Therefore E is the set that contains the joint support. We can decompose ${\tilde{\Sigma }}_{xy}$ as

$${\tilde{\Sigma }}_{xy}=\underset{{\mathrm{S}}_1}{\underbrace{{𝒫}_E\{{\tilde{\Sigma }}_{xy}\}}}+\underset{{\mathrm{S}}_2}{\underbrace{{𝒫}_F\{{\tilde{\Sigma }}_{xy}\}}}+\underset{{\mathrm{S}}_3}{\underbrace{{𝒫}_G\{{\tilde{\Sigma }}_{xy}\}}}.$$ (26)

where $𝒫$ is the projection operator defined in (4).

The usefulness of the decomposition in (26) is that S₁, S₂, and S₃ have different supports, which enables us to write

$$\eta ({\tilde{\Sigma }}_{xy})=\eta (S_1)+\eta (S_2)+\eta (S_3).$$

We can therefore analyze the three terms $\eta (S_1)$, $\eta (S_2)$, and $\eta (S_3)$ separately. In general, the thresholding operator η is not linear in that for matrices A and B, $\eta (A+B)=\eta (A)+\eta (B)$ generally does not hold.

As indicated above, we analyze the operator norms of $\eta (S_1)$, $\eta (S_2)$, and $\eta (S_3)$ separately. Among S₁, S₂, and S₃, S₁ is the only matrix that is supported on E, the true support. The basic idea of the proof is showing that co-ordinate thresholding preserves the matrix S₁, and kills off the other matrices S₂ and S₃, which contain the noise terms. S₁ includes the matrix $U{\Lambda }^{1∕2}{\mathbf{Z}}^T\mathbf{Z}{\Lambda }^{1∕2}{U}^T$. Because ${\mathbf{Z}}^T\mathbf{Z}$ concentrates around I_r by Bai-Yin law (cf. Lemma 4.7.1 of [42]), $U{\Lambda }^{1∕2}{\mathbf{Z}}^T\mathbf{Z}{\Lambda }^{1∕2}{U}^T$ concentrates around $U\Lambda V^T$. Therefore the analysis of η(S₁) is relatively straightforward.

Most of the proof is devoted towards showing $\Vert \eta (S_2){\Vert }_{op}$ and $\Vert \eta (S_3){\Vert }_{op}$ are small, i.e., co-ordinate thresholding kills off the noise terms. The difficulty arises because the threshold was kept smaller than the traditional threshold of order $\sqrt{\log (p+q)∕n}$ to adjust for the hard regime. Therefore the approaches of [50] or [28] do not work in this regime. The noise matrices S₂ and S₃ are sum of matrices of the form $M{\mathbf{Z}}^T{\mathbf{Z}}_{1}N$, $M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N$, or $M{\mathbf{Z}}^T{\mathbf{Z}}_{2}N$, or their transposes, where for rest of this section, M and N should be understood as deterministic matrices of appropriate dimension, whose definition can change from line to line. Analyzing $\Vert \eta (S_2){\Vert }_{op}$ and $\Vert \eta (S_3){\Vert }_{op}$ essentially hinges on Lemma 8, which upper bounds the operator norm of matrices of the form $\eta (M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N)$. The proof of Lemma 8 uses, among other tools, a sharp Gaussian concentration result from [1] (see Corollary 10 therein), and a generalized Chernoff’s inequality for dependent Bernoulli random variables [65]. Using Lemma 8, we can also upper bound operator norms of matrices of the form $\eta (M_1{\mathbf{Z}}_1^T\mathbf{Z}{N}_1+M_2{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_2)$ because $M_1{\mathbf{Z}}_1^T\mathbf{Z}{N}_1+M_2{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_2$ can be represented as $M_3[\mathbf{Z}{\mathbf{Z}}_1{]}^T{\mathbf{Z}}_2{N}_2$ for some matrix M₃ of appropriate dimension. Therefore, to show $\Vert \eta (S_2){\Vert }_{op}$ and $\Vert \eta (S_3){\Vert }_{op}$ are small, Lemma 8 suffices, which also completes the proof.

The proof of Theorem 4 has similarities with the proof of the analogous result for PCA in [1] (see Theorem 1 therein). However, one main difference is that for PCA, the key instrument is the representation of X as the spiked model [44], which yields the representation

$$\mathbf{X}=\mathbf{Z}M+\sigma {\mathbf{Z}}_1,$$ (27)

where $\mathbf{Z}\in {\mathbb{R}}^{n\times r}$ and ${\mathbf{Z}}_1\in {\mathbb{R}}^{n\times p}$ are standard Gaussian data matrices, and $M\in {\mathbb{R}}^{r\times p}$ is a deterministic matrix. The analysis in PCA revolves around the sample covariance matrix ${\widehat{\Sigma }}_{n,x}=X^{T}X∕n$, which, following (27), writes as

$${\widehat{\Sigma }}_{n,x}=\frac{1}{n}\left\{M^T{\mathbf{Z}}^T\mathbf{Z}M+\sigma {\mathbf{Z}}_1^T\mathbf{Z}M+\sigma M^T{\mathbf{Z}}^T{\mathbf{Z}}_1+{\sigma }^2{\mathbf{Z}}_1^T{\mathbf{Z}}_1\right\}.$$

From the above representation, it can be shown that the analogues of S₂ and S₃ in the PCA case are sum of matrices of the form $M_1{\mathbf{Z}}_1^T{\mathbf{Z}}_2$ or their transposes. [1] uses an upper bound on $\Vert \eta ({\mathbf{Z}}_1^T{\mathbf{Z}}_2){\Vert }_{op}$ to bound the PCA analogue of $\Vert \eta (S_2){\Vert }_{op}$ and $\Vert \eta (S_3){\Vert }_{op}$ (see Proposition 13 therein). In contrast, we encounter terms of the form $M_1{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_1$ since CCA is concerned with X^TY/n. To deal with these terms, we needed the upper bound result on $\Vert \eta (M_1{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_1){\Vert }_{op}$ instead, which requires a separate elaborate proof. Although the basic idea behind bounding $\Vert \eta (M_1{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_1){\Vert }_{op}$ and bounding $\Vert \eta ({\mathbf{Z}}_1^T{\mathbf{Z}}_2){\Vert }_{op}$ is similar, the proof of bounding $\Vert \eta (M_1{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_1){\Vert }_{op}$ is more involved. For example, some independence structures are destroyed due to the pre and post multiplication by the matrices M₁ and N₁, respectively. We required concentration inequalities on dependent Bernoulli random variables to tackle the latter.

IV. Numerical Experiments

This section illustrates the performance of different polynomial time CCA support recovery methods when the sparsity transitions from the easy to difficult regime. We base our demonstration on a Gaussian rank one model, i.e., (X, Y) are jointly Gaussian with covariance matrix ${\Sigma }_{xy}=\rho {\Sigma }_x\alpha {\beta }^T{\Sigma }_y$. For simplicity, we take p = q and s_x = s_y = s. In all our simulations, ρ is set to be 0.5, and $\alpha ={\alpha }^{\ast }∕\sqrt{({\alpha }^{\ast }{)}^T{\Sigma }_x{\alpha }^{\ast }}$, $\beta ={\beta }^{\ast }∕\sqrt{({\beta }^{\ast }{)}^T{\Sigma }_y{\beta }^{\ast }}$ where

$$\begin{gathered} {\alpha }^{\ast }=(1∕\sqrt{s},\dots ,1∕\sqrt{s},0,\dots ,0), \\ {\beta }^{\ast }=\left(\sqrt{1-(s-1)s^{-4∕3}},s^{-2∕3},\dots ,s^{-2∕3},0,\dots ,0\right) \end{gathered}$$

are unit norm vectors. Note that the order of most elements of β is O(s^−2/3), where a typical element of α is O(s^−1/2). Therefore, we will refer to α and β as the moderate and the small signal case, respectively. For the population covariance matrices Σ_x and Σ_y of X and Y, we consider the following two scenarios:

• A (Identity): Σ_x = I_p and Σ_y = I_q. Since p = q, they are essentially the same.

• B (Sparse inverse): This example is taken from [28]. In this case, ${\Sigma }_x^{-1}={\Sigma }_y^{-1}$ are banded matrices, whose entries are given by

  $$\begin{gathered} ({\Sigma }_x^{-1}{)}_{i,j}=1\{i=j\}+0.65\times 1\{\mid i-j\mid =1\} \\ +0.4\times 1\{\mid i-j\mid =2\}. \end{gathered}$$

Now we explain our common simulation scheme. We take the sample size n to be 1000, and consider three values for p: 100, 200, and 300. The highest value of p + q is thus 600, which is smaller than but in proportion to n regime. Our simulations indicate that all of the methods considered here requires n to be quite larger than p + q for the asymptotics to kick in at ρ = 0.5. We will later discuss this point in detail. We further let $s∕\sqrt{n}$ vary in the set [0.01, 2]. To be more specific, we consider 16 equidistant points in the set [0.01, 2] for the ratio $s∕\sqrt{n}$.

Now we discuss the error metric used here to compare the performance of different support recovery methods. Type I and type II errors are commonly used tools to measure the performance of support recovery [1]. In case of support recovery of α, we define the type I error to be the proportion of zero elements in α that appear in the estimated support $\widehat{D}(\alpha )$. Thus, we quantify the type I error of α by $\mid \widehat{D}(\alpha )\setminus D(\alpha )\mid ∕(p-s)$. On the other hand, the type II error for α is the proportion of elements in D(α) which are absent in $\widehat{D}(\alpha )$, i.e., the type II error is quantified by $\mid D(\alpha )\setminus \widehat{D}(\alpha )\mid ∕s$. One can define the type I and type II errors corresponding to β similarly. Our simulations demonstrate that often the methods with low type I error exhibit a high type II error, and vice versa. In such situations, comparison between the corresponding methods becomes difficult if one uses the type I and type II errors separately. Therefore, we consider a scaled Hamming loss type metric, which suitably combines the type I and type II error. The symmetric Hamming error of estimating D(α) by $\widehat{D}(\alpha )$ is [66, Section 2.1]

$$1-\frac{\mid D(\alpha )\cap \widehat{D}(\alpha )\mid }{\sqrt{\mid D(\alpha )\Vert \widehat{D}(\alpha )\mid }}.$$

Note that the above quantity is always bounded above by one. We can similarly define the symmetric Hamming distance between D(β) and $\widehat{D}(\beta )$. Finally, the estimates of these three errors (Type I, Type II, and scaled Hamming Loss) are obtained based on 1000 Monte Carlo replications.

Now we discuss the support recovery methods we compare here.

• Naïve SCCA. We estimate α and β using the SCCA method of [24], and set $\widehat{D}(\alpha )=\{i\in [p]:{\widehat{\alpha }}_i\ne 0\}$ and $\widehat{D}(\beta )=\{i\in [q]:{\widehat{\beta }}_i\ne 0\}$, where $\widehat{\alpha }$ and $\widehat{\beta }$ are the corresponding SCCA estimators. To implement the SCCA method of [24], we use the R code referred therein with default tuning parameters.

• Cleaned SCCA. This method implements RecoverSupp with the above mentioned SCCA estimators of α and β as the preliminary estimators.

• CT. This is the method outlined in Algorithm 2, which is RecoverSupp coupled with the CT estimators of α and β.

Our CT method requires the knowledge of the population covariance matrices Σ_x and Σ_y. Therefore, to keep the comparison fair, in case of the cleaned SCCA method as well, we implement RecoverSupp with the popular covariance matrices. Because of their reliance on RecoverSupp, both cleaned SCCA and CT depend on the threshold cut, tuning which seems to be a non-trivial task. We set $\text{cut}=C\sqrt{\log (p+q)s({\Sigma }_x^{-1})∕n}$, where C is the thresholding constant. Our simulations show that a large C results in high type II error, where insufficient thresholding inflates the type I error. Taking the hamming loss into account, we observe that C ≈ 1 leads to a better performance in case A in an overall sense. On the other hand, case B requires a smaller value of thresholding parameter. In particular, we let C to be one in case A, and set C = 0.05 and 0.2, respectively, for the support recovery of α and β in case B. The CT algorithm requires an extra threshold parameter, namely the parameter Thr in Algorithm 2, which corresponds to the co-ordinate thresholding step. We set Thr in accordance with Theorem 4 and Remark 8, with K being $1288{ℬ}^4$ and C₁ being $50{ℬ}^4$. We set $ℬ$ as in Remark 8, that is

$$ℬ=\max \{{\Lambda }_{max}({\Sigma }_x),{\Lambda }_{max}({\Sigma }_y),{\Lambda }_{max}({\Sigma }_x^{-1}),{\Lambda }_{max}({\Sigma }_y^{-1})\}.$$

The errors incurred by our methods in case A are displayed in Figure 2 (for α) and Figure 3 (for β). Figures 4 and 5, on the other hand, display the errors in the recovery of α and β, respectively, in case B.

Fig. 2:

Support recovery for α when ${\Sigma }_x=I_p$ and ${\Sigma }_y=I_q$. Here threshold refers to cut in Theorem 1.

Fig. 3:

Support recovery for β when ${\Sigma }_x=I_p$ and ${\Sigma }_y=I_q$. Here threshold refers to cut in Theorem 1.

Fig. 4:

Support recovery for α when ${\Sigma }_x$ and ${\Sigma }_y$ are the sparse covariance matrices. Here threshold refers to cut in Theorem 1.

Fig. 5:

Support recovery for β when ${\Sigma }_x$ and ${\Sigma }_y$ are the sparse covariance matrices. Here threshold refers to cut in Theorem 1.

Now we discuss the main observations from the above plots. When the sparsity parameter s is considerably low (less than ten in the current settings), the naíve SCCA method is sufficient in the sense that the specialized methods do not perform any better. Moreover, the naïve method is the most conservative one among all three methods. As a consequence, the associated type I error is always small, although the type II error of the naïve method grows faster than any other method. The specialized methods are able to improve the type II error at the cost of higher type I error. At a higher sparsity level, the specialized methods can outperform the naïve method in terms of the Hamming error, however. This is most evident when the setting is also complex, i.e., the signal is small, or the underlying covariance matrices are not identity. In particular, Figure 2 and 4 entail that when the signal strength is moderate and the sparsity is high, the cleaned SCCA has the lowest hamming error. In the small signal case, however, CT exhibits the best hamming error as $s∕\sqrt{n}$ increases; cf. Figure 3 and 5.

The Type I error of CT can be slightly improved if the sparsity information can be incorporated during the thresholding step. We simply replace cut by the maximum of cut and the s-th largest element of ${\widehat{V}}^{clean}$, where the latter is as in Algorithm RecoverSupp. See, e.g., Figure 6, which entails that this modification reduces the Hamming error of the CT algorithm in case A. our empirical analysis hints that the CT algorithm has potential for improvement from the implementation perspective. In particular, it may be desirable to obtain a more efficient procedure for choosing cut in a systematic way. However, such a detailed numerical analysis is beyond the scope of the current paper and will require further modifications of the initial methods for estimation of α, β both for scalability and finite sample performance reasons. We keep these explorations as important future directions.

Fig. 6:

Support recovery by the CT algorithm when we use the information on sparsity to improve the type I error. Here ${\Sigma }_x$ and ${\Sigma }_y$ are $I_p$ and $I_q$, respectively, and threshold refers to cut in Theorem 1. To see the decrease in type I error, compare the errors with that of Figure 2 and Figure 3.

It is natural to wonder what is the effect of cleaning via RecoverSupp on SCCA. As mentioned earlier, during our simulations we observed that a cleaning step generally improves the type II error of the naïve SCCA, but it also increases the type I error. In terms of the combined measure, i.e., the Hamming error, it turns out that cleaning does have an edge at higher sparsity levels in case B; cf. Figure 4 and Figure 5. However, the scenario is different in case A. Although Figures 2 and 3 indicate that almost no cleaning occurs at the set threshold level of one, we saw that cleaning happens at lower threshold levels. However, the latter does not improve the overall Hamming error of naïve SCCA. The consequence of cleaning may be different for other SCCA methods.

To summarize, when the sparsity is low, support recovery using the naïve SCCA is probably as good as the specialized methods. However, at higher sparsity level, specialized support recovery methods may be preferable. Consequently, the precise analysis of the apparently naïve SCCA will indeed be an interesting future direction.

V. Discussion

In this paper, we have discussed rate optimal behavior of information theoretic and computational limits of the joint support recovery for the sparse canonical correlation analysis problem. Inspired by recent results in the estimation theory of sparse CCA, a flurry of results in sparse PCA, and related developments based on low-degree polynomial conjecture – we are able to paint a complete picture of the landscape of support recovery for SCCA. For future directions, it is worth noting that our results are so far not designed to recover D(v_i) for individual i ∈ [r] separately (and hence the term joint recovery). Although this is also the case for most state of the art in the sparse pCA problem (results often exist only for the combined support [1] or the single spike model where r = 1 [29]), we believe that it is an interesting question for deeper explorations in the future. Moreover, moving beyond asymptotically exact recovery of support to more nuanced metrics (e.g., Hamming Loss) will also require new ideas worth studying. Finally, it remains an interesting question to pursue whether polynomial time support recovery is possible in the $\sqrt{n∕\log (p+q)}\ll s_x$, $s_y\ll \sqrt{n}$ regime using a CT type idea – but for unknown yet structured high dimensional nuisance parameters Σ_x, Σ_y.

Biographies

Nilanjana Laha received a Bachelor of Statistics in 2012 and a Master of Statistics in 2014 from the Indian Statistical Institute, Kolkata. Then she received a Ph.D. in statistics in 2019 from the University of Washington, Seattle. She was a postdoctoral research fellow at the department of Biostatistics at Harvard university from 2019 to 2022. She is currently an assistant professor in Statistics at Texas A & M University. Her research interests include dynamic treatment regimes, high dimensional association, and shape constrained inference.

Rajarshi Mukherjee received a Bachelor of Statistics in 2007 and a Master of Statistics in 2009 from the Indian Statistical Institute, Kolkata. He received his Ph.D. degree in Bisostatistics from Harvard University in 2014. He was a Stein fellow in the department of Statistics at Stanford University from 2014 to 2017. He was an assistant professor at the division of Biostatistics at the University of California, Berkeley, from 2017 to 2018. Since 2018, he has been an assistant professor at the department of Biostatistics at Harvard University. His research interests primarily lie in structured signal detection problems in high dimensional and network models, and functional estimation and adaptation theory in nonparametric statistics.

Appendix A. Full version of RecoverSupp

Algorithm 3 RecoverSupp: simultaneous support recovery of U and V

$$\begin{array}{cc}\hfill & \mathrm{Input}:1)\text{Preliminary estimations}{\widehat{U}}^{(1)}\text{and}{\widehat{V}}^{(1)}\text{of}U\text{and}\hfill \\ \hfill & V,\text{and estimators}{\widehat{\Gamma }}_n^{(1)}\text{and}{\widehat{\Omega }}_n^{(1)}\text{of}{\Sigma }_x^{-1}{\Sigma }_y^{-1},\text{re}\text{-}\hfill \\ \hfill & \text{spectively}.\text{All are based on smaple}{O}_1=(x_i,y_i{)}_{i=1}^{[n∕2]}.\hfill \\ \hfill & 2)\text{Estimator}{\widehat{\Sigma }}_{n,xy}^{(2)}\text{of}{\Sigma }_{xy}\text{based on sample}{O}_2=\hfill \\ \hfill & (x_i,y_i{)}_{i=[n∕2]+1}^n.\hfill \\ \hfill & 3){\text{Threshold levels cut}}_x,{\text{cut}}_y>0\text{and rank}r\in \mathbb{N}.\hfill \\ \hfill & \mathrm{Output}:\widehat{D}(U)\text{and}\widehat{D}(V),\text{estimators of}D(U)\text{and}D(V),\hfill \\ \hfill & \text{respectively}.\hfill \\ \hfill & 1)\mathrm{Cleaning}:{\widehat{V}}^{clean}\leftarrow {\widehat{\Omega }}_n^{(1)}{\widehat{\Sigma }}_{n,yx}^{(2)}{\widehat{U}}^{(1)};{\widehat{U}}^{clean}\leftarrow \hfill \\ \hfill & {\widehat{\Gamma }}_n^{(1)}{\widehat{\Sigma }}_{n,xy}^{(2)}{\widehat{V}}^{(1)}.\hfill \\ \hfill & 2)\mathrm{Threshold}:\text{Compute}\hfill \\ \hfill & \widehat{D}(U)≔\{i\in [p]:\mid {\widehat{U}}_{ik}^{clean}\mid >{\text{cut}}_x\text{for some}k\in [r]\}\hfill \\ \hfill & \text{and}\hfill \\ \hfill & \widehat{D}(V)≔\{i\in [q]:\mid {\widehat{V}}_{ik}^{clean}\mid >{\text{cut}}_y\text{for some}k\in [r]\}.\hfill \\ \hfill & \mathrm{return}:\widehat{D}(U)\text{and}\widehat{D}(V).\hfill \end{array}$$

In Algorithm 3, we used different cut-offs for estimating $\widehat{D}(U)$ and $\widehat{D}(V)$, which are cut_x and cut_y, respectively. In practice, one can choose the same threshold cut for both of them.

Appendix B. Proof preliminaries

The Appendix collects the proof of all our theorems and lemmas. This section introduces some new notations and collects some facts, which are used repeatedly in our proofs.

A. New Notations

Since the columns of ${\Sigma }_x^{1∕2}U$, i.e., [${\Sigma }_x^{1∕2}{U}_1,\dots ,{\Sigma }_x^{1∕2}{U}_r$] are orthogonal, we can extend it to an orthogonal basis of ${\mathbb{R}}^p$, which can also be expressed in the form [${\Sigma }_x^{1∕2}{u}_1,\dots ,{\Sigma }_x^{1∕2}{u}_p$] since Σ_x is non-singular. Let us denote the matrix [u₁,…,u_p] by $\tilde{U}$, whose first r columns form the matrix U. Along the same line, we can define $\tilde{V}$, whose first q columns constitute the matrix V.

Suppose $A\in {\mathbb{R}}^{p\times q}$ is a matrix. Recall the projection operator defined in (4). For any S ⊂ [p], we let $A_{S\ast }$ denote the matrix ${𝒫}_{S\times [q]}\{A\}$. Similarly, for $F\subset [q]$, we let A_F be the matrix ${𝒫}_{[p]\times F}\{A\}$. For $k\in \mathbb{N}$, we define the norms $\Vert A{\Vert }_{k,\infty }={\max }_{j\in [q]}\Vert A_j{\Vert }_k$ and $\Vert A{\Vert }_{\infty ,k}={\max }_{i\in [q]}\Vert A_i{\Vert }_k$. We will use the notation ∣A∣_∞ to denote the quantity ${\text{sup}}_{1\in [p],j\in [q]}\mid A_{i,j}\mid$.

The Kullback Leibler (KL) divergence between two probability distributions P₁ and P₂ will be denoted by KL(P₁ ∣ P₂). For $x\in \mathbb{R}$, we let $\lfloor x\rfloor$ denote greatest integer less than or equal to $x\in \mathbb{R}$.

B. Facts on $𝒫(r,s_x,s_y,ℬ)$

First, note that since $v_i^T{\Sigma }_y{v}_i=1$ by (2) for all i ∈ [q], we have $\Vert v_i{\Vert }_2\le \sqrt{ℬ}$. Similarly, we can also show that $\Vert u_i{\Vert }_2\le \sqrt{ℬ}$. Second, we note that $\Vert {\Sigma }_x^{1∕2}U{\Vert }_{op}=\Vert {\Sigma }_y^{1∕2}V{\Vert }_{op}=1$, and

$$\begin{gathered} \mid {\Sigma }_{yx}{\mid }_{\infty }\le \Vert {\Sigma }_{yx}{\Vert }_{op}=\Vert {\Sigma }_{y}V\Lambda U^T{\Sigma }_x{\Vert }_{op} \\ \le \Vert {\Sigma }_y^{1∕2}{\Vert }_{op}\Vert {\Sigma }_y^{1∕2}V{\Vert }_{op}\Vert \Lambda {\Vert }_{op}\Vert {\Sigma }_x^{1∕2}U{\Vert }_{op}\Vert {\Sigma }_x^{1∕2}{\Vert }_{op} \\ \le ℬ \end{gathered}$$ (28)

because the largest element of Λ is not larger than one. Since X_i’s and Y_i’s are Subgaussian, for any random vector v independent of X and Y, it follows that [45, Lemma 7]

$$\mid ({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx})v{\mid }_{\infty }\le C_{ℬ}\Vert v{\Vert }_2\sqrt{\frac{\log (p+q)}{n}}$$ (29)

with $\mathbb{P}$ probability 1 – o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$. Also, we can show that ${\Phi }_0={\Sigma }_y^{-1}$ satisfies

$$\begin{gathered} \Vert ({\Phi }_0{)}_k{\Vert }_{1,\infty }\le \sqrt{s({\Sigma }_x)}\Vert ({\Phi }_0{)}_k{\Vert }_{2,\infty }\le \sqrt{s({\Sigma }_x)}\Vert {\Phi }_0{\Vert }_{op} \\ \le \sqrt{s({\Sigma }_x)}ℬ, \end{gathered}$$

where Cauchy-Schwarz inequality was used in the first step.

C. General Technical Facts

Fact 1.For two matrices$A\in {\mathbb{R}}^{m\times n}$and$B\in {\mathbb{R}}^{n\times q}$, we have

$$\Vert AB{\Vert }_F^2\le \Vert A{\Vert }_{op}^2\Vert B{\Vert }_F^2,\Vert AB{\Vert }_F^2\le \Vert A{\Vert }_F^2\Vert B{\Vert }_{op}^2$$

Fact 2 (Lemma 11 of [1]). Let $\mathbf{Z}\in {\mathbb{R}}^{n\times p}$ be a matrix with i.i.d. standard normal entries, i.e., Z_i,j ~ N(0, 1). Then for every t > 0,

$$\mathbb{P}(\Vert \mathbf{Z}{\Vert }_{op}\ge \sqrt{p}+\sqrt{n}+t)\le \text{exp}(-t^2∕2).$$

As a consequence, there exists an absolute constant C > 0 such that

$$\mathbb{P}\left(\Vert \mathbf{Z}{\Vert }_{op}\ge \sqrt{2}(\sqrt{p}+\sqrt{n})\right)\le \text{exp}(-C(p+n)).$$

Recall that for $A\in {\mathbb{R}}^{p\times q}$, in Appendix B-A, we defined ∥A∥_1,∞ and ∥A∥_∞1 to be the matrix norms ${\max }_{j\in [q]}\Vert A_j{\Vert }_1$ and ${\max }_{i\in [p]}\Vert A_{i\ast }{\Vert }_1$, respectively.

The following fact is a Corollary to (29).

Fact 3. Suppose X and Y are jointly subgaussian. Then $\mid {\widehat{\Sigma }}_{n,xy}-{\Sigma }_{xy}{\mid }_{\infty }=O_p(\sqrt{\log (p+q)∕n})$.

Fact 4 (Chi-square tail bound). Suppose ${\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_k\stackrel{iid}{\sim }N(0,1)$. Then for any y > 5, we have

$$\mathbb{P}\left(\sum _{l=1}^k{\mathbb{Z}}_l^2\ge yk\right)\le \text{exp}(-yk∕5).$$

Proof of Fact 4. Since Z_l’s are independent standard Gaussian random variables, by tail bounds on Chi-squared random variables (The form below is from Lemma 12 of [1]),

$$\mathbb{P}\left(\sum _{l=1}^k{\mathbb{Z}}_l^2\ge k+2\sqrt{kx}+2x\right)\le \text{exp}(-x).$$

Plugging in x = y_k, we obtain that

$$\mathbb{P}\left(\sum _{l=1}^k{\mathbb{Z}}_l^2\ge (1+2\sqrt{y}+2y)k\right)\le \text{exp}(-yk),$$

which implies for y > 1,

$$\mathbb{P}\left(\sum _{l=1}^k{\mathbb{Z}}_l^2\ge 5yk\right)\le \text{exp}(-yk),$$

which can be rewritten as

$$\mathbb{P}\left(\sum _{l=1}^k{\mathbb{Z}}_l^2\ge yk\right)\le \text{exp}(-yk∕5)$$

as long as y > 5. □

Appendix C. Proof of Theorem 1

For the sake of simplicity, we denote ${\widehat{U}}^{(1)}$, ${\widehat{\Sigma }}_{n,xy}^{(2)}$, and ${\widehat{\Omega }}_n^{(1)}$ by $\widehat{U}$, ${\widehat{\Sigma }}_{n,xy}$, and ${\widehat{\Omega }}_n$, respectively. The reader should keep in mind that $\widehat{U}$ and ${\widehat{\Omega }}_n$ are independent of ${\widehat{\Sigma }}_{n,xy}$ and ${\widehat{\Omega }}_n$ because they are constructed from a different sample. Next, using Condition 1, we can show that there exists $(w_i,\dots ,w_p)\in \{\pm 1{\}}^p$ so that

$$\begin{gathered} \underset{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}{\text{inf}}\mathbb{P}(\underset{i\in [r]}{\max }\mid (w_i{\widehat{u}}_{n,i}-u_i{)}^T{\Sigma }_x(w_i{\widehat{u}}_{n,i}-u_i)\mid \phantom{)} \\ \phantom{(}<{\text{Err}}^2)\to 1. \end{gathered}$$

as n → ∞. Without loss of generality, we assume w_i = 1 for all i ∈ [r]. The proof will be similar for general w_i’s. Thus

$$\underset{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}{\text{inf}}\mathbb{P}\left(\underset{i\in [r]}{\max }\mid ({\widehat{u}}_{n,i}-u_i{)}^T{\Sigma }_x({\widehat{u}}_{n,i}-u_i)\mid <{\text{Err}}^2\right)\to 1$$ (30)

Therefore $\Vert {\widehat{u}}_{n,i}-u_i{\Vert }_2\le \text{Err}\sqrt{ℬ}$ for all i ∈ [r] with $\mathbb{P}$ probability tending to one.

Now we will collect some facts which will be used during the proof. Because ${\widehat{u}}_{n,i}$ and ${\widehat{\Sigma }}_{n,yx}$ are independent, (29) implies that

$$\mid ({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}{\mid }_{\infty }\le C_{ℬ}\Vert {\widehat{u}}_{n,i}{\Vert }_2\sqrt{\frac{\log (p+q)}{n}}.$$

Using (30), we obtain that $\Vert {\widehat{u}}_{n,i}{\Vert }_2\le \Vert {\widehat{u}}_{n,i}-u_i{\Vert }_2+\Vert u_i{\Vert }_2\le \sqrt{B}(\text{Err}+1)$. Because $\text{Err}<{ℬ}^{-1}\le 1$, we have

$$\begin{gathered} \underset{\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)}{\text{inf}}\mathbb{P}\left(\underset{i\in [r]}{\max }\mid ({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}{\mid }_{\infty }\le C_{ℬ}\sqrt{\frac{\log (p+q)}{n}}\right) \\ =1-o(1). \end{gathered}$$ (31)

Noting (28) implies $\mid {\Sigma }_{yx}{\widehat{u}}_{n,i}{\mid }_{\infty }\le \Vert {\Sigma }_{yx}{\Vert }_{op}\Vert {\widehat{u}}_{n,i}{\Vert }_2\le 2{ℬ}^{3∕2}$, and that $\log (p+q)=o(n)$, using (31), we obtain that

$$\underset{i\in [r]}{\max }\mid {\widehat{\Sigma }}_{n,yx}{\widehat{u}}_{n,i}{\mid }_{\infty }\le \mid ({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}{\mid }_{\infty }+\mid {\Sigma }_{yx}{\widehat{u}}_{n,i}{\mid }_{\infty }\le 3{ℬ}^{3∕2}$$ (32)

with $\mathbb{P}$ probability 1 – o(1).

Now we are ready to prove Theorem 1. We will denote the columns of ${\widehat{V}}_n^{clean}$ by ${\widehat{v}}_{n,i}^{clean}$ for i ∈ [r]. Because ${\Lambda }_i(v_i{)}_k=e_k^T{\Sigma }_y^{-1}{\Sigma }_{yx}{u}_i$, it holds that

$$\begin{gathered} ({\widehat{v}}_{n,i}^{clean}{)}_k-{\Lambda }_i(v_i{)}_k=e_k^T({\widehat{\Omega }}_n-{\Phi }_0){\widehat{\Sigma }}_{n,yx}{\widehat{u}}_{n,i} \\ +e_k^T{\Phi }_0({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i} \\ +e_k^T{\Phi }_0{\Sigma }_{yx}({\widehat{u}}_{n,i}-u_i) \end{gathered}$$

leading to

$$\begin{gathered} \mid ({\widehat{v}}_{n,i}^{clean}{)}_k-{\Lambda }_i(v_i{)}_k\mid \le \underset{T_1(i,k)}{\underbrace{\mid e_k^T({\widehat{\Omega }}_n-{\Phi }_0){\widehat{\Sigma }}_{n,yx}{\widehat{u}}_{n,i}\mid }} \\ +\underset{T_2(i,k)}{\underbrace{\mid e_k^T{\Phi }_0({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}\mid }} \\ +\underset{T_3(i,k)}{\underbrace{\mid e_k^T{\Phi }_0{\Sigma }_{yx}({\widehat{u}}_{n,i}-u_i)\mid }}. \end{gathered}$$

Handling the term T₂ is the easiest because

$$\begin{gathered} \underset{i\in [r],k\in [q]}{\max }{T}_2(i,k) \\ \le \Vert {\Phi }_0{\Vert }_{1,\infty }\mid ({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}{\mid }_{\infty } \\ \le C_{ℬ}\sqrt{\frac{s({\Sigma }_y^{-1})\log (p+q)}{n}} \end{gathered}$$

with $\mathbb{P}$ probability 1 – o(1) uniformly over $𝒫(r,s_x,s_y,ℬ)$, where we used (31) and the fact that $\Vert {\Phi }_0{\Vert }_{1,\infty }\le \sqrt{s({\Sigma }_y^{-1})ℬ}$. The difference in cases (A), (B), (C) arises only due to different bounds on T₁(i, k) in these cases. We demonstrate the whole proof only for case (A). For the other two cases, we only discuss the analysis of T₁(i, k) because the rest of the proof remains identical in these cases.

1). Case (A):

Since we have shown in (32) that $\mid {\widehat{\Sigma }}_{n,yx}{\widehat{u}}_{n,i}{\mid }_{\infty }\le 3{ℬ}^{3∕2}$, we calculate

$$\begin{gathered} \underset{i\in [r],k\in [q]}{\max }{T}_1(i,k)\le \Vert {\widehat{\Omega }}_n-{\Phi }_0{\Vert }_{1,\infty }\underset{i\in [r]}{\max }\mid {\widehat{\Sigma }}_{n,yx}{\widehat{u}}_{n,i}{\mid }_{\infty } \\ \le 3{ℬ}^{3∕2}{C}_{\text{pre}}s({\Sigma }_y^{-1})\sqrt{\frac{\log q}{n}} \end{gathered}$$

with $\mathbb{P}$ probability tending to one, uniformly over $𝒫(r,s_x,s_y,ℬ)$, where to get the last inequality, we also used the bound on $\Vert {\widehat{\Omega }}_n-{\Phi }_0{\Vert }_{\infty ,1}$ in case (A).

Finally, for T₃, we notice that

$$\begin{gathered} T_3(i,k)=\mid e_k^T{\Phi }_0{\Sigma }_{yx}({\widehat{u}}_{n,i}-u_i)\mid \\ =\mid e_k^T\sum _{j=1}^r{\Lambda }_j{v}_j{u}_j^T{\Sigma }_x({\widehat{u}}_{n,i}-u_i)\mid \\ \le \underset{j\in [r]}{\max }\mid (v_j{)}_k\mid \mid \sum _{j=1}^r{u}_j^T{\Sigma }_x({\widehat{u}}_{n,i}-u_i)\mid \end{gathered}$$

since Λ₁ ≥ 1. Since (v_j)_k = V_kj, it is clear that T₃(i, k) is identically zero if $k\notin D(V)$. Otherwise, Cauchy Schwarz inequality implies,

$$\begin{gathered} \mid \sum _{j=1}^r{u}_j^T{\Sigma }_x({\widehat{u}}_{n,i}-u_i)\mid \\ \le \sqrt{r}{\left(\sum _{j=1}^r(u_j^T{\Sigma }_x({\widehat{u}}_{n,i}-u_i){)}^2\right)}^{1∕2} \\ \le \sqrt{r}\Vert {\Sigma }_x^{1∕2}({\widehat{u}}_{n,i}-u_i){\Vert }_2 \end{gathered}$$

because ${\Sigma }_x^{1∕2}{u}_j’\mathrm{s}$ are orthogonal. Thus

$$\underset{i\in [r],k\in D(V)}{\max }\mid T_3(i,k)\mid \le \sqrt{r}\underset{j\in [r]}{\max }\mid (v_j{)}_k\mid \text{Err}.$$

Now we will combine the above pieces together. Note that

$$\begin{gathered} \underset{i\in [q]}{\max }\underset{k\in [r]}{\max }(\mid T_1(i,k)\mid +\mid T_2(i,k)\mid \\ \le C_{ℬ}\underset{{ϵ}_n}{\underbrace{C_{\text{pre}}s({\Sigma }_y^{-1})\sqrt{\frac{\log (p+q)}{n}}}}. \end{gathered}$$ (33)

For $k\notin D(V)$, denoting the i-th column of ${\widehat{V}}^{clean}$ by ${\widehat{v}}_{n,i}^{clean}$ we observe that,

$$\begin{gathered} \underset{k\notin D(V)}{\max }\underset{i\in [r]}{\max }\mid {\widehat{V}}_{ki}^{clean}\mid =\underset{k\notin D(V)}{\max }\underset{i\in [r]}{\max }\mid ({\widehat{v}}_{n,i}^{clean}{)}_k\mid \\ \le \underset{i\in [q]}{\max }\underset{k\in [r]}{\max }(\mid T_1(i,k)\mid +\mid T_2(i,k)\mid ) \\ \le C_{ℬ}{ϵ}_n \end{gathered}$$ (34)

with $\mathbb{P}$ probability 1 – o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$. On the other hand, if k ∈ D(v_i), then we have for all i ∈ [r],

$$\begin{gathered} \mid ({\widehat{v}}_{n,i}^{clean}{)}_k\mid >{\Lambda }_i\mid (v_i{)}_k\mid -\sqrt{r}\underset{j\in [r]}{\max }\mid (v_j{)}_k\mid \text{Err} \\ -\underset{i\in [q]}{\max }\underset{k\in [r]}{\max }(\mid T_1(i,k)\mid +\mid T_2(i,k)\mid ), \end{gathered}$$

which implies

$$\underset{i\in [r]}{\max }\mid {\widehat{V}}_{ki}^{clean}\mid >\underset{i\in [r]}{\max }{\Lambda }_i\mid (v_i{)}_k\mid -\sqrt{r}\underset{i\in [r]}{\max }\mid (v_i{)}_k\mid \text{Err}-C_{ℬ}{ϵ}_n.$$

Since $\text{Err}<{ℬ}^{-1}∕(2\sqrt{r})$ and ${ℬ}^{-1}<{\text{min}}_{i\in [r]}{\Lambda }_i$, we have

$$\begin{gathered} \underset{i\in [r]}{\max }{\Lambda }_i\mid (v_i{)}_k\mid -\sqrt{r}\underset{i\in [r]}{\max }\mid (v_i{)}_k\mid \text{Err} \\ >({ℬ}^{-1}-\sqrt{r}\text{Err})\underset{i\in [r]}{\max }\mid (v_i{)}_k\mid \\ >{ℬ}^{-1}\underset{i\in [r]}{\max }\mid (v_i{)}_k\mid ∕2. \end{gathered}$$

Thus, noting V_ki = (v_i)_k, we obtain that

$$\begin{gathered} \underset{k\in D(V)}{\text{min}}\underset{i\in [r]}{\max }\mid ({\widehat{v}}_{n,i}^{clean}{)}_k\mid =\underset{k\in D(V)}{\text{min}}\underset{i\in [r]}{\max }\mid {\widehat{V}}_{ki}^{clean}\mid \\ >\underset{k\in D(V)}{\text{min}}\underset{i\in [r]}{\max }\mid V_{ki}\mid ∕(2ℬ)-C_{ℬ}{ϵ}_n \end{gathered}$$

with $\mathbb{P}$ probability 1 – o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$. Suppose $C_{ℬ}^{\prime }=2ℬC_{ℬ}$. Note that

$$\underset{k\in [p]}{\text{min}}\underset{i\in [r]}{\max }\mid (v_i{)}_k\mid ={\theta }_n{C}_{ℬ}^{\prime }{ϵ}_n$$

where θ_n > 2. Then with $\mathbb{P}$ probability 1 – o(1) uniformly over $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$,

$$\underset{k\in D(V)}{\text{min}}\underset{i\in [r]}{\max }{\widehat{V}}_{ki}^{clean}>({\theta }_n-1)C_{ℬ}^{\prime }{ϵ}_n∕(2ℬ).$$

This, combined with (34) implies setting $\text{cut}\in [C_{ℬ}^{\prime }{ϵ}_n∕(2ℬ),({\theta }_n-1)C_{ℬ}^{\prime }{ϵ}_n∕(2ℬ)]$ leads to full support recovery with $\mathbb{P}$ probability 1 – o(1). The proof of the first part follows.

2). Case (B):

In the Gaussian case, we resort to the hidden variable representation of X and Y due to [64], which enables sharper bound on the term T₁(i, k). Suppose Z ~ N_r(0, I_r) where r is the rank of Σ_xy. Consider Z₁ ~ N_p(0, I_p) and Z₂ ~ N_q(0, I_q) independent of Z. Then X and Y can be represented as

$$X={𝒲}_{1}Z+{\mathscr{H}}_1{Z}_1\text{and}Y={𝒲}_{2}Z+{\mathscr{H}}_2{Z}_2,$$ (35)

where

$${𝒲}_1={\Sigma }_{x}U{\Lambda }^{1∕2},{𝒲}_2={\Sigma }_{y}V{\Lambda }^{1∕2},{\mathscr{H}}_1=({\Sigma }_x-{𝒲}_1{𝒲}_1^T{)}^{1∕2},$$

and

$${\mathscr{H}}_2=({\Sigma }_y-{𝒲}_2{𝒲}_2^T{)}^{1∕2}.$$

Here $({\Sigma }_x-{𝒲}_1{𝒲}_1^T{)}^{1∕2}$ is well defined because

$${\Sigma }_x-{𝒲}_1{𝒲}_1^T={\Sigma }_x\tilde{U}(I_p-{\Lambda }_x){\tilde{U}}^T{\Sigma }_x,$$

where Λ_x is a p × p diagonal matrix whose first p elements are Λ₁,…,Λ_r, and they rest are zero. Because Λ₁ ≤ 1, we have

$$({\Sigma }_x-{𝒲}_1{𝒲}_1^T{)}^{1∕2}={\Sigma }_x\tilde{U}(I_p-{\Lambda }_x{)}^{1∕2}{\tilde{U}}^T{\Sigma }_x.$$

Similarly, we can show that

$$({\Sigma }_y-{𝒲}_2{𝒲}_2^T{)}^{1∕2}={\Sigma }_y\tilde{V}(I_q-{\Lambda }_y{)}^{1∕2}{\tilde{V}}^T{\Sigma }_y,$$

where Λ_y is the diagonal matrix whose first r elements are Λ₁,…,Λ_r, and the rest are zero. It can be easily verified that

$$Var(X)={𝒲}_1{𝒲}_1^T+{\mathscr{H}}_1={\Sigma }_x,Var(Y)={𝒲}_2{𝒲}_2^T+{\mathscr{H}}_2={\Sigma }_y,$$

and

$${\Sigma }_{xy}={𝒲}_1{𝒲}_2^T={\Sigma }_{x}U\Lambda V^T{\Sigma }_y,$$

which ensures that the joint variance of (X, Y) is still α. Also, some linear algebra leads to

$$\max \left\{\Vert {\mathscr{H}}_1{\Vert }_{op}^2,\Vert {\mathscr{H}}_2{\Vert }_{op}^2,\Vert {𝒲}_1{\Vert }_{op},\Vert {𝒲}_2{\Vert }_{op}\right\}<ℬ.$$ (36)

Suppose we have n independent realizations of the pseudoobservations Z₁, Z₂, and Z. Denote by Z₁, Z₂, and Z, the stacked data matrices with the i-th row as (Z₁)_i, (Z₂)_i, and Z_i, respectively, where i ∈ [n]. Here we used the term data-matrix although we do not observe Z, Z₁ and Z₂ directly. Due to the representation in (35), the data matrices X and Y have the form

$$\mathbf{X}=\mathbf{Z}{𝒲}_1^T+{\mathbf{Z}}_1{\mathscr{H}}_1,\mathbf{Y}=\mathbf{Z}{𝒲}_2^T+{\mathbf{Z}}_2{\mathscr{H}}_2.$$

We can write the covariance matrix ${\widehat{\Sigma }}_{n,xy}={\mathbf{X}}^T\mathbf{Y}∕n$ as

$$\begin{gathered} {\widehat{\Sigma }}_{n,xy}=\frac{1}{n}\{{𝒲}_1{\mathbf{Z}}^T\mathbf{Z}{𝒲}_2^T+{𝒲}_1{\mathbf{Z}}^T{\mathbf{Z}}_2{\mathscr{H}}_2+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T\mathbf{Z}{𝒲}_2^T\phantom{\}} \\ \phantom{\{}+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\mathscr{H}}_2\}. \end{gathered}$$ (37)

Therefore, for any vector ${\theta }_1\in {\mathbb{R}}^p$ and ${\theta }_2\in {\mathbb{R}}^q$, we have

$$\begin{gathered} {\theta }_1^T({\widehat{\Sigma }}_{n,xy}-{\Sigma }_{xy}){\theta }_2={\theta }_1^T{𝒲}_1^T\left(\frac{{\mathbf{Z}}^T\mathbf{Z}}{n}-I_r\right){𝒲}_2{\theta }_2 \\ +\frac{1}{n}{\theta }_1^T\left({𝒲}_1{\mathbf{Z}}^T{\mathbf{Z}}_2{\mathscr{H}}_2+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T\mathbf{Z}{𝒲}_2^T+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\mathscr{H}}_2\right){\theta }_2. \end{gathered}$$ (38)

By Bai-Yin law on eigenvalues of Wishart matrices [67], there exists abolute constant C > 0 so that for any t > 1,

$$P\left({\Vert \frac{{\mathbf{Z}}^T\mathbf{Z}}{n}-I_r\Vert }_{op}<t\sqrt{r∕n}\right)\ge 1-2\text{exp}(-C{t}^{2}r),$$

which, combined with (36), implies

$$\begin{gathered} \underset{\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)}{\text{inf}}\mathbb{P}(\mid {\theta }_1^T{𝒲}_1^T({\mathbf{Z}}^T\mathbf{Z}∕n-I_r){𝒲}_2{\theta }_2\mid \phantom{)} \\ \phantom{(}\le t{ℬ}^2\Vert {\theta }_1{\Vert }_2\Vert {\theta }_2{\Vert }_2\sqrt{r∕n}) \\ \ge 1-2\text{exp}(-C{t}^{2}r). \end{gathered}$$

Now we will state a lemma which will be required to control the other terms on the right hand side of (38).

Lemma 3. Suppose ${\mathbf{Z}}_1\in {\mathbb{R}}^{n\times p}$ and ${\mathbf{Z}}_2\in {\mathbb{R}}^{n\times q}$ are independent Gaussian data matrices. Further suppose $x\in {\mathbb{R}}^p$ and $y\in {\mathbb{R}}^q$ are either deterministic or independent of both Z₁ and Z₂. Then there exists a constant C > 0 so that for any t > 1,

$$P\left(\mid x^T{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}y\mid >t\Vert x{\Vert }_2\Vert y{\Vert }_2\sqrt{n}\right)\le \text{exp}(-Cn)-\text{exp}(t^2∕2).$$

The proof of Lemma 3 follows directly setting b = 1 in the following Lemma, which is proved in Appendix H-D.

Lemma 4. Suppose ${\mathbf{Z}}_1\in {\mathbb{R}}^{n\times p}$ and ${\mathbf{Z}}_2\in {\mathbb{R}}^{n\times q}$ are independent standard Gaussian data matrices, and $D\in {\mathbb{R}}^{n\times k_1}$ and $B\in {\mathbb{R}}^{n\times k_2}$ are deterministic matrices with rank a and b, respectively. Let a ≤ b ≤ n. Then there exists an absolute constant C > 0 so that for any t ≥ 0, the following holds with probability at least $1-\text{exp}(-Cn)-\text{exp}(-t^2∕2)$:

$$\Vert D^T{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}B{\Vert }_{op}\le C\Vert D{\Vert }_{op}\Vert B{\Vert }_{op}\sqrt{n}\max \{\sqrt{b},t\}.$$

Lemma 3, in conjunction with (36), implies that there exists an absolute constant C > 0 so that

$$\begin{gathered} \frac{1}{n}\mid {\theta }_1^T\left({𝒲}_1{\mathbf{Z}}^T{\mathbf{Z}}_2{\mathscr{H}}_2+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T\mathbf{Z}{𝒲}_2^T+{\mathscr{H}}_1^T{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\mathscr{H}}_2\right){\theta }_2\mid \\ \le t{ℬ}^2\Vert {\theta }_1{\Vert }_2\Vert {\theta }_2{\Vert }_2{n}^{-1∕2} \end{gathered}$$

with $\mathbb{P}$ probability at least $1-\text{exp}(-Cn)-\text{exp}(t^2∕2)$ for all $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$. Therefore, there exists C > 0 so that

$$\begin{gathered} \mathbb{P}\left(\mid {\theta }_1^T({\widehat{\Sigma }}_{n,xy}-{\Sigma }_{xy}){\theta }_2\mid \le t\sqrt{r}{ℬ}^2\Vert {\theta }_1{\Vert }_2\Vert {\theta }_2{\Vert }_2{n}^{-1∕2}\right) \\ \ge 1-\text{exp}(-Cn)-\text{exp}(-C{t}^2). \end{gathered}$$ (39)

for all $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$. Note that

$$\begin{gathered} T_1(i,k)\le \underset{T_{11}(i,k)}{\underbrace{\mid {\left(({\widehat{\Omega }}_n{)}_{k\ast }-({\Sigma }_y^{-1}{)}_{k\ast }\right)}^T({\widehat{\Sigma }}_{n,yx}-{\Sigma }_{yx}){\widehat{u}}_{n,i}\mid }} \\ +\underset{T_{12}(i,k)}{\underbrace{\mid {\left(({\widehat{\Omega }}_n{)}_{k\ast }-({\Sigma }_y^{-1}{)}_{k\ast }\right)}^T{\Sigma }_{yx}{\widehat{u}}_{n,i}\mid }}. \end{gathered}$$

Now suppose ${\theta }_1=({\widehat{\Omega }}_n{)}_{k\ast }-({\Sigma }_y^{-1}{)}_{k\ast }$ and ${\theta }_2={\widehat{u}}_{n,i}$. By our assumption, $\Vert {\theta }_1{\Vert }_2\le C_{\text{pre}}\sqrt{s({\Sigma }_y^{-1})(\log q)∕n}$ with $\mathbb{P}$ probability 1 – o(1) uniformly across $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$. We also showed that $\Vert {\widehat{u}}_{n,i}{\Vert }_2\le 2\sqrt{ℬ}$. It is not had to see that

$$\underset{i\in [q],k\in [r]}{\text{sup}}{T}_{12}(i,k)\le 2{ℬ}^{3∕2}{C}_{\text{pre}}\sqrt{s({\Sigma }_y^{-1})(\log q)∕n}$$ (40)

with $\mathbb{P}$ probability 1 – o(1) uniformly across $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$. For T₁₁, observe that (39) applies because ${\theta }_i=({\widehat{\Omega }}_n{)}_{k\ast }-({\Sigma }_y^{-1}{)}_{k\ast }$ and ${\theta }_2={\widehat{u}}_{n,i}$ are independent of ${\widehat{\Sigma }}_{n,xy}$. Thus we can write that for any t > 1, there exists $C_{ℬ}>1$ such that

$$\begin{gathered} \underset{\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)}{\text{sup}}\mathbb{P}\left(\mid T_{11}(i,k)\mid >t{C}_{ℬ}{C}_{\text{pre}}\sqrt{rs({\Sigma }_y^{-1})\log q}∕n\right) \\ \le \text{exp}(-Cn)+\text{exp}(-C{t}^2). \end{gathered}$$

Applying union bound, we obtain that for any $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$,

$$\begin{gathered} \mathbb{P}\left(\underset{i\in [q]}{\max }\underset{k\in [r]}{\max }\mid T_{11}(i,k)\mid >\frac{t{C}_{ℬ}{C}_{\text{pre}}\sqrt{rs({\Sigma }_y^{-1})\log q}}{n}\right) \\ \le \text{exp}(-Cn+\log (qr))+\text{exp}(-C{t}^2+\log (qr)). \end{gathered}$$

Since r < q and log q = o(n), setting $t=2\sqrt{\log q}∕C$, we obtain that

$$\underset{\begin{array}{c}\hfill \mathbb{P}\in \hfill \\ \hfill {𝒫}_G(r,s_x,s_y,ℬ)\hfill \end{array}}{\text{sup}}\mathbb{P}\left(\underset{i\in [q]}{\max }\underset{k\in [r]}{\max }\mid T_{11}(i,k)\mid >C_{ℬ}{C}_{\text{pre}}\sqrt{rs({\Sigma }_y^{-1})}\frac{\log q}{n}\right)$$

is o(1). Using (33) and (40), one can show that

$${ϵ}_n=C_{\text{pre}}\sqrt{s({\Sigma }_y^{-1})(\log (p+q))∕n}\max \{\sqrt{r(\log q)∕n},1\}$$

in this case.

3). Case (C):

Note that when ${\widehat{\Omega }}_n={\Sigma }_y^{-1},T_1(i,k)=0$. Therefore, (33) implies ${ϵ}_n=\sqrt{s({\Sigma }_y^{-1})\log (p+q)∕n}$ in this case.

Appendix D. Proof of Theorem 2

Since the proof for U and V follows in a similar way, we will only consider the support recovery of U. The proof for both cases follows a common structure. Therefore, we will elaborate the common structure first. Since the model $𝒫(r,s_x,s_y,ℬ)$ is fairly large, we will work with a smaller submodel. Specifically, we will consider a subclass of the single spike models, i.e., r = 1. Because we are concerned with only the support recovery of the left singular vectors, we fix ${\beta }_0$ in ${\mathbb{R}}^q$ so that $\Vert {\beta }_0{\Vert }_2=1$. We also fix ρ ∈ (0, 1) and consider the subset $ℰ\subset \{\alpha \in {\mathbb{R}}^p:\Vert \alpha {\Vert }_2=1\}$. Both ρ and $ℰ$ will be chosen later. We restrict our attention to the submodel $ℳ(s_x,s_y,\rho ,ℰ)$ given by

$$\begin{gathered} \{\mathbb{P}\in 𝒫(1,s_x,s_y,ℬ):\mathbb{P}\equiv N_{p+q}(0,\Sigma )\text{where}\Sigma \phantom{\}} \\ \phantom{\{}\text{is of the form}(41)\text{with}\alpha \in ℰ,\beta ={\beta }_0\}, \end{gathered}$$

where (41) is as follows:

$$\Sigma =\left[\begin{array}{cc}\hfill I_p\hfill & \hfill \rho \alpha {\beta }^T\hfill \\ \hfill \rho \beta {\alpha }^T\hfill & \hfill I_q\hfill \end{array}\right].$$ (41)

That Σ is positive definite for ρ ∈ (0, 1) can be shown either using elementary linear algebra or the the hidden variable representation (35). During the proof of part (B), we will choose $ℰ$ so that ${\text{Sig}}_x^2\le (B^2-1)(\log (p-s_x))∕8n$, which will ensure that $ℳ(s_x,s_y,\rho ,ℰ)\subset {𝒫}_{\text{Sig}}(r,s_x,s_y,ℬ)$ as well.

Note that for $\mathbb{P}\in ℳ(s_x,s_y,\rho ,ℰ)$, U corresponds to α, and hence D(U) = D(α). Therefore for the proof of both parts, it suffices to show that for any decoder ${\widehat{D}}_{\alpha }$ of D(α),

$$\underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in ℳ(s_x,s_y,ℰ)}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right)>1∕2.$$ (42)

In both of the proofs, our $ℰ$ will be a finite set. Our goal is to choose $ℰ$ so that $ℳ(s_x,s_y,\rho ,ℰ)$ is structurally rich enough to guarantee (42), yet lends itself to easy computations. The guidance for choosing $ℰ$ comes from our main technical tool for this proof, which is Fano’s inequality. We use the verson of Fano’s inequality in [53] (Fano’s Lemma). Applied to our problem, this inequality yields

$$\begin{gathered} \underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in ℳ(s_x,s_y,\rho ,ℰ)}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right) \\ \ge 1-\frac{\frac{{\sum }_{{\mathbb{P}}_1,{\mathbb{P}}_2\in ℳ(s_x,s_y,\rho ,ℰ)}KL({\mathbb{P}}_1^n\mid {\mathbb{P}}_2^n)}{\mid ℳ(s_x,s_y,\rho ,ℰ){\mid }^2}+\log 2}{\log (\mid ℳ(s_x,s_y,\rho ,ℰ)\mid -1)}, \end{gathered}$$ (43)

where ${\mathbb{P}}_n$ denotes the product measure corresponding to n i.i.d. observations from $\mathbb{P}$. We also have the following result for product measures, $KL({\mathbb{P}}_1^n\mid {\mathbb{P}}_2^n)=nKL({\mathbb{P}}_1\mid {\mathbb{P}}_2)$. Moreover, when ${\mathbb{P}}_1$, ${\mathbb{P}}_2\in ℳ(s_x,x_y,\rho ,ℰ)$ with left singular vectors ${\alpha }_1$ and ${\alpha }_2$, respectively,

$$KL({\mathbb{P}}_1\mid {\mathbb{P}}_2)=\log \frac{\text{det}({\Sigma }_2)}{\text{det}({\Sigma }_1)}-(p+q)+Tr({\Sigma }_2^{-1}{\Sigma }_1),$$

where $\text{det}({\Sigma }_1)=\text{det}({\Sigma }_2)=1-{\rho }^2$ by Lemma 13, and

$$-(p+q)+Tr({\Sigma }_2^{-1}{\Sigma }_1)=\frac{2{\rho }^2}{1-{\rho }^2}\left(1-({\alpha }_1^T{\alpha }_2)\Vert {\beta }_0{\Vert }_2^2\right)$$

by Lemma 14. Noting ${\alpha }_1$, ${\alpha }_2$, and ${\beta }_0$ are unit vectors, we derive $KL({\mathbb{P}}_1\mid {\mathbb{P}}_2)={\rho }^2(\Vert {\alpha }_1-{\alpha }_2{\Vert }_2^2)∕(1-{\rho }^2)$. Therefore, in our case, (43) reduces to

$$\begin{gathered} \underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in ℳ(s_x,s_y,\rho ,ℰ)}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right) \\ \ge 1-\frac{n{\rho }^2{\text{sup}}_{{\alpha }_1,{\alpha }_2\in ℰ}\Vert {\alpha }_1-{\alpha }_2{\Vert }^2∕(1-{\rho }^2)+\log 2}{\log (\mid ℰ\mid -1)}. \end{gathered}$$ (44)

Thus, to ensure the right hand side of (44) is non-negligible, the key is to choose $ℰ$ so that the α’s in $ℰ$ are close in l₂ norm, but $\mid ℰ\mid$ is sufficiently large. Note that the above ensures that distinguishing the α’s in $ℰ$ is difficult.

A. Proof of part (A)

Note that our main job is to choose $ℰ$ and ρ suitably. Let us denote

$${\alpha }_0=(\underset{s_x\text{many}}{\underbrace{1∕{\sqrt{s}}_x,\dots ,1∕{\sqrt{s}}_x}},\underset{p-s_x\text{many}}{\underbrace{0,\dots ,0}}).$$

We generate a class of α’s by replacing one of the $1∕{\sqrt{s}}_x$ in ${\alpha }_0$ by 0, and one of the zero’s in ${\alpha }_0$ by $1∕{\sqrt{s}}_x$. A typical α obtained this way looks like

$$\alpha =\left(\underset{s_x\text{many}}{\underbrace{(1∕{\sqrt{s}}_x,\dots ,0,\dots 1∕{\sqrt{s}}_x}},\underset{p-s_x\text{many}}{\underbrace{0,\dots ,1∕\sqrt{{\mathrm{s}}_{\mathrm{x}}},\dots ,0}}\right).$$

Let $ℰ$ be the class, which consists of ${\alpha }_0$, and all such resulting α’s. Note that $\mid ℰ\mid =s_x(p-s_x)$, and ${\alpha }_1$, ${\alpha }_2\in ℰ$ satisfy

$$\Vert {\alpha }_1-{\alpha }_2{\Vert }_2^2\Vert \le \Vert {\alpha }_1-{\alpha }_0{\Vert }_2^2+\Vert {\alpha }_2-{\alpha }_0{\Vert }_2^2\le 4s_x^{-1}.$$

Because p > s_x > 1, we have

$$\log (s_x(p-s_x)-1)\ge \log (p-s_x).$$

Therefore, (44) leads to

$$\begin{gathered} \underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{\mathbb{P}\in ℳ(s_x,s_y,\rho ,ℰ)}{\text{sup}}\mathbb{P}\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right) \\ \ge 1-\frac{4{\rho }^{2}n{s}_x^{-1}∕(1-{\rho }^2)+\log 2}{\log (p-s_x)}, \end{gathered}$$

which is bounded below by 1/2 whenever

$$s_x>\frac{8{\rho }^{2}n}{(1-{\rho }^2)\{\log (p-s_x)-\log 4\}},$$

which follows if

$$s_x>\frac{16{\rho }^{2}n}{(1-{\rho }^2)\log (p-s_x)}$$

because $4=\sqrt{16}<\sqrt{p-s_x}$. To get the best bound on s_x, we choose the value of ρ which minimizes ρ²/(1 – ρ²) for $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$, that is $\rho =1∕ℬ$. Plugging in $\rho =1∕ℬ$, the proof follows.

B. Proof of part (B)

Suppose each $\alpha \in ℰ$ is of the following form

$$\alpha =\left(\underset{s_x-1\text{many}}{\underbrace{b,\dots ,b}},\underset{p-s_x+1\text{many}}{\underbrace{0,\dots ,0,z,0,\dots ,0}}\right).$$

We fix z ∈ (0, 1), and hence $b=\sqrt{(1-z^2)∕(s_x-1)}$ is also fixed. We will choose the value of ρ and z later so that ${𝒫}_{\text{Sig}}(r,s_x,s_y,ℬ)\supset ℳ(s_x,s_y,\rho ,ℰ)$. Since z is fixed, such an α can be chosen in p–s_x + 1 ways. Therefore $\mid ℰ\mid =p-s_x+1$. Also note that for α, ${\alpha }^{\prime }\in ℰ$, $\Vert \alpha -{\alpha }^{\prime }{\Vert }_2^2\le 2z^2$. Therefore (44) implies

$$\underset{{\widehat{D}}_{\alpha }}{\text{inf}}\underset{P\in ℳ(s_x,s_y,\rho ,ℰ)}{\text{sup}}P\left({\widehat{D}}_{\alpha }\ne D(\alpha )\right)$$ (45)

$$\ge 1-\frac{2n{\rho }^2{z}^2∕(1-{\rho }^2)+\log 2}{\log (p-s_x)},$$ (46)

which is greater than 1/2 whenever

$$z^2<\frac{1-{\rho }^2}{4n{\rho }^2}\log \left(\frac{p-s_x}{4}\right),$$

which holds if

$$z^2=\frac{1-{\rho }^2}{8n{\rho }^2}\log (p-s_x)$$

because 16 < p – s_x. To get the best bound on z, we choose the value of ρ for $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$ which maximizes (1 – ρ²)/ρ², that is $\rho =1∕ℬ$. Thus (42) is satisfied when $\rho =1∕ℬ$, and $ℰ$ corresponds to

$$z^2=({ℬ}^2-1)log(p-s_x)∕\left(8_n\right)$$

Since the minimal signal strength Sig_x for any $\mathbb{P}\in ℳ(s_x,s_y,{ℬ}^{-1},ℰ)$ equals min(z, b) ≤ z, we have ${𝒫}_{\text{Sig}}(r,s_x,s_y,ℬ)\supset ℳ(s_x,s_y,{ℬ}^{-1},ℰ)$, which completes the proof.

Appendix E. Proof of Theorem 3

We first introduce some notations and terminologies that are required for the proof. For $w\in {\mathbb{Z}}^m$, and $x\in {\mathbb{R}}^m$, we denote $w!={\prod }_{i=1}^m{w}_i!$ and $x^w={\prod }_{i=1}^m{x}_i^{w_i}$. In low-degree polynomial literature, when $w\in {\mathbb{Z}}^m$, the notation ∣w∣ is commonly used to denote the sum ${\sum }_{i=1}^n{w}_i$ for sake of simplicity. We also follow the above convention. Here the notation ∣·∣ should not be confused with the absolute value of real numbers. Also, for any function $f:{\mathbb{R}}^m\mapsto \mathbb{R}$, $w\in {\mathbb{Z}}^m$, and t = (t₁,…, t_m), we denote

$${\partial }_t^{w}f(t)=\frac{{\partial }^{\mid w\mid }}{\partial t_1^{w_1}\cdots \partial t_r^{w_r}}f(t).$$

We will also use the shorthand notation ${\mathbb{E}}_{\pi }$ to denote ${\mathbb{E}}_{\alpha \sim {\pi }_x,\beta \sim {\pi }_y}$, sometimes.

Our analysis relies on the Hermite polynomial, which we will discuss here very briefly. For a detailed account on the Hermite polynomials, see Chapter V of [62]. The univariate Hermite polynomials of degree k will be denoted by h_k. For k ≥ 0, the univariate Hermite polynomials $h_k:\mathbb{R}\mapsto \mathbb{R}$ are defined recursively as follows:

$$\begin{gathered} h_0(x)=1,h_1(x)=x{h}_0(x),\dots , \\ {h}_{k+1}(x)=x{h}_k(x)-h_k^{\prime }(x). \end{gathered}$$

The normalized univariate Hermite polynomials are given by ${\widehat{h}}_k(x)=h_k(x)∕\sqrt{k!}$. The univariate Hermite polynomials form an orthogonal basis of L₂(N(0, 1)). For $w\in {\mathbb{Z}}^m$, the m-variate Hermite polynomials are given by $H_w(y)={\prod }_{i=1}^m{h}_{w_i}(y_i)$, where $y\in {\mathbb{R}}^m$. The normalized version ${\widehat{H}}_w$ of H_w equals $H_w∕\sqrt{w!}$. The polynomials ${\widehat{H}}_w’\mathrm{s}$ form an orthogonal basis of L₂(N_m(0, I_m)). We denote by ${\Pi }_n^{\le D_n}$ the linear span of all n(p + q)-variate Hermite polynomials of degree at most D_n. Since ${\mathbb{L}}_n^{\le D_n}$ is the projection of ${\mathbb{L}}_n$ on ${\Pi }^{\le D_n}$, it then follows that

$$\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2=\sum _{\begin{array}{c}\hfill w\in {\mathbb{Z}}^{n(p+q)}\hfill \\ \hfill \mid w\mid \le D_n\hfill \end{array}}\langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^2.$$ (47)

From now on, the degree-index vector w of ${\widehat{H}}_w$ or H_w will be assumed to lie in ${\mathbb{Z}}^{n(p+q)}$. We will partition w into n components, which gives w = (w₁,…,w_n), where $w_i\in {\mathbb{Z}}^{p+q}$ for each i ∈ [n]. Clearly, i here corresponds to the i-th observation. We also separate each w_i into two parts $w_i^x\in {\mathbb{Z}}^p$ and $w_i^y\in {\mathbb{Z}}^q$ so that $w_i=(w_i^x,w_i^y)$. We will also denote $w^x=(w_1^x,\dots ,w_n^x)$, and $w_y=(w_1^y,\dots ,w_n^y)$. Note that $w^x\in {\mathbb{Z}}^{np}$ and $w^y\in {\mathbb{Z}}^{nq}$, but w ≠ (w^x, w^y) in general, although ∣w∣= ∣w^x∣+∣w^y∣.

Now we state the main lemmas which yields the value of $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$. The first lemma, proved in Appendix H-C, gives the form of the inner products $\langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}$.

Lemma 5. Suppose w is as defined above and ${\mathbb{L}}_n$ is as in (20). Then it holds that

$$\begin{gathered} \langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^2 \\ =\{\begin{array}{c}\frac{{ℬ}^{-\mid w\mid }}{w!}{\left\{{\mathbb{E}}_{\pi }\left[1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}{\alpha }^{{\sum }_{i=1}^n{w}_i^x}{\beta }^{{\sum }_{i=1}^n{w}_i^y}\right]\right\}}^2\hfill \\ \times {\left({\prod }_{i=1}^n\mid w_i^x\mid !\right)}^{2}if\mid w_i^x\mid =\mid w_i^y\mid foralli\in [n],\hfill \\ 0o.w.\hfill \end{array}\phantom{\}} \end{gathered}$$

Here the priors π_x and π_y are the Rademacher priors defined in (17).

Our next lemma uses Lemma 5 to give the form of $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$. This lemma uses replicas of α and β. Suppose ${\alpha }_1$, ${\alpha }_2\sim {\pi }_y$ and ${\beta }_1$, ${\beta }_2\sim {\pi }_y$ are all independent Rademacher priors, where π_x and π_y are defined as in (17). We overload notation, and use ${\mathbb{E}}_{\pi }$ to denote the expectation under ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$, and ${\beta }_2$.

Lemma 6. Suppose W is the indicator function of the event $\{\Vert {\alpha }_1{\Vert }_2\Vert {\beta }_1{\Vert }_2<ℬ$, $\Vert {\alpha }_2{\Vert }_2\Vert {\beta }_2{\Vert }_2<ℬ\}$. Then For any $D_n\in \mathbb{N}$, $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$ equals

$${\mathbb{E}}_{\pi }\left[W\sum _{d=0}^{\lfloor D_n∕2\rfloor }\left(\begin{array}{c}\hfill d+n-1\hfill \\ \hfill d\hfill \end{array}\right){\left\{{ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\right\}}^d\right].$$

The proof of Lemma 6 is also deferred to Appendix H-C. We remark in passing that the negative binomial series expansion yields

$$(1-x{)}^{-n}=\sum _{d=0}^{\infty }\left(\begin{array}{c}\hfill n+d-1\hfill \\ \hfill d\hfill \end{array}\right)x^d,\text{for}\mid x\mid <1,$$ (48)

whose D_n-th order truncation equals

$${\left((1-x{)}^{-n}\right)}^{\le D_n}=\sum _{d=0}^{D_n}\left(\begin{array}{c}\hfill n+d-1\hfill \\ \hfill d\hfill \end{array}\right)x^d.$$

Note that W is nonzero if and only if $\Vert {\alpha }_1{\Vert }_2\Vert {\beta }_1{\Vert }_2<ℬ$ and $\Vert {\alpha }_2{\Vert }_2\Vert {\beta }_2{\Vert }_2<ℬ$, which, by Cauchy Schwarz inequality, implies

$$\mid ({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\mid <{ℬ}^2.$$

Thus $\mid {ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\mid <1$ when W = 1. Hence Lemma 6 can also be written as

$$\begin{gathered} \Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2 \\ ={\mathbb{E}}_{\pi }\left[W{\left\{{\left(1-{ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\right)}^{-n}\right\}}^{\le \lfloor D_n∕2\rfloor }\right]. \end{gathered}$$

Now we are ready to prove Theorem 3.

Proof of Theorem 3. Our first task is to get rid of W from the expression of $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}$ in Lemma 6. However, we can not directly bound W by one since the term $({\alpha }_1^T{\alpha }_2{)}^d({\beta }_1^T{\beta }_2{)}^{d}W$ may be negative for odd $d\in \mathbb{N}$. We claim that $\mathbb{E}[({\alpha }_1^T{\alpha }_2{)}^d({\beta }_1^T{\beta }_2{)}^{d}W]=0$ if $d\in \mathbb{N}$ is odd. To see this, first we write

$$\mathbb{E}\left[({\alpha }_1^T{\alpha }_2{)}^d({\beta }_1^T{\beta }_2{)}^{d}W\right]=\mathbb{E}\left[\mathbb{E}\phantom{[}[({\alpha }_1^T{\alpha }_2{)}^{d}W\mid {\beta }_1,{\beta }_2]({\beta }_1^T{\beta }_2{)}^d\right].$$ (49)

Note that $({\alpha }_1^T{\alpha }_2{)}^{d}W\mid {\beta }_1$, ${\beta }_2$ has the same distribution as

$$1\{\Vert {\alpha }_1{\Vert }_2<ℬ\Vert {\beta }_1{\Vert }_2^{-1}\}1\{\Vert {\alpha }_2{\Vert }_2<ℬ\Vert {\beta }_2{\Vert }_2^{-1}\}({\alpha }_1^T{\alpha }_2).$$

Notice from (17) that marginally, ${\alpha }_1\stackrel{d}{=}-{\alpha }_1$, and ${\alpha }_1$ is independent of ${\alpha }_2$, ${\beta }_1$ and ${\beta }_2$. Therefore,

$$({\alpha }_1^T{\alpha }_2)W\mid {\beta }_1,{\beta }_2\stackrel{d}{=}-({\alpha }_1^T{\alpha }_2)W\mid {\beta }_1,{\beta }_2.$$

Hence, conditional on ${\beta }_1$ and ${\beta }_2$, $({\alpha }_1^T{\alpha }_2)W$ is a symmetric random variable, and $\mathbb{E}[({\alpha }_1^T{\alpha }_2{)}^d{W}^d\mid {\beta }_1,{\beta }_2]=0$ for any odd positive integer d. Since W is binary random variable, W^d = W. Thus, $\mathbb{E}[({\alpha }_1^T{\alpha }_2{)}^{d}W\mid {\beta }_1,{\beta }_2]=0$ as well for an odd number $d\in \mathbb{N}$. Thus the claim follows from (49). Therefore, from Lemma 6, it follows that

$$\begin{gathered} \Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2 \\ ={\mathbb{E}}_{\pi }\left[W\sum _{d=0}^{\lfloor \frac{\lfloor \frac{D_n}{2}\rfloor }{2}\rfloor }\left(\begin{array}{c}\hfill 2d+n-1\hfill \\ \hfill 2d\hfill \end{array}\right){\left\{{ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\right\}}^{2d}\right]. \end{gathered}$$

Observe that $\lfloor \lfloor D_n∕2\rfloor ∕2\rfloor \le D_n∕4$. Hence, $\lfloor \lfloor D_n∕2\rfloor ∕2\rfloor \le \lfloor D_n∕4\rfloor$. Also the summands in the last expression are non-negative. Therefore, using the fact that W ≤ 1, we obtain

$$\begin{gathered} \Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2 \\ \le {\mathbb{E}}_{\pi }\left[\sum _{d=0}^{\lfloor D_n∕4\rfloor }\left(\begin{array}{c}\hfill 2d+n-1\hfill \\ \hfill 2d\hfill \end{array}\right){\left\{{ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2)\right\}}^{2d}\right]. \end{gathered}$$ (50)

Our next step is to simplify the above bound on $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$. To that end, define the random variables ${\xi }_i={\alpha }_{1i}{\alpha }_{2i}$ for $i\in [p]$, and ${\xi }_j^{\prime }={\beta }_{1j}{\beta }_{2j}$ for $j\in [q]$. Denoting

$$\nu =(s_x∕p{)}^2,\text{and}\omega =(s_y∕q{)}^2,$$

we note that

$${\xi }_i=\{\begin{array}{cc}\frac{+1}{s_x}\hfill & w.p.\nu ∕2\hfill \\ \frac{-1}{s_x}\hfill & w.p.\nu ∕2\hfill \\ 0\hfill & w.p.1-\nu ,\hfill \end{array}\phantom{\}}\text{and}{\xi }_j^{\prime }=\{\begin{array}{cc}\frac{+1}{s_y}\hfill & w.p.\omega ∕2\hfill \\ \frac{-1}{s_y}\hfill & w.p.\omega ∕2\hfill \\ 0\hfill & w.p.1-\omega .\hfill \end{array}\phantom{\}}$$

Also, since ${\xi }_i$ and ${\xi }_j’\mathrm{s}$ are symmetric, $\mathbb{E}{\xi }_i^{2k+1}$ and $\mathbb{E}{\xi }_j^{2k+1}$ vanishes for any $k\in \mathbb{Z}$. Then for any $d\in \mathbb{Z}$,

$$\begin{gathered} {\mathbb{E}}_{\pi }\left[({\alpha }_1^T{\alpha }_2{)}^{2d}({\beta }_1^T{\beta }_2{)}^{2d}\right] \\ =E_{{\pi }_x}\left[{\left(\sum _{i=1}^p{\xi }_i\right)}^{2d}\right]E_{{\pi }_y}\left[{\left(\sum _{j=1}^q{\xi }_j^{\prime }\right)}^{2d}\right] \\ =\left(\sum _{\begin{array}{c}\hfill z\in {\mathbb{Z}}^p,\hfill \\ \hfill \mid z\mid =2d\hfill \end{array}}\frac{(2d)!}{z!}\prod _{i=1}^p\mathbb{E}\left[{\xi }_i^{z_i}\right]\right)\left(\sum _{\begin{array}{c}\hfill l\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid l\mid =2d\hfill \end{array}}\frac{(2d)!}{l!}\prod _{j=1}^q\mathbb{E}\left[({\xi }_j^{\prime }{)}^{l_j}\right]\right) \end{gathered}$$

by Fact 6. Since the odd moments of $\xi$ and ${\xi }^{\prime }$ vanish, the above equals

$$\begin{gathered} \left(\sum _{\begin{array}{c}\hfill z\in {\mathbb{Z}}^p,\hfill \\ \hfill \mid z\mid =2d\hfill \end{array}}\frac{(2d)!}{(2z)!}\prod _{i=1}^p\mathbb{E}\left[{\xi }_i^{2z_i}\right]\right)\left(\sum _{\begin{array}{c}\hfill l\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid l\mid =d\hfill \end{array}}\frac{(2d)!}{(2l)!}\prod _{j=1}^q\mathbb{E}\left[({\xi }_j^{\prime }{)}^{2l_j}\right]\right) \\ =\left(\sum _{\begin{array}{c}\hfill z\in {\mathbb{Z}}^p,\hfill \\ \hfill \mid z\mid =d\hfill \end{array}}\frac{{\nu }^{\mid D(z)\mid }(2d)!}{(2z)!}\prod _{i=1}^p{s}_x^{-2z_i}\right) \\ \times \left(\sum _{\begin{array}{c}\hfill l\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid l\mid =d\hfill \end{array}}\frac{{\omega }^{\mid D(z)\mid }(2d)!}{(2l)!}\prod _{j=1}^q{s}_y^{-2l_j}\right), \end{gathered}$$

where we remind the readers that ∣D(z)∣ denotes the cardinality of the support of z for any vector z. The above implies

$$\begin{gathered} {\mathbb{E}}_{\pi }\left[({\alpha }_1^T{\alpha }_2{)}^{2d}({\beta }_1^T{\beta }_2{)}^{2d}\right] \\ =(s_x{s}_y{)}^{-2d}\underset{𝒥(d;p)}{\underbrace{\sum _{\begin{array}{c}\hfill z\in {\mathbb{Z}}^p,\hfill \\ \hfill \mid z\mid =d\hfill \end{array}}\frac{(2d)!}{(2z)!}{\nu }^{\mid D(z)\mid }}}\underset{𝒥(d;q)}{\underbrace{\sum _{\begin{array}{c}\hfill l\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid l\mid =d\hfill \end{array}}\frac{(2d)!}{(2l)!}{\nu }^{\mid D(l)\mid }}}. \end{gathered}$$

Plugging the above into (50) yields

$$\begin{gathered} \Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2 \\ \le \sum _{d=0}^{\lfloor D_n∕4\rfloor }\left(\begin{array}{c}\hfill 2d+n-1\hfill \\ \hfill 2d\hfill \end{array}\right)(s_x{s}_y{)}^{-2d}{ℬ}^{-4d}𝒥(d;p){𝒥}_d(d;q) \\ \stackrel{(a)}{\le }\sum _{d=0}^{\lfloor D_n∕4\rfloor }{\left(\frac{(2d+n-1)e}{2d}\right)}^{2d}(s_x{s}_y{)}^{-2d}{ℬ}^{-4d}𝒥(d;p)𝒥(d;q), \end{gathered}$$

where (a) follows since $\left(\begin{array}{c}\hfill a\hfill \\ \hfill b\hfill \end{array}\right)\le (ae∕b{)}^b$ for a, $b\in \mathbb{N}$. Let us denote ${\mu }_x=\sqrt{ne}∕(\sqrt{p}ℬ)$ and ${\mu }_y=\sqrt{ne}∕(\sqrt{q}ℬ)$. By (21), ${\mu }_x$, ${\mu }_y<1∕\sqrt{3}$ and

$$D_n\le \frac{\text{min}\{s_y^2,s_x^2\}{ℬ}^2}{ne}.$$

Therefore we have

$${\mu }_x^2{D}_n<\frac{s_x^2}{p}\text{and}{\mu }_y^2{D}_n<\frac{s_y^2}{q}.$$

Hence Lemma 4.5 of [36] implies that for any 11 ≤ d ≤ D_n,

$$\begin{gathered} 𝒥(d;p)\lesssim (2d)!\left(\begin{array}{c}\hfill p\hfill \\ \hfill d\hfill \end{array}\right)\sqrt{d}{e}^{d^2∕p+d∕2}{2}^{-3d∕2}{\mu }_x^{-2d}{\nu }^d, \\ 𝒥(d;q)\lesssim (2d)!\left(\begin{array}{c}\hfill q\hfill \\ \hfill d\hfill \end{array}\right)\sqrt{d}{e}^{d^2∕q+d∕2}{2}^{-3d∕2}{\mu }_y^{-2d}{\omega }^d. \end{gathered}$$

For d ≤ 1, Theorem 5 of [68] gives

$$(2d)!\le \frac{(2d{)}^{2d+1}{e}^{-2d}\sqrt{2\pi }}{\sqrt{2d-1}}.$$

Also since $\left(\begin{array}{c}\hfill p\hfill \\ \hfill d\hfill \end{array}\right)\le (pe∕d{)}^d$, we have

$$\begin{gathered} 𝒥(d;p)\lesssim (2d{)}^{2d+1∕2}{\left(\frac{pe}{d}\right)}^d\sqrt{d}{e}^{d^2∕p-d}{2}^{-3d∕2}{\mu }_x^{-2d}{\nu }^d, \\ 𝒥(d;q)\lesssim (2d{)}^{2d+1∕2}{\left(\frac{qe}{d}\right)}^d\sqrt{d}{e}^{d^2∕q-d}{2}^{-3d∕2}{\mu }_y^{-2d}{\omega }^d, \end{gathered}$$

leading to

$$𝒥(d;p)𝒥(d;q)\lesssim d^{2d+2}{e}^{d^2∕p+d^2∕q}{2}^{d+1}({\mu }_x{\mu }_y{)}^{-2d}(\nu p{)}^d(\omega q{)}^d.$$

Therefore $\Vert {\mathbb{L}}_n^{\le D}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$ is bounded by a constant multiple of

$$\begin{gathered} \sum _{d=11}^{\lfloor D_n∕4\rfloor }{\left(\frac{(2d+n-1)e}{2d}\right)}^{2d}(s_x{s}_y{)}^{-2d}{d}^{2d+2}{e}^{d^2∕p+d^2∕q} \\ \times 2^{d+1}({\mu }_x{\mu }_y{)}^{-2d}(\nu p{)}^d(\omega q{)}^d{ℬ}^{-4d} \\ \lesssim \sum _{d=11}^{\lfloor D_n∕4\rfloor }d{\left\{\frac{{ℬ}^{-4}(2d+n-1{)}^2{e}^2}{2{\mu }_x^2{\mu }_y^{2}pq}\right\}}^d{e}^{d^2∕p+d^2∕q}. \end{gathered}$$

Since $D_n^2\le \text{min}\{p,q\}$, it follows that $e^{d^2∕p+d^2∕q}\le e^2$. Note that the above sum converges if

$$(D_n∕2+n-1{)}^2{e}^2<2{ℬ}^4{\mu }_x^2{\mu }_y^{2}pq=2n^2{e}^2,$$

or equivalently $(D_n∕2+n-1{)}^2<2n^2$, which is satisfied for all $n\in \mathbb{N}$ since $D_n<n$. Thus the proof follows. □

Appendix F. Proof of Theorem 4

We invoke the decomposition of ${\widehat{\Sigma }}_{n,xy}$ in (37). But first, we will derive a simplified form for the matrices ${\mathscr{H}}_1$ and ${\mathscr{H}}_2$ in (37). Note that we can write ${\mathscr{H}}_1$ as

$${\mathscr{H}}_1={\Sigma }_x^{1∕2}(I_p-{\Sigma }_x^{1∕2}U\Lambda U^T{\Sigma }_x^{1∕2}){\Sigma }_x^{1∕2}.$$

Let us denote

$$B_x=\text{diag}(\underset{r\text{times}}{\underbrace{1-{\Lambda }_1,\dots ,1-{\Lambda }_r}},\underset{p-r\text{times}}{\underbrace{1,\dots ,1}}).$$ (51)

Because ${\Sigma }_x^{1∕2}\tilde{U}$ is an orthogonal matrix, ${\Sigma }_x^{1∕2}\tilde{U}{B}_x{\tilde{U}}^T{\Sigma }_x^{1∕2}$ is a spectral decomposition, which leads to

$${\mathscr{H}}_1={\Sigma }_x^{1∕2}{\left({\Sigma }_x^{1∕2}\tilde{U}{B}_x{\tilde{U}}^T{\Sigma }_x^{1∕2}\right)}^{1∕2}{\Sigma }_x^{1∕2}={\Sigma }_x\tilde{U}{B}_x^{1∕2}{\tilde{U}}^T{\Sigma }_x.$$

Similarly, we can show that the matrix ${\mathscr{H}}_2$ in (37) equals ${\Sigma }_y\tilde{V}{B}_y^{1∕2}{\tilde{V}}^T{\Sigma }_y$, where

$$B_y=\text{diag}(\underset{r\text{times}}{\underbrace{1-{\Lambda }_1,\dots ,1-{\Lambda }_r}},\underset{q-r\text{times}}{\underbrace{1,\dots ,1}}).$$

Finally the fact that ${\mathscr{H}}_1={\Sigma }_{x}U{\Lambda }^{1∕2}$ and ${𝒲}_2={\Sigma }_{y}V{\Lambda }^{1∕2}$ in conjuction with (37) produces the following representation for ${\tilde{\Sigma }}_{xy}={\Sigma }_x^{-1}{\widehat{\Sigma }}_{n,xy}{\Sigma }_y^{-1}$:

$$\begin{gathered} {\tilde{\Sigma }}_{xy}=\frac{1}{n}\{U{\Lambda }^{1∕2}{\mathbf{Z}}^T\mathbf{Z}{\Lambda }^{1∕2}{V}^T+U{\Lambda }^{1∕2}{\mathbf{Z}}^T{\mathbf{Z}}_2{\Sigma }_y(\tilde{V}{B}_y{\tilde{V}}^T)\phantom{\}} \\ +(\tilde{U}{B}_y{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T\mathbf{Z}{\Lambda }^{1∕2}{V}^T \\ \phantom{\{}+(\tilde{U}{B}_x{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\Sigma }_y(\tilde{V}{B}_y{\tilde{V}}^T)\}. \end{gathered}$$

Now recall the sets E, F, and G defined in (24) and (25) in Section III-D, and the decomposition of ${\tilde{\Sigma }}_{xy}$ in (26). From (26) it follows that

$$\eta ({\tilde{\Sigma }}_{xy})=\eta ({𝒫}_E\{{\tilde{\Sigma }}_{xy}\})+\eta ({𝒫}_F\{{\tilde{\Sigma }}_{xy}\})+\eta ({𝒫}_G\{{\tilde{\Sigma }}_{xy}\}).$$

Recall that for any matrix $A\in {\mathbb{R}}^{p\times q}$, and $S\subset [p]$, we denote by $A_{S^{\ast }}$ the matrix ${𝒫}_{S\times [q]}\{A\}$. Then it is not hard to see that $U_{E_1^{\ast }}=U$ and $V_{E_2^{\ast }}=V$, which leads to

$$\begin{gathered} {\mathbf{S}}_1=\frac{1}{n}\{U{\Lambda }^{1∕2}{\mathbf{Z}}^T\mathbf{Z}{\Lambda }^{1∕2}{V}^T\phantom{\}} \\ +U{\Lambda }^{1∕2}{\mathbf{Z}}^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right) \\ +({\tilde{U}}_{E_1\ast }{B}_y{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T\mathbf{Z}{\Lambda }^{1∕2}{V}^T \\ \phantom{\{}+({\tilde{U}}_{E_1\ast }{B}_x{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)\}. \end{gathered}$$ (52)

Next, note that $U_{F_1\ast }=0$ and $V_{F_2\ast }=0$. Therefore,

$${\mathbf{S}}_2=\frac{1}{n}\left\{({\tilde{U}}_{F_1\ast }{B}_x{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{F_2\ast }{)}^T\right)\right\}.$$ (53)

Finally, we note that S₃ = (H₁ + H₂), where

$$\begin{gathered} {\mathbf{H}}_1=\frac{1}{n}\{(U{\Lambda }^{1∕2}{\mathbf{Z}}^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{F_2\ast }{)}^T\right)\phantom{\}} \\ \phantom{\{}+({\tilde{U}}_{E_1\ast }{B}_x{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{F_2\ast }{)}^T\right)\} \end{gathered}$$ (54)

and

$$\begin{gathered} {\mathbf{H}}_2=\frac{1}{n}\{({\tilde{U}}_{F_1\ast }{B}_y{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T\mathbf{Z}{\Lambda }^{1∕2}{V}^T\phantom{\}} \\ \phantom{\{}+({\tilde{U}}_{F_1\ast }{B}_x{\tilde{U}}^T){\Sigma }_x{\mathbf{Z}}_1^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)\}. \end{gathered}$$

Here the term S₁ holds the information about ${\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}=U\Lambda V^T$. Its elements are not killed off by co-ordinate thresholding because it contains the Wishart matrix ${\mathbf{Z}}^T\mathbf{Z}$ which concentrates around I_r by Bai-Yin law (cf. Theorem 4.7.1 of of [42]). The only term that contributes to ${\widehat{\Sigma }}_{n,xy}$ is S₁. Lemma 7 entails that η(S₁) concentrates around ${\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}$ in operator norm. The proof of Lemma 7 is deferred to Appendix H-B.

Lemma 7. Suppose $s_x$, $s_y<n$. Then with probability 1 – o(1),

$$\begin{gathered} \Vert \eta ({\mathbf{S}}_1)-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le \frac{Thr\text{min}\{s_x,s_y\}}{\sqrt{n}} \\ +C{ℬ}^2\frac{\max \{\sqrt{s_x},\sqrt{s_y}\}}{\sqrt{n}}. \end{gathered}$$

The entries of S₂ and S₃ are linear combinations of the entries of ${\mathbf{Z}}_1^T{\mathbf{Z}}_2$, ${\mathbf{Z}}^T{\mathbf{Z}}_1$ and ${\mathbf{Z}}^T{\mathbf{Z}}_2$. Since Z, Z₁, Z₂ are independent, the entries from the latter matrices are of order O_p(n^−1/2), and as we will see, they are killed off by the thresholding operator η. Our main work boils down to showing that thresholding kills off most terms of the noise matrices S₂ and S₃, making $\Vert \eta ({\mathbf{S}}_2){\Vert }_{op}$ and $\Vert \eta ({\mathbf{S}}_3){\Vert }_{op}$ small. To that end, we state some general lemmas, which are proved in Appendix H-B. That $\Vert \eta ({\mathbf{S}}_2){\Vert }_{op}$ and $\Vert \eta ({\mathbf{S}}_3){\Vert }_{op}$ are small follows as corollaries to this lemmas. Our next lemma provides a sharp concentration bound which is our main tool in analyzing the difficult regime, i.e., $s_x+s_y\approx \sqrt{p+q}$ case.

Lemma 8. Suppose ${\mathbf{Z}}_1\in {\mathbb{R}}^{n\times p}$ and ${\mathbf{Z}}_2\in {\mathbb{R}}^{n\times q}$ are independent standard Gaussian data matrices. Let us also denote ${\mathbf{Q}}_{M,N}=M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N$ where $M\in {\mathbb{R}}^{p^{\prime }\times p}$ and $N\in {\mathbb{R}}^{q\times q^{\prime }}$ are fixed matrices so that $p^{\prime }\le p$ and $q^{\prime }\le q$. Further suppose $\log (p\vee q)=o(n)$ and $\log n=o(\sqrt{p}\vee \sqrt{q})$. Let $K_0=161\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2$. Suppose K ≥ K₀ is such that threshold level τ satisfies $\tau \in [\sqrt{K_0},\sqrt{K\log (\max \{p,q\})}∕2]$. Then there exists a constant C > 0 so that with probability 1 – o(1),

$$\begin{gathered} \Vert \eta ({\mathbf{Q}}_{M,N};\tau ∕\sqrt{n}){\Vert }_{op}\le C\Vert M{\Vert }_{op}\Vert N{\Vert }_{op}\left(\sqrt{\frac{p+q}{n}}\vee \frac{p+q}{n}\right) \\ \times e^{-{\tau }^2∕K}. \end{gathered}$$

Our next lemma, which also is proved in Appendix H-B, handles the easier case when the threshold is exactly of the order $\sqrt{\log (p+q)}$. This thresholding, as we will see, is required in the easier sparsity regime, i.e., $s_x+s_y\ll \sqrt{p+q}$. Although Lemma 9 follows as a corollary to Lemma A.3 of [50], we include it here for the sake of completeness.

Lemma 9. Suppose Z₁, Z₂, M, N, and Q_M,N are as in Lemma 8, and $\log (p+q)=o(n)$. Further suppose $\Vert M{\Vert }_{op}$, $\Vert N{\Vert }_{op}\le Cℬ$ where C > 0 is an absolute constant. Let $\tau =\sqrt{C_1\log (p+q)}$. Here the tuning parameter $C_1>C{ℬ}^4$ where C > 0 is a sufficiently large constant. Then $\eta ({\mathbf{Q}}_{M,N};\tau ∕\sqrt{n})=0$ with probability tending to one.

We will need another technical lemma for handling the terms S₂ and S₃.

Lemma 10. Suppose $A\in {\mathbb{R}}^{m\times p}$ and $D=D_1\times D_2\subset [m]\times [p]$. Then the followings hold:

1. ${𝒫}_D(\eta (A))=\eta ({𝒫}_D(A))$.

2. $\Vert {𝒫}_D(A){\Vert }_{op}\le \Vert A{\Vert }_{op}$

Note that $M={\tilde{U}}_{F_1\ast }{B}_x{\tilde{U}}^T{\Sigma }_x$ satisfies

$$\Vert M{\Vert }_{op}\le \Vert {\Sigma }_x^{-1∕2}{\Vert }_{op}\Vert {\Sigma }_x^{1∕2}{\tilde{U}}_{F^{\ast }}{\Vert }_{op}\Vert B_x{\Vert }_{op}\Vert {\Sigma }_x^{1∕2}\tilde{U}{\Vert }_{op}\Vert {\Sigma }_x^{1∕2}{\Vert }_{op}.$$

However, $\Vert B_x{\Vert }_{op}\le 1$. Also because $\mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$, it follows that $\Vert {\Sigma }_x{\Vert }_{op},\Vert {\Sigma }_x^{-1}{\Vert }_{op}\le ℬ$. Moreover, since ${\Sigma }_x^{1∕2}\tilde{U}$ is orthogonal, $\Vert {\Sigma }_x^{1∕2}\tilde{U}{\Vert }_{op}=1$. Part B of Lemma 10 then yields $\Vert {\Sigma }_x^{1∕2}{\tilde{U}}_{F^{\ast }}{\Vert }_{op}\le \Vert {\Sigma }_x^{1∕2}\tilde{U}{\Vert }_{op}=1$. Therefore

$$\Vert M{\Vert }_{op}=\Vert {\tilde{U}}_{F_1\ast }{B}_x{\tilde{U}}^T{\Sigma }_x{\Vert }_{op}\le ℬ.$$ (55)

Similarly we can show that the matrix $N=\tilde{V}{B}_y({\tilde{V}}_{F_2\ast }{)}^T{\Sigma }_y$ satisfies $\Vert N{\Vert }_{op}\le ℬ$. Because ${\mathbf{S}}_2=\eta (M{Z}_1^T{Z}_{2}N)$ by (53), that $\eta ({\mathbf{S}}_2)$ is small follows immediately from Lemma 8. Under the conditions of Lemma 8, we have

$$\begin{gathered} \Vert \eta ({\mathbf{S}}_2){\Vert }_{op}\le C{ℬ}^2\left(\sqrt{\frac{p+q}{n}}\vee \frac{p+q}{n}\right) \\ \times e^{-{\text{Thr}}^2∕K} \end{gathered}$$ (56)

with high probability provided $K\ge 161{ℬ}^4$ and $\text{Thr}\in [13{ℬ}^2,\sqrt{K\log (\max \{p,q\})}∕2]$. On the other hand, under the setup of Lemma 9, $p(\Vert \eta (S_2){\Vert }_{op}=0){\to }_{n}1$. Lemma 11, which we prove in Appendix H-B, entails that the same holds for S₃.

Lemma 11. Consider the setup of Lemma 8. Suppose $K\ge 1288{ℬ}^4$ is such that $Thr\in [36{ℬ}^2,\sqrt{K\log (2\max \{p,q\})}∕2]$. Then there exists a constant C > 0 so that with probability tending to one,

$$\Vert \eta ({\mathbf{S}}_3){\Vert }_{op}\le C{ℬ}^2\left(\sqrt{\frac{p+q}{n}}\vee \frac{p+q}{n}\right)e^{-Th{r}^2∕K}.$$

Under the setup of Lemma 9, on the other hand, $\eta (\Vert \eta (S_3){\Vert }_{op})=0$ with probability tending to one.

We will now combine all the above lemmas and finish the proof. First, we consider the regime when $(s_x+s_y{)}^2\le (p+q)e$, so that there is thresholding, i.e., $\text{Thr}>0$. We split this regime into two subregimes: $2^{1∕4}(p+q{)}^{3∕4}\le (s_x+s_y{)}^2\le (p+q)e$ and $(s_x+s_y{)}^2\le 2^{1∕4}(p+q{)}^{3∕4}$.

1). Regime $2^{1∕4}(p+q{)}^{3∕4}\le (s_x+s_y{)}^2\le (p+q)∕e\colon\colon$

First, we explain why we needed to split the $e(s_x+s_y{)}^2\le p+q$ regime into two parts. Since s_x, $s_y<\sqrt{n}$, Lemma 7 applies. Note that if $\text{Thr}\in [36{ℬ}^2$, $\sqrt{K\log (\max \{p,q\})}∕2]$ with $K\ge 1288{ℬ}^4$, then Lemma 11 and (56) also apply. Therefore it follows that in this case

$$\begin{gathered} \Vert \eta ({\tilde{\Sigma }}_{xy})-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le C{ℬ}^2(\frac{(s_x+s_y)\text{Thr}}{\sqrt{n}}\phantom{)} \\ \phantom{(}+\frac{\sqrt{s_x+s_y}}{n}+\sqrt{\frac{p+q}{n}}\vee \frac{p+q}{n}{e}^{-{\text{Thr}}^2∕K}). \end{gathered}$$ (57)

We will shortly show that under $(s_x+s_y{)}^2\le (p+q)∕e$, setting ${\text{Thr}}^2=K\log ((p+q)∕(s_x+s_y{)}^2)$ ensures that the bound in (57) is small. However, for (57) to hold, ${\text{Thr}}^2$ needs to satisfy

$${\text{Thr}}^2∕K\le \frac{\log (\max \{p,q\}))}{4},$$

which holds with ${\text{Thr}}^2=K\log ((p+q)∕(s_x+s_y{)}^2)$ if and only if

$$\log \left((p+q)∕(s_x+s_y{)}^2\right)\le \log \left(\max \{p,q{\}}^{1∕4}\right).$$

Since $\max \{p,q\}\ge (p+q)∕2$ the above holds when

$$(p+q{)}^{3∕4}\le 2^{-1∕4}(s_x+s_y{)}^2.$$

Therefore, setting ${\text{Thr}}^2=K\log ((p+q)∕(s_x+s_y{)}^2)$ is useful when we are in the regime $2^{1∕4}(p+q{)}^{3∕4}\le (s_x+s_y{)}^2\le (p+q)∕e$. We will analyze the regime $(s_x+s_y{)}^2{\le }^{1∕4}(p+q{)}^{3∕4}$ using separate procedure.

In the $2^{1∕4}(p+q{)}^{3∕4}\le (s_x+s_y{)}^2\le (p+q)∕e$ case,

$$\begin{gathered} \sqrt{\frac{p+q}{n}}{e}^{-{\text{Thr}}^2∕K}=\sqrt{\frac{p+q}{n}}\frac{(s_x+s_y{)}^2}{(p+q)} \\ =\frac{(s_x+s_y)}{\sqrt{n}}\frac{s_x+s_y}{\sqrt{p+q}}<\frac{(s_x+s_y)}{\sqrt{en}} \end{gathered}$$

because $(s_x+s_y{)}^2\le (p+q)∕e$, and similarly,

$$\frac{p+q}{n}{e}^{-{\text{Thr}}^2∕K}=\frac{p+q}{n}\frac{(s_x+s_y{)}^2}{(p+q)}=\frac{(s_x+s_y)}{2\sqrt{n}}$$

since we also assume $s_x+s_y\le 2\sqrt{n}$. The above bounds entail that, in this regime, the first term on the bound in (57) is the leading term provided $\text{Thr}>1$, i.e.,

$$\begin{gathered} \Vert \eta ({\tilde{\Sigma }}_{xy})-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op} \\ \le C{ℬ}^2\left(\frac{(s_x+s_y)\text{Thr}}{\sqrt{n}}+\frac{(s_x+s_y)}{\sqrt{n}}\right) \\ \le C{ℬ}^2\frac{(s_x+s_y)\max (\text{Thr},1)}{\sqrt{n}} \end{gathered}$$

with probability $1-o(1)$. Plugging in the value of Thr leads to

$$\begin{gathered} \Vert \eta ({\tilde{\Sigma }}_{xy})-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op} \\ \le C{ℬ}^2\frac{s_x+s_y}{\sqrt{n}}{\left(\max \left\{K\log \left(\frac{(s_x+s_y{)}^2}{p+q}\right),1\right\}\right)}^{1∕2} \end{gathered}$$

in the regime $2^{1∕4}(p+q{)}^{3∕4}\le (s_x+s_y{)}^2\le (p+q)∕e$. In our case, $(s_x+s_y{)}^2∕(p+q)\ge e$. Also since $ℬ>1$ by definition of $𝒫(r,s_x,s_y,ℬ)$, we also have $K\ge 1$, indicating

$$\begin{gathered} \Vert \eta ({\tilde{\Sigma }}_{xy})-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op} \\ \le C{ℬ}^2\frac{s_x+s_y}{\sqrt{n}}{\left(K\log \left(\frac{(s_x+s_y{)}^2}{p+q}\right)\right)}^{1∕2}. \end{gathered}$$

2). Regime $(s_x+s_y{)}^2<2^{1∕4}(p+q{)}^{3∕4}:$

When $(s_x+s_y{)}^2<2^{1∕4}(p+q{)}^{3∕4}$, of course, the above line of arguments may not work although this indeed is an easier regime because $s_x+s_y$ is less than $\sqrt{(p+q)∕\log (p+q)}$. In this regime, we set $\text{Thr}=\sqrt{C_1\log (p+q)}$ where $C_1$ is a constant depending on $ℬ$ as in Lemma 9. For this τ, we have showed that $\Vert \eta (S_2){\Vert }_{op}=0$ with probability tending to one. Lemma 11 implies the same holds for $\Vert \eta (S_3){\Vert }_{op}$ as well. Thus from the decomposition of ${\tilde{\Sigma }}_{xy}$ in (26), it follows that the asymptotic error occurs only due to the estimation of ${\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}$ by $\eta (S_1)$. Using Lemma 7, we thus obtain

$$\Vert {\tilde{\Sigma }}_{xy}-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le C{ℬ}^2\frac{(s_x+s_y)\max \{\text{Thr},1\}}{\sqrt{n}}.$$

On the other hand, since $(p+q{)}^{3∕4}>2^{-1∕4}(s_x+s_y{)}^2$, rearranging terms, we have

$$\begin{gathered} \log \left((p+q)∕(s_x+s_y{)}^2\right)>\left(\log (p+q)-\log 2\right)∕4 \\ >C\log (p+q). \end{gathered}$$

Thus, in the regime $(s_x+s_y{)}^2<2^{1∕4}(p+q{)}^{3∕4}$, we have

$$\begin{gathered} \Vert {\tilde{\Sigma }}_{xy}-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op} \\ \le C{ℬ}^2\frac{s_x+s_y}{\sqrt{n}}\max \left\{\sqrt{C_1\log \left(\frac{p+q}{(s_x+s_y{)}^2}\right)},1\right\}. \end{gathered}$$ (58)

3). Regime $(s_x+s_y{)}^2>(p+q)∕e:$:

It remains to analyze the case when either $(s_x+s_y{)}^2>(p+q)∕e$. In that case, there is no thresholding, i.e., Thr = 0. We will show that the assertions of Theorem 4 holds in this case as well. To that end, note that (26) implies

$$\Vert {\tilde{\Sigma }}_{xy}-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le \Vert S_1-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}+\Vert S_2+S_3{\Vert }_{op}.$$

From the proof of Lemma 7 it follows that $\Vert S_1-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le {Cℬ}^2\max \{\sqrt{s_x},\sqrt{s_y}\}∕\sqrt{n}$. For S₂, we have shown that it is of the form $M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N∕n$ where $\Vert M{\Vert }_{op},\Vert N{\Vert }_{op}\le ℬ$. On the other hand, we showed that $S_3={\mathbf{H}}_1+{\mathbf{H}}_2$, where the proof of Lemma 11 shows H₁ and H₂ are of the form M AN where $\Vert M{\Vert }_{op}\Vert N{\Vert }_{op}\le 2{ℬ}^2$ and A is either $[\mathbf{Z}{\mathbf{Z}}_1{]}^T{\mathbf{Z}}_2∕n$ (for H₁) or ${\mathbf{Z}}_1^T[\mathbf{Z}{\mathbf{Z}}_2]∕n$ (for H₂). Therefore, it is not hard to see that $\Vert S_2+S_3{\Vert }_{op}$ is bounded by

$$C{ℬ}^2\left(\Vert {\mathbf{Z}}_1^T{\mathbf{Z}}_2{\Vert }_{op}+\Vert {\mathbf{Z}}_1^T[\mathbf{Z}{\mathbf{Z}}_2]{\Vert }_{op}+\Vert [\mathbf{Z}{\mathbf{Z}}_1{]}^T{\mathbf{Z}}_2{\Vert }_{op}\right).$$

For standard Gaussian matrices ${\mathbf{Z}}_1\in {\mathbb{R}}^{n\times p}$ and ${\mathbf{Z}}_2\in {\mathbb{R}}^{n\times q}$ it holds that $\Vert Z_1^T{Z}_2∕n{\Vert }_{op}\le C(\sqrt{(p+q)∕n}+(p+q)∕n)$ with probability $1-o(1)$ (cf. Theorem 4.7.1 of of [42]). Since $r\le \text{min}\{p,q\}$, it follows that $\Vert S_2+S_3{\Vert }_{op}\le C{ℬ}^2(\sqrt{p+q∕n}+(p+q)∕n)$ with probability $1-o(1)$. The above discussion leads to

$$\begin{gathered} \Vert {\tilde{\Sigma }}_{xy}-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le C{ℬ}^2({\left(\frac{s_x+s_y}{n}\right)}^{1∕2}+{\left(\frac{p+q}{n}\right)}^{1∕2}\phantom{)} \\ +\phantom{(}\frac{p+q}{n}) \\ \le 2C{ℬ}^2\left({\left(\frac{p+q}{n}\right)}^{1∕2}+\frac{p+q}{n}\right) \end{gathered}$$

because $s_x+s_y<p+q$. If $(p+q)\le e(s_x+s_y{)}^2$, the above bound is of the order $(s_x+s_y)∕\sqrt{n}$. Thus Theorem 4 follows.

Appendix G. Proof of Corollary 2

Proof of Corollary 2. We will first show that there exist $C_{ℬ}^{\prime },c_{ℬ}>0$ so that

$$\begin{gathered} \underset{i\in [r]}{\max }\Vert {\widehat{u}}_{n,i}-w{u}_i{\Vert }_2 \\ \le C_{ℬ}^{\prime }\frac{(s_x+s_y)}{\sqrt{n}}\max \left\{{\left(c_{ℬ}\log \left(\frac{p+q}{(s_x+s_y{)}^2}\right)\right)}^{1∕2},1\right\}. \end{gathered}$$ (59)

For the sake of simplicity, we denote the matrix ${\widehat{U}}^{(1)}$ in Algorithm 2 by $\widehat{U}$. Denoting ${ϵ}_n^{\prime }=\Vert \eta ({\tilde{\Sigma }}_{xy})-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}$, we note that

$$\Vert {\Sigma }_x^{1∕2}\eta ({\tilde{\Sigma }}_{xy}){\Sigma }_y^{1∕2}-{\Sigma }_x^{1∕2}U\Lambda V^T{\Sigma }_y^{1∕2}{\Vert }_{op}\le ℬ{ϵ}_n^{\prime }.$$

Also the matrix ${\widehat{U}}_{\text{pre}}$ defined in Algorithm 2 and ${\Sigma }_x^{1∕2}U$ are the matrices corresponding to the leading r singular vectors of ${\Sigma }_x^{1∕2}\eta ({\tilde{\Sigma }}_{xy}){\Sigma }_y^{1∕2}$ and ${\Sigma }_x^{1∕2}U\Lambda V^T{\Sigma }_y^{1∕2}$, respectively. By Wedin’s sin-theta theorem (we use Theorem 4 of [52]), for any $1\le i<r$,

$$\underset{w\in \{\pm 1\}}{\text{min}}\Vert {\widehat{U}}_i^{\text{pre}}-w{\Sigma }_x^{1∕2}{u}_i\Vert \le \frac{2^{3∕2}(2{\Lambda }_1+{ϵ}_n^{\prime }){ϵ}_n^{\prime }}{\text{min}\{{\Lambda }_{i-1}^2-{\Lambda }_i^2,{\Lambda }_i^2-{\Lambda }_{i+1}^2\}},$$

where Λ₀ is taken to be ∞, and

$$\underset{w\in \{\pm 1\}}{\text{min}}\Vert {\widehat{U}}_r^{\text{pre}}-w{\Sigma }_x^{1∕2}{u}_r{\Vert }_2\le \frac{2^{3∕2}(2{\Lambda }_1+{ϵ}_n^{\prime }){ϵ}_n^{\prime }}{{\Lambda }_{r-1}^2-{\Lambda }_r^2}.$$

Since $\mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$, ${\text{min}}_{i\in [r]}({\Lambda }_{i-1}-{\Lambda }_i)>{ℬ}^{-1}$ and ${\text{min}}_{i\in [r]}{\Lambda }_i>{ℬ}^{-1}$. Therefore, for ${ϵ}_n^{\prime }<1$, we have

$$\underset{i\in [r]}{\max }\underset{w\in \{\pm 1\}}{\text{min}}\Vert {\widehat{U}}_i^{\text{pre}}-w{\Sigma }_x^{1∕2}{u}_i{\Vert }_2\le C_{ℬ}{ϵ}_n^{\prime }.$$

We have to show ${ϵ}_n^{\prime }<1$. Theorem 4 gives a bound on ${ϵ}_n^{\prime }$, which can be made smaller than one if the $C_{ℬ}$ in (23) is chosen to be sufficiently large. Hence, the above inequality holds. Because ${\widehat{U}}_i^{\text{pre}}={\Sigma }_x^{1∕2}{\widehat{u}}_{n,i}$, using the fact $\Vert {\Sigma }_x{\Vert }_{op}\le ℬ$, the last display implies

$$\underset{i\in [r]}{\max }\underset{w\in \{\pm 1\}}{\text{min}}\Vert {\widehat{u}}_{n,i}-w{u}_i{\Vert }_2\le {ℬ}^{1∕2}{C}_{ℬ}{ϵ}_n^{\prime },$$

which, combined with Theorem 4, proves (59). Now note that the constant $C_{ℬ}$ in (23) can be chosen so large such that the right hand side of (59) is smaller than $1∕(2{ℬ}^2\sqrt{r})$. Since $\Vert {\Sigma }_x{\Vert }_{op}<ℬ$, it follows that Condition 1 is satisfied, and the rest of the proof then follows from Theorem 1.

Appendix H. Proof of Auxilliary Lemmas

A. Proof of Technical Lemmas for Theorem 2

The following lemma can be verified using elementary linear algebra, and hence its proof is omitted.

Lemma 12. Suppose Σ is of the form (41). Then the spectral decomposition of Σ is as follows:

$$\Sigma =\sum _{i=1}^{p-1}{x}_1^{(i)}(x_1^{(i)}{)}^T+\sum _{i=1}^{q-1}{x}_2^{(i)}(x_2^{(i)}{)}^T+(1+\rho )x_3{x}_3^T+(1-\rho )x_4{x}_4^T,$$

where the eigenvectors are of the following form:

1. For $i\in [p-1],x_1^{(i)}=(y_i,0_q)$, where $\{y_i{\}}_{i=1}^{p-1}\subset {\mathbb{R}}^p$ forms an orthonormal basis system of the orthogonal space of α.

2. For $i\in [q-1],x_2^{(i)}=(0_p,z_i)$, where $\{z_i{\}}_{i=1}^{q-1}\subset {\mathbb{R}}^p$ forms an orthonormal basis system of the orthogonal space of β.

3. $x_3=(\alpha ∕\sqrt{2},\beta ∕\sqrt{2})$ and $x_4=(\alpha ∕\sqrt{2},-\beta ∕\sqrt{2})$.

Here for $k\in \mathbb{N}$, 0_k denotes the k-dimensional vector whose all entries are zero.

Lemma 13. Suppose Σ is as in (41). Then $det(\Sigma )=1-{\rho }^2$ and

$$\begin{gathered} {\Sigma }^{-1}=\left[\begin{array}{cc}\hfill I-\alpha {\alpha }^T\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill I-\beta {\beta }^T\hfill \end{array}\right]+\frac{1}{2(1+\rho )}\left[\begin{array}{cc}\hfill \alpha {\alpha }^T\hfill & \hfill \alpha {\beta }^T\hfill \\ \hfill \beta {\alpha }^T\hfill & \hfill \beta {\beta }^T\hfill \end{array}\right] \\ +\frac{1}{2(1-\rho )}\left[\begin{array}{cc}\hfill \alpha {\alpha }^T\hfill & \hfill -\alpha {\beta }^T\hfill \\ \hfill -\beta {\alpha }^T\hfill & \hfill \beta {\beta }^T\hfill \end{array}\right]. \end{gathered}$$

Proof of Lemma 13. Follows directly from Lemma 12.

Lemma 14. Suppose Σ₁ and Σ₂ are of the form (41) with singular vectors α₁, β₁, α₂, and β₂, respectively. Then

$$Tr({\Sigma }_1{\Sigma }_2^{-1})=p+q+\frac{2{\rho }^2}{1-{\rho }^2}\left(1-({\beta }_1^T{\beta }_2)({\alpha }_1^T{\alpha }_2)\right).$$

Proof. Lemma 13 can be used to obtain the form of ${\Sigma }_2^{-1}$, which implies ${\Sigma }_1{\Sigma }_2^{-1}$ equals

$$\left[\begin{array}{cc}\hfill I_p\hfill & \hfill \rho {\alpha }_1{\beta }_1^T\hfill \\ \hfill \rho {\beta }_1{\alpha }_1^T\hfill & \hfill I_q\hfill \end{array}\right]\left[\begin{array}{cc}\hfill I_p+\rho C_{\rho }{\alpha }_2{\alpha }_2^T\hfill & \hfill -C_{\rho }{\alpha }_2{\beta }_2^T\hfill \\ \hfill -C_{\rho }{\beta }_2{\alpha }_2^T\hfill & \hfill I_q+\rho C_{\rho }{\beta }_2{\beta }_2^T,\hfill \end{array}\right]$$

where $C_{\rho }=\rho ∕1-{\rho }^2$. Since $Tr({\Sigma }_1{\Sigma }_2^{-1})$ equals the sum of the two p × p and q × q diagonal submatrices, we obtain that

$$\begin{gathered} Tr({\Sigma }_1{\Sigma }_2^{-1})=Tr\left(I_p+\rho C_{\rho }{\alpha }_2{\alpha }_2^T-\rho C_{\rho }({\beta }_1^T{\beta }_2){\alpha }_1{\alpha }_2^T\right) \\ +Tr\left(I_q+\rho C_{\rho }{\beta }_2{\beta }_2^T-\rho C_{\rho }({\alpha }_1^T{\alpha }_2){\beta }_1{\beta }_2^T\right) \\ =p+q+\frac{{\rho }^2}{1-{\rho }^2}(Tr({\alpha }_2^T{\alpha }_2)+Tr({\beta }_2^T{\beta }_2)\phantom{)} \\ -\phantom{(}({\beta }_1^T{\beta }_2)Tr({\alpha }_1{\alpha }_2^T)-({\alpha }_1^T{\alpha }_2)Tr({\beta }_1{\beta }_2^T)), \end{gathered}$$

where we used the linearity of Trace operator, as well as the fact that $Tr(AB)=Tr(BA)$. Noticing $\Vert {\alpha }_2{\Vert }_2=\Vert {\beta }_2{\Vert }_2=1$, the result follows.

B. Proof of Key Lemmas for Theorem 4

1). Proof of Lemma 7:

Proof of Lemma 7. Note that

$$\begin{gathered} \Vert \eta ({\mathbf{S}}_1)-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le \underset{T_1}{\underbrace{\Vert \eta ({\mathbf{S}}_1)-{\mathbf{S}}_1{\Vert }_{op}}} \\ +\underset{T_2}{\underbrace{\Vert {\mathbf{S}}_1-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}}}. \end{gathered}$$

We deal with the term T₁ first. Recall from (26) that ${\mathbf{S}}_1={𝒫}_{E_1\times E_2}({\tilde{\Sigma }}_{xy})$ is a sparse matrix. In particular, each row and column of S₁ can have at most s_y and s_x many nonzero elements, respectively. Now we make use of two elementary facts. First, for $x\ne 0$, $\mid \eta (x)-x\mid \le \text{Thr}∕\sqrt{n}$, and second, for any matrix $A\in {\mathbb{R}}^{p\times q}$,

$$\Vert A{\Vert }_{op}\le \underset{1\le i\le p}{\max }\sum _{j=1}^p\mid A_{ij}\mid \wedge \underset{1\le j\le q}{\max }\sum _{i=1}^n\mid A_{ij}\mid .$$

The above results, combined with the row and column sparsity of S₁, lead to

$$\begin{gathered} T_1=\Vert \eta ({\mathbf{S}}_1)-{\mathbf{S}}_1{\Vert }_{op} \\ \le \left(\underset{1\le i\le p}{\max }\Vert ({\mathbf{S}}_1{)}_{i\ast }{\Vert }_0\right)\wedge \left(\underset{1\le j\le q}{\max }\Vert ({\mathbf{S}}_1{)}_j{\Vert }_0\right)\frac{\text{Thr}}{\sqrt{n}} \\ \le \text{min}\{s_x,s_y\}\frac{\text{Thr}}{\sqrt{n}}, \end{gathered}$$

which is the first term in the bound of $\Vert \eta ({\mathbf{S}}_1)-{\Sigma }_{xy}{\Vert }_{op}$.

Now for T₂, noting ${\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}=U\Lambda V^T$, observe that

$$\begin{gathered} {\mathbf{S}}_1-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1} \\ =\underset{S_{11}}{\underbrace{U{\Lambda }^{1∕2}\left(\frac{{\mathbf{Z}}^T\mathbf{Z}}{n}-I_r\right){\Lambda }^{1∕2}{V}^T}} \\ +\underset{S_{12}}{\underbrace{U{\Lambda }^{1∕2}\frac{{\mathbf{Z}}^T{\mathbf{Z}}_2}{n}{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)}} \\ +\underset{S_{13}}{\underbrace{({\tilde{U}}_{E_1\ast }{B}_y{\tilde{U}}^T){\Sigma }_x\frac{{\mathbf{Z}}_1^T\mathbf{Z}}{n}{\Lambda }^{1∕2}{V}^T}} \\ +\underset{S_{14}}{\underbrace{({\tilde{U}}_{E_1\ast }{B}_x{\tilde{U}}^T){\Sigma }_x\frac{{\mathbf{Z}}_1^T\mathbf{Z}}{n}{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)}}. \end{gathered}$$

It is easy to see that

$$\begin{gathered} \Vert S_{11}{\Vert }_{op}\le \Vert {\Sigma }_x^{-1∕2}{\Vert }_{op}\Vert {\Sigma }_x^{1∕2}U{\Vert }_{op}\Vert {\Sigma }_y^{-1∕2}{\Vert }_{op}\Vert {\Sigma }_y^{1∕2}V{\Vert }_{op}\Vert \Lambda {\Vert }_{op} \\ \times {\Vert \frac{{\mathbf{Z}}^T\mathbf{Z}}{n}-I_r\Vert }_{op}. \end{gathered}$$

Since $(\mathbf{X},\mathbf{Y})\sim \mathbb{P}\in {𝒫}_G(r,s_x,s_y,ℬ)$, ${\Sigma }_x^{-1}$ and ${\Sigma }_y^{-1}$ are bounded it operator norm by $ℬ$. Also, ${\Sigma }_x^{1∕2}\tilde{U}$ and ${\Sigma }_y^{1∕2}\tilde{V}$ are orthonormal matrices. Therefore the operator norms of the matrices ${\Sigma }_x^{1∕2}U$, ${\Sigma }_y^{1∕2}V$, and Λ are bounded by one. On the other hand, by Bai-Yin’s law on eigenvalues of Wishart matrices (cf. Theorem 4.7.1 of [42]), $\Vert {\mathbf{Z}}^T\mathbf{Z}∕n-I_r{\Vert }_{op}\le C(\sqrt{r∕n}+r∕n)$ with high probability. Since $r<s_x<\sqrt{n}$, clearly $r∕n<1$. Thus $\Vert S_{11}{\Vert }_{op}\le ℬC\sqrt{r∕n}$ with high probability. Hence it suffices to show that the terms S₁₂, S₁₃, and S₁₄ are small in operator norm, for which, we will make use of Lemma 4. First let us consider the case of S₁₂. Clearly,

$$\begin{gathered} \Vert S_{12}{\Vert }_{op}\le \Vert {\Sigma }_x^{-1∕2}{\Vert }_{op}\Vert {\Sigma }_x^{1∕2}U{\Vert }_{op}\Vert {\Lambda }^{1∕2}{\Vert }_{op} \\ \times {\Vert \frac{{\mathbf{Z}}^T\mathbf{Z}}{n}{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)\Vert }_{op}. \end{gathered}$$

We already mentioned that $\Vert {\Sigma }_x^{-1}{\Vert }_{op}\le ℬ$, and $\Vert {\Sigma }_x^{1∕2}U{\Vert }_{op}$ and $\Vert \Lambda {\Vert }_p$ are bounded by one. Therefore, it follows that

$$\Vert S_{12}{\Vert }_{op}\le {ℬ}^{1∕2}{\Vert \frac{{\mathbf{Z}}^T{\mathbf{Z}}_2}{n}{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)\Vert }_{op}.$$

Now we apply Lemma 4 on the term ${\mathbf{Z}}^T{\mathbf{Z}}_2{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)$ with $A=I_r$, and $B={\Sigma }_y\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T$. Note that ${\Sigma }_y$, $\tilde{V}$, and $B_y$ are full rank matrices, i.e., they have rank q. Therefore, the rank of B equals rank of ${\tilde{V}}_{E_2\ast }$. Note that the rows of the matrix $\tilde{V}$ are linearly independent because the square matrix $\tilde{V}$ has full rank. Therefore, the rank of ${\tilde{V}}_{E_2\ast }$ is $\mid E_2\mid$, which is $s_y$. Hence, the rank of $B$ is also $s_y$. Also note that $(A)=r\le s_y\le n$. Therefore Lemma 4 can be applied with $a=r$ and $b=s_y$. Also, $\Vert A{\Vert }_{op}=1$ trivially follows. Using the same arguments which led to (55), on the other hand, we can show that $\Vert B{\Vert }_{op}\le ℬ$ by (26). Therefore Lemma 4 implies that for any t > 0, the following holds with probability at least $1-\text{exp}(-Cn)-\text{exp}(-t^2∕2)$:

$${\Vert \frac{{\mathbf{Z}}^T{\mathbf{Z}}_2}{n}{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)\Vert }_{op}\le Cℬ\frac{\max \{\sqrt{s_y},t\}}{\sqrt{n}},$$

which implies $\mid S_{12}\mid \le C{ℬ}^{3∕2}\max \{\sqrt{s_y},t\}∕\sqrt{n}$ with high probability. Exchanging the role of X and Y in the above arguments, we can show that $\mid S_{13}\mid \le C{ℬ}^{3∕2}\max \{\sqrt{s_x},t\}∕\sqrt{n}$ with high probability. For S₁₄, we note that

$$\Vert S_{14}{\Vert }_{op}\le {\Vert ({\tilde{U}}_{E_1\ast }{B}_x{\tilde{U}}^T){\Sigma }_x\frac{{\mathbf{Z}}_1^T{\mathbf{Z}}_2}{n}{\Sigma }_y\left(\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T\right)\Vert }_{op}.$$

We intend to apply Lemma 4 with $A={\Sigma }_x\tilde{U}{B}_x({\tilde{U}}_{E_1\ast }{)}^T$ and $B={\Sigma }_y\tilde{V}{B}_y({\tilde{V}}_{E_2\ast }{)}^T$. Arguing in the lines of the proof for the term S₁₂, we can show that A and B have rank $a=s_x$ and $b=s_y$, respectively. Without loss of generality we assume $s_y\ge s_x$, which yields $b\ge a$, as requred by Lemma 4. Otherwise, we can just take the transpose of C₁₄, which leads to $a=s_y$ and $b=s_x$, implying $b\ge a$. Using (55), as before, we can show that the operator norms of A and B are bounded by $ℬ$. Therefore, Lemma 4 implies that for all $t\ge 0$,

$$\Vert S_{14}{\Vert }_{op}\le C{ℬ}^2\frac{\max \{{\sqrt{s}}_x,{\sqrt{s}}_y,t\}}{\sqrt{n}}$$

with probability at least $1-\text{exp}(-Cn)-\text{exp}(-t^2∕2)$. Hence, it follows that with probability $1-o(1)$,

$$\Vert {\mathbf{S}}_1-{\Sigma }_x^{-1}{\Sigma }_{xy}{\Sigma }_y^{-1}{\Vert }_{op}\le C{ℬ}^2\frac{\max \{\sqrt{s_x},\sqrt{s_y}\}}{\sqrt{n}}.$$

2). Proof of Lemma 8:

Without loss of generality, we will assume that $p>q$. We will also assume, without loss of generality, that $p^{\prime }=p$ and $q^{\prime }=q$. If that is not the case, we can add some zero rows to M and zero columns to N, respectively, which does not change their operator norm, but ensures $p^{\prime }=p$ and $q^{\prime }=q$. For any $p\in \mathbb{N}$, let ${\mathbb{S}}^{p-1}$ denote the unit sphere in ${\mathbb{R}}^p$. We denote an ϵ-net (with respect to Eucledian norm) on any set $𝒳\subset {\mathbb{R}}^p$ by $T^{ϵ}(𝒳)$. When $𝒳={\mathbb{S}}^{p-1}$, there exists an ϵ-net of ${\mathbb{S}}^{p-1}$ so that

$$\mid T^{ϵ}({\mathbb{S}}^{p-1})\mid \le {\left(1+2∕ϵ\right)}^p.$$

By $T_p^{ϵ}$, we denote such an ϵ-net. Although $T_p^{ϵ}$ may not be unique, that is not necessary for our purpose. For a subset $S\subset [p]$, $T_p^{ϵ}(S)$ will denote an ϵ-net of the set $\{x\in {\mathbb{S}}^{p-1}:x_i=0\text{if}i\ne 0\}$. Note that each element of the latter set has at most $\mid S\mid -1$ many degrees of freedom, from which, one can show that $\mid T_k^{ϵ}(S)\mid \le (1+2∕ϵ{)}^{\mid S\mid }$. The following Fact on ϵ-nets will be very useful for us. The proof is standard and can be found, for example, in [42].

Fact 5. Let $A\in {\mathbb{R}}^{p\times q}$ for p, $q\in \mathbb{N}$. Then there exist $x\in T_p^{ϵ}$ and $y\in T_q^{ϵ}$ such that $\mid \langle x,Ay\rangle \mid \ge (1-2ϵ)\Vert A{\Vert }_{op}$.

Letting ${\mathbf{A}}_n=\eta (M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N)$, and using Fact 5, we obtain that

$$P(\Vert {\mathbf{A}}_n{\Vert }_{op}>\delta )\le P\left(\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x,{\mathbf{A}}_{n}y\rangle \mid \ge (1-2ϵ)\delta \right)$$

for any $\delta >0$. Proceeding like Proposition 15 of [1], we fix $1<J_{p,q}\le \text{min}\{p,q\}$, and introduce the sets

$$\begin{gathered} S_x=\{i\in [p]:\mid x_i\mid \ge \sqrt{J_{p,q}∕p}\} \\ {S}_y=\{i\in [q]:\mid y_i\mid \ge \sqrt{J_{p,q}∕q}\}, \end{gathered}$$ (60)

and their complements $S_x^c=[p]\setminus S_x$ and $S_y^c=[q]\setminus S_y$. The precise value of J_p,q will be chosen later. For any subset $A\subset [k]$, $k\in \mathbb{N}$, and vector $x\in {\mathbb{R}}^k$, we denote by $x_A$ the projection of x onto A, which means $x_A\in {\mathbb{R}}^p$ and $(x_A{)}_i=x_i$ if $i\in A$, and zero otherwise. Let us denote the projections of x and y on $S_x$, $S_x^c$, $S_y$, and $S_y^c$, by $x_{S_x}$, $x_{S_x^c}$, $y_{S_y}$, and $y_{S_y^c}$, respectively. Note that this implies

$$x=x_{S_x}+x_{S_x^c},y=y_{S_y}+y_{S_y^c},$$

as well as

$$x_{S_x},x_{S_x^c}\in {\mathbb{R}}^p,y_{S_y},y_{S_y^c}\in {\mathbb{R}}^q.$$

There are fewer elements the sets $S_x$ and $S_y$ compared to their complements. Therefore, we will treat these sets separately. To that end, we consider the splitting

$$\begin{gathered} P\left(\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x,{\mathbf{A}}_{n}y\rangle \mid \ge 4\delta (1-2ϵ)\right) \\ \le \underset{T_1}{\underbrace{P\left(\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x_{S_x},{\mathbf{A}}_n{y}_{S_y}\rangle \mid \ge \delta (1-2ϵ)\right)}} \\ +\underset{T_2}{\underbrace{P\left(\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x_{S_x},{\mathbf{A}}_n{y}_{S_y^c}\rangle \mid \ge \delta (1-2ϵ)\right)}} \\ +\underset{T_3}{\underbrace{P\left(\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x_{S_x^c},{\mathbf{A}}_{n}y\rangle \mid \ge \delta (1-2ϵ)\right)}} \end{gathered}$$ (61)

The term T₁ can be bounded by Lemma 15.

Lemma 15. Suppose M and N are as in Lemma 8 and ${\mathbf{A}}_n=\eta ({\mathbf{Q}}_{M,N})$ where ${\mathbf{Q}}_{M,N}=M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N∕n$. Then for any $\Delta >0$, there exist absolute constants C, $c>0$ such that

$$\begin{gathered} P\left\{\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x_{S_x},{\mathbf{A}}_n{y}_{S_y}\rangle \mid \ge \Delta \right\} \\ \le C\text{exp}((p+q)\frac{\log (C{J}_{p,q})}{J_{p,q}}\phantom{)} \\ -\phantom{(}\frac{n^2{\Delta }^2}{4C\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(2n+p+q)}) \\ +\frac{C}{{\Delta }^2}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(n(p+q){)}^C\left\{e^{-c(n+q)}+e^{-c(n+p)}\right\} \end{gathered}$$

We state another lemma which helps in controlling the terms T₂ and T₃.

Lemma 16. Suppose M, N, Z₁, Z₂, and A_n are as in Lemma 8. Let $K_0=161\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2$. Suppose $k>0$ is such that $K\ge K_0$ and moreover, $\tau \in [\sqrt{K_0},\sqrt{K\log p}∕2]$. Let ${𝒯}_2$ be either the set $T_q^{ϵ}$ or the set ${\tilde{T}}_q^{ϵ}=\{y_{S_y}:y\in T_q^{ϵ}\}$. Then there exist absolute constants C, $c>0$ such that the following holds for any $\Delta >0$;

$$\begin{gathered} P\left\{\underset{x\in T_p^{ϵ},y\in {𝒯}_2}{\max }\mid \langle x_{S_x^c},{\mathbf{A}}_{n}y\rangle \mid \ge \Delta \right\} \\ \le C\text{exp}\left(C(p+q)-\frac{{\Delta }^2{n}^2{e}^{{\tau }^2∕K}}{C\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2{J}_{p,q}(2n+p+q)}\right) \\ +\frac{C\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2}{{\Delta }^2}(n(p+q){)}^C\text{exp}\left(-c\text{min}(n,\sqrt{p})\right). \end{gathered}$$

Note that when $𝒟=T_q^{ϵ}$, Lemma 16 yields a bound on T₃. On the other hand, the case ${𝒯}_2={\tilde{T}}_q^{ϵ}$ yields a bound on the term

$$T_2^{\prime }=P\left(\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x_{S_x^c},{\mathbf{A}}_n{y}_{S_y}\rangle \mid \ge \delta (1-2ϵ)\right).$$ (62)

While $T_2^{\prime }$ is not exactly equal to T₂, interchanging the role of x and y in $T_2^{\prime }$ gives T₂. Since the upper bound on $T_2^{\prime }$ given by Lemma 16 is symmetric in p and q, it is not hard to see that the same bound works for T₂.

If we let $ϵ=1∕4$, then $\Delta =\delta ∕2$. Combining the bounds on T₁, T₂, and T₃, we conclude that the right hand side of (61) is $o(1)$ if ${\Delta }^2$ is larger than some constant multiple of

$$\begin{gathered} \max \{\frac{(n+p+q)(p+q)}{n^2}\left(\frac{\log J_{p,q}}{J_{p,q}}+J_{p,q}{e}^{-{\tau }^2∕K_0}\right)\phantom{\}}, \\ \phantom{\{}\frac{(n(p+q){)}^C}{\text{exp}\left(c\text{min}\{n,\sqrt{p}\}\right)}\}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2 \end{gathered}$$

where $K_0=320\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2$. We will show that the first term dominates the second term. By our assumption on τ, ${\tau }^2<80\log p\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2$, which implies ${\tau }^2∕K_0<\log (p\wedge q)∕2$, which combined with the fact $J_{p,q}>1$, yields $J_{p,q}\text{exp}(-{\tau }^2∕K_0)>J_{p,q}∕\sqrt{p\wedge q}$. On the other hand, under p > q, our assumption on n implies $\log n=o(\sqrt{p})$. Also because $p+q=o(\log n)$, it follows that $(n(p+q){)}^C\text{exp}(-c\text{min}\{n,\sqrt{p}\})$ is small, in particular

$$\begin{gathered} \frac{(n+p+q)(p+q)}{n^2}\left(\frac{\log J_{p,q}}{J_{p,q}}+J_{p,q}{e}^{-{\tau }^2∕K_0}\right) \\ \ge \frac{(n+p+q)(p+q)}{n^2\sqrt{p\wedge q}} \\ \gg (n(p+q){)}^C\text{exp}(-c\text{min}\{n,\sqrt{p}\}). \end{gathered}$$

Therefore, for $P(\Vert {\mathbf{A}}_n{\Vert }_{\delta }>\delta )$ to be small,

$$\begin{gathered} {\delta }^2>C\underset{1<J_{p,q}<p\wedge q}{\text{min}}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2\frac{(n+p+q)(p+q)}{n^2} \\ \times \left(\frac{\log J_{p,q}}{J_{p,q}}+J_{p,q}{e}^{-{\tau }^2∕K_0}\right) \end{gathered}$$

suffices. In particular, we choose $J_{p,q}=\text{exp}({\tau }^2∕(2K_0))$. Note that because ${\tau }^2\le K_0\log (p\wedge q)∕2$, this choice of J_p,q ensures that $J_{p,q}\ll \text{min}\{p,q\}$, as required. The proof follows noting this choice of J_p,q also implies

$$\begin{gathered} \frac{\log J_{p,q}}{J_{p,q}}+J_{p,q}{e}^{-{\tau }^2∕K_0}\le e^{-{\tau }^2∕(2.5K_0)} \\ ={\left\{\text{exp}\left(\frac{-{\tau }^2}{{40}^2\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2}\right)\right\}}^2. \end{gathered}$$

3). Proof of Lemma 9:

Proof of 9. For any $i\in [p]$ and $j\in [q]$,

$${\mathbf{Z}}_1{M}_{i\ast }∕\Vert M_{i\ast }{\Vert }_2\sim N(0,I_n)$$

and ${\mathbf{Z}}_2{N}_j∕\Vert N_j{\Vert }_2\sim N(0,I_n)$ are independent. In this case, there exist absolute constants δ, c and $C>0$, so that (cf. Lemma A.3 of [50])

$$P\left(\frac{\mid M_{i\ast }^T{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_j\mid }{\Vert M_{i\ast }{\Vert }_2\Vert N_j{\Vert }_2}\ge nt\right)\le C\text{exp}(-cn{t}^2)$$

for all $t\le \delta$. Since $(M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N{)}_{ij}=M_{i\ast }^T{\mathbf{Z}}_1^T{\mathbf{Z}}_2{N}_j$, and $\Vert M_{i\ast }{\Vert }_2,\Vert N_i{\Vert }_2\le ℬ$, using union bound we obtain

$$P\left(\mid M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N{\mid }_{\infty }\ge nt\right)\le C\text{exp}\left(\log (p^{\prime }{q}^{\prime })-cn{t}^2∕{ℬ}^4\right).$$

Letting $\tau ={ℬ}^2\sqrt{C^{\prime }\log (p+q)}$ and $t=\tau ∕\sqrt{n}$, we observe that for our choice of τ, $t<\delta$ for all sufficiently large n since $\log (p+q)=o(n)$. Therefore, the above inequality leads to

$$\begin{gathered} P(\eta ({\mathbf{Q}}_{M,N})\ne 0)=P\left(\mid {\mathbf{Q}}_{M,N}{\mid }_{\infty }\ge \tau ∕\sqrt{n}\right) \\ \le C\text{exp}(2\log (p^{\prime }+q^{\prime })-c{C}^{\prime }\log (p+q)). \end{gathered}$$

Because $p^{\prime }\le p$ and $q^{\prime }\le q$ by our assumption on M and N, $C^{\prime }>2∕c$ suffices. Hence the proof follows.

4). Proof of Lemma 11:

Proof of Lemma 11. From the definition of S₃ in (26), and (54), it is not hard to see that $\eta ({\mathbf{S}}_3)=\eta ({\mathbf{H}}_1)+\eta ({\mathbf{H}}_2)$. We will show that H₁ is of the form $M[\mathbf{Z}{\mathbf{Z}}_1{]}^T{\mathbf{Z}}_{2}N$ where $\Vert M{\Vert }_{op}\le 2ℬ$ and $\Vert N{\Vert }_{op}\le ℬ$. Then the first part would follow from Lemma 8, which, when applied to this case, would imply

$$\Vert \eta ({\mathbf{H}}_1){\Vert }_{op}\le C{ℬ}^2\left(\sqrt{\frac{p+q}{n}}\vee \frac{p+q}{n}\right)e^{-{\text{Thr}}^2∕K}$$

provided $\text{Thr}\in [36{ℬ}^2$, $\sqrt{K\log (\max p+r,q)}∕2]$ and $K\ge 1288{ℬ}^4$. Since $r<\text{min}\{p,q\}$, the upper bound of Thr becomes $\sqrt{K\log (2\max \{p,q\})}∕2$. The proof for $\Vert \eta ({\mathbf{H}}_2){\Vert }_{op}$ will follow in a similar way, and hence skipped.

Letting

$$\begin{gathered} A_1={\Lambda }^{1∕2}{U}^T,A_2={\Sigma }_x\tilde{U}{B}_x({\tilde{U}}_{E_1\ast }{)}^T, \\ {A}_3={\Sigma }_y\tilde{V}{B}_y({\tilde{V}}_{F_2\ast }{)}^T, \end{gathered}$$

we note that (54) implies ${\mathbf{H}}_1=A_1^T{\mathbf{Z}}^T{Z}_2{A}_3+A_2^T{\mathbf{Z}}_1^T{Z}_2{A}_3$, which can be written as

$${\mathbf{H}}_1=A_1^T{\left(\left[\mathbf{Z}{\mathbf{Z}}_1\right]\right)}^T{Z}_2{A}_3,\text{where}{A}_4=\left[\begin{array}{c}\hfill A_1\hfill \\ \hfill A_2\hfill \end{array}\right].$$

We will now invoke Lemma 8 because $Z_3=[\mathbf{Z}{\mathbf{Z}}_2]$ is a Gaussian data matrix with n rows and $p+r\le 2p$ columns, and the matrices A₄ and A₃ are also bounded in operator norm. To see the latter, first, noting $\Vert A_4{\Vert }_{op}=\sqrt{\Vert A_4^T{A}_4{\Vert }_{op}}$, and we observe that

$$\Vert A_4^T{A}_4{\Vert }_{op}=\Vert A_1^T{A}_1+A_2^T{A}_2{\Vert }_{op}\le \Vert A_1{\Vert }_{op}^2+\Vert A_2{\Vert }_{op}^2.$$

Therefore it suffices to bound the operator norms of A₁, A₂, and A₃ only. Using (55), we can show that the operator norm of the matrices of the form A₂, or A₃ is bounded by $ℬ$ for $(X,Y)\sim \mathbb{P}\in 𝒫(r,s_x,s_y,ℬ)$. Since ${\Sigma }_x^{1∕2}U$ has orthogonal columns, it can be easily seen that $\Vert A_1{\Vert }_{op}\le 1$. Therefore

$$\Vert A_4{\Vert }_{op}\le \Vert A_1{\Vert }_{op}+\Vert A_2{\Vert }_{op}\le 1+ℬ\le 2ℬ$$

because $ℬ>1$ as per the definition of $𝒫(r,s_x,s_y,ℬ)$. The proof of the first part now follows by Lemma 8. Because $\Vert A_4{\Vert }_{op}\le 2ℬ$ and $\Vert A_3{\Vert }_{op}\le ℬ$, the proof of the second part follows directly from Lemma 9, and hence skipped.

C. Proof of Additional Lemmas for Section III-C and Theorem 3

Proof of Lemma 2. To prove the current lemma, we will require a result on the concentration of $\alpha$ and $\beta$ under ${\pi }_x$ and ${\pi }_y$. To that end, for s, $m\in \mathbb{N}$ satisfying $s\le m$, let us define the set

$$𝒲(s,m)=\left\{x\in {\mathbb{R}}^m:\Vert x{\Vert }_0\in [s∕2,2s],\Vert x{\Vert }_2\in [0.9,1.1]\right\}.$$

Suppose ${\pi }_x$ and ${\pi }_y$ are the Rademacher priors on $\alpha$ and $\beta$ as defined in Section III-C. The following lemma then says that $\alpha$ and $\beta$ concentrates on $𝒲(s_x,p)$ and $𝒲(s_y,q)$ with probability tending to one.

Lemma 17. Suppose $s_y\to \infty$. Then

$$\underset{n}{\text{lim}}{\pi }_x(\alpha \in 𝒲(s_x,p))=1;\underset{n}{\text{lim}}{\pi }_y(\beta \in 𝒲(s_y,q))=1.$$ (63)

Here the probability ${\pi }_x(\alpha \in 𝒲(s_x,p))$ depends on n through $s_x$ and q. Similarly ${\pi }_y(\beta \in 𝒲(s_y,q))$ depends on n through $s_y$ and q.

Recall the definition of ${\mathbb{P}}_{\alpha ,\beta }$ from (19). Let us consider the class

$${𝒫}_{sub}(ℬ)=\left\{{\mathbb{P}}_{\alpha ,\beta }:\alpha \in 𝒲(s_x,p),\beta \in 𝒲(s_y,q)\right\}.$$

If $\alpha \in 𝒲(s_x,p)$ and $\beta \in 𝒲(s_x,p)$, than $\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2\le (1.1{)}^2<ℬ$ because $ℬ>2$. Therefore (19) implies that $(X,Y)\sim \mathbb{P}\in {𝒫}_{sub}(ℬ)$ has canonical correlation ${ℬ}^{-1}$. Thus ${𝒫}_{sub}(ℬ)\subset {𝒫}_G(r,2s_x,2s_y,ℬ)$, implying

$$\begin{gathered} \underset{n}{\text{lim}\text{inf}}\underset{{\mathbb{P}}_n\in {𝒫}_G(r,2s_x,2s_y,ℬ{)}^n}{\text{sup}}{\mathbb{P}}_n\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1)\right) \\ \ge \underset{n}{\text{lim}\text{inf}}\underset{{\mathbb{P}}_n\in {𝒫}_{sub}(ℬ)}{\text{sup}}{\mathbb{P}}_n\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1)\right). \end{gathered}$$

Suppose ${ℱ}_x$ and ${ℱ}_y$ are the Borel σ-field associated with $𝒲(s_x,p)$ and $𝒲(s_y,q)$, respectively. Define the probability measures ${\tilde{\pi }}_x$ and ${\tilde{\pi }}_y$ on $(𝒲(s_x,p),{ℱ}_x)$ and $(𝒲(s_y,q),{ℱ}_y)$, respectively, by

$${\tilde{\pi }}_x(A)=\frac{{\pi }_x(A)}{{\pi }_x(𝒲(s_x,p))}\text{for all}A\in {ℱ}_x,$$

and

$${\tilde{\pi }}_y(B)=\frac{{\pi }_y(B)}{{\pi }_y(𝒲(s_y,q))}\text{for all}B\in {ℱ}_y.$$

Note also that if $\alpha \in 𝒲(s_x,p)$ and $\beta \in 𝒲(s_y,q)$, then ${\mathbb{P}}_{\alpha ,\beta }\in {𝒫}_{sub}(ℬ)$. Therefore

$$\begin{gathered} \underset{n}{\text{lim}\text{inf}}\underset{{\mathbb{P}}_n\in {𝒫}_{sub}(ℬ)}{\text{sup}}{\mathbb{P}}_n\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1)\right) \\ \ge \underset{n}{\text{lim}\text{inf}}{\int }_{\begin{array}{c}\hfill 𝒲(s_x,p)\hfill \\ \hfill \times 𝒲(s_y,q)\hfill \end{array}}{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1\right)d{\tilde{\pi }}_x(\alpha )d{\tilde{\pi }}_y(\beta ) \\ =\frac{{\text{lim inf}}_n{\int }_{\begin{array}{c}\hfill 𝒲(s_x,p)\hfill \\ \hfill \times 𝒲(s_y,q)\hfill \end{array}}{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1\right)d{\pi }_x(\alpha )d{\pi }_y(\beta )}{{\text{lim sup}}_n\left({\pi }_x(𝒲(s_x,p)){\pi }_y(𝒲(s_y,q))\right)}, \end{gathered}$$

whose denominator is one by Lemma 17. Denoting $𝒲(s_y,q{)}^c={\mathbb{R}}^p\setminus 𝒲(s_y,q)$, we note that

$$\begin{gathered} {\int }_{{\mathbb{R}}^p\times 𝒲(s_y,q{)}^c}{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1\right)d{\pi }_x(\alpha )d{\pi }_y(\beta ) \\ \le 1-{\pi }_y(𝒲(s_y,q)){\to }_{n}0 \end{gathered}$$

by Lemma 17. Similarly, denoting $𝒲(s_x,p{)}^c={\mathbb{R}}^p\setminus 𝒲(s_x,p)$, we can show that

$${\int }_{𝒲(s_x,p{)}^c\times {\mathbb{R}}^y}{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1\right)d{\pi }_x(\alpha )d{\pi }_y(\beta ){\to }_{n}0.$$

Therefore, it holds that

$$\begin{gathered} \underset{n}{\text{lim}\text{inf}}\underset{𝒲(s_x,p)\times 𝒲(s_y,q)}{\int }{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=1\right)d{\pi }_x(\alpha )d{\pi }_y(\beta ) \\ =\&\underset{n}{\text{lim}\text{inf}}{\mathbb{E}}_{\pi }\left[{\mathbb{P}}_{n,\alpha ,\beta }\left({\Phi }_n(\mathbf{X},\mathbf{Y})=0\right)\right]. \end{gathered}$$

Thus the proof follows.

Proof of Lemma 17:

Proof of Lemma 17.. We are going to show (63) only for ${\pi }_x$ because the proof for ${\pi }_y$ follows in the identical manner. Throughout we will denote by ${\mathbb{E}}_{{\pi }_x}$ and ${\text{var}}_{{\pi }_x}$ the expectation and variance under ${\pi }_x$. Note that when $\alpha \sim {\pi }_x$, $\Vert \alpha {\Vert }_0={\sum }_{i=1}^{p}I[{\alpha }_i\ne 0]$, where $I[{\alpha }_i\ne 0]$’s are i.i.d. Bernoulli random variables with success probability $s_x∕p$. Therefore, Chebyshev’s inequality yields that for any $ϵ>0$,

$${\pi }_x\left(\mid \Vert \alpha {\Vert }_0-s_x\mid >s_xϵ\right)\ge p\frac{{\text{var}}_{{\pi }_x}(I[{\alpha }_i\ne 0])}{s_x^2{ϵ}^2}=\frac{1-s_x∕p}{s_x{ϵ}^2},$$

which goes to zero if $s_x\to \infty$. Therefore, for $ϵ=1∕2$, we have

$${\pi }_x\left(\Vert \alpha {\Vert }_0\in [s_x∕2,2s_x]\right)\le {\pi }_x\left(\mid \Vert \alpha {\Vert }_0-s_x\mid >s_xϵ\right)\to 0.$$

Also, since ${\mathbb{E}}_{{\pi }_x}[{\sum }_{i=1}^p{\alpha }_i^2]=1$, Chebyshev’s inequality implies that

$$\begin{gathered} {\pi }_x\left(\sum _{i=1}^p{\alpha }_i^2-1\ge ϵ\right)\le \frac{{\text{var}}_{{\pi }_x}\left({\sum }_{i=1}^p{\alpha }_i^2\right)}{{ϵ}^2} \\ \stackrel{(a)}{=}\frac{p.{\text{var}}_{{\pi }_x}({\alpha }_i^2)}{{ϵ}^2}\le \frac{p{\mathbb{E}}_{{\pi }_x}[{\alpha }_i^4]}{{ϵ}^2}=\frac{1}{s_x{ϵ}^2}, \end{gathered}$$

which goes to zero if $s_x\to \infty$ for any fixed $ϵ>0$. Here (a) uses the fact that ${\alpha }_i$’s are i.i.d. The proof now follows setting $ϵ=0.1$.

1). Proof of Lemma 5:

Proof of Lemma depends on two auxiliary lemmas. We state and prove these lemmas first.

Lemma 18. Suppose $w\in {\mathbb{Z}}^m$, and $A\in {\mathbb{R}}^{m\times m}$ is a matrix. Let $\mathbb{P}$ be the measure induced by the m-dimensional standard Gaussian random vector and denote by ${\mathbb{E}}_{\mathbb{P}}$ the corresponding expectation. Then for any $x\in {\mathbb{R}}^m$ we have

$$\sum _{j\in {\mathbb{Z}}^m}\frac{t^j}{j!}{E}_{\mathbb{P}}[H_j(AZ)]=e^{t^T(A^2-I)t∕2}.$$

Proof of Lemma 18. The generating function of H_w has the convergent expansion [69, Proposition 6]

$$\sum _{j\in {\mathbb{Z}}^m}\frac{t^j}{j!}{H}_j(x)=\text{exp}\left\{t^{T}x-t^{T}t∕2\right\}$$

for any $x\in {\mathbb{R}}^m$. Therefore,

$$\sum _{j\in {\mathbb{Z}}^m}\frac{t^j}{j!}{H}_j(Ax)=\text{exp}\left\{t^{T}Ax-t^{T}t∕2\right\}.$$

Multiplying both side by the density $d\mathbb{P}$ of $\mathbb{P}$ and then integrating over ${\mathbb{R}}^m$ gives us

$$\sum _{j\in {\mathbb{Z}}^m}\frac{t^j}{j!}{E}_{\mathbb{P}}[H_j(AZ)]=E_{\mathbb{P}}\left[e^{t^{T}AZ}\right]e^{-t^{T}t∕2}=e^{t^T(A^2-I)t∕2}.$$

Lemma 19. Let $\Sigma (\alpha ,\beta ,1∕ℬ)$ be as defined in (18). Suppose $z=(z_x,z_y)$ where $z_x\in {\mathbb{Z}}^p$ and $z_y\in {\mathbb{Z}}^q$. Then for any $t\in {\mathbb{R}}^{p+q}$, we have

$$\begin{gathered} {\phantom{\mid }{\partial }_t^z\text{exp}\left\{\frac{1}{2}{t}^T\left(\Sigma (\alpha ,\beta ,1∕ℬ)-I_{p+q}\right)t\right\}\mid }_{t=(0,\dots ,0)} \\ =\{\begin{array}{cc}{ℬ}^{-\mid z_x\mid }\mid z_x\mid !{\alpha }^{z_x}{\beta }^{z_y}\hfill & if\mid z_x\mid =\mid z_y\mid ,\hfill \\ 0\hfill & o.w.\hfill \end{array}\phantom{\}} \end{gathered}$$

Proof of Lemma 19. Let us partition t as $(t_x,t_y)$ where $t_x=(t_x(1),\dots ,t_x(p))\in {\mathbb{R}}^p$ and $t_y=(t_y(1),\dots ,t_y(q))\in {\mathbb{R}}^q$. We then calculate

$$\frac{t^T\left(\Sigma (\alpha ,\beta ,1∕ℬ)-I_{p+q}\right)t}{2}={ℬ}^{-1}{t}_x^T\alpha {\beta }^T{t}_y,$$

which implies

$$\begin{gathered} \text{exp}\left\{\frac{1}{2}{t}^T\left(\Sigma (\alpha ,\beta ,1∕ℬ)-I_{p+q}\right)t\right\} \\ =\text{exp}\left\{{ℬ}^{-1}\sum _{i=1}^p\sum _{j=1}^q{\alpha }_i{\beta }_j{t}_x(i)t_y(j)\right\} \\ =\sum _{k=0}^{\infty }{ℬ}^{-k}\frac{{\left({\sum }_{i=1}^p{\alpha }_i{t}_x(i)\right)}^k{\left({\sum }_{j=1}^q{\beta }_j{t}_y(j)\right)}^k}{k!} \end{gathered}$$

which equals

$$\begin{gathered} \sum _{k=0}^{\infty }\frac{{ℬ}^{-k}}{k!}\sum _{\begin{array}{c}\hfill z_x\in {\mathbb{Z}}^p,\hfill \\ \hfill \mid z_x\mid =k\hfill \end{array}}\sum _{\begin{array}{c}\hfill z_y\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid z_y\mid =k\hfill \end{array}}\frac{k!}{z_x!}\frac{k!}{z_y!}{\alpha }^{z_x}{\beta }^{z_y}{t}_x^{z_x}{t}_y^{z_y} \\ =\sum _{k=0}^{\infty }\sum _{\begin{array}{c}\hfill z_x\in {\mathbb{Z}}^p,\hfill \\ \hfill \mid z_x\mid =k\hfill \end{array}}\sum _{\begin{array}{c}\hfill z_y\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid z_y\mid =k\hfill \end{array}}{ℬ}^{-k}\frac{k!}{z!}{\alpha }^{z_x}{\beta }^{z_y}{t}_x^{z_x}{t}_y^{z_y} \\ \stackrel{(a)}{=}\sum _{\begin{array}{c}\hfill z\in {\mathbb{Z}}^{p+q}\hfill \\ \hfill \mid z_x\mid =\mid z_y\mid \hfill \end{array}}{ℬ}^{-\mid z_x\mid }\frac{\mid z_x\mid !}{z!}{\alpha }^{z_x}{\beta }^{z_y}{t}^z. \end{gathered}$$

In step (a), we stacked the variables $z_x$ and $z_y$ to form $z=(z_x,z_y{)}^T$. Note that following the terminologies set in the beginning of Appendix E, $z!=z_x!z_y!$ and $t^z=t_x^{z_x}{t}_y^{z_y}$. Note that if $\mid z_x\mid \ne \mid z_y\mid$, then the term $t^z$ has zero coefficient in the above expansion. Thus the lemma follows.

Proof of Lemma 5.

$$\begin{gathered} \langle {\mathbb{L}}_n,H_w{\rangle }_{L^2({\mathbb{Q}}_n)}={\mathbb{E}}_{(\mathbf{X},\mathbf{Y})\sim {\mathbb{Q}}_n}\left[{\mathbb{E}}_{\pi }\left[H_w(\mathbf{X},\mathbf{Y})\frac{d{\mathbb{P}}_{n,\alpha ,\beta }}{d{\mathbb{Q}}_n}\right]\right] \\ ={\mathbb{E}}_{\pi }\left[{\mathbb{E}}_{(\mathbf{X},\mathbf{Y})\sim {\mathbb{P}}_{n,\alpha ,\beta }}\left[H_w(\mathbf{X},\mathbf{Y})\right]\right] \\ \stackrel{(a)}{=}{\mathbb{E}}_{\pi }\left[\underset{i\in [n]}{{\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta },}}\left[\prod _{i\in [n]}{H}_{w_i}(X_i,Y_i)\right]\right] \\ ={\mathbb{E}}_{\pi }\left[\prod _{i\in [n]}{\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta }}\left[H_{w_i}(X_i,Y_i)\right]\right] \end{gathered}$$

where (a) follows because $(X_i,Y_i)$’s are independent observations. Now note that if $\Vert \alpha \Vert \Vert \beta {\Vert }_2\ge ℬ$, then (19) implies

$${\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta }}\left[H_{w_i}(X_i,Y_i)\right]={\mathbb{E}}_{(X_i,Y_i)\sim \mathbb{Q}}\left[H_{w_i}(X_i,Y_i)\right]=0,$$

where the last step follows because ${\mathbb{E}}_{Z\sim \mathbb{Q}}[H_{w_i}(Z)]=0$ for any $i\in [n]$. If $\Vert \alpha \Vert \Vert \beta {\Vert }_2<ℬ$, then $\Sigma (\alpha ,\beta ,1∕ℬ)$ defined in (18) is positive definite, and (19) implies

$$\begin{gathered} {\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta }}\left[H_{w_i}(X_i,Y_i)\right]={\mathbb{E}}_{\mathbf{Z}\sim \mathbb{Q}}\left[H_{w_i}\left(\Sigma (\alpha ,\beta ,1∕ℬ{)}^{1∕2}\mathbf{Z}\right)\right] \\ ={\phantom{\mid }{\partial }_t^{w_i}\left(\text{exp}\left\{\frac{1}{2}{t}^T\left(\Sigma (\alpha ,\beta ,1∕ℬ)-I_{p+q}\right)t\right\}\right)\mid }_{t=(0,\dots ,0)} \end{gathered}$$

by Lemma 18. Here $\Sigma (\alpha ,\beta ,1∕ℬ)$ is as in (18), and $\Sigma (\alpha ,\beta ,1∕ℬ)$ is positive definite because $\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ$, as discussed in Section III-C. Therefore, we can write

$$\begin{gathered} {\mathbb{E}}_{(X_i,Y_i)\sim {\mathbb{P}}_{\alpha ,\beta }}\left[H_{w_i}(X_i,Y_i)\right] \\ =1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\} \\ \times {\phantom{\mid }{\partial }_t^{w_i}\left(\text{exp}\left\{\frac{1}{2}{t}^T\left(\Sigma (\alpha ,\beta ,1∕ℬ)-I_{p+q}\right)t\right\}\right)\mid }_{t=(0,\dots ,0)} \end{gathered}$$

Lemma 19 gives the form of the partial derivative in the above expression, and implies that the partial derivative is zero unless $\mid w_i^x\mid =\mid w_i^y\mid$. Therefore, $\langle {\mathbb{L}}_n,H_w{\rangle }_{L^2({\mathbb{Q}}_n)}\ne 0$ only if $\mid w_i^x\mid =\mid w_i^y\mid$ for all $i\in [n]$. In this case, $\mid w_i\mid =2\mid w_i^x\mid$ is even, and by Lemma 19,

$$\begin{gathered} \langle {\mathbb{L}}_n,H_w{\rangle }_{L^2({\mathbb{Q}}_n)} \\ ={\mathbb{E}}_{\pi }\left[1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}\prod _{i\in [n]}{ℬ}^{-\mid w_i^x\mid }\mid w_i^x\mid !{\alpha }^{w_i^x}{\beta }^{w_i^y}\right] \\ =\left\{{ℬ}^{-{\sum }_{i=1}^n\mid w_i^x\mid }\prod _{i=1}^n\mid w_i^x\mid !\right\} \\ \times {\mathbb{E}}_{\pi }\left[1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}{\alpha }^{{\sum }_{i=1}^n{w}_i^x}{\beta }^{{\sum }_{i=1}^n{w}_i^y}\right] \\ ={ℬ}^{-\mid w\mid ∕2}\left\{\prod _{i=1}^n\mid w_i^x\mid !\right\} \\ \times {\mathbb{E}}_{\pi }\left[1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}{\alpha }^{{\sum }_{i=1}^n{w}_i^x}{\beta }^{{\sum }_{i=1}^n{w}_i^y}\right]. \end{gathered}$$

Therefore,

$$\begin{gathered} \langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^2 \\ =\{\begin{array}{c}\frac{{ℬ}^{-\mid w\mid }}{w!}{\mathbb{E}}_{\pi }{\left[1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}{\alpha }^{{\sum }_{i=1}^n{w}_i^x}{\beta }^{{\sum }_{i=1}^n{w}_i^y}\right]}^2\hfill \\ \times {\left\{{\prod }_{i=1}^n\mid w_i^x\mid !\right\}}^2\text{if}\mid w_i^x\mid =\mid w_i^y\mid \text{for all}i\in [n],\hfill \\ 0\text{o.w.}\hfill \end{array}\phantom{\}} \end{gathered}$$

2). Proof of Lemma 6:

Proof. Lemma 5 implies that ${\mathbb{L}}_n$ belongs to the subspace generated by those $H_w$’s whose degree-index ω has $\mid w_i^x\mid =\mid w_i^y\mid$ for all $i\in [n]$. The degree of the polynomial $H_w$ is $\mid w\mid$, which is even in the above case. Therefore, if $D_n\ge 1$ is odd, $\Vert {\mathbb{L}}_n^{\le D_n}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$ equals $\Vert {\mathbb{L}}_n^{\le (D_n-1)}{\Vert }_{L_2({\mathbb{Q}}_n)}^2$. Hence, it suffices to compute the norm of ${\mathbb{L}}_n^{\le 2{𝒟}_n}$, where ${𝒟}_n=\lfloor D_n∕2\rfloor$. Suppose $w\in {\mathbb{Z}}^{n(p+q)}$ is such that $\mid w_i^x\mid =\mid w_i^y\mid$ for all $i\in [n]$. Lemma 5 gives

$$\begin{gathered} \langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^2 \\ =\frac{{ℬ}^{-\mid w\mid }}{w!}{\left\{{\mathbb{E}}_{\pi }\left[1\{\Vert \alpha {\Vert }_2\Vert \beta {\Vert }_2<ℬ\}{\alpha }^{{\sum }_{i=1}^n{w}_i^x}{\beta }^{{\sum }_{i=1}^n{w}_i^y}\right]\right\}}^2 \\ \times {\left\{\prod _{i=1}^n\mid w_i^x\mid !\right\}}^2. \end{gathered}$$

Consider the pair of replicas ${\alpha }_1,{\alpha }_2\stackrel{iid}{\sim }{\pi }_x$ and ${\beta }_1,{\beta }_2\stackrel{iid}{\sim }{\pi }_y$. Letting W denote the indicator function of the event $\{\Vert {\alpha }_1{\Vert }_2\Vert {\beta }_1{\Vert }_2<ℬ,\Vert {\alpha }_2{\Vert }_2\Vert {\beta }_2{\Vert }_2<ℬ\}$, we can then write

$$\begin{gathered} \langle {\mathbb{L}}_n,{\widehat{H}}_w{\rangle }_{L^2({\mathbb{Q}}_n)}^2=\frac{{ℬ}^{-\mid w\mid }}{w!}{\mathbb{E}}_{\pi }\left[({\alpha }_1{\alpha }_2{)}^{{\sum }_{i=1}^n{w}_i^x}({\beta }_1{\beta }_2{)}^{{\sum }_{i=1}^n{w}_i^y}W\right] \\ \times {\left\{\prod _{i=1}^n\mid w_i^x\mid !\right\}}^2. \end{gathered}$$ (64)

Denote by $\overline{d}=(d_1,\dots ,d_n)\in {\mathbb{Z}}^n$. Using (64), we obtain the following expression:

$$\Vert {\mathbb{L}}_n^{\le 2{𝒟}_n}{\Vert }_{L_2(\mathbb{Q})}=\sum _{d=0}^{{𝒟}_n}{ℬ}^{-2d}\sum _{\overline{d}:\sum d_i=d}\sum _{\begin{array}{c}\hfill w:w_i^x\in {\mathbb{Z}}^p,\hfill \\ \hfill w_i^y\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid w_i^x\mid =\mid w_i^y\mid =d_i\hfill \end{array}}{T}_{\overline{d},w}$$

where

$$T_{\overline{d},w}={\mathbb{E}}_{\pi }\left[W\prod _{i=1}^n\left(\frac{d_i^2}{w_i^x!w_i^y!}({\alpha }_1{\alpha }_2{)}^{w_i^x}({\beta }_1{\beta }_2{)}^{w_i^y}\right)\right].$$

Therefore $\Vert {\mathbb{L}}_n^{\le 2{𝒟}_n}{\Vert }_{L_2(\mathbb{Q})}$ equals

$$\begin{gathered} \sum _{d=0}^{{𝒟}_n}{ℬ}^{-2d}\sum _{\overline{d}:\sum d_i=d}{\mathbb{E}}_{\pi }[W\sum _{\begin{array}{c}\hfill w:w_i^x\in {\mathbb{Z}}^p,\hfill \\ \hfill w_i^y\in {\mathbb{Z}}^q,\hfill \\ \hfill \mid w_i^x\mid =\mid w_i^y\mid =d_i\hfill \end{array}}\left(\prod _{i=1}^n\frac{d_i!}{w_i^x!}({\alpha }_1{\alpha }_2{)}^{w_i^x}\right)\phantom{]} \\ \times \phantom{[}\left(\prod _{i=1}^n\frac{d_i!}{w_i^y!}({\beta }_1{\beta }_2{)}^{w_i^y}\right)] \\ =\sum _{d=0}^{{𝒟}_n}{ℬ}^{-2d}\sum _{\overline{d}:\sum d_i=d}{\mathbb{E}}_{\pi }[W\left(\sum _{\begin{array}{c}\hfill w^x:w_i^x\in {\mathbb{Z}}^p\hfill \\ \hfill \mid w_i^x\mid =d_i\hfill \end{array}}\prod _{i=1}^n\frac{d_i!}{w_i^x!}({\alpha }_1{\alpha }_2{)}^{w_i^x}\right)\phantom{]} \\ \times \phantom{[}\left(\sum _{\begin{array}{c}\hfill w^y:w_i^y\in {\mathbb{Z}}^q\hfill \\ \hfill \mid w_i^y\mid =d_i\hfill \end{array}}\prod _{i=1}^n\frac{d_i!}{w_i^y!}({\beta }_1{\beta }_2{)}^{w_i^y}\right)] \end{gathered}$$

In the last step, we used the variables $w^x=(w_1^x,\dots ,w_n^x)$, and $w_y=(w_1^y,\dots ,w_n^y)$. Suppose $z_i\in {\mathbb{Z}}^p$ for each $i\in [n]$. For any $x\in {\mathbb{R}}^p$ and $y\in {\mathbb{R}}^q$, it holds that

$$\begin{gathered} \sum _{z_i\in {\mathbb{Z}}^p,\mid z_i\mid =d_i}\prod _{i=1}^n\frac{d_i!}{z_i!}{x}^{z_i}{y}^{z_i} \\ =\prod _{i=1}^n\sum _{z_i\in {\mathbb{Z}}^p,\mid z_i\mid =d_i}\frac{d_i!}{z_i!}{x}^{z_i}{y}^{z_i} \\ \stackrel{(a)}{=}\prod _{i=1}^n(x^{T}y{)}^{d_i}=(x^{T}y{)}^{{\sum }_{i=1}^n{d}_i}, \end{gathered}$$

where (a) follows from Fact 6.

Fact 6. [Multinomial Theorem] Suppose $\alpha \in {\mathbb{R}}^p$. Then for $m\in \mathbb{Z}$,

$${\left(\sum _{i=1}^p{\alpha }_i\right)}^m=\sum _{z\in {\mathbb{Z}}^p,\mid z\mid =m}\frac{k!{\alpha }^z}{z!}.$$

Therefore it follows that

$$\begin{gathered} \left(\sum _{\begin{array}{c}\hfill w^x:w_i^x\in {\mathbb{Z}}^p\hfill \\ \hfill \mid w_i^x\mid =d_i\hfill \end{array}}\frac{d_i!}{w_i^x!}({\alpha }_1{\alpha }_2{)}^{w_i^x}\right)\left(\sum _{\begin{array}{c}\hfill w^y:w_i^y\in {\mathbb{Z}}^q\hfill \\ \hfill \mid w_i^y\mid =d_i\hfill \end{array}}\frac{d_i!}{w_i^y!}({\beta }_1{\beta }_2{)}^{w_i^y}\right) \\ =({\alpha }_1^T{\alpha }_2{)}^{{\sum }_{i=1}^n{d}_i}({\beta }_1^T{\beta }_2{)}^{{\sum }_{i=1}^n{d}_i}, \end{gathered}$$

which implies

$$\begin{gathered} \Vert {\mathbb{L}}_n^{\le 2{𝒟}_n}{\Vert }_{L_2(\mathbb{Q})} \\ =\sum _{d=0}^{{𝒟}_n}{ℬ}^{-2d}\sum _{\overline{d}:\sum d_i=d}{\mathbb{E}}_{\pi }\left[W({\alpha }_1^T{\alpha }_2{)}^{{\sum }_{i=1}^n{d}_i}({\beta }_1^T{\beta }_2{)}^{{\sum }_{i=1}^n{d}_i}\right] \\ \stackrel{(a)}{=}\sum _{d=0}^{{𝒟}_n}{ℬ}^{-2d}\left(\begin{array}{c}\hfill d+n-1\hfill \\ \hfill d\hfill \end{array}\right){\mathbb{E}}_{\pi }\left[W({\alpha }_1^T{\alpha }_2{)}^d({\beta }_1^T{\beta }_2{)}^d\right] \\ ={\mathbb{E}}_{\pi }\left[W\sum _{d=0}^{{𝒟}_n}\left\{\left(\begin{array}{c}\hfill d+n-1\hfill \\ \hfill d\hfill \end{array}\right){\left({ℬ}^{-2}({\alpha }_1^T{\alpha }_2)({\beta }_1^T{\beta }_2\right)}^d\right\}\right]. \end{gathered}$$

where (a) follows since the number of $\overline{d}\in {\mathbb{Z}}^n$ such that $\mid \overline{d}\mid =d$ equals $\left(\begin{array}{c}\hfill n+d-1\hfill \\ \hfill d\hfill \end{array}\right)$. Noting ${𝒟}_n=\lfloor D_n∕2\rfloor$, the proof follows.

D. Proof of Technical Lemmas for Theorem 4

First, we introduce some additional notations and state some useful results that will be used repeatedly throughout the proof. Suppose $A\in {\mathbb{R}}^{p\times q}$. We can write A as

$$A=\left[A_{\ast 1}{A}_{\ast 2}\cdots A_{\ast q}\right].$$

We define the vectorization operator as

$$\text{Vec}(A)=\left[\begin{array}{c}\hfill A_{\ast 1}\hfill \\ \hfill \cdots \hfill \\ \hfill A_{\ast q}\hfill \end{array}\right].$$

We will use two well known operations on the vetorization operators, which follow from Section 10.2.2 of [70].

Fact 7. A. $Trace(A^{T}B)=Vec(A{)}^{T}Vec(B)$.

B. $Vec(AXB)=(B^T\otimes A)Vec(X)$ where $\otimes$ denotes the Kronecker delta product.

Often times we will also use the fact that [71, Theorem 13.12]

$$\Vert A\otimes B{\Vert }_{op}=\Vert A{\Vert }_{op}\Vert B{\Vert }_{op}.$$ (65)

Define the Hadamard product between vectors $x=(x_1,\dots ,x_p)$ and $y=(y_1,\dots ,y_p)$ by

$$x\circ y=(x_1{y}_1,\dots ,x_p{y}_p{)}^T.$$

Note that Cauchy-Schwarz inequality implies that

$$\Vert x\circ y{\Vert }_2\le \Vert x{\Vert }_2\Vert y{\Vert }_2$$ (66)

We will also often use of Fact 1, which states $\Vert AB{\Vert }_F^2\le \Vert A{\Vert }_{op}^2\Vert B{\Vert }_F^2$.

1). Proof of Lemma 10:

Proof. The first result is immediate. For the second result, denote by $x_D$ by the projection of y on $R^D$. Note that for any $x\in {\mathbb{R}}^m$ and $y\in {\mathbb{R}}^p$.

$$\frac{x^{T}D(A)y}{\Vert x\Vert \cdot \Vert y\Vert }=\frac{x_{D_1}^{T}A{y}_{D_2}}{\Vert x\Vert \cdot \Vert y\Vert }\le \frac{x_{D_1}^{T}A{y}_{D_2}}{\Vert x_{D_1}\Vert \cdot \Vert y_{D_2}\Vert }$$

Thus the maximum singular value of D(A) is smaller than that of A, indicating that

$$\Vert D(A)\Vert \le \Vert A\Vert .$$

2). Proof of Lemma 4:

First, we state and prove two facts, which are used in the proof of Lemma 4.

Fact 8. Suppose $A\in {\mathbb{R}}^{n\times r}$, $B\in {\mathbb{R}}^{p\times s}$ are potentially random matrices satisfying $A^{T}A=I_r$ and $B^{T}B=I_s$. Let $\mathbf{X}\in {\mathbb{R}}^{n\times p}$ be such that $r,s\le p$, and $\mathbf{X}\mid A,B$ is distributed as a standard Gaussian data matrix. Then the matrix $A^T\mathbf{X}B\mid A,B$ is distributed as a standard Gaussian data matrix.

Proof of Fact 8. $\mathbf{X}\in {\mathbb{R}}^{n\times p}$ is a Gaussian data matrix with covariance $\Sigma \in {\mathbb{R}}^{p\times p}$ if and only if

$$\text{Vec}({\mathbf{X}}^T)\sim N_{np}(0,I_n\otimes \Sigma ).$$ (67)

Now

$$\text{Vec}((A^T\mathbf{X}B{)}^T)=\text{Vec}(B^T{\mathbf{X}}^{T}A)\stackrel{(a)}{=}(A^T\otimes B^T)\text{Vec}({\mathbf{X}}^T)$$

where (a) follows from Fact 7B. However, since $(A^T\otimes B^T)\in {\mathbb{R}}^{rs\times np}$, (67) implies

$$(A^T\otimes B^T)\text{Vec}({\mathbf{X}}^T)\mid A,B\sim N_{rs}\left(0,(A^T\otimes B^T)(A\otimes B)\right),$$

but

$$(A^T\otimes B^T)(A\otimes B)=A^{T}A\otimes B^{T}B=I_r\otimes I_s=I_{rs}.$$

Therefore,

$$\text{Vec}((A^T\mathbf{X}B{)}^T)\mid A,B\sim N_{rs}(0,I_{rs}).$$

Then the result follows from (67).

In the above fact, it may appear that $A^T\mathbf{X}B$ is independent of matrices A and B since its conditional distribution is standard Gaussian. However, $A^T\mathbf{X}B$ still depends on A and B through r and s, which may be random quantities.

Fact 9. Suppose $A\in {\mathbb{R}}^{n\times k}$, $\mathbf{X}\in {\mathbb{R}}^{n\times p}$, $B\in {\mathbb{R}}^{p\times s}$ are such that conditional on A and B, X is distributed as a standard Gaussian data matrix. Further suppose that the rank of A and B are a and b, respectively. Then the following assertion holds:

$$\frac{\Vert A^T\mathbf{X}B{\Vert }_{op}}{\Vert A{\Vert }_{op}\Vert B{\Vert }_{op}}\le \Vert \mathbb{Z}{\Vert }_{op}$$

where $\mathbb{Z}\mid A,B$ is distributed as a standard Gaussian data matrix in ${\mathbb{R}}^{a\times b}$.

Proof of Fact 9. Suppose $P_A$ and $P_B$ are the projection matrices onto the column spaces of A and B, respectively. Then we can write $P_A=V_A{V}_A^T$ and $P_B=V_B{V}_B^T$, where $V_A\in {\mathbb{R}}^{n\times a}$ and $V_B\in {\mathbb{R}}^{p\times b}$ are matrices matrices with full column rank so that $V_A^T{V}_A=I_a$ and $V_B^T{V}_B=I_b$. Writing $A=P_{A}A$ and $B=P_{B}B$, we obtain that

$$\Vert A^T\mathbf{X}B{\Vert }_{op}=\Vert A^T{V}_A{V}_A^T\mathbf{X}{V}_B{V}_B^{T}B{\Vert }_{op}$$

which is bounded by

$$\Vert A{\Vert }_{op}\Vert V_A{\Vert }_{op}\Vert V_A^T\mathbf{X}{V}_B{\Vert }_{op}\Vert V_B{\Vert }_{op}\Vert B{\Vert }_{op}$$

That $\Vert V_A{\Vert }_{op}$ and $\Vert V_B{\Vert }_{op}$ are one follows from the definitions of $V_A$ and $V_B$. Fact 8 implies conditional on $V_A$ and $V_B$, $V_A^T\mathbf{X}{V}_B\in {\mathbb{R}}^{a\times b}$ is distributed as a standard Gaussian data matrix. Hence, the proof follows.

Proof of Lemma 4. Let us denote the rank of ${\mathbf{Z}}_{1}D$ by $a^{\prime }$. Note that $a^{\prime }\le \text{rank}(D)=a$. Letting $A={\mathbf{Z}}_{1}D$, and applying Fact 9, we have the bound

$$\Vert D^T{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}B{\Vert }_{op}\le \Vert {\mathbf{Z}}_{1}D{\Vert }_{op}\Vert \mathbf{Z}{\Vert }_{op}\Vert B{\Vert }_{op}$$

where $\mathbf{Z}\mid {\mathbf{Z}}_1$ is distributed as a standard Gaussian data matrix in ${\mathbb{R}}^{a^{\prime }\times b}$. Next we apply Fact 9 again, but now on the term $\Vert {\mathbf{Z}}_{1}D{\Vert }_{op}$, which leads to

$$\Vert {\mathbf{Z}}_{1}D{\Vert }_{op}\le \Vert D{\Vert }_{op}\Vert {\mathbf{Z}}^{\prime }{\Vert }_{op},$$

where ${\mathbf{Z}}^{\prime }\in {\mathbb{R}}^{n\times a}$ is a standard Gaussian data matrix. Therefore,

$$\Vert D^T{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}B{\Vert }_{op}\le \Vert A{\Vert }_{op}\Vert {\mathbf{Z}}^{\prime }{\Vert }_{op}\Vert \mathbf{Z}{\Vert }_{op}\Vert B{\Vert }_{op}.$$

We use the Gaussian matrix concentration inequality in Fact 2 to show that with probability at least $1-\text{exp}(-Cn),\Vert {\mathbf{Z}}^{\prime }{\Vert }_{op}\le \sqrt{2}(\sqrt{n}+\sqrt{a})$. Also, for $\mathbf{Z}\in {\mathbb{R}}^{a^{\prime }\times b}$, the first part of Fact 2 implies

$$\mathbb{P}\left(\Vert \mathbf{Z}{\Vert }_{op}\le \sqrt{a^{\prime }}+\sqrt{b}+t\mid {\mathbf{Z}}_1\right)\ge 1-\text{exp}(-t^2∕2)$$

for any $t>0$. Since $a^{\prime }\le a$, and $t$ is deterministic, the above implies

$$\mathbb{P}\left(\Vert \mathbf{Z}{\Vert }_{op}\le \sqrt{a}+\sqrt{b}+t\right)\ge 1-\text{exp}(-t^2∕2).$$

Hence, for any $t>0$, we have the following with probability at least $1-\text{exp}(-Cn)-\text{exp}(-t^2∕2)$:

$$\Vert D^T{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}B{\Vert }_{op}\le \sqrt{2}\Vert D{\Vert }_{op}\Vert B{\Vert }_{op}(\sqrt{n}+\sqrt{a})(\sqrt{a}+\sqrt{b}+t).$$

Since $a\le b\le n$, it follows that

$$\Vert D^T{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}B{\Vert }_{op}\le C\Vert D{\Vert }_{op}\Vert B{\Vert }_{op}\sqrt{n}\max \{\sqrt{b},t\}.$$

Therefore, the proof follows.

3). Proof of Lemma 15:

Proof of Lemma 15. Denoting

$$𝒯=\left\{(x^{\prime },y^{\prime })\in {\mathbb{R}}^p:x^{\prime }=x_{S_x},y^{\prime }=y_{S_y},x\in T_p^{ϵ},y\in T_q^{ϵ}\right\},$$

we note that

$$\underset{x\in T_p^{ϵ},y\in T_q^{ϵ}}{\max }\mid \langle x_{S_x},{\mathbf{A}}_n{y}_{S_y}\rangle \mid =\mid \underset{(x,y)\in T}{\max }\mid \langle x,{\mathbf{A}}_{n}y\rangle \mid .$$

Therefore it suffices to show that there exist absolute constants C, $c>0$ such that

$$\begin{gathered} P\left\{\underset{(x,y)\in 𝒯}{\max }\mid \langle x,{\mathbf{A}}_{n}y\rangle \mid \ge \Delta \right\} \\ \le C\text{exp}\left\{(p+q)\frac{\log (C{J}_{p,q})}{J_{p,q}}-\frac{n^2{\Delta }^2}{4C\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(2n+p+q)}\right\}. \\ +\frac{C}{{\Delta }^2}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(n(p+q){)}^C\left\{e^{-c(n+q)}+e^{-c(n+p)}\right\} \end{gathered}$$

Let us denote ${𝒵}_1=\text{Vec}({\mathbf{Z}}_1^T)$, ${𝒵}_2=\text{Vec}({\mathbf{Z}}_2^T)$, and $𝒵=({𝒵}_1^T,{𝒵}_2^T{)}^T$. Thus

$${𝒵}^T=\{({𝒵}_1{)}_{\ast 1}^T,\dots ,({\mathbf{Z}}_1{)}_{\ast p}^T,({\mathbf{Z}}_2{)}_{\ast 1}^T,\dots ,({\mathbf{Z}}_1{)}_{\ast q}^T\}.$$

Recalling ${\mathbf{Q}}_{M,N}=\frac{M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N}{n}$, we define

$$f_{x,y}({𝒵}_1,{𝒵}_2)=\langle x,\eta ({\mathbf{Q}}_{M,N})y\rangle =\langle x,{\mathbf{A}}_{y}y\rangle .$$ (68)

To obtain a tight concentration inequality for $f_{x,y}({𝒵}_1,{𝒵}_2)$, we want to use the following Gaussian concentration lemma due to [1]

Lemma 20 (Corollary 10 of [1]). Let $𝒵\sim N(0,I_n)$ be a vector of n i.i.d. standard Gaussian variables. Suppose $ℬ$ is a finite set and we have functions $F_b:{\mathbb{R}}^n\mapsto \mathbb{R}$ for every $b\in ℬ$. Assume $𝒢\in {\mathbb{R}}^n\times {\mathbb{R}}^n$ is a Borel set such that for lebesgue-almost every $(Z,Z^{\prime })\in 𝒢$ :

$$\underset{b\in ℬ}{\max }\underset{t\in [0,1]}{\text{sup}}\Vert \nabla F_b(\sqrt{t}Z+\sqrt{1-t}{Z}^{\prime }){\Vert }_2\le ℒ.$$

Then, there exists an absolute constant $C>0$ so that for any $\Delta >0$,

$$\begin{gathered} \mathbb{P}\left(\underset{b\in ℬ}{\max }\mid F_b(𝒵)-\mathbb{E}{F}_b(𝒵)\mid \ge \Delta \right) \\ \le C\mid ℬ\mid \text{exp}\left(-\frac{{\Delta }^2}{C{ℒ}^2}\right) \\ +\frac{C}{{\Delta }^2}\mathbb{E}\left[\underset{b\in ℬ}{\max }(F_b(𝒵)-F_b({𝒵}^{\prime }){)}^4\right]\mathbb{P}({𝒢}^c{)}^{1∕2}. \end{gathered}$$

Here ${𝒵}^{\prime }$ is an independent copy of $𝒵$.

In our case, the index b corresponds to (x, y), the set $ℬ$ corresponds to $𝒯$, and the function $F_b(𝒵)$ corresponds to $F_{x,y}(𝒵)$. To find the centering and the Lipschitz constant $ℒ$, we need to compute $\mathbb{E}{f}_{x,y}({𝒵}_1,{𝒵}_2)$ and ${\nabla }_{𝒵}{f}_{x,y}({𝒵}_1,{𝒵}_2)$, respectively.

First, note that since Z₁ and Z₂ are independent standard Gaussian data matrices, ${\mathbf{Q}}_{M,N}\stackrel{d}{=}-{\mathbf{Q}}_{M,N}$. Noting $\mathbb{E}\eta (X)=0$ for any symmetric random variable X, we deduce

$$\mathbb{E}\langle x,{\mathbf{A}}_{n}y\rangle =\langle x,E[\eta ({\mathbf{Q}}_{M,N})]y\rangle =0.$$

Using Lemma 21 we obtain that

$${\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}\Vert }_2\le \Vert g({\mathbf{Z}}_2){\Vert }_{op}{\Vert v\circ \nabla \eta (\text{Vec}({\mathbf{Q}}_{M,N}))\Vert }_2$$

and

$${\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_2}\Vert }_2\le \Vert h({\mathbf{Z}}_1){\Vert }_{op}{\Vert v\circ \nabla \eta (\text{Vec}({\mathbf{Q}}_{M,N}))\Vert }_2$$

where

$$\begin{gathered} v=\text{Vec}(x{y}^T),g({\mathbf{Z}}_2)={\mathbf{Z}}_{2}N\otimes M^T∕n \\ h({\mathbf{Z}}_1)={\mathbf{Z}}_1{M}^T\otimes N∕n. \end{gathered}$$

Because $\mid \nabla \eta (x)\mid <1$ for each $x\in \mathbb{R}$,

$$\begin{gathered} \Vert v\circ \nabla \eta (\text{Vec}({\mathbf{Q}}_{M,N})){\Vert }_2\le \underset{x}{\text{sup}}\nabla \mid \eta (x)\mid \Vert v{\Vert }_2 \\ \le \Vert v{\Vert }_2=\Vert x{\Vert }_2\Vert y{\Vert }_2 \end{gathered}$$

since $\Vert v{\Vert }_2^2=\Vert x{y}^T{\Vert }_F^2=\Vert x{\Vert }_2^2\Vert y{\Vert }_2^2$. Also, because $\Vert A\otimes B{\Vert }_{op}$ equals $\Vert A{\Vert }_{op}\Vert B{\Vert }_{op}$, we have

$$\begin{gathered} \Vert g({\mathbf{Z}}_2){\Vert }_{op}^2=\frac{\Vert {\mathbf{Z}}_{2}N\otimes M^T{\Vert }_{op}^2}{n^2}=\frac{\Vert {\mathbf{Z}}_{2}N{\Vert }_{op}^2\Vert M{\Vert }_{op}^2}{n^2} \\ \le \frac{\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2\Vert {\mathbf{Z}}_2{\Vert }_{op}^2}{n^2}. \end{gathered}$$ (69)

and similarly,

$$\Vert h({\mathbf{Z}}_1){\Vert }_{op}^2\le \frac{\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2\Vert {\mathbf{Z}}_1{\Vert }_{op}^2}{n^2}.$$ (70)

Therefore,

$$\begin{gathered} {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}\Vert }_2\le \Vert x{\Vert }_2\Vert y{\Vert }_2\frac{\Vert M{\Vert }_{op}\Vert N{\Vert }_{op}\Vert {\mathbf{Z}}_2{\Vert }_{op}}{n}, \\ {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_2}\Vert }_2\le \Vert x{\Vert }_2\Vert y{\Vert }_2\frac{\Vert M{\Vert }_{op}\Vert N{\Vert }_{op}\Vert {\mathbf{Z}}_1{\Vert }_{op}}{n}. \end{gathered}$$

Letting $\nabla f_{x,y}(𝒵)$ denote $\frac{\partial f_{x,y}(𝒵)}{\partial 𝒵}$, we note that the above two inequalities imply

$${\Vert \nabla f_{x,y}(𝒵)\Vert }_2^2\le \Vert x{\Vert }_2^2\Vert y{\Vert }_2^2\frac{\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(\Vert {\mathbf{Z}}_1{\Vert }_{op}^2+\Vert {\mathbf{Z}}_2{\Vert }_{op}^2)}{n^2}.$$

Because $\Vert x{\Vert }_2$, $\Vert y{\Vert }_2\le 1$, we have

$${\Vert \nabla f_{x,y}(𝒵)\Vert }_2^2\le \frac{\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(\Vert {\mathbf{Z}}_1{\Vert }_{op}^2+\Vert {\mathbf{Z}}_2{\Vert }_{op}^2)}{n^2}.$$ (71)

We choose a good set ${𝒢}_1$ where the above bound is small. To that end, we take ${𝒢}_1$ to be

$$\begin{gathered} {𝒢}_1=\{({\tilde{\mathbf{Z}}}_1,{\tilde{\mathbf{Z}}}_1^{\prime },{\tilde{\mathbf{Z}}}_2,{\tilde{\mathbf{Z}}}_2^{\prime }):{\tilde{\mathbf{Z}}}_1\in {\mathbb{R}}^{n\times p},{\tilde{\mathbf{Z}}}_1^{\prime }\in {\mathbb{R}}^{n\times p},{\tilde{\mathbf{Z}}}_2\in {\mathbb{R}}^{n\times q},\phantom{\}} \\ {\tilde{\mathbf{Z}}}_2^{\prime }\in {\mathbb{R}}^{n\times q},\max \{\Vert {\mathbf{Z}}_1{\Vert }_{op},\Vert {\mathbf{Z}}_1^{\prime }{\Vert }_{op}\}\le \sqrt{2}(\sqrt{n}+\sqrt{p}), \\ \phantom{\{}\max \{\Vert {\mathbf{Z}}_2{\Vert }_{op},\Vert {\mathbf{Z}}_2^{\prime }{\Vert }_{op}\}\le \sqrt{2}(\sqrt{n}+\sqrt{q})\}. \end{gathered}$$ (72)

Let us denote ${𝒵}_i=\text{Vec}({\mathbf{Z}}_i^T)$ and ${\widetilde{𝒵}}_i=\text{Vec}({\tilde{\mathbf{Z}}}_i^T)$. To apply Lemma 21, now we define the process

$${𝒵}_i(t)=\sqrt{t}{\widetilde{𝒵}}_i+\sqrt{1-t}{\widetilde{𝒵}}_i^{\prime },t\in [0,1],i=1,2.$$

Equation 71 implies that on ${𝒢}_1$,

$${\Vert {\nabla }_{𝒵}{f}_{x,y}\left({𝒵}_1(t),{𝒵}_2(t)\right)\Vert }_2^2\le \frac{4\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(2n+p+q)}{n^2}=ℒ.$$

We are now in a position to apply Lemma 21, which yields that

$$\begin{gathered} P\left(\underset{(x,y)\in 𝒯}{\max }\mid f_{x,y}({𝒵}_1,{𝒵}_2)\mid \ge \Delta \right) \\ \le C\mid 𝒯\mid \text{exp}\left(-\frac{{\Delta }^2}{C{ℒ}^2}\right)+\frac{C}{{\Delta }^2}E{\left[\underset{(x,y)\in T}{\max }{f}_{x,y}({𝒵}_1,{𝒵}_2{)}^4\right]}^{1∕2} \\ \times P({𝒢}_1^c{)}^{1∕2}. \end{gathered}$$ (73)

From equation 79 of [1] it follows that C can be chosen so large such that

$$\mid 𝒯\mid \le \text{exp}\left((p+q)\frac{\log (C{J}_{p,q})}{J_{p,q}}\right).$$

Thus, after plugging in the value of $ℒ$, the first term on the right hand side of (73) can be bounded above by

$$C\text{exp}\left\{(p+q)\frac{\log (C{J}_{p,q})}{J_{p,q}}-\frac{n^2{\Delta }^2}{4C\Vert M{\Vert }^2\Vert N{\Vert }^2(2n+p+q)}\right\}.$$

To bound the second term in (73), notice that Lemma 22 yields the bound

$$\mathbb{E}\left[\underset{(x,y)\in 𝒯}{\max }{f}_{x,y}({𝒵}_1,{𝒵}_2{)}^4\right]\le C\Vert M{\Vert }_{op}^4\Vert N{\Vert }_{op}^4(n(p+q){)}^C,$$

whereas Fact 2 leads to the bound

$$P({𝒢}_1^c{)}^{1∕2}\le 2\left(\text{exp}(-c(n+p))+\text{exp}(-c(n+q))\right).$$ (74)

Therefore the proof follows.

Lemma 21. Suppose $f_{x,y}$ is as defined in (68) and ${\mathbf{Q}}_{M,N}=M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N∕n$. Then

$$\begin{gathered} {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}\Vert }_2\le \Vert g({\mathbf{Z}}_2){\Vert }_{op}{\Vert v\circ \nabla \eta (Vec({\mathbf{Q}}_{M,N}))\Vert }_2, \\ {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_2}\Vert }_2\le \Vert h({\mathbf{Z}}_1){\Vert }_{op}{\Vert v\circ \nabla \eta (Vec({\mathbf{Q}}_{M,N}))\Vert }_2 \end{gathered}$$

where $v=Vec(x{y}^T)$, $g({\mathbf{Z}}_2)={\mathbf{Z}}_{2}N\otimes M^T∕n$, and $h({\mathbf{Z}}_1)={\mathbf{Z}}_1{M}^T\otimes N∕n$.

Proof. Using $v=\text{Vec}(x{y}^T)$, and the fact that $Tr(AB)=Tr(BA)$, we calculate that

$$\begin{gathered} f_{x,y}({𝒵}_1,{𝒵}_2)=Tr\left(y{x}^T\eta ({\mathbf{Q}}_{M,N})\right) \\ =Tr\left((x{y}^T{)}^T\eta \left(\frac{M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N}{n}\right)\right) \\ =\text{Vec}(x{y}^T{)}^T\text{Vec}\left(\eta \left(\frac{M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N}{n}\right)\right) \\ =v^T\eta \left(\text{Vec}\left(\frac{M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N}{n}\right)\right). \end{gathered}$$

Fact 7 implies

$$\text{Vec}({\mathbf{Q}}_{M,N})=\frac{(N^T{\mathbf{Z}}_2^T\otimes M)}{n}{𝒵}_1=g({\mathbf{Z}}_2{)}^T{𝒵}_1,$$ (75)

which yields $f_{x,y}({𝒵}_1,{𝒵}_2)=v^T\eta (g({\mathbf{Z}}_2{)}^T{𝒵}_1)$. Noting $v\in {\mathbb{R}}^{pq}$, we can hence write $f_{x,y}({𝒵}_1,{𝒵}_2)$ as

$$f_{x,y}({𝒵}_1,{𝒵}_2)=\sum _{i=1}^{pq}{v}_i\eta \left([g({\mathbf{Z}}_2{)}_i{]}^T{𝒵}_1\right).$$

Let us denote by $\nabla \eta (x)$ the derivative of $\eta (x)$ evaluated at $x\in \mathbb{R}$. For $A\in {\mathbb{R}}^{p\times q}$, we denote by $\nabla \eta (A)$ the matrix whose (i, j)-th entry equals $\nabla \eta (A_{i,j})$. Then we obtain that for $j\in [np]$,

$$\frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial ({𝒵}_1{)}_j}=\sum _{i=1}^{pq}{v}_i\nabla \eta \left([g({\mathbf{Z}}_2{)}_i{]}^T{𝒵}_1\right)g({\mathbf{Z}}_2{)}_{ij},$$

indicating that

$$\begin{gathered} \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}=\sum _{i=1}^{pq}{v}_i\nabla \eta \left([g({\mathbf{Z}}_2{)}_i{]}^T{𝒵}_1\right)g({\mathbf{Z}}_2{)}_i \\ =g({\mathbf{Z}}_2)\left[v\circ \nabla \eta \left(g({\mathbf{Z}}_2{)}^T{𝒵}_1\right)\right] \end{gathered}$$

where $\circ$ implies the Hadamard product. It follows that

$${\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}\Vert }_2\le \Vert g({\mathbf{Z}}_2){\Vert }_{op}{\Vert v\circ \nabla \eta \left(g({\mathbf{Z}}_2{)}^T{𝒵}_1\right)\Vert }_2.$$

Then the first part of the proof follows from (75). The proof of the second part follows similarly, and hence, skipped.

Writing $v^{\prime }=Vec(y{x}^T)$, we have

$$\begin{gathered} f_{x,y}({𝒵}_1,{𝒵}_2)=Tr\left(\eta \left(\frac{N^T{\mathbf{Z}}_2^T{\mathbf{Z}}_1{M}^T}{n}\right)x{y}^T\right) \\ =Tr\left(x{y}^T\eta \left(\frac{N^T{\mathbf{Z}}_2^T{\mathbf{Z}}_1{M}^T}{n}\right)\right), \end{gathered}$$

which equals

$$\begin{gathered} Tr\left((y{x}^T{)}^T\eta \left(\frac{N^T{\mathbf{Z}}_2^T{\mathbf{Z}}_1{M}^T}{n}\right)\right) \\ =\text{Vec}(y{x}^T{)}^T\text{Vec}\left(\eta \left(\frac{N^T{\mathbf{Z}}_2^T{\mathbf{Z}}_1{M}^T}{n}\right)\right) \\ =(v^{\prime }{)}^T\eta \left(\text{Vec}\left(\frac{N^T{\mathbf{Z}}_2^T{\mathbf{Z}}_1{M}^T}{n}\right)\right). \end{gathered}$$

Fact 7 implies that the above equals

$$(v^{\prime }{)}^T\eta \left(\frac{(M{\mathbf{Z}}_1^T\otimes N^T)}{n}{𝒵}_2\right)=(v^{\prime }{)}^T\eta \left(h({\mathbf{Z}}_1{)}^T{𝒵}_2\right).$$

where $h({\mathbf{Z}}_1)=\frac{{\mathbf{Z}}_1{M}^T\otimes N}{n}$. Thus, similarly we can show that

$$\begin{gathered} {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_2}\Vert }_2 \\ \le \Vert h({\mathbf{Z}}_1){\Vert }_{op}{\Vert v^{\prime }\circ \nabla \eta \left(h({\mathbf{Z}}_1{)}^T{𝒵}_2\right)\Vert }_2 \\ =\Vert h({\mathbf{Z}}_1){\Vert }_{op}{\Vert \text{Vec}\left((x{y}^T{)}^T\right)\circ \text{Vec}\left(\nabla \eta {\left(\left[\frac{M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N}{n}\right]\right)}^T\right)\Vert }_2 \\ =\Vert h({\mathbf{Z}}_1){\Vert }_{op}{\Vert \text{Vec}\left(x{y}^T\right)\circ \text{Vec}\left(\nabla \eta \left(\left[\frac{M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N}{n}\right]\right)\right)\Vert }_2 \\ =\Vert h({\mathbf{Z}}_1){\Vert }_{op}{\Vert v\circ \nabla \eta \left(g({\mathbf{Z}}_2{)}^T{𝒵}_1\right)\Vert }_2. \end{gathered}$$

Therefore, the proof follows.

Lemma 22. There exists an absolute constant C so that the function $f_{x,y}$ defined in (68) satisfies

$$\mathbb{E}\left[\underset{\Vert x{\Vert }_2\le 1,\Vert y{\Vert }_2\le 1}{\max }{f}_{x,y}({𝒵}_1,{𝒵}_2{)}^4\right]\le C\Vert M{\Vert }_{op}^4\Vert N{\Vert }_{op}^4(n(p+q){)}^C.$$

Proof. As usual, we let ${\mathbf{Q}}_{M,N}=M{\mathbf{Z}}_1^T{\mathbf{Z}}_{2}N∕n$. Since $\Vert x{\Vert }_2,\Vert y{\Vert }_2\le 1$, we have

$$\begin{gathered} f_{x,y}({𝒵}_1,{𝒵}_2{)}^4\le \Vert \eta ({\mathbf{Q}}_{M,N}){\Vert }_{op}^4\stackrel{(a)}{\le }\Vert \eta ({\mathbf{Q}}_{M,N}){\Vert }_F^4 \\ \stackrel{(b)}{\le }\Vert {\mathbf{Q}}_{M,N}{\Vert }_F^4\stackrel{(c)}{\le }{n}^{-4}\Vert M{\Vert }_{op}^4\Vert N{\Vert }_{op}^4\Vert {\mathbf{Z}}_1{\Vert }_F^4\Vert {\mathbf{Z}}_2{\Vert }_F^4. \end{gathered}$$

Here (a) follows because the operator norm is smaller than the Frobenius norm, (b) follows because $\mid \eta (x)\mid \le \mid x\mid$, and (c) follows from Fact 1. Since Z₁ and Z₂ are independent,

$$\begin{gathered} \mathbb{E}\left[\underset{\Vert x{\Vert }_2\le 1,\Vert y{\Vert }_2\le 1}{\max }{f}_{x,y}({𝒵}_1,{𝒵}_2{)}^4\right] \\ \le n^{-4}\Vert M{\Vert }_{op}^4\Vert N{\Vert }_{op}^4\mathbb{E}[\Vert {\mathbf{Z}}_1{\Vert }_F^4]\mathbb{E}[\Vert {\mathbf{Z}}_2{\Vert }_F^4]. \end{gathered}$$

Now note that since Z₁ and Z₂ are standard Gaussian data matrices,

$$\mathbb{E}[\Vert {\mathbf{Z}}_1{\Vert }_F^4]\le \mathbb{E}\left[Tr({\mathbf{Z}}_1^T{\mathbf{Z}}_1{)}^2\right]\le k_1(n+p{)}^{k_2}$$

for some absolute constants $k_1$ and $k_2$. We can choose C so large such that $k_1(n+p{)}^{k_2}\le C(n+p{)}^C$. Similarly, we can show that

$$\mathbb{E}[\Vert {\mathbf{Z}}_2{\Vert }_F^4]\le \mathbb{E}\left[Tr({\mathbf{Z}}_2^T{\mathbf{Z}}_2{)}^2\right]\le C(n+q{)}^C,$$

implying

$$\mathbb{E}\left[\underset{\Vert x{\Vert }_2\le 1,\Vert y{\Vert }_2\le 1}{\max }{f}_{x,y}({𝒵}_1,{𝒵}_2{)}^4\right]\le C\Vert M{\Vert }_{op}^4\Vert N{\Vert }_{op}^4(n(p+q){)}^C$$

for sufficiently large C.

4). Proof of Lemma 16:

Proof. The framework will be same as the proof of Lemma 15. Define $𝒯={𝒯}_1\times {𝒯}_2$ where

$${𝒯}_1=\left\{x^{\prime }\in {\mathbb{R}}^p:x^{\prime }=x_{S_x},x\in T_p^{ϵ}\right\}.$$

Let ${𝒵}_1$, ${𝒵}_2$, $𝒵$, and $f_{x,y}$ be as in Lemma 15. In this case, the main difference from Lemma 15 is that $\mid 𝒯\mid$ is much larger. Eventually we will arrive at (73) using the concentration inequality in Lemma 21, but large $\mid 𝒯\mid$ makes the right hand side of the inequality in (73) much larger. Therefore, we require a tighter bound on $ℒ$, which is the bound on the Lipschitz constant of $\nabla f_{x,y}(𝒵)$ on the good set, so that the concentration inequality in (73) is still useful. To bound the Lipschitz constant, as before, we bound $\Vert \nabla f_{x,y}({𝒵}_1,{𝒵}_2){\Vert }^2$ using Lemma 21, which implies that

$${\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}\Vert }_2\le \Vert g({\mathbf{Z}}_2){\Vert }_{op}{\Vert v\circ \nabla \eta (\text{Vec}({\mathbf{Q}}_{M,N}))\Vert }_2,$$

where $v=\text{Vec}(x{y}^T)$ and $g({\mathbf{Z}}_2)={\mathbf{Z}}_{2}N\otimes M^T∕n$. From (69) it follows that

$$\Vert g({\mathbf{Z}}_2){\Vert }_{op}^2\le \frac{\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2\Vert {\mathbf{Z}}_2{\Vert }_{op}^2}{n^2}.$$ (76)

In Lemma 15, we bounded $\Vert v\circ \nabla \eta (\text{Vec}({\mathbf{Q}}_{M,N})){\Vert }_2$ by $\Vert v{\Vert }_2$, which was later bounded by 1. We require a tighter bound on $\Vert v\circ \nabla \eta (\text{Vec}({\mathbf{Q}}_{M,N})){\Vert }_2$ this time. Note that $\nabla \eta (z)\le 1\{\mid z\mid \ge \tau ∕\sqrt{n}\}$ at all $z\in \mathbb{R}$ for any directional derivative of η. Noting $\Vert x{\Vert }_{\infty }\le \sqrt{J_{p,q}∕p}$ for $x\in {𝒯}_1$, we deduce that any $A\in {\mathbb{R}}^{p\times q}$ and $(x,y)\in 𝒯$ satisfy

$$\begin{gathered} \Vert v\circ \nabla \eta (\text{Vec}(A)){\Vert }_2^2=\sum _{i=1}^p\sum _{j=1}^q{x}_i^2{y}_j^2\eta (A_{i,j}{)}^2 \\ \le \frac{J_{p,q}}{p}\sum _{j=1}^q{y}_j^2\underset{j\in [q]}{\text{sup}}\sum _{i=1}^p\eta (A_{i,j}{)}^2 \\ =\frac{J_{p,q}}{p}\Vert y{\Vert }_2^2\underset{j\in [q]}{\text{sup}}\sum _{i=1}^{p}1\{\mid A_{i,j}\mid >\tau ∕\sqrt{n}\}, \end{gathered}$$

which is not greater than

$$J_{p,q}\underset{j\in [q]}{\text{sup}}\sum _{i=1}^{p}1\{\mid A_{i,j}\mid >\tau ∕\sqrt{n}\}∕p$$

because $\Vert y{\Vert }_2^2\le 1$ for $y\in {𝒯}_2$.

Thus, it follows that

$$\begin{gathered} {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_1}\Vert }_2^2\le \frac{2J_{p,q}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2\Vert {\mathbf{Z}}_2{\Vert }_{op}^2}{p{n}^2} \\ \times \underset{j\in [q]}{\text{sup}}\left\{\sum _{i=1}^{p}1\{\mid ({\mathbf{Q}}_{M,N}{)}_{i,j}\mid >\tau ∕\sqrt{n}\}\right\}. \end{gathered}$$

Similarly, we can show that

$$\begin{gathered} {\Vert \frac{\partial f_{x,y}({𝒵}_1,{𝒵}_2)}{\partial {𝒵}_2}\Vert }_2^2\le \frac{2J_{p,q}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2\Vert {\mathbf{Z}}_1{\Vert }_{op}^2}{p{n}^2} \\ \times \underset{j\in [q]}{\text{sup}}\left\{\sum _{i=1}^{p}1\{\mid ({\mathbf{Q}}_{M,N}{)}_{i,j}\mid >\tau ∕\sqrt{n}\}\right\}. \end{gathered}$$

Thus,

$$\begin{gathered} {\Vert \nabla f_{x,y}(𝒵)\Vert }_2^2\le \frac{2J_{p,q}\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2(\Vert {\mathbf{Z}}_1{\Vert }_{op}^2+\Vert {\mathbf{Z}}_2{\Vert }_{op}^2)}{n^2} \\ \times \underset{j\in [q]}{\text{sup}}\frac{\left\{{\sum }_{i=1}^{p}1\{\mid ({\mathbf{Q}}_{M,N}{)}_{i,j}\mid >\tau ∕\sqrt{n}\}\right\}}{p}. \end{gathered}$$

We want to define the good set ${𝒢}_2$ of $({\tilde{\mathbf{Z}}}_1,{\tilde{\mathbf{Z}}}_2,{\tilde{\mathbf{Z}}}_1^{\prime },{\tilde{\mathbf{Z}}}_2^{\prime })$ such that

$$Z_i(t)=\sqrt{t}{\tilde{\mathbf{Z}}}_i+\sqrt{1-t}{\tilde{\mathbf{Z}}}_i^{\prime },t\in [0,1],i=1,2,$$

satisfies both $\Vert {\mathbf{Z}}_1(t){\Vert }_{op}^2+\Vert {\mathbf{Z}}_2(t){\Vert }_{op}^2\le 4(2n+p+q)$ and

$$\underset{j\in [q]}{\text{sup}}\sum _{i=1}^{p}1\{\mid (M{\mathbf{Z}}_1(t{)}^T{\mathbf{Z}}_2(t)N{)}_{i,j}\mid >\tau \sqrt{n}\}\le 4p{e}^{-{\tau }^2∕K}.$$

We claim that the above holds if $({\tilde{\mathbf{Z}}}_1,{\tilde{\mathbf{Z}}}_2,{\tilde{\mathbf{Z}}}_1^{\prime },{\tilde{\mathbf{Z}}}_2^{\prime })\in {𝒢}_1$ defined in (72), and for all $j\in [q]$,

$$\begin{gathered} \sum _{i=1}^{p}1\{\mid (M{\tilde{\mathbf{Z}}}_1^T{\tilde{\mathbf{Z}}}_{2}N{)}_{i,j}\mid >\tau \sqrt{n}∕2\}, \\ \sum _{i=1}^{p}1\{\mid (M({\tilde{\mathbf{Z}}}_1^{\prime }{)}^T{\tilde{\mathbf{Z}}}_2^{\prime }N{)}_{i,j}\mid >\tau \sqrt{n}∕2\}\le 2p{e}^{-{\tau }^2∕K} \\ \sum _{i=1}^{p}1\{\mid (M({\tilde{\mathbf{Z}}}_1^{\prime }{)}^T{\tilde{\mathbf{Z}}}_{2}N{)}_{i,j}\mid >\tau \sqrt{n}∕2\}, \\ \sum _{i=1}^{p}1\{\mid (M({\tilde{\mathbf{Z}}}_1{)}^T{\tilde{\mathbf{Z}}}_2^{\prime }N{)}_{i,j}\mid >\tau \sqrt{n}∕2\}\le 2p{e}^{-{\tau }^2∕K}. \end{gathered}$$ (77)

The above claim follows from (89) and (90) of [1]. Therefore we define the good set ${𝒢}_2$ to be the subset of ${𝒢}_1$ where (77) is satisfied. Defining ${𝒵}_1(t)=\text{Vec}({\mathbf{Z}}_1(t{)}^T)$ and ${𝒵}_2(t)=\text{Vec}({\mathbf{Z}}_2(t{)}^T)$, we obtain that for some absolute constant $C>0$, it holds that

$$\begin{gathered} \Vert \nabla f_{x,y}({𝒵}_1(t),{𝒵}_2(t)){\Vert }_2^2 \\ \le qC\underset{{ℒ}^2}{\underbrace{\frac{J_{p,q}(2n+p+q)\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2{e}^{-{\tau }^2∕K_0}}{n^2}}}=C{ℒ}^2 \end{gathered}$$

provided ${\tilde{\mathbf{Z}}}_1,{\tilde{\mathbf{Z}}}_1^{\prime },{\tilde{\mathbf{Z}}}_2,{\tilde{\mathbf{Z}}}_2^{\prime }\in {𝒢}_2$. Similar to the proof of Lemma 15, using Lemma 21, we obtain that there exists an absolute constant C so that

$$\begin{gathered} P\left\{\underset{(x,y)\in 𝒯}{\max }\mid f_{x,y}({𝒵}_1,{𝒵}_2)\mid \ge \Delta \right\}\le C\mid 𝒯\mid \text{exp}\left(-\frac{{\Delta }^2}{C{ℒ}^2}\right) \\ +\frac{C}{{\Delta }^2}E{\left[\underset{(x,y)\in 𝒯}{\max }{f}_{x,y}({\mathbf{Z}}_1,{\mathbf{Z}}_2{)}^4\right]}^{1∕2}P({𝒢}_2^c{)}^{1∕2}. \end{gathered}$$ (78)

Now since $\mid 𝒯\mid \le \mid T_p^{ϵ}\mid \times \mid T_q^{ϵ}\mid$, and for any $k\in \mathbb{N}$, the ϵ-net $T_k^{ϵ}$ is chosen so as to satisfy $\mid T_k^{ϵ}\mid \le (1+2∕ϵ{)}^k$, we have $\mid 𝒯\mid \le (1+2∕ϵ{)}^{p+q}$. Therefore, we conclude that the first term of the bound in (78) is not larger than

$$C\text{exp}\left(-\frac{{\Delta }^2}{C{ℒ}^2}+(p+q)\log (1+2∕ϵ)\right).$$

Rest of the proof is devoted to bounding the second term of the bound in (78). The expectation term can be bounded easily using Lemma 22, which yields

$$\mathbb{E}\left[\underset{(x,y)\in T}{\max }{f}_{x,y}({\mathbf{Z}}_1,{\mathbf{Z}}_2{)}^4\right]\le C\Vert M{\Vert }_{op}^4\Vert N{\Vert }_{op}^4\{n(p+q){\}}^C.$$

We will now show that $P({𝒢}_2^c)$ is small. Note that by definition, ${𝒢}_2={𝒢}_1\cap 𝒱$, where $𝒱$ is the set of $({\tilde{\mathbf{Z}}}_1,{\tilde{\mathbf{Z}}}_2,{\tilde{\mathbf{Z}}}_1^{\prime },{\tilde{\mathbf{Z}}}_2^{\prime })$, which satisfies the equation system (77). Notice that by (74), we already have $P({𝒢}_1^c)\le e^{-c(n+p)}+e^{-c(n+q)}$ for some $c>0$. Thus it suffices to show that $P({𝒱}^c)$ is small. To this end, note that since ${\tilde{\mathbf{Z}}}_1$, ${\tilde{\mathbf{Z}}}_1^{\prime }$, ${\tilde{\mathbf{Z}}}_2$, ${\tilde{\mathbf{Z}}}_2^{\prime }$ are independent, (77) implies

$$\begin{gathered} P({𝒱}^c)\le 4P(\sum _{i=1}^{p}1\left\{\mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid >\tau \sqrt{n}∕4\right\}>2p{e}^{-{\tau }^2∕K}\phantom{)} \\ \phantom{(}\text{for all}j\in [q]). \end{gathered}$$

Defining the set ${𝒜}_j=\left\{\Vert {\tilde{\mathbf{Z}}}_2{N}_{\ast j}{\Vert }_2\le 2\sqrt{n}\Vert N_{\ast j}{\Vert }_2\right\}$, we bound the above probability as follows:

$$\begin{gathered} P({𝒱}^c)\le 4\sum _{j=1}^{q}P(\sum _{i=1}^{p}1\{\mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid >\tau \sqrt{n}∕4\phantom{)} \\ \phantom{(}\phantom{\mid }>2p\text{exp}(-{\tau }^2∕K_0)\mid {\tilde{\mathbf{Z}}}_2\in {𝒜}_j) \\ +4\sum _{j=1}^{q}P\left({\tilde{\mathbf{Z}}}_2\in {𝒜}_j^c\right). \end{gathered}$$ (79)

Now note that ${\tilde{\mathbf{Z}}}_2{N}_{\ast j}\sim N_n\left(0,\Vert N_{\ast j}{\Vert }_2^2{I}_n\right)$, or ${\tilde{\mathbf{Z}}}_2{N}_{\ast j}∕\Vert N_{\ast j}{\Vert }_2\sim N_n(0,I_n)$. Therefore, there exists a universal constant $c>0$ so that

$$\begin{gathered} \sum _{j=1}^{q}P({\tilde{\mathbf{Z}}}_2\in {𝒜}_j^c)=\sum _{j=1}^{q}P\left(\Vert N_{\ast j}{\Vert }_2^{-1}\Vert {\tilde{\mathbf{Z}}}_2{N}_{\ast j}{\Vert }_2>2\sqrt{n}\right) \\ \le q\text{exp}(-cn), \end{gathered}$$ (80)

where the last bound is due to the Chi-square tail bound in Fact 4 (see also Lemma 1 of [72] and Lemma 12 of [1]). Therefore, it only remains to bound the first term in (79). We begin with an expansion of $\mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid$ as follows

$$\begin{gathered} \mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid =\mid \sum _{l=1}^p\sum _{k=1}^n{M}_{il}({\tilde{\mathbf{Z}}}_1{)}_{kl}({\tilde{\mathbf{Z}}}_{2}N{)}_{kj}\mid \\ =\mid \sum _{l=1}^p{M}_{il}\underset{{\Psi }_l^j}{\underbrace{\sum _{k=1}^n({\tilde{\mathbf{Z}}}_1{)}_{kl}({\tilde{\mathbf{Z}}}_{2}N{)}_{kj}}}\mid . \end{gathered}$$

Since ${\tilde{\mathbf{Z}}}_1$ and ${\tilde{\mathbf{Z}}}_2$ are independent, ${\tilde{\mathbf{Z}}}_1$conditioned on ${\tilde{\mathbf{Z}}}_2$ is still a standard Gaussian data matrix. Hence, for $l\in [p]$, conditional on ${\tilde{\mathbf{Z}}}_2$, ${\Psi }_l^j$’s are independent $N(0,\Vert {\tilde{Z}}_2{N}_{\ast j}{\Vert }_2^2)$ random variables. As a result, for each $l\in [p]$ and $j\in [q]$, ${\Psi }_l^j$ can be written as $\Vert {\tilde{Z}}_2{N}_{\ast j}{\Vert }_2{\mathbb{Z}}_l$, where ${\mathbb{Z}}_l={\Psi }_l^j∕\Vert {\tilde{\mathbf{Z}}}_2{N}_{\ast j}{\Vert }_2$, and ${\mathbf{Z}}_1,\dots ,{\mathbb{Z}}_p\mid {\tilde{\mathbf{Z}}}_2\stackrel{iid}{\sim }N(0,1)$. Noting $\Vert N_j{\Vert }_2\le \Vert N{\Vert }_{op}$ for every $j\in [q]$, we derive the following bound provided ${\tilde{\mathbf{Z}}}_2\in {𝒜}_j$:

$$\begin{gathered} \sum _{i=1}^{p}1\{\mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid >\tau \sqrt{n}∕4\} \\ =\sum _{i=1}^{p}1\left[\Vert {\tilde{Z}}_2{N}_{\ast j}{\Vert }_2\mid \sum _{l=1}^p{M}_{il}{\mathbb{Z}}_l\mid >\tau \sqrt{n}∕4\right] \\ \le \sum _{i=1}^{p}1\left[\sqrt{2}\Vert N{\Vert }_{op}\mid \sum _{l=1}^p{M}_{il}{\mathbb{Z}}_l\mid >\tau ∕4\right]. \end{gathered}$$

Defining

$$f(x)\equiv f(x_1,\dots ,x_p)=\sum _{i=1}^p\frac{1\left[\mid {\sum }_{l=1}^p{M}_{il}{x}_l\mid >\tau ∕(4\sqrt{2}\Vert N{\Vert }_{op})\right]}{p},$$ (81)

we notice that the above calculations implies conditional on ${\tilde{\mathbf{Z}}}_2\in {𝒜}_j$,

$$\frac{{\sum }_{i=1}^p\mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid >\tau \sqrt{n}∕4]}{p}\le f({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_p).$$

Therefore,

$$\begin{gathered} P\left(\sum _{i=1}^{p}1\{\mid M_{i\ast }^T{\tilde{Z}}_1^T{\tilde{Z}}_2{N}_j\mid >\tau \sqrt{n}∕4\}>2p{e}^{-{\tau }^2∕K}\mid {\tilde{\mathbf{Z}}}_2\in {𝒜}_j\right) \\ \le P\left(f({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_p)>2\text{exp}(-{\tau }^2∕K)\mid {\tilde{\mathbf{Z}}}_2\in {𝒜}_j\right), \end{gathered}$$ (82)

which is is bounded by $\text{exp}(-2\sqrt{p})$ by Lemma 23. Therefore, (79), (80), and (82) jointly imply that

$$P({𝒱}^c)\le 4q\text{exp}(-cn)+4q\text{exp}(-2\sqrt{p}).$$

Therefore $P({𝒢}_2^c)$ is bounded by

$$\begin{gathered} \text{exp}(-c(n+p))+\text{exp}(-c(n+q))+4q\text{exp}(-cn) \\ +4q\text{exp}(-2\sqrt{p})\le 4q\text{exp}(-c\text{min}\{n,\sqrt{p}\}), \end{gathered}$$

which completes the proof.

Lemma 23. Suppose $160\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2<K$ and $\tau <\sqrt{K\log p}∕2$. Further suppose ${\mathbb{Z}}_1,\dots {\mathbb{Z}}_p$ are independent standard Gaussian random variables. Then the function f defined in (81) satisfies

$$\mathbb{P}\left(f({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_p)>2\text{exp}(-{\tau }^2∕K)\right)\le \text{exp}(-2\sqrt{p}).$$

Proof of Lemma 23. Note that $pf({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_p)$ is a sum of dependent Bernoulli random variables. Therefore the traditional Chernoffs or Hoeffding’s bound for inependent Bernoulli random variables will not apply. We use a generalized version of Chernoffs inequality, originally due to [65] (also discussed by [73], [74] among others), which applies to weakly dependent Bernoulli random variables.

Lemma 24 ([65]). Let $X_1,\dots ,X_p$ be Bernoulli random variables and $ϵ\in (0,1)$. Suppose there exists $\delta \in (0,ϵ)$ such that for any $ℬ\subset [p]$, the following assertion holds:

$$\mathbb{E}\left[\prod _{i\in ℬ}{X}_i\right]\le {\delta }^{\mid ℬ\mid }.$$ (83)

For $x,y\in (0,1)$, we denote

$$D(x\Vert y)=y\log (y∕x)+(1-y)\log ((1-y)∕(1-x)).$$

Then we have

$$\mathbb{P}\left[\frac{{\sum }_{i=1}^p{X}_i}{p}\ge ϵ\right]\le \text{exp}\left(-pD(\delta \Vert ϵ)\right).$$

Note that if we take $X_i=1\{\mid {\sum }_{l=1}^p{M}_{il}{\mathbb{Z}}_l\mid >\tau ∕(4\sqrt{2}\Vert N{\Vert }_{op})\}$ and $ϵ=2\text{exp}(-{\tau }^2∕K)$, then the above lemma can Ire applied to bound $P(f({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_p)>2\text{exp}(-{\tau }^2∕K))$ provided (83) holds, which will be referred as the weak dependence Condition from now on. Suppose $\mid ℬ\mid =k$. For the sake of simplicity, we take $ℬ=\{1,\dots ,k\}$. The arguments, which are to follow, would hold for any other choice of $ℬ$ as well as long as $\Vert ℬ\mid =k$. Denote by $M_k$ the submatrix of M containing only the first k rows of M. Let us denote ${\mathbb{Z}}_{1:k}=({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_k)$. Letting $t=\tau ∕(4\sqrt{2}\Vert N{\Vert }_{op})$, we observe that for our choice of $X_i$’s, $\mathbb{E}[{\prod }_{i\in ℬ}{X}_i]$ equals

$$\begin{gathered} P\left(\mid M_{i\ast }^T{\mathbb{Z}}_{1:k}\mid >t,l\in [k]\right)\le P\left({\mathbb{Z}}_{1:k}^T{M}_k^T{M}_k{\mathbb{Z}}_{1:k}>k{t}^2\right) \\ \le P\left(\Vert M_k^T{M}_k{\Vert }_{op}\sum _{i=1}^k{\mathbf{Z}}_l^2>k{t}^2\right). \end{gathered}$$

The operator norm $\Vert M_k^T{M}_k{\Vert }_{op}$ equals $\Vert M_k{\Vert }_{op}^2$, which is bounded by $\Vert M{\Vert }_{op}^2$ by Lemma 10B. Therefore, the right hand side of the last display is bounded by $P({\sum }_{l=1}^k{\mathbb{Z}}_l^2>k{t}^2∕\Vert M{\Vert }_{op}^2)$. By Chi-square tail bounds (see for instance Fact 4), the latter probability is bounded above by $\text{exp}(-k{t}^2∕(5\Vert M{\Vert }_{op}^2))$ for all $t>\sqrt{5}\Vert M{\Vert }_{op}$. Since $t=\tau ∕(4\sqrt{2}\Vert N{\Vert }_{op})$, note that $\tau >\sqrt{160}\Vert M{\Vert }_{op}\Vert N{\Vert }_{op}$ suffices. For such τ, we have thus shown that

$$\mathbb{E}\left[\prod _{i\in ℬ}{X}_i\right]\le \text{exp}\left(-\mid ℬ\mid \frac{{\tau }^2}{160\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2}\right).$$

Thus our $\delta =\text{exp}\left(-\frac{{\tau }^2}{160\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2}\right)$, which is less than $ϵ∕2=\text{exp}(-{\tau }^2∕K)$ because $K>160\Vert M{\Vert }_{op}^2\Vert N{\Vert }_{op}^2$. Thus our (δ, ϵ) pair satisfies the weak dependence condition. Therefore by Lemma 24, it follows that

$$\mathbb{P}\left(f({\mathbb{Z}}_1,\dots ,{\mathbb{Z}}_p)>2\text{exp}(-{\tau }^2∕K)\right)\le \text{exp}(-pD(\delta \Vert ϵ)).$$

We will now use the lower bound $D(x\Vert y)\ge 2(x-y{)}^2$ for $x,y\in (0,1)$. Because $\mid \delta -ϵ\mid \le ϵ∕2,D(\delta \Vert ϵ)\ge {ϵ}^2∕2$, indicating $pD(\delta \Vert ϵ)\ge 2p\text{exp}(-2{\tau }^2∕K)$, which is greater than $2\sqrt{p}\text{if}2{\tau }^2∕K\le \log p∕2$, or equivalently ${\tau }^2\le (K\log p)∕4$. Therefore, the current lemma follows.