Computational prediction of complex cationic rearrangement outcomes

Abstract

Recent years have seen revived interest in computer-assisted organic synthesis^1,2. The use of reaction- and neural-network algorithms that can plan multistep synthetic pathways have revolutionized this field^1,3–7, including examples leading to advanced natural products^6,7. Such methods typically operate on full, literature-derived ‘substrate(s)-to-product’ reaction rules and cannot be easily extended to the analysis of reaction mechanisms. Here we show that computers equipped with a comprehensive knowledge-base of mechanistic steps augmented by physical-organic chemistry rules, as well as quantum mechanical and kinetic calculations, can use a reaction-network approach to analyse the mechanisms of some of the most complex organic transformations: namely, cationic rearrangements. Such rearrangements are a cornerstone of organic chemistry textbooks and entail notable changes in the molecule’s carbon skeleton^8–12. The algorithm we describe and deploy at https://HopCat.allchemy.net/ generates, within minutes, networks of possible mechanistic steps, traces plausible step sequences and calculates expected product distributions. We validate this algorithm by three sets of experiments whose analysis would probably prove challenging even to highly trained chemists: (1) predicting the outcomes of tail-to-head terpene (THT) cyclizations in which substantially different outcomes are encoded in modular precursors differing in minute structural details; (2) comparing the outcome of THT cyclizations in solution or in a supramolecular capsule; and (3) analysing complex reaction mixtures. Our results support a vision in which computers no longer just manipulate known reaction types^1–7 but will help rationalize and discover new, mechanistically complex transformations.

Reactions involving sequences of carbocation rearrangements are important in biosynthesis^13,14 as well as organic synthesis, allowing for drastic reorganization of a complex scaffold hard to achieve by other methods. Such reactions have been used as key steps of some classic total syntheses^15,16 but their use remains limited as outcomes are not readily predictable, especially for unexplored substrates. So far, most approaches have relied on quantum mechanical calculations; these can be highly accurate and can account for nuanced effects such as posttransition state (p-TS) bifurcations¹² but can be computationally very costly^11,17 and have been used mostly to substantiate plausible pathways and products^11,17 rather than predict them de novo (but see refs. 18,19). Approximate graph- and rule-based models are significantly faster but have often been limited in scope^20,21, prone to false-positive predictions and not able to solve even moderate-complexity problems^22,23 (Supplementary Information section 6), although some proved useful in scaffold enumeration^24,25. The difficulty in generalizing and applying these methods ‘on-the-fly’ to arbitrary scaffolds seems to be twofold. On one hand, quantum approaches may be too fine as the number of degrees of freedom may be too large to consider the problem a priori, particularly for larger systems and multistep pathways. On the other hand, coarse-grained models may be too crude to properly define all intricacies (strain, stereochemistry and so on) of individual mechanistic steps and apply them only in appropriate situations, to yield realistic intermediates (Supplementary Information sections 6.1 and 6.2). We reasoned that the problem may become tractable at an intermediate level of description, one in which an adequately broad yet chemically accurate set of mechanistic and physical-organic rules limits the solution space to a network of mechanistic steps on which finer, quantum-level analyses are then performed.

Curation of mechanistic steps

With the above considerations in mind, our first objective was to catalogue all or nearly all universally accepted mechanistic steps with which even very complex cationic rearrangements could be explained. As mechanistic steps are not reported in repositories such as Reaxys or SciFinder (and cannot be just downloaded or machine-learned) we curated, over the years, a training set of 715 solution-based (that is, not gas-phase) examples, mostly from advanced-level total syntheses and involving diverse scaffolds. For each of these 715 reactions, we performed detailed mechanistic analysis, mapping individual atoms and assigning each mechanistic step to a particular class (Fig. 1a and all other examples posted at https://HopCatResults.allchemy.net/). Although the mechanisms are only chemically plausible (at the level of familiar arrow-pushing²⁶), they allow us to ascertain that all 715 sequences could be written out using a finite set of commonly accepted mechanistic transforms. Notably, this set was limited and, as we kept analysing the 715 reactions, the numbers of newly added transforms steadily decreased (Fig. 1b). Ultimately, our collection comprised 38 distinct ways of carbocation generation, 58 transforms for rearrangements and resonances, and 53 rules for cation quenching. We then followed the same strategy to curate two more collections: one set comprising 310 mechanistic emergent steps that are not (yet) commonly used in total syntheses (but enable retro alkyne exo cyclizations, 1,2 shifts for vinyl carbocations and so on) and the other grouping 30 steps specific to biosynthetic carbocationic rearrangements. All transforms are detailed in Supplementary Information section 2.

Fig. 1 |. Key aspects of a network-based algorithm to predict mechanisms and product distributions of complex carbocationic rearrangements.

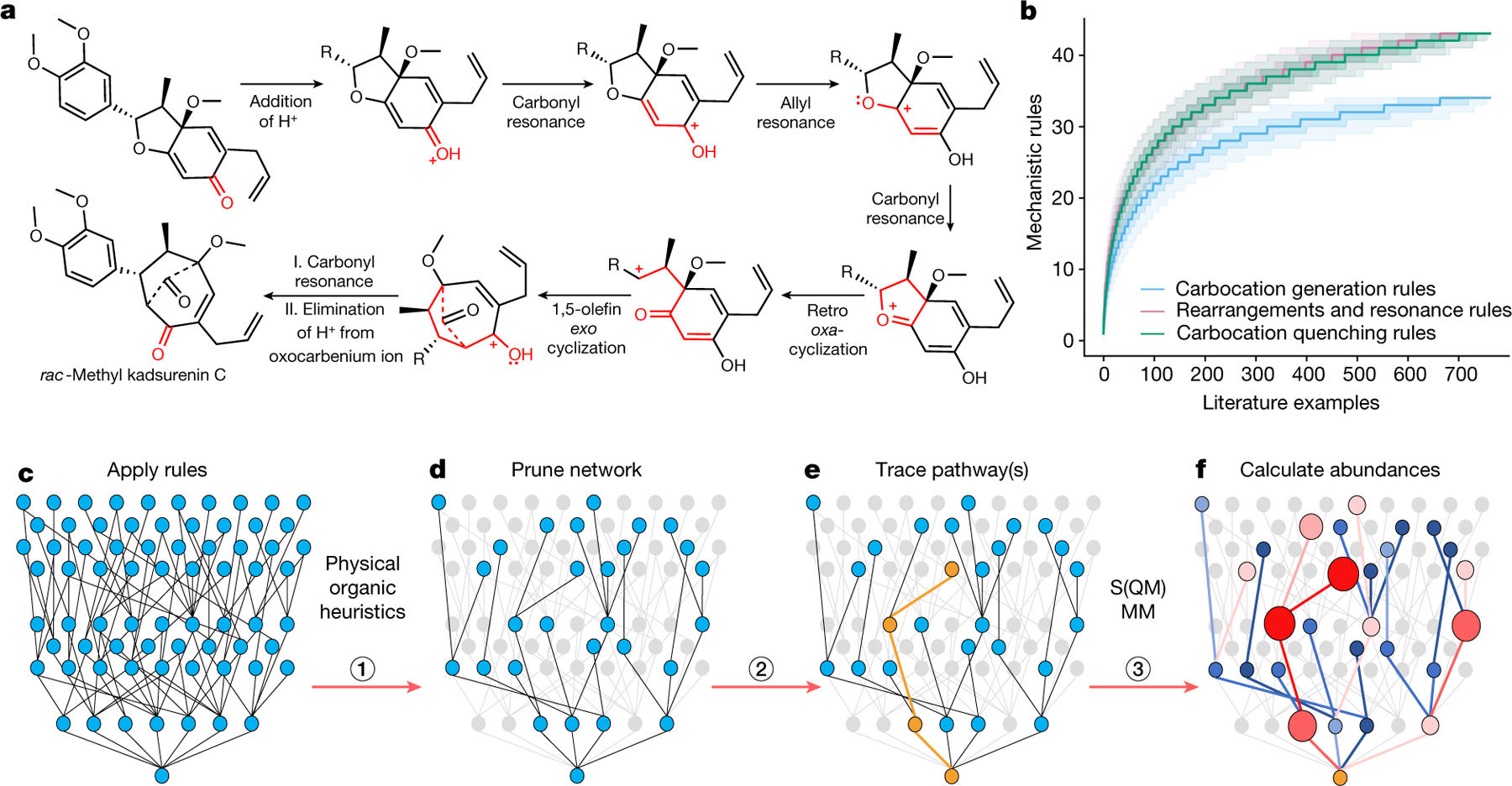
a, One of the literature examples (from total synthesis of methyl Kadsurenin C; ref. 46) analysed by expert chemists to assign individual mechanistic steps. Bonds and atoms coloured in red span the ‘cores’ of mechanistic transforms. b, The horizontal axis counts numbers of literature examples analysed (715 in total, all examples deposited at https://HopCatResults.allchemy.net/) to derive these rules. The vertical axis plots the number of mechanistic rules identified by analysing a given number of literature examples (note that certain rules are grouped, for example, ‘Addition of water 1’ and ‘Addition of water 2’ are counted as one). Blue curve, carbocation generation rules; red, rearrangements and resonances; green, carbocation quenches. For each set, analysis was repeated 10,000 times, each time with a different and random ordering of literature examples. The solid line represents the median; the dark and light shaded areas delineate interpercentile ranges 0.25–0.75 and 0.05–0.95, respectively. All curves flatten out suggesting that our sets of mechanistic rules are nearly complete (for all rules, see Supplementary Information section 2). c, The mechanistic steps thus derived are applied iteratively to propagate reaction networks commencing from arbitrary substrates (‘parent’ node at the very bottom). d, The networks are pruned according to physical-organic constraints (Supplementary Information section 3) to reduce network size by up to roughly 1,000 times. e, Subsequently, the algorithm can trace (orange) mechanistic pathway(s) between the substrate and some known product. Already at this stage, the algorithm can solve some complex mechanistic puzzles (Fig. 3 and Extended Data Figs. 1–3 and Supplementary Figs. 41–66). f, Calculation of energies of all nodes and/or molecules and energetic barriers of all edges and/or steps (Methods) yields kinetic rate constants (here, coloured blue to red to indicate slow to fast steps). Solution of kinetic equations then predicts the abundances of specific products, here indicated by the sizes of the nodes.

Rule encoding and additional constraints

Next, all transforms were encoded in the SMARTS (SMILES arbitrary target specification) notation as described in our previous works^1,3,6,27. However, they encompass only a few atoms and are unaware of a broader range of structures of (complex and diverse) scaffolds to which they may be applied: consequently, they can yield highly strained or structurally nonsensical products, or may not account for subtler effects such as p-TS bifurcations. To remedy this, we implemented several constraints grounded in physical-organic considerations. The first group (Supplementary Information section 3.1) evaluates transformation products and prevents the formation of, for example, highly strained bridge carbocations, most primary carbocations (with exception of those formed in 1,3-olefin exo cyclization, retro-1,3-olefin exo cyclization or allyl resonance), certain types of micro- and macrocycles, as well as any other forbidden, structurally improbable motifs (for example, three- and four-membered rings with unsaturations, or a tetrahedrane carbocation). The second group (Supplementary Information section 3.2) applies to specific reaction types and inspects whether the substrate is properly preorganized for the reaction to occur (for example, in 1,5-H shifts or 1,4-oxa cyclizations), whether participating rings are properly activated (for example, in aryl cyclizations) or whether certain substituents meet bulkiness criteria (for example, in silyl β elimination). The third group (Supplementary Information section 3.3) considers stereochemistry to prevent, for example, cyclizations of ring substituents trans to each other, cyclizations from unsuitable $E\text{/}Z$ configurations of double-bond systems, cyclizations ‘knitting through’ larger rings or hydride or alkyl migrations to different faces of a ring. Finally, the fourth group (Methods and Supplementary Information section 3.4) regards p-TS bifurcations and aims to eliminate steps that cannot occur due to nonequilibrium or dynamic effects^12,28.

Generation of mechanistic networks

Together, the transforms and constraints enable the generation of networks of mechanistic steps in an Allchemy-based²⁹ HopCat webapp (https://HopCat.allchemy.net/; for user manual, see Supplementary Information section 1 and, for illustration, Supplementary Video 1). In default settings, the program uses the core set of total-synthesis-oriented transforms and, optionally, also the 310 emergent and/or 30 biosynthetic ones. In a typical scenario, the software takes as input a starting carbocation (if a neutral molecule is input, possible starting carbocations are suggested to form generation G_n=0 of the network). Subsequently, the algorithm considers the starting cation and its possible resonant structures, and applies to them matching rearrangement steps and constraints to produce the first generation, G₁, of evolved carbocations and their resonant forms. These molecules are subjected to the next round of rearrangements and also cation quenching steps to give G₂. The still active, non-quenched carbocations can then be used to generate G₃ and the process is iterated until a user-specified limit of generations, G_nmax, is reached or all carbocations are quenched. At all stages, the structures are deduplicated but if the same molecules can be reached through different routes, all such routes are kept. Of note, the user can optionally allow for the quenched cations to be regenerated (as in syntheses in refs. 30,31); only one regeneration event is allowed per one route.

When the networks were propagated from the substrates of our 715 examples, all literature-reported products were identified within G₆ (95% within G₄ and roughly 50% within G₂). The networks varied in size from just teens to tens of thousands of nodes with calculation times on a multicore desktop ranging from seconds to several hours (typically, 1–10 min but, for example, as long as 3 hours for the 173,122-node network for homobrendane³²). The network size did not correlate with the substrate’s mass or the number of stereocentres but increased with the number of multiple non-aromatic bonds (Fig. 2a,b) that allow for multiple resonance structures (which in turn, enable different rearrangements) and can also serve as sources of electrons (for example, in olefin cyclizations). Irrespective of the substrate, the networks had a similar, branching structure; on average, each carbocation branched out into seven progeny carbocations (counting resonance structures) and three neutral and/or quenched products. These average branching factors did not depend on synthetic generation (Fig. 2c,d). We also note that the application of the physical-organic constraints described in the previous section was essential as it reduced the network size at least several hundred times (and more than 1,300 times for the G₄ network of a cycloaraneosene intermediate³³). For many examples, networks without constraints were simply too large to be calculated on time scales of days.

Fig. 2 |. Statistics of the mechanistic networks and model performance.

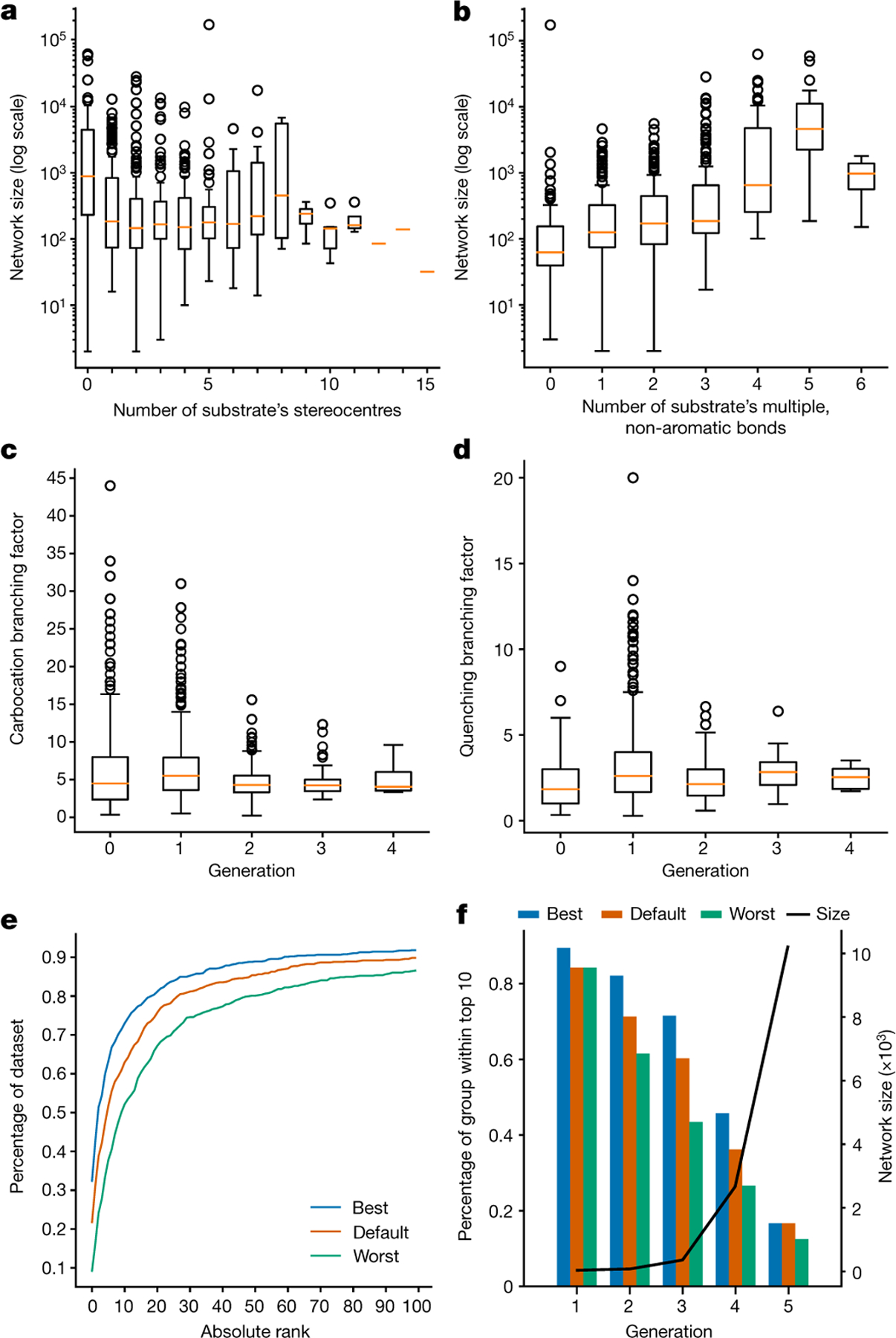
All analyses are based on the networks generated for the ‘715’ set. Orange lines indicate median, boxes envelop data between Q₁ and Q₃ quartiles; whiskers delineate the most spread pair of points within the (Q₁ − 1.5 × interquartile range, Q₃ + 1.5 × interquartile range) range, where the interquartile range is Q₃ – Q₁. a,b, Sizes of mechanistic networks do not correlate with, for example, a substrate’s molecular weight or the number of stereocentres (a) but increase with the number of multiple, non-aromatic bonds (b). c,d, Average branching factors remain similar irrespective of a network’s synthetic generation, G_n: carbocation (c) and quenching (d) branching factors. The branching factor for carbocations in a given G_n is the number of carbocations in G_n+1 divided by their number in G_n. The quench factor is the number of quenched and/or neutral products in G_n+1 divided by the number of carbocations in G_n. Performance of the kinetic model is quantified in e,f. e, The horizontal axis quantifies the absolute rank (best is zero) of the literature-reported product within the network. The vertical axis gives the percentage of the entire dataset (that is, all 715 networks) for which the predicted rank is not larger than the corresponding value on the x axis (top k statistic). Default settings use the default quench and generation parametrization with time and temperature either taken from literature or set to 298 K and 12 h. The best settings modify these parameters within 30% of the default values (0.7, 0.8, 1.2 and 1.3) and missing time data (here, 2 h and 12 h) that give the best top k statistics. The worst settings correspond to the worst result obtained with such modifications. f, Bars and the left axis quantify the dependence of the top ten statistics on the number of synthetic generations. The right axis and black line plot the average network size. As the networks become very large, the accuracy in predicting the literature product within the top ten decreases markedly.

Tracing of mechanistic pathways

Assuming the reaction product was found somewhere in the network, the mechanistic path(s) to the starting material were traced by a classic breadth-first search (in 312 out of 715 cases, these mechanistic solutions were unique). When the algorithm was tested on several examples from outside the 715 literature set, it identified the routes proposed by the authors of these works (Extended Data Figs. 1 and 2 and Supplementary Information section 5.2), provided solutions to problems that previously lacked mechanistic explanation (for example, ref. 34 and Fig. 3), and suggested plausible mechanisms for biosynthetic rearrangements (Extended Data Fig. 3).

Fig. 3 |. HopCat’s analysis of a carbocationic rearrangement in Kobayashi’s synthesis of a taxanine derivative.

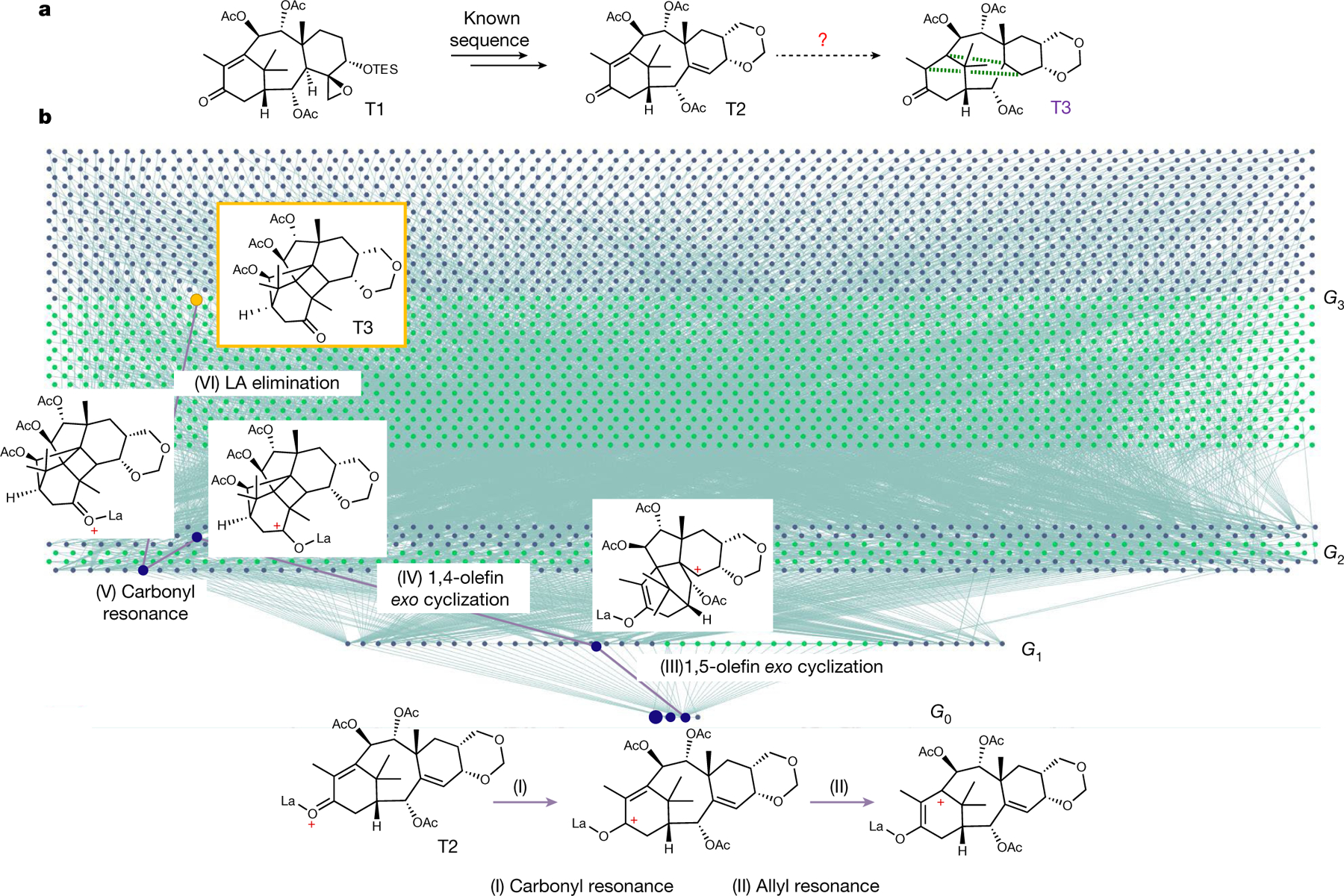
a, Reaction of β-4(20)-epoxy-5-O-triethylsilyltaxinine A, T1, which on treatment with BF₃×OEt₂ gives compound T3 containing a cyclobutane ring marked for clarity with green dotted bonds³⁴. Although the authors explained the mechanism for the T1 ➔ T2 step (Lewis acid-promoted liberation of formaldehyde followed by elimination of silyl ether and formation of 1,3-dioxane), step T2 ➔ T3 was referred to as curious⁴⁷ and had no mechanistic explanation even in a recent review⁴⁸ (published 20 years after the original paper). b, Screenshot of a fragment of the 3,404-node network—generated within a few minutes—illustrates HopCat’s analysis starting with LA-activated T2. Resonances correspond to horizontal connections in each synthetic generation G_n; rearrangements are connections between generations. Blue nodes are carbocationic intermediates; green are quenched molecules. The mechanistic route to the experimentally observed product is traced by purple lines. Miniatures showing the intermediates are overlaid on the network (Supplementary Figs. 1–9). Note that an alternative but longer pathway replacing 1,4-olefin exo cyclization with a sequence of 1,5-olefin endo and 1,2-C shift, and then replacing carbonyl resonance and elimination of the Lewis acid with elimination and enolization was also found. For additional problems solved by HopCat on similar time scales, see Extended Data Figs. 1 and 2 and Supplementary Figs. 41–43 and 50–66. The reader is encouraged to use https://HopCat.allchemy.net/ to solve other mechanistic riddles, starting from substrates and carbocations of their choice. OTES, triethylsilyl ether.

Estimating product distributions

Next we extended the algorithm to the challenging and practically important situation in which only the substrate and reaction conditions are given but the reaction outcome is unknown: that is, we wished to predict the main product and possible byproducts, and also estimate their distributions under given reaction conditions. This required energetic and kinetic calculations for the network’s molecules and reactions. Whereas different theoretical approaches can be imagined, we implemented methods that, without compromising accuracy too much, could perform network-wide calculations within times commensurate with the expectations of software’s users (minutes) and would not require expensive licences. These calculations are applicable to the core set of transforms for which many parameters can be adopted from previous studies. With the entire workflow detailed in the Methods section, its key stages were:

1. Augmentation of the initial network of directed (that is, irreversible) edges with edges corresponding to applicable reverse transformations. Such augmentation introduced reversibility and removed non-physical ‘sinks’ from the network.

2. Generation of the lowest-energy conformers (LECs), for all nodes in the network.

3. Generation of near-attack conformers³⁵ for steps requiring pronounced conformational changes (cyclizations, long-range H shifts).

4. Calculation of conformers’ energies by a semi-empirical method (for example, PM6) and calculation of substrate versus product energy differences, $\text{Δ}E\text{s}$, including additional substrates if present (for example, for eliminations, we included base and protonated base in energy calculations).

5. Estimation of steps’ contributions to activation barriers parametrized mostly on available literature data and quantum mechanical calculations of model systems. The only free parameters used in all examples discussed later were Hammond parameters $A_g$ and $B_g$ for olefin protonation and water elimination; these values were fitted at a single temperature against experimental data for linalool (below).

6. Coarsening of the network to group resonant structures into single nodes, identification of nodes corresponding to local energetic minima, calculation of the lowest-energy paths (LEPs) between the minima and calculation of the rate constants for all steps using the standard Eyring equation.

7. Numerical integration of the set of kinetic equations.

Of note, we implemented stages (1)–(7) for rearrangements taking place in solution and also under nanoscopic confinement. In the latter case, the analyses were limited to conformers that fitted into either a spherical or an ellipsoidal enclosure of user-specified dimensions. Individual steps were allowed only when the reacting motifs were within a certain distance (Methods). The impact of the environment (for example, slower deprotonation and/or quench process due to locking the conjugated base on the capsule’s wall³⁶) could also be modelled by changing the protonation and/or deprotonation (quench) barriers (see the user manual in Supplementary Information section 1).

Experimental validations

The performance of the model thus constructed was tested against both existing data from the literature and new experiments.

Retrospective data analyses

We first analysed how many of the products experimentally observed in the 715 literature reactions discussed earlier were also among HopCat’s top k predictions. Such an analysis is obviously limited in that many, especially older, publications do not report the exact nature of the acid used to generate the cation, as many as 228 examples provide no information about reaction temperature or time, 202 have only temperature and 109 only time; in addition, it is often not known whether the isolated product was the main or just the desired one. In such cases, we assigned reasonable default values (p-toluenesulfonic acid, 298 K, 12 h) or several such settings (for example, 2 and 12 h from which we then took the best and worst result). Even with these uncertainties, with the theoretical approximations involved and with no free parameters, the model did reasonably well, in roughly 70% of cases placing the literature-reported product within its top ten predictions (higher for smaller networks and decreasing steadily with network size, Fig. 2e,f).

Rearrangements of linalool and fenchol

Turning to our own experiments, we first focused on linalool (1 in Fig. 4) and fenchol (2 in Fig. 4), whose carbocationic rearrangements have been studied for decades and apparently in exhaustive detail^37–39. Here, we were interested not only in whether network analyses would rediscover mechanisms leading to the known products but also whether they would (1) reproduce experimentally observed product distributions at different temperatures and (2) perhaps identify some additional products not identified in previous studies, which they did.

Fig. 4 |. Experimental versus predicted product distributions emerging from rearrangements of linalool and fenchol at different temperatures.

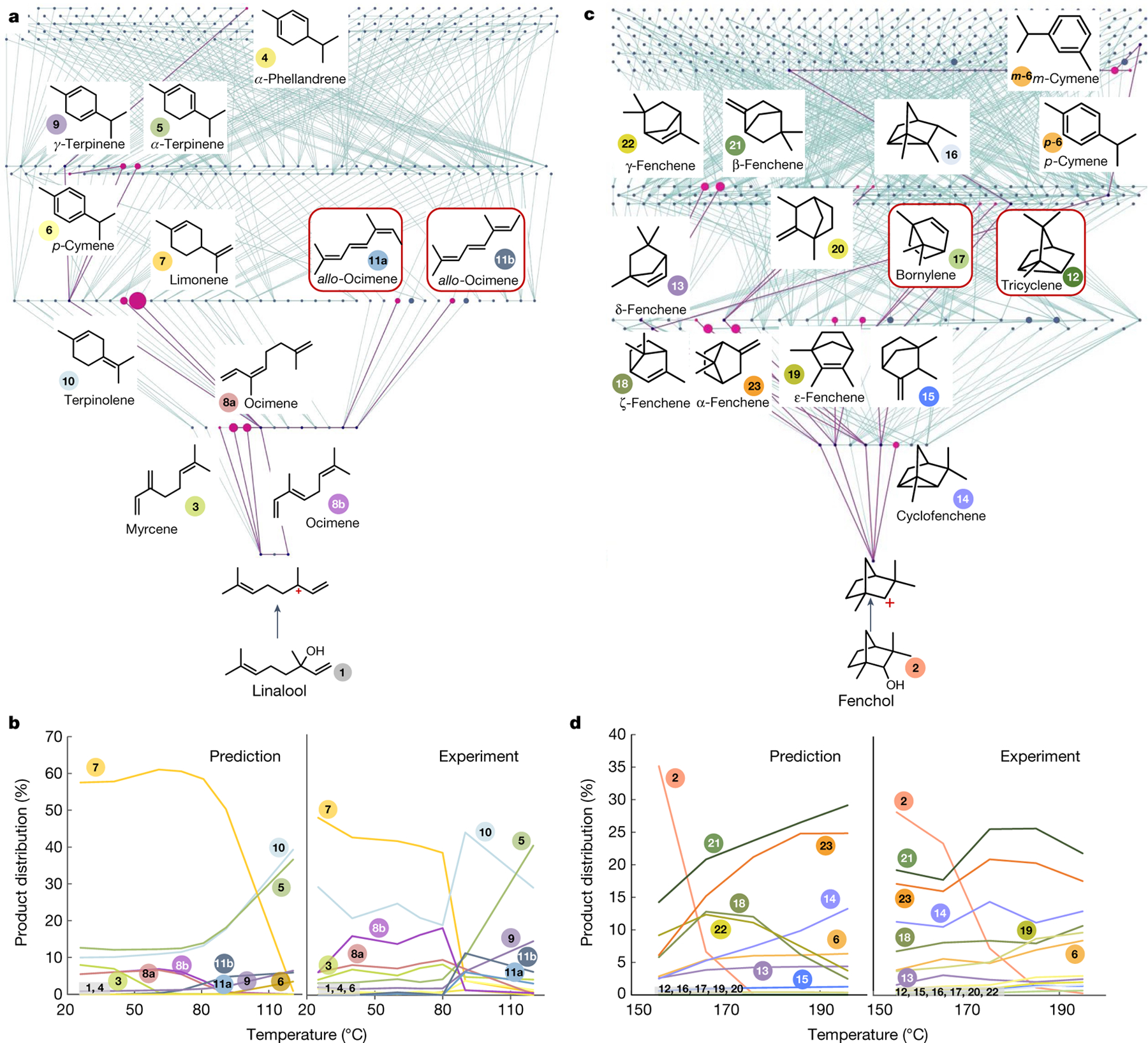
a,b, The data for linalool for which experimental conditions were: linalool 1 (0.65 mmol), TsOH•H₂O (0.65 mmol), MS 4 Å, dry benzene, Ar, 16 h. c,d, The data for fenchol for which experimental conditions were: fenchol 2 (1.95 mmol), KHSO₄ (1.95 mmol), MS 4 Å, neat, Ar, 16 h. For all experimental details, see Supplementary Information section 7. a,c, Screenshots of HopCat’s networks, both propagated up to G₄. Purple nodes are products observed experimentally and node sizes correspond to relative abundances of the products (see also the second part of Supplementary Video 1). Previously unreported products are in red frames. b,d, Comparisons of experimental versus predicted product distributions at different temperatures. Vertical axes quantify percentages of specific products in the reaction mixture (whenever applicable, in the model and in experiment, these percentages are sums of values for enantiomers and diastereoisomers). In the experiments, the crude mixture was analysed by GC–MS (see Methods and Supplementary Information section 7 for details).

For linalool, the G₄ network (Fig. 4a) contained all experimentally observed products 3–10. With only four Hammond $A_g$ and $B_g$ parameters fitted to experimental data only at a single temperature (T_fit = 80 °C), the model (1) rationalized the formation of trienes 11a and 11b not detected in previous studies (and in our experiments at T_fit seen in only trace amounts); (2) reproduced a switchover in product distribution around 80 °C (from dominant 7 below this temperature to 5, 10 above; Fig. 4b and a discussion of mechanism that appears in Supplementary Information section 7) and (3) did not predict false positives among the main products (at higher temperatures, $Z$ isomer of 11b—not detected in the experiment but probably a precursor to the $E$ isomer of 11b—was placed fifth, with abundance 0.6%; at lower temperatures, there were no false positives in the top seven and down to roughly 0.1% abundance). For fenchol, experiments identified 12 products, all found within the network (Fig. 4c) and with the first false-positive ranked fifth (with roughly 0.5% abundance). The exact abundances of products of longer paths were slightly underestimated at 50–170 °C but the agreement was better at higher temperatures (Fig. 4d). Molecules 17 and 12 were not previously described as products of fenchol’s rearrangement and, noteworthy, network analysis was instrumental in identifying 17, which was misidentified by the conventional Xcalibur/NIST assignment of the relevant gas chromatography with mass spectrometry (GC–MS) peak (Methods).

Substrate-controlled terpene cyclizations

Arguably, the most challenging set of validations was to predict the outcomes of a series of novel tail-to-head terpene (THT) cyclizations. In biosynthetic settings, such cyclizations take place in a catalyst-controlled modality, whereby different terpene synthases can act on the same linear precursor to yield various complex terpene frameworks. As an alternative, we wished to encode different cyclization outcomes by structural differences in the precursor molecules, with no individually tailored catalysts. Predictable conversion of structurally simple precursor molecules into complex scaffolds in this manner would represent a powerful approach for modular access to complex natural product structures. Here, information dictating the cyclization outcomes was preprogrammed into linear precursors, and, in turn, into building blocks from which those precursors are derived (Extended Data Fig. 5) in a manner that might be amenable with automated modular synthesis^40,41. The examples in Fig. 5a are especially challenging to predict, even to experienced synthesis experts, because the precursors differ solely in the positions of one methyl group and/or one double bond. Moreover, we studied these cyclizations not only in solution but also in the supramolecular resorcinarene capsule (roughly ellipsoidal) previously shown to catalyse related rearrangements with a Brønsted acid cocatalyst⁴²: rearrangements under such confinement are virtually intractable without the help of a computer because analysis of mechanistic pathways is coupled to the analysis of conformers that fit within the capsule’s enclosure.

Fig. 5 |. Experimental versus predicted outcomes for the THT cyclizations and uncertainty of theoretical predictions.

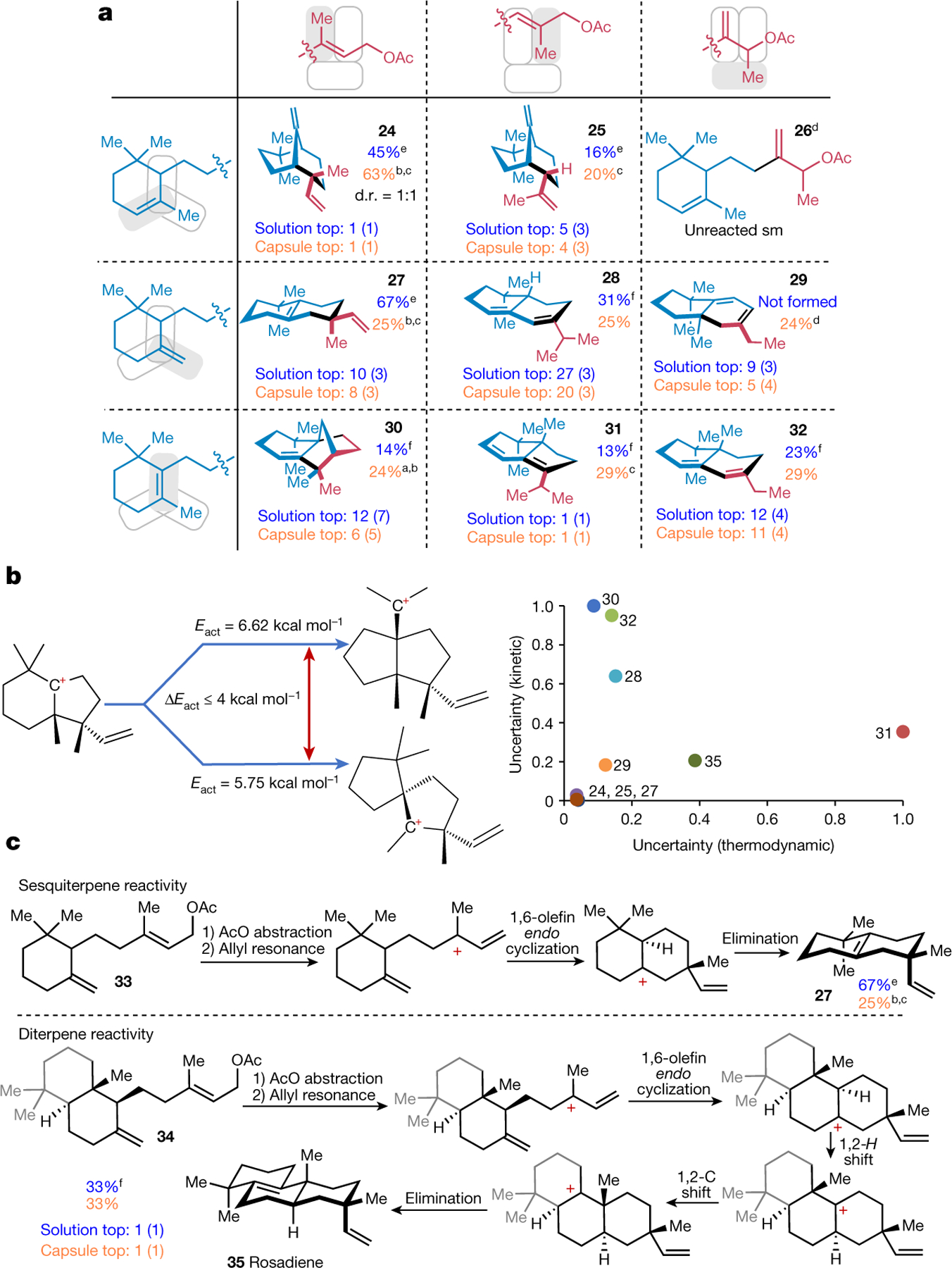
a, Table illustrating the building blocks (light-blue and red fragments) and the corresponding cyclized products, if observed. Methyl groups and the double bonds differing between the fragments are highlighted in grey. Within each tile, dark blue shows yields for solution experiments (determined by GC); orange shows yields for experiments performed in the capsule (isolated yields). The algorithm-predicted top k rankings are listed below the structures. Values in parentheses are rankings of the correct skeleton being formed (that is, with all stereochemical information and all double bonds removed). Unless otherwise noted, capsule reaction conditions were 20 mol% supramolecular capsule, 3 mol% HCl, CHCl₃ solvent and 40 °C. b, Scheme of a similar probability and thus high-uncertainty branching along a hypothetical fragment of a mechanistic route. In the graph, the vertical axis quantifies such kinetic uncertainty as the number of branchings (within 4 kcal mol⁻¹) normalized by the maximum value within the set. The horizontal axis plots the normalized numbers of products in each network whose energies are within 4 kcal mol⁻¹ of the correct one; this thermodynamic measure of uncertainty is not predictive. c, Mechanistic routes from two precursors differing only in the distal part (marked in grey in the lower structure). For the lower precursor, rosadiene was predicted as the top one (solution)/top one (capsule) outcome. Indeed, it was obtained in experiments in 33% yield. Note that despite seemingly similar precursors, the two mechanistic routes are markedly different. ^aGC yield. ^b10 mol% of capsule used, and reaction carried out at 30 °C. ^cProduct isolated after preparative scale reaction of alcohol substrate; in all these cases, the same main product is observed in the reaction of the acetate substrate. ^dSubstrate is an equimolar mixture of diastereomers. ^eHCl (1.0 equiv.). ^fBF₃×OEt₂ (1.0 equiv.) solution conditions.

The networks originating from various precursors spanned 94 to 8,284 nodes. Within these large spaces of potential outcomes, the algorithm performed well, as the products isolated in experiments were ranked, on average, ninth in solution and seventh in the capsule (for individual rankings; Fig. 5a and for mechanistic pathways see Supplementary Information section 8). Of note, the initial experiments yielded some products only in the capsule but not in solution (1 eq. HCl): nonetheless, even with adjustments of protonation and deprotonation rate parameters, the algorithm persisted in suggesting that these products (for example, 31) or skeletons (for example, 28) are comparably likely to form in solution. These predictions turned out to be correct and the products were indeed observed when ionization of the precursors was affected by BF₃×OEt₂ instead of HCl. In the end, only product 29 was not formed in solution and required the use of the capsule: this preference for the capsule was reflected by the algorithm’s rankings.

Analysing the poorest predictions (for example, 28 ranked only 27th in solution and 20th in the capsule, 30 ranked 12th or sixth or 32 ranked 12th or 11th), we observed that their mechanistic pathways had several similar-probability branchings: that is, several intermediates along these sequences could engage in side mechanistic steps having similar activation energies (Fig. 5b and Methods). Naturally, energy calculations entail inherent error, which for the PM6 method used here, was estimated⁴³ at 4–8 kcal mol⁻¹. Therefore, we reasoned that the presence of branchings for which activation energies are within a few kcal mol⁻¹ could be a rough measure of the uncertainty assigned to a given sequence and ranking prediction. For this metric, the Spearman correlation coefficient against predicted top k values was roughly 0.65 and, when it was applied to THT cyclizations, it correctly assigned the highest uncertainties to 30, 32 and 28 (Fig. 5b).

Synthesis of rosadiene natural product

Finally, we tested a pair of seemingly very similar terpene precursors, 33 and 34 in Fig. 5c. Although they differ only in the distal part of the molecule (coloured light-grey in 34), the outcomes were predicted to be markedly different. In particular, for compound 34, the early 1,6-olefin endo cyclization was predicted to be followed by 1,2-H and 1,2-C shifts, before final elimination gives rosadiene 35, a natural product previously obtained through 8,15-isopimaradiene rearrangement⁴⁴ or sclareol cyclization⁴⁵. This prediction was ranked top one (solution) and top one (capsule), and the product was obtained in both solution and capsule experiments in 33% yield.

Conclusions

Overall, these examples suggest that our multiscale, network-quantum mechanical algorithm can rapidly suggest plausible mechanisms and the most likely outcomes of non-trivial carbocationic rearrangements, and is capable of differentiating between minute structural differences in the substrate molecules. We envision its unique applicability in three areas: (1) to guide spectral and/or chromatographic assignments of complex products and/or product mixtures (including authentication of such mixtures in food or fragrance industries); (2) to study rearrangements under confinement (including microporous materials); and (3) to systematically survey large numbers of automatically synthesized^40,41, linear precursors for productive THT cyclizations yielding unprecedented numbers of new scaffolds. In the future, the workflow could benefit from the use of more accurate quantum mechanical methods (albeit at the expense of computing time) and could be adapted to other reaction classes, for example, radical-based rearrangements.

Methods

Physical-organic constraints

All constraints are discussed in detail in Supplementary Information section 3.

Energy and kinetic calculations

The overall relationships between the HopCat’s mechanistic networks and the potential energy surface can be phrased as follows: each node corresponds to a single valence bond structure of a molecule, whereas the (directed) edges represent minimum energy paths (MEPs) between these points. Compared to high-level quantum mechanical calculations, (1) potential energy surfaces we consider do not take into account non-statistical dynamic effects directly (although certain patterns of this kind are included in a heuristic manner by elimination of edges corresponding to dynamically improbable routes, see ‘Treatment of p-TSBs’ section below), and (2) the concatenation of many arrow-pushing steps into concerted processes is performed in a simplified manner (see ‘Graph transformation’ section below) although these concatenations are not manifest in the WebApp, which shows individual mechanistic steps.

To model the reaction kinetics within the network (and, thus, the distribution of products), one needs to determine (1) energy function of nodes, and (2) energy function of directed edges. Regarding (2), we define such a function as a non-negative estimate of the highest energy along the MEP between the starting and ending nodes, taken with respect to the energy of the starting node. For instance, for MEP containing a transition-state (TS) structure between nodes a and b, the corresponding edge energy is defined as $E_{\text{TS}}-E_{\text{a}}$, whereas for an interpolating (without a transition state) MEP, the edge energy is taken as $\text{max(}{E}_{\text{b}}-E_{\text{a}},0)$.

Choice of energy function.

First, as a benchmark, we computed SCS-MP2/aug-cc-pVDZ energy profiles for a set of model mechanistic steps: 1,2-C shift, 1,2-H shift, addition of water to a carbocation and addition of a carbocation to an alkene. In the case of 1,2 shifts, we considered six cases differing in the order of the starting and ending carbocations. The results of these model calculations demonstrate that (1) addition of a nucleophile (be it a lone pair of oxygen in water or double bond in alkene) follows the potential energy profile akin to bond dissociation (Extended Data Fig. 4d) and (2) that C/H shifts are effectively ‘barrierless’ when the stability difference between initial and ending carbocations is high (bottom panels in Extended Data Fig. 4b,c). The stability difference between carbocations of consecutive orders was in the range of 10–20 kcal mol⁻¹, in agreement with experimental stabilities reported in ref. 38 (Extended Data Fig. 4e). In the case of symmetric (that is, when the orders of initial and final carbocations are the same), H shift in the 2,3-dimethylbutyl system (top right panel in Extended Data Fig. 4e), the barrier of roughly 4 kcal mol⁻¹ coincides with the value from ref. 49.

Next, because density functional theory and ab initio calculations are too computationally demanding for high-throughput applications, in particular for energy calculations of hundreds or thousands of nodes within a single network, we tested energy profiles for these model systems using several semi-empirical quantum mechanical (SQM) methods: xTB³⁸, PM6 (ref. 49) and RM1 (ref. 50) (as implemented in OpenMopac^51,52). We also considered application of the neural network described in ref. 53, but it turned out to accept only neutral molecules as input. As can be seen in Extended Data Fig. 4, all SQM methods either overestimate barriers or produce non-physical ‘transition states’ along the paths, probably because of limitations originating from their underlying approximations (the minimal basis set and tight-binding or neglect of diatomic differential overlap assumptions, which seem to work well in the vicinity of valence bond structures but fail in between). The only exception is the xTB model, which performs well for our model C shifts (Extended Data Fig. 4c), but fails on some H shifts (Extended Data Fig. 4b).

Because of the abovementioned limitations, we could not use semi-empirical calculations to detect possible transition-state points between connected valence bond structures. Instead, we proceeded with the construction of a phenomenological model, in which the edge energy function was defined as

$$E_{\text{ab}}=\max (E_{\text{b}}-E_{\text{a}},P_{\text{ab}})$$ (1)

where $E_{\text{ab}}$ denotes edge energy, $P_{\text{ab}}$ is a non-negative edge-specific energy penalty (accounting for either an energy barrier or energy related to conformational change required for the step to occur) and $E_{\text{a}}$ and $E_{\text{b}}$ correspond to energies of nodes a and b, respectively.

As the edge energy function defined above explicitly depends on the node energy function, the next step was to benchmark SQM methods with respect to energy difference between the LECs of the starting and ending carbocations of a mechanistic step. To do so, we selected 127 representative mechanistic steps involving diverse scaffolds (in particular, 33 reverse olefin cyclizations, 29 oxa cyclizations, 28 C shifts, 25 olefin cyclizations, five H shifts, four alkyne cyclizations and three aryl cyclizations), For this set, we used the SCS-MP2/cc-pVDZ method as a reference and compared it with corresponding SQM energies (Extended Data Table 1), which revealed the xTB and PM6 families of methods to provide the most accurate step energies.

Choice of parameters.

With the overall objective to keep the number of adjustable parameters as small as possible, we assigned the following values (reasonable in the light of previous studies):

H and C shifts.

Here, we assign energy penalties $P_{\text{H}}$ and $P_{\text{C}}$ to 6 kcal mol⁻¹, which is close to the average of the values reported in ref. 49 for 1,2-H, 1,3-H and 1,4-H (4.96, 4.63 and 8.5 kcal mol⁻¹, respectively; Extended Data Fig. 4). Furthermore, we assign separate $P_{\text{C3}}$ and $P_{\text{Me}}$ parameters (set to 8 and 9 kcal mol⁻¹, respectively, based on experimental results obtained for fenchol system) to 1,3-C and 1,2-methyl shifts.

Cyclizations.

As addition of a nucleophile to a carbocation is expected to follow the bond dissociation curve when the corresponding atoms are in proximity, the remaining factor is the energy penalty related to bringing the substrate into a near-attack conformation (NAC). The NAC energy relative to the substrate constitutes the cyclization penalty $P_{\text{ab}}^{\text{NAC}}$. For reverse cyclizations, we assume no penalty.

Generation steps.

This process is assumed to be generally endoenergetic, and equation (1) is no longer suitable. Instead, we compute activation barriers for generation steps based on the Hammond postulate, which assumes a linear relationship between reaction energy and reaction activation energy, $\text{Δ}{E}_{\text{act}}=A_{\text{g}}(E_{\text{b}}-E_{\text{a}})+B_{\text{g}}$, where the Hammond parameters $A_g$ and $B_g$ are assigned to each generation rule $g$. We set the following $A_g$ and $B_g$ values: (0.6, −20) for olefin protonation and (0.2, −10) for water elimination from alcohol (fitted against distribution of linalool products at 80 °C). For other generation rules (for example, carbonyl protonation) we simply estimate $\text{Δ}{E}_{\text{act}}$ by the reaction energy $E_{\text{b}}-E_{\text{a}}$: in other words, we set $(A_{\text{g}},B_{\text{g}})=(1,0)$.

Quench steps.

As the profiles of addition of several nucleophiles to carbocations (Extended Data Fig. 4d) suggest that such an association process does not have an energy barrier by itself (in the sense of the transition-state theory), its rate should be only influenced by diffusion, desolvation effects and concentration of base. We incorporated these effects into parameter $P_{\text{q}}$, whose value we set to 8 kcal mol⁻¹.

Other cases.

A double bond adjacent to the formal carbocation may change its $E\text{/}Z$ regiochemistry due to a delocalization effect (allyl resonance), which makes rotation around this bond possible. We estimate these barriers by (1) generation of an approximate transition-state conformer (corresponding to the dihedral angle of 90°); (2) computing an energy barrier using a semi-empirical method and (3) linear transformation of this barrier. The coefficients for the last step were obtained by linear regression with B3LYP results for a set of allylic systems with different substitution patterns (Supplementary Information section 3.5). For the irreversible oxidation of dienes to aryls, we assigned $P_{\text{arom}}=26$ kcal mol⁻¹ (as reported in ref. 54).

Network initialization

Preparation of Allchemy’s mechanistic network for kinetic calculation entailed four steps: (1) assignment of structures (LEC and NAC calculations) followed by removal of improper nodes; (2) node energy calculations; (3) assignment of edge energies (according to equation (1) and Hammond parameters); and (4) transformation to a kinetic graph.

LEC calculations.

With RDKit’s implementation of the distance matrix algorithm and MMFF94 force field, we generated and optimized 50 conformers (with force tolerance set to 0.01) for each node in the network and took the one with the lowest energy as the LEC, saving its coordinates and MMFF94 energy. For calculations in capsules, 100 LECs were considered (100 is the maximum number of LECs that can be set in HopCat).

NAC calculations.

For each transformation, the substrate’s conformer resembling the product is calculated by bringing the reacting, non-hydrogen atoms to the distance of 3 Å and relaxing the rest of the molecule while keeping this distance fixed. Specifically, having identified substrate’s atoms that should be in close proximity but before conformer generation, we set coordinates of these atoms to (0,0,0) and (0,0,3). Using RDKit, we generated 50 such conformers for every relevant node molecule (specifically, only substrates to cyclizations), and selected the lowest-energy one as the NAC. The MMFF94 energy with respect to the substrate was taken as NAC energy (note that in some cases studied, for example, for a model limonene molecule, MMFF94 energy value of 4.6 kcal mol⁻¹ was closer to the B3LYP/6−31+G** result of 3.5 kcal mol⁻¹ than PM6, which provided only 2 kcal mol⁻¹). For calculations in capsules, 100 NACs were considered (100 is the maximum number of NACs that can be set in HopCat).

Detection of ‘improper’ conformers.

When the distance matrix algorithm failed to produce a valid conformer, it was assumed that the structure was impossible to construct without breaking bonds or flipping stereocentres. We detected two failure modes: either the function did not produce any conformer or the generated structure was entirely flat (one of xyz coordinates was zero for all atoms) despite having sp³-hybridized atoms. All nodes and edges with such improper structures were collected and scheduled for removal. In a typical network, about 2% of nodes were removed.

Removal of improper nodes.

All improper nodes were removed from the node list. All edges (both incoming and outgoing) that were either beginning or ending in any of the removed nodes were also removed. A BFS algorithm was then run starting from the initial carbocation (root of the network) to detect and remove any disconnected components (nodes that lost their connections to the rest of the network because of the removal of their ancestors).

Removal of improper edges.

Edges for which NAC calculations of the substrates failed were removed from the edge list. Then, detection and removal of disconnected components were performed as described in the previous point.

SQM calculations.

Single point calculations were performed with COSMO model of solvent (with the dielectric constant set to 2.27, corresponding to benzene). When testing different methods, neglect of diatomic differential overlap methods (PM6, RM1 and so on) were computed in OpenMopac⁵², whereas xTB was provided with its own package⁵⁰. In the final version of HopCat, the PM6 model was used.

Graph transformation

First, all nodes connected by resonance transformations were combined, as they represent the same physical entity. For $E\text{/}Z$ isomerization, we checked dihedral angles to group together nodes representing the same conformation of an allyl system. Then, the resonance nodes within a given group were assigned to a single ‘supernode’ representing the group’s structure. The supernode inherits all connections from the constituent nodes. Next, we identified local minima (MIN) in the graph (this operation is required to properly define the system of kinetic equations). These minima are defined as nodes for which all outgoing edges have non-zero value of edge energies $E_{\text{ab}}$. Then, to define the rate constants for transitions between different MINs, corresponding LEPs have to be found (as they give a leading contribution to the rate constant). MINs and LEPs define a kinetic graph, in which nodes correspond to MINs and edges to LEPs, with LEP energies related to the corresponding rate constants by the Eyring equation, $k=\frac{k_{B}T}{h}\exp \left(-\frac{\text{Δ}{E}_{\text{act}}}{RT}\right)$ (in which $k_B$ is the Boltzmann constant and $h$ is the Planck constant). As edge energies in the mechanistic graph are non-negative (equation (1)), the maximum energy along LEP—an approximation of transition state between MINs—is simply the sum of individual edge energies. However, to avoid double counting, the LEP connecting two MINs cannot pass through another MIN. Therefore, the algorithm to detect LEPs proceeded as follows:

1. All edges outgoing from any of MINs were (temporarily) removed from the graph and stored elsewhere.

2. For each MIN node $m$:

   1. The edges outgoing from $m$ were reintroduced into the graph,

   2. LEPs connecting $m$ to any other MIN node in the graph were found with Dijkstra algorithm,

   3. LEP energies for thus detected pairs of MIN nodes were transformed into rate constants using the abovementioned Eyring equation and stored,

   4. The edges outgoing from $m$ were once again removed from the graph.

Finally, for eliminations, we multiplied the corresponding rate constants by the number of symmetrically equivalent hydrogens that can be abstracted leading to the same product. For instance, abstraction of a proton from a terminal methyl group will be three times as fast as abstraction from tertiary carbon atoms, for example, C(CH)(C)[CH+] C>>CC(C)=CC.

Kinetic calculations

Once the kinetic graph is defined, we perform numerical integration⁵⁵ (using SciPy implementation of the backward differentiation method) with initial concentration vector set to 1 for the initial carbocation or substrate and 0 for other nodes in the network.

Calculations under confinement

For calculations mimicking nanoconfinement, for example, within the supramolecular capsule we used in some of our experiments, we imposed geometry-specific constraints on the generated conformers. If the confinement could be approximated as spherical, we (1) restricted the upper bound of the initial distance matrix to the diameter of the sphere, then (2) applied a distance-geometry algorithm with such modified bounds and finally (3) optimized the resulting geometry using MMFF94 force field with harmonic distance constraint applied to every atom, so as to keep the entire molecule inside the sphere (if possible). This last constraint was imposed by (1) addition of a fixed reference point $X_0$ in the current geometric centre of the molecule and (2) addition of an energy penalty of the form $k{\sum }_{\text{a}\in \text{atoms}\hspace{0.33em}\text{outside}\hspace{0.33em}\text{sphere}}{(|X_{\text{a}}-X_0|-R)}^2$, where $R$ is the sphere’s radius. After generation and optimization, we additionally removed conformers that (1) exceeded the confinement boundary by more than 1 Å (this also means that we accepted conformers for which, for instance, one hydrogen atom was only slightly outside the target sphere or ellipsoid) or (2) contained valence angles centred at each atom and deviating by more than 10° from the unconstrained structure. This pruning step was intended to remove unsuccessful optimization attempts as well as the structures that were unphysically squashed or twisted during optimization.

In the case of ellipsoidal confinement, the first two steps were the same as in the spherical case, with the largest axis taken as an upper bound of the distance matrix. The third step was conceptually identical, we optimized the geometry with harmonic constraint with respect to the ellipsoid’s surface and applied to the atoms outside the ellipsoid, but the mathematical complexity of the problem required certain modifications to the optimization procedure. First, we computed the minimum volume enclosing the ellipsoid of the generated conformer and used the result to rotate the molecule so as to align the axes of minimum volume enclosing the ellipsoid with the coordinate system (as we choose our confinement ellipsoid to be in standard orientation, that is, with principal axes oriented along x, y and z axes in order of their length). Second, we expressed the MMFF94 energy with confinement penalty as a function of rotatable dihedral angles instead of atomic coordinates, thus reducing the overall number of variables. We then optimized this target function with SciPy implementation of COBYLA algorithm^56–58. After generation and optimization, the set of conformers was pruned just as in the spherical case. Finally, we prohibited mechanistic steps that are geometrically disfavoured under confinement: that is, those in which bond-forming atoms are separated by more than 4.6 Å in all generated conformers.

Treatment of p-TSBs

The p-TS bifurcation (p-TSB) involve a pair of mechanistic steps sharing a common transition state after which the MEP bifurcates towards different products without additional barrier. In such a scenario, nonequilibrium or dynamic effects may effectively exclude one of these transitions in favour of the other. Typically, modelling of such phenomena requires high-level quantum mechanical calculations (possibly even ab initio molecular dynamics): clearly, an approach that cannot be applied effectively to reaction networks consisting of thousands of nodes. Instead, we aimed to capture p-TSB effects at an approximate level of knowledge-based rules reflecting various energetic and/or structural features. First, based on the available literature (that is, our set of 715 reactions spanning 4,174 mechanistic steps, all deposited at https://HopCatResults.allchemy.net), we identified three types of mechanistic step that (1) were reported or postulated to proceed through a non-classical carbocation and (2) are present in our literature dataset in numbers allowing for meaningful analysis: olefin cyclization^59,60 (347 examples), 1,2-C shift starting from cyclobutylcarbinyl cation^61,62 (53 examples) and retro-1,3-olefin cyclization originating from cyclopropylcarbinyl cation⁶² (80 examples). In the case of olefin cyclization, in which the two products arise from attacks on different atoms of the same C=C bond, we performed PM6 calculations that evidenced that in 96% of cases, a product with lower energy was preferred. This observation was encoded as a heuristic to eliminate higher-energy products; some additional subrules were applied to the remaining 4% of exceptions. For the remaining two classes, we also identified and encoded structural criteria (for example, based on the difference in connectivities of carbon atoms in the β position to carbocation in cyclopropylcarbinyl and cyclobutylcarbinyl carbocations) dictating the preferred product. For the remaining types of step and system (for example, pimarenyl cation, pimar-8-en-15-yl cation), we encoded the preferred products verbatim. All these rules are discussed in detail in Supplementary Information section 3.4.

GC–MS analyses

In experiments with linalool and fenchol, the products were analysed by GC–MS and assignments were proposed by Thermo Scientific Xcalibur v.2.1 with NIST 08 MS Library software. These assignments were further corroborated by comparison against reference compounds (purchased or synthesized separately) and available literature data, and by additional control experiments (for all experimental and spectroscopic details, see Supplementary Information section 7).

In the analysis of products of fenchol’s rearrangements, Xcalibur/NIST’s assignment of GC–MS peaks was correct for 12 (a tricyclene with a retention time of 8.65 min), but this software incorrectly suggested 17 (at 8.01 retention time) to be 1,5,5-trimethyl-3-propan-2-yli denecyclohexane. However, the formation of this molecule was mechanistically unlikely as it would require an unrealistically long sequence of seven mechanistic steps (1,2-C shift, retro-1,5-olefin exo cyclization, 1,2-C shift, 1,2-H shift, 1,3-olefin exo cyclization and retro-1,3-olefin exo cyclization, quench by elimination). Also, no products that branched off this path were experimentally observed, which suggested a wrong signal assignment. This made us reconsider some of the reference compounds we synthesized, identifying the same retention time for bornylene. For this compound, HopCat (1) suggested a concise three-step sequence (1,2-C shift, 1,2-C shift, elimination) and (2) indicated that the same network branch leads not only to 17 but also to experimentally observed compounds p-6 and 12 (see Supplementary Information sections 7.1 and 7.2 for, respectively, the scheme of the network and for HopCat’s screenshots of mechanistic pathways starting from linalool and fenchol). We highlight this example because it illustrates the benefits of combining conventional (GC–MS, Xcalibur) and mechanistic network analyses.

THT cyclization studies.

Synthesis of the cyclization substrates.

Details of all syntheses are included in Supplementary Information section 8. Briefly, the substrates were prepared by a Negishi coupling between an organozinc reagent (generated from the corresponding alkyl bromide) and a vinyl iodide. The alkyl bromide (3.0 equiv.) was dissolved in tetrahydrofuran (THF) (0.4 M) and t-BuLi (1.6 M in hexanes, 6.0 equiv.) was added at −78 °C. The solution was stirred at −78 °C for 30 min, then cannulated (rinsed with THF, 2 ml) to a flask containing ZnCl₂ (3.0 equiv.) suspended in THF (2 M). The resulting solution was stirred at room temperature for 20 min, then cannulated (rinsed with THF, 2 ml) to a flask containing the vinyl iodide (1.0 equiv.) and Pd(PPh₃)₄ (0.1 equiv.) dissolved in THF (0.6 M with respect to the vinyl iodide). The reaction mixture was shielded from light and stirred at room temperature for 18 h. Brine and EtOAc were then added, the layers separated and the aqueous layer further extracted with EtOAc. The combined organic layers were dried over Na₂SO₄ and the solvent removed in vacuo.

The crude residue was dissolved in THF (0.2 M) and tetrabutylammonium fluoride was added (2.2 equiv.). The reaction mixture was stirred at room temperature until complete consumption of the starting material was observed by TLC (3–18 h). Brine and EtOAc were then added, the layers separated and the aqueous layer further extracted with EtOAc. The combined organic layers were dried over Na₂SO₄, the solvent removed in vacuo and the crude residue purified by use of flash chromatography (hexanes:EtOAc 95:5 ➔ 9:1) to give the pure alcohol.

For the preparation of the corresponding acetate substrates, this alcohol (1.0 equiv.) was dissolved in dichloromethane (0.2 M) and Et₃N (2.5 equiv.), N,N-dimethyl 4-aminopyridine (0.4 equiv.) and acetic anhydride (2.0 equiv.) were added. The reaction mixture was stirred at room temperature until complete consumption of the starting material was observed by TLC (1–3 h). HCl 1 M aqueous solution was then added, the layers separated and the aqueous layer extracted with dichloromethane. The combined organic layers were washed with brine, dried over Na₂SO₄ and the solvent removed in vacuo. The crude residue was purified by means of flash chromatography (hexanes:EtOAc 97:3) to give the pure acetate.

Cyclizations using the resorcinarene capsule catalyst.

To the substrate dissolved in CHCl₃ (30 mM) was added the specified amount of resorcinarene capsule catalyst followed by an HCl stock solution in CDCl₃ (3 mol%), and the mixture was stirred at the specified temperature. Once the reaction was judged to be complete by GC analysis, the solvent was partially removed in vacuo (350 mbar at 40 °C for short timeframes of 10–15 min as longer evaporation times could lead to significant loss of the volatile sesquiterpene products) and the mixture was passed through a column of silica (eluting with pentane) to remove the capsule catalyst and polar byproducts (for reactions using 20 mol% of the capsule catalyst, two such passages may be required), followed by column chromatography using AgNO₃-impregnated silica to isolate the product of the reaction. Procedures for each compound and characterization data are available in Supplementary Information section 8.

Solution cyclizations using HCl.

To the substrate (16.7 μmol, 1.00 equiv.) dissolved in CDCl₃ (480–X μl, where X is the amount in μl of HCl stock solution in CDCl₃ to be added to the reaction, as determined after titration, vide infra) was added a n-decane stock solution in CDCl₃ (20 μl, 167 mmol l⁻¹, 3.34 μmol, 0.2 equiv.). An aliquot (roughly 10 μl) of the reaction mixture was diluted with 0.25 ml of hexane (containing 0.08% DMSO) and subjected to GC analysis (initial sample). An HCl stock solution in CDCl₃ (X μl, 1.0 equiv.) was then added and the mixture was stirred in a closed vial at the specified (internal) temperature. Further samples were taken at the indicated times and analysed by GC. Conversions and yields were calculated as described in our previous work³⁷.

Preparation and titration of HCl stock solution in CDCl₃.

HCl stock solution in CDCl₃ was prepared by passing HCl gas, generated by the dropwise addition of concentrated H₂SO₄ to dry NaCl, through CDCl₃ for roughly 30 min. The concentration of HCl in the resulting solution was determined as follows: HCl stock solution in CDCl₃ (100 μl) was added to a solution of phenol red in EtOH (0.002 wt%, 2.5 ml) by using a Microman M1 pipette equipped with plastic tips. On addition, the solution turned from yellow (neutral) to pink (acidic). The resulting solution was then titrated with a 0.100 M ethanolic solution of triethylamine. At the equivalence point, the solution turned from pink to yellow. The HCl stock solution was kept in the fridge, and the titration was repeated immediately before each use.

Solution cyclizations using BF₃×OEt₂.

To the substrate (16.7 μmol, 1.0 equiv.) dissolved in CDCl₃ (310 μl) was added a n-decane stock solution in CDCl₃ (20 μl, 167 mmol l⁻¹, 3.34 μmol, 0.2 equiv.). An aliquot (roughly 10 μl) of the reaction mixture was diluted with 0.25 ml of hexane (initial sample) and subjected to GC analysis. A BF₃×OEt₂ stock solution in CDCl₃ (0.1 M, 170 μl, 17.0 μmol, 1.0 equiv.) was then added and the mixture was stirred in a closed vial at the specified (internal) temperature, and further samples were taken at the indicated times and analysed by GC. Conversions and yields were calculated as described in our previous work³⁷.

Extended Data

Extended Data Fig. 1 |. HopCat’s mechanistic analysis of a reaction yielding a fused tetrahydropyran.

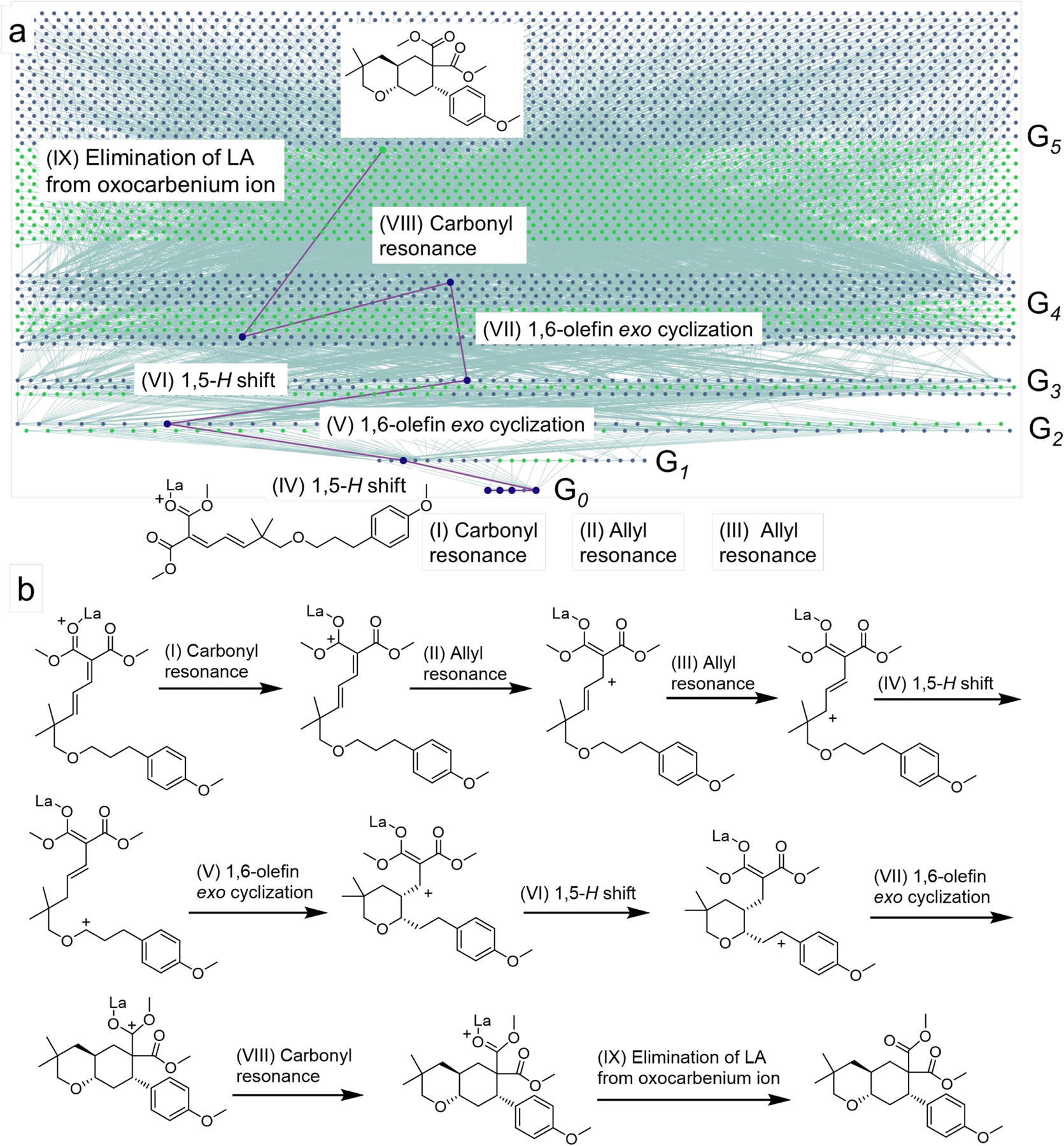
An example of a problem not “seen” by the machine during training on 715 literature examples. In the original publication⁶³, the authors focused on the double 1,5-H shifts as key steps and did not consider the full mechanism. HopCat’s calculations ran up to n = 4 generations and traced a complete and unique mechanistic pathway. This pathway starts with a series of carbonyl and allyl resonances placing positive charge at the position available for 1,5-H shift followed by 1,6-olefin exo cyclization. Subsequently, the sequence of 1,5-H shift and 1,6-olefin exo cyclisation steps is repeated to afford tetrahydropyran’s bicyclic scaffold. The last two mechanistic steps along the pathway are: (i) carbonyl resonance to form oxocarbenium species and (ii) elimination of Lewis acid yielding the final, quenched product. The software’s solution agrees with the partial mechanism postulated in the original publication. a, A screenshot showing a simplified network (without stereochemistry). In reality, the network was generated with full stereochemistry and comprised of ~28,000 nodes that cannot be clearly visualized as a miniature. b, Details of all mechanistic steps (for raw screenshots from HopCat, in traditional and atom-mapped visualization modalities, see Supplementary Section S5). Additional examples are also provided in Supplementary Section S5.

Extended Data Fig. 2 |. HopCat’s mechanistic analysis of a reaction leading to a tricyclic dienone.

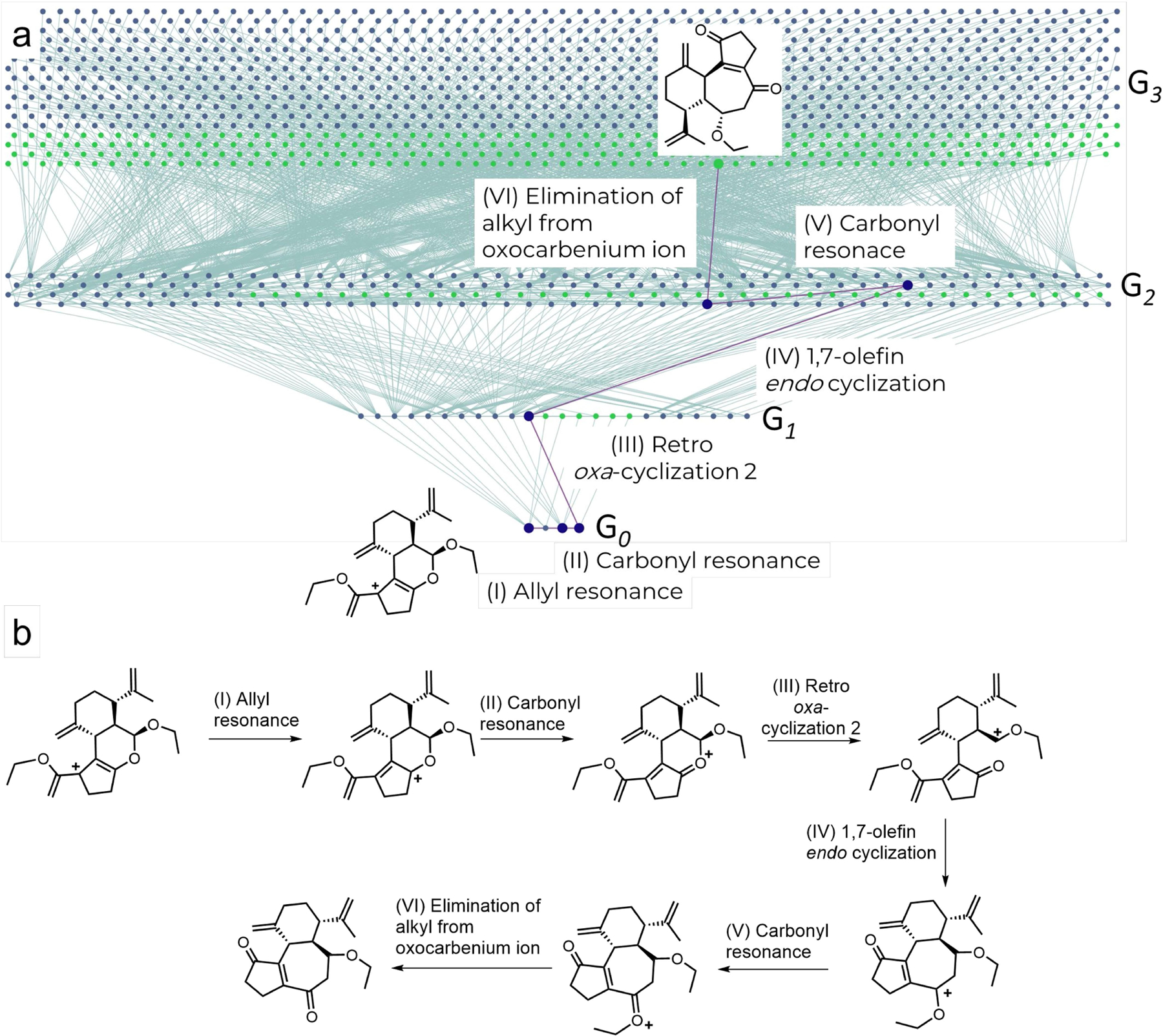
HopCat solves another problem not “seen” in the 715 training set. The dienone is an intermediate used in the recent synthesis of curcusone diterpenes⁶⁴. In the original publication, authors included a plausible arrow-pushing scheme of electron movements for the double deprotectionaldol sequence but did not support it with a more detailed mechanistic analysis. HopCat identifies the reaction’s product in G₄ and proposes a plausible and unique mechanistic route. Starting from a carbocation generated via elimination of substrate’s tertiary alcohol (bottom row of the network), this intermediate undergoes two consecutive resonances (allyl and carbonyl) that result in the formation of an oxocarbenium cation. Subsequent retro oxa-cyclization followed by ring closure constructs a seven-membered, central ring of the molecule. The last two steps describe deprotection of the enol ether. Formation of the oxocarbenium cation via carbonyl resonance makes the alkyl group on the oxygen a good leaving group, enabling its subsequent elimination and formation of the final product. The overall movement of electrons is consistent with the one proposed by the authors. a, A screenshot showing the network comprised of ~2,000 nodes. b, Details of all mechanistic steps (for raw screenshots from HopCat, in traditional and atom-mapped visualization modalities, see Supplementary Section S5). Additional examples are also provided in Supplementary Section S5.

Extended Data Fig. 3 |. A contested and only recently resolved⁶⁵ biosynthesis of spiroviolene relies on a macrocyclization step (1,11-olefin endo cyclization), which does not occur in abiotic set of carbocation transformations.

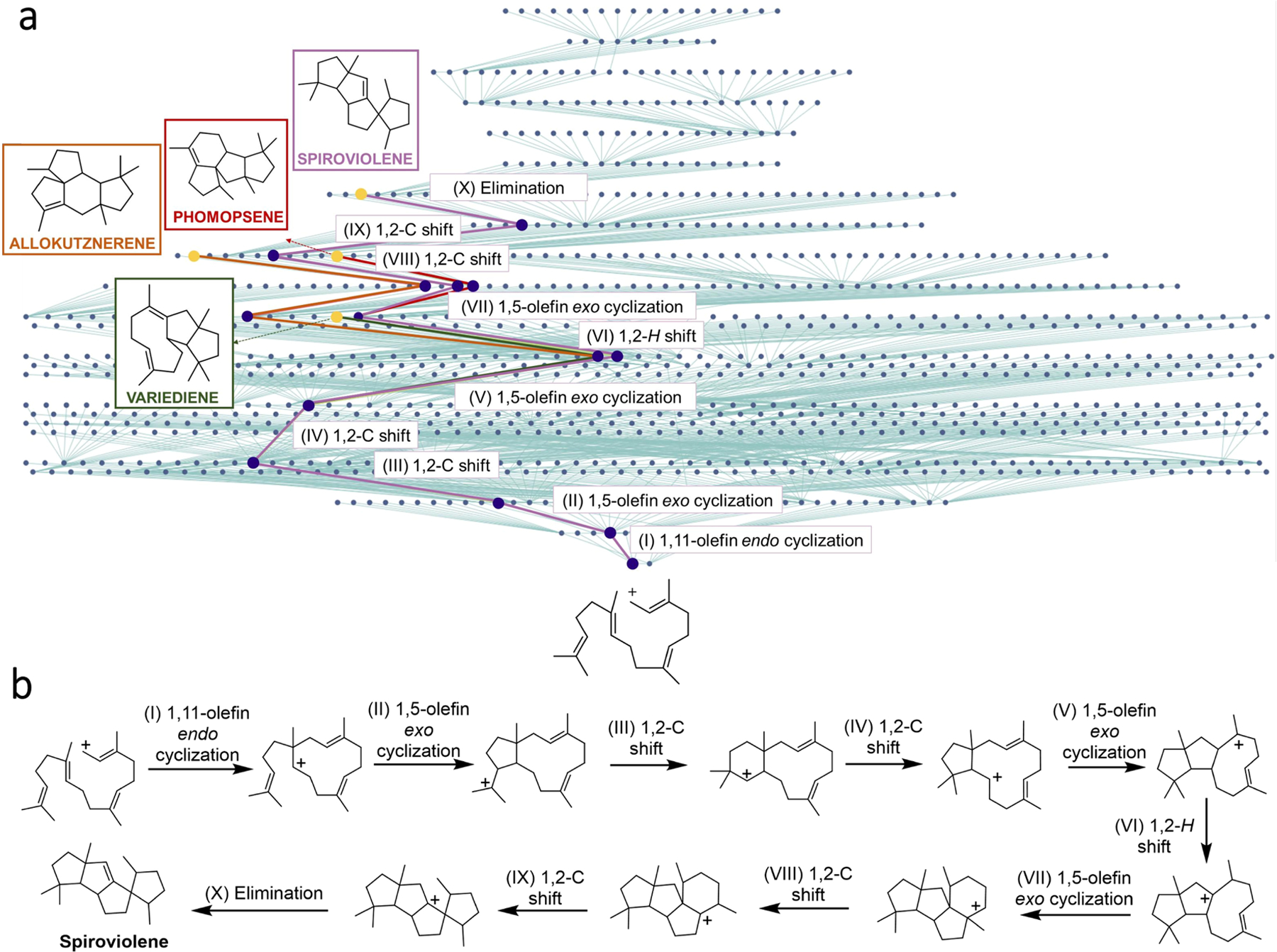
Identifying the mechanistic pathway for the biosynthesis of spiroviolene has proven a computationally challenging problem – in fact, the pathway was not found within G₇ and expansions to higher generations exceeded computing power. Accordingly, we implemented a “mixed” strategy search in which 7 generations were expanded from the substrate in the forward direction and 6 generations from the product in the retrosynthetic direction (using “reversed” mechanistic rules). This strategy considerably reduces the computational cost as the number of nodes in two smaller networks, each propagated to n generations and with branching factor m, scales as 2mⁿ vs. m²ⁿ for one forward network expanded to 2n generations (for n = m = 7, the difference is mⁿ /2 ~ 400,000 times). The algorithm then searched for common node(s) in the two networks and, when they were found, was able to concatenate a 10-step route. a, HopCat’s screenshot showing a grossly simplified network generated by a mixed forward-retro search. In reality, the network comprised of 909,937 nodes that could not be clearly visualized as a miniature. HopCat’s shortest route is marked with purple lines and agrees with the recently revised pathway⁶⁵. Also, in the same network, rearrangement sequences leading to three other natural products were found – phomopsene⁶⁶ (red lines and frame), allokutznerene⁶⁶ (orange) and variediene⁶⁷ (green); b, Details of all mechanistic steps for spiroviolene’s mechanistic route. For raw HopCat’s screenshots of the sequences leading to all four natural products, in traditional and atom-mapped visualization modalities, see Supplementary Section S5). Note: Akin to Fig. 4 and Extended Data Figs. 1, 2, none of the biosyntheses shown in this figure were considered when extracting mechanistic steps from literature examples.

Extended Data Fig. 4 |. Theoretical studies of model H- and C-shifts.

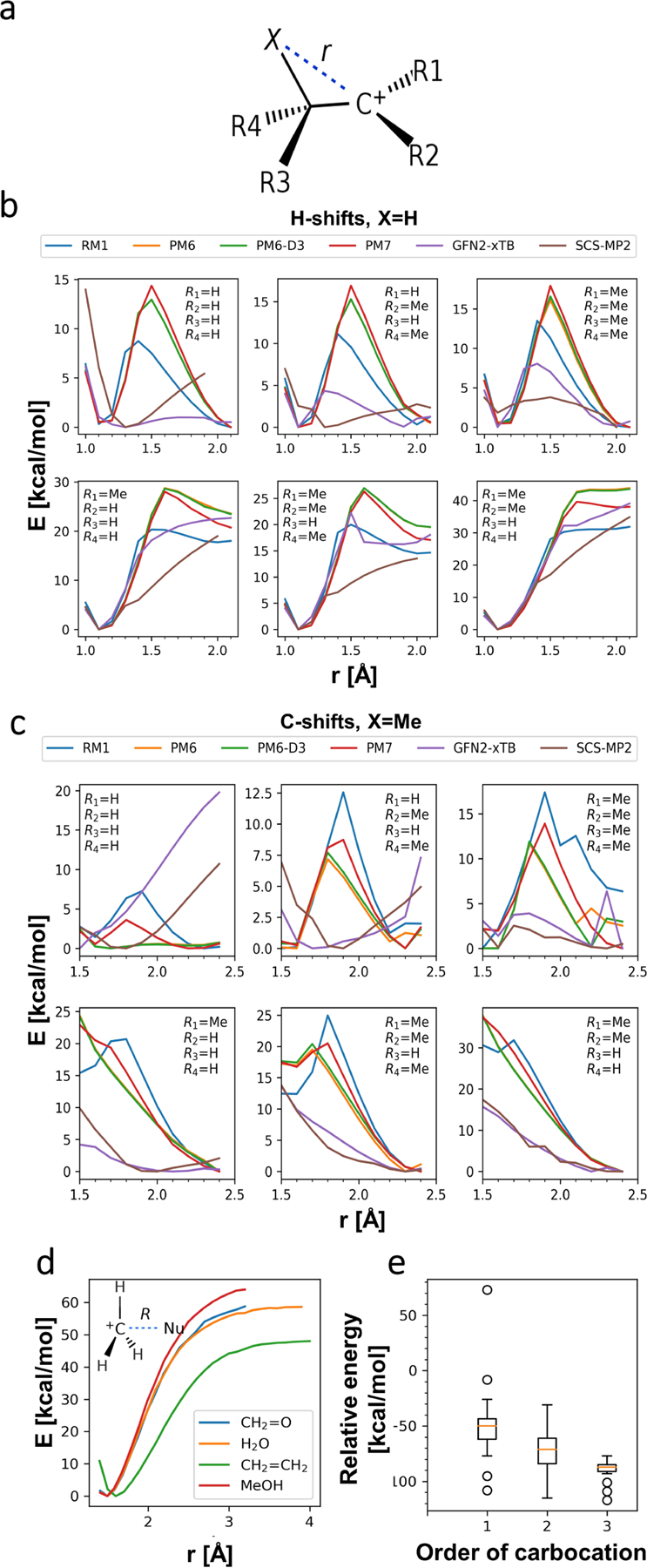
a, System setup. For all unique configurations of substituents R1-R4 (-H and -Me were considered), atom X was dragged along distance vector r so as to simulate the shift. Initial geometry was chosen such that the C-X bond was approximately perpendicular to the plane of the carbocation. All trajectories were subsequently verified by visual inspection. b, H-shifts (X = H). Top three panels represent symmetric shifts (such that the orders of initial and resulting carbocations are the same), with the order of carbocation increasing from the left to the right. In the bottom row, two leftmost panels represent shifts in which the carbocation changes order by one, whereas the rightmost panel represents an extreme example of transition between first-order and tertiary carbocations. c, C-shifts (X = Me). Top three panels represent symmetric shifts (such that the orders of initial and resulting carbocations are the same), with the order of carbocation increasing from left to right. In the bottom row, two leftmost panels represent shifts in which the carbocation changes order by one, whereas the rightmost panel represents an extreme example of transition between first-order and tertiary carbocations. d, Theoretical studies of carbocation association process. Each curve represents the SCS-MP2/aug-cc-pVDZ energy profile with PCM model of water, modelling approach of four nucleophiles (formaldehyde, water, methanol and ethene) towards CH₃⁺ along vector R (scheme inserted in the top left of the panel). e, Boxplot representing experimental stabilities of carbocations taken from³⁸ with respect to the CH₃⁺ cation. The data was grouped according to the order of a carbocation (number of non-hydrogen atoms directly connected to the formally charged carbon atom), showing the general trend in the stability: increasing the order of a carbocation lowers the energy, on average, by 10–20 kcal/mol.

Extended Data Fig. 5 |. General synthetic scheme for the preparation of the precursors employed in Fig. 5.

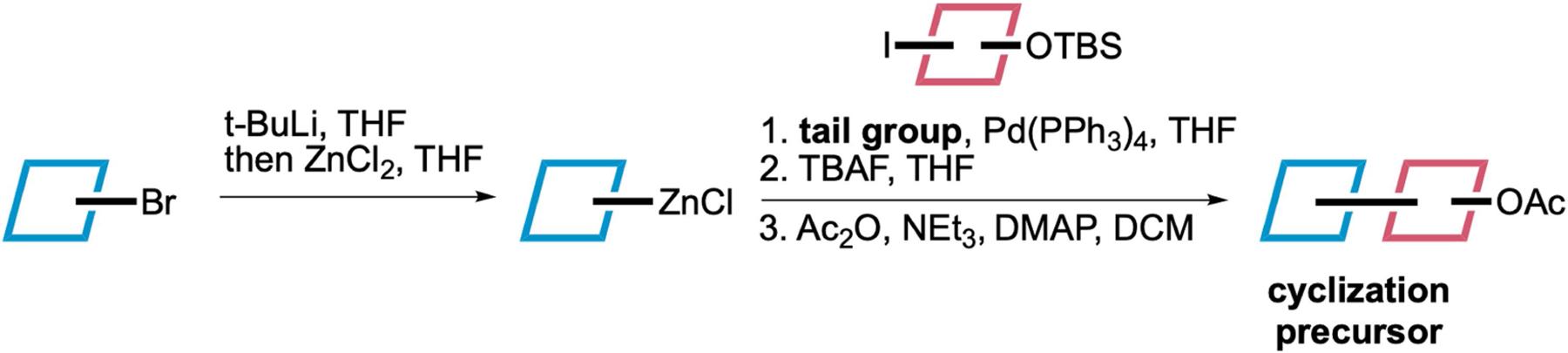
An alkyl bromide is converted into the corresponding organozinc reagent by sequential treatment with t-BuLi and ZnCl₂. This reagent is then used in a Negishi coupling with a vinyl iodide bearing a protected alcohol group. The coupling product is then deprotected to give the free alcohol, and the corresponding acetate is prepared by acetylation of this alcohol.

Extended Data Table 1 |.

Accuracy of $\text{Δ}E$ computed for representative rearrangement steps with semiempirical methods

Method	${\rho }_R$	${\rho }_S$	MAE
xTB	0.892	0.910	8.28
PM6-D3	0.894	0.848	8.215
PM6	0.891	0.841	8.384
PM7	0.853	0.789	9.685
RM1	0.821	0.759	9.872
PM3	0.774	0.67	10.932

SCS-MP2/aug-cc-pVDZ is taken as reference, ${\rho }_R$ is Pearson correlation coefficient, ${\rho }_S$ denotes Spearman rank correlation coefficient, and MAE is mean absolute error.

Data availability

Mechanistic reaction rules, physical-organic methods and the kinetic model are detailed in the main text, Methods and the Supporting Information. All 715 atom-mapped mechanistic pathways from which the mechanistic steps were extracted are posted at https://HopCatResults.allchemy.net. Therein, networks propagated from the literature substrates are also deposited. Experimental details including spectroscopic data can be found in Supplementary Information sections 7 and 8. We intend to update HopCat based on new literature findings; these improvements will be made available to the software’s users.