Impact of Beam Shape on Print Accuracy in Digital Light Processing Additive Manufacture

Abstract

Photopolymerization-based additive manufacturing requires selectively exposing a feedstock resin to ultraviolet (UV) light, which in digital light processing is achieved either using a digital micromirror device or a digital mask. The minimum tolerances and resolution for a multilayer process are separate for resolution through the Z-axis, looking through the thickness of a printed part, and resolution in the XY-axes, in the plane of the printed layer. The former depends wholly on the rate of attenuation of the incident UV light through the material relative to the mechanical motion of the build layer, while the latter is determined by a two-dimensional pattern of irradiance on the resin formed by the digital micromirror device or the digital mask. The size or the spacing of elements or pixels of this digital mask is frequently given by manufacturers as the “resolution” of the device, however, in practice the achievable resolution is first determined by the beam distribution from each pixel. The beam distribution is, as standard, modeled as a two-parameter Gaussian distribution but the key parameters of peak intensity and standard deviation of the beam are hidden to the user and difficult to measure directly. The ability of models based on the Gaussian distribution to correctly predict the polymerization of printed features in the microscale is also typically poor. In this study, we demonstrate an alternative model of beam distribution based on a heavy-tailed Lorentzian model, which is able to more accurately predict small build areas for both positive and negative features. We show a simple calibration method to derive the key space parameters of the beam distribution from measurements of a single-layer printed model. We propose that the standard Gaussian model is insufficient to accurately predict a print outcome as it neglects higher-order terms, such as beam skew and kurtosis, and in particular failing to account for the relatively heavy tails of the beam distribution. Our results demonstrate how the amendments to the beam distribution can avoid errors in microchannel formation, and better estimates of the true XY-axes resolution of the printer. The results can be used as the basis for voxel-based models of print solidification that allow software prediction of the photopolymerization process.

Introduction

Three-dimensional (3D) printing is transforming traditional processing methods for microscale applications. Research into microfluidics and lab-on-a-chip applications is well established,^1,2 while soft robotics applications are advancing.³ Control over local material properties is invaluable to four-dimensional (4D) printing and metamaterial applications,⁴ particularly prediction and control of the material stresses generated during the fabrication process.⁵ For all these microscale applications, digital light processing (DLP) remains attractive due to its high resolution and versatility. DLP is a maskless vat photopolymerization process, which uses an ultraviolet (UV) light field projected from a digital micromirror device to selectively polymerize a photosensitive resin. The majority of current systems use a bottom-up approach, where the light field is projected through the transparent base of a build tray and the printed part is raised upward with each successive layer, as opposed to a top-down, where the light source is placed above the build tray and the part must be lowered into the resin to continue printing.⁶

DLP's strength is the ability to create microscale structures within a larger build area,⁷ allowing the user to control material properties in the micrometer range by changing the resin feedstock properties and the irradiation intensity pattern of the incident UV light field.⁸

The two mechanisms for control are interrelated—a designed resin feedstock must initiate photopolymerization at a light frequency and energy level, which matches the projection system and the light field should not be so attenuated by the resin that the photopolymerization ceases before the structure is able to bond to the build plate or to a previous layer.

Matching these properties within a DLP and resin system is facilitated by the development of models of photopolymerization kinetics, which can be grouped into top-down and bottom-up approaches. The latter seeks to model the photochemical reaction details such as initiator photolysis and chain initiation and propagation.⁹ These models have high degrees of complexity, and primarily focus on the chemical reaction ––treating the UV light field as an averaged energy input to the system.¹⁰ The top-down approach relies on predicting solidification from easily measured and observable parameters, such as relating the depth of polymerization to exposure time and energy dosage through the Beer–Lambert law. A number of works have used this simple attenuation relationship to optimize the resolution of 3D prints along the Z-axis,^11–13 which is to say controlling the thickness of each build layer.

A well-designed match between the attenuative properties of the resin and extinction length of the incident UV light source allows small suspended layers to be printed, facilitating closed channels and bridges at microscale resolution.^14,15 The user needs to then develop only a relatively simple model to control the UV energy density, and hence the depth of polymerization, in the resin by changing the exposure time or light source intensity.¹⁵

These models view the incident light intensity as a flat field, and track only the attenuation of the energy through the feedstock material. Applications such as kirigami structures, structures which may change shape in response to environmental stimuli and metamaterial structures rely on the ability to change local material properties such as the stress gradient,¹⁶ Young's modulus,¹⁷ or water swelling behavior.¹⁸ In other fabrication or 3D printing processes, this might be achieved through changing the feedstock material, but for DLP processes multimaterial printing is cumbersome, expensive, and requires specialized processes.^19,20 Four-dimensional printing techniques and metamaterial printing using DLP processes have therefore focused on controlling the rate of change of material properties that occurs during the photopolymerization process, essentially allowing some regions of materials to cure more rapidly or more fully than surrounding regions to create a gradient of the desired material property through the build area.²¹

In the simplest case, this might involve lowering or gray scaling, a region of pixels to lower the energy dose over a small printed area resulting in a region with a higher through-thickness stress gradient and lower Young's modulus, which can be used to induce the structure to bend after printing.^16,22

Modeling of the 2D-structured UV intensity depends on the image projected from the digital micromirror device (DMD), which is typically modeled as a series of overlapping Gaussian distributions.^23,24 Examinations of print relation and light field intensity in these axes have been rarer as fixed optics limits the user's scope for control. In optical design, the issue of most concern in the misalignment of pixels and beam skew rather than the impact of the field on the material properties of the resin.^25–27

Modeling the 2D light field has been attempted by a number of groups with the strategy of superimposing a series of Gaussian profiles corresponding to each “on” pixel in the DMD.^28,29 This approach has not been widely adopted since for larger area builds, where the area of illuminated pixels corresponds to a printed area of greater than 1 mm², there is relatively little variation in the intensity field so the flat-field assumption of field intensity suffices.²³ Groups seeking to push microscale accuracy, on the other hand, have adopted iterative process control techniques.^3,30 Simply printing the same subject repeatedly at a series of exposure times and intensities and selecting the best or most accurate print makes clear sense given the quick build times and cheap fabrication of DLP-based building.

However, recent improvements in process control allow pixel-by-pixel intensity control for each build layer, which, in a recent series of microfluidics experiments at Brigham Young University, demonstrated printed microchannel widths down to 7 μm.³¹ Additionally, 2D and 3D models of the UV light field can be used to predict material properties in the build, which allows prediction of stress gradients and the resultant curvature and deformation upon release of the part from the substrate.³² This multiplication of process parameters and use cases suggest the need for more proactive, predictive modeling to supplant trial and error methods.

Of the works that have modeled the beam spread from a DMD pixel, the assumption of a Gaussian distribution is, to our knowledge, universal. In this work, we find the Gaussian distribution model does a poor job of predicting print features when the number of contiguous “on” pixels is small or exposure times are unusually long. Initial investigations of printed feature shape of columns of single “on” pixels showed a cross-section with distinctly sharper peaks and longer-tailed bases that might be expected from a standard three-parameter Gaussian. In this Gaussian model, the distribution will have position (mean), beam width at half power, and intensity at peak parameters, however, this does allow description of the shape of the beam profile. Elements such as beam kurtosis and skew require consideration of the higher-order measurable moments. This sharpness profile is also a measurement of the “tail-heaviness” of the beam relative to a mesokurtic distribution.³³

The source of this change in beam profile shape appears to be the optical path from the UV light source, in particular the fixed projection optics. DLP architectures will seek to flatten the project pattern from their light source through an integrator rod (Fig. 1). The light path directs to the digital micromirror device and the resin basin through the projection optics. As the DMD is small, for example 9.85 × 6.16 mm for a Texas Instruments DLP4500 DMD, the projection optics must then throw the pattern to a build area of two to three times the size. In this stage, the design of the projection lens, which is most likely to occur errors, for example offsets of a pixel from its intended position³⁴ and changes in the sharpness profile in the transmitted beam.^35,36

FIG. 1.

Overview of DLP optics in relation to build area and DMD. On the left the optical path to the build area, showing the projection of the DMD image to the build tray base. (Top right) The Z-axis resolution is primarily determined by the build layer step thickness of the build block, and by the attenuation of the UV light when printing over a void (e.g., Build Layer 3). (Bottom right) In the XY-axes, resolution is determined by the beam distribution of the DMD and projection system with each “on” pixel contributing a small amount of the total required energy for photopolymerization to take place. DLP, digital light processing; DMD, digital micromirror device; UV, ultraviolet.

This work deals with calibration and measurement of a DLP optics through a series of test prints. These methods are designed not to need recourse to direct measurement of the UV light field through charge-coupled device (CCD) profilers, but instead to infer properties such as the peak pixel intensity and beam half-width through direct measurements of the height and width of selected test structures.

The properties are calculated for a traditional Gaussian profile from each pixel, and compared with a Lorentzian function as a beam profile. The Lorentzian function was found to fit the sharpness profile of individual pixel-wide builds and to offer some explanation for overprints and layer structures, which occur at lower exposure times than would have been predicted with the Gaussian pixel model. The Lorentzian fit is then applied to polymerization models of positive feature prediction of 1- to 5-pixel structures, and to negative feature prediction of channels of 1- to 3-pixel width. The model predicts a much-reduced range of exposure times that will successfully allow a microchannel to be cleanly printed, and a strong dependence on the intensity profile in the surrounding structure due to the extended, Cauchy-like tails of the Lorentzian distribution.

Finally, we apply the Lorentzian profile model to a full 3D, layer-by-layer model of a challenging build and discuss the impact of the sharpness and tail heaviness of the beam profile on print resolutions and error prediction.

Materials and Methods

Resin formulation

All structures presented in this article were printed using poly(ethylene glycol) diacrylate (PEGDA, MW250). The photoinitiator was phenylbis(2,4,6-trimethylbonzoyl) phosphine oxide (Irgacure 819). Sudan I was used as an absorber in concentrations of 0.2% by weight/weight. This was held constant while the concentration of the photoinitiator varied from 0.2% to 1% (w/w). Preparations were sonicated for 30 min before use and stored in foiled wrapped containers to protect the resins from light. Test structures were created using a commercial 3D printer (Asiga Pico HD), with an advertised print resolution of 26 μm, although it should be noted that this figure actually represents the pixel pitch or the spacing between each pixel center at the resin surface. Slicing of computer aided design (CAD) models was performed by the manufacturer's software (Asiga Composer). Measurements of UV intensity and beam profile were made with a CCSD beam profiler and DataRay acquisition software. All printed parts were air dried and blotted due to the known impact of washing in IPA or other solvents on slender parts.

X-ray computer tomography measurements

X-ray computer tomography (CT) scans were performed using the Bruker Skyscan 1172, using an SHT 11 Megapixel camera and a Hamamatsu 80 kV (100 μA) source. The samples were held in a polystyrene mount and oriented vertically on a piece of dental wax. No filter was applied to the X-Ray source. The images generated were 1332 × 2000 pixels with a resolution of 4.98 μm per pixel. Reconstruction and measurement were performed by Bruker's CTAn software. The threshold for the attenuation signal was set by eye to cut speckle around the sample. The images were then further cleaned with a thresholding mask using Bruker's CTAn software. The images produced by the uCT are based on the level of attenuation through the sample, which is dependent on the thickness of the material and its absorption coefficient.

Print prediction

Full 3D model predictions of print geometry were made using software developed to estimate stress from the degree of conversion within the material and coded in MATLAB and Python. CAD files for 3D-printed parts were sliced using Autodesk's Netfabb. This generates a series of binary images corresponding to the state of each pixel (on/off) in each layer of the printed part. For each print layer, we calculate the irradiance pattern on the surface of the material from the pattern of “on” pixels. This is summed to the calculated dose on all preceding layers. Point clouds for the degree of polymerization throughout the model could then be generated (See Model Calibration). Two-dimensional models of individual slices of geometry and full 3D models were generated using iso2mesh.³⁷

Model calibration

Simulating and predicting a vat-based photopolymerization process requires integrated models of the photochemical reaction in the resin, the structured UV light field, and mechanical process parameters such as build platform movement and resin mixing strategy. We are primarily interested in the model of the UV light field in this work, however, validating the model in a 3D print requires us to establish a model for resin photopolymerization. Later we integrate this with a basic model of build platform motion to generate a full 3D model of the process.

Resin model

Theoretical approaches to photoinduced polymerization may model the reaction steps explicitly. This must at least include models of photoinitiation, chain propagation, and termination. This model has high complexity and require calculation or estimation of hidden- or difficult-to-measure parameters making it difficult to apply to mathematical modeling and print prediction. In this study, we model photopolymerization using a phenomenological approach following Vitale et al.³⁸ This approach relies on predicting resin solidification through a normalized degree of conversion parameter, $\varphi$, with a value of 0 indicating liquid resin and 1 indicating that the polymer chain propagation has been terminated. Within this range lies the gelation threshold, ${\varphi }_c$, which represents the liquid-to-solid transition and is accompanied by a rapid volumetric contraction of the material. The material properties continue to evolve with the polymer chains, typically increasing in stiffness and glass transition temperature as the reaction progresses.

The Vitale and Cabral model of photopolymerization describes the rate of change of the degree of conversion parameter, $\varphi$, in terms of the exposure time, i, light intensity I, and a reaction constant, K, which we must derive experimentally.

$$\frac{\partial \varphi \left(t\right)}{\partial t}=K\left[1-\varphi \left(t\right)\right]I\left(t\right)$$ (1)

Intensity attenuation along the light path obeys the Beer–Lambert law

$$\frac{\partial I\left(z\right)}{\partial z}=-\mu \left(z\right)I\left(z\right)$$ (2)

where μ is the extinction factor and z the light propagation distance. If we assume the extinction factor does not change significantly during the reaction, then the degree of conversion can be solved as

$$\varphi \left(z,t\right)=1-exp\left(-K{I}_{0}exp\left(-\mu z\right)t\right)$$ (3)

where I₀ = I (z = 0), the light intensity at the surface of the resin. Since in an unconstrained polymerization process the degree of conversion at the limits of the polymerization front will be ${\varphi }_c$ we can relate the, easily measurable, solidified thickness to the unknown extinction factor and reaction constant.

$$z_p=C_{d}ln\left[\frac{K{I}_{0}t}{ln\left(\frac{1}{1-{\varphi }_c}\right)}\right]$$ (4)

Here z_p is the measured solidified thickness and C_d is the reciprocal of the extinction factor μ referred to as the critical depth.

The generalized resin parameters K and C_d are measured by exposing a layer of resin to blanket illumination at a constant intensity. This is done in a single exposure without any build block or other constraints to ensure that the polymerization process will terminate at the gelation threshold. Sweeping the exposure time, the measured printed heights may be plotted against ln (I₀t) (Fig. 2), where a straight line fit of the data y = mx + c will yield the critical depth parameter as the gradient of the line (C_d = m) and the reaction constant K knowing the gelation point for PEGDA is ${\varphi }_c=0.22$.

FIG. 2.

Example resin model parameter estimation for PEGDA Mn250 with 0.2% wt/wt Irgacure and 0.2% wt/wt Sudan I. Print height was measured from exposure of the resin to UV light from Asiga pico HD printer with build block removed. Exposure area set by “.stl” models of a single-layer thickness and X-Y dimensions of 2 × 2 mm. The exposure time was controlled by the Asiga software with print height measured by a set of external calipers. (Top) Straight line fit to natural log of the dose (tI₀) gives the critical depth parameter as the gradient. (Bottom) Print height prediction graph for PEGDA resin with 0.2% wt/wt photoinitiator and 0.2% wt/wt Sudan I absorbent.

$$K=exp\left(\frac{-m}{c}\right)ln\frac{1}{1-{\varphi }_c}$$ (5)

The critical depth parameter is expected to be independent of the printer and light intensity parameters and is primarily controlled through the absorbent. For the purposes of this investigation, we prepared three resins with a constant critical depth parameter (constant 0.1% by weight of Sudan I) and varying levels of photoinitiator. The calculated critical depths and reaction constants are listed in Table 1.

Table 1.

Measured Critical Depth (Cd) and Reaction Coefficient (K) for Three Primary Resins Used in this Model

Resin	Critical depth (Cd)	Reaction coefficient (K)
PEGDA, 0.1% Irgacure, 0.1% Sudan I	113 μm	3.313
PEGDA, 0.2% Irgacure, 0.1% Sudan I	104 μm	10.62
PEGDA, 1% Irgacure, 0.1% Sudan I	118 μm	68.0

Light field model

The resin model assumes that the light intensity is constant in the XY-plane of illumination, an assumption that is accurate when a large area is being illuminated. The image used in the previous step is created by a digital micromirror device to control the pattern of irradiance on the surface of the resin. The digital mask might be considered an array of pixels, each with an overlapping distribution function of irradiance, which when summed will provide a stable flat field over the bulk of the resin. Smaller parts and narrow regions will have a lower maximum light intensity, being composed of fewer “on” pixels, and large variation in intensity over the resin surface. The distribution function for a single pixel is normally assumed to be a Gaussian distribution (considered in one dimension here).

$$I_{px}\left(x\right)=I_{peak}exp\left(-\frac{1}{2}{\left(\frac{d\left(x\right)}{\sigma }\right)}^2\right)$$ (6)

Each pixel has an intensity distribution based on the distance to the center of the pixel d (x) and the standard deviation of the function, $\sigma$, or half width half maximum of the beam. The intensity profile of any given mask can be calculated as the sum of the intensity distributions from all illuminated pixels.

In this study, for each pixel column (i) and row (j) the pixel center (X_i,_j, Y_i,j) is calculated, typically as a function of the pixel pitch. For the Asiga machine, we are using in this study, the pitch given as 26 μm. This presents us with two unknowns: the peak intensity for each pixel distribution (I_peak) and the standard deviation of the distribution, $\sigma$. It is possible to measure these directly using a CCD beam profiler, however, this requires equipment customized to the print and vat setup, which is expensive and time-consuming.

An alternative approach is to infer the peak intensity and standard deviation parameters from a printed calibration object. This second calibration step requires creating a series of single-layer, 2 × 2 mm grids with a crossbar thickness equivalent to 1, 2, 3, or 5 pixels. These pixel masks can be generated automatically by the slicing software by generating a CAD design with the crossbar thickness equivalent to the pixel pitch (Fig. 3a) and disabling X-Y correction and antialiasing features. The single-layer slice can then be inspected in standard graphics editing software to confirm the pixel mask dimensions. The measured heights and widths of these crossbars, along with the critical depth parameter measured in the previous calibration step, can be used to estimate the standard deviation of a single pixel spread. Since in an unconstrained print we know that the degree of conversion of the material will be ${\varphi }_c$ at the surface, which must also be the degree of conversion at the lateral extents of the exposed layer.

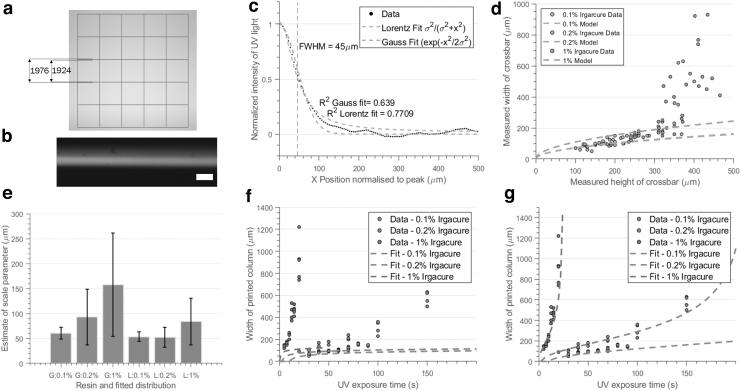
FIG. 3.

The method of determining the standard deviation of the pixel distribution uses a square array of single pixel filaments (a). Units in the figure are micrometers. The intensity distribution of these filaments can be measured with a CCD profiler (b) and the normalized intensity distribution curve fit to a distribution model. (c) The fit to the Gaussian and Lorentzian distributions and estimates a standard deviation of 45 μm. However, the Gaussian fit does not well predict the link between print width and print height expected from Equation 8 (d). The Lorentzian model's estimate of standard deviation (or half-width half-maximum) from measured print width is closer to the measured values (e) and predicts print width at higher exposure times much more accurately than the Gaussian model (f, g). CCD, charge-coupled device.

By setting $\varphi ={\varphi }_c$, and combining equations 4 and 6, we can derive an expression for the standard deviation of the beam profile, which depends only on the measured width of the part, w, the measured height, z_p, and the known critical depth C_d, and gelation point parameters.

$$\sigma =\sqrt{\frac{-w^2}{2ln\left(-\Gamma exp\left(-\frac{z_p}{C_d}\right)\right)}}$$ (8)

$$\Gamma =\frac{ln\left(1-{\varphi }_c\right)}{ln\left(\frac{1}{1-{\varphi }_c}\right)}$$ (9)

or,

$$\sigma =\sqrt{-\frac{w^2}{2ln\left(-ln\left(1-{\varphi }_c\right)K{I}_{max}t\right)}}$$ (10)

in terms of the reaction constant K and the exposure time t.

Figure 3c shows the measured print height against measured print width for resins with 0.1% wt/wt Irgacure, 0.2% wt/wt Irgacure, and 1% wt/wt Irgacure, as well as the predicted relationship between print width and height from Equation 8. The match is reasonable for print heights under 200 μm but quickly diverges after this point. Direct measurement of the beam profile through a CCD profiler and DataRay acquisition software (Fig. 3b) suggested the cause of this may be that the Gaussian model of pixel spreading did not capture the long tails of the measured intensity profile.

As, to the best of our knowledge, the beam distribution for 3D printing has only been modeled as a two-parameter Gaussian we attempted to curve fit the data using standard heavy-tail distributions. Figure 3c shows curve fit models of a Lorentzian distribution and a Gaussian distribution with an estimated scale parameter (standard deviation or half-width half-maximum) of 45 μm. Both curves show a similar coefficient of determination R², however, the distinction is small around the beam neck while Cauchy-like long tails of the distribution are more clearly visible and better matched to the Lorentzian distribution.

If we consider the pixel distribution of Equation 6, this time with a Lorentzian distribution

$$I_{px}=I_{max}\left[\frac{{\sigma }^2}{d{\left(x\right)}^2+{\sigma }^2}\right]$$ (11)

the relationship between the scale parameter $\sigma$ and the measured height and width would become

$$\sigma =\sqrt{\frac{-w^2\Gamma e\; xp\left(-\frac{z_p}{C_d}\right)}{1+\Gamma exp\left(-\frac{z_p}{C_d}\right)}}$$ (12)

or in terms of exposure time and reaction constant

$$\sigma =\sqrt{\frac{\frac{-w^2}{k{I}_{max}t}ln\left(\frac{1}{1-{\varphi }_c}\right)}{1+\frac{1}{k{I}_{max}t}ln\left(\frac{1}{1-{\varphi }_c}\right)}}$$ (13)

Figure 3e shows the estimated scale parameter $\sigma$ from the Gaussian distribution and Lorentzian distribution for the three resins with increasing weights of photoinitiator. From the direct measurement we expect a scale parameter of 45 μm, however, estimates based on the Gaussian distribution in Equation 8 show values ranging from 60 to 160 μm with increasing errors. The Lorentzian distribution estimation using Equation 12 shows a better estimate for the first two datasets of 53.4 and 52.2 μm, but produces a high reading of 83 μm for the case where 1% wt/wt photoinitiator is used.

In the case of very long exposure times, a thin film of printed material appears across the entire build area, which cannot be captured through the tailedness of the distribution and is likely a result of diffusion through the membrane. Our dataset pushes to the extreme ends of likely exposure energies, so a potential solution is simply to truncate the data before such print errors occur. Restricting the dataset to the first 25 data points (before the film has developed) allows a far more accurate estimate of 48.1, 41.4, and 47.0 μm for the Lorentz distribution. The same strategy for the Gaussian fit produced better but still increasingly inaccurate results of 47.2, 52.9, and 69.1 μm.

The impact of this on estimations of print dimensions is shown in Figure 3f and 3g, which give predictions of the print widths against exposure time for the grid structure. The rearranged Equations 10 and 13 are used to make the print width estimates in combination with a low constant irradiance C equivalent to 0.1% of the flat field irradiance to account for the presence of diffusion at longer exposure times. While the Lorentzian distribution fits the data at very high exposure times, it should be noted that the exposure times considered here are far larger than would be expected in a standard printing scenario. At the lower end of exposure times, the Gaussian model also provides a reasonable estimate of print width.

Mechanical model

In a bottom-up process, the build block is moved a fixed distance away from the Teflon film at the base of the build tray at every print stage (Fig. 1, top right); this distance represents the build layer thickness. At each successive movement of the build tray the resin is remixed, typically by tilting, scraping, or other physical agitation, and the next UV pattern is exposed onto the liquid resin. A full 3D model must at the minimum account for the impact of successive exposures to determine the total dose delivered within each layer. In this study, we use the approach described by Gong et al^8,15 to account for successive exposures in the z-dimension (through the thickness of the build layer) along with the voxel-based method we previously used to predict residual strain in DLP process.³² If we let z = 0 be the position of the surface of the build block, then the exposure surface of the current build layer is at position z = nz_th, where z_th is the build layer thickness and n the current layer number. Augmenting the Beer–Lambert equation to account from exposure through the Z-axis for each successive exposure gives:

$$I\left(z,n\right)=I_{0}exp\left(\frac{\left[\left(n+1\right)z_{th}-z\right]}{C_d}\right)$$ (14)

Now we use the 2D Lorentz equation to give the intensity distribution from the sum of pixels, again summing over the array of pixels (i,j) and centering each distribution on the x,y position at the center of the current pixel (X_i, Y_j).

The combined Equations 14 and 15 are repeated for every build layer, being careful to note that only layers preceding the current layer should have any UV dose. These layers are also summed to give a complete 3D matrix of UV light intensity throughout the build area.

Basic MATLAB scripts based on Equation 16 allow us to take a design model file, slice the model into a series of 2D bitmap images and build a 3D degree of conversion model to predict print solidification. In this model we also assume perfect mixing of the material between layers, resetting the degree of conversion for any material not fully cured during a single exposure to zero.

Results and Applications

Given that the exposure times over which the Lorentzian distribution model shows significant improvement over the typical Gaussian-based system is beyond the exposure times used in a standard print, this model refinement is only likely to be applicable to printing at the microscale. In this section, we compare the predictive accuracy of the two models to three edge cases for a DLP-based print in a single layer: a positive feature less than 10 pixels wide, a negative feature less than 5 pixels wide, and the combination of small pixel number positive and negative features (e.g., a thin-walled tube structure). All the test structures used to verify print prediction are made using PEGDA with 0.2% wt/wt Sudan I as with the model calibration and with 0.2% wt/wt photoinitiator.

Positive feature prediction

When a positive feature is 1- or 2-pixel widths across, the intensity of the UV irradiance is significantly reduced, resulting in a large range of exposure times possible. For example, using the Lorentzian model for distribution, a single-pixel-wide feature using a resin with a critical depth of 112 μm would require a minimum exposure time of 12.15 s to successfully print a 10-μm-thick build layer. The long exposure time occurs due to the low peak intensity of a single pixel, less than 20% of the flat field irradiance (Fig. 4c). At 3 pixels wide, this exposure time would be reduced to 5 s and the feature size would be 41 μm. These calculations suggest that reducing the print area in terms of number of pixels is likely to result in diminishing returns. Smaller number of contiguous pixels will require longer exposure times, exacerbating the impact of the long tails of the distribution (Table 2).

FIG. 4.

The measured height and width of a printed feature is plotted against exposure time for square array structures of 1, 3, and 5 pixels (a, b). In modeling the peak irradiance for a single pixel filament is less than a third of that of a 5-pixel wide filament, and less than 20% of the flat field irradiance (c). The model shape of a crossbar for 1-, 3-, and 5-pixel width (d) is presented for comparison with X-Ray images of 1-pixel- (e), 3-pixel- (f), and 5-pixel (g)-wide crossbars. Scale bars 100 μm.

Table 2.

Comparison Between Designed Part Size on the Image Mask Based on 26 μm Pixel Pitch and Printed Width Using Lorentzian Model

No. pixels	Width on digital mask (μm)	10 μm build layer height		50 μm build layer height
		Exposure time (s)	Model print width (μm)	Exposure time (s)	Model print width (μm)
1	26	12.14	53	17.04	121
3	78	4.25	57	6.06	131
5	130	2.82	73	4.03	163
11	286	1.8	145	2.57	279
21	546	1.47	319	2.09	515

Comparison between designed part size on the image mask based on 26 μm pixel pitch and printed width using Lorentzian model. The part width shows little sensitivity to the designed width on the digital mask at low pixel counts.

The relationship between the number of illuminated pixels and the output width is shown using a modification of the calibration grid used in the model setup. Now the grid comprises struts of 1-, 3-, and 5-pixels wide, which are exposed for up to 200 s. Figure 4b and c show the measured printed heights and widths along with the Lorentzian model. The timescales chosen are in the upper end of what would be necessary for a typical build, giving print heights of between 100 and 200 μm without the constraint of a build block of a previous layer. The impact of the long tails of the model is again clearly visible at longer exposure times and the higher irradiance of larger blocks of “on” pixels, however, the relative insensitivity of print width to the mask is particularly visible at low exposure times and pixel numbers. A change from a 1-pixel to a 3-pixel-wide strut, three times the illuminated area, results in an increase of print width from 200 to 260 μm at the longest exposure times measured. At shorter exposure times, the change in print thickness from 1- to 3-pixels is sufficiently small to be within the variance of both datasets.

In practice, this means that although it is possible in theory to print at below the pixel pitch resolution with appropriate process control, reducing the width of the pixel mask produces diminishing returns in the resolution, which dramatically increases print time to a point where it is likely incompatible with larger-scale features.

Negative feature prediction

The impact of the Lorentzian distribution on printing channels and voids within the material is perhaps of more practical interest, as the accurate fabrication of such negative features is crucial to applying 3D printing strategies to microfluidics applications. Perhaps the most surprising result from this investigation is that the successful printing of a microscale channel will depend on the width of the channel walls. The summative effect of the long-tails of each pixel distribution means that it is much more difficult to print single small channels within a bulk material, as would be necessary for standard microfluidics applications. The effect is illustrated in Figure 5, showing a 3-pixel-wide channel within a cup structure of varying wall widths. The channel with a 10-pixel-wide (∼260 μm wide on the pixel mask) wall prints successfully with a channel width of 200 μm. With a 15-pixel-wide surrounding wall, the channel width decreases to 40 μm and with a 20-pixel-wide surrounding wall, the channel is not printed. The channel width also naturally varies with the exposure time; however, the impact of the Lorentzian model is to cause the channel to fail to print much sooner than the Gaussian model.

FIG. 5.

Model and data on the impact of surrounding pixel intensity on microchannel formation. (a) 3-pixel channels (76 μm on the digital mask) are surrounded by walls on 10, 15, and 20 pixels. (b) A channel with designed wall widths of 10-pixels printed at increasing exposure times, compared with the printed widths from both Gaussian distribution model and Lorentzian. (c) The Lorentzian distribution model prediction of a 3-pixel channel with 10-pixel-wide walls (green), 15-pixel-wide walls (red) and 20-pixel-wide walls (blue) compared with X-ray CT scans of same channel with 10-pixel (d), 15-pixel (e), and 20-pixel walls (f). Scale bars 100 μm. CT, computer tomography.

Figure 5c shows the measured channel widths for a 3-pixel-wide channel printed with 10-pixel surrounds over a range of 1.8 to 2.6 s. The data range chosen represents the maximum range over which this resin could successfully print a channel in the top 10 layers of a material, with exposure times below this range failing to polymerize the wall regions and beyond this range printing over the channel region.

Recent work has used grayscale pixels around microchannels to reduce irradiance near the negative feature.³¹ Single-pixel channels, which we found not to be possible to print with our previous experimental setup and theoretically using the Lorentzian model, are possible with the reduction in intensity of the surrounding pixels. In the work cited above, a single pixel channel with 2-pixel grayscale surround was generated, creating a printed channel narrower than the pixel-pitch of their custom printer. Figure 6a and b show the Lorentzian model being applied to this gray-scaling approach, surrounding the single-pixel channel with 2 pixels at half-power, at quarter-power, and 3-pixels at one third power, showing that in theory we can also control the printed gap by grayscaling the surrounding pixels. To verify, we printed channels with 1-pixel gap width surrounded by 2-pixels on each side with a grayscale intensity from 0% to 30% of maximum—beyond which the channel was found not to print (Fig. 7c).

FIG. 6.

(a) The Lorentzian model was applied to channels formed of 1-pixel gaps with 2- to 3-pixels of fractional intensity. (b) The predicted print widths for 2 columns of surrounding pixels with increasing grayscale intensity from 0 to 1.0 in intervals of 0.1 and (c) the predicted channel print for 3-pixels at 1/3 power (green), 2-pixel columns at 1/4 power (red), and 2 pixels at 1/2 power (blue) showing a failure to print. The resultant channel cross-sections are shown in (d–f). Scale bar 20 μm.

FIG. 7.

Simulation of first two build layers of an angled microchannel. The color bar scale is the degree of conversion of the material. In the top row a single exposure brings the material just to gelation point, while the second exposure increases the degree of conversion of selected parts of the first layer. Scenario (a) shows the channel overprinted in the first layer, print failure is due to overexposure. Scenario (b) shows a channel successfully printed in one layer but second layer overprints, failure is due to gradient of channel or poor match of extinction scale of light to build layer thickness. Scenario (c) shows a successful microchannel print.

The channels retained the same parameters as the 3-pixel-wide models, having surrounding walls of 10-pixels, including the gray pixels and were all exposed at 2.5 s. The measured and predicted channel widths are given in Table 3 and shown in Figure 7D–F.

Table 3.

Predicted and Measured Channel Widths for 2-Pixel Grayscale Surround of 1-Pixel Channel

Grayscale ratio	Predicted channel width (μm)	Measured channel width (μm)
0	61	64
0.1	47	52
0.2	31	40
0.3	0	0

Wall widths were 10 pixels at an exposure time of 2.5 s.

Full layer-by-layer model

The most challenging structures to fabricate in layer-by-layer 3D printing require substantially different process controls. Thin walls or struts require long exposure times or high intensities to compensate for the lack of cumulative pixel intensity, however, this exacerbates the impact of the distribution tailedness giving these relatively low-intensity regions sufficient energy to reach the gelation point. Narrow gap voids require low exposure times and consideration of the intensity pattern in the surrounding print. Meanwhile suspended regions, a layer printed onto an empty space or channel, require a precisely calibrated exposure time to avoid overprinting into an intended void. In this last section, we apply the full layer-by-layer model incorporating the Lorentzian pixel distribution from equation 16. This approach follows the multilayer model developed by Gong et al and expands it to include intensity distribution from the pixel mask to create a voxel-based model of solidification. A demonstration of this voxel-based model is applied to a challenging build case in Figure 7: an angled microchannel, which combined narrow print gaps with overprinted regions.

This approach allows layer-by-layer troubleshooting of microchannels, distinguishing print flaw caused by overprinting in the plane of the build (scenario a) with those caused by overprinting from subsequent layers (scenario b).

The utility of calculation of these layer-by-layer effects using the voxel-based model limited by the memory requirements of such a process: a useful spatial resolution of 1 μm³ applied to a small-scale model of 20 × 20 × 10 mm required more than 15 GB. This brute force approach to modeling would require some adaptive refinement of mesh sizing before it could be applied to software control of a 3D printer.

Conclusion

We present a method of printer calibration and process control model tailored to microscale additive manufacture using a digital light projector maskless process. We focus on the prediction of print resolution in the plane of printing, and find a long-tailed Lorentzian distribution is a better fit and a better predictor of final print resolution than the more commonly used Gaussian fit. Using this model, we are able to evaluate the impact of the surrounding building on positive and negative feature formation and control the printed width of a microchannel to subpixel pitch resolution by a combination of exposure time control and grayscaling of adjacent pixels. The evaluation method and calibration steps will allow the user of a given DLP 3D printed to determine the resolution limit and simulate microscale designs at the edge of what is possible with their current technology.

Author Disclosure Statement

No competing financial interests exist.

Funding Information

This work was funded by a Leverhulme Trust Early Career Fellowship ECS-2019-185.