Highlights
-
•
Development of a powerful Deep Learning model (DenseNet) for automatically classifying spinal osteosarcoma and giant cell tumors in medical images.
-
•
Integration of a self-attention mechanism and multi-scale feature map extraction to enhance feature extraction capabilities.
-
•
Use of Grad-CAM for improved visualization of tumor regions during predictions.
-
•
Significant support for orthopedic physicians in accurate diagnostic classification, aiding in treatment and care plan development.
-
•
Acknowledges the need for a larger dataset to improve model performance and its applicability in diverse clinical settings.
Keywords: DenseNet, Self-attention mechanism, Spinal osteosarcoma, Giant cell tumors, Automatic classification and diagnosis
Abstract
Objective
This study aims to explore an optimized deep-learning model for automatically classifying spinal osteosarcoma and giant cell tumors. In particular, it aims to provide a reliable method for distinguishing between these challenging diagnoses in medical imaging.
Methods
This research employs an optimized DenseNet model with a self-attention mechanism to enhance feature extraction capabilities and reduce misclassification in differentiating spinal osteosarcoma and giant cell tumors. The model utilizes multi-scale feature map extraction for improved classification accuracy. The paper delves into the practical use of Gradient-weighted Class Activation Mapping (Grad-CAM) for enhancing medical image classification, specifically focusing on its application in diagnosing spinal osteosarcoma and giant cell tumors. The results demonstrate that the implementation of Grad-CAM visualization techniques has improved the performance of the deep learning model, resulting in an overall accuracy of 85.61%. Visualizations of images for these medical conditions using Grad-CAM, with corresponding class activation maps that indicate the tumor regions where the model focuses during predictions.
Results
The model achieves an overall accuracy of 80% or higher, with sensitivity exceeding 80% and specificity surpassing 80%. The average area under the curve AUC for spinal osteosarcoma and giant cell tumors is 0.814 and 0.882, respectively. The model significantly supports orthopedics physicians in developing treatment and care plans.
Conclusion
The DenseNet-based automatic classification model accurately distinguishes spinal osteosarcoma from giant cell tumors. This study contributes to medical image analysis, providing a valuable tool for clinicians in accurate diagnostic classification. Future efforts will focus on expanding the dataset and refining the algorithm to enhance the model's applicability in diverse clinical settings.
1. Introduction
Both spinal tumors and giant cell tumors can occur in the vertebral column, presenting similar clinical symptoms and imaging features such as lytic bone destruction, heterogeneous signal densities within the lesions, and the presence of cystic areas. If there are typical imaging characteristics, differentiation between the two can be relatively straightforward based on factors like age, lesion location, and characteristic imaging findings [1]. However, when the presentation is atypical, especially in the cervical and sacral vertebrae, particularly in the skull base and sacrum, these cases often lack the typical imaging features, making the differential diagnosis more challenging [2]. Research has shown a high misdiagnosis rate for spinal giant cell tumors, with common misdiagnoses as spinal tumors. In this study, an optimized DenseNet model is employed to classify spinal osteosarcoma and giant cell tumor images, with the primary goal of assessing its potential value in differentiating between these two conditions. The goal is to provide a reliable method for distinguishing spinal and giant cell tumors that are difficult to differentiate with conventional imaging techniques.
In recent years, radiology has witnessed a profound transformation driven by deep neural networks' emergence and rapid development. These networks have revolutionized the field by significantly enhancing feature extraction capabilities from medical images. Deep neural networks excel in detecting and interpreting intricate patterns and subtle details within images, making them invaluable tools for accurate diagnosis and treatment planning. The importance of feature extraction in medical image analysis cannot be overstated, as it forms the foundation for identifying abnormalities, diseases, and other medical conditions. The use of deep neural networks in radiology has ushered in a new era of precision and efficiency, enabling radiologists to provide more accurate assessments and better patient care. Convolutional Neural Networks (CNN) have garnered significant attention in histopathology image analysis due to their exceptional performance and stability in large-scale image processing tasks. CNNs are specifically designed for image analysis and have a natural ability to learn hierarchical features from images. In histopathology, where examining cellular structures and tissue abnormalities is crucial, CNNs shine by automatically extracting relevant features and patterns. Their adaptability to various scales and complexities of histopathological images and robust performance make them a preferred choice for accurate image analysis. Their application in histopathology has contributed to improved disease diagnosis, prognosis, and treatment planning. Song et al. [3] used the pre-trained VGG-VD model on ImageNet to extract local features from images and represented these features using Fisher Vector (FV) encoding. Murthy et al. [4] injected pre-extracted VGG features into the intermediate layers of a semi-supervised CNN to focus the CNN on the central region of images. Li et al. [5] used an improved CNN to segment tumors, replacing conventional radiological methods for calculating image feature segmentation, resulting in high-quality MRI features encoded as FV vectors. Lao et al. [6] first segmented medical images and then, using transfer learning, employed pre-trained CNNs to extract geometric, intensity, texture, and other deep features from the images.
The “vanishing gradients” problem is a critical challenge that emerges as deep neural networks increase in depth during training. This problem occurs when the gradients used for training deep networks diminish significantly as they propagate backward through the network's layers. As networks deepen, the gradients that signal how much each neuron's weight should be adjusted in response to training data tend to become very small. This leads to slow or stalled training, making it challenging to optimize deep networks effectively. The “vanishing gradients” issue can hinder the training of deep neural networks and affect their performance. Techniques like skip connections, batch normalization, and proper weight initialization have been introduced to address this challenge, allowing deep networks to be trained more efficiently and effectively. ResNet, a groundbreaking architecture, effectively mitigates this issue by introducing skip connections. These connections enable signals to bypass specific layers, ensuring that gradients do not vanish during training. This innovation has been instrumental in enabling the training of intense networks, which has further improved their performance. Nevertheless, ResNet has many parameters, as each layer has its weights, and research indicates that the contribution of many layers is minimal [7], [8].
To enhance feature extraction capabilities and reduce the likelihood of misclassifying tumors, the model designed in this paper is based on DenseNet, as proposed by Huang et al. [9]. DenseNet connects all layers directly, with each layer receiving additional input from the preceding layers, allowing direct access to gradients from the loss function and the original input signal, thereby mitigating gradient vanishing and strengthening feature propagation. Furthermore, DenseNet's approach maintains constant feature maps in its layers. Notably, while narrow DenseNet layers only contribute a fraction of the network's overall knowledge, most feature maps still need to be made public, thus promoting feature reusability and minimizing network parameters.
2. Material and methods
2.1. DenseNet
A Dense Convolutional Network is composed of multiple dense blocks, and each dense block contains multiple convolutional layers. The input to each convolutional layer is formed by concatenating the outputs of all previous convolutional layers with the original input, as follows:
| (1) |
Each dense block has a structure, as shown in Fig. 1. Each layer is composed of BN-ReLU-Conv (1 × 1) and BN-ReLU-Conv (3 × 3), where a combination of batch normalization [10] and rectified linear units [11] precedes each convolutional layer. The 1 × 1 convolutional layer is a bottleneck layer to reduce the number of input feature maps, improving computational efficiency. Within the architecture of deep neural networks, the 3 × 3 convolutional layer plays a vital role in maintaining the size of feature maps within a dense block. It employs one-pixel zero-padding to ensure that the feature map size remains constant as information passes through the network's layers.
Fig. 1.
Dense block structure. This structure comprises every layer consisting of BN-ReLU-Conv (1 × 1) and BN-ReLU-Conv (3 × 3), with batch normalization and rectified linear units applied before each convolutional layer.
Additionally, each dense block consistently produces a fixed number of k feature maps. This design not only aids in preserving critical spatial information but also provides a mechanism for controlling the complexity of the network, making it more manageable and interpretable. The DenseNet's dense connections are similar to ResNet's residual connections, but with a difference: the input to the current layer is not simply added to the input of the previous layer; instead, feature maps are concatenated to facilitate the flow of information between layers and promote feature reuse.
2.2. Multi-Scale feature map extraction
The concept of extracting multi-scale feature maps in this paper is inspired by the idea of scale space, initially proposed by Iijima [10] in 1962. The approach described involves designing multiple continuously varying scale parameters to generate a sequence of information representations at different scales. This process is fundamental in image analysis, where images can have varying levels of detail and resolution. By adapting to these changes in scale, the model can effectively capture features and details at different levels of granularity. Using continuously varying scale parameters ensures that the model is not limited to specific fixed scales but can adapt to a wide range of image resolutions. Subsequently, the primary outlines extracted from this sequence serve as a feature vector for various image-processing tasks, such as feature extraction and edge detection. The primary outlines represent a condensed yet informative summary of the image's essential features, regardless of its resolution. This feature vector effectively encapsulates the salient information necessary for these tasks, enabling the model to consistently perform tasks like edge detection or feature extraction across images with varying resolutions. This approach is precious in scenarios where images can have different levels of detail or are acquired using various devices with varying resolutions. The model can maintain its effectiveness in image analysis tasks by adapting to the scale variations and using the primary outlines as a feature vector. It is a versatile and robust technique for real-world computer vision and image processing applications.
In literature, a multi-scale convolutional network (MCNN) was introduced [11], which alternately stacked layers to capture nodule heterogeneity and designed to extract discriminative features. It used multi-scale nodule patches to quantify nodule features thoroughly. In another study [12], the Double-Tree Complex Wavelet Transform (DTCWT) was employed to extract information at different spatial scales from structural MRI data, enabling the differentiation of whether cases had multiple sclerosis based on multi-scale information. In neuroimaging for the diagnosis of neurological diseases, multi-scale feature extraction has gained substantial traction in recent research. Researchers have found that leveraging features at various scales within the brain's neural network can lead to more comprehensive and accurate disease diagnosis. This approach has been adopted widely because it allows for detecting subtle and complex patterns across different spatial scales in neuroimaging data. In SMSDNet, multi-scale feature extraction is applied. This paper employs down-sampling by adding average pooling layers between the four dense blocks to transform the scale of feature maps. The feature maps output by the first two dense blocks in the network have a larger size and a smaller receptive field, containing coarse-grained image information. After multiple pooling operations, the feature maps produced by the latter two dense blocks contain rich, detailed information. The paper under discussion presents a novel approach to feature fusion, specifically for deep learning applications. To achieve this, it performs cross-layer fusion of feature maps. This technique involves applying convolution operations to feature maps with larger scales in the upper layers. The purpose is to adjust their size to match the scale of the feature maps in the lower layers. Subsequently, these adjusted feature maps are added together. This approach improves the network's ability to capture multi-scale information, enhancing its performance in image classification and disease diagnosis tasks. The utilization of cross-layer feature fusion has demonstrated significant improvements in the effectiveness of deep learning models in handling complex medical data. Combining feature maps at different scales effectively enhances feature extraction and classification accuracy.
In SMSDNet, multi-scale feature extraction is implemented. The paper employs down-sampling as a critical technique to effectively manage the scale of feature maps. It incorporates average pooling layers between the four dense blocks. The role of these average pooling layers is to reduce the spatial dimensions of the feature maps. This down-sampling operation serves several purposes. First, it helps control the computational complexity of the network by reducing the number of parameters and computations in subsequent layers. Second, it enhances the network's ability to capture higher-level abstract features by aggregating information from more extensive regions of the input data. Third, it allows the network to recognize and focus on essential features while discarding less relevant or redundant information. This strategic feature map scaling through down-sampling is crucial for optimizing deep learning models for image analysis and classification tasks. The feature maps produced by the first two dense blocks in the network have a larger size and a smaller receptive field, containing coarse-grained image information. On the other hand, the feature maps generated by the latter two dense blocks contain rich, detailed information after undergoing multiple pooling operations.
The paper introduces a novel technique of cross-layer fusion of feature maps, which is instrumental in enhancing feature extraction and improving classification accuracy. This process involves applying convolution operations to feature maps with larger scales located in the upper layers of the network. These operations adjust the feature maps' size to match the feature maps' scale in the lower layers. Once the feature maps are suitably aligned in scale, they are added together. This technique allows the network to effectively capture information across different scales and resolutions, promoting the integration of fine-grained details with high-level context. The fusion of feature maps from various layers enhances the model's ability to recognize intricate patterns and make more accurate classifications by combining information from different levels of the network, providing a multi-scale view of the input data. This multi-scale approach enables the model to capture intricate patterns and details at various levels of abstraction, improving its performance in tasks that require recognizing complex patterns and making more accurate classifications. This cross-layer feature fusion is especially advantageous in tasks that require the extraction of multi-scale information, such as image classification and medical diagnosis.
2.3. Self-attention
The self-attention mechanism has been widely employed in RNN and long short-term memory (LSTM) models to handle decision tasks with sequential or causal relationships [13], [14], [15]. Building on this foundation, studies [16] and [17] introduced attention mechanisms into the transformer framework (encoder-decoder) to learn text representations by considering the relationships between the current word and its context. Transformers, in comparison to RNNs, offer distinct advantages in capturing long-term dependencies. The primary advantage of transformers over RNNs in handling long-term dependencies is their ability to consider and weigh different parts of the input sequence when making predictions. Unlike RNNs, which process data sequentially and may struggle with capturing long-range dependencies, transformers employ self-attention mechanisms that simultaneously analyze and assign relevance to various segments of the input sequence. This parallel processing capability enhances their efficiency and makes them more effective in various natural language processing and sequence-to-sequence tasks. Unlike RNNs, which sequentially process data and may struggle with long-range dependencies, transformers are highly parallelizable and can efficiently capture dependencies between distant tokens in the input sequence. This parallel processing capability makes them more effective in various natural language processing and sequence-to-sequence tasks.
Additionally, top-down attention mechanisms are crucial in Deep Boltzmann Machines (DBM) and image classification. Top-down attention mechanisms are crucial in Deep Boltzmann Machines and image classification. Deep Boltzmann Machines integrates these mechanisms into the training phase to guide the reconstruction process. By focusing on the high-level features and gradually refining the generated samples, Deep Boltzmann Machines can better capture the underlying structure of the data and learn more informative representations. Similarly, in image classification tasks, top-down attention mechanisms are widely used to direct the network's processing towards the most relevant parts of an image. This selective attention allows deep learning models to enhance their performance by prioritizing important features and disregarding noise or distractions, ultimately leading to more accurate and efficient image classification. This selective attention allows deep learning models to enhance their performance by prioritizing important features and disregarding noise or distractions, ultimately leading to more accurate and efficient image classification.
Similar to the approach in this paper, Wang et al. [18] designed a soft attention structure that incorporates both bottom-up and top-down feedforward structures as part of the attention module and adds soft weights to the features. Yuan et al. [19] proposed a self-attention deep learning framework called HybridAtt, which combines channel-aware perception attention (wise attention) and time attention. The channel-aware perception attention layer is used to infer the importance of Polysomnography (PSG) channels, while the time attention layer captures dynamic correlations between different timestamps.
In order to accommodate the nature of DenseNet's dense connections, SMSDNet has some differences in its self-attention mechanism:
(1) SMSDNet introduces a distinct approach to the self-attention mechanism compared to traditional DenseNet models. In SMSDNet, each dense block independently incorporates the self-attention mechanism to enhance the feature extraction process within the block itself. This self-attention mechanism enables the network to focus on relevant features and relationships between different parts of the input data, promoting more efficient and context-aware feature extraction. This is particularly beneficial in dense blocks, as it helps capture long-range dependencies and complex patterns within the feature maps. SMSDNet does not introduce a temporal attention mechanism, as it operates sequentially within each block, without temporal correlations between blocks. This design decision ensures efficiency and avoids introducing unnecessary complexity. Self-attention mechanisms allow the network to focus on relevant features and relationships between different parts of the input data, promoting more efficient and context-aware feature extraction. This is particularly beneficial in dense blocks, as it helps capture long-range dependencies and complex patterns within the feature maps. However, a temporal attention mechanism, which would capture dependencies between dense blocks across time, is not introduced because DenseNet's feature extraction operates sequentially within each block. Each block is designed to process and refine the features independently, and there are no temporal correlations between the blocks. Therefore, introducing a temporal attention mechanism would be unnecessary and could introduce complexity without significant benefits.
(2) For each layer, pixel matrices and index matrices are computed, and contribution weights are assigned to each output through convolution, matrix multiplication, and global pooling.
(3) previous research [20], [21] set weight thresholds to reduce computational complexity and model complexity, and layers with weights below the threshold were not used as inputs to later layers. However, in this work, every input is concatenated based on weight coefficients to maintain a fixed convolutional structure within the dense block. All previous feature maps are retained and combined with the current input to ensure no information is omitted. The weight coefficients determine the contribution of each feature map to the concatenated input, allowing the network to balance the importance of various features. This approach is crucial for preserving the network's ability to effectively capture multi-scale information and handle diverse features. Omitting layers or excluding inputs could lead to information loss and hinder the model's capacity to recognize intricate patterns.
2.4. A multi-scale DenseNet classification model with a self-attention mechanism
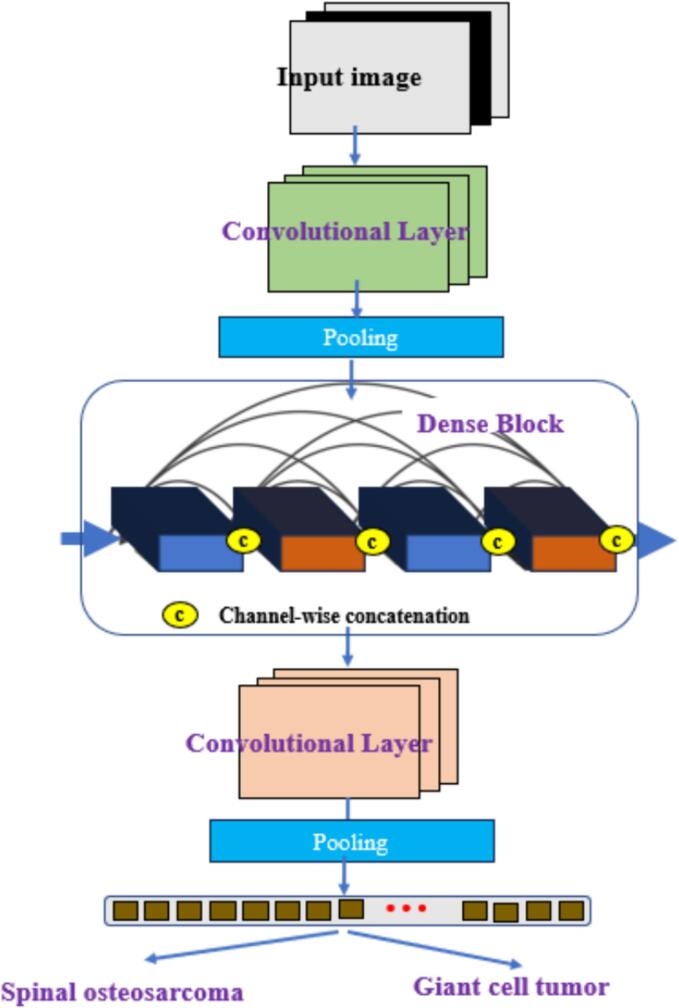
The SMSD-Net, a multi-scale DenseNet classification model, is enhanced with a self-attention mechanism. SMSD-Net effectively leverages multi-scale feature maps by incorporating a self-attention mechanism. This mechanism facilitates the capture of long-range dependencies and contextual information across the multi-scale feature maps. In the context of fusion images, it plays a critical role in enhancing the recovery of low-level features such as color and shape. By attending to relevant parts of the feature maps at different scales and considering their interactions, the self-attention mechanism assists the model in identifying and recovering fine-grained details and subtle characteristics in the fusion images. This comprehensive approach ensures that even low-level features are appropriately considered, ultimately improving classification task accuracy. In the context of fusion images, it plays a critical role in enhancing the recovery of low-level features such as color and shape. By attending to relevant parts of the feature maps at different scales and considering their interactions, the self-attention mechanism helps the model identify and recover fine-grained details and subtle characteristics in the fusion images. This, in turn, leads to improved accuracy in classification tasks by ensuring that even low-level features are appropriately considered. The SMSD-Net is employed for feature extraction and classification of spinal osteosarcoma and giant cell tumors of bone in medical images. The specific architecture of this model is illustrated in Fig. 2.
Fig. 2.
SMSDNet module architecture. A multi-scale DenseNet classification model with a self-attention mechanism is utilized for feature extraction and classification of spinal osteosarcoma and giant cell tumors in medical images.
The model is divided into four modules: (1) Color space conversion module. RGB color model is suitable for display and other luminous body displays; three primary colors of different brightness mix all color information. The HSV is a color model used to measure users' perceptions. channel represents color, represents depth, and represents light and shade. The HSV model plays a more significant role in image segmentation than the RGB model. In the RGB model, the image displayed through the three channels is brighter than the actual image, while in the HSV, the brightness can be represented by only one light and dark component, . In addition, HSV can directly represent the difference in tone and color depth between images. Convert RGB to HSV by the following formula:
| (2) |
When , .
| (3) |
| (4) |
| (5) |
(2) Dense convolutional network module with self-attention mechanism: Taking into account the nature of DenseNet's dense connections, where the input to each layer is the concatenation of all the previous layer's inputs, and with five dense layers designed as feature extractors within each dense block, a self-attention mechanism is applied to allocate weights to the various components of each layer's input, determining their respective contributions. This allows for the determination of the contribution ratio of each component.
(3) Multi-Scale Feature Map Information Fusion Module: The initial input image size is 256 256 3; after each dense network block, the image dimensions remain unchanged. Research in [22] and [23] suggests leveraging multi-scale information can enhance feature extraction. Following each dense network block, a transformation layer is introduced, consisting of a 1 1 Conv layer and a max-pooling layer. The max-pooling layer reduces the width and height of the dense block's output images to half their original size while keeping the number of channels the same. In SMSDNet, four dense network blocks correspond to four different feature maps with varying widths, heights, and 16 channels: , , , and . The feature maps and , output by the first two dense blocks, have larger dimensions and a wider receptive field containing coarse-grained image information. and , output by the latter two blocks after multiple max-pooling layers, have image dimensions of 32 32 and 16 16, and due to multiple feature extraction layers, they contain more detailed information. Given these facts, this paper first performs cross-layer fusion on the four output feature maps and then combines the results to obtain feature maps that include multi-scale information.
(4) Post-Processing Module: The fusion image undergoes four max-pooling layers, causing the loss of a significant amount of image detail. To recover low-level features of the fusion image, such as color and shape features, the post-processing module takes the multi-scale information feature maps and the feature map output by the final dense block as input. It uses upsampling and the same convolution operations to restore some of the lost details. Finally, the output feature map is passed through two neurons in a fully connected layer and a softmax classifier to obtain the probability of the image belonging to a tumor.
2.5. Dense block with self-attention mechanism
In SMSDNet, each dense block comprises five dense layers, and the inputs to each dense layer consist of the concatenation of all previous inputs. A self-attention mechanism is introduced to account for the relationships between these concatenated connections. This self-attention mechanism enables the network to dynamically weigh and prioritize different parts of the concatenated input feature maps. It considers the dependencies and interactions between the features at each layer, allowing the model to focus on the most relevant information. This, in turn, enhances the network's ability to capture multi-scale and contextually rich information, which is crucial for tasks like image classification, where features at different levels of abstraction are essential for accurate predictions. The core of this mechanism is to allocate weights to each output of the previous layer before concatenation. The dense block with the self-attention mechanism is depicted in Fig. 3.
Fig. 3.
Self-attention dense block. This mechanism's heart is the distribution of weights to each output from the preceding layer before concatenation.
The self-attention mechanism is divided into the following three steps:
(1) For each input corresponding to a feature map () with a size , two matrices are calculated for each layer: the fundamental matrix and the query matrix . Initially, . When calculating the input for the -dense layer, the query matrix of the layer is subjected to matrix multiplication with the vital matrix of all previous layers (including itself), resulting in a weight matrix .
(2) Since the size of each weight matrix is , a global pooling layer is applied to Kl for further refinement of the weight coefficients. Each shares a pooling matrix , which computes the weighted sum of each pixel in . After the global pooling operation, each layer obtains a numerical representation reflecting the weight. Subsequently, softmax is used to constrain these values within the range [0, 1], resulting in weight coefficients .
(3) Research in [24] and [25], as well as the current study, involves calculating weight proportions and setting weight thresholds. When the weight is below this threshold, it is not considered part of the input to reduce the number of parameters. However, the methods mentioned above have drawbacks. Each layer's input comprises partial outputs from the previous layer, not all outputs, making the model non-fixed. As a result, the number of convolutional kernel channels used in each layer's dense convolution can vary significantly. Additionally, the features the lower weight layers contribute will be minimal even after weight allocation. Hence, the lower weight outputs from previous layers are not removed. The formula for calculating the input to the dense layer is as follows:
| (6) |
Here, the original input is considered as the 0-th layer.
2.6. General information
A retrospective study was conducted at Anxi County Traditional Chinese Medicine Hospital in Quanzhou City, Fujian Province. The study included 300 patients diagnosed with spinal osteosarcoma and giant cell tumors between January 2019 and December 2020. Among them were 252 male and 48 female patients, with ages ranging from 41 to 90 years and an average age of 61 ± 19 years. After excluding 51 patients with poor CT image quality, 249 patients were included in the study.
The patients were diagnosed and classified by a senior attending physician with extensive experience based on the patient's clinical information. The TCM classifications for the patients were as follows: 168 cases with spinal osteosarcoma and 81 cases with giant cell tumors.
Out of the 249 patients, they were randomly divided into training and testing groups in a 7:3 ratio.
2.7. Instruments
A 64-slice Philips CT scanner was used for helical volume scanning. The scan parameters were as follows: 120 kV, automatic mA, 1 mm slice thickness, 1.0 pitch, collimation width of 64 × 0.625 mm, and a 1 mm slice interval. Patients were positioned supine with both arms raised above their heads. The scanning range extended from the thoracic inlet to the diaphragmatic surface at the lower border of the lungs.
3. Results
Due to the clear visibility of the images, as shown in Fig. 4, radiologists can use color visualization with Grad-CAM to pinpoint key diagnostic regions within medical images, aiding their decision-making. This method enhances interpretability, reduces oversight, and facilitates communication among medical professionals, making diagnoses more efficient and confident. By implementing the Grad-CAM technique, the proposed model, based on the classification of the spinal osteosarcoma image group, shows an accuracy of 0.821. As for the giant cell tumor image group classification model, the model shows an accuracy of 0.810. These results provide a better understanding of the predictions made by the deep learning model.
Fig. 4.
Visualization of spinal osteosarcoma and giant cell tumor images using Grad-CAM on the trained model. (a) Original image showing spinal osteosarcoma, (b) Original image showing spinal osteosarcoma, (c) Algorithm activation map showing giant cell tumor, (d) Class activation map showing giant cell tumor, (e) Showing Raw image of spinal osteosarcoma, (f) algorithm activation map showing giant cell tumor. [Note: High-intensity visuals (blue and green) reflect the regions of interest that our model focuses on when making predictions]. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The ROC curves for the classification models of the two medical diagnostic image groups are shown in Fig. 5. The performance of the image group classification models in the test group is presented in Table 1. For the spinal osteosarcoma image group classification model, the ROC curve shows an AUC of 0.814. As for the giant cell tumor image group classification model, the ROC curve indicates an AUC of 0.882.
Fig. 5.
ROC Curves of Image Group Classification Models for Spinal Osteosarcoma and Giant Cell Tumor. Note: (a) represents the ROC curve for the spinal osteosarcoma training group, (b) for the spinal osteosarcoma testing group, (c) for the giant cell tumor training group, and (d) for the giant cell tumor testing group.
Table 1.
Performance of automatic classification models for two easily confused medical conditions.
| Type of tumors being classified by model | AUC | 95 %CI | Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|---|
| Spinal osteosarcoma | 0.814 | 0.842 ∼ 0.903 | 0.821 | 0.870 | 0.824 |
| Giant cell tumor of bone | 0.882 | 0.863 ∼ 0.916 | 0.810 | 0.869 | 0.837 |
4. Analysis and discussion
Spinal osteosarcoma is a rare bone tumor that originates from residual embryonic remnants of the spinal cord. It accounts for 16.7 % of primary spinal tumors. Advances in diagnostics, research, and the accumulation of diverse case data have shifted the understanding of spinal osteosarcoma. While it was previously thought to occur primarily in vertebral ends, increasing reports now acknowledge its presence in mobile spinal segments, broadening our knowledge of the condition. In a study by Boriani et al. in 2006 [26], among 52 cases of mobile spine osteosarcomas, 29 % were in the cervical spine, 13 % in the thoracic spine, and 58 % in the lumbar spine.
Giant cell tumors of the spine are relatively rare and account for 2.5 % to 5.6 % of all giant cell tumors. They are less common than giant cell tumors in long bones. Diagnosing giant cell tumors in the vertebral column can be challenging because these tumors often lack the typical radiological features seen in giant cell tumors in long bones. In long bones, giant cell tumors often present with more distinctive radiological characteristics, such as well-defined borders and a characteristic “soap-bubble” appearance. In contrast, when they occur in the vertebral column, these tumors may not exhibit these classic features, making their identification and differentiation from other spinal conditions more difficult. This diagnostic challenge underscores the importance of relying on clinical symptoms and advanced imaging techniques to diagnose and distinguish these tumors in the vertebral column accurately. This complicates the radiological diagnosis, leading to potential misdiagnosis or missed diagnoses [2].
In terms of clinical presentation, as the tumor grows, it can lead to various symptoms, including pain, sensory disturbances, limb weakness, and even paralysis, resulting from compression of nerve roots or the spinal cord. Clinical symptoms of spinal osteosarcoma and giant cell tumors may not significantly differ. Both conditions can manifest with symptoms such as localized pain, neurological deficits, and structural changes in the spine. This similarity in clinical presentation can create challenges in differentiating between the two conditions based solely on symptoms. Accurate diagnosis often necessitates advanced imaging techniques, including MRI and CT, to assess the nature and location of the lesions. Moreover, due to their overlapping clinical symptoms, a histological examination of tissue samples is frequently required for definitive differentiation, highlighting the importance of comprehensive diagnostic approaches. Accurate preoperative imaging diagnosis is crucial for selecting appropriate clinical treatment methods and assessing prognosis [27].
This study employed an optimized DenseNet-based automatic classification algorithm. The results demonstrate that this classification model performs well in distinguishing between spinal osteosarcoma and giant cell tumors of bone. The model achieved an accuracy of over 80 %, sensitivity more significant than 80 %, specificity exceeding 80 %, and an average AUC of 0.914 and 0.882, respectively. This indicates that the model performs excellently and can provide a quantitative reference for physicians in developing treatment and care plans. Additionally, it reduces physicians' workload and enhances diagnostic classification accuracy.
The study acknowledges several vital limitations. One of the primary limitations stems from the relatively small sample size used in the research. This limited sample size impacted the breadth of the model's classifications and may have led to overfitting, making it challenging for the model to generalize to broader scenarios. To address this limitation, the manuscript suggests the need for future research efforts to expand the dataset significantly. By collecting a more diverse and extensive dataset, the model's performance will likely improve in accuracy and generalizability.
Additionally, the study recognizes the importance of refining the algorithm to cover a broader range of classification scenarios, enhancing the model's applicability in natural clinical settings where a more prominent and representative dataset is essential for robust and reliable diagnostic support. The small sample size restricts the model's generalization ability and may lead to overfitting. The study suggests expanding the sample size in future research efforts to address this limitation. By collecting a more diverse and extensive dataset, the model's performance will likely improve in accuracy and generalizability. Additionally, the study acknowledges the need for algorithm updates, ensuring that the model can cover a broader range of classification scenarios. This, in turn, will enhance the model's applicability in natural clinical settings, where a more prominent and more representative dataset is essential for robust and reliable diagnostic support.
The Grad-CAM visualization at the patch level demonstrates that the deep learning model can effectively overcome the interference caused by morphological heterogeneity within the same category of bone tumors. It accurately distinguishes bone tumors of different malignancies based on diagnostic morphological features. We hypothesize that the model accomplishes this by extracting and learning abstract pathological morphological features of undifferentiated or unclassified nature within benign and malignant bone tumor tissues, enabling correct binary classification at the patch level. However, more experiments are required to verify this hypothesis, which can be implemented in the future.
5. Conclusion
In conclusion, this study has presented a robust automatic classification model based on an optimized DenseNet algorithm for the differentiation of spinal osteosarcoma and giant cell tumors of the bone. The results indicate that the model achieved remarkable performance with an accuracy of over 80 %, sensitivity exceeding 80 %, and specificity surpassing 80 %. Moreover, it attained an average AUC of 0.814 for spinal osteosarcoma and 0.882 for giant cell tumors, demonstrating its effectiveness in distinguishing these challenging diagnoses. By utilizing this model, physicians can gain quantitative reference information to support their clinical decision-making, ultimately enhancing the accuracy of diagnostic classification.
While the study's findings are promising, it is essential to acknowledge that the limited sample size impacted the breadth of the model's classifications. Future efforts will focus on expanding the dataset and refining the algorithm to address this limitation. These steps will enhance the model's overall performance and ensure its applicability in diverse clinical settings.
This research contributes to medical image analysis, providing a valuable tool for clinicians in accurately differentiating spinal osteosarcoma and giant cell tumors of the bone.
Ethical approval
Every human participant in this study has provided written consent to participate in our research.
Funding
This research article did not receive any external funding.
CRediT authorship contribution statement
Jingteng He: Writing – original draft, Methodology, Investigation, Formal analysis, Conceptualization. Xiaojun Bi: Writing – review & editing, Validation, Supervision, Software, Project administration.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Si M.J., Wang C.S., Ding X.Y., et al. Differentiation of primary chordoma, giant cell tumor, and schwannoma of the sacrum by CT and MRI. Eur. J. Radiol. 2013;82(12):2309–2315. doi: 10.1016/j.ejrad.2013.08.034. [DOI] [PubMed] [Google Scholar]
- 2.Hunter C.L., Pacione D., Hornyak M., et al. Giant-cell tumors of the cervical spine: case report. Neurosurgery. 2006;59(5):E1142–E1143. doi: 10.1227/01.NEU.0000245589.08463.8D. [DOI] [PubMed] [Google Scholar]
- 3.Song Y., Zou J.J., Chang H., et al. 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI) IEEE; 2017. Adapting Fisher vectors for Histopathology image classification; pp. 600–603. [Google Scholar]
- 4.Murthy V., Hou L., Samaras D., et al. 2017 IEEE Winter Conference on Applications of Computer Vision (WACV) IEEE; 2017. Center-focusing multi-task CNN with injected features for classifying glioma nuclear images; pp. 834–841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Li Z, Wang Y, Yu J, et al. Deep Learning based Radiomic (DLR) and its usage in noninvasive IDH1 prediction for low-grade glioma. Sci. Rep., 2017, 7(1):5467. [DOI] [PMC free article] [PubMed]
- 6.Lao J., Chen Y., Li Z.C., et al. A deep learning-based radiomics model for survival prediction in glioblastoma multiforme. Sci. Rep. 2017;7(1):10353. doi: 10.1038/s41598-017-10649-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.He K, Zhang X, Ren S, et al. Deep residual Learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 770-778.
- 8.Huang G, Sun Y, Liu Z, et al. Deep networks with stochastic depth[C]//Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11–14, 2016, Proceedings, Part IV 14. Springer International Publishing, 2016: 646-661.
- 9.Huang G, Liu Z, Van Der Maaten L, et al. Densely connected convolutional networks. Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 4700-4708.
- 10.Iijima T. Basic theory on normalization of a pattern. Bull. Electro-Tech. Laboratory. 1962;26:368–388. [Google Scholar]
- 11.Raghu M., Zhang C., Kleinberg J., et al. Transfusion: Understanding transfer learning for medical imaging. Adv. Neural Inf. Proces. Syst. 2019;32 [Google Scholar]
- 12.Lewis J.J., O'c R.J., Nikolov S.G., et al. Pixel and region-based image fusion with complex wavelets. Inf. Fusion. 2007;8(2):119–130. [Google Scholar]
- 13.Srivastava R.K., Greff K., Schmidhuber J. Training very deep networks. Adv. Neural Inf. Proces. Syst. 2015;28 [Google Scholar]
- 14.Noh H., Hong S., Han B. Proceedings of the IEEE International Conference on Computer Vision. 2015. Learning deconvolution network for semantic segmentation; pp. 1520–1528. [Google Scholar]
- 15.Kim J.H., Lee S.W., Kwak D.H., et al. Conference on Neural Information Processing Systems(NIPS) 2016. Multimodal residual Learning for visual QA; pp. 361–369. [Google Scholar]
- 16.Tan Z, Wang M, Xie J, et al. Deep semantic role labeling with self-attention. Proceedings of the AAAI conference on artificial intelligence. 2018, 32(1).
- 17.Mu Z, Yang X, Dong Y. Review of end-to-end speech synthesis technology based on deep Learning. arXiv preprint arXiv:2104.09995, 2021.
- 18.Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision. Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2818-2826.
- 19.Yuan Y., Jia K., Ma F., et al. A hybrid self-attention deep learning framework for multivariate sleep stage classification. BMC Bioinf. 2019;20(16):1–10. doi: 10.1186/s12859-019-3075-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang R., Lei T., Cui R., et al. Medical image segmentation using deep learning: A survey. IET Image Process. 2022;16(5):1243–1267. [Google Scholar]
- 21.Schlemper J., Caballero J., Hajnal J.V., et al. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans. Med. Imaging. 2017;37(2):491–503. doi: 10.1109/TMI.2017.2760978. [DOI] [PubMed] [Google Scholar]
- 22.Pauly M., Keiser R., Gross M. Multi-scale feature extraction on point-sampled surfaces. Comput. Graphics Forum. 2003;22(3):281–289. [Google Scholar]
- 23.Reisman W.M. Puerto Rico and the International Process. Rev. Juridica U. Inter. PR. 1976;11:533. [Google Scholar]
- 24.An F.P., Liu J. Medical image segmentation algorithm based on multilayer boundary perception-self attention deep learning model. Multimed. Tools Appl. 2021;80(12):1–23. [Google Scholar]
- 25.Wu Y., Ma Y., Liu J., et al. Self-attention convolutional neural network for improved MR image reconstruction. Inf. Sci. 2019;490:317–328. doi: 10.1016/j.ins.2019.03.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Boriani S, Bandiera S, Biagini R, et al. Chordoma of the mobile spine: fifty years of experience. Spine (Phila Pa 1976), 2006, 31(4): 493-503. [DOI] [PubMed]
- 27.Samartzis D., Foster W.C., Padgett D., et al. Giant cell tumor of the lumbar spine: operative management via spondylectomy and short-segment, 3-column reconstruction with pedicle recreation. Surg. Neurol. 2008;69(2):138–141. doi: 10.1016/j.surneu.2007.01.038. [DOI] [PubMed] [Google Scholar]