Abstract
The traction converter modulation generates switching-frequencies current harmonics. The trapped filters can eliminate these switching harmonics, reducing total inductance and filter size. Nonetheless, in comparison with the typical inductor-capacitor-inductor (LCL) filter, the trap inductor needs a larger magnetic core. Moreover, the trapped filter has not been analyzed in the traction systems. This paper proposes a magnetic integrated inductor-trap-inductor (LLCL) filter to decrease the filter’s size and investigate its application in traction converters. In fact, the application range of this filter is quite broad, and it can be used in various electrical power systems, including industrial power systems, renewable energy systems, transportation systems, and building power systems. The LC-trap may be formed by connecting the equivalent trap inductor, introduced through the magnetic coupling between inverter-side and grid-side inductors, in series with the filter capacitor. Furthermore, for H-bridge unipolar pulse width modulation (PWM) traction converters, the prominent switching harmonics are concentrated at the double switching frequencies. Therefore, the stability zone is expanded by moving the resonance above the Nyquist frequency. The presented filter’s features and design are thoroughly analyzed. The proposed method is finally validated by the MATLAB/Simulink simulation and hardware-in-the-loop (HIL) experimental results. Compared to the discrete windings, the integrated ones can save two magnetic cores. Furthermore, the proposed filter can meet IEEE criteria with 0.3% for all the harmonics and total harmonic distortion (THD) of 2.15% of the grid‐side current.
1. Introduction
The electric multiple units (EMUs) with pulse width modulation (PWM) traction converters are often used on China’s high-speed railway (HSR) lines [1]. For modern railway traction power-supply systems (TPSS), the undesired current harmonics produced by modulating traction inverters are a well-known issue [2]. Such harmonics may result in various problems that reduce the performance of the traction network, including torque bursts, severe mistakes and disturbances, and communications system interruptions [3]. On several electric railways, harmonic resonance occurrences have led to the faulty triggering of protection systems, breakdown of high-voltage installations, and maybe train blockages [4]. Thus, one of the critical issues for HSR lines is correcting for and resolving harmonic pollution. The harmonics at low frequencies may be suppressed using adequately constructed repeated controllers [5] or proportional-resonant ones [6]. However, the high-frequency harmonics, especially those at the switching frequency and its multiples, could be mitigated by passive filters [7]. When connected to the TPSS, traction converters must adhere to the grid codes.
The problem of harmonics at high frequencies in HSR is frequently addressed using the traction network or the high-speed train (HST) driving system. The traction harmonics reduction in power networks has received the majority of research attention. Several studies employ passive filters for changing the harmonic impedance at the traction network [7]. Capacitor filter (C) and inductor-capacitor filter (LC) are examples of these filters. This method is very costly in TPSS with high power and voltage. For the HST driving system, there is an alternative method to decrease the harmonics generated by the traction inverters. This approach attenuates the HSR high-frequency harmonics by using the selective harmonics elimination (SHE) PWM approach [4]. The offline optimal PWM approach is very sensitive to system parameters and requires complex computations to solve the fundamental equations. High-frequency harmonics may be easily absorbed with large filter inductances. Even yet, a straightforward approach like this will ultimately increase the system’s size, expenses, and controller bandwidths. Except for a little additional capacitor utilized in the manner given in [8], the well-known LCL filters thus replaced the conventional L ones, where the total value of inductance is the same.
Over the past several years, network-tied converters have increasingly used LCL filters to minimize harmonics at high frequencies in the input or output current of renewable energies [9]. On the other hand, boost inverter filtered by traditional L filter has been heavily utilized by the HSTs, particularly as a grid-side converter. To maximize iron core consumption and meet the requirements for compact size and lightweight in HST equipment, the leakage inductance of the traction transformer (TT) was often employed as an inductance of the grid-side converter [10]. However, the LCL filters have severe limitations, including poor switching harmonics absorption, significant passive components, and electrical network resonance [11]. Different LCL-modified filter configurations have been presented in [12–23], where most of them are with extra LC traps connected in parallel or series and resonated to the dominant switching frequency. These traps enable bypassing or blocking of particular harmonics. The inductance and capacitance of the filters, as well as the total harmonic distortion (THD), will all be decreased due to removing these harmonics from the current fed into the network. Compared to other novel passive filters, the inductor-trap-inductor (LLCL) filter introduced in [24–30] has lately drawn more interest. The series LC trap was employed to substitute the capacitor in the LCL filter, where it is resonated to the switching frequency.
Most prior research has been on lowering the total inductance of power filters to decrease their expense and size. The magnetic cores are principally responsible for the total size of the power filters. Trapped filters, however, include additional magnetic cores that significantly increase the system size despite a significant decrease in overall inductance. The magnetic integration strategy, which integrates several discrete inductors onto a single magnetic core, is the most popular solution for that issue [10,31–37]. To decrease the core size and magnetically integrate single- or three-phase LCL filters, an EIE-type core has been suggested in [32,38] to boost converter efficiency. In [39], it is proposed to integrate LCL filters with a composite delta-yoke core magnetically. This core is over 10% smaller than the EIE one. Magnetic integration always leads to magnetic coupling, notwithstanding the possibility of decoupled core topologies like EIE and delta-yoke types. The magnetic coupling impacts the harmonic absorption of the LCL filter because it adds coupling inductance to the filter capacitor branch. For minimizing the effects of magnetic coupling, [38,40] employed a good-permeable I-type core in the EIE one. However, this constrains the design’s flexibility and parameters’ modification.
Meanwhile, the induced resonance may cause system stability problems. Several damping approaches, including passive damping [14,23,41], and active damping [42–46], have been proposed to ensure system stability. The passive damping influences would be much higher in actual implementations when the equivalent series resistance (ESR) of passive elements commonly rises in the high frequencies. It is also possible to make the system stable using a single-current loop controller with an unavoidable delay by configuring the filter resonance frequency suitably [47–49]. However, designing the resonant frequency beyond the Nyquist frequency, i.e., half the sampling frequency fs/2, is chosen because of the additional losses of passive dampening techniques and the great sensors expenses of active dampening methods [11,50].
An innovative single-phase magnetic integrated LLCL-type PWM rectifier for HSTs having resonant frequency beyond the Nyquist frequency has been designed using the expertise gained from creating grid-connected rectifiers and filters for renewable energy sources. Furthermore, since the switching harmonics of H-bridge unipolar PWM converters emerge around the double switching frequency, this design is advantageous for these devices because it is more economical when the resonance is set at high frequencies. The inverter-side and grid-side inductances, along with a trap with zero impedance at the resonant frequency, make up an integrated LLCL filter. The trap in the proposed filter attenuates harmonics at the double switching frequency, which dominates current harmonics. Therefore, the required number of filter inductors may be reduced since the filter deals with more minor harmonics in the higher multiples of the switching frequency. To minimize the current harmonics at high frequencies, which may cause resonances in the TPSS, this filter is meant to take the place of the conventional L and LCL ones.
The area needed for LCL-type filter devices also has to be reduced because of the space restriction in HSTs for air-core inductors, which is solved by the proposed filter. The presented filter, according to simulation and hardware-in-the-loop (HIL) experimental results, may meet the power quality criteria and the constrained space in the locomotive. The two windings of the filter could be coiled on one magnetic core. A good design, applicability, and linearity of the inductor are advantages of the proposed technique.
To show the filter’s feasibility, In the subsequent sections, it is evaluated against some passive filters, i.e., its counterpart discrete LLCL, LCL, and L ones. Only three passive filters were utilized to reduce harmonics in traction systems, i.e., the traditional L, LCL, and integrated filtering inductors LCL ones [8,10,51]. Thus, the presented filter is just compared to the LCL and L ones. To confirm the magnetic integration’s effectiveness and the filter design’s adaptability, the presented filter is also compared to the discrete LLCL one. Compared to the previous techniques, the model, analysis, and verification results reported in this paper demonstrate that the adopted one can minimize the needed passive components for the magnetic integrated LLCL filter, resulting in a more cost-effective design. Furthermore, the conventional LCL filter performs poorly at low-frequency harmonics. Moreover, the discrete LLCL filter requires an extensive size and is also sensitive to resonance. Therefore, the selection of the proposed filter has been guided by its advantages compared with the other filters. Thus, the integrated LLCL filter can be considered suitable for operating in traction network systems since this filter has a robust structure. The advantages of the presented filter can be summarized by:
reducing the size by winding many coils through magnetic integration,
attenuating the switching frequency and its multiple harmonics that reduce the current THD,
assuring durability against the filter parameters differences, and
preserving system stability under transient conditions.
Furthermore, SHE [52,53], which may eliminate selected harmonics using the controller system, has been compared with the proposed approach. SHE is only adequate for offline calculations, which calls for more detailed lookup tables at the low fundamental frequency and attenuates harmonics at low frequencies to increase ensuing harmonics at high frequencies [54–57]. In contrast, the proposed method is straightforward and able to achieve the SHE’s influence at low harmonics. In addition, the output waveforms are enhanced, the undesired harmonic distortion is removed, and the converter losses are decreased. Without using any extra elements, the LCL filter’s capacitor with the equivalent inductance created by the coupling effect between the two inductances produces the LC trap. The two inductors are also held together by a single magnetic core, which minimizes the total size and related expenses.
The research work has innovative ideas and a certain degree of theoretical innovation. The main innovations of this paper are as follows:
To decrease the large size of the conventional filters, this paper proposes designing a new passive filter, called the magnetic integrated LLCL filter, to attenuate the current switching harmonics with minimized size. In the proposed filter, two discrete windings are integrated on one magnetic core. The proposed filter is effective in reducing the harmonics to the standard allowed limits with a reduction of the filter size compared with the conventional passive filters.
To assess the resonance issue in passive integrated filters, this paper proposes establishing the magnetic integrated LLCL with resonance frequency beyond Nyquist frequency since. The proposed filter can suppress the current harmonics distortions and resonance with a small size.
To improve the problems in conventional solutions of harmonics mitigation in the traction converters, represented by the small area for large air-core inductors in the HST and weak harmonics suppression, this paper proposes an optimized integrated filter in the traction converters. The proposed integrated passive filter is applicable in the HSR traction converters for harmonics suppression and performance under different operation conditions.
The contributions of the paper are listed below:
An integrated LLCL filter with resonance beyond the Nyquist frequency is designed, simulated, and validated step-by-step.
A detailed analysis of the magnetic integration idea of many inductors in traction converters has been done.
The harmonics removal and size decrement are utilized to validate the proposed method.
The remainder of the article is arranged in the following manner. Section 2 will initially display the system structure of the integrated LLCL filter before studying the magnetic circuit. Section 3 presents the integrated LLCL parameters designing and modeling. Results from simulations and HIL experiments are presented in Section 4 to evaluate the feasibility of the filter. Lastly, Section 5 brings the article to the conclusion. This paper structure is shown in the flow chart in Fig 1, showing the processes and technical route.
Fig 1. Paper outline processes and technical route.
2. System structure and analysis of magnetic circuit
2.1. System structure
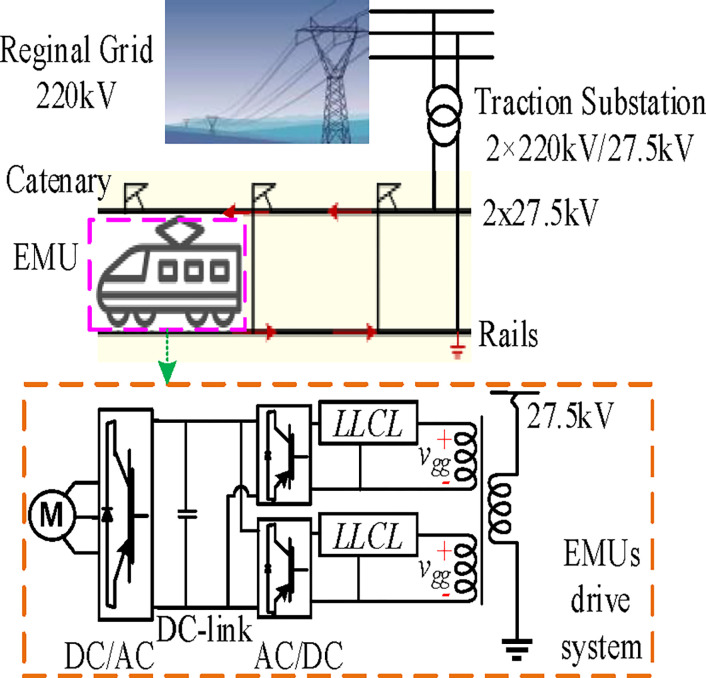
The standard TPSS structure utilized in China’s HSR is shown in Fig 2 [8]. To provide the all-parallel autotransformer (AT)-fed network via a V/x-structure TT, the three-phase 220 kV network voltage must be reduced to 27.5 kV single-phase double-feeders in the electrical supply substation. TTs may be connected using single-phase, Scott, V/v(V/x), and Ynd11, among other methods. The V/x-structure TT is used by German and Chinese HSR due to its excellent capacity utilization, straightforward wiring, and compatibility with AT catenary systems [1]. The all-parallel AT-fed TPSS grid architecture is commonly used in heavy-duty trains and HSR around the world due to its advantages of extended power supply, minimal voltage drop, and electromagnetic interference [31]. The ATs, mounted at the AT substation or section post, are spaced along the track by around 10 to 15 kilometers. In the complex AT traction electrical network, the feeders, contact lines, rail, protection wires, communication cables, and integrated grounding cables are considered multiconductor transmission lines.
Fig 2. Structure of traction power supply substation.
Fig 2 shows a single-phase inverter drive system for an equivalent HST. The line-side inverter in every HST’s power grid comprises two PWM rectifiers connected in parallel. Two interlaced two-level single-phase converters are used in the power conversion stage to achieve a high power factor and current carrying capacity. As presented in [1], the train inverters are frequently two-level, multi-interlaced, two- or three-level. Two interlaced two-level PWM inverter driving system of EMUs and all-parallel AT-fed network structures are used for analysis in this paper. However, there are several other grid modes and EMUs kinds, as was already indicated. However, the findings of the simulation and HIL experiments and the established rule of the researched filter are applicable for the other types, opening up the possibility of multiple distinct lines of future study.
As this paper mainly focuses on the application of the magnetic integrated LLCL filter, the detailed mathematical model of HSR and initial parameters are not presented here, which has already been elaborated in existing studies [1,2,7,8,58–60]. For example, a uniform mathematical model of TPSS and China HST is presented in [58] using the nodal admittance matrix. The HSR modeling can potentially affect the filtering effect of the passive filter. The modeling of the HSR system, including the power converters, power cables, and load, can affect the performance of the passive filter in several ways. For example, the impedance of the load and the power cables can influence the filter’s resonant frequency, which can, in turn, affect its ability to attenuate harmonics.
Additionally, the type and level of nonlinearities presented in the HSR system can affect the harmonic content of the signals transmitted through the filter, which can also impact its performance. As described in Fig 2, the passive filter is placed in the PWM-controlled train to suppress the harmonic generated by the traction converter since it is the origin of harmonics in the low voltage side of the TT. Therefore, the traction grid is seen from the filter as an ideal linear component, with vgg representing the contact-line voltage at the train location, while the equivalent load is seen as a fixed resistance [2,8,10,60]. Thus, to simplify the analysis, the values of the EMUs’ converter parameters affecting the filter design and performance are listed in Section 3.
Fig 3 shows the harmonics assessment circuit from the traction electrical network to the line-side traction converter with an integrated LLCL filter. Here, just a single integrated LLCL inverter is used for simplification. With a 27.5/1.55 transformation ratio, the TT is regarded as a standard linear component. The equivalent inductor of the secondary side of the TT is represented by Ls. It should be noted that this specific arrangement does not significantly limit the use of trapped filters. These filters may often be used in dc/ac or ac/dc generation systems that are either single-phase or three-phase, standalone or grid-connected [35].
Fig 3. H-bridge traction converter with int. LLCL filter.
In this case, Rdc is the equivalent load of a single integrated LLCL inverter in the traction inverter-motor driving system, Cdc is the dc-link capacitor, and IRdc and ICdc denote their currents. Four switches designated as S1, S2, S3, and S4 that operate at the switching frequency fsw convert the dc-link voltage Vdc into ac voltage vin that contains harmonics at the prominent switching frequency 2fsw and its multiples [61]. The harmonics are concentrated around 2fsw when using a unipolar sinusoidal PWM (SPWM). Thus, 2fsw is the actual switching frequency. It is also important to remember that harmonics at the double switching frequency 2fsw are much more prominent than those at high switching frequencies, which have the most output current harmonics. For this reason, the total harmonics can be effectively decreased by eliminating the harmonics at 2fsw. In real situations, one LC-trap is favoured due to its lower expense and size, and this is the approach that is further investigated in this work.
As discussed above, one of the biggest challenges for HSR operators is to keep the power quality at a high level by limiting the line voltage and currents’ THD at the point of common coupling (PCC). Since the current in these non-linear systems is still periodic (just not sinusoidal), this change in the nature of the current can be described in terms of the harmonic distortion of the current. Because the grid is assumed to provide a sinusoidal voltage, then there is no voltage at frequencies other than the fundamental. Therefore, only current harmonics must be continuously monitored for power quality. THD is a common measurement of the level of harmonic distortion present in electrical power networks. The THD term is expressed as the effective value of all harmonics divided by the effective value of its fundamental current. The distortion as a percentage of THD is defined as in (1), where In is the effective current of the nth harmonics and I1 is the effective current of the fundamental frequency. If the harmonic components are equal to the “0”, then THD will be equal to the “0”. The presence of harmonic currents and voltages in the power system means the distortion of sinusoidal waves. Deteriorated waves are called as non-sinusoidal waves. Voltage and current waveform distortion due to harmonics can lead to the high-voltage installations and HST either damaged or blockaded [62–65].
| (1) |
The TT might be viewed as a typical transformer. To create the worst instability situation, the equivalent series resistors of the filter components are disregarded. The inverter-side inductor Li and grid-side inductors Lg are connected in series, where their voltages are vi and vg, respectively, and their currents are ii and ig. At the same time, the dc bus current is represented by Idc. A shunt filter capacitor Cf has been inserted at the connection point of Li and Lg. The voltage at this point is denoted by vf, whereas if represents the current flowing through Cf. In addition, vpcc represents the voltage at the PCC. At this point, the inverter is tied to the grid.
The traction grid conditions may considerably impact the passive filter filtration effect. The traction network is assumed to be weak throughout this paper’s discussion, which means a low short-circuit ratio. As a result, the system impedance could change significantly [66]. For the worst stability case, an idealized voltage source with series inductance, denoted by Ls in Fig 3, is used to represent the grid. Since the network resistance would reduce the resonant peaks, the focus will only be on the impact of the network inductance.
Moreover, when several converters operate simultaneously to share power, the equivalent grid inductance detected by one converter is proportional to the number of inverters. The network impedance significantly impacts as the number of inverters rises [34]. According to [11], higher Ls may weaken the resonant poles. The filter was shown to undergo brief transient oscillations before returning to its setpoint. Despite this, compared to the strong grid circumstances, the system’s dynamic reaction took longer.
2.2. Proposed magnetic integration approach of LLCL filter
The proposed magnetic integration method for an LLCL filter will be covered in this section. In-depth discussions of the passive filter inductors’ design ideas may be found in the pertinent literature. The grid-side and inverter-side inductors in a typical LCL filter require the fabrication of two inductors since each has its own specific inductor. Assume that the LLCL filter [24–30], i.e., the equivalent discrete filter to the integrated LLCL one, as illustrated in Section 2.3, uses one LC-trap. In such an instance, in addition to the grid-side and inverter-side inductors, one more inductor must be fabricated. As a result, the discrete LLCL filter still has a big size and high expenses due to the requirement of another magnetic core for the trap inductor. This is still the case even if the total inductance is less than that of a conventional LCL filter. It is advised to apply magnetic integration, an excellent method that has already been employed in grid-tied converters for LCL [38,40], and LLCL [11,67] filters, to further increase the power density while minimizing expenses.
Fig 4(A) illustrates the magnetic integration for the LLCL filter. In contrast, Fig 5 depicts the electric connection schematic for such a circuit. By winding Li and Lg, with winding turns Ni and Ng, on the side limbs, the coupling influence may be fully used to lower the filter size. In such a magnetic core, the Li and Lg windings are negatively coupled because the flux directions at the side limbs are opposite. The central concept of the presented magnetic integration is constructing a trap-inductor via the magnetic coupling between Li and Lg inductors called an active trap inductor. In the proposed design, integrating Li and Lg introduces a coupling inductor for the LC trap. Based on Fig 4(B), Φi refers to the flux generated by Li winding. In contrast, Φim and Φig are the fluxes generated by Li winding and flowing across the central limb and Lg winding, respectively, as described in (2), where Ri, Rm, and Rg can refer to the magnetic resistors of the three limbs, respectively [11,34,35,68].
Fig 4. Proposed magnetic integration of LLCL filter.
Fig 5. Circuit diagram of an integrated LLCL filter.
| (2) |
Furthermore, the flux generated by Lg winding is Φg, where the fluxes generated by Lg and flowing across the central limb and Li winding are Φgm and Φgi, respectively, and it is easy to explain them in (3) [11,34,35,68].
| (3) |
Each inductor winding’s total flux consists of the self-flux and the mutual flux. Vi and Vg are determined as in (4) [11,68]. They could either be determined, according to (2)–(4), as in (5) [11,35]. The self-inductances Li and Lg and the mutual inductances Mig and Mgi could be described as in (6) [11,34,35,67].
| (4) |
| (5) |
| (6) |
It must be indicated that the Mig and Mgi are equal and thus can be referred to as Mig. The two inductors appear to be coupled according to (5) and (6), so (7) could represent Vi and Vg [11,67].
| (7) |
The self and mutual inductances are, based on (6), determined by the magnetic resistances that could be defined by (8). In this equation, the cross-sectional areas of the central and side limbs are represented by AC and AS, with AS = 1/2AC. lgc and lgs represent the air gap lengths of the central and side limbs. Moreover, μ0 = 4π × 10−7 N / A2 refers to the air permeability [11,34,35,67,68]. In the end, (9) is used to calculate the self and mutual inductances by substituting (8) into (6) [11,34,35]. As illustrated in (10), the ratio of the mutual inductance to the square root of the product of the self-inductances is known as the coupling coefficient kMig. Furthermore, it can be found that by adjusting the air gap lengths lgs and lgc, i.e., the ratio lgs/lgc, the coupling coefficient could be tuned effectively.
| (8) |
| (9) |
| (10) |
The magnetic coupling between two windings may be used in the approach method to create an equivalent trap inductor, as shown in Section 2.3. As a result, it is feasible to eliminate the requirement for two magnetic cores and reduce the expense and size of the LLCL filter. Furthermore, it is noted that there is no additional component in contrast to the discrete LLCL filter.
2.3. Properties and filtering effectiveness of the proposed filter
The integrated LLCL filter’s circuit construction is shown in Fig 5, with an inverter-side inductance Li, a grid-side inductance Lg, and an LC trap (Mig-Cf). This LC trap resonates at 2fsw, which is the dominant switching frequency. To reduce the switching harmonics, the mutual inductor Mig is used in the integrated LLCL filter to produce the resonant tank with Cf. The resonant tank removes the output current’s particular harmonics. The whole filter attenuates the other harmonics at the same time. The integrated LLCL filter is designed using a method described in this work that involves setting the series resonant frequency to 2fsw.
Furthermore, Fig 6 presents the block diagram of the proposed filter. From vin to ig, the integrated LLCL filter’s transfer function GLLCL(s) may be derived as in (11), where the coefficients are presented in the S1 Appendix.
Fig 6. Integrated LLCL filter block diagram.
| (11) |
It can be found that GLLCL(s) has a zero at ωt = (1/(CfMig))1/2, where ωt represents the trap angular frequency. Setting this frequency to the dominant switching frequency, as shown in (12), where ft is the trap frequency, will effectively suppress the corresponding switching harmonics. Furthermore, simulation and HIL experimental results will be used in Section 4 to confirm the THD reduction and validity of the proposed filter.
| (12) |
Employing the values in Table 1, Fig 7 displays the Bode diagrams ig(s)/vin(s) of the integrated LLCL and discrete LLCL, LCL, and L filters. These values are derived based on [8]. A detailed explanation of the procedures utilized to design these parameters is provided in Section 3. The integrated LLCL filter maintains the discrete LLCL filter’s characteristics, as shown in Fig 7, and produces a potent harmonics suppression at 2fsw, where this frequency has a magnitude trap. Furthermore, Fig 7 shows that the magnitude-frequency characteristics of GLLCL(s) have a conjugate resonant peak because the degree of their denominator is 3. This resonant peak is obtained by putting the denominator of GLLCL(s) in (11) equals zero, substituting s with jω. The integrated LLCL filter’s resonance frequency fr can be determined using (13) [11,67].
Table 1. Parameters values of the filters.
| Filter type | Integrated LLCL | Discrete LLCL | Discrete LCL [8] | Discrete L |
|---|---|---|---|---|
| Li(mH) | 1.63 | 1.63 | 1.63 | 2.93 |
| Lg(mH) | 1.3 | 1.3 | 1.3 | - |
| Cf(μF) | 125 | 125 | 125 | - |
| Lf(mH) | - | 0.167 | - | - |
| Mig(mH) | 0.167 | - | - | - |
| k Mig | 0.115 | - | - | - |
Fig 7. Bode diagrams for the four filters.
| (13) |
The discrete LCL filter has the highest roll-off rate of -60 dB/dec at the high-frequency domains, as shown in Fig 7, but since it lacks a trap magnitude, its suppression at the switching frequency is less. After the trap frequency, the proposed integrated LLCL filter has a harmonics suppression of -20 dB/dec. The resonant peaks may cause system stability problems. Designing the resonant frequency beyond the Nyquist frequency is adopted in this paper for assuring the system stability and exploring the new stability zone, which can be derived as in (14).
| (14) |
3. Integrated LLCL filter design and modeling
The parameters design of the proposed filter for traction converters is covered in this section. The Ls has been adjusted at 4 mH. The integrated LLCL filter parameters could be designed using the system parameters listed in Table 2 considering the criteria of the harmonic restrictions permitted by IEEE 519–2014 [8,69,70], the inverter-side current ripple ΔILi less than 40%, and utilizing below 5% of the reactive power. According to Rdc, the inverter works as a rectifier here. Moreover, designing Li, which may be done using the LCL filter’s designing approach [8], is the first step in the design process of the integrated LLCL filter. Consequently, with ΔILi ≤ 40%, Li is designed as in (15) for an H-bridge single-phase unipolar SPWM rectifier.
Table 2. Parameter values for the EMUs inverter.
| Description | Symbol | Value |
|---|---|---|
| Contact-line voltage (RMS) | V gg | 1550 V |
| System rated power | P o | 900 kW |
| DC-link capacitor | C dc | 4 mF |
| Load resistor | R dc | 10 Ω |
| DC-link voltage | V dc | 3000 V |
| Switching frequency | f sw | 550 Hz |
| Fundamental frequency | f o | 50 Hz |
| Network inductor | L s | 4 mH |
| (15) |
Design Lg is similar to Li to obtain the maximum amount of inductor utilization since such a system may attain the lowest resonance frequencies [36,37,50,71]. However, Lg has been reduced to 1.3 mH because the maximum and ripple currents have dropped by almost 40%.
It is necessary to check the total inductance Ltotal = Li + Lg in order to keep the inductors’ ac voltage drop lower than the 10% root-mean-square (RMS) value of vgg [72].
When selecting the filter capacitor Cf, It is necessary to strike a balance between reactive power consumed at the fundamental frequency and the elimination of harmonics at high frequencies [8,73]. Cf can be as low as 125 F while considering the permitted reactive power. However, the total capacitance Ctotal = Cf must be limited by the amount of reactive power used under the rated conditions to satisfy the power factor criteria. Moreover, the reactive current will be excessive if Ctotal is higher than 0.05 p.u [8,50]. The increase in filter inductance might solve this problem.
Moreover, Mig is designed by meeting (12)–(14), which means that the filter’s fr must fall between 1/2fsw and 5/6fsw, while ft must equal 2fsw = 1.1 kHz. fr = 2/3fsw = 367 Hz is chosen as the median value to increase stability and mitigate the loss of inductance with increasing current [11,50]. As a result, Mig has been determined to be 0.167 mH.
Furthermore, kMig, the pertinent coupling coefficient, is optimized to be 0.115 based on (10). Thus, the ratio of air gaps could be calculated as lgs/lgc = 3.85, demonstrating that Li and Lg are determined by lgs. In addition, Fig 8 displays the presented filter’s comprehensive designing flowchart.
Fig 8. Flowchart for the int. LLCL filter design method.
The discrete LLCL filter is designed using a similar procedure, which implies that Li, Lg, and Cf equal those of the proposed filter for providing a reasonable evaluation. The additional inductor Lf is determined by (12), replacing Mig with Lf, which is designed to be 0.167 mH.
By adopting an identical procedure, the LCL filter is designed, implying that Li, Lg, and Cf are similar to the presented filter to give a consistent evaluation.
Additionally, the L filter may be identical to the Ltotal of the proposed filter or equal to the LCL filter with setting Cf = 0 μF.
The parameters of the integrated LLCL, discrete LLCL, LCL, and L filters may be found in Table 1 following the application of these design processes. Furthermore, the traction converter with the proposed filter may be controlled similarly to that described in [35,51,54,60,74]. Thus, it will not be discussed here. For demonstrating the validity of the presented filter’s design, Section 4 will give the verification results.
As noticed, the proposed filter may create an equivalent extra inductor, saving one inductor and all of its parts. Additionally, one magnetic core may be saved by the proposed magnetic integration. This is because, unlike the discrete LLCL filter and other versions like LTCL and LCL-LC filters, which employ three magnetic cores, Li and Lg might be coiled on the side limbs of a single magnetic core.
It is essential to compare the sizes of integrated inductors with discrete inductors. The discrete inductors of the LLCL filter could be, respectively, wound on the central limbs of three cores. To enable proper comparison, the filter inductances of the integrated and discrete LLCL filters are configured similarly. The biggest filter is the discrete LLCL filter, which has three cores. While the integrated LLCL and discrete L filters each have one core, and the discrete LCL filter has two cores.
4. Simulation and HIL experimental verification
With the parameters listed in Tables 1 and 2, the configuration in Fig 3 was used to develop MATLAB/Simulink simulation and HIL models. The objective is to evaluate the efficacy of the presented filter design technique and to contrast it with the separate LLCL, LCL, and L filters. It must be kept in mind that an adaptive proportional-resonant controller was employed in the traction converter control system that is not discussed in this article. This research employs the symmetrical, unipolar, regular sampled SPWM.
The advantages and disadvantages of several passive filters are compared, along with their robustness, complexity, and size. To investigate the efficiency, transient performance, and harmonics attenuation ability of four filters, simulations and HIL tests are performed. The various performance indexes that have been computed are listed in Table 3.
Table 3. Performance indicators of the filters.
| Index | Integrated LLCL | Discrete LLCL | Discrete LCL | Discrete L |
|---|---|---|---|---|
| Dc Voltage fluctuation (V) | ±140 | ±145 | ±150 | ±130 |
| Size (number of cores) | 1 | 3 | 2 | 1 |
| Power losses (kW) | 23.34 | 22.72 | 24.31 | N/A |
| Harmonics around 2fsw (% Iref) | 0.02 | 0.01 | 0.10 | 0.19 |
| Harmonics around 4fsw (% Iref) | 0.01 | 0.01 | 0.03 | 0.12 |
| Harmonics around 6fsw (% Iref) | 0.01 | 0.02 | 0.02 | 0.09 |
| THD of ig (%) | 2.15 | 2.14 | 4.34 | 1.94 |
4.1. Simulation results
The simulated steady-state waveforms of ig, ii, vgg, and Vdc with the proposed integrated LLCL filter are depicted in Fig 9(A). It is shown that Vdc here approximates 3000 V, and the error is lower than 150 V (5%) due to the controller the voltage loop. In the steady state, ig is adequately filtered to be extremely sinusoidal. Fig 9(B) shows that its THD is just 2.15%, which is very low. This is mainly due to the proposed LLCL filter’s capability to reduce the low-order harmonics and double switching-frequency harmonics to a combined attenuation of 0.02%. With fourfold and sixfold switching-frequency harmonics of 0.01% and 0.01% of the fundamental current, the harmonic currents on the grid-side inductor are likewise attenuated satisfactorily. In this situation, all harmonic currents can be limited to less than 0.3%, which satisfies Table 3 displays the switching harmonics composition.
Fig 9. Simulation results using integrated LLCL filter.
For comparison, Fig 10(A) presents the simulated waveforms of a traction rectifier with a discrete LLCL filter. This section compares the proposed integrated filter’s performance to its discrete equivalent. As a result, Figs 9 and 10 indicate that the discrete LLCL filter likewise underwent the same test. When using the discrete LLCL filter in place of the integrated LLCL filter, the grid-side current waveform ig still maintains a sinusoidal shape, proving that the compensation of harmonics at low frequencies is unaffected. Furthermore, the harmonics at 2fsw of ig are significantly decreased, as seen in Fig 10(B). In addition, the ig harmonics over the double switching frequency are effectively suppressed. The fourfold sixfold switching-frequency harmonics are 0.01% and 0.01%, respectively, of the fundamental component, much lower than the limits. Table 3 shows that the specified LLCL filter can meet IEEE criteria with a grid-side current THD of 2.14% but with more extensive filter components. As demonstrated, the performance of the proposed filter, in general, is comparable to that of the discrete LLCL filter, indicating that it is effective with a small size.
Fig 10. Simulation results using discrete LLCL filter.
Fig 11 presents the simulated results of the traction PWM rectifier using a traditional LCL filter. The waveforms are presented in Fig 11(A), and the harmonic spectra of ig and ii are demonstrated in Fig 11(B). As seen in Fig 11(B), the 3rd harmonic of ig is approaching the threshold of 4.00% of the fundamental component. This unipolar modulated traction converter’s somewhat inferior performance can be attributed to its relatively low switching frequency and tiny filter inductances. THD of ig is 4.34%, less than the allowable level. The proposed filter only needs one magnetic core, while the discrete LCL one needs two cores.
Fig 11. Simulation results using discrete LCL filter.
The simulated results of a traction rectifier with an L filter are depicted in Fig 12(A). Only the simulated results for ig are presented because the simulations for ii are identical. Although ig is filtered to a sinusoidal shape and has the same phase of vgg, as shown in Fig 12(B), a current spiking at the 39th harmonic, near 4fsw, is observed. The grid code will be broken as a result. Moreover, the L filter will cause the dc-link voltage to decrease to around 2560 V, which will harm the converter’s performance and increase the risk of traction blockage. The 2560 V dc-link voltage is not allowed in real-world operation. As a result, more research on this problem is recommended.
Fig 12. Simulation results using discrete L filter.
As seen in Table 3, although the THDs of the four filters are satisfied at less than 5%, the required inductance of the output filter differs. Furthermore, the first two filters’ switching current harmonics at the LC-trap frequency are equal, supporting the viability of the presented method. Moreover, in comparison with the discrete LLCL filter and the discrete LCL filter, two magnetic cores and one magnetic core, respectively, are saved. As a result, the proposed filter minimizes expenses and size.
When comparing thoroughly, it is essential to consider the inductors’ power losses, even if the integrated LLCL filter is less in size and weight than the discrete LLCL and LCL filters. Since the L filter is unstable, it would not be taken into consideration hereunder. The detailed analysis of the inductors’ power losses, which has previously been explored in previous research [11], is not included here since this paper’s main emphasis is on the LLCL filter’s magnetic integration and usage in traction inverters. Inductors often lose power as a result of core and winding copper loss. Due to the numerous switching harmonics in the inverter output current ii and voltage vin, the inductors’ power losses are not easily computed or measured.
To assess the inductors’ power losses in the integrated LLCL, discrete LLCL, and LCL filters, the system efficiency is estimated under similar circumstances. When working under a unit factor, Pin denotes the input active power calculated using Pin = VggIgrms, while Po denotes the output active power computed using Po = VdcIdc. The ratio of Po/Pin is utilized to evaluate the efficiency of the system. The average values of idc and vdc, which may be determined using calculations or direct measurements, are Idc and Vdc. The RMS values of ig and vgg are Igrms and Vgg. To determine the power losses, Po would be subtracted from Pin. Although these losses seem high compared to the total power, they are much less than the allowed limits. The system efficiency of the integrated LLCL and discrete LLCL and LCL filters, if tested under conditions similar to full load, are 97.47%, 97.54%, and 97.37%, respectively. Since the efficiency is generally higher than 97.3%, there are not many power losses in the system. Thereby inferring that no additional countermeasures for power losses are not needed.
The proposed filter is subjected to load variation testing, and Fig 13 shows the associated simulated waveforms. The load was raised to 125% of its rated value (10 → 12.5) at t = 0.8 s. The entire fluctuation length was 0.13 s, which shows that the filter was designed well.
Fig 13. Simulation results of step-up load variation.
The simulation dynamic results of an integrated LLCL filter when the Vdc was suddenly stepped down by 300 V (3000 → 2700 V) at t = 0.8 s are shown in Fig 14. The presented method exhibits a well-designed filter in the dynamic phase and has strong harmonic switching elimination capabilities. Even though the filter experiences few transients, it finally stabilizes at its setpoint. The current requires about 0.12 s to follow its reference, even if it necessitates a longer time for the system to react dynamically.
Fig 14. Simulation dynamic waveforms.
The above results demonstrate good filtering performance, slight voltage variation, appropriate stability, quick dynamics features, and excellent resistance to the grid impedance of the proposed filter. The LCL filter also exhibits poor performance for harmonics at low frequencies. Furthermore, a significant size is required for the discrete LLCL filter. As a result, choosing the integrated LLCL filter is driven by its advantages over the alternatives.
Since the integrated LLCL filter possesses a sturdy structure, it may be inferred that it is appropriate for traction networks. The above simulation results are consistent with the above parts’ theoretical analyses.
4.2. HIL experimental results
The experiments are also carried out on the HIL platform for further verification. The HIL experimental platform has been set for verifying the superiority, feasibility, and applicability of the presented filter. The main advantage of the HIL experimental platform is that the actual model may be assessed without physical hardware, as shown in Fig 15 [75]. Another advantage is that the designer need not rely on environmental or naturalistic tests. The HIL platform’s use is practical and economical because the models can simulate plants. Using HIL, it would be feasible to reduce the expense of hardware verifications and the time and effort required for developing modifications in various applications [76,77].
Fig 15. HIL experimental platforms schematic diagram.
In addition, difficulties in recognizing and redesigning are easy, thanks to HIL experiments. Furthermore, it enables real-time tests to progress through the entire process faster than hardware tests. HIL is also more accurate and less expensive than physical testing because of its ability to be developed and executed on a schedule.
This method has shown considerable potential for both industry and academics because of HIL’s ability to provide riskless equipment and a speedy prototype procedure in research of engineering [4,8,11,31,35,60,75–84]. If a system with high power, such as TPSS, would be included, HIL tests may offer a safe testing environment. HIL is an attractive technique that offers the capabilities to test design methodology in a scenario of extensive systems with many complicated independent models that have high switching frequencies or quick dynamic behavior [4,8,31,60,76,82,84]. In addition, HIL is a contemporary technology frequently utilized for power electronic system design and validation. To address the problems of difficulty, complexity, and expense, HIL has been used to test power converters [75,77–81]. Results have demonstrated that HIL verification is a useful method for assessing the grid-connected passive-filtered inverter [8,11,31,35,78,79,83].
It should be made clear that the presented filter is currently in the research phase. It will be more cost effective to design and test the proposed filter utilizing the HIL platform in this step rather than the physical filter design that could happen in the subsequent phases because it is impossible to build an actual TPSS at laboratory tests. It is important to note that the HIL technology is an essential verification tool for new design techniques in large systems like TPSS. This technique allows for the examination of the accuracy and efficacy of the system under study with no spending expense of actual systems [4,8,31,60,76,82,84]. The standard method in the HIL technique is used in this work to model the proposed filter. Utilizing this standard method for the examined circuit, it is believed that the HIL technique produces relevant results that are extremely near to those of the actual tests, as in the systems presented in [8,11,31,35,78,79,83].
A fast control prototyping unit developed by StarSim modeling and integrated into the NI PXle-8821-FPGA-7868R real-time controller (RTC) and the NI PXle-8821- 7846R real-time simulator (RTS) are all part of the HIL [84], as shown in Fig 16. The HIL also includes a power system emulating unit, hardware input/output ports, an oscilloscope, and a host computer. The translucent backboard of the NI PXle-1082 has eight slots and offers exceptional performance and output power.
Fig 16. Configurations of HIL experiments.
Moreover, it provides a high degree of durability, which reduces the time needed for repairs [77]. It has improved synchronization capabilities and matches the OXI-5 PXI hardware requirements. The NI PXle-1071, on the other hand, is a 4-position PXI platform backboard, robust, and rack-attachable, indicating that its basic design was developed for optimum use and adaptability [84].
MATLAB/Simulink can be utilized for programming the control system, where the fixed-step solver can be used. Using the modeling program StarSim, the grid-connected rectifier with filter and control system models are uploaded into the HIL. Executing the grid-connected rectifier with filter model and control system model in RTS and RTC, respectively, results in constructing a closed loop. Like the simulation verification, identical parameters are used. The oscilloscope and monitor could be used for tracking the voltage and current waveforms. The oscilloscope may also provide data, such as S1 Data, for the experimental current/voltage waveforms, which might then be uploaded to the MATLAB/Simulink program and examined with the Powergui FFT Analysis Tool.
Fig 17 depicts the experimental results of a traction inverter with an integrated LLCL filter. These results match the simulation results in Fig 9. The prominent switching harmonics were mostly eliminated because the LC-trap frequency is adjusted at 2fsw. To meet the requirements of grid regulations, as tabulated in [70], it is possible to significantly reduce the THD of ig.
Fig 17. Experimental results using integrated LLCL filter.
The experimental results of the discrete LLCL filter are shown in Fig 18. These results demonstrate that harmonics of ig at the prominent switching frequency would not surpass the acceptable threshold. This filter’s LC-trap is the fundamental reason for this good performance, supporting the theoretical analysis and simulation findings in Fig 10.
Fig 18. Experimental results using discrete LLCL filter.
Fig 19 illustrates the experimental results of the discrete LCL filter. The low-frequency harmonics of ig at the were found to almost surpass the requirements. This problem is caused by the unipolar modulated traction rectifier’s low switching frequency and tiny filter inductors. As in the simulation results in Fig 11, the THD of ig could be seen as less than the acceptable levels.
Fig 19. Experimental results using discrete LCL filter.
Fig 20 displays the experimental results using the conventional L filter. Despite the ig being filtered to a sinusoidal shape and in phase with vgg, a current spiking in the 39th harmonic, beside 4fsw, was seen. There will be a breach of the grid codes as a result of this. In addition, Vdc would decrease to around 2560 V, like the simulated results presented in Fig 12. Thus, this situation may lead to poor converter performance or traction blockage. In real life, a Vdc of 2560 V would not be allowed. Therefore, additional research needs to investigate the problem more thoroughly.
Fig 20. Experimental results using traditional L filter.
The experimental results of an integrated LLCL filter with a 25% Rdc increment in varying load conditions are shown in Fig 21. The system can function appropriately in the face of transient occurrences.
Fig 21. Experimental results of step-up load variation.
The dynamic test was performed for the integrated LLCL filter, where Fig 22 shows the experimental results of a 300 V step-down variation in the Vdc (3000 → 2700 V). As can be observed, the waveforms are comparable to those simulated in Fig 14, proving that the filter can provide both stability and switching harmonic attenuation. The integrated LLCL filter is seen to have certain transient moments and then return to its setpoint with no fluctuation, which verifies the system’s robustness. Even though the transient phase only lasted for around 0.12 s, the system’s dynamic responsiveness needed a brief time till the current began following its reference.
Fig 22. Experimental dynamic results.
The experimental results are consistent with the simulated and theoretical analyses discussed in the previous sections. These simulation and experimental results verify the accuracy of the theoretical analysis and show that the proposed integrated LLCL filter maintains the benefits of the discrete LLCL and LCL ones while minimizing their drawbacks. The results demonstrate that the presented parameter design approach is successful, the proposed parameter robustness analysis technique is accurate, and the presented filter performs comparably to the discrete LLCL filter. The integrated LLCL filter is also flexible, improve filtering performance in the steady state, and effective in load variations and dynamics working conditions.
5. Conclusion
To reduce the size and weight of the inductors because high-speed trains have minimal space, an integrated LLCL filter with resonance frequency beyond the Nyquist frequency is proposed in this paper for traction rectifiers to suppress the dominant current switching harmonics. Based on the traditional LCL filter, an LC-trap could be created by introducing a coupling inductance into the filter capacitor branch via the magnetic coupling of the inverter-side and grid-side windings. It is possible to tune this LC trap to a specific harmonic frequency using a stepwise design method. The proposed filter can save two magnetic cores and achieve an identical harmonic suppression performance as the discrete LLCL filter. Furthermore, the proposed filter is with a magnetic core structure similar to the integrated LCL filter but performs better in harmonic suppression. The presented filter has been provided with a detailed step-by-step design method to facilitate the parameter choices. The developed filter could also withstand the grid impedance changes. After completing MATLAB/Simulink simulations and HIL experimental models, the verification results were provided to verify the following merits of the integrated LLCL filter:
The proposed filter has fewer discrete passive elements compared to the discrete LLCL and LCL filters, which enables decreasing the cores number of 1 and 2 respectively.
The proposed approach provides good harmonics reduction and resonance clearing compared to conventional passive filters, leading to a grid-side current THD value of 2.15%.
The method made it possible for the flexibility of filter design and efficacy of magnetic integration, which can provide a reference for designing new passive filters.
It further achieved durability and stability in transient occurrences, with an entire fluctuation length of only around 0.12 s.
However, the passive-filtered traction converters must maintain grid connectivity and carry out fault ride-through in the event of grid faults; else, system instability would occur. Hence, this instability problem and its solution must be adequately researched in the future.
Supporting information
(CSV)
(DOCX)
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
The author(s) received no specific funding for this work.
References
- 1.Hu H., Shao Y., Tang L., Ma J., He Z., and Gao S., “Overview of harmonic and resonance in railway electrification systems,” IEEE Trans. Ind. Appl., vol. 54, no. 5, pp. 5227–5245, 2018, doi: 10.1109/TIA.2018.2813967 [DOI] [Google Scholar]
- 2.Zhang R., Lin F., Yang Z., Cao H., and Liu Y., “A harmonic resonance suppression strategy for a high-speed railway traction power supply system with a SHE-PWM four-quadrant converter based on active-set secondary optimization,” Energies, vol. 10, no. 10, 2017, doi: 10.3390/en10101567 [DOI] [Google Scholar]
- 3.Kaleybar H. J., Brenna M., Foiadelli F., Fazel S. S., and Zaninelli D., “Power quality phenomena in electric railway power supply systems: An exhaustive framework and classification,” Energies, vol. 13, no. 24, 2020, doi: 10.3390/en13246662 [DOI] [Google Scholar]
- 4.Cui H., Song W., Fang H., Ge X., and Feng X., “Resonant harmonic elimination pulse width modulation-based high-frequency resonance suppression of high-speed railways,” IET Power Electron., vol. 8, no. 5, pp. 735–742, 2015, doi: 10.1049/iet-pel.2014.0204 [DOI] [Google Scholar]
- 5.Yang S., Wang P., Tang Y., Zagrodnik M., Hu X., and Tseng K. J., “Circulating current suppression in modular multilevel converters with even-harmonic repetitive control,” IEEE Trans. Ind. Appl., vol. 54, no. 1, pp. 298–309, 2018, doi: 10.1109/TIA.2017.2749257 [DOI] [Google Scholar]
- 6.Seifi K. and Moallem M., “An adaptive PR controller for synchronizing grid-connected inverters,” IEEE Trans. Ind. Electron., vol. 66, no. 3, pp. 2034–2043, 2019, doi: 10.1109/TIE.2018.2838098 [DOI] [Google Scholar]
- 7.Hu H., He Z., and Gao S., “Passive filter design for China high-speed railway with considering harmonic resonance and characteristic harmonics,” IEEE Trans. Power Deliv., vol. 30, no. 1, pp. 505–514, 2015, doi: 10.1109/TPWRD.2014.2359010 [DOI] [Google Scholar]
- 8.Song W., Jiao S., Li Y. W., Wang J., and Huang J., “High-frequency harmonic resonance suppression in high-speed railway through single-phase traction converter with LCL filter,” IEEE Trans. Transp. Electrif., vol. 2, no. 3, pp. 347–356, 2016, doi: 10.1109/TTE.2016.2584921 [DOI] [Google Scholar]
- 9.Wu W., Zhang Y., Chung H. S. H., and Blaabjerg F., “A new type of three-phase asymmetric-LCL power filter for grid-tied voltage source inverter with step-up transformer,” IEEE Trans. Ind. Electron., vol. 69, no. 12, pp. 11936–11945, 2021, doi: 10.1109/TIE.2021.3131867 [DOI] [Google Scholar]
- 10.Liu Y. et al. , “A novel harmonic suppression traction transformer with integrated filtering inductors for railway systems,” Energies, vol. 13, no. 2, pp. 1–18, 2020, doi: 10.3390/en13020473 [DOI] [Google Scholar]
- 11.Al-Barashi M., Wu S., Liu Z., Meng X., and Tasiu I. A., “Magnetic integrated LLCL filter with resonant frequency above Nyquist frequency,” IET Power Electron., vol. 15, no. 13, pp. 1409–1428, 2022, doi: 10.1049/pel2.12313 [DOI] [Google Scholar]
- 12.F. Wu, F. Shen, Z. Zhang, J. Ye, A. Shen, and J. Xu, “An LCPSL filter with multi-Tuned traps for grid-connected converters,” in 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics, COMPEL 2017, 2017, pp. 1–7, doi: 10.1109/COMPEL.2017.8013387 [DOI]
- 13.D. Pan, X. Wang, F. Blaabjerg, and H. Gong, “Active damping of LCL-filter resonance using a digital resonant-notch (biquad) filter,” in 2018 20th European Conference on Power Electronics and Applications, EPE 2018 ECCE Europe, 2018, p. P.1-P.9.
- 14.Beres R. N., Wang X., Blaabjerg F., Liserre M., and Bak C. L., “Optimal design of high-order passive-damped filters for grid-connected applications,” IEEE Trans. Power Electron., vol. 31, no. 3, pp. 2083–2098, 2016, doi: 10.1109/TPEL.2015.2441299 [DOI] [Google Scholar]
- 15.Xu J., Bian S., Qian Q., and Xie S., “Stability-oriented design for LCL-LC-trap filters in grid-connected applications considering certain variation of grid impedance,” in Proceedings—2018 IEEE International Power Electronics and Application Conference and Exposition, PEAC 2018, 2018, pp. 1343–1348, doi: 10.1109/PEAC.2018.8590452 [DOI] [Google Scholar]
- 16.Yao W., Yang Y., Xu Y., Blaabjerg F., Liu S., and Wilson G., “Phase reshaping via all-pass filters for robust LCL-filter active damping,” IEEE Trans. Power Electron., vol. 35, no. 3, pp. 3114–3126, 2020, doi: 10.1109/TPEL.2019.2927272 [DOI] [Google Scholar]
- 17.Zheng C. et al. , “An integrated design approach for LCL-type inverter to improve its adaptation in weak grid,” Energies, vol. 12, no. 13, 2019, doi: 10.3390/en12132637 [DOI] [Google Scholar]
- 18.Dragičević T., Zheng C., Rodriguez J., and Blaabjerg F., “Robust quasi-predictive control of LCL-filtered grid converters,” IEEE Trans. Power Electron., vol. 35, no. 2, pp. 1934–1946, 2020, doi: 10.1109/TPEL.2019.2916604 [DOI] [Google Scholar]
- 19.Awal M. A., Yu H., Della Flora L., Yu W., Lukic S., and Husain I., “Observer based admittance shaping for resonance damping in voltage source converters with LCL filter,” in 2019 IEEE Energy Conversion Congress and Exposition, ECCE 2019, 2019, pp. 4455–4462, doi: 10.1109/ECCE.2019.8913194 [DOI] [Google Scholar]
- 20.Pan D., Ruan X., and Wang X., “Direct realization of digital differentiators in discrete domain for active damping of LCL-type grid-connected inverter,” IEEE Trans. Power Electron., vol. 33, no. 10, pp. 8461–8473, 2018, doi: 10.1109/TPEL.2017.2780174 [DOI] [Google Scholar]
- 21.Tong L., Chen C., and Zhang J., “Iterative design method of LCL filter for grid-connected converter to achieve optimal filter parameter combination,” J. Eng., vol. 2019, no. 16, pp. 1532–1538, 2019, doi: 10.1049/joe.2018.8824 [DOI] [Google Scholar]
- 22.Saleem M., Choi K. Y., and Kim R. Y., “Resonance damping for an LCL filter type grid-connected inverter with active disturbance rejection control under grid impedance uncertainty,” Int. J. Electr. Power Energy Syst., vol. 109, no. 1, pp. 444–454, 2019, doi: 10.1016/j.ijepes.2019.02.004 [DOI] [Google Scholar]
- 23.Bian S., Xu J., Qian Q., and Xie S., “Design and analysis of different passive damping for grid-connected LCL filters to achieve desirable system performance,” in Proceedings—2018 IEEE International Power Electronics and Application Conference and Exposition, PEAC 2018, 2018, pp. 1740–1745, doi: 10.1109/PEAC.2018.8590359 [DOI] [Google Scholar]
- 24.Huang M., Wang X., Loh P. C., and Blaabjerg F., “LLCL-filtered grid converter with improved stability and robustness,” IEEE Trans. Power Electron., vol. 31, no. 5, pp. 3958–3967, 2016, doi: 10.1109/TPEL.2015.2467185 [DOI] [Google Scholar]
- 25.Wu W. et al. , “A robust passive damping method for LLCL-filter-based grid-tied inverters to minimize the effect of grid harmonic voltages,” IEEE Trans. Power Electron., vol. 29, no. 7, pp. 3279–3289, 2014, doi: 10.1109/TPEL.2013.2279191 [DOI] [Google Scholar]
- 26.Wu L., Liu T., and Hao X., “Coordination control strategy for LLCL-filter based grid-tied inverter with indirect sliding mode power control and virtual impedance,” J. Eng., vol. 2019, no. 16, pp. 2804–2809, 2019, doi: 10.1049/joe.2018.8506 [DOI] [Google Scholar]
- 27.Huang M., Wang X., Loh P. C., and Blaabjerg F., “Design of LLCL-filter for grid-connected converter to improve stability and robustness,” in Conference Proceedings—IEEE Applied Power Electronics Conference and Exposition—APEC, 2015, pp. 2959–2966, doi: 10.1109/APEC.2015.7104772 [DOI] [Google Scholar]
- 28.Wu W., He Y., and Blaabjerg F., “An LLCL power filter for single-phase grid-tied inverter,” IEEE Trans. Power Electron., vol. 27, no. 2, pp. 782–789, 2012, doi: 10.1109/TPEL.2011.2161337 [DOI] [Google Scholar]
- 29.Wu W. et al. , “A modified LLCL filter with the reduced conducted EMI noise,” IEEE Trans. Power Electron., vol. 29, no. 7, pp. 3393–3402, 2014, doi: 10.1109/TPEL.2013.2280672 [DOI] [Google Scholar]
- 30.Fang J., Xiao G., and Zhang Y., “An LCCL filter and its application to a Half-Bridge APF,” in 9th International Conference on Power Electronics—ECCE Asia: “Green World with Power Electronics”, ICPE 2015-ECCE Asia, 2015, pp. 2566–2573, doi: 10.1109/ICPE.2015.7168135 [DOI] [Google Scholar]
- 31.Tong N., Xu J., Xiang J., Liu Y., and Kong L., “High-order harmonic elimination and resonance damping based on inductive-filtering transformer for electrified railway transportation system,” IEEE Trans. Ind. Appl., vol. 58, no. 4, pp. 5157–5170, 2022, doi: 10.1109/tia.2022.3166722 [DOI] [Google Scholar]
- 32.T. K. and F. B. Gohil G., Bede L., Teodorescu R., “Optimized integrated harmonic filter inductor for dual-converter-fed open-end transformer topology,” IEEE Trans. Power Electron., vol. 32, no. 3, pp. 1818–1831, 2017, doi: 10.1109/TPEL.2016.2562679 [DOI] [Google Scholar]
- 33.Jiang S., Liu Y., Ye X., and Pan X., “Design of a fully integrated EMI filter for a single-phase grid-connected inverter,” IEEE Trans. Ind. Electron., vol. 68, no. 12, pp. 12296–12309, 2021, doi: 10.1109/TIE.2020.3047049 [DOI] [Google Scholar]
- 34.Fang J., Li X., Yang X., and Tang Y., “An integrated trap-LCL filter with reduced current harmonics for grid-connected converters under weak grid conditions,” IEEE Trans. Power Electron., vol. 32, no. 11, pp. 8446–8457, 2017, doi: 10.1109/TPEL.2017.2651152 [DOI] [Google Scholar]
- 35.Al-Barashi M., Liu Z., Saeed M. S. R., and Wu S., “Fully integrated TL-C-L filter for grid-connected converters to reduce current harmonics,” in 2021 IEEE 12th Energy Conversion Congress and Exposition–Asia (ECCE-Asia), 2021, pp. 1789–1794, doi: 10.1109/ECCE-Asia49820.2021.9479097 [DOI] [Google Scholar]
- 36.Xiaoqiang L., Jingyang F., Pengfeng L., and Yi T., “A common magnetic integration method for single-phase LCL filters and LLCL filters,” in 2017 IEEE Energy Conversion Congress and Exposition, ECCE 2017, 2017, pp. 5595–5600, doi: 10.1109/ECCE.2017.8096931 [DOI] [Google Scholar]
- 37.Li X., Fang J., Lin P., and Tang Y., “Active magnetic decoupling for improving the performance of integrated LCL-filters in grid-connected converters,” IEEE Trans. Ind. Electron., vol. 65, no. 2, pp. 1367–1376, 2017, doi: 10.1109/TIE.2017.2733445 [DOI] [Google Scholar]
- 38.Pan D., Ruan X., Bao C., Li W., and Wang X., “Magnetic integration of the LCL filter in grid-connected inverters,” IEEE Trans. Power Electron., vol. 29, no. 4, pp. 1573–1578, 2014, doi: 10.1109/TPEL.2013.2281763 [DOI] [Google Scholar]
- 39.Liu Y., See K. Y., Tseng K. J., Simanjorang R., and Lai J. S., “Magnetic integration of three-phase LCL filter with delta-yoke composite core,” IEEE Trans. Power Electron., vol. 32, no. 5, pp. 3835–3843, 2017, doi: 10.1109/TPEL.2016.2583489 [DOI] [Google Scholar]
- 40.Chen F., Jiang S., Jin D., and Mei Z., “Magnetic integrated LCL filter design for a 2.5 kW three-phase grid-connected inverter with double closed-loop control,” J. Power Electron., vol. 22, no. 2, pp. 338–350, 2022, doi: 10.1007/s43236-021-00365-y [DOI] [Google Scholar]
- 41.Xu J. and Xie S., “LCL-resonance damping strategies for grid-connected inverters with LCL filters: a comprehensive review,” J. Mod. Power Syst. Clean Energy, vol. 6, no. 2, pp. 292–305, 2018, doi: 10.1007/s40565-017-0319-7 [DOI] [Google Scholar]
- 42.Gaafar M. A., Ahmed E. M., and Shoyama M., “A two state feedback active damping strategy for the LCL filter resonance in grid-connected converters,” J. Power Electron., vol. 16, no. 4, pp. 1587–1597, 2016, doi: 10.6113/JPE.2016.16.4.1587 [DOI] [Google Scholar]
- 43.Wang X., Blaabjerg F., and Loh P. C., “Grid-current-feedback active damping for LCL resonance in grid-connected voltage-source converters,” IEEE Trans. Power Electron., vol. 31, no. 1, pp. 213–223, 2016, doi: 10.1109/TPEL.2015.2411851 [DOI] [Google Scholar]
- 44.Ben Said-Romdhane M., Naouar M. W., Slama-Belkhodja I., and Monmasson E., “Robust active damping methods for LCL filter-based grid-connected converters,” IEEE Trans. Power Electron., vol. 32, no. 9, pp. 6739–6750, 2017, doi: 10.1109/TPEL.2016.2626290 [DOI] [Google Scholar]
- 45.Roldan-Perez J., Bueno E. J., Peña-Alzola R., and Rodriguez-Cabero A., “All-pass-filter-based active damping for VSCs with LCL filters connected to weak grids,” IEEE Trans. Power Electron., vol. 33, no. 11, pp. 9890–9901, 2018, doi: 10.1109/TPEL.2017.2789218 [DOI] [Google Scholar]
- 46.Liu X., Qi Y., Tang Y., Guan Y., Wang P., and Blaabjerg F., “Unified active damping control algorithm of inverter for LCL resonance and mechanical torsional vibration suppression,” IEEE Trans. Ind. Electron., vol. 69, no. 7, pp. 6611–6623, 2021, doi: 10.1109/TIE.2021.3095796 [DOI] [Google Scholar]
- 47.Pan D., Ruan X., Wang X., Blaabjerg F., Wang X., and Zhou Q., “A highly robust single-loop current control scheme for grid-connected inverter with an improved LCCL Filter Configuration,” IEEE Trans. Power Electron., vol. 33, no. 10, pp. 8474–8487, 2018, doi: 10.1109/TPEL.2017.2783301 [DOI] [Google Scholar]
- 48.Wang J., Yan J. D., and Zou J., “Inherent damping of single-loop digitally controlled voltage source inverters with LCL filters,” in 2016 IEEE 25th International Symposium on Industrial Electronics (ISIE), 2016, pp. 487–492, doi: 10.1109/ISIE.2016.7744938 [DOI] [Google Scholar]
- 49.Xia W. and Kang J., “Stability of LCL-filtered grid-connected inverters with capacitor current feedback active damping considering controller time delays,” J. Mod. Power Syst. Clean Energy, vol. 5, no. 4, pp. 584–598, 2017, doi: 10.1007/s40565-017-0309-9 [DOI] [Google Scholar]
- 50.Tang Y., Yao W., Loh P. C., and Blaabjerg F., “Design of LCL filters with LCL resonance frequencies beyond the Nyquist frequency for grid-connected converters,” IEEE J. Emerg. Sel. Top. Power Electron., vol. 4, no. 1, pp. 3–14, 2016, doi: 10.1109/JESTPE.2015.2455042 [DOI] [Google Scholar]
- 51.Wu S. and Liu Z., “Low-frequency stability analysis of vehicle-grid system with active power filter based on dq-frame impedance,” IEEE Trans. Power Electron., vol. 36, no. 8, pp. 9027–9040, 2021, doi: 10.1109/TPEL.2021.3049145 [DOI] [Google Scholar]
- 52.Memon M. A., Mekhilef S., and Mubin M., “Selective harmonic elimination in multilevel inverter using hybrid APSO algorithm,” IET Power Electron., vol. 11, no. 10, pp. 1673–1680, 2018, doi: 10.1049/iet-pel.2017.0486 [DOI] [Google Scholar]
- 53.Kundu S., Bhowmick S., and Banerjee S., “Improvement of power utilisation capability for a three-phase seven-level CHB inverter using an improved selective harmonic elimination–PWM scheme by sharing a desired proportion of power among the H-bridge cells,” IET Power Electron., vol. 12, no. 12, pp. 3242–3253, 2019, doi: 10.1049/iet-pel.2018.5076 [DOI] [Google Scholar]
- 54.Tasiu I. A., Liu Z., Wu S., Yu W., Al-Barashi M., and Ojo J. O., “Review of recent control strategies for the traction converters in high-speed train,” IEEE Trans. Transp. Electrif., vol. 8, no. 2, pp. 2311–2333, 2022, doi: 10.1109/tte.2022.3140470 [DOI] [Google Scholar]
- 55.Sahoo S. K. and Bhattacharya T., “Phase-shifted carrier-based synchronized sinusoidal PWM techniques for a cascaded H-bridge multilevel inverter,” IEEE Trans. Power Electron., vol. 33, no. 1, pp. 513–524, 2018, doi: 10.1109/TPEL.2017.2669084 [DOI] [Google Scholar]
- 56.Ronanki D. and Williamson S. S., “Modular multilevel converters for transportation electrification: challenges and opportunities,” IEEE Trans. Transp. Electrif., vol. 4, no. 2, pp. 399–407, 2018, doi: 10.1109/TTE.2018.2792330 [DOI] [Google Scholar]
- 57.Priya M., Ponnambalam P., and Muralikumar K., “Modular-multilevel converter topologies and applications–a review,” IET Power Electron., vol. 12, no. 2, pp. 170–183, 2019, doi: 10.1049/iet-pel.2018.5301 [DOI] [Google Scholar]
- 58.He Z., Hu H., Zhang Y., and Gao S., “Harmonic resonance assessment to traction power-supply system considering train model in China high-speed railway,” IEEE Trans. Power Deliv., vol. 29, no. 4, pp. 1735–1743, 2014, doi: 10.1109/TPWRD.2013.2284233 [DOI] [Google Scholar]
- 59.Song K., Mingli W., Yang S., Liu Q., Agelidis V. G., and Konstantinou G., “High-order harmonic resonances in traction power supplies: a review based on railway operational data, measurements, and experience,” IEEE Trans. Power Electron., vol. 35, no. 3, pp. 2501–2518, 2020, doi: 10.1109/TPEL.2019.2928636 [DOI] [Google Scholar]
- 60.Geng Z., Liu Z., Hu X., and Liu J., “Low-frequency oscillation suppression of the vehicle–grid system in high-speed railways based on H∞ control,” Energies, vol. 11, no. 6, pp. 1–23, 2018, doi: 10.3390/en11061594 [DOI] [Google Scholar]
- 61.Holmes D. G. and Lipo T. A., Pulse width modulation for power converters: principles and practice. Hoboken, NJ, USA: Wiley Inc., 2003. [Google Scholar]
- 62.Adak S., Cangi H., and Yilmaz A. S., “Design of an LLCL type filter for stand-alone PV systems’ harmonics,” J. Energy Syst., vol. 3, no. 1, pp. 36–50, 2019, doi: 10.30521/jes.506076 [DOI] [Google Scholar]
- 63.Adak S., Cangi H., Eid B., and Yilmaz A. S., “Developed analytical expression for current harmonic distortion of the PV system’s inverter in relation to the solar irradiance and temperature,” Electr. Eng., vol. 103, pp. 697–704, 2021, doi: 10.1007/s00202-020-01110-7 [DOI] [Google Scholar]
- 64.Cangi H. and Adak S., “Analysis of solar inverter THD according to PWM’s carrier frequency,” in 2015 International Conference on Renewable Energy Research and Applications (ICRERA), 2015, pp. 194–198, doi: 10.1109/ICRERA.2015.7418694 [DOI] [Google Scholar]
- 65.Adak S., “Harmonics mitigation of stand‑alone photovoltaic system using LC passive filter,” J. Electr. Eng. Technol., vol. 16, pp. 2389–2396, 2021, doi: 10.1007/s42835-021-00777-7 [DOI] [Google Scholar]
- 66.Lu S., Xu Z., Xiao L., Jiang W., and Bie X., “Evaluation and enhancement of control strategies for VSC stations under weak grid strengths,” IEEE Trans. Power Syst., vol. 33, no. 2, pp. 1836–1847, 2018, doi: 10.1109/TPWRS.2017.2713703 [DOI] [Google Scholar]
- 67.Fang J., Li H., and Tang Y., “A magnetic integrated LLCL filter for grid-connected voltage-source converters,” IEEE Trans. Power Electron., vol. 32, no. 3, pp. 1725–1730, 2017, doi: 10.1109/TPEL.2016.2613578 [DOI] [Google Scholar]
- 68.Li X., Lin P., and Tang Y., “Magnetic integration of LTL filter with two LC-traps for grid-connected power converters,” IEEE J. Emerg. Sel. Top. Power Electron., vol. 6, no. 3, pp. 1434–1446, 2018, doi: 10.1109/JESTPE.2017.2764060 [DOI] [Google Scholar]
- 69.Assefa S. A., Kebede A. B., and Legese D., “Harmonic analysis of traction power supply system: case study of Addis Ababa light rail transit,” IET Electr. Syst. Transp., vol. 11, no. 4, pp. 391–404, 2021, doi: 10.1049/els2.12019 [DOI] [Google Scholar]
- 70.IEEE recommended practice and requirements for harmonic control in electric power systems, vol. 2014. IEEE Standard 519–2014, 2014.
- 71.Tang Y., Yoon C., Zhu R., and Blaabjerg F., “Generalized stability regions of current control for LCL-filtered grid-connected converters without passive or active damping,” in 2015 IEEE Energy Conversion Congress and Exposition, ECCE 2015, 2015, pp. 2040–2047, doi: 10.1109/ECCE.2015.7309948 [DOI] [Google Scholar]
- 72.Fang J., Xiao G., Yang X., and Tang Y., “Parameter design of a novel series-parallel-resonant LCL filter for single-phase half-bridge active power filters,” IEEE Trans. Power Electron., vol. 32, no. 1, pp. 200–217, 2017, doi: 10.1109/TPEL.2016.2532961 [DOI] [Google Scholar]
- 73.Jayaraman M. and Sreedevi V. T., “Power quality improvement in a cascaded multilevel inverter interfaced grid connected system using a modified inductive-capacitive-inductive filter with reduced power loss and improved harmonic attenuation,” Energies, vol. 10, no. 11, pp. 1–23, 2017, doi: 10.3390/en10111834 [DOI] [Google Scholar]
- 74.Wu S., Liu Z., Li Z., Zhang H., and Hu X., “Impedance modeling and stability analysis in vehicle-grid system with CHB-STATCOM,” IEEE Trans. Power Syst., vol. 35, no. 4, pp. 3026–3039, 2020, doi: 10.1109/TPWRS.2020.2963897 [DOI] [Google Scholar]
- 75.Liu C., Bai H., Ma R., Zhang X., Gechter F., and Gao F., “A network analysis modeling method of the power electronic converter for hardware-in-the-loop application,” IEEE Trans. Transp. Electrif., vol. 5, no. 3, pp. 650–658, 2019, doi: 10.1109/TTE.2019.2932959 [DOI] [Google Scholar]
- 76.Tasiu I. A., Liu Z., Qixiang Y., Hong C., Hu K., and Siqi W., “Fuzzy observer-based control for the traction dual rectifiers in high-speed train,” IEEE Trans. Veh. Technol., vol. 70, no. 1, pp. 303–318, 2021, doi: 10.1109/TVT.2020.3047663 [DOI] [Google Scholar]
- 77.Zhu L., Jiang D., Qu R., Tolbert L. M., and Li Q., “Design of power hardware-in-the-loop simulations for integrated starter-generator systems,” IEEE Trans. Transp. Electrif., vol. 5, no. 1, pp. 80–92, 2019, doi: 10.1109/TTE.2018.2881052 [DOI] [Google Scholar]
- 78.Feng F., Fang J., Manandhar U., Gooi H., and Xie P., “Impedance-based stability analysis of DAB converters with single-, double-, or cooperative triple-phase-shift modulations and input LC filter,” Front. Energy Res., vol. 10, pp. 1–12, 2022, doi: 10.3389/fenrg.2022.874477 [DOI] [Google Scholar]
- 79.T. D. C. Busarello, J. F. Guerreiro, M. G. Simoes, and J. A. Pomilio, “Hardware-in-the-loop experimental setup of a LCL-filtered grid-connected inverter with digital proportional-resonant current controller,” in 2021 IEEE 22nd Workshop on Control and Modelling of Power Electronics, COMPEL 2021, 2021, pp. 1–8, doi: 10.1109/COMPEL52922.2021.9646047 [DOI]
- 80.Zeni V. S., Munaretto L., Chaves H., Dal Pont N. C., Gruner V. F., and Finamor G., “Hardware-in-the-loop simulation of smart hybrid inverter: a comparison of online simulation and practical results,” in Conference Record of the IEEE Photovoltaic Specialists Conference, 2020, pp. 2005–2009, doi: 10.1109/PVSC45281.2020.9300809 [DOI] [Google Scholar]
- 81.Alvarez-gonzalez F., Griffo A., Sen B., and Wang J., “Real-time hardware-in-the-loop simulation of permanent-magnet synchronous motor drives under stator faults,” IEEE Trans. Ind. Electron., vol. 64, no. 9, pp. 6960–6969, 2017, doi: 10.1109/TIE.2017.2688969 [DOI] [Google Scholar]
- 82.Amin M. and Abdel Aziz G. A., “A Hardware-in-the-loop realization of a robust discrete-time current control of PMa-SynRM for aerospace vehicle applications,” IEEE J. Emerg. Sel. Top. POWER Electron., vol. 7, no. 2, pp. 936–945, 2019, doi: 10.1109/JESTPE.2018.2890592 [DOI] [Google Scholar]
- 83.Al-Barashi M., Meng X., Liu Z., Saeed M. S. R., Tasiu I. A., and Wu S., “Enhancing power quality of high-speed railway traction converters by fully integrated T-LCL filter,” IET Power Electron., vol. 16, no. 5, pp. 699–714, 2023, doi: 10.1049/pel2.12415 [DOI] [Google Scholar]
- 84.Liu C., Guo X., Ma R., Li Z., Gechter F., and Gao F., “A system-level FPGA-based hardware-in-the-loop test of high-speed train,” IEEE Trans. Transp. Electrif., vol. 4, no. 4, pp. 912–921, 2018, doi: 10.1109/TTE.2018.2866696 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(CSV)
(DOCX)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.