Prokrustean Graph: A substring index for rapid k-mer size analysis

Abstract

The widespread adoption of k-mers in bioinformatics has led to efficient methods utilizing genomic sequences in a variety of biological tasks. However, understanding the influence of k-mer sizes within these methods remains a persistent challenge, as the outputs of complex bioinformatics pipelines obscure this influence with various noisy factors. The choice of k-mer size is often arbitrary, with justification frequently omitted in the literature and method tutorials. Furthermore, recent methods employing multiple k-mer sizes encounter significant computational challenges.

Nevertheless, most methods are built on well-defined objects related to k-mers, such as de Bruijn graphs, Jaccard similarity, Bray-Curtis dissimilarity, and k-mer spectra. The role of k-mer sizes within these objects is more intuitive and can be described by numerous quantities and metrics. Therefore, exploring these objects across k-mer sizes opens opportunities for robust analyses and new applications. However, the evolution of k-mer objects with respect to k-mer sizes is surprisingly elusive.

We introduce a novel substring index, the Prokrustean graph, that elucidates the transformation of k-mer sets across k-mer sizes. Our framework built upon this index rapidly computes k-mer-based quantities for all k-mer sizes, with computational complexity independent of the size range and dependent only on maximal repeats. For example, counting maximal simple paths in de Bruijn graphs for $k=1,\dots ,100$ is achieved in seconds using our index on a gigabase-scale dataset. We present a variety of such experiments relevant to pangenomics and metagenomics.

The Prokrustean graph is space-efficiently constructed from the Burrows-Wheeler Transform. Through this construction, it becomes evident that other modern substring indices inherently face difficulties in exploring k-mer objects across sizes, which motivated our data structure.

Our implementation is available at: https://github.com/KoslickiLab/prokrustean.

1. Introduction

As the volume and number of sequencing reads and reference genomes grow every year, k-mer-based methods continue to gain popularity in computational biology. This simple approach—cutting sequences into substrings of a fixed length—offers significant benefits across various disciplines. Biologists consider k-mers as intuitive markers representing biologically significant patterns, bioinformaticians easily formulate novel methods by regarding k-mers as fundamental units that reflect their original sequences, and engineers leverage their fixed-length nature to optimize computational processes at a very low level. However, understanding the most crucial parameter, k, remains elusive, thereby leaving the accuracy of experimental results obscure to practitioners.

Two central challenges emerge in k-mer-based methods. First, the selection of the k-mer size is often arbitrary, despite its well-recognized influence on outcomes. This issue, though widely acknowledged, remains insufficiently addressed in the literature, with little formal guidance on determine an optimal k size for applications. The reasoning behind these choices is frequently unclear, typically confined to specific, unpublished experimental analyses (e.g., “we found that k=31 was appropriate...”). Second, methods attempting to utilize multiple k-mer sizes encounter significant computational burdens. The accuracy benefits of incorporating multiple k-mer sizes are overshadowed by the escalating computational costs with each additional k-mer size. Consequently, researchers often resort to “folklore” k values based on prior empirical results.

The influence of k-mer sizes within each method is a complex function reflecting bioinformatics pipelines that process k-mers. As biological adjustments and engineering strategies complicate the pipelines, their outputs obscure the impact of k-mer sizes with noisy factors, as simplified in the following abstraction:

pipeline (k-mer-based objects(sequences, k), biological adjustments, engineering.

Despite the complexity of the pipelines, there always exist mathematically well-defined k-mer-based objects that form the foundation of method formulation. These objects abstract the utilization of k-mers and depend solely on sequences and k-mer sizes. Thus, they offer potential for generalizability and quantification of the influence of k-mers in methods. Indeed, intuitive quantities have been derived from k-mer-based objects; however, there are challenges in actually computing them, as detailed in several examples we now present.

In genome analysis, the number of distinct k-mers is often used to reflect the complexity of genomes. Although the number varies by k-mer sizes, large data sizes restrict experiments to a few k values [9, 15, 39]. A recent study suggests that the number of distinct k-mers across all k-mer sizes provides additional insights into pangenome complexity [10]. Furthermore, the frequencies of k-mers provide richer information, as discussed in [1, 46], but their computation becomes more complicated and sometimes impractical, even with a fixed k-mer size [7].

In comparative analyses, Jaccard Similarity is utilized for genome indexing and searching by being approximated through hashing techniques [26, 34]. Experiments attempting to assess the influence of k-mer sizes on Jaccard Similarity must undergo tedious iterations through various k-mer sizes [8]. Additionally, Bray-Curtis dissimilarity is a k-mer frequency-based measure frequently used to compare metagenomic samples, where experimentalists face resource limitations due to the growing size of sequencing data, even with a fixed k-mer size. Yet, the demand for analyzing multiple k-mer sizes continues to increase [23, 35, 36].

Genome assemblers utilizing k-mer-based de Bruijn graphs are probably the most sensitive to k-mer sizes, and those employing multi-k approaches face significant computational challenges. The choice of k-mer sizes is particularly crucial in de novo assemblers, yet they predominantly rely on heuristic methods [19, 27, 38]. The topological features of de Bruijn graphs are succinctly summarized by the compacting process, where vertices represent simple paths called unitigs, but exploring these features across varying k-mer sizes is computationally intensive. Furthermore, the development of multi-k de Bruijn graphs continues to be a challenging and largely theoretical endeavor [22, 40, 43], with no substantial advancements following the heuristic selection of multiple k-mer sizes implemented by metaSPAdes [33].

These examples motivated the pressing need to generalize the exploration of k-mer-based objects across varying k-mer sizes. We introduce a computational framework for rapidly computing quantities derived from k-mer-based objects across a range of k sizes. The objective is clarified in Section 2, with experimental results in Section 3. The underlying substring index and its usage are briefly presented in Section 4 and Section 5.

Due to the length of proofs and algorithms, construction algorithms are left in Supplementary materials. We emphasize that distinctions between the new substring index and other modern substring indexes are only briefly covered in Section 5, while the construction algorithms provide essential insights. The new index can be built from the Burrows-Wheeler Transform (BWT), but the BWT alone is unlikely to achieve the same efficiency as our framework. It appears that modern substring indexes based on longest common prefixes, such as the BWT, suffix tree, FM-index, and r-index, share similar limitations.

2. Setup and main theorem

Let $\Sigma$ be our alphabet and let $S\in {\Sigma }^{\ast }$ represent a finite-length string, and $\mathcal{U}\subset {\Sigma }^{\ast }$ represent a set of strings. Consider the following preliminary definitions and main result detailing the Prokrustean graph utility:

Definition 1.

• A region in the string $S$ is a triple $(S,i,j)$ such that $1\le i\le j\le |S|$.

  ** See the example after definition 2 which justifies this non-standard region notation $(S,i,j)$.

• The string of a region is the corresponding substring: str $(S,i,j):=S_i{S}_{i+1}\dots S_j$.

• The size or length of a region is the length of its string: $\left|(S,i,j)\right|:=j-i+1$.

• An extension of a region $(S,i,j)$ is a larger region $\left(S,i^{\prime },j^{\prime }\right)$ including $(S,i,j)$:

  $$(S,i,j)⊊\left(S,i^{\prime },j^{\prime }\right):=i^{\prime }\le i\le j\le j^{\prime }\text{and}|(S,i,j)|<\left|\left(S,i^{\prime },j^{\prime }\right)\right|.$$
• The occurrences of $S$ in $\mathcal{U}$ are those regions in strings of $\mathcal{U}$ corresponding to $S$:

  $$oc{c}_{\mathcal{U}}(S):=\left\{\left(S^{\prime },i,j\right)\mid S^{\prime }\in \mathcal{U}\text{\&}str\left(S^{\prime },i,j\right)=S\right\}.$$

• $S$ is a maximal repeat in $\mathcal{U}$ if it occurs at least twice and more than any of its extensions: $\left|oc{c}_{\mathcal{U}}(S)\right|>1$, and for all $S^{\prime }$ a superstring of $S$, $\left|oc{c}_{\mathcal{U}}(S)\right|>\left|oc{c}_{\mathcal{U}}\left(S^{\prime }\right)\right|$. I.e., a maximal repeat $S$ is one that occurs more than once in $\mathcal{U}$ (i.e. is a repeat), and any extension of which has a lower frequency in $\mathcal{U}$ than $S$.

• Let ${\mathcal{R}}_{\mathcal{U}}$ represent the set of all maximal repeats in $\mathcal{U}$.

Theorem 1. (Main Result)

Given a set of sequences $\mathcal{U}$, there exists a substring representation ${\mathcal{G}}_{\mathcal{U}}$ of size $O\left(|\Sigma |\left|{\mathcal{R}}_{\mathcal{U}}\right|\right)$. ${\mathcal{G}}_{\mathcal{U}}$ can be used to compute k-mer quantities of $\mathcal{U}$ for all $k=1,\dots ,k_{\max }$ within $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$ time and space, where $k_{\max }$ is the length of the longest sequence in $\mathcal{U}$. The k-mer quantities are defined as follows:

• (Counts) The number of distinct k-mers, as used in genome cardinality DandD [10].

• (Frequencies) k-mer Bray-Curtis dissimilarities, as used in comparing metagenomic samples [36].

• (Extensions) The number of maximal unitigs in k-mer de Bruijn graphs, as used in analyses of reference genomes and genome assembly [29, 42].

• (Occurrences) The number of edges with annotated length of k in an overlap graph. [45].

Furthermore, ${\mathcal{G}}_{\mathcal{U}}$ can be constructed in $O\left(|bwt|+\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$ time and space utilizing bwt, a BWT representation of $\mathcal{U}$.

Proof. Section 4 defines ${\mathcal{G}}_{\mathcal{U}}$ and derives its size $O\left(|\Sigma |\left|{\mathcal{R}}_{\mathcal{U}}\right|\right)$. Section 5 introduces the computation of k-mer quantities, and the construction algorithm is introduced in the Supplementary Section S3. □

${\mathcal{G}}_{\mathcal{U}}$ is termed the Prokrustean graph of $\mathcal{U}$. The main contribution is that the time complexity for computing k-mer quantities for all $k\in \left[1,k_{\max }\right]$ is independent of the range, specifically $O(|{\mathcal{G}}_{\mathcal{U}}|)$. Notably, $|{\mathcal{G}}_{\mathcal{U}}|$ is sublinear relative to $N$, where $N$ is the cumulative sequence length of $\mathcal{U}$. In contrast, any direct computation of k-mer quantities from $\mathcal{U}$ for a fixed k-mer size demands, at best, $O(N)$ time. Extending this computation naively to $k=1,\dots ,k_{\max }$ increases the complexity to $O\left(N^2\right)$ to cover all possible substrings.

3. Results

The construction and four applications of the Prokrustean graph were conducted with various datasets that were randomly selected to represent a broad range of sizes, sequencing technologies, and biological origins. Diverse sequencing datasets were collected, including two metagenome short-read datasets, one metagenome long-read dataset, and two human transcriptome short-read datasets. The full list of datasets is provided in section S1. All experiments were performed on a Mac Studio equipped with an Apple M1 Max of 10 CPU cores and 64 GB memory.

3.1. Prokrustean graph construction with $k_{min}$

The construction algorithm is introduced in the Supplementary Section S3. The Prokrustean graph grows with the number of maximal repeats, i.e., $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)=O\left(|\Sigma |\cdot \left|{\mathcal{R}}_{\mathcal{U}}\right|\right)$. Also, the size of ${\mathcal{G}}_{\mathcal{U}}$ can be controlled by dropping maximal repeats of length below $k_{min}$. Then ${\mathcal{G}}_{\mathcal{U}}$ requires $O\left(|\Sigma |\cdot \left|{\mathcal{R}}_{\mathcal{U}}\left(k_{min}\right)\right|\right)$ space where ${\mathcal{R}}_{\mathcal{U}}\left(k_{min}\right)$ is the set of maximal repeats of length at least $k_{min}$. Then, subsequent sections cover the results of four applications that compute k-mer quantities for $k=k_{min},\dots ,k_{max}$. We assume $k_{max}$ is always less than $|{\mathcal{G}}_{\mathcal{U}}|$, even if the largest possible value is chosen, which is typical for sequencing data. Figure 1 shows how the graph size $\left(O\left(|\Sigma |\cdot \left|{\mathcal{R}}_{\mathcal{U}}\left(k_{min}\right)\right|\right)\right)$ of short sequencing reads decreases as $k_{min}$ increases.

Fig.1:

Size decay of a Prokrustean graph as a function of $k_{min}$. The sizes of Prokrustean graphs, i.e., number of vertices and edges, versus $k_{min}$ values for a short read dataset ERR3450203 are depicted. The size of the graph rapidly drops around $k_{min}=[11,\dots ,19]$, meaning the maximal repeats and locally-maximal repeat regions are dense when $k_{min}$ is under 11. The number of edges falls again around $k_{min}=100$ because the graph eventually becomes fully disconnected.

Table 1 shows that the size of the Prokrustean graphs is sublinear to that of their inputs. Also, the space occupancy is close to the inputs (read files) with practical $k_{min}$ values. We used $k_{min}=30$ that is common in genome assemblers and comparative microbiome analyses.

Table 1:

Prokrustean graph construction introduced in Section S3. Symbols M, B, mb, and gb denote millions, billions, megabytes, and gigabytes, respectively. $N$ represents the cumulative sequence length of $\mathcal{U}$. ${\mathcal{V}}_{\mathcal{U}}$ is the vertex set and ${\mathcal{E}}_{\mathcal{U}}$ is the edge set of ${\mathcal{G}}_{\mathcal{U}}$. Since $\left|{\mathcal{E}}_{\mathcal{U}}\right|\ll N$, the time complexity of subsequent applications $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right):=O\left(\left|{\mathcal{E}}_{\mathcal{U}}\right|\right)$ is sublinear to the input, even if all k-mer sizes are considered.

dataset	reads	N	$k_{min}$	time	memory	output size	$\left|{\mathcal{V}}_{\mathcal{U}}\right|$	$\left|{\mathcal{E}}_{\mathcal{U}}\right|$
SRR20044276 (metagenomic)	0.94M	72M	1	20s	200mb	40mb	8M	21M
SRR20044276 (metagenomic)	0.94M	72M	20	13s	180mb	35mb	2.7M	5.4M
ERR3450203 (metagenomic)	55M	4.5B	20	29min	12.7gb	3.1gb	254M	477M
ERR3450203 (metagenomic)	55M	4.5B	30	28min	11gb	2.7gb	221M	407M
SRR18495451 (metagenomic/long)	0.83M	11.3B	30	90min	43gb	14gb	890M	1.7B
SRR7130905 (human/rna-seq)	45M	6.8B	30	39min	18gb	4gb	280M	580M
SRR21862404 (human/rna-seq)	336M	22.3B	30	99min	37gb	5.9gb	330M	800M

Regarding subsequent results, note that, to our knowledge, no existing computational techniques perform the exact same tasks across a range of k-mer sizes, making performance comparisons inherently “unfair.” Readers are encouraged to focus on the overall time scale to gauge the efficiency of the Prokrustean graph. Additionally, discrepancies in output comparisons may arise due to practice-specific configurations in computational tools, such as the use of only ACGT (i.e., no “N”) and canonical k-mers in KMC. Consequently, we tested correctness on GitHub¹ using our brute-force implementations.

3.2. Counting distinct k-mers for $k=k_{min},\dots k_{max}$

The number of distinct k-mers is commonly used to assess the complexity and structure of pangenomes and metagenomes [13, 44]. A recent study by [10] spans multiple k contexts, suggesting that the number of k-mers across all k-mer sizes should be used to estimate genome sizes. The Supplementary Algorithm S1 counts distinct k-mers for all k-mer sizes in time $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$. We employed KMC [28], an optimized k-mer counting library designed for a fixed k size, for comparison, and used it iteratively for all k values.

3.3. Counting simple paths in de Bruijn graphs for $k_{min},\dots ,k_{max}$

A maximal unitig of a de Bruijn graph represents a simple path that cannot be extended further. Maximal unitigs are vertices of a compacted de Bruijn graph [20], reflecting a topological characteristic of the graph. More maximal unitigs generally indicate more complex graph structures, which significantly impact genome assembly performance [3, 14]. Therefore, their number across multiple k-mer sizes reflects the influence of k-mer sizes on the complexity of assembly. Algorithm S3 counts maximal unitigs for all k-mer sizes in time $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$.

We utilized GGCAT [20] for comparisons, a mature library constructing compacted de Bruijn graphs of a fixed k-mer size. We assumed their construction is equivalent to counting maximal unitigs. Again, computing maximal unitigs with the Prokrustean graph becomes more efficient as additional k-mer sizes are considered. Table 3 displays the comparison, and Figure 2 illustrates one of the outputs.

Table 3:

Counting maximal unitigs with GGCAT and Algorithm S3 using the Prokrustean Graph. GGCAT was executed iteratively for each k size, with each iteration taking approximately 1–5 minutes. The efficiency gap becomes clearer when there are many possible k-mer sizes, as in long reads. Both methods used 8 threads.

Dataset	k	GGCAT		Prokrustean Graph
		time	memory	time	memory
SRR20044276	20..150	13m	310mb	0.36s	70mb
ERR3450203	20..150	98m	1.1gb	21s	6.1gb
SRR18495451	30..50000	days	-	127s	26gb
SRR7130905	30...150	126m	1.4gb	46s	8.5gb
SRR21862404	30...150	168m	0.8gb	76s	13.8gb

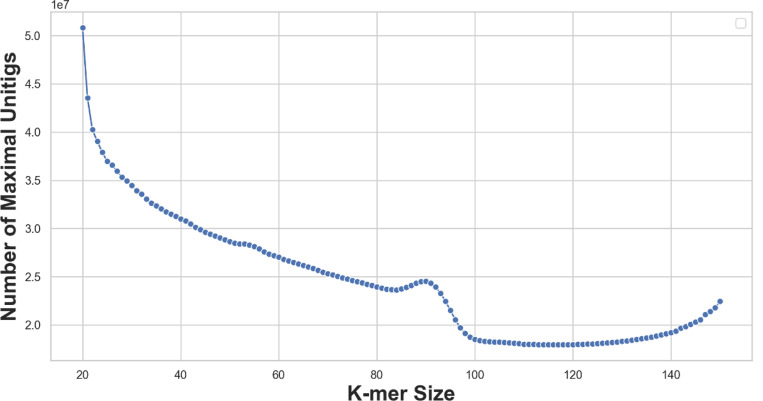
Fig.2:

The number of maximal unitigs in de Bruijn graphs of order k = 20,...,150 of metagenomic short reads (ERR3450203). A complex scenario is revealed: The decrease of the numbers fluctuates in k = 30,...,60, and the peak around k = 90 corresponds to the sudden decrease in maximal repeats. Lastly, further disconnections increase contigs and eventually make the graph completely disconnected.

3.4. Computing Bray-Curtis dissimilarities for $k_{min},\dots ,k_{max}$

The Bray-Curtis dissimilarity is a frequency-based metric that measures the dissimilarity between biological samples. The Bray-Curtis dissimilarity for k-mer sets is defined as follow:

$$BC\left({\mathcal{U}}_A,{\mathcal{U}}_B,k\right)=1-\frac{{\sum }_{w\in \left\{k\text{-mers in}{\mathcal{U}}_A\cup {\mathcal{U}}_B\right\}}2\cdot \min \left(\text{fre}{\text{q}}_A(w),\text{fre}{\text{q}}_B(w)\right)}{{\sum }_{w\in \left\{k\text{-mers in}{\mathcal{U}}_A\cup {\mathcal{U}}_B\right\}}\text{fre}{\text{q}}_A(w)+\text{fre}{\text{q}}_B(w)}.$$

This quantity is particularly popular in metagenomics analysis [23, 36]. In each citation we found, the dissimilarity scores are presented for a single k-mer size. However, the values are sensitive to the choice of k-mer sizes, so they are often calculated with multiple k-mer sizes for analyses [23, 36, 47], yet most state-of-the-art tools utilize a fixed k-mer size [7]. Algorithm S2 computes Bray-Curtis dissimilarities for all k-mer sizes in $O\left(\mid Pairs|\cdot |{\mathcal{G}}_{\mathcal{U}}\mid \right)$, where ${\mathcal{G}}_{\mathcal{U}}$ contains sequencing reads for samples, and Pairs is the sample pairs compared.

Figure 3 shows that dissimilarities between four example metagenome samples are not consistent in that at some k-mer sizes, one observed pattern of dissimilarity is completely flipped at another k-mer size. I.e. no k size is “correct”; instead, new insights are obtained from multiple k sizes. This task took about 10 minutes with the Prokrustean graph of four samples of 12 gigabase pairs in total, and the graph construction took around 1 hour. Computing the same quantity takes around 5 to 8 minutes for a fixed k-mer size with Simka [7], and no library computes it across k-mer sizes.

Fig.3:

Bray-Curtis dissimilarities between four metagenomic samples computed with Algorithm S2. We used the sequencing data of four samples derived from infant fecal microbiota, which were studied in [36]. Samples include two from 12-month-old human subjects and two from 3-week-olds. The relative order between values shift as k changes, e.g. compared to all other dissimilarities, the dissimilarity between sample 2 and 4 is highest at k = 8 but lowest at k = 21. Note that diverse k sizes (10, 12, 21, 31) are actively utilized in practice.

3.5. Counting vertex degrees of overlap graph of threshold $k_{min}$

Overlap graphs are extensively utilized in genome and metagenome assembly, alongside de Bruijn graphs. Although their definition appears unrelated to k-mers, we can view them as representing common suffix-prefix k-mers of sequences in $\mathcal{U}$. Overlap information is particularly crucial in read classification [2, 16, 31, 41] and contig binning [32, 45] in metagenomics. These applications interpret vertex degrees as (abundant-weighted) read coverage in samples, which exhibit high variances due to species diversity and abundance variability.

A common computational challenge is the quadratic growth of overlap graphs relative to the number of reads: $O\left(|\mathcal{U}{|}^2\right)$. In contrast, the Prokrustean graph, which encompasses the overlap graph as a sort of hierarchical form, requires $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$ space to access the structure of overlaps, enabling the efficient computation of vertex degrees.

Figure 4 is the result of computing the vertex degrees on a metagenomic short read dataset, as computed by Algorithm S4. With the Prokrustean graph of 27 million short reads (4.5 gigabase pairs in total; ERR3450203), the computation used 8.5 gigabytes memory and 1 minute to count all vertex degrees.

Fig.4:

Vertex degrees of the overlap graph of metagenomic short reads (ERR3450203) computed with Algorithm S4. The number of vertices per each degree is scaled as log log y. There is a clear peak around 10² at both incoming and outgoing degrees, which may imply dense existence of abundant species. The intermittent peaks after 10² might be related to repeating regions within and across species.

4. Prokrustean graph: A hierarchy of maximal repeats

The key idea of the Prokrustean graph is to recursively capture maximal repeats by their relative frequencies of occurrences in $\mathcal{U}$. Consider Figure 5 depicting repeats in three sequences ACCCT, GACCC, and TCCCG.

Fig.5:

Recursive repeats. At each sequence on the top level, locally-maximal repeat regions (indicated with blue underlining) are used to denote substrings that are more frequent than its superstring. The arrows then points to a node of the substring, and the process can repeat hierarchically.

Definition 2.

$(S,i,j)$ is a locally-maximal repeat region in $\mathcal{U}$ if:

$$\left|oc{c}_{\mathcal{U}}(str(S,i,j))\right|>\left|oc{c}_{\mathcal{U}}(S)\right|$$ (1)

and for each extension $\left(S,i^{\prime },j^{\prime }\right)$ of $\left(S,i,j\right)$,

$$\left|oc{c}_{\mathcal{U}}\left(str\left(S,i^{\prime },j^{\prime }\right)\right)\right|=\left|oc{c}_{\mathcal{U}}(S)\right|.$$ (2)

**Note that we often omit “in $\mathcal{U}$” when the context is clear.

A locally-maximal repeat region captures a substring that appears more frequently than the “parent” string, and any extension of the region captures a substring that appears as frequently as the parent string. Consider the previous example $\mathcal{U}=\left\{\text{ACCCT, GACCC, TCCCG}\right\}$. The region (ACCCT,1,4) is a locally-maximal repeat region capturing the substring ACCC in ACCCT. However, (ACCCT,2,4) is not a locally-maximal repeat region because the region capturing CCC in ACCCT can be extended to the left to capture ACCC which occurs more frequently than ACCCT.

Note, an alternative definition using substring notations, such as locally-maximal repeats, instead of regions, is not robust, hence the requirement for us to use region notation. Consider $\mathcal{U}=\left\{\text{ACCCTCCG, GCCC}\right\}$ and $S:=\text{ACCCTCCG}$. Observe that the region ($S,2,4$) capturing CCC is a locally-maximal repeat region because CCC occurs more frequently than $S$ in $\mathcal{U}$, but its immediate left and right extensions capture ACCC and CCCT that occur the same number of times as $S$. In constrast, a subregion ($S,2,3$) capturing CC is not a locally-maximal repeat region because an extension ($S,2,4$) still captures a string (CCC) which occurs 2 times in $\mathcal{U}$ which is more than $S$. However, ($S,6,7$), which also captures CC, is a locally-maximal repeat region because $\left|oc{c}_{\mathcal{U}}(\text{CC})\right|=5>\left|oc{c}_{\mathcal{U}}(S)\right|=1$ and $\left|oc{c}_{\mathcal{U}}(S)\right|=\left|oc{c}_{\mathcal{U}}(\text{TCC})\right|=\left|oc{c}_{\mathcal{U}}(\text{CCG})\right|$. Consequently, defining a locally-maximal repeat as S_6..7=CC becomes ambiguous when compared with S_2..3=CC, whereas an explicit expression of a region ($S,6,7$) more accurately reflects the desired property of hierarchy of occurrences.

The Prokrustean graph of $\mathcal{U}$ is simply a graph representation of the recursive structure. Its vertexes represent the substrings and edges represent locally-maximal repeat regions. The theorem below says that all maximal repeats in $\mathcal{U}$ are captured along the recursive description.

Proposition 1 (Complete).

Construct a string set $\mathbf{\text{R}}(\mathcal{U})$ as follows:

1. for each locally-maximal repeat region $(S,i,j)$ where $S\in \mathcal{U}$, add $\mathit{\text{str}}(S,i,j)$ to $\mathbf{\text{R}}(\mathcal{U})$ and

2. for each locally-maximal repeat region $(S,i,j)$ where $S\in \text{R}(\mathcal{U})$, add $\mathit{\text{str}}(S,i,j)$ to $\mathbf{\text{R}}(\mathcal{U})$.

Then it follows that $\mathbf{\text{R}}(\mathcal{U})={\mathcal{R}}_{\mathcal{U}}$ holds.

Proof. Any string in $\mathbf{\text{R}}(\mathcal{U})$ is a maximal repeat of $\mathcal{U}$, so the claim is satisfied if the process captures every maximal repeat of $\mathcal{U}$. Assume a maximal repeat $R$ is not in $\mathbf{\text{R}}(\mathcal{U})$. Consider any occurrence of $R$ in some $S\in \mathcal{U}$. Extending the maximal repeat $R$ within $S$ makes the number of its occurrences drop, but since $R$ cannot occur as a locally-maximal repeat region by assumption, it must be included in some locally-maximal repeat region that captures a maximal repeat $R_1$, hence $R_1\in \mathbf{\text{R}}(\mathcal{U})$, and $R$ is a proper substring of $R_1$. Now consider any occurrence of $R$ within $R_1$. This argument continues recursively, capturing maximal repeats $R_1,R_2,\dots$, but cannot extend indefinitely as $R_{i+1}$ is always shorter than $R_i$ for every $i\ge 1$. Eventually, $R$ must be occurring as a locally-maximal repeat region of some $R_n$, which is a contradiction. □

Therefore, we use maximal repeats as vertices of the Prokrustean graph, along with sequences, so $\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$.

Definition 3.

The Prokrustean graph of $\mathcal{U}$ is a directed multigraph ${\mathcal{G}}_{\mathcal{U}}:=\left({\mathcal{V}}_{\mathcal{U}},{\mathcal{E}}_{\mathcal{U}}\right)$:

• Vertex set ${\mathcal{V}}_{\mathcal{U}}:v_S\in {\mathcal{V}}_{\mathcal{U}}$ if and only if $S\in \mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$.

• Each vertex $v_S\in {\mathcal{V}}_{\mathcal{U}}$ is annotated with the string size, size $\left(v_S\right)=|S|$.

• Edge set ${\mathcal{E}}_{\mathcal{U}}:e_{S,i,j}\in {\mathcal{E}}_{\mathcal{U}}$ if and only if $(S,i,j)$ is a locally-maximal repeat region.

• Each edge $e_{S,i,j}\in {\mathcal{E}}_{\mathcal{U}}$ directs from $v_S$ to $v_{str}(S,i,j)$ and is annotated with the interval $\left(e_{S,i,j}\right):=(i,j)$, representing the locally-maximal repeat region.

Figure 6 visualizes how locally-maximal repeat regions are encoded in a Prokrustean graph. Next, the cardinality analysis of this representation reveals promising bounds.

Fig.6:

The Prokrustean graph of $\mathcal{U}=\left\{\text{ACCCT,GACCC,TCCCG,GGCG}\right\}$. The left graph illustrates the recursion of locally-maximal repeat regions, depicted as blue regions, following the same rule described in Figure 5. The Prokrustean graph on the right represents the same structure that white vertices correspond to sequences $\left(\mathcal{U}\right)$ and blue vertices represent maximal repeats $\left({\mathcal{R}}_{\mathcal{U}}\right)$ found through the recursion process shown in the left graph. The strings are not stored, so integer labels store the regions and the size of the substrings.

Theorem 2 (Compact).

$\left|{\mathcal{E}}_{\mathcal{U}}\right|\le 2|\Sigma |\left|{\mathcal{V}}_{\mathcal{U}}\right|$.

Proof. Every vertex in ${\mathcal{V}}_{\mathcal{U}}$ has at most one incoming edge per letter extension on the right (or similarly on the left), so has at most $2|\Sigma |$ incoming edges. Assume the contrary: a maximal repeat appears as two different locally-maximal repeat regions $(S,i,j)$ and $\left(S^{\prime },i^{\prime },j^{\prime }\right)$ within $S$, $S^{\prime }\in \mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$, and can extend by the same letter on the right, i.e., $(S,i,j+1)$ and $\left(S^{\prime },i^{\prime },j^{\prime }+1\right)$ capture the same string. Extending these regions further together will eventually diverge their strings, because either $S\ne S^{\prime }$ or the original two regions are differently located even if $S=S^{\prime }$. Consequently, at least one of them—$(S,i,j+1)$ without loss of generality—results in a decreased occurrence count of its string as it extends. Hence, $|occ\mathcal{U}(str(S,i,j+1))|>|occ\mathcal{U}(S)|$. This leads to contradiction because a locally-maximal repeat region $(S,i,j)$ should satisfy $|oc{c}_{\mathcal{U}}(S,i,j+1)|=|oc{c}_{\mathcal{U}}(S,1,|S|)|$. □

Assuing that $|\mathcal{U}|\ll \left|{\mathcal{R}}_{\mathcal{U}}\right|$, as is overwhelmingly the case in practice—meaning there are significantly more maximal repeats than sequences—we derive that $O\left(\left|{\mathcal{V}}_{\mathcal{U}}\right|\right)=O\left(\left|{\mathcal{R}}_{\mathcal{U}}\right|\right)$. Hence, $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right):=O\left(\left|{\mathcal{E}}_{\mathcal{U}}\right|\right)=O\left(\left|\Sigma \Vert {\mathcal{R}}_{\mathcal{U}}\right|\right)$ by the theorem. Given that $|\Sigma |$ is typically constant in genomic sequences (eg. $\Sigma =\{A,C,T,G\}$), the graph’s size depends on the number of maximal repeats. Letting $N$ be the accumulated sequence length of $\mathcal{U}$, it is a well-known fact that $\left|{\mathcal{R}}_{\mathcal{U}}\right|<N$ [25], so the graph grows sublinear to the input size. Furthermore, Section 3 restricted ${\mathcal{R}}_{\mathcal{U}}$ to maximal repeats of length at least $k_{\min }$. Setting a practical threshold $k_{\min }$ allows for significantly more efficient and configurable space usage.

4.1. Prokrustean graph construction

We leave the construction algorithm in Supplementary Section S3. However, we emphasize that the core insight of our study comes from the relationship between the Prokrustean graph and suffix trees. It turns out that a straightforward transformation can be defined with affix trees—the union of the suffix tree of $\mathcal{U}$ and the suffix tree of its reversed strings. A subset of edges of the affix tree of $\mathcal{U}$ corresponds to the reversed edge set of the Prokrustean graph of $\mathcal{U}$. But affix trees are resource-intensive, so our final algorithm utilizes the BWT of $\mathcal{U}$, adding more intermediate steps to compensate for the non-bidirectional substring representation.

5. Framework: Computing $k\text{-}mer$ quantities for all $k$ sizes

We first describe the type of information required to efficiently compute k-mer quantities (defined in Theorem 1) to elucidate the uniqueness of the Prokrustean graph. Specifically, why can’t other modern substring indexes be used for the computations in previous results? The answer also implies why developing efficient multi-k k-mer-based methods has been challenging.

5.1. A proxy problem: computing substring co-occurrence.

There exists a theoretical void in identifying when a k-mer and a k′-mer serve similar roles within their respective substring sets. Although close k-mer sizes generally yield comparable outputs, dissecting this phenomenon at the level of local substring scopes is unexpectedly challenging. For instance, de Bruijn graphs constructed from sequencing reads with k = 30 and k′ = 31 display distinct yet highly similar topologies [40]. However, anyone formally articulating the topological similarity would find it quite elusive, as vertex mapping and other techniques establishing correspondences between the two graphs fail to consistently explain it.

A common underlying difficulty is that the entire k-mer set undergoes complete transformations as the k-mer size changes. Since the role of a k-mer is assigned within its k-mer set, the role of a k′-mer within k′-mers cannot be “locally” derived. To address this issue, we propose substring co-occurrence as a generalized framework for consistently grouping k-mers of similar roles across varying k-mer sizes.

Definition 4.

A string $S$ co-occurs within a string $S^{\prime }$ in $\mathcal{U}$ if:

$$Sisasubstringof{S}^{\prime }and\left|oc{c}_{\mathcal{U}}(S)\right|=\left|oc{c}_{\mathcal{U}}\left(S^{\prime }\right)\right|.$$

Modern substring indexes built on longest common prefixes of suffix arrays are adept at capturing co-occurrence while extending a substring. In suffix trees, a substring that extends from $S$ to $S^{\prime }$ along an edge—without passing through a node—indicates preservation of co-occurrence. Similarly, the BWT and its variants represent both $S$ and $S^{\prime }$ with the same set of suffix array intervals to imply co-occurrence. However, there has been no recognized necessity for capturing co-occurrence for substrings rather than superstrings:

Definition 5.

$co-subst{r}_{\mathcal{U}}\text{(}S\text{)}$ is the set of substrings that co-occur within $S$.

Modern substring indexes would fail to “smoothly” move over the order $\left(k\right)$ unless $co-subst{r}_{\mathcal{U}}\text{(}S\text{)}$ is efficiently accessible. For instance, the variable-order de Bruijn graph and its variants extend a compact de Bruijn graph representation built on the Burrows-Wheeler Transform [12]. To address the large substring space, these solutions require non-trivial operation times for both forward moves and order changes [5, 11].

We argue the usefulness of $co-subst{r}_{\mathcal{U}}\text{(}S\text{)}$ with a simple yet foundational property.

Theorem 3 (Principle).

For any substring $S$ such that $oc{c}_{\mathcal{U}}(S)>0$,

$$S\mathit{co-occurs\; within\; exactly\; one\; sequence\; or\; maximal\; repeat\; in}\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}.$$

Proof. Assume the theorem does not hold, i.e., $S$ co-occurs within either no string or multiple strings in $\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$. Consider the former case: $S$ co-occurs within no string in $\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$, meaning $S$ occurs more than any of its superstrings in $\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$. Given that $S$ occurs in some string $S^{\prime }\in \mathcal{U}$ (since $occ{u}_{\mathcal{U}}(S)>0$, $S$ must be occurring more frequently than $S^{\prime }$ by assumption. Then, there exists a maximal repeat $R$ such that $S$ is a substring of $R$ and $R$ is a substring of $S^{\prime }$, because extending $S$ within $S^{\prime }$ decreases its occurrence at some point. Again, whenever $S$ is a substring of a maximal repeat $R$, $S$ must be occurring more frequently than $R$ by assumption. Following the similar argument above, there exists another maximal repeat $R^{\prime }$ such that $S$ is a substring of $R^{\prime }$ and $R^{\prime }$ is a proper substring of $R$. This recursive argument will eventually terminate as $R^{\prime }$ is strictly shorter than $R$. Thus, $S$ co-occurs within the last maximal repeat, which contradicts the assumption.

Now consider the latter case where $S$ co-occurs within at least two strings in $\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$. If $S$ is extended within these two strings, either to the right or left by one step at each time, the extensions eventually diverge into two different strings since the two superstrings differ, thereby reducing the number of occurrences. Hence, $S$ must be occurring more frequently than at least one of those two superstrings, leading to a contradiction. □

This theorem provides two insights. First, the sequences and maximal repeats $\mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$ comprehensively and disjointly cover the entire substring, i.e., every substring in $\mathcal{U}$ is in ${⨆}_{S\in \mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}}co-stac{k}_{\mathcal{U}}(S)$. Second, by computing $co-subst{r}_{\mathcal{U}}(S)$ for every $S\in \mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}$, we can categorize k-mers of similar roles across various lengths. Therefore, we aim to design a succinct representation of $co-subst{r}_{\mathcal{U}}\text{(}S\text{)}$ that can be accessed by the Prokrustean graph.

5.2. An algorithmic idea: co-occurrence stacks.

We apply the Prokrustean graph to compute k-mer quantities for all k sizes within the $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$ time and space. Previously, a toy example in Figure 5 depicted blue regions that cover locally-maximal repeat regions. Then, given a k-mer size, a complementary region is a maximal region that covers k-mers that are not included in a blue region. See the red regions underlining in Figure 7. An opportunistic property is that k-mers in red regions co-occur within their parent strings. The following notation captures substrings in red regions.

Fig.7:

Complementary regions. Blue underlining depicts locally maximal regions, and red underlining depicts regions that complement k-mers not covered in blue regions, given k values of 3 and 4. Every k-mer appears exactly once within a red region. For example, in the left image, the 3-mer ACC is included in a red region within ACCCC and does not appear again in any other red region. Note that red regions can include multiple co-occurring k-mers. So, in the right image, both 4-mers TCCC and CCCG co-occur within TCCCG.

Definition 6.

A string $S$ k-co-occurs within a string $S^{\prime }$ in $\mathcal{U}$ if:

$$everyk-merinSco-occurswithin{S}^{\prime }in\mathcal{U}.$$

Furthermore, $S$ maximally k-co-occurs within $S^{\prime }$ in $\mathcal{U}$ if no superstring of $S$ k-co-occurs within $S^{\prime }$ in $\mathcal{U}$. The red regions in Figure 7 identify maximal k-co-occurring substrings of $S^{\prime }$, so the Prokrustean graph can be used to efficiently compute co-occurring k-mers of a fixed k-mer size. Now, we extend red regions for all possible k values, as shown in Figure 8. Observe that stack-like structures are formed around locally-maximal repeat regions of the string. The shape motivated the following definition:

Fig.8:

Three types of maximal co-occurrence stacks. Maximal co-occurrence stacks of $S$ (sets of red rectangles) are introduced at each row for each type, given two locally-maximal repeat regions in $S$ (blue rectangles). The Rate column describes the change in the count of expressed k-mers as the k-mer size increases by 1. Hence, the rate is ${\delta }_l+{\delta }_r-1$. Also, ${\delta }_l$ and ${\delta }_r$ control the vertical shapes of stacks. For example, the Type 0 stack forms like a rectangle with ${\delta }_l={\delta }_r=0$, but the Type 1 stack forms like stairs on its left with ${\delta }_l=1$.

Definition 7.

Consider two strings $S$ and $T$ where $T$ is a substring of $S$, along with two numbers: a depth $d^{\ast }$ and a k-mer size $k^{\ast }$, each at least 1. A co-occurrence stack of $S$ in $U$ is defined as a 4-tuple:

$$\left(S,T,k^{\ast },d^{\ast }\right)$$

if for each $i=1,2,\dots ,d^{\ast }$, for $k_i=k^{\ast }-(i-1)$, and for change rates ${\delta }_l:={\mathit{1}}_T$ is NOT a prefix of $S$ and ${\delta }_r:={\mathit{1}}_T$ is NOT a suffix of $S$, the following holds:

$$str\left(T,1+{\delta }_l\cdot (i-1),\left|T\right|-{\delta }_r\cdot (i-1)\right)\text{maximally}{k}_i\text{-co-occurs within}S.$$

A co-occurrence stack expresses a k-mer if the k-mer is a substring of some k-co-occurring substring identified by the stack. A co-occurrence stack is maximal if its expressed k-mers are not a subset of those expressed by any other co-occurrence stack.

Let the set of all maximal co-occurrence stacks of $S$ in $\mathcal{U}$ as $co-stac{k}_{\mathcal{U}}(S)$. It is straightforward to check that no two stacks in $co-stac{k}_{\mathcal{U}}(S)$ express the same k-mer together. So, we can nicely cover $co-stac{k}_{\mathcal{U}}(S)$ with $co-stac{k}_{\mathcal{U}}(S)$. We extend the scheme to the substring space of $\mathcal{U}$. Define ${\mathcal{S}}_{\mathcal{U}}:={\cup }_{S\in \mathcal{U}\cup {\mathcal{R}}_{\mathcal{U}}}co-stac{k}_{\mathcal{U}}(S)$.

Theorem 4 (Framework).

${\mathcal{S}}_{\mathcal{U}}$ is a complete substring representation of $\mathcal{U}$ such that every substring (any k-mer of any k value) in $\mathcal{U}$ is expressed by exactly one stack in ${\mathcal{S}}_{\mathcal{U}}\cdot \left|{\mathcal{S}}_{\mathcal{U}}\right|$ is bounded by $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$, and can be enumerated in $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$ time given ${\mathcal{G}}_{\mathcal{U}}$.

Proof. Supplementary Section S2 derives this result.

5.3. Algorithms

${\mathcal{S}}_{\mathcal{U}}$ is used in the four algorithms computing the results in Section 3. For each stack in ${\mathcal{S}}_{\mathcal{U}}$, constant-time operations are defined, and since $\left|{\mathcal{S}}_{\mathcal{U}}\right|$ is $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$, the time complexity of the algorithms is independent of the k-mer size interval $\left[k_{min},k_{max}\right]$.

For example, consider using the stack in the first row of Figure 8 for counting distinct k-mers. The co-occurrence stack $\left(S,T=ACTCCGAAT,k^{\ast }=9,d^{\ast }=4\right)$ compactly represents the information of co-occurring substrings. From k = 6 to k = 9, the counts of expressed k-mers of $S$ consistently decrease by 1, starting from 4. Therefore, for a count vector defined for the interval $\left[k_{min},k_{max}\right]$, an algorithm can implement the contribution of the stack by “adding 4 to the count vector at k = 6” and “recording a change rate decrease of 1 at k = 6 and restoring it at k = 9.” Repeating this process for all stacks in ${\mathcal{S}}_{\mathcal{U}}$ counts all k-mers in $\mathcal{U}$ and takes $O\left(\mid {\mathcal{S}}_{\mathcal{U}}\right)\mid$ time. Refer to Supplementary Algorithm S1, Algorithm S2, Algorithm S3, and Algorithm S4 for the whole contexts.

6. Conclusion

We have introduced the problem of computing co-occurring substrings $co-subst{r}_{\mathcal{U}}\text{(}S\text{)}$ as a proxy to analyze the influence of k-mer sizes in k-mer-based methods. The Prokrustean graph facilitates access to $co-subst{r}_{\mathcal{U}}\text{(}S\text{)}$ by iterating over $co-stac{k}_{\mathcal{U}}(S)$, which is used to implement algorithms that compute k-mer-based quantities across a range of k sizes. Once the Prokrustean graph is constructed using the BWT in a space-efficient manner, the computation of k-mer-based quantities for all k-mer sizes becomes roughly equivalent to scanning the graph. Furthermore, we can control the performance by choosing $k_{min}$, the smallest maximal repeat size, so that the graph size is adjusted based on the needs of analyzed methods.

The Prokrustean graph and the affix tree have intuitive relationships, as shown in Supplementary Figure S10. The contrast lies in accessing the co-occurrence structure. Suffix trees represent co-occurrence by extending substrings, functioning as a “bottom-up” approach. The Prokrustean graph, however, follows a “top-down” approach, as co-occurring substrings (not superstrings) are identified in constant time. The issue with the bottom-up approach is that not all co-occurrence stacks $co-stac{k}_{\mathcal{U}}(S)$ are easily identified, even if bidirectional substring indexes are employed. For example, the Type-2 stack in Figure 8 requires information about two locally-maximal repeat regions within close proximity in a string, which is difficult to identify with substring extending operations. We therefore conjecture that exploring the space of k-mers with modern LCP-based substring indices presents an intrinsic challenge.

The results in Section 3.3 on counting maximal unitigs imply that a Prokrustean graph can smoothly explore de Bruijn graphs of all orders. Thus, the Prokrustean graph can advance the so-called variable-order scheme [11] by representing the union of de Bruijn graphs of all orders. A straightforward approach is to use the maximal co-occurrence stacks ${\mathcal{S}}_{\mathcal{U}}$ as a vertex set. We have confirmed that an edge set of size $O\left(\left|{\mathcal{G}}_{\mathcal{U}}\right|\right)$ can represent all extensions between the stacks. Since the Prokrustean graph does not grow faster than the number of maximal repeats, this new representation can serve as a compact multi-k assembly graph, more precisely identifying sequencing read errors, SNPs in population genomes, and genome contigs.

Thus, the open problem 5 in [40], which calls for a practical representation of variable-order de Bruijn graphs that generates assembly comparable to that of overlap graphs, can be answered with the Prokrustean graph. Recall that Section 3.5 analyzed the overlap graph of $\mathcal{U}$. The two popular objects used in genome assembly can be accessed together through the Prokrustean graph.

There is abundant literature analyzing the influence of k-mer sizes in various bioinformatics tasks, but little effort has been made to derive rigorous formulations or quantities to explain these phenomena. We expect our framework to contribute as an initial step toward understanding the influence, at least at the base level of k-mer-based objects of sequencing data or reference genomes.

Table 2:

Counting distinct k-mers with Prokrustean graphs with Algorithm S1. For comparisons, KMC had to be executed iteratively causing the computational time to increase steadily as the range of k increases. The running time of KMC took about 1–3 minutes for each k-mer size.

Dataset	k	KMC			Prokrustean Graph
		time	memory	threads	time (build)	memory	threads
SRR20044276	20...150	4.5m	840mb	8	0.36s (13s)	80mb	8
ERR3450203	20...150	50m	12gb	8	30s (29min)	6gb	8
SRR18495451	30...50000	days	-	8	88s (90min)	24gb	8
SRR7130905	30...150	66m	12gb	8	46s (39min)	8.5gb	8
SRR21862404	30...150	112m	13gb	8	74s (99min)	13.8gb	8