Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2024 May 23;9(22):23241–23251. doi: 10.1021/acsomega.3c09247

RamanFormer: A Transformer-Based Quantification Approach for Raman Mixture Components

Onur Can Koyun †,*, Reyhan Kevser Keser †, Safa Onur Şahin ‡, Damla Bulut ‡, Mustafa Yorulmaz ‡, Veysel Yücesoy ‡, Behçet Uğur Töreyin †
PMCID: PMC11154961  PMID: 38854537

Abstract

graphic file with name ao3c09247_0008.jpg

Raman spectroscopy is a noninvasive technique to identify materials by their unique molecular vibrational fingerprints. However, distinguishing and quantifying components in mixtures present challenges due to overlapping spectra, especially when components share similar features. This study presents “RamanFormer”, a transformer-based model designed to enhance the analysis of Raman spectroscopy data. By effectively managing sequential data and integrating self-attention mechanisms, RamanFormer identifies and quantifies components in chemical mixtures with high precision, achieving a mean absolute error of 1.4% and a root mean squared error of 1.6%, significantly outperforming traditional methods such as least squares, MLP, VGG11, and ResNet50. Tested extensively on binary and ternary mixtures under varying conditions, including noise levels with a signal-to-noise ratio of up to 10 dB, RamanFormer proves to be a robust tool, improving the reliability of material identification and broadening the application of Raman spectroscopy in fields, such as material science, forensics, and biomedical diagnostics.

1. Introduction

Raman spectroscopy is a powerful analytical technique for material identification. It can be utilized to measure the inelastic scattering of light by molecular vibrations in a material. The characteristic vibrational modes of molecules give rise to a unique Raman spectrum which can be used as the “fingerprint” of the material. Moreover, the chemical composition of the material can be identified. Hence, Raman spectroscopy can be utilized for the identification of the unknown materials. Moreover, this technology is a fast, label-free, and noninvasive tool.1,2

The advantages of Raman scattering lead to its use in various fields. It has a wide range of application areas including material identification, food analysis, disease diagnosis, and forensic analysis.3−6 As an example for food analysis, a study7 utilizes surface-enhanced Raman scattering (SERS) to analyze food colorants which are food blue, tartrazine, sunset yellow, and acid red. Another study8 classifies milk samples from different species by using Raman spectroscopy. Additionally, Raman scattering offers significant utility in forensic analysis, primarily because it is a noncontact and nondestructive method. For example, Gasser et al.9 design a hyperspectral Raman imager technique to detect and classify explosives at a distance of 15 m. Dies et al.10 utilize SERS to detect illicit drugs, such as cocaine. Doty and Lednev11 employ Raman spectroscopy with partial least-squares discriminant analysis (PLSDA), to differentiate human and animal blood.

On the other hand, Raman spectroscopy can also be utilized for disease diagnosis. For instance, Kim et al.12 design a chip fabrication method for SERS analysis to detect prenatal diseases from amniotic fluids. Lim et al.13 exploit SERS analysis as well, to identify cells infected with different influenza viruses. Further, they demonstrate that their approach can be utilized to detect newly emerging influenza viruses. Mineral identification is among a wide range of applications in which Raman spectroscopy serves as a powerful tool for material analysis. The majority14,15 of public and comprehensive Raman data sets consist of mineral spectra, while the research on mineral classification includes the works by Sang et al.,16 Liu et al.17 and Liu et al.18

Mixture analysis on the Raman spectrum is an open research direction, where the aim is identifying and quantifying the components in a given mixture spectrum. In this study, an approach for the identification and quantification of the components in a Raman mixture is proposed. For this purpose, we introduce RamanFormer, which is a transformer-based19 approach for Raman mixture analysis. To summarize, our contributions can be listed as follows:

  • 1.

    Introduction of RamanFormer, a novel transformer-based model specifically designed for the analysis of Raman spectroscopy mixtures, representing a significant advancement in the field of spectroscopy.

  • 2.

    Comprehensive evaluation of the model’s performance across various data samples, including binary and ternary chemical mixtures, showcasing its superior performance over traditional and contemporary methods in terms of root mean squared error (RMSE) and mean absolute error (MAE).

  • 3.

    Demonstration of RamanFormer’s robustness in challenging scenarios, such as those involving components present in low amounts and conditions of varying noise levels, highlighting its practical applicability in real-world spectroscopic analysis.

  • 4.

    Empirical evidence of the model’s adaptability and resilience, proving its capability to accurately identify and quantify components in mixtures under diverse conditions.

  • 5.

    Exploration of the potential of advanced machine learning architectures, like transformers, in spectroscopy, paving the way for future advancements in various applications including material science, food safety, forensics, and medical diagnostics.

2. Related Work

Raman spectrum analysis is an extensively studied area in the literature. Here, we specifically focus on the optimization-based algorithms, where we partition these methods as machine learning and deep learning methods for processing Raman signals.

2.1. Machine Learning and Deep Learning Methods for Raman Signal Analysis

2.1.1. Machine Learning Methods for Processing Raman Signals

Many supervised learning algorithms are used for Raman spectrum analysis.20 For instance, some studies utilize methods based on discriminant analysis, such as linear discriminant analysis (LDA)21,22 and PLSDA.23,24 Furthermore, some papers exploit artificial neural network (ANN) based models such as multilayer perceptron (MLP)25,26 and convolutional neural network (CNN).27,28 Moreover, some studies employ regression analysis-based methods, e.g., multiple linear regression (MLR),29 principal component regression (PCR),30 and partial least squares (PLS).22 Besides, Li et al.31 and Li et al.32 utilize k-nearest neighbor on Raman spectra for the detection of cancer types of breast and colon, respectively. Zivanovic et al.33 and Banaei et al.34 use the random forest approach for the identification of molecular colocalization and interactions of the drug molecules, and cancer diagnostic, respectively. Additionally, some studies employ support vector machine (SVM) on Raman signals for various fields such as the food industry and medicine.21,35,36

2.1.2. Deep Learning Methods for Processing Raman Signals

In general, Raman signal processing involves essential steps, such as data preprocessing, feature extraction (or selection), and data modeling. While classical machine learning techniques are commonly applied in Raman spectroscopy, these intricate processes can be performed by a singular neural network, given an adequate amount of training data. Depending on the output types, deep learning applications for Raman spectroscopy can be divided into four main parts: preprocessing, classification, regression, and spectral highlighting.37

As an example of preprocessing, Wahl et al.38 propose a one-step automatic Raman spectral preprocessing method using CNN. First, the authors create synthetic spectra by randomly adding signal peaks, baselines, and background noise. Then, they train a CNN model to map a set of input Raman spectra to the corresponding ideal spectrum. Furthermore, Valensise et al.39 apply a 1-D CNN model to subtract the nonresonant background (NRB) from broadband coherent anti-Stokes Raman scattering (B-CARS) spectra. This model is called SpecNet, which consists of five convolutional layers, followed by three fully connected layers.

Similar to the preprocessing phase, 1-D CNNs also hold considerable importance in the classification of Raman spectra. For instance, in the differentiation of human and animal blood, Dong et al.28 utilize a streamlined network adapted from the LeNet-5 architecture, incorporating only two convolutional layers for feature extraction, succeeded by a fully connected layer for classification. Consequently, the authors attain an accuracy of 96.33%. In another study, a 1-D CNN is used to detect prostate cancer from Raman spectra of extracellular vesicles.40 To assess the disease activity of ulcerative colitis (UC), Kirchberger-Tolstik et al.41 also use a 1-D CNN and achieve an average sensitivity of 78% and an average specificity of 93% for the four Mayo endoscopic scores. To detect microbial contamination, Maruthamuthu et al.42 use a 1-D CNN to distinguish the Raman spectra of Chinese hamster ovary (CHO) cells from 12 microbe species. In addition, a new approach called “deep learning-based component identification” (DeepCID) is introduced by Fan et al.43 Authors show that DeepCID achieves an accuracy of 98.8% for all 167 components. Fu et al.44 propose a lactose-dominated drug (LLD) quantity model which is based on the non-negative least-squares (NNLS) algorithm and DeepCID.

Autoencoders and ResNets are widely utilized for the classification of Raman spectra as well as 1-D CNNs. For example, Houston et al.45 use a locally connected neural network (LCNN) to create an accurate and robust two-stage classification model in the case of negative outliers. In this model, while the LCNN is designed to train data, an automatic encoder is used for outlier detection. Furthermore, Ho et al.46 propose a mesh with 25 convolutional layers for rapid bacterial identification. The antibiotic therapy identification accuracy of their model was 97.0 ± 0.3%. For pathogen classification, Yu et al. combine Raman spectroscopy with a generative adversarial network (GAN)47 to achieve high accuracy when the training data set is limited.48

Due to the limited size of the data set, other researchers observe the utility of employing transfer learning during the training of classification models for Raman spectroscopy. For example, Thrift and Ragan49 employ a CNN-based monomolecule SERS measurement method that transfers information from the Rhodamine 800 (R800) domain to the methylene blue (MB) domain. They show that SERS measurement methods can be quite satisfactory, even with only 50 new MB training samples. In addition, Zhang et al.50 pretrain a CNN model on a source data set consisting of Bio-Rad and RRUFF databases. Subsequently, they accomplish a 4.1% improvement in classification accuracy using solely 216 new spectra from the target data set.

2.2. Raman Mixture Analysis

Studies on Raman mixture analysis can be categorized into two groups based on the methodology. The first group contains studies that identify the components in a mixture without quantification of the components. For example, Pan et al.51 propose a deep neural network-based approach for ternary mixtures that contain oleic acid, palmitic acid, and retinyl palmitate. Wang et al.52 introduce a CNN-based method for the identification of chemical mixture components such as methanol, ethanol, and propylene glycol. In another study,53 an approach based on similarity analysis and sparse non-negative least squares is proposed to identify the components in liquid and powder mixtures. Zhao et al.54 introduce an approach called ConInceDeep, which combines continuous wavelet transform and Inception model55 to predict the binary existence of components in a mixture. Moreover, Fan et al.43 propose a CNN-based approach to determine the presence of components in a mixture where an individual model is employed for each component.

On the other hand, the second group of studies focuses on the quantification of the components in a mixture as well as the detection of their presence. For instance, Keren et al.56 utilize the least-squares method for mixture analysis on living subjects such as mice. Similarly, Zhang et al.57 exploit a modified reverse searching method and non-negative least squares for identification and quantification of the components in a mixture, respectively. Zeng et al.58 propose a mixture analysis approach based on a non-negative elastic net to quantify the components in mixtures that are measured or generated using the spectra of the components. Li et al.59 introduce a CNN-based approach for spectral unmixing of a mixture of various dyes for mRNA biomarker detection. In another study,60 a CNN-based approach is proposed to identify and quantify the components in SERS (surface-enhanced Raman spectroscopy) spectra of mixtures that contain chemicals widely used in agricultural production. Furthermore, a recent study61 introduces a Python package to generate Raman mixture data sets, where several algorithms are evaluated on these data sets for predicting the concentrations of mixture components.

3. Methodology

Our predictive model is based on a transformer,19 which is a deep neural network architecture designed to capture intricate patterns in the input. Transformers are initially proposed for NLP tasks. However, now they have been extensively utilized across various domains, including computer vision,62 chemistry,63 and life sciences,64 thanks to their success in numerous tasks. The main distinctive point that differentiates them from previous approaches is their self-attention mechanism. This mechanism is designed to enable the model to capture dependencies between words that are far apart in the sequence, making it effective for tasks that require an understanding of long-range dependencies, such as language translation and text summarization.

3.1. Preliminary: Transformer Layer

Transformer19 models have revolutionized the field of natural language processing (NLP) by introducing a novel architecture that eschews recurrent layers in favor of self-attention mechanisms and feed-forward neural networks. At the heart of the transformer architecture are the transformer layers, which are composed of several key components: the attention layer, feed-forward layers, layer normalization, and the Gaussian error linear unit (GELU) activation function. Further, in our proposed method, we employ three transformer encoder layers.

3.1.1. Attention Mechanism

The attention mechanism is the core component of transformer models, enabling the model to dynamically focus on different parts of the input sequence when an output sequence. The mechanism is mathematically represented as

3.1.1. 1

where Q, K, and V represent the query, key, and value matrices, respectively, derived from the input embeddings. The term dk represents the dimensionality of the key vector K, which is used to scale the dot product, thus helping in stabilizing the gradients during training.

3.1.2. Feed-Forward Layers

Following the attention mechanism in each transformer layer is a feed-forward network (FFN), which applies two linear transformations with a GELU activation in between:

3.1.2. 2

where x is the input. W1, W2, b1, and b2 are the weights and biases of the two linear layers, respectively.

3.1.3. Layer Normalization

Layer normalization is applied within the transformer layers to stabilize the activations across the network. It normalizes the inputs across the features for each data point in a mini-batch and is evaluated as follows:

3.1.3. 3

where μ and σ2 are the mean and variance of the input, ϵ is a small constant added for numerical stability, and γ and β are learnable parameters for scaling and shifting, respectively.

3.1.4. Gaussian Error Linear Unit

The GELU is a nonlinear activation function that has been shown to improve the performance of transformer models. It is defined as

3.1.4. 4

where Φ(x) is the cumulative distribution function of the standard normal distribution. The GELU function allows the model to capture nonlinearities in the data, contributing to the overall expressive power of the transformer.

Transformer layers, through the integration of attention mechanisms, FFNs, layer normalization, and GELU activation functions, provide a powerful framework for modeling sequential data. These components work in harmony to enable the transformer model to capture complex dependencies and relationships in the data, making it highly effective for a wide range of learning tasks.

3.2. Proposed Method: RamanFormer

As shown in Figure 1, our model consists of particular layers to achieve a successful mixture analysis. In the “patchify layer”, we extract nonoverlapping patches of 128 units in length from the Raman spectra data. These patches then undergo a linear transformation using a 128 × 256 weight matrix, followed by a ReLU activation to introduce nonlinearity, since nonlinearity is crucial to enable a neural network to approximate nonlinear functions effectively.

Figure 1.

Figure 1

Open in a new tab

Diagram illustrates the sequential composition of layers in the proposed model for robust spectral analysis and precise component ratio prediction. Here, N stands for the number of samples (eq 5).

Our model includes three transformer encoder layers, which are responsible for obtaining meaningful hidden representations from the input data. Within the transformer encoder layers, our model operates at a dimensionality of 256. The core element of a transformer encoder is the self-attention mechanism, which provides the model to learn the long-term dependencies of the input. We employ eight self-attention heads to capture various aspects of the data’s dependencies, while the feed-forward dimension is set to 1024, ensuring effective feature representation.

After the transformer encoder layers, data are fed into convolution layers, which provide capturing spatial hierarchies in the input. In our model, the convolution layers comprise 1-D filters (256 and 512 filters of size 9) with a stride of 2. To account for boundary effects, padding is applied with a width of 4 units. After each convolution layer, batch normalization and GELU activation are applied, where batch normalization is used to normalize the data and stabilize the training process, and GELU is employed to obtain a more stable training process due to its smooth nature.

The features obtained from these layers undergo global average pooling, which aggregates information across the temporal dimension, thereby compactly representing crucial details while mitigating noise. This pooled representation is then propagated through linear layers with ReLU activations, further enhancing the model’s capacity to capture complex patterns. These layers reduce the dimensions of data from 512 to 256 and subsequently to M, where M is the number of distinct components. In this study, we choose M as 3, since the mixtures in our data set consist of three components, at most. Hence, the last layer produces predicted component ratios as the final output. The model’s training employs an L1 loss function, as shown in eq 5, quantifying the absolute disparity between predicted and actual ratios:

3.2. 5

where yi and ŷi are the true and predicted values for the ith sample, respectively, and N is the number of samples.

These architecture details outline a comprehensive framework designed to extract, transform, and analyze spectral data, enabling an accurate prediction of component ratios.

3.3. Model Training

The proposed deep learning model is trained using a data set containing Raman spectra and corresponding ground truth component ratios. The training process involves the following steps:

  • 1.
    Data Augmentation: During training, each input spectrum is augmented by adding a small amount of random noise. This enhances the model’s robustness and generalization to noisy spectra. Given a clean signal x, the additive noise model applies Gaussian noise n with mean μ and standard deviation σ, resulting in a noisy signal y as follows:
    graphic file with name ao3c09247_m006.jpg 6
  • 2.

    Optimizer and Learning Rate Schedule: The stochastic gradient descent optimizer with momentum and weight decay is used for parameter optimization. A cosine annealing learning rate schedule is applied to reduce the learning rate during training gradually.

  • 3.
    Evaluation: We comprehensively evaluate our proposed model using a leave-one-out cross-Inline graphic (LOOCV) method due to limited data availability. We use MAE and RMSE metrics to evaluate the outputs of our algorithm given in eqs 7 and 8, respectively:
    graphic file with name ao3c09247_m008.jpg 7
    graphic file with name ao3c09247_m009.jpg 8
    We also utilized the signal-to-noise ratio (SNR) to assess the performance of our method against noise. Let Psignal and Pnoise be the signal power and noise power, respectively. SNR is defined in eq 9 as follows:
    graphic file with name ao3c09247_m010.jpg 9

4. Raman Spectroscopy Setup and Raman Spectral Mixture Data Set

We used a commercially available USB Raman spectrometer (QE Pro Raman+) for recording the Raman spectra. The laser excitation of the sample at 785 nm and Raman signal collection after excitation are performed by using a Raman fiber optic probe, which is equipped with excitation and collection fibers. The laser is coupled to the excitation fiber tip through the SMA-SMA connectors. It is then directed toward the chemical holder cuvette upon reflection off a dichroic mirror and is focused on the cuvette via a lens. The generated Raman signal is collected by the same lens, spectrally filtered, and coupled to the collection fiber tip. The collection fiber tip is then connected to the USB spectrometer.

We collect a Raman data set of 37 samples in total, to identify and quantify the components in a given mixture, where the data set contains three chemicals and their various binary and ternary mixtures. We choose methanol (Tekkim TK.911022.02501), isopropyl alcohol (Tekkim TK.090250.02501), and ethanolamine (Fisher Chemical E/0701/08), i.e., easily accessible chemicals in laboratories. For Raman spectroscopy, we prepare the chemicals and their mixtures in cuvettes (ISOLAB I.098.02.002.100) that are typically used in spectrophotometers. First of all, we measured the Raman spectra of individual chemicals to determine the spectral characteristics of the chemicals. We also collect the spectrum of the empty cuvette to account for the spectral lines emitted from the chemical holder, which is made of polystyrene. We then prepare numerous mixtures of two chemicals with alternating ratios, from methanol, isopropyl alcohol, and ethanolamine, to expose the proposed transformer-based algorithm with a spectrally wide range of samples.

We further examine the mixtures of chemicals that are prepared by using three chemicals to evaluate how the algorithm performs for differentiating the components of ternary mixtures. For this purpose, we prepare a 1:1:1 mixture of methanol, isopropyl alcohol, and ethanolamine, as well as the three-chemical mixtures with varying volume amounts. Figure 2 shows an exemplary spectrum of a mixture and the three main components in the data set, namely, methanol, isopropyl alcohol, and ethanolamine. Table 1 summarizes the component ratios of mixtures in our data set. It is important to note that for all measurements performed on mixtures 120 mW excitation laser power at 785 nm is used with an acquisition time of 5 s.

Figure 2.

Figure 2

Open in a new tab

Raman spectra presented here showcase a specific ternary mixture and its individual components: (a) methanol (M), (b) isopropyl alcohol (IPA), and (c) ethanolamine (E) and (d) Raman spectrum of a ternary mixture composed of M, IPA, and E. The respective ratios of these components in the mixture are methanol at 78.75%, isopropyl alcohol at 8.75%, and ethanolamine at 12.50%.

Table 1. Component Ratios for the Mixtures in Our Training Set, Which Are Controlled Series of Alternating Two- and Three-Chemical Mixtures with Depicted Varying Volume Amountsa.

mixture of M and IPA (%)
 mixture of M and E (%)
 mixture of IPA and E (%)
 mixture of M, IPA, and E (%)
M IPA M E IPA E M IPA E
10 90 10 90 10 90 8.75 78.75 12.50
20 80 20 80 20 80 17.50 70 12.50
40 60 40 60 40 60 35 52.50 12.50
50 50 50 50 50 50 33.33 33.33 33.33
60 40 60 40 60 40 52.50 35 12.50
80 20 80 20 80 20 70 17.50 12.50
90 10 90 10 90 10 78.75 8.75 12.50
Open in a new tab
a

M, IPA, and E represent methanol, isopropyl alcohol, and ethanolamine, respectively.

The volume of one chemical in the mixtures shown in Table 1 is limited to 8.75% at the lowest. Therefore, it is very beneficial to analyze cases where one chemical is dominant and the other chemical is in very low amounts, especially for forensic and pharmaceutical applications. For this aim, we also measure the Raman spectra of isopropyl alcohol and ethanolamine mixtures with alternating volume ratios of 1, 3, and 5%, which yields six extra samples in turn. These mixtures are used only for the evaluation of our algorithm in challenging scenarios; hence, they are not included in the training step of our model. The performances of our algorithm on challenging samples are presented in Figures 3–7 and Tables 2 and 3.

Figure 3.

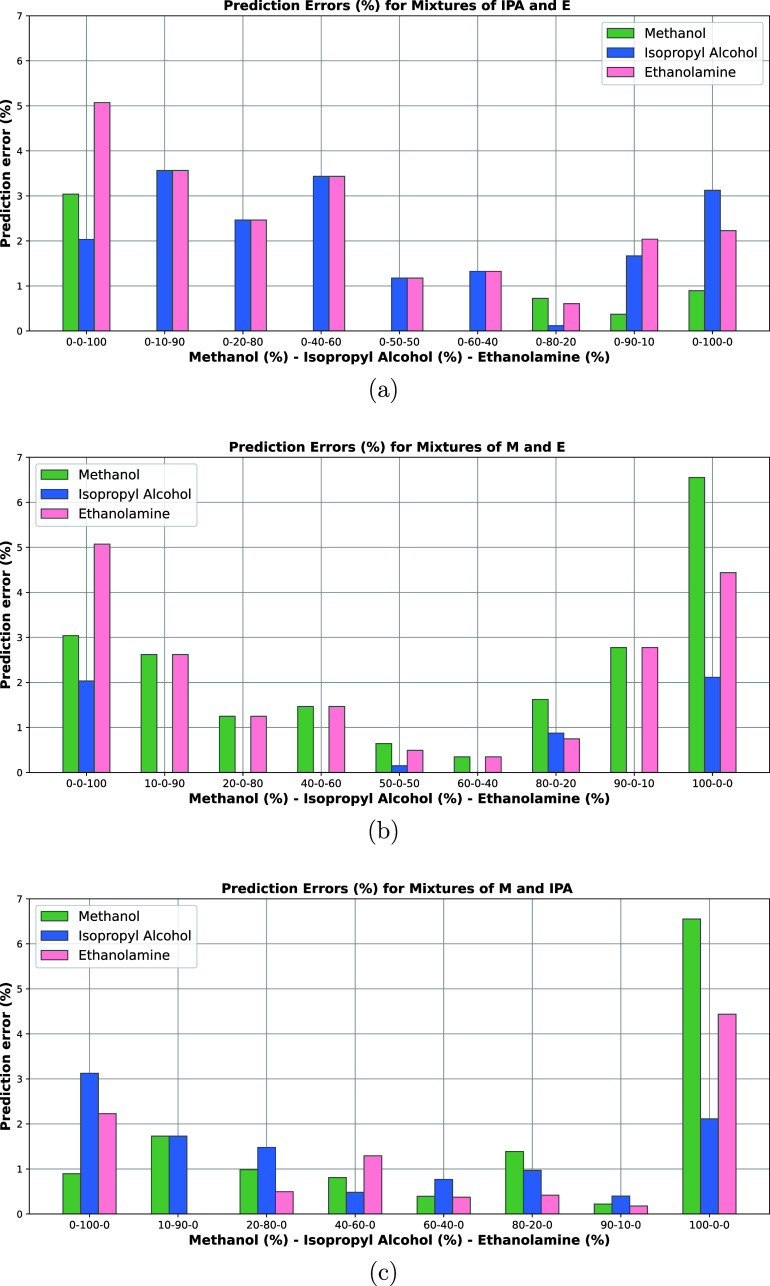
Figure 3

Open in a new tab

Prediction errors of methanol (M), isopropyl alcohol (IPA), and ethanolamine (E) in the mixtures of (a) isopropyl alcohol and ethanolamine, (b) methanol and ethanolamine, and (c) methanol and isopropyl alcohol. Actual mixture percentages of M, IPA, and E are specified under each bar plot, respectively.

Figure 7.

Figure 7

Open in a new tab

Evaluation of the RamanFormer model’s performance across different levels of additive noise, as measured by varying signal-to-noise ratios (SNR), showcasing its durability against noise in test data. Notably, RamanFormer remains effective against noise up to a 10 dB SNR threshold, after which error rates start to increase gradually.

Table 2. Comparison of Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) for Component Ratio Prediction Using LS,53,56−59 MLP,51 VGG11,51 and ResNet5051 Techniques.

method RMSE (%) MAE (%)
least squares53,56−59 3.6 3.1
MLP51 36.4 31.3
VGG1151 4.1 3.0
ResNet5051 3.2 2.9
RamanFormer (Ours) 1.6 1.4
Open in a new tab

Table 3. Variation of MAE and RMSE with Increasing Standard Deviation of Noise in the RamanFormer Resultsa.

standard deviation MAE (%) RMSE (%)
0.1 1.5 1.7
0.2 1.7 2.0
0.3 1.8 2.1
0.4 2.7 3.3
0.5 3.9 4.7
0.6 5.1 6.4
0.7 6.1 7.8
0.8 7.5 9.4
0.9 8.7 10.7
1.0 9.4 11.8
Open in a new tab
a

As the standard deviation escalates, both the mean absolute error (MAE) and the root mean square error (RMSE) demonstrate a progressive increase, signifying a decrement in predictive accuracy.

5. Results and Discussion

Upon training completion, the model is evaluated on a held-out test data set. The predicted component ratios are compared to the ground truth ratios, and various performance metrics are computed. To evaluate the power of our proposed model, we conduct comparative assessments against several established models/methods, which are the least squares, ResNet50, MLP, and VGG11, as demonstrated in Table 2.

The proposed transformer-based method yields encouraging outcomes in its capability to predict component ratios from Raman spectra. By combination of transformer encoders and convolutional layers, the model adeptly extracts both low-band and high-band characteristics of the Raman spectra, resulting in holistic representations of mixtures and components. This combination of distinctive layers effectively empowers the model to thoroughly comprehend the complex relationship between the spectral features and component ratios, thus enhancing the prediction performance. Consequently, our model emerged as the frontrunner in this comparative analysis, surpassing all aforementioned methods in terms of both RMSE and MAE metrics.

Furthermore, the prediction errors of methanol, isopropyl alcohol, and ethanolamine are plotted in a sample-wise manner in Figure 3. Although prediction errors for individual chemicals are only relatively high compared to the mixtures, where individual chemicals can be considered as some of the extreme cases. Moreover, the prediction errors of each component in the ternary mixture samples are plotted in Figure 4. The findings indicate that our approach can successfully quantify the components in the ternary mixtures with an average of 1.4% error.

Figure 4.

Figure 4

Open in a new tab

Prediction errors of methanol (M), isopropyl alcohol (IPA), and ethanolamine (E) in the ternary mixtures. Actual mixture percentages of M, IPA, and E are specified under each bar plot, respectively.

To further assess the performance of our approach, we validate RamanFormer on challenging scenarios of mixtures, where one chemical is dominant and the other chemical is present in very low amounts, which are 1, 3, and 5%. The prediction errors of the components in these mixtures are plotted in Figure 5. Results show that our approach can make more accurate predictions of the component ratios, in the case in which ethanolamine is the dominant chemical in the mixtures.

Figure 5.

Figure 5

Open in a new tab

Prediction errors of methanol (M), isopropyl alcohol (IPA), and ethanolamine (E) in the binary mixtures of challenging scenarios, where one chemical is dominant and the other chemical is present in very low amounts.

In another set of experiments, the robustness of our method was tested against noisy conditions. Initially, noise was incorporated into the training data set to simulate a variety of Raman signals characterized by different SNRs, achieved by introducing noise with varying standard deviation levels into the input signals. Figure 6 showcases the test error outcomes when the model is trained across these diverse SNR values. This visualization highlights the model’s ability to converge effectively under varying noise levels in the training data, demonstrating its adaptability and robustness in handling noisy spectroscopic data.

Figure 6.

Figure 6

Open in a new tab

Demonstration that when exposed to a noisy training set characterized by diverse signal-to-noise ratio (SNR) values, the model exhibits the capability to achieve convergence even with a signal-to-noise ratio (SNR) of 0 dB, though with a somewhat higher error. Training instances are augmented with additive Gaussian noise as in eq 6, while evaluation of the error is conducted on the clean, untouched test data.

Subsequently, to rigorously assess the robustness of our proposed methodology, noise was incorporated into the testing data set. During this phase, the model underwent training using data that had been deliberately disturbed with Gaussian noise, exhibiting a standard deviation of 0.1. The objective was to examine the model’s performance against variably noised test samples. The prediction errors over a range of SNR values are illustrated in Figure 7, providing a comprehensive evaluation of the model’s resilience. The analysis reveals that the model demonstrates consistent and reliable performance for test data characterized by SNR values exceeding 7.5 dB. This observation underscores the RamanFormer’s capacity to effectively handle noise, indicating its substantial robustness and applicability in the practical analysis of Raman spectroscopy data under noise-influenced conditions.

Moreover, Table 3 presents the performance of the proposed approach in terms of the MAE and RMSE for different standard deviation values of the added noise. As the standard deviation of the noise increases from 0.1 to 1.0, the table demonstrates a clear trend: both the MAE and RMSE metrics exhibit a progressive increase. This indicates that as the noise level in the test data becomes more pronounced, the model’s ability to accurately predict the component ratios diminishes. Specifically, at lower noise levels (standard deviation of 0.1), the model shows resilience with an MAE of 1.5% and an RMSE of 1.7%. These errors are relatively minimal, suggesting that RamanFormer maintains a high accuracy even in the presence of slight noise.

However, as the noise level escalates, the prediction errors increase noticeably. For example, when the standard deviation reaches 0.5, the MAE and RMSE jump to 3.9 and 4.7%, respectively. Beyond this point, the errors continue to grow more substantially, reaching an MAE of 9.4% and an RMSE of 11.8% at a standard deviation of 1.0. This pattern underscores the natural consequence of higher noise levels, making it more challenging for the model to decipher the underlying spectral signatures of the components, thus affecting its predictive performance.

Table 3 and Figure 7 provide quantitative insight into the robustness of the RamanFormer model against noise. While it demonstrates an expected decrease in performance with increasing noise, the gradual nature of this degradation suggests that RamanFormer is tolerant to noise to a certain degree. This analysis is critical for understanding the practical limitations and applications of the model, especially in real-world scenarios where noise is an inherent part of spectroscopic data.

In summary, the exceptional outcomes of our study emphasize the significant impact that our approach could have in enhancing the field of component ratio prediction using Raman spectroscopy. The ability of our model to outperform traditional methods confirms the benefits of adopting innovative strategies including the use of transformer encoders and convolutional layers. Additionally, the findings reveal our model’s proficiency in accurately quantifying mixture components under various challenging conditions. Moreover, the robustness of our approach against noise further validates its applicability and reliability in practical spectroscopic analysis scenarios.

6. Conclusions

This study introduces RamanFormer, a novel transformer-based approach for the identification and quantification of components in mixtures using Raman spectroscopy. Our model, characterized by an effective combination of transformer encoders and convolutional layers, is designed to effectively reveal the intricate patterns and dependencies in Raman spectra, thereby enabling an accurate prediction of component ratios. The architecture of RamanFormer, which incorporates transformer encoder layers, convolution layers, and global average pooling, demonstrates a sophisticated understanding of both low-band and high-band characteristics of the spectral data.

The comprehensive evaluation of RamanFormer across various data samples, including binary and ternary mixtures of chemicals, highlights its superior performance over traditional and contemporary approaches. Our model not only outperforms existing methods in terms of RMSE and MAE but also proves to be robust in challenging scenarios, where components are present in significantly low amounts. Moreover, the effectiveness of RamanFormer under conditions of varying noise levels underscores its practical applicability in real-world scenarios, where noise is an inevitable factor.

This study makes several significant contributions to the field of spectroscopy through the development, evaluation, and comparison of RamanFormer, a transformer-based model designed for Raman mixture analysis. First, the introduction of RamanFormer represents a noteworthy advancement in spectroscopy, leveraging transformer technology to tackle the complex challenge of mixture analysis. The model’s evaluation on a data set, encompassing both binary and ternary mixtures, highlights its adaptability and resilience, showcasing its ability to handle different scenarios with precision. Furthermore, the superior performance of RamanFormer demonstrated through a comparative analysis with existing methods, underscores its effectiveness in delivering accurate predictions of component ratios. These contributions collectively yield the potential of RamanFormer to revolutionize the approach to analyzing Raman spectroscopy data, offering enhanced accuracy and robustness.

Our findings indicate the potential of leveraging advanced machine learning architectures, such as transformers, in the realm of spectroscopy. By accurately identifying and quantifying the components of mixtures, RamanFormer paves the way for advancements in various applications, including materials science, food safety, forensics, and medical diagnostics. Future work may focus on further refining the model’s architecture to enhance its performance, exploring its applicability to other types of spectroscopic data, and extending its capabilities to handle larger and more complex data sets.

In conclusion, RamanFormer represents a significant step forward in the application of machine learning techniques to Raman spectroscopy. Its success in accurately predicting component ratios, coupled with its robustness to noise, holds promising implications for the broader field of spectroscopic analysis and beyond.

Acknowledgments

This project is funded by ASELSAN, their generous financial support and invaluable contributions have played a pivotal role in the successful execution of this research endeavor. The authors would like to thank Esra Ayantuna for the efforts on the early optical measurements and analysis, Bilal Kızılelma for the support on the sample preparations, and anonymous reviewers for improving the quality of the paper.

The authors declare no competing financial interest.

References

  1. Sigle M.; Rohlfing A.-K.; Kenny M.; Scheuermann S.; Sun N.; Graeßner U.; Haug V.; Sudmann J.; Seitz C. M.; Heinzmann D.; et al. Translating genomic tools to Raman spectroscopy analysis enables high-dimensional tissue characterization on molecular resolution. Nat. Commun. 2023, 14, 5799. 10.1038/s41467-023-41417-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Neng J.; Zhang Q.; Sun P. Application of surface-enhanced Raman spectroscopy in fast detection of toxic and harmful substances in food. Biosens. Bioelectron. 2020, 167, 112480 10.1016/j.bios.2020.112480. [DOI] [PubMed] [Google Scholar]
  3. Ryzhikova E.; Ralbovsky N. M.; Sikirzhytski V.; Kazakov O.; Halamkova L.; Quinn J.; Zimmerman E. A.; Lednev I. K. Raman spectroscopy and machine learning for biomedical applications: Alzheimer’s disease diagnosis based on the analysis of cerebrospinal fluid. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy 2021, 248, 119188 10.1016/j.saa.2020.119188. [DOI] [PubMed] [Google Scholar]
  4. Boonsit S.; Kalasuwan P.; van Dommelen P.; Daengngam C. Rapid material identification via low-resolution Raman spectroscopy and deep convolutional neural network. Journal of Physics: Conference Series. 2021, 1719, 012081 10.1088/1742-6596/1719/1/012081. [DOI] [Google Scholar]
  5. de Oliveira Penido C. A. F.; Pacheco M. T. T.; Lednev I. K.; Silveira L. Jr Raman spectroscopy in forensic analysis: identification of cocaine and other illegal drugs of abuse. J. Raman Spectrosc. 2016, 47, 28–38. 10.1002/jrs.4864. [DOI] [Google Scholar]
  6. Marigheto N.; Kemsley E.; Defernez M.; Wilson R. A comparison of mid-infrared and Raman spectroscopies for the authentication of edible oils. J. Am. Oil Chem. Soc. 1998, 75, 987–992. 10.1007/s11746-998-0276-4. [DOI] [Google Scholar]
  7. Ai Y.-J; Liang P.; Wu Y.-X.; Dong Q.-M.; Li J.-B.; Bai Y.; Xu B.-J.; Yu Z.; Ni D. Rapid qualitative and quantitative determination of food colorants by both Raman spectra and Surface-enhanced Raman Scattering (SERS). Food chemistry 2018, 241, 427–433. 10.1016/j.foodchem.2017.09.019. [DOI] [PubMed] [Google Scholar]
  8. Amjad A.; Ullah R.; Khan S.; Bilal M.; Khan A. Raman spectroscopy based analysis of milk using random forest classification. Vib. Spectrosc. 2018, 99, 124–129. 10.1016/j.vibspec.2018.09.003. [DOI] [Google Scholar]
  9. Gasser C.; GÖschl M.; Ofner J.; Lendl B. Stand-off hyperspectral Raman imaging and random decision forest classification: a potent duo for the fast, remote identification of explosives. Analytical chemistry 2019, 91, 7712–7718. 10.1021/acs.analchem.9b00890. [DOI] [PubMed] [Google Scholar]
  10. Dies H.; Raveendran J.; Escobedo C.; Docoslis A. Rapid identification and quantification of illicit drugs on nanodendritic surface-enhanced Raman scattering substrates. Sens. Actuators, B 2018, 257, 382–388. 10.1016/j.snb.2017.10.181. [DOI] [Google Scholar]
  11. Doty K. C.; Lednev I. K. Differentiation of human blood from animal blood using Raman spectroscopy: A survey of forensically relevant species. Forensic science international 2018, 282, 204–210. 10.1016/j.forsciint.2017.11.033. [DOI] [PubMed] [Google Scholar]
  12. Kim W.; Lee S. H.; Kim J. H.; Ahn Y. J.; Kim Y.-H.; Yu J. S.; Choi S. based surface-enhanced Raman spectroscopy for diagnosing prenatal diseases in women. ACS Nano 2018, 12, 7100–7108. 10.1021/acsnano.8b02917. [DOI] [PubMed] [Google Scholar]
  13. Lim J.-Y.; Nam J.-S; Shin H.; Park J.; Song H.-I; Kang M.; Lim K.-I; Choi Y. Identification of newly emerging influenza viruses by detecting the virally infected cells based on surface enhanced Raman spectroscopy and principal component analysis. Analytical chemistry 2019, 91, 5677–5684. 10.1021/acs.analchem.8b05533. [DOI] [PubMed] [Google Scholar]
  14. Lafuente B.; Downs R. T.; Yang H.; Stone N. 1. The power of databases: The RRUFF project. Highlights in mineralogical crystallography 2015, 1–30. 10.1515/9783110417104-003. [DOI] [Google Scholar]
  15. Berlanga G.; Williams Q.; Temiquel N. Convolutional neural networks as a tool for Raman spectral mineral classification under low signal, dusty Mars conditions. Earth Space Sci. 2022, 9, e2021EA002125 10.1029/2021EA002125. [DOI] [Google Scholar]
  16. Sang X.; Zhou R.-G; Li Y.; Xiong S. One-dimensional deep convolutional neural network for mineral classification from Raman spectroscopy. Neural Process. Lett. 2022, 54, 677–690. 10.1007/s11063-021-10652-1. [DOI] [Google Scholar]
  17. Liu J.; Gibson S. J.; Mills J.; Osadchy M. Dynamic spectrum matching with one-shot learning. Chemometrics and Intelligent Laboratory Systems 2019, 184, 175–181. 10.1016/j.chemolab.2018.12.005. [DOI] [Google Scholar]
  18. Liu J.; Osadchy M.; Ashton L.; Foster M.; Solomon C. J.; Gibson S. J. Deep convolutional neural networks for Raman spectrum recognition: a unified solution. Analyst 2017, 142, 4067–4074. 10.1039/C7AN01371J. [DOI] [PubMed] [Google Scholar]
  19. Vaswani A.; Shazeer N.; Parmar N.; Uszkoreit J.; Jones L.; Gomez A. N.; Kaiser Ł.; Polosukhin I.. Attention is all you need. In Advances in neural information processing systems; Curran Associates, Inc., 2017; Vol. 30. [Google Scholar]
  20. Ellis D. I.; Goodacre R. Metabolic fingerprinting in disease diagnosis: biomedical applications of infrared and Raman spectroscopy. Analyst 2006, 131, 875–885. 10.1039/b602376m. [DOI] [PubMed] [Google Scholar]
  21. Rebrošová K.; Šiler M.; Samek O.; Ržička F.; Bernatová S.; Holá V.; Ježek J.; Zemánek P.; Sokolová J.; Petráš P. Rapid identification of staphylococci by Raman spectroscopy. Sci. Rep. 2017, 7, 14846. 10.1038/s41598-017-13940-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Monavar H. M.; Afseth N.; Lozano J.; Alimardani R.; Omid M.; Wold J. Determining quality of caviar from Caspian Sea based on Raman spectroscopy and using artificial neural networks. Talanta 2013, 111, 98–104. 10.1016/j.talanta.2013.02.046. [DOI] [PubMed] [Google Scholar]
  23. Chawla K.; Bankapur A.; Acharya M.; D’Souza J. S.; Chidangil S. A micro-Raman and chemometric study of urinary tract infection-causing bacterial pathogens in mixed cultures. Anal. Bioanal. Chem. 2019, 411, 3165–3177. 10.1007/s00216-019-01784-4. [DOI] [PubMed] [Google Scholar]
  24. Roggo Y.; Degardin K.; Margot P. Identification of pharmaceutical tablets by Raman spectroscopy and chemometrics. Talanta 2010, 81, 988–995. 10.1016/j.talanta.2010.01.046. [DOI] [PubMed] [Google Scholar]
  25. Ibtehaz N.; Chowdhury M. E.; Khandakar A.; Kiranyaz S.; Rahman M. S.; Zughaier S. M. RamanNet: a generalized neural network architecture for Raman spectrum analysis. Neural Comput. Applic. 2023, 35, 18719–18735. 10.1007/s00521-023-08700-z. [DOI] [Google Scholar]
  26. Ullah R.; Khan S.; Ali Z.; Ali H.; Ahmad A.; Ahmed I. Evaluating the performance of multilayer perceptron algorithm for tuberculosis disease Raman data. Photodiagnosis and Photodynamic Therapy 2022, 39, 102924 10.1016/j.pdpdt.2022.102924. [DOI] [PubMed] [Google Scholar]
  27. Thrift W. J.; Cabuslay A.; Laird A. B.; Ranjbar S.; Hochbaum A. I.; Ragan R. Surface-enhanced Raman scattering-based odor compass: Locating multiple chemical sources and pathogens. ACS sensors 2019, 4, 2311–2319. 10.1021/acssensors.9b00809. [DOI] [PubMed] [Google Scholar]
  28. Dong J.; Hong M.; Xu Y.; Zheng X. A practical convolutional neural network model for discriminating Raman spectra of human and animal blood. J. Chemom. 2019, 33, e3184 10.1002/cem.3184. [DOI] [Google Scholar]
  29. Estienne F.; Massart D.; Zanier-Szydlowski N.; Marteau P. Multivariate calibration with Raman spectroscopic data: a case study. Anal. Chim. Acta 2000, 424, 185–201. 10.1016/S0003-2670(00)01107-7. [DOI] [Google Scholar]
  30. Uysal R. S.; Boyaci I. H.; Genis H. E.; Tamer U. Determination of butter adulteration with margarine using Raman spectroscopy. Food chemistry 2013, 141, 4397–4403. 10.1016/j.foodchem.2013.06.061. [DOI] [PubMed] [Google Scholar]
  31. Li Q.; Li W.; Zhang J.; Xu Z. An improved k-nearest neighbour method to diagnose breast cancer. Analyst 2018, 143, 2807–2811. 10.1039/C8AN00189H. [DOI] [PubMed] [Google Scholar]
  32. Li X.; Yang T.; Li S.; Wang D.; Song Y.; Zhang S. Raman spectroscopy combined with principal component analysis and k nearest neighbour analysis for non-invasive detection of colon cancer. Laser Physics 2016, 26, 035702 10.1088/1054-660X/26/3/035702. [DOI] [Google Scholar]
  33. Zivanovic V.; Seifert S.; Drescher D.; Schrade P.; Werner S.; Guttmann P.; Szekeres G. P.; Bachmann S.; Schneider G.; Arenz C.; Kneipp J. Optical nanosensing of lipid accumulation due to enzyme inhibition in live cells. ACS Nano 2019, 13, 9363–9375. 10.1021/acsnano.9b04001. [DOI] [PubMed] [Google Scholar]
  34. Banaei N.; Moshfegh J.; Mohseni-Kabir A.; Houghton J. M.; Sun Y.; Kim B. Machine learning algorithms enhance the specificity of cancer biomarker detection using SERS-based immunoassays in microfluidic chips. RSC Adv. 2019, 9, 1859–1868. 10.1039/C8RA08930B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Li J.-L.; Sun D.-W.; Pu H.; Jayas D. S. Determination of trace thiophanate-methyl and its metabolite carbendazim with teratogenic risk in red bell pepper (Capsicumannuum L.) by surface-enhanced Raman imaging technique. Food Chem. 2017, 218, 543–552. 10.1016/j.foodchem.2016.09.051. [DOI] [PubMed] [Google Scholar]
  36. Ou L.; Chen Y.; Su Y.; Huang Y.; Chen R.; Lei J. Application of silver nanoparticle-based SERS spectroscopy for DNA analysis in radiated nasopharyngeal carcinoma cells. J. Raman Spectrosc. 2013, 44, 680–685. 10.1002/jrs.4269. [DOI] [Google Scholar]
  37. Luo R.; Popp J.; Bocklitz T. Deep learning for Raman spectroscopy: a review. Analytica 2022, 3, 287–301. 10.3390/analytica3030020. [DOI] [Google Scholar]
  38. Wahl J.; Sjödahl M.; Ramser K. Single-step preprocessing of raman spectra using convolutional neural networks. Applied spectroscopy 2020, 74, 427–438. 10.1177/0003702819888949. [DOI] [PubMed] [Google Scholar]
  39. Valensise C. M.; Giuseppi A.; Vernuccio F.; De la Cadena A.; Cerullo G.; Polli D. Removing non-resonant background from CARS spectra via deep learning. APL Photonics 2020, 5, 061305 10.1063/5.0007821. [DOI] [Google Scholar]
  40. Lee W.; Lenferink A. T.; Otto C.; Offerhaus H. L. Classifying Raman spectra of extracellular vesicles based on convolutional neural networks for prostate cancer detection. Journal of raman spectroscopy 2020, 51, 293–300. 10.1002/jrs.5770. [DOI] [Google Scholar]
  41. Kirchberger-Tolstik T.; Pradhan P.; Vieth M.; Grunert P.; Popp J.; Bocklitz T. W.; Stallmach A. Towards an interpretable classifier for characterization of endoscopic Mayo scores in ulcerative colitis using Raman Spectroscopy. Anal. Chem. 2020, 92, 13776–13784. 10.1021/acs.analchem.0c02163. [DOI] [PubMed] [Google Scholar]
  42. Maruthamuthu M. K.; Raffiee A. H.; De Oliveira D. M.; Ardekani A. M.; Verma M. S. Raman spectra-based deep learning: A tool to identify microbial contamination. MicrobiologyOpen 2020, 9, e1122 10.1002/mbo3.1122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Fan X.; Ming W.; Zeng H.; Zhang Z.; Lu H. Deep learning-based component identification for the Raman spectra of mixtures. Analyst 2019, 144, 1789–1798. 10.1039/C8AN02212G. [DOI] [PubMed] [Google Scholar]
  44. Fu X.; Zhong L.-M.; Cao Y.-B.; Chen H.; Lu F. Quantitative analysis of excipient dominated drug formulations by Raman spectroscopy combined with deep learning. Analytical Methods 2021, 13, 64–68. 10.1039/D0AY01874K. [DOI] [PubMed] [Google Scholar]
  45. Houston J.; Glavin F. G.; Madden M. G. Robust classification of high-dimensional spectroscopy data using deep learning and data synthesis. J. Chem. Inf. Model. 2020, 60, 1936–1954. 10.1021/acs.jcim.9b01037. [DOI] [PubMed] [Google Scholar]
  46. Ho C.-S.; Jean N.; Hogan C. A.; Blackmon L.; Jeffrey S. S.; Holodniy M.; Banaei N.; Saleh A. A.; Ermon S.; Dionne J. Rapid identification of pathogenic bacteria using Raman spectroscopy and deep learning. Nat. Commun. 2019, 10, 4927. 10.1038/s41467-019-12898-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Goodfellow I.; Pouget-Abadie J.; Mirza M.; Xu B.; Warde-Farley D.; Ozair S.; Courville A.; Bengio Y.. Generative adversarial nets. In Advances in neural information processing systems; Curran Associates, Inc., 2014; Vol. 27. [Google Scholar]
  48. Yu S.; Li H.; Li X.; Fu Y. V.; Liu F. Classification of pathogens by Raman spectroscopy combined with generative adversarial networks. Sci. Total Environ. 2020, 726, 138477 10.1016/j.scitotenv.2020.138477. [DOI] [PubMed] [Google Scholar]
  49. Thrift W. J.; Ragan R. Quantification of analyte concentration in the single molecule regime using convolutional neural networks. Analytical chemistry 2019, 91, 13337–13342. 10.1021/acs.analchem.9b03599. [DOI] [PubMed] [Google Scholar]
  50. Zhang R.; Xie H.; Cai S.; Hu Y.; Liu G.-K; Hong W.; Tian Z.-Q Transfer-learning-based Raman spectra identification. J. Raman Spectrosc. 2020, 51, 176–186. 10.1002/jrs.5750. [DOI] [Google Scholar]
  51. Pan L.; Pipitsunthonsan P.; Daengngam C.; Channumsin S.; Sreesawet S.; Chongcheawchamnan M. Identification of complex mixtures for Raman spectroscopy using a novel scheme based on a new multi-label deep neural network. IEEE Sensors Journal 2021, 21, 10834–10843. 10.1109/JSEN.2021.3059849. [DOI] [Google Scholar]
  52. Wang X.; Pan Q.-H.; Fan X.-G.; Xu Y.-J Component identification for Raman spectra with deep learning network. J. Phys.: Conf. Ser. 2021, 1914, 012044 10.1088/1742-6596/1914/1/012044. [DOI] [Google Scholar]
  53. Zhao X.; Liu C.; Zhao Z.; Zhu Q.; Huang M. Performance Improvement of Handheld Raman Spectrometer for Mixture Components Identification Using Fuzzy Membership and Sparse Non-Negative Least Squares. Appl. Spectrosc. 2022, 76, 548–558. 10.1177/00037028221080205. [DOI] [PubMed] [Google Scholar]
  54. Zhao Z.; Liu Z.; Ji M.; Zhao X.; Zhu Q.; Huang M. ConInceDeep: A novel deep learning method for component identification of mixture based on Raman spectroscopy. Chemometrics and Intelligent Laboratory Systems 2023, 234, 104757 10.1016/j.chemolab.2023.104757. [DOI] [Google Scholar]
  55. Szegedy C.; Liu W.; Jia Y.; Sermanet P.; Reed S.; Anguelov D.; Erhan D.; Vanhoucke V.; Rabinovich A.. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition; IEEE, 2015; pp. 1–9. [Google Scholar]
  56. Keren S.; Zavaleta C.; Cheng Z. d.; de La Zerda A.; Gheysens O.; Gambhir S. Noninvasive molecular imaging of small living subjects using Raman spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2008, 105, 5844–5849. 10.1073/pnas.0710575105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Zhang Z.-M.; Chen X.-Q.; Lu H.-M.; Liang Y.-Z.; Fan W.; Xu D.; Zhou J.; Ye F.; Yang Z.-Y. Mixture analysis using reverse searching and non-negative least squares. Chemometrics and Intelligent Laboratory Systems 2014, 137, 10–20. 10.1016/j.chemolab.2014.06.002. [DOI] [Google Scholar]
  58. Zeng H.-T.; Hou M.-H.; Ni Y.-P.; Fang Z.; Fan X.-Q.; Lu H.-M.; Zhang Z.-M. Mixture analysis using non-negative elastic net for Raman spectroscopy. J. Chemom. 2020, 34, e3293 10.1002/cem.3293. [DOI] [Google Scholar]
  59. Li J. Q.; Dukes P. V.; Lee W.; Sarkis M.; Vo-Dinh T. Machine learning using convolutional neural networks for SERS analysis of biomarkers in medical diagnostics. J. Raman Spectrosc. 2022, 53, 2044–2057. 10.1002/jrs.6447. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zhang J.; Xin P.-L.; Wang X.-Y.; Chen H.-Y.; Li D.-W. Deep learning-based spectral extraction for improving the performance of surface-enhanced Raman spectroscopy analysis on multiplexed identification and quantitation. J. Phys. Chem. A 2022, 126, 2278–2285. 10.1021/acs.jpca.1c10681. [DOI] [PubMed] [Google Scholar]
  61. Antonio D.; OToole H.; Carney R.; Kulkarni A.; Palazoglu A. Assessing the Performance of 1D-Convolution Neural Networks to Predict Concentration of Mixture Components from Raman Spectra. arXiv preprint arXiv:2306.16621 2023, 10.48550/arXiv.2306.16621. [DOI] [Google Scholar]
  62. Dosovitskiy A.; Beyer L.; Kolesnikov A.; Weissenborn D.; Zhai X.; Unterthiner T.; Dehghani M.; Minderer M.; Heigold G.; Gelly S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv preprint arXiv:2010.11929 2020, 10.48550/arXiv.2010.11929. [DOI] [Google Scholar]
  63. Schwaller P.; Laino T.; Gaudin T.; Bolgar P.; Hunter C. A.; Bekas C.; Lee A. A. Molecular transformer: a model for uncertainty-calibrated chemical reaction prediction. ACS central science 2019, 5, 1572–1583. 10.1021/acscentsci.9b00576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Rives A.; Meier J.; Sercu T.; Goyal S.; Lin Z.; Liu J.; Guo D.; Ott M.; Zitnick C. L.; Ma J.; Fergus R. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. U. S. A. 2021, 118, e2016239118 10.1073/pnas.2016239118. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES