Effects of Macromolecular Cosolutes on the Kinetics of Huntingtin Aggregation Monitored by NMR Spectroscopy

Abstract

The effects of two macromolecular cosolutes, specifically the polysaccharide dextran-20 and the protein lysozyme, on the aggregation kinetics of a pathogenic huntingtin exon-1 protein (hht^ex1) with a 35 polyglutamine repeat, htt^ex1Q₃₅, are described. A unified kinetic model that establishes a direct connection between reversible tetramerization occurring on the microsecond time scale and irreversible fibril formation on a time scale of hours/days forms the basis for quantitative analysis of htt^ex1Q₃₅ aggregation, monitored by measuring cross-peak intensities in a series of 2D ¹H–¹⁵N NMR correlation spectra acquired during the course of aggregation. The primary effects of the two cosolutes are associated with shifts in the prenucleation tetramerization equilibrium resulting in substantial changes in concentration of “preformed” htt^ex1Q₃₅ tetramers. Similar effects of the two cosolutes on the tetramerization equilibrium observed for a shorter, nonaggregating huntingtin variant with a 7-glutamine repeat, htt^ex1Q₇, lend confidence to the conclusions drawn from the fits to the htt^ex1Q₃₅ aggregation kinetics.

Graphical Abstract

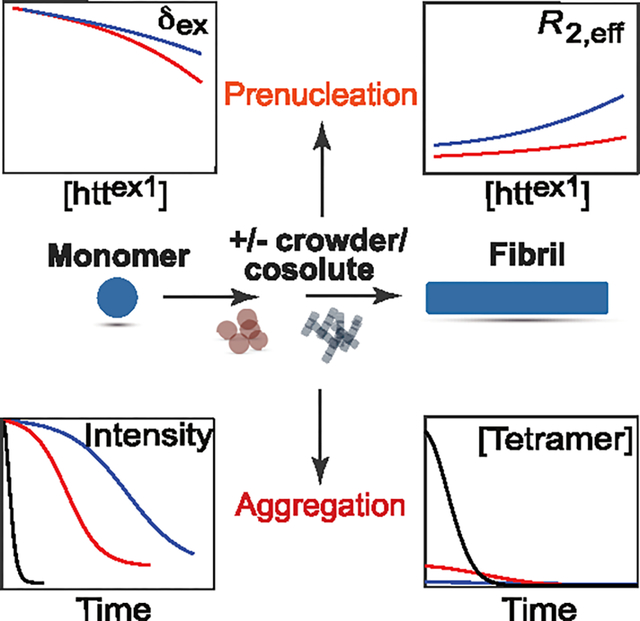
Huntington’s disease is a fatal neurodegenerative condition arising from aggregation of a huntingtin polypeptide and accumulation of fibrils within neuronal inclusion bodies.^1–3 The huntingtin exon-1 protein, htt^ex1Q_n, consists of a 16-residue N-terminal amphiphilic domain (NT), a polyglutamine stretch (polyQ) of variable length n, and a proline-rich domain (PRD) comprising two polyproline tracts separated by a 17-residue linker.⁴ The onset of Huntington’s disease is correlated with the length of the polyQ repeat, with a threshold value of ~35 for the number of Gln residues in the polyQ stretch.^4–6 Earlier exchange NMR-based studies have shown that huntingtin exon-1 constructs that aggregate very slowly on the order of several weeks, such as htt^ex1Q₇ or a minimalistic construct lacking the PRD domain, htt^NTQ₇, undergo reversible tetramerization of the NT domain on a time-scale of ~50 μs forming a sparsely populated four-helix bundle consisting of a dimer of dimers with D₂ symmetry.^7–9 This fast, reversible oligomerization that precedes nucleation,⁸ is a prerequisite for formation of htt^ex1 fibrils that occurs on a much slower time scale (typically, hours or days). In fact, it has been demonstrated that formation of fibrils can be effectively blocked by a number of mechanisms,^8,10–12 all of which involve reduction of the tetramer population, underscoring the critical role of prenucleation tetramerization for huntingtin aggregation.

Recently, we developed a unified kinetic model for aggregation of htt^ex1Q₃₅¹² – a construct with a 35-residue polyQ repeat–that establishes a direct link between fast, reversible tetramerization and slow, irreversible fibril formation (Figure 1).¹³ Monomers of htt^ex1Q₃₅ ($m$) reversibly self-associate on the microsecond time scale to yield sparsely populated dimers, $D$, which in turn equilibrate on a similar time-scale with lowly populated tetrameric species, $T$. These two reversible oligomerization processes are characterized by equilibrium constants $K_{\text{eq},1}$ and $K_{\text{eq},2}$, respectively. The tetramers $T$ are slowly and irreversibly converted (with a rate constant $k_{\mathrm{c}}$) in a monomer-independent manner into elongation-capable, “active” primary nuclei,¹⁴ followed by chain elongation¹⁴ (with a rate constant $k_{+}$) to produce mature fibrils $M$. The process of secondary nucleation^15–17 ($k_{\mathrm{s}}$) involves interactions of htt^ex1Q₃₅ monomers $m$ with fibrils $M$ to produce secondary nuclei that, albeit physically and kinetically distinct from their primary counterparts, add to the total pool of nuclei P (Figure 1). In this model, the connection between the processes of tetramerization and fibril formation involves an irreversible conversion of pre-equilibrated tetramers T to “active” primary nuclei via conformational rearrangement of the former with a monomer-independent rate.¹³ This slow rearrangement likely involves the polyQ repeats: while in the prenucleation tetramer, the polyQ stretches are intrinsically disordered, they are likely brought into the appropriate spatial configuration conducive to formation of a four-stranded β-sheet by the four-helix bundle formed by the amphiphilic NT domains (Figure 1) – a process similar to the “hydrophobic zipper” model of protein folding.^18,19

Figure 1.

Schematic representation of the unified model of htt^ex1Q₃₅ aggregation. The prenucleation tetramerization equilibrium (shown at the top) is coupled with monomer-independent conversion, chain elongation and fibril surface-mediated secondary nucleation stages (see text). The concentration of tetramers, [T], as a function of monomer concentration, [m], is expressed through the product of equilibrium constants, $K_{\mathrm{T}}={\left(K_{\text{eq},1}\right)}^2{K}_{\text{eq,}2}$.

Here we describe the effects of two macromolecular cosolutes, namely the polysaccharide dextran-20 (average molecular weight, MW = 20 kDa) and the protein hen egg white lysozyme (MW ~ 14 kDa), on the kinetics of htt^ex1Q₃₅ aggregation. Macromolecular cosolutes are commonly used to mimic the highly crowded cellular interior, where up to 30% of cell volume is occupied by macromolecules. The effects of cosolutes on protein folding and protein–protein interactions are well documented.^20–23 Much less is known, however, about how cosolutes influence aggregation of proteins in general and disordered proteins in particular.^24–27 The consolidated model of Figure 1 forms the basis for a combined quantitative analysis of reversible tetramerization and irreversible fibril formation from peak intensities in a series of two-dimensional ¹H–¹⁵N band-selective optimized flip-angle short-transient heteronuclear multiple quantum coherence (SOFAST-HMQC)^28,29 NMR spectra monitoring the progress of htt^ex1Q₃₅ aggregation. We show that the primary effect of both cosolutes on htt^ex1Q₃₅ aggregation kinetics relates to shifts in the prenucleation tetramerization equilibrium resulting in large changes in the concentration of “preformed” tetramers T. Although the presence of cosolutes affects the rate constants of htt^ex1Q₃₅ fibril formation to some extent, and for dextran-20, the observed acceleration of htt^ex1Q₃₅ fibril formation is in agreement with earlier reports for other protein systems,²⁶ these effects are relatively minor on the time scale of the aggregation process and are therefore deemed secondary.

It was realized at the early stages of the present study that profound effects exerted by the cosolutes on aggregation of htt^ex1Q₃₅ make the NMR tools that we have developed recently for quantitative studies of chemical exchange in aggregating protein systems,¹² inapplicable in the presence of either dextran-20 or lysozyme. Therefore, we turned first to characterization of the prenucleation tetramerization equilibrium, in the absence and presence of the two cosolutes, for a huntingtin construct, htt^ex1Q₇, that does not aggregate on the time scale of NMR experiments.^7,9 The rationale behind this approach is based on two factors: first, the close similarity between the characteristics of the tetramerization equilibrium for htt^ex1Q₇^8,9 and the longer, fast-aggregating htt^ex1Q₃₅ construct;^12,13 second, the expectation that the effects of cosolutes on tetramerization will follow the same trends for different htt^ex1 variants considering that all these variants share the same tetramer-forming N-terminal region. The use of a protein construct that is stable in solution with or without cosolutes for prolonged periods of time allowed us to record time-consuming NMR experiments–such as the measurements of concentration dependent exchange-induced chemical shift changes (δ_ex) of backbone amide ¹⁵N and ¹H_N nuclei, and concentration dependent ¹⁵N effective transverse relaxation rates (R_2,eff) derived from R_1ρ relaxation rates measured on-resonance with several radiofrequency (RF) spin-lock field strengths⁹ – that would be impossible to carry out for fast aggregating protein samples.

The concentration-dependent ¹⁵N/¹H_N-δ_ex and ¹⁵N-R_2,eff values obtained for several residues of htt^ex1Q₇ at 5 °C and pH 6.5 in the absence and presence of 200 mg/mL dextran-20 or 100 mg/mL hen egg white lysozyme, are compared in Figure 2A (see Supporting Information, SI, “Materials and Methods” for experimental details). The characteristic curvature at higher concentrations apparent for both NMR observables in the absence of cosolutes (shown in red) is a signature of increasing population of higher (>2) order oligomers, specifically htt^ex1Q₇ tetramers. The curvature is substantially enhanced in the presence of dextran (shown in blue) and practically eliminated in the presence of lysozyme (green), indicating that the overall tetramerization equilibrium (Figure 2B) is shifted to the right and left in the presence of dextran-20 and lysozyme, respectively, with dextran-20 and lysozyme respectively promoting and impeding production of htt^ex1Q₇ tetramers. As no significant ¹⁵N or ¹H chemical shift differences were observed between the low concentration (50 μM) htt^ex1Q₇ samples (where the monomer m is prevalent) in the absence or presence of dextran-20, we assumed that the chemical shift differences for both nuclei between the oligomeric (D and T; assumed to have the same chemical shifts since deviations of ¹⁵N and ¹H_N chemical shifts from their random coil values are dominated by the backbone secondary structure) and monomeric (m) states, Δω_N and Δω_H, are the same in the absence and presence of dextran-20. Further, we note that the volume fraction excluded from solution upon addition of 200 mg/mL of dextran-20 is estimated to be in the range of 0.16 to 0.20 (see SI, ‘Estimation of the fibril elongation rate enhancement Γ’). Not surprisingly, as the dextran-20 containing solution is highly nonideal, the corresponding (directly proportional to excluded volume fraction) increase in the effective concentration of htt^ex1Q₇ cannot account for the increase in the concentration/population of htt^ex1Q₇ tetramers (see SI, Figure S3).

Figure 2.

Effects of cosolutes on the tetramerization equilibrium for htt^ex1Q₇. (A) Examples of concentration-dependent chemical shift changes (¹⁵N/¹H_N-δ_ex) and effective transverse relaxation rates (¹⁵N-R_2,eff; RF spin-lock field strength of 750 Hz) obtained for htt^ex1Q₇ in the absence of cosolutes (red) and in the presence of 200 mg/mL dextran-20 (blue) and 100 mg/mL hen egg white lysozyme (green). Experimental data are shown with open circles; continuous solid lines represent the global best-fit to the 3-state exchange model in panel (B). The data in the presence of lysozyme were not best-fit, and the dashed green lines are drawn solely to guide the eye. The reduced χ² of the best-fit was 4.6. The full sets of concentration-dependent ¹⁵N/¹H_N-δ_ex and ¹⁵N-R_2,eff data obtained for htt^ex1Q₇ and best-fit to the model in panel (B), are provided in the SI, Figures S1 and S2, respectively. (B) The model of oligomerization used to fit the htt^ex1Q₇ data. The populations of each species (in monomer units; %) are reported for [htt^ex1Q₇] = 1.0 mM, in the absence of cosolutes (red) and in the presence of 200 mg/mL dextran-20 (blue). See SI, “Materials and Methods”, for NMR acquisition parameters and details of the fitting procedures. The NMR experiments were carried out at 5 °C and pH 6.5.

Global fitting of all concentration-dependent ¹⁵N/¹H_N-δ_ex and ¹⁵N-R_2,eff data for htt^ex1Q₇ in the absence and presence of dextran-20 under the assumption of equal $\mathrm{\Delta }{\omega }_{\mathrm{N}}$ and $\mathrm{\Delta }{\omega }_{\mathrm{H}}$ but different kinetics (rate constants) of tetramerization yielded similar time-scales, τ_ex (the inverse of the exchange rate) for the overall exchange process from monomer to tetramer in the absence and presence of dextran-20: τ_ex ~ 77–81 μs and ~42–72 μs, respectively, from the lowest (50 μM) to the highest (1 mM) concentration of htt^ex1Q₇ used (see SI, “Materials and Methods” for details of the calculations and fitting procedure; the data in the presence of lysozyme could not be analyzed quantitatively because of the very weak concentration dependence of the NMR observables as seen in Figure 2A; see SI Table S1, for the parameters of htt^ex1Q₇ tetramerization kinetics in the absence and presence of dextran-20, and Table S2, for the extracted values of $\mathrm{\Delta }{\omega }_{\mathrm{N}}$ and $\mathrm{\Delta }{\omega }_{\mathrm{H}}$). It is interesting to note that a slight increase in the overall tetramerization exchange rate for htt^ex1Q₇ is observed in the presence of dextran-20 despite the accompanying increase in viscosity which would be expected to result in a decrease in exchange rate³⁰ (see SI, Figure S4, for diffusion profiles of htt^ex1Q₇ in the absence and presence of cosolutes). Importantly, the product of equilibrium constants $K_{\mathrm{T}}={\left(K_{\text{eq},1}\right)}^2{K}_{\text{eq,}2}$ increases from 2.8 (±1.1) × 10⁶ M⁻³ in the absence of dextran-20 to 9.0 (±3.2) × 10⁶ M⁻³ in the presence of dextran-20, with directly proportional increases in the fractional population of tetramers (Figure 2B).

The above analysis shows that dextran-20 acts on the tetramerization equilibrium of htt^ex1Q₇ as a typical crowding agent.^{20,22,23,31–38} As folded proteins occupy less space in solution compared to unstructured (disordered) polypeptide chains, crowding agents at high concentrations typically stabilize folded conformations through (highly nonlinear) excluded volume effects.^{21,32,35,37,39–42} We therefore conclude that the (partially) folded tetramers of htt^ex1Q₇ are stabilized predominantly by “hard-core” repulsive interactions between dextran-20 and htt^ex1Q₇. Lysozyme, on the other hand, affects the tetramerization equilibrium in the opposite way to dextran-20, stabilizing the unfolded, monomeric state of htt^ex1Q₇. Considering that the net positive charges of +4 and +0.3 (+1.2) for lysozyme and the htt^ex1Q₇ monomer (tetramer), respectively, at pH 6.5 would lead to repulsive interactions between the two proteins that would likely favor the partially folded tetramers,^23,43–46 this effect may be attributable to some weak attractive (hydrophobic rather than electrostatic) interactions between htt^ex1Q₇ and lysozyme that stabilize the unfolded monomers of htt^ex1Q₇ (note that no changes in ¹H_N/¹⁵N chemical shifts could be detected upon addition of 100 mg/mL lysozyme to httex1Q7).^{23,37,43–45}

Having established the effects of cosolutes on the tetramerization equilibrium for a system that does not aggregate during the time required to record the various exchange-based NMR experiments, we turned next to the fast aggregating htt^ex1Q₃₅ construct. In the framework of the kinetic model in Figure 1, the time course of htt^ex1Q₃₅ aggregation (fibril formation), can be described by two ordinary differential equations,^13,14,47,48

$$\frac{dP}{dt}=k_{\mathrm{c}}{K}_{T}m{\left(t\right)}^4+k_{\mathrm{s}}m{\left(t\right)}^{n2}M(t)$$ (1.1)

$$\frac{dM}{dt}=-\frac{dm(t)}{dt}=2k_{+}m(t)P(t)$$ (1.2)

where the product of equilibrium constants, $K_T={\left(K_{\text{eq},1}\right)}^2\left(K_{\text{eq},2}\right)={\left(k_1/k_{-1}\right)}^2\left(k_2/k_{-2}\right)$ in units of M⁻³; $P(t)$ is the number concentration of extendable ends of the nascent fibrils; $M(t)$, the mass concentration of mature fibrils (in monomer units); the concentration of the monomer $m$ derives from material balance, $m(t)=m_{\text{tot}}-M(t)$, where $m_{\text{tot}}$ is the total concentration of htt^ex1Q₃₅; $k_{\mathrm{c}}$ is the rate constant for the conversion of tetramers to “active” nuclei in units of h⁻¹; n2, the order of secondary nucleation^15–17 (n2 = 1 for htt^ex1Q₃₅); $k_{\mathrm{s}}$, the secondary nucleation rate constant in units of M⁻ⁿ²h⁻¹; and $k_{+}$, the chain elongation rate constant in units of M⁻¹h⁻¹. Analysis of the kinetics of tetramerization and fibril formation according to eqs 1.1 and 1.2, assumes that the interconversion of the oligomeric species occurs fast on the time scale of aggregation, and the tetramerization equilibrium (Figure 2B) is established “instantaneously” at each sampled time-point during the course of aggregation.¹³ This assumption is based on the fact that prenucleation tetramerization occurs on the μs time scale while aggregation/fibril formation proceeds on a time scale of hours/days.

The product of the two constants in the first term of eq 1.1 ($k_{\mathrm{c}}{K}_{\mathrm{T}}$) is formally equivalent to the rate constant of primary nucleation (k_n) in “classical” formulations of protein aggregation kinetics.^14,47,48 This product makes the determination of each individual constant just from the best-fits of aggregation profiles impossible without prior knowledge of either of them from other types of experimental data. However, the rate constant for conversion of tetramers to elongation competent nuclei $,k_{\mathrm{c}}=0.068\pm 0.01{\mathrm{h}}^{-1}$, was established in our previous study of htt^ex1Q₃₅ aggregation kinetics in the absence of cosolutes from ¹⁵N/¹H_N-δ_ex and cross-peak volume/intensity ratios (V/I) obtained during the course of aggregation decay of NMR signals.¹³ Since $k_{\mathrm{c}}$ describes a very slow conformational rearrangement, we posit that this rate is unlikely to undergo significant changes in the presence of cosolutes. Therefore, integration of eqs 1.1 and 1.2 was performed with the value of $k_{\mathrm{c}}$ fixed to its previously determined value¹³ for all aggregation profiles here (with or without cosolutes). The values of $K_{\mathrm{T}}$ extracted from the best-fits to the model in eqs 1.1 and 1.2 are therefore predicated on the premise of $k_{\mathrm{c}}$ being invariant to cosolute effects. It is worth noting, however, that the remaining rate constants ($k_{+},k_{\mathrm{s}}$) in the model of eqs 1.1 and 1.2 are largely independent of this assumption since the process of primary nucleation is determined by the product $k_{\mathrm{c}}{K}_{\mathrm{T}}$ rather than individual constants in eqs 1.1 and 1.2.

The aggregation decay profiles, monitored by the measurement of cross-peak intensities in 2D ¹H–¹⁵N SOFAST-HMQC NMR spectra and best-fit to the model described by eqs 1.1 and 1.2, for the C-terminal residues of htt^ex1Q₃₅ (PRD domain) in the absence of cosolutes, along with the temporal changes in the concentration of tetramers T in monomer units (4[T]) occurring during the course of aggregation, are shown in Figure 3A. The corresponding htt^ex1Q₃₅ aggregation profiles and changes in tetramer concentrations in the presence of dextran-20 and lysozyme are shown in Figures 3B and 3C, respectively. The amount of tetrameric species available at the initial stages of aggregation determines the rate of primary nucleation, and is inversely proportional to the length of the lag period at the onset of fibril formation (Figure 3A–C). As time progresses, fibril-mediated secondary nucleation process ($k_{\mathrm{s}}$) gradually becomes the dominant nucleation mechanism, with the amount of tetramer and the rate of conversion from tetramer to “active” nuclei $P(k_{\mathrm{c}})$ losing their significance. Integration of eqs 1.1 and 1.2 was performed numerically using the initial conditions $P(0)$ obtained in each case from a coarse-grained grid-search and indicated in the caption of Figure 3, while $M(0)$ was set to 0 in all the cases. The optimal values of rate constants and $K_{\mathrm{T}}$ obtained from the fit are summarized in Table 1. It is important to note that the presence of a small amount of nuclei P at the start of fibril formation ($P(0\ne 0$) ensures at least partial decorrelation of otherwise highly correlated pairs of parameters: ($K_{\mathrm{T}};k_{+}$) and ($k_{\mathrm{s}};k_{+}$).⁴⁸ Residual anticorrelations between the ($K_{\mathrm{T}};k_{+}$) and ($k_{\mathrm{s}};k_{+}$) pairs of parameters are reflected in relatively higher errors for all parameters of htt^ex1Q₃₅ aggregation in the presence of dextran-20 (Table 1). Plots of reduced χ² of the fits in the presence of dextran-20 and lysozyme as a function of $K_{\mathrm{T}}$ and $k_{+}$, and $k_{\mathrm{s}}$ and $k_{+}$, generated while keeping the products $K_{\mathrm{T}}{k}_{+}$ and $k_{\mathrm{s}}{k}_{+}$ constant, are shown in the SI, Figure S5.

Figure 3.

Aggregation profiles and temporal changes in the concentration of tetramers T (in monomer units) for htt^ex1Q₃₅ in the absence of cosolutes (A), in the presence of 200 mg/mL dextran-20 (B), and 100 mg/mL lysozyme (C). The experimental data, recorded at 5 °C (800 MHz) and normalized to the first time point (t = 0), are shown with open circles. The best-fit curves are shown as black continuous lines and were obtained from a global fit to the kinetic scheme in Figure 1 and the model described by eqs 1.1 and 1.2. Initial concentrations of each sample, m_tot, are indicated on the plots. The following sets of initial conditions P(0) were used in the fits (in nanomolar, nM, units): {2; 4; 6} for htt^ex1Q₃₅ in the absence of cosolutes; {0.5; 1.0; 10} for htt^ex1Q₃₅ in the presence of dextran-20; and {0.5; 12; 60} in the presence of lysozyme. See SI, “Materials and Methods” for the details of the fitting procedure.

Table 1.

Parameters of htt^ex1Q₃₅ Aggregation Kinetics in the Absence and Presence of Macromolecular Cosolutes^a

Sample conditions	KT × 106 (M−3)	ks (M−1 h−1)	k+ × 105 (M−1 h−1)
No cosolute	7.4 ± 0.4	0.3 ± 0.02	6.4 ± 0.4
+ 200 mg/mL dextran-20	39 ± 8	1.4 ± 0.5	28 ± 9
+ 100 mg/mL lysozyme	2.9 ± 0.1	0.1 ± 0.01	4.5 ± 0.1

^aThe rate constant k_c was set to 0.068 h⁻¹ in all the fits (see text).

Plots of the time evolution of nuclei P (nM), mature fibrils M (μM), and the ratios $M/P$ extrapolated for $t\to \infty (M_{\infty }/P_{\infty })$, which serve as approximate measures of fibril length,^48,49 are shown in Figure 4. The ratio $M/P$ reaches approximately the same maximum of ~2,000 at t → ∞ in the absence and presence of cosolutes. Assuming the separation between polyQ β strands along the long axis of the fibril of ~5 Å, we estimate that the fibrils reach an approximate length of ~1 μm, in good agreement with the measurements from electron microscopy images of htt^ex1Q₃₅ fibrils in our earlier study.¹² In fact, the preservation of $M/P$ ratios in the presence of cosolutes can be predicted from simple analytical arguments. Specifically, using the ansatz about the “average” form of $P(t)$, $P_{av}(t)$, given by,^47,50 $P_{av}(t)=P_0(t)/\left(1+P_0(t)/P_{\mathrm{\infty }}\right)$, where $P_0$ stands for $P$ at the start of aggregation, we obtain an approximate analytical form for $P_{\mathrm{\infty }}$,

$$P_{\mathrm{\infty }}\approx \frac{\sqrt{{\left(2k_{+}{P}_0\right)}^2+K_T{k}_{+}{k}_{\mathrm{c}}{m}_{tot}^4+2k_{+}{k}_{\mathrm{s}}{m}_{tot}^2}}{2k_{+}}$$ (2)

Figure 4.

Time dependence of mature fibrils M, nuclei P, and the M/P ratios, simulated for htt^ex1Q₃₅ aggregation (5 °C) using the optimized parameters of the kinetic model in eqs 1.1 and 1.2 in the absence of cosolutes (A), and in the presence of 200 mg/mL dextran-20 (B) and 100 mg/mL lysozyme (C).

For nondissociative fibrils, the ratio $M_{\mathrm{\infty }}/P_{\mathrm{\infty }}$ is equal to $m_{\text{tot}}/P_{\mathrm{\infty }}$, and is given by

$$\frac{M_{\mathrm{\infty }}}{P_{\mathrm{\infty }}}\approx \frac{2k_{+}{m}_{\text{tot}}}{\sqrt{{\left(2k_{+}{P}_0\right)}^2+K_T{k}_1{k}_{\mathrm{c}}{m}_{\text{tot}}^4+2k_{+}{k}_{\mathrm{s}}{m}_{\text{tot}}^2}}$$ (3)

It follows from eq 3 that for $P_0\approx 0,M/P\equiv M_{\mathrm{\infty }}/P_{\mathrm{\infty }}\sim \sqrt{k_{+}}$, while for $P_0\approx 0$ and small $m_{tot}$, the first two terms under the square root contribute negligibly to the total sum, and $M/P\approx \sqrt{2k_{+}/k_{\mathrm{s}}}$. This relationship shows that for preservation of the average fibril length to hold, the change in one of the rate constants ($k_{+}$ or $k_{\mathrm{s}}$) due to some external factors such as cosolutes, should be accompanied by a proportional change in the other rate constant.

The primary effect of both cosolutes on htt^ex1Q₃₅ aggregation kinetics relates to the shifts in the tetramerization equilibrium (Figure 2B and the upper part of Figure 1) resulting in profound changes in concentrations of “preformed” tetramers. The shifts in this equilibrium under the effect of cosolutes follow the same trends as described above for the nonaggregating htt variant, htt^ex1Q₇, but are somewhat larger: while the presence of dextran-20 shifts the equilibrium far to the right increasing the value of $K_{\mathrm{T}}$ (and hence the rate of primary nucleation) 5.2-fold, the presence of lysozyme shifts the equilibrium slightly to the left by decreasing the value of $K_{\mathrm{T}}$ and the rate of primary nucleation 2.5-fold (Table 1). The partially folded tetramers of htt^ex1Q₃₅ are stabilized by excluded volume effects in the presence of dextran-20 which acts as a typical crowding agent.^{21,32,35,37,39,40,42} The effects of lysozyme on the tetramerization equilibrium are more subtle and are likely to arise from weak attractive interactions of a hydrophobic nature between the two proteins.^{23,37,43–45} We note that the modeling of aggregation kinetics according to eqs 1.1 and 1.2 provides only the product of equilibrium constants ($K_{\mathrm{T}}$) and does not bear any information on the partitioning between its constituents ($K_{\mathrm{e}\mathrm{q},1}$ and $K_{\mathrm{e}\mathrm{q},2}$). Assuming the same ratio of the two equilibrium constants determined in our earlier study of htt^ex1Q₃₅ tetramerization in the absence of cosolutes, $\left(K_{\text{eq},2}/K_{\text{eq},1}\right)=4737$,¹³ we estimate that $K_{\text{eq},1}=20.2{\mathrm{M}}^{-1}$, and $K_{\mathrm{e}\mathrm{q},2}=9.5\times {10}^4{\mathrm{M}}^{-1}$ in the presence of dextran-20, and $K_{\mathrm{e}\mathrm{q},1}=8.5{\mathrm{M}}^{-1},K_{\text{eq,}2}=4.0\times {10}^4{\mathrm{M}}^{-1}$ in the presence of lysozyme. Although exactly the same $\left(K_{\text{eq,}2}/K_{\text{eq,}1}\right)$ ratio (namely, the stability of the tetramer $T$ relative to that of the dimer $D$) cannot be guaranteed in the presence of cosolutes, an approximate lower bound on $\left(K_{\text{eq},2}/K_{\text{eq},1}\right)\sim 1000$, can be estimated from simulated ¹⁵N-δ_ex values as a function of both htt^ex1Q₃₅ monomer concentration and $\left(K_{\text{eq},2}/K_{\text{eq},1}\right)$ ratio.

Both cosolutes also affect the rate constants of htt^ex1Q₃₅ aggregation, and these changes occur in concert with the shifts in tetramerization equilibrium. In particular, whereas dextran-20 accelerates fibril formation by increasing $k_{+}$ and $k_{\mathrm{s}}$ ~ 4.5-fold, lysozyme slows it down ever so slightly by a concerted decrease in these two rate constants (Table 1). Although some effects of the crowded environment on the rates of protein aggregation/fibril formation were predicted from simulations or observed experimentally on several occasions previously,^{24–27,51–54} the mechanistic basis for these changes in each particular case is hard to pinpoint. We note that the acceleration of htt^ex1Q₃₅ fibril formation in the presence of 200 mg/mL dextran-20 is in quantitative agreement with earlier observations of Dobson and co-workers for the aggregation of a number of proteins in the presence of crowding agents.^24,26 In particular, significant enhancements, Γ, in fibril elongation rates (quantified as the ratio of fibril elongation rates with and without cosolutes) up to a factor of ~2.5 were reported for bovine insulin, human α-synuclein and lysozyme in the presence of 50 mg/mL dextran-200 (MW ~ 200 kDa), with Γ exponentially dependent on the concentration of dextran.²⁶ These enhancement factors were found to be consistent with predictions based on “scaled particle” theory⁵⁵ that provides a description of the volume fraction available to particles (including those of a fibril) upon their introduction into a bath of inert cosolute molecules. Using the parameters of the “scaled particle” model for nonspherical cosolutes (see SI, eq S3, and the accompanying explanations), we estimate Γ for htt^ex1Q₃₅ in the presence of 200 mg/mL dextran-20 to be 4.30, in good agreement with the value of 4.38 ± 1.43 for the experimental ratio of rate constants $k_{+}$ with and without dextran-20 reported in Table 1. Conversely, a slight slow-down of htt^ex1Q₃₅ aggregation in the presence of lysozyme may be attributed to minor changes in solution conditions and/or the mechanisms of chain elongation/secondary nucleation rather than to excluded volume effects.

In summary, we have described the effects of two macromolecular cosolutes, namely the polysaccharide dextran-20 (200 mg/mL) and the protein hen egg white lysozyme (100 mg/mL), on the aggregation kinetics of a pathogenic huntingtin exon-1 protein with 35 polyQ repeats, htt^ex1Q₃₅. The unified kinetic model shown in Figure 1 and described by eqs 1.1 and 1.2, forms the basis for a combined quantitative analysis of the fast, reversible tetramerization and much slower, irreversible fibril formation from cross-peak intensities in a series of 2D ¹H–¹⁵N SOFAST-HMQC NMR spectra acquired during the course of htt^ex1Q₃₅ aggregation. The primary effect of both cosolutes on htt^ex1Q₃₅ aggregation kinetics is associated with a shift in the tetramerization equilibrium resulting in profound changes in concentrations of “preformed” htt^ex1Q₃₅ tetramers. Similar effects of both cosolutes on the tetramerization equilibrium observed for a shorter, very slowly aggregating (on a time scale of weeks) huntingtin variant with 7 polyQ repeats, htt^ex1Q₇, lend confidence to the conclusions drawn from the modeling of htt^ex1Q₃₅ aggregation kinetics. The presence of cosolutes also affects to some extent the rate constants of htt^ex1Q₃₅ fibril formation. The observed acceleration of htt^ex1Q₃₅ fibril formation in the presence of dextran-20 is in qualitative agreement with earlier reports for other aggregating protein systems.²⁶