A comparative study of machine learning and response surface methodologies for optimizing wear parameters of ECAP-processed ZX30 alloy

Abstract

Magnesium, valued for its lightweight, recyclability, and biocompatibility, faces challenges like its poor wear behavior and mechanical properties that limit its adaptation for a multitude of applications. In this study, various statistical analyses, and machine learning (ML) techniques were employed to optimize equal channel angular pressing (ECAP) process parameters for improving the wear behavior of Mg-3wt.% Zn-0.7 wt% Ca alloy. ECAP was conducted up to four passes via route Bc at 250 °C. Wear testing of both as-annealed (AA) and ECAP-processed alloys was performed using the dry ball-on-flat wear method under varying loads, speeds, and time. One pass (1P) and 4Bc-ECAP resulted in a notable uniform grain refinement of 86 % and 91 %, respectively, compared to the AA. X-ray diffraction (XRD) analysis confirmed a refined structure attributed to extensive dynamic recrystallization. Mechanical wear testing revealed a significant reduction in volume loss (VL), up to 56 % and 28.5 % after 1P and 4Bc samples, respectively, compared to the AA sample, supported by the observed texture intensity. The coefficient of friction (COF) stabilizes at 0.30–0.45, indicating low friction characteristics. Next, by adjusting wear load and speed through design of experiments (DOE), the wear output responses, VL and COF, were experimentally investigated. The output responses were predicted in the second step using ML, 3D response surface plots, and statistical analysis of variance (ANOVA). According to the regression model, the minimal VL was attained at a 5 N applied load. Also, the wear speed and VL at different passes are inversely proportional. On the other hand, the optimal COF was obtained at applied load about 2–3 N and 250 mm/s at different passes. The wear process variables were then optimized using different optimization techniques namely, genetic algorithm (GA), hybrid DOE–GA, and multi-objective genetic algorithm (MOGA) approaches.

1. Introduction

Magnesium (Mg) alloys are highly esteemed in the aerospace, automotive, and electronic communication industries due to the exceptional mechanical properties they possess; namely their low density, high specific strength, and machinability [[1], [2], [3]]. Moreover, Mg alloys have emerged as potential substitutes for traditional orthopedic and cardiovascular biomaterial implants due to their favorable biocompatibility and biodegradability [4,5]. However, in practical applications, certain components fabricated from Mg alloys undergo friction and wear, leading to a reduction in their overall durability [6]. Mg–Zn–Ca-based alloys (designated as ZX alloys) have garnered considerable attention as bio-implant materials owing to their favorable mechanical properties, facilitated by the presence of zinc (Zn) and calcium (Ca), which are elements found naturally in the human body and proper nutrition requires their presence [7]. Zn and Ca effectively refine Mg grains, thereby enhancing ductility and contributing to improvements in mechanical performance [8]. However, these alloys’ mechanical strength often falls short of optimal levels, primarily due to the low content of alloying elements [9]. Meeting the demands for wear resistance under various service conditions remains a significant challenge, constituting a fundamental barrier in biomedical applications [10]. Consequently, there is an urgent need to explore methodologies capable of simultaneously improving the mechanical properties and wear resistance of ZX-Mg alloys to extend their operational lifespan.

To address these concerns, researchers have explored various methods including designing new alloys, developing composites, and surface modifications [11,12]. Dou et al. [13] studied the impact of various surface treatments on the friction and corrosion resistance of AZ31 alloy. Ultrasonic rolling + ion injection yielded the most significant reduction in surface roughness, lowest friction coefficient, and superior wear resistance. In a dry friction setup, wear tests were performed on Co–Mg alloy, both borided and unborided. Boriding significantly improved wear resistance, showing a wear rate of 25.89x10⁻⁵ to 94.95x10⁻⁵ mm³/N.m [14]. Somekawa et al. [15] investigated the wear and frictional characteristics of an Mg–Zn–Y alloy with quasi-crystalline phase dispersion. The uniform phase distribution within the coarse-grained matrix significantly enhanced the wear resistance. However, some techniques such as surface coating may introduce complications like decreased biocompatibility and mechanical properties, and poor bonding to the Mg surface [16]. Mechanical processing, including severe plastic deformation (SPD) techniques like equal channel angular pressing (ECAP) and high-pressure torsion (HPT), have garnered attention for their ability to enhance mechanical properties and refine grain structure, thereby influencing corrosion and wear resistance and other properties relevant to biomedical applications [[17], [18], [19]]. In addition, SPD processes offer the advantage of producing ultrafine-grained materials without the need for additional alloying elements, making them particularly suitable for biomaterials with stringent biocompatibility requirements [20].

SPD through ECAP has been hailed as a highly promising technique for altering the texture of ZX-Mg alloys [21]. Tong et al. [22] studied the effect of ECAP on Mg–Zn–Ca alloy using routes A, Bc, and C. Route Bc was the most effective in grain refinement. Huang et al. [23] achieved notable grain refinement (∼259 μm) in the Mg-1.1 % Ca- 2 % MgO composite alloy after four passes of ECAP, which significantly enhanced the mechanical properties, decreased the corrosion rate, and improved the biocompatibility. Martynenko et al. [24] reported that the corrosion resistance of Mg–Zn–Ca alloys subjected to Bc-ECAP did not exhibit any improvement, despite the doubling of its ductility. Therefore, the mechanical and corrosion properties of ZX alloys are significantly impacted by ECAP routes, owing to the induced plastic strain, alterations in microstructure, and texture modifications. On the other hand, while ECAP processing enhances tensile ductility and may improve other mechanical properties like fatigue strength and formability, its impact on wear resistance remains a topic of ongoing research [25]. Consequently, there is limited understanding regarding the wear characteristics of ECAPed Mg-ZX alloys.

Recently, various studies have been conducted on predicting and optimizing the ECAP parameters and characterizing wear performance via machine learning and statistical analysis techniques, such as response surface methodology (RSM), genetic algorithms (GA), hybrid design of experiments and GA, and multi-objective genetic algorithms (MOGAs) [[26], [27], [28], [29]]. Machine learning (ML) is a subset of artificial intelligence that focuses on creating models and algorithms that let computers learn and make decisions without explicit programming [[30], [31], [32]]. Saleh et al. [33] experimentally investigated the effect of dry sliding wear testing variables on the weight reduction of AZ91 produced by rotary die-equal channel angular pressing (RD-ECAP) method through 0, 8, and 16 passes. The results show that improvements in the wear resistance of AZ91 depend on the increase in the number of passes of RD-ECAP. However, increasing the applied load, sliding speed, and sliding time all resulted in a lower wear resistance, according to RSM analysis. Shaban et al. [34] used ML approaches to optimize the ECAPed-ZK30 parameters. A die angle of 90° and four passes via route Bc were found to produce the most grain refinement. Hence, a combination of optimization approaches proved effective for modelling and predicting the behavior of ECAPed materials.

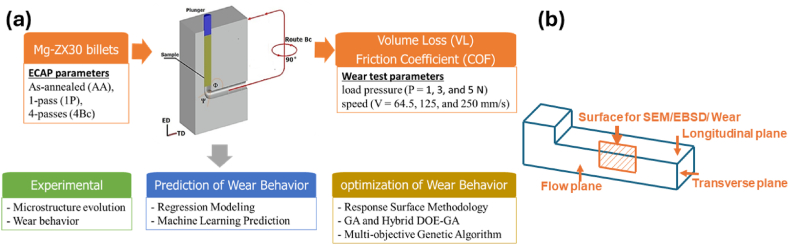
In summary, this study investigates the potential of ECAP to enhance the Mg-based ZX30 alloy's mechanical properties by producing an ultra-fine grain (UFG) structure, resulting in significant strengthening and improved structural homogeneity. This highlights the critical need to extend these advancements to tribological properties and implement appropriate optimization strategies. The objective of this research is to evaluate the influence of various ECAP processing parameters on the microstructural and tribological characteristics of ZX30-Mg alloy (Fig. 1a). Utilizing experimental results, optimization techniques such as machine learning (ML) and response surface methodology (RSM) are employed to determine the optimal processing conditions for realizing the highest performance in the Mg-ZX30 alloy.

Fig. 1.

(a) Flow chart of the research procedures, (b) Schematic of the ECAP sample and position for microstructure and wear characterization.

2. Experimental details and methodology

2.1. Materials and experimental procedures

In this research, ECAP was performed on a ZX30 Mg alloy with a chemical composition of Mg–3 wt.% Zn–0.7 wt% Ca. The as-received extruded bars were machined into billets with a diameter of 20 mm and a length of 60 mm. Before processing, ZK30 billets were annealed at 430 °C for 16 h, and then furnace cooled. As illustrated in Fig. 1a, the adopted ECAP die had two cylindrical channels intersecting at an angle (Φ) of 90° with an outer arc of curvature (Ψ) of 20°. The process was conducted at 250 °C. The ZX30 billets were processed through 1-pass (1P) and four passes via route Bc (4P) by rotating the sample in the same direction along their longitudinal axis by 90° before each new pass.

The microstructural characterization for both the as-annealed (AA) and ECAPed ZX30 alloys was performed after the samples were cut along their longitudinal cross-section (Fig. 1b), polished, and etched in a solution of 6 g picric acid, 5 mL acetic acid, 100 mL ethanol, and 10 mL deionized water. The microstructural evolution of the as-annealed and ECAPed ZX30 alloys, including grain size and grain orientation distribution maps, was examined using Electron Backscattered Diffraction (EBSD) interfaced with a field-emission gun scanning electron microscope (FEG-SEM). The EBSD analyses were performed on the billet's longitudinal section — that is the plane parallel to the processing direction (flow plane), as shown in Fig. 1b. The data was processed using the HKL Flamenco Channel 5 software program (Hitachi, Ltd., Tokyo, Japan). In order to achieve good statistical data, the SEM was operated at 15 kV and 1.5 nA, with a step size of 100 nm from the extrusion direction (ED) surface during EBSD. Furthermore, X-ray diffraction (XRD) was used to study the microstructure and to analyze the secondary phases.

The mechanical wear characterization of as-annealed and ECAPed ZX30 samples was investigated in terms of the VL and COF using a ball-on-flat test rig (Bruker's universal mechanical tester, USA). The tests were performed under three levels of applied loads (1, 3, and 5 N) and three levels of speeds (64.5, 125, and 250 mm/s). The wear test times were adjusted to be (410, 210, and 110 s, respectively) to ensure a consistent wear distance for all conditions, resulting in distances of approximately 26,445 mm, 26,250 mm, and 27,500 mm. This approach allowed us to observe the volume loss variation in response to different speeds, reflecting the material's behavior under applied force and friction. Before testing, the ZX30 samples were ground and polished to a mirror-like finish. The coefficient of friction (COF) values were smoothed using the least square method to minimize noise in the data, and the averages were calculated from the smoothed data. The volume loss values were measured using the final depth of the ball.

2.2. Machine learning methodology

A precise predictive machine learning model was developed to forecast the ECAP characteristics of ZX30 alloys. These models were built using the following fundamental techniques: linear regression (LR), Gaussian process (GP) for regression, and random forest (RF) [35]. These machine learning models work well together and have great potential for precisely predicting the ECAP parameters. These algorithms are employed to find characteristics, relationships, and patterns in the data under study. The following is used to describe a few of these techniques.

2.2.1. Linear regression

Linear regression is a fairly straightforward statistical method that maps the relation between a dependent variable and one or more independent variables. The machine learning model interprets the data as a linear equation and seeks to find the best-fit line that provides an accurate description of the data. This can be quantified as the line whose values produce the least difference from the actual dependent variable values. Linear regression equations are of the form shown in Eq. (1) [27]:

$$y=\sum _{i=1}^n{b}_i{x}_i+b_0$$ 1

where y is the dependent variable, x₁, x₂, …, x_n are the independent variables, b₀ is the intercept, and b₁, b₂, …, b_n are coefficients that describe how the independent and dependent variables interact. The ordinary least squares method is then used to calculate the coefficients that would lead to the best-fit line. This is accomplished by selecting the coefficients that minimize the sum of the squares of the differences between the predicted and actual values. After training the model, it can be used any number of times to predict the dataset's behavior by altering the values of the independent variable(s). However, multiple reasons might cause the overfitting of the model, in which case the model fails to predict values from new independent variables. As such, a number of methods can be used to mitigate overfitting behavior in the model, Regularized linear regression (RLR) is one such popular method [27]. It introduces a penalty term to the linear regression model that improves its generalization performance.

2.2.2. Gaussian process (GP)

A non-parametric probabilistic regression technique called GP regression is used to describe the relationship between the input and target variables. It views forecasts as a Gaussian process, with a range of likely functions defined by a covariance function (kernel) and a mean. Uncertainty may be evaluated since GPR produces a posterior distribution over the anticipated functions [36]. A general purpose function (GP) may be described by its covariance function, k(x,x'), which is the kernel function, and its mean function, m(x), where x and x' are two instances inside the input features matrix x. Consequently, the following is a description of the predicted y* values as a Gaussian process function (Eq. (2)) [36]:

$$y^{*}\sim GP\left(m\left(x\right),k\left(x,x^{\prime }\right)\right)$$ 2

2.2.3. Random forests (RF)

RF is an ensemble learning technique that produces a final prediction by using many decision trees and combining their forecasts. A random selection of training data attributes and samples is used to build each decision tree. All of the different tree projections are combined to create the final prediction (for example, a majority vote for classification or an average for regression). The equation (Eq. (3)) for random forest prediction is [37]:

$$y=mode\left(y1,y2,.‥,yn\right)$$ 3

Where yi stands for each tree's prediction, and mode is the average for regression or the most common prediction for classification.

2.3. Statistical analysis and regression modeling

In the present investigation, an ANOVA analysis was performed using the Design Expert program to analyze the experimental findings. The effects of the input parameters (P and V) on the output responses (VL and COF) were investigated. Table 1 summarizes the ANOVA results. At a 95 % confidence level, the adjusted R², expected R², p-value, adequate precision, and F-value are reported. p-values less than 0.05 and F-values greater than 4 were found in all of the responses, indicating that the independent parameters, individual model coefficients, and interaction terms were significant determinants of the responses obtained, and that the predicted models are adequate. For the three processing conditions, pressure had a significant effect on the VL, followed by speed. Wear speed has a significant effect on the COF at AA and four passes, followed by pressure. On the other hand, pressure had a significant effect on the COF at single pass followed by speed. The signal-to-noise ratio (S/N), which was determined with adequate accuracy and should be greater than four, was used to evaluate the model's validity.

Table 1.

Statistical analysis of VL and COF of ZX30 at AA, 1P and 4P.

Response	F-Value (F > 4)	p-Value (p < 0.05)	Adeq Precision (ratio >4)	R2	R2adj	R2pred
VLAA	294.59	<0.0001	44.6844	0.9952	0.9918	0.9870
COFAA	33.37	<0.0001	17.2511	0.9589	0.9302	0.8896
VL1P	46.89	<0.0001	17.6173	0.9624	0.9419	0.9113
COF1P	119.2	<0.0001	41.5266	0.9882	0.9799	0.9682
VL4P	1603.54	<0.0001	109.8441	0.9989	0.9982	0.9973
COF4P	65.66	<0.0001	21.6816	0.9787	0.9638	0.9427

Multiple regression transformation types and interactions between independent variables were examined to model wear-related responses. Quadratic regression was used to model the relationships between the provided parameters and the obtained responses. Equations (4)–(9) represent both the non-linear model of volume loss (VL) and the coefficient of friction (COF) at various passes as a function of speed (V) and applied load (P), together with their corresponding determination and adjusted coefficients. Statistical significance of the developed models was verified, which indicates that they can be utilized to predict the response of the system from the input parameters, as long as the best regression coefficient of prediction (R²) is near unity. Correlation coefficient R² and adjusted R² values in the present research ranged from 88.9 to 99.89 %, which is quite close to unity.

VL_AA = 2.17580 × 10⁻⁶+4.48554 × 10⁻⁹ × P+2.06712 × 10⁻¹¹ × V-9.12806 × 10⁻¹² × P × V-1.82219 × 10⁻⁹ × P²

+2.07911 × 10 ¹⁶ × V² + 6.74987 × 10⁻¹² × P² × V-7.8323 × 10⁻¹⁴ × P × V²

R² = 99.52% 4

COF_AA = −0.108819 + 0.245627 × P + 0.005772 × V - 0.002487 × P × V - 0.025489 × P² - 0.000016 × V²

+ 0.000175 × P² × V +4.51575 × 10⁻⁶ × P × V²

R²= 95.89 % 5

VL_1P = 9.54423 × 10⁻⁷+5.23418 × 10⁻⁹ × P+7.34019 × 10⁻¹¹ × V-4.82102 × 10⁻¹¹ × P × V- 7.125 × 10⁻¹⁰ × P²

−2.33249 × 10⁻¹³ × V² +1.32294 × 10⁻¹³ × P × V²

R²= 96.24% 6

COF_1P = −0.036654 + 0.127707 × P+0.009047 × V-0.002969 × P × V-0.00781 × P² -0.000026 × V²

+0.000193 × P² × V +5.69181 × 10⁻⁶ × P × V²

R²= 98.82% 7

VL_4P = 1.55980 × 10⁻⁶+3.80513 × 10⁻⁹ × P-3.01064 × 10⁻¹¹ × V-2.71112 × 10⁻¹¹ × P × V-8.83036 × 10⁻¹⁰ × P2

+1.36033 × 10⁻¹³ × V² +4.03665 × 10⁻¹² × P² × V

R² = 99.89% 8

COF_4P = 0.477336–0.019043 × P - 0.000941 × V+0.000154 × P × V - 0.000963 × P² + 6.58716 × 10⁻⁷ × V²

+ 0.000021 × P² × V - 7.12677 × 10⁻⁷ × P × V²

R² = 97.87% 9

3. Results and discussions

3.1. Experimental results

3.1.1. Grain structure and crystallographic texture

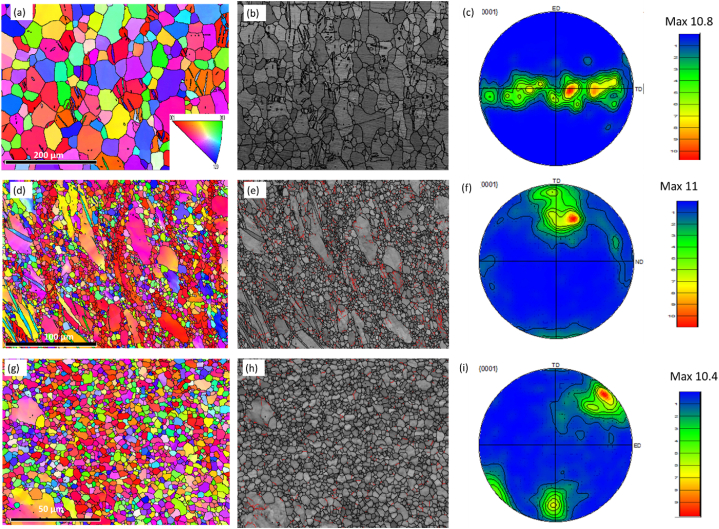
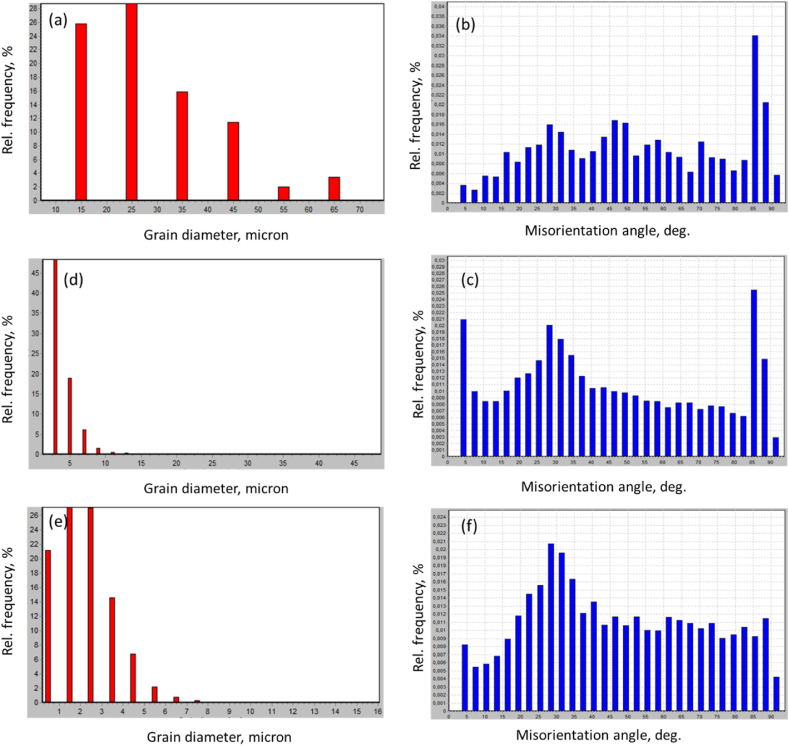
Fig. 2 displays an Inverse Pole Figure (IPF) map of each of the three samples alongside its corresponding grain boundaries (GB) map. The black lines denote high-angle grain boundaries (>15°), while the red lines represent low-angle grain boundaries (ranging from 5 to 15°). In addition, grain size distribution and misorientation angle distribution plots for each processing condition are shown in Fig. 3. For the as-annealed sample (Fig. 2a–c), the sample showcases uniform coarse equiaxed grains with an average diameter of 26 μm (Fig. 3a and b). This sample was annealed at 430 °C for 16 h, which caused some recrystallization twins to expectedly develop [38]. Post-1-pass processing (Fig. 2c–f), the grains show a wide range of orientations. This transformation resulted in elongated structures alongside refined ultrafine grains, indicating that an incomplete dynamic recrystallization was induced by ECAP [39]. Visible coarse elongated grains persisted after processing, which is likely due to their misalignment with the desired slip system during deformation. The inherent anisotropy of the crystal structure in HCP structural metals generally directs deformation towards {0001} <1120> basal slip at room temperature, though prismatic slip may occur under high applied stresses or temperatures [40]. After 1P processing, the grains showed a much narrower size range of 1–15 μm in diameter. The average grain diameter was 3.5 μm, and over 70 % of grains were finer than 4 μm (Fig. 3c and d). The IPF map for 4P similarly shows a blend of red, blue, and yellow orientations (Fig. 2g–i), yet the prevalence of fine equiaxed grains across the entire IPF map denotes a predominantly homogeneous microstructure. This suggests a uniform deformation process caused by dynamic recrystallization (DRX) throughout the entire microstructure. The 4Bc route produced a grain size range of 0.225 μm–16 μm, with an average size of 2.18 μm, as depicted in Fig. 2, Fig. 3e.

Fig. 2.

IPF coloring maps (a, d, g) and their corresponding GB maps with grain boundaries of misorientation angles >15° In black lines, 5°-15° in red lines (b, e, h) and (0001) pole figures for the ZX 30 alloy in its AA-condition (a, b, c) and the ECAP processed samples for (d, e, f) 1P, (g, h, i) 4BCE (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Fig. 3.

Grain size distribution histograms and misorientation angle distributions of ZX30 in the AA condition (a, b) and after ECAP processing through 1P (c, d), and (e, f) 4-Bc.

Analyzing the band contrast map of the annealed sample reveals the prevalence of high-angle grain boundary structures, indicative of complete recrystallization. Additionally, texture analysis indicates a significantly strong texture, approximately ten times stronger than random. Various shear texture components, such as the B fiber, show alignment of the 0001 poles parallel to the shear plane normal (SPN), which aligns with the TD. Post 1P, the texture intensifies further. The maximum intensity achieved was 11 times random and the basal plane was aligned roughly 10° relative to the TD. The crystallographic texture observations are consistent with previous studies conducted on ZX30 [41,42], ZK30 alloy [34], and AZ31 alloy [43]. Notably, examining the grain boundary map of 4P (Fig. 3f) highlights the dominance of high-angle grain boundaries (HAGBs), with few visible instances of low-angle grain boundaries (LAGBs). The smaller LAGB fraction in the 4P condition, with a total relative frequency of 0.0255 as confirmed by misorientation angle distributions, emphasizes the effectiveness of processing for 4-passes via route Bc.

After 1-pass ECAP, recrystallized grain formation reduces dislocation accumulation within the grains, subsequently causing their transforming into LAGBs [44]. The presence of large grains, as illustrated in Fig. 2d, hinders dislocation motion and results in their aggregation around these particles. During processing, this aggregation transforms into LAGBs and ultimately into new grains with HAGBs, a phenomenon known as particle stimulated nucleation (PSN) (Fig. 3b and c) [39]. This mechanism significantly influences grain development during ECAP processing, particularly at low strain rates [45]. Additionally, bulging of grain boundaries often precedes dynamic recrystallization (DRX), a process closely linked with strain-induced grain boundary migration, which becomes evident after 4 passes of route Bc. Moreover, nucleation within shear bands leads to the formation of grains with various orientations [46]. The effect of DRX is also discernible in the evolution of grain boundary distribution, as depicted in Fig. 2g, where the fraction of LAGBs decreases due to grain refinement mechanisms induced by DRX during ECAP processing. Consequently, this processing route promotes the development of a more uniform deformation field, facilitating the activation of different slip systems. The observed misorientation angle distribution and substantial reduction in grain size, in Fig. 3, strongly suggest enhancements in mechanical properties, consequently impacting the wear resistance of the ZX30 alloy.

3.1.2. X-ray diffraction (XRD)

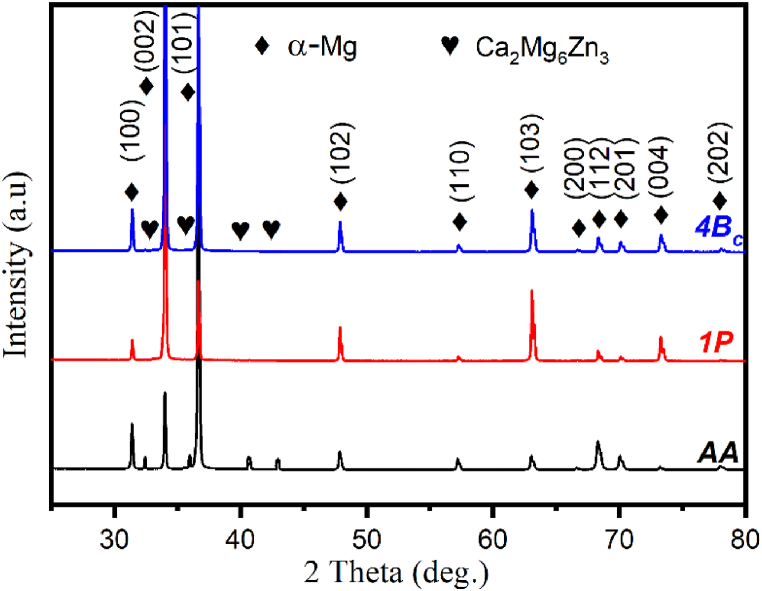
X-ray diffraction (XRD) analysis was employed to assess the impact of ECAP on both AA and ECAP-induced phases within ZX30 alloys, presented in Fig. 4. Predominantly, the identified peaks in the samples are associated with the α-Mg phase, signifying no presence of oxidation or the emergence of novel crystalline phases due to the extrusion process. Furthermore, the XRD investigation shows the presence of eutectic Ca₂Mg₆Zn₃ second phases only within the as-annealed (AA) billets, whereas it diminishes notably for 1P [47]. This observation reveals that as the Zn content within the alloy increases, the Mg₂Ca phase diminishes, leaving behind an α-Mg solid solution and Ca₂Mg₆Zn₃ phases. Such behavior points towards distinct precipitation tendencies. For the ZX30 alloy processed through 4P, XRD revealed a distinctive transformation: processing exclusively retained α-Mg peaks while the Ca₂Mg₆Zn₃ peaks disappeared. The dissolution is due to the elevated density of dislocations and vacancies generated by the ECAP process, creating pathways for enhanced diffusion of Zn and Ca atoms [48]. Concurrently, the intensities of these retained peaks exhibited broadening, indicative of a refined structure attributed to extensive dynamic recrystallization [34,49].

Fig. 4.

XRD Pattern for AA-ZX30 and ECAP processed billets.

3.1.3. Wear behavior

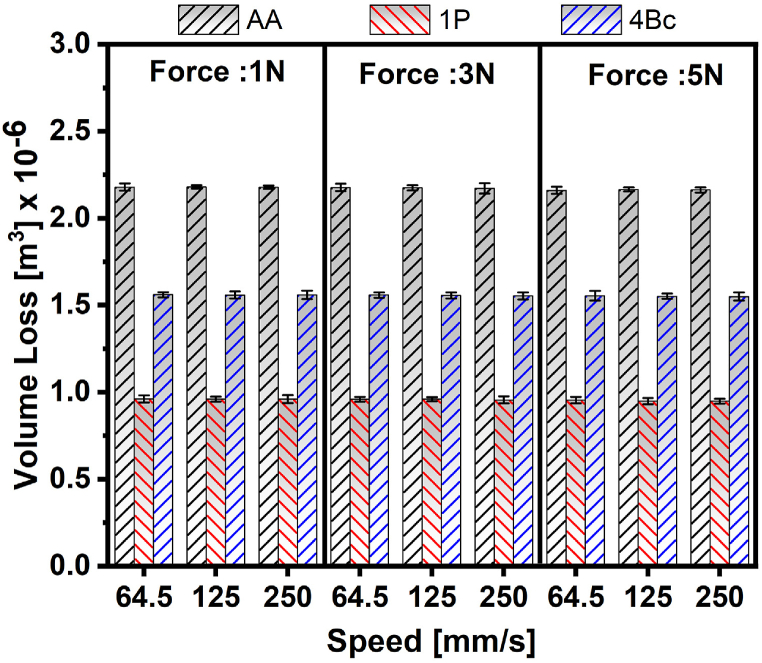
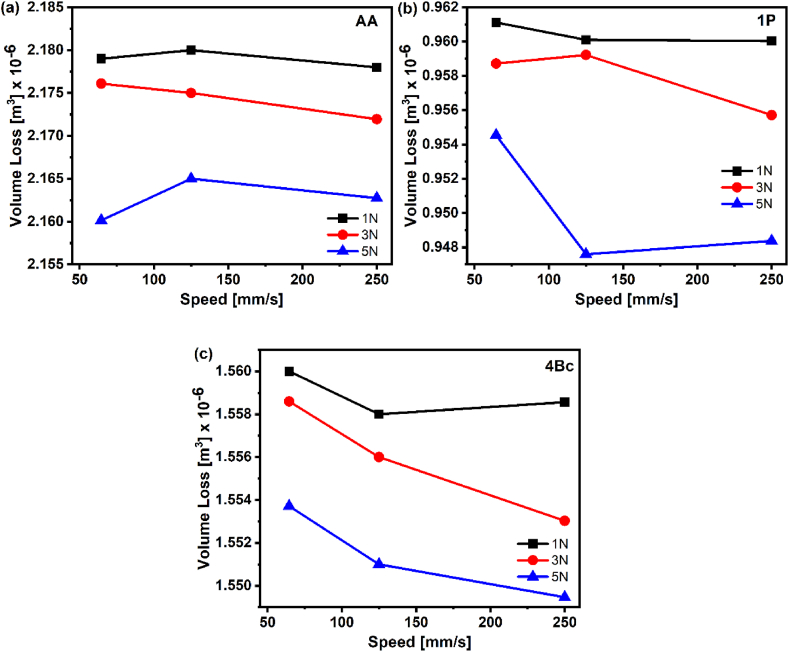
The volume loss assessment depicted in Fig. 5 for wear-tested ZX30 samples, for both AA and ECAP processed samples, highlights intriguing wear resistance patterns under varying applied wear loads. Notably, the wear resistance curves exhibit a consistent behavior with increasing sliding distance, showcasing nearly steady-state characteristics. Surprisingly, the volume loss remains mostly unaffected by rising wear loads from 1 to 5 N across all examined samples. The AA sample displays the highest volume loss at all applied wear loads, measuring 2.178x10⁻⁶ m³ (Fig. 5). However, post-1P ECAP processing, a substantial reduction in volume loss is evident, recorded at 0.958x10⁻⁶ m³, marking a remarkable 56 % decrease compared to the AA sample. Further processing via 4P shows an improved reduction in the volume loss by 28.5 % compared to the AA. Fig. 6 corroborates these findings, emphasizing the insignificant effect of applied loads within the range of 1–5 N across all ZX30 samples. The volume loss values remain between 2.164x10⁻⁶ to 2.178x10⁻⁶ m³ (Fig. 6a), 9.481x10⁻⁷ to 9.594x10⁻⁶ m³ (Fig. 6b), and 1.549x10⁻⁶ to 1.558x10⁻⁶ m³ (Fig. 6c), for AA, 1P, and 4P, respectively.

Fig. 5.

The volume loss of the AA and ECAPed ZX30 alloy under varying applied loads.

Fig. 6.

The volume loss over time for ZX30 subjected to (a) AA, (b) 1P, and (c) 4Bc.

These results suggest the formation of a mechanically mixed layer, extending the contact area between the sample and counter surface, thus enhancing wear behavior of ECAPed samples. The presence of intermetallic phases within the Mg matrix, noted for their high thermal stability, likely contributes to enhanced interfacial bonding, consequently boosting the wear resistance [50]. Comparable findings by Y. Hong et al. with an extruded AZ91 alloy highlight the role of fine Mg₁₇Al₁₂ particles in improving microhardness and, consequently, wear behavior [51]. Interestingly, the dominance of texture strengthening mechanisms over grain refinement effects, particularly evident in 1P and 4P samples, underscores the significance of texture intensity as shown in Fig. 7. Despite experiencing lower volume loss, the ECAPed samples exhibit lower texture intensity in the transverse direction (TD), extrusion direction (ED), and normal direction (ND) (Fig. 7). The AA condition revealed a maximum texture strength of 5.2 times random which was displayed at the ED as shown in Fig. 7a. Plastic straining through 1P displayed a maximum texture strength of 2.8 times random which was depicted at both TD and ND (Fig. 7b), while processing through 4P displayed a maximum texture strength of 1.5 times random (Fig. 7c). Accordingly, the severe reduction of grain size (Fig. 2) resulted in improving the wear behavior of ZX30 alloy (Fig. 4). On the other hand, increasing the ECAP passes from 1P up to 4P showed a notable deterioration in the wear behavior despite of decreasing the average grain size which was coupled with a decrease in the texture strength which indicated that the texture strengthening effect could dominate the effect of grain refinement effect. Accordingly, the effect of surface texture on the wear behavior was confirmed by Yuan et al. [52].

Fig. 7.

The Inverse Pole Figure (IPF) of along ZX30 alloy at its (a) AA, (b) 1P and (c) 4P condition along the Transverse Direction (TD), Extrusion Direction (ED), and Normal Direction (ND).

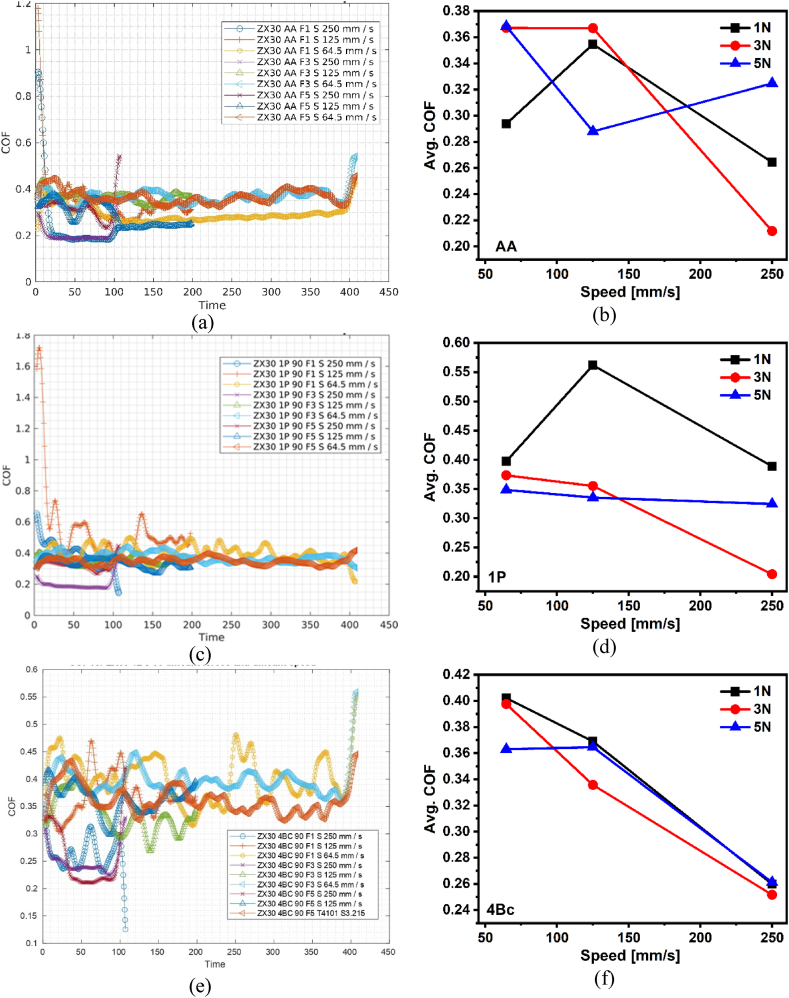
The friction coefficients obtained for the ZX30 alloy under different wear test conditions are shown in Fig. 8. The obtained friction coefficients for the ZX30 alloy across diverse wear test conditions portray distinct behaviors indicative of material response under varying loads and speeds. Initially exhibiting instability across all tested conditions, this is attributed to the repositioning of wear debris within the wear track upon contact initiation. Stabilization manifests as consistent values ranging between 0.30 and 0.45 (Fig. 8a–c, e), emphasizing the alloy's inherent low friction characteristics owing to its hexagonal crystal structure, facilitating shearing along basal planes. Notably, under higher wear speeds, a marked reduction in the COF to approximately 0.22 emerges under a 3 N load (Fig. 8b–d, f), aligning with observed wear rate trends. This decline correlates with the formation of an optimal contact area, fostering a protective layer on the refined structure induced by ECAP. This layer, reliant on both the robust surface and accumulated friction, appears to boost wear resistance [53]. The improved friction and wear properties are further attributed to the profound grain size reduction, heightened surface hardness, and the introduction of significant residual compressive stress into the surface layer, instigating a gradient nanostructure [54,55]. This nanostructure mitigates microcrack initiation and expansion, underscoring its role in augmenting the friction and wear performance of the processed alloy.

Fig. 8.

The coefficient of friction (COF) values, represented as (a, c, and e), along with the average COF values (b, d, and f), were determined for both as-annealed (AA) billets (a, b) and the ECAP-processed ZX30 alloy following routes (c, d) 1P and (e, f) 4Bc.

The wear mechanism can be divided into mild and severe wear according to the wear parameters such as applied load, speed, and wear distance [56]. In this study, the wear parameters lie in the mild wear region (applied load of 5 N and wear speed of 250 mm/s). In the mild wear regime, both oxidation wear and delamination wear mechanisms occur [57,58]. Fig. 9 shows the worn surface of ZX30 samples after wear testing. The wear grooves were aligned parallel to the wear direction as shown in Fig. 9. Furthermore, the worn surface morphology contained the adhesion region as well as the plastic deformation bands. In addition, the wear debris remained in adhesion with the worn surface of ZK30 which can be an indication for abrasion wear happening [59]. The hard particles in the contact surfaces scratched the samples and fragments of ZX30 were removed as reported by Lim et al. [60]. From Fig. 9a it can be revealed that the wear grooves of the AA condition were wider and deeper compared to the ECAP processed counterpart (Fig. 9b) which indicates that ECAP processing improved the wear behavior due to the developed ultrafine grained structure which improved the hardness of ZX30 alloy.

Fig. 9.

SEM micrographs of the worn surface of ZX30 alloy (a) AA and (b) ECAP-processed via 1P.

3.2. Prediction of wear characteristics

3.2.1. Machine learning prediction models

The aforementioned machine learning methods were used to analyze the collected data and derive correlations. The results obtained from these ML methodologies, along with a detailed discussion of the findings, are presented in this section.

Important insights into the interactions between these factors may be gained from the correlation plots and correlation coefficients (Fig. 10) between the two output variables (VL and COF) for data preprocessing of ML models and the input variables comprising number of paths (NP), applied force (P) and speed (V). The direction and strength of a linear relationship between the model's input and output variables may be examined using correlation plots. By looking at the scatterplots, we may first determine if there is a positive, negative, or no correlation between each pair of variables. This information facilitates understanding of how changes in one variable affect another. A high correlation coefficient suggests that an increase in one variable is associated with an increase in the other. On the other hand, the correlation coefficient provides a numerical evaluation of the linear relationship's strength and direction. Its range is between −1 to +1, where a strong negative correlation is indicated by a value near −1, a strong positive correlation by a value close to +1, and no or weak relationship is indicated by a value close to 0. When analyzing the connection between the force and speed input variables and the output variables it is crucial to look at the magnitude and significance of the correlation coefficients. An increase in one variable is thought to be related to an increase in the other if the correlation coefficient is high.

Fig. 10.

Correlation matrix of input and output variables showcasing the strength and direction of relationships between each two input-output variable using correlation coefficients.

Fig. 10 shows that there is no correlation between VL and NP, P, or V, as the correlation coefficient approaches zero. Furthermore, there is a weak negative correlation of −0.25 between VL and NP. Conversely, a strong negative correlation coefficient of −0.58 indicates the relationship between COF and speed.

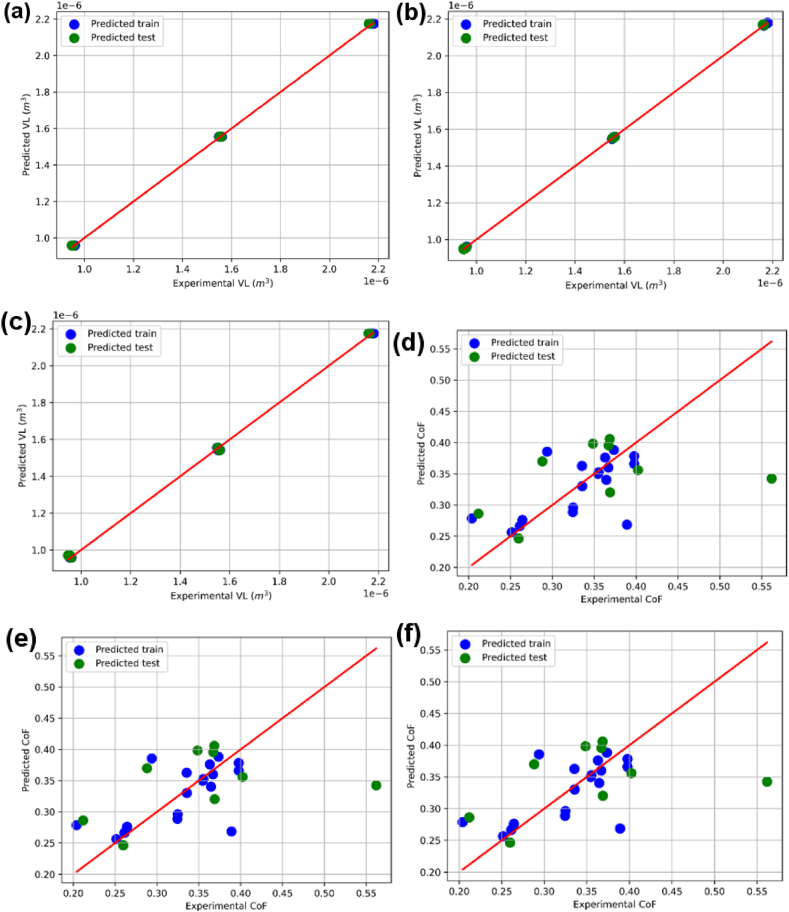
When comparing the predicted train and test VL values to the actual experimental data, as shown in Fig. 11, it is clear that the VL prediction model using the LR (Linear Regression) approach performed well. A common metric for evaluating a regression model's quality of fit is the R²-score. Higher numbers on the scale of 0–1 denote better performance. In this case, the ML model has created a substantial connection between the predicted VL and COF values and the actual data, as indicated by the R²-scores for both the training and test datasets, which vary from 0.96 to 0.99. This demonstrates that a substantial portion of the variability in VL and COF data can be explained by the indicated ML models. Fig. 11 shows the predicted test and train VL against the actual data calculated for various NP, P, and V. This allows for the performance evaluation of the best VL model obtained using LR, GP, and RF ML algorithms (Fig. 11 a, b, c). Similarly, LR, GP, and RF produced the calculated COF best performance models (Fig. 11 d, e, f).

Fig. 11.

Performance evaluation of predicted train and test VL models obtained through (a) LR, (b) GP, and (c) RF, as well as COF models produced by (d) LR, (e) GP, and (f) RF ML modeling.

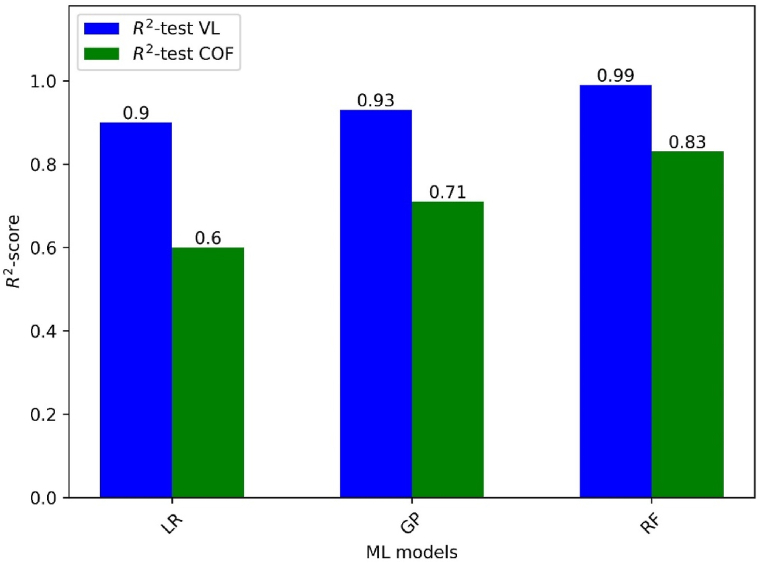
Fig. 12 summarizes the R²-scores for training and testing three different machine learning models for the output variables VL and COF. The coefficient of determination, or R²-score, is a statistic that goes from 0 to 1 that represents how well the model fits the data. The best R² values for the testing dataset for VL and COF, were obtained to be 0.99 and 0.83 respectively, suggesting that the RF ML model predicts the VL variable on unknown data with a high degree of accuracy as compared to other ML models of LR, GP.

Fig. 12.

Result summary of ML test datasets displaying R²-score achieved for each model.

3.2.2. Regression prediction models

Plots of the experimental data against the corresponding expected values of VL and COF for AA, single pass, and four pass samples are shown in Fig. S1 (supplementary material). The blue dots represent the minimum output value, while the red points represent the highest output value. The majority of the intersection points of the experimental and predicted values were found to be relatively close to the median line, indicating that the created regression models were effective, according to the analysis of the aforementioned charts.

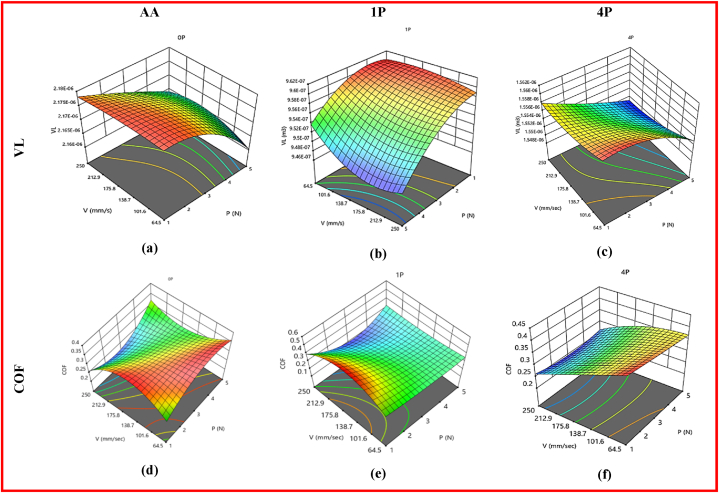
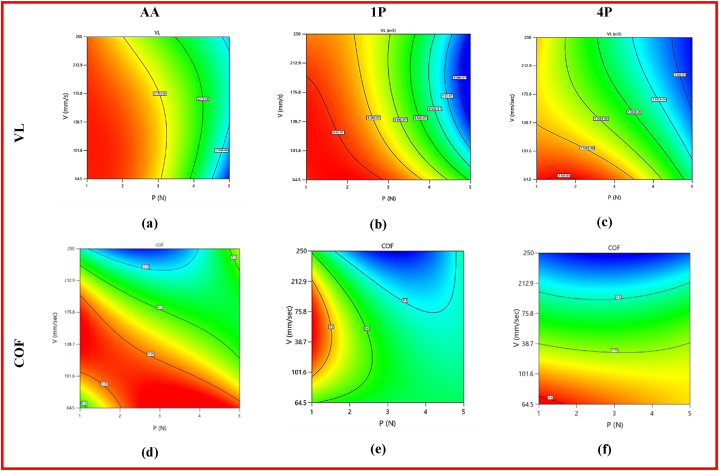
The 3D and 2D response plots depicted in Fig. 13, Fig. 14 were created using regression models. These plots were utilized to assess the variation in VL and COF in relation to wear variables (P and V) during numerous ECAP passes, specifically AA, single, and four passes.

Fig. 13.

Three-dimensional plot of ZX30's VL (a, b and c) and COF (d, e and f) at AA, 1P and 4P.

Fig. 14.

Two-dimensional plot of ZX30's VL (a, b and c) and COF (d, e and f) at AA, 1P and 4P.

Regarding VL, the relationship between P and VL at AA, 1P, and 4P is inversely proportional, as demonstrated in Fig. 13 (a, b, and c) and Fig. 14 (a, b, and c). It was observed that VL decreases when P increases throughout the wear process. Consequently, minimum VL is attained at a 5 N applied load. Additionally, the V of the wear process and VL are inversely proportional across all passes. It is evident that billets with varying numbers of passes require varied wear rates. Therefore, making more passes will require moving faster to reduce the quantity of VL. Fig. 14 (a, b, and c) illustrates the two-dimensional plot of VL values at AA, 1P, and 4P. The minimal VL_AA is 2.151 × 10⁻⁶ m³ obtained at 5 N and 64.5 mm/s as shown in Fig. 14 (a). Fig. 14 (b) shows the optimal VL_1P at single pass is 9.46373 × 10⁻⁷ m³ obtained at 5 N and 195 mm/s. Finally, the minimum VL_4P at four passes is 1.54907 × 10⁻⁶ m³ at 5 N and 250 mm/s as shown in Fig. 14 c.

The effect of wear parameters, P and V, on COF for ZX30 billets produced by ECAP at AA, 1P, and 4P, is shown in Fig. 13 d, e, and f. The COF drops as P increases until it reaches its lowest value at about 2–3 N. Following that, COF increases as P continues to increase. The applied V in the wear process and COF have an inverse proportionality. Consequently, ZX30's minimal COF value at AA, 1P, and 4P was achieved at 250 mm/s. Fig. 14 (d, e, and f) illustrates the two-dimensional plot of COF values regardless of processing route. The minimum COF_AA is 0.213515 and was obtained at 2.6 N and 250 mm/s as shown in Fig. 14 d. At 3.2 N and 250 mm/s, shown in Fig. 14 e, the lowest COF_1P is 0.186026. Finally, Fig. 14 f illustrates the minimum COF_4P is 0.246582813 at 3 N and 250 mm/s.

3.3. Optimization of wear characteristics

3.3.1. Response surface methodology (RSM) optimization

The key factors and outcomes of the RSM optimization of the VL and COF of ZX30 at AA, 1P and 4P are illustrated in Fig. S2, Fig. S3 and Fig. S4 (supplementary material). The red and blue dots, correspond to the wear parameters (P and V) and responses (VL and COF), respectively. With "minimize" as the suggested objective, the VL and COF optimization objective was created to be "in range," and the desirability function's intended output was in the form of "smaller-is-better".

For the AA condition, the optimal parameters for minimal VL have been found to be (A) P = 5 N and (B) V = 64.5 mm/s. Fig. S2 (a) (supplementary material) demonstrates that this outcome resulted in the lowest possible VL value of 2.16023 × 10⁻⁶ m³. Additionally, it had been found that (A) P = 2.5847 N and (B) V = 250 mm/s were the most appropriate COF conditions. As a result, the lowest COF value that could be obtained was 0.215294, as Fig. S2 (b) (supplementary material) showed.

For ZX30 alloy processed through 1P, the results of the RSM optimization carried out on the VL and COF are presented in Fig. S3 (supplementary material). The optimal circumstances for VL were identified to be V = 223.334 mm/s and P = 4.95 N, as shown in Fig. S3 (a) (supplementary material), which provided the lowest possible VL value of 9.47 × 10⁻⁷ m³. Additionally, it was found that (A) P = 3.177 N and (B) V = 249.708 mm/s were the most appropriate values for COF. Fig. S3 (b) (supplementary material) illustrates how this contributed to the lowest possible COF value of 0.196985.

For ZX30 billets processed through 4P, Fig. S4 (supplementary material) shows the results of the RSM optimization on the VL and COF, together with the associated variables. The values of V = 238.033 mm/s and P = 5 N were found to be the most appropriate conditions for VL. As shown in Fig. S4 (a) (supplementary material), this resulted in the lowest VL possible value of 1.54905 × 10⁻⁶ m³. The COF's ideal P and V values were determined to be (A) P = 2.5875 N and (B) V = 246.734 mm/s. This eventually resulted in the lowest possible COF value, which was 0.250088, as shown in Fig. S4 (b) (supplementary material).

3.3.2. Genetic algorithm and hybrid DOE-GA optimization

A genetic algorithm (GA) was used to identify the best suitable combination of wear-independent parameters which lead to the minimum feasible VL and COF. Equations (4)–(9) were applied to the wear boundary conditions, P and V, in order to obtain the objective function for each response. The following expression applies to the proposed objective functions:

Minimize (VL, COF) tested under the following ranges of wear conditions.

64.5≤ V ≤ 250 (mm/sec), 1 ≤ P ≤ 5 (N)

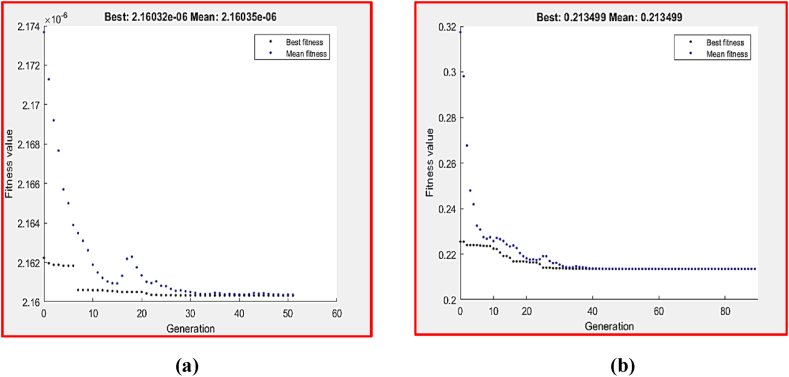
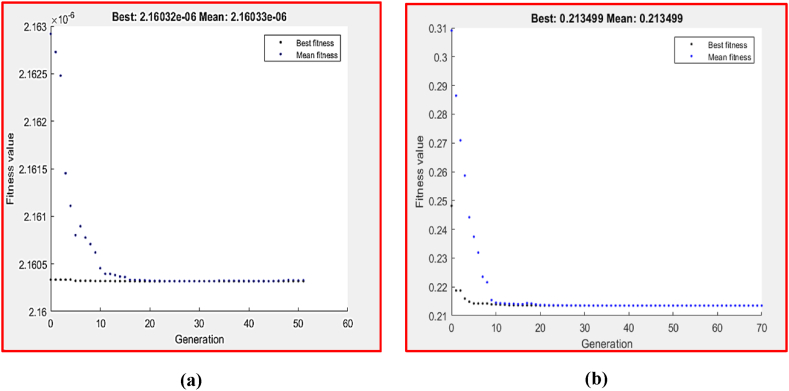
Fig. 15, Fig. 16 show the GA optimization technique's performance in terms of fitness value and run solver view, which were derived from MATLAB, together with the related wear conditions of the best VL and COF, respectively, at AA. The goal of minimizing the values of VL and COF was suggested by equations 4, 5, respectively. This function was then used as the fitness function and was subject to the wear boundary condition. The lowest value of VL that GA could obtain at P = 5 N and V = 64.506 mm/s was 2.16023 × 10⁻⁶ m3, as shown in Fig. 15-a. Additionally, at P = 2.571 N and V = 250 mm/s, the GA provided a minimum COF value of 0.213499 (Fig. 15-b).

Fig. 15.

Optimum wear responses by GA of ZX30 at AA: (a) VL and (b) COF.

Fig. 16.

Optimum wear responses by DOE-GA of ZX30 at AA: (a) VL and (b) COF.

To improve the GA results, design of experiments and hybrid analysis (DOE–GA) were conducted. The initial populations of hybrid DOE-GA have been identified using the optimum wear parameters of VL and COF at AA. Under 5 N load and a speed of 64.506 mm/s conditions, the hybrid DOE–GA produced a minimum VL value of 2.16023 × 10⁻⁶ m³ (Fig. 16-a). Likewise, the hybrid DOE–GA produced a minimum COF (Fig. 16-b) of 0.213499 with a load of 2.571 N at a speed of 250 mm/s.

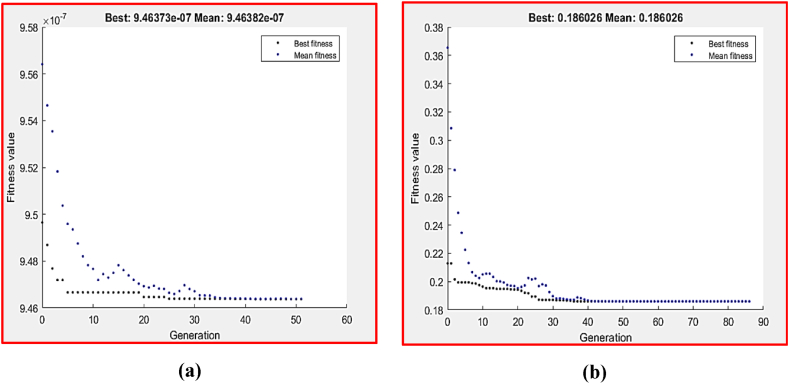
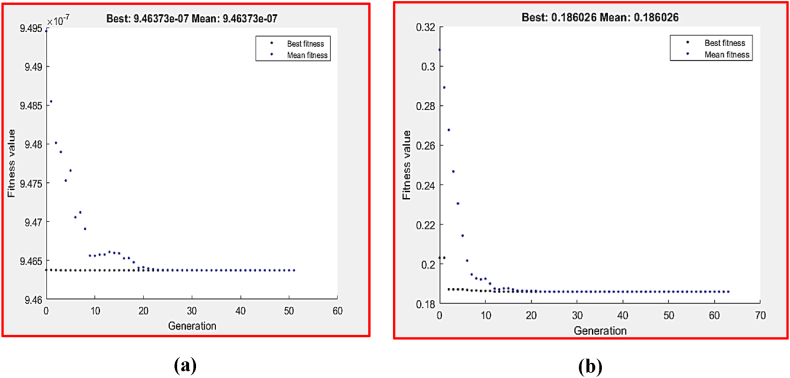
For ZX30 billets processed through 1P, the fitness function was the minimization of VL and COF at a single pass, as stated by Equations 6, 7, while subject to the wear boundary conditions. According to GA, the ideal values of VL and COF were 9.46373 × 10⁻⁷ m³ and 0.186026, respectively, as shown in Fig. 17a, b. The lowest observed VL was at 5 N and 195.75 mm/s. On the other hand, GA revealed that the best wear conditions for COF were determined to be 3.2 N and 250 mm/s.

Fig. 17.

Optimum wear responses by GA of ZX30 at 1P: (a) VL and (b) COF.

Fig. 18 (a) and (b) illustrate the hybrid DOE–GA values for optimum VL and COF of the alloy after being subjected to a single ECAP pass, which were 9.46373 × 10⁻⁷ m³ and 0.186026, respectively, acquired at 195.75 mm/s and 5 N for VL and 3.2 N and 250 mm/s for COF.

Fig. 18.

Optimum wear responses by DOE - GA of ZX30 at 1P: (a) VL and (b) COF.

Equations 8, 9 show the fitness function as the smallest possible value of VL and COF at 4P condition, while subject to the wear boundary condition. According to GA, the ideal values of VL and COF were 1.54905 × 10⁻⁶ m³ and 0.246559, respectively, as illustrated in Fig. 19 (a, b). At 238.033 mm/s and 5 N, the lowest VL value was observed. However, based on GA 250 mm/s and 2.926 N were the optimum wear parameters for COF.

Fig. 19.

Optimum wear responses by GA of ZX30 at 4P: (a) VL and (b) COF.

The hybrid DOE–GA results for the lowest possible VL and COF at four passes were 1.54905 × 10⁻⁶ m³ and 0.246559, respectively, as shown in Fig. 20 (a, b). For VL, the aforementioned results were attained at 237.98 mm/s and 5 N, and for COF, at 250 mm/s and 2.926 N.

Fig. 20.

Optimum wear responses by DOE-GA of ZX30 at 4P: (a) VL and (b) COF.

3.3.3. Multi-objective genetic algorithms (MOGAs)

Multi-objective genetic algorithms (MOGAs) are optimization methods designed to accomplish the difficult task of identifying a set of solutions for many objectives that are in conflict. In MATLAB 2020, a GA Toolbox can be used to address optimization issues with multiple objectives and find many possible solutions simultaneously. In order to solve optimization problems by GA, regression models known as objective functions were used as the fitness function. Three levels were used, with P and V serving as the upper and lower boundaries for the input wear parameter values. The Pareto front, also known as the non-dominated solution, is a solution set generated by MOGAs to address these multi-objective optimization problems. It achieves an appropriate equilibrium between multiple objectives without sacrificing any of them [[61], [62], [63], [64]].

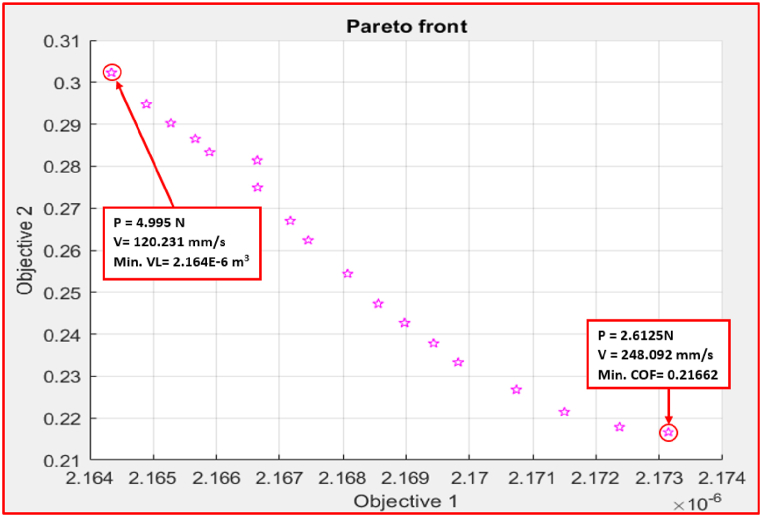
For the AA condition, the genetic algorithm, a non-traditional optimization method, was used to handle the two optimization goals as multi-objective functions in order to determine the lowest values of the VL and COF at AA. The fitness functions for VL and COF at AA for ZX30 were, respectively, expressed by Equation (4) and Equation (5). Fig. 21 displays the Pareto chart points for Objective 1 (VL) and Objective 2 (COF). Excessive VL was found to be the cause of a decrease in the COF. Therefore, sacrificing a drop in COF may lead to an increase in VL. The optimal VL was 2.164 × 10⁻⁶ m³ at 4.99 N and 120.231 mm/s, leading to a relatively large COF of 0.3022. On the other hand, the best COF was found to be 0.21662 at 2.61 N and 248 mm/s alongside the most undesirable VL of 2.173 × 10⁻⁶ m³.

Fig. 21.

Pareto front chart of VL and COF at AA.

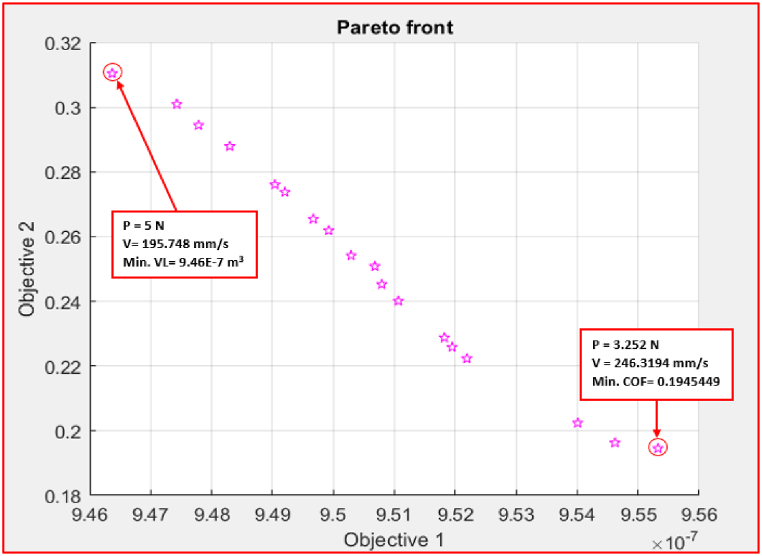
Equations 6, 7, respectively, represent the VL and COF fitness functions at 1P. The Pareto chart points for Objective 1 (VL) and Objective 2 (COF) for a single pass are shown in Fig. 22. It was observed that the COF decreased with increasing VL. The optimal VL for a single pass was 9.46 × 10⁻⁷ m³ at 5 N and 195.748 mm/s, with the associated worst maximum COF of 0.31. The lowest COF was 0.1945 at 3.252 N and 246.3 mm/s, with the associated highest VL value of 9.55 × 10⁻⁷ m³.

Fig. 22.

Pareto front chart of VL and COF at 1P.

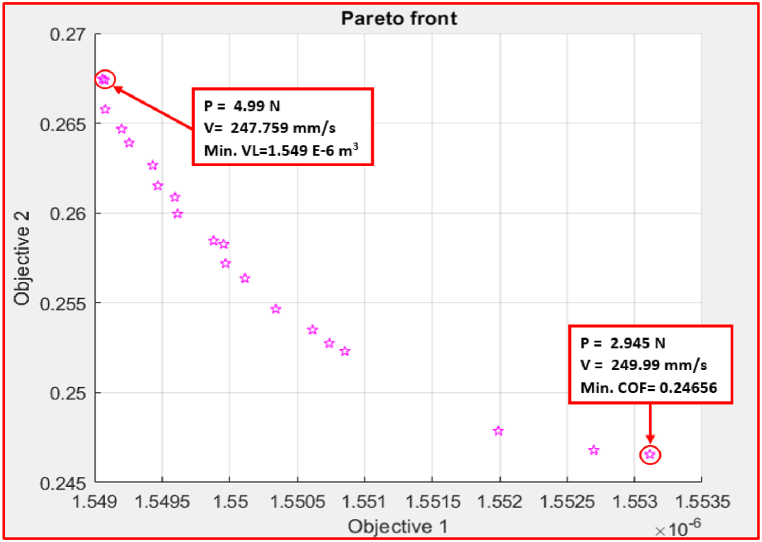
Equations 8, 9, respectively, reflect the VL and COF fitness functions for the 4P processing conditions. The Objective 1 (VL) and Objective 2 (COF) Pareto chart points for four passes are shown in Fig. 23. The minimum COF was 0.2465 obtained at P = 2.945 N and V = 249.9 mm/s with a VL of 1.55 × 10⁻⁶ m³. Consequently, the minimum VL was found to be 1.549 × 10⁻⁶ m³ at P = 4.9 N and V = 247.75 mm/s with a COF value of 0.2674. Table 2 summarizes the comparison of wear responses values using DOE, RSM, GA, hybrid DOE-GA and MOGA.

Fig. 23.

Pareto front chart of VL and COF at 4P.

Table 2.

Summary results of ZX30 wear process.

Response		DOE	RSM	GA	DOE-GA	MOGA
						VL	COF
VLAA	Value	2.160 × 10−6	2.16023 × 10−6	2.16023 × 10−6	2.16023 × 10−6	2.164 × 10−6
	P	5	5	5	5	4.99
	V	64.5	64.506	64.506	64.506	120.23
COFAA	Value	0.2117	0.215294	0.213499	0.213499		0.2166
	P	3	2.58474	2.571	2.571		2.612
	V	250	250	250	250		248.09
VL1P	Value	9.476 × 10−7	9.47 × 10−7	9.463 × 10−7	9.463 × 10−7	9.463 × 10−7
	P	5	4.95	5	5	5
	V	125	223.334	195.75	195.75	195.748
COF1P	Value	0.2040	0.196985	0.186026	0.186026		0.1945
	P	3	3.17722	3.2	3.2		3.252
	V	250	249.708	250	250		246.319
VL4P	Value	1.549 × 10−6	1.54905 × 10−6	1.54905 × 10−6	1.54905 × 10−6	1.549 × 10−6
	P	5	5	5	5	4.99
	V	250	238.033	238.033	237.98	247.759
COF4P	Value	0.2516	0.250088	0.246559	0.246559		0.2465
	P	3	2.5875	2.926	2.926		2.945
	V	250	246.734	250	250		249.9

3.3.4. Optimization of wear characteristics at large space

The ideal wear process conditions and accompanying responses—that is, ZX30's VL and COF at AA, single, and four passes—were suggested in this section. The recommended applied load and speed range for the test specimen were 1–30 N and 64.5–1000 mm/s, respectively, based on earlier tests of the ZX30, which determined the ideal wear parameters, P and V. The ideal wear process condition determined by the genetic algorithm (GA) and associated VL and COF values are shown in Table 3.

Table 3.

Optimal VL and COF of ZX30 at AA, single and four passes based on previous studies.

No. of passes		AA	1P	4P
VL	Value	1.04E-6	3.44E-7	1.06E-6
	Load	30	30	30
	Speed	64.5	183.76	64.5
COF	Value	0.101	0.0237	0.0346
	Load	1.74	2.5	4.8
	Speed	300	300	400

3.5. Validation for ECAPed ZX30

To comprehend how changes in applied load and speed impact the volume loss in the system, the above-mentioned ML models were employed to shed light on the relationship between volume loss and these input variables. Table 4 displays the results of a new, unseen dataset that was used to further investigate the validity of this ML modeling in terms of prediction accuracy and error. The achieved accuracy ranged from 75.6 % to 84.4 %, which is reasonably accepted and validates the performance of the predictive model.

Table 4.

Validation results of VL modeling using new unseen experimental dataset.

NP	P (N)	V(mm/sec)	Experimental VL	Predicted VL	Error (%)	Accuracy (%)
0	4	100	1.4805E-06	1.7108E-06	−15.6 %	84.4 %
0	4	300	1.4736E-06	1.7855E-06	−21.2 %	78.8 %
0	10	125	1.4668E-06	1.8085E-06	−23.3 %	76.7 %
0	10	175	1.4690E-06	1.8272E-06	−24.4 %	75.6 %

4. Conclusions

The ECAP of the ZX30 alloy was conducted to experimentally evaluate its effect on wear performance. Through subsequent experimentation that involved manipulating load pressure (P) and speed (V) using design of experiments (DOE), a thorough assessment of wear performance, specifically focusing on volume loss (VL) and coefficient of friction (COF), was achieved. This investigation was further enriched by predictive modeling techniques employing machine learning (ML), 3D response surface plots, and statistical analysis of variance (ANOVA). The comprehensive analyses serve to emphasize the influence of ECAP routes on optimizing the wear properties of ZX30 alloy. The following was concluded.

• 1.ECAP facilitates the dynamic recrystallization process, leading to significant grain refinement and the formation of a homogeneous ultrafine-grained structure. Processing four passes via route Bc produce an average grain size of 2.18 μm, characterized by a predominant presence of high-angle grain boundaries (HAGBs).
• 2.The texture intensity notably increases after one pass becoming approximately 11 times random with an alignment of approximately 10° relative to the TD. This alignment contributes to the occurrence of basal slip induced by SPD. Conversely, after 4 Bc a relatively strong simple shear texture with a comparable intensity is observed.
• 3.ECAP enhances wear resistance by reducing volume loss. Increasing the number of ECAP passes further facilitates the development of mechanically mixed layer and improves interfacial bonding.
• 4.The average coefficient of friction values stabilized between 0.30 and 0.45 even after the 4Bc-ECAP process. The fluctuations in the COF increased with increasing ECAP passes over all examined speeds.
• 5.The correlation coefficient R² and adjusted R² of the VL and COF regression models shows that the experimental and projected values are closely correlated. In the present study, R² and adjusted R² values varied from 88.9 to 99.89 %, which is close to unity.
• 6.3D plots show that the minimum VL was attained at a 5 N applied load. Also, V of the wear process and VL are inversely proportional regardless of number of passes.
• 7.The optimal COF was obtained at applied load of about 2–3 N and 250 mm/s at different passes.
• 8.The optimization results of VL and COF obtained by RSM, GA, hybrid DOE-GA and MOGA are compatible with experimental ones.
• 9.Unseen data was used to validate the VL_AA response model. The validity of the model was confirmed showing medium accuracy (53.15 %–56.72 %) between the practical and regression model.

Data availability

Correspondence and requests for materials should be addressed to corresponding author (A.I. Alateyah).

CRediT authorship contribution statement

Samar El-Sanabary: Writing – original draft, Validation, Data curation. Hanan Kouta: Validation, Software, Formal analysis. Mahmoud Shaban: Writing – original draft, Software, Formal analysis, Data curation. Abdulrahman Alrumayh: Writing – original draft, Methodology. Abdulrahman I. Alateyah: Supervision, Project administration, Funding acquisition, Conceptualization. Fahad Nasser Alsunaydih: Writing – review & editing, Software, Formal analysis. Majed O. Alawad: Methodology. Yasmine El-Taybany: Writing – original draft, Formal analysis. Mohamed S. El-Asfoury: Writing – review & editing, Resources, Methodology. Waleed H. El-Garaihy: Writing – review & editing, Writing – original draft, Project administration, Methodology, Investigation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following is the Supplementary data to this article.