Tensor Methods in Biomedical Image Analysis

Abstract

In the past decade, tensors have become increasingly attractive in different aspects of signal and image processing areas. The main reason is the inefficiency of matrices in representing and analyzing multimodal and multidimensional datasets. Matrices cannot preserve the multidimensional correlation of elements in higher-order datasets and this highly reduces the effectiveness of matrix-based approaches in analyzing multidimensional datasets. Besides this, tensor-based approaches have demonstrated promising performances. These together, encouraged researchers to move from matrices to tensors. Among different signal and image processing applications, analyzing biomedical signals and images is of particular importance. This is due to the need for extracting accurate information from biomedical datasets which directly affects patient’s health. In addition, in many cases, several datasets have been recorded simultaneously from a patient. A common example is recording electroencephalography (EEG) and functional magnetic resonance imaging (fMRI) of a patient with schizophrenia. In such a situation, tensors seem to be among the most effective methods for the simultaneous exploitation of two (or more) datasets. Therefore, several tensor-based methods have been developed for analyzing biomedical datasets. Considering this reality, in this paper, we aim to have a comprehensive review on tensor-based methods in biomedical image analysis. The presented study and classification between different methods and applications can show the importance of tensors in biomedical image enhancement and open new ways for future studies.

Introduction

Tensors have been proven to be effective tools for analyzing multimodal and multidimensional datasets.[1,2] Generally speaking, tensors are higher-order arrays, basically used for recording and representing higher-order datasets.[1] Vectors (1^st order tensors) and matrices (2^nd order tensors) can be considered as special cases of tensors.

Inefficiency of matrices in representing and analyzing multimodal and multidimensional datasets has been encouraged researchers to replace matrices with tensors.[3] Besides, emerging of new datasets with high dimensions and several modalities increases the need for tensor-based methods for data analysis. This has been widely affected different areas in signal and image processing domains, such as natural image analysis, blind source separation, machine learning, hyperspectral imaging, medical diagnosis, and so on.[4,5,6,7,8,9,10]

Among different image processing applications, biomedical image enhancement is of special consideration. Higher-quality biomedical images result in faster and more accurate diagnoses of diseases. In addition, sometimes, simultaneous analysis of several datasets recorded from one patient is inevitable for a more accurate investigation.[11,12,13] These facts, by keeping in mind that many biomedical images (datasets) are naturally of higher orders, show the importance of using tensor methods in biomedical image analysis (enhancement). Some examples of biomedical images are illustrated in Figure 1. In this figure, from left to right, an example of an optical coherence tomography (OCT) image[14] (https://people.duke.edu/~sf59/Fang_TMI_2013.htm) and a fundus fluorescein angiogram photograp[15] (https://misp.mui.ac.ir/en/fundus-fluorescein-angiogram-photographs-diabetic-patients-0) have been shown.

Figure 1.

Some examples of biomedical images. From left to right, examples of an optical coherence tomography image and fundus fluorescein angiogram image

Tensor decomposition is a common method for processing of higher-order datasets.[2] CP (CANDECOMP/PARAFAC) and Tucker decompositions are two well-known tensor decomposition methods.[16] The two methods have been widely used in different signal and image processing areas and resulted in promising performances.[16,17,18,19,20,21,22,23] However, Tucker decomposition suffers from the curse of dimensionality.[16] It means that the number of elements resulting from Tucker decomposition of a tensor increases exponentially with the tensor order. This limits using Tucker decomposition for higher-order tensors.

For mitigating the curse of dimensionality, several other tensor decomposition methods, called tensor networks, have been developed.[1] The important characteristic of tensor networks is that the number of elements resulting from decomposition of a tensor, increases linearly with tensor order. This makes tensor networks suitable for analyzing higher-order datasets. Two members of tensor networks which have been highly exploited in different signal and image processing areas are tensor train (TT) and tensor ring (TR) decompositions.[24,25]

Tensor networks are proper for analyzing higher-order tensors (more than 5^th order tensors), however, many of the actual datasets are not as high order as expected. For providing a situation for using tensor networks, low-order datasets are usually transferred into higher-order datasets.[26,27,28] This is done using different methods which are generally known as tensorization or folding methods. Hankelization or KET folding are the two well-known methods for transferring a low-order dataset into higher-order spaces.[6,29,30,31]

The main important issue when using tensor decomposition is selecting proper ranks. In general, the ranks determine the size of latent variables resulting from tensor decomposition. This includes the size of resulting factor matrices or core tensors. In addition, in some definitions, a tensor rank is the rank of different unfoldings of that tensor. There are different methods for determining the rank of a tensor such as using prior fixed ranks or rank incremental methods.[26,27,32] In the fixed rank methods, the ranks are determined in advance and as an input to the algorithm. In these methods, the ranks are not changed during the execution of the algorithm. In the rank incremental methods, the ranks are not set fixed but are increased gradually during several iterations. Simulations show that the rank incremental methods usually outperform fixed rank approaches.[26] However, an important assumption when using tensors, especially for the completion or denoising of different (biomedical) images, is low-rankness.[33,34,35,36,37] This means that the original tensor is low-rank or better to say, the matrices or tensors resulting from tensor decomposition have small sizes. In contrast to matrices, rank of a tensor does not have a unique definition and varies with the underlying tensor structure assumptions. Consequently, the low-rankness assumption also varies with the tensor structure. This will be discussed in more detail in the next sections.

In this paper, we have mainly focused on tensor methods for analyzing biomedical images. The importance of this study becomes clear when we know that many biomedical images are in tensor formats (usually low-order tensors). In this situation, matrix methods are usually inefficient due to the following reasons.[38,39]

1. Transferring a higher-order dataset into a matrix usually ignores local and spatial correlations among elements

2. Latent variables extracted by matrix factorization are usually less meaningful compared to information extracted by tensor decomposition.

Even, for low-order datasets (in matrix format), tensor-based methods can be more efficient compared to matrix-based methods.[3] The examples show that, despite the higher computational burden of tensor-based methods in comparison to the matrix-based approaches, their higher performance and applicability in different areas cannot be ignored.

Above-mentioned reasons demonstrate the need for using tensor methods for biomedical image analysis. Despite many papers that use the biomedical images in their initial formats (when using CP and Tucker decompositions), some of the recently proposed methods prefer to use biomedical images in higher order spaces (sometimes known as embedded space) and applying tensor networks.[28,31]

In this paper, the tensor-based methods used for the following three important categories have been studied.

1. Biomedical image completion (super-resolution)

2. Biomedical image denoising

3. Information fusion.

Tensor decomposition methods studied in this paper are limited to CP, Tucker, higher order singular value decomposition (HOSVD), TT, and TR decompositions. Some other tensor decomposition methods, such as block term decomposition (BTD) and tensor singular value decomposition (t-SVD) which have been also exploited for biomedical image analysis,[40,41,42,43,44,45] have not been reviewed in this paper. In addition, since this paper focuses on biomedical image processing methods, the tensor-based signal processing approaches have not been reviewed here.

The main advantage of this paper compared to the other review papers is that we do not limit the review to only one special tensor decomposition method[46] or a special application or dataset.[21,47,48,49] We tried to present a comprehensive review that encompasses different image processing applications with different datasets and different tensor decomposition methods.

The rest of this paper has been organized as: notations and preliminaries have been reviewed in section 2. Section 3 presented different tensor decomposition methods. Tenosrization methods and low-rankness are reviewed in sections 4 and 5, respectively. Tensor-based methods for medical image analysis have been studied in section 6. Discussion and future perspective are presented in section 7, and finally, the paper is concluded in section 8.

Notations and Preliminaries

In this section, we have reviewed the notations which will be used in the rest of the paper. The notations are the same as the notations used in.[16] Vectors and matrices are denoted by small boldface and capital boldface letters (x and X), respectively. Tensors are denoted by underlined capital bold letters, as Elements of a vector are denoted as x_i, while elements of a matrix or tensor are denoted as

Element wise (Hadamard), Khatri–Rao, Kronecker and outer products between two tensors (vectors or matrices) are denoted as and °, respectively.

Frobenius norm, nuclear norm, transpose, and pseudo-inverse of a matrix are denoted by ‖.‖_F, ‖.‖_*, ‖.‖^T and ‖.‖^†, respectively. Recall that the Frobenius norm of a tensor is defined as . Also, “tr” stands for the trace of a matrix, i.e. sum of its diagonal elements.

Matricization of a tensor, i.e., reshaping that tensor into a matrix format, is a useful tool when working with tensors. Depending on the shape of the resulting matrix, several methods are defined for matricization. Mod-{n} matricization of an N^th order tensor reshapes that tensor into a matrix of size and denoted by X_(n). Mod-{n} canonical unfolding of denoted by X_<n>, and is an matrix. Especial form of matricization, mainly used for TR decomposition, is X_[n] which reshapes a tensor into a matrix of size .

Notations used in this paper are summarized in Table 1. Furthermore, for more clarifying the paper, list of abbreviations used in the paper are presented in Table 2.

Table 1.

List of notations used in the paper

Vectors, matrices and tensors	x, X and X
Elements of a tensor
Element wise (Hadamard), Khatri-Rao, Kronecker and outer products	and °
Mod-{n} matricization and Mod-{n} canonical matricization of X	X(n) and X<n>
Frobenius norm, nuclear norm, transpose and pseudo-inverse operators	‖.‖F, ‖.‖*, ‖.‖T and ‖.‖†

Table 2.

List of paper abbreviations

Abbreviation	Full format
CP	CANDECOMP/PARAFAC
TT	Tensor train
TR	Tensor ring
SSA	Singular spectrum analysis
SVD	Singular value decomposition
HOSVD	Higher order singular value decomposition
t-SVD	Tensor singular value decomposition
BTD	Block term decomposition
OCT	Optical coherence tomography
MRI	Magnetic resonance imaging
fMRI	Functional magnetic resonance imaging
MDT	Multiway delay embedding transform
CT	Computed tomography
PET	Positron emission tomography
MRF	Magnetic resonance fingerprinting
SPECT	Single photon emission computed tomography
PSNR	Peak signal to noise ratio
SSIM	Structural similarity

Tensor Decomposition Methods

As mentioned in the introduction, tensor decomposition is a common method for analyzing a dataset with tensor structure.[1] There are several tensor decomposition methods, such as CP decomposition, Tucker decomposition, HOSVD, BTD, t-SVD, TT decomposition, TR decompositions, hierarchical Tucker decomposition, and so on.[16,24,25,50,51] In this paper, we have focused on five main decomposition methods, i.e. CP, Tucker, HOSVD, TT, and TR decompositions. These methods are reviewed in the following subsections.

CANDECOMP/PARAFAC decomposition

CP decomposition, illustrated in the first row of Figure 2 is a well-known tensor decomposition method among existing classic tensor decomposition methods. In CP decomposition, a tensor is decomposed as a sum of R rank-one tensors, where R is known as the CP rank. CP decomposition is denoted as[16]

Figure 2.

CANDECOMP/PARAFAC (first row) and Tucker (second row) decompositions of a 3^rd order tensor

where is an N^th order tensor to be decomposed, B⁽ⁿ⁾ is the n^th factor matrix of I_n × R size and Λ is a diagonal matrix. CP decomposition can also denoted as:[16]

where is the r^th column of is the B⁽ⁿ⁾, λ_r is the r^th diagonal element of Λ and is a rank-one tensor of size . Each element of tensor is computed as: [16]

where is the (i_n, r)-th element of B⁽ⁿ⁾.

Tucker decomposition

Another well-known approach for tensor decomposition is Tucker decomposition [illustrated in the second row of Figure 2]. In Tucker decomposition, an N^th order tensor of size I₁ × I₂ ×…× I_N is decomposed as.[16]

where is the core tensor of size R₁ × R₂ ×…× R_N and B⁽ⁿ⁾ is the n-th factor matrix of size I_N × R_N.

Vector [R₁, R₂,…, R_N] determines the size of core tensors and factor matrices. Tucker decomposition can be expressed in a mathematical format as.[16]

and the elements are calculated as: [16]

where, is the (r₁,r₂, … r_N) -th element of and is the (r_n, i_n)-th element of B⁽ⁿ⁾.

HOSVD can be considered as a special case for Tucker decomposition, where all of the factor matrices are orthogonal and the core tensor is all orthogonal, i.e. the lateral slices are mutually orthogonal.

Tensor train decomposition

TT decomposition is a simple member of tensor networks. It is well-known due to its simplicity and overcoming the curse of dimensionality. A tensor with TT structure is denoted as:[16,24]

where ⁽ⁿ⁾ is the n^th core tensor of size R_n-1 × I_n × R_n. In TT decomposition R₀ = R_N = 1, so the first and the last core tensors are two matrices.[24] The resulting core tensors are interconnected with each other linearly. It is clear that R_n’s indeed determine the size of core tensors, i.e. larger R_n’s result in larger core tensors.

The number of elements resulting from TT decomposition of an N^th order tensor is 2RI + (N - 2) R² I (considering I₁ = I₂ =…= I_N = I and R₁ = R₂ =…= R_n = R). Hence, the number of elements is linearly increased with the tensor order (N). For higher order tensors, i.e., larger values of N, the resulting elements of TT decomposition are much less than the resulting elements of Tucker decomposition which is equal to R^N + NRI. This shows that TT decomposition overcomes the curse of dimensionality.

Each element of a tensor with TT structure is computed as: [16,24]

where is the i_n -th lateral slice of the n -th core tensor.

Tensor ring decomposition

TR decomposition is another member of tensor networks which can be considered as a generalization of TT decomposition and denoted as:[25]

where, similar to TT decomposition, ⁿ is the n^th core tensor of size R_n-1 × I_n × R_n. In TR decomposition, the core tensors are interconnected in a ring, and in contrast to TT decomposition, R₀ = R_N > I.[25] The number of elements resulting from TR decomposition of an N^th order tensor is equal to NIR². It shows that the number of elements increases linearly with tensor order which overcomes the curse of dimensionality. Each element of a tensor with TR structure is computed as: [25]

Illustrations of TT and TR decomposition methods are shown in Figure 3. In this figure, each circle shows a third-order core tensor. In these two decompositions, an N^th order tensor is decomposed into N third order core tensors. In TT, the core tensors are connected linearly, while in TR, the core tensors are interconnected in a ring.

Figure 3.

Tensor train (first row) and tensor ring (second row) decompositions of an N^th order tensor

Coupled tensor decomposition

When working with big data or multimodal (multidimensional) datasets, sometimes, it is needed to decompose several datasets simultaneously. This enables exploiting common information among datasets which is not available when processing each dataset individually. This is an important issue in data fusion (will be discussed later).[52,53,54]

The coupled decomposition of datasets can be divided into several categories: Matrix-matrix decomposition, matrix-tensor decomposition, and tensor–tensor decomposition.[55,56] In this paper, we mainly focus on matrix-tensor and tensor–tensor decompositions. Coupled matrix-tensor decomposition can be modeled as: [55]

where X and are the two datasets, in matrix and tensor formats, respectively, which are factorized simultaneously. ^X(θ₁) and are the factorized versions of X and , respectively. ^X(θ₁) can be in different matrix factorization formats, while can be in the form of different tensor decompositions, such as CP decomposition, Tucker decomposition, TT or TR decompositions, and so on. θ₁ and θ₂ are the latent variables of each decomposition and have some common parameters, called shared factors. In other words, and , where and , are the specific (unshared) parameters of each dataset and θ^c contains the shared parameters between two datasets.

In a similar manner, coupled tensor–tensor factorization can be modeled as: [56]

where ₁ and ₂ are the first and second datasets (in tensor formats) to be factorized simultaneously, and and are the factorized versions in different tensor decomposition formats. θ₁ and θ₂ are the resulting latent variables that have some shared factors.

Based on the relation among shared factors, the datasets can be coupled in different ways, named, hard coupling, soft coupling, and multimodal soft coupling. In the hard coupling method, the shared factors among datasets are assumed to be exactly the same.[57,58] This is a good approach for coupling the datasets of the same type. In the soft coupling approach, the shared factors are not exactly the same, but they are similar. In this approach, a penalty term is added to the cost function which controls the similarity of the shared factors.[59] This method is preferred for datasets that have different types. Coupled tensor decomposition of two datasets with soft coupling of shared factors can be modeled as:

where and are the shared factors of the first and second datasets, respectively, and controls the similarity of the shared factors with weight λ .

In multimodal soft coupling, it is assumed that the shared factors are similar to a third factor resulting from another modality.[60] This method is applicable when working with datasets that have several modalities, like audiovisual datasets. Coupled matrix-tensor and tensor-tensor decompositions are illustrated in Figure 4.

Figure 4.

Matrix-tensor (first row) and tensor-tensor (second row) couplings of two datasets. The datasets are coupled along one mode

TT and TR decompositions (generally tensor networks) are mainly applicable for higher-order tensors. In addition, some papers show that transferring lower-order tensors into higher-order ones can increase the performance of the algorithms.[26,27,28,29,30,31,32] Due to these reasons, it is usually preferred to transfer the raw dataset into higher-order spaces, sometimes known as embedded space. These methods, generally known as tensorization methods, are reviewed in the next section.

Tensorization Methods

Tensorization methods are for transferring a dataset into a tensor. In this paper, we also consider the methods for transferring lower-order tensors into higher-order ones as tensorization methods.

Hankelization is a classic method for transferring a vector into a matrix with Hankel structure.[29,30,61] Recall that in a matrix with a Hankel structure, all of the elements in each skew diagonal are the same. This method is an initial step in an algorithm known as singular spectrum analysis (SSA), basically used for time series analysis.[29,30,61] Hankelization of a vector is shown in Figure 5.

Figure 5.

Hankelization of a vector. Using this method, a vector is transferred into a matrix with Hankel structure

Recently, Hankelization has been exploited in tensor-based algorithms and showed promising results in different applications. Multiway delay embedded transform (MDT) has been proposed in Yokota et al.’s study[26] for image completion. In this method, a lower-order dataset is first multiplied by special matrices, called duplication matrices, and then tensorized into higher-order spaces. Using MDT, an N^th order tensor is reformatted into a 2N^th order tensor.[26]

Patch Hankelization (Figure 6) is another method for providing higher-order tensors.[27] In patch Hankelization, patches of pixels or elements of a low-order dataset are used for tensorization. In this method, the original low-order dataset is multiplied by matrices, called patch duplication matrices, and then a folding step is applied. In patch Hankelization, a 3^rd order dataset is transferred into a 7^th order tensor. Patch Hankelization with overlapped patches has been also proposed by Sedighin et al.[28]

Figure 6.

Patch Hankelization of a matrix. Each square contains patch (blocks of elements) with size P × P

KET augmentation is another approach for transferring a low-order tensor into higher-order spaces.[31] It transfers a 2^nd order matrix into a 3^rd order tensor. The approach is done by extracting consecutive patches of the original matrix and stacked them into a 3^rd order tensor. Overlapped KET augmentation, known as OKET, has been also proposed.[62] In this method, the consecutive patches have overlap with each other. This provides a situation for applying two steps of augmentation and can produce a 4^th order tensor from a matrix.

There are also other reshaping methods such as decimation or segmentation which have been used for reshaping a low-order dataset into a tensor.[6]

Low-rankness

An important issue when working with tensors is determining proper ranks. In a simple word, the ranks of each decomposition determine the size of resulting latent factors. In CP decomposition, the low-rankness means that the original tensor is composed of small number of rank-one tensors, i.e., small R. This is the same for Tucker, TT and TR decompositions, where low-rankness is equivalent to smaller core tensors.

Low-rankness of the original tensor is a very useful and important assumption when the problem is tensor completion (super-resolution) or denoising.[3,35,37,63,64] Tensor completion (matrix completion) is the problem of recovering a tensor when only a small part of its elements is available. This is a very important issue in many fields, such as recommender systems, compressed sensing, image compression, etc. In the first look, the problem seems to be ill-posed, however, by assuming that the original tensor is low-rank, it is possible to recover the missed information.[3,35,37,63,65]

The rank of a matrix has a clear definition; however, the rank of a tensor does not have a unique definition. Different definitions for tensor rank result in different performances of the algorithms. In this section, we briefly review the different definitions of tensor ranks.

CP rank

As mentioned before, CP rank of a tensor is the number of rank-one tensors that construct the original tensor.[65] CP rank of a tensor is unique, however, its computation is difficult. That’s why in most of the research papers, it is replaced by other definitions of rank.

Tucker rank

A common definition for tensor rank is the Tucker rank which is defined as follows:[3]

where α’s are nonnegative weights <1 and . Considering the above definition, Tucker rank of a tensor is a weighted summation of different mod-{n} unfoldings of that tensor.

Computing the rank of each resulting matrix X_(n) is not easy, so the rank is replaced by the nuclear norm of that matrix, as: [3]

The algorithms based on minimizing the Tucker rank of a tensor try to minimize the above definition for rank. The main issue when using Tucker rank is that the size of X_(n) is I_n × I₁I₂…I_n-1I_n+1…I_N which is a highly unbalanced matrix and its rank is limited to I_N. This reduces the efficiency of the algorithms based on minimizing the Tucker rank.[3]

Tensor train rank

TT rank of a tensor is computed as follows:[37]

where . For simplicity in the computation, similar to the Tucker rank, the rank of matrices is replaced by their nuclear norms,[37] as:

The algorithms based on low-rankness of TT rank try to minimize the above rank of the original tensor. The superiority of using TT rank in comparison to the Tucker rank is that the mod-{n} canonical unfoldings of a tensor is of size I₁I₂…I_n × I_n+1…I_N, so the rank is bounded by min I₁I₂…I_n,I_n+1…I_N, which can be a larger value compared to the Tucker rank and imposes less limitation on the algorithm.[37] Therefore, in many of algorithms, the Tucker rank is replaced by the TT rank.[37]

Tensor-based Biomedical Image Analysis

In this section, we will review the biomedical image analysis methods using different tensor-based approaches. The methods have been categorized from two perspectives. First, the algorithms have been categorized into three groups based on their applications. The three groups are biomedical image completion, biomedical image denoising, and information fusion. Second, the algorithms have been categorized based on the tensor decomposition methods they have used.

Biomedical image completion

Image completion is an important issue in image processing area, including biomedical image analysis.[3,26,28,66] The problem of image completion, also known as image in-painting, is to recover the missed (or uncertain) elements of an image using its available ones.[3] The problem originated from the reality that sometimes, achieved biomedical images have missed elements due to many reasons such as noise, human mistakes, hardware failure, or low sampling rate. In the last case (low sampling rate), the problem of image completion is also known as image super-resolution.[66]

The problem of image completion (super-resolution) seems to be ill-posed in the first look. However, the researches show that if the underlying image is low-rank, it is possible to recover the missed elements using the observed ones.[3]

It is worth noting that tensor-based completion methods are usually categorized into two groups: The first group contains the low-rank-based methods. These methods are based on minimizing different ranks (defined before) of the tensor which is usually done by minimizing the nuclear norm of different unfoldings of the tensor. Recovering of a (biomedical) image, based on tensor rank minimization can be formulated as:

where and are the estimated and original tensors, respectively, and Ω is the subset of observed elements.

The second group is the decomposition-based methods.[32,67] These methods are based on the reality that the latent factors resulting from the decomposition of a tensor usually preserve the underlying structure of the original tensor and it is possible to recover the original (completed) tensor by factorizing the incomplete tensor into latent variables.[26,32]

CP decomposition has been used in papers such as Li and Hu, Becker et al., Zhou et al., Zhang and Hawkins, and Yokota et al.[17,21,46,68,69] for biomedical image completion. Li and Hu[17] proposed a low-rank CP decomposition framework for magnetic resonance fingerprinting (MRF) reconstruction. It is mentioned that the high acquisition speed of MRF results in aliasing artifacts in the final fingerprints which reduces the accuracy of the information. However, the high dimensional MRF is highly low-rank, and, hence, low-rank CP decomposition has been exploited for removing the artifacts and recovering the elements.

In Zhang and Hawkins’s study,[68] a Bayesian framework accompanied by the CP low-rank assumption has been used for magnetic resonance imaging (MRI) data completion. In this paper, the MRI is assumed to be a low-rank streaming dataset and CP decomposition with low-rankness has been applied for completion.

Smoothed low-rank CP decomposition has been proposed in[69] and shown to be effective for MRI data completion. In this method, smoothness has been applied to each latent factor resulting from CP decomposition. The superiority of this approach is that it is a rank incremental method. As mentioned before, in rank incremental methods, the ranks (here CP rank) are not set fixed and increased gradually during iterations.

Tucker decomposition has been also exploited for biomedical image completion. Most of these methods are based on minimizing the Tucker rank (defined in(15)) of the tensor.[3,70,71,72,73] However, there exist some methods based on using Tucker decomposition of the incomplete dataset.[26,72,74]

In Liu et al.’s study,[3] three methods based on minimizing Tucker rank have been proposed and tested for MRI data completion. The methods are simple low-rank tensor completion (SiLRTC), fast low-rank tensor completion (FaLRTC), and high accuracy low-rank tensor completion (HaLRTC). HaLRTC is based on the minimization of the following cost function, using alternating direction method of multipliers (ADMM).[3]

where is the original tensor and Ω denotes the subset of observed elements. is the estimated tensor and P_i(i)’s are the mod-{i} unfoldings of the tensor.

Results provided in,[3] show that low-rank Tucker decomposition has the ability of recovering missed elements in MRI images. However, these approaches are inefficient in recovering missed slices (will be discussed later).

MRI (and dynamic MRI) recovering from partially observed elements, using low-rank Tucker decomposition, has been also investigated in Banco et al., Roohi et al. and Wu et al.[71,73,75] In Roohi et al.,[73] the Tucker low-rank assumption (low Tucker rank) in addition to the sparsity constraint has been applied for MRI data recovery. A similar method has been exploited in Xu et al.[76] for OCT image reconstruction. In Guo et al.,[77] a patch-based method based on minimizing Tucker rank has been proposed for functional MRI (fMRI) super-resolution. In the mentioned paper, low-rankness has been imposed on each extracted patch, instead of the general image.

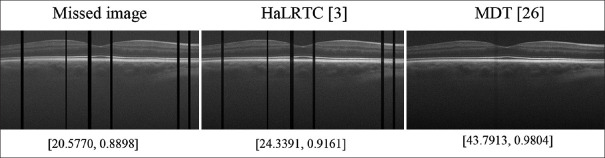
Methods proposed by Yokota et al., Hatvaniy et al. and Gui et al.[26,72,74] are based on direct Tucker decomposition. In[74] a Bayesian framework has been proposed for recovering MRI from 50% to 20% of the observed elements. Authors of[26] Proposed an approach that was capable of recovering missing slices (in contrast to HaLRTC method) based on transferring the original dataset into higher spaces and using Tucker decomposition with rank incremental. Figure 7 shows a better comparison between low-rank-based and decomposition-based methods. In this figure, we have compared a low-rank-based method and a tensor decomposition method for recovering missed slices of an OCT image. As this figure shows, HaLRTC (nuclear norm minimization method for low-rankness) was not able to recover the missed slices of a three dimensional (3D) OCT image of dataset,[14] while the method of,[26] called MDT, could recover the missed slices. The computed peak signal to noise ratio (PSNR) and structural similarity (SSIM) of the resulting images, also confirm the higher performance of the tensor decomposition method for recovering missed slices.[72] used tensor decomposition for dental computed tomography (CT) image super-resolution.

Figure 7.

Comparison of reconstruction of a sample B-scan of dataset[14] with missing slices, using HaLRTC and MDT algorithms. The results show that HaLRTC (low-rank based approach using nuclear norm minimization) could not recover the missed slices, while MDT (decomposition based approach) could recover the image. PSNR and SSIM for each image have been reported beneath each image

HOSVD has also been widely used for biomedical image completion.[78,79,80,81,82,83,84,85] In Liu et al.’s[78] and Yi et al.’s studies,[79] a tensor completion method based on deriving 3D tensors with Hankel structure and applying HOSVD has been proposed. Rank truncation is applied on the resulting factor matrices and core tensor to preserve the low-rankness of decomposition. The method has an iterative structure which repeats the procedure until convergence. The algorithm has been applied for MRI reconstruction.

In Zhang et al.’s study,[80] dynamic MRI reconstruction has been modeled as a low-rank tensor completion and sparse representation. For further improving the performance of the algorithm and utilizing the low-rank structure of dynamic MRI, a new nuclear norm has also been defined. Lu et al., proposed a method based on applying multiconvolutional filters to the input image.[82] Then the similar cubes of resulting filtered images are grouped together and HOSVD with low-rank assumption has been applied on each of them.[82] Another method based on stacking similar patches and applying low-rank HOSVD has been also used in Bustin et al. and Daneshmand et al.[84,85] for MRI and OCT images reconstruction, respectively. It is worth noting here that, in the mentioned approaches, low rankness for HOSVD is usually achieved by truncating the resulting factor matrices and core tensor.

TT and TR decompositions have been also exploited for biomedical image completion.[28,31,86,87] Methods proposed by Ma et al. and Chen and Cao[31,87] used low-rank TT decomposition (tensor with low TT rank) for MRI reconstruction and Guo et al.[86] exploited this approach for CT image completion.

In Sedighin et al.’s study,[28] a new method based on TR decomposition and overlapped patch Hankelization has been proposed for OCT image completion (super-resolution).

Biomedical image denoising

Denoising is one of the important pre-processing steps for the effective exploitation of medical images. Resulting biomedical images are usually contaminated by noise and accurate diagnosis is not possible unless proper denoising is applied. Different papers have been published for biomedical image denoising using tensor methods.[18,20,85,88,89,90,91,92]

Similar to image completion methods, the denoising methods can be divided into two groups: decomposition based[18,20] and low-rank-based methods.[85,89,94,95,96] The low-rank-based methods use the following cost function for denosing.

where is the observed noisy image (tensor) and is the estimated tensor which should be low-rank. Based on the underlying assumption for the structure of (CP, Tucker, HOSVD, TT/TR), different low-rank methods have been derived for biomedical image denoising.

CP decomposition has been used for biomedical image denoising. In Cui et al., and Cao et al.’s studies,[18,20] methods based on using Bayesian CP decomposition have been proposed for MRI image denoising.

In Zhang et al.’s study,[89] a low-rank Tucker-based method has been proposed for CT image denoising. In this method, small tensors (patches) have been extracted from the input multichannel CT image and low-rankness was applied to each extracted tensor.

HOSVD is one of the highly exploited tensor decomposition methods used for image denoising.[85,88,90,91,92,94,97] Fu et al. have proposed a low-rank-based method using HOSVD for MRI image denoising. This method exploited self-similarity between different 3D patched of the original MRI and construct 4D tensors by putting similar 3D patches together. Then by applying low-rankness and HOSVD, the denoised image has been recovered.[90] In[91] a Bayesian method has been proposed and tested for MRI image denoising.[91] Similar to Fu and Dong’s study,[90] similar patches are grouped together to provide a higher-order tensor and then low-rank HOSVD has been applied to the resulting tensor. Then, by assuming the Laplacian scale mixture for the resulting factors, a Bayesian framework has been presented for MRI image denoising. HOSVD accompanied with (first order and second order) total variation (TV) has been also proposed for denoising of OCT images.[85] In this method, similar patches of the 3D OCT are grouped to form a set of 3D tensors. Then, by applying HOSVD accompanied with low-rank assumption and TV, denoising of noisy OCT images is carried out. In Zhang et al.’s study,[92] a two-stage method based on putting similar patches together and applying HOSVD has been proposed. In the first stage, the input is the noisy image and for the second stage, the weighted summation of the original noisy image and the recovered image of the first stage is used as an input for the HOSVD. Zhang et al. have proposed a mixed approach for MRI image denoising.[98] In the first stage of this method, a low-rank HOSVD has been applied to the global 3D image. In the second stage of the algorithm, similar patches of the resulting image of the first stage is grouped together and HOSVD has been applied to the resulting higher-order tensor. In,[95] a patch-based method for positron emission tomography (PET) denoising has been proposed. The method was based on aggregating similar patches together to form a 4D tensor and applying HOSVD. Then, hard thresholding has been applied on the resulting factors to preserve low-rankness. Olesen et al. proposed an iterative method by using HOSVD and low-rank assumption for MRI denoising.[99] This method is also a patch-based method that applied low-rankness on each patch. Another paper that has been utilized HOSVD for MRI image denoising is provided by Yeganli et al.[94] In contrast to other mentioned papers, the method of[94] is not patch based and general MRI image has been used for image denoising. The sparsity constraint has also applied on the core tensor resulted from HOSVD for denoising. Low-rank HOSVD by exploiting a non-convex penalty function has been also proposed for MRI denoising by Wang et al.[97]

TT decomposition has also been exploited for OCT image denoising.[93] In this paper, low TT rank (defined in(17)) is used for OCT image denoising (despeckling).

Information fusion

Information fusion is an important issue when working with biomedical datasets. As mentioned earlier, information fusion enables the effective exploitation of common (shared) information among different modalities of multimodal datasets. In addition, by fusing several multimodal datasets, it is possible to use the unshared information of all datasets simultaneously, which is not possible when using each modality independently.

Tensor-based fusing of biomedical images has been widely studied in different literatures.[11,12,13,38,100,101,102,103,104,105,106,107,108,109,110,111] The methods are “usually” based of coupled decomposition of different datasets (Figure 4). However, some of fusion methods used the information of one modality for tensor decomposition of another modality, or applying tensor decomposition on a dataset which is composed of all modalities together.

Coupled CP decomposition has been exploited in[100] for extracting shared and distinct components among different fMRI tasks. The imposing constraint, results in more interpretable extracting components. Another CP-based fusion approach for multiparadigm fMRI has been proposed by Zhang et al.[101] In this method, correlation matrices extracted for subjects have been grouped together to form a 3D tensor. Then, CP decomposition with sparsity constraint of the latent factors has been applied for extracting parameters.

Joint analysis (fusion) of fMRI and electroencephalography (EEG) is an important task in neuroscience which is widely used for diagnosis of many diseases.[11,12,13,110] FMRI provides information about brain activities with high spatial resolution but low time resolution. Unlike fMRI, EEG can provide information with high time resolution but low spatial resolution. This is the key point that the fusion of EEG and fMRI can provide information with high spatial and time resolutions. For this aim, usually matrix-tensor coupling methods have been used. In,[11] fMRI and EEG fusion have been exploited for extracting patterns that differ between patients with schizophrenia and healthy groups. In this method, the EEG signals extracted from different subjects and different electrodes are reformatted into a tensor (subject × time × electrode) and fMRI extracted from different subjects are reformatted in a matrix (subject × voxel). Then these two datasets are coupled in their subject modes. A similar idea has been presented in,[110] however, hard coupling of the shared factors (equality of the shared factors) has been modified to the soft coupling (similarity of shared factors). Three neuroimaging modalities (instead of two modalities), including fMRI, EEG, and structural MRI (sMRI) have been fused together for capturing schizophrenia-related patterns.[12] In this method, two matrices, containing the fMRI and sMRI information and one tensor containing the EEG dataset are factorized together. Coupled CP (tensor-tensor) decomposition has been also exploited for EEG and fMRI fusion.[103] In such a method, in contrast to matrix-tensor coupling, the fMRI dataset is resorted into a tensor format. The time-frequency transforms of EEG signals have been grouped to form a fourth-order tensor and then the two datasets are coupled in their time and subject modes. In[13], the information extracted from EEG of different subjects has been used as a constraint for CP decomposition of fMRI of the corresponding subjects. In this way, they have detected the active areas in the brain during special periods.

Tucker decomposition has also been used for biomedical image fusion. In Zhang et al.’s study,[102] coupled tensor–tensor-based fusion methods (with Tucker decomposition) have been utilized for different medical image fusion. The low-frequency and high-frequency information of images are coupled to form a mixed band image. In the mentioned paper, fusions of CT and MRI, MRI and PET, MRI, and single photon emission CT (SPECT) have been investigated using coupled Tucker decomposition.

In studies by Thomason and Gregor,[108] fusing of different biomedical images into a single image using HOSVD has been studied. Several two-dimensional images have been grouped to form a 3D tensor and then HOSVD has been applied for fusion. The method has been tested for the fusion of MRI and CT images. In Yin et al.’s study,[104] a patch (block)-based method has been proposed for biomedical image fusion. HOSVD has been applied on each block by imposing sparsity on the core tensor. Then, by weighted averaging of the resulted coefficient of similar blocks of different input images, the final image has been reconstructed.

Discussion and Future Perspective

As we have reviewed in this paper, it is clear that the tensor methods have highly affected the area of biomedical image processing. Many biomedical image processing algorithms have been developed based on different tensor decomposition methods. The reviewed methods have been categorized based on tensor decomposition methods they have used and also based on their structures, and the results are shown in Table 3. It is clear that classic tensor decomposition methods, i.e. CP, Tucker, and HOSVD decompositions have been widely used for many algorithms. However, fewer algorithms exploited TT and TR decompositions methods. This can have several reasons; first, it can be due to their shorter lifespan comparing to other classic methods. Second, TT and TR decompositions are usually applicable for higher-order tensors. While many biomedical datasets are not as high order as expected. Hence, classic methods have been more exploited for analyzing biomedical datasets. However, recent studies have shown the effectiveness of Hankelization for image processing,[26,32] not only for improving the performance of the algorithms but also for transferring lower-order tensors into higher-order datasets. This is an important fact that provides a situation for exploiting tensor networks for analyzing biomedical images (or even biomedical signals).

Table 3.

Categorizing the reviewed papers based on the tensor decomposition methods

Application	Tensor decomposition method				Structure of the method
	CP	Tucker	HOSVD	TT/TR	Patch (block) based	Global
Completion	[17,21,46,68,69]	[3,26,70-74,77]	[78-85]	[28,31,86,87]	[28,70,77,82-85]	[3,17,31,68,69,26, 71-74,78-81,86,87]
Denoising	[18,20]	[89]	[85,88,90-92,94-97,98]	[93]	[85,88-92,95-98]	[18,20,93,94]
Fusion	[11,12,100,101,103,110]	[102]	[104,108]	-	[104]	[11,12,100-103,108]

In the patch (block) based methods, patches (blocks) of the input images have been used for processing, while in global methods, the whole images have been exploited. HOSVD – Higher order singular value decomposition; CP – CANDECOMP/PARAFAC; TT/TR – Tensor train/tensor ring

In Table 3, the algorithms have been also categorized based on their structures. In the patch-based methods, patches (blocks) of images have been used for processing instead of general image. In these methods, usually similar patches (blocks) have been extracted from the input image (images) and grouped to form a higher-order tensor which is usually low-rank. The low-rankness is usually accompanied by other constraints like sparsity which have been imposed on the latent variables resulting from decomposition of the tensor. On the contrary, in global methods, low-rankness has been applied to the whole image. Patch-based approaches usually have a higher computational burden comparing to the global methods, however, low-rank assumption is more applicable for patch-based methods. This is of high importance when the problem is completion or denoising where low-rankness plays an important role in recovering the images. Recent studies show that applying Hankelization or patch-based Hankelization methods also have the ability for deriving low-rank tensors. It is worth noting here that, Hankelization is usually applied for tensor decomposition-based methods, for example,[26,32] not low-rank-based methods. Recall that low-rank-based methods are based on minimizing the nuclear norm of the tensor, while tensor decomposition methods are based on decomposing the tensor into latent variables that preserve the underlying tensor structures. The important difference between these two methods is that the low-rank-based methods are usually unable to recover the missing slices of data, while tensor decomposition methods have this ability (Sedighin and Cichocki[32] and Figure 7). These together show the importance of using Hankelization with tensor decomposition methods, which, unfortunately, has been ignored in biomedical image processing and needs higher attentions in future.

As shown in Table 4, it is clear that many of tensor-based methods used MRI (dynamic MRI) for the simulations. MRI images are of high importance in diagnoses of different diseases. In addition, since MRI and dynamic MRI can be considered as (steaming) tensors, tensor methods are more preferred for analyzing MRI images. However, tensor methods can be effectively used for analyzing the vast majority of biomedical images (with the help of tensorization methods), which can be studied in future researches.

Table 4.

Categorizing the reviewed papers based on the target images they have been used

Application	Target image
	CT	MRI	fMRI	OCT	PET
Completion	[72,83,86]	[3,17,26, 31,68-71,73,74,78-82,84,87,98]	[77]	[28,85]	[95]
Denoising	[88], [89]	[18,20,90-92,94,96,97]	-	[85,93]	-
Fusion	[102]	[12,102,104,108]	[11-13,53,101,103,110]	-	[102]

CT – Computed tomography; MRI – Magnetic resonance imaging; FMRI – Functional magnetic resonance imaging; OCT – Optical coherence tomography; PET – Positron emission tomography

Conclusion

This study tries to investigate and categorize different tensor-based biomedical image processing methods. The algorithms have been categorized based on their applications and the tensor decomposition methods they have been used. It is shown that classic tensor decomposition methods have been widely used for different approaches, while TT and TR decompositions have been studied in a few biomedical image analysis papers. Furthermore, tensor methods are highly centered around MRI images and are less used for other biomedical images. These together, show a need for more attention in using tensor-based methods, especially tensor networks, for different biomedical image processing.

Financial support and sponsorship

This work has been supported by Isfahan University of Medical Sciences (Grant number: 2401120).

Conflicts of interest

There are no conflicts of interest.