Abstract
Predicting the spread trends of a pandemic is crucial, but long-term prediction remains challenging due to complex relationships among disease spread stages and preventive policies. To address this issue, we propose a novel approach that utilizes data augmentation techniques, compartmental model features, and disease preventive policies. We also use a breakpoint detection method to divide the disease spread into distinct stages and weight these stages using a self-attention mechanism to account for variations in virus transmission capabilities. Finally, we introduce a long-term spread trend prediction model for infectious diseases based on a bi-directional gated recurrent unit network. To evaluate the effectiveness of our model, we conducted experiments using public datasets, focusing on the prediction of COVID-19 cases in four countries over a period of 210 days. Experiments shown that the Adjust-R2 index of our model exceeds 0.9914, outperforming existing models. Furthermore, our model reduces the mean absolute error by 0.85–4.52% compared to other models. Our combined approach of using both the compartmental and deep learning models provides valuable insights into the dynamics of disease spread.
Keywords: Deep learning, Compartmental model, Infectious disease Prediction, Attention mechanism
Subject terms: Computational science, Data mining
Introduction
The emergence of pandemics, exemplified by the recent COVID-19 crisis, poses profound threats to global health and societal stability. Effective prediction of pandemic spread trends is crucial for governments to formulate proactive response strategies, allocate resources efficiently, and promote societal recovery.
Historically, compartmental models such as SIR (Susceptible-Infectious-Recovered) and SEIR (Susceptible-Exposed-Infectious-Recovered), which simulate the flow of individuals through disease states, have been foundational in studying infectious disease dynamics. These models provide valuable insights into epidemic behaviors such as peak infection rates and total case numbers. However, these models are constrained by fixed parameters and may struggle to capture the nuanced, evolving nature of pandemics1. Similarly, data mining-based models like ARIMA (AutoRegressive Integrated Moving Average) and SARIMA (Seasonal ARIMA) excel in linear modeling but often fail to account for the nonlinear characteristics inherent in pandemic spread dynamics, influenced by complex factors such as healthcare interventions, human behavior changes, and environmental influences2.
In recent years, machine learning techniques have emerged as promising tools to enhance prediction capabilities by extracting complex temporal dependencies in time-series data3. For instance, a model to predict COVID-19 cases was proposed based on multivariate shapelet learning from historical observations4. Deep learning, in particular, has demonstrated advantages in capturing nonlinear relationships and has been applied effectively in various predictive tasks5. Recent studies have explored the application of deep learning models in predicting pandemic spread trends6. Notably, these models have been employed to capture diverse temporal dependencies reflecting disease transmission patterns7, and address uncertain temporal dynamics in infectious disease time series8.
Despite these advancements, predicting the long-term spread trends of pandemics remains challenging. The ongoing mutations of COVID-19 and the emergence of various subtypes with differing infectious capabilities introduce variability that significantly impacts public policies and individual behaviors. At the same time, Government-implemented prevention and control measures also dynamically influence the spread of the disease. Consequently, the COVID-19 pandemic exhibits diverse spread trends over time, and the non-stationary nature of time-series data complicates prediction using traditional methods. Moreover, while deep learning models offer enhanced prediction accuracy, their black-box nature poses challenges in interpreting results, which is crucial for informed decision-making across healthcare, policy, and business sectors9.
In summary, this paper aims to propose a framework that integrates the strengths of deep learning and compartmental models to enhance the prediction of infectious disease spread. By leveraging deep learning’s ability to handle complex data patterns and compartmental models’ epidemiological insights, we seek to improve the accuracy and interpretability of pandemic spread predictions. We aim to augment time series related to the population with features from the compartmental model and prevention and control policies. Our approach leverages the self-attention mechanism to quantify variations in transmission capabilities of the infectious disease across stages segmented based on a breakpoint detection algorithm. The introduction of a Bidirectional Gated Recurrent Unit (Bi-GRU) network10 will enable long-term predictions of infected populations. This integrated framework addresses the limitations of compartmental models in incorporating covariates and enhances the interpretability often associated with deep learning models.
The paper’s expected contributions are as follows: (1) We enhance prediction accuracy by integrating disease prevention measures and compartmental model features into population data through augmentation. (2) To deepen understanding of infectious disease spread, we introduce a breakpoint detection algorithm that segments the transmission process into stages. We employ a self-attention mechanism to dynamically assign weights, quantifying transmission capabilities across stages and capturing temporal changes in transmission rates for more accurate predictions. (3) We propose a bi-directional gated recurrent unit (Bi-GRU) network model to predict long-term infectious disease spread trends. This model extracts temporal features from both pre- and post-specific time points, significantly improving prediction accuracy. By combining data augmentation, compartmental models, and advanced predictive techniques, our approach enhances interpretability and prediction performance. (4) We evaluate our approach on public COVID-19 pandemic datasets, demonstrating its advantages over existing methods.
The remainder of the paper are organized as follows. Section “Related work” provides a review of related work in the field, which leads to the development of new ideas related to disease spread process segmentation, weight addition, and feature fusion. Section “Stage-sensitive spread prediction model of infectious disease” presents a detailed description of the proposed prediction model, including its architecture, training, and components. In “Experiments”, the proposed prediction model is evaluated using infectious disease datasets from four different countries. The evaluation includes performance metrics, comparative analysis with existing models, and discussions on the results. Finally, “Conclusion” concludes the paper by summarizing the key findings and contributions of the study, and the potential future directions for improvements are also discussed.
Related work
Epidemic models
The compartmental model provides a framework for dividing the population into different categories, such as the susceptible, infected, and recovered individuals. Thus, the future evolution of each category can be predicted. Notably, the standard SIR compartmental model was employed to predict the spread of COVID-19 in several countries11. Considering that COVID-19 transmission has an incubation period, during which infected individuals are not yet contagious, the SEIR model was derived from the SIR model by adding an Exposed compartment (E)12. At the same time, social distancing is verified having impacts on curbing the development of virus, and is also incorporated into the SEIR model for infectious disease prediction13. Estimating the parameters of compartmental models is challenging, particularly during disease outbreaks when these parameters may vary. To address the problem, deep learning methods are combined with the compartmental model14.
Compartmental models supply a solid foundation for the prediction of infectious diseases, and have shown their advantages. However, the spread of the infectious diseases may be affected by the governmental control measures. Current compartmental models give little consideration to it. At the same time, compartmental models excels in discovering the interactions among population in different categories, but it is difficult for them to extract complex temporal dependencies in time series.
Data mining-based models
ARIMA is a time series analysis model widely used in forecasting outbreaks of various diseases. It has demonstrated good accuracy in predicting infectious diseases in the field of medicine15. For instance, it was applied to the dynamic prediction of hemorrhagic fever with renal syndrome16, hand-foot-mouth disease17, hepatitis B18, and also the COVID-19 pandemic recently19. An ARIMA-based model was also employed to forecast the infectious disease dynamics in India 20. Similarly, using the ARIMA model, a rapid increase of local infectious disease levels in the Arab region in April 2020 was predicted, leading to the recommendation of strict control measures to reduce the spread of the disease21.
The SARIMA model, an extension of ARIMA by incorporating seasonal factors, was applied to predict the third wave of the infectious disease in Malaysia22. Similarly, the incorporation of exogenous variables into the ARIMA model was explored in infectious disease prediction23. More recently, some studies combined compartmental models with statistical models to estimate the effective reproduction parameters of the compartmental model24. A Multivariate Shapelet Learning (MSL) model is proposed to learn shapelets from historical observations in multiple areas4. The learned shapelets can explain the increasing and decreasing trends of new confirmed cases, and reveal the COVID-19 incubation period.
These models usually perform well on linear prediction, but the spread of the infectious diseases is affected by various factors with complex interactions. Moreover, compared with deep learning-based models, these models also have disadvantages in predicting time series.
Deep learning-based models
Deep learning methods have been employed for infectious disease prediction, including Recurrent Neural Networks (RNN), Convolutional Neural Networks (CNN), attention-based networks, Graph Neural Networks (GCN), and so on25. For example, some studies utilized Long Short-Term Memory (LSTM) networks to forecast infectious disease levels in India and Canada26,27. A Gated Recurrent Network-based approach tried to examine the impact of non-pharmaceutical interventions on infectious disease development10. A multi-input deep CNN model was used to predict infectious disease levels in several cities of China28. An integrated model that combines Transformer and GCNs is introduced to predict infectious disease trends in three states in the United States29, which represented good predictive performance and model convergence. An oriented transformer (ORIT) model for infectious diseases has been introduced7. ORIT leverages multi-orientation context vectors to capture multidimensional temporal relationships within disease case data, while also addressing the variability in the incubation period for predicting different infectious disease cases. Additionally, a Dual-Grained Directional Representation (DGDR) model has been proposed to capture uncertain temporal dynamics from infectious disease time series for generating predictions8. Deep learning methods are capable of handling nonlinear relationships and multiple variables, learning complex feature representations, and rapidly analyzing and predicting real-time data.
The aforementioned methods give a solid foundation for the prediction of infectious disease. However, the spread of infectious diseases represents diverse development trends over different time periods. These variations can even arise due to either the changes of disease prevention and control measures or the evolving transmission capacity of the virus caused by mutations. Existing methods haven’t given enough consideration to this. Therefore, we try to combine compartmental model feature with policy measures feature and employs bidirectional gated recurrent networks for trend prediction.
Initially, we employ a breakpoint detection algorithm to segment the infectious disease time series, followed by the utilization of a self-attention mechanism to capture the relations among stages. The self-attention mechanism facilitates the identification of changes in the speed of infectious disease transmission. During periods of rapid spread and high transmission rates, stages with a greater impact on public health and prevention and control strategies may be assigned higher weights. We intend to study the long-term predictions by integrating compartmental model with deep learning models, which can overcome the limitations of compartmental model, lack the ability to incorporate covariates, and address the poor interpretability often associated with deep learning models.
Stage-sensitive spread prediction model of infectious disease
Architecture
A stage-sensitive prediction model for infectious disease is proposed in this paper. As shown in Fig. 1, the proposed model mainly consists of two modules, data augmentation and prediction. In data augmentation module, time series related to the population are segmented by a breakpoint detection algorithm at first. Then, the staged population data are fused with features from the compartmental model, and that about the prevention and control policies. Importantly, a self-attention mechanism is leveraged to quantify the variations in transmission capabilities of the infectious disease across stages. As to the prediction module, a Bidirectional Gated Recurrent Unit (Bi-GRU) network is used to predict the populations may be infected in a long-term.
Figure 1.
The proposed trend prediction model for infectious disease.
In Fig. 1, represents population data reflecting the number of uninfected individuals, infected individuals, recovered individuals and dead individuals, where , and indicates the population data on the t-th day. The time points, at which the number of infections seems to change largely, are detected and been used to divide the time series X into stages. These time points are also called breakpoints. Correspondingly, population features in all stages are denoted as , where , and indicates the population data on the stage p. The features from the SIRF model in all stages is termed as . The GI feature refers to the disease prevention and control measures taken by the government in each stage.
In order to deeply reveal the rules in virus transmission, the features Y from the SIRF model are fused with features G reflecting governmental control measures. We employ a self-attention mechanism to learn the transmission relationship among various stages. Thus, trainable weights will be assigned to time series in different stages. This can help more accurately reflect the dynamic changes and impacts of infectious disease transmission, thereby improving the prediction.
Finally, a Bi-GRU network is introduced to learn temporal dependencies from the augmented time series in both forward and backward directions, and predict the number of infections at a given future time point.
Transmission stage division
For a non-smooth time series, the breakpoint detection is to identify the positions of data mutations. On the curve of infected population, the segment between two consecutive breakpoints seems to be stable. So, this can be used to divide outbreak stages of an infectious disease.
Due to the complexity and non-stationarity of COVID-19 pandemic data, we adopt an adaptive breakpoint detection method, which can determine the optimal breakpoints. Given a time series of infected population, we denote the time series between breakpoints and as . For a given breakpoint , its score is calculated using as . The set of breakpoint scores, is denoted as . The idea is to build a contrast function, , that is the sum of loss functions c(X). This loss function represents the evaluation of the goodness of fit. In order to obtain the most accurate segmentation of the data, it is necessary to minimize the loss function of each segment, which is ultimately reflected in the minimization of the contrast function. The detected breakpoint values are shown as equation , where, P represents the number of breakpoints, and is the penalty for . The addition of this is aimed at balancing the reference function . If the penalty is small, it tends to use more segments to reduce V. Conversely, if the penalty is large, it tends to use fewer segments.
The mean shift model is the most widely used and simple loss function in breakpoint detection. This function follows a Gaussian distribution with a fixed variance. The loss function is also known as the quadratic error loss, , where, is the empirical mean of sub-signal .
To find the optimal breakpoints, a search method is required for the optimization. The penalty , which is also known as the linear penalty, is considered the most popular penalty. The penalty is denoted as , where is the smoothing parameter. Intuitively, the smoothing parameter controls the trade-off between complexity and goodness of fit. A low value of favors segmentation with many breakpoints, while a high value of discards most of the change points.
The Pruned Exact Linear Time (PELT) algorithm is used to find the exact solution for the penalty term . This method considers each sample in order and determines whether to discard it from the potential set of breakpoints based on explicit pruning rules.
Stage weight learning
When categorizing the stages of infectious disease transmission, the self-attention mechanism can be employed to assign weights to each stage, thus providing a more accurate representation of their importance and impact30. By leveraging the self-attention mechanism, the model can autonomously discern the correlations and interactions between different stages, facilitating the allocation of appropriate weights to each stage.
Self-attention is a variant of the traditional attention mechanism, which can capture the correlations of input sequences without additional knowledge. The self-attention mechanism adopts a query-key-value pattern. Given the input time series of fused features (see in Fig. 1), the calculation of the weight between the two sequences is described as Eq. (1), where , and denote the fused feature sequence in the p-th stage.
| 1 |
In Eq. (1), parameter , and are three trainable linear matrices, while , and are matrices composed of query vectors, key vectors, and value vectors, respectively. The attention weight matrix is denoted as A, and H is the time series matrix after adding the attention weight.
Feature fusion
The SIRF model, which is a variant of the traditional compartmental model, can describe the interaction and evolution of different population in infectious disease spread. Therefore, incorporating the prevention and control measures into such interactions will have impacts on the spread prediction of infectious disease. We suppose that S, , I, R, and F represent the susceptible population, asymptomatic population, confirmed cases, recovered population, and the fatalities, respectively. The interaction and evolution of different population in infectious disease spread can be represented as , , , where, , , , and refer to the asymptomatic fatality rate, the confirmed case fatality rate, the effective transmission rate, and the recovery rate, respectively.
Generally, there are , , and , and , where, represents the total population. Thus, the features from the infectious disease model are denoted as .
In this paper, we introduce 13 GI features for quantifying prevention and control measures into the prediction model, including Close Schools, Close Workplaces, Cancel Gatherings, Restrict Gatherings, Close Traffic, Restrict Staying Home, Restrict Domestic Travel, Restrict International Travel, Public Information Campaigns, Testing Policies, Contact Tracing, Infection Detection, and Deflationary Index. To be convenient for discussion, we shortly termed them as . Finally, we fuse these two kinds of features into (see in Fig. 1).
Spread trend prediction
The Bi-GRU network has advantages in modeling time series. By simultaneously extracting temporal features from both the period preceding and following a specific time point, it can significantly improve the prediction accuracy. As shown in Fig. 1, the Bi-GRU network used in the proposed model contains an input layer, a forward hidden layer, a backward hidden layer, and an output layer. At each time step, the input data is transmitted to both the forward and backward hidden layers. The output of the output layer is determined by the combined representations of the two hidden layers.
The Bi-GRU network receives the weighted time series as input, where , and is the input vector of the p-th stage. The feature extraction of the Bi-GRU network is simply represented as follows:
| 2 |
where, and represent the update gate and reset gate, respectively; represents the candidate hidden state; and represent the hidden state at stages and p , respectively; , , , , and are trainable weights; b is a bias; represents the sigmoid function. It can be found, from the equations above, that a GRU can either remember or forget some previous temporal features through learning parameters and , thereby improving the temporal dependencies extraction from time series. Thus, the mathematical expression of the Bi-GRU network structure is as follows:
| 3 |
where, and are the states of the forward and backward hidden layers at stage p, respectively; and are the weights of the forward and backward hidden layers at stage p, respectively; is the bias of the hidden layer at time p. Thus, the Bi-GRU network can extract the long-term temporal dependencies, thereby improving the prediction of time series.
Experiments
Datasets
The data used in the experiments was obtained from the Coronavirus Resource Center established by Johns Hopkins University (CRC) (https://coronavirus.jhu.edu/region), and the COVID-19 Government Response Tracker by the University of Oxford (OxCGRT). The CRC has collected infectious disease data from countries and regions worldwide since early 2020. The OxCGRT gathered governmental policies related to containment and closure, economic, health system, and the miscellaneous31. These policies are quantified based on their extent of implementation, and the scores are aggregated to form a set of policy indicators. We selected four countries with high infection rates worldwide for the experiments. Among these countries, France, South Korea, and Germany have the highest infection rates. Despite Japan ranking sixth, we included it due to its exceptionally high urbanization rate. This choice also aimed to balance geographical diversity, as otherwise the fourth and fifth countries would both be European. For each country, the dataset was divided into training and testing sets with a ratio of 7:3, allowing us to generate a long-term prediction spanning 210 days. Both the training and testing data were normalized by the maximum-minimum normalization.
Experiment design
The experiment was conducted on a Windows 11 system, utilizing an NVIDIA 3080 GPU. The environment was configured with Python 3.8 and TensorFlow’s Keras library. The experiment employed a Bi-GRU network architecture consisting of an input layer, 5 hidden layers, and an output layer. The input layer processed a total of 18 features with a time step of 10. A batch size of 128 and a hidden size of 64 were used. The activation function ReLU and optimizer Adam were applied. Dropout regularization with a rate of 0.2 and a learning rate set to 0.001 were also utilized. The model training iterates up to 1000 times.
The proposed method is evaluated using widely accepted indicators, including Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), and Adjusted. The definition of the MAPE and the are given as follows,
| 4 |
where, represents the ground truth, represents the predicted value, n represents the length of the time range to be predicted, a represents the number of samples, and m represents the number of features.
Prediction results analyses
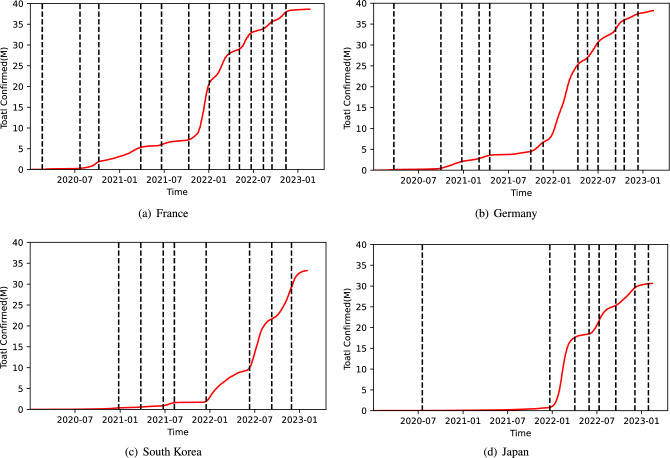
Figure 2 illustrates the cumulative confirmed cases in France, Germany, Japan and South Korea, respectively, as well as their breakpoints detected by the proposed algorithm. Using the obtained time points, the time series of infectious disease cases is divided into different stages.
Figure 2.
The cumulative confirmed cases and the spread stages detected.
We compare the proposed model with six baseline models, including LSTM, AutoEncoder (AE), ARIMA, SEIR, CNN, and Transformer-GCN (TF-GCN), in the trend prediction of confirmed cases in four countries mentioned above.
Figure 3 illustrates the relative error of each model on the prediction of infected cases in four countries every 10 days. It can be found that our model maintains the smallest relative error at the majority of time points. It is also found that our model is more stable in relative prediction error than others in a long time period, and more adaptive to different datasets.
Figure 3.
Relative errors of different models..
In order to further evaluate the fitting capability of the proposed model, we conducted comparative analyses of different models using three indicators, MAE, MAPE, and . Figure 4 shows that our model can reduce the average MAE in the four countries by about 0.85–4.52% compared with others. It can also be found that the proposed model has advantages over others in MAPE. Figure 5 compares different models on average MAPE when they are used to predict the confirmed cases in all the four countries. It shows that the proposed model achieves the smallest average MAPE of 0.43% in all models. Comparatively, the AutoEncoder-based model, which ranks in the second position, can only achieve an average MAPE of 1.28%. The ARIMA-based prediction model even has an average MAPE beyond 4.95%. Furthermore, we can find that the most widely used model in infectious disease prediction, SEIR, shows disadvantages in MAPE compared with others except ARIMA and Transformer-GCN. At the same time, though LSTM and Transformer both are considered having perfect performance in the prediction of time series, they do not perform well in the prediction of infectious diseases.
Figure 4.

Average MAEs of different models.
Figure 5.

Average MAPEs of different models.
As to the index, our model also shows advantages over others, since it is more than 0.99 when used to predict infectious cases in all four countries. Figure 6 gives the average of all models in the prediction of cases in the four countries. It is also found that the proposed model perform best, and the AutoEncoder and CNN models rank in the second and third position, respectively. On the other hand, SEIR achieves an average index of 0.912225, which ranks only in the fifth position.
Figure 6.

Average adjusted-R2 of different models.
In summary, when considering the capability of trend fitting, MAPE, and of each model, it is found that existing models show disadvantages in capture the variations of viral transmission capabilities in different outbreak stages. The disadvantage will be magnified in long-term predictions, leading to low prediction accuracy. In contrast, our model considers the variations in transmission capabilities across different stages of the infectious disease, and incorporates an attention mechanism to assign higher weights to stages with stronger transmission rates. Importantly, the proposed model also integrates features from infectious disease models and control policies, enabling the Bi-GRU to capture more comprehensive information from the time series. The experiments verify that this integration improves prediction accuracy and reduces errors in long-term predictions.
Sensitivity analysis and ablation studies
To evaluate the robustness and relative importance of various parameters in our model, we conducted sensitivity analysis experiments. We varied two parameters of the proposed model, the hidden layer size and batch size, and observed their effects. The vertical axis of Fig. 7 represents the average MAE when the proposed model is used to predict the infectious cases in the four countries. From the figure, it can be observed that the model demonstrates reasonable variations in MAE under different hyperparameter settings. Notably, the model represents the best performance when the Batch-size is set to 128, and the Hidden-size to 64.
Figure 7.

Sensitivity of the proposed model with different hyperparameters.
To further validate the rationality of the proposed model, we conducted ablation experiments using its two variations. The two variations excluded the SIRF and self-attention mechanism modules from the original model, respectively. We compared their performance using the MAE and RMSE metrics on datasets about the four countries.
As shown in Fig. 8, both SIRF and the attention mechanism play significant roles in reducing the MAE. It seems that the self-attention mechanism has greater impact on the overall performance of the model. Figure 9 shows that both SIRF and the attention mechanism are critical to reduce the RMSE of the proposed model, thereby making the model more stable and adaptive to different datasets. Similarly, the self-attention mechanism contributes more in reducing the RSME than the SIRF model.
Figure 8.

MAEs of the proposed approach and its variations.
Figure 9.

RMSEs of the proposed approach and its variations.
Discussion
Based on experimental results and analysis, our proposed model exhibits the strongest ability to fit infectious disease data over a considerable period compared to state-of-the-art models. In contrast, the ARIMA model exhibits the weakest ability to fit data due to its limitations in modeling nonlinear and non-stationary time series. While LSTM and AutoEncoder are recognized for their strong performance in time series prediction, they show drawbacks in stability and long-term infectious disease forecasting compared to our model. This is likely due to their limited capacity to extract inter-feature relationships. The TF-GCN model, combining Transformer and GCN, excels in extracting temporal features and capturing feature relationships in time series data. However, it struggles with stability in predicting long-term infectious disease trends and demonstrates poor adaptability across different datasets. Variations in disease transmission capabilities across stages significantly impact TF-GCN’s predictive performance. SEIR, widely used in infectious disease prediction, performs poorly on two of four datasets due to limitations in long-term time series modeling.
Our findings indicate significant variations in the stages of COVID-19 spread, ranging from approximately one to six months, resulting in non-stationary time series of cases across different countries. Our ablation studies highlight the effectiveness of segmenting disease spread into stages and utilizing a self-attention mechanism to dynamically weigh these stages based on variations in disease transmission dynamics. Implementing these strategies in our model led to substantial improvements, with a reduction in Mean Absolute Error (MAE) by approximately 56.2% and Root Mean Square Error (RMSE) by 51.4% on average for long-term predictions.
Furthermore, we observed considerable impacts of preventive measures such as Home Confinement, Contact Tracing Policy, and Vaccination Status on the spread of infectious diseases. This underscores their critical role in predictive modeling. Our research also validates the effectiveness of data augmentation through compartmental models and the integration of preventive policies, resulting in an average decrease in MAE by 36.32% and RMSE by 21.98%.
In conclusion, integrating compartmental models with machine learning techniques, alongside adaptive stage segmentation of disease spread and inclusion of preventive policy data, represents a robust and effective approach for predicting long-term trends in infectious diseases.
Conclusion
By incorporating the compartmental model and Bi-GRU network, the prediction of long-term trends in infectious disease spread can be significantly improved. Additionally, data augmentation that consider disease prevention and control policies contributes to enhancing the accuracy of predictions. Furthermore, the application of a weighted stage division approach using self-attention mechanisms further enhances the predictive performance.
In the future, we will explore a multi-factor comprehensive prediction model by incorporating additional variables related to infectious diseases, such as meteorological environment and population mobility data, in order to improve the accuracy of our predictions. Furthermore, we intend to investigate the prediction of infectious diseases by considering the sparsity of time series data to improve the adaptability of the prediction model.
Supplementary Information
Author contributions
Wanghu Chen and Heng Luo wrote the main manuscript text, and Jing Li and Jiacheng Chi prepared the datasets. All authors reviewed the manuscript.
Funding
The work is supported by the National Natural Science Foundation of China (No. 62462059, 61967013).
Data availibility
The data utilized in the paper are publicly provided by third-party organizations. The URLs for downloading the data or references to the data have been included in the manuscript. For further needs, please contact corresponding author. The infectious disease data can be downloaded from https://coronavirus.jhu.edu/region. The data about the policies is introduced in “Hale, T. et al. A global panel database of pandemic policies (oxford covid-19 government response tracker). Nat. human behaviour 5, 529-538 (2021).”
Code availibility
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-72005-x.
References
- 1.Di Giamberardino, P., Iacoviello, D., Papa, F. & Sinisgalli, C. Dynamical evolution of covid-19 in Italy with an evaluation of the size of the asymptomatic infective population. IEEE J. Biomed. Health Inform.25, 1326–1332. 10.1109/JBHI.2020.3009038 (2021). 10.1109/JBHI.2020.3009038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Masum, M., Masud, M., Adnan, M. I., Shahriar, H. & Kim, S. Comparative study of a mathematical epidemic model, statistical modeling, and deep learning for covid-19 forecasting and management. Socioecon. Plann. Sci.80, 101249 (2022). 10.1016/j.seps.2022.101249 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Watson, G. L. et al. Pandemic velocity: Forecasting covid-19 in the us with a machine learning & bayesian time series compartmental model. PLoS Comput. Biol.17, e1008837 (2021). 10.1371/journal.pcbi.1008837 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wang, Z. & Cai, B. Covid-19 cases prediction in multiple areas via shapelet learning. Appl. Intell.52, 595–606 (2022). 10.1007/s10489-021-02391-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen, Z., Ma, M., Li, T., Wang, H. & Li, C. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion97, 101819 (2023). 10.1016/j.inffus.2023.101819 [DOI] [Google Scholar]
- 6.Shoeibi, A. et al. Automated detection and forecasting of covid-19 using deep learning techniques: A review. Neurocomputing577, 127317. 10.1016/j.neucom.2024.127317 (2024). 10.1016/j.neucom.2024.127317 [DOI] [Google Scholar]
- 7.Wang, Z. et al. Oriented transformer for infectious disease case prediction. Appl. Intell.53, 30097–30112 (2023). 10.1007/s10489-023-05101-6 [DOI] [Google Scholar]
- 8.Zhang, P., Wang, Z., Huang, Y. & Wang, M. Dual-grained directional representation for infectious disease case prediction. Knowl.-Based Syst.256, 109806 (2022). 10.1016/j.knosys.2022.109806 [DOI] [Google Scholar]
- 9.Li, X. et al. Interpretable deep learning: Interpretation, interpretability, trustworthiness, and beyond. Knowl. Inf. Syst.64, 3197–3234 (2022). 10.1007/s10115-022-01756-8 [DOI] [Google Scholar]
- 10.Bi, L., Fili, M. & Hu, G. Covid-19 forecasting and intervention planning using gated recurrent unit and evolutionary algorithm. Neural Comput. Appl.34, 17561–17579 (2022). 10.1007/s00521-022-07394-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cooper, I., Mondal, A. & Antonopoulos, C. G. A sir model assumption for the spread of covid-19 in different communities. Chaos Solitons Fract.139, 110057 (2020). 10.1016/j.chaos.2020.110057 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Battineni, G., Chintalapudi, N. & Amenta, F. Sars-cov-2 epidemic calculation in italy by seir compartmental models. Appl. Comput. Inf.20, 251–261 (2024). [Google Scholar]
- 13.Mwalili, S., Kimathi, M., Ojiambo, V., Gathungu, D. & Mbogo, R. Seir model for covid-19 dynamics incorporating the environment and social distancing. BMC. Res. Notes13, 1–5 (2020). 10.1186/s13104-020-05192-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gan, Y., & Yu, W. Epidemics trend prediction model of covid-19. CAAI Trans. Intell. Syst.16, 528–536 (2021).
- 15.Zaki, M. J. Scalable algorithms for association mining. IEEE Trans. Knowl. Data Eng.12, 372–390 (2000). 10.1109/69.846291 [DOI] [Google Scholar]
- 16.Zhao, Y. et al. A new seasonal difference space-time autoregressive integrated moving average (sd-starima) model and spatiotemporal trend prediction analysis for hemorrhagic fever with renal syndrome (hfrs). PLoS ONE13, e0207518 (2018). 10.1371/journal.pone.0207518 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu, L., Luan, R., Yin, F., Zhu, X. & Lü, Q. Predicting the incidence of hand, foot and mouth disease in sichuan province, china using the arima model. Epidemiol. Infect.144, 144–151 (2016). 10.1017/S0950268815001144 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cai, X.-H., He, M.-Z., Zhou, Z. & Xu, M.-G. Forecasting hapetitis b epidemic situation by applying the arima model. World J. Infect.10, 25–28 (2010). [Google Scholar]
- 19.Somyanonthanakul, R. et al. Forecasting covid-19 cases using time series modeling and association rule mining. BMC Med. Res. Methodol.22, 281 (2022). 10.1186/s12874-022-01755-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Swaraj, A. et al. Implementation of stacking based Arima model for prediction of Covid-19 cases in India. J. Biomed. Inform.121, 103887 (2021). 10.1016/j.jbi.2021.103887 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Alzahrani, S. I., Aljamaan, I. A. & Al-Fakih, E. A. Forecasting the spread of the covid-19 pandemic in Saudi Arabia using Arima prediction model under current public health interventions. J. Infect. Public Health13, 914–919 (2020). 10.1016/j.jiph.2020.06.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tan, C. V. et al. Forecasting Covid-19 case trends using Sarima models during the third wave of Covid-19 in Malaysia. Int. J. Environ. Res. Public Health19, 1504 (2022). 10.3390/ijerph19031504 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Aji, B. S., & Rohmawati, A. A. Forecasting number of covid-19 cases in Indonesia with arima and arimax models. In 2021 9th international conference on information and communication technology (ICoICT), pp. 71–75 (IEEE, 2021).
- 24.Kiarie, J., Mwalili, S. & Mbogo, R. Forecasting the spread of the covid-19 pandemic in kenya using seir and arima models. Infecti. Dis. Model.7, 179–188 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ajagbe, S. A. & Adigun, M. O. Deep learning techniques for detection and prediction of pandemic diseases: A systematic literature review. Multimed. Tools Appl.83, 5893–5927 (2024). 10.1007/s11042-023-15805-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Pillai, P. K., Durairaj, D. & Samivel, K. Deep learning-based forecasting of Covid-19 in India. J. Test. Eval.50, 225–242. 10.1520/JTE20200574 (2022). 10.1520/JTE20200574 [DOI] [Google Scholar]
- 27.Chimmula, V. K. R. & Zhang, L. Time series forecasting of covid-19 transmission in Canada using lstm networks. Chaos Solitons Fract.135, 109864 (2020). 10.1016/j.chaos.2020.109864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Huang, C.-J., Chen, Y.-H., Ma, Y. & Kuo, P.-H. Multiple-input deep convolutional neural network model for Covid-19 forecasting in China. MedRxiv 2020-03 (2020).
- 29.Li, Y., Wang, Y. & Ma, K. Integrating transformer and gcn for covid-19 forecasting. Sustainability14, 10393 (2022). 10.3390/su141610393 [DOI] [Google Scholar]
- 30.Jung, S., Moon, J., Park, S. & Hwang, E. Self-attention-based deep learning network for regional influenza forecasting. IEEE J. Biomed. Health Inform.26, 922–933. 10.1109/JBHI.2021.3093897 (2022). 10.1109/JBHI.2021.3093897 [DOI] [PubMed] [Google Scholar]
- 31.Hale, T. et al. A global panel database of pandemic policies (oxford covid-19 government response tracker). Nat. Hum. Behav.5, 529–538 (2021). 10.1038/s41562-021-01079-8 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data utilized in the paper are publicly provided by third-party organizations. The URLs for downloading the data or references to the data have been included in the manuscript. For further needs, please contact corresponding author. The infectious disease data can be downloaded from https://coronavirus.jhu.edu/region. The data about the policies is introduced in “Hale, T. et al. A global panel database of pandemic policies (oxford covid-19 government response tracker). Nat. human behaviour 5, 529-538 (2021).”