Abstract
Wildfires are among the most common natural disasters in many world regions and actively impact life quality. These events have become frequent due to climate change, other local policies, and human behavior. Fire spots are areas where the temperature is significantly higher than in the surrounding areas and are often used to identify wildfires. This study considers the historical data with the geographical locations of all the “fire spots” detected by the reference satellites covering the Brazilian territory between January 2011 and December 2022, comprising more than 2.2 million fire spots. This data was modeled with a spatio-temporal generalized linear mixed model for areal unit data, whose inferences about its parameters are made in a Bayesian framework and use meteorological variables (precipitation, air temperature, humidity, and wind speed) and a human variable (land-use transition and occupation) as covariates. The meteorological variables humidity and air temperature showed the most significant impact on the number of fire spots for each of the six Brazilian biomes.
Keywords: Brazilian wildfires, Spatio-temporal modeling, Wildfires risk factors, Bayesian modeling
Subject terms: Ecology, Environmental sciences, Mathematics and computing
Introduction
Brazil, the fifth country in the world in territorial extension, has a vast wealth in several categories, its biodiversity being one of them. Considered by many experts as the “country of megadiversity”, given that 15–20% of the known species in the world are found in its territory1, its fauna and flora are officially separated into six biomes: Amazônia, Caatinga, Cerrado, Mata Atlântica, Pampas, and Pantanal (see Fig. S1 of the supplementary material for more details on the location of each biome).
The Amazônia biome includes about 60% of the largest rainforest in the world, with extensive mineral reserves and 20% of the world’s water availability2. The Caatinga is in a semi-arid climate, with great biological richness and unique species3. The Cerrado is recognized as the richest savanna in the world in terms of biodiversity, having remained unchanged until the 1950s when the federal capital was transferred to Brasília4. The Mata Atlântica is located on the Brazilian coast, thus being the most threatened biome in the country, where only 27% of the original forest cover is still preserved5. The Pampas is characterized by a rainy climate without a dry period and negative temperatures during the winter6. Finally, the Pantanal is recognized as the planet’s most extensive continuous floodplain7. Further official details can be found on the website of the Brazilian Institute of Geography and Statistics (IBGE; Instituto Brasileiro de Geografia e Estatística; https://www.ibge.gov.br)8.
Despite all the wealth and beauty, a somewhat chronic problem has become increasingly worse in Brazil during the last few years: wildfires9–12. Wildfires, fires that occur in natural areas such as forests and woods, which can be caused by various factors such as human activities, uncontrolled fires, and natural causes, are one of the most common forms of natural disasters in many world regions and actively affect the quality of life13–15. These events have become more frequent with the increasing effect of climate change, other local policies, and human behavior16–18.
In particular, the Amazon rainforest has been deforested over the years, increasingly reducing its area19–22, either from the overthrow of trees or wildfires. The PRODES - Amazônia project has been monitoring this deforestation since 1988, having reached a deforestation “peak” of 13 thousand km2 in the last ten years in 2021. However, something different has been happening in recent years: wildfires that were more commonly seen primarily in the Amazon rainforest have spread to other Brazilian biomes, causing natural disasters such as the devastation of approximately one-third of the Pantanal in the 2020 wildfires23 and the arrival of smoke caused by fires in the Pantanal in 2020 to the cities of São Paulo, Rio de Janeiro, and Curitiba24.
Given the importance and consequences of Brazilian wildfires, locally and globally, and their increase in recent years, much research has been done on the topic. For example10, used data from satellite images and discussed the characteristics of wildfires from a broader perspective, including the whole Brazilian territory, some regions of the USA, and Australia25 gave an overview of the fires in Pantanal26, discussed the economic footprint of the 2018 wildfires of California, and27 provided an extensive analysis of forest fires in the Pantanal biome during 202028 analyzed forest fires caused by lightning in central Brazil, a region comprising parts of the biomes Mata Atlântica, Cerrado, and Pantanal. The impacts of the mega-fire campaign in the Cerrado biome in 2017 from a biophysical point of view, energy balance, and evapotranspiration were presented by29,30 analyzed the effectiveness of using prescribed fires in fire-prone areas to prevent large fires, using the Brazilian Cerrado as a research site. More recently, a study by31 used hierarchical time series forecasting to compare models and reconciliation techniques in forecasting the number of fire spots at municipality, biome, and country levels.
From a space-time point of view32, provided an analysis of the processes that drove deforestation in the Amazon forest with an analysis of the impacts of agriculture in the state of Mato Grosso between 2006 and 2017, using a spatial panel model that makes it possible to identify the factors that affect deforestation33 carried out a spatial analysis that allowed the quantification of forest degradation in the Brazilian Amazon rainforest between 1992 and 2014, and34 used a coupled ecosystem-fire model to quantify the effects of climatic events and land use in forest fires in the Amazônia9 presented a general analysis of forest fires’ temporal and spatial aspects in the Mata Atlântica biome in the south of Bahia state and the north part of Espírito Santo35 used a sample-based approach to consistently quantify tree cover loss from 2000 to 2013 in the Brazilian legal Amazon, comprising land area from nine Brazilian states, across all forest types in the region, primary forest and non-primary forest.
Unlike previous studies focusing mainly on localized wildfire analyses within specific regions or biomes, this research provides a comprehensive understanding of fire spot dynamics across Brazil. Considering the entire Brazilian territory spanning twelve years, our study aims to fill a notable gap in the literature by offering a national-scale analysis of fire spot patterns. Moreover, our approach integrates meteorological variables and human-induced land-use transitions as covariates, allowing for a holistic examination of the complex interactions driving fire spot occurrences. By applying sophisticated statistical modeling techniques, including a Bayesian framework for parameter inference, we seek not only to describe but also to elucidate the underlying mechanisms shaping fire spot dynamics at a national level. By addressing this broader scope, our research aims to contribute novel insights to the field of wildfire research and inform proactive strategies for wildfire management and mitigation.
In this paper, after a temporal and spatial analysis of the number of fire spots that were detected in the entire Brazilian territory between January 1, 2011, and December 31, 2022, we used a spatio-temporal approach to model the number of fire spots per Brazilian municipality and biome, using meteorological and human-based explanatory variables considering the data between the years 2012 and 2021. We used a spatio-temporal generalized linear mixed model for areal unit data, whose inferences about its parameters are made in a Bayesian framework with covariates.
The remainder of this paper is organized as follows. First, we describe data collection, data organization, and data imputation, which come from three sources: (i) satellite images that resulted in a dataset with all fire spots between January 1, 2011, and December 31, 2022, throughout the Brazilian territory, and its geographic location; (ii) weather data from all weather stations available in Brazil between January 1, 2012, and December 31, 2021; and (iii) land use and occupation year by year between January 1, 2012, and December 31, 2021. In addition, we present the full details of a Bayesian spatio-temporal generalized linear mixed model for areal unit data. Section 3 presents the results from a vast descriptive and exploratory data analysis (fire spots, climatic data, and land use), followed by the results obtained by the Bayesian spatio-temporal generalized linear mixed model for areal unit data and their discussion. The paper ends in Section 4 with some concluding remarks and possible future research directions.
Materials and methods
The detailed flowchart of the methodology proposed and used in this paper is presented in Fig. 1, which sets the structure of this section: data collection, data treatment, and data organization being the subsections with three paragraphs each, one for each data set. This section ends with detailed information about a Bayesian spatio-temporal generalized linear mixed model for areal unit data. The complete data collection, treatment, and organization details are listed below to allow for reproducible science.
Figure 1.
Detailed flowchart of the methodology used in this paper, including the data collection, data treatment, data organization, data visualization, and spatial-temporal modeling. Blue arrows are related to the steps and operations from data collection to data treatment, organization, and visualization. Red arrows are associated with the spatio-temporal modeling.
Data collection
This study used complex data from three different sources, considering a time interval of twelve years between January 1, 2011, and December 31, 2022. The data sources used were: (i) satellite images that resulted in a data set containing all fire spots in the whole Brazilian territory during the twelve years; (ii) hourly climatic data from all available meteorological stations in Brazil during the ten years used for modeling, i.e., between January 1, 2012, and December 31, 2021; and (iii) data related to land use and land-use transition during the ten years used for modeling, i.e. between January 1, 2012, and December 31, 2021. The difference in data collection periods was due to data availability. Land use and land-use transition are made available with a large delay. Thus, we decided to present a temporal and spatial descriptive and exploratory analysis of the number of fire spots considering 12 years (2011-2022) and model building considering 10 years (2012–2021).
Fire spots - Time and geographical locations The response variable was obtained from the Brazilian National Institute for Space Research (INPE; Instituto Nacional de Pesquisas Espaciais; http://queimadas.dgi.inpe.br). The original raw data included 12 files, one per year, with all fire spots detected on Brazilian territory by the INPE reference satellite AQUA M-T. These raw files have the date, hour, satellite (several satellites are available), Brazilian state, Brazilian municipality, biome, number of days without rain, precipitation, fire risk, latitude, longitude, and relative firepower. For the 12 years considered in this study, the AQUA M-T satellite detected approximately 2.2 million fire spots, having the associated database the same number of rows.
According to INPE36, fire spots detected by polar-orbiting satellites like AQUA are identified by field validation to measure around 30 meters long by 1 meter wide or larger. However, the pixel size of MODIS sensors, like those on AQUA and TERRA satellites, is typically 1 km × 1 km or larger. Therefore, even small burns of a few tens of square meters are detected as covering at least one km2. This means that a burning pixel could represent various fire sizes within its detection area, from small to large fires.
Meteorological data - Variables from all available meteorological stations in Brazil This data set was obtained from the Brazilian National Institute of Meteorology (INMET; Instituto Nacional de Meteorologia; http://portal.inmet.gov.br). The original raw data includes one file for each of the meteorological stations, whose number increases with time, starting with 468 in 2012 and reaching 588 in 2021 (468, 473, 475, 484, 529, 563, 596, 589, and 588 for the years between 2012 and 2021, respectively). These raw files include the date, time, total precipitation, atmospheric pressure (hourly, maximum, and minimum), global radiation, air temperature, dew point temperature (hourly, maximum, and minimum), hourly temperature (minimum and maximum), humidity (hourly, minimum and maximum), wind (direction, maximum gust, and hourly speed). From these meteorological variables, a total of four variables were considered in this study: precipitation, air temperature, humidity, and wind speed, measured in millimeters (mm), degrees Celsius (°C), percentage (%), and meters per second (m/s) respectively. Each file contained 8760 rows for “typical” years and 8784 for leap years.
Land use This data set was obtained from the Brazilian Annual Land Use and Land Cover Mapping Project in Brazil (MapBiomas; Projeto de Mapeamento Anual do Uso e Cobertura da Terra no Brasil; http://mapbiomas.org)37. Unlike the fire spots and climate data, land use data directly results from human activity. This data includes variables that measure land use and occupation and transition values between how the land was used from one year to the next, between 2011 and 2021. In this case, land use refers to the type of use at that given moment of the soil representing hectares of area, while land use transition will be exactly the number of hectares of area that changed between one year and the following year, with the possibility of loss or area gain. This data is organized into six main categories, which are defined and presented in Table 1 and consists of the total land use (in thousands of hectares) in each category (and several sub-categories) per municipality and year.
Table 1.
Land use and occupation and transition categories.
| Main classes | Secondary classes |
|---|---|
| Forest | Forest Formation, Savanna Formation, Mangrove and Wooded Restinga |
| Non Forest Natural Formation | Wetland, Grassland, Salt Flat, Rocky Outcrop and Other non-Forest Formation |
| Farming | Pasture, Agriculture, Forest Plantation and Mosaic of Agriculture and Pasture |
| Non Vegetated Area | Beach, Dune, Sand Spot, Urban Area, Mining and Other non Vegetated Areas |
| Water | River, Lake, Ocean and Aquaculture |
| Non Observed | – |
Data treatment
Many problems might arise when dealing with observational data that require intensive data cleaning and data treatment. In this study, we have to deal with missing value imputation, data aggregation, data extrapolation, data interpolation, and data transformation. In what follows, we explain in detail the treatment that each data set needed before the analysis could be performed.
Fire spots In this data set, the main challenge for data treatment was related to data aggregation per day. Based on the geographic locations of each fire spot, it was associated with the municipality, state, and biome where it occurred. After establishing this association, the data were aggregated per day for each municipality, state, and biome. This resulted in a database with as many rows as the number of days between January 1, 2011, and December 31, 2022. The days without observations for a given municipality, state, or biome were assigned the value zero, as no fire spot was observed on that day/location.
Climate data In this data, two main problems had to be dealt with: (i) not all Brazilian municipalities have a meteorological station, and (ii) for some meteorological stations, especially at the beginning of the ten-year historical period, a high number of observations were missing. We considered daily observations of four meteorological variables: precipitation, air temperature, humidity, and wind speed. As the data was collected hourly, the monthly averages were taken for each meteorological station, then used for data extrapolation for every Brazilian municipality, and considered in the Bayesian spatio-temporal modeling. This data treatment for the meteorological variables was organized into three steps:
Data aggregation per month: For each of the four meteorological variables, precipitation, air temperature, humidity, and wind speed, the monthly average was obtained for each meteorological station;
- Data extrapolation from meteorological station to municipality: To estimate the meteorological variables, and also to impute missing values, in a given municipality and in a given month, a weighted average between the values of the three closest stations to that municipality geographic center were considered. After identifying and selecting the three closest stations, , , the values of the environmental/meteorological variable for each of the stations are extracted and denoted by , , respectively. Then, the Euclidean distances between the geographic center of the municipality with the missing observation and the three closest stations, , , is obtained and represented by , . In this way, when we identify a missing value for that meteorological variable in a given municipality, it is estimated as
In this approach, we give higher weights to stations closer to the meteorological station with the missing observation. The closer a station is to the geographic center of a municipality with the missing observation, the more weight it has to estimate the missing value. In the case of missing observations in the meteorological variable for any of the closest stations, those will not be used for the estimation. The value of the meteorological variable in the time t and municipality k will remain missing if not observed in any of the three closest stations.1 Missing value imputation: After data extrapolation, there were still several missing values because, in some cases, the three meteorological stations closest to the municipality without a station had missing values for a given meteorological variable in one or more months. To deal with these missing values, we use the package imputeTS38 of the R software39 to impute them. Due to spatial heterogeneity, we impute the values of the time series of each municipality individually. The imputation was based on the exponential weighted moving average method, considering as the integer width of the moving average window, i.e., it expands to both sides of the center element, being k on the left and k on the right.
Land use In this data set, the main challenge was that the land-use transition variables are available for each municipality per year, while the modeling phase needs monthly observations. Data interpolation from year to month was considered using imputation techniques to solve that problem, i.e., for variables related to land use, we assume that the monthly values of these variables between January and December of the same year are equal to the corresponding average annual value. The measurement level of these variables was transformed to thousands of hectares.
Data organization
Fire spots - Total numbers per day, month, biome, and municipality After the treatment of the raw data, six data sets were created to be used in the descriptive analysis, data visualization, and spatio-temporal modeling: (i) the number of fire spots per day per Brazilian municipality; (ii) the number of fire spots per day per Brazilian state; (iii) the number of fire spots per day per Brazilian biome; (iv) the number of fire spots per month per Brazilian municipality; (v) the number of fire spots per month per Brazilian state; (vi) the number of fire spots per month per Brazilian biome. All the 5570 Brazilian municipalities, the 27 states (including the federal district), and the six biomes were considered. These data files are available as supplementary material for this paper. The R code to obtain the data files is available upon request from the corresponding author of this paper.
Climate data - Precipitation, air temperature, humidity, and wind speed per month and municipality After the treatment of the raw data, eight data sets were created to be used in the descriptive analysis, data visualization, and spatio-temporal modeling: (i) monthly averages of precipitation per municipality; (ii) monthly averages of air temperature per municipality; (iii) monthly averages of humidity per municipality; (iv) monthly averages of wind speed per municipality. The data sets are available upon request from the corresponding author of this paper.
Land use - Gain and loss of green area and farming area, and land-use transition After the treatment of the raw data, five data sets were created, four to be used in the descriptive analysis and data visualization: (i) yearly gain and loss of green area per municipality, in thousands of hectares; (ii) yearly gain and loss of green area per municipality, in thousands of hectares, weighted by the area of the municipality; (iii) yearly gain and loss of farming area per municipality, in thousands of hectares; and (iv) yearly gain and loss of farming area per municipality, in thousands of hectares, weighted by the area of the municipality; and one to be used for the spatio-temporal modeling: (v) monthly “land-use transition” from a green area (forest and non-forest natural formation) to a farming area (in thousands of hectares), for each of the 5570 municipalities. The first four variables can help measure the deforestation between the year t and the year .
Model description
Some strategies to model aggregated data in time-varying areas include the space-time auto-regressive moving average (or STARMA, in short) models within the most widely used40. However, this class of models does not allow for the incorporation of explanatory variables into the model.
Our objective with this analysis is to model the total number of fire spots, aggregated by municipality and month, by including explanatory variables such as precipitation, temperature, humidity, radiation, and land-use transition. Since the standard linear regression model assumes that observations are independent, it does not address our need to accommodate dependencies in time and space. As we deal with panel data (counts) that vary in time and space, we decided to work with a spatio-temporal generalized linear mixed model for areal unit data developed by41. Models of this class help to fit areal unit data given in discrete periods while allowing the inclusion of explanatory variables, which have already been used in works by42–45. In the next paragraphs, we will briefly review this model.
Consider N non-overlapping areal units. Data is recorded for each unit in T consecutive time periods. For modeling purposes, in our case, time is given in months and Brazilian municipalities are the areal units. Let be the number of fire spots observed in municipality and at time . Suppose that to model count data, where , is the risk of fire spot in municipality i during month t relative to an offset , and denotes the conditional expectation operator. Working with the default log link function, we have:
| 2 |
where:
is a p-dimensional vector of known covariates for municipality i and time period t, whose entries form the -th row of the design matrix ;
is a p-dimensional vector of covariate regression parameters and its prior distribution, specified as by41, has mean vector and diagonal covariance matrix ;
is a latent component for municipality i and time period t encompassing one or more sets of spatio-temporally autocorrelated random effects.
Note that we have a traditional Poisson log-linear model if for all and . Since there is often interest in checking whether there is any simple linear trend in the random effects for each region i41 proposed the use of the following specification to estimate autocorrelated linear time trends for each areal unit:
| 3 |
where:
comes from the covariate component in (2) and represents the overall intercept parameter;
is the incremental intercept parameter for the i-th municipality;
is the overall slope parameter, with prior distribution ;
is the incremental slope parameter for the i-th municipality; and
is the average time.
According to41, the specification given in (3) is recommended if the aim of the analysis is to estimate which areas exhibit increasing or decreasing linear trends in the response over time. As a consequence of this formulation, each municipality i is allowed to have its own risk profile over time whose intercept is and whose trend is 46. In other words, the model gives the spatio-temporal pattern in the mean response with a spatially varying linear time trend.
Let be a symmetric non-negative neighborhood matrix, where represents the spatial closeness between municipalities. The diagonal elements of this matrix are equal to zero. The off-diagonal elements () receive the following binary specification: , if municipalities i and share a common border; and , otherwise. To ensure model identifiability, the elements of vectors and satisfy . Write and to denote the vectors and without their corresponding i-th entries, respectively. To complete the model41 specify the following prior distributions:
| 4 |
and
| 5 |
where:
and are spatial dependence (or auto-regression) parameters for the intercept () and slope () processes, respectively, which are specified with independent prior distributions over the unit interval [0, 1] so that zero corresponds to independence and one corresponds to strong spatial smoothness;
and are random effects variance parameters for the intercept () and slope () processes, respectively, which are specified with independent conjugate prior distributions.
The vector of observations is . The collection of parameters is , whose parameter space is . Since the density of the posterior distribution does not have a closed-form, one can use the Markov chain Monte Carlo (MCMC) algorithm to sample from this density. The correlated linear time trends model is officially implemented in the ST.CARlinear function of the R package CARBayesST41. Alternatively, one can fit this model using the Bcartime function of the R package bmstdr47. The hyperparameters , , a, b, , and are chosen to have flat prior distributions for all model parameters, which were specified as: , , , , , and .
Computational resources
All analyses were conducted using the R programming language (version 4.3.2)39, on a personal computer with the following configuration: (i) Processor: Intel Core i7-6500U CPU @ 2.50 GHz; (ii) Installed RAM: 16 GB; (iii) Operating system: Windows 10 64-bit.
Results and discussion
Spatial and temporal data visualization
In this section, we document temporal and spatial patterns in the number of fire spots in the whole Brazilian territory, per municipality (administrative region), and per biome (large region of vegetation and wildlife adapted to a specific climate). The temporal analysis was done by organizing the data in terms of daily observations, and the spatial analysis was done by considering all 5570 Brazilian municipalities. Table 2 shows the total number of fire spots in the Brazilian territory per year and its variation rate (i.e., the percentage change from one year to the next) compared with the previous year, and Fig. 2 depicts the total daily number of fire spots in the Brazilian territory between January 1, 2011, and December 31, 2022.
Table 2.
Total number of fire spots in the Brazilian territory per year, between January 1, 2011, and December 31, 2022, and its variation rate compared with the previous year.
| Year | Fire Spots | Variation Rate (%) |
|---|---|---|
| 2011 | 158,099 | – |
| 2012 | 217,238 | 37 |
| 2013 | 128,149 | − 41 |
| 2014 | 175,900 | 37 |
| 2015 | 216,782 | 23 |
| 2016 | 184,218 | − 15 |
| 2017 | 207,511 | 13 |
| 2018 | 132,872 | − 36 |
| 2019 | 197,632 | 49 |
| 2020 | 222,798 | 13 |
| 2021 | 184,081 | − 17 |
| 2022 | 200,763 | 9 |
Figure 2.

Daily number of fire spots in the Brazilian territory between January 1, 2011, and December 31, 2022.
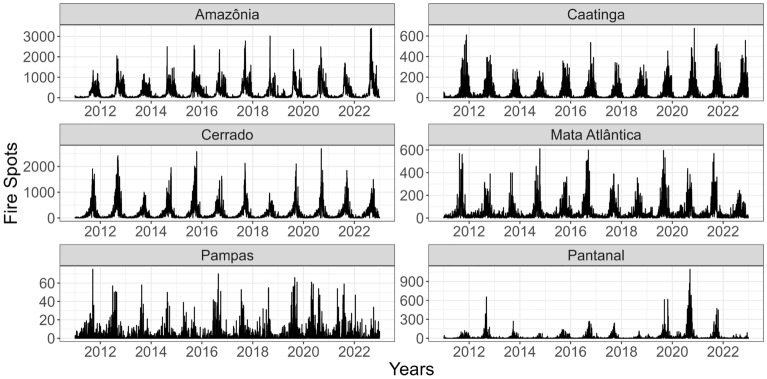
Figure 3 shows the total daily number of fire spots per biome between January 1, 2011, and December 31, 2022. A seasonal effect and an increase in fire spots are visible in several biomes for 2019 and 2020 compared with the years before, especially for Pantanal. When we look at the Amazônia, it is possible to notice that after a drop in 2021, a new rise in the number of fire spots is visible in 2022.
Figure 3.
Daily number of fire spots between January 1, 2011, and December 31, 2022, for each of the six biomes: Amazônia, Cerrado, Atlantic forest (Mata Atlântica), Caatinga, Pampa, and Pantanal, respectively.
Figure 4 shows the heat map with the total number of fire spots for each of the 5570 Brazilian municipalities per year, where we can see the temporal trend for each municipality. It is visible that Amazônia has been fustigated by forest fires year after year, and the Pantanal had an increase in the number of fire spots in 2019-2021.
Figure 4.
Heat map with the total number of fire spots per year for each of the 5570 Brazilian municipalities. The lines represent the borders of the Brazilian states. The plots were generated with the R software39.
Figure 5 shows the heat map with the monthly average number of fire spots for each of the 5570 municipalities between 2011 and 2022, i.e., the number of fire spots in a given municipality in a given month is the average of all fire spots in that municipality for that month using the 12 years available. The highest number of fire spots are observed in August, September, and October, with a significant incidence in the biomes of Amazônia, Pantanal, and parts of Cerrado.
Figure 5.
Heat map with the monthly average number of fire spots for each of the 5570 municipalities between 2011 and 2022. The lines represent the borders of the Brazilian states. The plots were generated with the R software39.
The temporal and spatial plots related to the meteorological variables and variables associated with the land-use transitions are available in the supplementary material. Figures S2–S5 show the monthly average for the meteorological variables precipitation, air temperature, humidity, and wind speed, respectively, between January 1, 2012, and December 31, 2021, for each Brazilian biome. The geographic locations of all Brazilian meteorological stations are depicted in Fig. S1 of the supplementary material.
Figure S6 of the supplementary material shows the evolution of land use and occupation by green areas (forests or non-forest natural formations) between January 1, 2011, and December 31, 2021, for each Brazilian municipality. The maps show the difference in the green area occupation between the years t and , for , in thousands of hectares (overall numbers per municipality). Figure S7 is similar to Figure S6, where the total number of hectares is weighted by the municipality’s area. In both plots, there is a predominance of red over green, representing a loss in the land occupation of green areas from one year to the next, being more extreme between 2019 and 2020, reaching the worst situation in 2021. Figures S8 and S9 are similar to Figures S6 and S7, respectively, being the heat maps obtained by considering the year 2011 as the reference. This allows a cumulative comparison with 2011 regarding land use and occupation by green areas.
Figure S10 shows the evolution of land use and occupation by farming between January 1, 2011, and December 31, 2021, for each Brazilian municipality. The maps show the difference in the green area occupation between the years t and , for , in thousands of hectares (overall numbers per municipality). Figure S11 is similar to Figure S10, where the total number of hectares is weighted by the municipality’s area. In both plots, there is a predominance of red color over green, representing a gain in the land occupation with farming from one year to the next, being more extreme between 2019 and 2020, reaching the worst situation in 2021. Figures S12 and S13 are similar to Figures S10 and S11, respectively, being the heat maps obtained by considering the year 2011 as the reference. This allows a cumulative comparison with the year 2011 regarding land use and occupation by farming.
Spatio-temporal modeling
Based on the data visualization results, and as expected, we noticed that the number of fire spots depends on time and space. In addition, we noted that the number of fire spots varies greatly per biome. Due to the heterogeneity among biomes, instead of simultaneously proposing a model for all Brazilian municipalities, we adjusted a statistical model per biome to model each municipality’s monthly totals of fire spots. Here, we work with a Bayesian spatio-temporal generalized linear mixed model proposed by41 and called correlated linear time trends model, which was reviewed in Subsection 2.4, as it is more suitable for count data and allows the inclusion of explanatory variables.
We worked with of the 5570 Brazilian municipalities in the spatio-temporal modeling, excluding two islands due to a limitation of the neighborhood matrix. This matrix requires non-zero rows, implying that each municipality needs at least one neighbor. Moreover, we considered months equally spaced in time (ten years, from 2012 to 2021).
Initially, the six models, one per biome, included all available explanatory variables: land-use transition (LUT), precipitation (PREC), temperature (TEMP), humidity (HUMID), and wind speed (WSPD). Due to the strong correlation among some atmospheric explanatory variables and the risk of having multicollinearity, we performed a selection of variables where only atmospheric explanatory variables most correlated with the response variable and least correlated with each other were considered in each model, one per biome. We consider the municipal area, expressed in hectares, as an offset (), which is sent to the six models on the log-scale. Writing in terms of (2), the six models, one for each biome, have the following structure:
| 6 |
We have data for months, corresponding to years. Let be the year. As the values are the same for the twelve months of each year of the study, we have:
| 7 |
We ran the MCMC algorithm 30,000 times to estimate the parameters of the models fitted for each biome, excluding the first 15,000 iterations (burn-in period) and taking samples from the posterior distribution every 15th iteration to reduce autocorrelation in the chains, which formed a sample of size 1,000 from the posterior distribution. Table 3 shows some statistics of model parameters for each biome. Firstly, note that the spatial dependence parameters ( and ) are significant for all models and present greater intensity in the models for the Pampas and Pantanal biomes. To assess the convergence of the chains, one can study the behavior of the trace plots and compute Geweke’s statistics. According to48, values for Geweke’s statistic must be between and 1.96 to indicate convergence. The results obtained for this statistic indicate convergence for all parameters of the six models. The acceptance rates for parameters and are equal to 100%, since their full conditional distributions are known due to the use of conjugate prior distributions. Table 4 shows the acceptance rates for the other parameters sampled by the Metropolis-Hastings algorithm for each model. Table 5 shows some fit criteria for each model.
Table 3.
Statistics of model parameters for each biome: posterior mean and its 95% credibility interval (CI), effective sample size (ESS), and Geweke’s statistic (GS).
| Parameters | Post. mean | 95% CI | ESS | GS |
|---|---|---|---|---|
| Amazônia | ||||
| − 7.6545 | (− 7.7199, − 7.5852) | 123.0 | − 0.5 | |
| − 0.0047 | (− 0.0050, − 0.0044) | 129.6 | 0.1 | |
| − 0.0622 | (− 0.0625, − 0.0619) | 112.9 | 0.5 | |
| 0.2169 | (0.2148, 0.2189) | 154.6 | 0.3 | |
| − 0.4174 | (− 0.4365, − 0.3982) | 635.1 | 0.1 | |
| 1.1985 | (1.0284, 1.4093) | 1000.0 | 0.5 | |
| 1.0287 | (0.8510, 1.2649) | 891.7 | − 0.2 | |
| 0.0211 | (0.0008, 0.0589) | 918.2 | 1.0 | |
| 0.0304 | (0.0018, 0.0847) | 696.3 | − 0.1 | |
| Caatinga | ||||
| − 6.4695 | (− 6.6459, − 6.3186) | 65.9 | − 0.6 | |
| 0.0913 | (0.0844, 0.0982) | 98.2 | 1.1 | |
| − 0.0895 | (− 0.0903, − 0.0886) | 82.3 | − 0.7 | |
| 0.1623 | (0.1574, 0.1676) | 67.2 | 0.9 | |
| 0.1723 | (0.1233, 0.2182) | 725.3 | − 0.7 | |
| 2.7714 | (2.4229, 3.2521) | 707.7 | − 1.2 | |
| 2.1794 | (1.8987, 2.5082) | 764.3 | 1.8 | |
| 0.0274 | (0.0021, 0.0674) | 615.4 | − 0.9 | |
| 0.0125 | (0.0004, 0.0407) | 878.6 | − 0.2 | |
| Cerrado | ||||
| − 2.7890 | (− 2.8374, − 2.7322) | 42.1 | 1.3 | |
| − 0.0153 | (− 0.0162, − 0.0142) | 102.2 | − 1.1 | |
| − 0.0794 | (− 0.0797, − 0.0792) | 101.8 | − 1.3 | |
| 0.0453 | (0.0432, 0.0470) | 43.5 | − 1.2 | |
| − 0.0768 | (− 0.0973, − 0.0566) | 825.3 | − 0.8 | |
| 0.9776 | (0.8884, 1.0986) | 1000.0 | 1.1 | |
| 1.1143 | (0.9938, 1.2770) | 654.2 | 0.2 | |
| 0.0103 | (0.0003, 0.0318) | 1000.0 | − 0.1 | |
| 0.0150 | (0.0008, 0.0444) | 621.5 | 0.4 | |
| Mata Atlântica | ||||
| 2.8770 | (2.8061, 2.9537) | 241.2 | − 0.6 | |
| − 0.0300 | (− 0.0397, − 0.0199) | 147.3 | − 1.8 | |
| − 0.1093 | (− 0.1101, − 0.1085) | 166.4 | 0.2 | |
| − 0.1217 | (− 0.1236, − 0.1198) | 276.7 | 0.8 | |
| 0.0766 | (0.0465, 0.1073) | 813.4 | 1.4 | |
| 1.3385 | (1.2488, 1.4441) | 1000.0 | − 0.3 | |
| 1.8315 | (1.6782, 2.0320) | 659.1 | − 0.2 | |
| 0.0068 | (0.0002, 0.0190) | 883.1 | − 0.5 | |
| 0.0088 | (0.0003, 0.0284) | 628.4 | 1.0 | |
| Pampas | ||||
| 0.8876 | (0.5054, 1.2512) | 231.0 | − 0.9 | |
| − 0.0368 | (− 0.0669, − 0.0028) | 56.7 | 0.9 | |
| − 0.0781 | (− 0.0822, − 0.0742) | 260.0 | 0.8 | |
| − 0.1848 | (− 0.1916, − 0.1782) | 309.3 | 0.5 | |
| 0.3151 | (0.1900, 0.4365) | 742.5 | 0.6 | |
| 3.1092 | (2.4505, 3.9517) | 1000.0 | 0.2 | |
| 2.0882 | (1.3573, 3.1047) | 536.2 | − 0.8 | |
| 0.7711 | (0.5771, 0.9351) | 1000.0 | − 0.2 | |
| 0.4752 | (0.1784, 0.7932) | 446.5 | 0.0 | |
| Pantanal | ||||
| − 0.7567 | (− 0.9013, − 0.6131) | 321.0 | − 0.3 | |
| − 0.0225 | (− 0.0239, − 0.0213) | 202.2 | − 0.4 | |
| − 0.1028 | (− 0.1039, − 0.1018) | 174.6 | 1.6 | |
| 0.0292 | (0.0246, 0.0334) | 355.0 | − 0.6 | |
| 0.6831 | (0.6004, 0.7604) | 637.1 | − 1.2 | |
| 0.8953 | (0.4185, 1.8148) | 861.1 | − 0.1 | |
| 1.0254 | (0.4856, 2.1762) | 1000.0 | − 0.7 | |
| 0.1935 | (0.0052, 0.6162) | 1000.0 | − 0.6 | |
| 0.0846 | (0.0014, 0.3809) | 802.6 | − 1.8 | |
Table 4.
Acceptance rate (%) of model parameters per biome sampled from the posterior distribution using the Metropolis-Hastings algorithm.
| Biome | ||||||
|---|---|---|---|---|---|---|
| Amazônia | 42.3 | 34.8 | 41.9 | 41.3 | 40.2 | 43.8 |
| Caatinga | 41.6 | 39.4 | 48.8 | 49.5 | 43.1 | 46.7 |
| Cerrado | 40.2 | 36.1 | 41.4 | 48.0 | 48.3 | 39.0 |
| Mata Atlântica | 46.1 | 36.2 | 49.4 | 48.5 | 44.7 | 42.2 |
| Pampas | 43.2 | 36.1 | 48.1 | 47.9 | 41.4 | 46.0 |
| Pantanal | 44.5 | 33.6 | 43.0 | 44.4 | 49.3 | 56.3 |
Table 5.
Fit criteria for each model by biome. DIC abbreviates Deviance Information Criterion, is the estimated effective number of parameters, LMPL abbreviates Log Marginal Predictive Likelihood, WAIC abbreviates Watanabe-Akaike Information Criterion, is the estimated number of effective parameters, and is the natural logarithm of the likelihood function.
| Biome | DIC | WAIC | LMPL | |||
|---|---|---|---|---|---|---|
| Amazônia | 1552262.9 | 1118.6 | 1592961.6 | 57088.9 | − 774444.7 | − 775012.9 |
| Caatinga | 438833.0 | 2095.7 | 457118.5 | 20618.2 | − 223568.7 | − 217320.8 |
| Cerrado | 1158941.8 | 2710.8 | 1201742.8 | 43203.9 | − 591431.2 | − 576760.1 |
| Mata Atlântica | 595699.2 | 4967.3 | 609729.8 | 17140.3 | − 304474.6 | − 292882.3 |
| Pampas | 36530.4 | 336.3 | 37068.5 | 822.1 | − 18535.4 | − 17928.9 |
| Pantanal | 87130.4 | 103.4 | 118373.9 | 22646.5 | − 43433.6 | − 43461.8 |
Let be the -th column of the design matrix , . The effect of variable on the number of fire spots is quantified as relative risk, for a fixed increase in the value of this variable49 recommends using to represent a realistic increase in the current value , where is the sample standard deviation of covariate . According to41 and exponentiating (2), the relative risk for an increase in variable is calculated by
| 8 |
We compute to estimate the relative risk given in Equation (8), where is the posterior median of . Table 6 shows the relative risks for each model by variable. An increase of one standard deviation unit in the current value of decreases the risk of fire spots by 45.1% in the Amazônia, 68.0% in the Caatinga, 62.0% in the Cerrado, 61.4% in the Mata Atlântica, 39.9% in the Pampas, and 67.4% in the Pantanal. On the other hand, an increase of one standard deviation unit in the current value of increases the risk of fire spots by 34.9% in the Amazônia, 47.4% in the Caatinga, 14.4% in the Cerrado, and 6.7% in the Pantanal. An increase of one standard deviation unit in reduced the risk of fire outbreaks by 35.7% in the Mata Atlântica, and 51.1% in the Pampas, which may be related to the increase in the number of fire outbreaks due to the fall in relative air humidity during winter50. Although the value one is outside the 95% CI of the relative risk of , the effect of adding one standard deviation unit on this variable is low in all models.
Table 6.
Sample standard deviation (SD), posterior median of relative risk (RR) and 95% credible interval (CI) for RR, per variable of each model.
| Biome | Variable | SD | RR | 95% CI |
|---|---|---|---|---|
| Amazônia | LUT | 7.6397 | 0.965 | (0.9623, 0.9673) |
| HUMID | 9.6260 | 0.549 | (0.5477, 0.5509) | |
| TEMP | 1.3804 | 1.349 | (1.3452, 1.3527) | |
| Caatinga | LUT | 1.2516 | 1.121 | (1.1114, 1.1307) |
| HUMID | 12.7339 | 0.320 | (0.3165, 0.3237) | |
| TEMP | 2.3890 | 1.474 | (1.4564, 1.4923) | |
| Cerrado | LUT | 2.3065 | 0.965 | (0.9633, 0.9678) |
| HUMID | 12.1639 | 0.380 | (0.3792, 0.3818) | |
| TEMP | 2.9749 | 1.144 | (1.1372, 1.1500) | |
| Mata Atlântica | LUT | 0.8465 | 0.975 | (0.9669, 0.9833) |
| HUMID | 8.7139 | 0.386 | (0.3832, 0.3884) | |
| TEMP | 3.6243 | 0.643 | (0.6390, 0.6477) | |
| Pampas | LUT | 1.9251 | 0.930 | (0.8791, 0.9946) |
| HUMID | 6.5237 | 0.601 | (0.5850, 0.6163) | |
| TEMP | 3.8678 | 0.489 | (0.4767, 0.5019) | |
| Pantanal | LUT | 9.8376 | 0.801 | (0.7906, 0.8111) |
| HUMID | 10.9043 | 0.326 | (0.3221, 0.3297) | |
| TEMP | 2.2285 | 1.067 | (1.0563, 1.0773) |
Let be a collection of K MCMC samples of the posterior distribution. Since , the (i, t)-th predicted value based on the k-th MCMC sample is calculated as:
| 9 |
Using (9), some summary statistics can be calculated. For instance, the posterior mean of the (i, t)-th predicted value is . In addition, one can consider the temporally varying values, aggregated over all municipalities, to quantify changes in temporal trends. Based on47, in Fig. 6 we evaluate the average observed values and the average fitted values over time for each model. Based on the “peaks” of each of the subfigures, it is noted that most biomes show an increase in the number of fire spots in 2020–2021 compared to 2018–2019. Attention is focused on the totals observed in the Amazônia biome and, mainly, in the Pantanal biome.
Figure 6.
Observed and fitted average number of fire spots, per model. Observed values are represented by black dots, fitted values are represented by the solid blue line, and 95% CI are represented by dashed red lines. The plots were generated with the R software39.
The incremental slope parameter is also called the “differential trend of the i-th areal unit”, , which is the interaction between the time effect and the municipality effect. According to the interpretation given by46, it is known that is negative (positive, respectively) when the temporal trend of the municipality i is less steep (steeper, respectively) than the mean trend . In this work, we say that is null if zero is contained within its 95% credible interval. Figure 7 shows the municipalities where is positive, null or negative by biome, which can be useful especially in Amazônia, Cerrado, and Pantanal biomes, since they are related to high total fire spots.
Figure 7.
Heat maps with the sign of the incremental slope parameter relative to the i-th Brazilian municipality by biome, being null if zero is contained within its 95% credible interval. The plots were generated with the R software39. The limits of the municipalities belonging to the Mata Atlântica biome were removed to allow better visualization, given their small sizes.
To assess whether the model adequately captures the structure and variability of the observed data, a residual analysis of the model and the Posterior Predictive Checks (PPC) can be performed.
The (i, t)-th “raw” residual is defined as . Specifically for Poisson models, the (i, t)-th Pearson residual is . To obtain the spatial Pearson residual for each municipality i, aggregated across all time periods47, suggests to compute . The spatial residuals shown in Fig. 8 indicate good fit for the six models.
Figure 8.
Heat maps with the spatial Pearson residuals for Brazilian municipalities, per model. The plots were generated with the R software39. The limits of the municipalities belonging to the Mata Atlântica biome were removed to allow better visualization, given their small sizes.
Define . PPC involves simulating data from the posterior predictive distribution and comparing the simulated data to the observed data. If the resulting distributions are similar, it indicates that the model in use is capturing the underlying distribution of the data and is therefore considered valid. Under the conditional independence assumption, is given by:
| 10 |
Since the integral that appears in (10) is not analytically tractable, one may use Monte Carlo methods to approximate it in two steps. For each municipality , time and MCMC sample , firstly compute using (9) and then generate from the distribution. Working with counts, PPC consists of comparing the relative frequencies of (observed data) with those of (simulated data). Figure 9 shows that the differences between the relative frequencies of observed data and simulated data in all models are small, indicating that the adjustments are adequate.
Figure 9.
Relative frequencies of observed data and simulated data from the posterior predictive distribution, for all six models. The plots were generated with the R software39.
Concluding remarks
This paper explores and models the behavior of the number of fire spots in the whole Brazilian territory between January 1, 2011, and December 31, 2022, considering meteorological variables (precipitation, air temperature, humidity, and wind speed) and a human variable (land-use transition) as covariates.
In the descriptive analysis, we found out that the number of fire spots has a seasonal pattern and has been increasing in the last years of our study, particularly in 2019 and 2020 (Figs. 2, 3 and 4), with the Pantanal biome showing the most important increase in the number of fire spots in the years 2020–2021 (Fig. 3). The most affected biomes are Amazônia, Cerrado, and Pantanal (Figs. 3 and 4), having the state of Pará the highest concentration in the number of fire spots (Figs. 4 and 5). The highest incidence of fire spots is in August, September, and October (Fig. 5).
Concerning land-use and occupation behavior by green areas (forests or non-forest natural formations) between 2011 and 2021, a loss is observed from one year to the next, more extreme between 2020 and 2021 (Figs. S6 and S7). An opposite trend was observed for land use and occupation by farming, with a gain in land occupation from one year to the next, being more extreme between 2020 and 2021 (Figs. S10 and S11).
The spatio-temporal modeling (Table 3) showed that the meteorological variables humidity and air temperature significantly impacted the number of fire spots for each of the six Brazilian biomes. Although the value one is outside the 95% CI of the relative risk of land use transition (Table 6), the effect of adding one standard deviation unit on this variable is low in all models. A limitation of this class of models is that it cannot consider overdispersion and zero-inflated data.
Our research significantly advances wildfire analysis in Brazil by focusing on studying fire spot dynamics. Firstly, our national-scale analysis spanning twelve years goes beyond localized studies, providing a broader understanding of fire spot patterns. Secondly, by integrating meteorological variables and human-induced land-use transitions, we reveal the complex drivers of fire spots. Thirdly, our methodological rigor, including Bayesian inference, enhances the reliability of our findings. Lastly, our study offers practical implications for wildfire management, guiding proactive strategies. These contributions deepen our understanding of wildfire dynamics and provide valuable stakeholder insights.
The strategies and approach proposed in this paper are of great generality and can be applied to study and understand the behavior of similar data sets in other world regions and in different fields of application where the data has a similar structure.
Besides a comparative analysis with other spatiotemporal models, future research should focus on forecasting wildfire fire spots to provide insights for proactive wildfire management and mitigation strategies. Examining the effects of different land management practices on fire frequency and intensity could offer practical recommendations for reducing wildfire risks. These studies could explore how variations in agricultural practices, reforestation efforts, and urban development influence wildfire dynamics across diverse biomes. Moreover, it is essential to continue monitoring wildfire fire spots’ spatial and temporal dynamics, particularly in the context of climate change and evolving land-use patterns. Longitudinal studies are needed to assess the long-term impact of land management practices on fire frequency and intensity.
Supplementary Information
Author contributions
P.C.R. designed the study. J.P. and R.B. performed the analysis. P.C.R., J.P., and R.B. interpreted the results. J.P. prepared the figures. P.C.R., J.P., and R.B. prepared the manuscript. P.C.R. and J.P. prepared the supplementary information. P.C.R. coordinated and supervised the project. P.C.R., J.P., and R.B. participated in the writing of the manuscript.
Data availability
All data generated and analyzed during this study are included in this published article and its supplementary information files and available at https://github.com/SaLLy-laboratory/Brazilian-wildfires.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Jonatha Sousa Pimentel, Rodrigo S Bulhões and Paulo Canas Rodrigues.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-70082-6.
References
- 1.Marasini, J. B. Plantas alimentícias não convencionais em Urubici, SC. (2018).
- 2.Lemos, A. L. F. & Silva, J. D. A. Desmatamento na Amazônia Legal: Evolução, causas, monitoramento e possibilidades de mitigação através do Fundo Amazônia. Floresta e Ambiente18, 98–108 (2024). 10.4322/floram.2011.027 [DOI] [Google Scholar]
- 3.Noutcheu, R., Oliveira, F. M., Wirth, R., Tabarelli, M., & Leal, I. R. (2024). Chronic human disturbance and environmental forces drive the regeneration mechanisms of a Caatinga dry tropical forest. Persp. Ecol. Conser.
- 4.Hidasi-Neto, J., Gomes, N. M. A. & Pinto, N. S. A vegetação nativa do Cerrado é um refúgio para as aves na trajetória atual da mudança climática. Austral Ecol.49(1), e13336 (2024). 10.1111/aec.13336 [DOI] [Google Scholar]
- 5.Gonçalves, A. D. S. Arquivos pessoais de cientistas e conservacionistas: A experiência do Instituto Nacional da Mata Atlântica (INMA). Estudos Históricos (Rio de Janeiro)36, 5–22 (2023). 10.1590/s2178-149420230202 [DOI] [Google Scholar]
- 6.Pires, M. M., Pallaoro, R. B. & Périco, E. Environmental changes in a key region of the Pampa: A quantitative analysis of land use in the ibirapuitã environmental protection area (Rio Grande do Sul) and surroundings. Revista de Gestão Social e Ambiental18(1), e04234–e04234 (2024). 10.24857/rgsa.v18n1-012 [DOI] [Google Scholar]
- 7.Novais, J. W. Z. et al. Modelagem do Fluxo de Calor no Solo em Área de Pastagem no Pantanal Mato-Grossense. Revista Brasileira de Geografia Física17(1), 564–579 (2024). 10.26848/rbgf.v17.1.p564-579 [DOI] [Google Scholar]
- 8.IBGE, Biomas Brasileiros - IBGE Educa Jovens. Avaliable in https://bit.ly/3snoveu. Accessed in: March 12, 2023.
- 9.Eugenio, F. C. et al. Causal, temporal and spatial statistics of wildfires in areas of planted forests in Brazil. Agricultural and Forest Meteorology266, 157–172 (2019).
- 10.Kganyago, M. & Shikwambana, L. Assessment of the characteristics of recent major wildfires in the USA, Australia and Brazil in 2018–2019 using multi-source satellite products. Remote Sens.12(11), 1803 (2020). 10.3390/rs12111803 [DOI] [Google Scholar]
- 11.Bonilla-Aldana, D. K. et al. Brazil burning! What is the potential impact of the Amazon wildfires on vector-borne and zoonotic emerging diseases?-A statement from an international experts meeting. Travel Med. Infect. Dis.31, 101474–101474 (2019). [DOI] [PubMed]
- 12.Aragão, L. E. O. C. et al. 21st Century drought-related fires counteract the decline of Amazon deforestation carbon emissions. Nat. Commun.9, 536 (2018). 10.1038/s41467-017-02771-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Caúla, R. H. et al. to 2011.”. Environ. Earth Sci.74(2015), 1497–1508 (1998).
- 14.Silva Junior, C. A., et al. Persistent fire foci in all biomes undermine the Paris Agreement in Brazil. Sci. Rep.10, 16246 (2020). [DOI] [PMC free article] [PubMed]
- 15.de Oliveira-Junior, J. F., et al. Fire foci related to rainfall and biomes of the state of Mato Grosso do Sul, Brazil. Agric. Forest Meteorol.282, 107861 (2020).
- 16.Williams, A. P. et al. Observed impacts of anthropogenic climate change on wildfire in California. Earth’s Future7(8), 892–910 (2019). 10.1029/2019EF001210 [DOI] [Google Scholar]
- 17.Dupuy, J. L. et al. Climate change impact on future wildfire danger and activity in southern Europe: a review. Annal. For. Sci.77(2), 1–24 (2020).
- 18.Clarke, H., Cirulis, B., Borchers-Arriagada, N., Bradstock, R., Price, O., & Penman, T. (2023). Health costs of wildfire smoke to rise under climate change. NPJ Clim. Atmos. Sci.6(1), 102.
- 19.Shukla, J., Nobre, C. & Sellers, P. Amazon deforestation and climate change. Science247(4948), 1322–1325 (1990). 10.1126/science.247.4948.1322 [DOI] [PubMed] [Google Scholar]
- 20.Werth, D., & Avissar, R. The local and global effects of Amazon deforestation. J. Geophys. Res. Atmos.107(D20), LBA-55 (2002).
- 21.Ometto, J. P., Aguiar, A. P. D. & Martinelli, L. A. Amazon deforestation in Brazil: Effects, drivers and challenges. Carbon Manag.2(5), 575–585 (2011). 10.4155/cmt.11.48 [DOI] [Google Scholar]
- 22.Ellwanger, J. H., Kulmann-Leal, B., Kaminski, V. L., Valverde-Villegas, J. A. C. Q. U. E. L. I. N. E., VEIGA, A. B. G., Spilki, F. R., Chies, J. A. B. (2020). Beyond diversity loss and climate change: Impacts of Amazon deforestation on infectious diseases and public health. Anais da Academia Brasileira de Ciências92. [DOI] [PubMed]
- 23.Martins, P. I., Belém, L. B. C., Szabo, J. K., Libonati, R. & Garcia, L. C. Prioritising areas for wildfire prevention and post-fire restoration in the Brazilian Pantanal. Ecol. Eng.176, 106517 (2022). 10.1016/j.ecoleng.2021.106517 [DOI] [Google Scholar]
- 24.Libonati, R., DaCamara, C. C., Peres, L. F., Sander de Carvalho, L. A. & Garcia, L. C. Rescue Brazil’s burning Pantanal wetlands. Nature588(7837), 217–219 (2020). 10.1038/d41586-020-03464-1 [DOI] [PubMed] [Google Scholar]
- 25.Leal Filho, W., Azeiteiro, U. M., Salvia, A. L., Fritzen, B. & Libonati, R. Fire in Paradise: Why the Pantanal is burning. Environ. Sci. Policy123, 31–34 (2021). 10.1016/j.envsci.2021.05.005 [DOI] [Google Scholar]
- 26.Wang, D. et al. Economic footprint of California wildfires in 2018. Nat. Sustain.3, 252–260 (2021). [Google Scholar]
- 27.Garcia, L. C. et al. Record-breaking wildfires in the world’s largest continuous tropical wetland: Integrative fire management is urgently needed for both biodiversity and humans. J. Environ. Manag.293, 112870 (2021). [DOI] [PubMed]
- 28.Schumacher, V. et al. Characteristics of lightning-caused wildfires in central Brazil in relation to cloud-ground and dry lightning. Agric. For. Meteorol.312, 108723 (2022). 10.1016/j.agrformet.2021.108723 [DOI] [Google Scholar]
- 29.Ivo, I. O., Biudes, M. S., Vourlitis, G. L., Machado, N. G. & Martim, C. C. Effect of fires on biophysical parameters, energy balance and evapotranspiration in a protected area in the Brazilian Cerrado. Remote Sens. Appl. Soc. Environ.19, 100342 (2020). [Google Scholar]
- 30.Santos, F. L. et al. Prescribed burning reduces large, high-intensity wildfires and emissions in the Brazilian savanna. Fire4(3), 56 (2021). 10.3390/fire4030056 [DOI] [Google Scholar]
- 31.Pinheiro, A. C. & Rodrigues, P. C. Hierarchical time series forecasting of fire spots in Brazil: A comprehensive approach. Stats7(3), 647–670 (2024). 10.3390/stats7030039 [DOI] [Google Scholar]
- 32.Kuschnig, N., Cuaresma, J. C., Krisztin, T. & Giljum, S. Spatial spillover effects from agriculture drive deforestation in Mato Grosso, Brazil. Sci. Rep.11(1), 21804 (2021). 10.1038/s41598-021-00861-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Matricardi, E. A. T. et al. Long-term forest degradation surpasses deforestation in the Brazilian Amazon. Science369(6509), 1378–1382 (2020). 10.1126/science.abb3021 [DOI] [PubMed] [Google Scholar]
- 34.Brando, P. M., Soares-Filho, B., Rodrigues, L., Assunção, A., Morton, D., Tuchschneider, D., Coe, M. T. (2020). The gathering firestorm in southern Amazonia. Sci. Adv.6(2), eaay1632. [DOI] [PMC free article] [PubMed]
- 35.Tyukavina, A. et al. Types and rates of forest disturbance in Brazilian Legal Amazon, 2000–2013. Sci. Adv.3(4), e1601047 (2017). 10.1126/sciadv.1601047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Programa Queimadas do INPE. Avaliable in http://bit.ly/3wBUSeM. Accessed in: February 25, 2024.
- 37.MapBiomas Project–Collection 7 of the Annual Series of Land Cover and Use Maps of Brazil, accessed on 10 December 2022 through the link: http://mapbiomas.org/.
- 38.Moritz, S. & Bartz-Beielstein, T. imputeTS: Time series missing value imputation in R. R J.9(1), 207 (2017). 10.32614/RJ-2017-009 [DOI] [Google Scholar]
- 39.R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria (2023). https://www.R-project.org/.
- 40.Banerjee, Sudipto, Bradley P. Carlin, & Alan E. Gelfand. Hierarchical Modeling and Analysis for Spatial Data. Chapman and Hall/CRC (2003).
- 41.Lee, D., Rushworth, A. & Napier, G. Spatio-temporal areal unit modeling in R with conditional autoregressive priors using the CARBayesST package. J. Stat. Softw.84, 1–39 (2018).30450020 10.18637/jss.v084.i09 [DOI] [Google Scholar]
- 42.Salan, M. S. A. et al. Measuring the impact of climate change on potato production in Bangladesh using Bayesian Hierarchical Spatial-temporal modeling. PLoS ONE17, e0277933 (2022). 10.1371/journal.pone.0277933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lubinda, J., Haque, U., Bi, Y., Hamainza, B., & Moore, A. J. (2021). Near-term climate change impacts on sub-national malaria transmission. Sci. Rep.11. [DOI] [PMC free article] [PubMed]
- 44.Bravo, M. A. et al. Where is air quality improving, and who benefits? A study of PM2.5 and ozone over 15 years. Am. J. Epidemiol.191, 1258–1269 (2022). 10.1093/aje/kwac059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Galarza, C. R. C. et al. Bayesian spatio-temporal modeling of the dynamics of COVID-19 deaths in Peru. Entropy26(6), 474 (2024). 10.3390/e26060474 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Bernardinelli, L. et al. Bayesian analysis of space’time variation in disease risk. Stat. Med.14(21–22), 2433–2443 (1995). 10.1002/sim.4780142112 [DOI] [PubMed] [Google Scholar]
- 47.Sahu, S. Bayesian Modeling of Spatio-Temporal Data with R. (Chapman and Hall/CRC, 2022).
- 48.Geweke, J. Evaluating the accuracy of sampling-based approaches to the calculation of posterior moments. Staff Report 148, Federal Reserve Bank of Minneapolis (1991).
- 49.Lee, D. A tutorial on spatio-temporal disease risk modelling in R using Markov chain Monte Carlo simulation and the CARBayesST package. Spatial Spatio-temporal Epidemiol.34, 100353 (2020). 10.1016/j.sste.2020.100353 [DOI] [PubMed] [Google Scholar]
- 50.Desmatamento nos Biomas do Brasil Cresceu 22.3% em 2022, Mapbiomas. Avaliable in https://bit.ly/3XqfO3r. Acessed in: June 10, 2024.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data generated and analyzed during this study are included in this published article and its supplementary information files and available at https://github.com/SaLLy-laboratory/Brazilian-wildfires.