Abstract
Background and purpose
Monte Carlo (MC) based dose calculations are widely used in radiotherapy with a low statistical uncertainty, being accurate but slow. Increasing the uncertainty accelerates the calculation, but reduces quality. In online adaptive planning, however, dose is recalculated every treatment fraction, potentially decreasing the cumulative calculation error. This study aimed to evaluate the effect of higher MC statistical uncertainty in the context of daily online plan adaptation.
Materials and methods
For twenty prostate cancer patients, daily plans were simulated for 5 fractions and three modes of variation: rigid whole body translations, local-rigid prostate translations and local-rigid prostate rotations. For each mode and fraction, adaptive plans were generated from a clinical reference plan using three MC uncertainty values: 1 % (standard), 2 % and 3 % per plan. Dose-volume criteria were evaluated for accumulated doses, checking plan acceptability and comparing higher uncertainty plans to the standard.
Results
Increasing the statistical uncertainty setting from 1 % to 2–3 % caused an accumulated median target D98% reduction of 0.1 Gy, with interquartile ranges (IQRs) up to 0.12 Gy. Rectum V35Gy increased in median up to 0.16 cm3 with IQRs up to 0.33 cm3. The bladder V28Gy and V32Gy showed median increases up to 0.24 %-point, with IQRs up to 0.54 %-point. Using 2 % uncertainty reduced calculation times by more than a minute for all modes of variation, with no further time gain when increasing to 3 %.
Conclusion
A 2–3 % MC statistical uncertainty was clinically feasible. Using a 2 % uncertainty setting reduced calculation times at the cost of limited relative dose-volume differences.
1. Introduction
Dose calculation based on Monte Carlo (MC) simulations is considered the most accurate for radiotherapy treatments [1], [2], [3]. Treatment planning systems based on such dose engines use a pre-set (user-defined) uncertainty to effectively determine the number of particle histories to be calculated in the dose calculation or to determine when to stop the simulation. A lower uncertainty runs more particle histories, leading to a more accurate dose distribution but also longer calculation times [4], [5], [6].
In daily online plan adaptation, the plan is adjusted to the daily patient position and anatomy just prior to delivery of the treatment. In a typical workflow, a scan is made, the target and healthy tissues are re-delineated, and the plan is re-optimized on the new anatomy [7], [8], [9], [10], [11], [12], [13], [14]. To minimize intrafraction motion, and maximize treatment slot and staff utilization, this process should be performed as fast as possible.
In current clinical practice, a Monte Carlo statistical uncertainty setting of 1–2 % per plan is commonly used, both in the generation of the reference plan, and for the online adaptation. Using a higher uncertainty will speed up daily plan adaptation, at the cost of daily plan quality. However, due to the random nature of the uncertainty introduced, deterioration of quality of the full treatment plan delivered over multiple fractions might be limited. Extensive research has been done into the accuracy of Monte Carlo dose calculations and the effect of its statistical uncertainties on qualitative evaluation of treatment plans [3], [4], [5], [6], [15], [16], [17], [18]. To our knowledge, no literature however yet exists on any systematic effect of the statistical uncertainty setting when considering daily online adaptive workflows including dose accumulation.
The aim of this study was to evaluate the effect of different Monte Carlo statistical uncertainty settings on the accumulated dose of fractionated treatments. In particular, for fractionated treatments using online adaptive planning, the noise due to a high MC uncertainty may average out over the full treatment. To this end we compared daily adapted plans generated using different values of Monte Carlo uncertainty, and evaluated the differences between the accumulated dose distributions.
2. Materials and methods
2.1. Patient data, treatment volumes and dose prescription
Data of twenty prostate cancer patients who were treated on the Unity 1.5 T MR-Linac were included in this study. For all patients one planning computed tomography (CT) scan and five T2-weighted daily magnetic resonance imaging (MRI) scans were acquired during the course of the treatment. For this study the planning CT scans were used to simulate online adaptations. Approval from the institutional review board was obtained (approval number IRBd20-008).
All plans in this study were generated in the Monaco Treatment Planning System (TPS) (Elekta AB, Stockholm, Sweden, research version 5.59.11a), which uses the GPUMCD algorithm for Monte Carlo dose calculations. The clinically used reference plans prescribing 5 × 7.25 Gy, optimized for the planning scans by expert planners were re-optimized in this version as well, using the same optimization objectives as the clinical reference plan. Reference plans were all optimized using a Monte Carlo uncertainty of 1 % per plan.
2.2. Daily adaptation, Monte Carlo uncertainty settings and daily variations
The Unity MR-Linac allows for an adapt-to-shape (ATS) workflow for daily plan adaptation [13], [14], [19], [20], [21]. This workflow takes the optimization objectives used in a patient-specific reference plan and uses these to optimize a new plan on the daily scan.
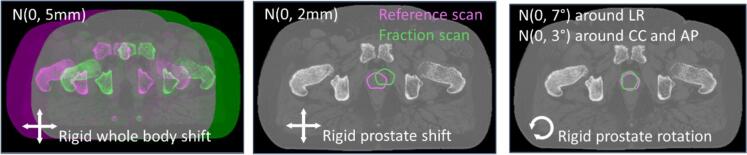
To investigate the effect of daily plan adaptations, we simulated three modes of variations for each patient, as schematically shown in Fig. 1. First, to simulate the effect of setup errors, we sampled five (one for each fraction) rigid whole body shifts from a normal distribution with mean 0 and Standard Deviation (SD) = 5 mm isotropic for each patient. Second, five rigid prostate shifts were sampled per patient from a normal distribution with mean 0 and SD = 2 mm isotropic. The planning scans were deformed using an in-house tool, translating the prostate and gradually changing the anatomy in a surrounding ring to match the outer anatomy [22]. Third, prostate rotations were sampled from a normal distribution with mean 0 and SD = 7° around the Left-Right axis, and from a normal distribution with mean 0 and SD = 3° around the other axes. Using the same in-house tool [22], the planning scans were now adjusted by rotating the prostate and gradually changing the anatomy in a surrounding ring of up to 2 cm to match the outer anatomy.
Fig. 1.
A schematic of the three modes of simulated variation. For visibility, all simulated variations are exaggerated.
For each mode of variation we thus obtained five (one per fraction) simulated daily scans with delineations for each patient. To run the dose calculation, the structures on these daily scans were assigned relative electron densities equal to their average electron density on the planning CT.
We evaluated three MC uncertainty settings: 1 % (the clinical value), 2 %, and 3 % per plan. For simplicity we will refer to these settings from here on as MC1, MC2 and MC3, respectively. For each simulated daily scan, we applied the ATS workflow in Monaco to yield daily plans, optimized and calculated using all three MC uncertainty settings. To ensure fair comparisons, no tweaking was done on the optimization objectives in the ATS workflow [23].
As was used in the clinical treatments, dose calculation gridsizes were kept at 3 × 3 × 3 mm3 throughout all simulations. To achieve a fair comparison, the dose of all plans optimized with a MC setting >1 % was afterwards recalculated using a 1 % uncertainty setting. Recalculated MC2 and MC3 plans will be referred to as MC2R and MC3R plans.
To evaluate the effect of the applied MC uncertainty setting on the whole treatment, for each daily variations mode, for each MC setting, the five fraction plans were transformed back to the planning scan, on which the dose was accumulated. For each MC value, for each mode of variation, we had a total of 100 daily plans and 20 accumulated doses.
2.3. Evaluation of the planning methods
According to institutional protocol, an adapted plan was deemed clinically acceptable when the planning target volume (PTV) D2% and D98% values were at most 0.5 Gy worse than the reference plan values. For the organs at risk (OARs, here the rectum and the bladder) the clinical dose-volume criteria for daily adaptation were identical to the reference plan criteria.
Two types of evaluation were performed. Firstly for plan acceptability, the dose-volume criteria were evaluated for each daily plan to check for clinical acceptability (Table S1 in the Supplementary Materials). This would be the evaluation which is performed on the day of treatment. The accumulated dose distribution over the whole treatment was also evaluated against the same criteria. Secondly a comparison to the clinical standard was performed. For plans generated using MC2R and MC3R, the obtained dose-volume values were compared to those values from the corresponding MC1 plan. This comparison was done both per treatment fraction and on the accumulated dose, in terms of median differences and interquartile ranges (IQRs). All differences were obtained in the respective units of the criteria (e.g. Gy, cm3 or %-point, see Table S1 in the Supplementary Materials).
For all Monte Carlo uncertainty values, the duration of the optimization and recalculation steps were recorded. All simulations were performed on a dual Intel Xeon Gold 6132 server with 128 GB RAM. All dose calculations were done on a single NVIDIA GeForce RTX 2080 Ti GPU with 11 GB GDDR6-memory.
2.4. Statistical analysis
Differences between the individual fraction dose distributions using MC1 and MC2R or MC3R were tested for statistical significance using the Wilcoxon signed-rank test for clustered data with significance level α = 0.05 [24], [25]. For the differences between the accumulated dose distributions, statistical significance was tested using the Wilcoxon signed-rank test with significance level α = 0.05.
3. Results
3.1. Daily plans – Plan acceptability
For all modes of anatomical variation, plans optimized using MC1 yield acceptable PTV coverage in ≥97 % of the plans over the modes of variations (Table 1). Increasing to MC2 and MC3 yielded acceptable PTV coverage in ≥93 % of the plans. For MC2R and MC3R, PTV acceptability decreased slightly, but remained ≥94 % when dealing with whole body shifts and prostate translations, and ≥87 % when dealing with prostate rotations. The overall plan acceptability was mostly affected by the OAR criteria, with the rectum V35Gy being the most limiting.
Table 1.
The number of daily plans meeting the different dosimetric criteria. MC1, MC2, and MC3 are the plans obtained directly through optimization using 1%, 2% and 3% MC uncertainty per plan respectively. MC2R and MC3R are the plans optimized using 2% or 3% uncertainty per plan, and subsequently recalculated using a 1% MC uncertainty per plan. Between parentheses the number of patients for whom all fractions meet the criteria is provided. In total there are 100 daily plans per MC uncertainty value and daily mode of variation and 20 patients.
| 100 daily plans (20 patients) | MC1 | MC2 | MC2R | MC3 | MC3R | |
|---|---|---|---|---|---|---|
| Whole body shift | PTV D98% | 98 (18) |
98 (19) |
97 (18) |
99 (19) |
95 (16) |
| PTV D2% | 100 (20) |
100 (20) |
100 (20) |
100 (20) |
100 (20) |
|
| OARs | 90 (17) |
80 (12) |
80 (12) |
83 (14) |
83 (14) |
|
| All Combined | 89 (16) |
80 (12) |
79 (12) |
82 (13) |
78 (11) |
|
| Prostate translation | PTV D98% | 97 (18) |
97 (18) |
94 (17) |
97 (18) |
95 (17) |
| PTV D2% | 99 (19) |
98 (19) |
98 (18) |
99 (19) |
99 (19) |
|
| OARs | 87 (16) |
70 (8) |
70 (8) |
79 (11) |
79 (11) |
|
| All Combined | 85 (15) |
67 (6) |
65 (4) |
77 (9) |
75 (9) |
|
| Prostate rotation | PTV D98% | 97 (18) |
93 (16) |
87 (15) |
95 (18) |
87 (15) |
| PTV D2% | 98 (18) |
99 (19) |
100 (20) |
97 (19) |
99 (19) |
|
| OARs | 77 (12) |
88 (16) |
88 (16) |
72 (8) |
72 (8) |
|
| All Combined | 75 (10) |
83 (13) |
79 (13) |
69 (7) |
64 (5) |
|
3.2. Daily plans – comparison to clinical standard
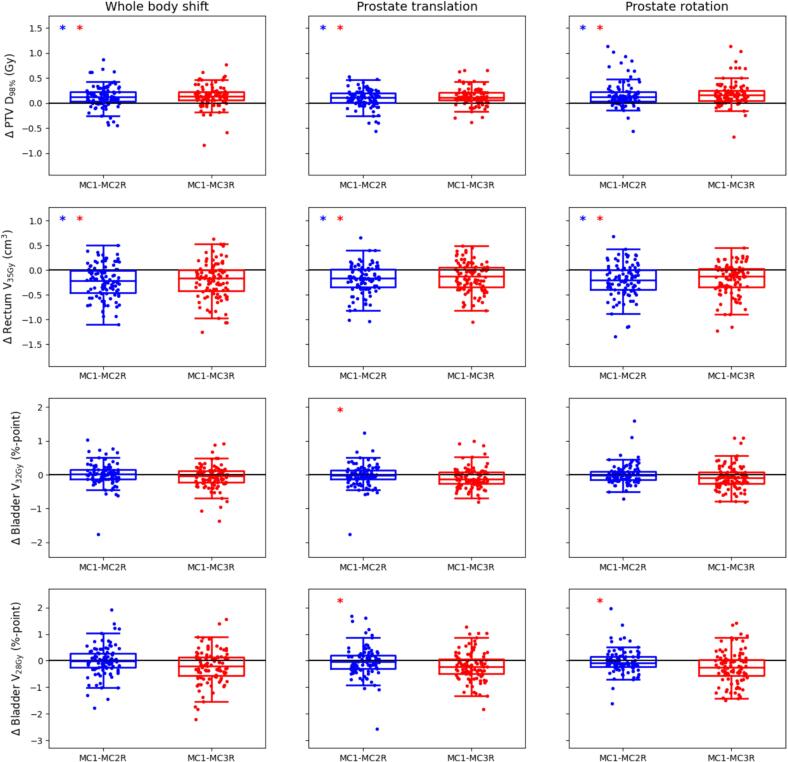
For the PTV D98% the MC1 values were in median between 0.1 and 0.2 Gy higher than the MC2R and MC3R values (Fig. 2). For all modes of anatomical variation the IQRS of the differences between MC1 and MC2R values and between MC1 and MC3R values were 0.2 Gy or less.
Fig. 2.
Boxplots showing the differences between the dose-volume values obtained in the individual plans generated using MC1 and those obtained with MC2R (blue) and MC3R (red). Each row represents one of the most limiting dose-volume criteria. Results are shown for plans simulating whole body shifts (left column), prostate translations (middle column) and prostate rotations (right column). The dots represent the individual difference values for all 100 fractions. Each box indicates the median and the 25th and 75th percentiles of the obtained differences. The vertical whiskers depict the remaining points up to 1.5 times the interquartile range. Statistically significant differences between MC1 and MC2R are indicated by blue asterisks in the top left corner, statistically significant differences between MC1 and MC3R by red asterisks. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
For the rectum V35Gy the opposite was seen, where the MC2R and MC3R values were in median up to 0.25 cm3 higher than the MC1 values, with IQRs up to 0.45 cm3. For the bladder the differences were in median ranging between −0.13 and 0.01 %-point (V32Gy) and −0.26 and −0.02 %-point (V28Gy). IQRs for these criteria were between 0.25 and 0.69 %-point.
3.3. Accumulated dose distributions – plan acceptability
While the number of accumulated dose distributions with acceptable target coverage were different depending on the used MC uncertainty when looking at prostate translations, for whole body shifts and prostate rotations no effect of the MC uncertainty could be observed (Table 2).
Table 2.
The number of patients (out of 20) meeting the different dose-volume criteria for the accumulated dose distributions.
| MC1 | MC2R | MC3R | ||
|---|---|---|---|---|
| Whole body shift | PTV D98% | 20 | 19 | 20 |
| PTV D2% | 20 | 20 | 20 | |
| OARs | 18 | 16 | 17 | |
| All Combined | 18 | 16 | 17 | |
| Prostate translation | PTV D98% | 19 | 17 | 16 |
| PTV D2% | 20 | 20 | 20 | |
| OARs | 16 | 13 | 13 | |
| All Combined | 15 | 11 | 11 | |
| Prostate rotation | PTV D98% | 17 | 17 | 17 |
| PTV D2% | 20 | 20 | 20 | |
| OARs | 16 | 14 | 15 | |
| All Combined | 14 | 12 | 13 | |
Similar to individual fraction plans, overall plan acceptability was mostly affected by the OAR criteria. It could be observed that the number of patients meeting the dose-volume criteria for all fractions (Table 1) was lower than the number of patients meeting the criteria after dose accumulation.
3.4. Accumulated dose distributions – comparison to clinical standard
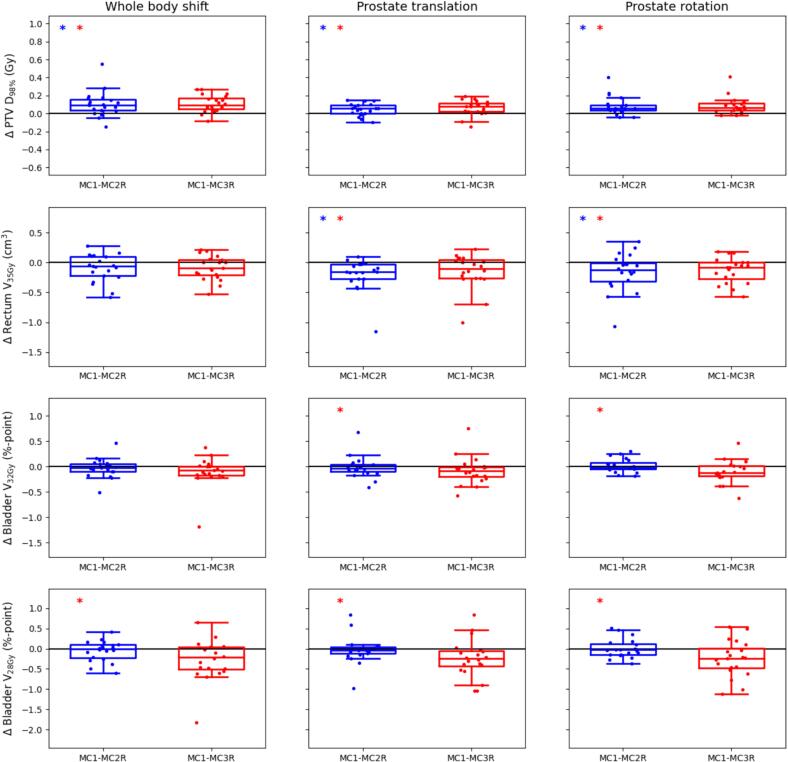
Similar to the differences seen for the daily plans, the accumulated PTV D98% values obtained with MC2R and MC3R were slightly lower than those obtained with MC1 (in median up to 0.1 Gy), with IQRs up to 0.12 Gy (Fig. 3). For the rectum V35Gy the MC2R and MC3R values were in median up to 0.16 cm3 higher than the MC1 values, with IQRs up to 0.33 cm3. For the bladder the MC2R and MC3R values were in median up to 0.12 %-point and 0.24 %-point higher than in MC1 plans, for the V32Gy and V28Gy respectively. IQRs for these criteria were up to 0.21 and 0.54 %-point respectively.
Fig. 3.
Boxplots showing the differences between the dose-volume values obtained in the accumulated dose distributions generated using MC1 and those obtained with MC2R (blue) and MC3R (red). Each row represents one of the most limiting dose-volume criteria. Results are shown for plans simulating whole body shifts (left column), prostate translations (middle column) and prostate rotations (right column). The dots represent the individual difference values for all 20 patients. Each box indicates the median and the 25th and 75th percentiles of the obtained differences. The vertical whiskers depict the remaining points up to 1.5 times the interquartile range. Statistically significant differences between MC1 and MC2R are indicated by blue asterisks in the top left corner, statistically significant differences between MC1 and MC3R by red asterisks. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
3.5. Timing
Recalculating the MC2 and MC3 plans using a 1 % statistical uncertainty per plan took on average 30 s. Timing differences were only observed in the second optimization phase, which exists of the segment shape optimization and the segment weight optimization (Table 3). There it could be seen that in moving from MC1 to MC2 one could win more than a minute for all modes of anatomical variation. Increasing from MC2 to MC3 however did not lead to any more time gain.
Table 3.
Average timing (in seconds) results of the different optimization steps for the three modes of daily variation and the 3 used MC uncertainty values, as well as the number of segments and monitor units obtained in the plans. FMO is the fluence map optimization. The second optimization phase includes the segment shape optimization (SSO) and the segment weight optimization (SWO). The full optimization includes everything from start to finish, hence including some overhead steps on top of the FMO, SSO and SWO.
| MC1 | MC2 | MC3 | ||
|---|---|---|---|---|
| Whole body shift | FMO (s) | 16 (11–25) | 16 (10–24) | 17 (11–28) |
| SSO+SWO (s) | 279 (205–340) | 205 (133–278) | 202 (115–285) | |
| Total optimization (s) | 306 (231–376) | 233 (159–308) | 230 (141–318) | |
| #Segments | 61 (33–96) | 62 (34–98) | 62 (29–98) | |
| #MU | 1481 (1206–1805) | 1466 (1214–1781) | 1465 (1212–1831) | |
| Prostate translation | FMO (s) | 18 (11–35) | 18 (11–35) | 18 (11–31) |
| SSO+SWO (s) | 317 (204–651) | 223 (156–351) | 222 (159–332) | |
| Total optimization (s) | 349 (233–683) | 254 (185–388) | 254 (189–365) | |
| #Segments | 62 (35–99) | 62 (35–96) | 62 (36–98) | |
| #MU | 1463 (1199–1811) | 1451 (1195–1784) | 1445 (1204–1861) | |
| Prostate rotation | FMO (s) | 18 (11–30) | 18 (12–28) | 19 (12–29) |
| SSO+SWO (s) | 321 (215–658) | 225 (126–324) | 226 (148–320) | |
| Total optimization (s) | 352 (244–685) | 256 (155–360) | 258 (176–352) | |
| #Segments | 63 (35–98) | 62 (36–98) | 62 (37–99) | |
| #MU | 1477 (1231–1934) | 1451 (1220–1826) | 1454 (1207–1903) | |
4. Discussion
In this study we have evaluated the effect of Monte Carlo uncertainty when simulating full online adaptive prostate cancer treatments. We compared the clinical setting of 1 % MC uncertainty per plan with 2 % and 3 % uncertainty per plan, while simulating whole body shifts and rigid prostate translations and rotations. Plans optimized using 2 % and 3 % were subsequently recalculated using a 1 % MC uncertainty. Plan acceptability was evaluated for both the individual fraction plans as well as after dose accumulation.
Evaluating the plans obtained immediately after optimization, just prior to treatment, shows that target coverage is immediately achieved for all MC settings for all modes of daily variation for the majority of the fractions (Table 1). After recalculating with a 1 % MC uncertainty setting, the PTV D98% acceptability rates decreased. While the acceptability of MC2 and MC3 remained comparable, the difference with respect to the MC1 plans increased slightly.
While target coverage acceptability after dose accumulation decreased about 25 % when using MC3 instead of MC1 (Table 2), the actual PTV D98% differences between MC2R or MC3R and MC1 were small (−0.2 Gy – 0.6 Gy, Fig. 3). The same was seen for the bladder V32Gy and V28Gy with median increases up to 0.24 %-point. With the statistical uncertainty being 2–3 %, these order of variations could possible also be observed without any anatomical changes. The higher sensitivity of the rectum V35Gy can be explained by its very low objective of 2 cm3.
Wendykier et al. [4] investigated the optimal statistical uncertainty values for the electron Monte Carlo dose engine in the Eclipse TPS (Varian Medical Systems, Palo Alto, CA) in terms of calculation time and dose uncertainty. Comparing the calculated dose to measured dose, different settings were tested, varying among other the statistical uncertainty setting. Overall they found that when combined with specific other settings, a 2 % statistical uncertainty was the optimal value for this algorithm.
When comparing plans calculated using uncertainty settings of 0.5 % versus 1 % per plan for stereotactic treatments, Goodall et al. [6] report up to 1.1 % median decrease in PTV coverage. The difference between settings of 1 % and 2 % per plan, while not directly reported, can visually be observed as smaller. In our study performing full optimizations, we similarly find small median decreases in PTV coverage of 0.2 Gy, which are further reduced after dose accumulation.
In this study all reference plans were made using a MC1 uncertainty setting, and thus might not necessarily be clinically acceptable when re-optimized using a higher MC uncertainty. The effects as observed in this study could possibly thus be further reduced by checking for plan acceptability for higher MC uncertainty in the process of generating the reference plan.
A limitation of this study is that we only included data of prostate cancer patients, and only considered user designed anatomical variations. For cases with more OARs and/or more daily variation, the effect of the MC uncertainty could increase as the effect of small fluctuations will affect more dose-volume criteria. While we believe the absolute differences with respect to the current standard will remain small, further research is required to test this. It should furthermore be noted that the settings for the dose calculation gridsizes in this study (3x3x3 mm3) were specific for these data, and are not necessarily suitable for smaller targets. The results of this study may therefore not be directly applicable to those types of treatments, and more testing to find the appropriate combination of gridsizes and MC uncertainty settings should be performed.
An interesting observation from this study is that the dose-volume criteria value of an accumulated dose distribution was sometimes clinically unacceptable, while all fraction doses were acceptable. For plans dealing with prostate rotations, we observed PTV D98%, accum < min(PTV D98%, daily) for 5/20 patients, for at least one of the MC uncertainty values (Figure S1 of the Supplementary Materials). This contradicts the naive assumption that daily underdosage averages out over fractionated treatment plans. We observed that this phenomenon can occur when evaluating volumetric criteria, whenever voxels not meeting the criteria are in different locations each treatment day. While the actual underdosage per voxel will be small because it does average out, the volumetric criteria worsens as more voxels experience underdosage. The obvious issue in this phenomenon is that one cannot predict this when only evaluating the individual fraction plans. One possible solution would be to perform in-between dose accumulation, which would require accurate dose accumulation techniques. It should be noted that this result was observed for all MC uncertainties, including the current standard of 1 %. No clear correlation could be observed between the occurrence of this phenomenon and the applied MC uncertainty. A more extensive study should be done to evaluate how often this phenomenon occurs when dealing with true clinical cases.
In our study using MC2 instead of MC1 yielded a time gain of more than a minute. While the overall speed has since improved, similar time differences were already observed in the first tests of the GPUMCD model including magnetic fields [16]. The optimization times of the MC2 and MC3 plans were, however, very similar (Table 3). Goodall et al. [6] evaluated the effect of using different statistical uncertainty values on dose calculations for stereotactic radiotherapy plans. They report that the observed calculation times did not match the expectations, stating this to be due to the MC dose engine in the Monaco TPS. Amongst others, safety measures are implemented to limit the overall statistical uncertainty to 12 % per control point. In our study another attributing factor is that during full plan optimization the dose is continuously being calculated and the selected MC uncertainty thus affects the entire optimization path. This could suggest that a higher MC uncertainty causes a slower convergence of the problem, needing more steps and higher calculation times. Furthermore a research version GPU was used in this study, overall limiting the achievable speed of the MC implementation. As also observed by Fracchiolla et al. [5], the calculation times of GPU-based MC systems depend on many factors, including the amount and types of GPUs, gridsizes, and MC uncertainty values.
Optimizing the trade-off between speed and quality of the dose calculation, naturally depends on the application at hand. E.g. for phantom verification of an independent dose check, Nachbar et al. use 0.5 % in the TPS and 0.1 % in the secondary check [17]. On the other hand, to calculate the additional dose during (kV and MV) image guidance LeDeroff et al. accepted 5 % to keep calculation times acceptable [18].
While this study focuses on TPS using Monte Carlo dose calculation algorithms, other algorithms like the faster collapsed cone (CC) algorithms are also widely used in radiotherapy. As these algorithms do not have a statistical uncertainty, no speed up as investigated in this work could be achieved. It should be noted that due to the magnetic field, CC algorithms are not available for MR-Linac treatment planning.
In conclusion, the effects on dose-volume values when using increased Monte Carlo uncertainty settings in the application of online daily plan adaptation in prostate cancer treatments as described in this study are limited when compared to the current clinical standard. A time gain can be expected, as was seen in this study when moving from 1 % uncertainty per plan to 2 % uncertainty per plan. Increasing MC uncertainty from the widely accepted value of 1 % uncertainty per plan to 2 % uncertainty per plan can thus be done safely, with the benefit of reducing treatment times for the patients.
5. Disclosures
Netherlands Cancer Institute is a member of the Elekta AB (Stockholm, Sweden) MR-Linac consortium. This work uses TPS Monaco Research version 5.59.11a, which is made available to the Netherlands Cancer Institute as part of a research collaboration.
This research was supported by an institutional grant of the Dutch Cancer Society and of the Dutch Ministry of Health, Welfare and Sport.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: T. Janssen reports institutional funding from Elekta AB (Stockholm). J.-J. Sonke reports research grants from Elekta AB (Stockholm). Our department receives license fees from Elekta AB (Stockholm) for IGRT software.
Acknowledgements
The authors want to thank Peter de Ruiter, Tineke Vijlbrief-Bosman, Lisa Wiersema, Joeke van der Linden, Joyce Bilderbeek and Vivian van Pelt for their advice on treatment plan acceptability and the clinical dose-volume criteria. The authors furthermore want to thank Peter Voet from Elekta for the technical support and Sami Hissoiny from Elekta and Marnix de Witte for their feedback on the manuscript.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.phro.2024.100636.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Ma C.M.C., Chetty I.J., Deng J., Faddegon B., Jiang S.B., Li J., et al. Beam modeling and beam model commissioning for Monte Carlo dose calculation-based radiation therapy treatment planning: Report of AAPM Task Group 157. Med Phys. 2020;47:e1–e18. doi: 10.1002/mp.13898. [DOI] [PubMed] [Google Scholar]
- 2.Ma C.-M., Li J.S., Deng J., Fan J. Implementation of Monte Carlo Dose calculation for CyberKnife treatment planning. J Phys Conf Ser. 2008;102 doi: 10.1088/1742-6596/102/1/012016. [DOI] [Google Scholar]
- 3.Heath E., Seuntjens J., Sheikh-Bagheri D. Dosimetric evaluation of the clinical implementation of the first commercial IMRT Monte Carlo treatment planning system at 6 MV. Med Phys. 2004;31:2771–2779. doi: 10.1118/1.1786172. [DOI] [PubMed] [Google Scholar]
- 4.Wendykier J., Wojtyna E., Bekman B., Bekman A., Woźniak B., Niewiadomska B., et al. Optimal values of the Electron Monte Carlo dose engine parameters. Rep Pract Oncol Radiother. 2023;28:416–428. doi: 10.5603/RPOR.a2023.0044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fracchiolla F., Engwall E., Janson M., Tamm F., Lorentini S., Fellin F., et al. Clinical validation of a GPU-based Monte Carlo dose engine of a commercial treatment planning system for pencil beam scanning proton therapy. Phys Med. 2021;88:226–234. doi: 10.1016/j.ejmp.2021.07.012. [DOI] [PubMed] [Google Scholar]
- 6.Goodall S.K., Ebert M.A. Recommended dose voxel size and statistical uncertainty parameters for precision of Monte Carlo dose calculation in stereotactic radiotherapy. J Appl Clin Med Phys. 2020;21:120–130. doi: 10.1002/acm2.13077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de Jong R., Visser J., van Wieringen N., Wiersma J., Geijsen D., Bel A. Feasibility of conebeam CT-based online adaptive radiotherapy for neoadjuvant treatment of rectal cancer. Radiat Oncol. 2021;16:1–11. doi: 10.1186/s13014-021-01866-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu X., Liang Y., Zhu J., Yu G., Yu Y., Cao Q., et al. A fast online replanning algorithm based on intensity field projection for adaptive radiotherapy. Front Oncol. 2020;10:1–10. doi: 10.3389/fonc.2020.00287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Van Timmeren J.E., Chamberlain M., Krayenbuehl J., Wilke L., Ehrbar S., Bogowicz M., et al. Treatment plan quality during online adaptive re-planning. Radiat Oncol. 2020;15:1–11. doi: 10.1186/s13014-020-01641-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Finazzi T., Palacios M.A., Spoelstra F.O.B., Haasbeek C.J.A., Bruynzeel A.M.E., Slotman B.J., et al. Role of on-table plan adaptation in MR-guided ablative radiation therapy for central lung tumors. Int J Radiat Oncol Biol Phys. 2019;104:933–941. doi: 10.1016/j.ijrobp.2019.03.035. [DOI] [PubMed] [Google Scholar]
- 11.Henke L., Kashani R., Robinson C., Curcuru A., DeWees T., Bradley J., et al. Phase I trial of stereotactic MR-guided online adaptive radiation therapy (SMART) for the treatment of oligometastatic or unresectable primary malignancies of the abdomen. Radiother Oncol. 2018;126:519–526. doi: 10.1016/j.radonc.2017.11.032. [DOI] [PubMed] [Google Scholar]
- 12.Bernatowicz K., Geets X., Barragan A., Janssens G., Souris K., Sterpin E. Feasibility of online IMPT adaptation using fast, automatic and robust dose restoration. Phys Med Biol. 2018;63 doi: 10.1088/1361-6560/aaba8c. [DOI] [PubMed] [Google Scholar]
- 13.Intven M.P.W., de Mol van Otterloo S.R., Mook S., Doornaert P.A.H., de Groot-van Breugel E.N., Sikkes G.G., et al. Online adaptive MR-guided radiotherapy for rectal cancer; feasibility of the workflow on a 1.5T MR-linac: clinical implementation and initial experience. Radiother Oncol. 2021;154:172–178. doi: 10.1016/j.radonc.2020.09.024. [DOI] [PubMed] [Google Scholar]
- 14.Winkel D., Bol G.H., Kroon P.S., van Asselen B., Hackett S.S., Werensteijn-Honingh A.M., et al. Adaptive radiotherapy: The Elekta Unity MR-linac concept. Clin Transl Radiat Oncol. 2019;18:54–59. doi: 10.1016/j.ctro.2019.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Buffa F.M., Nahum A.E. Monte Carlo dose calculations and radiobiological modelling: analysis of the effect of the statistical noise of the dose distribution on the probability of tumour control. Phys Med Biol. 2000;45:3009–3023. doi: 10.1088/0031-9155/45/10/318. [DOI] [PubMed] [Google Scholar]
- 16.Hissoiny S., Raaijmakers A.J.E., Ozell B., Després P., Raaymakers B.W. Fast dose calculation in magnetic fields with GPUMCD. Phys Med Biol. 2011;56:5119–5129. doi: 10.1088/0031-9155/56/16/003. [DOI] [PubMed] [Google Scholar]
- 17.Nachbar M., Mönnich D., Dohm O., Friedlein M., Zips D., Thorwarth D. Automatic 3D Monte-Carlo-based secondary dose calculation for online verification of 1.5 T magnetic resonance imaging guided radiotherapy. Phys Imaging Radiat Oncol. 2021;19:6–12. doi: 10.1016/j.phro.2021.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Le Deroff C., Berger L., Bellec J., Boissonnat G., Chesneau H., Chiavassa S., et al. Monte Carlo-based software for 3D personalized dose calculations in image-guided radiotherapy. Phys Imaging Radiat Oncol. 2022;21:108–114. doi: 10.1016/j.phro.2022.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kontaxis C., Bol G.H., Lagendijk J.J.W., Raaymakers B.W. A new methodology for inter- and intrafraction plan adaptation for the MR-linac. Phys Med Biol. 2015;60:7485–7497. doi: 10.1088/0031-9155/60/19/7485. [DOI] [PubMed] [Google Scholar]
- 20.Raaymakers B.W., Lagendijk J.J.W., Overweg J., Kok J.G.M., Raaijmakers A.J.E., Kerkhof E.M., et al. Integrating a 1.5 T MRI scanner with a 6 MV accelerator: Proof of concept. Phys Med Biol. 2009;54:N229–N237. doi: 10.1088/0031-9155/54/12/N01. [DOI] [PubMed] [Google Scholar]
- 21.Lagendijk J.J.W., Raaymakers B.W., van Vulpen M. The magnetic resonance imaging-linac system. Semin Radiat Oncol. 2014;24:207–209. doi: 10.1016/j.semradonc.2014.02.009. [DOI] [PubMed] [Google Scholar]
- 22.Licup A., Van Kranen S., Buijs M., Koetsveld F., Sonke J., Remeijer P. EP-2053 Pelvic plan adaptation to manage systematic rotations without CT re-imaging. Radiother Oncol. 2019;133:S1129–S1130. doi: 10.1016/S0167-8140(19)32473-9. [DOI] [Google Scholar]
- 23.Jagt T.Z., Janssen T.M., Betgen A., Wiersema L., Verhage R., Garritsen S., et al. Benchmarking daily adaptation using fully automated radiotherapy treatment plan optimization for rectal cancer. Phys Imaging Radiat Oncol. 2022;24:7–13. doi: 10.1016/j.phro.2022.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jiang Y., He X., Lee M.L.T., Rosner B., Yan J. Wilcoxon rank-based tests for clustered data with r package clusrank. J Stat Softw. 2020;96(1–26) doi: 10.18637/jss.v096.i06. [DOI] [Google Scholar]
- 25.Rosner B., Glynn R.J., Lee M.L.T. The Wilcoxon signed rank test for paired comparisons of clustered data. Biometrics. 2006;62:185–192. doi: 10.1111/j.1541-0420.2005.00389.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.