Abstract
Retinal surgery is a challenging procedure requiring precise manipulation of the fragile retinal tissue, often at the scale of tens-of-micrometers. Its difficulty has motivated the development of robotic assistance platforms to enable precise motion, and more recently, novel sensors such as microscope integrated optical coherence tomography (OCT) for RGB-D view of the surgical workspace. The combination of these devices opens new possibilities for robotic automation of tasks such as subretinal injection (SI), a procedure that involves precise needle insertion into the retina for targeted drug delivery. Motivated by this opportunity, we develop a framework for autonomous needle navigation during SI. We develop a system which enables the surgeon to specify waypoint goals in the microscope and OCT views, and the system autonomously navigates the needle to the desired subretinal space in real-time. Our system integrates OCT and microscope images with convolutional neural networks (CNNs) to automatically segment the surgical tool and retinal tissue boundaries, and model predictive control that generates optimal trajectories that respect kinematic constraints to ensure patient safety. We validate our system by demonstrating 30 successful SI trials on pig eyes. Preliminary comparisons to a human operator in robot-assisted mode highlight the enhanced safety and performance of our system.
Keywords: Vision-Based Navigation, Computer Vision for Medical Robotics, Medical Robots and Systems
I. Introduction
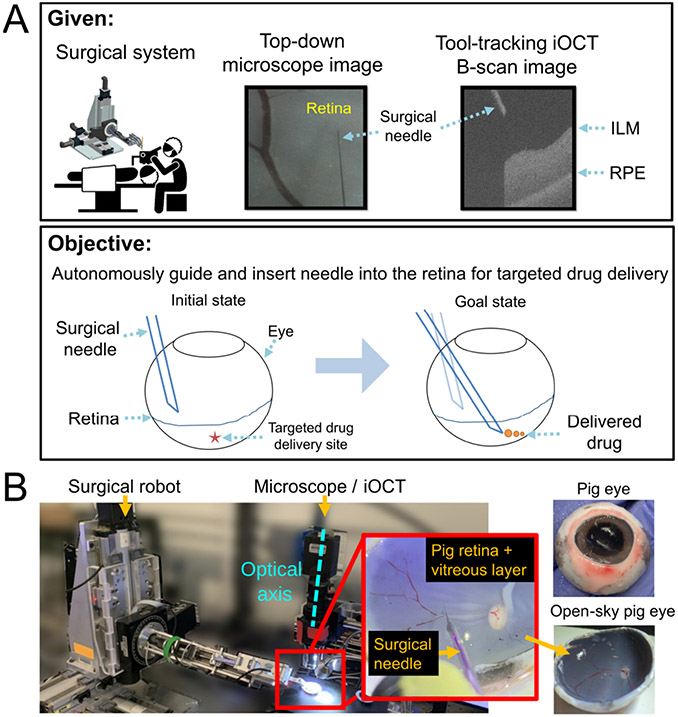
Subretinal injection (SI) is a procedure that involves inserting a micro-needle between the retina’s photoreceptor layer and the underlying retinal pigment epithelium (RPE) layer for the purpose of targeted drug delivery (Fig. 1). SI typically proceeds with the surgeon inserting a surgical tool through the sclertomy port of the eye and visualizing the retina from a top-down view using a surgical microscope. The task requires precisely navigating the surgical needle to a desired location above the retina, gently landing its tip on the retinal surface, and inserting it to reach a specific depth. The needle-tip position is then sustained for drug delivery. SI is a promising approach to treat inherited retinal dystrophies (IRDs), a class of rare eye diseases impairing vision and known to affect ~2 million people world-wide [1].
Fig. 1.
(A) Problem statement; Our imaging system provides a simultaneous view of the surgical tool and the B-scan image which dynamically tracks the surgical instrument (B) Experimental setup
However, SI presents significant challenges. Surgeons must control their natural hand tremor (~180μm in amplitude), which is comparable to the thickness of the fragile retina (~200μm) [2]. They also face difficulties with depth perception due to the top-down view of the surgery, hindering their ability to perform precision-driven tasks. Moreover, maintaining the needle position for extended periods during drug infusion can be challenging due to microjerks, which can push its tip away by more than 250μm [3]. All taken together, unassisted SI pushes surgeons to their physiological limits [4].
To address the challenges of SI, prior works have introduced robotic assistance and intraoperative optical coherence tomography (iOCT) for depth guidance. iOCT is an imaging modality that provides cross-sectional (B-scan) or volumetric (C-scan) views of the surgical workspace, providing depth perception between the surgical tool and the underlying retinal tissue. Using such systems, prior works have demonstrated robot-assisted SI under teleoperated control by a surgeon [4]. More recent works have also explored the use of iOCT for automating navigation tasks in SI. For example, [5] and [6] developed workflows that allowed surgeons to select a goal waypoint in the iOCT view. The robot then navigated the needle-tip to the selected waypoint below the retina to accomplish SI.
However, these works presents several critical limitations. Firstly, these works lacked real-time capabilities due to reliance on slow volumetric C-scans. For instance, the state-of-the-art Leica iOCT system in [6] required 7.69 seconds to scan a 2.5mm × 2.5mm (100 B-scans) square patch of the retina. Such scanning speed is inadequate considering the potential occurrence of involuntary patient motion during that time period [4]. While relying on smaller C-scans or a single B-scan is possible [5], the resulting scanning region may become too limited, leading to the risk of the surgical instrument leaving the viewable field due to patient motion. Secondly, prior works focused exclusively on utilizing iOCT views, neglecting the rich information provided in the microscope view. The microscope view provides global and familiar information to surgeons and should be utilized to easily identify affected regions (e.g., areas of bleeding). Lastly, prior works have not accounted for the important remote-center-of-motion (RCM) constraint when designing their workflows, which is essential for ensuring the safety of the patient.
In this paper, we address the above limitations by first developing a custom imaging system that integrates the microscope and iOCT in a real-time manner, as demonstrated in our project website1. Unlike prior works which relied on slow volume scans [6] or fixed cross-sectional scans [5], we develop a hybrid approach where a small iOCT scanning region dynamically tracks the surgical instrument. Even if the surgical tool moves, the B-scan automatically tracks the tool, thereby enabling real-time depth feedback between the needle and the underlying retinal tissue. Given such a capable imaging system, we design an intuitive autonomous SI workflow by combining automated perception and model predictive control (MPC) which ensures the critical kinematic safety constraints of the surgery. These contributions address the limitations of prior works mentioned above, specifically those relating to the slow speed of the imaging system, utilizing both RGB and depth views for comprehensive visualization, and ensuring critical constraints for patient safety. In summary, our contributions include:
Designing an integrated hardware and software system with real-time microscope and iOCT feedback, deeplearning based perception, and MPC for trajectory optimization which satisfies safety-related kinematic constraints
Outlining a strategy for calibrating the microscope and iOCT to generate tool-axis-aligned B-scans.
Validating the system via 30 successful autonomous trials on three cadaveric pig eyes, achieving mean needle insertion accuracy of 26 ± 12μm to various subretinal goals while requiring a mean duration of 55 ± 10.8 seconds. Preliminary comparisons to a human operator in robot-assisted mode highlight the enhanced safety and performance of our system.
II. Related Works
Most prior works in robot-assisted retinal surgery have focused on developing assistive technologies, primarily via the development of robot-assisted platforms, integration of novel sensors on the surgical tool, and software frameworks aiding with active intervention for enhanced safety, which are exhaustively covered in [7]. More recently, there has been a growing number of works addressing automation in retinal surgery, in particular as demonstrated by [6], [5], and [8]. A key differentiating factor between prior works and ours is the ability to provide real-time RGB-D feedback in an efficient manner via dynamic tracking of the surgical instrument. Such capability unlocks compelling possibilities when combined with automated perception and task & motion planning, enabling real-time applications as we demonstrate in this work. On the imaging side, we highlight [9], which demonstrated dynamic tracking of OCT B or C-scans by detecting the surgical tool from spectrally encoded reflectometry images in a similar fashion to our system. However, their work primarily focused on developing an imaging system without robotic integration or experimental validation using animal tissues, which we focus more in this study.
III. Problem Formulation
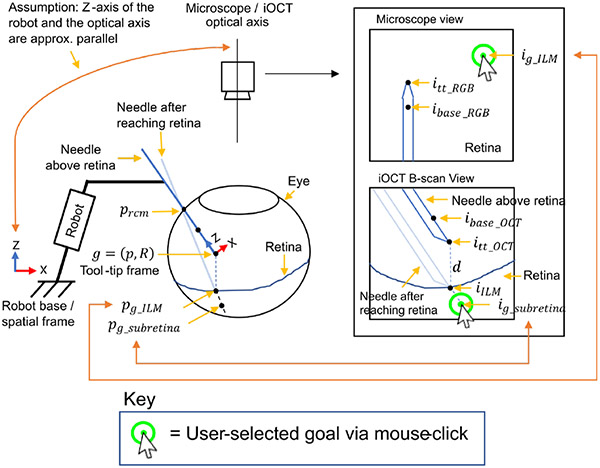
Consider a robotic manipulator with a surgical tool attached at its end-effector, as illustrated in Fig. 3. The key variables mentioned throughout this section are also illustrated in Fig. 3. We define the robot states as , where and . denotes the tool-tip position, the orientation, and and the tool-tip-frame translational and angular velocity. Let the robot occupy a region in the workspace , where denotes the robot joint angles.
Fig. 3.
Key variables used are shown. Double arrows are shown to indicate that the pixel goals and correspond to and respectively in euclidean space.
The tool-tip state is fully-observable using high-precision motor encoders and precise knowledge of the robot forward kinematics. Additionally, the system includes a monocular microscope camera generating top-down observations of the surgical environment from space of images at a given time . A co-axially mounted OCT generates B-scan images . The B-scan plane dynamically tracks the tool such that the scanning plane is always aligned with the tool axis, thereby providing depth feedback between the needle and the underlying retina at all times.
Initially, the surgeon manually introduces the surgical tool into the eye through a sclera entry point, , which is recorded at the time of entry. The sclera point should remain fixed after each entry to avoid unsafe forces exerted on the sclera tissue. Once the tool-tip is within the microscope’s view, its key points are detected in the microscope and B-scan views using two CNNs. Specifically, the detected tool-tip and its base are denoted as , in the microscope image and , in the B-scan image. These detected points also define the axis of the tools in the respective images (illustrated in Fig. 2). Simultaneously, the ILM and RPE layers are segmented using another CNN, generating binary segmentation masks and . Using the detected tool-tip and the segmented ILM layer , the projection of the tool-tip to the ILM layer below (i.e. along the same B-scan image column index) is computed and denoted in the B-scan view.
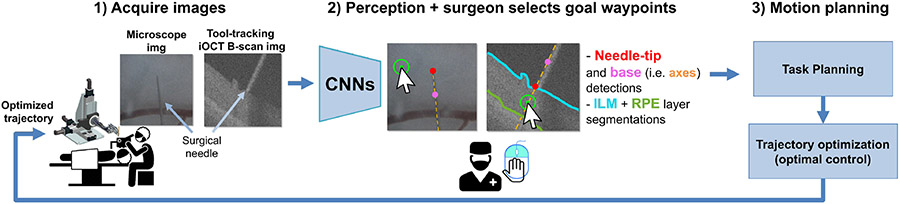
Fig. 2.
High-level workflow; 1) the microscope image and the iOCT B-scan images are acquired. 2) Three CNNs provide needle-tip detections and retinal layer segmentations. The surgeon provides two waypoint goals in the microscope and B-scan images via two mouse-clicks. The waypoint goal is first specified in the microscope image, then in the B-scan image before insertion. 3) The relevant task and motion is planned, and an optimized trajectory is sent to the robot for trajectory-tracking.
Given this setup, the surgeon selects a 2D pixel goal via a mouse-click in the top-down microscope image. This goal denotes the desired waypoint through which the needle is introduced into the retina from the microscope view. It also corresponds to a 3D euclidean point on the retina’s surface w.r.t the robot’s spatial frame. We seek to reach , however, its exact location is unknown. Instead of estimating directly, we propose to reach it approximately by employing a specific visual-servoing strategy (Section IV). After is reached using this strategy, the surgeon specifies another goal waypoint along the axis of the needle and below the retina in the B-scan view via a mouse-click. Note that at this point in time, the needle is placed on the retinal surface, as illustrated in Fig. 3 (labelled as “Needle after reaching retina”). The goal corresponds to a 3D euclidean point defined w.r.t the robot spatial frame. This subretinal goal is the final drug-delivery site. Since the iOCT B-scan is always aligned with the needle-axis, can be reached by simply inserting it along its axis.
In summary, the objective is to navigate the needle-tip to two sequential goals: and then , given the user-clicked goals and respectively. We thus consider the following two problems:
Navigating the needle above the retinal surface: navigate the needle-tip to the desired needle insertion point on the retinal surface given the clicked goal .
Needle insertion: insert the needle along its axis to reach the goal insertion waypoint given the clicked goal .
The objective is to autonomously perform the above tasks while relying on monocular top-down images, tool-axis aligned B-scan images, and three CNNs automatically providing detections and segmentations necessary for task autonomy. Additionally, kinematic constraints concerned with the safety of the surgery must be satisfied while ensuring smooth robot motion.
IV. Technical Approach
The following sections provide greater details on the technical approach and implementation. We begin by providing a high-level description of the needle insertion strategy (Section IV-A, IV-B) and then dive in more detail into the calibration procedures (Section IV-C, IV-D), visual-servoing (Section IV-D, IV-E), and network implementation details (IV-F).
A. Navigation above the retina
The first step of the navigation procedure is positioning the needle-tip at the first desired waypoint given the user-selected goal . Recall that is only a 2D pixel goal. Therefore, the corresponding 3D location is unknown. One possible approach may be to estimate directly using images and/or iOCT. However, this can be challenging in retinal surgery where unknown distortion is present due to the patient’s lens and cornea which is in the optical path. Instead, we propose a straightforward navigation procedure in which can be approximately reached without directly estimating its 3D position. At a high level, this procedure first consists of aligning the needle-tip with the clicked goal from the top-down microscope view via 2D planar motion. Then, the needle is simply lowered towards the retina while relying on the B-scan for depth feedback. The specific procedure is as follows:
Step 1: Align the needle-tip with the clicked goal via 2D visual-servoing i.e. via actutation only along the robot’s spatial XY plane (the robot’s spatial XY frame is shown in Fig. 3). This step effectively aligns the needle-tip with the clicked goal pixel from the top-down microscope view.
Step 2: Lower the needle towards the retinal surface via incremental motion along the robot’s spatial Z-axis. This step moves the needle-tip closer to the retinal surface in the B-scan view, while mostly keeping the needle-tip aligned with the clicked goal from the microscope view.
Step 3: Repeat the above two steps until (Fig. 3) is reached in the B-scan view.
The underlying assumption here is that the optical axis of the microscope and the robot’s spatial Z-axis are approximately parallel, as illustrated in Fig. 3. Therefore, during 2D planar motion (step 1), the observed motion of the needle-tip is a corresponding planar motion in the microscope image. During the needle lowering step (step 2), the observed motion is a corresponding needle-lowering motion in the B-scan view. However, during step 2, the tool-tip may deviate from the clicked goal in the microscope view, since the optical axis and the robot’s spatial Z-axis are only approximately parallel. Therefore, steps 1 and 2 must be repeated (step 3) whenever a pixel error above a small threshold is observed to realign the needle-tip with the clicked goal. In terms of implementation details, the 2D navigation step was repeated whenever pixel error > 1 pixel was observed, and the maximum navigation distance was set at 200μm increments. During Z-axis motions, the needle was lowered at the maximum of 50μm steps and when the distance to was within 60μm, the remaining distance was navigated in open-loop. Also, in order to avoid potential collision between the needle and the retina, we enforced a safety factor by offsetting by 30μm above the retinal surface. Ultimately, this iterative procedure enables accurate needle-tip placement anywhere on the retinal surface.
We also provide a few comments on the approximate parallelism between the optical axis and the robot’s spatial Z-axis and its effect on the navigation procedure when violated. In general, the more parallelism is violated, the more 2D corrective actions may be required. If the parallelism is heavily violated, in which case corrective 2D actions may be required frequently, then it may be worth performing hand-eye calibration to compute which direction of travel on the robot is along the camera’s optical axis.
B. Needle insertion
Once the needle-tip is approximately placed on (Section IV-A), the surgeon specifies another goal waypoint in the B-scan view via a mouse click. The desired insertion distance is obtained as follows:
| (1) |
where is converted to microns using a conversion factor (Table I). The needle is then simply inserted along its axis to reach .
TABLE I.
Conversion factors for converting pixel distance to microns
| Image Type | Conversion factor (μm / pixel) |
|---|---|
| Microscope image | 13.6 |
| B-scan (along img height) | 2.6 |
| B-scan (along img width) | 5.3 |
| B-scan (between B-scan slices) | 13.6 |
C. Microscope-OCT Calibration
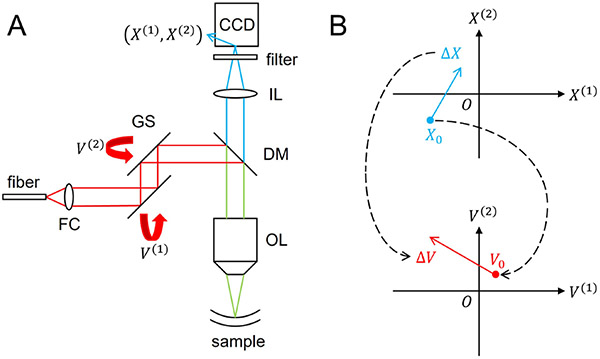
The microscope-OCT setup combines a 100 kHz swept source OCT system [10] with a microscope for simultaneous OCT and microsopic imaging. A charged-coupled device (CCD) is added to the OCT system to capture microscopic images [11]. Both the OCT and the CCD share the same objective lens, ensuring precise alignment and consistent working distance. A short-pass dichroic mirror with a 650 nm cutting-off wavelength splits the light into reflection and transmission. It reflects near infrared light back to the OCT system while transmitting visible light to the CCD for microscopic imaging. The transmitted visible light is focused onto the CCD by an imaging lens, and a short-pass filter is employed to reduce near infrared noise. Two galvo mirrors are utilized to tilt the collimated beam from the fiber collimator, and thus control the OCT scanning position. This integrated microscope-OCT setup facilitates a comprehensive OCT and microscopic visualization.
In the OCT system, the laser scanning position in a microscopic image is determined by the rotation angles of two orthogonal Galvo mirrors, which are controlled through voltages. Specifically, we use a pair of Galvo mirrors (GVS001, Thorlabs), where the scanning angle is linearly proportional to the applied voltage with a 99.9% linearity. Moreover, we use a scan lens (LSM04-BB, Thorlabs) in which the scanning position is linearly proportional to the scanning angle with a F-Theta distortion less than 1.1%. Therefore, we assume a linear relationship between the laser scanning position and the applied voltages, given by the equation:
| (2) |
where represents the laser scanning position in the microscopic image, corresponds to the voltages applied to the two galvo mirrors, and are linear parameters that convert the applied voltages to the corresponding laser scanning position in the microscopic image. The mapping between the laser scanning position and the applied voltage is shown in Fig. 4(b).
Fig. 4.
(A) Microscope-OCT system setup. FC, fiber collimator; GS, galvo scanners; DM, dichroic mirror; IL, imaging lens; OL, objective lens. (B) The mapping between the laser scanning position and the applied voltage.
The linear parameters and need to be calibrated. We use a laser viewing card to visualize and locate the laser scanning position in the microscopic image. We record a set of laser scanning positions when applying voltages according to a predefined voltage set . The linear parameters and are calibrated by minimizing the least square error:
| (3) |
where refers to Euclidean norm. It can be derived that:
| (4) |
| (5) |
where and are matrices that are expressed as:
| (6) |
| (7) |
and , .
To generate OCT B-scan that is aligned with the needle axis in the microscopic image, we need the needle tip position, needle orientation and a predefined scanning length in the microscopic image frame. The central voltage is determined by:
| (8) |
where is the needle tip position in the microscopic image. The voltages are determined on the tangent space at through the equation:
| (9) |
where is the tangent vector at describing the voltage amplitude and the voltage angle, and is the tangent vector at describing the needle orientation and the predefined scanning length. Therefore, to generate a scanning cross section along the needle axis and centered at the needle tip that is described by:
| (10) |
where is a normalized time parameter, we should control the voltage according to:
| (11) |
D. Real-Time Hand-Eye Calibration and Visual Servoing
In order to navigate the needle-tip to the clicked goal (i.e. during step 1 in Section IV-A), the calibration parameters between the robot and the microscope must be ascertained. To avoid complex calibration procedure such as in [5], we choose a visual servoing strategy which relies on real-time iterative updates to the calibration matrix based on the observed robot motions in real-time [12]. This effectively enables real-time adaptation to the changing intrinsic and extrinsic properties of the camera, enabling the surgeon to change the microscope position, magnification, or add distortive optics (e.g. BIOME or contact-lenses) during the procedure, without needing to perform a calibration procedure repeatedly.
Since the robot’s spatial Z-axis and the camera’s optical axis are approximately parallel (Section IV-A), the calibration is only performed between the robot’s spatial XY plane and the image plane. To simplify the notation, we introduce a variable , which simply denotes the XY components of the surgical tool-tip position, where the selector matrix picks out the first two elements of the vector it operates on. is defined as:
| (12) |
Consider an unknown function which converts the tool-tip XY position to its corresponding image coordinates. implicitly contains the intrinsic and extrinsic parameters of the camera. In other words,
| (13) |
We may approximate the unknown using the first-order Taylor series approximation:
| (14) |
| (15) |
where is a Jacobian matrix that relates the change in tool-tip XY position Apk to the corresponding change in image coordinates . denotes the iteration step, since the Jacobian is iteratively updated to adapt to observed motions. Specifically, the Jacobian is recalculated whenever a significant change and is observed. In our experiments, we updated the when pixels and was observed.
Borrowing from [12], we use an online update rule to estimate the Jacobian in real-time based on the observed robot motions. The method utilizes Broyden’s update formula to estimate the Jacobian, given as:
| (16) |
where is the step size for updating the Jacobian [13]. We chose . This is an iterative approach where the Jacobian is initialized as an arbitrary non-singular matrix (e.g. an identity matrix) and after several updates it converges to the true Jacobian. To use the Jacobian to guide the needle to , we reformulate Eq. 15 as
| (17) |
where is the desired motion vector in image coordinates, and is the desired change in tool-tip position to align the needle-tip with the clicked goal.
Using , the desired waypoint to reach can be given as:
| (18) |
where the motion along robot’s spatial Z-axis is zero. To be clear, . can be considered as an intermediate waypoint that is constantly updated (e.g. every time the Jacobian is updated), such that the tool-tip will be eventually aligned with in the microscope view.
E. Optimal Control Formulation
Once a desired goal waypoint is determined (Section IV-D) it is used by an optimal control framework to generate an optimal trajectory to the goal. The formulation and implementation follows our previous work [14].
F. Network Detail
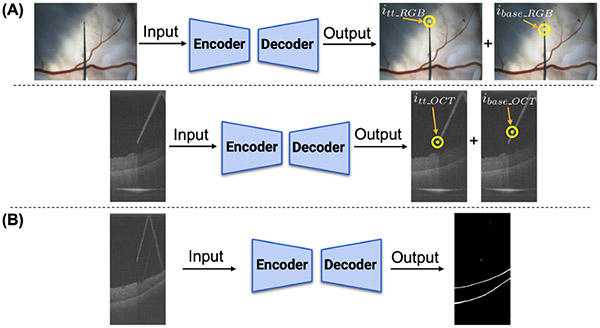
Two CNNs are implemented for the tool-tip and its base predictions (Fig. 5A). One network is used for the microscope images and another network for the B-scan images. Both networks are identical and adopt a U-Net-like [15] architecture, using Resnet-18 [16] as a backbone. After the image is encoded into feature vectors, two decoders are used to predict the tool-tip and its base respectively. The output sizes are identical to the input sizes (480 × 640 × 3 and 1024 × 512 for the microscope and B-scan images respectively). In order to enforce consistency, the distance between the tool-tip and its base are set to be 50 and 100 pixels in the microscope and B-scan images respectively. We implement a third CNN to segment the ILM and the RPE layer in the B-scan image, as shown in Fig. 5B. The encoder of the segmentation network is identical to the B-scan image network. We modify the decoder to output three channels, predicting the background, ILM layer, and the RPE layer respectively.
Fig. 5.
Network architectures: (A) Two networks are trained to detect the needle tip and its base (thus defining its axis), one for microscope and another for iOCT images. (B) A third network is trained to the ILM and RPE layer segmentations
To train the networks, cross-entropy loss was used for the tool-tip and its base predictions and the retinal layers segmentation. For the tool-tip and its base predictions, an additional mean squared error (MSE) loss was used to enforce consistent distance spacing between the predicted points (i.e. 50 or 100 pixels). Also, to balance the errors among the three labels during segmentation training, we set the weights for the background, ILM, and RPE layer to be 0.001, 0.4995, and 0.4995 respectively. 2000 microscope images and 1050 B-scan images were collected from 4 pig eyes for training and validation, with a split ratio of 4:1. Note that these four pig eyes are only used during the training phase, and during testing completely different set of pig eyes are used. All labels were manually annotated using a labeling tool called Supervisely. During training, batch size was set to be 24. Several data augmentations, including shifting, scaling, rotating, blurring, and dropout, were applied to increase the robustness of the network.
G. Hardware
Our system consisted of three computers: one computer for controlling the robot, another for iOCT hardware, and another for data-intensive processing. B-scan images were acquired at 11Hz, and the camera images were acquired at 30Hz. The inference speed of all the networks in IV-F exceeded 40Hz, deployed on an NVIDIA RTX 3090 GPU.
V. Experiments
As shown in Fig. 1B, the experimental setup consists of the Steady Hand Eye Robot (SHER) [17], a silver-coated glass pipette attached at the robot handle (30μm tip diameter), a microscope-integrated OCT, and an open-sky pig eye filled with vitreous.
We validated our system through 30 autonomous subretinal injection trials on 3 open-sky pig eyes (Fig. 1B). For each eye, 10 trials were performed. The experimental procedure follows the description provided in Section III. We evaluate our system based on the following metrics:
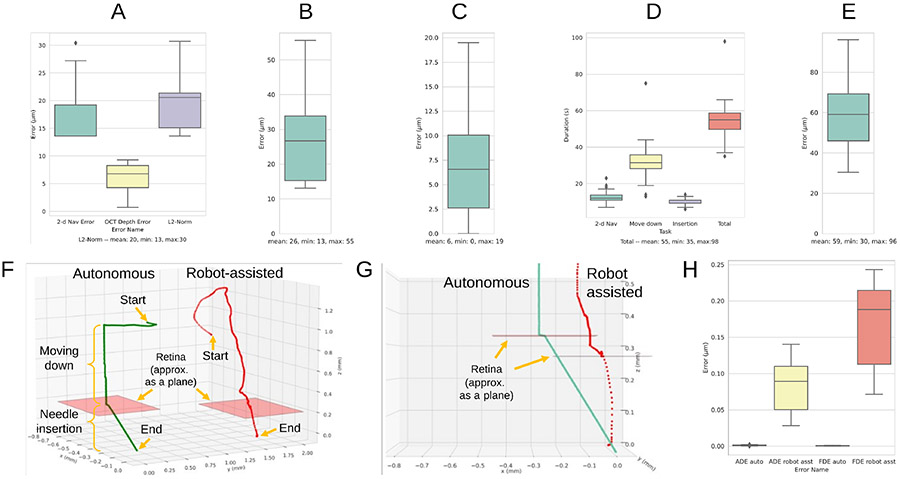
1). Navigation error on the retinal surface goal (Fig. 6A):
Fig. 6.
Experimental metrics are shown (see Section V): (A) navigation error on the retinal surface goal (B) needle-insertion error at the drug delivery site (C) RCM error (D) total duration of the surgery by task (E) 2D navigation error to the clicked goal from the microscope view during robot-assisted mode (F) qualitative comparison between autonomous and robot-assisted modes (G) same comparison from a close-up side view during needle insertion (H) comparing the deviation of the needle-tip from the insertion axis during needle insertion; ADE (average displacement error), FDE (final displacement error).
this metric measures how closely the needle-tip is placed on the retinal surface goal after performing the navigation procedure described in Section IV-A. Recall that we did not estimate of directly. Therefore, we approximate the error by combining the 2D navigation error between the clicked goal () and the needle-tip () in the microscope view and the depth error between the needle-tip () and the retinal goal () in the B-scan view to obtain the navigation error in 3D.
Specifically, we compute the 2D navigation error in the microscope view using the following formula (2D Nav Error in Fig. 6A): , where is the ground-truth needle-tip pixel coordinate obtained via manual annotation. We compute the depth error using the depth component of the B-scan view via the following formula (OCT Depth Error in Fig. 6A): , where is the ground-truth needle-tip pixel coordinate in the B-scan image obtained via manual annotation, and is a selector vector that picks out the second element of the vector it operates on (i.e. the pixel index along the B-scan image height). Specifically, . Finally, these two errors are combined using the L2-norm metric (L2-Norm in Fig. 6A). The computed pixel errors are converted into micrometers using the relevant conversion factors listed in Table I.
2). Needle insertion error (Fig. 6B):
this metric measures how closely the needle-tip reaches the desired insertion goal below the retina based on the acquired volume scans after needle insertion. The error is calculated using the following L2-norm metric: , where is the ground-truth B-scan slice index which the needle is expected to land and is the B-scan slice index which the needle actually lands after needle insertion. The computed voxel errors are converted to micrometers using the relevant conversion factors in Table I. Note that a volumetric scan was performed after needle insertion (i.e. multiple B-scans or “slice” of images were collected) to compute this error.
3). RCM error (Fig. 6C):
this metric measures how closely the needle-axis is aligned with the RCM point throughout the entire procedure, computed using robot kinematics data [14].
4). Task duration (Fig. 6D):
this metric measures the duration taken for each task and their total sum. We include the duration of the navigation procedure and the insertion procedure, excluding the time taken by the user to specify goal waypoints.
VI. Results and Discussion
We discuss the results for the metrics provided in Section V. During the 30 autonomous SI trials, the needle-tip reached the desired retinal surface goal with mean error of 20 ± 6μm w.r.t the L2-norm metric as shown in Fig. 6A. As shown in Fig. 6B, the subretinal goal was reached with mean error of 26 ± 12μm. Note that reaching the desired depth is the most critical requirement while reaching , to avoid potential damage to the retina, and the mean error along the depth dimension was 7 ± 11μm. In comparison, such level of accuracy may be difficult to achieve for human surgeons, since the mean hand-tremor amplitude during retinal surgery is approximately 180μm [2]. Our navigation accuracy in reaching the subretinal goal is comparable to prior work of [6], which reported mean error of 32±4μm and of [5], which reported 50.4±29.8μm. Note that the detailed experimental conditions, constraints, and workflow design vary significantly between these studies, thus we avoid making any claims regarding which work demonstrates superior performance. Throughout the entire procedure, the mean RCM error was kept low at 6 ± 4μm as shown in Fig. 6C. The mean total duration of the surgery was 55 ± 10.8 seconds as shown in Fig. 6D.
We also show a preliminary comparison to a human performing SI in robot-assisted mode. The control scheme follows the prior work described in [17]. A total of 10 trials were performed. Qualitatively, as shown in Fig. 6F, the autonomous trajectory appears more stable and efficient. Quantitatively, the robot-assisted trajectory was less accurate in reaching the top-down clicked goal. Specifically, the mean navigation error for robot-assisted mode was 59 ± 19 μm (Fig. 6E), while for autonomous mode it was 19 ± 6μm (2D Nav Error in Fig. 6A) with p = 4.15 × 10−12 using a two-sided T-test. A closer side view comparison in Fig. 6G shows that, for the autonomous mode, the needle insertion trajectory was nearly perfect along the needle’s axis. However, this is difficult to achieve in robot-assisted mode, since this constraint is difficult for humans to enforce by hand. We quantitatively show the deviation of the needle-tip trajectory from the originally intended insertion axis in Fig. 6H, by considering a commonly-used average displacement (ADE) and final displacement error (FDE) metric for comparing trajectories. Both ADE and FDE errors are near zero in autonomous mode, whereas in robot-assisted mode, the errors are in the order of hundreds of micrometers.
We also note that while all 30 autonomous trials were successful, 2 trials required human intervention. Intervention was necessary during the initial 2D navigation step above the retina due to perception error, when the CNN failed to detect the needle-tip position in the microscope image. When this occurred, the operator simply intervened and initialized the needle at a different location and the trial was resumed. This error did not lead to any damage on the retina, since the errors occurred during the navigation step above the retinal surface.
Also, our system was demonstrated on a simplified open-sky eye filled with vitreous, which introduced some distortion. In a closed-eye setting, however, there will be other optical elements such as the patient’s lens and cornea, which will introduce further distortion. Such distortions may affect our 2D visual-servoing strategy (Section IV-D) and we provide explanation of how our approach may still work in heavier distortive settings. Specifically, our 2D visual-seroving strategy relies on a Jacobian matrix that assumes a linear relationship between and (Section IV-D). Generally, this relationship holds locally even in a distortive environment. Beacuse this Jacobian is updated when small local tool-tip motion is observed (> 8 pixels and > 20μm in robot coordinates, see Setion IV-D), as long as the linear relation generally holds within such local environment, our 2D navigation approach would work. In practice, the observed phenomena in our open-sky eye setting (filled with distortive vitreous) was that as the needle-tip navigated to the clicked goal, the Jacobian was constantly updated such that it locally adpated to the distortive environment, which ultimately enabled precise navigation to the goal.
VII. Conclusion
We demonstrated a real-time autonomous system and workflow for subretinal injection. This was enabled by the global view provided by microscope images and dynamically-aligned B-scan images that tracked the needle axis for real-time depth feedback. Future work will consider extending this work to closed pig eye settings and other dextrous surgical manipulation tasks.
Supplementary Material
Acknolwedgement
This work was supported by U.S. National Institutes of Health under the grants number 2R01EB023943-04A1 and 1R01 EB025883-01A1, and partially by JHU internal funds
Footnotes
References
- [1].Berger W, Kloeckener-Gruissem B, and Neidhardt J, “The molecular basis of human retinal and vitreoretinal diseases,” Progress in Retinal and Eye Research, vol. 29, no. 5, pp. 335–375, 2010. [Online]. Available: https://www.sciencedirect.com/science/article/pii/S135094621000025X [DOI] [PubMed] [Google Scholar]
- [2].Singh S and Riviere C, “Physiological tremor amplitude during retinal microsurgery,” in Proceedings of the IEEE 28th Annual Northeast Bioengineering Conference (IEEE Cat. No.02CH37342), 2002, pp. 171–172. [Google Scholar]
- [3].Xue K, Edwards T, Meenink H, Beelen M, Naus G, Simunovic M, De Smet M, and MacLaren R, Robot-Assisted Retinal Surgery: Over-coming Human Limitations, 05 2019, pp. 109–114. [Google Scholar]
- [4].Cehajic-Kapetanovic J, Xue K, Edwards TL, Meenink TC, Beelen MJ, Naus GJ, de Smet MD, and MacLaren RE, “First-in-human robot-assisted subretinal drug delivery under local anesthesia,” Am. J. Ophthalmol, vol. 237, pp. 104–113, May 2022. [DOI] [PubMed] [Google Scholar]
- [5].Mach K, Wei S, Kim JW, Martin-Gomez A, Zhang P, Kang JU, Nasseri MA, Gehlbach P, Navab N, and Iordachita I, “Oct-guided robotic subretinal needle injections: A deep learning-based registration approach,” in 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). IEEE, 2022, pp. 781–786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Dehghani S, Sommersperger M, Zhang P, Martin-Gomez A, Busam B, Gehlbach P, Navab N, Nasseri MA, and Iordachita I, “Robotic navigation autonomy for subretinal injection via intelligent real-time virtual ioct volume slicing,” 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Iordachita II, De Smet MD, Naus G, Mitsuishi M, and Riviere CN, “Robotic assistance for intraocular microsurgery: Challenges and perspectives,” Proceedings of the IEEE, vol. 110, no. 7, pp. 893–908, 2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Gerber MJ, Hubschman J-P, and Tsao T-C, “Automated retinal vein cannulation on silicone phantoms using optical-coherence-tomography-guided robotic manipulations,” IEEE/ASME Transactions on Mechatronics, vol. 26, no. 5, pp. 2758–2769, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Tang EM, El-Haddad MT, Patel SN, and Tao YK, “Automated instrument-tracking for 4d video-rate imaging of ophthalmic surgical maneuvers,” Biomed. Opt. Express, vol. 13, no. 3, pp. 1471–1484, Mar 2022. [Online]. Available: https://opg.optica.org/boe/abstract.cfm?URI=boe-13-3-1471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Wei S, Guo S, and Kang JU, “Analysis and evaluation of bc-mode oct image visualization for microsurgery guidance,” Biomedical optics express, vol. 10, no. 10, pp. 5268–5290, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wei S, Kim JW, Martin-Gomez A, Zhang P, Iordachita I, and Kang JU, “Region targeted robotic needle guidance using a camera-integrated optical coherence tomography,” in Optical Coherence Tomography. Optica Publishing Group, 2022, pp. CM2E–6. [Google Scholar]
- [12].agersand MJ and Nelson RC, “Adaptive differential visual feedback for uncalibrated hand-eye coordination and motor control,” 1994. [Google Scholar]
- [13].Broyden CG, “A class of methods for solving nonlinear simultaneous equations,” Mathematics of Computation, vol. 19, pp. 577–593, 1965. [Google Scholar]
- [14].Kim JW, Zhang P, Gehlbach PL, Iordachita II, and Kobilarov M, “Towards autonomous eye surgery by combining deep imitation learning with optimal control,” Proceedings of machine learning research, vol. 155, pp. 2347–2358, 2020. [PMC free article] [PubMed] [Google Scholar]
- [15].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in Medical Image Computing and Computer-Assisted Intervention. Springer, 2015, pp. 234–241. [Google Scholar]
- [16].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778. [Google Scholar]
- [17].Üneri A, Balicki MA, Handa J, Gehlbach P, Taylor RH, and Iordachita I, “New steady-hand eye robot with micro-force sensing for vitreoretinal surgery,” in Biomedical Robotics and Biomechatronics (BioRob), 2010 3rd IEEE RAS and EMBS International Conference on. IEEE, 2010, pp. 814–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.