Abstract
The rapid advancement in Artificial Intelligence (AI) and big data has developed significance in the water sector, particularly in hydrological time-series predictions. Recurrent Neural Networks (RNNs) and Long Short-Term Memory (LSTM) networks have become research focal points due to their effectiveness in modeling non-linear, time-variant hydrological systems. This review explores the different architectures of RNNs, LSTMs, and Gated Recurrent Units (GRUs) and their efficacy in predicting hydrological time-series data.
-
•
RNNs are foundational but face limitations such as vanishing gradients, which impede their ability to model long-term dependencies. LSTMs and GRUs have been developed to overcome these limitations, with LSTMs using memory cells and gating mechanisms, while GRUs provide a more streamlined architecture with similar benefits.
-
•
The integration of attention mechanisms and hybrid models that combine RNNs, LSTMs, and GRUs with other Machine learning (ML) and Deep Learning (DL) has improved prediction accuracy by capturing both temporal and spatial dependencies.
-
•
Despite their effectiveness, practical implementations of these models in hydrological time series prediction require extensive datasets and substantial computational resources.
Future research should develop interpretable architectures, enhance data quality, incorporate domain knowledge, and utilize transfer learning to improve model generalization and scalability across diverse hydrological contexts.
Keywords: Recurrent neural networks, Long short-term memory, Deep learning, Hydrological prediction, Artificial intelligence
Method name: RNN and LSTM variants for Time Series Prediction.
Graphical abstract
Specifications table
| Subject area: | Engineering |
| More specific subject area: | Modeling and Forecasting |
| Name of the reviewed methodology: | Recurrent Neural Networks and Long Short-term Memory |
| Keywords: | Recurrent Neural Networks, Long Short-Term Memory, Deep Learning, Hydrological Prediction, Artificial Intelligence |
| Resource availability: | N.A. |
| Review questions: | RQ-1: What are the key architectural differences and advancements between traditional RNNs, LSTM networks, and GRU networks, and how do these differences impact their performance in hydrological predictions? RQ-2: How have LSTM networks been adapted or modified to improve their accuracy and efficiency in hydrological time series forecasting, and what innovative methodologies have been introduced in recent research? RQ-3: In what ways have RNN, LSTM, and GRU models been implemented in hydrological applications, and what case studies highlight their effectiveness and limitations in real-world scenarios? RQ-4: What are the significant trends in the application of hybrid models in hydrological predictions over the past decade? RQ-5: What gaps exist in the current literature on the use of RNNs, LSTMs, and GRUs for hydrological forecasting, and what future research directions are suggested to address these gaps and enhance the models' predictive capabilities? |
Background
Developments in Deep learning (DL) techniques have enabled scientists to extract facts from a wide range of data types [1]. Given the several features of input time series data, DL includes recurrent neural networks (RNNs) [[2], [3], [4], [5], [6], [7]], deep neural networks (DNNs) [[8], [9], [10], [11], [12]], Feedforward neural networks (FFNNs) [[13], [14], [15]], and convolutional neural networks (CNNs) [[16], [17], [18], [19], [20]]. While CNNs and DNNs struggle with temporal information in input data, RNNs excel in fields that need sequential information, such as time series, text, audio, and video [21]. This subject extends FFNNs to allow variable or indefinite length sequences, covering notable recurrent architectures such as LSTM and gated recurrent units (GRUs) [22]. RNNs can be divided into discrete-time and continuous-time RNNs [5]. Cyclic connections are a critical component of RNN architecture, allowing the network to update its current state based on previous states and current input [3]. Fully connected RNNs [23] and selective RNNs [24], which use typical recurrent cells such as sigma cells, have proven effective in specific applications. However, when there is a substantial gap between crucial input data points, these RNNs struggle to connect the dots [24]. RNNs overcome short-term dependencies caused by challenges such as the vanishing or expanding gradient problem. However, RNNs have limits. Pre-segmented training data is required, as is output post-processing to convert it into labeled sequences [22]. To address “long-term dependencies,” Hochreiter and Schmidhuber (1997) created LSTM [25]. The most prominent advances in RNNs have been driven by LSTM, making it a focus point in DL. RNN and the LSTM networks are sequential frameworks that use prior sequence items to predict future components. Recent research has shown that processing sequences bidirectionally can improve performance, particularly in offline processing settings where sequence fragments can be stored and analyzed rather than streamed [26]. As a result, bidirectional RNNs [2] and bidirectional LSTMs [27,28] were developed to process sequences in both forward and backward directions. LSTMs and RNNs have been widely adopted for various tasks, including hydrological prediction [[29], [30], [31]], speech recognition [28,[32], [33], [34]], trajectory prediction [[35], [36], [37], [38]], and correlation analysis [[39], [40], [41], [42]].
In predicting hydrological components, traditional forecasting models struggle to capture the complex temporal dependencies and non-linear relationships present in hydrological data [43]. Many researchers have used LSTM and RNNs to solve various problems in water treatment and management systems. For example, Aslam et al. (2021) compared advanced DL models (LSTM, GRU) to conventional models (RNN, Support Vector Regression (SVR), FFNN) for forecasting global solar radiation (GSR) and found that DL models performed better [44]. For flood forecasting, Kao et al. (2020) suggested an encoder-decoder model based on LSTM [45]. Pham et al. (2021) investigated flood susceptibility modeling with DL [46]. Ni et al. (2020) employed LSTM for streamflow and rainfall prediction, building two models: one incorporating the wavelet network with LSTM and the other combining CNNs with LSTM to improve performance [47]. Li et al. (2023) proposed a soft sensor water quality forecasting system. This model's reliability for anaerobic processes is estimated using evaluation and probability projection [48]. Similarly, Wongburi and Park (2023) developed prediction models for runoff variables using basic RNN and LSTM architectures. The efficiency of these models is carefully validated using different training data conditions and model designs [49]. For precipitation forecasting, Waqas et al. (2024) used hybrid models, a combination of LSTM and RNNs, to decompose wavelets for daily and monthly forecasts [29,30]. LSTM-RNNs were also employed by Wangwongchai et al. (2023) to estimate the missing daily rainfall dataset [50]. It has numerous uses in water quality prediction; for example, Liu et al. (2019) used the LSTM network to develop a model to assess drinking water quality in the Yangtze River basin. The LSTM network can forecast drinking water's pH, DO, COD, and NH3-N concentrations [51]. The LSTM network was also used to predict water temperature [52]. Barzegar et al. (2020) suggested a hybrid model that employs CNN and LSTM to determine DO and chlorophyll-a (Chl-a) concentrations in Greece's Small Prespa Lake. Their findings demonstrated that the combined CNN-LSTM model outperformed standalone machine learning (ML) models such as CNN, LSTM, SVR, and decision trees (DTs) [53].
The selection and implementation of RNNs and LSTM variants, independently or in combination with other models, necessitates a profound grasp of their architectural intricacies and operational mechanisms. While numerous review studies explain these aspects, a critical need remains for a comprehensive exploration of their recent applications in hydrological time-series predictions. Therefore, this review stems from the need to enhance hydrological forecasting models by leveraging advancements in RNN, LSTM, and GRU architectures. Traditional models struggle with complex temporal dependencies and non-linear relationships, while recent DL techniques have demonstrated superior performance. By examining theoretical foundations and practical applications, this review aims to bridge gaps in the current literature and highlight the potential of these advanced models in improving hydrological predictions. This study investigates RNNs, GRUs, and LSTM networks, with advancements in LSTM cell design that set it apart from other RNN architectures. The study is structured into three main sections, transitioning from theoretical foundations to practical applications. The first section studies RNN, LSTM, and GRU components, their architecture, interactions, and implementation methodologies, catering to readers seeking a deep theoretical understanding of these models. The second section presents applications of RNNs, LSTMs, GRUs, and their variants in hydrological time series forecasting. Finally, the review assesses the deployment of these models in hydrological predictions over recent years, concluding with insights that have the potential to enhance the accuracy and efficiency of hydrological forecasting models.
Method details
This review was initiated with a comprehensive search strategy to identify relevant literature on RNNs, LSTM, and GRU networks. The search included papers containing the terms “Recurrent Neural Networks” or “RNN,” “Long Short-Term Memory” or “LSTM,” and “Gated Recurrent Unit” or “GRU” in their titles, abstracts, or keywords. Databases and search engines such as Google Scholar, SpringerLink, ScienceDirect, IEEE Xplore, ACM Digital Library, and Web of Science were utilized. To ensure the inclusion of high-quality and impactful research, we focused on papers published in reputable peer-reviewed journals. We presented at major conferences, including those on Neural Data Processing Systems (NeurIPS), AI, Deep Learning (DL), and ML, with a focus on hydrological predictions.
Emphasis was placed on papers that significantly contributed to the theoretical advancements or practical applications of LSTM, including foundational works, innovative methodologies, and impactful case studies. Given the rapid evolution of the field, priority was given to recent publications to capture the latest advancements and trends. The initial search yielded a total of 223 papers. The screening process involved a review of titles and abstracts to assess the relevance of each paper, followed by a full-text review for those that passed the initial screening. Duplicate papers were identified and removed to ensure each study was considered only once. The selected papers extracted critical information consisting of authorship, publication year, title, source of publication, research objectives, hypotheses, methodologies, key findings, contributions, applications in hydrological predictions, limitations, and future research directions. The extracted data was synthesized to provide a comprehensive overview of advancements in LSTM research, structured to cover foundational concepts, methodological innovations, practical implementations, significant findings, and emerging trends.
Hydrological time series prediction and RNN, LSTM, and GRU-based models
Hydrological time series prediction is a critical study area for managing water resources in the face of climate change and increasing water demand [54]. ML and DL address different hydrological challenges, such as river flow, rainfall, and water levels [55,56]. RNN, Long LSTM, GRU variants, and hybrid models have emerged as powerful tools for predicting various hydrological variables [56]. This section synthesizes the application of these models, the types of input datasets used, and their effectiveness in different hydrological prediction scenarios. RNNs have shown utility in short-term and seasonal hydrological predictions [57]. For example, in sequence-based hydrological downscaling, RNNs have improved over traditional methods, providing more accurate short-term predictions [58]. Similarly, LSTMs have been employed to predict river flow [59], rainfall-runoff prediction [60], and lake water levels [61]. Studies have shown that LSTMs outperform traditional methods and basic RNNs, particularly for long-term predictions. For example, LSTM models have been used to predict lake water levels with significant accuracy for 60-day ahead forecasts, showing a 78 % improvement over the Naïve Method [62]. GRU models have been shown to handle longer prediction periods effectively, such as 120-day ahead forecasts of water levels, where GRU achieved better performance metrics compared to both RNNs and LSTMs [62]. GRUs allow faster training times, making them suitable for real-time hydrological predictions where quick model updates are necessary [63]. Hybrid models, which combine and integrate RNN, LSTM, and GRU algorithms with other statistical, ML, and DL techniques such as LSTM-CNN [64], wavelet decomposed LSTM [65], wavelet decomposed AutoRegressive Integrated Moving Average (ARIMA)-LSTM [66], hybrid RNN-LSTM [67], hybrid LSTM-GRU [56,68] and ARIMA-GRU [69] has also gained traction in hydrological time series prediction. These models leverage the strengths of individual components to improve overall predictive performance. For example, hybrid models that combine CNNs with LSTMs (CNN-LSTM) have been used to predict outlet water temperature [70]. The CNN component captures spatial features from the data, while the LSTM component models the temporal dependencies. Such hybrid models have shown improved accuracy over standalone LSTM or CNN models, particularly in complex urban environments where both spatial and temporal patterns are crucial.
The effectiveness of standalone RNN, LSTM, and GRU models in hydrological prediction largely depends on the quality and quantity of input data [56]. High-dimensional datasets, which include various hydrological and meteorological variables, enhance the model's ability to capture complex relationships in the data [71]. One of the significant challenges in applying DL models to hydrological prediction is the availability of high-quality, continuous data [72]. Missing or inconsistent data can significantly impact the model's performance. Therefore, data preprocessing techniques such as imputation and normalization are critical steps in preparing datasets for model training [50]. Additionally, the interpretability of DL models remains a concern. The “black-box” nature of these models makes it difficult to understand how they arrive at their predictions, which can hinder their adoption in operational and policy-making contexts [73].
RNNs, LSTMs, GRUs, and hybrid models have demonstrated significant potential in hydrological time series prediction. While challenges such as data quality, model interpretability, and computational demands need to be addressed, the benefits of these models in improving water resource management and planning are substantial. Therefore, there is a need to understand these model's architectures and variants before implementation in hydrological predictions.
Theoretical foundations of the RNN and LSTM
DL has become a critical tool in hydrological time series forecasting and modeling, which provides a data-driven approach to predicting complex hydrological trends. Enhanced computational power and greater data availability have further pushed the adoption of DL in this domain [74]. Fig. 1 shows the types of DL and the iterative DL process in hydrology. This critical review is focused on RNN, LSTM, and GRU variants. RNNs are artificial neural networks (ANNs) created for sequence prediction applications. RRNs are excellent in the determination of temporal relationships in sequential data since they use internal memory to interpret variable-length input sequences.
Fig. 1.
(a): Different DL models and (b): the iterative DL prediction process.
Recurrent neural networks
Hopfield introduced the RNN in 1982 [75]. Neural network structures were developed based on the theory that human cognition relies on experience and memory [7]. In 1990, Elman introduced RNNs trained through backpropagation methods [23]. These methods underscored significant challenges in capturing long-term dependencies due to issues with vanishing and exploding gradients [23]. This issue was first identified by Bengio and Hochreiter in 1991, although their findings were written in German [76,77]. While gradient clipping can mitigate exploding gradients, vanishing gradients require more advanced solutions. One of the pioneering and influential methods was the LSTM model, introduced by Hochreiter and Schmidhuber [25]. RNNs are dynamic systems with internal states at each time step, facilitated by cyclic connections between neurons and potential self-feedback mechanisms. These feedback connections allow RNNs to transmit information from previous events to current processing steps, thus creating a memory of time series occurrences [[4], [5], [6]].
An RNN processes a sequence of inputs x1, x2…………., xt. At each time step “t,” the network updates its hidden state. “ by considering both the current input “xt” and the hidden state from the previous time step “ht-1” (Fig. 2). This hidden state is calculated using the following equation:
| (1) |
Fig. 2.
Flow Diagram of a Recurrent Neural Network (the sequential processing of inputs, hidden states, and outputs across time steps).
Where:
is the hidden state at the current time step “t.”
is the hidden state from the previous time step “t-1.”
xt is the input at the current time step “t.”
is the weight matrix associated with the hidden state.
is the weight matrix for the input.
is the bias vector.
“σ” is the non-linear activation function, typically a function like tanh or ReLU, which introduces non-linearity to the network and helps it learn complex patterns.
The output at each time step “yt” is computed using the current hidden state with the following equation:
| (2) |
Where:
is the output at time step “t.”
is the weight matrix for the output layer,
is the bias vector for the output,
“Φ” is the activation function used at the output layer.
RNNs are trained by minimizing a loss function L across the entire sequence, calculated as the sum of individual losses at each time step:
| (3) |
Where:
is the loss at time step “t.”
is the predicted output at time step “t.”
is the actual target output at time step “t.”
T is the total number of time steps in the sequence.
Backpropagation Through Time (BPTT) is used to train the RNN. The gradients of the loss function are computed by applying the chain rule to the sequence. The gradient of the loss concerning the hidden state at time step “t” is:
| (4) |
Where:
is the gradient of the loss for the hidden state ,
is the gradient of the loss for the output ,
is the gradient of the output for the hidden state,
is the gradient of the loss for the previous hidden state ,
is the gradient of the hidden state at time step “t − 1” for the hidden state at time step “t”.
This recurrent computation is at the core of BPTT, enabling the RNN to learn from the entire sequence and adjust the weights to minimize the loss.
RNNs can be seen as FFNNs enhanced with loops in their architecture. As shown in Fig. 3, an RNN, like an FFNN, includes an input layer (with nodes such as x1, x2, etc.), a hidden layer (with nodes such as h1, h2, etc.), and an output layer. The critical difference lies in the interconnections of the hidden layer nodes. These connections are unidirectional, meaning h2 depends on h1 (and x2), and h3 depends on h2 (and x3). This configuration ensures that each hidden node relies on the previous hidden node, creating a sequential process. This interconnected structure allows RNNs to retain and leverage the context of preceding inputs, enhancing prediction accuracy.
Fig. 3.
Architectures of general FFNNs and RNNs.
The vanishing gradients issue occurs when gradients of the loss function of RNN parameters become exceedingly small or large over time. As shown in Fig. 4, the color gradient of nodes in the unfolded network signifies their responsiveness to initial inputs, which diminishes as subsequent inputs overwrite activations in the hidden layer, leading the network to 'forget' initial inputs.
Fig. 4.
Vanishing gradient problem for RNNs.
Long short-term memory (LSTM)
The LSTM is meant to overcome the problems of exploding and vanishing gradients during training, even after long delays [78]. This problem is alleviated using a constant error carousel (CEC) that holds the error within each unit's cell [25]. Such cells are recurrent networks with a distinct topology in which the CEC is supplemented by input and output gates, resulting in a memory cell. The self-recurrent links within these cells allow feedback with a one-step delay [25]. The term “long short-term memory” originates from the concept that simple RNNs possess long-term memory encoded in weights that change slowly during training (Fig. 4), capturing overarching information about the data. Short-term memory is represented by transient activations exchanged between nodes [22]. The LSTM model features a memory cell composed of simpler nodes arranged in a predefined connectivity pattern, distinguished by the inclusion of multiplicative nodes [79]. LSTMs are designed to ease the challenges associated with long-term dependencies [30]. LSTM excels at retaining information over extended durations, which is inherent to their operational design rather than a learned behavior. While all RNNs are cyclic structures comprising a single tanh layer (Fig. 5(a)). In contrast, LSTMs maintain this sequential architecture with a repeating module structure that integrates four interacting layers. Within an LSTM, the repeating module consists of four interconnected layers (Fig. 5(b)).
Fig. 5.
The difference between LSTM and RNN (a): RNN contains a single layer, and (b): LSTM contains four interacting layers.
Memory cell
The LSTM architecture's memory cell incorporates an internal state and multiplicative gating mechanisms, each overseeing distinct functions (Fig. 5(b)). These functions include (i) modulation of the impact of new input vectors on the internal state via the input gate, (ii) control of the retention or disposal of information within the internal state through the forget gate, and (iii) determining the extent to which the internal state of the neuron contributes to the cell's output via the output gate.
Gates in LSTM memory cell
The LSTM design employs gating mechanisms that accept input vectors from the current time (t) and hidden state vectors from the previous time step, as shown in Fig. 6(a). These vectors change three fully linked layers, each using a sigmoid activation function so that the resulting gate values—the input gate, forget gate, and output gate—are confined within the interval [0,1]. An additional input node, typically activated by a tanh function, plays a crucial role in this process, as shown in Fig. 6(b). To understand it numerically, assume there are “h” hidden units, “n,” and g inputs. The input is , and the hidden state from the previous time step is . Similarly, the gates at time step t are specified as follows. The input gate is . The forget gate is . The output gate is . and can be determined using the following formulas:
| (5) |
| (6) |
| (7) |
where , , are biases and , , and , , are weights.
Fig. 6.
(a): In an LSTM model, many key components contribute to its functionality. The memory cell includes input gates, output gates, forget gates, and input nodes, each playing a crucial role in regulating information flow (b): The internal state of the memory cell maintains a record of past information, updated through interactions with these gates. (c): the hidden state of the LSTM model serves as its output, capturing the network's learned representations and insights from the input sequence.
Input node and internal state
In LSTM networks, the computation at the input node involves three gates, each employing an activation function with a specific value range. At “t,” the input gate. “” controls the incorporation of new data via. “” during the forget gate. “ controls the extent to which the previous cell is recalled. These gates utilize the elementwise Hadamard product, pointwise operator . Mathematically, this relationship can be expressed as:
| (8) |
Where and are weight and is a bias.
Hidden state
LSTMs differ from basic RNNs in that they employ gating mechanisms in the hidden state. These mechanisms allow precise control over when to update or reset the hidden state, addressing issues like vanishing and exploding gradients. During training, these mechanisms are learned, enabling LSTMs to retain valuable information early in a sequence, skip irrelevant observations, and reset the state as needed. In LSTMs, the output gate regulates how much the memory cell's internal state influences subsequent layers. A high gate value (near 1) allows considerable influence, while a low value (near 0) limits impact, enabling the cell to accumulate information over time and impact the network strategically.
| (9) |
Gated recurrent unit
Cho et al. (2014) introduced the GRU, a kind of RNN architecture [80]. It was created to solve the drawbacks of conventional RNNs. GRUs are a popular option since they maintain comparable performance while simplifying the architecture of LSTM networks [81]. GRU attempted to improve the architecture of LSTMs. These gates control the information flow within the unit, allowing the model to identify temporal relationships and manage long-term memory [82,83] (Fig. 7).
Fig. 7.
Difference between LSTM and GRU.
The update gate ( controls how much of the previous memory will be carried over to the next step, as shown in Fig. 8. It merges the features of the input and forgets the gates in LSTM. The reset gate ( controls how much of the previous memory is to be forgotten. It helps the model decide the extent to which the past state should be ignored. The is defined as follows:
| (10) |
Fig. 8.
Architecture of Gated Recurrent Unit.
Here, denotes the weight matrix at (, is the concatenation of the prior hidden state with the current input , where σ is the sigmoid activation function.
| (11) |
is the weight matrix at (.
The current memory ( represents a possible hidden state that includes the reset gate. It mixes the new input and the previous concealed state.
| (12) |
W is the weight matrix, and tanh is the hyperbolic tangent activation function.
The final hidden state ( is a mixture of the prior hidden state and the current memory content , operated by the update gate.
| (13) |
Bidirectional LSTM
In a basic LSTM, the hidden outputs are passed between LSTM layers to both neighboring LSTM cells and used as inputs for the subsequent LSTM cell [22,74]. A Bidirectional LSTM architecture enhances this by allowing information to flow forward and backward (Fig. 9). In a Bidirectional LSTM, the forward flow captures system variations, while the backward flow helps to smooth the predictions [84]. The outputs from the forward and backward paths are then concatenated. The output is obtained by combining the results from both directions. The governing equations for a Bidirectional LSTM are as follows:
| (14) |
| (15) |
| (16) |
Fig. 9.
The architecture of Bi-LSTM.
Here, is a hidden state at time step iii for the forward LSTM layer, and “f” is the activation function, such as ReLU or tanh, applied to the weighted sums. are weight matrices for the input-to-hidden connections in the forward LSTM layer. are weight matrix for the hidden-to-hidden connections in the forward LSTM layer and V weight matrix used to transform the concatenated hidden states from the forward and backward LSTM layers.
Stacked LSTM
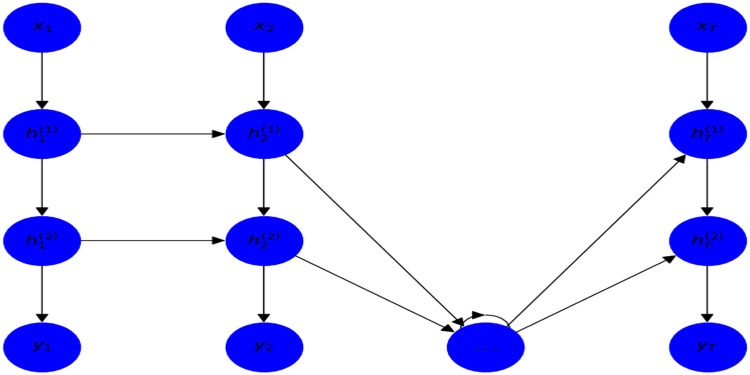
Stacked LSTM networks are composed of multiple LSTM layers stacked on top of one another, which is the model used to detect more complicated patterns and connections in the data [85,86]. Each LSTM layer evaluates data sequences and feeds its output into the next layer[85]. In a stacked LSTM network, the hidden state output of one LSTM layer is used as input for the next LSTM layer, as shown in Fig. 10.
Fig. 10.
The architecture of stacked LSTM.
Mathematically, the first LSTM layer:
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
Mathematically, the second LSTM layer:
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
Output Layer:
| (29) |
Where, are the hidden states of the first and second LSTM layers, respectively, at time step t. are the cell states of the first and second LSTM layers, respectively, at time step t. W and V are weight matrices.
Convolutional LSTM
Convolutional LSTM (ConvLSTM) networks enhance the regular LSTM [87] by introducing convolutional elements into the LSTM design to handle spatiotemporal data [88], as shown in Fig. 11. ConvLSTM excels in spatially organized data applications like precipitation forecasting [89] and hydrological modeling [64]. ConvLSTM replaces LSTM's fully linked operations with convolutional operations. It enables the network to capture spatial and temporal dependencies in the data [88]. The ConvLSTM architecture can be stated as follows:
- Input Gate:
(30) - Forget Gate:
(31) - Cell State:
(32) - Output Gate:
(33) - Hidden State:
(34)
Fig. 11.
The architecture of Convolutional LSTM memory cell.
Hybrid models in time series prediction
Many hybrid LSTM models have been implemented for time series prediction in recent years, as mentioned in Table 1. The LSTM-CNN model, applied for rainfall prediction in India in 2022, improved accuracy by capturing spatial features and temporal dependencies, though at the cost of high computational requirements [90]. Similarly, the LSTM-SVR model, used for streamflow forecasting in Malaysia in 2023, enhanced prediction accuracy by combining LSTM's temporal modeling capabilities with SVR's handling of non-linear relationships despite its sensitivity to hyperparameter settings [64]. The wavelet decomposed LSTM model for precipitation forecasting in Thailand achieved higher accuracy than other models by capturing non-linear relationships through wavelet decomposition, while it requires more data for practical training [29]. In Japan, the LSTM-SOM model, developed for anomaly detection in 2019, showed improved performance by clustering input features with SOM before feeding them into LSTM, but dependency on input data quality was a limitation [91]. The LSTM-GRU hybrid model, designed for short-term runoff prediction in China in 2020, enhanced computational efficiency and prediction accuracy compared to traditional LSTM models. It necessitated more training data than simpler models [92]. For streamflow prediction in China in 2023, the LSTM-DNN model demonstrated improved generalization and robustness by integrating deep neural networks with LSTM. It was sensitive to the design of its architecture [93]. The LSTM-Attention model applied for multi-step ahead prediction in South Korea in 2023 advanced from an attention mechanism that focused on relevant input features, enhancing forecasting performance, and complexity required careful tuning of attention parameters [94]. The LSTM-Transformer model, used for time series power forecasting in China in 2023, combined LSTM's sequential modeling with the Transformer's self-attention mechanism to improve accuracy but at a higher computational and memory cost [95]. In Algeria in 2022, the LSTM- Support Vector Machine (SVM) model for water quality prediction had good accuracy by integrating SVM with LSTM, though it was sensitive to kernel and regularization parameter choices [96]. Lastly, the LSTM-RNN model for extreme event prediction in China in 2021 improved forecasts of extreme hydrological events by combining RNN with LSTM, yet its complex structure limited interpretability [97,98].
Table 1.
Overview of implementation of different hybrid LSTM models in time series prediction.
| Hybrid Model | Purpose | Country/Region | Year | Study Findings | Limitations | Sources |
|---|---|---|---|---|---|---|
| LSTM-CNN | Rainfall Prediction | India | 2022 | Improved accuracy in capturing spatial features and temporal dependencies | High computational cost | [90] |
| LSTM-SVR | Streamflow forecasting | Malaysia | 2023 | Enhanced prediction accuracy by combining LSTM's temporal modeling with SVR's non-linear relationship handling | Sensitivity to hyperparameters | [64] |
| Wavelet decomposed STM | Precipitation Forecasting | Thailand | 2024 | Enhanced prediction accuracy by decomposed wavelet LSTM and well-captured non-linear relationship handling | May require more data for training | [29] |
| LSTM-SOM | Anomaly detection | Japan | 2019 | Improved anomaly detection using SOM to cluster input features before feeding into LSTM | Dependency on the quality of input data | [91] |
| LSTM-GRU | Short-term runoff prediction | China | 2020 | Enhanced computational efficiency compared to traditional LSTM while maintaining prediction accuracy. | It requires more data for training compared to simpler models | [92] |
| LSTM-DNN | Streamflow Prediction | China | 2023 | Improved generalization and robustness in predicting streamflow using deep neural networks | Sensitivity to architecture design choices | [93] |
| LSTM-Attention | Multi-step ahead prediction | South Korea | 2023 | Enhanced performance in multi-step ahead streamflow forecasting by attending to relevant input features | Complexity in tuning attention mechanism parameters | [94] |
| LSTM-Transformer | Time series power forecasting | China | 2023 | Combined advantages of LSTM's sequential modeling and Transformer's self-attention mechanism for improved accuracy | Higher computational cost and memory requirements | [95] |
| LSTM-SVM | Water quality prediction | Algeria | 2022 | Enhanced prediction accuracy for water quality parameters by integrating SVM with LSTM | Sensitivity to kernel and regularization parameters | [96] |
| LSTM-RNN | Extreme event prediction | China | 2021 | Improved prediction of extreme hydrological events using a recursive neural network in conjunction with LSTM | Limited interpretability of complex model structures | [97,98] |
This comparative analysis evaluates the efficacy of RNNs, LSTM, and GRUs in hydrological forecasting. LSTM networks have superior performance over traditional RNNs and GRUs due to their advanced memory cells and gating mechanisms, which enhance their ability to capture long-term dependencies essential for hydrological predictions [93]. These attributes enable LSTMs to manage complex temporal relationships effectively, providing robust forecasts for streamflow and rainfall. In contrast, GRUs, although simpler by integrating input and forget gates into a single update gate, offer a balance between computational efficiency and performance, making them suitable for scenarios with limited resources [94]. Despite their efficiency, GRUs slightly lag LSTMs in capturing intricate dependencies. Traditional RNNs, constrained by vanishing and exploding gradient issues, are less effective for long-term forecasting but remain helpful for short-term predictions due to their simple structure and faster training times. LSTMs have been widely adopted in hydrological applications, including precipitation forecasting and flood prediction, owing to their capacity for handling long-term dependencies [29]. GRUs also show promise in hydrological predictions, providing a viable alternative to LSTMs in resource-constrained environments. RNNs, while less effective for long-term tasks, are valuable for short-term forecasts and baseline comparisons [99].
RNNs, LSTMs, and GRUs, as well as their derivatives, have been applied to a different hydrological problem (rainfall-runoff prediction); their advantages and shortcomings are shown in Table 2. RNNs have demonstrated efficacy in capturing temporal dependencies across various regions, including India and Taiwan, where they have been used for monthly and daily rainfall-runoff modeling. Despite their strength in short-term predictions and managing noisy data, RNNs are limited by the vanishing gradient problem, which hampers their ability to capture long-term dependencies, as observed in applications within the Bardha Watershed and North Carolina (e.g., [100,101]). LSTM networks, an advanced variant of RNNs, have been applied extensively across different geographical regions, including the UK and the USA, and are notably effective in addressing the vanishing gradient problem. LSTMs are proficient in capturing long-term dependencies and managing complex temporal relationships, making them suitable for diverse hydrological time series applications. However, their computational intensity and sensitivity to hyperparameters are significant drawbacks, as seen in studies involving watersheds in Iowa and the Brays Bayou watershed, Texas ([60,102]). GRU networks, a more simplified variant, have shown promise in short-term runoff prediction with faster training times and comparable performance to LSTM models. GRUs are particularly effective in real-time applications and managing high-dimensional data, as demonstrated in regions like Southeast China and Bhutan. However, their simplified architecture may struggle with capturing long-term dependencies, and their effectiveness diminishes with smaller datasets, as highlighted in studies conducted in the Fujian Province and the Wei River Basin, Shaanxi, China ([92,103]). The effectiveness of these networks varies depending on the application context, with each model exhibiting specific advantages and limitations that must be considered for optimal hydrological modeling outcomes.
Table 2.
RNN, LSTM, GRU variants in hydrological (Rainfall-runoff) times series predictions.
| Network Type | Application | Input Data | Output | Study Region | Effectiveness | Advantages | Disadvantages | Source |
|---|---|---|---|---|---|---|---|---|
| RNN | Monthly Rainfall-runoff modeling | Historical monthly rainfall and runoff data | Predicted runoff | Bardha Watershed, India | RNN-based model outperformed in both training and testing periods. | Captures temporal dependencies in data | vanishing gradient problem | [100] |
| Rainfall-runoff | Historical rainfall data | Predicted runoff | Five small Amazon Basins | RNN-based models are capable of spatial and temporal changes that influence long-term simulations | Suitable for short-term predictions | High requirement for historical data | [104] | |
| Rainfall-runoff | Gridded and Meteorological Historical rainfall and runoff data | Predicted daily runoff | North Carolina, USA | RNN models demonstrated the superiority of LSTM and GRU. | Effective in capturing seasonal variations | Limited ability to capture long-term dependencies | [101] | |
| Reconstruction of rainfall-runoff processes | Historical rainfall data | Predicted runoff | Taiwan's Wu-Tu watershed | RNN-based models are appropriate for the reconstruction of rainfall-runoff processes | Timely predictions, managing noisy data | Requires significant data preprocessing | [105] | |
| Rainfall-runoff | Historical rainfall and runoff data | Predicted runoff | Daning and Lushui River Basins, China | The proposed showed promising results in both river basins | Robust against data irregularities | Susceptible to outliers | [106] | |
| LSTM | Rainfall-runoff | Historical rainfall and runoff data | Predicted runoff | Two watersheds in the State of Iowa, USA | The proposed model is effective for short-term flood forecast applications | Addresses vanishing gradient problem | Computationally intensive, requires careful tuning of hyperparameters | [60] |
| Rainfall-runoff | Grided and meteorological observations and streamflow records and evaporation | Predicted runoff | 241 catchments in the UK | Findings showed the potential of the LSTM for hydrological modeling applications. | Effective in capturing long-term dependencies | High computational cost | [107] | |
| Rainfall-runoff | CAMELS and meteorological Historical datasets | Predicted runoff | Various River basins in the UK | The proposed model improved the performance of daily runoff prediction and multistep ahead prediction | Manages complex temporal relationships | Vulnerable to overfitting | [108] | |
| Rainfall-runoff | Historical rainfall data | Predicted runoff | Brays Bayou watershed, Texas | LSTM model improved the outputs | Suitable for various hydrological time series applications | Sensitivity to initial conditions | [102] | |
| Rainfall-runoff Simulation | Hourly Historical rainfall and runoff data | Predicted runoff | 3 water basins from different provinces of China | The proposed LSTM model showed better simulation and was more intelligent than the ANN model | Effective in learning non-linear relationships | Requires significant data preprocessing | [109] | |
| GRU | Short-term runoff prediction | Hourly Historical precipitation and runoff dataset | Predicted runoff | Fujian Province, Southeast China | GRU performs better than LSTM in some cases. | Simplified architecture compared to LSTM | May struggle with long-term dependencies | [92] |
| Rainfall-runoff prediction | Historical rainfall data | Predicted runoff | Simtokha, Bhutan | The proposed model outperformed LSTM | Faster training times | Less effective with small datasets | [110] | |
| Runoff Prediction | Historical meteorological and runoff data | Predicted runoff | Bailong River watershed, China | The developed model has better predictivity and adaptability. | Robust performance in real-time applications | Limited interpretability | [103] | |
| Runoff Prediction | Historical rainfall data | Predicted runoff | Wei River Basin, Shaanxi, China | The changes in this study enhanced the performance of the GRU runoff forecasting model. | Comparable performance to LSTM | Requires more data for training | [111] | |
| Runoff Estimation | Historical rainfall and runoff data | Predicted runoff | India | The result suggests that GRU's result is at par with its compatriot LSTM model | Manages high-dimensional data effectively | Limited by network depth and complexity | [112] |
Computational efficiency and resource consumption in hydrological prediction
The computational efficiency and resource consumption of RNNs, LSTMs, and GRUs in hydrological forecasting vary when dealing with large-scale datasets. Traditional RNNs, due to their simpler architecture, tend to have lower computational requirements and faster training times, making them suitable for smaller datasets or short-term predictions [79]. However, their inability to capture long-term dependencies efficiently limits their applicability in large-scale, complex hydrological forecasting [22].
LSTMs, equipped with advanced memory cells and gating mechanisms, excel in capturing long-term dependencies and non-linear relationships, but this comes at a high computational [78]. Their training times are longer and require substantial computational resources in large-scale applications [67]. LSTMs also demand more memory due to their complex architecture, which can be a limiting factor when working with extensive datasets [42].
GRUs offer a balance between LSTMs and RNNs, providing improved computational efficiency while still retaining some ability to capture longer dependencies [81]. GRUs have fewer parameters than LSTMs, which results in faster training times and lower resource consumption [113]. However, GRUs may struggle with very long-term dependencies and often require larger datasets for optimal performance. GRUs offer a middle ground for hydrological forecasting with more favorable computational efficiency than LSTMs [114].
Effectiveness to outliers, noisy data, and missing data
RNNs, LSTMs, and GRUs exhibit varying levels of robustness to outliers, noisy data, and missing data, which are common in time series datasets. RNNs tend to struggle the most with these issues due to their simple architecture. While they can capture temporal dependencies, RNNs are vulnerable to outliers, which can distort the learning process and lead to inaccurate predictions [22]. Their performance also decreases in the presence of noisy data, as they lack advanced mechanisms to filter out irrelevant variations [115]. Missing data further complicates RNN. It needs imputation techniques or data preprocessing before training to avoid model failure [116].
LSTM networks, in contrast, are more resilient to outliers and noise due to their memory cells and gating mechanisms, which allow them to selectively retain relevant information and filter out less critical data points. This capacity makes LSTMs more effective at handling noisy datasets commonly found in hydrological applications, such as rainfall-runoff modeling and streamflow forecasting [67]. LSTMs are also better equipped to manage missing data due to their ability to maintain context over long sequences, making them less reliant on continuous data [50]. However, even with their robustness, LSTMs can be sensitive to extreme outliers, which still necessitate preprocessing techniques such as outlier removal or normalization to maintain performance [43].
GRUs, like LSTMs, exhibit a higher tolerance to noise and missing data compared to traditional RNNs. Their simpler architecture, while faster and more computationally efficient, includes mechanisms to retain essential information, which helps them maintain stability in the presence of data inconsistencies [117]. GRUs handle noisy data effectively in applications like drought prediction and runoff modeling [101] but are less effective than LSTMs when managing complex temporal relationships in particularly noisy or incomplete datasets [113].
Impact of hyperparameter tuning on prediction performance
Hyperparameter tuning is critical in determining the prediction performance of RNNs, LSTMs, and GRUs [118]. The selection of appropriate hyperparameters, such as the number of layers, the size of hidden states, learning rate, batch size, and dropout rate, can impact a model's ability to capture temporal dependencies and generalize to unseen data [119,120]. Poorly tuned hyperparameters can result in underfitting or overfitting, where the model either fails to capture essential patterns or fits too closely to the training data, leading to poor generalization [121].
For RNNs, hyperparameter tuning is more straightforward compared to LSTMs and GRUs [122]. However, due to their susceptibility to the vanishing gradient problem, tuning learning rates and the number of hidden units are critical to stability and convergence. In the case of LSTMs, the challenge of tuning hyperparameters increases due to their complex architecture. The number of memory cells, the size of the hidden state, and the learning rate must be carefully optimized to balance performance and computational cost [65]. LSTMs are sensitive to the choice of hyperparameters, and improper tuning can exacerbate issues such as overfitting or instability during training [30].
GRUs, with their simple structure, are easier to tune than LSTMs but still require careful optimization of parameters such as the learning rate, number of layers, and batch size [123]. Due to their faster training times and reduced computational demands, GRUs are often more forgiving when it comes to hyperparameter selection [123,124]. However, as with LSTMs, suboptimal tuning can hinder the model's ability to capture long-term dependencies and lead to reduced prediction accuracy [78].
RNNs, LSTMs, and GRUs differ in their robustness to noisy, outlier-laden, or missing data. Their performance is highly dependent on effective hyperparameter tuning. The right combination of hyperparameters is crucial for unlocking the full potential of these models, particularly for complex hydrological forecasting tasks.
Potential limitations and factors affecting hydrological time series prediction
The vanishing gradient problem of RNNs delays the ability to capture long-term dependencies, which results in low accuracy in long-term predictions [5]. LSTMs address these issues but are computationally intensive and prone to overfitting with small datasets [64]. GRUs offer a balance but may struggle with complex, long-term dependencies and require larger datasets for optimal performance [117]. Familiar sources of error in these models include inaccurate input data, insufficient training data, model overfitting, and sensitivity to hyperparameter settings [120]. Solutions to these limitations involve using regularization techniques like dropout to reduce overfitting, employing data augmentation to enhance training sets, and optimizing hyperparameters through cross-validation [120]. Factors affecting hydrological time series prediction include the quality of input data [125] (e.g., historical rainfall or streamflow [30]), data preprocessing methods, model architecture, and the length of temporal sequences. External factors such as climate variability, land-use changes, and human interventions (e.g., data collection and handling [50]) also play a crucial role [126]. Tackling these factors requires incorporating diverse data sources, employing advanced preprocessing techniques (e.g., wavelet decomposition [65]), and utilizing ensemble methods to enhance robustness in hydrological forecasting.
Answers to RQs
RQ-1: What are the key architectural differences and advancements between traditional RNNs, LSTM networks, and GRU networks, and how do these differences impact their performance in hydrological predictions?
Traditional RNNs had a simple architecture consisting of a single recurrent layer that fed its output back into itself, allowing them to capture temporal dependencies. However, they suffered from the vanishing gradient problem, which hindered their ability to learn long-term dependencies. LSTM networks addressed this issue with a more complex architecture that included memory cells and gates (input, output, and forget) to regulate the flow of information, making them more effective at capturing long-term dependencies. GRU networks, a variant of LSTMs, simplified this architecture by combining the forget and input gates into a single update gate and merging the cell state and hidden state. These advancements enhanced the performance of LSTMs and GRUs in hydrological predictions by improving their ability to model complex temporal patterns and handle long-term dependencies more efficiently.
RQ-2: How have LSTM networks been adapted or modified to improve their accuracy and efficiency in hydrological time series forecasting, and what innovative methodologies have been introduced in recent research?
LSTM networks have been adapted in various ways to enhance their accuracy and efficiency in hydrological time series forecasting. One common approach is the integration of attention mechanisms, which allow the model to focus on relevant parts of the input sequence, thereby improving prediction accuracy. Hybrid models combining LSTMs with CNNs have been introduced to capture both spatial and temporal dependencies in hydrological data. Wavelet transform has been employed to decompose the time series into different frequency components before feeding them into LSTM networks, enhancing the model's ability to capture multi-scale features. Recent research also explores the use of encoder-decoder architectures and ensemble learning techniques to combine multiple LSTM models, leading to more robust and accurate predictions in hydrological forecasting.
RQ-3: In what ways have RNN, LSTM, and GRU models been implemented in hydrological applications, and what case studies highlight their effectiveness and limitations in real-world scenarios?
RNN, LSTM, and GRU models have been implemented in various hydrological applications, including streamflow prediction, rainfall forecasting, and water quality monitoring. For example, LSTM networks have been used to predict streamflow in river basins, demonstrating superior performance over traditional models due to their ability to capture complex temporal dependencies. In rainfall forecasting, hybrid models combining LSTMs with wavelet transforms have shown enhanced accuracy by effectively decomposing and modeling the time series data. However, these models face limitations, such as the need for large datasets for training and computational intensity. Case studies, such as the application of LSTM models in the Yangtze River basin for water quality prediction, highlight their effectiveness in capturing intricate patterns in hydrological data. They also underscore the challenges in model generalization and scalability across different hydrological settings.
RQ-4: What are the significant trends in the application of hybrid models in hydrological predictions over the past decade?
Over the past decade, significant trends in the application of hybrid models for hydrological predictions have emerged, focusing on integrating various machine learning techniques to enhance prediction accuracy. A prominent trend is the combination of LSTM networks with CNNs to capture both spatial and temporal dependencies in hydrological data, leading to improved performance in tasks like rainfall and streamflow forecasting. Another trend is the use of wavelet transforms to decompose time series data into different frequency components before feeding them into LSTM models, allowing for better multi-scale feature extraction. Ensemble learning techniques, which combine multiple models to improve robustness and accuracy, have also gained traction. These hybrid approaches have shown considerable promise in addressing the complex and non-linear nature of hydrological systems, leading to more reliable and accurate predictions.
RQ-5: What gaps exist in the current literature on the use of RNNs, LSTMs, and GRUs for hydrological forecasting, and what future research directions are suggested to address these gaps and enhance the models' predictive capabilities?
Despite significant advancements, several gaps exist in the current literature on using RNNs, LSTMs, and GRUs for hydrological forecasting. One crucial gap is the limited understanding of these models' interpretability, making it challenging to explain and trust their predictions. Additionally, there is a need for more research on the generalization capabilities of these models across different hydrological settings and regions. Data scarcity and quality also pose significant challenges, as high-quality, extensive datasets are crucial for training these models effectively. Future research should focus on developing more interpretable model architectures and enhancing data collection and preprocessing methods. Exploring the integration of domain knowledge into model training and leveraging transfer learning techniques can help improve model generalization. Addressing these gaps will enhance the predictive capabilities of RNNs, LSTMs, and GRUs in hydrological forecasting.
Conclusion
This review has examined the different variants and applications of RNN, LSTM, and GRU architectures in hydrological time-series forecasting.
-
•
Traditional RNNs, although foundational in temporal sequence modeling, are hindered by the vanishing gradient problem, restricting their ability to capture long-term dependencies. LSTM networks address this limitation through advanced architecture, incorporating memory cells and gating mechanisms to enhance their capacity for modeling extended temporal dependencies. GRU networks, as a streamlined variant of LSTMs, integrate the forget and input gates into a single update gate, offering comparable performance with improved computational efficiency.
-
•
Recent innovations, such as hybrid models combining LSTMs with other ML and DL models (e.g., CNNs), have shown improved capabilities. The use of wavelet transforms to decompose time-series data before LSTM processing has further enhanced these models' ability to capture multi-scale features. Encoder-decoder architectures and ensemble learning techniques, which aggregate multiple LSTM models, have also been explored, contributing to more robust and precise predictions.
-
•
Despite the promising outcomes of these models in applications such as streamflow prediction, rainfall forecasting, and water quality assessment, challenges persist regarding the need for extensive training datasets and the high computational demands of these models. As the field advances, addressing issues related to model interpretability, generalization, and data quality will be critical for improving the scalability and applicability of these architectures across diverse hydrological contexts.
Future research should focus on predicting and understanding the discrepancies between real and simulated environments to enhance model accuracy and applicability. By identifying the factors that cause these differences, researchers can develop more robust and generalizable models. This approach will be crucial in refining simulation techniques, improving data quality, and ensuring that models better reflect real-world hydrological systems.
Limitations
This review focuses on architectural and methodological innovations in RNN, LSTM, and GRU variants, with limited research on practical implementation challenges. Further empirical validation across diverse hydrological settings would be necessary to substantiate the findings and ensure their generalizability.
Ethics statements
No data was used in this research.
Funding
No Funding was used in this research.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The authors would like to express their gratitude to The Joint Graduate School of Energy and Environment (JGSEE), King Mongkut's University of Technology Thonburi and the Center of Excellence on Energy Technology and Environment (CEE), Ministry of Higher Education, Science (MHESI), Research and Innovation for providing us with this opportunity.
This research project is supported by King Mongkut's University of Technology Thonburi (KMUTT), Thailand Science Research and Innovation (TSRI), and the National Science, Research and Innovation Fund (NSRF) Fiscal year 2024.
Data availability
No data was used for the research described in the article.
References
- 1.Najafabadi M.M., et al. Deep learning applications and challenges in big data analytics. J. Big Data. 2015;2:1–21. [Google Scholar]
- 2.Schuster M., Paliwal K.K. Bidirectional recurrent neural networks. IEEE Transact. Signal Process. 1997;45(11):2673–2681. [Google Scholar]
- 3.Salehinejad H., et al. 2017. arXiv preprint. [Google Scholar]
- 4.Medsker L.R., Jain L. Recurrent neural networks. Des. Applic. 2001;5(64–67):2. [Google Scholar]
- 5.Grossberg S. Recurrent neural networks. Scholarpedia. 2013;8(2):1888. [Google Scholar]
- 6.Caterini A.L., et al. Recurrent neural networks. Deep Neur. Netw. Math. Framew. 2018:59–79. [Google Scholar]
- 7.Medsker L., Jain L.C. CRC press; 1999. Recurrent Neural networks: Design and Applications. [Google Scholar]
- 8.Grünig M., et al. Applying deep neural networks to predict incidence and phenology of plant pests and diseases. Ecosphere. 2021;12(10):e03791. [Google Scholar]
- 9.Szegedy C., Toshev A., Erhan D. Deep neural networks for object detection. Adv. Neur. Inf. Process. Syst. 2013:26. [Google Scholar]
- 10.Sze V., et al. Efficient processing of deep neural networks: a tutorial and survey. Proceed. IEEE. 2017;105(12):2295–2329. [Google Scholar]
- 11.Samek W., et al. Explaining deep neural networks and beyond: a review of methods and applications. Proceed. IEEE. 2021;109(3):247–278. [Google Scholar]
- 12.Larochelle H., et al. Exploring strategies for training deep neural networks. J. Mach. Learn. Res. 2009;10(1) [Google Scholar]
- 13.Bebis G., Georgiopoulos M. Feed-forward neural networks. IEEE Potent. 1994;13(4):27–31. [Google Scholar]
- 14.Svozil D., Kvasnicka V., Pospichal J. Introduction to multi-layer feed-forward neural networks. Chemometr. Intell. Lab. Syst. 1997;39(1):43–62. [Google Scholar]
- 15.Glorot X., Bengio Y. Proceedings of the thirteenth international conference on artificial intelligence and statistics. 2010. Understanding the difficulty of training deep feedforward neural networks. JMLR Workshop and Conference Proceedings. [Google Scholar]
- 16.O'shea K., Nash R. 2015. arXiv preprint. [Google Scholar]
- 17.Vedaldi A., Lenc K. Proceedings of the 23rd ACM international conference on Multimedia. 2015. Matconvnet: convolutional neural networks for matlab. [Google Scholar]
- 18.Gu J., et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018;77:354–377. [Google Scholar]
- 19.Kattenborn T., et al. Review on Convolutional Neural Networks (CNN) in vegetation remote sensing. ISPRS J. Photogrammetr. Remote Sens. 2021;173:24–49. [Google Scholar]
- 20.Li Z., et al. A survey of convolutional neural networks: analysis, applications, and prospects. IEEE Trans. Neur. Netw. Learn. Syst. 2021;33(12):6999–7019. doi: 10.1109/TNNLS.2021.3084827. [DOI] [PubMed] [Google Scholar]
- 21.Yu J., de Antonio A., Villalba-Mora E. Deep learning (CNN, RNN) applications for smart homes: a systematic review. Computers. 2022;11(2):26. [Google Scholar]
- 22.DiPietro R., Hager G.D. Elsevier; 2020. Deep learning: RNNs and LSTM, in Handbook of Medical Image Computing and Computer Assisted Intervention; pp. 503–519. [Google Scholar]
- 23.Elman J.L. Finding structure in time. Cogn. Sci. 1990;14(2):179–211. [Google Scholar]
- 24.Šter B. Selective recurrent neural network. Neural Process. Lett. 2013;38:1–15. [Google Scholar]
- 25.Hochreiter S., Schmidhuber J. Long short-term memory. Neural Comput. 1997;9(8):1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 26.Ghojogh B., Ghodsi A. 2023. arXiv preprint. [Google Scholar]
- 27.Graves A., Schmidhuber J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neur. Netw. 2005;18(5–6):602–610. doi: 10.1016/j.neunet.2005.06.042. [DOI] [PubMed] [Google Scholar]
- 28.Graves A., Jaitly N., Mohamed A.-r. 2013 IEEE workshop on automatic speech recognition and understanding. IEEE; 2013. Hybrid speech recognition with deep bidirectional LSTM. [Google Scholar]
- 29.Waqas M., et al. Advancements in daily precipitation forecasting: a deep dive into daily precipitation forecasting hybrid methods in the tropical climate of Thailand. MethodsX. 2024 [Google Scholar]
- 30.Waqas M., et al. Incorporating novel input variable selection method for in the different water basins of Thailand. Alexandr. Eng. J. 2024;86:557–576. [Google Scholar]
- 31.Johny K., Pai M.L., Adarsh S. A multivariate EMD-LSTM model aided with Time Dependent Intrinsic Cross-Correlation for monthly rainfall prediction. Appl. Soft. Comput. 2022;123 [Google Scholar]
- 32.Shashidhar R., Patilkulkarni S., Puneeth S. Combining audio and visual speech recognition using LSTM and deep convolutional neural network. Int. J. Inform. Technol. 2022;14(7):3425–3436. [Google Scholar]
- 33.Bhaskar S., Thasleema T. LSTM model for visual speech recognition through facial expressions. Multimed. Tool. Appl. 2023;82(4):5455–5472. [Google Scholar]
- 34.Wang Q., et al. A novel privacy-preserving speech recognition framework using bidirectional LSTM. J. Cloud Comput. 2020;9(1):36. [Google Scholar]
- 35.Quan R., et al. Holistic LSTM for pedestrian trajectory prediction. IEEE Transact. Image Process. 2021;30:3229–3239. doi: 10.1109/TIP.2021.3058599. [DOI] [PubMed] [Google Scholar]
- 36.Xie G., et al. Motion trajectory prediction based on a CNN-LSTM sequential model. Sci. China Inform. Sci. 2020;63:1–21. [Google Scholar]
- 37.Song X., et al. Pedestrian trajectory prediction based on deep convolutional LSTM network. IEEE Transact. Intell. Transport. Syst. 2020;22(6):3285–3302. [Google Scholar]
- 38.Rossi L., et al. Vehicle trajectory prediction and generation using LSTM models and GANs. PLoS ONE. 2021;16(7) doi: 10.1371/journal.pone.0253868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Peng X., Li Y. A fusion method based on EEMD, Pearson correlation analysis, improved LSTM, and Gaussian function-Trust region algorithm for state of health Prediction of lithium-ion Batteries. J. Electrochem. Energy Convers. Storage. 2022;19(3) [Google Scholar]
- 40.Wang J.Q., Du Y., Wang J. LSTM based long-term energy consumption prediction with periodicity. Energy. 2020;197 [Google Scholar]
- 41.Dubey A.K., et al. Study and analysis of SARIMA and LSTM in forecasting time series data. Sustain. Energy Technolog. Assessm. 2021;47 [Google Scholar]
- 42.Wei J., et al. Ultra-short-term forecasting of wind power based on multi-task learning and LSTM. Int. J. Electr. Power Energy Syst. 2023;149 [Google Scholar]
- 43.Waqas M., et al. A deep learning perspective on meteorological droughts prediction in the Mun River Basin, Thailand. AIP Adv. 2024;14(8) [Google Scholar]
- 44.Aslam S., et al. A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 2021;144 [Google Scholar]
- 45.Kao I.-F., et al. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020;583 [Google Scholar]
- 46.Pham B.T., et al. Can deep learning algorithms outperform benchmark machine learning algorithms in flood susceptibility modeling? J. Hydrol. 2021;592 [Google Scholar]
- 47.Ni L., et al. Streamflow and rainfall forecasting by two long short-term memory-based models. J. Hydrol. 2020;583 [Google Scholar]
- 48.Li J., et al. Water quality soft-sensor prediction in anaerobic process using deep neural network optimized by Tree-structured Parzen Estimator. Front. Environ. Sci. Eng. 2023;17(6):67. [Google Scholar]
- 49.Wongburi P., Park J.K. Prediction of wastewater treatment plant effluent water quality using recurrent neural network (RNN) models. Water (Basel) 2023;15(19):3325. [Google Scholar]
- 50.Wangwongchai A., et al. Imputation of missing daily rainfall data; A comparison between artificial intelligence and statistical techniques. MethodsX. 2023;11 doi: 10.1016/j.mex.2023.102459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Liu P., et al. Analysis and prediction of water quality using LSTM deep neural networks in IoT environment. Sustainability. 2019;11(7):2058. [Google Scholar]
- 52.Hu Z., et al. A water quality prediction method based on the deep LSTM network considering correlation in smart mariculture. Sensors. 2019;19(6):1420. doi: 10.3390/s19061420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Barzegar R., Aalami M.T., Adamowski J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stochast. Environ. Res. Risk Assessm. 2020;34(2):415–433. [Google Scholar]
- 54.Zubaidi S.L., et al. A method for predicting long-term municipal water demands under climate change. Water Resour. Manag. 2020;34:1265–1279. [Google Scholar]
- 55.Sit M., et al. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020;82(12):2635–2670. doi: 10.2166/wst.2020.369. [DOI] [PubMed] [Google Scholar]
- 56.Zhang Y. University of Guelph; 2024. Utilizing Hybrid LSTM and GRU Models for Urban Hydrological Prediction. [Google Scholar]
- 57.Yang S., et al. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019;579 [Google Scholar]
- 58.Wang Q., et al. Sequence-based statistical downscaling and its application to hydrologic simulations based on machine learning and big data. J. Hydrol. 2020;586 [Google Scholar]
- 59.Le X.-H., et al. Application of long short-term memory (LSTM) neural network for flood forecasting. Water (Basel) 2019;11(7):1387. [Google Scholar]
- 60.Xiang Z., Yan J., Demir I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020;56(1) [Google Scholar]
- 61.Liu Y., et al. Short term real-time rolling forecast of urban river water levels based on LSTM: a case study in Fuzhou City, China. Int. J. Environ. Res. Public Health. 2021;18(17):9287. doi: 10.3390/ijerph18179287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ozdemir S., Ozkan Yildirim S. Prediction of Water Level in Lakes by RNN-Based Deep Learning Algorithms to Preserve Sustainability in Changing Climate and Relationship to Microcystin. Sustainability. 2023;15(22):16008. [Google Scholar]
- 63.Moura R., et al. International Conference on Optimization, Learning Algorithms and Applications. Springer; 2023. Predicting flood events with streaming data: a preliminary approach with GRU and ARIMA. [Google Scholar]
- 64.Dehghani A., et al. Comparative evaluation of LSTM, CNN, and ConvLSTM for hourly short-term streamflow forecasting using deep learning approaches. Ecol. Inform. 2023;75 [Google Scholar]
- 65.Waqas M., et al. Advancements in daily precipitation forecasting: a deep dive into daily precipitation forecasting hybrid methods in the tropical climate of Thailand. MethodsX. 2024;12 [Google Scholar]
- 66.Wang Z., Lou Y. 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC) IEEE; 2019. Hydrological time series forecast model based on wavelet de-noising and ARIMA-LSTM. [Google Scholar]
- 67.Sahoo B.B., et al. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019;67(5):1471–1481. [Google Scholar]
- 68.Muhammad A.U., Li X., Feng J. Machine Learning and Intelligent Communications: 4th International Conference, MLICOM 2019, Nanjing, China, August 24–25, 2019, Proceedings 4. Springer; 2019. Using LSTM GRU and hybrid models for streamflow forecasting. [Google Scholar]
- 69.Niknam A.R.R., et al. Comparing ARIMA and various deep learning models for long-term water quality index forecasting in Dez River, Iran. Environ. Sci. Pollut. Res. 2024:1–17. doi: 10.1007/s11356-024-32228-x. [DOI] [PubMed] [Google Scholar]
- 70.Zhang W., et al. Outlet water temperature prediction of energy pile based on spatial-temporal feature extraction through CNN–LSTM hybrid model. Energy. 2023;264 [Google Scholar]
- 71.Mazher A. Visualization framework for high-dimensional spatio-temporal hydrological gridded datasets using machine-learning techniques. Water (Basel) 2020;12(2):590. [Google Scholar]
- 72.Shen C., Lawson K. Deep Learning for the Earth Sciences: A Comprehensive Approach to Remote Sensing, Climate Science, and Geosciences. 2021. Applications of deep learning in hydrology; pp. 283–297. [Google Scholar]
- 73.Razavi S. Deep learning, explained: fundamentals, explainability, and bridgeability to process-based modelling. Environ. Modell. Softw. 2021;144 [Google Scholar]
- 74.Waqas M., et al. Potential of artificial intelligence-based techniques for rainfall forecasting in thailand: a comprehensive review. Water (Basel) 2023;15(16):2979. [Google Scholar]
- 75.Hopfield J.J. Neural networks and physical systems with emergent collective computational abilities. Proceed. Nat. Acad. Sci. 1982;79(8):2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Bengio Y., Simard P., Frasconi P. Learning long-term dependencies with gradient descent is difficult. IEEE Transact. Neur. Netw. 1994;5(2):157–166. doi: 10.1109/72.279181. [DOI] [PubMed] [Google Scholar]
- 77.Hochreiter S., et al. A Field Guide to Dynamical Recurrent Neural Networks. IEEE Press In; 2001. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. [Google Scholar]
- 78.Hochreiter S., Schmidhuber J. LSTM can solve hard long time lag problems. Adv. Neur. Inf. Process. Syst. 1996;9 [Google Scholar]
- 79.Zhao J., et al. International Conference on Machine Learning. PMLR; 2020. Do RNN and LSTM have long memory? [Google Scholar]
- 80.Cho K., et al. 2014. arXiv preprint. [Google Scholar]
- 81.Chung J., et al. 2014. arXiv preprint. [Google Scholar]
- 82.Jozefowicz R., Zaremba W., Sutskever I. International conference on machine learning. PMLR; 2015. An empirical exploration of recurrent network architectures. [Google Scholar]
- 83.Greff K., et al. LSTM: a search space odyssey. IEEE Trans. Neur. Netw. Learn. Syst. 2016;28(10):2222–2232. doi: 10.1109/TNNLS.2016.2582924. [DOI] [PubMed] [Google Scholar]
- 84.Cui Z., et al. 2018. arXiv preprint. [Google Scholar]
- 85.Ma M., et al. Predicting machine's performance record using the stacked long short-term memory (LSTM) neural networks. J. Appl. Clin. Med. Phys. 2022;23(3):e13558. doi: 10.1002/acm2.13558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Wang J., Peng B., Zhang X. Using a stacked residual LSTM model for sentiment intensity prediction. Neurocomputing. 2018;322:93–101. [Google Scholar]
- 87.Luo W., Liu W., Gao S. 2017 IEEE International conference on multimedia and expo (ICME. IEEE; 2017. Remembering history with convolutional lstm for anomaly detection. [Google Scholar]
- 88.Su J., et al. Convolutional tensor-train LSTM for spatio-temporal learning. Adv. Neur. Inf. Process. Syst. 2020;33:13714–13726. [Google Scholar]
- 89.Kim S., et al. 2017. arXiv preprint. [Google Scholar]
- 90.Singh D.K., Sahoo A. A hybrid CNN–LSTM deep learning model for rainfall prediction. NeuroQuantology. 2022;20(14):813. [Google Scholar]
- 91.Phiboonbanakit T., et al. Unsupervised hybrid anomaly detection model for logistics fleet management systems. IET Intell. Transp. Syst. 2019;13(11):1636–1648. [Google Scholar]
- 92.Gao S., et al. Short-term runoff prediction with GRU and LSTM networks without requiring time step optimization during sample generation. J. Hydrol. 2020;589 [Google Scholar]
- 93.Lin Y., et al. Bias learning improves data driven models for streamflow prediction. J. Hydrol.: Region. Stud. 2023;50 [Google Scholar]
- 94.Aslam M., Kim J.-S., Jung J. Multi-step ahead wind power forecasting based on dual-attention mechanism. Energy Rep. 2023;9:239–251. [Google Scholar]
- 95.Zhu J., et al. Time-series power forecasting for wind and solar energy based on the SL-transformer. Energies. 2023;16(22):7610. [Google Scholar]
- 96.Khelil M.I., et al. Self-organizing maps-based features selection with deep LSTM and SVM classification approaches for advanced water quality monitoring. Int. J. Intell. Eng. Syst. 2022;15(3) [Google Scholar]
- 97.Yan D., et al. Characteristics and prediction of extreme drought event using LSTM model in Wei River Basin. Terrest. Atmosph. Ocean. Sci. 2021;32(2) [Google Scholar]
- 98.Chen Y., et al. An LSTM-based neural network method of particulate pollution forecast in China. Environ. Res. Lett. 2021;16(4) [Google Scholar]
- 99.Abotaleb M., Dutta P.K. Hybrid Information Systems: Non-Linear Optimization Strategies with Artificial Intelligence. 2024. Optimizing long short-term memory networks for univariate time series forecasting: a comprehensive guide; p. 427. [Google Scholar]
- 100.Shekar P.R., et al. A combined deep CNN-RNN network for rainfall-runoff modelling in Bardha Watershed, India. Artif. Intell. Geosci. 2024;5 [Google Scholar]
- 101.Tabas S.S., Samadi S. Variational Bayesian dropout with a Gaussian prior for recurrent neural networks application in rainfall–runoff modeling. Environ. Res. Lett. 2022;17(6) [Google Scholar]
- 102.Li W., Kiaghadi A., Dawson C. High temporal resolution rainfall–runoff modeling using long-short-term-memory (LSTM) networks. Neur. Comput. Applic. 2021;33(4):1261–1278. [Google Scholar]
- 103.Yao Z., et al. An ensemble CNN-LSTM and GRU adaptive weighting model based improved sparrow search algorithm for predicting runoff using historical meteorological and runoff data as input. J. Hydrol. 2023;625 [Google Scholar]
- 104.de Mendonça L.M., Blanco C.J.C., de Oliveira Carvalho F. Recurrent neural networks for rainfall-runoff modeling of small Amazon catchments. Model. Earth Syst. Environ. 2023;9(2):2517–2531. [Google Scholar]
- 105.Pan T.y., Wang R.y. Using recurrent neural networks to reconstruct rainfall-runoff processes. Hydrolog. Process.: Int. J. 2005;19(18):3603–3619. [Google Scholar]
- 106.Wu C., Chau K.W. Rainfall–runoff modeling using artificial neural network coupled with singular spectrum analysis. J. Hydrol. 2011;399(3–4):394–409. [Google Scholar]
- 107.Kratzert F., et al. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018;22(11):6005–6022. [Google Scholar]
- 108.Yin H., et al. Rainfall-runoff modeling using long short-term memory based step-sequence framework. J. Hydrol. 2022;610 [Google Scholar]
- 109.Hu C., et al. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water (Basel) 2018;10(11):1543. [Google Scholar]
- 110.Chhetri M., et al. Deep BLSTM-GRU model for monthly rainfall prediction: a case study of Simtokha, Bhutan. Remote Sens. (Basel) 2020;12(19):3174. [Google Scholar]
- 111.Wang Q., et al. Impact of input filtering and architecture selection strategies on GRU runoff forecasting: a case study in the Wei River Basin, Shaanxi, China. Water (Basel) 2020;12(12):3532. [Google Scholar]
- 112.Nath A., Barman D., Saha G. Proceedings of the International Conference on Computing and Communication Systems: I3CS 2020, NEHU, Shillong, India. Springer; 2021. Gated Recurrent Unit: an effective tool for runoff estimation. [Google Scholar]
- 113.Mateus B.C., et al. Comparing LSTM and GRU models to predict the condition of a pulp paper press. Energies. 2021;14(21):6958. [Google Scholar]
- 114.ArunKumar K., et al. Comparative analysis of Gated Recurrent Units (GRU), long Short-Term memory (LSTM) cells, autoregressive Integrated moving average (ARIMA), seasonal autoregressive Integrated moving average (SARIMA) for forecasting COVID-19 trends. Alexandr. Eng. J. 2022;61(10):7585–7603. [Google Scholar]
- 115.Hu S., et al. Deep neural network for robust modulation classification under uncertain noise conditions. IEEE Transact. Vehicul. Technol. 2019;69(1):564–577. [Google Scholar]
- 116.Das S., Datta S., Chaudhuri B.B. Handling data irregularities in classification: foundations, trends, and future challenges. Pattern Recognit. 2018;81:674–693. [Google Scholar]
- 117.Weerakody P.B., et al. A review of irregular time series data handling with gated recurrent neural networks. Neurocomputing. 2021;441:161–178. [Google Scholar]
- 118.Buslim N., et al. 2021 9th International Conference on Cyber and IT Service Management (CITSM) IEEE; 2021. Comparing bitcoin's prediction model using GRU, RNN, and LSTM by hyperparameter optimization grid search and random search. [Google Scholar]
- 119.Garbin C., Zhu X., Marques O. Dropout vs. batch normalization: an empirical study of their impact to deep learning. Multimed. Tool. Appl. 2020;79(19):12777–12815. [Google Scholar]
- 120.Hewamalage H., Bergmeir C., Bandara K. Recurrent neural networks for time series forecasting: current status and future directions. Int. J. Forecast. 2021;37(1):388–427. [Google Scholar]
- 121.Jaiswal G., et al. Integration of hyperspectral imaging and autoencoders: benefits, applications, hyperparameter tunning and challenges. Comput. Sci. Rev. 2023;50 [Google Scholar]
- 122.Fekri M.N., et al. Deep learning for load forecasting with smart meter data: online adaptive recurrent neural network. Appl Energy. 2021;282 [Google Scholar]
- 123.Gür Y.E. Comparative analysis of deep learning models for silver price prediction: CNN, LSTM, GRU and hybrid approach. Akdeniz İİBF Dergisi. 2024;24(1):1–13. [Google Scholar]
- 124.Abbasimehr H., Paki R. Improving time series forecasting using LSTM and attention models. J. Ambient Intell. Human. Comput. 2022;13(1):673–691. [Google Scholar]
- 125.Machiwal D., Jha M.K. Time series analysis of hydrologic data for water resources planning and management: a review. J. Hydrol. Hydromech. 2006;54(3):237–257. [Google Scholar]
- 126.Himeur Y., et al. Using artificial intelligence and data fusion for environmental monitoring: a review and future perspectives. Inform. Fus. 2022;86:44–75. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No data was used for the research described in the article.