Abstract
The relationship between weather and acute coronary syndrome (ACS) incidence has been the subject of considerable research, with varying conclusions. Harnessing machine learning techniques, our study explores the relationship between meteorological factors and ACS presentations in the emergency department (ED), offering insights into seasonal variations and inter-day fluctuations to optimize patient care and resource allocation. A retrospective cohort analysis was conducted, encompassing ACS presentations to Dutch EDs from 2010 to 2017. Temporal patterns were analyzed using heat-maps and time series plots. Multivariable linear regression (MLR) and Random Forest (RF) regression models were employed to forecast daily ACS presentations with prediction horizons of one, three, seven, and thirty days. Model performance was assessed using the coefficient of determination (R²), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). The study included 214,953 ACS presentations, predominantly unstable angina (UA) (94,272; 44%), non-ST-elevated myocardial infarction (NSTEMI) (78,963; 37%), and ST-elevated myocardial infarction (STEMI) (41,718; 19%). A decline in daily ACS admissions over time was observed, with notable inter-day (estimated median difference: 41 (95%CI = 37–43, p = < 0.001) and seasonal variations (estimated median difference: 9 (95%CI 6–12, p = < 0.001). Both MLR and RF models demonstrated similar predictive capabilities, with MLR slightly outperforming RF. The models showed moderate explanatory power for ACS incidence (adjusted R² = 0.66; MAE (MAPE): 7.8 (11%)), with varying performance across subdiagnoses. Prediction of UA incidence resulted in the best-explained variability (adjusted R² = 0.80; MAE (MAPE): 5.3 (19.1%)), followed by NSTEMI and STEMI diagnoses. All models maintained consistent performance over extended prediction horizons. Our findings indicate that ACS presentation exhibits distinctive seasonal changes and inter-day differences, with marked reductions in incidence during the summer months and a distinct peak prevalence on Mondays. The predictive performance of our model was moderate. Nonetheless, we obtained good explanatory power for UA presentations. Our model emerges as a potentially valuable supplementary tool to enhance ED resource allocation or future predictive models predicting ACS incidence in the ED.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-024-73291-1.
Subject terms: Environmental sciences, Cardiology
Introduction
Emergency department (ED) crowding is an increasing problem for hospitals globally1,2. Traditionally, EDs have been predominantly staffed to align with average patient influx requirements3. This approach necessitates a critical evaluation in the context of fluctuating patient volumes, the increasing dilemma of ED crowding, and staffing shortages4–6. Future possibilities to mitigate these problems call for agile and responsive emergency care. The optimization of patient-staffing ratios, ideally with a concurrent increase in ED output possibilities, such as proactive bed management, could aid in improving patient flow and care7,8.
Emergency departments evaluating patients with suspected acute coronary syndrome (ACS) are particularly impacted by crowding, as chest pain is the second most frequent reason for ED visits worldwide. In the United States, approximately 7–8 million patients, or 6–7% of ED visits, present with symptoms suggestive of ACS9. Similarly, in The Netherlands, around 15% of ED presentations are suspected cases of ACS10.
A potential tool to alleviate ED crowding is dynamic predictions of daily ACS presentations, which could offer early insights into the anticipated activity levels in cardiac emergency rooms11. On days with a predicted higher incidence of ACS, increased vigilance or a reduced workload for medical personnel could be achieved through optimized patient-staffing ratios. Ideally, these predictions should be based on inputs that vary over short periods and should be publicly available. This approach could enhance future collaborative efforts in the field of ED visit predictions12.
Current literature suggests that both weather conditions and calendar data may influence the incidence of ACS13,14. However, the existing evidence is inconsistent and sometimes conflicting15–20. The assumed association between weather and specific diseases has an extensive history, dating back to 430 B.C. with Hippocrates’ first recorded attempt21. In modern times, prediction of the overall number of patients presenting in the emergency department based on meteorological and calendar data has been attempted. Unfortunately, previous studies had underwhelming predictive abilities and lacked focus on specific diagnoses22,23.
The primary aim of this study is to examine temporal patterns in daily ED presentations for ACS and for its subdiagnoses, including unstable angina, ST-elevated myocardial infarction, and non-ST-elevated myocardial infarction. Second, we used a data-driven approach to examine whether ED presentations for ACS and its subtypes can be accurately predicted using meteorological and calendar data.
Methods
Study design and population
This study is a retrospective nationwide cohort analysis of daily acute coronary syndrome presentations to emergency departments in the Netherlands. Data were gathered over a period extending from the 1st of January 2010 through to the 31st of December 2017—this collection period comprised 2,922 days, providing an expansive timeline for analytical examination. All ACS diagnoses were conducted, registered, and claimed to Dutch health insurance by a treating physician.
Acute coronary syndrome consists of a combination of diagnoses, including unstable angina (UA), ST-elevated myocardial infarction (STEMI), and non-ST-elevated myocardial infarction (NSTEMI)24.
Data collection
The dataset was extracted from a comprehensive database curated by Statistics Netherlands (CBS, The Hague)25. The sources of this database encompassed the Diagnostic Information System of the Dutch Healthcare Authority (NZa) for the years 2010 to 2015 and the national medical insurance claim database (Vektis C.V., Zeist, the Netherlands) for the years 2016 through 201726,27.
All ED visit data within the Netherlands were collected in compliance with national legislative frameworks and the European General Data Protection Regulations (GDPR). Ethical committee approval and participant informed consent were deemed unnecessary for this study due to the utilization of exclusively anonymized national statistical data in accordance with the Central Committee on Research involving human subjects. The research protocol employed in this study has been formally registered with Statistics Netherlands and is identifiable through the reference number PR000330. The execution and documentation of this study adhered to the guidelines and checklist of the TRIPOD statement, as detailed in Supplemental Table S3.
Calendar and meteorological data
Using literature review, we identified calendar and meteorological data as potential predictive abilities in different world regions15–20,28–41. In relation to calendar data, variables such as day of the week, month, and year were incorporated into our analysis. Furthermore, we included the number of ED presentations on the previous day as a predictive variable, thereby introducing an autoregressive component to the model, a commonly applied forecasting method42,43. Resulting in 28 calendrical variables.
Meteorological data were extracted from the publicly available database of the Royal Netherlands Meteorological Institute (KNMI, De Bilt, Netherlands). Comprehensive daily characteristics of the temperature, sunshine, humidity, wind, and precipitation in the Netherlands were collected by the KNMI. The national climate can be described as temperate and is equal across the country44.
All weather variables included in this analysis are shown in Table 2. We included the seven- and 14-day moving averages for each meteorological variable, the maximum inter-day difference of the previous three days, and the trending direction of the weather for the past two days, resulting in 112 meteorological variables.
Table 2.
Descriptive characteristics and univariate analysis of meteorological data.
| Meteorological data | Median [Q1–Q3] | Daily number of ED presentations (β (95% CI)) | |||
|---|---|---|---|---|---|
| ACS | UA | NSTEMI | STEMI | ||
| Mean daily temperature (°C) | 10.6 [6.2–15.5] | − 0.06 (− 0.07– − 0.06) | − 0.04 (− 0.04– − 0.03) | − 0.02 (− 0.02– − 0.01) | − 0.01 (− 0.01– − 0.01) |
| Maximum daily temperature (°C) | 14.6 [9.2–20.0] | − 0.05 (− 0.06– − 0.05) | − 0.03 (− 0.03– − 0.03) | − 0.01 (− 0.01– − 0.01) | − 0.01 (− 0.01– − 0.01) |
| Minimum daily temperature (°C) | 6.6 [2.3–10.7] | − 0.08 (− 0.08– − 0.07) | − 0.04 (− 0.05– − 0.04) | − 0.02 (− 0.02– − 0.01) | − 0.01 (− 0.02– − 0.01) |
| Minimum temperature at 10 cm surface (°C) | 4.7 [0.4–8.9] | − 0.08 (− 0.09– − 0.07) | − 0.05 (− 0.05– − 0.04) | − 0.02 (− 0.02– − 0.01) | − 0.01 (− 0.02– − 0.01) |
| Daily temperature difference (°C) | 0.8 [0.5–1.1] | − 0.07 (− 0.08– − 0.07) | − 0.03 (− 0.04– − 0.03) | − 0.02 (− 0.03– − 0.02) | − 0.02 (− 0.02– − 0.01) |
| Daily sunshine duration (h) | 4.1 [1.0–7.7] | − 0.08 (− 0.09– − 0.07) | − 0.03 (− 0.04– − 0.02) | − 0.03 (− 0.03– − 0.02 | − 0.02 (− 0.02– − 0.01) |
| Percentage of daily potential sunshine duration (%) | 34 [9–61] | − 0.08 (− 0.09– − 0.06) | − 0.04 (− 0.05– − 0.02) | − 0.02 (− 0.03– − 0.01) | − 0.02 (− 0.02– − 0.02) |
| Daily global radiation (J/cm2) | 863.0 [323.0–1583.8] | − 3.77 (− 4.28– − 3.26) | − 1.45 (− 1.91– − 0.99) | − 1.51 (− 1.73– − 1.28) | − 0.81 (− 0.94– − 0.69) |
| Daily evaporation (mm) | 1.3 [0.4–2.5] | − 0.24 (− 0.27– − 0.21) | − 0.1 (− 0.13– − 0.07) | − 0.09 (− 0.11– − 0.08) | − 0.05 (− 0.06– − 0.04) |
| Mean daily atmospheric pressure (hPa) | 1015.9 [1010.0 − 1021.5] | − 12.04 (− 12.1– − 11.98) | − 16.75 (− 16.81– − 16.7) | 5.78 (5.75–5.8) | − 1.06 (− 1.08– − 1.05) |
| Maximum daily atmospheric pressure (hPa) | 1018.7 [1013.1 − 1024.1] | − 11.32 (− 11.38– − 11.26) | − 20.29 (− 20.34– − 20.23) | 8.79 (8.76–8.81 | 0.18 (0.16–0.19) |
| Minimum daily atmospheric pressure (hPa) | 1013.0 [1006.5 − 1018.9] | − 11.87 (− 11.93– − 11.8) | − 12.89 (− 12.94– − 12.83) | 2.99 (2.97–3.02) | − 1.97 (− 1.99 – − 1.96) |
| Daily atmospheric pressure difference (hPa) | 0.5 [0.3–0.8] | 0.03 (0.02–0.04) | − 0.03 (− 0.04– − 0.02) | 0.04 (0.03–0.04) | 0.02 (0.02–0.02) |
| Mean daily atmospheric humidity (%) | 82 [74–88] | 0.2 (0.2–0.21) | 0.08 (0.08–0.09) | 0.08 (0.08–0.08) | 0.04 (0.04–0.04) |
| Maximum daily atmospheric humidity (%) | 97 [94–98] | − 0.31 (− 0.31– − 0.3) | − 0.11 (− 0.12– − 0.11) | − 0.12 (− 0.12– − 0.12) | − 0.07 (− 0.07– − 0.07) |
| Minimum daily atmospheric humidity (%) | 63 [52–74] | 0.17 (0.16–0.18) | 0.08 (0.08–0.09) | 0.06 (0.05–0.06) | 0.03 (0.03–0.04) |
| Daily atmospheric humidity difference (hPa) | 32 [21–43] | − 0.21 (− 0.23– − 0.2) | − 0.1 (− 0.12– − 0.09) | − 0.07 (− 0.08– − 0.06) | − 0.04 (− 0.05– − 0.04) |
| Daily precipitation duration (h) | 0.2 [0.0–2.7] | 0.08 (0.05–0.1) | 0.04 (0.01–0.06) | 0.02 (0.01–0.03) | 0.02 (0.01–0.02) |
| Daily amount of precipitation (mm) | 0.1 [0.0–2.6] | − 0.03 (− 0.05– − 0.01) | − 0.01 (− 0.03–0.0) | − 0.01 (− 0.02–0.0) | − 0.01 (− 0.01– − 0.0) |
| Maximum hourly amount of precipitation (mm) | 0.1 [0.0–1.1] | − 0.18 (− 0.23– − 0.12) | − 0.07 (− 0.11– − 0.02) | − 0.06 (− 0.08– − 0.04) | − 0.05 (− 0.06– − 0.04) |
| Daily cloud coverage (%) | 75 [50–100] | − 0.55 (− 0.65– − 0.44) | − 1.82 (− 1.92– − 1.73) | 1.0 (0.95–1.05) | 0.27 (0.25–0.3) |
| Mean daily wind speed (m/s) | 3.2 [2.4–4.1] | 0.19 (0.17–0.21) | 0.08 (0.06–0.1) | 0.07 (0.06–0.07) | 0.05 (0.04 − 0.05) |
| Maximum daily wind speed (m/s) | 5 [4–6] | 0.08 (0.07–0.09) | − 0.0 (− 0.01–0.01) | 0.05 (0.05–0.06) | 0.03 (0.03–0.03) |
| Minimum daily wind speed (m/s) | 1 [1, 2] | 0.25 (0.22–0.29) | 0.1 (0.07–0.13) | 0.1 (0.08–0.11) | 0.05 (0.05–0.06) |
| Daily maximum wind gust (m/s) | 10 [7–12] | − 0.02 (− 0.03– − 0.02) | − 0.05 (− 0.06– − 0.05) | 0.02 (0.02–0.02) | 0.01 (0.01–0.01) |
| Daily vector average wind direction (degrees) | 210 [133–251] | − 0.05 (− 0.05– − 0.04) | − 0.04 (− 0.04– − 0.03) | − 0.01 (− 0.01– − 0.01) | − 0.0 (− 0.0– − 0.0) |
| Daily Vector average wind speed (m/s) | 2.8 [1.9–3.8] | 0.22 (0.2–0.24) | 0.1 (0.08–0.11) | 0.07 (0.06–0.08) | 0.05 (0.04–0.05) |
| Presentations on the day before | |||||
| Number of ACS presentations on the day before | N.A | 0.2 (0.19–0.21) | N.A | N.A | N.A |
| Number of UA presentations on the day before | N.A | N.A | 0.69 (0.67–0.7) | N.A | N.A |
| Number of NSTEMI presentations on the day before | N.A | N.A | N.A | 0.24 (0.23–0.25) | N.A |
| Number of STEMI presentations on the day before | N.A | N.A | N.A | N.A | 0.07 (0.06–0.08) |
ACS Acute coronary syndrome, CI Confidence Interval, df degrees of freedom, UA unstable angina pectoris, NSTEMI non ST − elevated myocardial infarction, STEMI ST − elevated myocardial infarction, N.A. Not applicable, °C degrees Celsius, h hour, J/cm2 Joule per square centimeter as measure of surface tension, hPa hectopascal, mm millimeters, m/s meter per second.
aCalendar data Day of the week, Month, Season, and Year are analyzed using Kruskal − Wallis test with H − statistics as output. Consequently, post hoc Dunn’s tests with Bonferroni correction were performed with the first category Monday, January, Winter, and 2010 as reference categories.
Bold indicates significance (p < 0.05).
Prediction outcome
A substantial aim of this study was to forecast the daily number of ED visits related to ACS one day prior to their occurrence. The secondary objectives included predicting the daily frequency of ED visits for each ACS subdiagnosis. Furthermore, we aspired to expand the predictive horizon to forecast ED visits three-, seven-, and 30 days in advance.
Statistical analysis
Temporal patterns of daily ED visits for ACS and its subtypes were analyzed using a 30-day moving average. Heat-maps were used to visualize absolute differences in ED presentations for ACS and its subtypes. A non-parametric analysis of variance (Kruskal–Wallis test) and Dunn’s post hoc analysis with Bonferroni correction was conducted to compare differences in median ED presentations between groups. Estimated median differences (EMD) with a 95% confidence interval (CI) between variables were calculated with bootstrap resampling, and differences were assessed with a Mann–Whitney U test. Descriptive statistics were computed for each potential predictor variable, and univariate linear regression, combined with an offset, was performed to estimate regression coefficients (β) and corresponding 95% CI between each predictor and ED presentations for ACS and its subtypes.
Consecutively, the dataset was randomly split into a train (75%) and a test (25%) dataset, and model training was performed on the training dataset. Z-score normalization was used to standardize our variables for continuous features. Z-score normalization standardizes features by removing the mean and scaling to unit variance, resulting in a feature with a mean of 0 and a standard deviation of 1.
Model development
Multivariable linear regression (MLR) and machine learning algorithms represent the most prevalent modeling approaches for predicting ED visitations42,43. Therefore, we investigated two modeling approaches: MLR and Random Forest Regression (RF) with hyperparameter optimization. Least Absolute Shrinkage and Selection Operator (LASSO) regression was employed to identify the most relevant predictors for ED presentations in the MLR model. Feature importance factor was employed in order to identify most relevant features in the RF model. To calculate the best fitting controlling hyperparameter alpha (α) for the LASSO model, a standard tenfold cross-validation was performed. Regarding the RF model, hyperparameter optimization was initially conducted through random grid cross-validation to determine the most suitable hyperparameter grids. Our hyperparameter grid included: minimal samples leaf, minimal samples split, and number of estimators, all other parameters were standard values. Subsequently, a fivefold grid search cross-validation was employed for the precise identification of optimal hyperparameters. This procedure evaluates all potential combinations within our specified hyperparameter grid. The optimal set of hyperparameters is determined based on achieving the best performance score, measured using the mean squared error criterion. K-fold cross-validation involves partitioning the dataset into k subsets and iteratively training the model on k-1 subsets while testing the remaining subsets to minimize the risk of overfitting our model.
Model performances were evaluated using (adjusted) R-squared (R2). This metric quantifies the proportion of variance in the outcome explained by the selected predicting variables. Notably, these values were adjusted to the number of predictors used. Adjusted R2 adjusts the statistic based on the number of independent variables in the model. It penalizes the addition of predictors that do not improve the model. R2 values range from 0 to 1, with values closer to 1 indicating a greater proportion of the variance of ACS incidence explained by the model.
Validation
The test dataset (25%) was used to internally validate the predictive models to accurately evaluate the performance. The model fit to the test dataset was assessed using Mean Absolute Error (MAE) and Mean Absolute Percentage Error (MAPE). The MAE represents the average discrepancy between the model-predicted ED visits and the actual daily ED visit counts; lower MAE values indicate a higher degree of model accuracy. Mean absolute error is instrumental as it represents prediction errors in the same unit as the original data, which, in this context, is the number of patients. Mean Absolute Percentage Error is a validation metric similar to MAE; however, it quantifies the error in terms of a relative percentage rather than an absolute value.
All analyses were performed using the Anaconda Distribution for Python 3.9 visualized in JUPYTER Notebooks. We used the following packages: Pandas45, Numpy46, Statistics47, Statsmodels. API48 (v0.13.2) and Sci-Kit Learn49 (v1.0.2) libraries.
Results
During the study period, a total of 214,953 patients presented to emergency departments in the Netherlands with ACS. The majority of presentations were for unstable angina (94,272; 44%), followed by non-ST-elevated myocardial infarction (78,963; 37%) and ST-elevated myocardial infarction (41,718; 19%). There were no missing values for the meteorological, calendar, or patient presentation data.
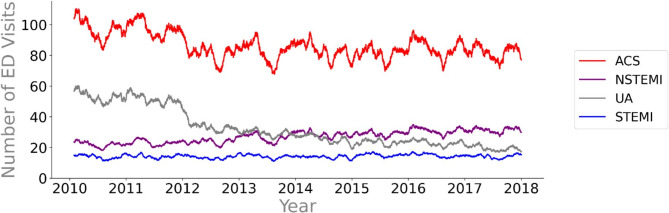
Figure 1 shows the 30-day moving average of ED visits for ACS and its subtypes. The overall incidence of ACS decreased after 2011, and the number of presentations remained stable from 2012 to 2018. The median daily ED presentations for ACS decreased from 96 [82–110] in 2010 to 81 [68–95] in 2017 (EMD; 15, 95%CI = 12–18, p = < 0.001). This decrease can be attributed to a sharp decrease in UA diagnoses after 2011. This decrease in daily UA diagnoses coincides with an increase in NSTEMI diagnoses. Daily diagnoses of STEMI remained stable over the 8-year inclusion period. The temporal patterns for ACS show distinct seasonal trends, with a noticeable drop during the summer months.
Figure 1.
Temporal pattern of ACS emergency department visits. The temporal trends and fluctuations were visualized by plotting 30-day moving averages of daily emergency department visits for ACS and its subdiagnoses. ACS Acute coronary syndrome, ED emergency department, UA unstable angina pectoris, NSTEMI non ST-elevated myocardial infarction, STEMI ST-elevated myocardial infarction.
Calendar characteristics
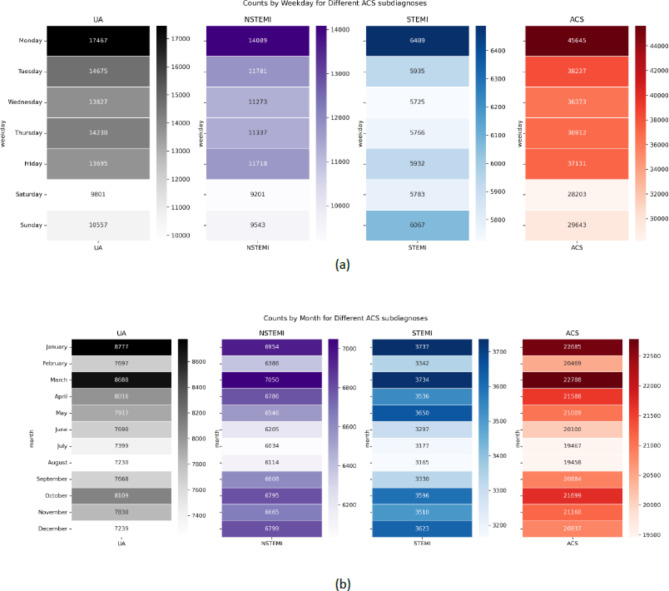
Figure 2a shows variation in absolute ED presentations for ACS by day of the week, with a peak on Mondays and fewer presentations during the weekend (H-statistic = 1169.98, p-value < 0.01). Specifically, on Mondays, there was a median of 110 [97–123] ED presentations for ACS compared to a median of 69 [61–80] cases on Sundays, for an EMD of 41 (95%CI = 37–43, p = < 0.001). This pattern was observed for each subdiagnosis of ACS as well.
Figure 2.
(a) Heat-map visualizing the sum of absolute ED presentations per weekday. (b) Fig. 2b Heat-map visualizing the sum of absolute ED presentations per month.
Similarly, statistically significant differences in median daily ED visits per month were observed (H-statistic = 136.11, p-value < 0.001). Post-hoc analyses revealed statistically significant differences in the median number of presentations in May, June, July, August, and December compared to January. Figure 2b shows that the summer (June, July, August) months had lower absolute presentations for ACS compared to the other seasons (EMD; 9 (95%CI 6–12, p = < 0.001). Elaborate descriptive statistics of all calendar variables are shown in Table 1.
Table 1.
Descriptive characteristics of all calendar variables.
| Calendar data | Median [Q1–Q3] daily ED presentations | |||
|---|---|---|---|---|
| Variable | ACS | UA | NSTEMI | STEMI |
| Day of the weeka (H − statistic with df:6) | 1169.98; p < 0.001 | 462.23; p < 0.001 | 611.02; p < 0.001 | 53.71; p < 0.001 |
| Monday | 110 [97–123] | 37 [29–52] | 33 [28–39] | 15 [13–18] |
| Tuesday | 90 [80–103] | 31 [24–45] | 28 [23–33] | 14 [11–17] |
| Wednesday | 87 [77–96] | 30 [23–42] | 27 [23–31] | 14 [11–16] |
| Thursday | 89 [77–98] | 30 [23–42] | 27 [22–32] | 14 [11–16] |
| Friday | 88 [79–98] | 28 [23–43] | 28 [23–33] | 14 [11–17] |
| Saturday | 67 [59–76] | 20 [15–30] | 22 [18–26] | 14 [11–17] |
| Sunday | 69 [61–80] | 21 [17–31] | 23 [19–27] | 14 [12–17] |
| Monthsa (H − statistic with df:11) | 136.11; p < 0.001 | 50.56; p < 0.001 | 100.15; p < 0.001 | 94.71; p < 0.001 |
| January | 91 [75–104] | 30 [23–47] | 27.5 [22–33] | 15 [12–17] |
| February | 89 [76–104] | 28.5 [23–43] | 28 [23–32] | 15 [12–17] |
| March | 91 [79–106] | 31 [24–44] | 28 [22–34] | 15 [12–18] |
| April | 89 [75–104] | 30 [22–43] | 28 [23–33] | 15 [12–18] |
| May | 83 [71–95] | 30 [20–41] | 26 [21–32] | 14 [12–17] |
| June | 83 [69–98] | 28 [21–41] | 26 [20–31] | 14 [11–16] |
| July | 78 [64–89] | 27 [20–38] | 24 [19–28] | 13 [10–15] |
| August | 77 [66–89] | 26 [19–37] | 23 [20–28] | 13 [10–16] |
| September | 85 [73–100] | 28 [21–40] | 27 [22–32] | 14 [11–16] |
| October | 86 [75–97] | 29 [21–41] | 27 [23–32] | 14 [12–17] |
| November | 88 [74–99] | 29 [21–40] | 27 [22–34] | 14 [12–18] |
| December | 84 [69–96] | 26 [19–36] | 27 [22–32] | 14 [11–17] |
| Seasona (H − statistic with df:3) | 90.0 p < 0.001 | 18.6 p < 0.001 | 80.7 p < 0.001 | 81.1 p < 0.001 |
| Winter | 88 [74–101] | 29 [21 − 40.25] | 27 [22–32] | 15 [12–17] |
| Spring | 88 [73–103] | 30 [22–42] | 27 [22–32] | 15 [12–18] |
| Summer | 79 [66–92] | 27 [20–38] | 27 [22–32] | 13 [10–16] |
| Autumn | 86 [74–99] | 29 [21–40] | 24 [20–29] | 14 [12–17] |
| Yeara (H − statistic with df: 7) | 293.67; p < 0.001 | 1744.44; p < 0.001 | 596.47; p < 0.001 | 44.28; p < 0.001 |
| 2010 | 96 [82–110] | 52 [44–60] | 22 [18–26] | 14 [11–17] |
| 2011 | 97 [84–110] | 51 [43–60] | 23 [19–27] | 14 [12–17] |
| 2012 | 81 [69–94] | 33 [27–40] | 24 [20–28] | 13 [11–16] |
| 2013 | 83 [70–95] | 29 [23–35] | 27 [22–31] | 14 [11–17] |
| 2014 | 82 [69–94] | 25 [20–30] | 28 [23–33] | 14 [10–16] |
| 2015 | 80 [67–92] | 23 [19–28] | 28 [24–34] | 15 [12–18] |
| 2016 | 85 [71–97] | 23 [18–27] | 31 [26–36] | 15 [12–18] |
| 2017 | 81 [68–95] | 19 [15–23] | 31 [26–36] | 14 [12–17] |
ACS Acute coronary syndrome, CI Confidence Interval, df degrees of freedom, UA unstable angina pectoris, NSTEMI non ST − elevated myocardial infarction, STEMI ST − elevated myocardial infarction, NA Not applicable, °C degrees Celsius, h hour, J/cm2 Joule per square centimeter as measure of surface tension, hPa hectopascal, mm millimeters, m/s meter per second.
aCalendar data Day of the week, Month, Season, and Year are analyzed using Kruskal − Wallis test with H − statistics as output. Consequently, post hoc Dunn’s tests with Bonferroni correction were performed with the first category Monday, January, Winter and 2010 as reference categories.
Bold indicates significance (p < 0.05).
Meteorological data
Table 2 shows the descriptive characteristics and univariate analyses of overall weather variables examined in this study. The results of the univariate analyses are presented as correlation coefficients for each ACS and each subtype of ACS. We identified numerous statistically significant possible predictive weather features that could impact the incidence of ACS. Supplemental table S1 shows all 112 meteorological variables and their univariate calculations.
Our analysis revealed that temperature, sunshine, atmospheric pressure, humidity, rain, wind speed, and wind direction, as well as their derived parameters, showed statistically significant correlations with emergency department visits for ACS. For instance, a 0.1° Celsius decrease in mean daily temperature resulted in a 0.07 (CI 95% 0.08 — 0.06) absolute increase in daily ACS emergency department presentations on average.
Machine learning-based predictions of ED presentations for ACS
The variability in the data explained by each modeling approach is shown in Table 3. When appropriate, the optimal set of hyperparameters is likewise explicated per modeling approach. The highest (adjusted) R2 was obtained using MLR analyses compared to other predictive modeling approaches. Emergency department presentations due to ACS can be predicted using meteorological and calendar data in a moderate manner, where 66% of the variance in daily ACS presentations in the Netherlands can be explained. The explained variance remained similar as the prediction horizon was extended towards 3-, 7-, and 30 days.
Table 3.
Model performances per ACS and subdiagnoses using calendar and meteorological data.
| MLR | Primary outcome | Secondary outcomes | ||||||
|---|---|---|---|---|---|---|---|---|
| Day 1 | Day 3 | Day 7 | Day 30 | |||||
| Diagnosis | R2 | R2 | R2 | R2 | ||||
| ACS | 0.66 | 0.67 | 0.66 | 0.65 | ||||
| UA | 0.80 | 0.80 | 0.81 | 0.79 | ||||
| NSTEMI | 0.45 | 0.47 | 0.45 | 0.47 | ||||
| STEMI | 0.06 | 0.07 | 0.05 | 0.07 | ||||
| Random forest | Primary outcome | Secondary outcomes | ||||||
|---|---|---|---|---|---|---|---|---|
| Day 1 | Day 3 | Day 7 | Day 30 | |||||
| Diagnosis | R2 | Hyperparameters | R2 | Hyperparameters | R2 | Hyperparameters | R2 | Hyperparameters |
| ACS | 0.61 |
MSL = 4 NEst = 900 |
0.60 |
MSL = 8 NEst = 900 |
0.58 |
MSL = 6 NEst = 1000 |
0.63 |
MSL = 10 NEst = 900 |
| UA | 0.75 |
MSL = 4 NEst = 1200 |
0.77 |
MSL = 3 NEst = 800 |
0.75 |
MSL = 2 NEst = 1100 |
0.79 |
MSL = 2 NEst = 1100 |
| NSTEMI | 0.34 |
MSL = 6 NEst = 900 |
0.33 |
MSL = 6 NEst = 1200 |
0.38 |
MSL = 2 NEst = 1200 |
0.41 |
MSL = 10 NEst = 1200 |
| STEMI | 0.04 |
MSL = 9 NEst = 1100 |
0.02 |
MSL = 10 NEst = 1000 |
0.04 |
MSL = 6 NEst = 800 |
0.04 |
MSL = 9 NEst = 1200 |
| LASSO | Primary outcome | Secondary outcomes | ||||||
|---|---|---|---|---|---|---|---|---|
| Day 1 | Day 3 | Day 7 | Day 30 | |||||
| Diagnosis | R2 | Hyperparameter (α) | R2 | Hyperparameter (α) | R2 | Hyperparameter (α) | R2 | Hyperparameter (α) |
| ACS | 0.65 | α = 0.22 | 0.66 | α = 0.25 | 0.65 | α = 0.23 | 0.64 | α = 0.21 |
| UA | 0.79 | α = 0.16 | 0.80 | α = 0.15 | 0.77 | α = 0.19 | 0.78 | α = 0.13 |
| NSTEMI | 0.45 | α = 0.06 | 0.47 | α = 0.07 | 0.45 | α = 0.06 | 0.47 | α = 0.05 |
| STEMI | 0.03 | α = 4.9 | 0.02 | α = 4.3 | 0.02 | α = 4.2 | 0.07 | α = 0.08 |
ACS acute coronary syndrome, LASSO least absolute shrinkage and selection operator regression, MLR multivariable linear regression, MSL minimal sample leaf, Nest number of estimators, NSTEMI non − ST elevated myocardial infarction, R2 explained variance in outcome (for example ACS) incidence, STEMI ST elevated myocardial infarction, UA unstable angina, α alpha (regularization parameter as cost function to control for outliers and prevent overfitting).
For MLR and LASSO R2, adjusted for number of features, was reported. To calculate α, 10 − fold cross − validation was used for the tuning of hyperparameter value (α).
The reported R2 of the Random Forest regressor algorithm are the mean average of all five computed models, which were calculated using 5 − fold grid search cross − validation for hyperparameter tuning.
The reported hyperparameters for the Random Forest Regressor algorithm included a minimal sample split of 2 (standard) as optimal for all models. The random state was set to 42 in all models; for all other hyperparameters, standard values were used.
A total of 140 predictive features (both meteorological and calendar) were used.
Unstable angina pectoris was best predicted using calendar and meteorological data, resulting in 80% of the variance in ED presentations for UA being explained by the data when predicting 1-day ahead. The R2 value for NSTEMI diagnoses was 0.45, indicating that our model explained 45% of the variance in NSTEMI visits to the ED. For STEMI presentations to the ED, our explained variance was approximately zero, regardless of modeling approach employed.
The LASSO regression model identified 46 of the 140 predictive features as most relevant for predicting ACS. The LASSO regression model yielded an explained variance (adjusted R2) of 65% for ACS presentations to the ED, compared to an explained variance of 66% by the MLR model (with 140 predictive features). A similar result was obtained using the RF model compared to the MLR/LASSO approach. Both meteorological and calendar data explained 63% of the variance of emergency department presentations due to ACS. Likewise, similar results were obtained for UA, NSTEMI, and STEMI diagnoses.
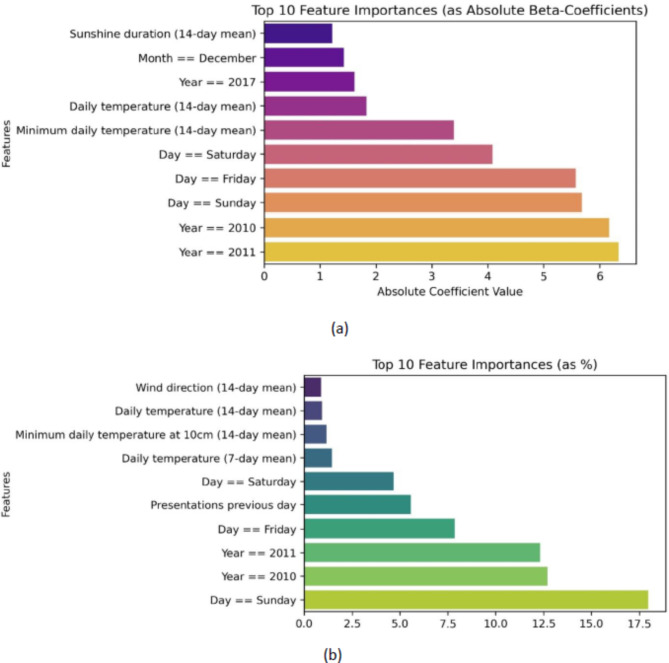
Figure 3 shows a condensed depiction (top 10) of the feature importance for the RF and LASSO/MLR regression models. The most important predictors for predicting ACS incidence are the day of the week (especially Sunday), year 2010/2011, and temperature.
Figure 3.
(a) Feature importance of Random Forest model. (b) Feature importance of the LASSO model. The top 10 importance of individual predictors for machine learning algorithms predicting ACS incidence with a one-day prediction horizon. Abbreviations: LASSO: Least Absolute Shrinkage and Selection Operator. LASSO was employed concurrently with the Multivariable Linear Regression model to serve as a feature selection tool.
Internal validation of modeling approaches
The modeling approaches employed in the present study were subjected to internal validation using the test dataset. When applied to the prediction of ED visits for ACS over the course of the subsequent day, the resulting MAE (MAPE) was 7.8 (11.0%). This value can be interpreted as an average deviation of 7 to 8 cases of actual ED presentations for ACS per day compared to the predicted number. A detailed breakdown of the MAE (MAPE) values corresponding to the subdiagnoses of ACS is shown in Table 4.
Table 4.
Internal validation per modeling approach.
| Diagnosis | Primary outcome | Secondary outcomes | ||
|---|---|---|---|---|
| Day 1 | Day 3 | Day 7 | Day 30 | |
| MAE (MAPE) | MAE (MAPE) | MAE (MAPE) | MAE (MAPE) | |
| MLR/LASSO | ||||
| ACS | 7.8 (11.0) | 8.2 (12.0) | 8.0 (11.9) | 8.0 (11.4) |
| UA | 5.3 (19.1) | 5.5 (20.7) | 5.6 (21.2) | 5.3 (19.3) |
| NSTEMI | 4.4 (17.6) | 4.6 (18.9) | 4.6 (19.0) | 4.7 (19.1) |
| STEMI | 3.3 (28.2) | 3.5 (26.7) | 3.3 (27.0) | 3.4 (27.0) |
| LASSO | ||||
| ACS | 7.8 (11.0) | 8.2 (11.8) | 8.0 (11.9) | 8.1 (11.5) |
| UA | 5.7 (20.3) | 5.8 (21.9) | 5.9 (22.5) | 5.8 (20.8) |
| NSTEMI | 4.7 (18.4) | 4.7 (19.6) | 4.8 (20.1) | 4.8 (19.7) |
| STEMI | 3.4 (28.4) | 3.5 (26.7) | 3.3 (27.0) | 3.4 (27.1) |
| Random forest | ||||
| ACS | 8.2 (11.6) | 8.5 (12.6) | 8.1 (11.6) | 8.3 (11.8) |
| UA | 5.9 (21.2) | 5.8 (21.9) | 5.7 (20.0) | 5.4 (19.6) |
| NSTEMI | 4.7 (19.2) | 4.7 (19.1) | 4.8 (19.7) | 4.6 (19.1) |
| STEMI | 3.4 (28.4) | 3.2 (26.9) | 3.3 (28.3) | 3.3 (27.7) |
ACS acute coronary syndrome, LASSO least absolute shrinkage and selection operator regression, MLR multivariable linear regression, NSTEMI non − ST elevated myocardial infarction, MAE mean absolute error, MAPE mean absolute percentage error, STEMI ST elevated myocardial infarction, UA unstable angina.
Discussion
Summary of findings
Our study aimed to investigate the temporal patterns and predictive factors of ED presentations for ACS in the Netherlands, a temperate climate zone, over an 8-year period.
We observed a reduction in ACS incidence during this period, particularly in the summer months, with a negative correlation between temperature and ACS incidence. Temperature emerged as a key meteorological predictive factor alongside calendar variables.
Second, after 2011, there was a notable decline in ACS occurrence, primarily attributed to a significant decrease in UA cases. Concurrently, there was an increase in the incidence of NSTEMI diagnoses. This decrease and subsequent increase in UA and NSTEMI diagnoses are possibly due to a reclassification of UA. They might be associated with the introduction of high sensitive cardiac troponin assays50. This advance in diagnostics increases the ability of physicians to rule out UA or to rule in NSTEMI cases in patients presenting with similar symptoms51,52. The incidence of STEMI diagnoses remained stable throughout the study period. These trends have been similarly observed in German and Swedish ACS registries53,54.
Furthermore, our descriptive analyses showed considerable daily variations in ACS presentations, with peak incidence on Mondays and a low incidence on weekend days. Our results align with previous literature; a distinct increase in incidence on Mondays and a decrease in presentations during the weekend has been described before13,55. However, the exact mechanism underlying this peak remains unknown. It is speculated that factors such as employment-related stress, inactivity, overconsumption of alcoholic beverages, or registration errors may play significant roles56. Furthermore, a decrease in ACS incidence was observed during the summer months. Seasonal variations in cardiovascular risk factors may explain this trend. A cross-sectional study encompassing data from 24 population-based studies across 15 countries demonstrated a reduction in cardiovascular risk factors during the summer months57.
Our study identified statistically significant correlations between individual weather parameters and ED presentations for ACS. This aligns with a body of research investigating the association between weather and the incidence of ACS58–62.
Predictive modeling
The predictive performance for acute coronary syndrome was moderate (adjusted R2 = 0.66; MAE (MAPE): 7.8 (11.0%), while the performance for subdiagnoses of ACS varied substantially. The prediction of unstable angina pectoris resulted in a good explained variance by our model (adjusted R2 = 0.80; MAE (MAPE): 5.3 (19.1%)). However, the predictive performances for NSTEMI (adjusted R2 = 0.45; MAE (MAPE): 4.4 (17.6%)) and STEMI (adjusted R2 = 0.06; MAE (MAPE): 3.3 (28.2%)) were poor. This implies that on a median day with 85 ACS presentations, our model would forecast an average range of 77 to 93 patients. Similarly, for UA, on this day with a median presentation of 29 patients to the ED, our model’s prediction would averagely span from 23 to 35 patients.
Extending the prediction horizon up to 30 days resulted in a minor decrease in predictive performance. This minor decrease could be explained by the relatively high importance of calendar features compared to meteorological features. The stability of our model, even with an extended prediction horizon, bolsters the potential for their concurrent application with other models predicting ACS in the ED. Furthermore, it strengthens the model’s potential as an instrument for enhancing ED operational efficiency.
Our results indicate that a non-linear machine learning approach using Random Forest regression was not superior to conventional multivariate linear regression. Contradicting our initial hypothesis, a tree-based machine learning algorithm (for example, an RF regression algorithm) would better deal with the multicollinearity of weather and calendar data and thus make more accurate predictions. Previous research proposed using RF machine learning algorithms to explore the complex interactions between weather parameters and cardiovascular events61,62. A possible rationale for this absence of superiority might be a lack of complex non-linear interactions between the input features and the outcome. Alternatively, a lack of connection between the selected variables and the outcome variable, in general, could explain the poor predictive performance of the RF algorithms. The absence of a relationship between our variables and STEMI diagnoses might, in turn, explain poor predictions of STEMI presentations for both modeling approaches. Our results are consistent with those of previous research, which reported an R2 value of 0.67 for predicting ACS incidence using a Random Forest algorithm in a study conducted in a province of Poland that analyzed 106,000 cases of ACS and the influence of weather parameters. This study, however, also incorporated patient characteristics such as medical history and demographic information. Furthermore, this study predicted the overall incidence of ACS in this region, not specifically focusing on ED presentations62.
Feature importance
Feature importance analyses, shown in Fig. 3, revealed that both the LASSO and Random Forest models notably adjusted for the years 2010 and 2011, likely attributed to the shift in the quantification of diagnoses of acute coronary syndrome mentioned above. Although univariate weather correlations were weak, weather parameters were identified for their predictive performance in both LASSO and RF models. Both models underscore the importance of the day of the week and temperature to predict ACS.
Strengths and limitations
In current literature, our research stands as the most comprehensive study concerning both the volume of patients and the duration of the study period assessing ACS incidence in the ED. While the relationship between meteorological conditions and daily or monthly variations has been previously explored, our work uniquely integrates these publicly available factors into predictive models for ACS incidence in the ED. This novel approach holds significant potential for enhancing future research in this field. For instance, the application of ensemble modeling techniques could refine the accuracy of both existing and forthcoming prediction models. For example, new machine learning-based decision support systems have been proposed to prevent unnecessary hospital admissions and enhance the early diagnosis of myocardial infarction63–65. In these studies, machine learning-based classification models have demonstrated superior performance compared to conventional diagnostic pathways and provide quicker identification of low-risk ACS patients. Similarly, prehospital algorithms for diagnosing ACS have been developed. If implemented, these models could optimize the recognition of ACS patients before they present to the ED66,67. Combining advanced prediction models with our model for predicting ACS presentations to the ED could significantly enhance patient care by reducing unnecessary admissions, improving early diagnosis, and optimizing resource allocation.
This study, while providing valuable insights into the temporal patterns of ACS incidence and the prediction of ED presentations for ACS with publicly available data, has several limitations which should be considered when interpreting the results. A notable limitation of our study was the incorporation of ‘Year’ as a predictive variable. The use of ‘Year’ is restrictive because its effects can only be evaluated retrospectively. It is useful for future predictions only if the model is recalibrated annually. To address this, we conducted a supplemental analysis (Table S2), where we excluded the predictor variables for the years 2012 to 2017. The remaining dummy coded variables for the years 2010 and 2011 were retained, essentially serving as an added constant to adjust for the noted change in incidence after these years. In this subanalysis, we observed a minor reduction in R2 (from 0.66 to 0.65) and similar results in our validation metrics, with an MAE (MAPE) of 7.8 (11%). This indicates that our model maintains its robustness even without including yearly trend variables. These supplementary findings suggest that a yearly trend predictor is not essential for our predictions.
Another limitation of our study was the choice of cross-validation (CV) method. We opted for random cross-validation instead of sequential cross-validation. This decision was influenced by the change in ACS classification post-2012 and the transition to a new organization (Vektis, starting in 2016) responsible for the counting and processing of diagnoses and insurance claims. While the change after 2016 did not manifest in the temporal patterns of our data, they could still impact the daily count of ACS diagnoses. Nevertheless, it is important to note that random CV also offers several advantages. A significant benefit is that the predictions derived from random CV tend to be more generalizable compared to those from sequential CV. In our study, we utilized data points from the entire study period (2010–2017) for both training and validation. This approach, stemming from the nature of random CV, potentially reduces the risk of bias and the likelihood of overfitting the models.
An additional limitation of our study is the reliance solely on anonymized data, which limits our ability to evaluate the impact of weather conditions on specific patient comorbidities, such as advanced age, sex, diabetes mellitus, or other concurrent diseases. Due to the nature of our data, we were unable to analyze diurnal variations in our predictions. Consequently, our model provides insights for an entire 24-h period rather than for specific times of the day, which could have had an additional benefit in the optimization of staffing schedules.
Conclusion
The present study sheds light on the temporal patterns of daily emergency department presentations for acute coronary syndrome and its subdiagnoses in the Netherlands. Our findings indicate that ACS presentations exhibit distinctive seasonal changes, with marked reductions in incidence during the summer months. Despite the modest predictive performance of the model using calendar and meteorological features to predict ACS presentations, our results demonstrate that the prediction of ED presentations for unstable angina using these variables has good predictive performance, even when extending the prediction horizon. Future research should focus on identifying new input parameters, such as calculating new non-linear weather features, examining which patients with comorbid diseases are more prone to be affected by meteorological changes, and examining the effect on ACS incidence. Furthermore, future research should include other diagnoses and a combination of modeling approaches to improve the accuracy of predicting overall ED patient presentations. Additionally, our findings could lead to improvement in patient flow within the emergency department and have the potential to assist in refining ED staffing schedules.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
Acknowledgements We would like to thank Andrea Pagani, PhD and Jan Willem Noteboom, MSc (both working at the KNMI DataLab) for their contributions and advices concerning the interpretation of all meteorological data and Miriam de Roos, MSc (researcher at Statistics Netherlands) for her assistance in the data extraction from Statistics Netherlands. We also thank the office of the CIO of the Dutch Ministry of Health, and the CIO, Mr. Ron Roozendaal, specifically for enabling this research project.
Author contributions
VCK wrote main manuscript & contributed to analyses. JS and BS contributed to writing and analyses. DV, JT, AV and BG contributed to writing. All Authors reviewed the manuscript.
Funding
This trial was partly funded by the Dutch Ministry of Health.
Data availability
Data Availability StatementThe data supporting the findings of this study are available upon reasonable request. The datasets, which include detailed information provided by the Dutch Ministry of Health, are not publicly accessible due to privacy and ethical considerations. Interested researchers may contact the corresponding author, Vincent C. Kurucz, MD, BSc, at V.C.Kurucz@amsterdamumc.nl, for data access requests, subject to compliance with applicable data protection regulations.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Van Der Linden, C. et al. Emergency department crowding in the Netherlands: Managers’ experiences. Int. J. Emerg. Med.6, 1–8 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pines, J. M. et al. International perspectives on emergency department crowding. Acad. Emerg. Med.18, 1358–1370 (2011). [DOI] [PubMed] [Google Scholar]
- 3.Affleck, A., Parks, P., Drummond, A., Rowe, B. H. & Ovens, H. J. Emergency department overcrowding and access block. Can. J. Emerg. Med.15, 359–370 (2013). [DOI] [PubMed] [Google Scholar]
- 4.Ramsey, Z. et al. Decreased nursing staffing adversely affects Emergency Department Throughput Metrics. Western J. Emerg. Med.19, 496 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.How The Nursing Shortage Affects The ER—And What To Do. About It - NurseJournal. https://nursejournal.org/articles/nursing-shortage-er-nurses/
- 6.Groot personeelstekort op spoedeisende hulp. : UMC vraagt andere afdelingen bij te springen - NH Nieuws. https://www.nhnieuws.nl/nieuws/319745/groot-personeelstekort-op-spoedeisende-hulp-umc-vraagt-andere-afdelingen-bij-te-springen
- 7.Morley, C., Unwin, M., Peterson, G. M., Stankovich, J. & Kinsman, L. Emergency department crowding: a systematic review of causes, consequences and solutions. PLoS One13, (2018). [DOI] [PMC free article] [PubMed]
- 8.Hoot, N. R. & Aronsky, D. Systematic Review of Emergency Department crowding: Causes, effects, and solutions. Ann. Emerg. Med.52, 126–136e1 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Center for Health Statistics, N. National Hospital Ambulatory Medical Care Survey. 2021 Emergency Department Summary Table (2021).
- 10.Update cijfers acute. zorg 2019 - Nederlandse Zorgautoriteit. https://puc.overheid.nl/nza/doc/PUC_301126_22/1/.
- 11.Ortíz-Barrios, M. A. & Alfaro-Saíz, J. J. Methodological approaches to support process improvement in Emergency departments: A systematic review. Int. J. Environ. Res. Public. Health 202017, 2664 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Frye, M., Mohren, J. & Schmitt, R. H. Benchmarking of data preprocessing methods for machine learning-applications in production. Procedia CIRP104, 50–55 (2021). [Google Scholar]
- 13.Willich, S. N. et al. Weekly variation of acute myocardial infarction. Increased Monday risk in the working population. Circulation90, 87–93 (1994). [DOI] [PubMed] [Google Scholar]
- 14.Mohammad, M. A. et al. Christmas, national holidays, sport events, and time factors as triggers of acute myocardial infarction: SWEDEHEART observational study 1998–2013. BMJ363, (2018). [DOI] [PMC free article] [PubMed]
- 15.Bhaskaran, K. et al. Effects of ambient temperature on the incidence of myocardial infarction. Heart95, 1760–1769 (2009). [DOI] [PubMed] [Google Scholar]
- 16.Sun, Z., Chen, C., Xu, D. & Li, T. Effects of ambient temperature on myocardial infarction: A systematic review and meta-analysis. Environ. Pollut.241, 1106–1114 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Ezekowitz, J. A. et al. The relationship between meteorological conditions and index acute coronary events in a global clinical trial. Int. J. Cardiol.168, 2315–2321 (2013). [DOI] [PubMed] [Google Scholar]
- 18.Panagiotakos, D. B. et al. Climatological variations in daily hospital admissions for acute coronary syndromes. Int. J. Cardiol.94, 229–233 (2004). [DOI] [PubMed] [Google Scholar]
- 19.Ravljen, M., Bilban, M., Kajfež-Bogataj, L., Hovelja, T. & Vavpotič, D. Influence of daily individual meteorological parameters on the incidence of acute coronary syndrome. Int. J. Environ. Res. Public Health11, 11616–11626 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wijnbergen, I., van’t Veer, M., Pijls, N. H. J. & Tijssen, J. Circadian and weekly variation and the influence of environmental variables in acute myocardial infarction. Neth. Heart J.20, 354–359 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Heineman, W. H. S. J. Hippocrates’ Air, Waters and Places (X, 1923).
- 22.Singh Erkamp, N., Van Dalen, H. & De Vries, E. D. Predicting emergency department visits in a large teaching hospital. 10.1186/s12245-021-00357-6. [DOI] [PMC free article] [PubMed]
- 23.Sudarshan, V. K., Brabrand, M., Range, T. M. & Wiil, U. K. Performance evaluation of Emergency Department patient arrivals forecasting models by including meteorological and calendar information: A comparative study. Comput. Biol. Med.135, 104541 (2021). [DOI] [PubMed] [Google Scholar]
- 24.Singh, A. & Museedi, A. S. G. SA. Acute Coronary Syndrome. StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing (2022).
- 25.(KNMI, Royal Netherlands Meteorological Institute & De Bilt Netherlands).
- 26.English | Nederlandse Zorgautoriteit. https://www.nza.nl/english.
- 27.Vektis - business intelligence centrum voor de zorg | Vektis.nl. https://www.vektis.nl/.
- 28.Spencer, F. A., Goldberg, R. J., Becker, R. C. & Gore, J. M. Seasonal distribution of acute myocardial infarction in the second National Registry of myocardial infarction. J. Am. Coll. Cardiol.31, 1226–1233 (1998). [DOI] [PubMed] [Google Scholar]
- 29.Fischer, T., Lundbye-Christensen, S., Johnsen, S. P., Schønheyder, H. C. & Sørensen, H. T. Secular trends and seasonality in first-time hospitalization for acute myocardial infarction–a Danish population-based study. Int. J. Cardiol.97, 425–431 (2004). [DOI] [PubMed] [Google Scholar]
- 30.Loughnan, M. E., Nicholls, N. & Tapper, N. J. Demographic, seasonal, and spatial differences in acute myocardial infarction admissions to hospital in Melbourne Australia. Int. J. Health Geogr.7, (2008). [DOI] [PMC free article] [PubMed]
- 31.Rumana, N. et al. Seasonal pattern of incidence and case fatality of acute myocardial infarction in a Japanese population (from the Takashima AMI Registry, 1988 to 2003). Am. J. Cardiol.102, 1307–1311 (2008). [DOI] [PubMed] [Google Scholar]
- 32.Kriszbacher, I., Bódis, J., Csoboth, I. & Boncz, I. The occurrence of acute myocardial infarction in relation to weather conditions. Int. J. Cardiol.135, 136–138 (2009). [DOI] [PubMed] [Google Scholar]
- 33.Kriszbacher, I., Boncz, I., Koppán, M. & Bódis, J. Seasonal variations in the occurrence of acute myocardial infarction in Hungary between 2000 and 2004. Int. J. Cardiol.129, 251–254 (2008). [DOI] [PubMed] [Google Scholar]
- 34.Abrignani, M. G. et al. Influence of climatic variables on acute myocardial infarction hospital admissions. Int. J. Cardiol.137, 123–129 (2009). [DOI] [PubMed] [Google Scholar]
- 35.Leibowitz, D., Planer, D., Weiss, T. & Rott, D. Seasonal variation in myocardial infarction is limited to patients with ST-elevations on admission. Chronobiol Int.24, 1241–1247 (2007). [DOI] [PubMed] [Google Scholar]
- 36.Savopoulos, C., Ntaios, G. & Hatzitolios, A. Is there a geographic variation in the seasonal distribution of acute myocardial infarction and sudden cardiac death? Int. J. Cardiol.135, 253–254 (2009). [DOI] [PubMed] [Google Scholar]
- 37.Houck, P. D., Lethen, J. E., Riggs, M. W., Gantt, D. S. & Dehmer, G. J. Relation of atmospheric pressure changes and the occurrences of acute myocardial infarction and stroke. Am. J. Cardiol.96, 45–51 (2005). [DOI] [PubMed] [Google Scholar]
- 38.Baumer, H., Ruhenstroth-Bauer, G., Burkel, E. M., Sönning, W. & Filipiak, B. Myocardial infarction and the weather: a significant positive correlation between the onset of heart infarct and 28 kHz atmospherics–A pilot study. Clin. Cardiol.8, 149–151 (1985). [DOI] [PubMed] [Google Scholar]
- 39.Barnett, A. G. et al. Cold periods and coronary events: An analysis of populations worldwide. J. Epidemiol. Community Health (1978)59, 551–557 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hopstock, L. A. et al. The effect of daily weather conditions on myocardial infarction incidence in a subarctic population: The Tromsø Study 1974–2004. J. Epidemiol. Community Health66, 815–820 (2012). [DOI] [PubMed] [Google Scholar]
- 41.Ryti, N. R. I. et al. Cold Weather and Cardiac arrest in 4 Seasons: Helsinki, Finland, 1997–2018. Am. J. Public. Health112, 107–115 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jiang, S., Liu, Q. & Ding, B. A systematic review of the modelling of patient arrivals in emergency departments. Quant. Imaging Med. Surg.13, 1957–1971 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wargon, M., Guidet, B., Hoang, T. D. & Hejblum, G. A systematic review of models for forecasting the number of emergency department visits. Emerg. Med. J.26, 395–399 (2009). [DOI] [PubMed] [Google Scholar]
- 44.Peel, M. C., Finlayson, B. L. & McMahon, T. A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci.11, 1633–1644 (2007). [Google Scholar]
- 45.pandas - Python. Data Analysis Library. https://pandas.pydata.org/.
- 46.NumPy https://numpy.org/.
- 47.statistics · PyPI. https://pypi.org/project/statistics/.
- 48.API Reference. - statsmodels 0.14.0. https://www.statsmodels.org/stable/api.html.
- 49.scikit-learn. machine learning in Python — scikit-learn 1.3.1 documentation. https://scikit-learn.org/stable/.
- 50.Lazar, D. R. et al. High-Sensitivity Troponin: A Review on Characteristics, Assessment, and Clinical Implications. Dis. Markers (2022). (2022). [DOI] [PMC free article] [PubMed]
- 51.Eggers, K. M., Jernberg, T. & Lindahl, B. Unstable angina in the era of Cardiac Troponin assays with improved Sensitivity-A clinical dilemma. Am. J. Med.130, 1423–1430e5 (2017). [DOI] [PubMed] [Google Scholar]
- 52.Braunwald, E. & Morrow, D. A. Unstable Angina Circulation127, 2452–2456 (2013). [DOI] [PubMed] [Google Scholar]
- 53.Neumann, J. T. et al. Temporal trends in incidence and outcome of acute coronary syndrome. Clin. Res. Cardiol.109, 1186–1192 (2020). [DOI] [PubMed] [Google Scholar]
- 54.Jernberg, T. Swedeheart Annual Report for 2018. (2019).
- 55.Witte, D. R., Grobbee, D. E., Bots, M. L. & Hoes, A. W. A meta-analysis of excess cardiac mortality on Monday. Eur. J. Epidemiol.20, 401–406 (2005). [DOI] [PubMed] [Google Scholar]
- 56.Barnett, A. G. & Dobson, A. J. Excess in cardiovascular events on mondays: A meta-analysis and prospective study. J. Epidemiol. Community Health (1978)59, 109–114 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Marti-Soler, H. et al. Seasonality of cardiovascular risk factors: an analysis including over 230 000 participants in 15 countries. Heart100, 1517–1523 (2014). [DOI] [PubMed] [Google Scholar]
- 58.Yang, J. et al. Cardiovascular mortality risk attributable to ambient temperature in China. Heart101, 1966–1972 (2015). [DOI] [PubMed] [Google Scholar]
- 59.Goerre, S. et al. Impact of weather and climate on the incidence of acute coronary syndromes. Int. J. Cardiol.118, 36–40 (2007). [DOI] [PubMed] [Google Scholar]
- 60.Nia, H. S. et al. Weather fluctuations: predictive factors in the prevalence of acute coronary syndrome. Health Promot Perspect.9, 123 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Wang, Y. et al. A random forest model to predict heatstroke occurrence for heatwave in China. Sci. Total Environ.650, 3048–3053 (2018). [DOI] [PubMed] [Google Scholar]
- 62.Wlodarczyk, A. et al. Machine learning analyzed Weather conditions as an effective means in the Predicting of Acute Coronary Syndrome Prevalence. Front. Cardiovasc. Med.9, 786 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Boeddinghaus, J. et al. Machine learning for myocardial infarction compared with Guideline-recommended diagnostic pathways. Circulation149, 1090–1101 (2024). [DOI] [PubMed] [Google Scholar]
- 64.Doudesis, D. et al. Machine learning for diagnosis of myocardial infarction using cardiac troponin concentrations. Nat. Med.29, 1201–1210 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bouzid, Z. et al. In search of an optimal subset of ecg features to augment the diagnosis of acute coronary syndrome at the emergency department. J. Am. Heart Assoc.10, 1–13 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Knoery, C. R. et al. Systematic review of clinical decision support systems for Prehospital Acute Coronary Syndrome Identification. Crit. Pathw. Cardiol.19, 119–125 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Takeda, M. et al. Prehospital diagnostic algorithm for acute coronary syndrome using machine learning: A prospective observational study. Sci. Rep.12, 14593 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data Availability StatementThe data supporting the findings of this study are available upon reasonable request. The datasets, which include detailed information provided by the Dutch Ministry of Health, are not publicly accessible due to privacy and ethical considerations. Interested researchers may contact the corresponding author, Vincent C. Kurucz, MD, BSc, at V.C.Kurucz@amsterdamumc.nl, for data access requests, subject to compliance with applicable data protection regulations.