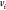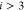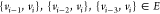Abstract
The discovery of the three-dimensional shape of protein molecules using interatomic distance information from nuclear magnetic resonance (NMR) can be modeled as a discretizable molecular distance geometry problem (DMDGP). Due to its combinatorial characteristics, the problem is conventionally solved in the literature as a depth-first search in a binary tree. In this work, we introduce a new search strategy, which we call frequency-based search (FBS), that for the first time utilizes geometric information contained in the protein data bank (PDB). We encode the geometric configurations of 14,382 molecules derived from NMR experiments present in the PDB into binary strings. The obtained results show that the sample space of the binary strings extracted from the PDB does not follow a uniform distribution. Furthermore, we compare the runtime of the symmetry-based build-Up (SBBU) algorithm (the most efficient method in the literature to solve the DMDGP) combined with FBS and the depth-first search (DFS) in finding a solution, ascertaining that FBS performs better in about 70% of the cases.
Introduction
The determination of the three-dimensional structure of protein molecules represents a profoundly complex challenge within structural biochemistry. This task necessitates a multidisciplinary strategy that melds mathematical modeling, judicious use of computational resources, and experimental data.1,2 Among the models developed to tackle this challenge, the discretizable molecular distance geometry problem (DMDGP) utilizes nuclear magnetic resonance (NMR) data to compute the Cartesian coordinates of atoms within the molecule based on distance measurements provided by NMR techniques.3−5
In the ideal scenario where the distances between all pairs of atoms in a protein are known, the DMDGP can be solved efficiently in linear time.6 However, NMR experiments typically provide only partial and approximate distance data, represented as lower and upper limits, rather than precise values.7 A common assumption in the literature is to fix bond lengths and bond angles of the protein molecule whose 3D structure we want to determine,8 which despite simplifying the problem, allows us to use a mathematical model (the DMDGP) that exploits the important combinatorial features of the problem, not considered in the continuous approach (see the subsequent sections for further discussion).
The most efficient method proposed in the literature to solve the DMDGP is the symmetry-based build-up (SBBU) algorithm,9 which employs a depth-first search (DFS) that explores the search space of the DMDGP, represented as a binary tree.3 While DFS is known for its low memory footprint,10 it does not incorporate biochemical information about proteins. In this paper, for the first time, we leverage data from the protein data bank (PDB)11 to propose an alternative search strategy to DFS.
The DMDGP Search Tree
The DMDGP is a specific subclass of the molecular distance geometry problem (MDGP),12 which is defined as follows.
Given a weighted undirected graph G = (V, E, d), where V represents the set of atoms in the molecule and E is the set of atom pairs with known distances given by 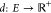 , solving the MDGP involves
finding a function
, solving the MDGP involves
finding a function 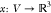 such that
such that
| 1 |
The DMDGP is an MDGP
with a particular ordering of the vertices
of 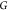 and specific conditions on the known distances.
Specifically, in the DMDGP, each vertex
and specific conditions on the known distances.
Specifically, in the DMDGP, each vertex 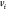 (for
(for 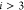 ) must be connected
to its three immediate
predecessors
) must be connected
to its three immediate
predecessors 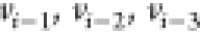 with known distances.
The conditions for
the ordering
with known distances.
The conditions for
the ordering 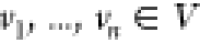 are as follows
(since the DMDGP can also
be defined in other dimensions k, represented as
are as follows
(since the DMDGP can also
be defined in other dimensions k, represented as  , for notational simplicity we simply write
DMDGP for the particular case
, for notational simplicity we simply write
DMDGP for the particular case 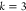 ):
):
A simplified notation is used where the
vertices 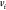 are represented by their indices
are represented by their indices 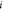 only. Thus,
only. Thus, 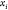 represents the coordinates of the vertex
represents the coordinates of the vertex 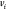 and
and  represents
the distance between vertices
represents
the distance between vertices 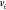 and
and  .
.
To eliminate solutions obtained merely by the rotations and translations of a given solution, the positions of the first three atoms can be fixed as follows:
forming the vertices of a triangle
with sides 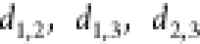 , where θ2,3 is the angle
at
, where θ2,3 is the angle
at 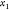 determined by the Law of Cosines.
determined by the Law of Cosines.
Subsequently,
in an iterative construction approach to solving
the DMDGP, under hypothesis H2 (we say that the immediate
predecessors 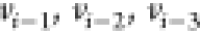 serve as reference
vertices for vi and that
the distances
serve as reference
vertices for vi and that
the distances 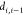 ,
, 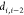 ,
,  are called discretization
distances,13 we can solve the following
system:
are called discretization
distances,13 we can solve the following
system:
 |
2 |
Each of these constraints defines
a sphere centered at one of the immediate predecessors, with a radius
equal to the distance between this center and point 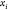 . Therefore,
. Therefore, 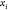 must lie in the intersection of these three
spheres. Assuming a solution exists for the DMDGP and that the points
must lie in the intersection of these three
spheres. Assuming a solution exists for the DMDGP and that the points  are not collinear, the intersection
of
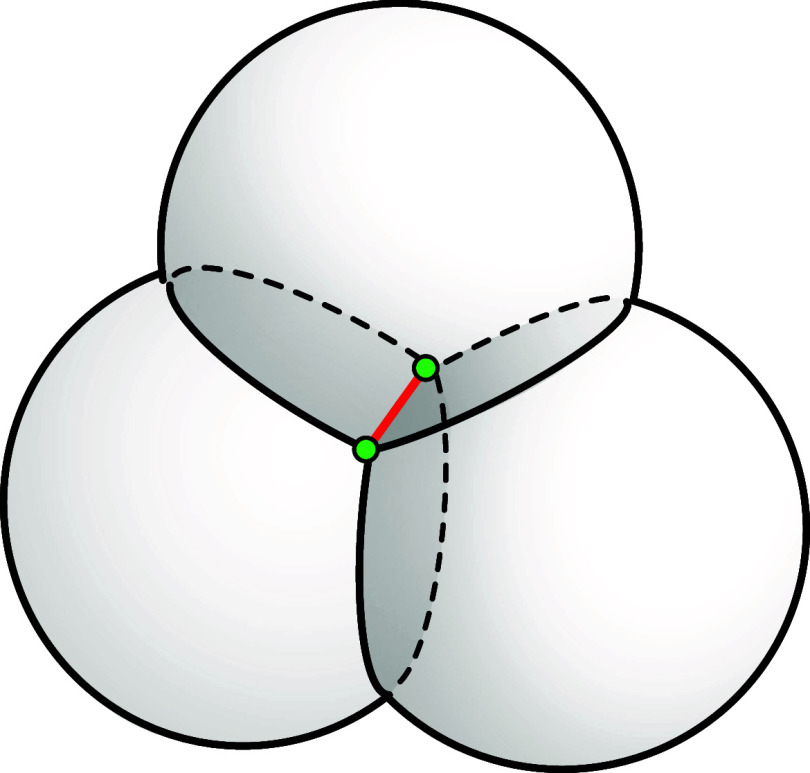
these three spheres will consist of at most two points (see Figure 1).
are not collinear, the intersection
of
these three spheres will consist of at most two points (see Figure 1).
Figure 1.
Two points (green) are in the intersection of three spheres.
Through this constructive procedure, once atoms  are fixed, atom
are fixed, atom 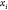 will have two possible positions,
will have two possible positions, 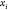 or
or 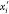 in
in 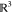 , obtained from system
(2). Once
, obtained from system
(2). Once 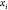 is chosen from the two possibilities,
we
can continue the process by fixing point
is chosen from the two possibilities,
we
can continue the process by fixing point 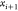 .
.
A natural representation for all
possible configurations is a binary
tree, where 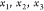 are represented as a single root node (since
they are fixed) and their two children represent the two possibilities
for
are represented as a single root node (since
they are fixed) and their two children represent the two possibilities
for 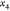 , and for each of these, we have two possibilities
for
, and for each of these, we have two possibilities
for 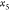 , and so on (see Figure 2).
, and so on (see Figure 2).
Figure 2.

Binary tree associated with a DMDGP instance with six atoms.
If we designate the left node
as child 0 and the right one as child
1, we can also map the relative position of each realization of 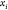 with respect to the plane πi defined by
with respect to the plane πi defined by  , which are the
immediate predecessors of
, which are the
immediate predecessors of  . Specifically, we can define the vectors
. Specifically, we can define the vectors
and assign orientation 0 if  , and 1 otherwise (see Figure 3).
, and 1 otherwise (see Figure 3).
Figure 3.
Plane πi and the positions xi and 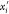 associated
with orientations 0 and 1. The
possible immersion points (in
associated
with orientations 0 and 1. The
possible immersion points (in 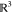 ) for the vertex vi are xi and
) for the vertex vi are xi and 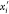 : the
point “above” the plane
πi is xi and has orientation bi = 1; the point “below” πi is
: the
point “above” the plane
πi is xi and has orientation bi = 1; the point “below” πi is 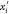 and
has orientation bi =
0.
and
has orientation bi =
0.
When additional distances are
known (namely dij, where j is not one of
the immediate predecessors of atom i), the viable
configurations are reduced by the presence of the additional constraint 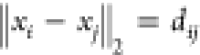 . These additional
distances are referred
to as pruning distances because they make the branches in the DMDGP
binary tree infeasible.13
. These additional
distances are referred
to as pruning distances because they make the branches in the DMDGP
binary tree infeasible.13
Together with the definition of the DMDGP, the branch-and-prune (BP) algorithm13−15 was designed to solve the problem by intelligently traversing the DMDGP search tree. Using the pruning constraints, it prunes branches that are identified as infeasible, thus eliminating the need to explore the entire tree.
Since there exists an algorithm that outperforms BP (the SBBU algorithm,9 as we mentioned in the introduction, we will use it to compare two different approaches to explore the DMDGP binary tree (we will give more details about SBBU in Extracting binary sequences).
The SBBU algorithm was originally developed to use a depth-first search (DFS) strategy that arbitrarily favors the 0 nodes of the binary tree. For example, in a binary tree of length two, the explored paths would be 00, 01, 10, 11.
DFS is a fundamental algorithm used in tree traversal,10 characterized by exploring a branch as deeply as possible before backtracking to explore other branches. While it always finds solutions in finite trees, DFS is notable for its memory efficiency, as it needs to store only a stack of nodes on the current path from the root node. However, it is important to note that DFS does not guarantee the shortest path to the solution.
In contrast to DFS, we propose a best-first search strategy called frequency-based search (FBS), an algorithm that traverses the tree by selecting which path to follow based on an evaluation function that estimates which nodes are most likely to lead to a solution.
An FBS Approach Defined by the PDB
The protein data bank (PDB) is a crucial resource for scientific advancement, containing over one terabyte of structural data for proteins, DNA, and RNA. The archive grows by nearly 10% per year and facilitates over 5 million structure data file downloads daily.16 There are 194,992 protein-related entries in the PDB, of which 14,382 were obtained through NMR.17
To assemble
our data repository, we selected all protein structures derived from
NMR experiments present in the PDB, considering the relevance of such
a technique to the scope of our research. From the first model of
each selected PDB file, we extracted the following information for
the backbone atoms of the protein in question: its unique index, its
name (N, Cα, C, H, Hα), and its coordinates in  , as well as the index
and three-letter
abbreviation of the residue to which it belongs.
, as well as the index
and three-letter
abbreviation of the residue to which it belongs.
It is important to highlight that some PDB files do not completely describe the protein backbone. For example, there are files in which some residues are missing, and in others, some atoms are missing. We also chose to remove proline and glycine residues, as these amino acids exhibit unique geometric characteristics and are often studied separately in the literature.18,19
We refer to the stretches of the backbone formed by contiguous residues after the removal of prolines and glycines as protein segments. Thus, associated with each PDB file, we generated several files, one for each protein segment. The total number of protein segments obtained from all the NMR files in the PDB was 73,675.
A DMDGP Order to Be Used in the FBS
The first step in establishing an FBS strategy that incorporates PDB data is to determine a DMDGP order for the atoms in the backbone. We present a DMDGP order that utilizes the lengths of covalent bonds, bond angles, and the geometric properties of peptide planes (in order to maintain the DMDGP symmetry properties,20,21 some of the atoms must be repeated in the order.22
In the context of
protein geometry, it is considered that bond lengths and bond angles
are fixed, despite the natural internal motions of proteins. This
assumption is known as the rigid geometry hypothesis.23 Consequently, the distances between atoms connected by
one or two covalent bonds are known. In addition to this distance
information, it is well established in the biological literature that
the atoms “around” a peptide bond belong to the same
plane, implying that all distances between these atoms are also known.24 Since the peptide bond connects the carboxyl
carbon of the i-th residue (Ci) to the amine nitrogen of the (i+1)-th residue (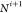 ), the atoms in the i-th
peptide plane are
), the atoms in the i-th
peptide plane are  , Ci,
, Ci, 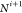 ,
, 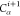 (see Figure 4). We
also consider that the distances between Hi,
(see Figure 4). We
also consider that the distances between Hi,  , and
, and 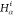 ,
, 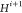 can be detected by NMR.25−27
can be detected by NMR.25−27
Figure 4.

Order ρ of a 3-residue
peptide backbone. The number inside
each circle represents the position of the respective atom in the
order of ρ. The repetition of 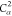 is the
10th element of ρ.
is the
10th element of ρ.
Based on these properties, we use the following DMDGP order for atoms in the protein backbone:
| 3 |
Note that for each intermediary residue we repeat the Cα after the occurrence of the C atom.
Figure 4 illustrates the order ρ for a three-residue peptide (the numbers inside the circles indicate the index of the atoms in the order) and Table 1 gives more information about ρ.
Table 1. Reference Atoms in Order ρa.
| Order | Atom | Predecessor Positions | Predecessor Atoms | ||||
|---|---|---|---|---|---|---|---|
| 1 | N1 | ||||||
| 2 | 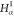 |
||||||
| 3 | C1 | ||||||
| 4 |  |
3 | 2 | 1 | C1 | 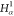 |
N1 |
| 5 | H2 | 4 | 3 | 2 | 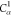 |
C1 | 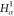 |
| 6 | N2 | 5 | 4 | 3 | H2 | 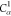 |
C1 |
| 7 |  |
6 | 5 | 4 | N2 | H2 | 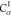 |
| 8 | 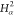 |
7 | 6 | 5 | 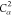 |
N2 | H2 |
| 9 | C2 | 8 | 7 | 6 | 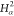 |
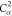 |
N2 |
| 10 | 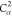 |
9 | 8 | 7 | C2 | 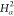 |
 |
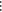 |
|||||||
 |
Hi |  |
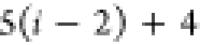 |
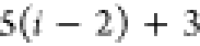 |
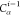 |
 |
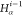 |
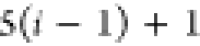 |
Ni | 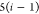 |
 |
 |
Hi | 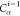 |
 |
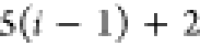 |
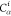 |
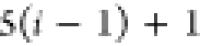 |
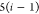 |
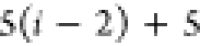 |
Ni | Hi | 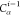 |
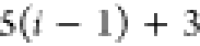 |
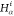 |
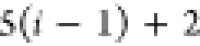 |
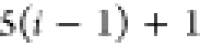 |
 |
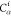 |
Ni | Hi |
 |
Ci | 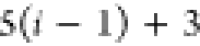 |
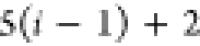 |
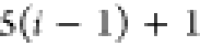 |
 |
 |
Ni |
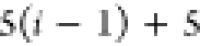 |
 |
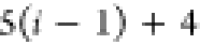 |
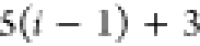 |
 |
Ci |  |
 |
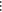 |
|||||||
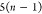 |
Hn | 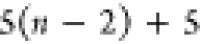 |
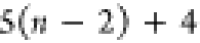 |
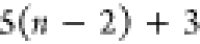 |
 |
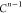 |
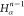 |
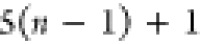 |
Nn | 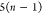 |
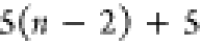 |
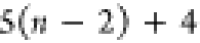 |
Hn | 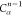 |
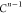 |
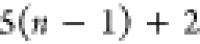 |
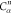 |
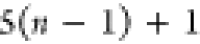 |
 |
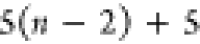 |
Nn | Hn | 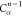 |
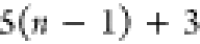 |
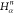 |
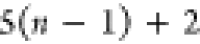 |
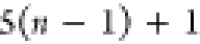 |
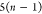 |
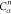 |
Nn | Hn |
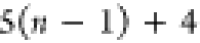 |
Cn | 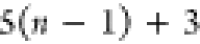 |
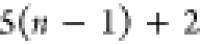 |
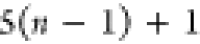 |
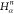 |
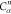 |
Nn |
For each atom in ρ, the first column displays its position; the second column displays its symbol; the third column displays the positions in ρ of its reference atoms; and the fourth column displays the symbols of its reference atoms.
Binary Representation for the Protein Backbone
There are different representations for proteins. In principle, they can be represented by strings formed from 23 characters, each representing one of the possible amino acid residues. This is a unique representation but is not geometric. Another possible representation is a list of 3D coordinates defining the location of each atom composing the protein.
Since the solution space of a DMDGP can be organized as a binary
tree, a solution can be represented as a binary string that incorporates
geometric information. Formally, following the ordering ρ (given
in (3)), each atom at position xi can be associated with a bit bi based on its relative position
to the plane formed by its reference atoms. Thus, the Cartesian coordinates
of each protein segment can be mapped, in a one-to-one relationship,
to a binary sequence .
.
Given that the first three
atoms of ρ are easily fixed in 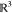 and have no reference
atoms (see Figure 4), we consider b1 = b2 = b3 = 0, without loss of
generality (although
a repeated vertex vi can
have reference atoms, the calculation of xi results in a point identical to the first occurrency
of the atom of vi. In
this case, consider it has a fixed
and have no reference
atoms (see Figure 4), we consider b1 = b2 = b3 = 0, without loss of
generality (although
a repeated vertex vi can
have reference atoms, the calculation of xi results in a point identical to the first occurrency
of the atom of vi. In
this case, consider it has a fixed 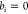 ). We can notice that for
the fourth atom
of ρ, the two possible positions for immersing it in
). We can notice that for
the fourth atom
of ρ, the two possible positions for immersing it in  (resulting from the intersection
of the
spheres associated with x1, x2, x3) are always feasible,
as v4 never has a fourth preceding neighbor.
This implies that for every solution x where b4 = 0, there exists another solution x′, where b4 = 1, obtainable by reflecting x with respect to
the plane π4 that passes through points x1, x2, x3.
(resulting from the intersection
of the
spheres associated with x1, x2, x3) are always feasible,
as v4 never has a fourth preceding neighbor.
This implies that for every solution x where b4 = 0, there exists another solution x′, where b4 = 1, obtainable by reflecting x with respect to
the plane π4 that passes through points x1, x2, x3.
As a direct consequence of this unique characteristic
of v4, we know that the binary representation
of x′ is the total inversion of
the bits
of b from the fourth position onward (except for
binary variables of repeated vertices). Therefore, to reduce the representation
of structures obtained in this manner, we normalize our data set by
inverting all binary representations where b4 = 1. With this choice, the binary representations in our
database have the format 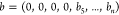 . We adopt the reduced representation
. We adopt the reduced representation 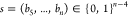 , removing the first four fixed bits.
, removing the first four fixed bits.
Extracting Binary Sequences from the PDB
The SBBU algorithm
solves one pruning constraint at a time. The constraints are of the
form 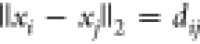 when represented in Cartesian coordinates,
but each of these constraints has a binary version,
when represented in Cartesian coordinates,
but each of these constraints has a binary version, 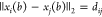 , where
, where 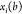 is the coordinate of xi as a function of the binary representation b. A change in the bits bk, for
is the coordinate of xi as a function of the binary representation b. A change in the bits bk, for 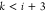 , may alter the coordinates of
, may alter the coordinates of 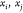 but does not affect the distance
between
them. Therefore, only the bits
but does not affect the distance
between
them. Therefore, only the bits 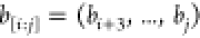 are “relevant” (we will use
this term as a definition) for satisfying the associated constraint.
are “relevant” (we will use
this term as a definition) for satisfying the associated constraint.
In SBBU,9 the pruning edges are ordered
and the associated constraints are solved sequentially. When a constraint
is coupled with a preceding one, that is, if it shares
relevant binary variables, we can utilize an important result from
the DMDGP symmetries.28 This result states
that if 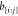 is a viable binary sequence for
is a viable binary sequence for 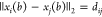 , then the only other viable binary
sequence
for this constraint is the complete flip of
, then the only other viable binary
sequence
for this constraint is the complete flip of 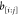 . This means
that when we have coupled constraints,
we can take advantage of part of the solution already found as well
as being part of the other constraint (of course, considering also
its complete flip).
. This means
that when we have coupled constraints,
we can take advantage of part of the solution already found as well
as being part of the other constraint (of course, considering also
its complete flip).
When a constraint does not share relevant binary variables, we refer to it as an independent constraint, and in such cases, SBBU must perform an exhaustive search for viable binary sequences.
The symmetric properties of the DMDGP20 allow us to derive all solutions from a single solution. Consequently, it is unnecessary to determine the PDB conformation as we can directly utilize the first solution found by SBBU. Therefore, when constructing our database, instead of extracting the binary sequences of independent constraints directly from the PDB, we solve the associated DMDGP instances and extract the binary sequences from the first solution that SBBU identifies for each independent constraint.
As the next step,
we organize the extracted binary sequences by
their first and last atoms as well as their lengths. For example,
consider d2,11, an independent pruning
distance related to the molecule illustrated in Figure 4. The atomic names of vertices 2 and 11 are Hα and H, respectively,
and the length of the segment 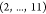 is 10. Thus, we classify the binary solution
associated with d2,11 into the group
is 10. Thus, we classify the binary solution
associated with d2,11 into the group 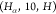 .
.
Our complete data set, comprising 73,675 three-dimensional configurations and their respective binary codings, can be automatically generated using the Python script available in the repository https://github.com/romulomarques/proteinGeometryData(accessed on 30 May, 2024). Additionally, this repository includes a .csv file containing the PDB IDs of all of the instances we downloaded.
The FBS in the SBBU Algorithm
As we already mentioned, the original version of the SBBU algorithm utilizes a DFS strategy. However, we can employ a more sophisticated search method that takes into account the probability distributions of viable binary sequences associated with solutions of DMDGP instances.
The new search
strategy, FBS, is based on identifying a viable path by analyzing
the frequency of binary sequences associated with specific independent
edges. More specifically, we group the viable binary sequences of
independent edges into categories such as 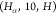 , as mentioned above. For example, another
group utilized is
, as mentioned above. For example, another
group utilized is 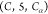 , which contains all constraints
, which contains all constraints 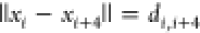 , where atom i is carbon
and atom i + 4 is α-carbon. Subsequently, we
sort the sequences within each group, prioritizing the most probable
ones (i.e., those with the highest frequency).
, where atom i is carbon
and atom i + 4 is α-carbon. Subsequently, we
sort the sequences within each group, prioritizing the most probable
ones (i.e., those with the highest frequency).
The optimal tree
search strategy minimizes the number of visited
nodes. In FBS, paths associated with the most frequent sequences are
tested first. Assuming the binary solution is  , each alternative path is tested
separately:
if the position of b in the FBS order is kb, then kb paths of length n must
be tested, resulting in a total cost of
, each alternative path is tested
separately:
if the position of b in the FBS order is kb, then kb paths of length n must
be tested, resulting in a total cost of
| 4 |
DFS operates in a similar manner within the SBBU algorithm. However, tree paths are ordered from the leftmost to the rightmost. If the position of b in this default ordering is lb, the number of visited nodes is given by
| 5 |
Figure 5 illustrates a binary tree of height four, composed of nodes numbered from 1 to 15. Below the tree representation, squares indicate the FBS ordering of the eight paths from the root to the leaves (ordering learned from the PDB), and triangles indicate the DFS default ordering. Suppose that the path (1, 9, 13, 14), highlighted in blue, represents the binary solution. Additionally, assume that b is in the third position in the FBS order. Under these assumptions, only the rightmost path would not be evaluated by DFS in the search for solution b, while the FBS algorithm would evaluate three paths of length four, involving a total of 12 nodes: (1, 9, 10, 11), (1, 2, 6, 7), and (1, 9, 13, 14).
Figure 5.
Binary tree nodes visited by DFS and FBS. The number in each node represents its position in the DFS visiting order. The number within a square at the bottom of each tree leaf indicates the position of the respective root–leaf path in the FBS. Similarly, the number within a triangle denotes the position of the path in DFS. The blue arcs highlight the root–leaf path corresponding to the solution. Blue squares and gray triangles illustrate which root–leaf paths are explored, respectively, by FBS and DFS until a solution is found (marked with *).
Applying eqs 5 and 4, we obtain
and
Therefore, FBS can reduce the number of visited nodes compared with DFS by prioritizing paths with frequent sequences. In the next section, we present a comparative analysis of SBBU combined with FBS and DFS to demonstrate this performance difference.
Computational Results
In this section, we present a descriptive statistical analysis of the binary sequences processed from our PDB data set. We highlight that the distribution of these sequences is not uniform. Furthermore, we randomly split the protein segment instances into training and test sets with an 80%–20% ratio, respectively. The training set provides the binary sequence frequency information that is used in the FBS strategy. Then, we compare the performances of DFS and FBS in terms of the execution time of the SBBU algorithm.
The SBBU algorithm was implemented in C++, with output processing handled in Python. The experiments were run on a machine equipped with a 13th Gen Intel(R) Core(TM) i9–13900H processor (2.60 GHz), 16GB RAM, and a Linux operating system.
Although there
may be independent pruning edges of other types,
we restrict our analysis to sequences of types 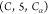 ,
, 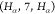 , and
, and 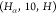 for two reasons: (i) the SBBU algorithm
works by identifying viable binary sequences and then assembling them
together. Hence, the algorithm underperforms when searching for the
solution of independent constraints involving many binary variables
because the search space size is an exponential function of the binary
sequence length; (ii) the frequency of larger sequences is relatively
low compared to the number of sequences of smaller lengths.
for two reasons: (i) the SBBU algorithm
works by identifying viable binary sequences and then assembling them
together. Hence, the algorithm underperforms when searching for the
solution of independent constraints involving many binary variables
because the search space size is an exponential function of the binary
sequence length; (ii) the frequency of larger sequences is relatively
low compared to the number of sequences of smaller lengths.
In Table 2, we observe that for all edge types, the fraction of observed binary sequences (k/kmax) is equal to 1. This indicates that every possible binary sequence of the specified length is present in our data set. Additionally, the ratio of Count to kmax varies significantly across different edge types, reflecting the differing frequencies of each sequence. For instance, the edge type HA-7-HA with a length of 4 has a Count/kmax ratio of 25,225.25. If we had a uniform distribution of sequences, we would expect each unique sequence to be observed 25,000 times on average. In contrast, the C-5-CA edge type with a length of 2 has a ratio of 2913.00, indicating a lower average frequency per sequence.
Table 2. Frequency Information on Binary Sequences for Each Edge Typea.
| Edge Type | Length | Count | k | kmax | k/kmax | Count/kmax |
|---|---|---|---|---|---|---|
| HA-10-H | 7 | 78,943 | 64 | 64 | 1.00 | 1,233.48 |
| HA-7-HA | 4 | 201,802 | 8 | 8 | 1.00 | 25,225.25 |
| C-5-CA | 2 | 5,826 | 2 | 2 | 1.00 | 2,913.00 |
The second column shows the binary sequence lengths (remember that the first three bits are already fixed); the third column shows the number of binary sequences processed from PDB; the fourth column shows the number of unique binary sequences collected; the fifth column shows the number of unique binary sequences that are mathematically possible to exist; the sixth and seventh columns represent the ratios of the third and fourth columns to the fifth column, respectively.
For each edge type, the FBS strategy sorts the binary sequences in descending order, with respect to their occurrence probabilities. In the following, we normalize the order indices by dividing them by the total number of sequences of each length. As a result, the normalized indices have values in the range (0, 1]. That is, if we have ordered sequences s1, s2, and s3, then the normalized indices would be 1/3, 2/3, and 1, respectively.
Figure 6 presents the accumulated probabilities for sequences of each edge type using the same normalized indices. It is observable that edges of the types HA-7-HA and C-5-CA have a distribution close to the uniform distribution. On the other hand, the edge type HA-10-H has a distribution with a sharp peak at the beginning, followed by a rapid decline. Therefore, for the edge type HA-10-H, a small number of sequences concentrate most of the probability mass. By giving priority to the most frequent sequences, we can significantly reduce the computational cost to find a feasible solution to edges in the HA-10-H class.
Figure 6.
Accumulated probability of the occurrence of the protein binary sequences. For each type of independent pruning distance, each binary sequence configuration processed from PDB is mapped, in descending order of probabilities, to an index in the interval (0, 1]. The dashed line represents the accumulated probabilities of a uniform distribution.
In order to compare the performance of DFS and FBS, for each instance of the problem, we measured the execution time of the SBBU algorithm to solve each edge, for each edge type, and also the total execution time.
Figure 7 shows the accumulated probability distribution for the relative time (speedup) of DFS over FBS for each edge type. In this context, a speedup greater than 1 indicates the superior performance of the FBS algorithm compared to DFS. As can be seen, for the edge type HA-10-H, FBS is better than DFS in approximately 80% of the cases. For the edge type HA-7-HA, FBS is better than DFS in approximately 60% of the cases. For edge type C-5-CA, FBS is worse than DFS in approximately 90% of the cases.
Figure 7.
Probability that the time speedup (the ratio of SBBU-DFS time to SBBU-FBS time) for binary sequences of different types of independent pruning distances is less than α, where α can go up to 100. If α is greater than 1, it means that FBS performs better than DFS.
The poor performance of FBS in the C-5-CA class does not affect its overall performance. In fact, Figure 8 shows that the speedup of solving the instances completely is greater than 1 in approximately 68.8% of the cases, which means that FBS is better in almost 70% of the tested problems. This is also reinforced by the right-skewed distribution.
Figure 8.
Histogram of the total time speedup (the ratio of the time that SBBU-DFS spent to solve an instance completely to the respective SBBU-FBS time). The hatched area indicates the number of instances where FBS is better than DFS, which corresponds to 68.8% of all of the tested proteins.
Figure 9 shows the average portion of the time spent by the SBBU algorithm in each edge class. On average, for DFS, the edge types HA-10-H and HA-7-HA correspond to 39% and 17% of the total time, respectively, while the time spent solving the C-5-CA edge type is almost negligible. On the other hand, the FBS strategy reduces the portion of time spent solving HA-10-H edges from 39% to 12%. The efficiency of FBS observed in Figure 8 can be explained by leveraging the edge types HA-10-H and HA-7-HA, as shown in Figure 7, and their relative importance in the total time. For FBS, the last column of Figure 9 shows an increase in the relative time spent solving dependent pruning edges as a consequence of the reduced time spent on HA-7-HA and, more significantly, on HA-10-H edges.
Figure 9.
Median relative time of each type of independent pruning distance when the problems are solved using DFS (blue) and FBS (in red). The relative time of a pruning distance type is the fraction of the total time spent solving all instances that corresponds to that type of distance. The “others” column corresponds to the relative time of all dependent pruning distances combined.
Our experiments demonstrate a clear advantage of the FBS method over the traditional DFS, thereby fulfilling the primary objective of this paper. Although the binary sequences extracted and analyzed from the PDB represent a specific subset of proteins, particularly those characterized by using NMR techniques, the data provide a robust foundation for our analysis and support the effectiveness of the FBS method within this context.
Conclusions
This study represents a pioneering effort in integrating data from the protein data bank (PDB) to address the discretizable molecular distance geometry problem (DMDGP), a central model in protein structure determination using nuclear magnetic resonance (NMR) data.
Our methodology exploits the combinatorial structure of the DMDGP, where the solution space is organized as a binary tree. By developing a binary string representation for protein backbone atomic coordinates, we identified nonuniform frequency patterns. This discovery led to the creation of the frequency-based search (FBS) method, which utilizes these patterns to enhance the search efficiency within the DMDGP solution space.
We incorporated FBS into the symmetry-based build-up (SBBU) method, the current state-of-the-art approach for solving DMDGP instances. Replacing the traditional depth-first search (DFS) with FBS in the SBBU framework resulted in an efficiency improvement in approximately 70% of tested instances, as evidenced by reduced computational time. This improvement is due to a significant decrease in the number of nodes traversed. Unlike DFS, FBS employs a data-driven strategy based on PDB-derived patterns, increasing the likelihood of identifying viable conformations and enhancing the search efficacy.
The results indicate that future research should focus on adapting FBS to other variants of the distance geometry problem (DGP)29,30 and expanding its application to additional structure determination techniques.
Acknowledgments
This research was funded by the Brazilian research agencies FAPESP (grant numbers 2013/07375-0 and 2023/08706-1), CAPES (grant number 88887.609785/2021-00), and CNPq (grant numbers 305227/2022-0 and 300809/2024-7). We also extend our gratitude to the anonymous reviewers for their substantial contributions to improving this paper.
Data Availability Statement
The codes provided by the authors at https://github.com/romulomarques/proteinGeometryData (accessed on 30 May 2024) progressively generates all files and folders used in this research. However, since some of these folders occupy a significant amount of memory, such as the folder containing the files downloaded from the PDB, which amounts to 25 Gigabytes, the authors have decided to make available in the GitHub repository the folder containing the data of protein segments, which is the necessary information to actually reproduce the experiment. In addition, in the same repository, the authors provide a .csv file that lists the PDB IDs of all the downloaded 3D structures. This Github project also provides the C++ implementation of the SBBU algorithm with both of DFS and FBS searches, and the Python codes that generate the graphics of the paper.
The Article Processing Charge for the publication of this research was funded by the Coordination for the Improvement of Higher Education Personnel - CAPES (ROR identifier: 00x0ma614).
The authors declare no competing financial interest.
References
- Donald B. R.Algorithms in Structural Molecular Biology; MIT Press, 2011. [Google Scholar]
- Schlick T.Molecular modeling and simulation: an interdisciplinary guide; Springer, 2010. [Google Scholar]
- Lavor C.; Liberti L.; Maculan N.; et al. The discretizable molecular distance geometry problem. Comput. Optim. Appl. 2012, 52, 115–146. 10.1007/s10589-011-9402-6. [DOI] [PubMed] [Google Scholar]
- Lavor C.; Liberti L.; Maculan N. Recent advances on the discretizable molecular distance geometry problem. Eur. J. Oper. Res. 2012, 219, 698–706. 10.1016/j.ejor.2011.11.007. [DOI] [Google Scholar]
- Mucherino A.; Lavor C.; Liberti L. The discretizable distance geometry problem. Opt. Lett. 2012, 6, 1671–1686. 10.1007/s11590-011-0358-3. [DOI] [PubMed] [Google Scholar]
- Dong Q.; Wu Z. A linear-time algorithm for solving the molecular distance geometry problem with exact inter-atomic distances. J. Glob. Optim. 2002, 22, 365–375. 10.1023/A:1013857218127. [DOI] [Google Scholar]
- Wüthrich K. Protein Structure Determination in Solution by Nuclear Magnetic Resonance Spectroscopy. Science 1989, 243, 45–50. 10.1126/science.2911719. [DOI] [PubMed] [Google Scholar]
- Crippen G.; Havel T.. Distance Geometry and Molecular Conformation; Research Studies Press, 1988. [Google Scholar]
- Gonçalves D. S.; Lavor C.; Liberti L.; Souza M. A new algorithm for the k dmdgp subclass of distance geometry problems with exact distances. Algorithmica 2021, 83, 2400–2426. 10.1007/s00453-021-00835-6. [DOI] [Google Scholar]
- Cormen T. H.; Leiserson C. E.; Rivest R. L.; Stein C.. Introduction to algorithms; MIT press, 2022. [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liberti L.; Lavor C.; Maculan N.; Mucherino A. Euclidean distance geometry and applications. SIAM Rev. 2014, 56, 3–69. 10.1137/120875909. [DOI] [Google Scholar]
- Liberti L.; Lavor C.; Maculan N. A branch-and-prune algorithm for the molecular distance geometry problem. Int. Trans. Oper. Res. 2008, 15, 1–17. 10.1111/j.1475-3995.2007.00622.x. [DOI] [Google Scholar]
- dos Santos Carvalho R.; Lavor C.; Protti F. Extending the geometric build-up algorithm for the molecular distance geometry problem. Inf. Process. Lett. 2008, 108, 234–237. 10.1016/j.ipl.2008.05.009. [DOI] [Google Scholar]
- Malliavin T. E.; Mucherino A.; Lavor C. Systematic exploration of protein conformational space using a distance geometry approach. J. Chem. Inf. Model. 2019, 59, 4486–4503. 10.1021/acs.jcim.9b00215. [DOI] [PubMed] [Google Scholar]
- About Us - Research Collaboratory for Structural Bioinformatics Protein Data Bank (RCSB PDB). https://www.rcsb.org/pages/about-us/index. accessed on 6–October–2024.
- RCSB PDB Statistics: Growth of Structures from NMR Experiments Released per Year. https://www.rcsb.org/stats/growth/growth-nmr. accessed 6–October–2024.
- Lovell S. C.; Davis I. W.; Arendall W. B. III; De Bakker P. I. W.; Word J. M.; Prisant M. G.; Richardson J. S.; Richardson D. C. Structure Validation by Cα Geometry: ϕ, ψ and Cβ Deviation. Proteins 2003, 50, 437–450. 10.1002/prot.10286. [DOI] [PubMed] [Google Scholar]
- Read R. J.; Adams P. D.; Arendall W. B.; Brunger A. T.; Emsley P.; Joosten R. P.; Kleywegt G. J.; Krissinel E. B.; Lütteke T.; Otwinowski Z. A new generation of crystallographic validation tools for the protein data bank. Structure 2011, 19, 1395–1412. 10.1016/j.str.2011.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mucherino A.; Lavor C.; Liberti L. Exploiting symmetry properties of the discretizable molecular distance geometry problem. J. Bioinform Comput. Biol. 2012, 10, 1242009. 10.1142/S0219720012420097. [DOI] [PubMed] [Google Scholar]
- Lavor C.; Oliveira A.; Rocha W.; Souza M. On the optimality of finding DMDGP symmetries. Comput. Appl. Math. 2021, 40 (3), 98. 10.1007/s40314-021-01479-6. [DOI] [Google Scholar]
- Lavor C.; Souza M.; Carvalho L. M.; Liberti L. On the polynomiality of finding KDMDGP re-orders. Discrete Appl. Math. 2019, 267, 190–194. 10.1016/j.dam.2019.07.021. [DOI] [Google Scholar]
- Gibson K. D.; Scheraga H. A. Energy minimization of rigid-geometry polypeptides with exactly closed disulfide loops. J. Comput. Chem. 1997, 18, 403–415. . [DOI] [Google Scholar]
- Lavor C.; Liberti L.; Donald B.; Worley B.; Bardiaux B.; Malliavin T. E.; Nilges M. Minimal NMR distance information for rigidity of protein graphs. Discrete Appl. Math. 2019, 256, 91–104. 10.1016/j.dam.2018.03.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Güntert P. Structure calculation of biological macromolecules from NMR data. Q. Rev. Biophys. 1998, 31, 145–237. 10.1017/S0033583598003436. [DOI] [PubMed] [Google Scholar]
- Rowland R. S.; Taylor R. Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii. J. Phys. Chem. 1996, 100, 7384–7391. 10.1021/jp953141+. [DOI] [Google Scholar]
- Billeter M.; Braun W.; Wüthrich K. Sequential Resonance Assignments in Protein H Nuclear Magnetic Resonance Spectra: Computation of Sterically Allowed Proton-Proton Distances and Statistical Analysis of Proton-Proton Distances in Single Crystal Protein Conformations. J. Mol. Biol. 1982, 155, 321–346. 10.1016/0022-2836(82)90008-0. [DOI] [PubMed] [Google Scholar]
- Liberti L.; Masson B.; Lee J.; Lavor C.; Mucherino A. On the number of realizations of certain Henneberg graphs arising in protein conformation. Discrete Appl. Math. 2014, 165, 213–232. 10.1016/j.dam.2013.01.020. [DOI] [Google Scholar]
- Mucherino A.; Lavor C.; Liberti L., et al. Distance geometry: theory, methods, and applications; Springer Science & Business Media, 2012. [Google Scholar]
- Billinge S. J.; Duxbury P. M.; Gonçalves D. S.; et al. Recent results on assigned and unassigned distance geometry with applications to protein molecules and nanostructures. Ann. Oper. Res. 2018, 271, 161–203. 10.1007/s10479-018-2989-6. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The codes provided by the authors at https://github.com/romulomarques/proteinGeometryData (accessed on 30 May 2024) progressively generates all files and folders used in this research. However, since some of these folders occupy a significant amount of memory, such as the folder containing the files downloaded from the PDB, which amounts to 25 Gigabytes, the authors have decided to make available in the GitHub repository the folder containing the data of protein segments, which is the necessary information to actually reproduce the experiment. In addition, in the same repository, the authors provide a .csv file that lists the PDB IDs of all the downloaded 3D structures. This Github project also provides the C++ implementation of the SBBU algorithm with both of DFS and FBS searches, and the Python codes that generate the graphics of the paper.