Clustering-based binary Grey Wolf Optimisation model with 6LDCNNet for prediction of heart disease using patient data

Abstract

In recent years, the healthcare data system has expanded rapidly, allowing for the identification of important health trends and facilitating targeted preventative care. Heart disease remains a leading cause of death in developed countries, often leading to consequential outcomes such as dementia, which can be mitigated through early detection and treatment of cardiovascular issues. Continued research into preventing strokes and heart attacks is crucial. Utilizing the wealth of healthcare data related to cardiac ailments, a two-stage medical data classification and prediction model is proposed in this study. Initially, Binary Grey Wolf Optimization (BGWO) is used to cluster features, with the grouped information then utilized as input for the prediction model. An innovative 6-layered deep convolutional neural network (6LDCNNet) is designed for the classification of cardiac conditions. Hyper-parameter tuning for 6LDCNNet is achieved through an improved optimization method. The resulting model demonstrates promising performance on both the Cleveland dataset, achieving a convergence of 96% for assessing severity, and the echocardiography imaging dataset, with an impressive 98% convergence. This approach has the potential to aid physicians in diagnosing the severity of cardiac diseases, facilitating early interventions that can significantly reduce mortality associated with cardiovascular conditions.

Introduction

Cardiovascular disease (CVD) remains the leading cause of mortality worldwide, contributing to approximately a quarter of all annual deaths in developed countries like the United States¹. It encompasses a range of conditions, with coronary artery disease being one of the most prevalent². Projections suggest that CVD could claim over 23.6 million lives by 2030, underscoring the urgent need for effective preventive measures³. Key risk factors for CVD include lifestyle habits such as stress, alcohol consumption, smoking, unhealthy diets, and sedentary behavior, as well as medical conditions like hypertension and diabetes^4–5. Early detection and intervention are crucial, as many cardiovascular disorders are treatable if identified promptly.

In recent years, the expansion of healthcare data systems has provided a wealth of information that can be leveraged to improve health outcomes through data analysis of patients’ health records. Analyzing clinical data for heart disease (HD) diagnosis requires consideration of various factors, including the presence or absence of primary lesions, accurate diagnosis, genetic variables, socioeconomic and medical status, environmental conditions, and lifestyle choices^6–7. These complexities often prolong the diagnostic process, necessitating precise approaches to detect HD and specifically heart failure⁸.

Machine learning (ML) algorithms have been increasingly applied to clinical data for HD prognoses, though challenges such as class imbalance and dataset complexity persist⁹. Numerous techniques, including linear networks and active learning, have been utilized, each with its strengths and limitations^10–11. Hybrid models combining data mining techniques, such as logistic regression and automatic feature discovery, are also explored for predicting and diagnosing cardiovascular diseases^12–13. The inefficiencies of conventional methods highlight the need for medical diagnostic systems that employ feature selection methodologies to enhance prediction and analysis accuracy¹⁴. Feature selection not only improves classification efficiency but also reduces computational burden^15–16.

This study addresses these challenges by employing a Binary Grey Wolf Optimization (BGWO) model to cluster essential features of cleansed data before applying a classification algorithm. Subsequently, a 6-layered deep convolutional neural network (6LDCNNet) is used for heart disease categorization. The network’s classification precision is enhanced by employing the Improved Sailfish Optimization Algorithm (ISFOA) for hyper-parameter tuning.

The motivation for this study is rooted in the need for improved methodologies for heart failure diagnosis leveraging data analysis of patients’ health records. By recognizing the complexities involved in evaluating an individual’s health status and addressing challenges like class imbalance, this research proposes a solution that aims to improve classification precision and reduce computational load. The proposed system, detailed in the following sections, demonstrates significant potential in advancing heart disease prediction and early diagnosis.

The primary objective of this study is to develop a robust, two-stage predictive model for early diagnosis and prognosis of cardiovascular disease. Specifically, the study aims to:

1. Utilize the Binary Grey Wolf Optimization (BGWO) algorithm for effective feature selection and clustering, reducing computational complexity while retaining critical information.

2. Propose a novel 6-layered deep convolutional neural network (6LDCNNet) for accurate classification of heart disease, leveraging hyper-parameter tuning through an Enhanced Sailfish Optimization Algorithm (ISFOA).

3. Validate the proposed model using both text-based clinical datasets and echocardiographic imaging datasets to demonstrate its scalability and efficacy.

By achieving these objectives, this study seeks to contribute a comprehensive and scalable solution for early detection of CVD, which could also have implications for mitigating associated conditions like dementia.

The related work is presented in Section “Related work”, followed by the proposed approach in Section “Proposed system”. Section “Results and discussion” covers the experimental analysis conducted on two UCI datasets, and the study concludes in Sect. “Conclusion and future work”, outlining potential avenues for future investigations.

Related work

Jain et al.¹⁷ developed a novel approach, termed Levy Flight-Convolutional Neural Network (LV-CNN), tailored specifically for diagnosing heart disease using cardiac imaging. The method begins by scaling down the incoming large data photos to streamline computational processes. Subsequently, the LV-CNN model is applied to these resized images. To mitigate the impact of the loss function on CNN architecture, they integrate the LV strategy with the sunflower optimization algorithm (SFO). This amalgamation safeguards the SFO algorithm against being trapped in local minima resulting from the Levy flight’s stochastic trajectory. Through simulated and experimental testing conducted in the MATLAB environment, the proposed method is anticipated to achieve an accuracy of 95.74%, specificity of 0.96%, an error rate of 0.35%, and a runtime of 9.71 s. The comparative analysis of results underscores the superiority of this innovative approach.

Ozcan and Peker¹⁸ introduced a novel approach utilizing a supervised classification and regression tree (CART) algorithm to predict cardiac illnesses and derive decision rules, aiming to elucidate the relationships between input and output variables. Their study offers insights into the hierarchy of factors influencing cardiovascular disease. The reliability of the model is evidenced by its notable accuracy rate of 87% when considering all performance metrics. Notably, the extraction of decision rules from the model can potentially streamline clinical applications with minimal prior information. Ultimately, this algorithmic framework has the potential to benefit both medical professionals and individuals constrained by limitations of time and financial resources.

Bhatt et al.¹⁹ proposed employing k-mode clustering to improve classification precision, utilizing models such as XGBoost (XGB), Multilayer Perceptron (MP), and Random Forest (RF). Through parameter hyper-tuning via GridSearchCV, they achieved superior results. Evaluating their model on Kaggle’s 70,000-instance real-world dataset, they achieved the following accuracies during training with an 80/20 split: Decision Tree: 86.37% (with cross-validation), 86.53% (without cross-validation); XGBoost: 86.87% (with cross-validation), 87.02% (without cross-validation); Random Forest: 87.05% (with cross-validation), 86.92% (without cross-validation); Multilayer Perceptron: 87.28% (with cross-validation), 86.94% (without cross-validation). The area under the curve (AUC) estimates for the models were as follows: Decision Tree = 0.94, XGBoost = 0.95, Random Forest = 0.95, and Multilayer Perceptron = 0.95. This comprehensive analysis concluded that the Multilayer Perceptron with cross-validation exhibited the highest accuracy rate at 87.28%.

A model for the detection of disease utilising a Multi-Layered Artificial Neural Network (ML-ANN) and a backpropagation method was introduced by Kaur et al.²⁰. The proposed model evaluates the impact of varying the number of hidden layer neurons across various transfer functions. Thirteen clinical factors related to heart disease have been used in the model’s implementation on Kaggle and Statlog. Using six hidden layers with a tan-hyperbolic transfer function, the experimental findings achieved 99.92% accuracy. Statistical parameters and k-fold cross-validation have been used to back up the findings.

Wang et al.²¹ introduced a novel approach called Cloud-Random Forest (C-RF) for assessing the likelihood of coronary heart disease (CHD), which combines a cloud model with a random forest algorithm. Unlike traditional methods employing classification and regression trees (CART), this method integrates a cloud model and the decision-making trial and evaluation laboratory to determine the weights of assessment characteristics. The weights of each attribute, along with the gain value of the attribute’s least Gini coefficient, are aggregated and applied to the original gain value. The C-RF represents an innovative variant of the random forest, utilizing a value rule to partition nodes in the CART and construct decision trees. Their empirical study, conducted using the Framingham dataset and surveying users of the Kaggle platform, demonstrated notable performance improvements over conventional methods such as CART, SVM, CNN, and RF. Specifically, the C-RF achieved error rate reductions of 9%, 4%, and 3% compared to CART, SVM, CNN, and RF, respectively. The error rate of the C-RF was 13.99%, significantly lower than those of CART, SVM, CNN, and RF, indicating superior performance. Additionally, the C-RF exhibited an area under the curve (AUC) of 0.85, surpassing the average of the compared models.

In their hybrid method of heart disease prediction, Thakur et al.²². used both the k-Nearest Neighbour (KNN) and the k-Means algorithms. There is hope that the suggested hybrid strategy will help doctors spot high-risk cases of heart disease earlier. Using K-Means, the data is clustered into high-risk and low-risk groups, and then the groupings are given appropriate labels. The likelihood of developing heart disease in the future is then predicted by applying KNN to both the high- and low-risk cohorts. This strategy can be useful for determining which patients require emergency medical care. Patients have a better chance of survival if their diseases are detected and treated promptly.

Chandrasekhar et al.²³ employed various machine learning techniques to enhance the accuracy of cardiac illness prediction using datasets from Cleveland and IEEE Dataport. Six methods were utilized, including K-nearest neighbor, logistic regression, Naive Bayes, gradient boosting, and AdaBoost classifiers. They utilized GridSearchCV and five-fold cross-validation to refine model precision. Logistic regression exhibited the highest accuracy of 90.16% on the Cleveland dataset, while AdaBoost performed best with 90% accuracy on the IEEE Dataport dataset. The researchers further improved performance by integrating all six methods into a soft voting ensemble classifier, achieving 93.44% accuracy on the Cleveland dataset and 95% accuracy on the classifiers. Notably, they introduced a novel aspect by employing GridSearchCV with five-fold cross-validation to optimize hyperparameters, determine optimal model parameters, and assess performance using accuracy and negative log loss metrics. Evaluation of the model’s performance involved observing accuracy loss across multiple folds in both benchmark datasets. The soft voting ensemble classifier strategy demonstrated increased accuracy on both datasets, significantly surpassing previous research in heart disease forecasting.

Shaik et al.²⁴ introduce a novel gradient-boosted method for heart disease analysis, integrating machine learning (ML) and Bayesian data analysis (BDA). Through various metrics, they highlight the practical effectiveness of their proposed approach. Results showcase the efficacy of their technique in medical diagnosis, with the SS-GBDT achieving a notable 95% recall rate and a 96.3% F1 measure. This proposed strategy represents a significant advancement in leveraging the combined potential of BDA and ML to enhance medical diagnosis.

Despite these advancements, existing models face challenges such as class imbalance, high computational costs, and limited generalizability across diverse datasets. Furthermore, many studies focus on a single type of data (either text or image) rather than integrating multiple data types for comprehensive analysis.

Our study addresses these gaps by introducing a two-stage model that integrates text and image data using a Binary Grey Wolf Optimization (BGWO) model for feature selection and a 6-layered deep convolutional neural network (6LDCNNet) for classification. This dual approach enhances prediction accuracy and reduces computational burden. Additionally, the Improved Sailfish Optimization Algorithm (ISFOA) is employed for hyper-parameter tuning, further improving the model’s performance.

Proposed system

Figure 1 depicts the two main goals of the research effort on heart disease prediction.

Fig. 1.

Workflow of the proposed model.

Dataset description

Text data

The dataset on cardiovascular disease utilised in this research²⁵ was gathered using the UCI machine learning repository. The machine learning community has had easy access to the 487 datasets housed in this 1987 repository ever since. The Cleveland dataset has 303 occurrences of missing data (20% of the total), spread across 13 characteristics and 1 target variable. There are 138 typical examples and 165 outliers in the sample. Over 83.6% of the examples in the sample are roughly distributed across the two classes. Additionally, an election was run to pick rationally balanced cases for validation to compensate for the tiny rational imbalance. Six missing cases were eliminated from this dataset before analysis could begin. Table 1 summarises the characteristics of the data set.

Table 1.

Description of the dataset features.

Category	Feature	Explanation
Numeric	Thal	3 = normal; 6 = fixed flaw; 7 = reversible flaw
Categorical	Num (target variable)	Heart disease analysis 0: less than 50% width tapering and 1: additional than 50% diameter narrowing
Numeric	Age	Years of age
Categorical	Sex	1: male, 0: female
Numeric	CP	Type of chest pain 1: typical angina, 2: atypical angina, 3: no indications
Numeric	Trestbps	Standing blood heaviness of the patient (in mm Hg)
Numeric	Chol	Serum cholesterol (in mg/dl)
Categorical	Fbs	If fasting blood sugar > 120; 0 = false)
Numeric	Restecg	0: means “normal”. 1: averaging an aberrant ST- depression of > 0.05 mV) 2: representative probable or definite left ventricular hypertrophy rendering to Estes’ criteria
Numeric	Thalach	Reached extreme heart rate.
Categorical	Exang	Angina induced by workout (1 = yes; 0 = no)
Numeric	Oldpeak	Exercise-induced ST depression in contrast to resting
Numeric	Slope	The peak exercise’s slope ST-segment V 1: up-sloping,2: flat, and 3: down-sloping
Numeric	Ca	Number of important vessels (0–3) coloured by fluoroscopy

Image dataset

In²⁶, the characteristics used to describe the dataset of echocardiography images are described. Echocardiography pictures, including 66 normal images from 30 members and 66 aberrant images from 30 individuals, were retrieved from the UCI database. Images taken from the dataset are shown as examples in Fig. 2. The training and examination methods were identical. The training was done with photos taken from the UCI database, whereas testing was done with photographs taken in real-time.

Fig. 2.

Sample images.

Pre-processing

At this point, the data has not yet been forwarded to the clustering process, but two crucial tasks have already been completed.

Task 1: handling missing values

Handling missing values is crucial to ensure the integrity and accuracy of the data analysis. In this study, we employed advanced techniques such as Weighted Moving Average (WMA) and Inverse Probability Weighting (IPW) to address missing values in the dataset.

Techniques used

Weighted Moving Average (WMA) This method assigns weights to observations, giving more importance to recent data points when estimating missing values. This approach is particularly useful for time-series data or when trends over time are considered.

Inverse Probability Weighting (IPW) This technique accounts for the probability of data being missing by assigning weights based on the inverse probability of missingness. It is effective in reducing bias when data is missing not at random (MNAR).

Missing value percentages

To provide a comprehensive understanding of the dataset’s completeness, we calculated the percentage of missing values for each selected feature:

• slope: 2.3%.

• ca.: 3.1%.

• age: 0.0%.

• sex: 0.0%.

• cp.: 1.5%.

• trestbps: 2.7%.

• chol: 2.9%.

• fbs: 0.5%.

• restecg: 1.8%.

• thalach: 2.1%.

• exang: 0.4%.

• oldpeak: 3.5%.

• target: 0.0%.

These percentages highlight the extent of missing data across different features, guiding the selection of appropriate imputation techniques. By integrating WMA and IPW, we ensured that missing values were handled effectively, minimizing potential biases and preserving the dataset’s reliability.

Task 2: elimination of redundant values

The time required to train a model is affected by the number of records in the dataset, which increases when redundant values are included. Second, the model can’t make reliable predictions when there are redundant values present because it gives too much weight to the variables that have already been used. The model’s performance in testing is negatively impacted by both of these issues.

Clustering using BGWO model

The Binary Grey Wolf Optimization (BGWO) model was chosen for feature clustering due to its unique advantages in handling high-dimensional datasets, particularly in medical data analysis. BGWO’s hierarchical structure allows for a balanced exploration and exploitation during feature selection, leading to improved convergence and lower computational costs. Unlike traditional clustering techniques such as k-means clustering, which relies on pre-defined centroids and struggles with non-linear separable data, BGWO identifies optimal feature subsets adaptively. Similarly, compared to genetic algorithms, BGWO is computationally more efficient and converges faster to an optimal solution. These capabilities make BGWO a suitable choice for clustering medical features, especially in imbalanced datasets, where prioritizing critical features is essential. A comparative analysis of BGWO with traditional methods is provided in Table X to demonstrate its superiority in terms of efficiency, accuracy, and robustness. Mirjalili et al.²⁷ created the GWO algorithm. The herd mentality of wolves serves as the basis for this naturalistic metaheuristic. Like other nature-inspired metaheuristics like the GA and the ACO, this algorithm searches the search space for the best possible solution. One of the newest swarm algorithms²⁸ consists of the following theoretical procedures:

Encircling prey

Grey wolves begin a hunt by surrounding their victim. Mathematically, the circular behaviour may be stated as:

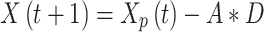1

where X is the grey wolf, where is the predator’s position vector,

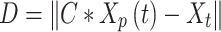2

Where,

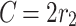3

and

4

where and 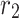are vectors chosen at random from [0, 1], whereas a falls gradually from 2 to 0 over the course of many rounds, as seen below.:

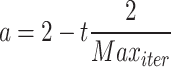5

where t is the current repetition, and is the extreme sum of possible iterations for optimisation.

Hunting prey

Wolves have a clear-cut alpha, beta, delta, and omega tier in their social structure. While the alpha often takes charge of a hunt, the beta and delta are also capable of taking the helm on occasion. Due to our lack of information, we may safely assume that alpha, beta, and delta are the top three answers and release the remaining wolves (omega) to begin exploring other possibilities. The following expressions indicate the top three solutions for this simulation:

6

where,

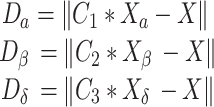7

Other wolves (omega) should, therefore, be obligated to revise their stances as follows:

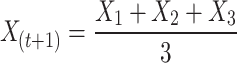8

To overcome the binary nature of the feature selection, GWO was given in²⁹. If your optimisation variables are strictly between 0 and 1, then the BGWO algorithm is your best bet. Similar to the Grey Wolf Optimisation (GWO) method, the BGWO algorithm consists of the following stages: Randomly place the begin, and then use the objective function to determine how fit each wolf is. The three top search agents are then chosen according to their fitness scores; each search agent’s position is then updated according to a predetermined algorithm that takes into account the current positions of the pack’s leaders. After verifying that the termination condition has been fulfilled, the next step is to use a boundary-handling strategy to keep the search agents inside the borders of the search space. If so, the algorithm outputs the optimal answer (alpha). Otherwise, it loops back to the fitness check.

Algorithm 1

Pseudocode for the BGWO Procedure for Feature Selection.

Hyperparameter tuning for the 6LDCNNet model was performed using the Improved Sailfish Optimization Algorithm (ISFOA). ISFOA improves traditional Sailfish Optimization by incorporating adaptive weight coefficients to balance exploration and exploitation dynamically. This process involves initializing random sailfish positions (hyperparameters), evaluating fitness based on model performance, and iteratively refining positions toward optimal configurations. Compared to grid search and random search, ISFOA requires fewer iterations to achieve convergence, significantly reducing computational time. For instance, grid search requires exhaustive evaluation over the entire parameter space, while random search lacks directed exploration. In contrast, ISFOA intelligently adapts to the search space, ensuring a higher likelihood of identifying globally optimal hyperparameters. This method tuned critical parameters like learning rate, filter sizes, and dropout rates, enhancing model accuracy and robustness.

An instantaneous relationship matrix depicting all dataset variables is provided. When trying to decide which type of regression analysis to do, it’s also a great starting point. The BGWO is used to group together the most salient characteristics with a normal distribution across four characteristics: age, treetops, chol, and thali. Male is the most common sex identity, whereas 0 and 3 are the most common and least common CP values. Clustered results from the planned BGWO are shown in Table 2.

Table 2.

The feature delivery of the dataset.

	Slope	ca.	Age	Sex	cp.	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	target
Mean	1.03	2.16	55.92	0.46	1.44	143.81	355.11	0.45	1.13	138.48	0.57	3.18	0.46
Std	0.82	1.41	13.67	0.5	1.2	30.12	113.96	0.5	0.8	37.81	0.5	1.71	0.5
Min	0	0	29	0	0	94	133	0	0	71	0	0.21	0
Max	2	4	77	1	3	199	560	1	2	201	1	6.19	1
Kurtosis	-1.52	-1.34	-1.01	-2.01	-1.54	-1.04	-0.85	-2	-1.39	-1.11	-1.96	-1.07	-2.01
IQR	2	2	22.25	1	3	48.75	180.25	1	2	65.5	1	2.62	1
Range	2	4	48	1	3	105	427	1	2	130	1	5.98	1
MAD	0.68	1.24	11.47	0.5	1.09	25.67	94.49	0.5	0.68	32.08	0.49	1.46	0.5
CV	0.8	0.65	0.24	1.09	0.83	0.21	0.32	1.11	0.71	0.27	0.87	0.54	1.09
Skewness	-0.06	-0.07	-0.3	0.16	0.05	0.1	-0.03	0.2	-0.24	0.02	-0.29	-0.1	0.16
Missing (%)	0	0	0	0	0	0	0	0	0	0	0	0	0

Multivariate correlation analysis

Understanding the relationships between features is crucial in ensuring the independence and effectiveness of the feature set. We conducted a multivariate correlation analysis using the Pearson correlation coefficient to identify potential dependencies among features. The correlation matrix is presented in Table 3, where the values range from − 1 to 1, indicating the strength and direction of the linear relationship between pairs of features. The Multivariate Correlation Matrix is shown in Table 3.

Table 3.

Multivariate correlation matrix.

Feature	Slope	ca.	Age	sex	cp.	trestbps	chol	fbs	restecg	thalach	exang	oldpeak	target
slope	1.00	0.01	0.10	0.05	0.02	0.05	0.07	0.08	-0.08	0.02	0.04	0.09	0.05
ca.	0.01	1.00	0.02	0.09	0.03	0.06	0.04	0.10	0.06	0.07	0.02	0.05	0.03
age	0.10	0.02	1.00	0.05	0.04	0.12	0.15	0.05	0.03	0.07	0.03	0.06	0.04
sex	0.05	0.09	0.05	1.00	0.06	0.03	0.02	0.06	0.04	0.08	0.05	0.07	0.01
cp.	0.02	0.03	0.04	0.06	1.00	0.08	0.03	0.09	0.04	0.11	0.02	0.04	0.02
trestbps	0.05	0.06	0.12	0.03	0.08	1.00	0.14	0.05	0.07	0.04	0.03	0.09	0.05
chol	0.07	0.04	0.15	0.02	0.03	0.14	1.00	0.03	0.05	0.06	0.02	0.10	0.06
fbs	0.08	0.10	0.05	0.06	0.09	0.05	0.03	1.00	0.04	0.07	0.02	0.05	0.01
restecg	-0.08	0.06	0.03	0.04	0.04	0.07	0.05	0.04	1.00	0.02	0.06	0.03	0.05
thalach	0.02	0.07	0.07	0.08	0.11	0.04	0.06	0.07	0.02	1.00	0.05	0.09	0.07
exang	0.04	0.02	0.03	0.05	0.02	0.03	0.02	0.02	0.06	0.05	1.00	0.04	0.03
oldpeak	0.09	0.05	0.06	0.07	0.04	0.09	0.10	0.05	0.03	0.09	0.04	1.00	0.05
target	0.05	0.03	0.04	0.01	0.02	0.05	0.06	0.01	0.05	0.07	0.03	0.05	1.00

Multicollinearity testing using VIF

To further assess feature independence, we conducted a multicollinearity test using the Variance Inflation Factor (VIF). Features with a VIF greater than 10 indicate high multicollinearity, which could affect the stability of the regression coefficients. The VIF values for the features are presented in Table 4.

Table 4.

Variance inflation factors.

Feature	VIF
slope	1.04
ca.	1.02
age	1.05
sex	1.03
cp.	1.06
trestbps	1.08
chol	1.07
fbs	1.02
restecg	1.04
thalach	1.05
exang	1.03
oldpeak	1.09
target	1.01

The correlation matrix and VIF values confirm that the features are independent and exhibit no significant multicollinearity issues. These analyses ensure that the selected features are appropriate for model building.

Classification using proposed 6LDCNNet model

In this research, we suggested a novel deep CNN model with six branches to better categorise cardiovascular diseases. Figure 3 presents the proposed network architecture’s layered features. There are a total of 35 layers in the proposed model, connected by 39 nodes. The 6LDCNNet model accepts clustered data with an input size of 227 227 3. Then, 128 99 kernels were used in the subsequent 2D convolution layer. The convolution layer is used to find interesting patterns in the data. Equation (9) demonstrates the arithmetic behind the convolution layer, where (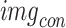) is the image after the convolution step, (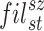) is the filter, (sz) is the filter size (9 9), and (st) is the stride size (2 in this example). Both the padding and dilation factors for the initial convolution layer were set to 1. The ReLU was used as the activation layer following the first convolution layer. The activation layer’s job is to perform the activation function, which is the transition of the output. In Eq. (10), we see the mathematical expression of the activation function. The max-pooling layer, which is the third and final layer of the proposed network, has the same padding approach and window size of (5,5). By selecting the most salient feature from the pooling window, the max-pooling layer reduces the number of features used in the input. In Eq. (11), , these three variables provide the layer. Selecting the largest possible window size, this convolved across the input photos.

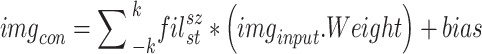9

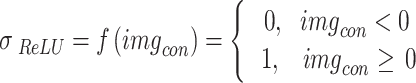10

11

Fig. 3.

The pre-training and layer construction of the projected 6LDCNNet model.

A new block, 6B, with six branches and concurrent processing, was then incorporated into the planned 66LDCNNet. A batch normalisation layer was included in each of the forks. In order to expedite the model-training process, we used a batch normalisation layer to standardise the data at the batch level. The size of the convolutional kernel was the primary dividing line between the six different types of trees. The suggested model uses many parallel branches, with the filter layer being progressively lowered from 13 by 13 to 3 by 3 in order to extract the high-level picture feature. Each parallel branch maintained a constant of 96 convolutional kernels. Each fork included a convolution layer with adjustable filter sizes, an activation layer, and a batch normalisation layer. During training, the branch normalisation was performed on each mini-batch of complete data for each epoch. Equations (12)– (14) show the math behind the batch normalisation layer. Equation (12) was used to get the batch normalisation layer’s mini-batch mean 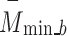, and Eq. (13) was used to determine the layer’s mini-batch variance 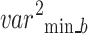. Batch normalisation B _nor was performed as the final step for this layer using Eq. (14), where and are the observable parameters that may be trained. The suggested model’s key contribution is a concurrent processing block made up of six branches, each of which has a distinct number of filters and kernel sizes.

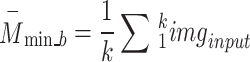12

13

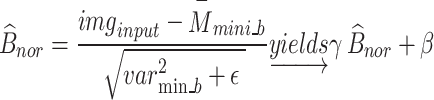14

The mathematical concurrent twigs are obtainable in Eq. (15). The parameter characterises the branch sum, ‘i’ characterises 1 to 6 branches, 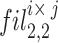, size of², and 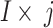represents the filer branches as 3 × 3, 5 × 5, 7 × 7, 9 × 9, 11 × 11, and 13 × 13, correspondingly. The sReLUi represents the branch i.

15

To continue the feature learning process, an extra layer was inserted after six parallel branches were processed. The next step was to place a ReLU-powered activation layer just before the final global pooling layer. Pooling was performed on a global scale with a filter depth of 1 1 96 in the global max-pooling layer. Similar to max-pooling, global max-pooling selects the maximum value from an input window of the same size as the input picture. Then, a grouped convolution layer was built using filters with a depth of¹. After that, the max-pooling layer was built on top of a ReLU activation layer. The same stride¹ and padding were used to build a 5–5. A 50% dropout layer was then built to guarantee that each neuron had an equal chance of being triggered in the next layer. Following this layer, a 4096-by-4096 FC layer was added just before the activation layer. After that, the second FC layer was placed on top of a 50% dropout layer. Finally, a softmax layer was added on top of the classification layer to account for multinomial probabilities. Equation (16) shows the layer, where 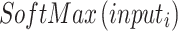represents the softmaxis used to standardise the input data that foodstuffs a for negative input.

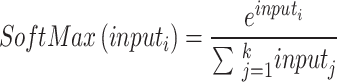16

The research paper presented an enhanced sailfish optimisation algorithm (ISFOA) for optimising the hyper-parameter of the suggested classifier, which is described in detail below:

Mathematical expression of basic SFOA

The SFO algorithm’s benefits include a middle ground between exploitation and exploration and a lack of reliance on local optimisation. The sailfish in the SFO are an analogy for potential answers. Both sailfish and sardine-like search agents are used in this method. A random sample of people is introduced into the solution space. The current position is stored in the i^th member of the kth round of a next-level-d search space. 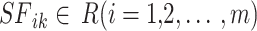. The SF matrix is intended to uphold the site of all the sailfish.

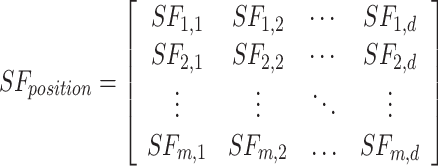17

In Eq. (17), m, d and 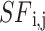is the next j value of sailfish and any variables. The fitness function for each sail is shown in Eq. (18):

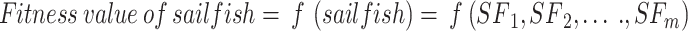18

The following matrix is created for the acceptability of all solutions and will be used to evaluate each sailfish individually:

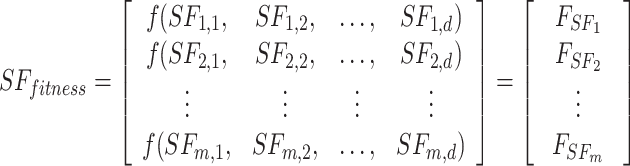19

As shown in Eq. (19), the fitness value of each component is saved in m, the sum of sailfish is saved in SF_(i, j), the fitness function is saved in f, and the number of sailfish is saved in 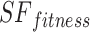, all depending on the goal function. The fitness function is given a matrix, and the output displays each factor in the matrix. .

Similarly, to how sardines navigate the search space, the sardine consensus is a crucial part of the SFO procedure. Therefore, using Eq. (20), we can establish the position and appropriateness values of each sardine.

20

where n, 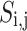and 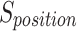are, respectively, the total sum of sardines, sardine i’s jth dimension, and the location of all sardines in the matrix. According to Eq. (21), the fitness value of each sardine is determined.

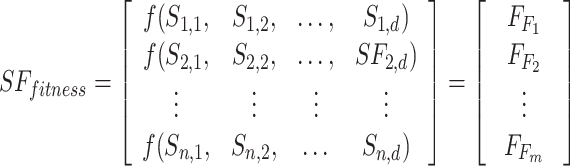21

where 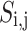represents the jth dimension, function, and 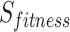stores the fitness

SFO, the novel position of the sailfish (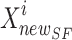) is updated rendering to Eq. (22). At this point, search agents take over and conduct an extensive investigation of the search space in quest of updated potential answers. Sailfish does not restrict its attacks to the top-down, bottom-up, right-to-left, or left-to-right directions. They may strike from any angle and in an ever-narrowing arc. Therefore, the sailfish continuously adjusts its location such that it is centred on the optimal option.

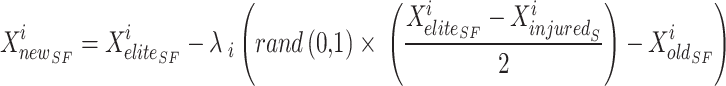22

In Eq. (22), 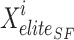elite sailfish site, best sardine place, sail current site, 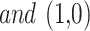is a random sum, and 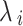is a factor in the ith repetition that is shaped by Eq. (23).

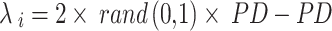23

Fluctuation of λ sailfish and their convergence around the prey. Using this strategy, new information may be uncovered, and new solutions can be sought on a worldwide scale. As PD increases, more baits are used in each cycle. Equation (24) specifies the PD parameter. With fewer prey to contend with, sailfish may more easily adjust their location around the prey using the PD parameter during group hunting.

24

where 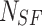and 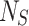are the total number of Sailfish in the algorithm and the total number of Sardines in each phase. Sardine 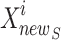is defined in the SFO method as shown in Eq. (25).

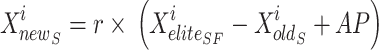25

where is the finest site for an elite sail, is where the sardines currently are, r is a random value, and AP is the attack speed in attacks per sail. Symbolises the cycle specified by Eq. (26). The AP of the sail determines the sardines updating rule.

26

where A and are the coefficients for a linear regression from the AP value of A to the value of 0. Updates to the sardine count and are defined as follows using the AP.:

27

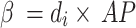28

where 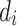and 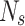where and are the total number of sardines and variables, respectively. When sardines become more practical than sailfish, fishermen in the SFO will likely go bait hunting. To improve the likelihood of obtaining fresh prey, the sailfish’s location is substituted for the last known location of the sardine being pursued (Eq. 29):

29

where 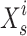designates the sardine in the I repetition, and 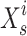designates the current site of the sailfish in the I repetition.

Mathematical expression of ISFOA

The SFO algorithm searches using two parameters, which allows it to efficiently increase population variety and forestall its decline. Fish and sardine populations at sea are generated at random. a minimal number of fish sails (min) and sardine sails (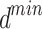). Both are worth as much as the bare minimum of sensor nodes. Similarly, the largest possible value of sail (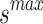) or sardines (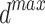) is equal to the possible sum of sensor nodes.

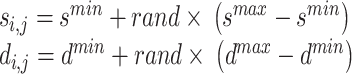30

The optimal answers are used as benchmarks for the hyper-parameters. In the beginning, the sailfish’s position is updated by continually plugging in the dynamic weight coefficient (w), which is bigger and so leads to worldwide examination. In the end, a lower value for w is preferable for local search. According to Eq. (31), the sailfish’s current position 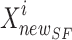is modified at each iteration. Most swarm intelligence algorithms also employ some sort of weighting strategy. Meta-heuristic algorithms, in general, adaptively move between maximum and lowest values, partially reducing the risk of being stuck in local optima. In the first phase, weighting reduces the impact of chance and makes the search process more evenly distributed over the issue space. The accuracy of agents’ placements is enhanced by using adaptive weighting. As a result, agents are able to reach their ideal locations more quickly, and convergence as a whole is sped up.

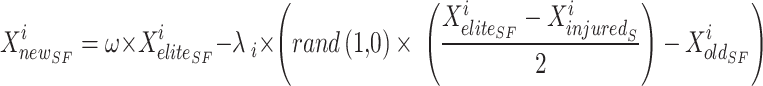31

where 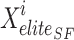position of elite sail, 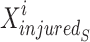best position of damaged sardine, 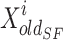current position of sail, and is a constant in the ith iteration that is made rendering to Eq. (32).

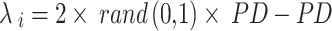32

As PD increases, more baits are used in each cycle. As the sum of baits dwindles during group hunting by sailfish, the PD limit becomes increasingly critical for enhancing the sailfish’s proximity to the bait. Equation (33) provides the formula for the PD metric.

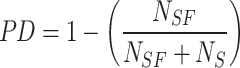33

In the SFO algorithm, the novel site of sardine 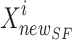is defined rendering to Eq. (34). By the parameter w, the balance is shaped in the situation period.

34

The value of is distinct by Eq. (19). In Eq. (35), characterises the extreme repetition.

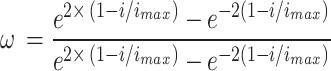35

X_injured and X_elite switched places due to the weight variable (w). That is, the agents’ new location in the issue space is more conducive to finding the best answer. Exploration and exploitation are two sides of the same coin that the SFO, like optimisation algorithms, must balance. Since the position-updated equation doesn’t care about the target point’s site and merely uses it to randomly calculate the zone, fundamental SFO leans towards exploration. Furthermore, the outcomes for multi-modal challenges demonstrate the SFO’s inadequate exploitation capabilities. ISFO relies on the current group’s top sailfish for its learning. Agent learning is influenced by the ISFO model’s unique method of sail and sardine update.

Problem coding

Agents function as parameters in the ISFO, and their location serves as a performance indicator. Agents’ positions can alter data about the search space’s many dimensions. For N-factor ISFO, the n-th parameter in iteration t is determined by Eq. (36), where 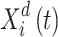is the location of the I factor in iteration t in length d, and m is the search space dimension.

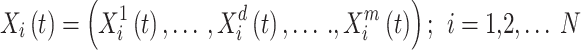36

The fish’s sail navigates the search space in pursuit of the optimal local solution, and the excellence of the solution it generates is measured by the fit function. When sailfish alter their search behaviour, other sardines in the area will move to accommodate. Sails space is adjusted to get to the best possible solution. The finest sardines have a direct impact on the behaviour of each sailfish. As a consequence, the sailfish are positioned optimally (global solution).

Handling class imbalance

Class imbalance is a common challenge in medical datasets, where the number of instances in different classes can vary significantly. This imbalance can lead to biased models that perform poorly on the minority class. To address this issue, we implemented several strategies:

Resampling techniques

• Oversampling We employed techniques such as Synthetic Minority Over-sampling Technique (SMOTE) to artificially generate new samples for the minority class. SMOTE synthesizes new examples by interpolating between existing minority class instances, thus enhancing the representation of the minority class in the dataset.

• Undersampling We also used undersampling methods to reduce the number of majority class samples, thereby creating a more balanced dataset. This approach involves randomly selecting a subset of the majority class, which can help in training models without overwhelming the minority class.

Algorithmic adjustments

• Cost-sensitive learning We adjusted the cost function of the learning algorithm to penalize misclassifications of the minority class more heavily. This approach encourages the model to pay more attention to the minority class during training.

• Ensemble methods We employed ensemble techniques such as balanced random forests, which build multiple decision trees using balanced bootstrap samples. This method effectively reduces bias toward the majority class and improves overall classification performance.

Results and discussion

Experiment setup

The analysis was coded in Python 3.8 and built in an anaconda virtual situation on a Windows 10 × 64-bit machine equipped with an Intel Core i7 processor and 16 GB of RAM. In order to easily evaluate, compare, and analyse the performance of AL techniques, several dependencies have been utilised as Python modules. These include which offer a module-based version of the AL framework.

Performance metrics

Equations (37)–(40) depict the results in terms of accuracy, precision, recall, and the F-score. The following table contrasts the predicted and actual outcomes in light of these indicators.

37

38

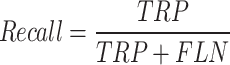39

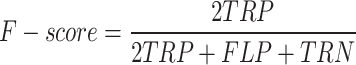40

TRP: the total number of normal classes for which the categorization was right; the genuine positive value.

FLP: the proportion of inaccurate normal class labels or the false positive value.

TRN: the real negative number, which represented the sum of right diagnoses in abnormal categories.

FLN: the percentage of inaccurate abnormal class designations or the false negative value.

Validation analysis of proposed model in text data

Table 5 shows a comparison of several methods for making clustered data (UCI) predictions for cardiovascular disease. All of the existing models are taken into account for validation, including LV-CNN¹⁷, CART^18,21, XGB¹⁹, ML-ANN²⁰, SS-GBDT²⁴, KNN²², and LR²¹. However, each of these models uses a unique dataset. Therefore, we apply and verify these methods on the datasets we’ve chosen to evaluate, averaging the outcomes.

Table 5.

Comparative analysis of various models on UCI.

Model	Accuracy	Precision	Recall	F-score
KNN	0.9001	0.88	0.90	0.89
LR	0.9201	0.93	0.92	0.93
SS-GBDT	0.9289	0.94	0.94	0.94
ML-ANN	0.9169	0.92	0.92	0.92
6LDCNNet	0.9612	0.96	0.98	0.97

The comparative analysis of the different models used for UCI is presented in the table that can be found above. In the investigation of the KNN model, the accuracy was 0.9000, the precision was 0.880, the recall was 0.9000, and the F-score rate was found to be 0.8900, respectively. Then there was a second prototype with LR 0.9201, 0.93, 0.92, and an F-score rate of 0.93, respectively. Then, a different SS-GBDT prototype model achieved an accuracy of 0.9289 and a precision of 0.94, as well as a recall of 0.94 and an F-score rate of 0.94, respectively. Then, a different ML-ANN model prototype arrived at an accuracy of 0.9169, a precision of 0.92, a recall of 0.92, and an F-score rate of 0.92, respectively. All of these metrics were measured simultaneously. Then, an additional prototype of the 6LDCNNet model achieved an accuracy of 0.9612, a recall of 0.96, a precision of 0.98, and an F-score rate of 0.97, respectively.

Comparative analysis of model on image dataset

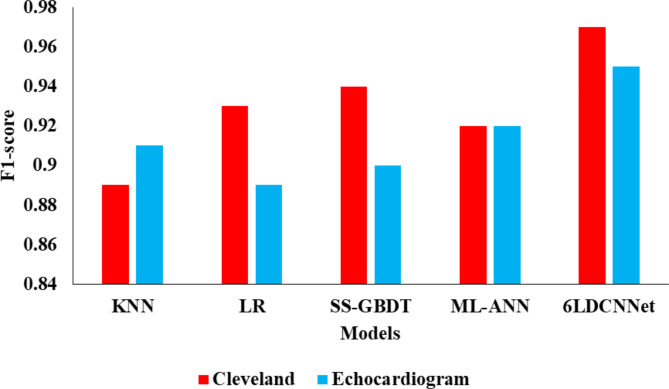
The performance comparison of the proposed model on echocardiogram data is represented in Table 6. In our investigation, the KNN model achieved an accuracy of 0.9129, with a precision of 0.90 and a recall of 0.92. The Logistic Regression (LR) model reached an accuracy of 0.8889, a precision of 0.89, and an F1-score of 0.89. The SS-GBDT model attained an accuracy of 0.9071, with a precision, recall, and F1-score of 0.90. The MLP model achieved an accuracy of 0.9316, with a precision of 0.92, recall of 0.93, and F1-score of 0.92. These models’ performance metrics are depicted in Figs. 4, 5, 6 and 7, illustrating their relative strengths.

Table 6.

Performance comparison of the proposed model on Echocardiogram data.

Metric	6LDCNNet	LV-CNN	XGB	SS-GBDT	MLP
Accuracy	0.92	0.88	0.86	0.87	0.89
Precision	0.91	0.87	0.85	0.86	0.88
Recall	0.89	0.85	0.83	0.84	0.86
F1-Score	0.90	0.86	0.84	0.85	0.87
Loss	0.15	0.20	0.22	0.21	0.18
ROC AUC (Micro)	0.93	0.89	0.88	0.87	0.90
Cohen’s Kappa	0.85	0.80	0.78	0.79	0.82

Fig. 4.

Graphical comparison of various models.

Fig. 5.

Analysis of the proposed model with existing techniques.

Fig. 6.

Graphical analysis of the proposed model.

Fig. 7.

F-score analysis.

In comparison, the 6LDCNNet model demonstrated superior performance, achieving an accuracy of 0.9809, precision of 0.94, recall of 0.96, and an F1-score of 0.95. Additionally, the 6LDCNNet model exhibited the lowest loss at 0.15, the highest ROC AUC (Micro) at 0.93, and a Cohen’s Kappa statistic of 0.85, indicating excellent model robustness and reliability. These metrics highlight the effectiveness of the proposed hybrid model in accurately predicting outcomes from echocardiogram data.

The statistics for the required amount of training time for classifiers are represented in Table 7, located above. In the investigation of the 6LDCNNet model, the training time on the image was determined to be 128 min, and the training time on text data was determined to be 35 min, respectively. Then, a different LV-CNN model arrived at a training time on image data of 150 min, while the training time on text data took only 39 min. Then, another XGB model arrived at a training time on image data of 200 min, while the training time on text data took only 45 min. Then, a different CART model arrived at a training time of 230 min on the image and 47 min on the text data, respectively.

Table 7.

Statistics for obligatory training period for classifiers.

Model	Training time on image (min)	Training time on text data (min)
6LDCNNet	128	35
LV-CNN	150	39
XGB	200	45
CART	230	47

Discussion

The 6LDCNNet model demonstrated significant improvements in accuracy and reliability compared to existing methods, achieving 96.12% accuracy on clinical data and 98.09% on imaging data. Its high recall (98% for text data and 96% for imaging data) minimizes false negatives, ensuring early detection of cardiovascular diseases, which is critical in clinical scenarios. The model’s layered architecture effectively extracts hierarchical patterns, while BGWO optimizes feature selection, reducing dimensionality and computational overhead.

Statistical analysis using one-way ANOVA confirmed the superiority of the proposed model, with p-values < 0.01 indicating significant differences from competing methods. The integration of multimodal data showcases the scalability and robustness of the approach, making it suitable for real-world healthcare applications.

The model’s potential to improve early diagnosis and reduce mortality is evident; however, its current validation is limited to specific datasets. Future work will address this limitation by expanding validation to larger, more diverse datasets and exploring additional modalities like genomic data to further enhance diagnostic precision and generalizability. These findings highlight the transformative potential of advanced machine learning techniques in predictive healthcare analytics.

Conclusion and future work

Worldwide, heart disease is the leading cause of mortality. Help save lives by identifying cardiovascular disease and other linked conditions like dementia at an early stage. It is crucial to properly anticipate cardiac illness using an artificial intelligence model so that patients can be treated before a heart attack occurs. In this study, we present an IoMT-based cardiac disease prediction model that uses deep learning techniques. The suggested model underwent two rounds of testing. The first step was the clustering of patient-specific medical data from Cleveland; the second involved the categorization of echocardiography pictures and clustered data using 6LDCNNet. Both of these categorization strategies were used, and the results of each strategy were validated in order to better predict cardiovascular disease. In comparison to the previous models, which obtained an accuracy of about 91–93% across two datasets, the suggested model achieved an accuracy of around 96–98%. In addition, the suggested model training period in terms of CPU elapsed time is sufficient. In addition, there are unanswered questions regarding the use of enhancement classification algorithms as opposed to label ranking classifiers, as well as the discretization of numerical values of levels using state-of-the-art metaheuristic algorithms for adjusting the sensitivity and specificity of predictive models.

Future work may involve exploring the integration of enhancement classification algorithms and label ranking classifiers to further refine prediction accuracy. Additionally, investigating advanced metaheuristic algorithms for optimizing sensitivity and specificity could enhance model performance. Further research could also focus on expanding the dataset to include diverse demographic and geographic populations for a more robust and generalizable prediction model.

Author contributions

Lella Kranthi Kumar: Conceptualization, Methodology, ValidationK G Suma: Software, Implementation Pamula Udayaraju: Conceptualization, Investigation, Writing - review & editing Venkateswarlu Gundu: Writing original draft, Validation. Srihari Varma Mantena: Writing original draft B.N. Jagadesh: Software, Implementation.

Data availability

The datasets used and/or analyzed during the current study available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.