Numerical and experimental methods for the assessment of a human finger-inspired soft pneumatic actuator for gripping applications

Abstract

The increasing demand for soft robotic systems in agricultural, biomedical and other applications has driven the development of actuators that can mimic the flexibility and adaptability of human muscles. Several studies have explored the design and implementation of soft actuators for robotic applications, however, there is a need for soft actuators demonstrating delicate gripping capabilities but also excel in specific biomedical applications, such as therapeutic massaging. The objective of this work is to develop a multi-finger soft pneumatic actuator mimicking human fingers for Ayurvedic therapeutic massaging and gripping applications. The actuator is geometrically modeled to mimic the dexterity and flexibility of a human finger and its mechanical behavior such as bending angle and gripping force under air pressure is studied through finite element analysis (FEA). The simulation results are experimentally validated. The finger-based actuator is fabricated using liquid silicone rubber, and its performance namely, bending deformation and gripping force generated at various pressure is determined and these results are compared with the simulated test cases. The study also provides a detailed analysis of the performance of the actuator, thus providing detailed insights into its applicability in therapeutic purposes.

• •Human finger inspired actuators are expected to demonstrate the dexterity and flexibility of human hands, which poses challenges in its modeling and analysis.
• •The load carrying capacity and bending movements of the actuator is assessed using numerical method of Finite Element Analysis.
• •Simulation results are validated through an experimental method using force sensors and image analysis of the bending movement of the soft actuator.

Graphical abstract

Specifications table

Subject area:	Engineering
More specific subject area:	Soft robotics
Name of your method:	Numerical and experimental methods
Name and reference of original method:	NA
Resource availability:	The authors can make the data available upon a reasonable request.

Background

By imitating the composition and behavior of live things, soft robotics holds great promise for both practical applications and expanding our knowledge of biological systems [1]. Soft robots in this discipline are extremely autonomous and versatile in complicated situations such as underwater or planetary exploration, because they blend sensor and feedback systems to enable real-time environmental perception and response [2]. Soft robotics has the potential to grow significantly and achieve game-changing discoveries thanks to continued advancements in materials science and manufacturing. Soft robots that can dynamically adjust their stiffness and compliance based on the task at hand can provide safer and more comfortable interactions with humans, whether it's assisting with daily tasks for the elderly or providing therapeutic support for individuals with physical disabilities [[3], [4], [5]].

Rehabilitation, prosthetics and orthotics are key areas of research and development in soft robotics. These robots often incorporate advanced technologies such as electromyography (EMG) sensors to monitor muscle activity and provide real-time feedback to patients and therapists [6]. Researchers are exploring the integration of machine learning algorithms to predict and anticipate users’ movements, allowing prosthetic limbs to respond more intuitively and naturally [7,8]. These advancements underscore the transformative potential of robotics in therapeutic applications, offering innovative solutions to enhance human health, well-being, and quality of life. These advancements underscore the transformative potential of robotics in therapeutic applications, offering innovative solutions to enhance human health, well-being, and quality of life.

Quach et al. [9] devised a low-cost, portable electropneumatic control system driven soft actuator which combines a closed-loop controller to control air pressure with pneumatic pressure sensors. Gunawardane et al. [10] examined a bilateral system design using a soft actuator that is teleoperated and delayed. In their proposed setup, the control signals from hand gestures are recognized over the internet and used to regulate the setup. The force and bending angle produced during gentle holding was determined using a data glove. Liu et al. [11] presented a concept for a soft pneumatic bending actuator making use of a topology optimization process to optimize the bending capabilities and, consequently, raise the soft grippers’ permissible payload. Vo et al. [12] outlined the basic layout of a soft robotic glove that uses soft pneumatic actuators for hand rehabilitation.

Soft robotics imitating and inspired by the functionality and dexterity of the human hand have been developed for biomedical applications [[13], [14], [15]]. Wang et al. [16] designed and analyzed a five segmented pneumatic network (PneuNet)-based bending actuator composed of elastomer to build a soft pneumatic glove. Duanmu et al. [17] created a soft pneumatic glove to improve finger knuckle rehabilitation that is driven by an elliptical cross-sectional guided bending bellows. Parsa et al. [18] presented the feasibility research and conceptual design for an elastomer-based, pneumatically operated soft hand prosthesis for amputees. Liu et al. [19] demonstrated a soft robotic gripper with two fingers that can be used in pinching and enveloping gripping modes. Takashima et al. [20] created a temperature-sensitive pneumatic artificial rubber muscle with a bending actuation that can be adjusted using two shape memory polymer sheets.

This work proposes a numerical-experimental combined method for analysis for soft actuators intended for gripping and biomedical therapeutic applications. Firstly, detailed numerical computations are carried out to evaluate the bending and gripping performance of the proposed finger-like soft actuator. The stress and strain response of the actuator is estimated to assess its mechanical integrity and stiffness. The actuator's performance is evaluated numerically for the massaging of a human arm. Secondly, the proposed actuator is fabricated with an elastomeric material and is tested experimentally for its bending deformations and gripping force generation to validate the simulation method. The gripping capability of the developed actuator is established through practical demonstrations by gripping some day-to-day objects. The method hopes to further the field of soft robotics by accomplishing these goals and enhancing the functionality and design of soft robotic hands for applications requiring flexibility and sensitive handling.

Method details

Geometrical modelling

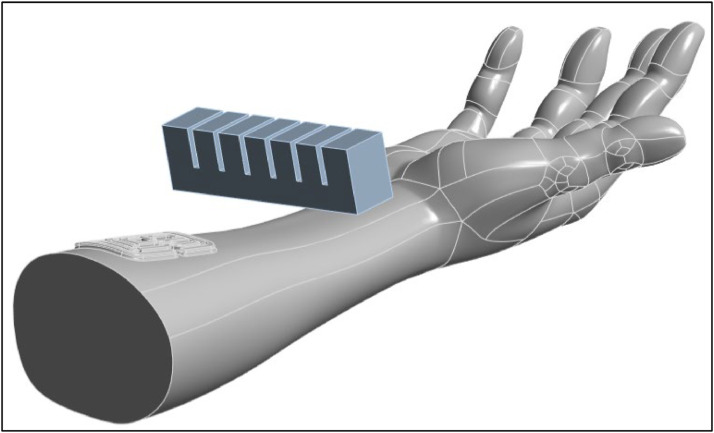
Geometrical modeling of a pneumatic soft actuator involves creating a representation of its external shape and internal structure to allow for air-flow passages. The overall shape of the actuator must be determined while considering factors like its intended application and range of motion. The proposed finger-like actuator is designed with multiple rectangular segments followed by narrow portions to allow for a bending motion upon inflation (refer Fig. 1). The dimensions are approximately chosen to emulate a typical human finger. The actuator is tested for its bending performance, and subsequently analyzed for its evaluation for massaging applications. For this purpose, the computer-aided design (CAD) model of a human arm is collected from Free3D®, an open-source platform for CAD models. The arrangement of actuator and human hand is shown in Fig. 2.

Fig. 1.

Geometric model of the proposed actuator.

Fig. 2.

The soft actuator and human hand CAD models for massaging simulation.

Finite element model development

After the creation of geometric model, the finite element (FE) model development involves two major aspects – applying the appropriate material model and prescribing the realistic boundary conditions (definitions of loading, contact regions and element discretization). Soft robotic actuators are often made from elastomers like silicone rubber, polyurethane, or elastomeric composites. The choice of the material significantly influences factors like flexibility, durability and response to stress and strain. In this study, the liquid silicone rubber (LSR) has been chosen for the actuator, is a popular material choice for soft robotics due to its mechanical properties [[21], [22], [23]]. LSR exhibits high flexibility, allowing soft robotic actuators to deform and adapt to various shapes and movements. It has excellent tensile strength, resisting forces applied in tension without rupturing. LSR is thus found to be a near suitable material considering factors such as stretchability and stiffness to transfer the pressure to body under the applied pressure. Also, it is biocompatible and non-toxic, making it suitable for applications that require contact with the human body [24,25]. Although selection of a different type of material can change the deformation behaviors and load carrying capability of the developed actuator, the method of its experimental and numerical evaluation would remain the same [26,27]. Therefore, LSR has been chosen for this work. Since the material selected is hyperelastic in nature, a 2nd order Yeoh model was used to describe the material model as shown in Eq. (1), where Here, W is the strain-energy potential, $I_1$ is the first invariant of the right Cauchy-Green deformation tensor, and $C_i$ are the material constants. The material constants used are listed in Table 1 [[28], [29], [30]].

$$W=\sum _{i=1}^2{C}_i{\left(I_1-3\right)}^i+D\left[compressionterms\right]$$ (1)

Table 1.

Material constants of Yeoh model used for the soft actuator [[28], [29], [30]].

Constant	Values (MPa)
C1	0.11
C2	0.03
D	0

The material behavior of compliant soft actuators made of hyperelastic solids under static equilibrium is described using the governing differential equation called the Navier-Cauchy equation, which is expressed as [31].

$$\nabla ·\sigma +\mathbf{F}=0$$ (2)

where the first term represents the divergence of the Cauchy stress tensor ($\sigma$) and second term represents the body force per unit volume ($\mathbf{F}$) induced by gravity. The Navier-Cauchy equation illustrates the necessity of balance between the applied external forces and the internal resistance forces for static equilibrium. The first term concisely denotes the total nine stress components of the stress tensor, describing the nature of distribution of internal forces within the body. The second term denotes the body force vector, i.e., the intensity of external forces. In FE software, the weak form of the above governing equation is set up using the principle of virtual work for solving static structural hyperelastic problems. The stress-strain relationship being nonlinear in case of hyperelastic materials, a consistent tangent stiffness is calculated for each incremental load using Newton-Raphson scheme of numerical methods. Here, we assume that the material is homogeneous, isotropic and incompressible, which is a common representation of elastomeric materials [[27], [28], [29], [30]]. The scope of the study being quasi-static gripping applications, the time-dependent behavior of the elastomeric material has been neglected [32].

To approximately mimic the property of a human hand, which is predominantly composed of muscular elements [33], an isotropic linear-elastic model is assumed for simplicity. Based on the Young's modulus reported for whole thigh muscles [34] and Poisson's ratio determined for passive skeletal muscle tissues [35] they are assumed as, E = 270 MPa and ν = 0.47, respectively.

Boundary conditions for numerical analysis

In this study, the structures are presumed to undergo quasi-static deformations, with negligible effects of inertia. The outer faces of the actuator with possibility of establishment of contact as well as the interacting faces of actuator and the rigid body are applied frictionless contact definitions to allow for a smooth sliding in the tangential direction between the interacting surfaces. Standard earth gravity is enabled to consider the natural tendency of motion of objects in the downward direction. Further, large deformation effects are activated to simulate the effects of material nonlinearity due to hyperelasticity [[36], [37], [38]]. For the bending analysis, the actuator is fixed on one of its end faces and other regions are left free to deform with the internal pressurization (refer Fig. 3). In case of the contact force (gripping force) evaluation, a rigid block is placed to obstruct the bending motion to measure the reaction force generated (refer Fig. 3(b)). This is a standard boundary condition which has been applied for the deformation and stress/strain analysis of soft pneumatic actuators [[27], [28], [29], [30],32]. These boundary conditions enable the actuator to inflate without any obstruction under the inflation pressure in the inner walls of the actuator, assisting in the analysis of its bending deformations and stress-strain variations.

Fig. 3.

(a) The inner walls of the actuator subjected to fluid pressure and (b) outer walls highlighted with possible interaction (contacts).

The actuator is discretized using second-order tetrahedral elements because they are more compliant compared to their linear counterparts. The element size is chosen as 3 mm by conducting mesh-independence study, resulting in 63,772 elements (refer Fig. 4). The boundary conditions applied in the FE models are depicted in Fig. 5. For contact force simulations, a rigid block is constrained in all directions, and the reaction force is calculated at its base with pressurization of the actuator. For the massaging simulation, the ends of the arm are fixed (highlighted in blue color in Fig. 5). The actuator is brought in contact with the area of the arm at around 30 mm from the wrist joint, which is the region a rich presence of nerves, veins and muscular tissues in the human arm. The massaging in these regions is found to give relaxing experiences to the human body. The actuation pressure for massaging simulation is kept as 90 kPa, considering a safety factor of 2 compared to the pressure discomfort threshold reported for muscular tissues of around 180 kPa [39,40].

Fig. 4.

Meshed model of the actuator.

Fig. 5.

Prescribed boundary conditions used for (a) contact force and (b) massing analysis: the blue colored portions are constrained in all directions.

Experimental testing and validation

Fabricating and soft robotic actuator is the first step in the experimental phase of this work. After creating the CAD model of the soft robotic actuator, a mold is modeled which outlines the desired shape and internal network of air chambers. The mold is fabricated using a 3D printer. For the fabrication of the actuator, the required amount of LSR is then poured into a beaker and its weight is measured. Then the catalyst is added to this beaker by 3 % of the weight of silicone used [41,42]. The mixture is stirred at an even and steady pace for about 2 min to ensure uniformity in the cured actuator and then poured into the two-part mold. The openings or gaps between the top mold parts are sealed by clay to ensure no leakage occurs. After this has been cured, the upper part of the actuator that consists of the chambers is taken out and placed on the cured base where more mixture is poured which after curing becomes one whole actuator without any openings or other similar defects ensuring the manufacturing of an enclosed actuator with an opening for the pneumatic control. The fabricated grippers were tested for their bending deformations, contact (gripping) force, and grasping capabilities. The fabricated single finger-like actuator is shown in Fig. 6. The gripping force measurements were carried out by using a force resisting sensor (Make: Robodo, Model: SEN38, Square size: 38.1 mm). Four trials were conducted at each inflation pressure to check for repeatability of results. The experimental setup used to this end is shown in Fig. 7.

Fig. 6.

Fabricated soft actuator.

Fig. 7.

(a) Experimental setup for force sensing resistor readings, (b) circuit for force sensing sensor readings.

Method validation

Bending response validation using numerical and experimental methods

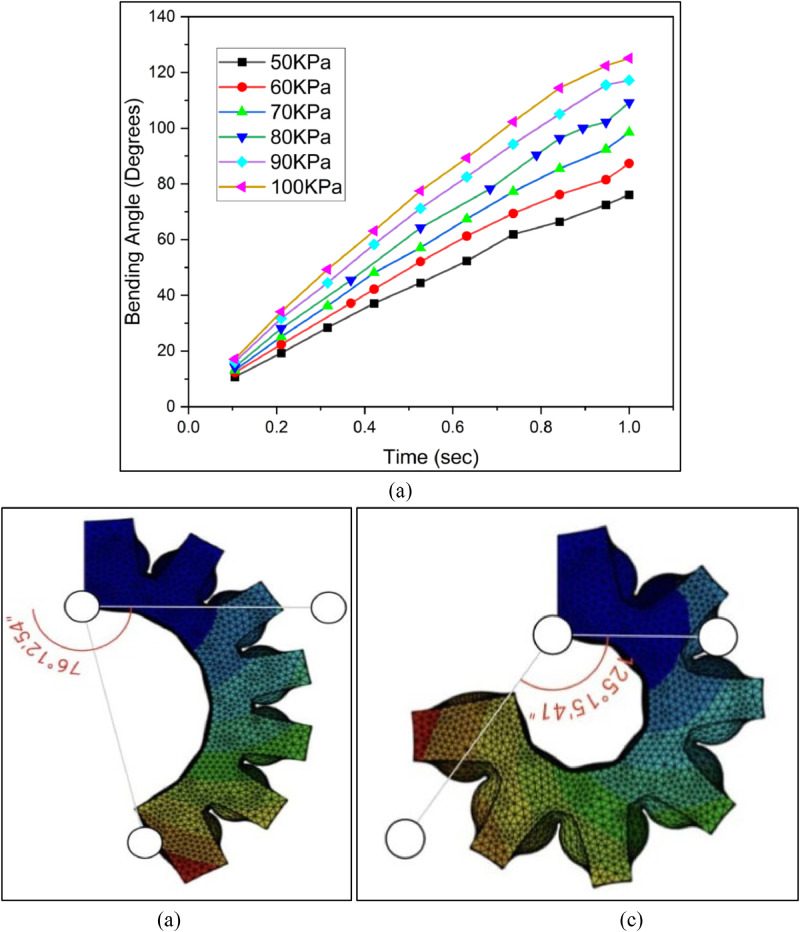
Fig. 8(a) shows the variations of actuator bending angle at different inflation pressures with respect to the time of loading during the static structural FE simulations. The bending angle obtained at 1 second is the obtained bending angle at fully loaded condition at a particular pressure value. Fig. 8, Fig. 8 show the results obtained in FE simulations at pressure of 60 kPa and 100 kPa, respectively. The relationship between bending angle and time depicted in the graph suggests a clear trend of a linear increase in bending angle over time across different input pressure levels.

Fig. 8.

(a) Bending angle variations obtained in the FE simulations at different pressures with respect to time, bending profiles obtained at (b) 60 kPa and (c) 100 kPa.

The relationship between bending angle and inflation pressure is shown in Fig. 9(a). The linear relationship between bending angle and pressure provides a predictable behavior which can be used to design systems to precisely control the actuator motion with respect to pressure conditions. The absolute percentage error between numerical and experimental results is depicted in Fig. 9(b).

Fig. 9.

(a) The bending angle variation with inflation pressures, (b) absolute percentage error between numerical and experimental results at different pressure levels.

The numerical results are validated through experimental observations by applying the corresponding values of inflation pressures in the fabricated actuator. Fig. 10(a) shows the experimentally measured bending angles at different actuation pressures. The data obtained from practical experimentation, showcasing the fluctuating relationship between bending angle and time for the soft actuator under varying pressure levels, demonstrates a notably intricate and non-linear trajectory, in contrast with simulation results. However, the bending angles observed in the experiments at full-pressure conditions are comparable to the simulation results (refer Fig. 9). Fig. 10(b) shows the maximum deformations exhibited by the soft actuator at different pressure levels.

Fig. 10.

(a) Bending angle variations obtained in experiments, (b) bending deformations observed at various pressures.

Gripping force validation using numerical and experimental methods

Fig. 11 shows the relationship between actuation pressure and gripping force in terms of reaction force generated by the rigid body in the FE simulations. The general tendency is seen as a progressive increase in force with higher pressures. It is found that the actuator could generate a gripping force ranging between 2 N and 2.71 N with corresponding variation pressure between 50 kPa and 100 kPa. Further, the gripping capability of the actuator is experimentally measured by means of a force sensor. Fig. 12 shows the mean values of results obtained from these experiments (standard deviations were found to be within 9.58 % of the mean). It is observed that the force increases in a stepped manner due to the program rounding the detected pressure to the nearest whole number. The FE simulations showed a maximum force of 2.71 N at 100 kPa of input pressure whereas experimental data obtained through the force sensitive resistor showed 5 N at 100 kPa input pressure. This can be attributed to the longer duration of regulated flow of air into the actuator in the experiments when compared to the FE simulations. These results are comparable to those reported for soft robotic grippers [43,44].

Fig. 11.

Reaction force variations obtained in the FE simulations at different pressures with respect to time.

Fig. 12.

Reaction force variations obtained in the experiments at different pressures with time.

Fig. 13 shows the total deformation experienced by the human arm under the action of the actuator inflated at 100 kPa. A uniform distribution of deformation is observed in the surface of the arm. Fig. 13 shows the total deformation experienced by the human arm under the action of the actuator inflated at 100 kPa. A uniform distribution of deformation is observed in the surface of the arm.

Fig. 13.

Total deformation (in m) observed in the human arm model.

Stress and strain variation assessment using numerical method

The linearized equivalent stress is examined along the length of the actuator with free inflation condition (refer Fig. 14). It is found that noticeable spikes in stress emerge at specific points along the actuator's length, particularly in regions coinciding with the presence of inter-chamber passages. This fundamental relationship highlights the expected mechanical response of the actuator to varying pressure inputs. Along the total of 6 inter-chamber passages, particularly the four central chambers are found to experience higher stresses consistently compared to other two chambers. This phenomenon suggests inherent structural or design characteristics that predispose these specific chamber regions to stress concentration. Two aspects may be attributed for this tendency: (1) Firstly the rectangular shape of the actuator gives rise to sharp corners which is a natural stress raiser. (2) Secondly, the root areas connecting two adjacent chambers come in contact during their bulging causing contact stresses to build up. This will be especially higher in the central portion of the actuator because of the larger deformations in this region leading to higher stresses. Similar observations have also been made in studies on soft pneumatic actuators [[45], [46], [47]]. The average equivalent stress and strain variations with pressure levels is shown in Fig. 15, which provides information on the mechanical stiffness of the actuator. The stress variations observed are found to be in the range of 0.1 to 0.5 MPa, which is comparable to the reported values in the literature under an inflation pressure of 100 kPa [29,30,48,49]

Fig. 14.

Linearized equivalent stress along the length of the actuator obtained in FE simulations.

Fig. 15.

Average equivalent (a) stress and (b) strain variations obtained in the FE simulations at different pressures with respect to time.

Practical demonstrations

The gripping capability of the fabricated actuator is assessed by picking some simple light-weight objects. A 3D-printed gripper holder capable of accommodating these actuators was fabricated for this purpose (refer Fig. 16(a)). By integrating the three actuators into the holder, a functional three-finger gripper system was created. Utilizing this innovative gripper, its capability is demonstrated to lift objects, such as a small cup with ease (refer Fig. 16, Fig. 16).

Fig. 16.

(a) Three-finger actuator, actuator (b) before and (c) after pressurization.

Limitations

Since, in the current work, the effects of dynamic loading scenarios were not simulated and the focus was only on static response of the actuator, the inertial effects were not incorporated in the analysis. The effect of friction between the object and the grabber has not been considered in the present analyses. This could lead to an underestimation of the gripping forces developed. The numerically computed stresses developed in the actuator were not experimentally validated. These aspects can form the avenues of future research work in this topic.

Credit author statement

Subraya Krishna Bhat: Writing – original draft, Writing - review & editing, Data collection and Validation; Deepak Doreswamy: Resources, Supervision, Writing – original draft, Writing - review & editing, Data collection; Aman H Hegde: Investigation, Software, Writing – original draft, Writing - review & editing; Vamsi Krishna Nukarapu: Investigation, Software, Writing – original draft, Writing - review & editing; Sathvik Bhat: Investigation, Software, Writing – original draft, Writing - review & editing; Puneeth S: Investigation, Software, Writing – original draft, Writing - review & editing; Vaibhav Das: Investigation, Software, Writing – original draft, Writing - review & editing; Aiman Aatif Bayezeed: Investigation, Software, Writing – original draft, Writing - review & editing; Anupkumar M Bongale: Supervision, Writing – original draft, Writing - review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.