Abstract
Living tissues are active multifunctional materials capable of generating, sensing, withstanding and responding to mechanical stress. These capabilities enable tissues to adopt complex shapes during development, to sustain those shapes during homeostasis, and to restore them during healing and regeneration. Abnormal stress is associated with a broad range of pathologies, including developmental defects, inflammatory diseases, tumor growth and metastasis. Here we review techniques that measure mechanical stress in living tissues with cellular and subcellular resolution. We begin with 2D techniques to map stress in cultured cell monolayers, which provide the highest resolution and accessibility. These techniques include 2D traction microscopy, micro-pillar arrays, monolayer stress microscopy, and monolayer stretching between flexible cantilevers. We next focus on 3D traction microscopy and the micro-bulge test, which enable mapping forces in tissues cultured in 3D. Finally, we review techniques to measure stress in vivo, including servo-null methods for measuring luminal pressure, deformable inclusions, FRET sensors, laser ablation and computational methods for force inference. Whereas these techniques remain far from becoming everyday tools in biomedical laboratories, their rapid development is fostering key advances in the way we understand the role of mechanics in morphogenesis, homeostasis and disease.
Introduction
Adherent animal cells are able to generate mechanical stresses to move, divide, remodel, and sense their mechanochemical microenvironment. The generation and transmission of stresses in a tissue can give rise to collective cellular phenomena of diverse complexity, from the relatively simple contraction of striated muscle to the intricate folding of an epithelium. The role of mechanical stresses in biological systems is particularly apparent in early development, when cellular layers of different identity undergo pronounced 3D movements to shape tissues1. However, living tissues are mechanically active throughout life. For instance, the intestinal epithelium self-renews every 3-5 days through a series of mechanical functions such as division, migration and extrusion2,3. Mechanical stresses also play a critical role in wound healing, where they enable cell migration towards the wounded area and supracellular contraction to seal the wound4. Conversely, aberrant stresses mediate devastating diseases such as myopathies or cancer5,6. Unlike in passive materials, stresses in living tissues are transduced by cells to trigger and regulate biological responses7. For example, an increase in tension causes cell proliferation whereas a decrease induces cell extrusion8-10.
A number of tools have been developed to measure mechanical stress over multiple length scales, from the single molecule to the entire organ. Here we will review technologies to measure stress in tissues with cellular and subcellular resolution. Because our focus will be on stress, we will exclude technologies to measure other relevant mechanical quantities such as stiffness, viscoelasticity or poroelasticity. Therefore, we will not discuss techniques such as magnetic tweezers11,12, optical tweezers13,14, acoustic tweezers15, atomic force microscopy16, micropipette aspiration17, microindentation18, microplate actuators19, Brillouin microscopy20,21, or tissue dissection and relaxation22. The reader is referred to excellent recent reviews on these techniques23-34.
We begin reviewing fundamental concepts in continuum mechanics, which might be familiar to most physicists and engineers but not to the broad biomedical community interested in cell and tissue mechanobiology. We continue presenting the techniques developed to measure tissue stress in vitro and ex vivo, starting with the techniques applicable to 2D cultures, such as 2D traction force microscopy, micro-pillar arrays, monolayer stress microscopy and tensile tests of cultured tissues. We then introduce the methods applied to 3D cultures, including 3D traction force microscopy and the micro-bulge test. We finally discuss the techniques compatible with in vivo samples, such as servo-null methods, inclusions, FRET sensors, laser ablation and force inference.
1. The concept of stress and traction
A force is an interaction that tends to deform or change the velocity of an object. Forces acting on any material can be classified as internal or external. For a given cell in a tissue, internal forces are generated by subcellular components such as the actomyosin cytoskeleton, whereas external forces are exerted by the surrounding extracellular matrix (ECM) or neighboring cells. The mechanics of deformable continuum materials is not formulated in terms of force, however, but rather in terms of force per unit area, a physical quantity known as stress. The need for the concept of stress can be simply understood by noticing that the same force applied over smaller or larger areas of a material will cause a different deformation.
The force per unit area acting on any internal or external surface of a material is called traction vector . It is assumed that the traction vector only depends on the location within the material and on the unit normal vector to the surface (Cauchy’s stress postulate). Therefore, the traction vectors that act on opposite sides of a surface are equal in magnitude and opposite in sign (Newton’s 3rd law) (Box 1). In general, the traction vector is not perpendicular to the surface, and it can be decomposed into normal and tangential vector components. Normal tractions can be compressive (negative) or tensile (positive) depending on their sign relative to (Box 1).
Box 1. the traction vector.
Box 1. Geometric representation of the traction vector, (red), acting at point A of a body subject to external forces (green arrows).
A given body can be cut by infinitely many imaginary planes passing through a point A. Each cut will define two sub-bodies and a pair of surfaces with outer normal vectors and . The traction vector is defined as the force between these adjacent surfaces divided by their surface area. It is linearly related to the stress tensor and to the normal vector by Cauchy’s stress theorem, Eq. (1). The traction vector may have any direction relative to the surface. Therefore, it is conveniently decomposed into its normal (, indicating compression or tension) and tangential (, indicating shear) vector components:
| (10) |
| (11) |
Normal tractions can be tensile (pulling) when they point in the direction of the outer normal , or compressive when they point in the opposite orientation (pushing). In the specific case of TFM, the surface of interest where tractions are defined is the interface between cells and their ECM.
As there are infinitely many surfaces passing through a point A, there are also infinitely many traction vectors acting on that point. Therefore, to fully characterize the stress state of a tissue we introduce the stress tensor field σ(A), a second order mathematical entity that contains all the stress information at a given point A. It can then be proven that the traction vector depends in a linear way on :
| (1) |
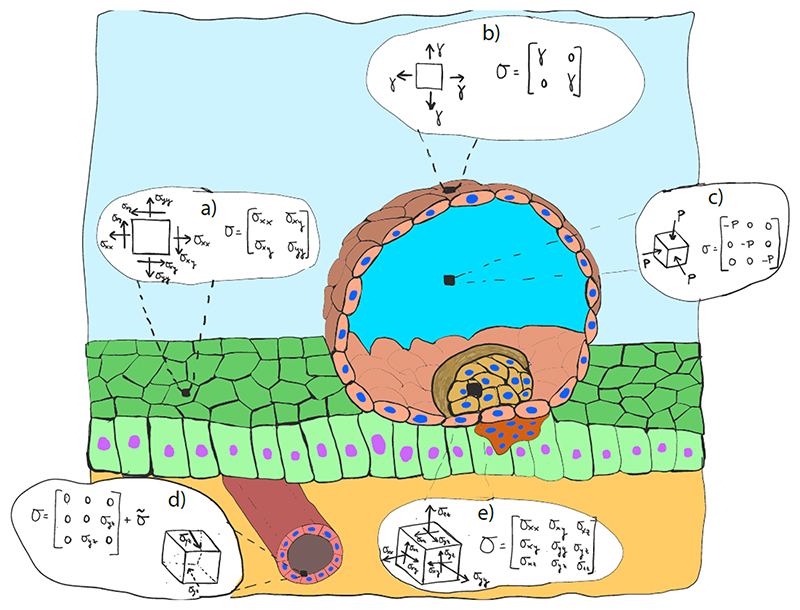
At any point A, the stress tensor σ(A) is a 3x3 symmetric matrix (Box 2). Depending on the geometry of the material and the loading conditions, it can adopt distinct forms. We illustrate the most characteristic of such forms in Box 3, using the process of blastocyst implantation as an example.
Box 2. the stress tensor.
Box 2. Geometric representation of the stress tensor σ at point A of a body under a load .
There are infinitely many traction vectors acting on a point A as there are infinitely many planes cutting through that point. The stress state at point A is, however, completely defined by 6 orthogonal planes infinitely close to A (defining an infinitesimal cube centered in A), and their associated tractions (Box 2a). In equilibrium, the traction vectors in parallel faces are equal and opposite and, therefore, only three traction vectors, , and are needed to describe the stress state at point A. For any given coordinate system, the components of these three traction vectors (Box 2b) can be organized in a 3x3 matrix called the stress tensor σ, which owing to balance of angular momentum is symmetric:
| (12) |
As a result of the spectral theorem, we can always find an orthonormal coordinate system where the matrix is diagonal (Box 2c).
| (13) |
When σ has a diagonal form, its three independent values (its eigenvalues) are called principal stresses (σ1 ≥ σ2 ≥ σ3). When they are equal, the stress state is called hydrostatic or spherical, and in any orthonormal coordinate system σ is proportional to 1, the identity 3x3 matrix. For instance, fluids at rest have a uniform (independent of A) stress state of the form
| (14) |
where P is the pressure. In this situation, the traction vector is always parallel to and thus perpendicular to any surface (the tangential component of the traction is identically zero) and compressive of magnitude P.
In a general case, the stress tensor σ can always be decomposed in its spherical or hydrostatic part (that produces tractions perpendicular to any surface) and its remaining deviatoric part:
| (15) |
| (16) |
| (17) |
The deviatoric part, which is represented as a traceless matrix, is responsible for the shear stresses.
When modeling thin objects such as plates placed parallel to the (x-y) plane, it may be justified to assume that the traction vector normal to the top and bottom free surfaces of the plate is identically zero and that the stress tensor does not depend on z. Since the normal vector to those surfaces is parallel to the z-direction, the stress tensor takes the form
| (18) |
These conditions are referred to as plane stress. Under these conditions, the stress state becomes two-dimensional, and an interaction of the thin plate with a substrate (e.g. a measured traction between a cell monolayer and its substrate) becomes a body force rather than a surface traction, see Eqns. (4)-(5).
Box 3. Stress tensor in biological tissues.
Box 3. Illustrative sketch of different representative stress states that are present during embryo implantation.
The stress tensor σ is, in general, a 3x3 symmetric full matrix, where all normal and tangential elements are non-zero (Box 3e). However, for specific geometries and loading conditions, it will adopt simplified forms. Here, we illustrate some characteristic mechanical configurations by using the process of blastocyst implantation as an example203.
The inner cell mass (Box 3e) is a 3D body in a 3D stress state, and therefore σ is in general a 3x3 full matrix. By contrast, the blastocoel (Box 3c) is a fluid filled cavity in a 3D hydrostatic state, and thus σ is a 3D diagonal matrix whose elements are equal. The endometrium (Box 3a) is a flat monolayer in a state of plane stress. Therefore, σ can be reduced to a full 2D matrix, with both normal and tangential components. Conversely, the blastocyst’s wall (trophectoderm) (Box 3b) is in a state of capillary (surface) tension due to the internal pressure exerted by the blastocoel. σ is then reduced to a 2D diagonal matrix with equal diagonal components. Finally, the endothelial surface of a blood capillary is subjected to a combination of shear stress, hydrostatic pressure and surface tension. σ can then be expressed as a sum of two matrices, one with only shear components owing to blood flow and one with a more complex structure due the vessel geometry, hydrostatic pressure and surface tension, generally expressed in cylindrical coordinates (Box 3d).
Force balance in a tissue is defined by Newton’s second law. For a tissue in equilibrium modeled as a continuum material and ignoring inertial forces, Newton’s second law is expressed in terms of the stress tensor as (see Box 4 for the derivation)
| (2) |
where ∇ · indicates the divergence operator, which applied to the stress tensor produces a vector expressing the out-of-equilibrium force density in the material, and where is an externally applied force density. When there are no external forces applied to the system, i.e. , the internal stresses are balanced at every point and the divergence in Eqn. (2) is identically zero. The above equilibrium equation, together with its boundary conditions, govern the mechanics of the system. In 3D, σ has 6 independent components and the equilibrium (vector) equation only provides 3 independent equations. In 2D, where stress is sometimes referred to as tension, σ has 3 independent components and equilibrium provides 2 independent equations. In general, we need extra conditions, called constitutive equations, to have a closed problem. Constitutive equations model the stress-generation mechanisms of the material under consideration, and for a living tissue they may include elastic (relating stress and deformation), viscous (relating stress and deformation rate), and active (involving internal consumption of chemical energy) components. The simplest of these relations is provided by isotropic linear elasticity, which relates σ and the deformation in a linear way through two coefficients: Young’s modulus E and Poisson’s ratio v. Constitutive equations of higher complexity are used when elasticity is not applicable, invoking viscosity35, hyperelasticity36, superelasticity37, plasticity38, viscoelasticity34, poroelasticity39 or polarity40. For some particular cases with highly symmetric geometries, such an expanding cell monolayer (2.3) or a spherical dome (3.2), the stress can be fully determined without specifying the constitutive equation by simply invoking equilibrium37,41.
Box 4. Equilibrium equation for a continuum.
The resultant of all external forces applied on a sub-volume V of a tissue bounded by the surface S is the sum of all surface forces acting on its boundary and of all body forces acting on its volume:
| (19) |
where the last step was obtained by invoking the divergence theorem.
Newton’s second law can then be written as:
| (20) |
where is the acceleration and ρ is the mass density. Despite the fact that tissues are dynamic systems that change in time, we can assume that they relax instantly to their closest state of mechanical equilibrium185. In this approximation, the tissue is said to be in a quasi-equilibrium state, which since the sub-volume is arbitrary, results in equilibrium Eqn. (2):
| (21) |
When there are no body forces acting on a tissue, i.e. , the internal stress gradients balance themselves at each point of the tissue:
| (22) |
2. Techniques to measure stress in tissues cultured in 2D
Biological tissues display great variability in their geometrical and mechanical configuration (Box 3). Leukocytes can crawl as single cells on 2D surfaces and invade the 3D ECM during the inflammatory response; epithelial cell monolayers cover the internal and external surfaces of our body, often withstanding a 2D plane stress (Box 2); the early mammalian embryo behaves as a thin walled spherical vessel under pressure; a tumor is a 3D material subjected to compressive stress due to its growth and to stromal forces. Each of these systems displays different mechanical states, and thus requires different techniques to measure the generated stresses. In the following sections, we will discuss techniques developed to measure stress in living tissues and their range of applicability. We will first review techniques applicable to in vitro and ex vivo 2D systems, while later sections will focus on in vitro and ex vivo 3D samples and in vivo systems. The techniques discussed in this section, together with their main features and selected bibliography, are summarized in Table 1.
Table 1. Summary of the techniques available to measure the mechanical stresses of living tissues.
| Technique | Measured quantity | Output | Strengths | Limitations | Bibliography |
|---|---|---|---|---|---|
| 2D IN VITRO AND EX VIVO | |||||
| 2D Traction Force Microscopy | 2D displacement of the substrate’s top surface. | 2D traction vector. | Absolute measurement. Simple implementation. Mechanical properties of the substrate can be tuned. |
Very sensitive to noise. Neglects out-of-plane tractions. |
4,35,36,42-73 |
| Micropillars | 2D displacement of pillar tip. | 2D traction force. | Absolute measurement. No reference image is needed. Clear physical interpretation of the measured force. |
Discrete adhesion. How topography affects cell behavior is unclear. Deformable substrate under pillars affects measurements. |
4,74,75,77-83 |
| Monolayer Stress Microscopy | Displacement of the substrate. | Local internal monolayer stress tensor. | Accesses local internal stresses of the tissue. | Linear, uniform and isotropic elasticity is generally assumed for the tissue. Uniform thickness is assumed. |
35,40,41,60-62,84-94,206 |
| Suspended monolayers | Cantilever displacement. | Average internal monolayer stress. |
Stress or strain are imposed by the user. | Local stress is not obtained. | 95-101 |
| 3D IN VITRO AND EX VIVO | |||||
| 2.5D Traction Force Microscopy | 3D displacement of a gel substrate. | 3D traction vector. | 3D traction can be measured. | Anisotropic 3D point spread function. Very sensitive to noise (high quality measured displacements are needed). Computational complexity. |
37,72,73,104-108,116-118 |
| 3D Traction Force Microscopy | 3D displacement of the ECM surrounding the tissue. | 3D traction vector. | 3D traction can be measured. Physiologically relevant ECM. |
Anisotropic 3D point spread function. Non-linear material behavior of the surrounding ECM. Cells remodel and degrade ECM. Computational complexity. |
38,103,109-115 |
| Micro-bulge test (domes) | 3D displacement of the substrate surface. | Luminal pressure and internal stress of curved monolayer. | No need to assume any constitutive behavior for cells. Accessing internal tension for curved monolayers. |
Only applicable to cell types that form domes. | 37,121 |
| IN VIVO | |||||
| Servo-null methods (pressure gauges) | Electrical resistance at the capillary tip. | Luminal pressure. | Direct access to luminal interstitial pressure. | Invasive. Complex experimental setup. |
121,128-142 |
| Inclusions | Inclusion shape/deformation. | Local tissue stress tensor components. | Able to report 3D tissue stress. | Only accesses stress value near to the inclusion. Might perturb force transmission in the tissue. Requires microinjection in vivo |
39,143-148,156,157,205 |
| FRET sensors | Fluorescence intensity. | Local tension at the molecular level. | Genetically encoded. Local measurement. |
Only reports tension, not compression. Calibration issues. No directional information. Unclear effect of the surrounding medium and fluorophore stability. |
151,158-167,169 |
| Laser ablation | Recoil velocity. | Relative tissue stress. | High spatio-temporal control of the perturbation. Easy implementation. |
Invasive. Relative measurements unless viscosity of the tissue is assumed. |
170-181 |
| Force inference | Tissue shape. | Relative local internal stress. | Very simple experimental implementation. Non-invasive. |
Only relative measurements. Computational complexity. Highly sensitive to segmentation noise. |
37,182-192,194-202,204 |
2.1. Traction Force Microscopy in 2D (TFM 2D)
Traction Force Microscopy (TFM) is the first and most standard technique used to measure the tractions exerted by single cells and tissues on soft elastic substrates. A first qualitative implementation of TFM showed that single cells were able to wrinkle a thin and soft silicon rubber substrate on which they were adherent42. Subsequent improvements attempted the quantification of the tractions underlying such deformations by modeling the substrate as a flat thin membrane under plane stress43-45. Following these seminal contributions, the technique was reformulated to its current implementation, which measures the 2D tractions exerted by cells on flat substrates of known thickness46. Typical substrates are polyacrylamide (PAA) and soft polydimethylsiloxane (PDMS) gels, which are transparent, tunable in stiffness and can be coated with ECM proteins. As detailed in a number of studies and reviews, TFM 2D directly measures the displacements that cells generate on the upper surface of their underlying substrate47,48. These displacements are measured relative to a reference state typically obtained by detaching all the cells from the substrate and thus relaxing it to its non-deformed configuration (Figs. 1a and 1b). Displacements are entirely caused by the tractions that cells exert on the substrate and they are computed by imaging fiducial markers that are embedded in the substrate or attached to its surface. Recent implementations of TFM 2D eliminate the need to image the relaxed configuration by distributing the markers into a regular array that serves as theoretical reference36,49.
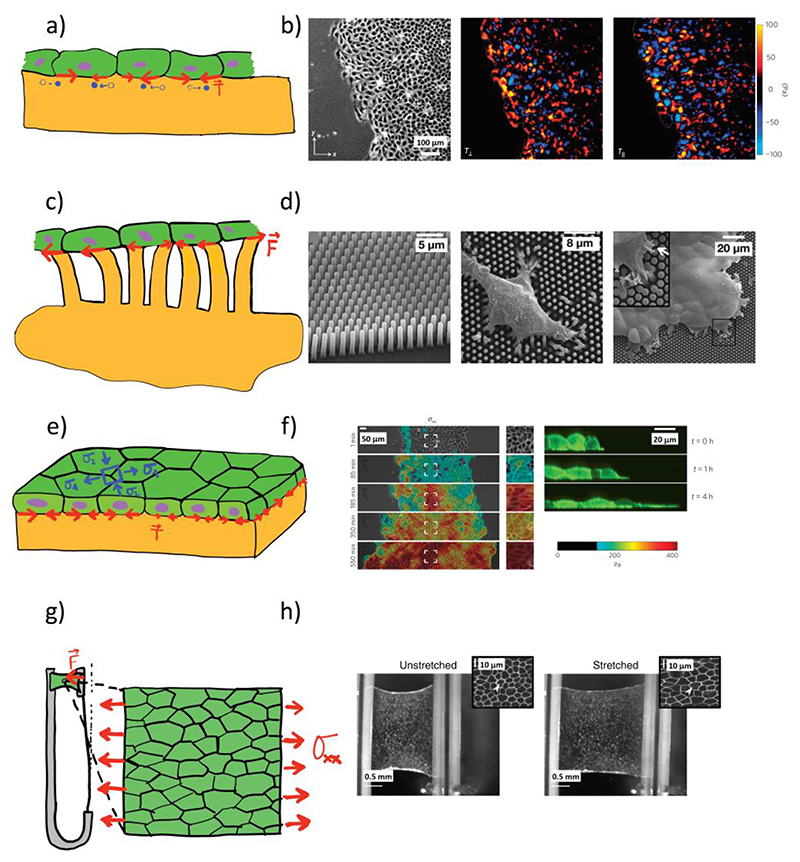
Figure 1. Techniques used to measure tractions and internal stresses in 2D tissues.
(a) In TFM 2D, a flat elastic gel is synthetized, and a tissue is allowed to attach to its surface. Cells exert tractions on the substrate and the resulting deformation can be tracked by adding fluorescent particles in or onto the substrate and comparing their position with an image of the substrate at rest. Tractions are then calculated by using different computational and analytical approaches. (b) Representative TFM 2D experiment. Phase contrast image of a flat cell monolayer on top of a polyacrylamide gel (left) together with the tractions exerted by the cells in the directions parallel (center) and perpendicular (right) to the advancing edge60. (c) In the micropillar technique, cells are seeded on top of an array of micropillars, whose deflection is proportional to the locally applied force. (d) Representative micropillar experiment. Scanning electron micrograph of a micropillar array (left) with a single cell (center) and a cell monolayer (right) lying on top of it78. (e) Using MSM, the internal stresses of a flat cell monolayer can be calculated from the tractions it applies on an elastic substrate. (f) Representative MSM experiment. Expanding cell monolayer with overlaid color-coded internal stresses calculated with MSM61 (left). Side view of an expanding monolayer (right). (g) The tensional state of a flat monolayer can be directly measured and controlled with a micromanipulator. (h) Representative suspended cell monolayer experiment. Monolayer before (center) and after (right) stretch applied with a micromanipulator96. Insert: zoom in a region of a monolayer before and after stretch97.
Different strategies are available to obtain the tractions that cause the measured surface displacements. In all cases, mechanical equilibrium Eqn. (2) (Box 4) is imposed to the substrate, and a constitutive behavior is chosen to establish a closed problem. The substrate is commonly considered uniform and isotropic, and its constitutive behavior is typically assumed linear elastic, with known Young’s modulus E and Poisson ratio v. TFM 2D can be used when the out-of-plane tractions exerted by the sample tissue are negligible compared to the in-plane tractions, yielding a 2D traction vector on the substrate surface50.
By also assuming a simple geometry (as a half-space or a finite thickness substrate) and small displacements (infinitesimally smaller than any relevant dimension of the gel), several computational methods have been developed to obtain the tractions. These methods take advantage of linear superposition and of the availability of analytical forms for the Green’s function of the problem, which provides the displacement field in the substrate under the action of a point surface load. In most cases, tractions are calculated as the solution to an inverse problem, typically computed in Fourier space to accelerate computational performance50,51. In some applications, the inversion can also be performed in real space using the Boundary Element Method46. Regardless of the specific computational formulation, the inverse problem is mathematically ill-posed, and because of the long-ranged decay of the Green’s function, the computed tractions are very sensitive to small variations or noise in the displacement data. This difficulty can be mitigated by using regularization techniques during the solution of the inverse problem52,53 or Bayesian methods54. When the previous hypotheses do not hold, as for example when the substrate is not uniform because there is a gradient of stiffness (E), when the geometry of the substrate is complex, or when there are large displacements, tractions need to be computed from the displacements using the Finite Element Method (FEM)55.
A different strategy is to directly compute the substrate deformation from the spatial derivatives of the displacement field56. The stress tensor σ is then directly computed from the deformation using the constitutive equation of the substrate material. Finally, the traction vector is obtained simply as . The main shortcoming of this approach is the noise in the displacement field, which arises from optical microscopy limitations, from the image analysis algorithms and from the material heterogeneities of the substrate. Noise in the measurements are strongly amplified when calculating the displacement derivatives, and the calculated σ might not satisfy the equilibrium Eqn. (2).
TFM has been pivotal in the emergence and growth of the field of mechanobiology. At the single cell level, TFM made visible for the first time the tractions that cells exert when they migrate46, divide57 and interact with their mechanical environment58,59. At the tissue level, TFM has been used to establish how cells coordinate local traction generation during collective cell migration60, how mechanical waves propagate in a cell monolayer61, and how cells combine different motility modes to heal wounds4. Other discoveries enabled by TFM include collective durotaxis62, kenotaxis63 and cell jamming64. Whereas most TFM expertiments have been performed using cultured monolayers, the technique has also been applied to tissue explants65.
Key advantages of TFM over other techniques are its straightforward implementation, its potential to be applied at different scales, and its high versatility, which has enabled its use in physics and engineering problems48 such as wetting35,66, fracture67,68 or adhesion69-71 both in living and inert materials. A major disadvantage is that retrieving the tractions from the displacements is an ill-posed problem and thus it is very sensitive to experimental noise. Furthermore, TFM 2D is by definition restricted to measuring tangential in-plane tractions, but deformations on flat gels might be due to out-of-plane tractions, resulting in errors in the traction field measured with TFM 2D72,73.
2.2. Micropillars
The use of micropillars to measure tractions exerted by a tissue is conceptually similar to TFM, but the continuous flat gel substrate is substituted by a discrete array of vertical slender micropillars of micron-size cross-section, typically fabricated with PDMS74. Because of the localized nature of adhesion to the substrate, micropillars measure an integrated traction over a small region, that is, a net force. Micropillars are physically anchored at their bottom and free at their tip, in a vertical cantilever beam configuration. Cell attachment is restricted to the pillar top surface, which defines the area of force application (Figs. 1c and 1d). The in-plane component of the forces applied on the substrate can be calculated from the displacements of the micropillars tips. Owing to the inherent locality and discreteness of the mechanical problem, the implementation of the technique is mathematically and computationally simpler than TFM. For deflections much smaller than the micropillar length, applied net force and tip displacement are linearly related through the elastic spring equation
| (3) |
where F is the applied force, E is Young’s modulus, I is the moment of inertia, L is the length of the micropillar and δ is the measured displacement. Eqn. (3) is only valid for slender pillars, i.e. with a length larger than 10 times their radius, of uniform cross-section. Micropillars are microfabricated following a regular lattice, which provides a reference from which deflection can be calculated. Particle tracking software is used to find the centroid of each tip and its location is compared to the theoretical position of the pillar in the ideal lattice. According to Eqn. (3), the substrate stiffness and stiffness gradient felt by the cells can be modified by tuning the pillar material, length74 and/or cross section75. A variant of this technique uses only two thick vertical micropillars76,77. Contractile cells, such as fibroblasts76 and cardiomyocytes76,77 are seeded between them surrounded by ECM proteins, mimicking a three-dimensional microtissue. Because the pillars are not slender and lack uniform cross-section, their response is not linear as in Eqn. (3), and their force-deflection curve needs to be experimentally calibrated.
Arrays of micropillars have been used to quantify forces during single and collective cell migration4,74,78, yielding force patterns comparable to those reported by TFM. In static monolayers, micropillar arrays have been exploited to study the tangential forces helping neutrophils to transmigrate through the endothelium79. This technique has also been used to study the role of tractions in the healing of wounds4, and to elucidate the role of leading cells in collective cell migration80. By modifying the geometrical properties of the micropillars, i.e. length and cross-sectional shape, cells were shown to increase the force generated with increasing the stiffness of the pillar81 and to elongate in the direction of highest stiffness75. This approach has also been employed to study the link between rigidity sensing of the environment and cancer cell growth82.
Compared with TFM 2D, micropillar-based traction microscopy has the advantage of providing a direct local interpretation of the relation between applied force and pillar deflection. Tracking the displacements of the pillars is simpler than following patterns of bead markers, and cells do not need to be detached to capture a reference image, given that the reference position of the pillars is calculated from an ideal grid. Furthermore, the mathematical and computational methods to calculate the forces are straightforward. A final advantage of micropillar arrays is that they provide a way to create stiffness gradients in the substrate by varying the shape of the pillars rather than their material properties. However, this technique presents some drawbacks, mostly associated with the discrete nature of the adhesion of cells to the pillars. Indeed, micropillar arrays provide the cells with topological cues affecting their behavior. Moreover, despite a correct substrate functionalization, cells still tend to enter the empty space between pillars. This technique requires very slender micropillars, which poses microfabrication and handling challenges. Furthermore, it only allows us to measure in-plane displacements of the micropillar tips, and thus vertical tractions are disregarded. Given that the actual relaxed position of the micropillars might deviate from their ideal location, the use of a theoretical reference image introduces random noise in the deflection and, therefore, in the force measurement. Finally, the presence of a deformable substrate under the pillars has been reported to induce an overestimation of the tractions applied by the tissues under study and, consequently, correction factors need to be introduced and validated83.
2.3. Monolayer Stress Microscopy
Given the traction field exerted by a tissue on a flat substrate and invoking simple force equilibrium arguments and mechanical assumptions, it is possible to calculate the internal stress distribution in the tissue (Figs. 1e and 1f). This approach, generally known as Monolayer Stress Microscopy (MSM), was first proposed to measure the average internal stress in a single cell41. This idea was then applied to measure the internal tension distribution in an expanding cell monolayer60, and later on, in cell doublets84,85, triplets86 and larger cell clusters87.
In MSM, the cell monolayer is modeled as a very thin flat plate under plane stress conditions88,89. In this 2D setting, the equilibrium Eqns. (2) take the form (Box 4)
| (4) |
| (5) |
where σxx, σyy and σxy are the components of the stress tensor in the tissue, h is the mean height of the monolayer, and Tx and Ty are the tractions measured by TFM 2D, which in this 2D approximation take the role of in Eqn. (2). These two partial differential equations, insufficient to determine the three unknown stress components, are then complemented by the Michell-Beltrami compatibility condition
| (6) |
This equation implicitly assumes a linearly elastic isotropic behavior of the tissue. The MSM inference of the tissue stress is then obtained by solving Eqns. (4)-(6) with suitable boundary conditions88,89.
This approach requires knowledge of Poisson’s ratio ν of the monolayer, but not its Young’s modulus E. An alternative approach has been proposed to calculate the monolayer internal stresses from the substrate displacements (rather than tensions) by solving the elasticity equations for the monolayer90. This approach has the advantage of not requiring the calculation of the tractions exerted on the substrate and allowing for non-uniformities in E and v of the monolayer. However, uncertainties in the values of the monolayer’s mechanical properties will greatly impact the calculated tensions.
For monolayers that cannot be modeled as elastic and isotropic, Eqn. (6) does not hold, and the problem is underdetermined unless a constitutive model is assumed. A Bayesian inversion method, Bayesian Inversion Stress Microscopy (BISM), has been proposed to solve Eqns. (4)-(5) independently of a constitutive model91. This approach, which can be interpreted as an unbiased regularization, is in principle devoid of free parameters and has been shown to be robust with respect to the underlying statistical model.
Recently, a mathematical framework has been developed to quantify bending moments in the cell monolayer from the out-of-plane tractions exerted on the substrate92. The problem is decomposed into a plane MSM state (governed by Eqns. 4-6), and a bending state induced by the out-of-plane components of the traction vector92,93.
MSM has been pivotal in describing emerging phenomena such as plithotaxis, i.e. the tendency of cells to follow the direction of maximum principal stress89, active de-wetting of epithelial islands35, collective durotaxis of epithelial monolayers62, cell extrusion at topological defects40, and the role of mechanical interactions between follower cells in the emergence of leaders during epithelial migration94.
Monolayer Stress Microscopy has the advantage of accessing the internal stresses of a tissue, as opposed to the interactions of the tissue with its surrounding environment, in a non-invasive way. However, it is built around the assumption of uniform elastic mechanical properties of the tissue and restrictive geometric constraints such as considering a flat monolayer with uniform thickness. These limitations are absent in formulations of MSM in quasi-1D configurations, such as cell chains or monolayers expanding from a rectangular pattern61. In 2D monolayers, the impact of MSM assumptions in the recovered stress field has been analyzed in detail88. Monolayer mechanical properties are dependent on cell type and microenvironment, and they might not be fully described by an elastic constitutive equation37. Similarly, cell monolayers might not present a uniform height. Finally, the original implementation of MSM makes the assumption of planar stress state, which might not be applicable to all types of monolayers. This limitation has been partially addressed by including the bending moments of the monolayer92.
2.4. Suspended monolayers
A direct tensile testing of in vitro and ex vivo cell cultures can be performed by using suspended cell monolayers95. These tensile assays enable the quantification of both the rheology of the monolayer95 and its stress response to mechanical deformations96. In these experiments, a freely suspended cell monolayer is attached at its two ends to one rigid and one flexible rod, used as manipulators to apply a given strain or stress, and as transducers to measure the conjugated stress or strain exerted by the monolayer97 (Figs. 1g and 1h). The suspended monolayer is physically and optically accessible, enabling the direct visualization of the tissue while being stretched.
Tensile tests of suspended cell monolayers have been used to characterize mechanical properties at the tissue, cellular and subcellular scales95, and these experiments have been computationally simulated with vertex models98. Tensile tests have also been applied to study the contribution of cell division to stress relaxation and tissue homeostasis99, with results well-captured by vertex model simulations100. More recently, tensile tests have shown that the stress response of cell monolayers to applied strains is controlled by the actomyosin cortex both in cell monolayers grown in vitro and in multilayered explants of Drosophila larval wing discs cultured ex vivo96. Furthermore, compression tests have been used to study the mechanoresponse of the actomyosin cytoskeleton, and to identify a buckling threshold above which monolayers remain folded101. Finally, mechanical probing of curls formed at the edges of suspended monolayers provides a method to measure the out-of-plane mechanics of tissues102.
The biggest advantage of this technique is its ability to perform tensile and compression tests of a cell monolayer devoid of matrix, hence directly testing the cellular material. Moreover, it is very well suited to image the cell monolayer while being manipulated, potentially enabling the combination with computational force inference methods (section 4.5). The technique has the disadvantage of requiring a very specialized and low-throughput protocol for sample preparation and testing.
3. Techniques to measure stress in tissues cultured in 3D
Specific techniques have been developed to measure the tractions and stresses in tissues cultured in 3D. They will be discussed here and summarized in Table 1.
3.1. Traction Force Microscopy in 3D
It is well known that cells impose 3D displacements on their extracellular matrix by applying 3D forces103. Even when attached to flat surfaces, tissues exert normal forces on their substrate. These normal forces are sometimes comparable in magnitude to their in-plane counterparts104,105. In those cases, TFM 2D is not a valid approach, and a different technique needs to be used. A natural extension to TFM in 2D (section 2.1) is to relax the hypothesis of zero normal tractions at the substrate surface. In this extension, a 3D displacement field of the top layer of the substrate needs to be measured to infer the 3D traction vector field (Figs. 2a and 2b). This method is also known as 2.5D because it involves calculating a 3D traction field applied on a 2D substrate. To obtain 3D tractions from 3D measured displacements, the same mathematical and computational approaches that were explained for TFM 2D can be used. Under the assumptions of a uniform, isotropic and linear elastic substrate, with simple geometry and small displacements, 3D traction fields were first calculated from displacements by following a direct approach and evaluating the constitutive elastic equation for the substrate106,107. Subsequently, a Boundary Element Method was proposed to generalize Dembo and coworkers’ solution46, by considering an incompressible substrate (v = 0.5) and thus uncoupling the normal and tangential problems108. Alternatively, 3D tractions fields can be calculated from displacements using the Fourier transform and the known Green’s function for the problem72. For other cases, where the aforementioned hypotheses do not hold, a Finite Element Method is needed104.
Figure 2. Techniques used to measure tractions and internal stresses in 3D tissues in vitro.
(a) In TFM 2.5D, a tissue is seeded on top of a 2D elastic substrate, and the displacements of the substrate are measured in 3D. From these displacements, the 3D traction field can be calculated. For simple geometries like spherical caps, the internal stresses of the tissue can be recovered with a micro-bulge test. (b) Representative TFM 2.5D experiment. 3D traction field (green arrows) generated by an epithelial dome (side view) on a flat substrate37. (c) By applying TFM 3D to tissues grown inside a deformable matrix with particle tracers, the full 3D displacement field can be measured, and from it the full 3D traction field can be inferred. (d) Representative TFM 3D experiment. Breast cancer spheroid embedded in a 3D collagen I matrix. Bright field image with superimposed ECM displacements (left) and fluorescent image of the spheroid and matrix (right) (courtesy of Nadine Grummel, David Böhringer and Ben Fabry).
To study some physiological processes such as tumor invasion or angiogenesis it may be more pertinent to measure the tractions exerted by a tissue embedded in a 3D ECM. The quantification of a 3D traction field from a 3D displacement field is fundamentally more challenging from the conceptual, experimental and computational points of view (Figs. 2c and 2d). A central conceptual hurdle of this technique is that cells continuously synthetize and remodel their ECM and, as a consequence, it is unclear if the measured displacements are produced by the tractions exerted by the cells or if they are the result of remodeling of the ECM33. Furthermore, the 3D imaging of the ECM completely surrounding the tissue might be too aggressive for the sample and induce phototoxicity. Another problem arises from the fact that the physiological 3D ECM includes fibers and thus cannot be modeled by linear elasticity. An early implementation of TFM 3D estimated the traction exerted by the invading front of a cancer spheroid embedded in a Matrigel matrix by tracking the motion of embedded microparticles109. This approach is limited by the assumption of linear elasticity, the measurement of the particle displacements in only one plane through bright field illumination, and the assumption that the traction force points in the direction of the average particle displacement. However, this work paved the way for more sophisticated studies. To tackle some of the problems of TFM 3D, some researchers have used well-characterized viscoelastic materials such as agarose110 or engineered synthetic matrices that behave as linear elastic materials111. Other groups have characterized the non-linear constitutive behavior for physiologically relevant ECMs such as collagen gels38,112. Recently, a simplification of TFM 3D has been applied to tumor spheroids113. By taking advantage of the approximately spherical geometry of the tissue and assuming spherical symmetry of the stress state, only an equatorial plane of the spheroid and the ECM is imaged. The radial far-field displacements of the ECM are measured as a function of the distance to the spheroid, and a scalar value of the tissue contractility is calculated through a Finite Element Method. In a particularly simplified implementation of TFM 3D, spherical tissues such as cancer spheroids114 and blastocysts115 are encapsulated within a spherical hydrogel drop. By measuring the radius and wall thickness of the hydrogel capsule, the normal stresses exerted by the spherical tissues are inferred.
TFM in 2.5D has been used to elucidate the interplay between normal and tangential forces during single cell migration105, the influence of 3D traction stresses in the protease-dependent invasion of cancer116, and diapedesis of leukocytes through a vascular endothelial monolayer117. It has also been employed to simultaneously measure traction forces and the substrate’s Poisson’s ratio from the displacements of fiducial markers at different substrate locations118. TFM 3D has been used to describe the invasion, in physiologically relevant conditions, of healthy111 and disease model cells112.
The main advantage of TFM in 2.5D is that it builds on top of TFM 2D, keeping its experimental and analytical simplicity while qualitatively improving the scope of its measurements by correctly quantifying 3D tractions. However, this technique also shares the drawbacks of TFM 2D, such as the high sensitivity to experimental noise. With regard to TFM 3D, its biggest benefit is the ability of using physiologically relevant ECMs. The main limitation is the need to deal with non-linear constitutive behaviors and 3D materials that can be degraded and remodeled by the cells. Furthermore, these techniques are affected by the current imaging limitations of 3D optical microscopy, such as a lower resolution in the z direction compared to the in-plane resolution, and a decline in image quality with the thickness of the sample.
3.2. Micro-bulge test
Recently, a bulge test has been implemented to investigate the stress state of curved epithelial monolayers37 (Figs. 2a and 2b). This technique is based on inducing the formation of out-of-plane domes over a soft, impermeable and elastic substrate119. Domes are blister-like structures that enclose a pressurized fluid-filled lumen120. The cell monolayer is idealized as a structural membrane supporting two-dimensional tangential stress and uniform transepithelial pressure121. Bending moments and out-of-plane shear stresses are neglected, consistent with the sharp contact angle of the domes with the substrate. The lumen’s fluid will indent the soft elastic substrate with a pressure that can be computed by applying TFM in 2.5D37 (Section 3.1) or servo null methods121 (Section 4.1), with similar quantitative results. The fact that dome geometry is very close to a spherical cap implies that its tangential stress is uniform, isotropic and completely described by a scalar value as in a capillary system. As a result of the axisymmetry of the system, the stress state of the dome can be fully computed by imposing mechanical equilibrium (Laplace’s law122,123)
| (7) |
where σ is the tangential uniform and isotropic stress, R is the dome radius (readily measured from a 3D confocal microscopy stack) and ΔP is the lumen hydrostatic pressure.
The stress-strain relationship for the suspended and curved epithelia showed an unexpected mechanical behavior termed active superelasticity37. This constitutive behavior allows tissues to undergo very large and reversible deformations at a constant tension. The plateau in tension is explained by a phase transformation between barely stretched and super-stretched cells that coexist in the epithelial dome. The phase transformation mechanism includes cortical depletion under stretch and re-stiffening at extreme deformations to stabilize the super-stretched phase. Active superelasticity may explain how epithelia actively maintain their integrity in many important physiological processes such as swelling and hatching of mammalian blastocysts37,124,125.
The main advantage of this technique is the robustness of the stress measurement because it is only based on mechanical equilibrium, and thus there is no need to assume any constitutive behavior for the epithelia. As a main drawback, it can only be applied to cell types that spontaneously form domes unless transepithelial pressure is externally controlled.
4. Techniques to measure stress in vivo
The techniques discussed in the previous sections were applicable to samples grown in vitro or ex vivo. Here, we discuss the techniques available to measure tractions and stresses in vivo. They are summarized in Table 1.
4.1. Servo-null methods for measuring luminal pressure
The development of closed cavities with a pressurized fluid-filled lumen is crucial for morphogenesis at different scales, from tissues to organs126. The hydrostatic pressure in such cavities can be measured by directly puncturing the lumen with a micropipette connected to a micropressure measuring system (Figs. 3a and 3b). Although the quantitative measurement of pressure in animals dates back to the eighteenth century127, the measurement of luminal pressure in micron-size tissue structures was more recently achieved thanks to the development of servo-null devices128. These devices use a glass micropipette filled with a saline solution electrolyte of very low electrical impedance, much lower than the luminal contents under study. When the tip is punctured into a fluid-filled pressurized cavity, the luminal content will be pushed inside the tip, effectively increasing the electrical impedance measured at the micropipette. A servomechanism is then used to read the impedance at the tip and send a signal to a pressure transducer that will push the electrolyte towards the lumen until the original impedance is restored. The counterpressure applied by the transducer is assumed to be the pressure of the luminal cavity129.
Figure 3. Techniques to measure internal stresses in vivo.
(a) Servo-null methods measure the luminal pressure of a tissue by inserting a capillary probe directly into the lumen. (b) The servo-null method applied to the luminal cavity of a mouse blastocyst before (left) and during (right) measurement140. (c) Inert deformable probes can be inserted in a specimen to assess its local stress state. (d) Liquid drop inserted in a tissue, before (left) and after (center and right) deformation205. (e) Fret sensors are genetically encoded molecular springs whose deformation is reported by a pair of resonant fluorophores. (f) Junctional tension reported by FRET sensors in an epithelial monolayer and in an epithelial acini167. (g) In the laser ablation technique, a specimen is cut by using a pulsed laser, and its internal stress is released. (h) Circular laser cut (left) performed in a Drosophila melanogaster embryo, and asymmetric retraction (center and right) of the cut patch due to the differential internal tension along the x and y axes172. (i) With force inference methods, cellular pressures and inter-cellular tensions can be inferred from the geometry of the tissue. (j) Illustration of a force inference method. Cell monolayer segmentation (left), tension and pressure location (center), and calculated values for the cellular pressure and cell-junction tension (right)33,194.
Although servo-null methods were originally developed to measure the pressure in the microcirculation128,130, they have been extensively used in diverse systems and length-scales, from the cytoplasm131,132 to whole animal organs133-136. Servo-null methods have also shown to be powerful tools for quantifying pressure in tissues. They were used early on to characterize pressurized domes formed by in vitro grown epithelia121, a tissue system where luminal pressure is key for its correct 3D morphogenesis (Section 3.2). They have also been used to assess the key role of luminal pressure during the development of the embryonic heart of zebrafish137 and chicken138 embryos, as well as for quantifying the relation between luminal pressure and successful brain formation of chicken embryos139. More recently, experiments at different stages of mouse blastocyst formation have shown that luminal pressure regulates cell fate specification and tissue patterning by influencing cell division and positioning140. Servo-null methods have also been used to study the mechanoregulation of tissue morphogenesis via hydraulic feedback in the developing inner ear of zebrafish141.
Despite their unique potential to measure pressure at the microscale, servo-null methods present several disadvantages. Typically, the tip resistance and compliance are neglected, overlooking a possible quantitative bias in the pressure measurements. From an experimental perspective, the meticulous filling of the tip needs to be assessed at all times, given that even small bubbles will highly impact the measurement. Moreover, puncturing micropipettes are prone to clogging, affecting the pressure readings. Finally, the probing tips need to be exceptionally thin to avoid leakage at the puncture site. Thus, this technique is highly complex and prone to very subtle but catastrophic errors both in the data collection and interpretation142.
4.2. Inclusions
A novel approach to measuring tissue stress in vivo and in vitro is based on introducing force transducers into the tissue and reading out their output signal through optical means (Figs. 3c and 3d). The probes used in these techniques need to have controlled size, shape and known visco-poro-elastic properties. Moreover, their mechanical properties must be stable in time. For this reason, cells themselves cannot be used as force transducers, and these techniques resort to synthetic inclusions39.
The first reported application of exogenous inserts as force transducers used fluorescently labeled liquid microdroplets of biocompatible fluorocarbon oils coated with adhesion molecules143. These microdroplets are injected into a tissue, and their 3D shape is imaged through confocal microscopy. By knowing the surface tension of the microdroplet and assuming a spherical reference configuration, part of the deviatoric stress (Box 2) locally applied on the surface of the microdroplet can be calculated. A critical step of this method is the assumption of constant and uniform surface tension of the microdroplets. This surface tension can be modified when proteins are adsorbed on the microdroplet’s surface, and thus it needs to be saturated with surfactants prior to injection32. One fundamental limitation of this implementation is the use of incompressible liquids, which impairs the measurement of the hydrostatic stress component and of the full deviatoric stress component (Box 2). This limitation has been overcome by using elastic reporters144. Furthermore, the use of exotic liquids such as ferromagnetic fluids enables the active application of forces on the surrounding tissue145.
A similar approach uses poroelastic polyacrylamide hydrogel microbeads rather than oil droplets146,147. Thanks to their poroelastic nature, these microbeads are able to report on the hydrostatic stress component (the pressure). When the microbeads are subjected to a hydrostatic stress, their polymer volume fraction changes and, consequently, the diffusion time of a small fluorescent tracer varies. By measuring this diffusion time one can calculate the hydrostatic component of the stress applied on the microbeads. A more advanced approach uses alginate hydrogel microbeads with fluorescent nanobeads embedded in them148. A Fast Iterative Digital Volume Correlation (FIDVC) algorithm149 applied to microbead images enables the calculation of the full deformation configuration of each microbead. The full stress state on the microbead surface is then calculated from the deformation by using a Finite Element Method.
A novel and promising generation of transducers for force measurement of in vivo specimens are Lanthanide-doped nanoparticles150,151. These nanoparticles change their molecular structure when subjected to a mechanical stress, effectively varying their fluorescence emission intensity152. They can be used as force reporters in the nano- to micro-Newton regime153. Although these nanoparticles have been extensively used as bioprobes150, they remain to be used as force transducers in biological applications. In the same vein, Wispering Galery Mode Microlasers are micron-sized deformable optical microresonators able to emit laser light pulses with a frequency dependent on their geometry154, and thus enabling the quantification of their deformation from their emission spectrum. These reporters have been inserted into the cytoplasm of contractile cardiomyocytes and in zebrafish hearts to monitor cell and organ contractility155, but they remain to be used as direct force reporters.
Oil microdroplet force transducers have been employed to study the stresses exerted by tooth mesenchymal cells in mandible explants ex vivo143 and in 3D multicellular spheroids in vitro156. Conversely, elastic hydrogel force transducers have been used to measure the hydrostatic stress in 3D multicellular spheroids146,147. Maps of the complete stress tensor have been obtained both in 3D tumor spheroids in vitro and in zebrafish embryos in vivo by using viscoelastic hydrogel force transducers148.
The main advantage of force transducers is their ability to report the 3D internal stresses both in vitro and in vivo143. Thanks to their size and to their mechanical and chemical properties, their injection does not compromise embryo viability. One limitation of using microdroplets as force transducers is the need to know the surface tension of the microdroplet, and the assumption that it does not change when the microdroplet is injected into the sample. Moreover, they only enable the measurement of some components of the stress tensor. These two disadvantages can be overcome by using hydrogel reporters144,146-148,157. Additional limitations include that the introduction of an exogenous body into the tissue might impact the measured stress distribution and affect tissue biochemical interactions, for example by serving as a potential sink for lipophilic growth factors or by altering diffusion patterns in the tissue.
4.3. FRET tension sensors
FRET (Förster Resonance Energy Transfer) tension sensors are composed of a molecular spring of known elastic constant and a fluorescence complex reporting the spring elongation158,159 (Figs. 3e and 3f). Sensors can be either encoded genetically or synthesized and coupled to an inert material. Different molecular springs have been designed and their elastic properties and force range have been characterized in vitro160,161. The elongation reporter system comprises two fluorophores, a donor and an acceptor, with different but overlapping excitation and emission spectra151. The rate of energy transfer between the two fluorophores, first described by Theodore Förster162, has the form:
| (8) |
where κ is the relative dipolar orientation between the donor and acceptor, J is the integral of the overlap between the donor emission and acceptor excitation spectra, kf is the radiative emission rate of the donor, n is the refraction index of the medium and r is the distance between the donor and the acceptor151. Because the rate of energy transfer depends on the separation between fluorophores, it can be converted into a tension readout after careful calibration.
FRET tension sensors have been extensively applied to the study of force transmission at focal adhesions in single cells161. At the multicellular level, they have been used to study intercellular tension in endothelial cell monolayers subjected to fluid shear163, to elucidate the mechanical role of E-cadherin during collective cell migration in the Drosophila ovary164, and to characterize the tension sustained by E-cadherin and desmosomes165 during cell stretch166 and swelling of epithelial acini167, among other applications.
FRET tension sensors have the advantage that they are genetically encoded and, therefore, they can be expressed in virtually any living tissue, both in vitro and in vivo. Moreover, they have the potential to report the forces sustained by different cellular components. They are non-invasive and can be used with a relatively high throughput. Despite the enormous potential of this technique, it presents several limitations that restrict its range of applicability and question the interpretation of its results168. It is typically assumed that FRET sensors are surrounded by a medium with the index of refraction of water, but local concentration changes might greatly impact the measurements151,169. Furthermore, it is assumed that the FRET sensor emission will only be affected by the applied tension, but local chemical interactions with the microenvironment might impact its spring constant or introduce hysteresis31,32. The readout of FRET sensors is affected by fluorophore stability, and its quality is severely decreased in thick samples, where the signal to noise ratio is reduced31,151. Another drawback of the technique, is that it can measure tension but not compression31. Importantly, it only provides the magnitude of tension, not its direction32. Finally, besides these technical considerations, it is worth emphasizing that molecular tension does not necessarily reflect tissue stress. Indeed, tissue stress is supported by many different proteins arranged in parallel, and the tensional state of one of such proteins does not necessarily reflect the stress of the tissue.
4.4. Laser ablation
Laser ablation is used to assess the stress state of cohesive tissues. It is based on simultaneously severing a group of cells to generate a sudden force imbalance. The movement of cells surrounding the ablated area to recover mechanical equilibrium is then used to compute relative values of stress before ablation170,171 (Figs. 3g and 3h). The ablation is performed with near-infrared femtosecond lasers or pulsed UV lasers. Strain and stress anisotropy can be quantified by ablating a supracellular annular region of the tissue172 or by severing circular areas173.
The main assumptions underlying this technique are that the tissue is at mechanical equilibrium before and after the cut, that the ablation is able to release tissue tension, and that, during relaxation, dissipative forces outweigh inertia172,174. By further assuming that dissipation is due to tissue viscosity and friction, the initial recoil velocity and its spatial profile provide information about the stress-to-viscosity and the friction-to-viscosity ratios172. However, given the complex rheological nature of tissues, it might not be accurate to assume a pure viscous response or uniform frictional properties, and therefore data from laser ablation experiments needs to be combined with an appropriate analysis of tissue rheology175,176. The combination of non-uniform or anisotropic rheological descriptions with Finite Element models can provide more accurate interpretations of laser ablation experiments176.
Laser ablation has been extensively used to study early morphogenesis and wound healing. For example, it has been used to show that dorsal closure in the Drosophila embryo is mechanically governed by the contractile forces exerted by purse strings at the leading edge of the lateral epidermis and by the actomyosin cortex of amnioserosa cells174,177. By ablating one amnioserosa cell, researchers showed that dorsal closure is favored by acto-myosin pulsed apical constrictions that pull on the epidermis178. Ion flux between cells has also been related to the generation of contractile forces, measured with laser ablation during dorsal closure179. In the Drosophila embryonic tissue, laser ablation showed that a contractile actomyosin cable forms along the wound margin, acting as a purse string180. In the zebrafish embryo, the tissue tension has been related to the orientation of the spindle by measuring and manipulating the stress state using laser ablation181.
The main advantages of laser ablation are that it can be used in vivo and in a wide variety of tissues, and its relatively easy implementation in many optical microscopy setups. As a major drawback, this technique only offers relative stress measurements unless a tissue rheology is assumed. Moreover, the measurement damages the sample severely, thereby impeding time-lapse recordings. Finally, current laser ablation implementations and analysis are largely restricted to a single optical plane, which prevents a full study of curved tissues.
4.5. Force inference
Geometric Force inference methods compute the internal force balance of a tissue from images of the cellular contours (Figs. 3i and 3j). Internal forces include surface tensions (arising from the cortical cytoskeleton, adhesion proteins, or the plasma membrane), internal pressures, and the elastic and viscous response of the cellular components33. By neglecting inertial forces, viscous dissipation and elastic contributions (assuming long time scales), only two force sources are generally considered: cellular surface tensions and internal pressure. Force inference methods assume that tensions and pressures equilibrate at the vertices of the junctional network and at cell-cell interfaces, where Laplace’s law, relating surface tension, pressure difference and curvature is invoked, Eqn. (7). With the assumptions mentioned above, relative tensions and pressures can be calculated without the need for a specific constitutive model of the system. Therefore, the tensions and pressure differences calculated with inference methods are determined up to a scaling constant factor, which can be obtained through an independent technique such as micropipette aspiration182,183 or TFM184.
The assumptions behind force inference methods for epithelial tissues can be formalized using vertex models185,186 (Box 5). In a vertex model, the arrangement of cells in the tissue is described by a set of vertices that define the intersection of three or more cells. The mechanical state of the monolayer can be described by a work function, W, accounting for the work performed by cellular pressure and by surface tensions as the configuration of the tissue is perturbed. The out-of-balance forces at each vertex in the model can then be computed as
| (9) |
where fν represents the total force acting on vertex ν, δW is the variation of work function and δxν denotes the variation of the position of vertex ν along the coordinate xν (Box 5). Mechanical equilibrium requires that fν = 0, providing one equation per vertex, which linearly depends on the unknown pressure and tension of adjacent cells. Thus, it is possible to establish an algebraic system of equations for cell pressure and surface tension just from the geometrical information of the epithelium187. However, by imposing force-balance at the vertices where multiple cells meet, this system of equations is underdetermined188. Different approaches have been used to make the problem overdetermined, so the force balance equation can be solved in the least squares sense. One option is to assume uniform tension, thereby reducing the unknowns to only the cell pressures189. This simplification is exact for foams and has been applied to model specific tissues such as the ommatidia of the Drosophila retina190. Alternatively, it can be assumed that every cell has the same pressure, keeping only the tensions as unknowns in the force equilibrium equation191. In a different approach, by observing that most of the cell interfaces in epithelia are under positive tension, Bayesian statistics have been applied to reduce the number of unknowns while calculating both internal pressures and cortical tensions188.
Box 5. Vertex models.
Box 5.
Illustrative representation of the parameters and variables of a vertex model: vertex v, edge λ, face κ, cell α, edge length lλ, face area Aκ, cell volume Vα, vertex applied force , edge tension Λλ, surface tension Tκ and cell pressure Pα.
A vertex model describes the geometry of a tissue as a set of vertices marking the confluence of three or more cells, i.e. triple junctions. The mechanical description of vertex models can be formulated by means of the work function, with an internal and an external component:
| (23) |
The external work differential accounts for any external force applied on the vertices
| (24) |
The internal work differential can be generally written as
| (25) |
where α labels each cell, κ and λ label each cell surface and edge, respectively, and ν labels each vertex. δVα, δAκ, δlλ and δxν represent variations in cell volume, surface area, edge length and vertex position, respectively; while Pα, Tκ, Λλ and indicate each cell’s intracellular pressure, surface and line tensions, and internal dissipative forces applied on each vertex. A particular dissipative process is the internal viscosity of the epithelium, that can be modeled as
| (26) |
The equations describing the system are simplified for 2D flat monolayers, where the cells are assumed to be columnar and to have a uniform height. Thus, in Eqn. (2525), the cell area takes the role of cell volume and the cell interfaces are treated as line edges with uniform line tension. Other energy functionals alternative to that in Eqn. (25) have been proposed in the literature204, with similar results.
Recently, force inference has been combined with TFM 2D (section 2.1) to study motile confluent epithelia, in an experimental setup similar to MSM184 (section 2.3). By knowing the tractions applied by the epithelial tissue, this approach enables the calculation of both the absolute tissue tensions and pressures as well as the rheology of the monolayer.
All the previous methods model the cell edges as straight lines between vertices, a geometry that is not always seen in epithelia. By relaxing the straight cell interface assumption, the force balance equations become overdetermined192. This method, called CellFIT-2D192 or Laplace inference193, demands a much higher accuracy of image segmentation algorithms to detect the curvature of cell boundaries194. Furthermore, the curvature of a cell-cell boundary in a 2D image will be smaller in general than that of the actual 3D surface. Laplace inference is well suited for tissues with high cell-edge curvature that is uniform along each cell boundary. However, for small or non-uniform curvatures along a cell edge, it is prone to artifacts and errors that propagate to cell neighbors. These errors are shown to increase with increasing tissue size193.
The problem of geometric force inference in 3D has been undertaken as an extension of CellFIT-2D called CellFIT-3D195. The geometry of the sample is detected by segmentation of 3D image stacks. Due to the complexity of accurately segmenting fluorescent 3D images of cells and the subsequent extraction of surface curvatures, CellFIT-3D is only used to calculate cell tensions, while a natural theoretical extension to calculate pressures is suggested.
In experimental setups where slow motions cannot be assumed, the introduction of viscosity in the force balance equation is required. In those cases, vertex models have been used to calculate the viscosity component of the internal forces of a cell monolayer196,197. In an approach called Cinemechanometry (CMM)186 or Video Force Microscopy198, cell pressures and tensions have been computed from the time evolution of the monolayer shape.
Geometric Force Inference methods have been successfully applied in vivo to study the mechanics of development in Drosophila198,199 and C. elegans 200. They have also been pivotal to understand the role of cell shape and mechanical stress orientation in mitosis in ex vivo models of xenopus tissue201. Among other contributions, force inference methods have also been used to study the process of hair-cell determination in the avian cochlea191, and the effect of interstitial fluid osmolarity in the tissue surface tension in progenitor cell segmentation during gastrulation of the Zebrafish embryo in vivo202.
Force inference methods have many advantages32: they are non-destructive, only requiring imaging of the tissue, they make minimal assumptions about the origin of the forces, they are well suited to be combined with other methods such as suspended monolayers (section 2.4), and they provide cellular and tissue resolution. Limitations include that they assume positive and constant tensions along each cell edge, which might not be true for wiggly junctions193; they only calculate ratios of tensions and pressure differences unless other techniques such as micropipette aspiration are used to provide absolute measurements of tensions182,183; they depend on the accurate segmentation of the cell contour in the tissue; and the calculation is currently limited to tractions transmitted between cells by contact, disregarding any force exerted by the cells on the substrate. The assumptions behind force-inference methods can be systematically tested in various ways, including the geometrical inspection of the junctional network (wiggly junctions or non-uniform curvature being signs of non-compliance), the a posteriori quantification of the error in the force-balance equations fν = 0, or comparisons with measurements relying on other techniques such as servo-null pressure measurements, extended micro-pipette aspiration or laser ablation tension measurements193. Furthermore, observation of cellular processes with mechanical consequences but not accounted for in the conceptual framework underlying force inference, such as protrusive behavior, cortex polarization or the presence of actin belts, may require reconsideration of the results or refinements of the underlying model.
5. Conclusions and outlook
A large and diverse suite of techniques is now available for researchers to measure stress with subcellular resolution in living tissues (see summary in Table 1). These techniques remain experimentally and computationally challenging, but their use is becoming progressively widespread thanks to the increased availability of open source software47 and standardized protocols. No technique is a one-size-fits-all solution, and there are a number of considerations that need to be taken into account before deciding which technique is more suitable to address a specific question. The highest resolution is provided by tools to measure stress in 2D cultured monolayers, but these flat monolayers do not capture essential features of tissues in vivo. Conversely, in vivo technologies might have more physiological relevance, but they generally do not provide absolute values of stress. The techniques reviewed here are not only relevant to illuminate biological processes in development, homeostasis and disease, but also to advance our understanding of active matter physics. In this context, measuring stress in reductionist tissues like micropatterned monolayers, or even unidimensional multicellular chains, is the pertinent strategy to address questions such as what are the master equations that govern the dynamics of aggregates of active particles. A general problem of the techniques reviewed here is that they are still limited to a relatively low throughput. Overcoming this limitation is crucial to bring mechanobiology from the basic science arena to applications in industry and medicine.
Selected Bibliography
First qualitative implementation of TFM, based on the observation that cells are able wrinkle thin polymer substrates 42
This paper marks the first quantitative implementation of TFM 2D46.
This paper formulates Fourier TFM 2D50, speeding up traction calculations by orders of magnitude.
This paper pioneered the use of micropillar arrays for force quantification74.
Description of the general concept underlying MSM, applied here to the inference of internal stress in a single cell41.
This paper marks the rigorous mathematical formulation of MSM to compute all components of the stress tensor in a cell monolayer89.
This paper shows the first implementation of the suspended monolayer technique95.
This paper formulates Fourier TFM 2.5D72.
This paper shows a pioneering implementation of TFM 3D109.
This paper shows the first use of the micro-bulge test to measure the internal stress of a curved epithelium37.
Implementation of servo-null systems and their application to measure pulsatile pressure in a capillary128.
This paper shows the first application of a servo-null device to an in vitro grown cell tissue121.
This paper shows the first use of exogenous inclusions as cell force transducers143.
This paper is a pioneering work in the implementation of laser ablation as a tissue stress inference method177.
One of the earliest implementations of a force inference method applied to a cellular tissue189.
Key Points.
Mechanical stresses generated by cells determine the fate, form and function of living tissues.
Several techniques have been developed to measure tissue stress with subcellular resolution.
State-of-the-art technologies now enable high-resolution mapping of time-varying stress fields in 2D and 3D cell cultures.
Measuring stresses in vivo remains an outstanding challenge that is currently addressed through the combination of image-based computational modelling and the insertion of soft inclusions in tissues of interest.
Acknowledgements
We apologize to the many colleagues whose work could not be cited owing to space constraints. We thank Nadine Grummel, David Böhringer and Ben Fabry for the gift of Fig. 2d, and Ariadna Marin-Llauradó and Tom Golde for critical reading of the manuscript. The authors are funded by Spanish Ministry for Science, Innovation and Universities MICCINN/FEDER (PGC2018-099645-B-I00 to XT, DPI2015-71789-R to MA), the Generalitat de Catalunya (2017-FI-B1-00068 grant to EL, SGR-2017-01602 to XT, 2014-SGR-1471 to MA, the CERCA Programme, and “ICREA Academia” award to MA), the European Research Council (CoG-616480 to XT and CoG-681434 to MA), the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 797621 to MGG, Obra Social “La Caixa”, Fundació la Marató de TV3 (project 201903-30-31-32 to XT). IBEC is recipient of a Severo Ochoa Award of Excellence from the MINECO.
References
- 1.Guillot C, Lecuit T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science. 2013;340:1185–1189. doi: 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]
- 2.Barker N. Adult intestinal stem cells: critical drivers of epithelial homeostasis and regeneration. Nature Reviews Molecular Cell Biology. 2014;15:19–33. doi: 10.1038/nrm3721. [DOI] [PubMed] [Google Scholar]
- 3.Krndija D, et al. Active cell migration is critical for steady-state epithelial turnover in the gut. Science. 2019;365:705–710. doi: 10.1126/science.aau3429. [DOI] [PubMed] [Google Scholar]
- 4.Brugués A, et al. Forces driving epithelial wound healing. Nature Physics. 2014;10:683–690. doi: 10.1038/nphys3040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Northey JJ, Przybyla L, Weaver VM. Tissue Force Programs Cell Fate and Tumor Aggression. Cancer Discovery. 2017;7:1224–1237. doi: 10.1158/2159-8290.CD-16-0733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nia HT, et al. Solid stress and elastic energy as measures of tumour mechanopathology. Nature Biomedical Enginnering. 2016;1 doi: 10.1038/s41551-016-0004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hannezo E, Heisenberg C-P. Mechanochemical Feedback Loops in Development and Disease. Cell. 2019;178:12–25. doi: 10.1016/j.cell.2019.05.052. [DOI] [PubMed] [Google Scholar]
- 8.Gudipaty SA, et al. Mechanical stretch triggers rapid epithelial cell division through Piezo1. Nature. 2017;543:118–121. doi: 10.1038/nature21407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Benham-Pyle BW, Sim JY, Hart KC, Pruitt BL, Nelson WJ. Increasing beta-catenin/Wnt3A activity levels drive mechanical strain-induced cell cycle progression through mitosis. eLIFE. 2016;5 doi: 10.7554/eLife.19799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Uroz M, et al. Regulation of cell cycle progression by cell-cell and cell-matrix forces. Nature Cell Biology. 2018;20:646–654. doi: 10.1038/s41556-018-0107-2. [DOI] [PubMed] [Google Scholar]
- 11.Crick FHC, Hughes AFW. The physical properties of cytoplasm. Experimental Cell Research. 1950;1:37–80. doi: 10.1016/0014-4827(50)90048-6. [DOI] [Google Scholar]
- 12.Bausch AR, Möller W, Sackmann E. Measurement of local viscoelasticity and forces in living cells by magnetic tweezers. Biophysical Journal. 1999;76:573–579. doi: 10.1016/S0006-3495(99)77225-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ashkin A. Acceleration and Trapping of Particles by Radiation Pressure. Physical Review Letters. 1970;24:156–159. doi: 10.1103/PhysRevLett.24.156. [DOI] [Google Scholar]
- 14.Ashkin A, Dziedzic JM, Bjorkholm JE, Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Optics Letters. 1986;11:288–290. doi: 10.1364/ol.11.000288. [DOI] [PubMed] [Google Scholar]
- 15.Wu J. Acoustical tweezers. The Journal of the Acoustical Society of America. 1991;89:2140–2143. doi: 10.1121/1.400907. [DOI] [PubMed] [Google Scholar]
- 16.Binnig G, Quate CF, Gerber C. Atomic force microscope. Physical Review Letters. 1986;56:930–933. doi: 10.1103/PhysRevLett.56.930. [DOI] [PubMed] [Google Scholar]
- 17.Mitchison JM, Swann MM. The mechanical properties of the cell surface I. The cell elastimeter. Journal of Experimental Biology. 1954;31:443–460. [Google Scholar]
- 18.Zamir EA, Srinivasan V, Perucchio R, Taber LA. Mechanical asymmetry in the embryonic chick heart during looping. Annals of Biomedical Engineering. 2003;31:1327–1336. doi: 10.1114/1.1623487. [DOI] [PubMed] [Google Scholar]
- 19.Foty RA, Forgacs G, Pfleger CM, Steinberg MS. Liquid properties of embryonic tissues: Measurement of interfacial tensions. Physical Review Letters. 1994;72:2298–2301. doi: 10.1103/PhysRevLett.72.2298. [DOI] [PubMed] [Google Scholar]
- 20.Brillouin L. Diffusion de la lumière et des rayons X par un corps transparent homogène. Annales de Physique. 1922;9:88–122. doi: 10.1051/anphys/192209170088. [DOI] [Google Scholar]
- 21.Scarcelli G, Yun SH. Confocal Brillouin microscopy for three-dimensional mechanical imaging. Nature Photonics. 2007;2:39–43. doi: 10.1038/nphoton.2007.250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Moore AR, Burt AS. On the locus and nature of the forces causing gastrulation in the embryos of Dendraster excentricus. Journal of Experimental Zoology. 1939;82:159–171. doi: 10.1002/jez.1400820107. [DOI] [Google Scholar]
- 23.Rehfeldt F, Schmidt CF. Physical probing of cells. Journal of Physics D: Applied Physics. 2017;50 doi: 10.1088/1361-6463/aa8aa6. [DOI] [Google Scholar]
- 24.Basoli F, et al. Biomechanical Characterization at the Cell Scale: Present and Prospects. Front Physiol. 2018;9:1449. doi: 10.3389/fphys.2018.01449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang H, Liu K-K. Optical tweezers for single cells. Journal of the Royal Society Interface. 2008;5:671–690. doi: 10.1098/rsif.2008.0052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Favre-Bulle IA, Stilgoe AB, Scott EK, Rubinsztein-Dunlop H. Optical trapping in vivo: theory, practice, and applications. Nanophotonics. 2019;8:1023–1040. doi: 10.1515/nanoph-2019-0055. [DOI] [Google Scholar]
- 27.Ozcelik A, et al. Acoustic tweezers for the life sciences. Nature Methods. 2018;15:1021–1028. doi: 10.1038/s41592-018-0222-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Krieg M, et al. Atomic force microscopy-based mechanobiology. Nature Reviews Physics. 2018;1:41–57. doi: 10.1038/s42254-018-0001-7. [DOI] [Google Scholar]
- 29.Hochmuth RM. Micropipette aspiration of living cells. Journal of Biomechanics. 2000;33:15–22. doi: 10.1016/s0021-9290(99)00175-x. [DOI] [PubMed] [Google Scholar]
- 30.González-Bermúdez B, Guinea GV, Plaza GR. Advances in Micropipette Aspiration: Applications in Cell Biomechanics, Models, and Extended Studies. Biophysical Journal. 2019;116:587–594. doi: 10.1016/j.bpj.2019.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Campàs O. A toolbox to explore the mechanics of living embryonic tissues. Seminars in Cell & Developmental Biology. 2016;55:119–130. doi: 10.1016/j.semcdb.2016.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sugimura K, Lenne P-F, Graner F. Measuring forces and stresses in situ in living tissues. Development. 2016;143:186–196. doi: 10.1242/dev.119776. [DOI] [PubMed] [Google Scholar]
- 33.Roca-Cusachs P, Conte V, Trepat X. Quantifying forces in cell biology. Nature Cell Biology. 2017;19:742–751. doi: 10.1038/ncb3564. [DOI] [PubMed] [Google Scholar]
- 34.Prevedel R, Diz-Muñoz A, Ruocco G, Antonacci G. Brillouin microscopy: an emerging tool for mechanobiology. Nature Methods. 2019;16:969–977. doi: 10.1038/s41592-019-0543-3. [DOI] [PubMed] [Google Scholar]
- 35.Pérez-González C, et al. Active wetting of epithelial tissues. Nature Physics. 2019;15:79–88. doi: 10.1038/s41567-018-0279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bergert M, et al. Confocal reference free traction force microscopy. Nature Communications. 2016;7:12814. doi: 10.1038/ncomms12814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Latorre E, et al. Active superelasticity in three-dimensional epithelia of controlled shape. Nature. 2018;563:203–208. doi: 10.1038/s41586-018-0671-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ban E, et al. Mechanisms of Plastic Deformation in Collagen Networks Induced by Cellular Forces. Biophysical Journal. 2018;114:450–461. doi: 10.1016/j.bpj.2017.11.3739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Girardo S, et al. Standardized microgel beads as elastic cell mechanical probes. Journal of Materials Chemistry B. 2018;6:6245–6261. doi: 10.1039/c8tb01421c. [DOI] [PubMed] [Google Scholar]
- 40.Saw TB, et al. Topological defects in epithelia govern cell death and extrusion. Nature. 2017;544:212–216. doi: 10.1038/nature21718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang N, et al. Cell prestress. I. Stiffness and prestress are closely associated in adherent contractile cells. American Journal of Physiology-Cell Physiology. 2002;282:C606–C616. doi: 10.1152/ajpcell.00269.2001. [DOI] [PubMed] [Google Scholar]
- 42.Harris AK, Wild P, Stopak D. Silicone rubber substrata: a new wrinkle in the study of cell locomotion. Science. 1980;208:177–179. doi: 10.1126/science.6987736. [DOI] [PubMed] [Google Scholar]
- 43.Lee J, Leonard M, Oliver T, Ishihara A, Jacobson K. Traction forces generated by locomoting keratocytes. Journal of Cell Biology. 1994;127:1957–1964. doi: 10.1083/jcb.127.6.1957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Oliver T, Dembo M, Jacobson K. Traction forces in locomoting cells. Cell Motility and the Cytoskeleton. 1995;31:225–240. doi: 10.1002/cm.970310306. [DOI] [PubMed] [Google Scholar]
- 45.Dembo M, Oliver T, Ishihara A, Jacobson K. Imaging the traction stresses exerted by locomoting cells with the elastic substratum method. Biophysical Journal. 1996;70:2008–2022. doi: 10.1016/S0006-3495(96)79767-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dembo M, Wang Y-L. Stresses at the Cell-to-Substrate Interface during Locomotion of Fibroblasts. Biophysical Journal. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schwarz US, Soiné JRD. Traction force microscopy on soft elastic substrates: A guide to recent computational advances. Biochimica et Biophysica Acta. 2015;1853:3095–3104. doi: 10.1016/j.bbamcr.2015.05.028. [DOI] [PubMed] [Google Scholar]
- 48.Style RW, et al. Traction force microscopy in physics and biology. Soft Matter. 2014;10:4047–4055. doi: 10.1039/c4sm00264d. [DOI] [PubMed] [Google Scholar]
- 49.Polio SR, Rothenberg KE, Stamenović D, Smith ML. A micropatterning and image processing approach to simplify measurement of cellular traction forces. Acta Biomaterialia. 2012;8:82–88. doi: 10.1016/j.actbio.2011.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Butler JP, Tolić-Nørrelykke IM, Fabry B, Fredberg JJ. Traction fields, moments, and strain energy that cells exert on their surroundings. American Journal of Physiology-Cell Physiology. 2002;282:C595–C605. doi: 10.1152/ajpcell.00270.2001. [DOI] [PubMed] [Google Scholar]
- 51.del Álamo JC, et al. Spatio-temporal analysis of eukaryotic cell motility by improved force cytometry. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:13343–13348. doi: 10.1073/pnas.0705815104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Schwarz US, et al. Calculation of Forces at Focal Adhesions from Elastic Substrate Data: The Effect of Localized Force and the Need for Regularization. Biophysical Journal. 2002;83:1380–1394. doi: 10.1016/S0006-3495(02)73909-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Sabass B, Gardel ML, Waterman CM, Schwarz US. High resolution traction force microscopy based on experimental and computational advances. Biophysical Journal. 2008;94:207–220. doi: 10.1529/biophysj.107.113670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang Y, et al. Traction force microscopy with optimized regularization and automated Bayesian parameter selection for comparing cells. Scientific Reports. 2019;9:539. doi: 10.1038/s41598-018-36896-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yang Z, Lin J-S, Chen J, Wang JH-C. Determining substrate displacement and cell traction fields--a new approach. Journal of Theoretical Biology. 2006;242:607–616. doi: 10.1016/j.jtbi.2006.05.005. [DOI] [PubMed] [Google Scholar]
- 56.Griffin BP, Largaespada CJ, Rinaldi NA, Lemmon CA. A novel method for quantifying traction forces on hexagonal micropatterned protein features on deformable poly-dimethyl siloxane sheets. MethodsX. 2019;6:1343–1352. doi: 10.1016/j.mex.2019.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Burton K, Taylor DL. Traction forces of cytokinesis measured with optically modified elastic substrata. Nature. 1997;385:450–454. doi: 10.1038/385450a0. [DOI] [PubMed] [Google Scholar]
- 58.Elosegui-Artola A, et al. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nature Cell Biology. 2016;18:540–548. doi: 10.1038/ncb3336. [DOI] [PubMed] [Google Scholar]
- 59.Balaban NQ, et al. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nature Cell Biology. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 60.Trepat X, et al. Physical forces during collective cell migration. Nature Physics. 2009;5:426–430. doi: 10.1038/nphys1269. [DOI] [Google Scholar]
- 61.Serra-Picamal X, et al. Mechanical waves during tissue expansion. Nature Physics. 2012;8:628–634. doi: 10.1038/nphys2355. [DOI] [Google Scholar]
- 62.Sunyer R, et al. Collective cell durotaxis emerges from long-range intercellular force transmission. Science. 2016;353:1157–1161. doi: 10.1126/science.aaf7119. [DOI] [PubMed] [Google Scholar]
- 63.Kim JH, et al. Propulsion and navigation within the advancing monolayer sheet. Nature Materials. 2013;12:856–863. doi: 10.1038/nmat3689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Park J-A, et al. Unjamming and cell shape in the asthmatic airway epithelium. Nature Materials. 2015;14:1040–1048. doi: 10.1038/nmat4357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Uroz M, et al. Traction forces at the cytokinetic ring regulate cell division and polyploidy in the migrating zebrafish epicardium. Nature Materials. 2019;18:1015–1023. doi: 10.1038/s41563-019-0381-9. [DOI] [PubMed] [Google Scholar]
- 66.Jerison ER, Xu Y, Wilen LA, Dufresne ER. Deformation of an elastic substrate by a three-phase contact line. Physical Review Letters. 2011;106:186103. doi: 10.1103/PhysRevLett.106.186103. [DOI] [PubMed] [Google Scholar]
- 67.Xu Y, et al. Imaging in-plane and normal stresses near an interface crack using traction force microscopy. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:14964–14967. doi: 10.1073/pnas.1005537107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Casares L, et al. Hydraulic fracture during epithelial stretching. Nature Materials. 2015;14:343–351. doi: 10.1038/nmat4206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Oria R, et al. Force loading explains spatial sensing of ligands by cells. Nature. 2017;552:219–224. doi: 10.1038/nature24662. [DOI] [PubMed] [Google Scholar]
- 70.Nguyen DT, et al. Surface Pressure and Shear Stress Fields within a Frictional Contact on Rubber. The Journal of Adhesion. 2011;87:235–250. doi: 10.1080/00218464.2011.557340. [DOI] [Google Scholar]
- 71.Chateauminois A, Fretigny C. Local friction at a sliding interface between an elastomer and a rigid spherical probe. The European Physical Journal E Soft Matter. 2008;27:221–227. doi: 10.1140/epje/i2008-10376-5. [DOI] [PubMed] [Google Scholar]
- 72.del Álamo JC, et al. Three-dimensional quantification of cellular traction forces and mechanosensing of thin substrata by fourier traction force microscopy. PLoS One. 2013;8:e69850. doi: 10.1371/journal.pone.0069850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Álvarez-González B, et al. Cytoskeletal Mechanics Regulating Amoeboid Cell Locomotion. Applied Mechanics Reviews. 2014;66:050804. doi: 10.1115/1.4026249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Tan JL, et al. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Saez A, Ghibaudo M, Buguin A, Silberzan P, Ladoux B. Rigidity-driven growth and migration of epithelial cells on microstructured anisotropic substrates. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:8281–8286. doi: 10.1073/pnas.0702259104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Legant WR, et al. Microfabricated tissue gauges to measure and manipulate forces from 3D microtissues. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:10097–10102. doi: 10.1073/pnas.0900174106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Boudou T, et al. A microfabricated platform to measure and manipulate the mechanics of engineered cardiac microtissues. Tissue Engineering: Part A. 2012;18:910–919. doi: 10.1089/ten.tea.2011.0341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.du Roure O, et al. Force mapping in epithelial cell migration. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:2390–2395. doi: 10.1073/pnas.0408482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Rabodzey A, Alcaide P, Luscinskas FW, Ladoux B. Mechanical forces induced by the transendothelial migration of human neutrophils. Biophysical Journal. 2008;95:1428–1438. doi: 10.1529/biophysj.107.119156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Reffay M, et al. Interplay of RhoA and mechanical forces in collective cell migration driven by leader cells. Nature Cell Biology. 2014;16:217–223. doi: 10.1038/ncb2917. [DOI] [PubMed] [Google Scholar]
- 81.Saez A, et al. Traction forces exerted by epithelial cell sheets. Journal of Physics: Condensed Matter. 2010;22:194119. doi: 10.1088/0953-8984/22/19/194119. [DOI] [PubMed] [Google Scholar]
- 82.Yang B, et al. Stopping transformed cancer cell growth by rigidity sensing. Nature Materials. 2020;19:239–250. doi: 10.1038/s41563-019-0507-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Schoen I, Hu W, Klotzsch E, Vogel V. Probing cellular traction forces by micropillar arrays: contribution of substrate warping to pillar deflection. Nano Letters. 2010;10:1823–1830. doi: 10.1021/nl100533c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Liu Z, et al. Mechanical tugging force regulates the size of cell-cell junctions. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:9944–9949. doi: 10.1073/pnas.0914547107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Bastounis E, Álvarez-González B, del Álamo JC, Lasheras JC, Firtel RA. Cooperative cell motility during tandem locomotion of amoeboid cells. Molecular Biology of the Cell. 2016;27:1262–1271. doi: 10.1091/mbc.E15-12-0836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Maruthamuthu V, Sabass B, Schwarz US, Gardel ML. Cell-ECM traction force modulates endogenous tension at cell-cell contacts. Proceedings of the National Academy of Sciences of the United States of America. 2011;108:4708–4713. doi: 10.1073/pnas.1011123108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Ng MR, Besser A, Brugge JS, Danuser G. Mapping the dynamics of force transduction at cell-cell junctions of epithelial clusters. eLIFE. 2014;3:e03282. doi: 10.7554/eLife.03282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Tambe DT, et al. Monolayer stress microscopy: limitations, artifacts, and accuracy of recovered intercellular stresses. PLoS One. 2013;8:e55172. doi: 10.1371/journal.pone.0055172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Tambe DT, et al. Collective cell guidance by cooperative intercellular forces. Nature Materials. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Moussus M, et al. Intracellular stresses in patterned cell assemblies. Soft Matter. 2014;10:2414–2423. doi: 10.1039/c3sm52318g. [DOI] [PubMed] [Google Scholar]
- 91.Nier V, et al. Inference of Internal Stress in a Cell Monolayer. Biophysical Journal. 2016;110:1625–1635. doi: 10.1016/j.bpj.2016.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Serrano R, et al. Three-Dimensional Monolayer Stress Microscopy. Biophysical Journal. 2019;117:111–128. doi: 10.1016/j.bpj.2019.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Timoshenko S, Woinowsky-Krieger S. Theory of Plates and Shells. Second edn. 1959. [Google Scholar]
- 94.Vishwakarma M, et al. Mechanical interactions among followers determine the emergence of leaders in migrating epithelial cell collectives. Nature Communications. 2018;9:3469. doi: 10.1038/s41467-018-05927-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Harris AR, et al. Characterizing the mechanics of cultured cell monolayers. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:16449–16454. doi: 10.1073/pnas.1213301109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Khalilgharibi N, et al. Stress relaxation in epithelial monolayers is controlled by the actomyosin cortex. Nature Physics. 2019;15:839–847. doi: 10.1038/s41567-019-0516-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Harris AR, et al. Generating suspended cell monolayers for mechanobiological studies. Nature Protocols. 2013;8:2516–2530. doi: 10.1038/nprot.2013.151. [DOI] [PubMed] [Google Scholar]
- 98.Merzouki A, Malaspinas O, Chopard B. The mechanical properties of a cell-based numerical model of epithelium. Soft Matter. 2016;12:4745–4754. doi: 10.1039/c6sm00106h. [DOI] [PubMed] [Google Scholar]
- 99.Wyatt TPJ, et al. Emergence of homeostatic epithelial packing and stress dissipation through divisions oriented along the long cell axis. Proceedings of the National Academy of Sciences of the United States of America. 2015;112:5726–5731. doi: 10.1073/pnas.1420585112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Xu G-K, Liu Y, Zheng Z. Oriented cell division affects the global stress and cell packing geometry of a monolayer under stretch. Journal of Biomechanics. 2016;49:401–407. doi: 10.1016/j.jbiomech.2015.12.046. [DOI] [PubMed] [Google Scholar]
- 101.Wyatt TPJ, et al. Actomyosin controls planarity and folding of epithelia in response to compression. Nature Materials. 2020;19:109–117. doi: 10.1038/s41563-019-0461-x. [DOI] [PubMed] [Google Scholar]
- 102.Fouchard J, et al. Curling of epithelial monolayers reveals coupling between active bending and tissue tension. bioRxiv. 2019 doi: 10.1073/pnas.1917838117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Bloom RJ, George JP, Celedon A, Sun SX, Wirtz D. Mapping local matrix remodeling induced by a migrating tumor cell using three-dimensional multiple-particle tracking. Biophysical Journal. 2008;95:4077–4088. doi: 10.1529/biophysj.108.132738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Hur SS, Zhao Y, Li Y-S, Botvinick E, Chien S. Live Cells Exert 3-Dimensional Traction Forces on Their Substrata. Cell and Molecular Bioengineering. 2009;2:425–436. doi: 10.1007/s12195-009-0082-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Álvarez-González B, et al. Three-dimensional balance of cortical tension and axial contractility enables fast amoeboid migration. Biophysical Journal. 2015;108:821–832. doi: 10.1016/j.bpj.2014.11.3478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Maskarinec SA, Franck C, Tirrell DA, Ravichandran G. Quantifying cellular traction forces in three dimensions. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:22108–22113. doi: 10.1073/pnas.0904565106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Toyjanova J, et al. High resolution, large deformation 3D traction force microscopy. PLoS One. 2014;9:e90976. doi: 10.1371/journal.pone.0090976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Delanoë-Ayari H, Rieu JP, Sano M. 4D traction force microscopy reveals asymmetric cortical forces in migrating Dictyostelium cells. Physical Review Letters. 2010;105:248103. doi: 10.1103/PhysRevLett.105.248103. [DOI] [PubMed] [Google Scholar]
- 109.Gordon VD, et al. Measuring the mechanical stress induced by an expanding multicellular tumor system: a case study. Experimental Cell Research. 2003;289:58–66. doi: 10.1016/s0014-4827(03)00256-8. [DOI] [PubMed] [Google Scholar]
- 110.Zhou J, Pal S, Maiti S, Davidson LA. Force production and mechanical accommodation during convergent extension. Development. 2015;142:692–701. doi: 10.1242/dev.116533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Legant WR, et al. Measurement of mechanical tractions exerted by cells in three-dimensional matrices. Nature Methods. 2010;7:969–971. doi: 10.1038/nmeth.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Steinwachs J, et al. Three-dimensional force microscopy of cells in biopolymer networks. Nature Methods. 2016;13:171–176. doi: 10.1038/nmeth.3685. [DOI] [PubMed] [Google Scholar]
- 113.Mark C, et al. Collective forces of tumor spheroids in three-dimensional biopolymer networks. bioRxiv. 2019 doi: 10.7554/eLife.51912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Alessandri K, et al. Cellular capsules as a tool for multicellular spheroid production and for investigating the mechanics of tumor progression in vitro. Proceedings of the National Academy of Sciences of the United States of America. 2013;110:14843–14848. doi: 10.1073/pnas.1309482110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Leonavicius K, et al. Mechanics of mouse blastocyst hatching revealed by a hydrogel-based microdeformation assay. Proceedings of the National Academy of Sciences of the United States of America. 2018;115:10375–10380. doi: 10.1073/pnas.1719930115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Aung A, et al. 3D traction stresses activate protease-dependent invasion of cancer cells. Biophysical Journal. 2014;107:2528–2537. doi: 10.1016/j.bpj.2014.07.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Yeh Y-T, et al. Three-dimensional forces exerted by leukocytes and vascular endothelial cells dynamically facilitate diapedesis. Proceedings of the National Academy of Sciences of the United States of America. 2018;115:133–138. doi: 10.1073/pnas.1717489115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Álvarez-González B, et al. Two-Layer Elastographic 3-D Traction Force Microscopy. Scientific Reports. 2017;7:39315. doi: 10.1038/srep39315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Leighton J, Brada Z, Estes LW, Justh G. Secretory activity and oncogenicity of a cell line (MDCK) derived from canine kidney. Science. 1969;163:472–473. doi: 10.1126/science.163.3866.472. [DOI] [PubMed] [Google Scholar]
- 120.Rabito CA, Tchao R, Valentich J, Leighton J. Effect of cell-substratum interaction on hemicyst formation by MDCK cells. In Vitro. 1980;16:461–468. doi: 10.1007/BF02626458. [DOI] [PubMed] [Google Scholar]
- 121.Tanner C, Frambach DA, Misfeldt DS. Transepithelial transport in cell culture. A theoretical and experimental analysis of the biophysical properties of domes. Biophysical Journal. 1983;43:183–190. doi: 10.1016/S0006-3495(83)84339-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Laplace PS. Sur L’Action Capillaire. Vol. 4. Chez J. B. M. Duprat; 1805. Ch. Supplément au dixième livre du Traité de Mécanique Céleste. [Google Scholar]
- 123.Lamb H. Statics: Including Hydrostatics and the Elements of the Theory of Elasticity. 3rd edn. Cambridge University Press; 1960. [Google Scholar]
- 124.Hildebrand S, et al. The E-cadherin/AmotL2 complex organizes actin filaments required for epithelial hexagonal packing and blastocyst hatching. Scientific Reports. 2017;7:9540. doi: 10.1038/s41598-017-10102-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Deglincerti A, et al. Self-organization of the in vitro attached human embryo. Nature. 2016;533:251–254. doi: 10.1038/nature17948. [DOI] [PubMed] [Google Scholar]
- 126.Navis A, Bagnat M. Developing pressures: fluid forces driving morphogenesis. Current Opinion in Genetics & Development. 2015;32:24–30. doi: 10.1016/j.gde.2015.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Hales S. Statical Essays: containing haemastaticks; or, an account of some hydraulick and hydrostatical experiments made on the blood and blood-vessels of animals. W. Innys and R. Manby; 1733. [DOI] [PubMed] [Google Scholar]
- 128.Wiederhielm CA, Woodbury JW, Kirk S, Rushmer RF. Pulsatile Pressures in the Microcirculation of Frog’s Mesentery. American Journal of Physiology. 1964;207:173–176. doi: 10.1152/ajplegacy.1964.207.1.173. [DOI] [PubMed] [Google Scholar]
- 129.Petrie RJ, Koo H. Direct measurement of intracellular pressure. Current Protocols in Cell Biology. 2014;63:121911–121919. doi: 10.1002/0471143030.cb1209s63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Falchuk KH, Berliner RW. Hydrostatic pressures in peritubular capillaries and tubules in the rat kidney. American Journal of Physiology. 1971;220:1422–1426. doi: 10.1152/ajplegacy.1971.220.5.1422. [DOI] [PubMed] [Google Scholar]
- 131.Kelly SM, Macklem PT. Direct measurement of intracellular pressure. American Journal of Physiology. 1991;260:C652–C657. doi: 10.1152/ajpcell.1991.260.3.C652. [DOI] [PubMed] [Google Scholar]
- 132.Petrie RJ, Koo H, Yamada KM. Generation of compartmentalized pressure by a nuclear piston governs cell motility in a 3D matrix. Science. 2014;345:1062–1065. doi: 10.1126/science.1256965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Myers RR, Rydevik BL, Heckman HM, Powell HC. Proximodistal gradient in endoneurial fluid pressure. Experimental Neurology. 1988;102:368–370. doi: 10.1016/0014-4886(88)90233-6. [DOI] [PubMed] [Google Scholar]
- 134.Wit HP, Thalen EO, Albers FWJ. Dynamics of inner ear pressure release, measured with a double-barreled micropipette in the guinea pig. Hearing Research. 1999;132:131–139. doi: 10.1016/s0378-5955(99)00048-9. [DOI] [PubMed] [Google Scholar]
- 135.Avila MY, Carré DA, Stone RA, Civan MM. Reliable measurement of mouse intraocular pressure by a servo-null micropipette system. Investigative Ophthalmology & Visual Science. 2001;42:1841–1846. [PubMed] [Google Scholar]
- 136.Hu N, Yost HJ, Clark EB. Cardiac morphology and blood pressure in the adult zebrafish. The Anatomical Record. 2001;264:1–12. doi: 10.1002/ar.1111. [DOI] [PubMed] [Google Scholar]
- 137.Hu N, Sedmera D, Yost HJ, Clark EB. Structure and function of the developing zebrafish heart. The Anatomical Record. 2000;260:148–157. doi: 10.1002/1097-0185(20001001)260:2<148::AID-AR50>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 138.Stekelenburg-de Vos S, et al. Systolic and diastolic ventricular function assessed by pressure-volume loops in the stage 21 venous clipped chick embryo. Pediatric Research. 2005;57:16–21. doi: 10.1203/01.PDR.0000147734.53277.75. [DOI] [PubMed] [Google Scholar]
- 139.Desmond ME, Levitan ML, Haas AR. Internal luminal pressure during early chick embryonic brain growth: descriptive and empirical observations. The Anatomical Record Part A: Discoveries in Molecular, Cellular, and Evolutionary Biology. 2005;285:737–747. doi: 10.1002/ar.a.20211. [DOI] [PubMed] [Google Scholar]
- 140.Chan CJ, et al. Hydraulic control of mammalian embryo size and cell fate. Nature. 2019;571:112–116. doi: 10.1038/s41586-019-1309-x. [DOI] [PubMed] [Google Scholar]
- 141.Mosaliganti KR, et al. Size control of the inner ear via hydraulic feedback. eLIFE. 2019;8 doi: 10.7554/eLife.39596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Lorenz JN. Micropuncture of the kidney: a primer on techniques. Comprehensive Physiology. 2012;2:621–637. doi: 10.1002/cphy.c110035. [DOI] [PubMed] [Google Scholar]
- 143.Campàs O, et al. Quantifying cell-generated mechanical forces within living embryonic tissues. Nature Methods. 2014;11:183–189. doi: 10.1038/nmeth.2761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Vorselen D, et al. Microparticle traction force microscopy reveals subcellular force exertion patterns in immune cell-target interactions. Nature Communications. 2020;11:20. doi: 10.1038/s41467-019-13804-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Serwane F, et al. In vivo quantification of spatially varying mechanical properties in developing tissues. Nature Methods. 2017;14:181–186. doi: 10.1038/nmeth.4101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Ingremeau F, et al. Optical sensing of mechanical pressure based on diffusion measurement in polyacrylamide cell-like barometers. Soft Matter. 2017;13:4210–4213. doi: 10.1039/c6sm02887j. [DOI] [PubMed] [Google Scholar]
- 147.Dolega ME, et al. Cell-like pressure sensors reveal increase of mechanical stress towards the core of multicellular spheroids under compression. Nature Communications. 2017;8:14056. doi: 10.1038/ncomms14056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Mohagheghian E, et al. Quantifying compressive forces between living cell layers and within tissues using elastic round microgels. Nature Communications. 2018;9:1878. doi: 10.1038/s41467-018-04245-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Bar-Kochba E, Toyjanova J, Andrews E, Kim KS, Franck C. A Fast Iterative Digital Volume Correlation Algorithm for Large Deformations. Experimental Mechanics. 2014;55:261–274. doi: 10.1007/s11340-014-9874-2. [DOI] [Google Scholar]
- 150.Shen J, Sun L-D, Yan C-H. Luminescent rare earth nanomaterials for bioprobe applications. Dalton Transactions. 2008:5687–5697. doi: 10.1039/b805306e. [DOI] [PubMed] [Google Scholar]
- 151.Mehlenbacher RD, Kolbl R, Lay A, Dionne JA. Nanomaterials for in vivo imaging of mechanical forces and electrical fields. Nature Reviews Materials. 2017;3:17080. doi: 10.1038/natrevmats.2017.80. [DOI] [Google Scholar]
- 152.Wisser MD, et al. Strain-induced modification of optical selection rules in lanthanide-based upconverting nanoparticles. Nano Letters. 2015;15:1891–1897. doi: 10.1021/nl504738k. [DOI] [PubMed] [Google Scholar]
- 153.Lay A, et al. Upconverting Nanoparticles as Optical Sensors of Nano-to Micro-Newton Forces. Nano Letters. 2017;17:4172–4177. doi: 10.1021/acs.nanolett.7b00963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Humar M, Yun SH. Intracellular microlasers. Nature Photonics. 2015;9:572–576. doi: 10.1038/nphoton.2015.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Schubert M, et al. Monitoring contractility in single cardiomyocytes and whole hearts with biointegrated microlasers. bioRxiv. 2019 doi: 10.1101/605444. [DOI] [Google Scholar]
- 156.Lucio AA, et al. Spatiotemporal variation of endogenous cell-generated stresses within 3D multicellular spheroids. Scientific Reports. 2017;7:12022. doi: 10.1038/s41598-017-12363-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Traeber N, et al. Polyacrylamide Bead Sensors for in vivo Quantification of Cell-Scale Stress in Zebrafish Development. Scientific Reports. 2019;9:17031. doi: 10.1038/s41598-019-53425-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Gayrard C, Borghi N. FRET-based Molecular Tension Microscopy. Methods. 2016;94:33–42. doi: 10.1016/j.ymeth.2015.07.010. [DOI] [PubMed] [Google Scholar]
- 159.Yasunaga A, Murad Y, Li ITS. Quantifying molecular tension-classifications, interpretations and limitations of force sensors. Physical Biology. 2019;17:011001. doi: 10.1088/1478-3975/ab38ff. [DOI] [PubMed] [Google Scholar]
- 160.Meng F, Suchyna TM, Sachs F. A fluorescence energy transfer-based mechanical stress sensor for specific proteins in situ. The FEBS journal. 2008;275:3072–3087. doi: 10.1111/j.1742-4658.2008.06461.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Grashoff C, et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Förster T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Annalen der Physik. 1948;437:55–75. doi: 10.1002/andp.19484370105. [DOI] [Google Scholar]
- 163.Conway DE, et al. Fluid shear stress on endothelial cells modulates mechanical tension across VE-cadherin and PECAM-1. Current Biology. 2013;23:1024–1030. doi: 10.1016/j.cub.2013.04.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Cai D, et al. Mechanical feedback through E-cadherin promotes direction sensing during collective cell migration. Cell. 2014;157:1146–1159. doi: 10.1016/j.cell.2014.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Price AJ, et al. Mechanical loading of desmosomes depends on the magnitude and orientation of external stress. Nature Communications. 2018;9:5284. doi: 10.1038/s41467-018-07523-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Borghi N, et al. E-cadherin is under constitutive actomyosin-generated tension that is increased at cell-cell contacts upon externally applied stretch. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:12568–12573. doi: 10.1073/pnas.1204390109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Narayanan V, et al. Osmotic Gradients in Epithelial Acini Increase Mechanical Tension across E-cadherin, Drive Morphogenesis, and Maintain Homeostasis. Current Biology. 2020;30:624–633. doi: 10.1016/j.cub.2019.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Eder D, Basler K, Aegerter CM. Challenging FRET-based E-Cadherin force measurements in Drosophila. Scientific Reports. 2017;7:13692. doi: 10.1038/s41598-017-14136-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Stabley DR, Jurchenko C, Marshall SS, Salaita KS. Visualizing mechanical tension across membrane receptors with a fluorescent sensor. Nature Methods. 2011;9:64–67. doi: 10.1038/nmeth.1747. [DOI] [PubMed] [Google Scholar]
- 170.Colombelli J, Solon J. Force communication in multicellular tissues addressed by laser nanosurgery. Cell and Tissue Research. 2013;352:133–147. doi: 10.1007/s00441-012-1445-1. [DOI] [PubMed] [Google Scholar]
- 171.Zulueta-Coarasa T, Fernandez-Gonzalez R. In: Integrative Mechanobiology: Micro- and Nano-Techniques in Cell Mechanobiology. Kim D, Sun Y, Simmons C, editors. Vol. 8. Cambridge University Press; 2015. pp. 128–147. [Google Scholar]
- 172.Bonnet I, et al. Mechanical state, material properties and continuous description of an epithelial tissue. Journal of the Royal Society Interface. 2012;9:2614–2623. doi: 10.1098/rsif.2012.0263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Etournay R, et al. Interplay of cell dynamics and epithelial tension during morphogenesis of the Drosophila pupal wing. eLIFE. 2015;4:e07090. doi: 10.7554/eLife.07090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Hutson MS, et al. Forces for morphogenesis investigated with laser microsurgery and quantitative modeling. Science. 2003;300:145–149. doi: 10.1126/science.1079552. [DOI] [PubMed] [Google Scholar]
- 175.Ma X, Lynch HE, Scully PC, Hutson MS. Probing embryonic tissue mechanics with laser hole drilling. Physical Biology. 2009;6:036004. doi: 10.1088/1478-3975/6/3/036004. [DOI] [PubMed] [Google Scholar]
- 176.Hutson MS, et al. Combining laser microsurgery and finite element modeling to assess cell-level epithelial mechanics. Biophysical Journal. 2009;97:3075–3085. doi: 10.1016/j.bpj.2009.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Kiehart DP, Galbraith CG, Edwards KA, Rickoll WL, Montague RA. Multiple forces contribute to cell sheet morphogenesis for dorsal closure in Drosophila. Journal of Cell Biology. 2000;149:471–490. doi: 10.1083/jcb.149.2.471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Solon J, Kaya-Çopur A, Colombelli J, Brunner D. Pulsed forces timed by a ratchet-like mechanism drive directed tissue movement during dorsal closure. Cell. 2009;137:1331–1342. doi: 10.1016/j.cell.2009.03.050. [DOI] [PubMed] [Google Scholar]
- 179.Hunter GL, Crawford JM, Genkins JZ, Kiehart DP. Ion channels contribute to the regulation of cell sheet forces during Drosophila dorsal closure. Development. 2014;141:325–334. doi: 10.1242/dev.097097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Fernandez-Gonzalez R, Zallen JA. Wounded cells drive rapid epidermal repair in the early Drosophila embryo. Molecular Biology of the Cell. 2013;24:3227–3237. doi: 10.1091/mbc.E13-05-0228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Campinho P, et al. Tension-oriented cell divisions limit anisotropic tissue tension in epithelial spreading during zebrafish epiboly. Nature Cell Biology. 2013;15:1405–1414. doi: 10.1038/ncb2869. [DOI] [PubMed] [Google Scholar]
- 182.Maître J-L, et al. Asymmetric division of contractile domains couples cell positioning and fate specification. Nature. 2016;536:344–348. doi: 10.1038/nature18958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Maître J-L, Niwayama R, Turlier H, Nédélec F, Hiiragi T. Pulsatile cell-autonomous contractility drives compaction in the mouse embryo. Nature Cell Biology. 2015;17:849–855. doi: 10.1038/ncb3185. [DOI] [PubMed] [Google Scholar]
- 184.Yang X, et al. Correlating cell shape and cellular stress in motile confluent tissues. Proceedings of the National Academy of Sciences of the United States of America. 2017;114:12663–12668. doi: 10.1073/pnas.1705921114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Alt S, Ganguly P, Salbreux G. Vertex models: from cell mechanics to tissue morphogenesis. Philosophical Transactions of the Royal Society B: Biological Sciences. 2017;372:20150520. doi: 10.1098/rstb.2015.0520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Cranston PG, Veldhuis JH, Narasimhan S, Brodland GW. Cinemechanometry (CMM): A method to determine the forces that drive morphogenetic movements from time-lapse images. Annals of Biomedical Engineering. 2010;38:2937–2947. doi: 10.1007/s10439-010-9998-1. [DOI] [PubMed] [Google Scholar]
- 187.Ishihara S, et al. Comparative study of non-invasive force and stress inference methods in tissue. The European Physical Journal E Soft Matter. 2013;36:9859. doi: 10.1140/epje/i2013-13045-8. [DOI] [PubMed] [Google Scholar]
- 188.Ishihara S, Sugimura K. Bayesian inference of force dynamics during morphogenesis. Journal of Theoretical Biology. 2012;313:201–211. doi: 10.1016/j.jtbi.2012.08.017. [DOI] [PubMed] [Google Scholar]
- 189.Stein MB, Gordon R. Epithelia as bubble rafts: A new method for analysis of cell shape and intercellular adhesion in embryonic and other epithelia. Journal of Theoretical Biology. 1982;97:625–639. doi: 10.1016/0022-5193(82)90363-0. [DOI] [PubMed] [Google Scholar]
- 190.Hayashi T, Carthew RW. Surface mechanics mediate pattern formation in the developing retina. Nature. 2004;431:647–652. doi: 10.1038/nature02952. [DOI] [PubMed] [Google Scholar]
- 191.Chiou KK, Hufnagel L, Shraiman BI. Mechanical stress inference for two dimensional cell arrays. PLoS Computational Biology. 2012;8:e1002512. doi: 10.1371/journal.pcbi.1002512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Brodland GW, et al. CellFIT: a cellular force-inference toolkit using curvilinear cell boundaries. PLoS One. 2014;9:e99116. doi: 10.1371/journal.pone.0099116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Kong W, et al. Experimental validation of force inference in epithelia from cell to tissue scale. Scientific Reports. 2019;9:14647. doi: 10.1038/s41598-019-50690-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Veldhuis JH, Mashburn D, Hutson MS, Brodland GW. Practical aspects of the cellular force inference toolkit (CellFIT) Methods in Cell Biology. 2015;125:331–351. doi: 10.1016/bs.mcb.2014.10.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Veldhuis JH, et al. Inferring cellular forces from image stacks. Philosophical Transactions of the Royal Society B: Biological Sciences. 2017;372:20160261. doi: 10.1098/rstb.2016.0261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Chen HH, Brodland GW. Cell-level finite element studies of viscous cells in planar aggregates. Transactions-American Society of Mechanical Engineers Journal of Biomechanical Engineering. 2000;122:394–401. doi: 10.1115/1.1286563. [DOI] [PubMed] [Google Scholar]
- 197.Brodland GW, Viens D, Veldhuis JH. A new cell-based FE model for the mechanics of embryonic epithelia. Computer Methods in Biomechanics and Biomedical Engineering. 2007;10:121–128. doi: 10.1080/10255840601124704. [DOI] [PubMed] [Google Scholar]
- 198.Brodland GW, et al. Video force microscopy reveals the mechanics of ventral furrow invagination in Drosophila. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:22111–22116. doi: 10.1073/pnas.1006591107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Sugimura K, Ishihara S. The mechanical anisotropy in a tissue promotes ordering in hexagonal cell packing. Development. 2013;140:4091–4101. doi: 10.1242/dev.094060. [DOI] [PubMed] [Google Scholar]
- 200.Xu M, Wu Y, Shroff H, Wu M, Mani M. A scheme for 3-dimensional morphological reconstruction and force inference in the early C. elegans embryo. PLoS One. 2018;13:e0199151. doi: 10.1371/journal.pone.0199151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Nestor-Bergmann A, et al. Decoupling the Roles of Cell Shape and Mechanical Stress in Orienting and Cueing Epithelial Mitosis. Cell Reports. 2019;26:2088–2100.:e2084. doi: 10.1016/j.celrep.2019.01.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Krens SFG, et al. Interstitial fluid osmolarity modulates the action of differential tissue surface tension in progenitor cell segregation during gastrulation. Development. 2017;144:1798–1806. doi: 10.1242/dev.144964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Barresi MJF, Gilbert SF. Developmental Biology. 12th edn. Oxford University Press; 2019. [Google Scholar]
- 204.Farhadifar R, Röper J-C, Aigouy B, Eaton S, Jülicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Current Biology. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- 205.Mongera A, et al. A fluid-to-solid jamming transition underlies vertebrate body axis elongation. Nature. 2018;561:401–405. doi: 10.1038/s41586-018-0479-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 206.Notbohm J, Kim JH, Asthagiri AR, Ravichandran G. Three-dimensional analysis of the effect of epidermal growth factor on cell-cell adhesion in epithelial cell clusters. Biophysical Journal. 2012;102:1323–1330. doi: 10.1016/j.bpj.2012.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]