Skip to main content
NCBI home page
Resuscitation Plus logoLink to Resuscitation Plus
. 2025 Feb 18;22:100910. doi: 10.1016/j.resplu.2025.100910

Assessment of heart and lung morphology in a single case during cardiopulmonary resuscitation: A virtual simulation

Jafar Moradicheghamahi a, Gerard Fortuny a, Josep M López a, Dolors Puigjaner a, Joan Herrero b, Youcef Azeli c,d,e,⁎
PMCID: PMC11914767  PMID: 40104099

Abstract

Background

Basic science research in cardiopulmonary resuscitation (CPR) is limited by challenges in obtaining haemodynamic data from models that simulate physiological processes. In this study, we assessed the morphology of the heart and lungs and calculated the ejection fractions of cardiac chambers during CPR using a virtual simulation.

Methods

A finite element model of a complete thorax, including internal organs, thoracic rib cage, spine, musculature, and a generic material representing soft tissues, was constructed from magentic resonance images of a man. Twelve chest compression simulations were performed with forces ranging from F = 50 to 600 N. During compression, lung and heart volumes were assessed, and the ejection fraction of each cardiac chamber was calculated.

Results

In our numerical simulations a compression depth of 5.06 cm was reached with a force of 450 N. At this depth, the right and left ventricular ejection fractions were 34.0% and 14.4%, respectively, while the right and left atrial ejection fractions were 22.1% and 24.2%, respectively. The cross-sectional area of the outflow tract decreased by 27.5% and 15.6% in the right and left ventricles, respectively. Lung volumes decreased by 193 cm3 and 169 cm3 in the right and left lungs, respectively, representing 11.2% of the total lung volume.

Conclusion

The right ventricle exhibited the highest ejection fraction among the cardiac chambers, and the left atrium showed a higher ejection fraction than the left ventricle during CPR.

Keywords: Cardiopulmonary resuscitation, Haemodynamics, Finite element model

Introduction

Sudden cardiac death is a leading cause of mortality in industrialised countries, and despite substantial research investment, survival rates for sudden cardiac death barely reach 10%.1, 2 Basic science research in cardiopulmonary resuscitation (CPR) is constrained by the difficulty of obtaining data from models simulating haemodynamics. Cardiac output during CPR is driven by two main mechanisms. The cardiac pump theory posits that direct sternal compression impacts the left ventricle, generating antegrade aortic flow and closing the mitral valve. By contrast, the thoracic pump theory suggests that direct ventricular compression is unnecessary; rather, flow is produced through the transmission of intrathoracic pressure over the left chambers, which act as a single conduit.3 Cardiac output relies on venous return to fill the heart chambers before each chest compression, making it essential to preserve sternal recoil and thoracic biomechanics.4

Since the 1960s, evidence in the field of haemodynamics in resuscitation science has primarily come from animal models.5 However, these results are not easily extrapolated to humans because of anatomical and biomechanical differences, particularly with deep and prolonged chest compression.6 The use of transoesophageal ultrasound has provided valuable haemodynamic data, enabling the determination of transvalvular flow behaviour, detection of left ventricular outflow tract obstruction, assessment of cardiac chamber compressibility, and evaluation of left ventricular systolic function through calculation of the ejection fraction. Nonetheless, transoesophageal ultrasound does not provide a comprehensive view and is technically challenging to perform.7, 8, 9, 10, 11

Mathematical models have been employed to study CPR haemodynamics, although they are complex and visually non-intuitive.12 Recently, chest biomechanics during CPR were investigated in a study of 216 virtually reproduced ribcages using a realistic finite element model (FEM), which demonstrated that wider chests experience lower stress levels on the ribs and carry a lower risk of fractures.13 However, data on changes in the global morphology of intrathoracic organs during CPR remain limited.14 In the present study, we used a virtual simulation based on FEM to assess the morphology of intrathoracic organs and calculate the ejection fraction of each cardiac chamber during a series of progressively deeper chest compressions.

Methods

Geometry model and mesh generation

Geometric data were derived from high-resolution whole-body magnetic resonance images (Signa Hispeed LX; GE Medical System, Milwaukee, WI, USA) obtained from the 3D Body Parts database for anatomy.15, 16 Slices were taken every 2 mm from an adult male Japanese volunteer of 173 cm in height, 65.0 kg in weight, and with a body mass index of 21.6 and a skin surface area of 1.69 m2. For imaging, the volunteer lay on his back with hands and arms positioned at his sides. Using specialised software, three-dimensional triangular surface meshes segmented into 51 different tissues and organs were generated.

Each of these individual surface meshes, defining the boundary of each organ, was imported into Gmsh software to create three-dimensional tetrahedral meshes.17 A refined and physically consistent model was then produced by eliminating any undesirable intersections between elements. This study protocol was approved by the Research Ethics Committee of the Pere Virgili Research Institute (Ref 168/2018).

Fig. 1 in the Supplementary Materials presents the overall view of the geometry model used. This model is shaped as a torso without a head or hands, incorporating the most relevant thoracic organs. Fig. 1Sb displays the subset of the geometry model representing the rib cage, which was developed in our previous study.13 In the current study, additional organs were incorporated into the geometry model, including the skin surface, lungs, heart, major blood vessels surrounding the heart, and a generic material representing the other soft tissues within the chest.

The heart muscle in this model weighs 291 g, assuming a myocardium density of ρm = 1.055 g/cm3.18 The heart model excludes valves and other internal heart structures, assuming instead that the entire volume of the four heart chambers is filled with blood. The ensemble of the volume meshes representing the internal organs is encased by an additional tetrahedral mesh for the remaining soft tissues. This geometry model was constructed as a continuum, with each segment meshed and characterised according to its specific tissue type. The computational mesh comprises a total of 6,112,533 linear tetrahedrons.

Material constitutive models

Material constitutive models are often characterized by three key parameters: Young’s modulus, Poisson’s ratio, and tensile strength. Young’s modulus (E) quantifies a material’s stiffness by measuring its resistance to deformation under tensile or compressive stress. Poisson’s ratio (η) describes how a material deforms in directions perpendicular to an applied load when stretched or compressed; it typically ranges from 0 to 0.5, with higher values indicating lower compressibility. Tensile strength (σY) is the maximum stress a material can withstand under tension before breaking.

E, η, and σY, along with the mathematical models used for different tissues, are presented in Table 1S of the supplementary material. Further details on these tissues are available in a previous study.13

In this study, the values of E and σY for bone tissue were adjusted to bring the compression force used in the simulation for a CPR depth close to the 5-cm target into better alignment with prior real-world data.19, 20 Is important to note that the E values for bone tissue used in previous work were overestimated because the model did not account for internal organs or soft tissues, which contribute to overall chest resistance to compression.21

Generally, adipose tissue and internal organs, including the lungs, liver, pancreas, and thymus, have a E values within the 1 kPa ≤ E ≤ 10 kPa range.22, 23, 24 For the generic soft tissue material, we assumed E = 5.0 kPa and a Poisson’s ratio of η = 0.4995. This value, nearing the incompressibility limit of η = 0.5, allowed the soft tissue to nearly preserve its volume in the simulations, ensuring that the continuity condition was consistently applied across all material boundaries.

The E values reported in the literature for adult human heart tissue vary widely, ranging from 5 kPa to 50 kPa.25 In this model, it is assumed that the heart is in the diastolic phase during cardiac arrest, thus setting E at 30 kPa for myocardial tissue based on previous findings.26 Table 1S also shows that blood in this study was modelled as a soft material with E = 3 kPa and Poisson’s ratio η = 0.35. However, sections of the major blood vessels in the heart model (inferior and superior vena cava, aorta, and pulmonary arteries) were modelled with a higher Poisson’s ratio, η = 0.499, to reflect the increased rigidity of the vessel walls.

Numerical simulation

In total, 12 simulations were conducted using the open-source software Code Aster.27 Compression forces ranged from F = 50 to 600 N, with increments of 50 N. The compression force was applied to a rounded 10-cm2 surface area above the skin, located on the lower half of the sternum, as shown in blue in Fig. 1Sa. Chest compression progressed linearly, reaching maximum depth at 0.6 s. The compression depth was measured on the skin surface patch where the force was applied. The patient was assumed to be in a supine position, with no-displacement boundary conditions enforced on various skin surface patches along the back.

Volume and area assessment

In each simulation, the FEM software output the computed displacement of each computational cell in response to the applied compression force. These displacements were then used to calculate the area and volume changes in various organs. For area assessments, slices were generated by defining cutting planes through specific organs. An advantage of this approach is that area or volume changes can be assessed even as the organ moves from its initial relative position.

Measurements for the cross-sectional area (CSA) of the ventricular outflow tract were taken at the aortic and pulmonary valve level. To assess cardiac chamber volumes, the entire surface of the endocardium was used, with the positions of the mitral and tricuspid annuli defining the boundary between the atria and ventricles. The reference uncompressed volumes of the intrathoracic organs are presented in Table 1.

Table 1.

Volumes (in cm3) of the whole heart, cardiac chambers, and lungs in the present model.

Whole Heart Left Ventricle Left Atrium Right Ventricle Right Atrium Myocardium Left Lung Right Lung
594 90 45 105 78 276 1465 1763
Open in a new tab

Ejection fraction calculation

The left ventricular ejection fraction (LVEF) and right ventricular ejection fraction (RVEF) were calculated from the end-diastolic volume in the uncompressed geometry and the end-systolic volume at maximum compression, as follows:

  • LVEF = (EDVLV − ESVLV)/EDVLV.

  • RVEF = (EDVRV − ESVRV)/EDVRV.

where EDVLV and ESVLV are the end-diastolic and end-systolic volumes of the left ventricle, respectively, and EDVRV and ESVRV are the end-diastolic and end-systolic volumes of the right ventricle, respectively.

The left atrial ejection fraction (LAEF) and right atrial ejection fraction (RAEF) were calculated as in previous studies, using the maximum volume in the uncompressed geometry and minimum volume at the point of maximum compression of the right atrium and left atrium, respectively28:

  • LAEF = (VmaxLA − VminLA)/VmaxLA.

  • RAEF = (VmaxRA − VminRA)/VmaxRA.

where VmaxLA and VminLA are the maximum and minimum volumes of the left atrium, respectively, and VmaxRA and VminRA are the maximum and minimum volumes of the right atrium, respectively.

Results

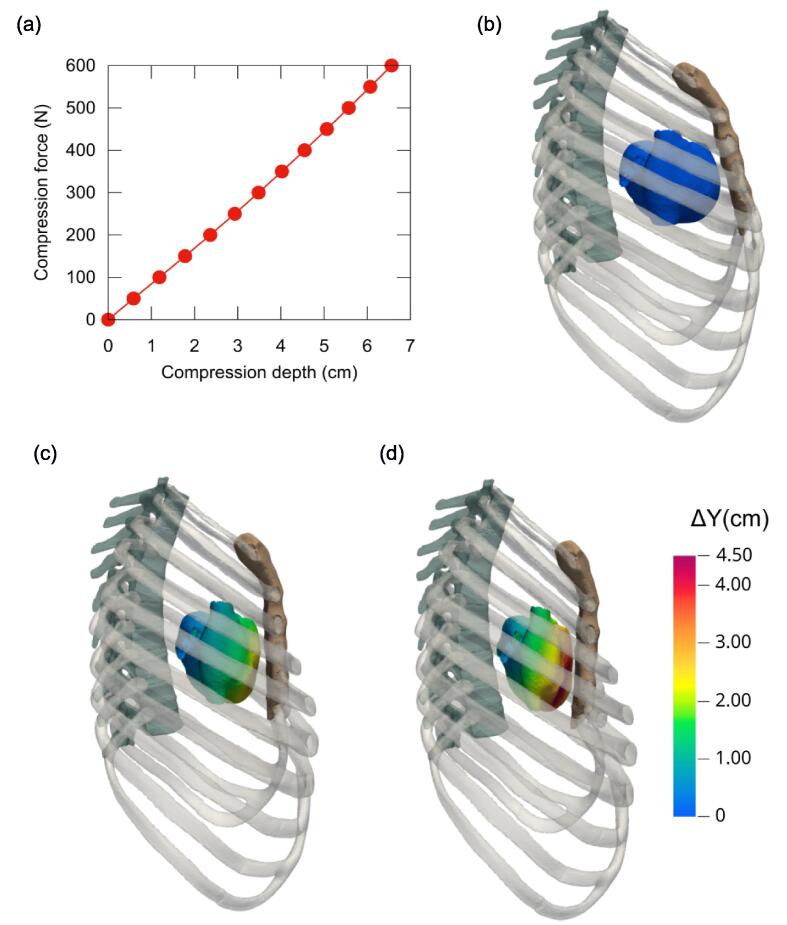
In this FEM simulation, a compression depth of 5.06 cm was achieved with a compression force of 450 N. Fig. 1a displays the computed chest compression depth as a function of the applied compression force.

Fig. 1.

Fig. 1

Open in a new tab

(a) Compression depth achieved as a function of the applied force. (b–d) Side view from the right of the rib cage and external heart structure, with (b) the uncompressed reference state and the computed geometries for compression forces of (c) F = 300 N and (d) F = 500 N. In (c, d), the heart surface is coloured to indicate displacement levels (ΔY) along the normal direction (aligned with the y-axis in the model setup).

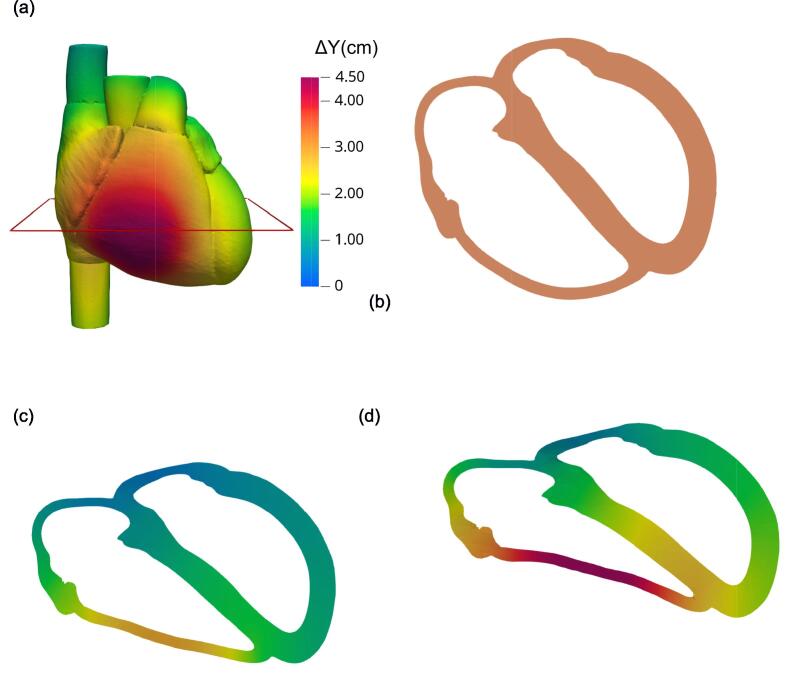
Fig. 1b–d shows the progressive compression of the heart due to rib cage compression. It illustrates how the sternum, fixed at its upper end, moves like a hinge, as previously described.29 The greatest displacement occurred at the distal end, specifically the xiphoid process. Fig. 2a, an anterior view of the heart, shows that the free wall of the right ventricle experienced the most backward displacement. The greatest compression of the heart occurred at an axial level between the fifth and sixth sternocostal joints. Fig. 2b–d shows an axial slice of the four cardiac chambers, with Fig. 2d showing the entire heart being displaced backward. At a chest compression depth of 5.6 cm (F = 500 N), the backward displacement of the right ventricle’s free wall reached 4.5 cm, while the septal wall and the left ventricle’s lateral wall, positioned closer to the spinal column, exhibited displacements of nearly 2.5 cm and 1.5 cm, respectively.

Fig. 2.

Fig. 2

Open in a new tab

Simulated compression of the heart. (a) Front view of the external heart surface, coloured to indicate levels of normal backward displacement (ΔY). (b–d) Deformation of the myocardium and compression of the heart chambers plotted on the axial slice marked in (a), with compression levels of (b) F = 0 (reference, uncompressed state), (c) F = 300 N, and (d) F = 500 N. In (c, d), colours indicate normal backward displacement levels as shown in the colour scale in (a).

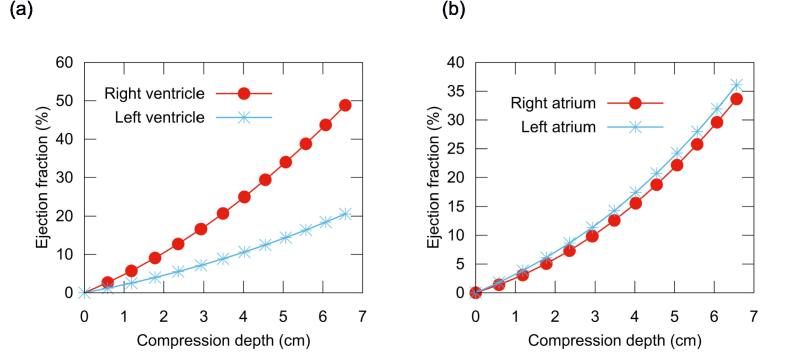
Fig. 3 presents the ejection fraction for each heart chamber as a function of chest compression depth. At a depth of 5.06 cm, the RVEF and LVEF were 34.0% and 14.4%, respectively, while the RAEF and LAEF were 22.1% and 24.2%.

Fig. 3.

Fig. 3

Open in a new tab

Computed ejection fraction of the heart chambers during chest compression. (a) Left and right ventricles. (b) Left and right atria.

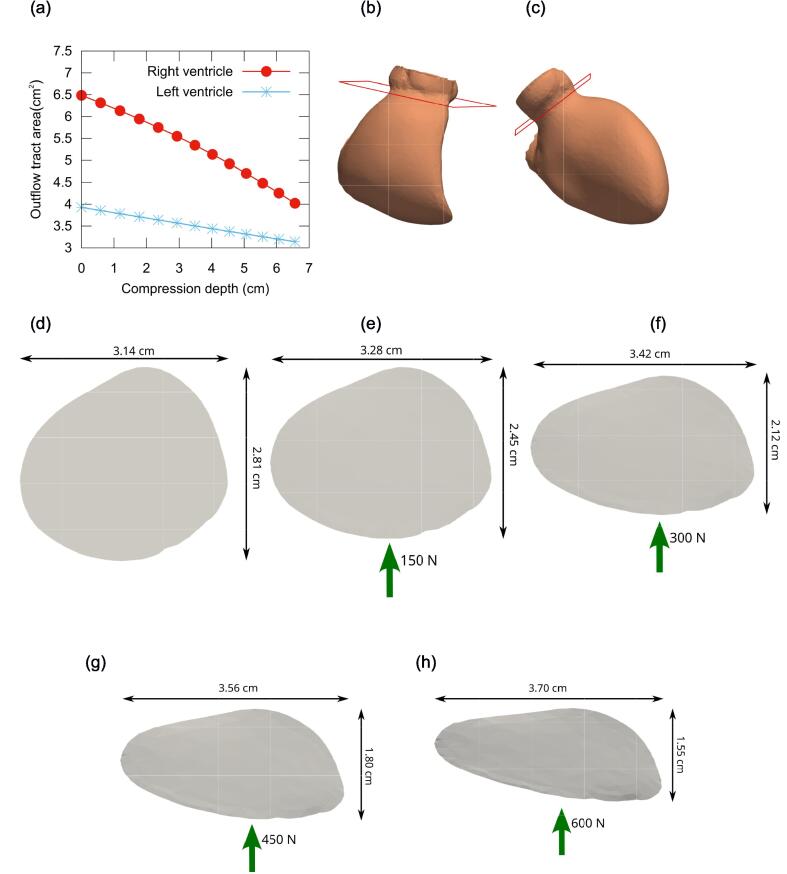
Fig. 4a depicts the variation of the CSA in the left ventricular outflow tract (LVOT) or the right ventricular outflow tract (RVOT) with chest compression. At a depth of 5.06 cm, the CSA decreased by 27.5% and 15.6% in the RVOT and LVOT, respectively. In the uncompressed geometry, as shown in Fig. 4d, the CSA shape of RVOT is approximately circular. With chest compression, the deformed RVOT became progressively more elliptical (Fig. 4e–h), with the major axis lengthening and the minor axis shortening. At a chest compression depth of 5.06 cm (F = 450 N), the decrease in the minor axis relative to the original geometry was calculated as (2.81 − 1.80)/2.81 = 0.36.

Fig. 4.

Fig. 4

Open in a new tab

(a) Variation of the cross-sectional area of the right and left ventricular outflow tract with chest compression depth. (b, c) Right and left ventricles in the uncompressed geometry, showing the slice used to measure the cross-sectional area. (d) Cross-sectional area of the right ventricular outflow tract in the uncompressed geometry. (e–h) Cross-sectional area of the right ventricular outflow tract deformed under compression forces of (e) F = 150 N, (f) F = 300 N, (g) F = 450 N, and (h) F = 600 N.

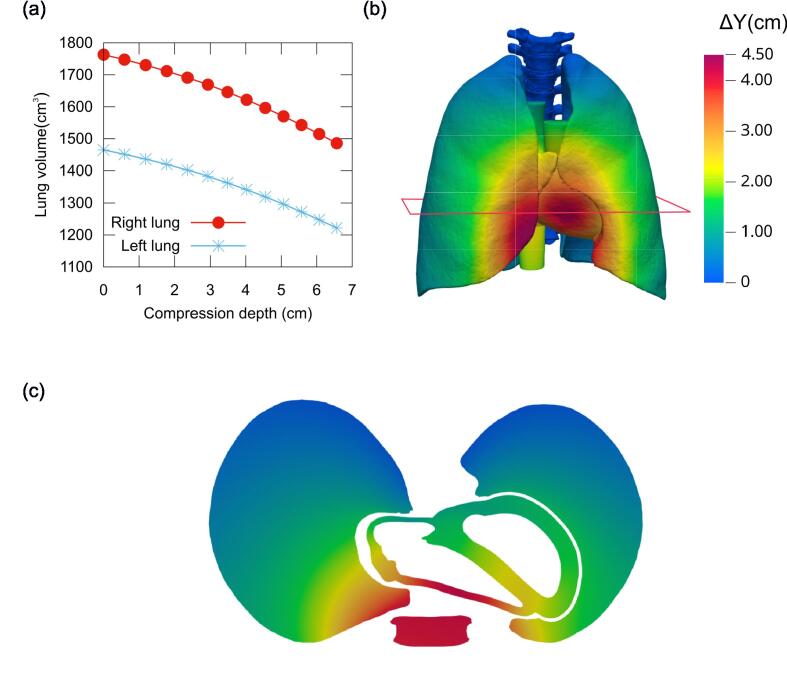
The present FEM simulations also characterised the lung volume reduction, as shown in Fig. 5. At a compression depth of 5.06 cm, the right lung volume decreased by 193 cm3 and the left lung by 169 cm3. This amounted to a total volume reduction of 362 cm3, or 11.2% of the total lung volume.

Fig. 5.

Fig. 5

Open in a new tab

(a) Lung volume variation with chest compression depth. (b) Slightly slanted front view of lungs and heart under a chest compression force of F = 450 N, with surfaces coloured to show backward displacement levels (ΔY) as indicated in the colour scale. (c) Lungs and heart in the axial slice marked in (b), with the cross-section of the sternum also shown for reference.

Discussion

This realistic FEM-based simulation has provided the first comprehensive assessment of the morphological changes of a patient’s heart and lungs during CPR, along with part of the haemodynamic assessment data. As the sternum was displaced, a progressive deformation of the cardiac chambers was observed, starting with those closest to the sternum. The heart as a whole shifted backward, a phenomenon previously observed in a study based on computed tomography images.14 The extent of this backward movement may depend on the relative distance between the lateral heart wall and the spine. The size, position of the heart, and chest geometry may thus play a critical role in the ejection fraction of each cardiac chamber. The volume of the ventricles and atria according to the body surface area of our model are within the normal range described in the literature.30, 31 Likewise the heart weight in our model falls within the standard deviation of the mean (330 ± 85 g) for an individual of the same size and weigth.32

Regarding heart position, the right and left ventricles are located at the level of the fourth and sixth intercostal spaces, with the LVOT positioned between the second and fourth intercostal spaces, consistent with findings from computed tomography-based studies.33

From a biomechanical perspective, the force required to achieve the 5-cm compression depth recommended in the guidelines aligns with values from other studies based on real cases. Reported force values to achieve a 53-mm compression depth range from 219 to 568 N.20 The force needed in this simulation was comparable to mean values reported in previous studies, such as the 441 N required for men at the onset of mechanical chest compression and the 430 N for groups with a lower incidence of rib fractures.19, 20

From a haemodynamic perspective, this simulation has enabled the first precise calculation of ejection fractions for all cardiac chambers during CPR. The normal mean LVEF value at rest is approximately 62%, while the RVEF averages around 52%.34 In this simulation, the LVEF and RVEF achieved were roughly one-fifth and two-thirds of these normal values, respectively. The literature suggests that even with optimal CPR, cardiac output typically reaches only 25–40% of pre-arrest levels.35

The RVEF was more than twice the LVEF, likely because the right chambers, being closer to the sternum, undergo greater deformation. Reduced left ventricular contractility is frequently observed during CPR using transoesophageal echocardiography.36, 37 This phenomenon is influenced by factors such as compression depth, compression point, and the duration of cardiac arrest.38, 39, 40, 41 For the correct interpretation of these results, how the characteristics of the myocardium may evolve over time should be taken into account. When CPR is delayed by more than 7 min or continues for more than 30 min in prolonged cases, a ‘stone heart’ phenomenon has been reported, where the ventricular walls stiffen, impeding left ventricular compression.41, 42 However, the right ventricle, with its thinner muscular wall, remains more compressible.

Another notable aspect is that the LAEF is larger than the LVEF. During CPR, significant changes in left atrial volume with minimal changes in left ventricular volume have been reported.9, 38 Ma et al. described a ‘left atrial pump’ mechanism, where left atrial compression is predominant.7 Some authors have proposed that the left atrium is the main contributor to flow during CPR, with a pressure gradient following the order: left atrium > left ventricle > aorta.9

An essential element of monitoring resuscitation manoeuvres is assessing left and right ventricular outflow tract obstruction because this has been linked to haemodynamic decline and reduced survival rates.8, 11 The values in our model align with the right ventricular outflow tract fractional shortening range reported by Catena et al.11

Regarding lung volume changes, the values in this model closely resemble those reported by Cordioli et al., who observed a mean lung volume decrease of 335 mL in a patient series.43 Anatomical lung dead space is estimated to range from 150 to 200 mL.44 In real-world patients, the tidal volume generated passively during chest compression may reach 108 mL but typically remains well below the anatomical dead space, contributing minimally to ventilation.45, 46 However, novel forms of passive ventilation using continuous airway pressure have shown promising results in the early minutes of resuscitation, and future FEM studies on lung volume changes with various chest compression methods could yield valuable insights.47

The clinical implications of this three-dimensional simulation are significant in basic resuscitation science, offering a unique perspective that is challenging to obtain with other models. Quantifying the ejection fraction as a function of different chest compression techniques, chest shapes, heart positions, cardiac dimensions, and myocardial stiffness could enhance our understanding of CPR haemodynamics and contribute valuable data for personalised CPR approaches. Use a series of FEM-models with different characteristics as it has been done previously will be useful to develop models to predict serious chest injuries to guide the best chest compression depth balancing the risk and benefit especially in prolonged CPR.13

The primary limitation of this study is that it is based on a single-patient simulation, making generalisation difficult. Additionally, the geometry model lacks complete realism because heart valves are not included. While the model shows reductions in heart chamber volumes to assess the ejection fraction, assumptions regarding blood flow or intrathoracic pressures are not yet feasible. Currently, there are no data on the variation of Young’s modulus over the course of cardiac resuscitation, representing a gap in the literature that warrants further investigation.

In this model, a generic material represents all soft tissues and organs not individually accounted for, including skin, pericardium, muscles, tendons, adipose tissue, trachea, oesophagus, stomach, and the major vessels and other digestive components within the chest. Because these omitted tissues and organs do not share identical mechanical properties, this soft tissue approximation serves to provide an estimated representation of their collective mechanical effect.

Conclusion

This virtual simulation enabled a comprehensive assessment of the relationship between the rib cage and key intrathoracic organs during CPR. In this case, the right ventricle exhibited an ejection fraction more than twice that of the left ventricle. The left atrium showed a higher ejection fraction than the left ventricle, suggesting its role in generating forward flow, consistent with the left atrial pump mechanism. This simulation has also provided insights into lung volume reduction during chest compression, aligning with observations in real patients.

Sources of funding

This work was supported by Universitat Rovira i Virgili under grant 2018PFR-URV-B2-29.

Credit authorship contribution statement

Jafar Moradicheghamahi: Writing – original draft, Visualization, Software, Investigation, Data curation. Gerard Fortuny: Writing – original draft, Visualization, Software, Investigation, Funding acquisition, Data curation. Josep M. López: Writing – original draft, Visualization, Software, Investigation, Funding acquisition, Data curation. Dolors Puigjaner: Writing – original draft, Visualization, Software, Investigation, Funding acquisition, Data curation. Joan Herrero: Writing – original draft, Visualization, Software, Resources, Investigation, Formal analysis. Youcef Azeli: Writing – review & editing, Writing – original draft, Methodology, Investigation, Conceptualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Footnotes

Appendix A

Supplementary material to this article can be found online at https://doi.org/10.1016/j.resplu.2025.100910.

Appendix A. Supplementary material

The following are the Supplementary material to this article:

Supplementary Data 1
mmc1.docx (3.6MB, docx)

References

  • 1.Tsao C.W., Aday A.W., Almarzooq Z.I., et al. Heart disease and stroke statistics—2022 update: a report from the American Heart Association. Circulation. 2022;145:e153–e639. doi: 10.1161/CIR.0000000000001052. [DOI] [PubMed] [Google Scholar]
  • 2.Gräsner J.T., Wnent J., Herlitz J., et al. Survival after out-of-hospital cardiac arrest in Europe – results of the EuReCa TWO study. Resuscitation. 2020;148:218–226. doi: 10.1016/j.resuscitation.2019.12.042. [DOI] [PubMed] [Google Scholar]
  • 3.Georgiou M., Papathanassoglou E., Xanthos T. Systematic review of the mechanisms driving effective blood flow during adult CPR. Resuscitation. 2014;85:1586–1593. doi: 10.1016/j.resuscitation.2014.08.032. [DOI] [PubMed] [Google Scholar]
  • 4.Azeli Y., Lorente Olazabal J.V., Monge García M.I., Bardají A. Understanding the adverse hemodynamic effects of serious thoracic injuries during cardiopulmonary resuscitation: a review and approach based on the Campbell diagram. Front Physiol. 2019;10:1475. doi: 10.3389/fphys.2019.01475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Sladen A. Landmark perspective: closed-chest massage, Kouwenhoven, Jude, Knickerbocker. JAMA. 1984;251:3137–3140. [PubMed] [Google Scholar]
  • 6.Neurauter A., Nysaether J., Kramer-Johansen J., et al. Comparison of mechanical characteristics of the human and porcine chest during cardiopulmonary resuscitation. Resuscitation. 2009;80:463–469. doi: 10.1016/j.resuscitation.2008.12.014. [DOI] [PubMed] [Google Scholar]
  • 7.Ma M.H.M., Hwang J.J., Lai L.P., et al. Transesophageal echocardiographic assessment of mitral valve position and pulmonary venous flow during cardiopulmonary resuscitation in humans. Circulation. 1995;92:854–861. doi: 10.1161/01.cir.92.4.854. [DOI] [PubMed] [Google Scholar]
  • 8.Hwang S.O., Zhao P.G., Choi H.J., et al. Compression of the left ventricular outflow tract during cardiopulmonary resuscitation. Acad Emerg Med. 2009;16:928–933. doi: 10.1111/j.1553-2712.2009.00497.x. [DOI] [PubMed] [Google Scholar]
  • 9.Rich S., Wix H.L., Shapiro E.P. Clinical assessment of heart chamber size and valve motion during cardiopulmonary resuscitation by two-dimensional echocardiography. Am Heart J. 1981;102:368–373. doi: 10.1016/0002-8703(81)90311-2. [DOI] [PubMed] [Google Scholar]
  • 10.Skulec R., Vojtisek P., Cerny V. Correlation between end-tidal carbon dioxide and the degree of compression of heart cavities measured by transthoracic echocardiography during cardiopulmonary resuscitation for out-of-hospital cardiac arrest. Crit Care. 2019;23:334. doi: 10.1186/s13054-019-2607-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Catena E., Ottolina D., Fossali T., et al. Association between left ventricular outflow tract opening and successful resuscitation after cardiac arrest. Resuscitation. 2019;138:8–14. doi: 10.1016/j.resuscitation.2019.02.027. [DOI] [PubMed] [Google Scholar]
  • 12.Babbs C.F. Effects of an impedance threshold valve upon hemodynamics in standard CPR: studies in a refined computational model. Resuscitation. 2005;66:335–345. doi: 10.1016/j.resuscitation.2005.03.023. [DOI] [PubMed] [Google Scholar]
  • 13.Moradicheghamahi J., Fortuny G., López J.M., Puigjaner D., Herrero J., Azeli Y. The effect of thoracic dimensions on compression depth during cardiopulmonary resuscitation. Numer Methods Biomed Eng. 2023;39:e3718. doi: 10.1002/cnm.3718. [DOI] [PubMed] [Google Scholar]
  • 14.Hansen K., Machin R., James J., Coats T., Rutty G.N. A look inside cardiopulmonary resuscitation: a 4D computed tomography model of simulated closed chest compression. A proof of concept. Resuscitation. 2020;153:149–153. doi: 10.1016/j.resuscitation.2020.05.037. [DOI] [PubMed] [Google Scholar]
  • 15.Nagaoka T., Watanabe S., Sakurai K., et al. Development of realistic high-resolution whole-body voxel models of Japanese adult males and females of average height and weight, and application of models to radio-frequency electromagnetic-field dosimetry. Phys Med Biol. 2004;49:1–15. doi: 10.1088/0031-9155/49/1/001. [DOI] [PubMed] [Google Scholar]
  • 16.Mitsuhashi N., Fujieda K., Tamura T., Kawamoto S., Takagi T., Okubo K. BodyParts3D: 3D structure database for anatomical concepts. Nucleic Acids Res. 2009;37:D782–D785. doi: 10.1093/nar/gkn613. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Geuzaine C., Remacle J.F. Gmsh: a 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int J Numer Methods Eng. 2009;79:1309–1331. [Google Scholar]
  • 18.Fuchs A., Mejdahl M.R., Kühl J.T., et al. Normal values of left ventricular mass and cardiac chamber volumes assessed by 320-detector computed tomography angiography in the Copenhagen General Population Study. Eur Heart J Cardiovasc Imaging. 2016;17:1009–1017. doi: 10.1093/ehjci/jev337. [DOI] [PubMed] [Google Scholar]
  • 19.Azeli Y., Barbería E., Fernández A., García-Vilana S., Bardají A., Hardig B.M. Chest wall mechanics during mechanical chest compression and its relationship to CPR-related injuries and survival. Resusc Plus. 2022;10 doi: 10.1016/j.resplu.2022.100242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Beesems S.G., Hardig B.M., Nilsson A., Koster R.W. Force and depth of mechanical chest compressions and their relation to chest height and gender in an out-of-hospital setting. Resuscitation. 2015;91:67–72. doi: 10.1016/j.resuscitation.2015.03.020. [DOI] [PubMed] [Google Scholar]
  • 21.Suazo M., Herrero J., Fortuny G., Puigjaner D., López J.M. Biomechanical response of human rib cage to cardiopulmonary resuscitation maneuvers: effects of the compression location. Numer Methods Biomed Eng. 2022;38:e3585. doi: 10.1002/cnm.3585. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Guimarães C.F., Gasperini L., Marques A.P., Reis R.L. The stiffness of living tissues and its implications for tissue engineering. Nat Rev Mater. 2020;5:351–370. [Google Scholar]
  • 23.Singh G., Chanda A. Mechanical properties of whole-body soft human tissues: a review. Biomed Mater. 2021;16 doi: 10.1088/1748-605X/ac2b7a. [DOI] [PubMed] [Google Scholar]
  • 24.Concha F., Sarabia-Vallejos M., Hurtado D.E. Micromechanical model of lung parenchyma hyperelasticity. J Mech Phys Solids. 2018;112:126–144. [Google Scholar]
  • 25.Domian I.J., Yu H., Mittal N. On materials for cardiac tissue engineering. Adv Healthc Mater. 2017;6 doi: 10.1002/adhm.201600768. [DOI] [PubMed] [Google Scholar]
  • 26.Emig R., Zgierski-Johnston C.M., Timmermann V., et al. Passive myocardial mechanical properties: meaning, measurement, models. Biophys Rev. 2021;13:587–610. doi: 10.1007/s12551-021-00838-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Code_Aster – Structures and thermomechanics analysis for studies and research, Électricité de France. https://code-aster.org/. Accessed 19 January 2023.
  • 28.Kanagala P., Arnold J.R., Cheng A.S.H., et al. Left atrial ejection fraction and outcomes in heart failure with preserved ejection fraction. Int J Cardiovasc Imaging. 2020;36:101–110. doi: 10.1007/s10554-019-01684-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Pickard A., Darby M., Soar J. Radiological assessment of the adult chest: implications for chest compressions. Resuscitation. 2006;71:387–390. doi: 10.1016/j.resuscitation.2006.04.012. [DOI] [PubMed] [Google Scholar]
  • 30.Lang R.M., Badano L.P., Mor-Avi V., et al. Recommendations for cardiac chamber quantification by echocardiography in adults: an update from the American Society of Echocardiography and the European Association of Cardiovascular Imaging. J Am Soc Echocardiogr. 2015;28:1–39.e14. doi: 10.1016/j.echo.2014.10.003. [DOI] [PubMed] [Google Scholar]
  • 31.Aune E., Baekkevar M., Roislien J., Rodevand O., Otterstad J.E. Normal reference ranges for left and right atrial volume indexes and ejection fractions obtained with real-time three-dimensional echocardiography. Eur J Echocardiogr. 2009;10:738–744. doi: 10.1093/ejechocard/jep054. [DOI] [PubMed] [Google Scholar]
  • 32.Vanhaebost J., Faouzi M., Mangin P., Michaud K. New reference tables and user-friendly Internet application for predicted heart weights. Int J Legal Med. 2014;128:615–620. doi: 10.1007/s00414-013-0958-9. [DOI] [PubMed] [Google Scholar]
  • 33.Papadimitriou P., Chalkias A., Mastrokostopoulos A., Kapniari I., Xanthos T. Anatomical structures underneath the sternum in healthy adults and implications for chest compressions. Am J Emerg Med. 2013;31:549–555. doi: 10.1016/j.ajem.2012.10.023. [DOI] [PubMed] [Google Scholar]
  • 34.Pfisterer M.E., Battler A., Zaret B.L. Range of normal values for left and right ventricular ejection fraction at rest and during exercise assessed by radionuclide angiocardiography. Eur Heart J. 1985;6:647–655. doi: 10.1093/oxfordjournals.eurheartj.a061916. [DOI] [PubMed] [Google Scholar]
  • 35.Chalkias A., Xanthos T. Pathophysiology and pathogenesis of post-resuscitation myocardial stunning. Heart Fail Rev. 2011;17:117–128. doi: 10.1007/s10741-011-9255-1. [DOI] [PubMed] [Google Scholar]
  • 36.Edmiston T., Sangalli F., Soliman-Aboumarie H., Bertini P., Conway H., Rubino A. Transoesophageal echocardiography in cardiac arrest: from the emergency department to the intensive care unit. Resuscitation. 2024;203 doi: 10.1016/j.resuscitation.2024.110372. [DOI] [PubMed] [Google Scholar]
  • 37.Uenishi M., Sugimoto H., Sawada Y., Terai C., Yoshioka T., Sugimoto T. Transesophageal echocardiography during external chest compression in humans. Anesthesiology. 1984;60:618. doi: 10.1097/00000542-198406000-00035. [DOI] [PubMed] [Google Scholar]
  • 38.Zanatta M., Lorenzi C., Scorpiniti M., Cianci V., Pasini R., Barchitta A. Ultrasound-guided chest compressions in out-of-hospital cardiac arrests. J Emerg Med. 2020;59:e225–e233. doi: 10.1016/j.jemermed.2020.07.005. [DOI] [PubMed] [Google Scholar]
  • 39.Marshall R.A., Morton J.S., Luchkanych A.M.S., et al. Left ventricle chest compression improves ETCO2, blood pressure, and cerebral blood velocity in a swine model of cardiac arrest and cardiopulmonary resuscitation. Resusc Plus. 2022;12 doi: 10.1016/j.resplu.2022.100326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Chang C.J., Sun J.T., Ma M.H.M., Chiang W.C., Chu S.E. Precise identification of area of maximal compression using transesophageal echocardiography during cardiopulmonary resuscitation. Resuscitation. 2023;187 doi: 10.1016/j.resuscitation.2023.109804. [DOI] [PubMed] [Google Scholar]
  • 41.Klouche K., Weil M.H., Sun S., et al. Evolution of the stone heart after prolonged cardiac arrest. Chest. 2002;122:1006–1011. doi: 10.1378/chest.122.3.1006. [DOI] [PubMed] [Google Scholar]
  • 42.Bartos J.A., Grunau B., Carlson C., et al. Improved survival with extracorporeal cardiopulmonary resuscitation despite progressive metabolic derangement associated with prolonged resuscitation. Circulation. 2020;141:877–886. doi: 10.1161/CIRCULATIONAHA.119.042173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Cordioli R.L., Lyazidi A., Rey N., et al. Impact of ventilation strategies during chest compression. An experimental study with clinical observations. J Appl Physiol. 2016;120:196–203. doi: 10.1152/japplphysiol.00632.2015. [DOI] [PubMed] [Google Scholar]
  • 44.Fowler W.S. Lung function studies. II. The respiratory dead space. Am J Physiol-Legacy Content. 1948;154:405–416. doi: 10.1152/ajplegacy.1948.154.3.405. [DOI] [PubMed] [Google Scholar]
  • 45.McDannold R., Bobrow B.J., Chikani V., Silver A., Spaite D.W., Vadeboncoeur T. Quantification of ventilation volumes produced by compressions during emergency department cardiopulmonary resuscitation. Am J Emerg Med. 2018;36:1640–1644. doi: 10.1016/j.ajem.2018.06.057. [DOI] [PubMed] [Google Scholar]
  • 46.Charbonney E., Delisle S., Savary D., et al. A new physiological model for studying the effect of chest compression and ventilation during cardiopulmonary resuscitation: the Thiel cadaver. Resuscitation. 2018;125:135–142. doi: 10.1016/j.resuscitation.2018.01.012. [DOI] [PubMed] [Google Scholar]
  • 47.Van Eijk J.A., Doeleman L.C., Loer S.A., Koster R.W., Van Schuppen H., Schober P. Ventilation during cardiopulmonary resuscitation: a narrative review. Resuscitation. 2024;203 doi: 10.1016/j.resuscitation.2024.110366. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data 1
mmc1.docx (3.6MB, docx)

Articles from Resuscitation Plus are provided here courtesy of Elsevier

RESOURCES