Bridging electron and nuclear motions in chemical reactions through electrostatic forces from reactive orbitals

Abstract

This study presents a physics-based framework for understanding chemical reactions, highlighting the critical role of the occupied reactive orbital, the most stabilized occupied orbital during a reaction, in guiding atomic nuclei via electrostatic forces. These forces, termed reactive-orbital-based electrostatic forces, arise from the negative gradient of orbital energy, creating a direct connection between orbital energy variations and nuclear motion. Through the analysis of 48 representative reactions, we identify two predominant types of force behavior: reactions that sustain reaction-direction forces either from the early stages or just before the transition state. These forces carve grooves along the intrinsic reaction coordinates on the potential energy surface, shaping the reaction pathway. This clarifies which types of electron transfer contribute to lowering the reaction barrier. This study provides a framework for understanding the driving forces behind chemical transformations, offering insights into the electronic basis of reaction mechanisms.

Understanding the coupling between electronic and nuclear motions in chemical reactions is crucial for elucidating how electrons drive chemical transformations. In this study, the authors present a unified theoretical framework that integrates electronic and nuclear motion theories based on variations in orbital energies and demonstrate that electrostatic forces arising from reactive orbitals contribute as a driving force in chemical reactions.

Introduction

What drives chemical reactions: electron motion or nuclear motion? The theoretical understanding of chemical reactions, grounded in the elucidation of molecular electronic structures via quantum mechanics, has historically diverged into two perspectives: electronic theories, such as the theory of organic reaction mechanisms¹ and frontier orbital theory², which emphasize electron motion, and nuclear motion theories, rooted in the potential energy surface (PES) framework³, which focus on atomic nuclei motions. Despite addressing the same fundamental phenomenon, the interrelation between these theories remains largely unexplored. Electronic theories propose that electron motion orchestrates molecular structural transformations during chemical reactions. However, this assertion has neither been rigorously validated nor supported by quantitative evidence. Conversely, nuclear motion theories, which quantitatively describe energetic changes related to nuclear motions, have become the dominant paradigm for predicting reaction rates. Bridging the gap between electronic motion and nuclear motion theories establishes a paradigm shift in chemical reactivity analysis.

To reconcile electron and nuclear motions in chemical reactions, it is essential to identify the specific electron motions that dictate reaction pathways. Reactive-orbital energy theory (ROET)⁴ addresses this challenge by leveraging a statistical mechanical framework⁵ to identify the molecular orbitals, both occupied and unoccupied, with the largest orbital energy variations before and after the reaction as the reactive orbitals. In contrast to conventional electronic analysis methods, such as the natural bond orbital^6,7 and intrinsic bond orbital methods⁸, which rely on localized orbitals, ROET examines canonical orbitals, which possess clear physical significance as described by generalized Koopmans’ theorem⁹. According to this theorem, the occupied and unoccupied orbital energies must, in theory, correspond to the ionization potentials (IP) and the electron affinities, respectively, both of which are experimentally measurable via photoelectron spectroscopy. This approach enables a comprehensive elucidation of the electronic roles played by cocatalysts and auxiliary reagents in metal-catalyzed reactions, as well as proteins in enzymatic processes, offering broader insights into their contributions to reaction mechanisms. Interestingly, reactive orbitals identified by ROET are often neither the HOMO nor the LUMO. This distinction becomes particularly pronounced in catalytic reactions involving transition metals, where low-energy valence orbitals with high electron densities frequently serve as the reactive orbitals.

The development of ROET was made possible by advancements in long-range corrected (LC) density functional theory (DFT)^10,11, enabling accurate and quantitative orbital energy calculations. Recent comparative studies of molecular orbital densities obtained from LC-DFT canonical orbitals and Dyson orbitals derived from the coupled-cluster method have demonstrated the exceptional fidelity of LC-DFT in replicating both orbital shapes and energies¹². ROET analysis of organic reactions revealed that transitions between reactive orbitals correspond closely to the directions of curly arrows used to represent reaction mechanisms¹³. Furthermore, ROET applied to the comprehensive reaction pathways of glycine demonstrated a one-to-one correspondence between reaction pathways and their respective reactive orbitals, offering a perspective on electron motion in chemical reactions¹⁴.

To connect these electron motions with nuclear motions, we turn to electrostatic force theory¹⁵, which quantifies the forces exerted by electronic configurations on molecular nuclei through Hellmann-Feynman forces¹⁶. By integrating ROET with electrostatic force theory, it becomes possible to identify the forces exerted by molecular orbitals that drive the reaction on the nuclei and to evaluate their alignment with the reaction pathway. When these forces align with the reaction direction, they carve reaction pathways on the PES, directly linking the nuclear motion with the motion of electrons driven by molecular orbitals.

Recent years have seen a growing interest in molecular orbitals, spurred by significant advancements in molecular orbital imaging techniques within experimental research^17–22. Notably, we recently demonstrated that valence electron densities of glycine and cytidine, visualized using synchrotron X-ray diffraction, exhibit remarkable agreement with those obtained through LC-DFT calculations²³. Furthermore, by subtracting LC-DFT molecular orbital densities from the total electron densities, we successfully reconstructed 2pπ orbital density images, reminiscent of those familiar from chemistry textbooks. This achievement enables direct analysis of electron motion that drives chemical reactions through molecular orbitals, enabled by the seamless integration of experimental and theoretical approaches. A deeper understanding of the electronic forces governing chemical transformations requires elucidating the electrostatic forces generated by reactive orbitals, which act as the fundamental driving forces along the reaction pathway.

In this study, we elucidate the driving forces of chemical reactions by calculating the electrostatic forces exerted by reaction-driving electrons on the nuclei of molecules. Using reactive orbitals identified through ROET, we compute the Hellmann-Feynman forces within the framework of electrostatic force theory. This integrated approach enables an examination of the implicit common understanding in electronic theories that electron motion mediated by molecular orbitals directs molecular structural transformations, thereby providing a framework for understanding the interplay between electron and nuclear motions in chemical reactions.

Theory

Electrostatic forces exerted by electrons on nuclei

To understand the forces acting on nuclei during chemical reactions, we begin by examining the electrostatic forces exerted by all electrons on the nuclei within a molecule. The Hamiltonian, $\widehat{H}$, governing the system of electrons and nuclei²⁴, is given by

$$\widehat{H}=\sum _i^{n_{\mathrm{elec}}}\left(-\frac{1}{2}{\nabla }_i^2-\sum _A^{n_{\mathrm{nuc}}}\frac{Z_A}{r_{iA}}\right)+\sum _{i<j}^{n_{\mathrm{elec}}}\frac{1}{r_{ij}}+\sum _{A<B}^{n_{\mathrm{nuc}}}\frac{Z_A{Z}_B}{R_{AB}},$$ 1

where ${\nabla }_i^2$ denotes the Laplacian with respect to electron i, r_iA is the distance from electron i to nucleus A, r_ij is the inter-electronic distance between electrons i and j, R_AB represents the internuclear distance between nuclei A and B, Z_A is the charge of nucleus A, and n_elec and n_nuc represent the numbers of electrons and nuclei, respectively. Atomic units are used (ℏ  =  e² =  m =  1, energies are in hartree, and distances are in bohr). Building upon electrostatic theory¹⁵, the Hellmann-Feynman force exerted by the electrons and nuclei on nucleus A is expressed as

$${\mathbf{F}}_A=-\frac{\partial }{\partial {\mathbf{R}}_A}⟨\mathrm{\Psi }∣\widehat{H}∣\mathrm{\Psi }⟩=-⟨\mathrm{\Psi }∣\frac{\partial \widehat{H}}{\partial {\mathbf{R}}_A}∣\mathrm{\Psi }⟩\simeq Z_A\int d\mathbf{r}\rho \left(\mathbf{r}\right)\frac{\mathbf{r}-{\mathbf{R}}_A}{\mid \mathbf{r}-{\mathbf{R}}_A{\mid }^3}-Z_A\sum _{B\left(\ne A\right)}^{n_{\mathrm{nuc}}}{Z}_B\frac{{\mathbf{R}}_{AB}}{{R_{AB}}^3},$$ 2

where ρ(r) represents the electron density at position r, and R_A and R_AB are position vector of nucleus A and vector from nucleus A to nucleus B, respectively. According to the Hellmann-Feynman theorem, these forces represent classical electrostatic forces when the electron distribution is determined variationally¹⁶. The approximation in the right-hand side of Eq. (2) neglects physical effects that depend on nuclear coordinates, such as dispersion forces, which scale with the inverse sixth power of the interatomic distance. It is known that while dispersion forces can affect the structures of weakly bound molecules, they have little influence on molecular orbitals. Therefore, their contribution can generally be neglected, except in cases where the Hellmann-Feynman force is extremely weak.

For a wavefunction describing all electrons, the electron density is given by

$$\rho \left({\mathbf{r}}_1\right)=N\int d{s}_{1}d{\mathbf{x}}_2\cdots d{\mathbf{x}}_N{\mathrm{\Psi }}^{*}\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\right)\times \mathrm{\Psi }\left({\mathbf{x}}_1,{\mathbf{x}}_2,\cdots ,{\mathbf{x}}_N\right),$$ 3

which is integrated over all spatial and spin coordinates, x_n = (r_n, s_n) for n  = 1 to N, except r₁. Within independent electron approximations²⁵, such as the Kohn-Sham method²⁶, the electron density simplifies to

$$\rho \left(\mathbf{r}\right)=\sum _i^{n_{\mathrm{elec}}}{\rho }_i\left(\mathbf{r}\right)=\sum _i^{n_{\mathrm{elec}}}{\varphi }_i^{*}\left(\mathbf{r}\right){\varphi }_i\left(\mathbf{r}\right),$$ 4

where ϕ_i is the i-th spin orbital wavefunction. The total electrostatic force on nucleus A is then expressed as the sum of contributions from electrons (${\mathbf{F}}_A^{\mathrm{elec}}$) and other nuclei (${\mathbf{F}}_A^{\mathrm{nuc}}$),

$${\mathbf{F}}_A={\mathbf{F}}_A^{\mathrm{elec}}+{\mathbf{F}}_A^{\mathrm{nuc}}\simeq Z_A\sum _i^{n_{\mathrm{elec}}}{\mathbf{f}}_{iA}-Z_A\sum _{B\left(\ne A\right)}^{n_{\mathrm{nuc}}}{Z}_B\frac{{\mathbf{R}}_{AB}}{{R_{AB}}^3},$$ 5

where the force contribution from the i-th orbital on nucleus A is

$${\mathbf{f}}_{iA}=\int d\mathbf{r}{\varphi }_i^{*}\left(\mathbf{r}\right)\frac{\mathbf{r}-{\mathbf{R}}_A}{\mid \mathbf{r}-{\mathbf{R}}_A{\mid }^3}{\varphi }_i\left(\mathbf{r}\right),$$ 6

Using this framework, the influence of reactive orbitals on nuclear forces can be isolated. The force contribution from an occupied reactive orbital (ORO) is given by

$${\mathbf{f}}_A^{\mathrm{ORO}}=\int d\mathbf{r}{\varphi }^{\mathrm{ORO*}}\left(\mathbf{r}\right)\frac{\mathbf{r}-{\mathbf{R}}_A}{\mid \mathbf{r}-{\mathbf{R}}_A{\mid }^3}{\varphi }^{\mathrm{ORO}}\left(\mathbf{r}\right),$$ 7

where ϕ^ORO represents the wavefunction of the ORO. This formulation allows for the direct assessment of how variations in reactive orbitals influence nuclear forces during chemical reactions.

In this study, we investigate the primary electrostatic forces driving nuclear motions in chemical reactions, focusing specifically on the forces generated by variations in the ORO. The progression of electron transfer throughout a reaction is characterized by changes in OROs¹³. The electrostatic force vector resulting from ORO variations can be expressed as:

$${\mathbf{F}}_A^{\mathrm{ROEF}}=Z_A{\mathbf{f}}_A^{\mathrm{ORO}}.$$ 8

where we refer to ${\mathbf{F}}_A^{\mathrm{ROEF}}$ as the reactive orbital-based electrostatic force (ROEF) vector. This formulation isolates the contribution of ORO variations along the reaction pathway, which may involve interactions with unoccupied orbitals, while neglecting the contributions from other orbitals.

Relationship between electrostatic forces and orbital energies

Next, we examine the relationship between ROEF and the Kohn-Sham orbital energies²⁴. The Kohn-Sham orbital energy, ϵ_i, is defined as

$${ϵ}_i=h_i+\sum _j^{n_{\mathrm{elec}}}{J}_{ij}+\int d\mathbf{r}{\rho }_i\left(\mathbf{r}\right)v_{\mathrm{xc}},$$ 9

where v_xc is an exchange-correlation potential functional, and h_i represents the one-electron Hamiltonian, given by

$$h_i=\int d\mathbf{r}{\varphi }_i^{*}\left(\mathbf{r}\right)\left\{-\frac{1}{2}{\nabla }^2-\sum _A^{n_{\mathrm{nuc}}}\frac{Z_A}{r_{iA}}\right\}{\varphi }_i\left(\mathbf{r}\right).$$ 10

The derivative of the orbital energy with respect to the coordinates of nucleus A is then expressed as

$$\frac{\partial {ϵ}_i}{\partial {\mathbf{R}}_A}=\frac{\partial }{\partial {\mathbf{R}}_A}\left\{h_i+\sum _j^{n_{\mathrm{elec}}}{J}_{ij}+\int d\mathbf{r}{\rho }_i\left(\mathbf{r}\right)v_{\mathrm{xc}}\right\}=\frac{\partial h_i}{\partial {\mathbf{R}}_A}.$$ 11

where contributions from the v_xc term are negligible due to its limited explicit dependence on nuclear positions.

Reactive-orbital-based electrostatic force (ROEF)

The total electrostatic force vector on nucleus A, derived from the Kohn-Sham electronic energy, E_KS, can be written as

$${\mathbf{F}}_A^{\mathrm{elec}}=-\frac{\partial E_{\mathrm{KS}}}{\partial {\mathbf{R}}_A}=-\frac{\partial }{\partial {\mathbf{R}}_A}\left\{\sum _i^{n_{\mathrm{elec}}}{h}_i+\sum _i^{n_{\mathrm{elec}}}\sum _{j\left(\ne i\right)}^{n_{\mathrm{elec}}}{J}_{ij}+E_{\mathrm{xc}}\right\}=-\sum _i^{n_{\mathrm{elec}}}\frac{\partial h_i}{\partial {\mathbf{R}}_A}=-\sum _i^{n_{\mathrm{elec}}}\frac{\partial {ϵ}_i}{\partial {\mathbf{R}}_A},$$ 12

indicating that the force contribution from each orbital is proportional to its energy gradient with respect to nuclear coordinates. Substituting this relationship, the ROEF vector can be expressed as

$${\mathbf{F}}_A^{\mathrm{ROEF}}=-\frac{\partial {ϵ}^{\mathrm{ORO}}}{\partial {\mathbf{R}}_A},$$ 13

where ϵ^ORO is the orbital energy of the ORO. This equation directly relates the orbital energy gradients to the forces exerted on the nuclei, providing a quantitative link between electronic structure and nuclear motion. By focusing on the ORO, this approach establishes a direct connection between orbital energy variations and nuclear forces, enabling a more detailed understanding of the forces driving chemical reactions at the atomic level.

Accuracy and interpretation of ROEF

From the relationship established in Eq. (13), we infer that orbital energy variations influence electrostatic forces during chemical reactions. Specifically, for OROs that exhibit decreasing orbital energies as the reaction progresses, the resulting electrostatic forces are expected to align with the reaction direction, as described in Eq. (8). These reaction-aligned electrostatic forces create trenches on the PES, delineating the intrinsic reaction coordinate (IRC) and defining the reaction pathway. OROs act as the driving force for a reaction when their electrostatic forces are sufficiently strong to establish the IRC. Since orbital energy remains constant during idealized electron transfer²⁷, orbital energy variations are minimal in reaction stages dominated by electron transfer. This behavior is reflected in the early stages of many reactions, as shown in Figs. S1 and S2 of the Supplementary Information. According to Eq. (13), when the orbital energy gradient approaches zero, the corresponding electrostatic force vector vanishes. However, even small gradients in orbital energy, arising from structural transformations along the IRC, determine the magnitude of the electrostatic force. Accurate calculation of these forces, therefore, hinges on precise determination of orbital energy variations induced by structural changes. This underscores the necessity of a robust theoretical framework capable of reliably predicting orbital energy gradients across different molecular structures. LC-DFT provides a critical tool in this regard, as it quantitatively reproduces orbital energies with high fidelity, making it indispensable for such analyses.

The Pulay force, an artificial force arising from the use of basis sets, is a factor potentially related to ROEFs^28–30. Previous studies report that the magnitude of Pulay forces for all electrons is less than 10 kJ mol⁻¹ bohr⁻¹, with even smaller contributions for individual molecular orbitals. By contrast, ROEF derived from orbital energy gradients are on the order of several hundred kJ mol⁻¹ bohr⁻¹. Given the negligible magnitude of Pulay forces compared to ROEFs, they are excluded from this analysis for simplicity.

An important insight from the interplay between ROEFs and orbital energy variations relates to the virial theorem³¹, which states that the kinetic energy is half the potential energy but with the opposite sign for nuclear-electron interactions. Under independent electron approximations, this relationship holds for individual electrons³². When orbital energy variations during orbital mixing are small, nuclear-electron potential changes are similarly minimized, suppressing fluctuations in ROEFs, as shown in Eqs. (10) and (12). While electron transfer induces polarization in the electron distribution, ROEF remains stable. However, structural deformations near the transition state can generate significant ROEFs, influencing the reaction pathway.

This study highlights the critical role of electron transfer as the driving force for structural transformations during reactions. By calculating the electrostatic forces associated with ORO energy gradients along the IRC, we trace the forces exerted on atomic nuclei, revealing how changes in electron distribution induced by electron transfer shape the reaction pathway.

Three-body model for evaluating ROEFs

Using the framework of ROEFs, we analyze a diverse set of atom-transfer reactions, comprising 16 hydrogen transfer reactions, one heavy atom transfer, two nucleophilic substitutions, and five unimolecular reactions, for the forward and backward processes, based on their calculated IRCs. For the ROEF analysis, atom-transfer reactions were modeled using a three-body approach.

Figure 1 illustrates this framework, applied to the NH + CH₄ → NH₂ + CH₃ reaction (a) and the ROEF vector calculation method (b). These ROEF values provide insight into the forces driving atomic movement caused by electron redistribution during ORO variations. This three-body model provides a simple and intuitive way to visualize the correlation between the reaction direction and electrostatic forces. However, it should be noted that this model is not applicable to more complex reactions such as catalytic or enzymatic processes, which are beyond the scope of the present study. To visualize such correlations in complex reactions, a new model will be required—one that projects the electrostatic force vectors onto the nuclear displacement vectors along the reaction coordinate. ROEF variations along the IRCs for all calculated reactions, along with corresponding molecular structures and atomic coordinates, are presented in Figs. S1 and S2 of the Supplementary Information.

Fig. 1. Three-body model for evaluating ROEFs in atom-transfer reactions.

a Example calculation model for the NH + CH₄  → NH₂ + CH₃ reaction at the transition state, where atoms C1, N2, and H6 are labeled as A, B, and C, and the movement of atom C from A to B is considered. b Method for calculating ROEFs in atom-transfer reactions: F_A, F_B, and F_C are the ROEF vectors calculated for atoms A, B, and C, respectively, ${\mathbf{F}}_{\mathrm{A}}^{\prime }$ and ${\mathbf{F}}_{\mathrm{C}}^{\prime }$ are the projection vectors of F_A and F_C in the direction of the A-C bond, F_C” and F_B” are the projection vectors of F_C and F_B in the direction of the C-B bond. These projections enable the calculation of ROEF vectors, F_BC and F_CA, crucial to the reaction. For unimolecular reactions, only one ROEF vector set corresponds to the reaction direction, and the remaining vectors are set to zero.

Results and discussion

Reaction types classified by ROEFs

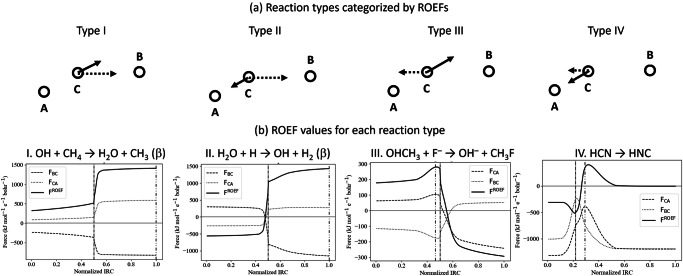
To elucidate the role of ROEF in chemical reactions, we examined their behavior along IRCs and identified four distinct patterns of ROEF variations. Figure 2a provides a conceptual diagram of ROEFs for each reaction type, using the three-body model shown in Fig. 1b.

Fig. 2. Variations in ROEF vectors categorized into four reaction types and their corresponding ROEF changes.

a Conceptual diagrams of the three-body model depicting ROEF vectors for four reaction types, with solid and dotted arrows representing electron transfer before and after the TS, respectively; b Representative reactions for each type, illustrating ROEF variations along normalized IRCs. The force magnitudes for the B-C and C-A bonds, F_BC  =  ∣F_BC∣ and F_CA = ∣F_CA∣, are shown as dotted and dashed curves, respectively, with the combined ROEF (F_ROEF  =  F_CA  −  F_BC) depicted as a solid curve. Definitions of F_BC and F_CA vectors are provided in Fig. 1b. Dash-dot lines indicate TS locations, while dash-dot-dot lines mark points where F_ROEF reaches its maximum. For open-shell reactions, the spin states of the reactive orbitals contributing the largest ROEF values are noted in parentheses next to the reaction formulas. For ROEF variations in reaction pathways other than those presented here, see Figs. S1 and S2.

ROEFs were classified into the following four patterns:

• I.Continuous forward ROEFs throughout the reaction
• II.Sudden forward ROEFs just before the TSs, maintained afterward
• III.Forward ROEFs until the TSs, followed by backward ROEFs
• IV.Backward ROEFs even after the TSs

Figure 2b illustrates representative reactions and ROEF variations for each type. The force magnitudes F_BC and F_CA, based on definitions in Fig. 1b, were calculated for the IRCs of four characteristic atom-transfer reactions. When F_BC is negative and F_CA is positive, the electrostatic forces are aligned with the reaction direction. The maximum force along the reaction path occurs where the difference F_CA  −  F_BC (solid curve) is greatest. Figures S1 and S2 present ROEF variations for both forward and backward processes. Forward ROEFs act along the reaction direction, while backward ROEFs oppose it. The distribution of reactions across the four categories is summarized in Fig. 2. Forward reactions are predominantly type I (11 reactions) and type II (10 reactions), with fewer in types III (2 reactions) and IV (1 reaction). Similarly, backward reactions are primarily type I (12 reactions) and type II (9 reactions), with only 1 and 2 reactions in types III and IV, respectively. Most reactions exhibit forward ROEFs immediately before the TS, which continue beyond the TS.

Peak ROEF values for forward reaction processes

Figure 3a highlights the peak ROEF values along the reaction pathways for forward processes, derived from ORO variations. The data for this figure are available in the Supplementary data.

Fig. 3. Peak ROEF values calculated from OROs of 24 atom-transfer reactions.

a The peak ROEF values for the forward processes, and b those for the backward processes. Black bars represent maximum forward ROEFs, while white bars show minimum backward ROEFs. These ROEF values correspond to the combined force F^ROEF  =  F_CA  −  F_BC along the B-C and C-A bonds, as defined in Fig. 1b. Reaction formulas are accompanied by the spin states of the reactive orbitals (noted in parentheses), along with their corresponding reaction types.

In many forward reactions, peak forward ROEFs significantly exceed the backward ROEFs. Notably, higher backward ROEF peaks are observed only in three type II reactions, two type III reactions, and one type IV reaction. The substantial forward ROEFs in types I and II suggest strong forces acting on atomic nuclei near and beyond the TS, implying that OROs generate trenches along the IRCs on the PES for most forward processes.

Reactions classified as types I and II dominate forward processes, accounting for 21 out of 24 reactions (detailed ROEF variations are provided in Fig. S1). In type I reactions, ROEFs are consistently directed along the reaction path from the onset, remaining constant throughout the reaction. Examples include reactions involving hydrogen atom exchange with OH, CH₃, or C₂H₅ molecules. These reactions are primarily driven by an electrostatic potential gradient established by the electron distribution from the start. In type II reactions, ROEFs initially oppose the reaction progression but shift direction just before the TS, aligning with the reaction path and persisting beyond the TS. This behavior is frequently observed in reactions producing hydrogen or NH₂ molecules through hydrogen atom exchange. The shift in ROEF direction occurs because orbital energy remains constant during electron transfer, and accumulated energy is released through structural deformations near the TS. These reactions are electron transfer-driven, with forces acting primarily near the TS or from the beginning of the reaction. In both types I and II, ROEF creates depressions along the IRC on the PES, forming the reaction pathway. However, for type II reactions, this effect is more localized to the region near the TS.

Peak ROEF values for backward reaction processes

Figure 3b illustrates the peak directional ROEF values derived from OROs for backward processes. In type II reactions, five cases exhibit higher backward ROEFs compared to forward ones, whereas this occurs in only one type IV reaction. The elevated backward ROEFs in type II likely contribute to slower reaction rates. In most other reactions, forward ROEFs dominate during the early stages, generating electrostatic fields that carve trenches along the IRC on the PES. Notably, electron transfer also contributes to shaping the IRC in backward processes.

Backward processes show a similar distribution to forward processes, with 21 out of 24 reactions classified as types I and II (see Fig. S2). This finding indicates that electron-driven forces influencing reaction progression are generally applied near the TS or from the start. A notable difference is the presence of an additional type IV reaction in the backward processes. Type IV reactions exhibit backward ROEFs even beyond the TS, indicating a persistent electron distribution bias in the backward direction. This bias does not drive the reaction forward, explaining the slower rates observed in these reactions. For example, the CH₄ + Cl  → CH₃ + HCl reaction proceeds electrostatically without such a bias. Conversely, the HNC  → HCN reaction involves an H atom circling the NC molecule, rendering the three-body model in Fig. 1b less applicable. Nevertheless, many backward processes remain influenced by electrostatic forces arising from ORO electron distributions.

The roles of ROEFs as the driving force of chemical reactions

These findings reveal that changes in the electron distribution within OROs generate electrostatic forces acting on atomic nuclei, playing a pivotal role in shaping the IRC on the PES. Furthermore, they establish a direct connection between electronic motion theories and nuclear motion theories, encompassing both forward and reverse reaction processes. A particularly noteworthy insight is that, for each reaction pathway, the electrostatic forces driving the reaction predominantly originate from the ORO that most effectively lowers orbital energy in the reaction direction. In reverse reactions, analysis of ROEFs generated by the ORO that most significantly reduces orbital energy in the reverse direction demonstrates that these forces naturally act on the nuclei, driving the reaction backward. Additionally, when orbital energy displays peak- or valley-like patterns, reverse-directed electrostatic forces emerge before and after the extrema, respectively. This behavior underscores the nuanced interplay between orbital energy variations and nuclear forces, highlighting the critical role of OROs in guiding reaction dynamics. These findings suggest the conclusion that changes in the ORO that most effectively lower orbital energy in the reaction direction serve as the driving force behind chemical reactions, uniting electronic and nuclear motion theories under a cohesive framework.

In conclusion, this study elucidates the pivotal role of ROEFs, arising from variations in OROs, in driving the motion of nuclei within reacting molecules. These findings bridge the electron transfer processes described in curly arrow-like representation with the concepts of the PES. ROEFs, defined by the negative gradients of ORO energies, facilitate reaction progress by mediating electron transfer. Our analysis of 24 atom-transfer reactions, encompassing both forward and backward mechanisms, revealed that ROEFs can be classified into four distinct types: I. continuous forward ROEFs throughout the reaction, II. sudden forward ROEFs just before the TSs that are maintained afterward, III. forward ROEFs until the TSs, followed by backward ROEFs, and IV. backward ROEFs even after the TSs. Notably, reactions in types I and II dominate both forward and backward processes, indicating that OROs primarily generate forward-directed ROEFs after the TS. These ROEFs lower the reaction barrier along the reaction pathway. Furthermore, OROs produce significant positive ROEFs that directly drive reaction progression. These observations underscore the critical role of ROEFs in shaping the IRCs on the PES.

Our findings demonstrate that chemical reactions are fundamentally driven by electrostatic forces from ORO variations, which define the reaction pathways on the PES. This enables a unified discussion of electron transfer and the resulting electrostatic forces. Through these insights, we establish a meaningful connection between electron motion theories and nuclear motion theories grounded in PES frameworks, offering a unified perspective on the mechanics of chemical reactions. It is noteworthy that ROEF- and ROET-based analyses rely solely on molecular orbitals and orbital energies, making these approaches theoretically extendable to ab initio wavefunction methods using Dyson orbitals^33,34. These insights offer additional opportunities for analyzing reaction mechanisms in complex systems, including catalytic and enzymatic processes, using ROEF-based frameworks.

Methods

Transition state and IRC calculations were performed with the LC-BLYP+LRD/aug-cc-pVTZ method^35,36, which incorporates long-range exchange and dispersion correlation effects to ensure accurate orbital energies and molecular geometries, implemented within the GAMESS program³⁷. Molecular orbital correspondences along the IRCs were established with an in-house program designed to automatically trace orbital energies and wavefunctions throughout the reaction pathway¹³. The reaction pathway with the higher experimental reaction rate was designated as the forward process, while the reverse process was treated as the backward process. The ORO was identified as the orbital maximizing the relative change in orbital energy between reactants and products. This change is quantified as $2\left({ϵ}_i^{\mathrm{prod}}-{ϵ}_i^{\mathrm{reac}}\right)/\mid {ϵ}_i^{\mathrm{prod}}+{ϵ}_i^{\mathrm{reac}}\mid$, where ${ϵ}_i^{\mathrm{reac}}$ and ${ϵ}_i^{\mathrm{prod}}$ are the energies of the i-th molecular orbital in the reactant and product states, respectively.

Author contributions

Conceptualization, Tsuneda; Methodology, Tsuneda; Software, Tsuneda; Validation, Tsuneda; Investigation, Tsuneda; Writing—original draft, Tsuneda; Writing—review and editing, Taketsugu; Visualization, Tsuneda; Supervision, Taketsugu; Project administration, Tsuneda; Funding acquisition, Taketsugu.

Peer review

Peer review information

Communications Chemistry thanks the anonymous reviewers for their contribution to the peer review of this work.

Data availability

The data related to Fig. 3 are compiled in the Supplementary Data 1. The data generated and/or analyzed in this study are available from the corresponding author, Takao Tsuneda, upon reasonable request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s42004-025-01556-5.