Abstract
Reducing friction has been a human pursuit for centuries, and is especially important for the development of nanotechnology. Nowadays, with the atomic-level understanding of friction, it is possible to reduce friction by modulating the configuration and motion of interfacial atoms. However, how to further reduce friction by modulating the interfacial electronic properties is still unclear. Here we show a strategy to achieve friction and wear reduction through inducing dynamic electronic density redistribution via alternating electric current. The friction force between conductive Ir AFM tip and graphene on Ni substrate can be reduced to 1/4 under 1 kHz alternating current, and maintain for more than 70,000 s under 9.1 GPa contact pressure without any obvious wear. An electronic-level friction model (PTT-E model) is presented to unravel and quantify the tuning effect, showing that the alternating current induced dynamic electron density redistribution is the key to friction reduction. This work proposes a feasible and robust method to reduce friction and wear in nanomechanical devices, and advances the understanding and predicting of electronic contribution in friction tuning.
Subject terms: Mechanical engineering, Electronic properties and materials
Friction and wear cause widespread energy loss and damage. Here, the authors propose a strategy to reduce friction and wear through inducing dynamic electronic density redistribution via alternating electric current.
Introduction
Friction is a common phenomenon in nature, and also a key technology that enabled human civilization1. Since Leonardo da Vinci studied friction in the 15th century, researchers have been striving to explore the key factors of friction and control it2–4. Nowadays, the fundamental law of friction has been investigated to improve the service life and reliability of micro-nano electromechanical systems (NEMS)5–7, to magnify the energy harvest efficiency of triboelectric nanogenerator (TENG)8, to enhance the dexterity of robotic grasping9, and to achieve haptic feedback for virtual reality10.
With a deeper understanding of atomic-level friction11, researchers have achieved friction control by regulating atomic motion through thermal activation or nanoscale mechanical vibration12–25. In terms of thermal activation, Krylov et al. revealed thermally activated jumps of the atomic-force microscopy (AFM) tip over the sliding barrier, demonstrating a pathway to nearly vanishing friction24. Tshiprut et al. theoretically predicted that vibrations could significantly enhance surface diffusivity and mobility while reducing nanoscale friction.12
In terms of applying mechanical vibration, Socoliuc et al. observed a significant reduction in friction between an AFM tip and an insulating NaCl surface when vibrations were excited. The mechanical excitation induced premature jumps over sliding energy barriers are found to be the key to friction reduction, inspired the field of dynamic superlubricity13. Lantz et al. further demonstrated that mechanical vibration could eliminate wear between a silicon AFM tip and a polymer surface, highlighting its potential for friction and wear reduction16. Since then, dynamic superlubricity has shown success in friction minimization14,15,17–19. Recently, a 2D piezoelectric thin film was applied along the contact interface to induce mechanical vibrations via the inverse piezoelectric effect, enabling active friction modulation without an external vibration source17.
However, these methods demand that the actuation frequency is precisely tuned to match the resonant frequency of the system, and it usually requires a high actuation voltage to induce sufficient amplitude of vibration (several nanometers), especially under high normal load17. Additionally, frequent mechanical vibrations may cause fatigue and failure in the system and interfere with device functionality26,27.
In recent years, tuning interface electronic properties via an external electric field or current has emerged as a promising approach for friction control. This method offers high flexibility, reversibility, low driving voltage, and vibration-free operation5,28–40. Park et al. reported a significant friction increase when an AFM tip slid against p-type doped silicon under an electrical current, attributing the effect to carrier accumulation and depletion29,30. Subsequent studies have observed similar electric field/current-induced friction modulation in various tribosystems31–33,35,36,41. However, applying an electric field perpendicular to the interface usually led to increased friction between the AFM tip and materials (such as silicon29, GaAs32, graphene oxide33, graphite31, graphene on Ru (0001)41, MoS236, MoSe242, h-BN35), yet how to reduce friction is still unclear.
The mechanisms underlying electric field/current-induced friction modulation remain unclear, making theoretical predictions challenging. Existing atomic-scale friction models, such as the Prandtl-Tomlinson (PT) and Frenkel-Kontorova (FK) models, describe friction as the process of overcoming potential energy barriers caused by atomic stacking changes. These models account for wear, plastic deformation, chemical reactions, and thermal activation23–25,43–45, but overlook electronic contributions to friction under an electric field or current28–30,34,46.
In this research, the friction force and wear at the interface of conductive AFM tip and 2D materials is reduced by applying an alternating electric current. The friction force when the Ir tip slides along the graphene on Ni substrate (i.e., Ir/Gr/Ni interface) can be reduced to 1/4 under an alternating electric current with bias voltage amplitude / frequency as low as 1 V and 1 kHz. This low friction force was sustained for over 70,000 s under a normal load of 840 nN ( ≈ 9.1 GPa contact pressure), without noticeable wear. Our theoretical calculation revealed that the alternating electric current activates the dynamic electronic density redistribution and atomic force perturbation (i.e., electrical activation), which assists the tribosystem to overcome the sliding barrier. Based on these, we put forward a friction model incorporating electrical activation (PTT-E model) to calculate atomic-scale friction under an alternating current. This mechanism of electrically activated friction reduction is applicable to various conductive 2D material interfaces, providing a theoretical framework for understanding and predicting electronic contributions to friction modulation.
Results
Friction and wear reduction induced by alternating current
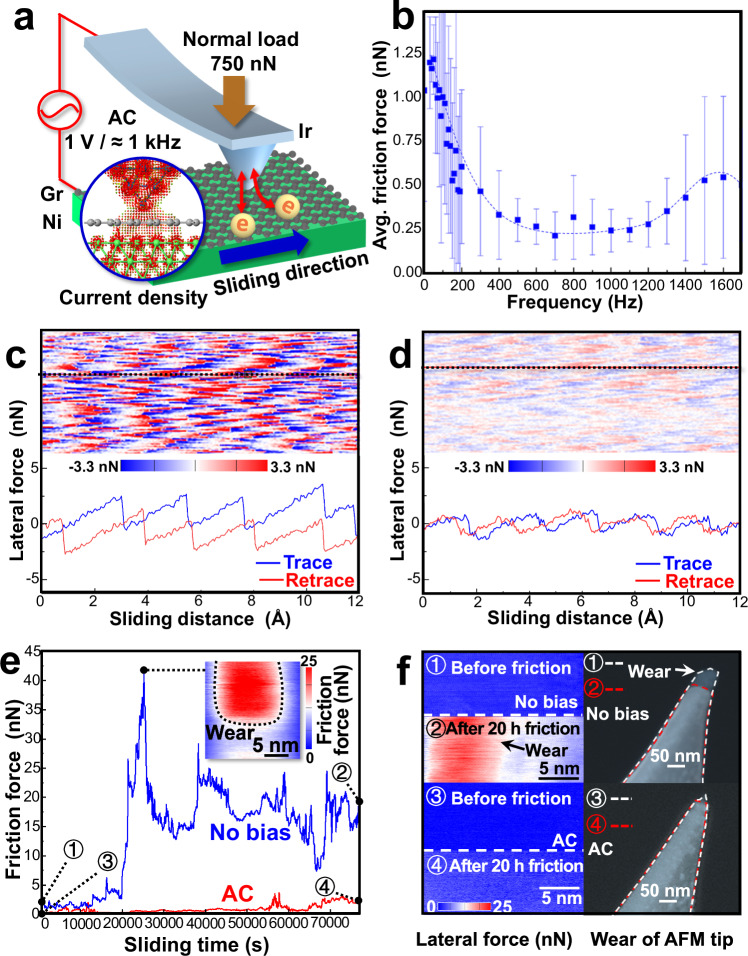
The impact of alternating electric current on friction force is investigated using conductive atomic force microscopy (c-AFM). The AFM tips (ASYELEC 01-R2) are made of doped monolithic silicon with a ≈ 23 nm Ir coating (tip radius R ≈ 25 nm, force constant k = 2.8 N m⁻¹, lateral sensitivity = 2.52 nN (mV)−1, resonant frequency = 77 kHz). The lateral force maps, friction loops and current maps of Ir/Gr/Ni interface are measured under 0-1.6 kHz alternating voltage with 1 V amplitude and 750 nN normal load, as shown in Fig. 1a. When applying the alternating voltage, the averaged friction force of the scan region can be reduced to 1/4 at frequency around 1 kHz (from 500 to 1200 Hz, the minimum is at 700 Hz), as shown in Fig. 1b. Atomically resolved lateral force maps and friction loops measured under no bias (Fig. 1c) and 1 V / 1 kHz alternating voltage (Fig. 1d) indicate a reduction in maximum lateral force during each atomic-scale stick-slip cycle.
Fig. 1. Tuning friction force and reducing wear via applying alternating electric current in conductive AFM experiments.
a The c-AFM experimental setups and current density calculated by DFT + NEGF of Ir/Gr/Ni interface. b The averaged friction force of the scan region under 1 V alternating voltage with different frequencies, under 2.4 nm s−1 sliding velocity. Error bars indicate the standard deviation of the friction force obtained from 1024 friction loops. c, d The lateral force maps and friction loops (along the black dashed lines) measured before (c) and after applying 1 V / 1 kHz alternating voltage (d). eThe friction force evolution of Ir/Gr/Ni interface under 1 V amplitude and 1 kHz frequency alternating voltage (red line) and no bias voltage (blue line). f The lateral force maps measured before (①③) and after 20 h friction (②④) under 840 nN normal load with (③④) and without (①②) alternating current. The SEM images of the AFM tips observed before (①③) and after (②④) 20 h friction under 840 nN normal load with (③④) and without (①②) alternating current. Source data are provided as a Source Data file.
The durability of the low-friction state induced by the alternating voltage is further evaluated (Fig. 1e). Experiments are conducted in an atmospheric environment with a normal load of 840 nN applied to the AFM tip, corresponding to a 9.1 GPa contact pressure based on the JKR model (for calculation details, see “Methods”). The normal load is much higher than the previous AFM experiments (2.73-208 nN13,16,17) where friction is reduced through mechanical vibration induced by alternating electric field.
Under such high contact pressure, graphene exhibited wear after ≈ 25,000 s of sliding without an alternating voltage (inset of Fig. 1e), accompanied by a sharp increase in friction. The AFM tip is also severely worn as shown in the scanning electron microscopy (SEM) images (see Fig. 1f). The SEM images of the tip before and after the friction experiment are colored blue and gray with white and red outlines, respectively. By overlapping the SEM images of the tip before and after friction, we can clearly see that the tip apex wore off about 50 nm.
In contrast, under 1 V amplitude and 1 kHz frequency alternating voltage, the low friction state maintains for more than 70,000 s (red line, Fig. 1e). The post-experiment friction force map (see Fig. 1f) revealed no significant friction increase, indicating negligible graphene wear. Meanwhile, SEM images confirmed that the AFM tip did not show any obvious wear neither (Fig. 1f). These results demonstrate that applying an alternating voltage effectively reduces wear and sustains a robust low-friction state.
Influencing factors of friction under alternating current
To gain a more comprehensive understanding of the friction-reducing effect induced by electric current, the influencing factors under applied alternating current are further investigated. Firstly, the variation of friction with bias voltage amplitude is investigated using c-AFM (Fig. 2a–c). As the amplitude of the bias voltage increases, a reduction in lateral force during sliding is observed (Fig. 2a). Meanwhile, the enclosed area between the trace and retrace curves decreases (Fig. 2b), indicating a decrease in friction force. The relationship between the average friction force within the scanning area and the bias voltage amplitude is shown in Fig. 2c. A nonlinear decrease in friction force is observed at low bias voltage amplitudes ( < 0.35 V), followed by an approximately linear decline at higher bias voltage amplitudes.
Fig. 2. Influencing factors of friction under alternating current.
a Lateral force maps and (b) lateral force loops measured under different bias voltage amplitudes. The blue and red lines represent the lateral forces during the trace and retrace processes, respectively. c Variation of friction force with the bias voltage amplitude. Error bars indicate the standard deviation of the friction force obtained from 512 friction loops. d–f The relationship between friction force and alternating current frequency measured at 2 nm s−1 (d), 500 nm s−1 (e) and 1000 nm s−1 (f) sliding velocity. g The relationship between friction force and AC frequency of Ir/h-BN/Au and Ir/Gr/Cu tribosystem measured by the c-AFM under 1 V alternating voltage amplitude. Error bars indicate the standard deviation of the friction force obtained from 512 friction loops. (h) The relationship between conductance and friction reduction ratio of the tribosystems measured in the experiment. The green, orange, and yellow colors represent the results of the Ir/Gr/Ni, Ir/Gr/Cu, and Ir/h-BN/Au, respectively. Source data are provided as a Source Data file.
Secondly, the effect of alternating current on friction under different sliding velocities is investigated. The friction force under different f (0–80 kHz) and v (2500, and 1000 nm s−1) is measured using c-AFM, as shown in Fig. 2d–f. At every sliding velocity, the friction force exhibits a similar trend with the increase of f, i.e., it firstly decreases and then increases. Yet the frequency leading to the lowest friction is not a constant, which shows an increasing trend with the sliding velocity.
Thirdly, the frictional behavior of different material interfaces under applied alternating current is investigated. The friction force of an Ir AFM tip sliding on graphene-covered Cu (Ir/Gr/Cu interface) and on h-BN-covered Au (Ir/h-BN/Au interface) is measured using c-AFM, as shown in Fig. 2g. The results show that all investigated interfaces exhibit a reduction in friction under alternating current. However, the degree of friction reduction varies among the interfaces and is positively correlated with the interfacial conductivity, as illustrated in Fig. 2h and Supplementary Fig. 1.
Finally, the effect of sliding direction is studied, as shown in Supplementary Fig. 2 and Supplementary Discussion 1. The friction force significantly decreases under alternating electric current in all sliding direction we have tested, and the relationships between friction and alternating current frequency are similar.
Mechanism and theoretical model of friction reduction
To fundamentally unravel the mechanism of friction reduction, the changes in interfacial charge density and atomic forces under various bias voltage and electric current are calculated using density functional theory combined with nonequilibrium Green’s function (DFT + NEGF). To ensure the applicability of the computational results to the experiment, the electric field distribution at the tip-sample interface is analyzed using the multi-physics coupled finite element method (FEM). The FEM results indicate that the electric field at the interface is approximately perpendicular to the surface, with a small radial component at the edge of the tip, as shown in Supplementary Fig. 3b, c. Accordingly, tip models with different curvature radii in contact with graphene are constructed. The r ≈ ∞ tip (i.e., Ir surface contact) closely resembles the perpendicular-to-interface field, while the r ≈ 1 nm tip accounts for the radial component of the electric field, as shown in Fig. 3a, b. In the following calculations, we refer to them as “flat contact (r ≈ ∞)” and “tip contact (r ≈ 1 nm)”, respectively. In addition, a layer of Ar atoms is introduced at the interface to simulate the tunneling barrier effect caused by adsorbed molecules under ambient conditions.
Fig. 3. Charge density redistribution and atomic force change under various bias voltage.
a, b External electrostatic potential distributions at the tip-sample interface for different atomic configurations of the tip calculated via DFT + NEGF. c, d Charge density redistribution Δρ = ρ(Vb) – ρ(0) calculated via DFT + NEGF under a + 0.4 V bias voltage. e, f Profiles of the charge density redistribution along the dashed lines indicated in (c)(d). Red and blue curves represent the results under +0.4 V and –0.4 V bias voltages, respectively. g, h The charge density redistribution as a function of bias voltage amplitude. The charge density redistribution value is taken as the value with largest absolute magnitude around the interfacial Ir atoms. The red/blue curves correspond to the cases with positive/negative applied bias voltage. i, j The total force FE on the contact region Ir atoms for different tip configurations as a function of bias voltage amplitude. The force perturbation ∆FE(Vb) = (FE(Vb)-F0)/F0, where FE(Vb) and F0 represent the forces under bias voltage Vb and zero bias voltage, respectively. Source data are provided as a Source Data file.
Under the applied bias voltage, the charge redistribution at the interface mainly concentrates between the Ir tip and the adsorbates, as well as between the adsorbates and graphene, as shown in Fig. 3c, d. This redistribution of charge density leads to changes in the forces acting on the Ir atoms at the interface, as illustrated in Fig. 3i, j. For both tip configurations, the bias-induced charge redistribution and force variations exhibit similar trends with increasing bias voltage amplitude, as shown in Fig. 3g–j. Due to the apex-enhanced electric field effect of the tip contact, the charge density redistribution and the variations in atomic forces are more pronounced, as shown in Fig. 3e–j.
To illustrate the effect of the charge density redistribution and atomic force variations on friction, we incorporated these effects into the Prandtl-Tomlinson (P-T) friction model, and developed the electrically activated P-T (PT-E) model. The P-T model is expressed in Eq. (1)47:
| 1 |
This model describes the sliding motion of a spring–mass oscillator with mass m and spring stiffness k, moving at velocity v over a periodic potential with period a and corrugation amplitude U₀. It is widely used to simulate friction in c-AFM experiments, where the AFM tip is treated as the spring–mass oscillator. The force F0 acting on the tip in the periodic potential can be expressed in Eq. (2):
| 2 |
When an alternating current is applied, the atomic force variations will be induced by charge density redistribution, and F0 will be changed into FE, which represents the force acting on the tip under electric current. FE can be obtained by fitting the DFT + NEGF calculation results (Fig. 3i, j). Taking the flat contact configuration as an example:
| 3 |
where is the force on the tip under an applied bias voltage Vb. Considering a sinusoidal altering bias voltage Vb = Vb0 sin(2πƒt+φ), substituting it into Eq. (3) yields the time-dependent force on the tip under the alternating bias voltage FE(t). By replacing F0 in Eq. (1) with the FE(t), we obtain the PT-E model (Fig. 4a), which enables the calculation of frictional force under an alternating current.
Fig. 4. Friction model under alternating electric current.
a The schematic of the electrically-thermally activated PT (PTT-E) model. The lateral force (b, c), x direction displacement of tip - sliding time (d, e) and the trajectory (f, g) of the tip apex (translucent blue cycle) sliding along the potential energy surface (PES, orange dash lines) pulled by the driver (gray square) with 10 nm s−1 speed, under 500 Hz alternating current (left) and no external field (right). The red and gray curves in (b) and (c) represent the calculated results of the PTT-E and PT-E models, respectively. Source data are provided as a Source Data file.
Furthermore, by introducing a random thermal noise term ξ(t) to consider the thermal effect14,47, the electrically-thermally activated PT model (PTT-E) model can be expressed in Eq. (4):
| 4 |
The thermal noise term ξ(t) satisfies the fluctuation–dissipation relation:
| 5 |
where is the Boltzmann constant, is the Dirac delta function.
To illustrate the mechanism of friction reduction induced by force perturbation, the oscillator’s trajectory and lateral force are analyzed using the PT-E and PTT-E models, under a 1 V / 500 Hz alternating current at a sliding velocity of 10 nm s−1. Model parameters are provided in the “Methods” section. FE(t) is fitted from the DFT + NEGF calculation results of the flat contact configuration. According to the PT-E model, without the application of an alternating current, the oscillator remains in the stick state until 0.05 s (Fig. 4c). During this period, the oscillator’s positions cluster near the potential energy minimum, resulting in a trajectory that appears as solid blue, as indicated by the red arrows in Fig. 4g.
When a 500 Hz alternating current is applied, the force perturbation induces back-and-forth oscillations along the sliding direction, referred to as displacement perturbations (Δx) in Fig. 4d. These perturbations lead to a broader distribution of positions during sticking, represented by semi-transparent blue regions in the trajectory, as shown by the purple arrows in Fig. 4f. The displacement perturbation facilitates an earlier transition from stick to slip, with the oscillator crossing the critical slip position at ≈ 0.03 s. The time of the slip occurred in advance is marked by the green arrows in Fig. 4c–e. This slip in advance also exists when the thermal effects are considered, as shown by the gray lines in Fig. 4b, c. In the experiment, we also observed the phenomenon of the slip in advance, as marked by the green arrow in Supplementary Fig. 4b, which is consistent with our computational results. This advancement in the slip event is accompanied by a reduction in the maximum lateral force, as indicated in Fig. 4b.
Validation of the friction model
The PT-E and PTT-E models are used to investigate and clarify the influence of various factors—including bias voltage amplitude, AC frequency, sliding velocity, and material—on friction under the alternating current. Firstly, the variation of friction with bias voltage amplitude is calculated, as shown in Fig. 5a, b, corresponding to the tip contact and flat contact configurations, respectively. For both configurations, friction decreases with increasing bias voltage amplitude, showing consistence with our experiments (Fig. 2c).
Fig. 5. Investigation of friction influencing factors under applied alternating current using the PT-E and PTT-E models.
a, b Variation of friction with bias voltage amplitude at different temperatures. The sliding velocity is set to 10 nm s−1, and the calculations are based on the tip contact (a) and flat contact configuration (b). The red and blue curves in (a) and (b) represent the calculated results of the PTT-E and PT-E models. c The relationship between the absolute value of atomic force change |ΔFE| and change density redistribution |Δρ| for different interfaces. The green, cyan, orange, and yellow markers represent the calculated results for the Ir/Gr/Ni interface, the Ir/Gr/Ni interface with a layer of Ar atoms as adsorbates, the Ir/Gr/Cu interface, and the Ir/h-BN/Au interface, respectively. d The relationship between friction force and alternating current frequency calculated via PT-E and PTT-E model at 2 nm s−1 (d), 500 nm s−1 (e) and 1000 nm s−1 (f). g The relationship between the AC frequency f corresponding to the minimum friction force and the sliding velocity v obtained from the experiment (gray stars) and calculated using PT-E model (blue triangles) and PTT-E model (red cycles). h–k The schematic of the tip apex sliding along the potential energy surface under different f v−1a. Source data are provided as a Source Data file.
Meanwhile, using the PT-E model, the influence of AC frequency ƒ and sliding velocity on friction is investigated, as shown in Fig. 5d–g. The ΔFE(t) fitted from flat contact configuration is used. At all sliding velocities, friction first decreases and then increases with increasing ƒ (Fig. 5d–f). Moreover, the frequency corresponding to the minimum friction increases with sliding velocity, which agrees with the experimental results (Fig. 5g).
To understand at which frequency the friction force reaches its minimum, we calculate the oscillator’s trajectory and the lateral force at different speeds (2500 and 1000 nm s−1) and AC frequencies, as shown in Supplementary Figs. 5–7. Meanwhile, we calculate the variation of displacement perturbation Δx with frequency, as shown in Supplementary Fig. 8. At all speeds, the lowest friction occurs at the frequency where the displacement perturbation is largest. This is because larger displacement perturbation will cause the oscillator to pass the energy barrier earlier, thus leading to a larger reduction in friction force.
Depending on the relative magnitude of the alternating current frequency f and the frequency at which the oscillator crosses the energy barrier (i.e., the washboard frequency v/a, where v is the speed and a is the lattice constant), there are two scenarios (A more detailed discussion can be seen in Supplementary Discussion 2):
When the frequency of the alternating current is lower than the washboard frequency (f < v/a), it takes v/(a·f) ( >1) stick-slip periods to activate a displacement perturbation Δx, as shown in Fig. 5h and Supplementary Fig. 5e. In this frequency range, the average Δx per stick-slip period is a·f/v (<1) times of its maximum value. As the frequency increases, the displacement perturbation occurs more frequently, the average Δx per stick-slip period increases, thus the friction shows a decreasing trend with frequency.
When the AC frequency is larger than (or equal to) the washboard frequency (f ≥ v/a), the displacement perturbation will be activated at least once in each stick-slip period. Further increasing the frequency helps to ensure that at least an effective displacement perturbation can be activated within one stick-slip period, regardless of the AC phase (the impact of AC phase on friction will be detailed discussed in Supplementary Fig. 7 and Supplementary Discussion 2), thus reducing the averaged friction. However, too high frequency will cause the Δx decrease due to the damping force induced dissipation, leading to an increase in friction, as shown in Fig. 5i and Supplementary Fig. 6g–i.
Therefore, the lowest friction will occur around the frequency range that is 1-2 orders of magnitude higher than the washboard frequency, as shown in Fig. 5k, and the specific value can be quantitatively calculated through the PTT-E model.
Furthermore, the interfacial charge density redistribution and atomic force changes of the Ir/Gr/Cu and Ir/h-BN/Au tribosystems are calculated using DFT + NEGF, as shown in Fig. 5c. Under an applied bias voltage, electron density redistribution (Δρ) occurs at all interfaces, resulting in atomic force perturbations (ΔFE), as illustrated in Fig. 5c. For the conductive interfaces - Ir/Gr/Ni and Ir/Gr/Cu - both Δρ and ΔFE are more pronounced compared to the insulating Ir/h-BN/Au interface. This behavior arises from the higher density of free electrons in conductive systems, which are more responsive to external electric fields. Consequently, a more substantial friction modulation is observed experimentally at interfaces with higher conductivity.
Discussion
Applying mechanical vibrations to reduce nanoscale friction was proposed by the Socoliuc et al.13 The concept of mechanically induced premature transitions over the sliding energy barrier pioneers a field of dynamic superlubricity. In our research, we find that this transition can also be induced by the electron density redistribution, which shows differences with mechanical vibrations. In terms of experimental phenomena: (1) The relationship between friction and frequency is different. The minimum friction value appears at the resonance frequency of the cantilever when mechanical vibrations are applied, because the vibration amplitude is the largest at this frequency13,17. In contrast, in our experiments, the frequency corresponding to the minimum friction is not fixed but is related to the sliding speed. (2) The mechanical fluctuation remains at the scale of 0.05 nm under alternating bias voltage (Supplementary Fig. 9), which is far below the magnitude required to reduce friction as reported in refs. 17,18. (3) Applying mechanical vibrations often cause significant fluctuations in the normal force during the friction process, and the normal interaction at the interface can even change from repulsive to attractive18. In contrast, in our experiments, as the normal load is much higher, the interfacial atoms always maintain a strong and almost constant repulsive force, as shown in Supplementary Fig. 10.
From the perspective of physical essence, to reduce friction via mechanical vibrations, the change in the distance between interface atoms is crucial according to existing theories47. This is a prerequisite for altering the potential energy surface. In contrast, we applied a normal load as high as 750 nN, which is much higher than the magnitude of the electrostatic force generated by a 1 V alternating voltage30. In this case, the electrostatic force is unlikely to cause a significant change in the interface distance and friction force. From a quantitative perspective, our first-principles calculations indicate that the force changes on interfacial atoms in the x (sliding direction) and z (normal direction) due to charge redistribution under an external field are on the order of 0.1 eV Å−1. This magnitude of force is negligible compared to the large normal load of 750 nN (i.e., 469 eV Å−1), but it is of the same order as the friction force ( ≈ 1 nN). Therefore, the external field and current can effectively tune the lateral forces of interfacial atoms without significantly affecting the normal force. Meanwhile, to estimate the impact of mechanical fluctuation, we also recorded the variation in the z-direction (perpendicular to the interface) position of the tip (ΔZ) during the friction process. As the bias voltage amplitude increases, the variation in the z position of the tip does not change significantly (less than 10%), with the standard deviation σz ≈ 0.05 nm regardless of the bias voltage amplitude, as shown in Supplementary Fig. 9. In contrast, the friction reduction exceeds 60%. For comparison, in the friction experiment between an AFM tip and a mica surface in an atmospheric environment, achieving the same magnitude of friction reduction requires a mechanical fluctuation amplitude >5 nm18. In a recent experiment about friction reduction between AFM tip and periodically poled lithium niobate (PPLN) surface, the mechanical fluctuation amplitude required to reduce friction is 1.6–5.9 nm17. Therefore, considering only mechanical fluctuation, it is difficult to quantitatively describe the friction reduction in our experiment.
Moreover, the friction reduction in our experiments is not due to thermal activation effects. This is because if the friction reduction is solely due to Joule heating, the friction should not change with the frequency of the alternating current. At the same time, we also calculated the temperature rise at the interface using the multi-field coupled finite element method (specific results in Supplementary Fig. 11 and Supplementary Discussion 3). The results show that even if we use the lowest thermal conductivity values reported in the literature for graphite/graphene and their interfaces, the temperature rise at the interface is only 69 °C. Accordingly, the calculated friction reduction is about 14.6%, still significantly lower than the results measured in our experiments.
Finally, the advantages of reducing friction via alternating electric current-induced dynamic electronic density redistribution are as followed. First, this method enables dynamic control of friction, that is, friction can be flexibly and instantly adjusted by changing the amplitude and frequency of the alternating current. Secondly, activating electron density redistribution does not rely on the changes in the atomic configuration, thus theoretically it causes almost no damage to the material, avoiding fatigue, failure and interference with device function caused by high temperature or frequent mechanical vibration19,26,27. Actuating dynamic electronic density redistribution instead of mechanical vibration is beneficial to the reliability and performance of devices. Thirdly, mechanical vibrations are difficult to maintain under high contact pressure. In contrast, actuating dynamic electronic density redistribution does not require high actuating voltage or precise control of frequency, which can be easily realized without the additional boost circuit or vibration source used in refs. 14,18,19, which means that it could solve the key issue hindering the practical application of MEMS/NEMS last for decades, i.e., severe wear under high mechanical load48.
In summary, through applying an alternating current, the friction force between the conductive AFM tip and graphene can be reduced to 1/4 and maintain more than 70,000 s under 9.1 GPa normal load, without apparent wear and mechanical vibration. Theoretical calculations show that the alternating current activates the dynamic electron density redistribution of the tribosystem, which further induces the atomic force perturbation that assist the tribosystem to overcome the sliding barrier. Based on these findings, we propose the PTT-E model which quantifies the friction reduction induce by electrical activation. This work proposed a feasible and robust strategy to reduce the friction and wear in nanomechanical devices, and sheds light on understanding and predicting the electronic contribution in friction tuning.
Methods
c-AFM experiment
The c-AFM experiments were carried out by Cypher c-AFM (made by Oxford Instruments) under the ambient atmosphere (temperature ≈ 25 °C, relative humidity ≈ 20%). A Ti/Ir coated tip (ASYELEC.01-R2, tip radius R ≈ 25 nm, force constant k = 2.8 N m−1, lateral sensitivity = 2.52 nN mV−1 calibrated with a diamagnetic levitation spring system) was used to measure the friction force under alternating current. The normal load was set to 750 nN during sliding unless otherwise specified, and the scanning rate was set to 1 Hz. The friction force was calculated as half of the difference in lateral force between the trace and retrace. The conductivity was calculated as the dI/dV of the I-V curve at zero bias voltage. The Gr/Cu sample was fabricated via chemical vapor deposition (CVD)49, while the Gr/Ni sample was purchased from Graphene Laboratories Inc., and h-BN/Au sample was fabricated through transferring mechanically exfoliated h-BN layers (purchased from HQ Graphene) to Au-plated silicon wafer.
Calculation of contact pressure and radius
According to the contact mechanics model (JKR model)50, we can estimate the radius of contact pressure as follows. The relationship between the averaged contact pressure P, contact area radius a, radius of tip curvature R, normal load F and surface energy per unit contact area γ can be written as follows:
| 6 |
| 7 |
where R = 25 nm, F = 840 nN, , , = , present the Poisson’s ratio and Young’s modulus of tip materials Ir, present the Poisson’s ratio and Young’s modulus of graphene substrate. According to the above calculation, we can obtain the averaged contact pressure is about 9.1 GPa, and the contact radius is about 5.4 nm.
Ab-initio calculations
The calculations of electron density and atomic force of tribosystems under electric current were implied in Quantum ATK. The Fritz-Haber Institute (FHI) type of pseudopotentials was used in all calculations. The Grimme method (DFT + D3) was used for dispersion force corrections. To consider the spin polarization of the Ni substrate, we use the spin-generalized gradient approximation (SGGA) based on Perdew-Burke-Ernzerhof (PBE) as the exchange-correlation functional. Before calculating the electronic properties, the atomic configurations of the tribosystems are optimized until the forces on all the relaxed atoms are less than 0.01 eV Å−1. To calculate the non-equilibrium electron density and electronic properties of the tribosystems when electric current flows, the non-equilibrium Green’s function method was used. When calculating the atomic force of tribosystems under electric current, their atomic configurations are fixed to ensure that the atomic force change is purely induced by electron density redistribution.
PT-E model calculations
The Langevin equation in the PT-E model is solved using the fourth-order Runge–Kutta algorithm17,47. The sliding barrier U0 is set to 2 eV. a is set to 2.46 Å, equal to the graphene lattice parameter. Other parameters k = 7 N m−1, m = 2 × 10−12 kg, 0.025 ns−1 are set to the magnitude commonly used in the PT model.
Supplementary information
Source data
Acknowledgements
The authors acknowledge the support of the National Natural Science Foundation of China (Grant Nos. 52225502 to T. Ma, 52305200 to A. Song, 52363033 to H. Wu), Key Research and Development Program of Yunnan Province (202203ZA080001-3 to H. Wu), New Cornerstone Science Foundation through the XPLORER PRIZE to T. Ma, Yunnan Precious Metals Laboratory Science Program (YPML-2023050251 to A. Song), Scientific and Technological Project of Yunnan Precious Metals Laboratory (YPML-20240502088 to H. Wu).
Author contributions
T.M. conceived the project. A.S. carried out the first-principles calculations. J.Z., X.T. and A.S. performed the c-AFM experiments. Z.X. carried out the FEM calculations. A.S., J.C. and Q.L. developed the model. A.S. and T.M. wrote the manuscript. J.L., H.Wu., Y.Hu., X.Li, X.L. and H.W. gave suggestions to the experiment and theoretical works. A.S., J.Z. and X.T. contribute equally to the work. All authors analyzed and discussed the results.
Peer review
Peer review information
Nature Communications thanks Florian Pape, Martin Rejhon, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request. Source data are provided within this paper. Source data are provided with this paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Aisheng Song, Jian-Xun Zhao, Xin Tang.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-025-59989-4.
References
- 1.Holmberg, K. & Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction5, 263–284 (2017). [Google Scholar]
- 2.Berman, D., Deshmukh, S. A., Sankaranarayanan, S. K., Erdemir, A. & Sumant, A. V. Macroscale superlubricity enabled by graphene nanoscroll formation. Science348, 1118–1122 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Zhang, S., Ma, T. B., Erdemir, A. & Li, Q. Y. Tribology of two-dimensional materials: From mechanisms to modulating strategies. Mater. Today26, 67–86 (2019). [Google Scholar]
- 4.Carpick, R. W. Physics - Controlling friction. Science313, 184–185 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Bresme, F., Kornyshev, A. A., Perkin, S. & Urbakh, M. Electrotunable friction with ionic liquid lubricants. Nat. Mater.21, 848–858 (2022). [DOI] [PubMed] [Google Scholar]
- 6.Wang, X. et al. Atomic-scale friction between single-asperity contacts unveiled through in situ transmission electron microscopy. Nat. Nanotechnol.17, 737–745 (2022). [DOI] [PubMed] [Google Scholar]
- 7.He, Y. et al. Atomistic observation on diffusion-mediated friction between single-asperity contacts. Nat. Mater.21, 173–180 (2022). [DOI] [PubMed] [Google Scholar]
- 8.Liu, J. et al. Direct-current triboelectricity generation by a sliding Schottky nanocontact on MoS2 multilayers. Nat. Nanotechnol.13, 112–116 (2018). [DOI] [PubMed] [Google Scholar]
- 9.Peng, Y. H. et al. Elastohydrodynamic friction of robotic and human fingers on soft micropatterned substrates. Nat. Mater.20, 1707 (2021). [DOI] [PubMed] [Google Scholar]
- 10.Aymard, A., Delplanque, E., Dalmas, D. & Scheibert, J. Designing metainterfaces with specified friction laws. Science383, 200–204 (2024). [DOI] [PubMed] [Google Scholar]
- 11.Koren, E., Lortscher, E., Rawlings, C., Knoll, A. W. & Duerig, U. Adhesion and friction in mesoscopic graphite contacts. Science348, 679–683 (2015). [DOI] [PubMed] [Google Scholar]
- 12.Tshiprut, Z., Filippov, A. E. & Urbakh, M. Tuning diffusion and friction in microscopic contacts by mechanical excitations. Phys. Rev. Lett.95, 016101 (2005). [DOI] [PubMed] [Google Scholar]
- 13.Socoliuc, A. et al. Atomic-scale control of friction by actuation of nanometer-sized contacts. Science313, 207–210 (2006). [DOI] [PubMed] [Google Scholar]
- 14.Shi, S., Guo, D. & Luo, J. Micro/atomic-scale vibration induced superlubricity. Friction9, 1163–−1174 (2020). [Google Scholar]
- 15.Iizuka, H., Nakamura, J. & Natori, A. Control mechanism of friction by dynamic actuation of nanometer-sized contacts. Phys. Rev. B80, 155449 (2009). [Google Scholar]
- 16.Lantz, M. A., Wiesmann, D. & Gotsmann, B. Dynamic superlubricity and the elimination of wear on the nanoscale. Nat. Nanotechnol.4, 586–591 (2009). [DOI] [PubMed] [Google Scholar]
- 17.Cao, J. & Li, Q. Vibration-induced nanoscale friction modulation on piezoelectric materials. Friction10, 1650–−1659 (2022). [Google Scholar]
- 18.Gnecco, E. et al. Dynamic superlubricity on insulating and conductive surfaces in ultra-high vacuum and ambient environment. Nanotechnology20, 025501 (2009). [DOI] [PubMed] [Google Scholar]
- 19.Pedraz, P., Wannemacher, R. & Gnecco, E. Controlled suppression of wear on the nanoscale by ultrasonic vibrations. ACS Nano9, 8859–8868 (2015). [DOI] [PubMed] [Google Scholar]
- 20.Dong, Y. et al. Phononic origin of structural lubrication. Friction11, 966–976 (2023). [Google Scholar]
- 21.Liu, L. et al. Recent advances in friction and lubrication of graphene and other 2D materials: mechanisms and applications. Friction7, 199–216 (2019). [Google Scholar]
- 22.Cannara, R. J. et al. Nanoscale friction varied by isotopic shifting of surface vibrational frequencies. Science318, 780–783 (2007). [DOI] [PubMed] [Google Scholar]
- 23.Jinesh, K. B., Krylov, S. Y., Valk, H., Dienwiebel, M. & Frenken, J. W. M. Thermolubricity in atomic-scale friction. Phys. Rev. B78, 155440 (2008). [DOI] [PubMed] [Google Scholar]
- 24.Krylov, S. Y., Jinesh, K. B., Valk, H., Dienwiebel, M. & Frenken, J. W. M. Thermally induced suppression of friction at the atomic scale. Phys. Rev. E71, 065101 (2005). [DOI] [PubMed] [Google Scholar]
- 25.Krylov, S. Y. & Frenken, J. W. M. The physics of atomic-scale friction: Basic considerations and open questions. Phys. Status Solidi B251, 711–736 (2014). [Google Scholar]
- 26.Choudhary, N. & Kaur, D. Vibration damping materials and their applications in nano/micro-electro-mechanical systems: a review. J. Nanosci. Nanotechnol.15, 1907–1924 (2015). [DOI] [PubMed] [Google Scholar]
- 27.van Spengen, W. M. MEMS reliability from a failure mechanisms perspective. Microelectron. Reliab.43, 1049–1060 (2003). [Google Scholar]
- 28.Krim, J. Controlling friction with external electric or magnetic fields: 25 examples. Front. Mech. Eng. -Switz.5, 22 (2019). [Google Scholar]
- 29.Park, J. Y., Ogletree, D. F., Thiel, P. A. & Salmeron, M. Electronic control of friction in silicon pn junctions. Science313, 186 (2006). [DOI] [PubMed] [Google Scholar]
- 30.Park, J. Y., Qi, Y., Ogletree, D. F., Thiel, P. A. & Salmeron, M. Influence of carrier density on the friction properties of siliconpnjunctions. Phys. Rev. B76, 064108 (2007). [Google Scholar]
- 31.Lang, H. J., Peng, Y. T., Cao, X. A. & Zou, K. Atomic-scale friction characteristics of graphene under conductive afm with applied voltages. ACS Appl. Mater. Interfaces12, 25503–25511 (2020). [DOI] [PubMed] [Google Scholar]
- 32.Qi, Y. B., Park, J. Y., Hendriksen, B. L. M., Ogletree, D. F. & Salmeron, M. Electronic contribution to friction on GaAs: an atomic force microscope study. Phys. Rev. B77, 184105 (2008). [Google Scholar]
- 33.Jiang, Y. et al. Tribological behavior of a charged atomic force microscope tip on graphene oxide films. Nanotechnology23, 495703 (2012). [DOI] [PubMed] [Google Scholar]
- 34.Yildiz, D., Kisiel, M., Gysin, U., Gurlu, O. & Meyer, E. Mechanical dissipation via image potential states on a topological insulator surface. Nat. Mater.18, 1201–1206 (2019). [DOI] [PubMed] [Google Scholar]
- 35.Chen, X. Y., Huang, Y., Zou, K. & Peng, Y. T. The controllable tuning of nanofriction on atomically thin hexagonal boron nitride with external electric field. Appl. Surf. Sci.581, 152361 (2022). [Google Scholar]
- 36.Zeng, Y. M., He, F., Wang, Q., Yan, X. H. & Xie, G. X. Friction and wear behaviors of molybdenum disulfide nanosheets under normal electric field. Appl. Surf. Sci.455, 527–532 (2018). [Google Scholar]
- 37.Acharya, B., Seed, C. M., Brenner, D. W., Smirnov, A. I. & Krim, J. Tuning friction and slip at solid-nanoparticle suspension interfaces by electric fields. Sci. Rep.9, 18584 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kisiel, M. et al. Mechanical dissipation from charge and spin transitions in oxygen-deficient SrTiO3 surfaces. Nat. Commun.9, 2946 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Tan, S. C. et al. Electric field controlled superlubricity of fullerene-based host-guest assembly. Nano Res16, 583–588 (2023). [Google Scholar]
- 40.Mao, J. H. et al. Realization of a tunable artificial atom at a supercritically charged vacancy in graphene. Nat. Phys.12, 545–549 (2016). [Google Scholar]
- 41.Song, A. S. et al. Fluctuation of Interfacial Electronic Properties Induces Friction Tuning under an Electric Field. Nano Lett.22, 1889–1896 (2022). [DOI] [PubMed] [Google Scholar]
- 42.Peng, J. F. et al. Friction behavior of monolayer molybdenum diselenide nanosheet under normal electric field. Phys. Lett. A384, 126166 (2020). [Google Scholar]
- 43.Tomlinson, G. A. A molecular theory of friction. Philos. Mag.7, 905–939 (1929). [Google Scholar]
- 44.Frenkel, J. & Kontorova, T. On the theory of plastic deformation and twinning. J. Phys. -Ussr1, 137–149 (1939). [Google Scholar]
- 45.Dong, Y. L., Li, Q. Y. & Martini, A. Molecular dynamics simulation of atomic friction: a review and guide. J. Vac. Sci. Technol. A31, 030801 (2013). [Google Scholar]
- 46.Kisiel, M. et al. Suppression of electronic friction on Nb films in the superconducting state. Nat. Mater.10, 119–122 (2011). [DOI] [PubMed] [Google Scholar]
- 47.Dong, Y., Vadakkepatt, A. & Martini, A. Analytical models for atomic friction. Tribol. Lett.44, 367 (2011). [Google Scholar]
- 48.Loh, O. Y. & Espinosa, H. D. Nanoelectromechanical contact switches. Nat. Nanotechnol.7, 283–295 (2012). [DOI] [PubMed] [Google Scholar]
- 49.Sun, L. Z. et al. Visualizing fast growth of large single-crystalline graphene by tunable isotopic carbon source. Nano Res10, 355–363 (2017). [Google Scholar]
- 50.Johnson, K. L., Kendall, K. & Roberts, A. D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A324, 301–313 (1971). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding authors upon request. Source data are provided within this paper. Source data are provided with this paper.