Assessing the impact of architectural and behavioral interventions for controlling indoor COVID-19 infection risk: An agent-based approach

Abstract

The COVID-19 pandemic changed our lives, forcing us to reconsider our built environment. In some buildings with high traffic flow, infected individuals release viral particles during movement. The complex interactions between humans, building, and viruses make it difficult to predict indoor infection risk by traditional computational fluid dynamics methods. The paper developed a spatially-explicit agent-based model to simulate indoor respiratory pathogen transmission for buildings with frequent movement of people. The social force model simulating pedestrian movement and a simple forcing method simulating indoor airflow were coupled in an agent-based modeling environment. The impact of architectural and behavioral interventions on the indoor infection risk was then compared by simulating a supermarket case. We found that wearing a mask was the most effective single intervention, with all people wearing masks reducing the percentage of infections to 0.08%. Among the combined interventions, the combination of customer control is the most effective and can reduce the percentage of infections to 0.04%. In addition, the extremely strict combination of all the interventions makes the supermarket free of new infections during its 8-h operation. The approach can help architects, managers, or the government better understand the effect of nonpharmaceutical interventions to reduce the infection risk and improve the level of indoor safety.

1. Introduction

Over the past 40 years, the frequency of outbreaks of respiratory infectious diseases has increased significantly [1]. The global coronavirus disease 2019 (COVID-19) pandemic caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has caused negative impacts on health and tremendous losses of human lives, with over 632 million confirmed cases and 6.5 million deaths (as of Nov 17, 2022) [2]. More than 90% of infections occurred indoors [3] due to difficulties in maintaining social distancing and limited ventilation [4]. It is reported that the indoor infection risk is 18.7 times higher than outdoors [5]. However, currently many studies on infection risk prediction focus on the city or country scale [6,7], and there are relatively few indoor infection risk prediction tools for various building types and occupant characteristics [8].

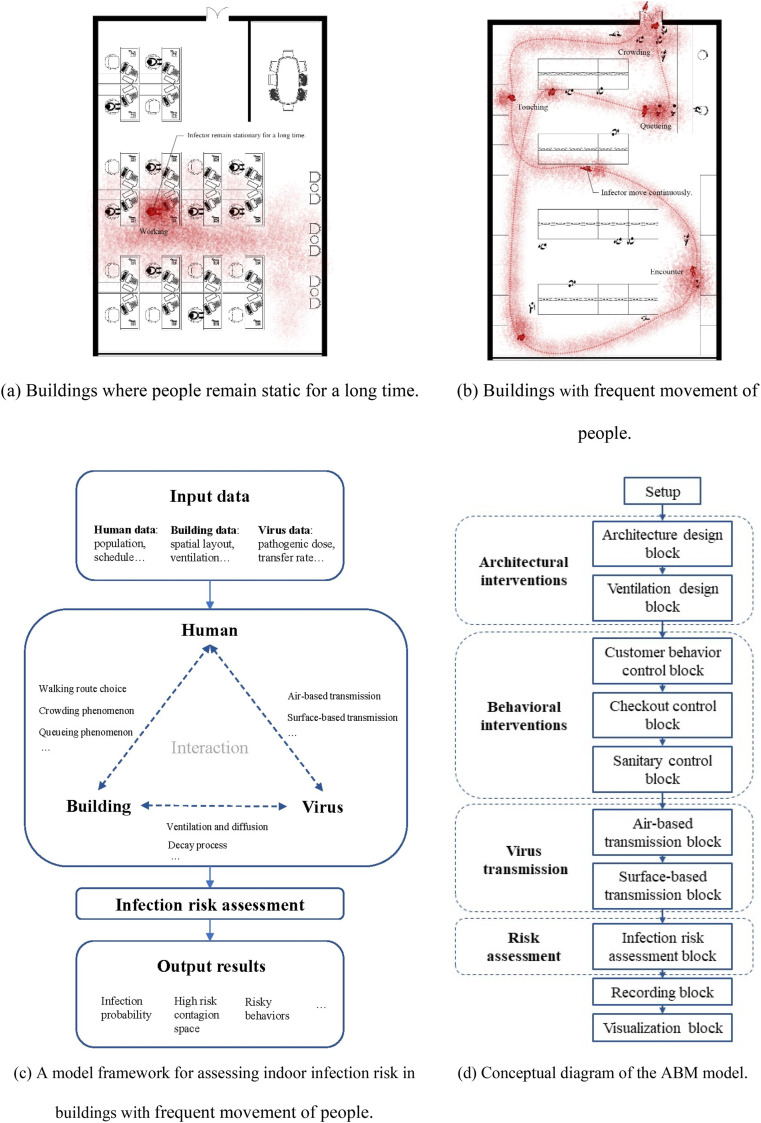
Public buildings such as offices, railway stations, supermarkets, hospitals, schools, etc. are the main places where respiratory infectious diseases spread [9]. These buildings here can be divided into two categories: one is the buildings with relatively fixed spatial positions of indoor occupants, such as office buildings, hotels or hospital wards, etc., where occupants remain relatively static for a long time; the other type is the buildings with the frequent internal pedestrian flow, such as airports, subway stations, supermarkets, etc., where the spatial positions of the occupants are constantly changing (Fig. 1 (a) (b)). The former has been studied by many researchers using Computational Fluid Dynamic (CFD) calculation [10] or the tracer gas method [11]. However, for the latter building category, indoor virus transmission simulation is more difficult. First, since the location of the infected individual is constantly changing, it is difficult for the traditional CFD method to handle this kind of dynamic simulation. Second, people's indoor positions are constantly changing due to the influence of environmental factors, such as spatial scale and real-time pedestrian flow. The complexity of the interactions between building, humans, and viruses makes it difficult to predict the infection risk of people in such buildings.

Fig. 1.

Scenarios of indoor infection risk assessment and the ABM modeling framework and approach.

Regarding human-building interaction, some researchers have explored the field of thermal performance. Hong et al. [12], Langevin et al. [13] and Zhang et al. [14] studied the effects of people opening/closing windows, turning on/off heaters, and clothing adjustment on building energy consumption and thermal comfort. For indoor virus transmission, it is more important that spatial factors affect people's paths, stay time, gathering conditions, etc. [15]. For instance, when people are looking for the products they want in a supermarket, the destinations and paths will vary depending on the spatial layout. Furthermore, in the process of moving to the destination, crowding may be caused due to the variation of spatial scale. In addition, queuing may occur due to the artificial division of some areas into linear spaces. These are human-building interactions closely related to the spread of diseases in indoor spaces [16].

Human-virus interaction mainly includes two categories: air-based transmission and surface-based transmission. For the former, high-speed camera equipment was used to capture the distribution characteristics of droplets sprayed from the mouth when people breathe, talk, cough, sneeze [17], or sing [18]. Wei et al. [19] established a mathematical model to calculate the short-range airborne transmission of SARS-CoV-2 considering the talking and coughing. For the latter, touching-related parameters and models were also established. Duives et al. [15] described and modeled in detail the process of contamination of surfaces by infected individuals and touching of surface viruses by susceptible individuals associated with SARS-CoV-2 transmission. Zhang et al. [20] established a hand contact model in an office setting to simulate the effectiveness of disinfection and behavioral interventions.

The virus-building interaction mainly includes the flow or decay of viruses caused by environmental conditions such as ventilation, temperature, and humidity. For ventilation, many researchers have used CFD methods to simulate virus flow under different ventilation conditions. Li et al. [21], Vuorinen et al. [22] and Arpino et al. [23] modeled the aerosol transmission in restaurants, retail-store, car cabins, etc. However, this method is limited by the assumption that the infected individual is fixed, which makes it difficult to simulate scenarios where people move frequently. On the other hand, the stability characteristics of viruses in different mediums, temperatures, and humidity have also been explored by medical researchers. Studies have shown that SARS-CoV-2 can remain infective on plastic surfaces for up to 9 days [24], but the survival time on copper surfaces does not exceed 4 h [25]. These studies provide basic valid data for virus-building interaction modeling.

This paper explores the prediction of infection risk of respiratory infectious disease in buildings with high traffic flow. It focuses on the interaction between humans, building, and viruses, and uses the agent-based modeling (ABM) method to couple the three kinds of interactions. Taking a supermarket as a case, we built a spatially-explicit building-scale model, based on which a parametric study was done to explore the impact of different building and behavioral measures on indoor infection risk. Through this analysis, we provide guidance for minimizing SARS-CoV-2 transmission during indoor gatherings.

2. Background

Studies on the evaluation of indoor COVID-19 infection risk of buildings can be divided into several categories, one of which is dominated by CFD simulations. Li et al. [26] performed detailed CFD simulations to simulate the spread of fine exhaled droplets in a restaurant in China to assess the possibility of airborne transmission and to characterize the associated environmental conditions. Vuorinen et al. [22] give various examples on the transport and dilution of aerosols over distances in a supermarket by using CFD simulations. In addition, Motamedi et al. [27] proposed a framework based on CFD method to evaluate the effect of different ventilation strategies on infection probability in an office room.

The other category is based on statistical data and mathematical formulas for indoor infection risk prediction. For example, Peng et al. [28] combine the key factors that control indoor airborne disease transmission including aerosol-generation rate, breathing flow rate, masking, ventilation and aerosol-removal rates, number of occupants, and duration of exposure, and finally proposed two indicators of infection risk, i.e., relative risk parameter and risk parameter.

In addition, some studies base on ABM method have coupled pedestrian models and viral transmission models for indoor infection risk prediction. D'Orazio et al. [29] proposed a probabilistic simulation model based on consolidated proximity and exposure-time-based rules to evaluate the effectiveness of mask wearing, density control and access control solutions for COVID-19 spreading in university buildings. Antczak et al. [30] built an agent-based model for evaluating the effectiveness of social distancing and checkout zone design in supermarkets during COVID-19 breaks. Alvarez & Ford [31] proposed a geospatial 3D agent-based model to explore the effect of face masks, lockdown, and self-isolation on the transmission of COVID-19 in university campuses. Harweg et al. [32] proposed an agent-based simulation of pedestrian dynamics to assess the distance measures to control close contact transmission of COVID-19. Farthing and Lanzas [33] developed an agent-based model for simulating indoor respiratory pathogen transmission in a single room scenario. The efficacy of four interventions including mask use, ventilation, pedestrian movement and social distancing was examined. Moreover, Lee et al. [34] proposed an OccSim system built in C# that generates occupancy behaviours in a 3D model of a building and helps users analyze the potential effect of virus transmission. Air-based transmission and surface-based transmission routes were both included in the model. Ronchi and Lovreglio [35] developed an occupant exposure model “EXPOSED” based on microscopic crowd models to assess the occupant exposure level in confined spaces. Additionally, Duives et al. [15] coupled a microscopic simulation model (Nomad) and a virus spread model (QVEmod) to investigate the spread of SARS-CoV-2 in indoor spaces. A restaurant was studied as a case study, and the effect of ventilation rate and face masks was compared.

Table 1 summarizes the building scenarios, interventions, involved transmission routes, methods of the model and implementation tools of recent studies on indoor infection risk assessment. Although there are many studies on indoor COVID-19 infection risk, there is still room for improvement: (1) Most of the models only cover mostly one or two transmission routes, while models combining multiple transmission routes containing air-based routes and surface-based routes are rare. Architects are difficult to obtain an overall assessment of the risk of infection in a certain spatial context covering all transmission routes. (2) Traditional CFD methods are mostly used to assess the effectiveness of ventilation interventions. It is difficult to apply CFD methods to buildings with frequent movement of occupants, where the source of contamination is not static. Therefore, it is necessary to develop an indoor infection risk assessment method that can integrate multiple transmission routes, and can quickly predict the infection risk in buildings with frequent movement of people to help architects and managers make better decisions. The flexible behavior simulation of the ABM model provides an opportunity to simulate indoor virus transmission in buildings with high traffic flow.

Table 1.

Typical research on the indoor COVID-19 infection risk assessment model.

Building scenario	Interventions	Transmission routes	Methods of the model	Implementation tools	Ref.
Restaurant	Ventilation	Short-range airborne route, Long-range airborne route	CFD method	Ansys Fluent	[26]
Supermarket	Ventilation	Short-range airborne route, Long-range airborne route	CFD, Monte-Carlo method	PALM, OpenFOAM, NS3dLab, Fire Dynamics Simulator	[22]
Office room	Ventilation	Short-range airborne route, Long-range airborne route	CFD method	Ansys Fluent	[27]
Classrooms, subway, supermarket, Stadium etc.	Ventilation rate, occupant density, mask efficiency	Long-range airborne route	Statistics-based method	Excel	[28]
University building	Wearing masks, density control, access control	Short-range airborne route	Statistics-based method	NetLogo	[29]
Supermarket	Social distancing, Checkout zone design	Short-range airborne route	Agent-based method	NetLogo	[30]
University campus	Face masks, lockdown, self-isolation	Short-range airborne route	Agent-based method	GAMA	[31]
Supermarket	Social distancing	Short-range airborne route	Agent-based method	–	[32]
Single room	Mask use, ventilation, pedestrian movement, social distancing	Short-range airborne route, Long-range airborne route	Agent-based method	NetLogo	[33]
Confined space	Occupant density	Short-range airborne route, Long-range airborne route	Agent-based method	–	[35]
Office building	Architecture design, facility and behavior management,	Short-range airborne route, Long-range airborne route, Environmental fomite route	Agent-based method	C#	[34]
Restaurant	Ventilation rate, face masks	Short-range airborne route, Long-range airborne route, Environmental fomite route	Agent-based method	–	[15]

The novelty of this study are as follows: (1) A spatially-explicit agent-based model that integrates building space, human behavior, and virus transmission to determine the efficacy of different types of interventions on the indoor infection risk was proposed. (2) The social force model simulating pedestrian movement and a simple forcing method simulating indoor airflow were coupled in an agent-based modeling environment. This study can provide architects and researchers with more comprehensive and in-depth understanding of the impact of architectural and behavioral interventions on indoor COVID-19 infection risk.

3. Methodology

3.1. Modeling framework for simulating indoor SARS-CoV-2 transmission

The above analysis indicates that an integrated model simulating the human-building-virus interaction is required to model indoor SARS-CoV-2 transmission for buildings with frequent movement of people (Fig. 1 (b)). We have designed an agent-based model, which focuses on simulating three types of interactions during indoor SARS-CoV-2 transmission: human-building interaction, human-virus interaction, and virus-building interaction. The model framework is shown in Fig. 1 (c).

The first step is to collect parametric data for humans, building, and viruses. The input variables consist of two categories. One is the fixed variables in the model, which is a constant, such as the decay rate of a virus. The other is the variables that can be changed, which can be adjusted and optimized to reduce the probability of indoor infection. This paper studies the impact of architectural and behavioral interventions on infection risk, so the adjustable variables are mainly building-related parameters and human-related parameters. The second step is to simulate the interaction of humans, building, and viruses, which includes three aspects. Human-building interaction modeling mimics indoor human activities due to architecture design, which includes walking route choice, crowding, and queuing phenomena. Human-virus interaction modeling refers to changes in virus transmission caused by various human behaviors, including air-based transmission and surface-based transmission. Virus-building interaction modeling includes two types: one is the effect of ventilation on the flow of viruses in the air, while the other is the effect of environmental media, temperature, and humidity on the virus decay rate. The third step is the infection risk assessment. The total exposure of individuals through air-based and surface-based transmission routes is counted, and then the individual infection probability is determined according to the dose-response equation. The last step is to output the predicted results, including the percentage of probable infections, high-risk contagion space, risky behavior, etc. The output data includes real-time situated visualization and timeline-based analysis.

The model was created using the open-source modeling software NetLogo and is available at https://github.com/zax1111/Indoor-COVID-19-Infection-Risk-Assessment-Model. Fig. 1 (d) shows the conceptual diagram of the model. At the beginning of the model is the input panel, which covers both building interventions and behavioral interventions. The architectural interventions rely on the building design block for inputting building plan information and the ventilation design block for inputting ventilation conditions. The behavioral interventions include a customer control block, a checkout control block, and a sanitary control block, which regulate customer shopping behavior, checkout management, and hygiene behavior, respectively. Then comes the virus transmission module, which includes the air-based transmission block and the surface-based transmission block. Finally, there is a risk assessment block, followed by a logging block and a visualization block to record data and plot real-time images.

3.2. Human-building interaction modeling

3.2.1. Route choice

When people go to their destination, the route selection problem will arise. People choose different paths in different architectural scenarios. In a familiar environment, people tend to choose the shortest path [36]. Since it is difficult to determine whether the occupants are familiar with the built environment or not, the shortest route toward one's destination is adopted in this paper. Algorithms for the shortest route include Dijkstra's algorithm [37], best-first search algorithm [38], and A-star algorithm [39], etc. We choose the A-star algorithm which is a combination of the former two.

3.2.2. Crowding phenomenon

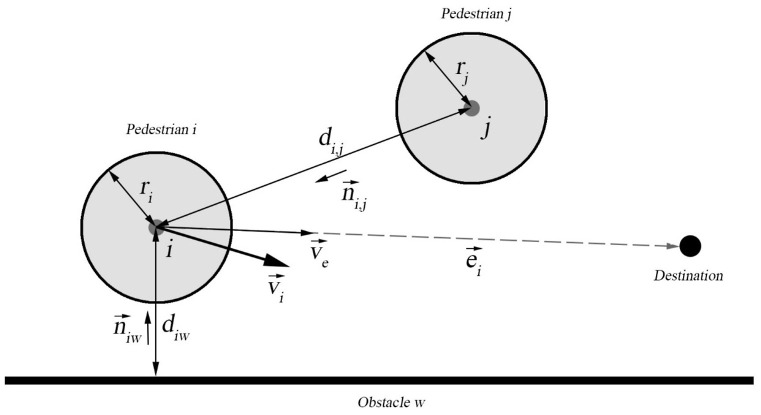
Crowding in space means that the distance between people has decreased dramatically, and this has a strong correlation with the transmission of respiratory diseases. Many pedestrian models have been proposed to characterize crowds, among which physics-based approaches are most common. Well-known examples are the fluid-dynamic model [40] and the social force model [41,42]. This paper chooses the social force model of Helbing and Peter [43], which uses driving and repulsive forces to describe the aggregation and dissipation of crowds under the variation of spatial scale. It successfully reproduced the “faster is slower” effect when crowded people push each other to go through a narrow opening. The social force model here mainly includes three types of forces, namely the driving force, the force from other pedestrians, and the force from obstacles (Fig. 2 ). We obtained the surveillance video of the case supermarket, extracted the crowd density and throughput rate at the entrance and compared them with the simulation data in the same spatial range to calibrate and enhance the model parameters. The validation and improvement process are detailed in Appendix S1.

Fig. 2.

Diagram of social force model to simulate the indoor crowding phenomenon.

3.2.3. Queuing phenomenon

Queuing is also a common phenomenon in buildings, due to the linear division of space or linear restrictions on crowd behavior. For queuing behavior, we designate a specific queuing zone in the building, where people in the zone cannot move freely but can only move in a certain direction. Furthermore, the distance between the queues can be set to reflect the effectiveness of social distancing measures.

3.3. Human-virus interaction modeling

3.3.1. Air-based transmission

Air-based transmission mainly includes two processes. One is the exhalation process, in which a person spread the virus into the air through breathing, speaking, coughing, etc. While the other is the inhalation process, in which a person inhales the virus in the air through breathing.

To describe this human-virus interaction process in the air, the model space is divided into grid cells. Each grid is 0.5 m × 0.5 m and is assumed to store air and droplets. When an infected person performs contagion-related behaviors, e.g., breathing, speaking, coughing, etc., the number of droplets in specific grids nearby will increase. All droplets are assumed to be ejected at an average human height of 1.7 m [44]. Besides, the model time step Δt is set to 0.25 s. We assume that a COVID-19 patient has the same cough frequency as a common chronic cough patient, with a 19% probability of coughing per minute [45,46], so the cough probability per Δt is 19%/60 × 0.25 = 7.92 × 10⁻⁴.

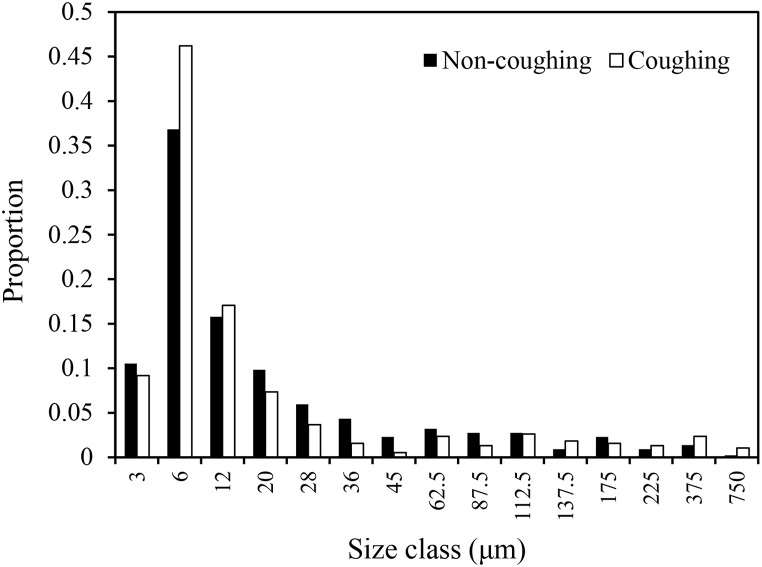
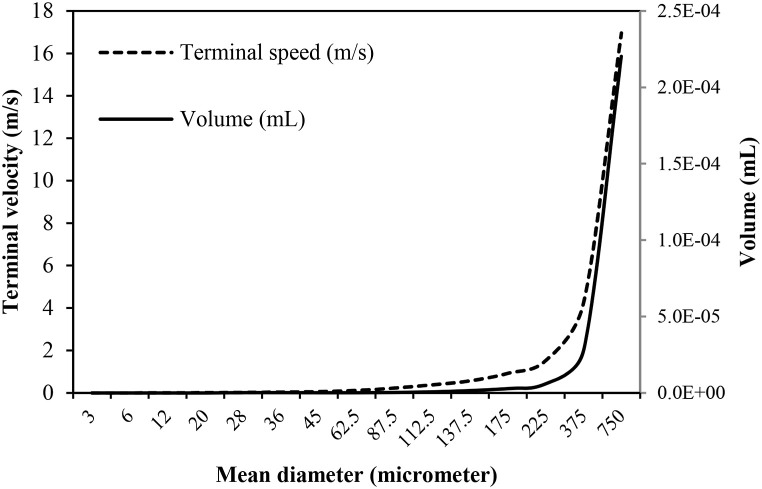
The droplets emitted from the human body vary in size, quantity, and distance in terms of different ejection activities. Although many studies classify “aerosols” (small) and “droplets” (large) by size, in this paper, we refer to all the ejected particles as “droplets” regardless of size for convenience. The droplets were classified into 16 size classes ranging from 3 μm to 750 μm in diameter as adopted from Duguid [33,47]. The distribution of droplet sizes is shown in Fig. 3 . Distributions of size classes during coughing and non-coughing events are based on the experimental findings of Chao et al. [48], which were recorded 60 mm away from people's mouths following these activities. And the air temperature and RH averaged from all experiments were 24.9 °C and 73.9%, respectively. For the droplets’ quantity, the average value of the droplet count is set to 9.7 × 10⁵ droplets/expectoration with a standard deviation of 3.9 × 10⁵ based on the model described in Ref. [33], which is derived from the Skagit County choir COVID-19 outbreak event [49]. These values are approximately equal to 970 (SD = 390) quanta/hr.

Fig. 3.

Distribution of droplet sizes during expectoration events.

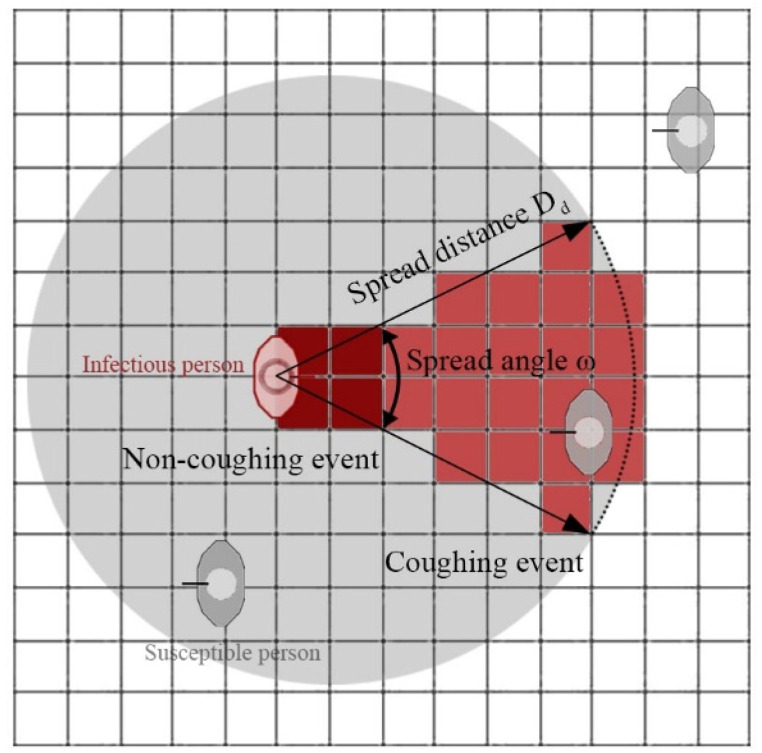
The spreading distance and angle differ for coughing and non-coughing event. Many studies have used high-speed cameras or CFD methods to collect droplet data under different behaviors, and the spatial range of droplets obtained is generally fan-shaped. We use the spread distance and spread angle index to describe the distribution of droplets in space (Fig. 4 ). Here the log-normal distributions are used to describe the randomness of the two variables [50]. Travel distances for coughing events follow the distribution with a mean of 5 m and a standard deviation of 0.256 m [51]. Travel distances for non-coughing events follow the distribution with a mean of 0.55 m and a standard deviation of 0.068 m based on Das et al.’ finding [52]. They found that the majority of 100 μm droplets will fall 0.55–2.35 m away from the expelling individual, depending on initial velocity. Since the spatial distribution of droplets is similar to a fan, the in-cone function in NetLogo is used. The cone is defined by two inputs, the distance and the angle which may range from 0 to 360 and is centered around the agent's current heading. The spread angle during coughing and non-coughing expectations were 35° and 63.5°, respectively according to Kwon et al. [53] and Gupta et al. [54]. Table 2 summarizes the parameters under coughing and non-coughing event.

Fig. 4.

Schematic diagram of spread angle and distance during coughing and non-coughing event.

Table 2.

Droplets spreading parameters under coughing and non-coughing event.

	Spread angle	Spread distance (mean)	Spread distance (standard deviation)	Number(mean)	Number(standard deviation)
Non-coughing	63.5°	0.55 m	0.068 m	9.7 × 105	3.9 × 105
Coughing	35°	5 m	0.256 m	9.7 × 105	3.9 × 105

For the inhalation process, if a susceptible person is located in the contaminated cell, the droplets containing the virus will be inhaled at a certain speed, and the virus exposure of the individual is reached. The inhalation rate for simulated individuals was set to 0.023 m³ air/min, equivalent to light physical activity for adults [55,56]. The number of droplets inhaled by an individual is calculated using Eq. (4).

$${\mathrm{D}}_{inhale}\left(t\right)=\frac{D}{V_{cell}}{\gamma }_{inhale}\Delta t$$ (4)

Where D _inhale (t) is the number of droplets inhaled by a person during (t-Δt, t), D is the total number of droplets in the unit cell, V _cell is the volume of the spatial unit grid, and γ _inhale is the inhalation rate of the person.

The total amount of viruses inhaled by a person is the sum of the number of viruses contained in droplets of each size, while the number of viruses per droplet scales with droplet size. We assume that the droplets are spherical [57] and hence the volume can be estimated as shown by the solid line in Fig. 5 . Furthermore, we set ρ _virus equals 2.35 × 10⁹ viruses/mL fluid according to the findings of Wölfel et al. [58] and Villers et al. [59]. Finally, the individual's virus exposure is calculated as shown in Eq. (5).

$${\mathrm{V}}_{inhale}\left(t\right)=\sum D_{inhale}\left(t\right)V_{droplets}{\rho }_{virus}\times \left(1-M\right)$$ (5)

Where V _inhale (t) is the number of viruses inhaled by a person during (t-Δt, t), V _droplets is the volume of droplets, ρ _virus is the number of viruses per mL fluid, M denotes the filter efficiency of face masks against droplets. It is noted that here we have added M as a parameter indicating the filtration efficiency of the mask to measure the efficacy of mask interventions.

Fig. 5.

The volume and terminal speed of droplets of different sizes in the model.

3.3.2. Surface-based transmission

A person can be exposed to the virus by touching a contaminated surface with their hands and then touching the mucous membranes of the body, which is surface-based transmission. It includes two processes: one is the contamination of environmental surfaces, while the other is the intake of viruses triggered by touching.

For the contamination process, there are two sources of viruses on indoor environmental surfaces. One is the deposition of droplets caused by activities such as speaking or coughing when an infected person is close to an environmental surface. The other is virus transmission due to an infected person touching a surface with their hands. Since the number of viruses transmitted by the hands of the infector is quite limited and difficult to determine, only the former source is considered here. That means the only way for an environmental surface to be contaminated is if it is spoken or coughed on, not through contact in this model.

When an infectious person speaks or coughs toward an object, the droplets may settle to the surface. Here, we assume that when the object is within the spreading distance and spreading angle of the infected person, the droplets in this cell will be evenly deposited on its surface, and the object becomes a "fomite" (Eq. (6)).

$${\mathrm{F}}_{surface}\left(t\right)=D_{cell}\left(t\right)$$ (6)

Where F _surface denotes the viruses on the environmental surfaces, and D _cell denotes the viruses sprayed into the cell in the form of droplets.

When a susceptible person touches a contaminated surface with hands, the virus is transferred to his/her hands. Eq. (7) is used to calculate the number of viruses received by the hands.

$${\mathrm{F}}_{hands}\left(t\right)=F_{surface}\left(t\right)T_{sh}\frac{{\mathrm{A}}_{\text{hand}}}{A_{surface}}$$ (7)

Where F _hands denotes the amount of virus that hands acquire from the environment susceptible individuals, and F _surface represents the viruses on the environmental surfaces involved in the touch. T _sh is the transfer efficiency from the environmental surface to the hands. A _hand denotes the contaminated hand surface area. A _surface is the average environmental surface area touched per hand contact. Virus transfer efficiency from a nonporous surface to a fingertip has been estimated to be 0.5% per touch per fingertip [56,60]. The authors could not locate published data on the virus transfer efficiency from porous surfaces to fingertips, but the transfer efficiency for bacteria from a porous surface has been estimated to be 0.1% per touch per fingertip [60]. Therefore, for all the indoor surfaces in general we assumed that T _sh equals 0.3% [61]. A _hand is set to 10 cm², which is approximately the area of five fingertips [62]. A _surface here is set to 50 cm × 50 cm = 2500 cm², which is the area of a grid cell [63].

In addition, supermarkets have their particularity for surface-based transmission, since the virus is deposited on the surface of the goods while the goods will be continuously taken away due to shopping activity. We roughly assume that each cell representing a shelf is loaded with approximately 10 goods, so each time a customer takes away the goods in the grid, it will take away 1/10 of the virus on the surface of the cell.

For some environmental surfaces that people stay nearby for a relatively long time, such as counters in supermarkets, people will touch them with a certain frequency. Therefore, such high-touch surfaces are assumed to be touched by proximate individuals at a constant rate as shown in Eq. (8).

$${\mathrm{F}}_{hands}\left(t\right)=F_{surface}\left(t\right){\mathrm{F}}_{sh}{T}_{sh}\frac{{\mathrm{A}}_{\text{hand}}}{A_{surface}}\Delta t$$ (8)

Where F _sh is the probability of hand contact with certain high-touch surfaces during (t-Δt, t). For example, in the supermarket case in this paper, we set the probability of people touching the counter surface as 0.2 times/min based on the observation of the supermarket counter [64,65].

Susceptible people usually touch their facial mucous membranes with a certain frequency, so that the viruses enter the body and lead to infection. Similar to contact with high-touch surfaces, we use Eq. (9) with a frequency index to calculate the amount of virus transferred during this process.

$${\mathrm{E}}_{face}\left(t\right)=F_{hand}\left(t\right){\mathrm{F}}_{hf}{T}_{hf}\frac{{\mathrm{A}}_{\text{face}}}{A_{hand}}\Delta t$$ (9)

Where E _face denotes the amount of virus that facial mucous membranes acquire from hands, and F _hand denotes the viruses on the hands involved in the touch. F _hf is the probability of hand contact with facial mucous membranes during (t-Δt, t). T _hf is the transfer efficiency from hands to the facial membranes per touch. A _face denotes the facial mucosal membranes area touched, and A _hand is the contaminated hand surface area. F _hf was set to 1.6 × 10⁻¹ per min based on the observation of 26 persons who collectively touched facial mucosal membranes unconsciously 1024 times in 4 h [66,67]. T _hf from a fingertip to facial mucosal membranes per touch was set to 0.35 [62,67]. Considering that the touch involves one fingertip of the five fingers on the same hand, A _face/A _hand was set to 0.2 [67].

3.4. Virus-building interaction modeling

3.4.1. Droplet deposition

Droplets may deposit to the surface of the environment due to the force of gravity after being ejected from the mouth. Droplets have different terminal speeds due to their different sizes and masses. According to Anchordoqui and Eugene [57], we assume that each droplet is spherical to obtain different terminal speeds for different sizes of droplets, which is shown by the dotted line in Fig. 5.

3.4.2. Droplet flow

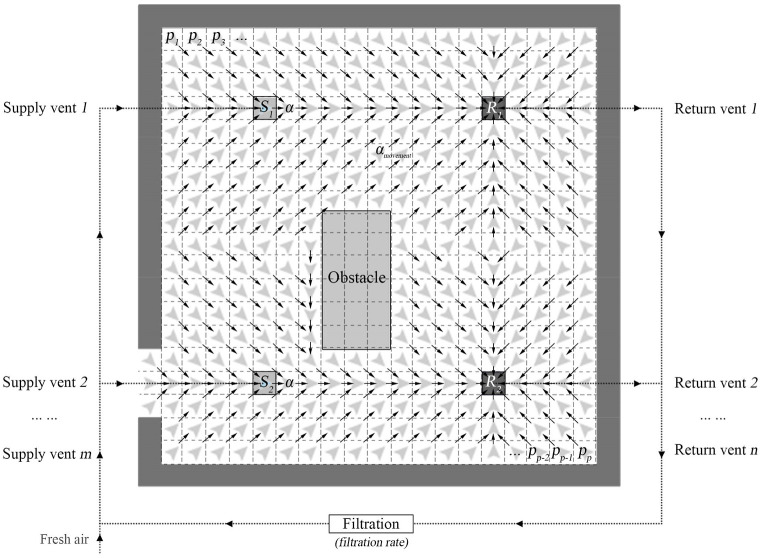
Some small droplets can float in the air for a long time, which allows the droplets to move throughout the space via forced airflow before the droplets settle to the ground. Here we designed a simple forcing method to simulate indoor airflow (Fig. 6 ). In a mechanically ventilated space, the air will generally flow continuously from the supply vents to return vents. Therefore, special supply vent cells and return vent cells were designed in NetLogo, and the undeposited droplets in other cells will gradually move toward the return vent according to certain rules. For the indoor airflow process, we consider three important indicators: air path, air change rate, and air filtration rate. The mechanism of the simple forcing method is detailed in Appendix S2.

Fig. 6.

Simple forcing method for simulating indoor airflow by agent-based modeling.

3.4.3. Droplet diffusion

In addition to flow by ventilation, droplets in the air will also spontaneously diffuse, which is caused by the diffusion properties of the gas itself. We set the droplets to diffuse to 8 surrounding cells with no walls or furniture at a rate of 1.5 × 10⁻³ m³/min according to the findings of Castillo and Weibel [68].

3.4.4. Virus decay

Viruses gradually decay in the air and on environmental surfaces. Half-life values are often used to describe the stability of viruses in different mediums. For the convenience of calculation, the variation of decay rate over time was simplified as linear regression. We assume that the viruses in the air decay at a rate of 1.27 × 10⁻⁴/s in terms of the half-life median of SARS-CoV-2 [25,69].

For the supermarket case we studied, an investigation of the surface material shows that the surfaces of the goods and shelves in the supermarket are mostly plastic, while the surfaces of the counters are made of stainless steel. Therefore, the virus decay rate on store shelves was set to 2.04 × 10⁻⁵/s [70], and the virus decay rate on counters was set to 2.47 × 10⁻⁵/s [70]. The decay rate here is the rate when the ambient temperature is 21 °C–23 °C and the relative humidity is 40%. Since the indoor temperature and humidity fluctuations are relatively small, the influence of indoor temperature and humidity variations on the decay rate is not considered [70].

3.5. Infection risk assessment

We modeled the relationship between exposure and infection risk using an exponential dose-response relationship [71] (Eq. (10)).

$$p\left(d\right)=1-\exp \left(-\frac{d}{k}\right)$$ (10)

Where p(d) is the risk of illness at the dose of d; and parameter k equals the reciprocal of the probability that a single pathogen will initiate the response. The value of k is set to 4.1 × 10² according to Watanabe et al.'s research on SARS Coronavirus [72]. In addition, viruses that enter the body from different mucous membranes are simplified here as being of equal efficacy.

The main parameter settings adopted for the indoor SARS-CoV-2 transmission model are summarized in Table 3 . It is worth noting that there are many variants of SARS-CoV-2 virus, e.g., Delta and Omicron, and these variants may have an impact on parameters such as the amount of virus exhaled by infected patients, the rate of viral decay and the pathogenic dose. For example, Lina et al. proved that more SARS-CoV-2 particles were exhaled by the Omicron patients than the Delta patients [73]. To avoid confounding of the results by variant factors, the original strain (D614) data were used in this paper to better facilitate comparison of the role of architectural and behavioral factors.

Table 3.

Parameters for the agent-based indoor SARS-CoV-2 transmission model.

Model parameter	Value (s)/Distribution	Reference (s)
Human-related parameters
Expectoration height	1.7 m	[44]
Interaction intensity (A)	2000 N/m	[74]
Interaction range (B)	0.5 m	[75]
Relaxation time ($T_{\alpha }$)	0.5 s	[75]
Expected speed (ve)	ve ∼ N (1.29, 0.262) m/s	[76]
Pedestrian mass (mi)	mi ∼ N (65, 52) kg	[77]
Anisotropy index (${\lambda }_i$)	0	[77]
Cough frequency	0.19 coughs/min	[45,46]
Inhalation rate	0.023 m3 air/min	[55,56]
Virus-related parameters
Droplets number (Dn)	ln Dn ∼ N (9.7 × 105, (3.9 × 105)2)/expectoration	[33,49]
Droplets spread angle-coughing (ωcoughing)	35°	[53,54]
Droplets spread angle-not coughing (ωnot-coughing)	63.5°	[53,54]
Droplets spread distance-coughing (Dd-coughing)	Dd-coughing ∼ N (5, 0.2562) m	[51]
Droplets spread distance-not coughing (Dd-not-coughing)	Dd-not-coughing ∼ N (0.55, 0.0682) m	[52]
Viruses density in droplets (ρvirus)	2.35 × 109 viruses/mL	[58,59]
Transfer efficiency from surfaces to hands (Tsh)	3 × 10−3	[56,60,61]
Transfer efficiency from hands to facial membranes (Thf)	0.35	[62]
Hand surface area (Ahand)	10 cm2	[62]
Touch frequency with counter surface (Fsh)	0.2 times/min	[64,65]
Touch frequency with target facial membranes (Fhf)	1.6 × 10−1 times/min	[66,67]
Viruses' decay rate in the air	1.27 × 10−4/sec	[25,69]
Viruses' decay rate on the plastic	2.04 × 10−5/sec	[25,70]
Viruses' decay rate on the steel	2.47 × 10−5/sec	[25,70]
Infection risk of a single virion (k)	4.1 × 102	[72]
Diffusion rate	1.5 × 10−3 m3/min	[68]
Building-related parameters
Size of spatial cell	0.5 m × 0.5 m	–

3.6. Case study

3.6.1. The underground supermarket and customer activity at Tianjin University, China

The case is an underground supermarket located in Tianjin University, China, as shown in Fig. 7 . The supermarket has a rectangular shape with an area of 217.5 m². It has only one entrance and exit and the shelves are distributed in rows. There are five checkouts in the supermarket, but they are not always open. The supermarket is open from 9:00 to 17:00 daily. The supermarket has three air supply vents in the central part, but only one return vent in the corner. Most of the customers are students, who come to buy some daily necessities such as fruit and vegetables. Crowding and queuing often occur in the supermarket according to site investigation.

Fig. 7.

The underground supermarket at Tianjin University, China.

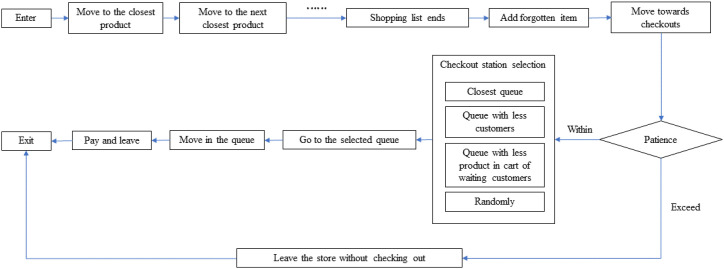
Based on the detailed observations of the customers in the supermarket and previous studies [78,79], consumer behavior rules in the supermarket were developed (Fig. 8 ). We assume that each consumer enters the supermarket with a specifically defined shopping list [80]. The consumer first moves to the closest product, picks up the item and adds it to his/her hands or shopping cart, and then walks to the next closest product. Moreover, customers often want to buy something impromptu, or forget about something they want to buy and return to buy it according to some studies [81,82]. To describe the shopping behavior more accurately, we add a recall mechanism when the shopping list ends, i.e., if the consumer forgets to buy something, he/she can add the item to the shopping list and go get it. When all the items on the shopping list are picked up, the consumer will move towards the checkout stations.

Fig. 8.

The customer's activity flow and checkout selection strategies.

According to the questionnaire survey of customers, customers mainly have several cashier selection strategies: (1) choosing the queue closest to him, (2) choosing the queue with the least number of customers, (3) choosing the queue with the least number of products in the hands/carts of waiting customers, and (4) choosing randomly. This is consistent with the findings of some studies on queuing behavior in supermarkets [83,84]. A random function was set up and customers will choose one of the above queuing strategies randomly. In addition, if there are too many customers in the current queue, which exceeds the patience of some customers, he/she will choose to leave the supermarket directly without checking out [85]. When queuing, the customer's route is a straight line, and the moving speed is determined by the checkout speed of the cashier. Finally, when payment is made, the customer leaves the supermarket through the exit. Fig. 8 presents the customer's activity flow and checkout selection strategies.

3.6.2. Architectural and behavioral interventions

Among prospective preventions [24,[86], [87], [88]], five types of possible and pragmatic architectural and behavioral interventions were considered: (a) spatial layout, (b) air ventilation, (c) customer control, (d) checkout control, and (e) sanitary measures.

• (a)Spatial layout

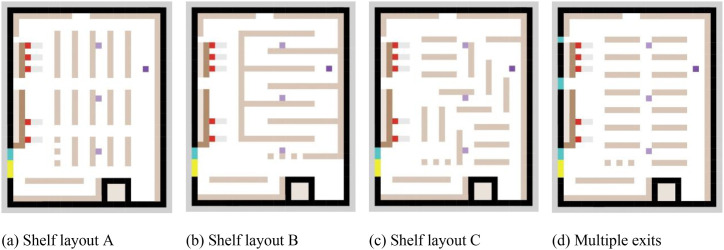
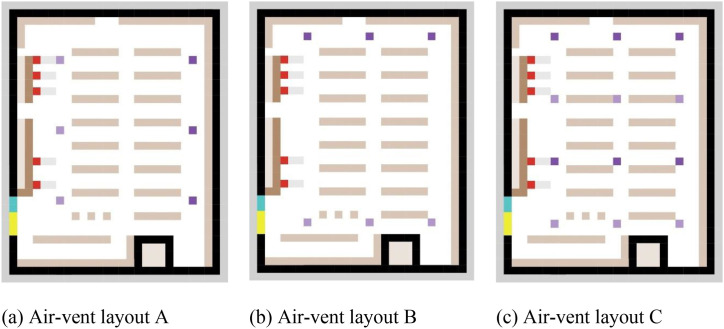
The spatial layout can change the movement trajectory of the crowd and form different gathering or contact situations, resulting in different infection risks. Taking the supermarket as the case, we mainly consider changing the layout of supermarket shelves and entrances/exits, which is an intervention that can be easily realized. Here, under the premise of ensuring the same quantity of goods, we designed three types of shelf layouts (with one exit), as shown in Fig. 9 (a) (b) (c). Supermarket Layout B is based on the special control measures for supermarkets in some areas of China during the epidemic period. According to the Operational Guidelines for Prevention and Control of COVID-19 Epidemic issued by the Chinese government, supermarkets, restaurants et al. may have one-way pedestrian flow restrictions to control indoor infection risk. Literatures such as Ying, F. and O'Clery, N [89]. also studied the effect of supermarket one-way aisle layout on indoor transmission of COVID-19. Therefore, we set up Layout B that restricts people to one-way walking routes to investigate the effect of one-way pedestrian flow layout on the indoor infection risk. On the other hand, Layout C was designed to cope with the increasing variety of supermarket shelf layout designs. The design of supermarket shelves is pushing forward, and some more flexible layouts are starting to emerge [90,91], instead of the traditional constant rows and columns. Therefore, we designed a flexible shelf Layout C to explore the impact of a looser planar organization on the indoor infection risk. In addition, two exits were added to the layout of the base scenario with only one exit to reduce the possibility of congestion as shown in Fig. 9 (d). After checking out customers will choose the nearest exit to leave.

• (b)Air ventilation

Fig. 9.

Scenarios with different spatial layouts.

Three factors are considered for the ventilation system, including air change rate, air-vent layout, and filter efficiency. For the air change rate, we assumed that the ACH of the supermarket was increased to 10 times/hour, 15 times/hour, and 20 times/hour from the baseline of 5 times/hour. For filter efficiency, we assume that the filter efficiency varies from 40% to 60%, 80%, and 100%. Additionally, three types of the air-vent layout were designed for comparison as shown in Fig. 10 .

• (c)Customer control

Fig. 10.

Scenarios with different air-vent layouts.

For customer control, four interventions were explored. One intervention is to control the maximum number of customers in the supermarket, including 50 people (base scenario), 30 people, and 20 people. The second is to control the time interval for the flow of people entering the supermarket, which are 5s (base scenario), 10s, and 15s respectively. The third is controlling physical distance when queuing. We assumed a greater physical distance of 1.0 m between customers while queuing to check out than the base scenario (0.5 m).

• (d)Checkout control

Checkout control refers to adjusting the open percentage of checkout, which are 50% (base scenario), 20%, 80%, and 100% open respectively.

• (e)Sanitary measures

According to previous reports on mask efficiency, we assumed that face mask-wearing could reduce the emission of viruses by 95% [92]. Furthermore, the use of masks reduced the probability of facial mucous membrane touch per min from 1.6 × 10⁻¹ per min to 5.4 × 10⁻² per min, because touches of the eyes accounted for 33% of the facial mucosal membrane touches involving the eyes, nose, and mouth [66]. In addition, if the infected person wears a mask, the spread distance and angle were set to 0. Here we assume three scenarios: the proportion of people wearing masks is 0% (base scenario), 50%, and 100% respectively. Surface cleaning can eliminate viruses on the surface of objects. We assumed that 99.9% of the viruses on the environmental surface were removed through decontamination when being cleaned [24]. According to our survey of several supermarkets, we found that the supermarkets on campus were mostly cleaned in the early morning, lunchtime and dinner time with an interval of approximately 4 h. Therefore, two cleaning scenarios were explored, the base scenario with no cleaning and cleaning every 4 h.

All the architectural and behavioral interventions involved are presented in Table 4 together with their variable values. In addition, the initial number of infections was set to 5%. The simulation period is 8 h (9:00–17:00). Due to the randomness of the simulation, we performed 10 simulations for each scenario to overcome the fluctuation of results due to randomness. A total of 38 × 10 = 380 simulations were performed, and each simulation took about 6 h on a desktop with an i7-CPU 3.60 GHz processor and 8 GB of RAM. The results of each metric are stored as NetLogo “list” data, and each data in the list corresponds to a time t. These data have two destinations: first, they are processed in NetLogo and programmed into “World” interface for real-time monitoring of spatial aggregation status, virus exposure and number of infections etc.; second, the multiple list data including the time list, are combined as a matrix and exported as.csv data, which was then imported into IBM SPSS Statistics software for further statistical analysis.

Table 4.

Descriptions and values of architectural and behavioral interventions.

Interventions	Variables	Values	Unit
Spatial layout	Shelf layout	Layout (base), A, B, and C	–
	Exit	Single exit (base), Multiple exits	–
Air ventilation	Air change rate	5 (base), 10, 15, 20	times/hour
	Filter efficiency	0.4 (base), 0.6, 0.8, 1.0	–
	Air-vent layout	Layout (base), A, B, and C	–
Customer control	Maximum customer number	50 (base), 30, 20	–
	Enter interval	5 (base), 10, 15	second
	Queueing distance	0.5 (base), 1.0	m
Checkout control	Checkout open percentage	20%, 50% (base), 80%, 100%	–
Sanitary measures	Mask percentage	0 (base), 50%, 100%	–
	Surface cleaning interval	No cleaning (base), 4.0	hour

4. Results

4.1. The base scenario

4.1.1. Real-time situated visualization

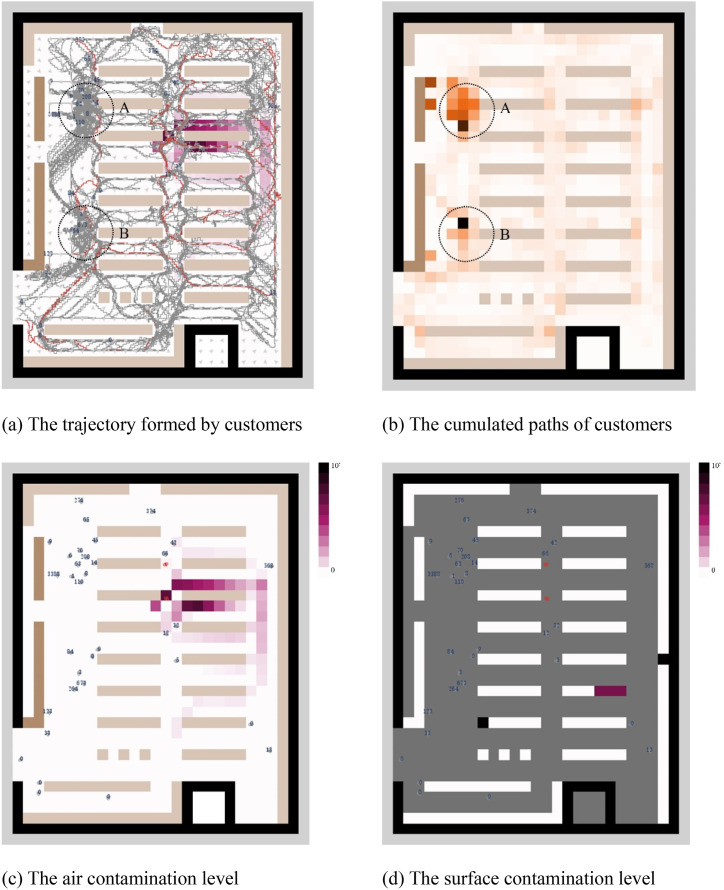
An interface showing the movement of people and environmental pollution in real time was created. Fig. 11 shows the instantaneous state of a simulation of the base scenario at the fifth minute. Fig. 11 (a) shows the movement paths of all customers in the supermarket in the first 5 min. And Fig. 11 (b) is the heat map of the cumulated path, indicating the number of times people pass by here. It can be seen that the flow of people mainly moves along the three longitudinal aisles formed by the shelves, while the spaces in front of the checkout are the area where people pass the most. Crowding is easy to form in two local spaces (areas “A” and “B”) with high traffic near checkouts, which are relatively high-risk spaces for virus transmission.

Fig. 11.

The real-time visualization of customers’ status and environmental contamination level of a simulation for the base scenario at the fifth minute. Crowding is easy to form in two local spaces (areas “A” and “B”) with high traffic near checkouts. The degree of air contamination between the infected individual and the return air vent is higher than in other directions, and the shelves near the entrance have been polluted to a high degree.

Fig. 11 (c) shows the air contamination level of the supermarket at 5 min. Red dots are infectious people who were originally infected by default. It can be seen that air contamination levels are much higher near infectious people. The instantaneous number of viruses in the cell where the infectious person is located can reach 7.36 × 10⁴. The high-concentration virus air will float to the return vent after being exhaled, increasing the air contamination level on the right side of the infectious person. Fig. 11 (d) shows the contamination level of shelves and counter surfaces at 5 min. It indicates that the shelves near the entrance have been polluted to a high degree, which is most likely due to the large number of people passing by here. In other words, this real-time spatially-based visualization can detect high-risk local spaces that are prone to congestion or environmental surfaces prone to be contaminated.

4.1.2. Timeline-based analysis

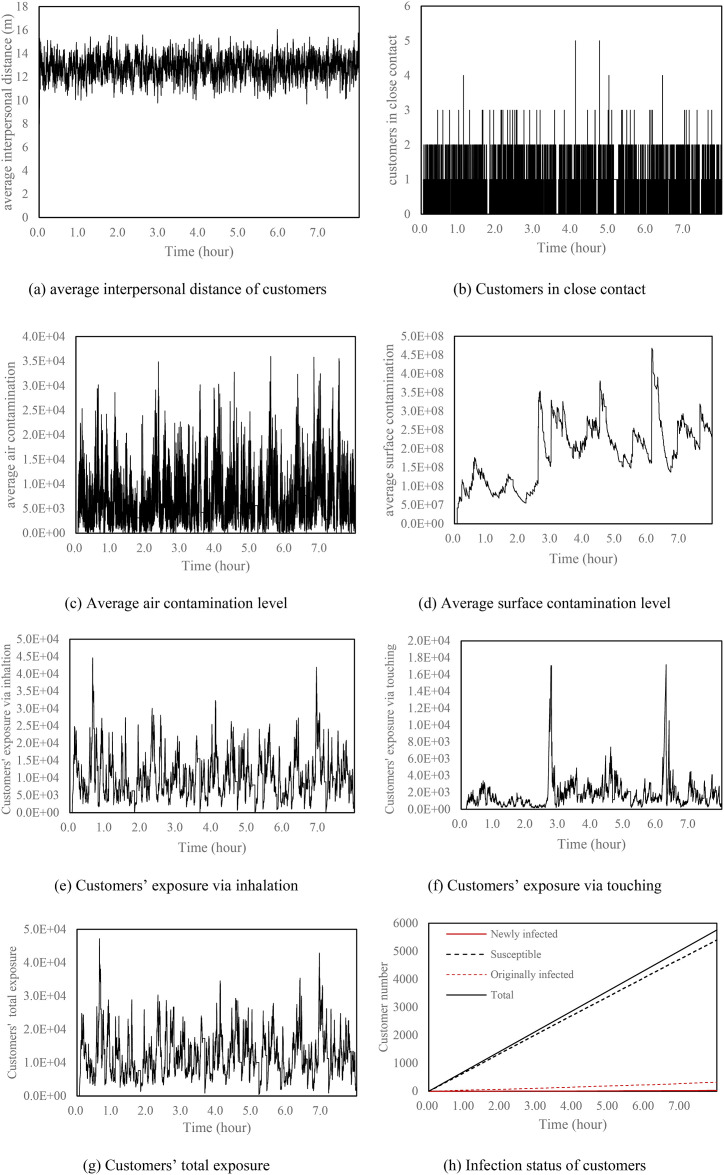
The timeline-based analysis includes three levels: space-oriented analysis, environment-oriented analysis, and occupant-oriented analysis. Fig. 12 shows the timeline-based analysis of a base scenario simulation.

Fig. 12.

The 8-h variations of customer exposure and environmental contamination of a simulation for the base scenario of the supermarket.

The space-oriented analysis includes two indicators: average interpersonal distance and customers in close contact. Average interpersonal distance refers to the average distance between every customer and other customers in the supermarket at a certain moment. It can be seen from Fig. 12 (a) that the average distance between people in the supermarket fluctuates around 12.8 m. Customers in close contact (Fig. 12 (b)) refers to the number of customers in the cone of the infectious people at each tick. It can be seen that the number of close contacts in the supermarket is 1 or 2 most of the time. Rarely do 3 or more close contacts occur at the same time. During the 8 h of simulation, a total of 33624 close contacts occurred.

The environment-oriented analysis includes two indicators: air contamination level and surface contamination level. Fig. 12 (c) shows the average air contamination level of the supermarket, namely the average number of viruses per cell. Results show that the instantaneous contamination level of indoor air can reach up to 3.59 × 10⁴, and the average value is 6.53 × 10³. Fig. 12 (d) shows the average surface contamination level variation. The overall upward trend of viruses on environmental surfaces is mainly due to the absence of surface cleaning measures. The decline of surface viruses can only be caused by the removal of goods during customers’ shopping process. The average surface contamination level of the supermarket is 1.90 × 10⁸.

The occupant-oriented analysis includes customers' inhaled viruses, customers' touched viruses, and total exposed viruses as well as changes in the infection status of the supermarket population. Fig. 12 (e) shows the virus exposure of all customers through inhalation at each tick, and the peak value can reach 4.33 × 10⁴. The cumulative respiratory exposure of all customers in the 8-h simulation period is 1.19 × 10⁹. Fig. 12 (f) shows the variation of virus exposure through surface-based transmission, of which the highest value is 1.66 × 10⁴. It can be seen that the virus exposure obtained through surface-based transmission is much smaller than the air-based transmission route, which is consistent with many existing studies [93,94]. This also resulted in the total exposure curve (Fig. 12 (g)) being very similar to the exposure curve via inhalation. Fig. 12 (h) shows the infection status of supermarket customers over time. The supermarket received a total of 5758 people in 8 h. When the initial infection rate was 5%, 29 people were eventually infected by entering the supermarket for shopping.

4.2. Effect of single intervention on customer exposures and infections

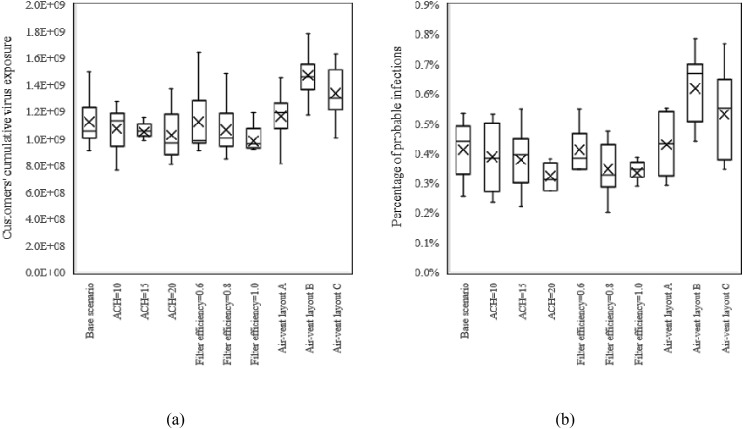
4.2.1. Spatial layout

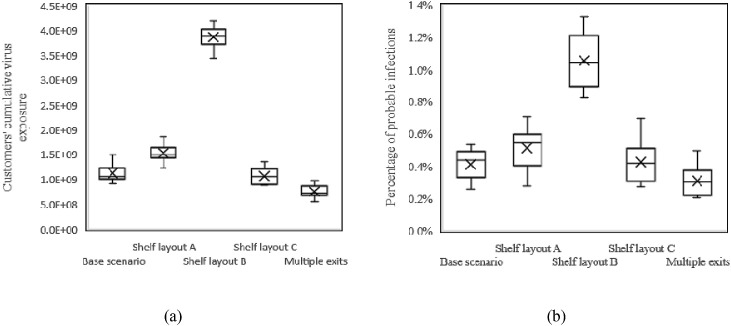
Fig. 13 (a) shows the difference in virus exposure of customers caused by various spatial layout interventions. The mean cumulative virus exposure ($\overline{E_v}$) of customers for the base scenario is 1.12 × 10⁹. The $\overline{E_v}$ under shelf layout A, shelf layout C and multiple exits scenarios all decreased, among which the virus exposure of multiple exits was the least, with an average of 7.57 × 10⁸. However, the $\overline{E_v}$ of shelf layout B increased significantly, with an average of 3.87 × 10⁹.

Fig. 13.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for different spatial layout scenarios.

The percentage of probable infections (p _i) has been chosen as the primary indicator of effectiveness as it is unaffected by the number of customers served. Here p _i is defined as a ratio of newly infected and initially healthy customers (Eq. (11)):

$$p_i=\frac{N_{\inf ected}^{newly}}{N_{total}-N_0}$$ (11)

Where p _i is the percentage of probable infections, N _total is the total number of people entering the supermarket, and N ₀ is the number of initially infected customers.

Fig. 13 (b) shows the p _i distribution for different spatial interventions, which is consistent with the trend of virus exposure. The average p _i ($\overline{p_i}$) under the base scenario is 0.41%, while the $\overline{p_i}$ of shelf layout B reaches 1.06%. On the other hand, the $\overline{p_i}$ of multiple exits decreased to 0.31%. The $\overline{p_i}$ of other distributed spatial layouts, namely layout B and layout C, also decreased. The single-aisle design of shelf layout B makes customers walk back and forth in the narrow aisle to find products, resulting in an increase in people's stay time and the number of close contacts. While the scattered layout of shelves and multiple exits can greatly reduce the congestion of people in supermarkets, thereby reducing the number of close contacts and the infection probability. This indicates that unreasonable space design can significantly increase the risk of infection, while proper space measures such as scattered furniture layout and multiple exits can effectively reduce the indoor infection risk.

4.2.2. Air ventilation

Fig. 14 shows the effect of different air ventilation interventions on cumulative virus exposure and infection risk. Trends in virus exposure and infection probability were similar across scenarios. As ACH increases from 5 times/hour to 20 times/hour, $\overline{E_v}$ gradually decreases from 1.12 × 10⁹ to 1.03 × 10⁹, and $\overline{p_i}$ has also dropped from 0.41% to 0.32%. Furthermore, as the filter efficiency increased from 0.4 to 1.0, the $\overline{E_v}$ decreased to 9.80 × 10⁸, and $\overline{p_i}$ gradually decreased to 0.33%. As for different air-vent layouts, results show that the $\overline{E_v}$ and $\overline{p_i}$ of air-vent layout A is slightly higher than that of the base scenario, while air-vent layouts B and C are much higher. The $\overline{p_i}$ of air-vent layout B and air-vent layout C reach 0.62% and 0.53% respectively. The possible reason is that though the number of vents was increased in this experiment, the ACH did not increase. More return vents resulted in indoor air flowing at a slower rate to the return vents, and contaminated air residing longer in the room, leading to more virus exposure. This suggests that we should not arbitrarily increase the number of air vents while the ACH remains the same, which will cause a greater risk of indoor infection.

Fig. 14.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for different air ventilation scenarios.

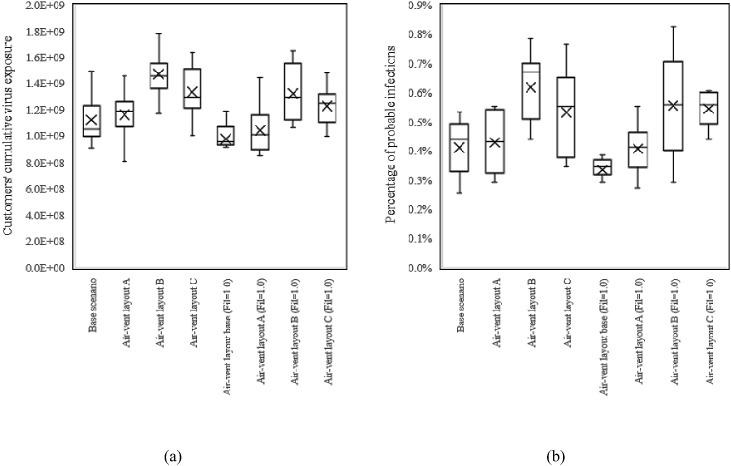
We posited that air-vent layout and filter efficiency may have cross-effects, so we added a set of control experiments to simulate three air-vent layouts with a filter efficiency of 1.0. Results show that the changing trends of the three air-vent layouts are consistent when the filter efficiency is 1.0 and 0.4, all of which are $\overline{p_i}$ (layout B) > $\overline{p_i}$ (layout C) > $\overline{p_i}$ (layout A) > $\overline{p_i}$ (layout base) (Fig. 15 ). This shows that increasing filter efficiency only uniformly reduces the E _v and p _i of different air-vent layouts, and does not change their trend, which means that the cross-effect between the two is very small.

Fig. 15.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for various air-vent layouts under filter efficiency 0.4 and 1.0.

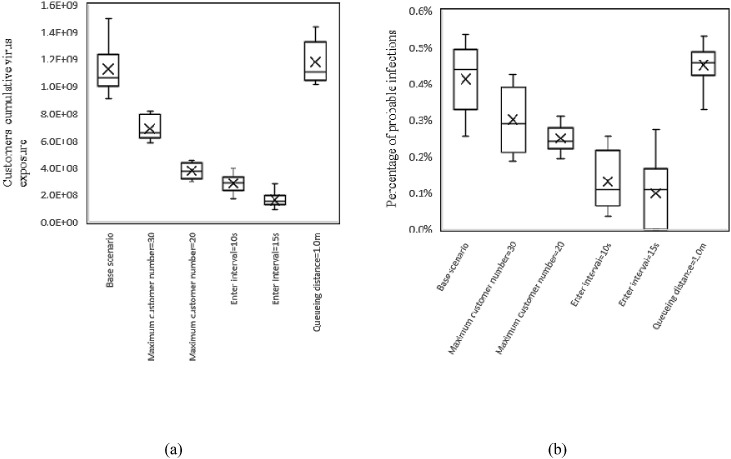
4.2.3. Customer control

The effect of customer control interventions is shown in Fig. 16 . Results show that as the maximum customer number decreased from 50 (base scenario) to 20, the customer's $\overline{E_v}$ decreased significantly to 3.76 × 10⁸ and $\overline{p_i}$ is reduced to 0.25%. Furthermore, increasing the entry interval of customers has a more pronounced effect. When the entry interval increased from 5s (base scenario) to 10s, the $\overline{E_v}$ decreased sharply to 2.85 × 10⁸, and $\overline{p_i}$ decreased to 0.13%. And as the time interval further increased to 15s, the $\overline{E_v}$ decreased to 1.62 × 10⁸, and $\overline{p_i}$ decreased to 0.10%. Reducing the maximum number of customers and increasing the entry time interval will reduce the real-time number of people in the supermarket, thereby reducing the probability of contact between susceptible people and infectious people, leading to a decrease in infection risk.

Fig. 16.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for different customer control scenarios.

Furthermore, we were surprised to find that when the queue spacing rose from 0.5 m to 1.0 m, the mean virus exposure rose slightly to 1.18 × 10⁸ and $\overline{p_i}$ increased slightly to 0.45%. This is likely due to the narrower aisle in front of the supermarket checkout in this case. The longer queue spacing led to more traffic congestion at the end of the queue, increasing the number of close contacts. This indicates that the queue spacing should be adjusted according to the actual space conditions and should not overly squeeze the traffic space.

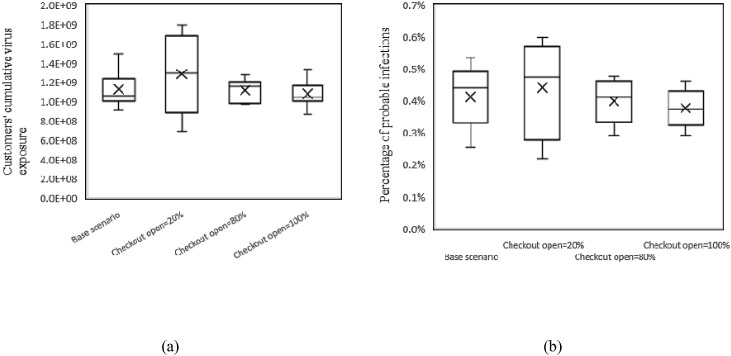
4.2.4. Checkout control

Fig. 17 shows the variation of virus exposure and infection probability due to checkout control. Results show that when the checkout open proportion is reduced to 20%, the $\overline{E_v}$ increases to 1.29 × 10⁹ and $\overline{p_i}$ increases to 0.44%. When the proportion of open checkout is increased to 80% and 100%, the $\overline{E_v}$ decreases to 1.11 × 10⁹ and 1.08 × 10⁹, and $\overline{p_i}$ decreases to 0.40% and 0.38%, respectively. It is obvious that the proportion of open percentage of checkout greatly change the infection risk of customers.

Fig. 17.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for different checkout control scenarios.

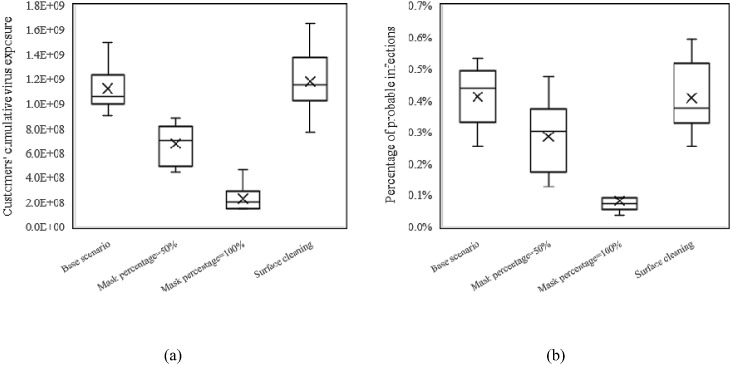
4.2.5. Sanitary measures

Sanitary measures include wearing masks and surface cleaning. Fig. 18 shows that when 50% of the population wears a mask, the $\overline{E_v}$ drops dramatically to 6.76 × 10⁸ and the $\overline{p_i}$ drops to 0.29%. And when 100% of the population wears masks, the $\overline{E_v}$ drops to an even lower 2.29 × 10⁸ and the $\overline{p_i}$ drops to a very low level of 0.08%. This suggests that wearing masks is a very useful measure to reduce the risk of indoor infection. However, the effect of surface cleaning measures was minimal. There was almost no change in $\overline{E_v}$ with surface cleaning every 4 h, and $\overline{p_i}$ also remained at the original 0.41%. This indicates that the effect of surface-cleaning measures on the control of indoor infection is very limited. The main reason for this is that exposure via the surface-based transmission route is well below that of airborne transmission, and changes in virus exposure due to cleaning have little effect on the infection probability.

Fig. 18.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for different sanitary measures.

4.3. Effect of combined interventions on customer exposures and infections

After the parametric study of single interventions, we attempted to combine measures to determine the possible infection reduction potential of each category of measures. The best parameters for each category of interventions were combined as (1) combination of spatial interventions: shelf layout C + multiple exits, (2) combination of ventilation interventions: ACH 20 + filter efficiency 1.0 + Air-vent layout base, (3) combination of customer control interventions: max customer number 20 + enter interval 15s + queueing distance 1.0 m, (4) checkout control interventions: checkout open 100%, (5) combination of sanitary interventions: mask percentage 100% + surface cleaning interval 4 h, and (6) combination of all single interventions as an extremely harsh measure. It is worth noting that these combined designs may have been used in combination during the epidemic period, but that does not mean they are optimal, as there may be interactions between these variables.

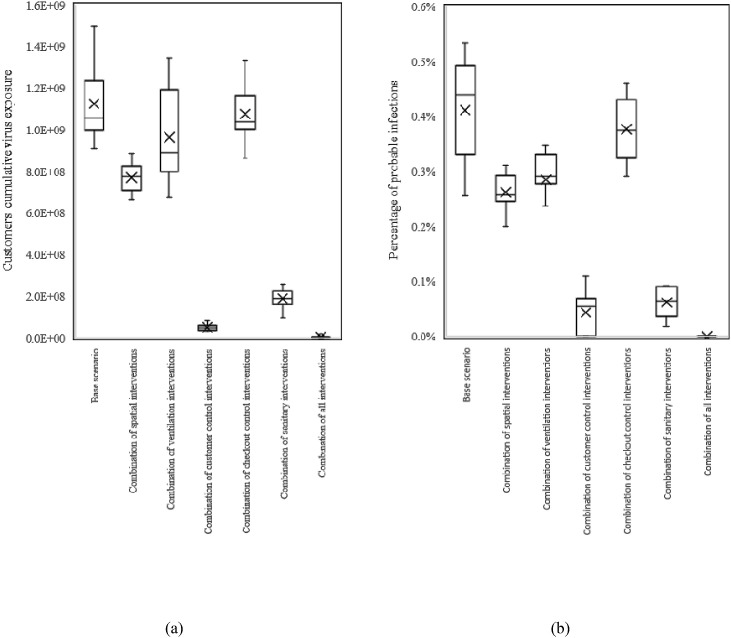
Fig. 19 shows the effect of different categories of interventions on customer virus exposure and infection risk. It can be seen that customer behavior control is the most effective category of interventions, with a significant reduction in $\overline{E_v}$ to 5.11 × 10⁷ and a reduction in $\overline{p_i}$ to 0.04%. The reason lies in the strict combination of the maximum number of customers and the entry interval, which makes the customers finish the shopping process and leave the supermarket quickly in a very short time, largely avoiding the encounter with infectious people in the supermarket.

Fig. 19.

Customers’ cumulative virus exposure (a) and percentage of probable infections (b) for different combinations of measures.

Furthermore, sanitary interventions were the second most effective. The combination of mask-wearing and surface cleaning reduces $\overline{E_v}$ to 1.89 × 10⁸ and $\overline{p_i}$ to 0.06%.

The third is the combination of spatial interventions. The scattered shelf layout and multiple exit design reduce $\overline{E_v}$ to 7.71 × 10⁸ and $\overline{p_i}$ to 0.26%. For checkout control, 100% open checkout reduces $\overline{E_v}$ to 1.08 × 10⁹ and $\overline{p_i}$ to 0.38%. The effectiveness of both types of interventions is to reduce the probability of customer encounters or stopping in the space, reduce the probability of close contact, and thus reduce the risk of infection.

The combination of ventilation interventions led to a decrease in $\overline{E_v}$ to 9.64 × 10⁸ and $\overline{p_i}$ to 0.29%. It is interesting to note that the effect of ventilation measures on viral exposure was not as significant as in several other categories, which differs from the general sense of perception. The reason is that the main transmission routes differ in various spatial scenarios due to different behaviors of people. In such high-traffic but low-stay venues, close contact transmission becomes the dominant transmission route. Therefore, it is more effective to reduce the probability of close contact by changing the spatial layout or controlling the behavior of customers. Ventilation interventions affect mainly aerosols that are suspended in the air for a long time. For some places where people remain relatively stationary for a long time (e.g., offices, wards, etc.), ventilation measures might be more effective when the cumulative inhalation of aerosols by people becomes the main infection factor.

Finally, the combination of "extremely strict" interventions resulted in an $\overline{E_v}$ of only 3.04 × 10⁶ and a $\overline{p_i}$ of 0. This proves the effectiveness of non-pharmaceutical measures, which may be used for supermarket control in some extreme outbreaks.

5. Discussion and future works

5.1. Application of the agent-based indoor SARS-CoV-2 transmission model

We developed an agent-based model that integrates building space, human behavior, and virus transmission to determine the efficacy of different types of interventions on indoor infection risk. The social force model simulating pedestrian movement and a simple forcing method simulating indoor airflow were coupled. Moreover, a user interface (Appendix S3) was designed so that the user can freely customize space configurations (e.g., changing shelf layout, adding exits) and occupant behaviors (e.g., entering interval, mask-wearing) to see the impact of each design decisions on infection risk. This approach can effectively help architects, supermarket managers, or the government to understand the impact of various measures on infection risk.

The model can be used to detect high-risk spaces, environmental surfaces, or behaviors. On one hand, real-time situated visualization shows spaces in buildings that are prone to crowding or congestion, and these are precisely the spaces at high risk of close contact. The model can show the contamination level of indoor air and surfaces, and diagnose localized spaces or surfaces that are vulnerable to contamination to take countermeasures. On the other hand, timeline-based analysis allows long-term monitoring of space, environment, or customers to determine the possible risks in the time dimension.

A relative comparison of the impacts of different measures is more valuable, which can help determine the effectiveness of the measures and take the most efficient measures. However, it should be noted that in different building scenarios, the impact of different measures is likely to be different. In supermarket buildings with a frequent flow of people, close contact is the main route of virus exposure. In this case, the proximity of people due to measures such as spatial layout and behavioral control becomes the main cause of infection. In some buildings such as offices and wards, people may stay in one spatial location for a long time. In this case, instead, people inhale aerosols for a long time and the accumulated viruses may become the main contributor to infection, and then ventilation will probably be a more important control factor. Therefore, each kind of building and behavior scenario should be analyzed specifically.

5.2. Limitations and future research

This agent-based model lacks validation, which is a problem that many infection prediction models currently face [95]. It is difficult to perform actual experimental validation and obtain data for the spread of the virus indoors. With the increase in medical tests, it may be possible to obtain some field data for validation in the future.

Second, the ventilation involved in the model only includes mechanical ventilation. Natural ventilation is too complicated to mimic in the ABM environment until now. Simulating natural ventilation in an ABM environment is challenging because it is affected by many factors such as wind speed, wind direction, air temperature difference between indoor and outdoor, and building layout. These parameters will have large fluctuations within a day, or even within an hour. Therefore, simulation of natural ventilation requires a high level of detail in modeling the physical environment. Moreover, the vertical airflow is not reflected in this model due to the limitations of the current ABM environment. However, due to the flattening of supermarket spaces with a length/width to height ratio greater than 3:1, horizontal airflow is more important than the vertical direction in this case. Furthermore, due to the initial spraying angle of the coughing action and the gravitational acceleration of droplets, most of the dispersal of the sprayed droplets is below the height of a person, i.e., below the level of 1.7 m height. The height of the supermarket shelf is approximately 1.6 m, which means that most of the droplets will be blocked by the shelf in the horizontal direction. Therefore, for the shelf in the supermarket we mainly focus on its airflow blocking effect in the horizontal direction. Coupled with the need to obtain indoor infection risks more efficiently and quickly to assist architects or managers in the decision-making process, complex vertical airflow was not considered in this study.

Third, the surface-based transmission simulation in the model needs to be supported by more measurement and experimental data. Supermarkets have their special characteristics in surface-based transmission because the virus falls on the goods, and the goods will be taken away continuously as the shopping process goes on. We roughly assume here that each grid is loaded with about 10 copies of goods. Each time the goods of the grid are taken away, 1/10 of the amount of virus of the grid will be taken away. However, the surface area varies depending on the goods, so it is difficult to estimate an accurate value of the surface area. For instance, vegetables and fruits cannot be fully “cleaned”. On the other hand, we also found that one of the major problems in simulating surface-based transmission is the lack of specific behavioral data. For example, what are the touching habits of people when selecting goods, and whether they will make some touching but not buy? These underlying data affect the accuracy of the model. Although some touch behaviors in offices have been studied by researchers such as Zhang et al. [20], this is a relatively uncharted territory that needs to be carefully studied and explored in the future.

In addition, there is a corresponding cost behind each intervention. For example, the best type of intervention in terms of reducing the probability of infection may be to restrict customer behavior, but this is likely to result in lower sales. Increasing ACH will increase operating costs while opening more checkouts will increase labor costs. This involves a decision balance problem, i.e., what decision is the most cost-effective? This model can provide benefits in terms of infection risk reduction for making more scientific decisions.

Finally, there is the problem of high time cost. In this paper, an 8-h supermarket simulation takes up to 6 h on a desktop with an i7-CPU 3.60 GHz processor. On the one hand, the use of a large number of cells to slice the space and store different sizes of droplet variables, which is similar to the CFD gridding simulation method, takes up a lot of memory and computation time. On the other hand, the social force model needs to calculate the driving force and repulsive force of each customer at each tick to arrive at the next position. This is more time-consuming than some algorithms that use fixed points and networks [89]. However, the problem of high time cost can be resolved by the use of hybrid models. For instance, Lutz and Giabbanelli [96] have developed machine leaning regression models for 4 COVID-19 ABMs to assist in fast decision-making. With the continuous improvement of hardware computing power and supervised learning algorithms, time cost will become less of a problem.

6. Conclusion

A spatially-explicit agent-based model for studying indoor respiratory pathogen transmission was proposed and used to demonstrate the potential effectiveness of multiple interventions for reducing SARS-CoV-2 transmission in the case study of a supermarket. The social force model simulating pedestrian movement and a simple forcing method simulating indoor airflow were coupled in the NetLogo modeling environment.

The results of the supermarket case study showed that for a single intervention, wearing a mask was the most effective, with all masks worn by the population reducing the $\overline{p_i}$ to 0.08%. In addition, customer control interventions were also quite effective, where tripling the entry interval reduced the $\overline{p_i}$ to 0.10%. Among the spatial interventions, the design of multiple exits was the most effective, reducing $\overline{p_i}$ to 0.31%. It was also found that some unreasonable space layouts can significantly increase the $\overline{p_i}$ and should be prevented in advance. Among the ventilation interventions, increasing the filter efficiency is the most effective, the $\overline{p_i}$ can be decreased to 0.33% when the filter efficiency is 1.0. Finally, opening all checkouts reduces $\overline{p_i}$ to 0.38%.

For the combination of measures, the customer control combination is the most effective and can reduce $\overline{p_i}$ to 0.04% by controlling the maximum number of customers, the customer entry interval, and the number of the customers shopping. The main reason is that customer control directly and significantly reduces the probability of contact between susceptible people and infected people in the same space. This is even more effective than the combination of sanitary measures, of which the $\overline{p_i}$ is 0.06%. Furthermore, the combination of space interventions through scattered shelf layouts and multiple exit design reduces $\overline{p_i}$ to 0.26%, which is more effective than the combination of ventilation interventions with a $\overline{p_i}$ of 0.29%. This is because close contact becomes the main source of virus exposure in buildings like supermarkets where people move frequently and stay less. Finally, the extremely stringent combination of all interventions can achieve an 8-h infection-free situation in supermarkets. This suggests that the risk of indoor infection can be reduced to a large extent by combining various non-pharmaceutical measures.

The findings of this study have some implications. The results of different architectural and behavioral interventions on indoor virus transmission can help architects, supermarket managers, and the government to better understand and choose epidemic prevention interventions to control indoor infection risk. Furthermore, this model can be easily adapted and applied to other building types and behavioral scenarios, particularly buildings with high traffic flow. User can freely customize space configurations and occupant behaviors to check the impact of decisions on indoor infection risk through the user-defined interface.

Finally, there are some limitations to this study which need to be considered. One of the limitations of this study is the lack of validation due to the difficulty of collecting virus data in the field and tracking the infection status of people. Future studies will use experimental or real-world measurements to further mine indoor viral and human behavior data and validate the model to enhance its accuracy.

CRediT authorship contribution statement

Anxiao Zhang: Conceptualization, Methodology, Software, Visualization, Writing – original draft. Qi Zhen: Data curation, Formal analysis, Writing – review & editing. Chi Zheng: Investigation, Validation. Jing Li: Data curation, Supervision. Yue Zheng: Data curation, Supervision. Yiming Du: Supervision. Qiong Huang: Supervision. Qi Zhang: Funding acquisition.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article:

Data availability

Data will be made available on request.