Abstract
Traditional concepts of river health and methods for identifying ecological river disconnection are not applicable to seasonal rivers. Given the substantial negative impact of ecological river disconnection on river ecosystems and the importance of groundwater and soil moisture for the ecology of seasonal rivers in arid and semi-arid regions, developing a comprehensive index for accurately identifying ecological river disconnection in these rivers is crucial. This study introduces a new Standardized Seasonal River Disconnection Index (SSRDI), which is based on a Standardized Index (SCI) and a three-variable Copula function. The SSRDI integrates surface water, groundwater, and soil water information to reveal the true hydrological conditions of seasonal rivers and provides a comprehensive analysis of ecological river disconnection patterns in Tabu River from 2002 to 2020. The findings are as follows: (1) The Gaussian Copula is most suitable for constructing the SSRDI for Tabu River. Optimal distribution functions vary across regions, times, and datasets; therefore, using the best monthly distribution functions to compute SRI, SGDI, and SSMI provides a more scientifically robust mathematical and statistical basis. (2) The SSRDI, which combines surface water, groundwater, and soil water, is more consistent with the actual hydrological conditions of Tabu River compared to the three univariate indices. (3) From 2002 to 2020, the SSRDI for Tabu River shows a continuous declining trend, albeit at a slowing rate. The overall pattern exhibits a cyclical trend of worsening followed by improvement, with June being the month of most severe ecological river disconnection. (4) The seasonal component of the SSRDI from 2002 to 2020 displays cyclical changes, with a mutation in June 2004. The trend component shows a general decline, with two mutations observed in April 2005 and February 2007. This study provides valuable insights for identifying ecological river disconnection of seasonal rivers. The index can be applied to monitoring, forecasting, and mitigating ecological river disconnection in arid and semi-arid river systems, and can more accurately and comprehensively grasp the true health status of seasonal rivers, which is of great significance for the sustainable development of seasonal river ecological environment.
Keywords: Seasonal river, Comprehensive river Disconnection index, Copula, Tabu river
Subject terms: Ecology, Environmental sciences, Hydrology, Natural hazards
Introduction
River ecosystems represent a unified entity formed by the integration of river biota and the river environment. They are among the most crucial ecosystems for both socio-economic benefits and natural functions, playing a vital role in the hydrological cycle1,2. As a key component of freshwater resources, rivers are closely linked to human origins3,4. However, the continuous intensification of global climate change and regional population growth have led to significant degradation of river ecosystems, posing severe threats to human survival and sustainable societal development5,6. From a systems perspective, rivers exhibit strong resistance to disturbances. Nevertheless, their self-repair capability is limited, meaning that when external disturbances exceed their capacity, river ecosystems will irreversibly degrade, leading to a decline or even loss of many ecosystem services7. Therefore, accurately assessing river health and ensuring ecosystem well-being are crucial for achieving sustainable development8,9.
The concept of river health has been a topic of debate among researchers for years. Karr (2001) defined river health from the perspectives of aquatic ecosystem health and ecological stability. As research has advanced, more scholars argue that river health should also encompass its service value to human society10. However, existing studies mainly focus on perennial rivers, with relevant concepts and methods applicable only to them. Seasonal rivers, also known as non-perennial rivers, rely primarily on precipitation or glacial meltwater and are significantly affected by seasonal variations. They may experience high flows during wet periods and reduced or even zero flow during dry periods or specific seasons11,12. Seasonal rivers are widespread globally, especially in arid and semi-arid regions13. Messager et al.14 predicted that 51-60% of the world’s rivers experience flow cessation for at least one day each year. Moreover, climate change, which affects temperature and precipitation, as well as surface water use and groundwater extraction, is increasing the proportion of seasonal rivers15. However, research on the distribution, functioning, and evolution of seasonal rivers remains insufficient and lacks a mature theoretical framework16,17. Thus, to thoroughly study and manage the flow characteristics and functional integrity of seasonal rivers, new concepts and models specific to seasonal rivers need to be developed.
Seasonal rivers differ from perennial ones in that their primary water sources are more singular, mainly from precipitation or snowmelt, with a significant dependence on groundwater. Previous assessments of seasonal river health or restoration efforts generally focused only on surface water, equating ecological restoration with surface water restoration. This approach overlooks the crucial impact of groundwater on river ecosystems, particularly in arid regions where groundwater has a profound influence on vegetation growth18,19. Zhao et al.20 found that vegetation coverage in the Heihe River Basin in China is constrained by groundwater levels, with groundwater depth determining vegetation types. Han et al.21proposed an ecohydrological method to predict regional vegetation and groundwater responses in China’s northwest arid region. Jin et al.22studied the relationship between vegetation growth, groundwater depth (DWT), and total dissolved solids (TDS) in the Yinchuan Plain in northwest China. Extensive research shows that vegetation growth in arid and semi-arid regions is highly sensitive to groundwater changes. Riparian vegetation, as a crucial component of river ecosystems, performs vital functions such as filtration, purification, carbon sequestration, and soil erosion control23,24. Therefore, in studies of seasonal river health in arid and semi-arid regions, groundwater’s influence on rivers must be considered. Soil moisture, as a link between surface and groundwater and a medium for material and energy exchange in terrestrial hydrological cycles, has significant ecological impacts25,26. Soil moisture is a direct water source for vegetation growth, especially in arid and semi-arid areas where it is a decisive factor in vegetation growth and distribution patterns27. Vegetation, as an indicator of ecological changes, plays a key role in the ecosystem’s self-regulation capabilities and is irreplaceable in maintaining climate stability, promoting land water cycles, and influencing surface conditions and carbon balance28. In ecologically fragile areas, vegetation communities directly engage in biochemical cycles, mitigating the lag and cumulative effects of climate change and enhancing water use efficiency, thus playing a crucial role in improving and maintaining ecological environments29,30. Hence, the role of soil moisture should not be overlooked in discussions of seasonal river health in arid and semi-arid regions.
To improve the accuracy and applicability of seasonal river health monitoring, a composite index that integrates surface water, groundwater, and soil moisture characteristics should be developed. This will support management efforts to accurately understand river health and timely formulate appropriate measures. Recently, scholars have begun to combine multiple variables to construct composite indices, making progress in the hydrometeorological field. Common methods include weighted methods, machine learning, principal component analysis (PCA), and multivariate approaches. Zhang and Jia et al.31used a linear combination method to allocate different weights to indices of precipitation, temperature, and soil moisture, creating the Microwave Integrated Drought Index (MIDI). Liu et al.32proposed a composite drought index based on PCA, integrating precipitation, evapotranspiration, soil moisture, runoff, and other hydrometeorological factors. However, weighted and hierarchical methods are subjective and prone to significant error, while PCA reduces dimensionality, potentially losing information and affecting assessment accuracy. Machine learning can handle large datasets efficiently but is region-specific and depends heavily on model parameter settings33. Copula functions can combine multiple variables based on their correlations, avoiding issues related to marginal distributions and preserving variable information, thereby overcoming the aforementioned problems34–36. Scholars have increasingly used Copula functions to construct composite drought indices. Hao and AghaKouchak et al.37 developed the Meteorological and Agricultural Drought Index (MSDI) using Copula functions to combine precipitation and soil moisture. Guo et al.38 proposed an improved Copula-based multi-variable standardized reliability and resilience index to assess socio-economic drought risks, providing new insights into dynamic drought risk assessment in changing environments.
Tabu River (TBR), located in northern China’s agricultural-pastoral zone, is an important water source. The basin experiences a dry climate, scarce rainfall, complex meteorological conditions, and fragile ecological environments, with a high dependence on groundwater. Therefore, accurately assessing the true status of water in the basin is essential for ensuring sustainable water use and combating desertification. This study focuses on TBR in Inner Mongolia, a typical seasonal river in China, to establish a Copula-based Standardized Ecological River Disconnection Index (SSRDI). This index integrates surface water, groundwater, and soil water to comprehensively characterize the true status of seasonal river flow.
The main objectives of this study are: (1) to calculate SRI, SGDI, and SSMI based on optimal marginal distribution functions; (2) to develop and validate a new Copula-based Standardized Ecological Flow Index; and (3) to identify temporal changes in TBR flow cessation using the Bayesian Estimator of Abrupt Seasonal and Trend change algorithm (BEAST). The findings will provide more reasonable and beneficial indicators for river health monitoring and can be applied to other research fields.
Study area and dataset
Study area description
TBR, the largest inland river in the northern foothills of the Yin Mountains, is located in central Inner Mongolia. It originates in Guyang County, Baotou City, with geographic coordinates of 110°34′−112°11′E longitude and 41°02′−42°23′N latitude. The river extends approximately 323.2 km and has a total basin area of about 11,191 km². The middle reach of the river is monitored by the Xichanghanying Hydrological Station. TBR lies within an arid to semi-arid continental climate zone and is predominantly seasonal. Precipitation is sparse, with most rainfall occurring between mid-July and early September, accounting for about 80% of the annual total. The river system is underdeveloped, with a low river network density and frequent flow interruptions during dry periods. Vegetation in the basin is mainly desert grassland. The southern part of the basin features densely distributed settlements, artificial surfaces, and cultivated land, while the northern part consists of desert grassland and exposed surfaces, resulting in a generally harsh ecological environment. The location of the study area is shown in Fig. 1.
Fig. 1.
Location of the study area.
Dataset
The SSRDI developed in this study primarily utilizes runoff, groundwater storage, and soil moisture data.
Monthly runoff data from 2002 to 2020 were collected from the Xichanghanying hydrological station in the study area. Located in the midstream of the basin, the Xichanghanying station is situated in a region where the upstream TBR relies mainly on high-altitude ice and snowmelt for replenishment. As the river flows downstream, the lack of rainfall in the mountainous areas, combined with evaporation and seepage, leads to a reduction in river flow, leaving the downstream region nearly dry without water for most of the year. Consequently, the recorded runoff at the Xichanghanying station can be considered representative of the basin’s runoff and used to reflect runoff conditions in the study area. Runoff data were obtained from Yinshanbeilu Grassland Eco-hydrology National Observation and Research Station.
Groundwater storage data were obtained from GRACE and GLDAS datasets. The GRACE satellite data, to date, primarily come from the Center for Space Research (CSR), the German Research Centre for Geosciences (GFZ), and the Jet Propulsion Laboratory (JPL). The main data products commonly used to estimate changes in land water reserves at present are Mascon, L3, and L2 (spherical harmonic coefficients). The Mascon product applies the spherical harmonic coefficients corresponding to the ocean scale atmospheric ocean model (G: geopotential coefficients, A: average of any background model over a time period, D:bottom-pressure over oceans, zero over land, GAD), glacial isostatic adjustment to correct it, then replace the C20 and C30 data in the gravity field model with the values calculated by satellite laser ranging, so it can be directly used for estimating changes in land water reserves39,40. This study extracts monthly abnormal data on land water storage provided by the GRACE RL06 Mascon satellite product released by CSR(https://www2.csr.utexas.edu/grace). The time is from January 2002 to December 2020, with a spatial resolution of 0.25°× 0.25°. Due to the loss of GRACE data from satellite sensors, linear interpolation was used to complete it. The missing month data is interpolated using the average of the months corresponding to the adjacent years of that month. The interpolated dataset is verified by comparing it with the changes in groundwater depth in some measured monitoring wells in the study area41.
GLDAS is jointly established by NASA and the National Centers for Environmental Prediction (NCEP) to provide data. It generates land surface fluxes by using advanced land surface models and data assimilation techniques, combined with satellite and ground observation data. To facilitate comparison with the GRACE mascon model, a Noah model with the same spatial resolution (0.25°) as the Grace dataset was selected. The download address is as follow (https://disc.gsfc.nasa.gov/datasets/).
Soil moisture data were sourced from the FLDAS dataset. FLDAS land surface assimilation data is a dataset output by the FLDAS land surface data assimilation system. It is a global high-resolution land surface data assimilation system dataset developed based on the Land Information System (LIS) and released by NASA in 2020. FLDAS dataset provides monthly global soil moisture data from 1982 to the present, with a spatial resolution of 0.1°× 0.1°. To facilitate harmonization with the GRACE dataset, the data were resampled using ArcGIS 10.2 to match the resolution of 0.25°. We resampled the data using the four methods (Nearest, Majority, Bilinear, Cubic) provided in ARCGIS 10.2 and ultimately chose the result of Bilinear as the basis for subsequent calculations. The download address is as follow (https://disc.gsfc.nasa.gov/datasets/).
Methodology
Permission was obtained from Yinshanbeilu National Field Research Station of Steppe Eco-hydrological System to conduct research in the Tabu River basin.
Definition of seasonal river health
Previously, definitions of seasonal river disconnection have equated it with the disconnection in perennial rivers, and believed that any river disconnection was unhealthy. This view is one-sided to the seasonal river, ignoring the importance of groundwater and soil water to the seasonal river health. Therefore, seasonal river health was defined in this study based on the characteristics of dual-layer river42. A dual-layer river describes a river where surface and groundwater coexist during high-flow periods and transition complementarily with seasonal changes. As upstream water decreases and surface runoff diminishes, groundwater flow rates and depths also decrease. When the surface flow reaches zero, the physical disconnection occurs, but at this time the groundwater can play its main ecological function and the seasonal river is still considered healthy. If groundwater flow rates and depths fall below a critical threshold, resulting in impaired ecological functions, ecological river disconnection occurs and the seasonal river is considered unhealthy.
Calculation of groundwater reserves
According to GRACE, the change in land water storage (ΔTWS) is the total change that includes changes in surface water storage and groundwater storage. The change in surface water storage can be obtained from GLDAS data, which includes changes in vegetation canopy water equivalent, snow water equivalent, and soil water equivalent43. Therefore, the change in groundwater storage can be obtained by subtracting the change in land water storage obtained from GRACE and the change in surface water storage obtained from GLDAS data, as shown in Eq. (1).
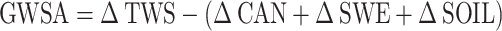 |
1 |
where GWSA is the change in groundwater reserves; ΔTWS is the change in land water reserves; ΔCAN is the change in vegetation canopy water equivalent; ΔSWE is the change in snow water equivalent; ΔSOIL represents the change in soil water equivalent.
Standardized indices
Since its introduction, standardized indices like the SPI have been widely used in drought research, applying sample data to runoff and soil moisture data in the studies of hydrological and agricultural droughts44,45. This study aims to extend the use of standardized indices to riverine ecological river disconnection research, offering a novel approach to identify ecological river disconnection in seasonal rivers.
Given the pivotal role of soil water as a link between surface water and groundwater, and its importance in energy conversion and the water cycle, three standardized indices—Standardized Runoff Index (SRI), Standardized Groundwater Index (SGDI), and Standardized Soil Moisture Index (SSMI)—are chosen as variables for constructing a comprehensive drought index46,47. These indices effectively describe surface water, groundwater, and soil moisture conditions, respectively. All indices are computed using the Standardized Climate Index (SCI) package in R.
The traditional SPI index fits precipitation data using a Gamma distribution, which remains unchanged when applied to other indices48.It is important to note that seasonal rivers are highly influenced by climate factors, causing variations in the optimal distribution of indices across regions, times, and indices49,50. Therefore, to ensure accuracy, the optimal distribution functions for flow, groundwater storage, and soil moisture should be selected separately21. Five distributions—Log-Logistic (Log-L), Weibull (Wbl), Generalized Pareto (GP), Gamma, and Log-normal (Logn)—are used to determine the optimal distribution function51,52. Additionally, the Root Mean Square Error (RMSE) criterion and Akaike Information Criterion (AIC) are used to evaluate the fit of the distribution functions53. Detailed procedures can be referenced from Vicente-Serrano (2012).
Copula-based standardized seasonal river disconnection index (SSRDI)
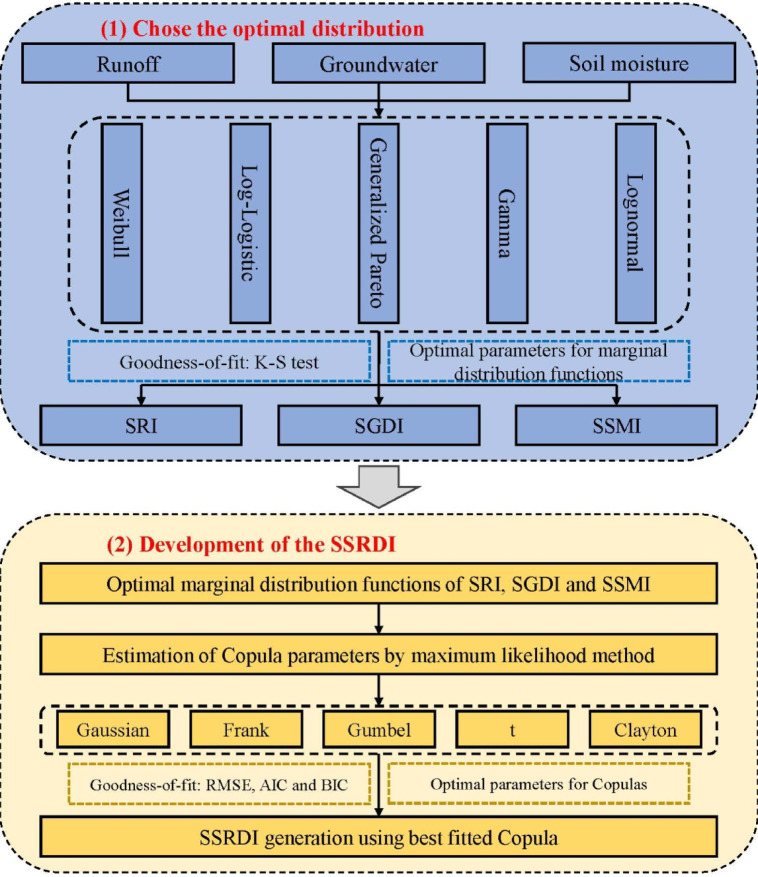
The Copula method is a crucial tool for constructing multivariate joint distributions and analyzing the correlation structures between random variables. It combines the joint distribution functions of multiple variables with their respective marginal distributions, enabling the construction of joint distributions with various marginal distributions54. Introduced by Sklar et al.55 and later developed by Nelsen et al.56the Copula method has found widespread application in statistics and finance57,58. Recently, its use has extended to hydrology, demonstrating effective predictive and application capabilities in studies of drought59,60precipitation61and design floods62,63. After computing the SRI, SGDI, and SSMI, their marginal distribution functions were combined to construct a new SSRDI based on the Copula function. The flowchart is shown in Fig. 2.
Fig. 2.
Flowchart for building SSRDI.
Step 1: Collect runoff, groundwater, and soil moisture data for the study area, and perform data preprocessing, including interpolation for missing station data and calculation of groundwater reserves.
Step 2: Select five distribution types (Log-L, Wbl, GP, Gamma, and Logn) to determine the marginal distribution functions for SRI, SGDI, and SSMI.
Step 3: Calculate the marginal distributions for SRI, SGDI, and SSMI, primarily using the Gringorten formula64.
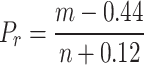 |
2 |
where m is the ranking of the data when sorted in descending order and n is the sample size.
Step 4: To determine the optimal copula function, the root mean square error (RMSE), Akaike information criterion (AIC), and Bayesian information criterion (BIC) were used to evaluate the fitted copula function. The smaller the values of AIC, BIC and RMSE, the stronger the fitting effect of the copula function. In this paper, we used five Copula functions (Table 1) to join the marginal distribution function, and choose the most suitable Copula function to build SSRDI.
Table 1.
Copula functions adopted in this study.
| Copula function | Mathematical formula | Parameter range |
|---|---|---|
| Gumbel |
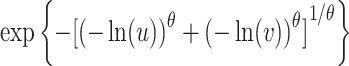
|
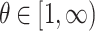
|
| Gaussian |
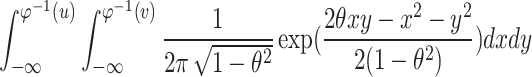
|
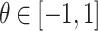
|
| Clayton |
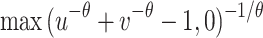
|
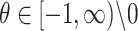
|
| t |

|
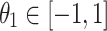 and and 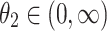
|
| Frank |
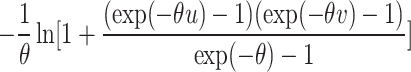
|
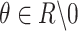
|
Step5: After determining the optimal copula function, the inverse normal function of the cumulative density function fitted by copula is used to obtain SSRDI. Calculate SSRDI using the following formula:
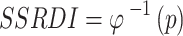 |
3 |
where 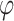 is the normal distribution function and p is the cumulative joint probability.
is the normal distribution function and p is the cumulative joint probability.
Due to the scarcity of precipitation and water in the TBR, only providing water for vegetation growth in the basin is considered as its basic function, without considering the water needed for human production activities. Therefore, the monthly average Vegetation Health Index (VHI) of TBR from 2002 to 2020 was calculated. When VHI is less than a certain threshold, it is defined as vegetation drought. At this time, the vegetation growth condition is poor, indicating that the ecological function of the river is damaged and ecological river disconnection has occurred65. Among the 228 months, 127 months experienced vegetation drought. Based on the empirical frequency of SSRDI, the SSRDI=−1.5 corresponding to 55.7% frequency was used as the threshold to determine whether ecological interruption occurred. That is, when the SSRDI is less than − 1.5, it is considered that ecological river disconnection has occurred. Furthermore, the SRI threshold was determined by modifying the Tennant method. This involved calculating the minimum ecological flow and setting the threshold based on the frequency of flow rates below this minimum and empirical SRI frequencies, as detailed in Yang et al.66. The SGDI threshold was set according to the standardized groundwater drought index calculated by Wang et al.41while the SSMI threshold was based on the study by Yan et al.67. Flow disruption severity was categorized into five levels, as shown in Table 2.
Table 2.
Classification of the SRI, SGDI, SSMI and SSRDI used in this study.
| Classification | SRI | SGDI | SSMI | SSRDI |
|---|---|---|---|---|
| No disconnection | (0,+∞) | (−0.5,+∞) | (0,+∞) | (−1.5,+∞) |
| Mild disconnection | (−0.5,0] | (−1,−0.5] | (−0.5,0] | (−2,−1.5] |
| Moderate disconnection | (−1.0,−0.5] | (−1.5,−1] | (−1.0,−0.5] | (−2.5,−2] |
| Severe disconnection | (−1.5,−1.0] | (−2.0,−1.5] | (−1.5,−1.0] | (−3.0,−2.5] |
| Extreme disconnection | (-∞,−1.5] | (-∞,−2.0] | (-∞,−1.5] | (-∞,−3.0] |
Bayesian estimator of abrupt seasonal and trend change algorithm (BEAST)
In this study, we used the BEAST method to decompose the constructed SSRDI time series to obtain seasonal changes, trend changes, and mutation points. BEAST is a time series decomposition algorithm based on Bayesian statistical theory, which has been well applied in fields such as water resource management and crop phenomenon analysis68,69. The difference between its BEAST change point monitoring algorithm mainly lies in two aspects. Firstly, traditional methods only select one best fit model, which ignores the uncertainty and error range of the model. However, BEAST uses a mechanism called Bayesian model averaging to aggregate many models into an average model, avoiding the randomness caused by a single model70,71. Secondly, most existing change detection algorithms produce binary results that are either right or wrong, while BEAST quantifies the relative usefulness of individual models and incorporates all models into inference through ensemble learning to obtain the probability of any given time point of change. This effectively avoids the uncertainty that non-Bayesian methods can easily cause.
From a mathematical perspective, BEAST divides time series into three parts:
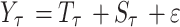 |
3 |
where Sτ is the seasonal variation item, Tτ is the trend change item, ε is the noise term.
The seasonal term Sτ is fitted in segments by a variable order sheet harmonic function, expressed as:
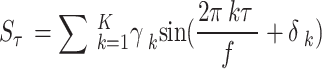 |
4 |
where γk, δk and f are amplitude, phase and the period of seasonal term, respectively.
The trend term is modeled by a piecewise polynomial linear function. Assuming that the trend term 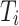 detects τ1, …, τm breakpoints, the linear expression of the trend term is:
detects τ1, …, τm breakpoints, the linear expression of the trend term is:
 |
5 |
where i represents the site of abrupt point, αi and βi represent the intercept and slope of the linear model on both sides of the abrupt point, respectively.
In addition, the trend and seasonal changes can be divided into 8 categories: monotonic increase (no mutation), monotonic decrease (no mutation), monotonic increase (positive mutation), monotonic decrease (negative mutation), interrupted increase, interrupted decrease, increase to decrease, and decrease to increase (Fig. 3).
Fig. 3.
Schematic diagram of change trend types based on BEAST algorithm.
Results
Construction of the SSRDI
This study first calculates the SRI, SGDI and SSMI. It then developed a novel Copula-based SSRDI, designed to identify whether seasonal river flows experience ecological river disconnection. To better align with the characteristics of the original data, the calculation process for SRI, SGDI, and SSMI is slightly modified. Given the seasonal distribution patterns of these elements, and to eliminate the influence of multi-year series values on the SSRDI, the runoff, groundwater, and soil moisture series are divided into 18 monthly sequences from 2002 to 2020. Each sequence is fitted separately, ensuring that the SRI, SGDI, and SSMI calculated using the optimal distribution function have a solid mathematical and statistical foundation. Five distribution functions (Log-L, Wbl, GP, Gamma, and Logn) are employed to determine the best fit for the monthly runoff, soil moisture, and groundwater data. Figures 4 and 5, and Fig. 6 display the empirical probability-probability (P-P) plots for runoff, groundwater, and soil moisture, respectively, which are nearly linear. This indicates that the chosen distribution functions fit the data well and can be used to accurately compute SRI, SGDI, and SSMI in the study area. Specifically, the optimal distribution varies by month: Wbl is used for runoff data in January, February, March, May, August, September, October, November, and December, while Logn and Gamma are used for the remaining months. Groundwater data consistently use the LOG-L distribution. For soil moisture data, Gamma is used in January, February, March, April, May, June, October, November, and December, with Logn used in the other months. After calculating SRI, SGDI, and SSMI, SSRDI is constructed according to Eqs. (2) and (3). Goodness-of-fit (GOF) tests for Copula functions are performed by calculating RMSE, AIC, and BIC values. Based on the principle that a lower RMSE, AIC, and BIC indicates a better fit, the best Copula function for the study area is the Gaussian Copula (Table 3). Therefore, SSRDI is derived using the selected optimal Copula function.
Fig. 4.
P-P plot of runoff for calculating SRI in the TBR. (a)-(l) represent January, February, March, April, May, June, July, August, September, October, November and December, respectively.
Fig. 5.
P-P plot of groundwater for calculating SGDI in the TBR. (a)-(l) represent January, February, March, April, May, June, July, August, September, October, November and December, respectively.
Fig. 6.
P-P plot of groundwater for calculating SGDI in the TBR. (a)-(l) represent January, February, March, April, May, June, July, August, September, October, November and December, respectively.
Table 3.
Goodness of fit (GOF) evaluation of different copula functions in the TBR.
| Copula | RMSE(*10−2) | AIC | BIC |
|---|---|---|---|
| Clayton | 8.4112 | −92.2187 | −65.3594 |
| Frank | 7.3418 | −112.3177 | −75.2591 |
| Gumbel | 7.3341 | −110.7574 | −76.4293 |
| t | 12.9897 | 160.1095 | 35.8124 |
| Gaussian | 5.1266 | −159.1482 | −141.4156 |
Performance of the SSRDI
Figure 7(a) illustrates the monthly SSRDI, SRI, SGDI, and SSMI from 2002 to 2020. The trends and variations in the monthly SSRDI are generally consistent with those of SRI, SGDI, and SSMI, indirectly validating the effectiveness of the calculated SSRDI. The data suggest that using SSRDI for describing and monitoring ecological river disconnection can be considered reliable. Notably, the green line representing SSRDI is slightly lower than the others, indicating that SSRDI reflects a more severe river disconnection than individual indices. To provide a clearer comparison, changes in SSRDI, SRI, SGDI, and SSMI from 2015 to 2020 are depicted in Fig. 7(b). It is widely acknowledged that ecological river disconnection occurs when surface river discharge falls below the minimum ecological flow or reaches zero. Seasonal rivers, due to limited and unstable recharge sources, often experience low or zero surface flow for extended periods. Typically, groundwater plays a crucial ecological role in these cases. Therefore, using only surface river disconnection to judge ecological river disconnection in seasonal rivers is inadequate. As shown in rectangular boxes a and c, SRI identifies moderate river disconnection, but with soil moisture (SSMI) and groundwater (SGDI) at healthy levels, SSRDI indicates light river disconnection or no disconnection. This suggests that despite surface river disconnection, groundwater and soil moisture still provide sufficient water for vegetation, maintaining ecological function and preventing severe ecological river disconnection. However, in September 2015, a sharp decline in SSMI, combined with surface flow and groundwater disconnection, resulted in severe ecological river disconnection. Similarly, as indicated in rectangular box b, while SRI does not detect river disconnection or identifies only light disconnection, SSRDI identifies severe river disconnection. This discrepancy arises because low SGDI and SSMI values indicate a lack of groundwater and soil moisture, resulting in insufficient water for vegetation and leading to ecological river disconnection.
Fig. 7.
(a): Comparison between monthly SSRDI and three single variable indexes from 2002 to 2020 in the TBR; (b): Details of comparison for monthly SSRDI and 3 single variable indexes from 2015 to 2021 in the TBR.
The correlation between SSRDI and the three univariate indices (SRI, SGDI, and SSMI) is detailed in Table 4; Fig. 8. SSRDI exhibits a positive correlation with each of these indices. Notably, both Spearman and Pearson correlation coefficients for SSRDI and each univariate index are significant at the P < 0.01 level. Specifically, the Spearman correlation coefficients are 0.531, 0.565, and 0.427, while the Pearson coefficients are 0.563, 0.568, and 0.446, all significant at P < 0.01.At the monthly scale, the minimum correlation coefficient (r) between SSRDI and SRI occurs in June (0.276), while the maximum is observed in August (0.681). For SSRDI and SGDI, the lowest r is in July (0.305) and the highest is in May (0.689). SSRDI and SSMI show their minimum r in April (0.228) and maximum in July (0.658). Overall, SSRDI demonstrates a strong correlation with SRI, SGDI, and SSMI, with the r value between SSRDI and SGDI generally exceeding that of SSRDI with the other two indices. Excluding May, June, and October, all other r values between SSRDI and SRI are significantly correlated, with March, April, July, August, and September passing the P < 0.05 significance test. Similarly, all r values between SSRDI and SGDI, except for June and July, are significantly correlated, with January, February, March, April, May, and August passing the P < 0.05 significance test. In summary, the Copula-based SSRDI developed in this study demonstrates reliability, sensitivity, and comprehensiveness. SSRDI effectively integrates information from the three indices, allowing for a more systematic and thorough identification of ecological river disconnection, proving to be highly effective in the TBR context.
Table 4.
The spearman and pearson correlation coefficient between SSRDI and different univariate indices.
| Rank correlation coefficient | SRI | SGDI | SSMI |
|---|---|---|---|
| Spearman | 0.531 | 0.565 | 0.427 |
| Pearson | 0.563 | 0.568 | 0.446 |
Fig. 8.
The Pearson correlations r between SSRDI and different univariate indices on a monthly scale in the TBR from 2002 to 2020.
As shown in Fig. 7(a), the green dashed line representing SSRDI is consistently lower than the black dashed line for SRI, the red dashed line for SGDI, and the blue dashed line for SSMI. To investigate whether this indicates a “severity” of ecological river disconnection by SSRDI, statistical correlations between the indices and disconnection occurrence were analyzed for the SSRDI, SRI, SGDI, and SSMI series, each comprising 228 samples. The study found that for 15 cases, all indices were below the threshold (i.e., all three disconnection types occurred along with ecological river disconnection). In 35 cases, all indices were above the threshold (i.e., neither the three disconnection types nor ecological river disconnection occurred). There were no cases where all three disconnection types occurred without ecological river disconnection or where ecological river disconnection occurred without the three disconnection types. This indirectly validates SSRDI’s effectiveness in TBR. Specifically, SSRDI was below the threshold (indicating ecological river disconnection) in 113 instances and above the threshold (indicating no ecological river disconnection) in 115 instances. Among the cases where only one index from SRI, SGDI, or SSMI was below the threshold and SSRDI was below the threshold (indicating ecological river disconnection due to one type of disconnection), there were 40 cases. Of these, 8 cases had both SSRDI and SRI below the threshold, while SGDI and SSMI were above the threshold; 1 case had both SSRDI and SGDI below the threshold, while SRI and SSMI were above the threshold; and 31 cases had both SSRDI and SSMI below the threshold, while SRI and SGDI were above the threshold. In cases where only one index from SRI, SGDI, or SSMI was below the threshold and SSRDI was above the threshold (indicating one type of disconnection occurred but did not lead to ecological river disconnection), there were 63 instances. Specifically, there were 23 cases where SRI was below the threshold, and SSRDI, SGDI, and SSMI were above the threshold; 1 case where SGDI was below the threshold, and SSRDI, SRI, and SSMI were above the threshold; and 39 cases where SSMI was below the threshold, and SSRDI, SRI, and SGDI were above the threshold. For cases where two indices from SRI, SGDI, or SSMI were below the threshold and SSRDI was below the threshold (indicating ecological river disconnection due to two types of disconnection), there were 59 instances. Specifically, there were 38 cases where SRI, SGDI, and SSRDI were below the threshold, while SSMI was above the threshold; 17 cases where SRI, SSMI, and SSRDI were below the threshold, while SGDI was above the threshold; and 4 cases where SGDI, SSMI, and SSRDI were below the threshold, while SRI was above the threshold. For cases where two indices from SRI, SGDI, or SSMI were below the threshold and SSRDI was above the threshold (indicating two types of disconnection occurred but did not lead to ecological river disconnection), there were 16 instances. Specifically, there were 9 cases where SRI and SGDI were below the threshold, while SSMI and SSRDI were above the threshold; 7 cases where SRI and SSMI were below the threshold, while SGDI and SSRDI were above the threshold; and no cases where SGDI and SSMI were below the threshold, while SRI and SSRDI were above the threshold. The probabilities of ecological river disconnection occurring with zero, one, two, or three types of disconnection are 0%, 38.8%, 78.7%, and 100%, respectively. This indicates that while one or two types of disconnection have some impact on rivers, they do not necessarily lead to comprehensive ecological river disconnection, and the likelihood of a comprehensive ecological river disconnection increases with the number of disconnection types.
Temporal changes of ecological river Disconnection
The variations in SSRDI over different decadal scales are illustrated in Fig. 9(a) and (b). In the 2000 s and 2010 s, the mean SSRDI values were − 1.211 and − 1.686, respectively. Specifically, SSRDI showed a declining trend in both decades, though the rate of decline differed, with linear trends of −0.900/10a and − 0.498/10a, respectively. The decline in the 2010 s slowed down. Figure 9(c) displays the monthly and seasonal distributions of SSRDI values for TBR from 2002 to 2020, with seasons defined as follows: spring (March-May), summer (June-August), autumn (September-November), and winter (December-February). On a monthly scale, the differences in average SSRDI values are minimal, with the highest value occurring in August and the lowest in June. Seasonally, winter experiences the most severe ecological flow disruption, followed by spring. Overall, the annual trend in ecological flow disruption shows some alleviation from January to March, worsening significantly from April to June to a minimum, easing from July to August to a peak, and worsening again from September to December. This pattern highlights that TBR’s extreme precipitation distribution leads to peak SSRDI values during concentrated rainfall in July and August.
Fig. 9.
(a), (b): The SSRDI change characteristics at the decadal scale in the 2000 s and 2010s. (c): SSRDI of the TBR in different months and seasons from 2002 to 2020.
Using the BEAST algorithm, we performed a mutation analysis on the SSRDI from 2002 to 2020. The seasonal, trend, and residual components of SSRDI are shown in Fig. 10. The seasonal component exhibits clear periodic changes, with an 89.02% probability of a seasonal mutation occurring in June 2004. The confidence interval for this mutation is from January 2004 to January 2006 (indicated by the green transparent curve in the figure), with mean SSRDI values of −0.65 and − 1.58 before and after the mutation, respectively, and the mutation being a monotonic decrease. For the trend component, two potential mutations in SSRDI during the study period are identified: the first in April 2005, with a 73.15% probability and a confidence interval from February 2005 to November 2005, characterized by a mutation from decrease to increase; the second in February 2007, with a 58.0% probability and a confidence interval from May 2006 to October 2007, characterized by a monotonic increase. At the first trend mutation point, SSRDI dropped sharply to its lowest point, showing no significant improvement within a year. Although SSRDI increased before and after the second mutation point, it remained below the pre-mutation level, indicating an overall declining trend.
Fig. 10.
Seasonal component, trend component, and residual component of SSRDI based on BEAST algorithm in the TBR during 2002–2020.
Discussion
Advantages of SSRDI
In arid and semi-arid regions with limited precipitation, high evaporation rates, and fragile ecosystems, surface water and groundwater frequently interchange72,73. Due to climate change and human activities, many arid and semi-arid regions experience perennial dry riverbeds, with the ecological environment heavily reliant on groundwater. This has led to an ecosystem model dominated by groundwater74. Current studies on seasonal rivers in these regions often focus solely on either surface water or groundwater, neglecting the interaction between them and the crucial role of soil moisture as a link between the two75,76. This study introduces a comprehensive index, the SSRDI, based on three-dimensional Copula functions and standardized indices, to assess ecological river disconnection in the TBR by integrating surface runoff, groundwater, and soil moisture. Due to the strong climatic influence on TBR’s hydrological conditions, optimal distributions vary across time and indices77. Therefore, prior fitting of runoff, groundwater, and soil moisture data is conducted to obtain the most accurate distribution functions for calculating SRI, SGDI, and SSMI49. SSRDI results indicate a continuous decline in TBR’s SSRDI from the early 2000 s to the late 2010 s, signaling increasingly severe ecological river disconnection. This finding is consistent with Luo et al.78 and Jin et al.73confirming the reliability of the SSRDI. Furthermore, the observed decrease in runoff in some regions of northwestern China’s arid inland river basins reported by Luo et al.78aligns with the temporal trends of SSRDI in this study, further validating its applicability in water-scarce areas. Thus, the proposed composite index holds practical application value.
Single types of disconnection do not necessarily lead to ecological river disconnection, and vice versa. A single type of disconnection may not necessarily lead to ecological river disconnection, and when ecological river disconnection occurs, a certain type of disconnection may also not occur. As illustrated in Fig. 11, focusing solely on surface runoff while neglecting groundwater and soil moisture may miss potential ecological river disconnection issues. Potential problems of ecological river disconnection may be missed until vegetation growth deteriorates and the ecological environment is severely damaged, and surface water supply and irrigation are difficult to fundamentally solve the problem75,79. At this point, addressing ecological river disconnection should focus on groundwater replenishment and maintaining groundwater ecology76,80. Conversely, if surface runoff is insufficient and leads to surface disconnection, unnecessary surface water supplementation is not required as adequate groundwater and soil moisture can still support vegetation growth, thus preventing ecological river disconnection79. From the perspective of water resource planning and efficient utilization, it is of great significance for local ecological environment protection and can provide effective reference for watershed water resource planning and management.
Fig. 11.
Schematic diagram of ecological river disconnection in different situations.
It is important to note that when both groundwater and soil moisture experience disconnection simultaneously, a comprehensive ecological flow interruption will inevitably occur (Table 5). This is due to the critical role of groundwater and soil moisture in sustaining vegetation growth in arid and semi-arid environments81,82. In such conditions, vegetation growth relies on the root system’s ability to absorb sufficient soil moisture through capillary action, with groundwater serving as a vital source of soil moisture47. The growth and distribution of vegetation are highly dependent on both groundwater and soil moisture28,81. Therefore, when both groundwater and soil moisture experience interruptions, vegetation roots cannot absorb adequate water, limiting growth and indicating damage to the ecological environment19,83. The SSRDI, therefore, is more sensitive to detecting the occurrence of disconnection compared to single indices, effectively capturing interruptions and non-interruptions under these conditions. It should be noted that SSRDI is not intended to completely replace any individual index but demonstrates strong correlations with SRI, SGDI, and SSMI. From an application and management perspective, using these indices in conjunction will provide the most comprehensive results.
Table 5.
The number of months in which comprehensive ecological river disconnection occurs and does not occur when different combinations of water types occur from 2002 to 2020 in TBR.
| Type | Surface water disconnection | Groundwater disconnection | Soil water disconnection | Comprehensive ecological river disconnection | Total | |
|---|---|---|---|---|---|---|
| Occur | Not occur | |||||
| 0 types of occurrences | No | No | No | 0 | 35 | 35 |
| 1 type of occurrences | Yes | No | No | 8 | 23 | 31 |
| No | Yes | No | 1 | 1 | 2 | |
| No | No | Yes | 31 | 39 | 70 | |
| 2 types of occurrences | Yes | Yes | No | 38 | 9 | 47 |
| Yes | No | Yes | 17 | 7 | 24 | |
| No | Yes | Yes | 4 | 0 | 4 | |
| 3 types of occurrences | Yes | Yes | Yes | 15 | 0 | 15 |
Furthermore, variations in threshold settings for different indices can significantly impact the identification results. In this study, four indices—SRI, SGDI, SSMI, and the newly constructed SSRDI—employ distinct threshold settings. This is done to ensure that the thresholds are as reasonable and applicable to the region as possible. For instance, the SRI threshold is derived from the study by Yang et al.66which employs an improved Tennant method to calculate the minimum ecological flow. According to this method, if the flow in a given month falls below this minimum ecological flow, it is classified as a flow interruption. By analyzing the frequency of such interruptions and the empirical frequency of SRI, the SRI value corresponding to the minimum ecological flow is determined as the interruption threshold. The traditional Tennant method uses a fixed percentage of the long-term average flow, which does not account for intra-annual variations in water flow or seasonal changes in river discharge84. The improved Tennant method addresses this by selecting a typical year with flow values closest to the long-term average, thereby reflecting the river’s seasonal flow characteristics more accurately66. The SSRDI threshold, on the other hand, is set based on vegetation health. Vegetation condition serves as an indirect indicator of the health of seasonal rivers. The Vegetation Health Index (VHI), which combines the advantages of both the Vegetation Condition Index and the Temperature Condition Index, provides a robust measure of vegetation health65. In this study, the monthly VHI data from 2002 to 2020 were used to identify months with vegetation drought occurrences. Combining this with the empirical frequency of SSRDI, the SSRDI value corresponding to periods of vegetation drought was established as the disconnection threshold85.
Uncertainties and limitations
Several uncertainties are present in this study. First, remote sensing datasets can be affected by cloud cover and adverse weather conditions, which may still impact the accuracy of the data5,41. Standardized indices are widely used in various models and assessments due to their computational efficiency77,86,87. However, different distribution functions applied during the normalization process may yield varying results89. This study identifies the optimal distribution among five parameter distributions: Log-L, Wbl, GP, Logn, and Gamma. Similarly, the choice of Copula function introduces uncertainty. The Copula function selected for constructing SSRDI in the TBR region is the Gaussian Copula, though this choice may vary across different regions and time periods.
The study has limitations. It analyzes temporal variations in SSRDI for the entire TBR region without assessing spatial scales within sub-regions. Future research could expand the index to larger spatial scales for evaluation88,89. Additionally, this study considers only five Copula functions; exploring other types could provide further insights90. Further investigation into seasonal river flow issues in arid and semi-arid areas could also integrate additional factors beyond surface water, groundwater, and soil moisture, applying higher-dimensional Copula functions to model the joint distribution of more variables91.
Conclusions
This study proposes a novel Copula-based standardized ecological river disconnection index (SSRDI) for seasonal river in the arid and semi-arid areas. SSRDI integrates information from surface water, groundwater, and soil moisture by employing SRI, SGDI, and SSMI. It provides a more accurate and scientific assessment of the onset of seasonal river disconnection compared to single-variable indices. Although SSRDI was applied to the TBR in this study, it has potential for broader application in other arid and semi-arid regions. The main findings are as follows:
Different optimal distribution functions for monthly runoff, groundwater, and soil moisture data were used to calculate SRI, SGDI, and SSMI, offering a more robust mathematical and statistical foundation. The Gaussian Copula was identified as the most suitable for constructing the SSRDI for TBR.
SSRDI demonstrated good correlation with the three single-variable indices, with Spearman and Pearson correlation coefficients passing significance tests at P < 0.01. SSRDI’s trends and variations align well with those of SRI, SGDI, and SSMI, providing a closer representation of river disconnection. By integrating surface water, groundwater, and soil moisture, SSRDI offers a more comprehensive and accurate assessment of seasonal river disconnection.
From 2002 to 2020, SSRDI for TBR showed a persistent decline, although the rate of decrease has slowed. On a decadal scale, the decline was more pronounced in the 2000 s compared to the 2010s. Seasonally, SSRDI reached its lowest in June and its highest in August, indicating the most severe river disconnection in June and relief in July and August. The annual pattern shows a cyclical trend of deterioration and recovery.
Seasonal components of SSRDI displayed periodic changes with a mutation in June 2004, altering the periodicity before and after this point, and a decrease in SSRDI’s mean value. The trend component showed an overall decline with two mutations occurring in April 2005 and February 2007.
Overall, this study validates the Copula-based SSRDI and provides valuable insights for identifying river disconnection in seasonal rivers of arid and semi-arid regions.
Acknowledgements
This research was supported by the Yinshanbeilu Grassland Eco-hydrology National Observation and Research Station (YSS2022020) and the Key Special Project of the “Science and Technology Revitalization of Mongolia” Action (grant number 2022EEDSKJXM004-4).
Author contributions
W.Z.: Formal analysis, Investigation, Methodology, Visualization, Writing – original draft, Writing – review & editing. Q.Q.: Conceptualization, Funding acquisition, Methodology, Writing – review & editing. Z.Z.: Investigation, Funding acquisition, Conceptualization., Writing – review & editing.Y.H.: Investigation, Funding acquisition. Writing – review & editingW.F.: Writing – review & editing. Methodology, Supervision.F.K.: Writing –review & editing.Methodology, Supervision.L.H.: Writing –review & editing, Visualization.Z.Y.: Writing –review & editing, Visualization.All authors reviewed the manuscript.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Palmer, M. & Ruhi, A. Linkages between flow regime, biota, and ecosystem processes: implications for river restoration. Science365, eaaw2087 (2019). [DOI] [PubMed] [Google Scholar]
- 2.Zhao, Q. et al. Evaluating a river’s ecological health: A multidimensional approach. Environ. Sci. Ecotechnology. 21, 100423 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen, W., Lu, S., Pan, N. & Jiao, W. Impacts of long-term reclaimed water irrigation on soil salinity accumulation in urban green land in Beijing. Water Resour. Res.49, 7401–7410 (2013). [Google Scholar]
- 4.Best, J. Anthropogenic stresses on the world’s big rivers. Nat. Geosci.12, 7–21 (2019). [Google Scholar]
- 5.Feng, K. et al. Three-dimensional perspective on the characterization of the Spatiotemporal propagation from meteorological to agricultural drought. Agric. Meteorol.353, 110048 (2024). [Google Scholar]
- 6.Graham, D. J., Bierkens, M. F. P. & van Vliet, M. T. H. Impacts of droughts and heatwaves on river water quality worldwide. J. Hydrol.629, 130590 (2024). [Google Scholar]
- 7.Jiang, S. et al. Development of a comprehensive framework for quantifying the impacts of climate change and human activities on river hydrological health variation. J. Hydrol.600, 126566 (2021). [Google Scholar]
- 8.Hanna, D. E. L., Tomscha, S. A., Ouellet Dallaire, C. & Bennett, E. M. A review of riverine ecosystem service quantification: research gaps and recommendations. J. Appl. Ecol.55, 1299–1311 (2018). [Google Scholar]
- 9.Lim, S. & Do, Y. Macroinvertebrate conservation in river ecosystems: challenges, restoration strategies, and integrated management approaches. Entomol. Res.53, 271–290 (2023). [Google Scholar]
- 10.Johnson, L. B., Breneman, D. H. & Richards, C. Macroinvertebrate community structure and function associated with large wood in low gradient streams. River Res. Appl.19, 199–218 (2003). [Google Scholar]
- 11.Sauquet, E. et al. Classification and trends in intermittent river flow regimes in australia, Northwestern Europe and USA: A global perspective. J. Hydrol.597, 126170 (2021). [Google Scholar]
- 12.Wang, H. et al. Anthropogenic climate change has influenced global river flow seasonality. Science383, 1009–1014 (2024). [DOI] [PubMed] [Google Scholar]
- 13.Bishop-Taylor, R., Tulbure, M. G. & Broich, M. Surface water network structure, landscape resistance to movement and flooding vital for maintaining ecological connectivity across australia’s largest river basin. Landsc. Ecol.30, 2045–2065 (2015). [Google Scholar]
- 14.Messager, M. L. et al. Global prevalence of non-perennial rivers and streams. Nature594, 391–397 (2021). [DOI] [PubMed] [Google Scholar]
- 15.Foulquier, A. et al. Unravelling large-scale patterns and drivers of biodiversity in dry rivers. Nat. Commun.15, 7233 (2024). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shanafield, M., Bourke, S. A., Zimmer, M. A. & Costigan, K. H. An overview of the hydrology of non-perennial rivers and streams. WIREs Water. 8, e1504 (2021). [Google Scholar]
- 17.Stubbington, R., England, J., Wood, P. J. & Sefton, C. E. M. Temporary streams in temperate zones: recognizing, monitoring and restoring transitional aquatic-terrestrial ecosystems. WIREs Water. 4, e1223 (2017). [Google Scholar]
- 18.El-Rawy, M. et al. Assessment of groundwater quality in arid regions utilizing principal component analysis, GIS, and machine learning techniques. Mar. Pollut Bull.205, 116645 (2024). [DOI] [PubMed] [Google Scholar]
- 19.Li, W., Kang, S., Du, T., Ding, R. & Zou, M. Optimal groundwater depth and irrigation amount can mitigate secondary salinization in water-saving irrigated areas in arid regions. Agric. Water Manag. 302, 109007 (2024). [Google Scholar]
- 20.Zhao, C., Li, S., Jia, Y. & Jiang, Y. [Dynamic changes of groundwater level and vegetation in water table fluctuant belt in lower reaches of Heihe river: coupling simulation]. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol.19, 2687–2692 (2008). [PubMed] [Google Scholar]
- 21.Han, M. et al. An eco-hydrological approach to predicting regional vegetation and groundwater response to ecological water conveyance in dryland riparian ecosystems. Quat Int.380–381, 224–236 (2015). [Google Scholar]
- 22.Jin, X., Wan, L., Zhang, Y., Xue, Z. & Yin, Y. A study of the relationship between vegetation growth and groundwater in the Yinchuan plain. Earth Sci. Front.14, 197–203 (2007). [Google Scholar]
- 23.Baattrup-Pedersen, A. et al. Structural and functional responses of plant communities to climate change-mediated alterations in the hydrology of riparian areas in temperate Europe. Ecol. Evol.8, 4120–4135 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gill, K. M., Goater, L. A., Braatne, J. H. & Rood, S. B. The irrigation effect: how river regulation can promote some riparian vegetation. Environ. Manage.61, 650–660 (2018). [DOI] [PubMed] [Google Scholar]
- 25.Agboma, C. & Itenfisu, D. Investigating the Spatio-Temporal dynamics in the soil water storage in alberta’s agricultural region. J. Hydrol.588, 125104 (2020). [Google Scholar]
- 26.Zhu, L., Sun, S., Li, Y., Liu, X. & Hu, K. Effects of climate change and anthropogenic activity on the vegetation greening in the Liaohe river basin of Northeastern China. Ecol. Indic.148, 110105 (2023). [Google Scholar]
- 27.Liu, Y., Cui, Z., Huang, Z., López-Vicente, M. & Wu, G. L. Influence of soil moisture and plant roots on the soil infiltration capacity at different stages in arid grasslands of China. CATENA182, 104147 (2019). [Google Scholar]
- 28.Li, B. B. et al. Deep soil moisture limits the sustainable vegetation restoration in arid and semi-arid loess plateau. Geoderma399, 115122 (2021). [Google Scholar]
- 29.Guillen-Cruz, G., Rodríguez-Sánchez, A. L. & Fernández-Luqueño, F. Flores-Rentería, D. Influence of vegetation type on the ecosystem services provided by urban green areas in an arid zone of Northern Mexico. Urban Urban Green.62, 127135 (2021). [Google Scholar]
- 30.Tugwell-Wootton, T., Skrzypek, G., Dogramaci, S., McCallum, J. & Grierson, P. F. Soil moisture evaporative losses in response to wet-dry cycles in a semiarid climate. J. Hydrol.590, 125533 (2020). [Google Scholar]
- 31.Zhang, A. & Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ.134, 12–23 (2013). [Google Scholar]
- 32.Liu, Y. et al. On the mechanisms of two composite methods for construction of multivariate drought indices. Sci. Total Environ.647, 981–991 (2019). [DOI] [PubMed] [Google Scholar]
- 33.Wu, Z., Cheng, D., He, H., Li, Y. & Zhou, J. Research progress of composite drought index. Water Resour. Prot.37 (1), 36–45 (2021). (in Chinese). [Google Scholar]
- 34.Mishra, A. K. & Singh, V. P. Drought modeling – A review. J. Hydrol.403, 157–175 (2011). [Google Scholar]
- 35.Wang, W. et al. Trivariate copula functions for constructing a comprehensive atmosphere-land surface-hydrology drought index: A case study in the yellow river basin. J. Hydrol.642, 131784 (2024). [Google Scholar]
- 36.Guo, L. et al. Developing a multivariate drought index to assess drought characteristics based on the SWAT-Copula method in the Poyang lake basin, China. Ecol. Indic.170, 113123 (2025). [Google Scholar]
- 37.Hao, Z. & AghaKouchak, A. Multivariate standardized drought index: A parametric multi-index model. Adv. Water Resour.57, 12–18 (2013). [Google Scholar]
- 38.Guo, Y. et al. Copulas-based bivariate socioeconomic drought dynamic risk assessment in a changing environment. J. Hydrol.575, 1052–1064 (2019). [Google Scholar]
- 39.Rowlands, D. D. et al. Global mass flux solutions from GRACE: A comparison of parameter Estimation strategies—Mass concentrations versus Stokes coefficients. J Geophys. Res. Solid Earth115, B01403 (2010).
- 40.Save, H., Bettadpur, S. & Tapley, B. D. High-resolution CSR GRACE RL05 mascons. J. Geophys. Res. Solid Earth. 121, 7547–7569 (2016). [Google Scholar]
- 41.Wang, F. et al. Spatio-temporal evolution and teleconnection factor analysis of groundwater drought based on the GRACE Mascon model in the yellow river basin. J. Hydrol.626, 130349 (2023). [Google Scholar]
- 42.Qu, S. et al. Large-scale surface water-groundwater origins and connectivity in the Ordos basin, china: insight from hydrogen and oxygen isotopes. Environ. Res.236, 116837 (2023). [DOI] [PubMed] [Google Scholar]
- 43.Zhang, K., Xie, X., Zhu, B., Meng, S. & Yao, Y. Unexpected groundwater recovery with decreasing agricultural irrigation in the yellow river basin. Agric. Water Manag. 213, 858–867 (2019). [Google Scholar]
- 44.Mckee, T. B., Doesken, N. J. & Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. (1993).
- 45.Alam, N. M. et al. Evaluation of drought using SPEI drought class transitions and log-linear models for different agro-ecological regions of India. Phys. Chem. Earth Parts ABC. 100, 31–43 (2017). [Google Scholar]
- 46.Pohl, F. et al. Long-term daily hydrometeorological drought indices, soil moisture, and evapotranspiration for ICOS sites. Sci. Data. 10, 281 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Deng, Y., Ye, X., Feng, J., Guo, H. & Du, X. Assessment of soil-groundwater nitrogen cycling processes in the agricultural region through flux model, stable isotope. J. Hydrol.639, 131604 (2024). [Google Scholar]
- 48.Vicente-Serrano, S. M., Beguería, S. & López-Moreno, J. I. A multiscalar drought index sensitive to global warming: the standardized precipitation evapotranspiration index. J. Clim.23, 1696–1718 (2010). [Google Scholar]
- 49.Bloomfield, J. P. & Marchant, B. P. Analysis of groundwater drought Building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci.17, 4769–4787 (2013). [Google Scholar]
- 50.Wang, F. et al. A new copula-based standardized precipitation evapotranspiration streamflow index for drought monitoring. J. Hydrol.585, 124793 (2020). [Google Scholar]
- 51.Hosking, J. R. M., Wallis, J. R. & Wood, E. F. Estimation of the generalized Extreme-Value distribution by the method of Probability-Weighted moments. Technometrics27, 251–261 (1985). [Google Scholar]
- 52.Hosking, J. R. M. & L-Moments Analysis and Estimation of distributions using linear combinations of order statistics. J. R Stat. Soc. Ser. B Methodol.52, 105–124 (1990). [Google Scholar]
- 53.Sherly, M. A., Karmakar, S., Chan, T. & Rau, C. Design Rainfall Framework Using Multivariate Parametric-Nonparametric Approach. (2016).
- 54.AghaKouchak, A., Feldman, D., Hoerling, M., Huxman, T. & Lund, J. Water and climate: recognize anthropogenic drought. Nature524, 409–411 (2015). [DOI] [PubMed] [Google Scholar]
- 55.Sklar, M. Fonctions de répartition à N dimensions et leurs Marges. Ann. ISUP. VIII, 229–231 (1959). [Google Scholar]
- 56.Nelsen, R. B. An Introduction To Copulas (Springer, 1998).
- 57.Wu, Z. X., Chen, M., Ye, W. & Miao, B. Risk analysis of portfolio by copula-GARCH. Xitong Gongcheng Lilun Yu ShijianSystem Eng. Theory Pract.26, 45–52 (2006). [Google Scholar]
- 58.Khan, M. A. et al. Modeling drought duration and severity using two-dimensional copula. J. Atmospheric Sol -Terr Phys.214, 105530 (2021). [Google Scholar]
- 59.Yusof, F., Hui-Mean, F., Suhaila, J. & Yusof, Z. Characterisation of drought properties with bivariate copula analysis. Water Resour. Manag. 27, 4183–4207 (2013). [Google Scholar]
- 60.Zin, W. & Ibrahim, K. Analysis of drought condition and risk in Peninsular Malaysia using standardised precipitation index. Theor Appl. Climatol111, 559–568 (2012).
- 61.Janga Reddy, M. & Ganguli, P. Bivariate flood frequency analysis of upper Godavari river flows using archimedean copulas. Water Resour. Manag26, 3995–4018 (2012).
- 62.Chebana, F. & Ouarda, T. B. M. J. Multivariate non-stationary hydrological frequency analysis. J. Hydrol.593, 125907 (2021). [Google Scholar]
- 63.Zscheischler, J., van den Hurk, B., Ward, P. J. & Westra, S. Chapter 4 - Multivariate extremes and compound events. in Climate Extremes and Their Implications for Impact and Risk Assessment (eds. Sillmann, J., Sippel, S. & Russo, S.) 59–76Elsevier, (2020). 10.1016/B978-0-12-814895-2.00004-5
- 64.Gringorten, I. I. A plotting rule for extreme probability paper. J. Geophys. Res.1896–1977 68, 813–814 (1963). [Google Scholar]
- 65.Du, L. et al. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs Geoinf.23, 245–253 (2013). [Google Scholar]
- 66.Yang, F., Xia, Z., Yu, L. & Guo, L. Calculation and analysis of the instream ecological flow for the Irtysh river. Procedia Eng.28, 438–441 (2012). [Google Scholar]
- 67.Yan, W., Yang, F., Zhou, J. & Wu, R. Droughts force Temporal change and Spatial migration of vegetation phenology in the Northern hemisphere. Agric. Meteorol.341, 109685 (2023). [Google Scholar]
- 68.Yang, X., Tian, S., You, W. & Jiang, Z. Reconstruction of continuous GRACE/GRACE-FO terrestrial water storage anomalies based on time series decomposition. J. Hydrol.603, 127018 (2021). [Google Scholar]
- 69.Pattathal, V., Karnieli, A. & A. & Deep feature learning and latent space encoding for crop phenology analysis. Expert Syst. Appl.187, 115929 (2022). [Google Scholar]
- 70.Cai, Y., Liu, S. & Lin, H. Monitoring the vegetation dynamics in the Dongting lake wetland from 2000 to 2019 using the BEAST algorithm based on dense Landsat time series. Appl. Sci.10, 4209 (2020). [Google Scholar]
- 71.White, J. H. R., Walsh, J. E. & Thoman, R. L. Using bayesian statistics to detect trends in Alaskan precipitation. Int J. Climatol41, 2045–2059 (2021).
- 72.Yang, N. et al. Triple isotopes (δD, δ18O, δ17O) characteristic of river water and groundwater in an arid watershed from Qaidam basin, Northwestern china: implications for hydrological cycle. Sci. Total Environ.927, 172229 (2024). [DOI] [PubMed] [Google Scholar]
- 73.Jin, J., Liu, T., Liao, Z., Wang, M. & Wang, Z. Interaction between intermittent river and groundwater in arid and semiarid basin considering the influence of evaporation on isotopic compositions. J. Hydrol. Reg. Stud.54, 101876 (2024). [Google Scholar]
- 74.Wang, Z. et al. River-groundwater interaction affected species composition and diversity perpendicular to a regulated river in an arid riparian zone. Glob Ecol. Conserv.27, e01595 (2021). [Google Scholar]
- 75.Huang, F., Ochoa, C. G. & Chen, X. Assessing environmental water requirement for groundwater-dependent vegetation in arid inland basins by combining the copula joint distribution function and the dual objective optimization: an application to the Turpan basin, China. Sci. Total Environ.799, 149323 (2021). [DOI] [PubMed] [Google Scholar]
- 76.Mpakairi, K. S., Dube, T., Dondofema, F. & Dalu, T. Spatio–temporal variation of vegetation heterogeneity in groundwater dependent ecosystems within arid environments. Ecol. Inf.69, 101667 (2022). [Google Scholar]
- 77.Wang, Y., Duan, L., Liu, T., Li, J. & Feng, P. A. Non-stationary standardized streamflow index for hydrological drought using climate and human-induced indices as covariates. Sci. Total Environ.699, 134278 (2020). [DOI] [PubMed] [Google Scholar]
- 78.Luo, J., Yu, R., Liang, W. & Hao, Y. Scale-specific controls of monthly suspended sediment load in a typical inland river. J. Hydrol.641, 131847 (2024). [Google Scholar]
- 79.Glanville, K., Sheldon, F., Butler, D. & Capon, S. Effects and significance of groundwater for vegetation: A systematic review. Sci. Total Environ.875, 162577 (2023). [DOI] [PubMed] [Google Scholar]
- 80.Anurag, H., Ng, G. H. C., Tipping, R. & Tokos, K. Modeling the impact of Spatiotemporal vegetation dynamics on groundwater recharge. J. Hydrol.601, 126584 (2021). [Google Scholar]
- 81.Eamus, D. & Froend, R. Groundwater-dependent ecosystems: the where, what and why of GDEs. Aust J. Bot.10.1071/BT06029 (2006). [Google Scholar]
- 82.Wang, Y., Zheng, C., Ma, R. & Review Safe and sustainable groundwater supply in China. Hydrogeol. J.26, 1301–1324 (2018). [Google Scholar]
- 83.Cooper, D. J., Sanderson, J. S., Stannard, D. I. & Groeneveld, D. P. Effects of long-term water table drawdown on evapotranspiration and vegetation in an arid region phreatophyte community. J. Hydrol.325, 21–34 (2006). [Google Scholar]
- 84.Huang, S., Chang, J., Huang, Q., Wang, Y. & Chen, Y. Calculation of the Instream Ecological Flow of the Wei River Based on Hydrological Variation. J. Appl. Math. (2014). (2014).
- 85.Bento, V. A., Gouveia, C. M., DaCamara, C. C. & Trigo I. F. A Climatological assessment of drought impact on vegetation health index. Agric. Meteorol.259, 286–295 (2018). [Google Scholar]
- 86.Zhang, Y. et al. Assessment of drought evolution characteristics based on a nonparametric and trivariate integrated drought index. J. Hydrol.579, 124230 (2019). [Google Scholar]
- 87.Secci, D., Tanda, M. G., D’Oria, M., Todaro, V. & Fagandini, C. Impacts of climate change on groundwater droughts by means of standardized indices and regional climate models. J. Hydrol.603, 127154 (2021). [Google Scholar]
- 88.Yang, C. et al. A novel comprehensive agricultural drought index accounting for precipitation, evapotranspiration, and soil moisture. Ecol. Indic.154, 110593 (2023). [Google Scholar]
- 89.Suo, N., Xu, C., Cao, L., Song, L. & Lei, X. A copula-based parametric composite drought index for drought monitoring and applicability in arid central Asia. CATENA235, 107624 (2024). [Google Scholar]
- 90.Fenech, J. P., Vosgha, H. & Shafik, S. Loan default correlation using an archimedean copula approach: A case for recalibration. Econ. Model.47, 340–354 (2015). [Google Scholar]
- 91.Oh, D. H. & Patton, A. J. High-dimensional copula-based distributions with mixed frequency data. J. Econom. 193, 349–366 (2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.