Temperature-tunability of perovskite quasi-bound states in the continuum-metastructure for enhanced terahertz performance and CO₂ sensing

Abstract

This study explores the optical and mechanical properties, along with the thermodynamical and thermal stability of methylammonium lead iodide (MAPbI₃), specifically for terahertz (THz) applications, utilizing first-principles density functional theory and finite element analysis. The refractive index of MAPbI₃ remains stable in the THz region, showing no dispersion or loss, and can be finely tuned by temperature, exhibiting pronounced changes around the 60 °C phase transition. We propose a tunable metastructure that integrates MAPbI₃, featuring periodic circular slot rings, to investigate bound states in the continuum (BICs) and quasi-BICs. By employing symmetry-breaking techniques, we effectively convert BICs into quasi-BICs, revealing temperature-tunable frequency shifts and quality factors that highlight the potential for innovative THz optoelectronic devices. Furthermore, our research examines the structure’s capability for carbon dioxide gas sensing, achieving impressive results with a maximum sensitivity of 0.301 THz/RIU and a figure of merit of 1.911 × 10⁵.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-025-09961-5.

Introduction

Carbon dioxide (CO₂) is one of the major greenhouse gases contributing significantly to global warming and climate change. Recently, CO₂ sensing technology has gained considerable attention for its potential to enhance environmental monitoring and improve industrial processes. Various advances in gas sensing technologies, including the development of highly sensitive and selective CO₂ sensors, have been reported in recent studies^1–4. These technologies not only contribute to reducing CO₂ levels but also enable real-time monitoring of air quality, making them essential tools in both environmental and industrial applications.

Terahertz (THz) waves, positioned between microwaves and infrared waves in the electromagnetic spectrum, have attracted considerable interest in various domains, including biomedicine, materials science, and chemistry⁵. This attention stems from their ability to penetrate deeply, nonionizing and nondestructive characteristics and their effectiveness in identifying molecular signatures⁶. However, the advancement of THz devices is hindered by their longer wavelengths and the limited availability of natural materials that can respond effectively to THz waves⁷. Metasurfaces offer a promising approach to overcome these obstacles. The unique periodic structure of these metasurfaces imparts remarkable properties⁸. In recent decades, a variety of metasurfaces have been conceptualized and developed. In addition to conventional metallic metasurfaces, innovative types such as all-dielectric metasurfaces⁹, flexible metasurfaces¹⁰, and liquid crystal metasurfaces have been proposed and fabricated¹¹. In these studies, only a limited number of materials are utilized for the THz range. Silicon and lithium tantalate are frequently employed in dielectric metasurfaces because of their high refractive index and minimal loss in the THz spectrum. Nevertheless, even with advancements in this area, it is crucial to explore new materials.

Recently, metasurfaces that incorporate bound states in the continuum (BICs) have gained considerable attention due to their infinite quality (Q) factor¹². Initially identified in quantum mechanics, the BIC concept has since been adapted for optical applications. In practice, BICs are often realized as quasi-BICs, which exhibit high but finite Q factors and appear as super cavity modes, enhancing spectral selectivity¹³. These high Q resonances are spectrally distinct, occurring at specific wavelengths, making them particularly effective for eliminating unwanted background spectra without additional filters⁵. Several researches have demonstrated that quasi-BICs with ultrahigh Q factors are highly effective for optoelectronic purposes. For example, we developed a perovskite-based metastructure for optical applications in the THz range¹⁴. Additionally, we designed and analyzed dielectric metasurfaces to form an ultrasensitive, label-free structure for sensing biological substances, gases, and temperature changes⁵. These findings underscore the spectral control capabilities of BIC metasurfaces, emphasizing their potential in optoelectronic applications. Typically, most dielectric metasurfaces have fixed functionalities after fabrication, preventing dynamic resonance and limiting their practical uses. However, reports of all-dielectric BIC metasurfaces with adjustable resonance frequencies are rare.

The chemical structure of three-dimensional (3D) metal halide perovskites is represented as ABX₃, where A signifies a monovalent cation, B denotes a divalent metal cation, and X indicates a halogen anion that bonds with the metal cations¹⁵. To substitute the A-site cation, organic compounds such as methylammonium (MA) or formamidinium can be used, along with inorganic ions like cesium. The B-site metal is commonly lead or tin. Hybrid perovskites, which combine organic and inorganic materials, exhibit numerous beneficial properties, including high charge mobility, low effective mass, high optical absorption coefficient, large dielectric constant, and a tunable bandgap^16–21. Methylammonium lead iodide (MAPbI₃) undergoes a phase transition from tetragonal to cubic at approximately 330 K²², making it suitable for thermally tunable metastructures.

In this study, we employ first-principles density functional theory (DFT) to examine the optical and stability properties of MAPbI₃ at various temperatures, to assess its potential for THz applications. The results indicate that the refractive index of MAPbI₃ can be modified by changing the temperature. This material exhibits a high dielectric constant, zero loss in the THz range, and tunability. Furthermore, we present a tunable metastructure incorporating periodic circular slot rings within a 3D perovskite layer (MAPbI₃). By displacing the inner ring from the center, we disrupt the symmetry of the structure, resulting in a zero-order channel that transforms dark modes into quasi-bound states in continuum states with finite linewidth. Through mathematical analysis using group theory and finite element calculations, we show that the proposed metastructure can excite multiband high-quality q-BICs, including the magnetic toroidal dipole and electric toroidal dipole. This study is a valuable reference for advancing THz applications, such as nonlinear optics, polarization-dependent switches, polarization-dependent filters, and multi-channel biochemical sensors. For example, we investigate the ability of this structure to carbon dioxide gas sensing and bidirectional optical switch.

Materials and methods

Structure

The proposed metastructure consists of a PDMS substrate (n = 1.4) topped with a thin layer of MAPbI₃, arranged in a periodic pattern of slot rings (Fig. 1a). The asymmetric unit cells are depicted in Fig. 1b, with structural parameters detailed in²³. An asymmetric structure is created by varying the offset distance of the inner ring (d). The optical properties of the metastructure are analyzed using the finite element method, applying Floquet-Bloch periodic boundary conditions along the x–z and y–z planes, with two perfectly matched layers along the z-axis. The unperturbed unit cell displays a 2D geometrical symmetry group referred to as C_4υ in Schoenflies notation. Table 1 presents the four dark modes (BICs) characterized by their irreducible representations: A₁, B₁, A₂, and B₂. Four BICs possess symmetries different from the incident electric field, preventing their excitation since these modes are orthogonal to the electric field components. To excite these BICs, it is necessary to reduce the symmetry of the structure. This can be accomplished by lowering the symmetry from C_4υ to C_s.

Fig. 1.

(a) The schematic of the metasurface and (b) the asymmetric unit cell.

Table 1.

Dark modes of C_4υ²³.

C4υ	C2	C4	C− 14	σx	σy	σxy	σ−xy
A1	1	1	1	1	1	1	1
A2	1	1	1	-1	-1	-1	-1
B1	1	-1	-1	1	1	-1	-1
B2	1	-1	-1	-1	-1	1	1

We then examine two additional structures that belong to the C_4v symmetry class. These structures feature a square unit cell and a cyclic unit cell (the inverse of the previous structure) (Fig. 2). It is important to note that the types of modes in these two structures are the same as in the previous structure, due to their similar symmetry class. The results in Table 2 indicate that the quality factor of the modes in the previous structure is higher compared to those in the two new structures. In addition, fabricating the previous structure from a square configuration is much simpler and less affected by non-uniformity. Therefore, we choose the structure presented in Fig. 1 as our primary structure.

Fig. 2.

Various structures belonging to the C_4υ symmetry class.

Table 2.

The quality factors of different C_4υ structures.

Structure	Q-factors of A1 (d = 0.5 μm)	Q-factors of B1 (d = 0.5 μm)	Q-factors of A2 (d = 0.5 μm)	Q-factors of B2 (d = 0.5 μm)
Main structure	1.4 × 104	5.85 × 105	5.50 × 105	4.68 × 104
Square structure	1.39 × 104	5.78 × 105	5.47 × 105	4.61 × 104
Reverse structure	3.27 × 103	6.46 × 104	5.19 × 104	5.52 × 103

Results and discussion

MAPbI₃ characteristics

The complex refractive index of MAPbI₃ is calculated using Eqs. (1–5) in the supplementary information and is depicted in Fig. 3. Since we use x- and y-polarized light to investigate the optical response of the metastructure, we should set the polarization vector of the incident light (u) to (100) and (010) when calculating the optical coefficients, as outlined in Eq. 2. The results in Table 3; Fig. 3 show that this perovskite exhibits no dispersion or loss in the THz region, making it highly suitable for applications within this spectral range. In addition, this material exhibits anisotropic properties (Table 3). This behavior is suitable for applications such as optical circuits, anti-reflective coatings, optoelectronic devices, and optical sensing systems. The refractive index of MAPbI₃ is influenced by temperature changes, which affect the lattice constant²². Table 3; Fig. 3 demonstrate how variations in temperature impact the lattice constant and, in turn, the refractive index of MAPbI₃. Notably, this material experiences a phase transition at 60 °C, shifting from the tetragonal phase (β-MAPbI₃) to the cubic phase (α-MAPbI₃)²², resulting in significant optical variations.

Fig. 3.

The refractive index of MAPbI₃ for different temperatures (25–60℃) with x-polarization (a) real part and (b) imaginary part.

Table 3.

Changes in lattice parameter and refractive index of MAPbI₃ with temperature.

Temperature	Lattice parameters of MAPbI3 (Å)22	Refractive index (N = n + ik) of MAPbI3 with x-polarization (Our DFT calculation)	Refractive index (N = n + ik) of MAPbI3 with y-polarization (Our DFT calculation)
25℃	a = b = 8.851, c = 12.444	2.5714 + 0i	2.5785 + 0i
30℃	a = b = 8.853, c = 12.443	2.5711 + 0i	2.5737 + 0i
35℃	a = b = 8.855, c = 12.446	2.5704 + 0i	2.5710 + 0i
40℃	a = b = 8.860, c = 12.453	2.5689 + 0i	2.5698 + 0i
45℃	a = b = 8.861, c = 12.460	2.5684 + 0i	2.5690 + 0i
50℃	a = b = 8.865, c = 12.477	2.5669 + 0i	2.5676 + 0i
55℃	a = b = 8.864, c = 12.497	2.5662 + 0i	2.5672 + 0i
60℃	a = b = c = 6.276	2.2503 + 0i	2.2577 + 0i

Next, we investigate the thermodynamic and thermal stability of MAPbI₃ at temperatures between 25 and 60 ℃. According to the results shown in Table 4 (Eq. 20 in the supplementary information), MAPbI₃ remains thermodynamically stable within this temperature range, as indicated by its negative formation energy values. However, as the temperature rises, the thermodynamic stability decreases because the unit cell volume increases. Interestingly, at 60 ℃, a crystal phase change causes the unit cell volume to decrease resulting in a higher stability.

Table 4.

Formation energy of MAPbI₃ with different temperatures (25–60℃).

Temperature	FE (eV)	E (ABX3) (eV)	E (AX) (eV)	E (BX2) (eV)
25℃	-0.190	-3126.309	-2288.287	-837.133
30℃	-0.173	-3126.285	-2288.981	-837.131
35℃	-0.132	-3126.277	-2289.015	-837.130
40℃	-0.106	-3126.271	-2289.033	-837.132
45℃	-0.0881	-3126.265	-2289.049	-837.128
50℃	-0.0550	-3126.252	-2289.067	-837.130
55℃	-0.0239	-3126.240	-2289.085	-837.131
60℃	-0.197	-3126.311	-2288.982	-837.132

The thermal stability of MAPbI₃ explored through AIMD analysis, is illustrated in Fig. 4. Between 25 and 60 ℃ the energy variation with temperature changes is minimal, indicating that MAPbI₃ maintains thermal stability across this temperature range.

Fig. 4.

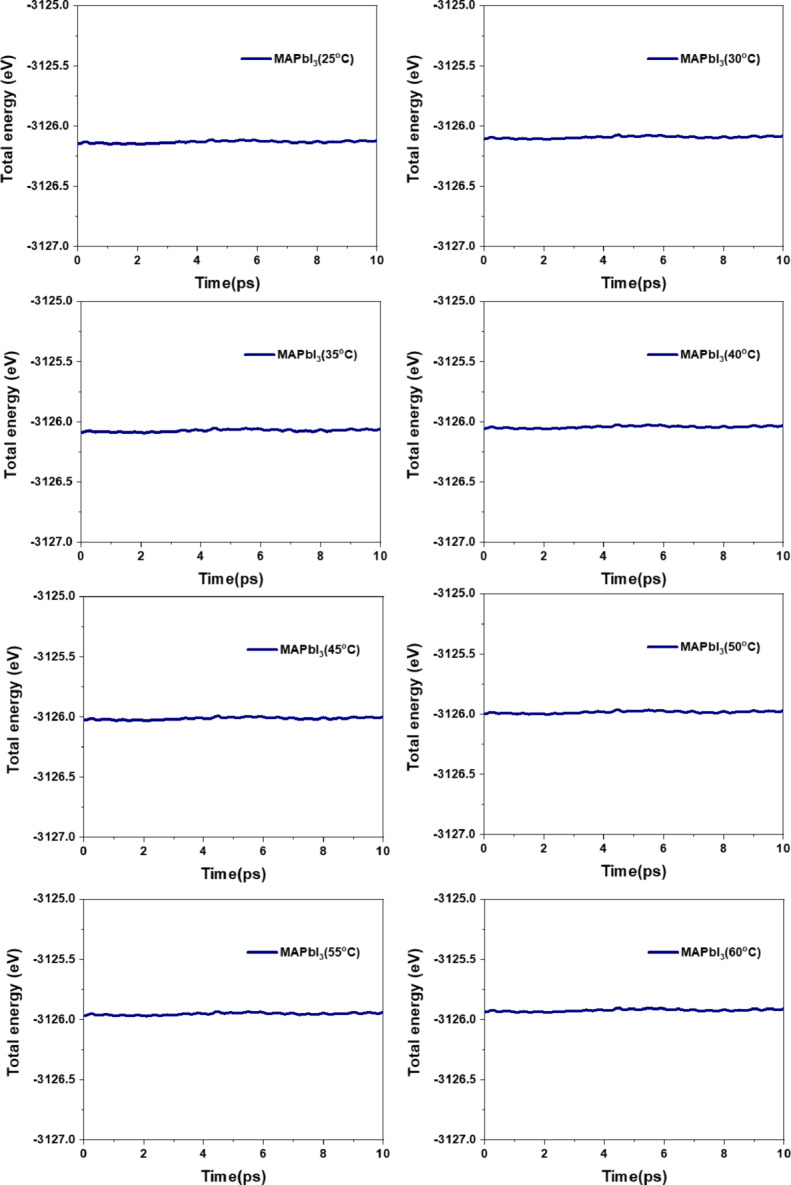
Thermal stability of MAPbI₃ at different temperatures (25–60℃).

Table 5 illustrates the mechanical properties of MAPbI₃ according to the Voigt-Reuss-Hill approximations. The data indicates that this material is ductile, with a bulk-to-shear modulus ratio greater than 1.75 or a Poisson’s ratio exceeding 0.26, and it is also flexible. In comparison, silicon and GaAs exhibit significantly higher Young’s modulus values of 174.8 GPa and 87 GPa, respectively²³, making them stiffer than MAPbI₃, which has a Young’s modulus ranging from 24 to 27 GPa. Consequently, MAPbI₃-based metasurfaces are suitable for use in wearable photonic devices. Furthermore, as the temperature rises, the mechanical modulus tends to decrease and flexibility increases. This enhanced flexibility is attributed to the elongation of the lead-iodine bond length. However, at 60 degrees, during a phase transition, the flexibility diminishes due to a reduction in unit cell volume and a decrease in lead-iodine bond length.

Table 5.

Mechanical properties of MAPbI₃ with different temperatures (25–60℃).

Mechanical properties		25℃	30℃	35℃	40℃	45℃	50℃	55℃	60℃
Voigt	Bv (GPa)	20.553	20.492	20.487	20.457	20.394	20.387	20.387	20.618
	Gv (GPa)	11.510	11.333	11.165	10.767	10.689	10.576	10.89	12.223
	Ev (GPa)	29.100	28.707	28.347	27.482	27.298	27.051	26.203	30.619
	BV/Gv	1.785	1.808	1.834	1.899	1.907	1.927	2.000	1.686
	υV	0.264	0.266	0.269	0.276	0.276	0.278	0.285	0.252
Reuss	BR (GPa)	20.449	20.366	20.449	20.366	20.408	20.325	20.280	20.576
	GR (GPa)	8.744	8.883	8.892	8.797	8.825	8.750	8.326	8.548
	ER (GPa)	22.960	23.266	23.299	23.069	23.141	22.956	21.971	22.525
	BR/GR (GPa)	2.308	2.292	2.298	2.315	2.312	2.322	2.435	2.407
	υR	0.312	0.309	0.310	0.311	0.311	0.311	0.319	0.317
Hil	BH (GPa)	20.501	20.429	20.468	20.411	20.401	20.356	20.334	20.597
	GH (GPa)	10.195	10.108	10.028	9.782	9.757	9.663	9.257	10.385
	EH (GPa)	26.030	25.986	25.823	25.275	25.219	25.003	24.114	26.572
	BH/GH (GPa)	2.010	2.021	2.041	2.086	2.109	2.106	2.196	2.094
	υH	0.288	0.287	0.289	0.293	0.293	0.294	0.302	0.284
Type of material		Ductile	Ductile	Ductile	Ductile	Ductile	Ductile	Ductile	Ductile

Metastructure characteristics

We perform eigenfrequency analysis for the metasurface shown in Fig. 1 at various temperatures. The results in Table 6 indicate that the frequency of BICs varies with temperature. As the temperature increases, the BICs experience a blue shift due to the reduction in the effective refractive index of the structure. Therefore, the proposed structure can be tuned by temperature. In addition, because the resonance frequencies change with temperature, this structure can be used as a temperature sensor. It should be noted that the resonance frequencies obtained in the eigenvalue analysis are entirely real, meaning they do not leak and have an infinite Q factor. To convert BICs into quasi-BICs, we break the symmetry of the structure. The Q factors obtained at different temperatures for d = 0.5 μm are listed in the third column of Table 6. As the temperature increases, the Q factor of the modes decreases due to the reduction in the effective refractive index of the structure.

Table 6.

The resonance frequencies and Q factors with different temperatures (25–60℃).

Temperature	fresonance	Q factor (d = 0.5 μm)
25℃	fA1:0.93097	QA1:1.4046 × 104
	fB1:0.92150	QB1:5.8525 × 105
	fA2:0.81780	QA2:5.5013 × 105
	fB2:0.91220	QB2:4.6820 × 104
30℃	fA1:0.93107	QA1:1.4041 × 104
	fB1:0.92160	QB1:5.8506 × 105
	fA2:0.81789	QA2:5.4995 × 105
	fB2:0.91230	QB2:4.6805 × 104
35℃	fA1:0.93133	QA1:1.4040 × 104
	fB1:0.92185	QB1:5.8500 × 105
	fA2:0.81811	QA2:5.4993 × 105
	fB2:0.91255	QB2:4.6801 × 104
40℃	fA1:0.93187	QA1:1.4034 × 104
	fB1:0.92239	QB1:5.8475 × 105
	fA2:0.81859	QA2:5.4966 × 105
	fB2:0.91308	QB2:4.6780 × 104
45℃	fA1:0.93205	QA1:1.4027 × 104
	fB1:0.92257	QB1:5.8450 × 105
	fA2:0.81875	QA2:5.4944 × 105
	fB2:0.91326	QB2:4.6762 × 104
50℃	fA1:0.93260	QA1:1.4022 × 104
	fB1:0.92311	QB1:5.8425 × 105
	fA2:0.81923	QA2:5.4914 × 105
	fB2:0.91379	QB2:4.6738 × 104
55℃	fA1:0.93285	QA1:1.4016 × 104
	fB1:0.92336	QB1:5.8405 × 105
	fA2:0.81945	QA2:5.4902 × 105
	fB2:0.91404	QB2:4.6725 × 104
60℃	fA1:1.06381	QA1:1.2441 × 104
	fB1:1.05299	QB1:5.1835 × 105
	fA2:0.93449	QA2:4.8423 × 105
	fB2:1.04230	QB2:4.1468 × 104

To intuitively illustrate the resonances, we analyze the near-field distributions of the displacement current, electric field, and magnetic field, as shown in Fig. 5. In mode A₁, the magnetic moments are arranged in a head-to-tail configuration, with current loops in the perpendicular plane indicating the magnetic toroidal dipole mode. Mode B₁ exhibits non-parallel magnetic moments, corresponding to a magnetic quadrupole. In mode A₂, the field map reveals a vortex of displacement currents threading through the inner ring, while magnetic moments form a vortex perpendicular to the current, indicating an electric toroidal dipole. Finally, mode B₂ is identified as an electric quadrupole mode, characterized by antiparallel electric moments.

Fig. 5.

Displacement currents, electric, and magnetic fields for (a) A₁, (b) B₁, (c) A₂, and (d) B₂.

To conduct a thorough analysis of the properties of q-BIC, we employ the exact multipole decomposition method²⁴. This approach involves integrating the displacement current density within the unit cell to better understand the electromagnetic source distribution in the far-field. These calculations consider the electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ), magnetic quadrupole (MQ), electric toroidal dipole (ETD), and magnetic toroidal dipole (MTD). As illustrated in Fig. 6, the primary multipole components for A₁, B₁, A₂, and B₂ are MTD, MQ, ETD, and EQ, respectively. These findings align perfectly with the data presented in Fig. 5.

Fig. 6.

Multipole decomposition for q-BICs.

We now investigate the impact of the inner ring’s offset distance from the center on the Q value of the q-BICs, as shown in Fig. 7. The findings indicate that the Q-factor of the q-BICs is highly sensitive to variations in the asymmetry parameters. Specifically, when moves away from 0, there is an exponential reduction in the Q-factor (Q∝d⁻²). This exponential decrease in the Q-factor aligns well with earlier research, which showed that increasing the asymmetry parameter led to a similar pattern^25,26. Therefore, the Q value of q-BIC modes can be effectively adjusted by manipulating the asymmetric parameters.

Fig. 7.

Q factors as a function of the asymmetry parameters for (a) A₁, (b) B₁, (c) A₂, and (d) B₂.

To assess the effect of fabrication process tolerance on the q-BICs, we investigated the Q-factor and resonance frequency of the modes with a ± 5% variation in the structural parameters. The results presented in Table 7 show that even with a ± 5% change in the metastructure parameters, the Q-factors of the modes remain in the same order. Thus, high Q-factors can be expected in real-world applications. To understand the red and blue shifts of the modes, we refer to the Mie resonance frequency of the dielectric resonator, as described in²⁷:

1

Table 7.

Impact of fabrication tolerance on q-BICs.

Fabrication tolerance		fres (P/h/r) THz	fres (P/h/r-5%) THz	fres (P/h/r + 5%) THz	Q-factor (P/h/r)	Q-factor (P/h/r-5%)	Q-factor (P/h/r + 5%)
P±5%	A1	0.93097	0.96527	0.89736	1.40 × 104	1.17 × 104	1.19 × 104
	B1	0.92150	0.96508	0.88258	5.85 × 105	5.72 × 105	5.81 × 105
	A2	0.81780	0.85799	0.78063	5.50 × 105	4.18 × 105	5.46 × 105
	B2	0.91220	0.95418	0.86292	4.68 × 104	3.15 × 104	4.44 × 104
h±5%	A1	0.93097	0.93906	0.90880	1.40 × 104	1.15 × 104	1.35 × 104
	B1	0.92150	0.93058	0.90500	5.85 × 105	5.60 × 105	5.71 × 105
	A2	0.81780	0.82114	0.80898	5.50 × 105	4.18 × 105	4.66 × 105
	B2	0.91220	0.91615	0.90905	4.68 × 104	4.57 × 104	4.63 × 104
r1, r2±5%	A1	0.93097	0.95897	0.90087	1.40 × 104	1.39 × 104	× 104
	B1	0.92150	0.96490	0.87750	5.85 × 105	5.62 × 105	5.73 × 105
	A2	0.81780	0.86484	0.77384	5.50 × 105	4.62 × 105	4.97 × 105
	B2	0.91220	0.95425	0.87075	4.68 × 104	4.33 × 104	4.50 × 104

In this equation, V(x, y, z) is associated with the resonator’s size, while µ and ε denote its permeability and permittivity, respectively. Additionally, θ is a constant for a specific resonance. Variations in height, radius, and period can cause the volume of the device to increase or decrease, resulting in a redshift or blueshift in the resonance frequency. Hence, the changes in resonance frequencies due to these parameters align with the Mie theory.

Application

Bidirectional switch

The proposed asymmetric structure perturbs the modes, as illustrated in Fig. 8. The arrow sizes vary slightly to reflect the lack of symmetry along that axis. It is evident that breaking the symmetry along the y-axis results in corresponding asymmetry in the modes along that axis, while the symmetry along the x-axis remains unaffected. As shown in the figure, after the disturbance, modes A₁ and A₂ become coupled to x and y polarizations, respectively, indicating the potential for their selective excitation. These findings also can be applied to modes B₁ and B₂. Thus, the proposed structure can function as a polarization-dependent notch filter or bidirectional switch in the THz region.

Fig. 8.

Depiction of the interaction between plane waves and the perturbed modes with electric fields indicated by arrows.

The polarization angle (θ) represents the angle between the y-axis and the direction of the incoming electric field, as shown in Fig. 9a. In Fig. 9b, the transmittance curves for q-BICs are displayed for various polarization orientations, allowing for the tuning of the transmittance intensity of these modes. In contrast to previously documented structures^28,29, our proposed design demonstrates distinct behavior. As the polarization angle shifts from 0° to 90°, the A₂ and B₂ modes vanish, while new q-BICs (A₁ and B₁) emerge at different frequencies. Notably, at a polarization angle of 0°, the switching state of q-BICs is (1,1,0,0), and when the angle reaches 90°, the switching state transitions to (0,0,1,1). This observation indicates potential uses for the metasurface in bidirectional optical switching.

Fig. 9.

(a) Schematic representation of the structure with varying polarization angles, (b) Transmittance curves for different polarization angles at 25 °C.

Gas sensor

The detection and sensing of CO₂ are crucial in various fields, including environmental monitoring, industrial processes, and healthcare. As a significant greenhouse gas, CO₂ plays a pivotal role in climate change, making its accurate measurement essential for effective climate action and policy-making. Furthermore, in indoor environments, elevated CO₂ levels can indicate poor ventilation, leading to health risks such as headaches, fatigue, and impaired cognitive function. Advanced CO₂ sensing technologies not only enhance the ability to monitor air quality but also contribute to energy efficiency in buildings and industrial settings by optimizing ventilation systems^30,31. Therefore, developing reliable and sensitive CO₂ sensors is vital for safeguarding public health.

The importance of gas sensing is highlighted by several recent studies that present diverse approaches to enhance sensor performance. For instance, a flexible CO₂ sensor based on a silver nanowire/polydimethylsiloxane composite was demonstrated for high sensitivity and mechanical robustness, suitable for wearable applications³². Similarly, an SnO₂-modified carbon dot for rapid CO₂ detection with a response time of 7 s was used for real-time monitoring³³. A laser-induced graphene sensor coated with polyaniline and copper oxide exhibited a detection limit of 10 ppm for CO₂, demonstrating the efficacy of hybrid materials³⁴.

For sensing applications, as shown in Fig. 10, we place CO₂ gas on the surface of MAPbI₃. It is crucial to assess the stability of MAPbI₃ in the presence of CO₂. To this end, we calculate the formation energy of MAPbI₃ with the results presented in Table 8. As shown, the formation energy of MAPbI₃ remains negative when exposed to the CO₂ gas, indicating that MAPbI₃ maintains thermodynamic stability. Additionally, we calculated the adsorption energy of CO₂ gas on MAPbI₃ using the equation E_ads=E_{adsorbate/sub}−(E_adsorbate+E_sub), where the adsorbate refers to a CO₂ molecule, and the substrate (sub) corresponds to a MAPbI₃. The values obtained in the third column of Table 8 are negative, indicating that MAPbI₃ has an affinity for adsorbing carbon monoxide. It is also crucial to assess the stability of the MAPbI₃ structure when exposed to CO₂ gas over time. To do this, we conducted AIMD simulations, and the results are presented in the fourth column of Table 8. As shown, the energy fluctuations are minimal, indicating that the structure remains stable over time.

Fig. 10.

Adsorption cases of 25% CO₂ on MAPbI₃.

Table 8.

Formation energy and gas adsorption energy of MAPbI₃.

Perovskite	FE (eV)	Eads (eV)	Energy variations (eV)	Refractive index (x-polarization)	Refractive index (y-polarization)
MAPbI3 + 25% CO2	-0.162	-1.05	0.025	2.8957	2.7027
MAPbI3 + 50% CO2	-0.149	-1.89	0.021	3.0456	2.9982
MAPbI3 + 75% CO2	-0.133	-2.53	0.017	3.3145	3.2147

To calculate the effective refractive index of MAPbI₃ with CO₂ gas (25% concentration), we consider 12 cases and compute the average of these cases (Fig. 10). Also, to calculate the effective refractive index of MAPbI₃ at different concentrations of CO₂ (50% and 75%), we examine different possible cases (30 and 40 cases, respectively). We then input these refractive indices into the metasurface to obtain the resonance frequency of q-BICs. The results in Table 9 show that an increase in the effective refractive index of the medium leads to a redshift in the q-BIC frequency, with minimal effect on modulation depth and Q-factor. This redshift can be described by perturbation theory as (δω/ω₀)=− (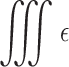∣E∣²dV/2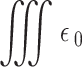∣E∣²dV), where δω, ω₀, and ε₀ refer to the resonance shift, resonance frequency, and change in the dielectric constant, respectively. A higher dielectric constant in the structure results in a redshift of the resonances.

Table 9.

The resonance frequencies with CO₂.

Perovskite	fresonance
MAPbI3 + 25% CO2	fA1:0.86125 fB1:0.82389 fA2:0.78700 fB2:0.88525
MAPbI3 + 50% CO2	fA1:0.82902 fB1:0.77877 fA2:0.71372 fB2:0.82113
MAPbI3 + 75% CO2	fA1:0.77127 fB1:0.69790 fA2:0.65830 fB2:0.77261

To evaluate sensing performance, we define bulk sensitivity as⁵:

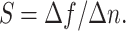2

and the figure of merit (FoM) as:

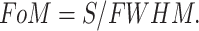3

Here, Δn represents the change in refractive index, Δf denotes the shift in resonance frequency, and FWHM is the full width at half maximum of the resonance linewidth.

The results in Table 10 indicate that the sensitivity of the various modes differs due to their distinct field distributions. The highest sensitivity and figure of merit are achieved for mode B₁, with values of 0.301 THz/RIU and 1.911 × 10⁵, respectively. The results highlight the significant potential of MAPbI₃ as a stable and sensitive material for CO₂ sensing applications, paving the way for further advancements in photonic sensor technology. Also, we compared the refractive index, Q-factor, and sensing performance of MAPbI₃ with other materials, and the results are presented in Table 11.

Table 10.

The sensor characteristics for different modes.

q-BICs	S (THz/RIU)	Q factor	FoM (RIU− 1)
A1	0.215	1.4046 × 104	0.324 × 104
B1	0.301	5.8525 × 105	1.911 × 105
A2	0.248	5.5013 × 105	1.668 × 105
B2	0.217	4.6820 × 104	1.113 × 104

Table 11.

Comparison of quality factor and refractive index parameters in room temperature.

Material	Refractive index	Q-factor	Sensitivity (THz/RIU)
PEA2PbI4 14	2.100 + 0i	5 × 105	*
BA2PbI4 14	2.104 + 0i	5.46 × 105	*
Silicon35	3.673 + 0.005	270	0.226
LiTaO336	2.033	1.2 × 105	0.489
MAPbI3 (This work)	2.5714 + 0i	5.85 × 105	0.301

Conclusion

In this work, we explored the temperature-tunable optical and mechanical properties of MAPbI₃ and their application in a novel metastructure design for THz applications. The DFT calculations confirmed that MAPbI₃ is thermally stable within the 25–60 °C range and maintains a high refractive index with no loss in the THz region. By introducing asymmetry in the metastructure, we successfully converted BICs into quasi-BICs, with their frequencies and quality factors tunable by temperature. This tunability highlights the potential of the proposed metastructure for applications in THz temperature sensing, bidirectional switch, and gas sensing. We investigate the ability of this structure to CO₂ gas sensing and achieve a maximum sensitivity of 0.301 THz/RIU and a figure of merit of 1.911 × 10⁵ which is defined by FoM = S/FWHM. Our findings provide a foundation for further development of high-performance THz devices leveraging the unique properties of MAPbI₃.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Author contributions

S.B. S.: Conceptualization; Data curation; Formal analysis; Investigation; Methodology; Software; Validation; Visualization; Roles/Writing - original draft.V.A.: Conceptualization; Data curation; Formal analysis; Funding acquisition; Project administration; Resources; Supervision; Validation; Visualization; Roles/ Writing - review & editing.

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

Declarations

Competing interests

The authors declare no competing interests.