Abstract
This study examines self-motion perception incorporated into motion sickness models. Research on modeling self-motion perception and motion sickness has advanced independently, though both are thought to share neural mechanisms, making the construction of a unified model opportune. Models based on the Subjective Vertical Conflict (SVC) theory, a refinement of the neural mismatch theory, have primarily focused on motion sickness, with limited validation for self-motion perception. Emerging studies have begun evaluating the perceptual validity of these models, suggesting that some models can reproduce perception in specific paradigms, while they often struggle to jointly capture motion perception and sickness. One prior study demonstrated that one of the SVC models could replicate illusory tilt during centrifugation, while others produced unrealistic responses, such as persistent tilt after motion cessation. In reality, under steady-state conditions such as being motionless, perceived motion is expected to settle to an appropriate state regardless of prior states. Based on the idea that this behavior is closely related to the equilibrium points and stability of the model dynamics, this study theoretically analyzed 6DoF-SVC models with a focus on them. Results confirmed that only one model ensures convergence from any state to a unique equilibrium point corresponding to plausible perception. In contrast, other SVC models and a conventional self-motion perception model converged to values dependent on earlier states. Further analysis showed that only this model captured both the somatogravic and Ferris wheel illusion. In conclusion, this 6DoF-SVC model unifies motion perception and sickness modeling, with theoretical convergence of the perceptual state.
Keywords: Vestibular self-motion perception, Computational model, Motion sickness, Subjective vertical conflict theory
Introduction
With the rapid advancement of technology, particularly in advanced transportation systems such as automated vehicles and virtual reality, several studies have emphasized that these technologies increase the possibility of motion sickness (Sivak and Schoettle 2015; Diels and Bos 2016; Wada 2016; Caserman et al. 2021; Keshavarz and Golding 2022). The experience of motion sickness, characterized by symptoms ranging from mild discomfort to severe nausea and even vomiting, undermines not only comfort but also the safety and efficiency of travel and the usability of immersive technologies. The importance of understanding, predicting, and mitigating motion sickness has, therefore, increased in recent years.
One of the most widely accepted computational models for motion sickness employs the Motion Sickness Dose Value (MSDV) as specified in (ISO2631-1 1997), further simply referred to as ISO). According to the ISO, multiplication of the MSDV with a gender-dependent constant predicts the severity of motion sickness for those exposed to pure vertical motion by integrating frequency-weighted acceleration over exposure time. Efforts have been made to expand our understanding of motion sickness across wider scenarios, including the effects of different motion directions such as fore-aft direction (Golding and Markey 1996; Golding et al. 1997, 2001) and lateral direction (Griffin and Mills 2002; Donohew and Griffin 2004), differences in body posture (Golding et al. 1995), and post-exposure effects such as recovery from (Golding and Stott 1997) or habituation (Golding and Stott 1995) to motion stimuli, among others. These investigations have led to an increased momentum in the revision of the ISO (Bos et al. 2022, 2024). In addition to these models, several computational models based on hypotheses of the mechanisms of motion sickness have been developed. For example, a pioneering conceptual model based on the neural mismatch theory (Reason 1978), which postulates that motion sickness arises from the accumulation of discrepancies between integrated sensory afferents and those expected, estimated through past experiences or internal models, was turned into a computational model first by Oman (Oman 1982). In this computational model, the self-motion perception process is modeled using the Observer Theory, and the errors used to improve motion perception are considered neural mismatches, based on the assumption that both self-motion perception and motion sickness share certain neural mechanisms. This approach was further refined by Bles et al. in their Subjective Vertical Mismatch (or Subjective Vertical Conflict: SVC) theory (Bles et al. 1998), which focused on verticality estimation as the source of motion sickness, while retaining feedback mechanisms for angular velocity and inertial acceleration to maintain perceptual consistency. It was and elaborated on numerically in one dimension by Bos and Bles (1998) and multiple dimensions by Bos et al. (2002). It is worth noting that the literature (Bos and Bles 1998) explained for the first time the peak in sickness incidence at a frequency of about 0.2 Hz, as observed by O’Hanlon and McCauley (1974) and modeled also by ISO, by fitting a single free gain parameter while fixing the time constant based on vertical perception studies. Following this, models further expanding on this SVC model, including rotational motion, were initiated by Kamiji and Wada (Kamiji et al. 2007; Wada et al. 2018), and several variations were subsequently introduced (Wada et al. 2020; Wada 2021; Inoue et al. 2023; Sousa Schulman et al. 2023; Liu et al. 2024). Moreover, these SVC models have been applied in engineering contexts, such as algorithms for vehicle motion control in automated vehicles (Wada 2016; Ukita et al. 2020; Yunus et al. 2022), and algorithms to generate visual stimuli aimed at minimizing motion sickness for passengers (Tamura et al. 2023). Overall, these SVC models are among the most elaborate and promising models.
On the other hand, the prediction of motion perception is also of significant academic and practical importance, and numerous studies have developed computational models for self-motion perception. Among these, a model proposed by Merfeld et al. (Merfeld and Zupan 2002) is representative of self-motion perception via vestibular sensations, and has been validated through various motion paradigms. Recently, Allred and Clark (2024) applied the Merfeld model to develop a computational model of motion sickness based on the sensory conflict theory, in which a weighted sum of discrepancies between sensory afferents from the otolith and canals and the corresponding expected signals is considered the source of the conflict leading to sickness. Furthermore, there exists research that has elucidated the correlation between parameters related to subjective vertical perception derived from Merfeld and Zupan (2002) and motion sickness observed in experiments (Irmak et al. 2021). The Merfeld model (Merfeld and Zupan 2002) and the SVC models (Kamiji et al. 2007; Inoue et al. 2023) are both based on the internal model hypothesis, which postulates that humans hold internal representations of sensory organs in the central nervous system, to enhance the accuracy of self-motion perception. More specifically, not only both of them but also many motion perception models are based on Merfeld et al. (1993). This paper (Merfeld et al. 1993) is the first to quantitatively demonstrate that human motion perception, including the velocity storage mechanism, could be represented by expressing the internal model hypothesis through an observer theoretical framework. Note that in Merfeld et al. (1993), the model was validated from the viewpoint of the reflexive eye movements of monkeys instead of the motion perception of humans. The major differences between the motion perception parts of the SVC models and the Merfeld model (Merfeld and Zupan 2002) are as follows: (1) Methods to resolve gravito-inertial acceleration (GIA) into gravity and inertial acceleration differ, leading to a difference in the behaviors of the perceived gravity vector; and (2) angular velocity perception is not influenced by the otolith signal in the SVC models, whereas it is in the Merfeld model (see the discussion section for details).
Based on the above consideration, these SVC models based on human motion perception mechanisms offer advantages when extended to modeling motion sickness induced by multisensory inputs such as vestibular-visual interactions (Wada et al. 2020; Liu et al. 2024). In addition, one model (Wada 2021) has the ability to describe the influence of humans’ anticipation on sickness, which has been observed in several studies (e.g., Kuiper et al. (2019, 2020); Reuten et al. (2024a, b). Moreover, the 6DoF-SVC models were evaluated and validated for motion sickness under various scenarios, including car sickness (Wada et al. 2018; Buchheit et al. 2022). On the other hand, emerging research has also begun to explore the validity of these models from the perspective of motion perception, though the range of motion paradigms explored to date has been limited. For example, Irmak et al. (2023) evaluated three models—an SVC model, the Merfeld model, and a particle filter model—from the perspectives of both motion perception and motion sickness prediction. For motion perception, the results of assessments using three paradigms- centrifugation, Earth-vertical axis rotation (EVAR), and off-vertical axis rotation (OVAR)- showed that all models aligned well with the observed data. In terms of motion sickness prediction, the evaluation was not based on direct symptom reports, but rather on simulated sensory conflict signals derived from each model. Analysis of these signals in the frequency domain showed that the SVC model provided the best overall match to known sensitivity curves. Nevertheless, none of the models were able to identify parameter sets that simultaneously and accurately described both perception and motion sickness. In contrast, Inoue et al. (2023) focused on structural variations within the SVC models and compared several versions through numerical simulations of subjective verticality changes during centrifugation. They demonstrated the existence of a model that could adequately reproduce experimentally observed tendencies. However, some model structures produce responses that are not observed in reality, such as the subjective vertical remaining tilted even after the motion has ceased, indicating that the influence of prior states on motion perception persists. Although comparable after-effects are known (e.g. Gillingham (1992)), this does not hold for the effect we report here, as clarified below. Given that motion perception is represented as a dynamical system, the evolution of the future states should be affected by their prior states. In addition to this, considering the various types of noise that can affect the system, even a transient perturbation of the state could lead to persistent effects on perception, potentially affecting one’s behavior for the rest of their life, which would be unrealistic. This makes it reasonable to assume the existence of a calibration mechanism that enables the system to converge to a plausible estimate of the actual state regardless of the prior states, under certain stationary conditions, such as being motionless relative to the Earth. Such a property is fundamentally linked to the concept of equilibrium points and the asymptotic stability of the system under stationary conditions.
Therefore, the primary purpose of the present study is to theoretically examine models of vestibular motion perception within the computational framework of motion sickness by focusing on their equilibrium points and the stability around these equilibrium points in a stationary state. This analysis was conducted in comparison with variations of the SVC model family (Inoue et al. 2023) and one of the frequently cited motion-perception models proposed in Merfeld and Zupan (2002). Furthermore, this study aimed to investigate how SVC models describe or predict perceived motion in specific motion paradigms in which the otolith-canal interaction plays important roles. Two of these will be elaborated in particular: the somatogravic effect, where the direction of perceived gravity shifts in an inertial acceleration environment, and the Ferris wheel illusion, where the sensation of rotation disappears during constant velocity rotation orthogonal to Earth’s gravity, leading to the illusion of circular motion without a change in orientation (Mayne 1974; Bos and Bles 2002). The results of the model analysis are then discussed.
The remainder of this paper is structured as follows. Section 2 presents an analysis of the dynamic equations of the SVC models to consider the appropriate model structure from the perspective of motion perception. Sections 3 and 4 present numerical simulations investigating the ability of the 6DoF-SVC model to describe the Ferris wheel and somatogravic illusions, respectively, in comparison with the motion perception model (Merfeld and Zupan 2002). Finally, Sect. 4 provides a detailed discussion of the results and presents the conclusions drawn from the study.
Computational models of SVC theory of vestibular motion sickness
In this section, the SVC models are introduced, and the dynamic equation of one of their variations is derived as an ordinary differential equation. The features of the motion perception component of the model are then discussed and compared with those of other models, including other variations of the SVC model family (Inoue et al. 2023) as well as a representative motion perception model (Merfeld and Zupan 2002). Specifically, we analyzed the equilibrium points of the model and the stability (convergence) around these equilibrium points in the stationary state.
The motivation for this analysis stems from the following considerations. The trajectories of the states in dynamical systems vary depending on the prior system states. Given that various types of noise can affect the system, it is reasonable to hypothesize the existence of a calibration mechanism facilitating the acquisition of an appropriate state. If state variables converge to specific values regardless of the prior states, under certain stationary conditions, such as being stationary with respect to Earth, this characteristic can function as the calibration mechanism. To investigate whether the models satisfy such conditions, we analyzed models under stationary conditions to determine the equilibrium point of the system state and to assess its asymptotic stability.
SVC models for vestibular motion sickness for 6DoF motion
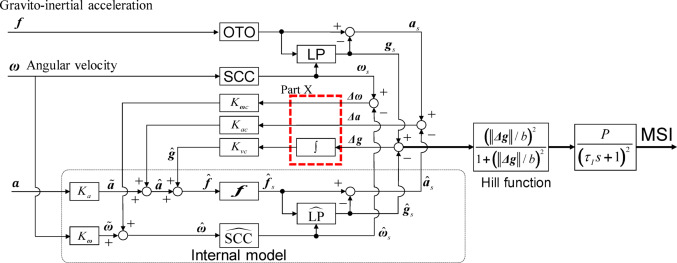
Even when focusing specifically on vestibular motion sickness in 6DoF head motion, multiple versions of computational models based on the SVC theory have been developed (see Introduction). One model version, elaborated by Inoue et al. (2023) is illustrated in Fig. 1. As shown in the figure, this model adopts an observer-theoretic framework and includes three feedback processes for the sensory conflict signals, depicted as  1,
1,  , and
, and 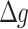 . Variations in the models, as also elaborated by Inoue et al. (2023), arise depending on the presence or absence of integrators in these feedback processes. Only one integrator applied to
. Variations in the models, as also elaborated by Inoue et al. (2023), arise depending on the presence or absence of integrators in these feedback processes. Only one integrator applied to 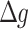 is referred to as In1, including two integrators applied to
is referred to as In1, including two integrators applied to 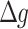 and
and  , referred to as In2, and three integrators applied to
, referred to as In2, and three integrators applied to  ,
,  , and
, and 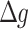 , referred to as In3. Notably, the In3 model corresponds to the original 6DoF-SVC model (Kamiji et al. 2007; Wada et al. 2018).
, referred to as In3. Notably, the In3 model corresponds to the original 6DoF-SVC model (Kamiji et al. 2007; Wada et al. 2018).
Fig. 1.
Overview of the 6DoF-SVC (In1) model (Inoue et al. 2023). There are several possible forms of the model, which differ in terms of the existence and absence of integrals the feedback process depicted in part X. For example, the original 6DoF-SVC model (Kamiji et al. 2007) (later (In3) model) includes integrals for all three feedback signals
The numerical simulations with these SVC models shown in a previous study (Inoue et al. 2023) suggest that unnatural drift in motion perception occurs in all versions except for the In1 model; thus, this section mainly focuses on the In1 model shown in Fig. 1. Note that the reasons for the occurrence of such drift in models, except for the In1 model, and the suitability of the In1 model will be elucidated through theoretical analysis in Sect. 2.2 and 2.3, where we analyze the dynamic equation, including the equilibrium point and the stability of the model. In addition to focusing on the In1 model in Sect. 2.2 and 2.3, detailed analyses of In2, In3, and the Merfeld model (a representative model of self-motion perception) are provided in the Appendix for comparison, following the same approach as in Sect. 2.2 and 2.3.
Dynamic equation of 6DoF-SVC (In1) model
The inputs to In1 are the angular velocity  and gravito-inertial acceleration (GIA) f, which is defined as the vector sum of the gravitational acceleration g and inertial acceleration a:
and gravito-inertial acceleration (GIA) f, which is defined as the vector sum of the gravitational acceleration g and inertial acceleration a:
 |
1 |
It should be noted that the direction of g is defined as the opposite of the gravitational force. In physics, gravitational acceleration is typically defined as the inertial acceleration of a mass when it is subjected only to a gravitational force, meaning that it should be in the same direction as the gravitational force, which is opposite to the definition of g in the present paper. However, when considering how the organs of balance sense acceleration and gravity, the otolith organs, in particular, acting as inertial linear accelerometers, cannot distinguish between the following two scenarios: (1) being stationary in a gravitational environment and (2) moving with an inertial acceleration that is equal in magnitude to the gravitational acceleration but in the opposite direction of the gravitational force. This phenomenon is a direct consequence of Einstein’s equivalence principle (Bos and Bles 2002). It should also be noted that in the Merfeld model (Merfeld and Zupan 2002), g is defined in the same direction as the gravitational force, which is opposite to its definition in the 6DoF-SVC model.
Currently, the output of the model is motion sickness incidence (MSI), which is defined as the percentage of people who would vomit due to the given motion stimulus. As indicated in (Bos et al. 2022), the expansion of the models would benefit from also considering pre-vomiting symptoms, and advances in this direction have recently been described (Bos et al. 2024). Moreover, very recently, an extended version of the SVC models outputting the MIsery SCale or Motion Illness Symptoms Classification (Bos et al. 2005; Reuten et al. 2021) has been recently published (Kotian et al. 2023; Inoue 2023; Inoue et al. 2024, 2025), taking into account the observation that motion sickness symptoms progress over time in a specific order during accumulation, with vomiting being the endpoint of that scale (Reuten et al. 2021).
The upper part of the model describes information processing by sensory organs, and the estimation of inertial and gravitational acceleration and angular velocity based on the sensory afferents (otoliths and semicircular canals, respectively). Although this comprises 3 × 3 = 9 degrees of motion freedom, they are mutually related by the laws of physics, actually resulting in six DOFs. Importantly, and actually being at the basis of motion illusions and motion sickness, the brain does not necessarily consider these laws of physics. Moreover, the control of posture and gait, for example, does benefit from discriminating gravity from inertia; for this reason, the 6DoF-SVC models explicitly assume that the brain deals with nine DOFs arranged in the three vectors a for linear self-motion, g for self-orientation with respect to gravity, and  for angular self-motion. The lower part of the model in the block depicted by the thin black dotted line represents the internal model of the sensory organs, and the expected afferent signals related to inertial and gravity accelerations and angular velocity. The discrepancies between the three sensory and expected vectors are fed back into the internal model to decrease their difference, ultimately resulting in an estimation of the actual state of the body, that is,
for angular self-motion. The lower part of the model in the block depicted by the thin black dotted line represents the internal model of the sensory organs, and the expected afferent signals related to inertial and gravity accelerations and angular velocity. The discrepancies between the three sensory and expected vectors are fed back into the internal model to decrease their difference, ultimately resulting in an estimation of the actual state of the body, that is, ,
,  , and
, and  being as close as possible to the actual state of the body, as given by a, g, and
being as close as possible to the actual state of the body, as given by a, g, and  . It is considered that the update of the expected afference signals is also aided by external signals related to knowledge of the exposed motion, such as efference copies and predicted motion signals, including those obtained from exposure to repetitive movements (Wada 2021).
. It is considered that the update of the expected afference signals is also aided by external signals related to knowledge of the exposed motion, such as efference copies and predicted motion signals, including those obtained from exposure to repetitive movements (Wada 2021).
In the SVC theory, it is assumed that only 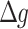 , the discrepancy between the sensed and expected gravitational acceleration, leads to motion sickness. MSI is then calculated from
, the discrepancy between the sensed and expected gravitational acceleration, leads to motion sickness. MSI is then calculated from 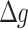 through the Hill function and a critically damped 2nd -order transfer function with a time constant on the order of minutes. This approach is based on the insight that a specific threshold likely exists, as minor discrepancies, even if sustained over a long period, do not cause motion sickness, and that the progression of motion sickness symptoms manifests in the order of (tens of) minutes. In addition, the Hill function considers an asymptotic behavior of sickness accumulation for larger conflicts, where sickness does exceed 100% of a population, reaching the limit of vomiting, meaning that individual symptoms do not worsen beyond vomiting (which may be different from considering the unpleasantness associated with symptoms; see (Reuten et al. 2021).
through the Hill function and a critically damped 2nd -order transfer function with a time constant on the order of minutes. This approach is based on the insight that a specific threshold likely exists, as minor discrepancies, even if sustained over a long period, do not cause motion sickness, and that the progression of motion sickness symptoms manifests in the order of (tens of) minutes. In addition, the Hill function considers an asymptotic behavior of sickness accumulation for larger conflicts, where sickness does exceed 100% of a population, reaching the limit of vomiting, meaning that individual symptoms do not worsen beyond vomiting (which may be different from considering the unpleasantness associated with symptoms; see (Reuten et al. 2021).
The OTO block represents the dynamics of the otolith organ and is assumed to be a unit matrix, indicating its function as an accelerometer sensing the GIA f = a + g. The SCC block depicts semi-circular canals, whose dynamic equation is given by
 |
2 |
This function considers the fact that humans exposed to constant angular motion initially perceive the rotation whereas the perception typically decreases exponentially to nil within tens of seconds. The LP block, which represents the method for resolving the internal representation of gravitational acceleration gs from the afferent signal of GIA, is described in Eq. (3), which has been termed the generalized Mayne equation (Bos and Bles 2002), after Mayne (Mayne 1974), who was the first to publish the idea of frequency filtering to differentiate between inertia and gravity.
 |
3 |
Blocks with hat notation, such as  , represent the internal models of those without hat notation, such as OTO. It is assumed that under optimal conditions and habituated to a natural environment,
, represent the internal models of those without hat notation, such as OTO. It is assumed that under optimal conditions and habituated to a natural environment,  and
and  are identical to OTO and LP, respectively, whereas
are identical to OTO and LP, respectively, whereas  is given by the following equation:
is given by the following equation:
 |
4 |
Please refer to (Inoue et al. 2023) for further details of the model. The model parameters used in the present study were also taken directly from that publication, and are summarized in Table 1.
Table 1.
Parameter values used in the 6DoF SVC (In1) model
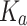
|
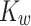
|

|

|

|
 [s] [s] |
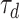 [s] [s] |
 [s] [s] |
|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 10.0 | 0.5 | 5.0 | 2.0 | 7.0 | 190 |
The differential equation expression encompassing all subsystems is given by Eq. (5) (refer to Appendix C for the derivation):
 |
5 |
where state vector x and input u are defined as
 |
6 |
 |
7 |
where M denotes MSI, and with intermediate variables defined as
 |
8 |
 |
9 |
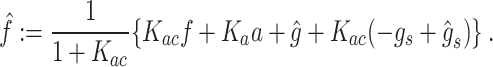 |
10 |
Among the motion perception vectors, the perceived gravity 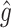 is obtained as a state variable, whereas the perceived inertial acceleration and angular velocity are given as functions of the state variables and inputs as follows:
is obtained as a state variable, whereas the perceived inertial acceleration and angular velocity are given as functions of the state variables and inputs as follows:
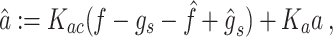 |
11 |
 |
12 |
Dynamics of In1 model with no motion inputs and its properties
Equilibrium points
Let us consider the case of no external motion inputs, which is characterized by a = 0 and  , hence
, hence  . The importance of this condition lies in the assumption that most animals, especially humans experience this state for most of their lives. In Bayesian terms, this condition can therefore also be considered as a dominant contributor to the prior distribution over internal states. From a simple calculation, the equilibrium points of system (5) under the no external motion case are given as
. The importance of this condition lies in the assumption that most animals, especially humans experience this state for most of their lives. In Bayesian terms, this condition can therefore also be considered as a dominant contributor to the prior distribution over internal states. From a simple calculation, the equilibrium points of system (5) under the no external motion case are given as
 |
13 |
where 
The intermediate variables at 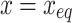 are obtained as follows:
are obtained as follows:
 |
14 |
 |
15 |
Thus, the resultant perceived motion at the equilibrium point is given as follows:
 |
16 |
 |
17 |
where they demonstrate that all the calculated perceived angular velocity, inertial acceleration, and gravitational acceleration converge to the actual state of the body in the absence of physical motion.
Stability analysis
We analyze the stability of the system (5) around the equilibrium points given by (13) under the condition a = 0, and hence  and
and  . Since the dynamics of the final path from
. Since the dynamics of the final path from 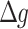 to M is obviously asymptotically stable, we consider a system that excludes M and
to M is obviously asymptotically stable, we consider a system that excludes M and 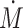 from the state variables. The dynamic equation was linearized using the Taylor expansion around the equilibrium point with a = 0 and hence
from the state variables. The dynamic equation was linearized using the Taylor expansion around the equilibrium point with a = 0 and hence 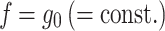 and
and  (refer to eq. (76) in Appendix D for the linearized dynamical system). The eigenvalues of the system matrix of the linearized system are expressed as
(refer to eq. (76) in Appendix D for the linearized dynamical system). The eigenvalues of the system matrix of the linearized system are expressed as
 |
18 |
each which has a multiplicity of three. For all eigenvalues to have negative real parts, it is required that  . Thus, this condition is satisfied if all gains and time constants in the model are positive.
. Thus, this condition is satisfied if all gains and time constants in the model are positive.
The above analysis proves that the state variables x converge to constant values, including M = 0, while the perceived motion converges to the actual self-motion in the physical world, irrespective of the initial values x(0). The significance of this property of the 6DoF-SVC (In1) model becomes more pronounced when compared to the other models (see below).
Namely, while the details are omitted here due to space constraints, similar analyses conducted on the 6DoF-SVC models (In2) and (In3) demonstrated that even in a stationary state, the state variables converge to values dependent on the initial values of the state variables for both models (See Appendix A). This dependency results in an unexpected drift in 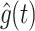 depending on the prior system states. For the Merfeld model (Merfeld and Zupan 2002), as shown in eqs. (52) and (61) of Appendix B, the model guarantees that the perceived gravity
depending on the prior system states. For the Merfeld model (Merfeld and Zupan 2002), as shown in eqs. (52) and (61) of Appendix B, the model guarantees that the perceived gravity 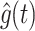 can converge to Earth’s gravity
can converge to Earth’s gravity 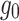 in its direction, but not in its magnitude, because
in its direction, but not in its magnitude, because 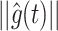 cannot change over time. However, accurately perceiving both Earth’s gravity g under stationary conditions requires that both the direction and magnitude of
cannot change over time. However, accurately perceiving both Earth’s gravity g under stationary conditions requires that both the direction and magnitude of 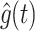 match the actual gravity vector. This means that the model should be able to hold or estimate the true magnitude of gravity as well. Therefore, if there are any discrepancies or fluctuations in the magnitude of
match the actual gravity vector. This means that the model should be able to hold or estimate the true magnitude of gravity as well. Therefore, if there are any discrepancies or fluctuations in the magnitude of  , a mechanism is required to correct them to maintain accurate motion perception. Indeed, related approaches have been proposed. Specifically, Kravets et al. (2021) and Allred et al. (2023) recently developed self-motion perception models to describe adaptation to altered gravity environments by incorporating additional mechanisms into the Merfeld model. Note that substituting f = g0 in eq.(60) yields
, a mechanism is required to correct them to maintain accurate motion perception. Indeed, related approaches have been proposed. Specifically, Kravets et al. (2021) and Allred et al. (2023) recently developed self-motion perception models to describe adaptation to altered gravity environments by incorporating additional mechanisms into the Merfeld model. Note that substituting f = g0 in eq.(60) yields . Thus, if
. Thus, if 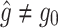 , the perceived inertial acceleration
, the perceived inertial acceleration  becomes non-zero, nevertheless under conditions where humans do not move physically.
becomes non-zero, nevertheless under conditions where humans do not move physically.
The aforementioned characteristic of the In1 model suggests that even if some perturbation occurs to the system state, the state will return or converge to ‘appropriate’ values as long as the no physical motion condition persists. This implies that neural information processing involved does not require the presence of any specific initial values, which might reflect its inherent robustness in humans. Furthermore, from a practical standpoint of using the model with experimental data to estimate motion perception and sickness, the aforementioned property of the In1 model also serves as an advantage. This allows for the initialization of the model’s state variables by conducting model calculations while maintaining a stationary condition, regardless of how the IMU sensor is positioned.
Motion perception simulation of Ferris wheel illusion
Ferris wheel illusion
Humans rotating with a constant angular velocity around the Earth horizontal axis first perceive an angular motion close to the veridical motion, which, after tens of seconds, changes into a persistent circular motion opposite to the true rotation without a change in body orientation (Stone and Letko 1964; Mittelstaedt 1983). This illusory perceived motion is referred to as the Ferris wheel illusion (Mayne 1974; Lackner and Graybiel 1978; Bos and Bles 2002). In this section, we conduct numerical simulations using the 6DoF-SVC (In1) model and the Merfeld model (Merfeld and Zupan 2002) to investigate how these models predict the perceived motion in the motion paradigm considered here.
Simulation conditions
First, the x and y axes of the head coordinate system were defined as the naso-occipital axis, with the anterior direction being positive, and the interaural axis, with the left direction being positive, respectively. The z-axis was selected to form a right-handed coordinate system, i.e., directed upward (see also ISO 8727 (1997). Second, the head was initially assumed to be in an upright Earth vertical orientation. Subsequently, rotation was considered around the x-axis (i.e., in roll) at a constant velocity initiated from the initial state. The GIA f and angular velocity  as inputs to the model for such motion exposure can be described as follows:
as inputs to the model for such motion exposure can be described as follows:
 |
19 |
where q(t) denotes the angle of body posture at time t measured from the Earth’s vertical direction in radians and the constant value  denotes the angular velocity. In the present study,
denotes the angular velocity. In the present study, 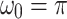 is used for the simulation.
is used for the simulation.
The 6DoF-SVC (In1) and Merfeld models were used for simulations to compare the results. As mentioned earlier, the definitions of both g and  are opposite between the 6DoF-SVC model and the Merfeld model. However, in the visualization of
are opposite between the 6DoF-SVC model and the Merfeld model. However, in the visualization of  in Fig. 2, the results of the Merfeld model were adjusted to align with the definition used in the 6DoF-SVC model. The parameters of the 6DoF-SVC (In1) and Merfeld models were used exactly as described in the publications Inoue et al. (2023) and Merfeld and Zupan (2002), and their values are listed in Table 1 and Table 2, respectively.
in Fig. 2, the results of the Merfeld model were adjusted to align with the definition used in the 6DoF-SVC model. The parameters of the 6DoF-SVC (In1) and Merfeld models were used exactly as described in the publications Inoue et al. (2023) and Merfeld and Zupan (2002), and their values are listed in Table 1 and Table 2, respectively.
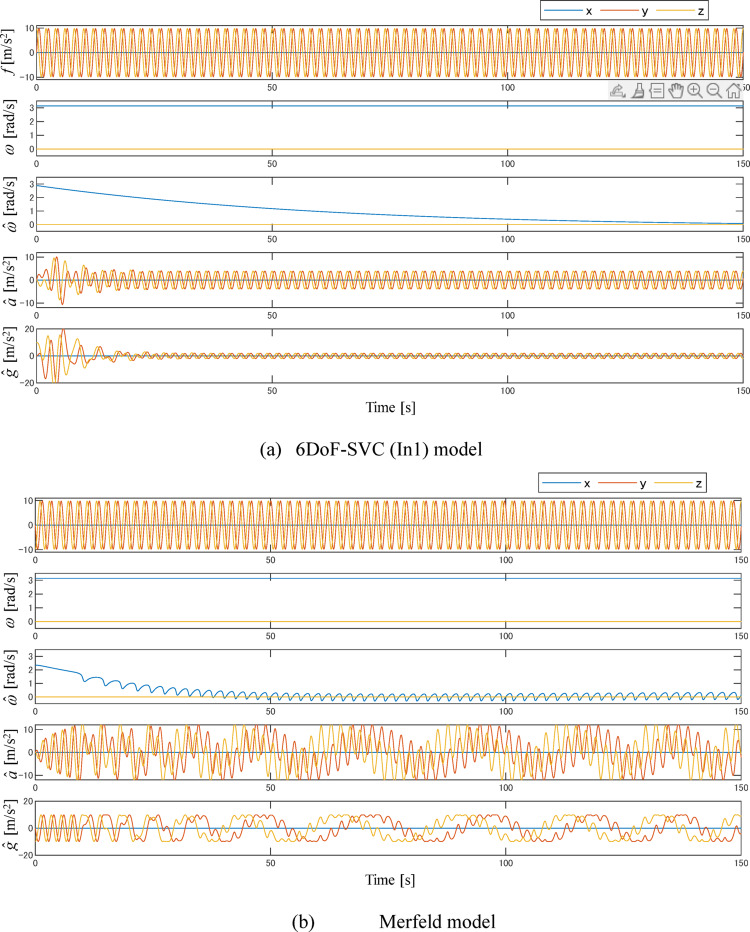
Fig. 2.
Simulation results for the Ferris wheel illusion with (a) the 6DoF-SVC (In1) model and (b) the Merfeld model. The upper two signals represent inputs of the models: GIA f and angular velocity 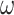 . The lower three signals are the model simulated perceived motion:
. The lower three signals are the model simulated perceived motion:  ,
,  , and
, and 
Table 2.
Parameter values used in the Merfeld model
|
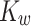
|
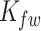
|
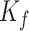
|
 [s] [s] |
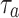 [s] [s] |
|---|---|---|---|---|---|
| −2.0 | 3.0 | 2.0 | 2.0 | 5.0 | 80 |
Simulation results
Figure 2 shows the simulation results for the Ferris wheel illusion using the (a) 6DoF-SVC (In1) model and (b) Merfeld model.
With the 6DoF-SVC model results, (1)  converges to
converges to  , (2)
, (2)  converges to sine waves in a quadrature phase relationship, and (3)
converges to sine waves in a quadrature phase relationship, and (3)  converges to a small value that is significantly less than 9.81. On the other hand, with the Merfeld model, (1)
converges to a small value that is significantly less than 9.81. On the other hand, with the Merfeld model, (1)  decreases while continuing to oscillate around a non-zero value, (2)
decreases while continuing to oscillate around a non-zero value, (2)  does not converge to sine waves, and (3)
does not converge to sine waves, and (3)  does not converge to any fixed pattern while it exhibits oscillatory behavior over time with a time-variant sine wave-like pattern overlaid with higher-frequency oscillations. The behaviors of the model-predicted (1) perceived angular velocity
does not converge to any fixed pattern while it exhibits oscillatory behavior over time with a time-variant sine wave-like pattern overlaid with higher-frequency oscillations. The behaviors of the model-predicted (1) perceived angular velocity  and (2) inertial acceleration
and (2) inertial acceleration  indicate that the 6DoF-SVC (In1) model has the ability to describe the Ferris wheel illusion, whereas the Merfeld model does not. Note, however, that perceived radius of the illusory motion in the Ferris wheel illusion has not, to our knowledge, been quantitatively assessed in previous studies (see Discussion section).
indicate that the 6DoF-SVC (In1) model has the ability to describe the Ferris wheel illusion, whereas the Merfeld model does not. Note, however, that perceived radius of the illusory motion in the Ferris wheel illusion has not, to our knowledge, been quantitatively assessed in previous studies (see Discussion section).
Motion perception simulation of somatogravic effect
Somatogravic effect
Humans exposed to linear forward acceleration while remaining erect perceive a backward tilt increasing asymptotically within seconds to the tilt of the GIA. Because studying this phenomenon requires relatively long linear tracks, it has often been studied in centrifuges (e.g. (Clark and Graybiel 1965; Cohen et al. 1973). In a fixed radius with the participant “fixed” erect to the centrifuge arm, the tilt due to the centripetal acceleration is perceived as tilted away from the rotation center, and the tilt is affected by the angular motion (Seidman et al. 1998; Bos and Bles 2002; Correia Grácio et al. 2013). This illusory perceived motion is referred to as the somatogravic illusion (Bos and Bles 2002; Correia Grácio et al. 2013). A specific detail is that this effect was originally studied using a visual analog, specifically the perceived displacement of a visual target, then referred to as the oculogravic illusion. In this section, we conduct numerical simulations using the 6DoF-SVC (In1) model and Merfeld model (Merfeld and Zupan 2002) to investigate how these models predict the perceived motion in the motion paradigm described above.
Simulation conditions
The parameters of both the 6DoF-SVC and Merfeld models were used as described in publications Inoue et al. (2023) and Merfeld and Zupan (2002), respectively, consistent with the approach taken in Sect. 3. The conditions regarding motion exposure are the same as the experiments conducted in (Merfeld et al. 2001), which examined the perceived roll tilt and reflexive eye movements in humans in the dark using two different centrifugation motion paradigms (fixed radius and variable radius). In the fixed-radius condition, the distance from the center to where the participant sat remained unchanged; however, the speed of rotation was altered to produce variations in the centrifugal acceleration. Conversely, in the variable-radius condition, the speed of rotation was kept constant, and the radius of the rotation was changed over time to achieve a centrifugal acceleration that closely matched that observed in the fixed-radius condition. The resultant GIA detected by the otolith organs under both conditions was virtually the same; the main distinction was whether yaw rotation signals from the canals were present (fixed-radius condition) or not (variable-radius condition). The details of this process are as follows.
Fixed-radius condition
The centrifugation radius was fixed at 0.54 m. The chair carrying the participant started at an initial velocity of 0 °/s and accelerated uniformly to reach 250 °/s in 10 s. This angular velocity was maintained for 120 s, after which it decelerated to zero over another 10 s and stopped. Assuming that the rotation occurred counterclockwise and the participant always faced forward in a direction tangential to the circle of rotation, the centripetal acceleration acted to the left of the participant. During steady state rotation at an angular velocity 250 °/s, the centripetal acceleration reached approximately 1 G.
Variable-radius condition
In the variable-radius condition, chair rotation was maintained at a constant speed of 250 °/s throughout the experiment. Initially, the centrifugation radius was set to 0 m, indicating concentric rotation. The participants were exposed to this rotation for sufficient time for the canals to no longer signal angular motion, which was set to 200 s in the present simulation study, whereas 5 min was employed for the experiments (Merfeld et al. 2001). After this initial period, the radius was increased in a quadratic manner over 10 s to achieve the same lateral acceleration as that employed in the fixed-radius condition while maintaining the rotational speed at 250 °/s. This phase was followed by 120 s of rotation at a constant radius of 0.54 m, after which the radius was reduced back to zero in another 10 s.
Simulation results
Figure 3 shows the simulation results for the somatogravic illusion using the (1) 6DoF-SVC model and (2) Merfeld model under (A) fixed- and (B) variable- radius conditions. In each graph, the upper two signals represent the inputs of the models: GIA f and angular velocity  . The two lower signals are the model-simulated perceived motion
. The two lower signals are the model-simulated perceived motion  and perceived head-tilt
and perceived head-tilt 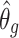 , which is defined as follows:
, which is defined as follows:
 |
20 |
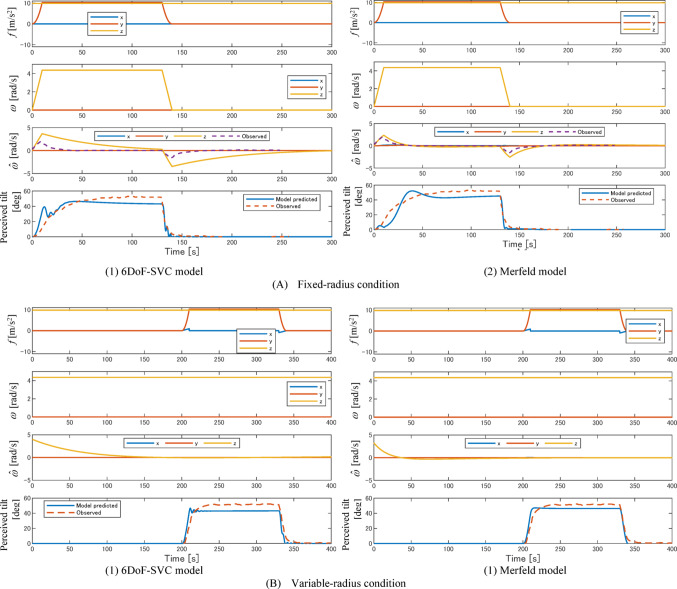
Fig. 3.
Simulation results for the somatogravic effect with (A) the fixed-radius condition and (B) the variable-radius conditions. For each condition, the left and right figures illustrate the results using (1) the 6DoF-SVC (In1) model and (2) the Merfeld model. For each graph, the upper two signals represent inputs of the models: GIA f and angular velocity  . The lower two signals are the model simulated perceived motion:
. The lower two signals are the model simulated perceived motion:  and perceived head tilt calculated from
and perceived head tilt calculated from  . The perceived tilt plots also include the average response obtained from multiple participants, digitized from Merfeld et al. (2001) for direct comparison. Similarly, the slow-phase velocity of the horizontal VOR obtained from Merfeld et al. (2001), inverted in sign, is overlaid with the plots of
. The perceived tilt plots also include the average response obtained from multiple participants, digitized from Merfeld et al. (2001) for direct comparison. Similarly, the slow-phase velocity of the horizontal VOR obtained from Merfeld et al. (2001), inverted in sign, is overlaid with the plots of 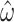 for the fixed-radius condition. For the variable-radius condition, however, the result was not overlaid because the experimental data provided in that paper correspond only to the steady-state phase (at 200 s in the figure), and they show values close to zero, which is consistent with the simulated results
for the fixed-radius condition. For the variable-radius condition, however, the result was not overlaid because the experimental data provided in that paper correspond only to the steady-state phase (at 200 s in the figure), and they show values close to zero, which is consistent with the simulated results
where  and the definition of
and the definition of  is according to Eq. (6). Consistent with Fig. 2, the definition of
is according to Eq. (6). Consistent with Fig. 2, the definition of  in Fig. 3 adheres to that provided by the 6DOF-SVC model.
in Fig. 3 adheres to that provided by the 6DOF-SVC model.
The results in Fig. 3(A) under the fixed-radius condition for both models demonstrate that the model-predicted perceived tilt increases with the lateral acceleration with some delay, eventually converging towards the GIA direction (45 °) for both models. Conversely, during deceleration, the predicted perceived tilt converges to 0 ° without delay. This trend was consistent with the experimental data, which were digitized from the results in (Merfeld et al. 2001), and overlaid with the simulation results for direct comparison.
In contrast, in Fig. 3(B), for the variable-radius condition, neither model exhibited the aforementioned delay for both the acceleration and deceleration phases, and the predicted perceived tilt aligned with the GIA direction in the steady-state. This result aligns with the trends observed in the participant experiments as previously described (Merfeld et al. 2001).
For both the fixed- and variable-radius conditions, exhibited behavior that decayed over time, which is qualitatively consistent with the observed VOR responses. However, the time constant of the signal differs between the models: the Merfeld model shows a closer match to the observed VOR velocity (digitized from Merfeld et al. (2001), whereas the 6DoF-SVC model exhibits a longer time constant, particularly under the fixed-radius condition.
Discussion and conclusion
Theoretical analysis of the 6DoF-SVC models and the Merfeld model in Sect. 2 revealed that among their structures, only the In1 model shows that the equilibrium points coincide with perceived motion thought to be ‘appropriate’ when assuming the body is at rest, regardless of the earlier system states, including initial value. Furthermore, the asymptotic stability of the dynamic equation of the In1 model to the equilibrium point has been proven. Note that for the other two 6DoF-SVC models, including the original 6DoF-SVC model (called the In3 model in the present study), as well as the Merfeld model, the equilibrium points depend on the prior states, though the calculations were omitted due to space constraints. This feature of the In1 model is significant, because it shows that the internal state can return to the appropriate values, even after being perturbed, when left undisturbed. The other models require the assumption of a mechanism for continuously maintaining accurate states to obtain appropriate state variables and, hence, perceived motion. Similar discussions have been made previously by (Bos and Bles 2002) regarding the GIA resolution using the generalized Mayne equation described in Eq. (3), which generates the sensory afferent level and can be regarded as a part of the self-motion perception model based on the internal model hypothesis employed in the present study. The contribution of the present research is to extend this discussion to the perceived motion as calculated by the motion perception model through the stability analysis of the model dynamics. In Sects. 3 and 4, we specifically addressed the Ferris wheel and somatogravic illusions as motion paradigms, where the otolith-canal interaction, more specifically the GIA resolution, plays a significant role. By comparing the 6DoF-SVC (In1) model with Merfeld’s model, it was demonstrated that the Ferris wheel illusion can be described by the 6DoF-SVC model, but not by the Merfeld model, while both models reproduced the somatogravic illusion. To the best of our knowledge, the 6DoF-SVC model is the only model capable of describing both phenomena. Inoue et al. (2023) conducted numerical simulations focusing on structural variations within the SVC models and demonstrated that the In1 model is capable of replicating the somatogravic illusion under fixed-radius centrifugation without any unnatural drift after motion exposure. However, they did not perform theoretical analyses on the equilibrium point of the model and its asymptotic stability. Irmak et al. (2023) compared three models—one of the SVC models, the Merfeld model, and a particle filter model—to investigate their capabilities in describing both motion perception and motion sickness. Their study revealed that while all models aligned well with observed data in motion perception paradigms such as centrifugation with fixed-radius conditions, EVAR, and OVAR, none could identify parameter sets that simultaneously and accurately described both perception and motion sickness. Notably, their analysis did not include the 6DoF-SVC (In1) model, on which the present study focuses, because our theoretical analysis demonstrates that this model uniquely satisfies asymptotic stability to a unique physiologically plausible equilibrium point. From these discussions, the contributions of the present study are first to demonstrate that asymptotic stability around the equilibrium point is an essential factor for motion perception models, and that only the In1 model satisfies this among the 6DoF-SVC models and the Merfeld model. Another contribution is to demonstrate that the In1 model qualitatively reproduces motion perception in the Ferris wheel illusion, and in the somatogravic illusion under fixed-radius and variable-radius conditions—whereas the Merfeld model is incapable of representing the Ferris wheel illusion.
The 6DoF-SVC (In1) model described the Ferris wheel illusion based on certain signal behaviors: (a) the perceived angular velocity converges to zero, and (b) the perceived inertial acceleration exhibits sinusoidal waves in a quadrature phase relationship. This combination should lead to a sensation of moving along a circular path with zero angular velocity. However, with respect to the perceived orientation, the model does not sufficiently represent it. In the Ferris wheel illusion (Stone and Letko 1964; Bos and Bles 2002), the perceived orientation is believed to rely on the path integration of canal afferents, idiotropic vectors (Mittelstaedt 1983), somatosensory cues (Bos and Bles 2002), and (c)  , which represents the perceived gravity derived from GIA resolution via the otolith signal (Bos and Bles 2002). Indeed, it has been observed that applied body pressure affects the perceived orientation in this illusion (Lackner and Graybiel 1978). In our simulation results with the 6DOF-SVC (In1) model (Fig. 2(a),
, which represents the perceived gravity derived from GIA resolution via the otolith signal (Bos and Bles 2002). Indeed, it has been observed that applied body pressure affects the perceived orientation in this illusion (Lackner and Graybiel 1978). In our simulation results with the 6DOF-SVC (In1) model (Fig. 2(a),  decayed over time to a value significantly less than 9.81. However, when
decayed over time to a value significantly less than 9.81. However, when  is smaller, the norm of
is smaller, the norm of  remains near 9.81 and continues to exhibit sinusoidal waves in a quadrature phase relationship (not provided in this paper). Experimentally, it has been observed that the Ferris wheel illusion can occur even at low angular velocities (Stone and Letko 1964). When
remains near 9.81 and continues to exhibit sinusoidal waves in a quadrature phase relationship (not provided in this paper). Experimentally, it has been observed that the Ferris wheel illusion can occur even at low angular velocities (Stone and Letko 1964). When  decays with larger
decays with larger  , the otolith signal might become ambiguous, suggesting that the aforementioned other cues may play a dominant role in determining the perceived orientation. Conversely, it is necessary to consider that other cues can dominate in determining perceived orientation, even in cases where
, the otolith signal might become ambiguous, suggesting that the aforementioned other cues may play a dominant role in determining the perceived orientation. Conversely, it is necessary to consider that other cues can dominate in determining perceived orientation, even in cases where  does not decay. However, the explanation of such mechanisms is beyond the ability of the 6DoF-SVC (In1) model, which is based only on vestibular sensation. Understanding and modeling these mechanisms remains an important topic for future research. Furthermore, model calculations using the 6DOF-SVC (In1) model predict that the perceived radius of the Ferris wheel gradually decreases as
does not decay. However, the explanation of such mechanisms is beyond the ability of the 6DoF-SVC (In1) model, which is based only on vestibular sensation. Understanding and modeling these mechanisms remains an important topic for future research. Furthermore, model calculations using the 6DOF-SVC (In1) model predict that the perceived radius of the Ferris wheel gradually decreases as 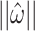 increases (not provided in this paper), in line with the predictions by (Stone and Letko 1964; Mayne 1974; Bos and Bles 2002). However, there is no study, including (Stone and Letko 1964), that has clearly reported the observed phenomenon in which the perceived radius of the illusory motion decreases as the rotational velocity increases. Instead, observations (Stone and Letko 1964) indicate that, as the rotational velocity increases, the perceived circular motion becomes anisotropic, meaning that the motion deviates from a circular path and takes on an elliptical trajectory, and eventually transitions to linear motion, with the amplitude of this linear motion gradually decreasing. Except for the presence of such anisotropy, this behavior might be considered in line with the decrease in amplitude due to increasing velocity. It should be noted that the current 6DoF-SVC (In1) model cannot replicate the shift from circular to elliptical perceived motion reported in the previous study. It is worth noting here that no studies to date have explicitly and quantitatively investigated this perception in the Ferris wheel illusion using rigorous psychophysical methods. This highlights the need for future research employing these techniques to validate perceptual dynamics in such paradigms.
increases (not provided in this paper), in line with the predictions by (Stone and Letko 1964; Mayne 1974; Bos and Bles 2002). However, there is no study, including (Stone and Letko 1964), that has clearly reported the observed phenomenon in which the perceived radius of the illusory motion decreases as the rotational velocity increases. Instead, observations (Stone and Letko 1964) indicate that, as the rotational velocity increases, the perceived circular motion becomes anisotropic, meaning that the motion deviates from a circular path and takes on an elliptical trajectory, and eventually transitions to linear motion, with the amplitude of this linear motion gradually decreasing. Except for the presence of such anisotropy, this behavior might be considered in line with the decrease in amplitude due to increasing velocity. It should be noted that the current 6DoF-SVC (In1) model cannot replicate the shift from circular to elliptical perceived motion reported in the previous study. It is worth noting here that no studies to date have explicitly and quantitatively investigated this perception in the Ferris wheel illusion using rigorous psychophysical methods. This highlights the need for future research employing these techniques to validate perceptual dynamics in such paradigms.
The key differences between the motion perception components of the SVC models and the Merfeld model are as follows. (1) In the SVC models, the magnitude of the perceived gravity vector can change over time, whereas it cannot in the Merfeld model. This difference highlights one of the reasons why the Merfeld model requires “appropriate” initial values of the state variables. (2) In the SVC models, perceived angular velocity  is not affected by the otolith signal, while in the Merfeld model, it is influenced by the otolith signal, specifically by changes in the direction of the GIA. Related to point (1) above, as described in Sect. 2.3.2, the Merfeld model can update the direction of the perceived gravity vector, but not its magnitude, which precludes it from correcting any deviations caused by internal noise or perturbations. Consequently, the Merfeld model may allow the unrealistic persistence of perceptual errors. This limitation suggests the relevance of incorporating a calibration mechanism—such as that introduced in the In1 model—which allows all state variables, including the perceived gravity magnitude, to converge to plausible values even in the presence of internal noise or perturbations and irrespective of prior states. In this regard, Kravets et al. (2021) and Allred et al. (2023) proposed models in which additional mechanisms were incorporated into the Merfeld model to describe adaptation to altered gravity environments. These extensions may also be useful for maintaining a correct magnitude of gravity in the above context. Since the present research has proven that perceived motions in the Merfeld model converge to appropriate states for all variables except the magnitude of perceived gravity, such additions may enable convergence of all state variables to physiologically plausible values. Investigating this possibility remains an important direction for future research. On the other hand, although the present study focused on motion perception under stationary Earth-gravity conditions, another important direction for future research is to investigate adaptation to altered gravity environments. This direction of research could be pursued within the same modeling framework by analyzing the time course of perceived gravity. The point described in (2) above differentiates between the SVC model and the Merfeld model in terms of their ability to describe the Ferris wheel illusion. The feature that
is not affected by the otolith signal, while in the Merfeld model, it is influenced by the otolith signal, specifically by changes in the direction of the GIA. Related to point (1) above, as described in Sect. 2.3.2, the Merfeld model can update the direction of the perceived gravity vector, but not its magnitude, which precludes it from correcting any deviations caused by internal noise or perturbations. Consequently, the Merfeld model may allow the unrealistic persistence of perceptual errors. This limitation suggests the relevance of incorporating a calibration mechanism—such as that introduced in the In1 model—which allows all state variables, including the perceived gravity magnitude, to converge to plausible values even in the presence of internal noise or perturbations and irrespective of prior states. In this regard, Kravets et al. (2021) and Allred et al. (2023) proposed models in which additional mechanisms were incorporated into the Merfeld model to describe adaptation to altered gravity environments. These extensions may also be useful for maintaining a correct magnitude of gravity in the above context. Since the present research has proven that perceived motions in the Merfeld model converge to appropriate states for all variables except the magnitude of perceived gravity, such additions may enable convergence of all state variables to physiologically plausible values. Investigating this possibility remains an important direction for future research. On the other hand, although the present study focused on motion perception under stationary Earth-gravity conditions, another important direction for future research is to investigate adaptation to altered gravity environments. This direction of research could be pursued within the same modeling framework by analyzing the time course of perceived gravity. The point described in (2) above differentiates between the SVC model and the Merfeld model in terms of their ability to describe the Ferris wheel illusion. The feature that  is unaffected by the otolith signal in the SVC model results in the canal afferent converging to zero even when exposed to off-vertical rotation at a constant velocity. This contributes to achieving
is unaffected by the otolith signal in the SVC model results in the canal afferent converging to zero even when exposed to off-vertical rotation at a constant velocity. This contributes to achieving  , as actually observed in the Ferris wheel illusion. In contrast, the feature that the otolith signal influences
, as actually observed in the Ferris wheel illusion. In contrast, the feature that the otolith signal influences  in the Merfeld model, results in
in the Merfeld model, results in  potentially not reaching zero even after the canal afferent converges to zero. This non-zero
potentially not reaching zero even after the canal afferent converges to zero. This non-zero  further impacts
further impacts  and ultimately contributes to preventing
and ultimately contributes to preventing  from becoming sinusoidal. Bos and Bles explained the Ferris wheel illusion using the generalized Mayne Eq. (3) itself, which is used in GIA resolution (Bos and Bles 2002). In the present study, we assumed an internal model to also include the generalized Mayne equation, and perceived gravity was considered to be represented by
from becoming sinusoidal. Bos and Bles explained the Ferris wheel illusion using the generalized Mayne Eq. (3) itself, which is used in GIA resolution (Bos and Bles 2002). In the present study, we assumed an internal model to also include the generalized Mayne equation, and perceived gravity was considered to be represented by 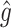 . Based on this, the present research demonstrated for the first time that both the Ferris wheel and somatogravic illusions can be represented using this
. Based on this, the present research demonstrated for the first time that both the Ferris wheel and somatogravic illusions can be represented using this  in 6DoF-SVC (In1) model. Another key difference is that the Merfeld model was not originally designed to predict motion sickness; thus, it requires an extension to account for the conflict signals employed in the sensory conflict or neural mismatch theory (Reason 1978). Oman’s model (Oman 1982) pioneered in addressing this, and the computational models of SVC theory (Bos and Bles 1998; Kamiji et al. 2007; Inoue et al. 2023) have subsequently been developed as a refinement of this formulation. Notably, Allred and Clark (2024) recently proposed a computational model of motion sickness based on the sensory conflict theory, using the Merfeld model (Merfeld and Zupan 2002). In that model, a weighted sum of discrepancies between sensory afferents from the otolith and canals and the corresponding expected signals is considered the source of the conflict leading to sickness. Given the work by Allred and Clark (2024), comparing these models from the viewpoint of motion sickness prediction remains an important direction for future research.
in 6DoF-SVC (In1) model. Another key difference is that the Merfeld model was not originally designed to predict motion sickness; thus, it requires an extension to account for the conflict signals employed in the sensory conflict or neural mismatch theory (Reason 1978). Oman’s model (Oman 1982) pioneered in addressing this, and the computational models of SVC theory (Bos and Bles 1998; Kamiji et al. 2007; Inoue et al. 2023) have subsequently been developed as a refinement of this formulation. Notably, Allred and Clark (2024) recently proposed a computational model of motion sickness based on the sensory conflict theory, using the Merfeld model (Merfeld and Zupan 2002). In that model, a weighted sum of discrepancies between sensory afferents from the otolith and canals and the corresponding expected signals is considered the source of the conflict leading to sickness. Given the work by Allred and Clark (2024), comparing these models from the viewpoint of motion sickness prediction remains an important direction for future research.
The present research, though, has some limitations. For instance, the discussion regarding the model’s ability to describe human self-motion perception in this study remains qualitative, implying that a quantitative analysis is required. Note that a previous study (Inoue et al. 2023) quantitatively demonstrated that the 6DoF-SVC (In1) model can describe the somatogravic illusion for fixed-radius centrifugation observed in Merfeld et al. (2001). Furthermore, the investigation in the present study was limited to the two motion paradigms of the Ferris wheel and somatogravic illusion. Thus, an investigation in contexts other than these two paradigms is an important direction for future research. Moreover, because this study focused only on models utilizing the vestibular system, validation was limited to motion perception in the dark. The validation of models incorporating vestibular-visual interactions is also an important area for future research. A recent study (Kotian et al. 2024) has explored visual contributions to both motion perception and motion sickness using models including SVC models and a conventional motion perception model, primarily focusing on validation through numerical simulations across multiple paradigms. However, theoretical analyses of equilibrium points and their stability—such as those presented in the present study—remain limited and warrant further investigation.
In the present study, it is assumed that perceived signals such as  and
and  are inputs to the internal models of sensory dynamics, similar to Merfeld’s model (Merfeld and Zupan 2002). This assumption is based on the idea that these inputs are expected to be optimal estimates of physical motion based on the observer theory and are believed to be used for motion control. However, observations in multisensory integration research (de Winkel et al. 2018) suggest that self-motion perception can be reported for each sensory modality, raising the possibility that either the sensory afferent (e.g.,
are inputs to the internal models of sensory dynamics, similar to Merfeld’s model (Merfeld and Zupan 2002). This assumption is based on the idea that these inputs are expected to be optimal estimates of physical motion based on the observer theory and are believed to be used for motion control. However, observations in multisensory integration research (de Winkel et al. 2018) suggest that self-motion perception can be reported for each sensory modality, raising the possibility that either the sensory afferent (e.g.,  in the model) or the expected sensory afferent calculated by the internal model (e.g.,
in the model) or the expected sensory afferent calculated by the internal model (e.g.,  in the model) might be another candidate for perceived motion. In addition, some research (Bos et al. 2008; Bos and Correia Grácio 2015) have argued that inertial acceleration of self-motion cannot be perceived. These issues remain a topic of debate.
in the model) might be another candidate for perceived motion. In addition, some research (Bos et al. 2008; Bos and Correia Grácio 2015) have argued that inertial acceleration of self-motion cannot be perceived. These issues remain a topic of debate.
In conclusion, this paper aimed at a unified model of self-motion perception and motion sickness. To this end, it conducted a theoretical analysis of the self-motion perception part of 6DoF-SVC models for vestibular motion sickness, along with numerical simulations in two motion paradigms where otolith-canal interaction plays a significant role, comparing them with a frequently-cited motion perception model. As a result, the 6DoF-SVC (In1) model was identified as the most promising candidate due to its ability to ensure that the predicted self-motion perception converges to “appropriate” values under rest conditions, regardless of the prior system states, as well as its capability to describe the two motion scenarios. However, it should be noted that the conditions examined in this study represent only a subset of the broader range of relevant conditions, such as tilt damping and the hilltop illusion. Additionally, many uncertainties remain regarding human perception itself, including whether changes in tilt perception influence angular velocity perception. In this sense, the current study represents one of the foundational steps in a broader exploration, with many steps yet to be taken.
Acknowledgements
This work was partially supported by the JSPS KAKENHI, Japan (Grant No.: 21K18308 and 24H00298).
Appendix A: Equilibrium point of the other vestibular 6DoF-SVC models
Appendix A provides the detailed equilibrium analysis for other SVC models mentioned in Sect. 2.
SVC model family
As discussed in Inoue et al. (2023), there exist multiple versions of models based on the SVC theory for vestibular motion sickness involving 6DoF motions. The only difference among them is the presence or absence of integrals within the feedback process, highlighted in Part X and enclosed by the red dotted lines in Fig. 1. The main body of the present paper has focused on the theoretical analysis of the In1 model, as described in Sect. 2. Here, we conducted theoretical analyses of the following other models:
In3: Integrals are present in all three error signals (Kamiji et al. 2007; Wada et al. 2018).
In2- : Integrals are present in two signals, excluding
: Integrals are present in two signals, excluding  .
.
In2-a: Integrals are present in two signals, excluding  .
.
Equilibrium points of the In3 model (the original model)
The dynamics of the In3 model is given as follows:
 |
A1 |
where state vector x and input u are defined as
 |
A2 |
 |
A3 |
where M denotes MSI, and with intermediate variables defined as
 |
A4 |
 |
A5 |
 |
A6 |
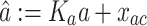 |
A7 |
 |
A8 |
The equilibrium points of the above dynamics under the condition with no external motion inputs, which are characterized by  and
and  , are given as
, are given as
 |
A9 |
where  , and
, and
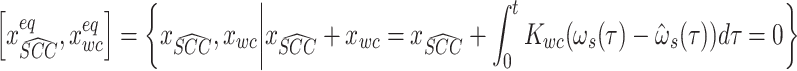 |
A10 |
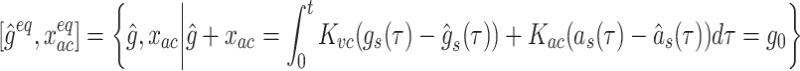 |
A11 |
suggesting that the elements of the equilibrium points in (A10) and (A11) are not determined uniquely, but form a set, and the state variables converge to a specific point within this set depending on the initial values, and by extension, the history of the state vectors. This is the cause of the drift in perceived variables, including  , as explained in Sect. 2 of the present study. The resultant perceived motion variables corresponding to the set of the equilibrium points given by the above are
, as explained in Sect. 2 of the present study. The resultant perceived motion variables corresponding to the set of the equilibrium points given by the above are 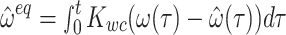 and
and  .
.
Equilibrium points of the In2- model
model
The dynamics of the IN2- model is given by
model is given by
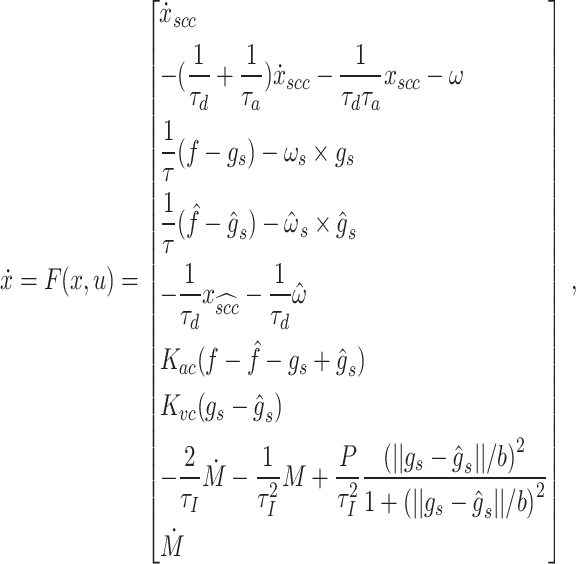 |
A12 |
where state vector x and input u are defined as
 |
A13 |
 |
A14 |
where intermediate variables defined as
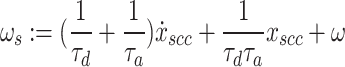 |
A15 |
 |
A16 |
 |
A17 |
 |
A18 |
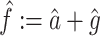 |
A19 |
The equilibrium points of the above dynamics under the condition with no external motion inputs, which are characterized by  and
and  , are given as
, are given as
 |
A20 |
where
 |
A21 |
suggesting that the element of the equilibrium point in (A21) is not determined uniquely, but forms a set, and the state variables converge to a specific point within this set depending on the initial values, and by extension, the history of the state vectors. This is the cause of the drift in perceived variables, including  , as explained in Sect. 2 of the present study. The resultant perceived motion variables corresponding to the set of the equilibrium points given by the above are
, as explained in Sect. 2 of the present study. The resultant perceived motion variables corresponding to the set of the equilibrium points given by the above are  and
and  .
.
Equilibrium point of the In2-amodel
The dynamics of the In2-a model is given as follows:
 |
A22 |
where state vector x and input u are defined as
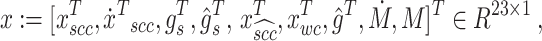 |
A23 |
 |
A24 |
where M denotes MSI, and with intermediate variables defined as
 |
A25 |
 |
A26 |
 |
A27 |
 |
A28 |
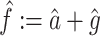 |
A29 |
The equilibrium points of the above dynamics under the condition with no external motion inputs, which are characterized by  and
and  , are given as
, are given as
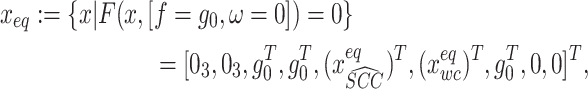 |
A30 |
where 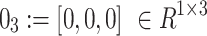 , and
, and
 |
A31 |
suggesting that the element of the equilibrium point in (A31) is not determined uniquely but forms a set, and the state variables converge to a specific point within this set depending on the initial values, and by extension, the history of the state vectors. This is the cause of the drift in perceived variables, including  , as explained in Sect. 2 of the present study. The resultant perceived motion variables corresponding to the set of the equilibrium points given by the above are
, as explained in Sect. 2 of the present study. The resultant perceived motion variables corresponding to the set of the equilibrium points given by the above are  , which can take non-zero values even though now
, which can take non-zero values even though now  is considered.
is considered.
Appendix B: Equilibrium points of the Merfeld model
Appendix B provides the detailed equilibrium analysis for the Merfeld model (Merfeld and Zupan 2002), a frequently-cited motion perception model.
The dynamics of the Merfeld model is given by
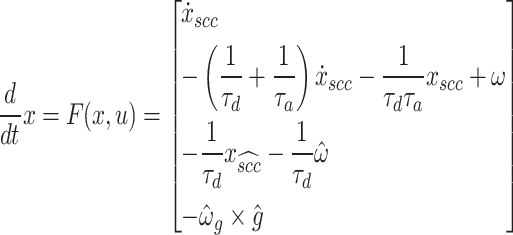 |
A32 |
where state vector x and input u are defined as
 |
A33 |
 |
A34 |
where
 |
A35 |
 |
A36 |
 |
A37 |
 |
A38 |
 |
A39 |
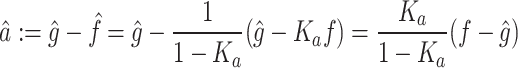 |
A40 |
The equilibrium points of the above dynamics under the condition with no external motion inputs, which are characterized by 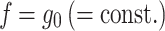 and
and 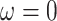 , are given as
, are given as
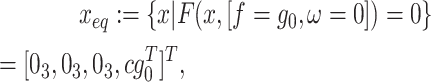 |
A41 |
where c denotes a constant scalar. Given this, vectors describing self-motion perception satisfy 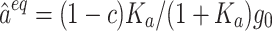 ,
,  , and
, and  . This means that the perceived gravity
. This means that the perceived gravity 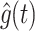 cannot be guaranteed to converge to the physical gravity
cannot be guaranteed to converge to the physical gravity 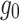 in its magnitude because
in its magnitude because 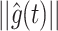 cannot change over time according to eq. (A32). Given them, to achieve
cannot change over time according to eq. (A32). Given them, to achieve  or accurately predict physical gravity in the steady state when humans are without physical motion, it is necessary to know the magnitude of gravity
or accurately predict physical gravity in the steady state when humans are without physical motion, it is necessary to know the magnitude of gravity  accurately. This also indicates that if any fluctuation occurs in
accurately. This also indicates that if any fluctuation occurs in  , a mechanism to resolve it should be added to the model to correct it. Please note that one of the major differences between the 6DoF-SVC (In1) model and the Merfeld model is that the perceived angular velocity
, a mechanism to resolve it should be added to the model to correct it. Please note that one of the major differences between the 6DoF-SVC (In1) model and the Merfeld model is that the perceived angular velocity  is affected by the otolith signal in the Merfeld model, as shown in (A36) and (A38), but not in the In1 model as illustrated Eq. (12). This difference is considered to be one of the reasons why the Ferris wheel illusion cannot be described by the Merfeld model.
is affected by the otolith signal in the Merfeld model, as shown in (A36) and (A38), but not in the In1 model as illustrated Eq. (12). This difference is considered to be one of the reasons why the Ferris wheel illusion cannot be described by the Merfeld model.
Please refer to Merfeld and Zupan (2002) for further details of the model. The parameter values used in the numerical simulations of the present study were also adopted directly from that publication, and are summarized in Table 2.
Appendix C: Derivation of Eq. (5)
According to Fig. 1, the dynamic equations of the 6DoF-SVC (In1) model are described by Eq. (1) through (4), together with the following equations:
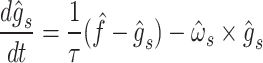 |
A42 |
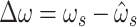 |
A43 |
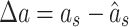 |
A44 |
 |
A45 |
 |
A46 |
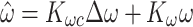 |
A47 |
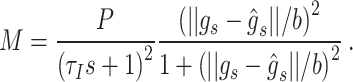 |
A48 |
By introducing the following new vector:
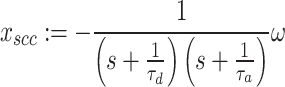 |
A49 |
Equation (2) can be rewritten in the time domain as follows:
 |
A50 |
Transforming eq. (A4) into the time domain yields:
 |
A51 |
By introducing the following new vector:
 |
A52 |
Equation (4) can be rewritten in the time domain as follows:
 |
A53 |
Transforming eq. (A52) into the time domain yields:
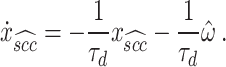 |
A54 |
Additionally, transforming eq. (68) into the time domain yields:
 |
A55 |
The differential equations (A51), (3), (A42), (A54),(A45), and (A55) can be expressed in the form of Eq. (5), provided that the state variable vector is defined as Eq. (6), that is,  . Note that the right-hand side of Eq. (5) includes variables
. Note that the right-hand side of Eq. (5) includes variables 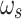 ,
, , and
, and  that are neither state variables nor inputs. However, as shown in Eqs. (8), (9), (12), and (10) together with (11), all of these can be expressed solely in terms of the state variables and inputs.
that are neither state variables nor inputs. However, as shown in Eqs. (8), (9), (12), and (10) together with (11), all of these can be expressed solely in terms of the state variables and inputs.
Appendix D: Linearized dynamics of 6DoF-SVC (In1) model
Eq. (A56) is a linear dynamical system obtained by linearizing the dynamics of 6DoF-SVC (In1) model (Eq. (5)) using the Taylor expansion around the equilibrium point. Note that  and
and  are excluded from the equation.
are excluded from the equation.
 |
A56 |
where  denotes a 3 × 3 skew-symmetric matrix that corresponds to cross products with vector z, and O3 and I3 denote the 3 × 3 zero and identity matrices, respectively. Please also refer to Sect. 2.3.2.
denotes a 3 × 3 skew-symmetric matrix that corresponds to cross products with vector z, and O3 and I3 denote the 3 × 3 zero and identity matrices, respectively. Please also refer to Sect. 2.3.2.
Author contributions
Conceptualization: T.W. and J.B.; Methodology: T.W. and J.B.; Formal analysis: T.W.; Writing - original draft preparation: T.W.; Writing - review and editing: T.W. and J.B.
Funding
This study was partially supported by JSPS KAKENHI (grant numbers 21K18308 and 24H00298).
Data availability
No datasets were generated or analysed during the current study.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Throughout this paper, vectors are represented in bold italics, while scalars are represented in italics.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Allred AR, Clark TK (2024) A computational model of motion sickness dynamics during passive self-motion in the dark. Exp Brain Res 242:1127–1148. 10.1007/s00221-024-06804-z [DOI] [PubMed] [Google Scholar]
- Allred AR, Kravets VG, Ahmed N, Clark TK (2023) Modeling orientation perception adaptation to altered gravity environments with memory of past sensorimotor States. Front Neural Circuits 17. 10.3389/fncir.2023.1190582 [DOI] [PMC free article] [PubMed]
- Bles W, Bos JE, de Graaf B et al (1998) Motion sickness: only one provocative conflict?? Brain Res Bull 47:481–487 [DOI] [PubMed] [Google Scholar]
- Bos JE, Bles W (1998) Modeling motion sickness and subjective vertical mismatch detailed for vertical motions. Brain Res Bull 47:537–542 [DOI] [PubMed] [Google Scholar]
- Bos JE, Bles W (2002) Theoretical considerations on canal-otolith interaction and an observer model. Biol Cybern 86:191–207. 10.1007/s00422-001-0289-7 [DOI] [PubMed] [Google Scholar]
- Bos JE, Correia Grácio BJ (2015) Perceived radial translation during centrifugation. J Vestib Res 25:119–124. 10.3233/VES-150555 [DOI] [PubMed] [Google Scholar]
- Bos JE, Bles W, Dallinga R (2002) Prediction of Seasickness with More Than One Degree of Freedom. In: Human Factors in Ship Design and Operation. pp 57–62
- Bos JE, MacKinnon SN, Patterson A (2005) Motion sickness symptoms in a ship motion simulator: effects of inside, outside, and no view. Aviat Space Environ Med 76:1111–1118 [PubMed] [Google Scholar]
- Bos JE, Bles W, Groen EL (2008) A theory on visually induced motion sickness. Displays 29:47–57. 10.1016/j.displa.2007.09.002 [Google Scholar]
- Bos JE, Diels C, Souman JL (2022) Beyond seasickness: A motivated call for a new motion sickness standard across motion environments. Vibration 5:755–769. 10.3390/vibration5040044 [Google Scholar]
- Bos JE, Souman JL, Nooij S, Diels C (2024) Advancing ISO 2631-1 by considering pre-emesis symptoms in carsickness. In: Prceedings of Driving Simulator Conference Europe
- Buchheit B, Schneider EN, Alayan M et al (2022) Motion sickness prediction in Self-Driving cars using the 6DOF-SVC model. IEEE Trans Intell Transp Syst 23:13582–13591. 10.1109/TITS.2021.3125802 [Google Scholar]
- Caserman P, Garcia-Agundez A, Gámez Zerban A, Göbel S (2021) Cybersickness in current-generation virtual reality head-mounted displays: systematic review and outlook. Virtual Real 25:1153–1170. 10.1007/s10055-021-00513-6 [Google Scholar]
- Clark B, Graybiel A (1965) Perception of the visual horizontal in normal and labyrinthine defective subjects during prolonged rotation. NSAM-936. Research report Naval School of Aviation Medicine (U S) [PubMed]
- Cohen MM, Crosbie RJ, Blackburn LH (1973) Disorienting effects of aircraft catapult launchings. Aerosp Med 44:37–39 [PubMed] [Google Scholar]
- Correia Grácio BJ, De Winkel KN, Groen EL et al (2013) The time constant of the somatogravic illusion. Exp Brain Res 224:313–321. 10.1007/s00221-012-3313-3 [DOI] [PubMed] [Google Scholar]
- de Winkel KN, Katliar M, Diers D, Bülthoff HH (2018) Causal inference in the perception of verticality. Sci Rep 8:5483. 10.1038/s41598-018-23838-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diels C, Bos JE (2016) Self-driving carsickness. Appl Ergon 53:374–382. 10.1016/j.apergo.2015.09.009 [DOI] [PubMed] [Google Scholar]
- Donohew BE, Griffin MJ (2004) Motion sickness: effect of the frequency of lateral Oscillation. Aviat Space Environ Med [PubMed]
- Gillingham KK (1992) The spatial disorientation problem in the United States Air Force. J Vestib Res 2:297–306. [PubMed]
- Golding JF, Markey HM (1996) Effect of frequency of horizontal linear Oscillation on motion sickness and somatogravic illusion. Aviat Space Environ Med 67:121–126 [PubMed] [Google Scholar]
- Golding JF, Stott JRR (1995) Effect of sickness severity on habituation to repeated motion challenges in aircrew referred for airsickness treatment. Aviat Space Environ Med 66: 625-30 [PubMed]
- Golding JF, Stott JRR (1997) Objective and subjective time courses of recovery from motion sickness assessed by repeated motion challenges. J Vestib Res 7. 10.1016/s0957-4271(96)00175-9 [PubMed]
- Golding JF, Markey HM, Stott JR (1995) The effects of motion direction, body axis, and posture on motion sickness induced by low frequency linear Oscillation. Aviat Space Environ Med 66:1046–1051 [PubMed] [Google Scholar]
- Golding JF, Finch MI, Stott JR (1997) Frequency effect of 0.35-1.0 hz horizontal translational Oscillation on motion sickness and the somatogravic illusion. Aviat Space Environ Med 68:396–402 [PubMed] [Google Scholar]
- Golding JF, Mueller AG, Gresty MA (2001) A motion sickness maximum around the 0.2 hz frequency range of horizontal translational Oscillation. Aviat Space Environ Med 72:188–192 [PubMed] [Google Scholar]
- Griffin MJ, Mills KL (2002) Effect of magnitude and direction of horizontal Oscillation on motion sickness. Aviat Space Environ Med 73:640–646 [PubMed] [Google Scholar]
- Inoue S (2023) Development of Computational Models To Predict Motion Sickness Symptom Levels Considering Visual and Vestibular Sensations. Master thesis, Nara Institute of Science and Technology
- Inoue S, Liu H, Wada T (2023) Revisiting motion sickness models based on SVC theory considering motion perception. In: SAE Technical Paper
- Inoue S, Liu H, Wada T (2024) A Digital Human Model for Symptom Progression of Vestibular Motion Sickness based on Subjective Vertical Conflict Theory. In: 2024 AHFE International Conference on Human Factors in Design, Engineering, and Computing
- Inoue S, Dang VT, Liu H, Wada T (2025) Construction of a computational model of individual progression of motion sickness symptoms based on subjective vertical conflict theory. Exp Brain Res 243:108. 10.1007/s00221-025-07052-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irmak T, de Winkel KN, Pool DM et al (2021) Individual motion perception parameters and motion sickness frequency sensitivity in fore-aft motion. Exp Brain Res 239:1727–1745. 10.1007/s00221-021-06093-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- Irmak T, Pool DM, de Winkel KN, Happee R (2023) Validating models of sensory conflict and perception for motion sickness prediction. Biol Cybern. 10.1007/s00422-023-00959-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- ISO 8727 (1997) Mechanical vibration and shock - Human exposure - Biodynamic coordinate systems. Geneva, Switzerland [Google Scholar]
- ISO2631-1 (1997) Mechanical vibration and shock–Evaluation of human exposure to Whole-body vibration- Part1, Geneva, Switzerland.
- Kamiji N, Kurata Y, Wada T, Doi S (2007) Modeling and validation of carsickness mechanism. In: Proceedings of International Conference on Instrumentation, Control and Information Technology. pp 1138–1143
- Keshavarz B, Golding JF (2022) Motion sickness: current concepts and management. Curr Opin Neurol 35:107–112. 10.1097/WCO.0000000000001018 [DOI] [PubMed] [Google Scholar]
- Kotian V, Pool DM, Happee R (2023) Modelling individual motion sickness accumulation in vehicles and driving simulators. In: Proceedings of the 22nd Driving Simulation & Virtual Reality Conference
- Kotian V, Irmak T, Pool D, Happee R (2024) The role of vision in sensory integration models for predicting motion perception and sickness. Exp Brain Res 242:685–725. 10.1007/s00221-023-06747-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kravets VG, Dixon JB, Ahmed NR, Clark TK (2021) COMPASS: computations for orientation and motion perception in altered sensorimotor States. Front Neural Circuits 15. 10.3389/fncir.2021.757817 [DOI] [PMC free article] [PubMed]
- Kuiper OX, Bos JE, Schmidt EA et al (2019) Knowing what’s coming: unpredictable motion causes more motion sickness. Hum Factors: J Hum Factors Ergon Soc 62:1339–1348. 10.1177/0018720819876139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuiper OX, Bos JE, Diels C, Schmidt EA (2020) Knowing what’s coming: anticipatory audio cues can mitigate motion sickness. Appl Ergon 85:103068. 10.1016/j.apergo.2020.103068 [DOI] [PubMed] [Google Scholar]
- Lackner JR, Graybiel A (1978) Postural illusions experienced during Z-axis recumbent rotation and their dependence upon somatosensory stimulation of the body surface. Aviat Space Environ Med 49:484–488 [PubMed] [Google Scholar]
- Liu H, Inoue S, Wada T (2024) Subjective vertical conflict model with visual vertical: predicting motion sickness on autonomous personal mobility vehicles. IEEE Trans Intell Transp Syst 25:9878–9894. 10.1109/TITS.2024.3357170 [Google Scholar]
- Mayne R (1974) A systems concept of the vestibular organs. In: Kornhuber HH (ed) Vestibular system part 2: psychophysics, applied aspects and general interpretations volume 6 /. 2 of the series Handbook of Sensory Physiology. Springer, Berlin Heidelberg, pp 493–580 [Google Scholar]
- Merfeld DM, Zupan LH (2002) Neural processing of gravitoinertial cues in humans. III. Modeling Tilt and translation responses. J Neurophysiol 87:819–833. 10.1152/jn.00485.2001 [DOI] [PubMed] [Google Scholar]
- Merfeld DM, Young LR, Oman CM, Shelhamer MJ (1993) A multidimensional model of the effect of gravity on the Spatial orientation of the monkey. J Vestib Res 3:141–161 [PubMed] [Google Scholar]
- Merfeld DM, Zupan LH, Gifford A (2001) Neural processing of Gravito-Inertial cues in humans. II. Influence of the semicircular canals during eccentric rotation. J Neurophysiol 85:1648–1660 [DOI] [PubMed] [Google Scholar]
- Mittelstaedt H (1983) A new solution to the problem of the subjective vertical. Naturwissenschaften 70:272–281. 10.1007/BF00404833 [DOI] [PubMed] [Google Scholar]
- O’Hanlon JF, McCauley ME (1974) Motion sickness incidence as A function of the frequency and acceleration of vertical sinusoidal motion. Aerosp Med 45:366–369 [PubMed] [Google Scholar]
- Oman CM (1982) A heuristic mathematical model for the dynamics of sensory conflict and motion sickness. Acta Otolaryngol Suppl 392:1–44 [PubMed] [Google Scholar]
- Reason JT (1978) Motion sickness adaptation:a neural mismatch model. J R Soc Med 71:819–829. 10.1177/014107687807101109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuten AJC, Nooij SAE, Bos JE, Smeets JBJ (2021) How feelings of unpleasantness develop during the progression of motion sickness symptoms. Exp Brain Res. 10.1007/s00221-021-06226-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reuten AJC, Bos JE, Martens MH et al (2024a) Mitigating motion sickness by anticipatory cues. Vibration 7:1266–1278. 10.3390/vibration7040065 [Google Scholar]
- Reuten AJC, Yunus I, Bos JE et al (2024b) Anticipatory cues can mitigate car sickness on the road. Transp Res Part F Traffic Psychol Behav 105:196–205. 10.1016/j.trf.2024.07.006 [Google Scholar]
- Seidman SH, Telford L, Paige GD (1998) Tilt perception during dynamic linear acceleration. Exp Brain Res 119:307–314. 10.1007/s002210050346 [DOI] [PubMed] [Google Scholar]
- Sivak M, Schoettle B (2015) Motion Sickness in Self-driving Vehicles. UMTRI Report No. UMTRI-2015-2, University of Michigan Transportation Research Institute, Ann Arbor, MI.
- Sousa Schulman D, Jalgaonkar N, Ojha S et al (2023) A Visual-Vestibular model to predict motion sickness for linear and angular motion. Hum Factors: J Hum Factors Ergon Soc. 10.1177/00187208231200721 [DOI] [PubMed] [Google Scholar]
- Stone RW, Letko W (1964) Some observations during weightlessness simulation with subject immersed in a rotating water tank. NASA TN D-2195. NASA Contract Rep NASA CR 1–20 [PubMed]
- Tamura Y, Wada T, Liu H (2023) Generating Visual Information for Motion Sickness Reduction Using a Computational Model Based on SVC Theory. In: 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC). IEEE, pp 5066–5071
- Ukita R, Okafuji Y, Wada T (2020) A Simulation Study on Lane-Change Control of Automated Vehicles to Reduce Motion Sickness Based on a Computational Model. In: Proceedings of the IEEE International Conference on Systems, Man and Cybernetics (SMC). pp 1745–1750
- Wada T (2016) Motion Sickness in Automated Vehicles. In: Meyer G, Beiker S (eds) International Symposium on Advanced Vehicle Control. Springer International Publishing, Cham
- Wada T (2021) Computational model of motion sickness describing the effects of learning exogenous motion dynamics. Front Syst Neurosci 15. 10.3389/fnsys.2021.634604 [DOI] [PMC free article] [PubMed]
- Wada T, Fujisawa S, Doi S (2018) Analysis of driver’s head Tilt using a mathematical model of motion sickness. Int J Ind Ergon 63:89–97. 10.1016/j.ergon.2016.11.003 [Google Scholar]
- Wada T, Kawano J, Okafuji Y et al (2020) A Computational Model of Motion Sickness Considering Visual and Vestibular Information. In: 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC). IEEE, pp 1758–1763
- Yunus I, Lundin A, Papaioannou G et al (2022) Trajectory planning to minimise motion sickness in autonomous driving. In: Proceedings of 15th International symposium on advanced vehicle control
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
No datasets were generated or analysed during the current study.