Combined experimental and computational investigation of vildagliptin: spectroscopy, electronic structure, MD and Docking to EGFR, VEGFR2, and HER2 anticancer targets

Abstract

This study combines experimental and computational approaches to investigate the molecular geometry and physicochemical properties of vildagliptin (VILD). Using methods such as UV-Vis, spectrofluorimetry, FTIR/Raman, and circular dichroism alongside DFT, molecular docking, and dynamics simulations, a reliable molecular model was obtained that aligns closely with X-ray crystallographic data. This model enabled accurate predictions of vibrational frequencies and systematic assignments of vibrational modes. Analyses, including Hirshfeld surface mapping, molecular electrostatic potential, HOMO-LUMO energetics, Fukui indices, and natural population analysis, provided clear insights into VILD’s reactivity, while NBO and TD-DFT studies elucidated key stabilizing interactions and high-energy electronic transitions. NTO visualization further clarified orbital dynamics, and circular dichroism measurements explained the molecular basis of the Cotton effect. Additionally, molecular docking and molecular dynamics simulations confirmed the formation of stable complexes with EGFR, VEGFR2, and HER2 receptor proteins, suggesting potential anticancer activity. The main purpose of this publication is to fill existing gaps in our understanding of VILD’s molecular behavior and offer a robust foundation for rational drug design and improved therapeutic strategies.

Supplementary Information

The online version contains supplementary material available at 10.1007/s10822-025-00646-9.

Introduction

Gliptins, including the representative agent vildagliptin, represent a relatively recent class of oral antihyperglycemic agents used in the management of type 2 diabetes mellitus. Their therapeutic effect primarily stems from the inhibition of the dipeptidyl peptidase-4 (DPP-4) enzyme, which physiologically inactivates incretin hormones such as glucagon-like peptide-1 (GLP-1) and glucose-dependent insulinotropic polypeptide (GIP). By attenuating DPP-4 activity, these agents modulate glucose homeostasis through multiple pathways: enhancing glucose-dependent insulin secretion, delaying gastric emptying, reducing postprandial glucose excursions, and suppressing appetite [1]. The modest elevation in endogenous GLP-1 levels observed with gliptin therapy may explain their limited impact on weight reduction, contrasting with GLP-1 receptor agonists that sustain supraphysiological incretin concentrations, leading to more pronounced weight loss [2].

The ubiquitous expression of DPP-4 in human tissues raises potential concerns regarding off-target effects. Nevertheless, gliptins are generally well-tolerated, with a low incidence of class-specific adverse events. Reported complications include gastrointestinal disturbances (nausea, vomiting), instances of ketoacidosis following insulin discontinuation [3], debated associations with pancreatitis risk [4–7], and hypersensitivity reactions [8, 9]. Notably, vildagliptin has not received FDA approval due to unresolved safety signals related to arthralgia [10, 11], though it remains authorized by the EMA.

Vildagliptin (2S)-1-[2-[(3-hydroxy-1-adamantyl)amino]acetyl]pyrrolidine-2-carbonitrile (VILD) is a cyanopyrrolidine derivative that incorporates a distinctive adamantane scaffold. The nitrile moiety is relatively prone to oxidation, first yielding an amide and subsequently a carboxylic acid, and it may also undergo cyclization with an amino group - processes that contribute to some of the main impurities in the active pharmaceutical ingredient [12].

The first therapeutic agent featuring an adamantane motif was amantadine, which was initially employed for its antiviral properties and later recognized for its efficacy in treating Parkinson’s disease. Two additional compounds with antiviral activity include rimantadine and tromantadine [13]. Memantine is used as an anti-dementia agent in Alzheimer’s disease, while adapalene, applied topically, serves as an anti-inflammatory drug. Saxagliptin and vildagliptin belong to the class of antidiabetic medications [14].

In recent years, the adamantane framework has attracted considerable interest among medicinal chemists due to its presence in compounds with diverse pharmacodynamic profiles. The literature includes hundreds of studies exploring the biological potential of various adamantane derivatives. Structurally, adamantane is a rigid, symmetrical tricyclic hydrocarbon (point group T_d), which enables precise three-dimensional positioning of substituents. This spatial arrangement facilitates the optimization of binding affinity and selectivity toward biological targets. The incorporation of adamantane into drug structures is often employed as a strategy to “escape from flatland” [15]. Introducing large lipophilic groups such as adamantane (sometimes referred to as the “lipophilic bullet”) can transform highly hydrophilic molecules (logP ≪ 0) into more lipophilic and clinically useful compounds [13, 16]. This modification enhances blood-brain barrier (BBB) permeability, improves membrane solubility, and prolongs plasma half-life, as the rigid cage structure protects the pharmacophoric moiety from metabolic degradation [17–19].

Numerous studies have been dedicated to designing novel adamantane-containing derivatives for potential use in the treatment of neurodegenerative diseases [20] as well as for their antibacterial and antiviral [21–25], antimalarial [26, 27], anti-inflammatory [28, 29], and anticancer activities [30–36].

Despite recent reports indicating that vildagliptin may exert antiproliferative effects in various cancer cell lines [37, 38], the molecular basis of this activity remains poorly understood. Existing spectroscopic investigations of vildagliptin, particularly FTIR and Raman studies, have been limited to superficial band assignments and often omit key vibrational modes associated with its cyano and adamantane moieties. Similarly, computational efforts to date have focused on isolated electronic transitions, without incorporating detailed density functional theory (DFT) analyses of reactivity descriptors in conjunction with molecular docking and molecular dynamics (MD) simulations. Consequently, there is a need for an integrated computational-experimental approach that fully assigns vibrational modes, elucidates the electronic structure and reactivity of vildagliptin, and evaluates the stability and dynamics of its complexes with key anticancer kinases (EGFR, HER2, VEGFR2). By combining FTIR, FT-Raman, UV-Vis, three-dimensional spectrofluorimetry, and circular dichroism measurements with DFT-based vibrational, NBO, NLO, and MEP analyses, alongside blind docking and MD simulations, the present study addresses this gap and provides a robust molecular rationale for repurposing vildagliptin in anticancer drug design. A thorough characterization of the physicochemical properties of vildagliptin is essential to facilitate the discovery of compounds with fewer adverse effects, improved storage stability, and to support the rational design of new therapeutic agents with analogous chemical frameworks.

Materials and methods

Materials

Vildagliptin (purity ≥ 98%) and spectroscopic-grade solvents were purchased from Sigma-Aldrich (USA).

Experimental methods

The FTIR transmission spectrum was recorded using a Nicolet 6700 spectrometer (Thermo Scientific, USA). The sample was mixed with anhydrous KBr in a 1:300 ratio, and the resulting mixture was pressed into a pellet. Spectral data were collected over the range 4000–400 cm⁻¹. The FT-Raman spectrum, acquired over 3700–150 cm⁻¹, was obtained with a Nicolet 8700 A spectrometer equipped with a neodymium Nd: YVO₄ laser (2 W, 1064 nm) and a germanium detector (NXR Genie). The UV-Vis spectrum of a methanolic solution (0.0005% concentration) was measured using a U-2001 spectrophotometer (Hitachi, Japan) in the 200–400 nm range. Three-dimensional fluorescence spectra were collected on the same solution using an RF-6000 spectrofluorimeter (Shimadzu, Japan) with excitation wavelengths spanning 200–500 nm and emission wavelengths from 200 to 600 nm. Finally, the circular dichroism spectrum of the methanolic solution was recorded in the range of 195–400 nm using a J-815 spectropolarimeter (Jasco, Japan).

Molecular modeling

The molecular structure of vildagliptin was investigated theoretically using density functional theory (DFT) calculations performed in Gaussian 16 Rev. B.01 [39]. Initial geometry was derived from crystallographic data [40]. Gas-phase geometry optimization was executed at the B3LYP/6-311++G(2d, p) level, incorporating Grimme’s D3 dispersion correction with Becke-Johnson damping (D3BJ) [41]. The optimized structure was subsequently used for vibrational frequency and thermodynamic calculations, employing the same functional, basis set, and dispersion correction. The absence of imaginary frequencies confirmed the stability of the minimized geometry. Scaled harmonic vibrational frequencies (scaling factor: 0.965) were analyzed using VEDA 4 [42] to assign atomic group vibrations and quantify potential energy distribution (PED).

Natural bond orbital (NBO) analysis [43] and Fukui function calculations [44] were conducted on the same model. Preliminary studies revealed that the CAM-B3LYP functional [45], combined with the 6-311++G(2d, p) basis set, provided superior agreement with experimental electronic excitation data. Therefore geometry optimization in solvent (using the IEFPCM solvation model [46] in methanol) was performed also incorporating D3BJ correction. Time-dependent DFT (TD-DFT) simulations on the CAM-B3LYP-optimized structure were performed to model electronic transition spectra and electronic circular dichroism. Additionally, geometry optimization of the first excited state was carried out using TD-CAM-B3LYP to simulate emission spectra.

Docking and molecular dynamics

The vacuum-optimized geometry of vildagliptin was employed for molecular docking and dynamics simulations. Crystal structures of tyrosine kinase domain of epidermal growth factor receptor (EGFR, PDB: 1M17) [47], kinase domain of human epidermal growth factor receptor 2 (HER2, PDB: 3PP0) [48] and kinase domain of vascular endothelial growth factor receptor 2 (VEGFR2, PDB: 4AG8) [49] were retrieved from Protein Data Bank. Protein and ligand preparation - including ligand rotatable bond assignment, hydrogen atom addition, and charge assignment - was performed using AutoDockTools [50]. Blind docking was implemented by generating grid boxes encompassing the entire protein structures to exhaustively sample potential binding poses. Docking simulations in AutoDock Vina [51] identified the highest-affinity ligand conformations, with protein-ligand interactions visualized via LigPlot+ [52] and Discovery Studio.

To validate docking-derived complexes, molecular dynamics (MD) simulations were conducted for three protein-ligand systems using GROMACS 2025.1 [53] with the CHARMM36 force field [54]. Ligand topology was generated via the SwissParam server [55]. Each system was solvated in a dodecahedral box with a 1.0 nm spacing between the protein and box edges, followed by TIP3P water molecule addition at 1 g/cm² density. Ionization (Cl⁻/Na⁺) neutralized the system charge. Energy minimization was performed via steepest descent (50000 steps), followed by equilibration in NVT (100 ps, 300 K, Berendsen thermostat) and NPT (100 ps, 1 bar, C-rescale barostat) ensembles. Production MD runs were executed for 100 ns under constant temperature and pressure (300 K, 1 bar).

Results and discussion

Geometric parameters

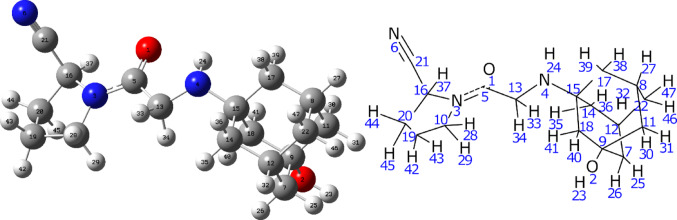
The vacuum-optimized geometry of vildagliptin (Fig. 1) closely aligns with its X-ray diffraction (XRD)-derived crystal structure. Selected geometric parameters are summarized in Table 1, with complete data provided in Table S1. The RMSD for interatomic distances between experimental and calculated values is 0.09 Å, indicating a strong correlation. As shown in Figure S1, the deviations primarily involve distances between hydrogen atoms and heavier atoms, which can be attributed to the nature of the XRD method, where the positions of lighter atoms are associated with greater uncertainty. The RMSD for bond angles between individual atoms is 1.11 degrees, indicating good agreement between the calculated and experimental data (Figure S2). The strong agreement between computationally derived and experimental structures underscores the robustness of the theoretical model, enabling detailed analysis of the compound’s geometric features. Minor discrepancies between DFT-optimized and XRD-determined geometries primarily involve bond lengths (e.g., O2-H23) and bond angles within non-cyclic amino, methylene, and carbonyl groups. These variations likely arise from structural relaxation in vacuum conditions and the absence of intermolecular interactions present in the crystalline environment.

Fig. 1.

Optimized structure of vildagliptin and atom numbering

Table 1.

Selected geometrical parameters of vildagliptin optimized in vacuum

Bond length [Å]	DFT	XRD	Bond angle [o]	DFT	XRD	Bond dihedral [o]	DFT	XRD
O1–C5	1.2216	1.2257	C9–C18–C15	110.82	109.81	O1–C5–C13–N4	11.16	13.46
O2–C9	1.4328	1.4339	O2–C9–C11	111.39	110.19	C16–N3–C10–C19	− 6.31	− 4.58
O2–H23	0.9645	0.82	O2–C9–C7	111.18	110.53	C10–N3–C16–C20	− 17.26	− 20.24
N3–C5	1.3622	1.3538	O2–C9–C18	106.33	107.85	N3–C10–C19–C20	27.44	27.65
N3–C10	1.4696	1.4791	C13–N4–C15	117.79	117.09	C5–N3 -C16–C21	− 87.19	− 95.54
N3–C16	1.4627	1.4619	O1–C5–C13	122.34	121.73
N4–C13	1.445	1.4585	N3–C5–C13	115.98	115.82
N4–C15	1.4641	1.4775	C10–N3–C16	112.51	111.65
N4–H24	1.0166	0.9277	N6–C21–C16	178.20	177.84
C5–C13	1.5218	1.5215
N6–C21	1.1498	1.1453
C16–C20	1.539	1.5292
C16–C21	1.4746	1.479

The carbon-carbon bond lengths within the adamantane scaffold align with literature-reported values for such bonds, averaging approximately 1.54 Å. Similarly, carbon-hydrogen bond lengths (≈ 1.09 Å) closely match theoretical predictions, though they exhibit a ~ 10% elongation compared to experimental data - a well-documented discrepancy in XRD studies.

The C16–C20 bond in the pyrrolidine ring is elongated relative to other C–C bonds in the system, likely due to steric and electronic effects arising from the substitution of a hydrogen atom at C16 with a nitrile moiety. Conversely, the C16–C21 bond length is shorter than typical single C–C bonds, attributed to electron density redistribution influenced by the adjacent nitrogen atom connected to C21.

Oxygen-carbon bond lengths further highlight structural specificity: the C9–O2 bond measures 1.433 Å, consistent with a single bond, while the C5-O1 bond (1.222 Å) reflects its double-bond character within the carbonyl group. The O2–H23 bond length (0.965 Å) aligns with standard values for hydroxyl-group interactions, corroborating the integrity of the hydrogen-bonding network in the optimized structure.

Most of the bonds connecting carbon and nitrogen atoms in the VILD molecule measure around 1.46 Å, with two notable exceptions: the C21–N6 and C5–N3 bonds. The former is a triple bond with an interatomic distance of 1.15 Å, while the latter is a single bond measuring 1.362 Å. The unusually short length of the C5–N3 bond can be attributed to an electron density shift from the carbon atom, induced by its adjacent double bond to a highly electronegative oxygen atom, thereby imparting a partial double-bond character.

Within the adamantane scaffold, most bond angles between carbon atoms are close to 109°, consistent with sp² hybridization. An outlier is the angle defined by atoms C15-C18-C9, which measures 110.8°. The terminal atoms in this angle (C15 and C9) are bonded to heteroatoms - nitrogen and oxygen, respectively, whose lone pairs slightly perturb the ideal tetrahedral geometry of the neighboring carbon atoms. Furthermore, the C11–C9–O2 and C7–C9–O2 angles are approximately 111°, whereas the C18–C9–O2 angle is reduced to 106°.

The C13–N4–C15 bond angle (117.8°) deviates markedly from the idealized tetrahedral geometry, suggesting localized electronic perturbations. In contrast, angles within the amide functional group - C13–C5–O1 (≈ 122°), N3–C5–O1 (≈ 122°), and C13–C5–N3 (116°) - align with literature-reported values for amide-bonded systems, confirming the structural integrity of this motif.

Within the pyrrolidine ring, bond angles generally conform to literature values, with the exception of the C10–N3–C16 angle (112°), which exhibits slight expansion likely attributable to steric strain from adjacent substituents. Atoms C16, C21, and N6 are almost collinear, forming an angle of 178.2°, while the carbonyl and amino groups display near-coplanar alignment (N4–C13–C5–O1 dihedral angle: 11°).

Non-planarity of the pyrrolidine ring is evident: atoms C16–N3–C10–C19 lie nearly coplanar (dihedral angle: 6.3°), whereas C20 resides out-of-plane. Dihedral angles for C10–N3–C16–C20 (17.3°) and N3–C10–C19–C20 (27.4°) further underscore the ring’s puckered conformation. The nitrile group adopts a near-perpendicular orientation relative to the carbonyl moiety (C5–N3–C16–C21 dihedral angle: 87.2°), reflecting steric and electronic constraints imposed by the adamantane scaffold.

Vibrational frequency analysis

Vildagliptin’s vibrational wavenumbers were analyzed by comparing experimental FTIR and FT-Raman spectra with DFT-simulated spectra. Theoretical spectra were scaled by a factor of 0.965 to improve alignment with experimental data, a standard correction to account for phase discrepancies (gas-phase calculations vs. solid-state measurements) [56]. Figure S3 presents the RMSD dependence of experimentally and computationally obtained peak wavenumbers on the scaling factor, varied from 1.000 to 0.900. The absence of imaginary frequencies in the computational output confirms the optimized geometry resides at a true potential energy minimum.

The FTIR spectra are partially discussed in the study [57], however, that manuscript provides only a superficial interpretation of the VILD FTIR spectrum and contains some rather obvious errors. The spectra are also addressed in the paper [58], but this work also omits most of the vibrational modes, such as those originating from the cyano group.

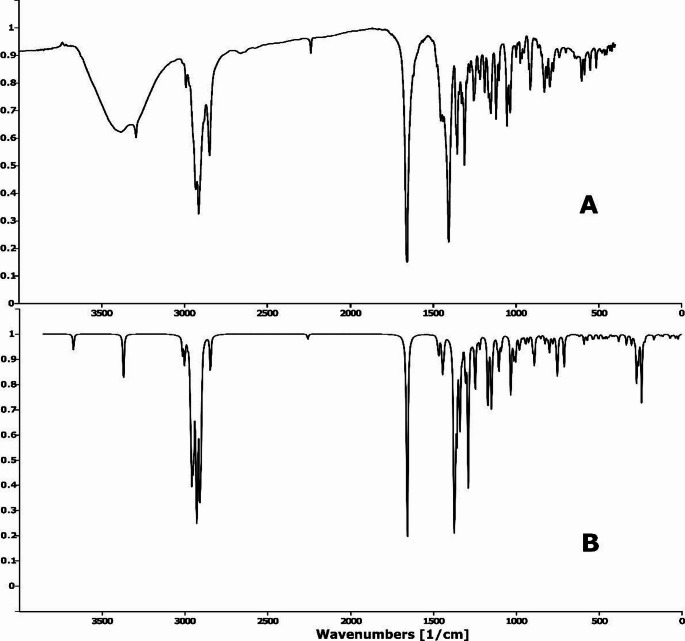
The molecule, exhibiting C1 symmetry, comprises 47 atoms and 135 fundamental vibrational modes. Each mode was optimized using algorithms in the VEDA 4 software, and its potential energy distribution (PED) was determined accordingly. Experimental and simulated FTIR spectra are presented in Fig. 2, while normalized Raman spectra are shown in Fig. 3. The spectra were not subjected to baseline correction. A comprehensive vibrational assignment, correlating observed wavenumbers with theoretical modes, is detailed in Table 2.

Fig. 2.

Experimental A and theoretical, B FTIR spectra of vildagliptin

Fig. 3.

Experimental A and theoretical, B Raman spectra of vildagliptin

Table 2.

Experimental and calculated vibrational frequencies (cm^− 1) with respective assignments and PED values

FTIR	Raman	Calc	Scal	IR int.	Raman int.	Assignments with PED(%)
3385(s)	–	3807	3674	12.83	174.67	νOH(100)
3293(s)	3293(m)	3494	3372	39.86	83.28	νNH(100)
3012(w)	3013(m)	3125	3016	13.94	97.94	νasCH2PR(77)+νasCH2PR(11)
2994(w)	2993(m)	3111	3002	20.44	124.36	νasCH2PR(79)
2971(w)	2973(m)	3092	2984	4.46	82.94	νCHPR(98)
–	–	3077	2969	23.35	89.30	νasCH2PR(78)+νasCH2PR(10)
2957(w)	–	3070	2963	45.76	84.06	νasCH2AR(88)
–	–	3067	2959	62.14	111.22	νasCH2AR(69)
2951(w)	2950(m)	3061	2954	12.10	35.09	νssCH2PR(78)+νasCH2MG(10)
–	–	3060	2952	30.78	117.41	νasCH2AR(79)
–	–	3059	2952	17.82	73.53	νasCH2AR(68)
–	2947(s)	3054	2947	11.03	139.08	νssCH2PR(84)
–	–	3054	2947	35.50	38.06	νasCH2AR(69)+νssCH2AR(10)
–	–	3051	2944	17.19	42.91	νasCH2AR(79)
–	2934(s)	3041	2935	51.59	541.85	νssCHAR(83)
2932	–	3035	2929	92.31	107.11	νssCHAR(82)
–	–	3030	2924	58.60	55.77	νssCH2AR(87)
–	2917(s)	3020	2914	21.81	120.51	νssCH2PR(79)
2915(s)	–	3018	2913	74.20	23.58	νssCH2PR(74)
–	–	3015	2910	17.29	49.55	νssCH2AR(80)
–	–	3014	2908	14.08	101.84	νssCH2AR(92)
–	–	3012	2906	12.07	32.92	νasCH2AC(78)
2882(m)	2882(s)	3009	2904	65.76	111.25	νssCH2AR(85)
–	–	3003	2898	9.08	24.21	νssCH2AR(11)+νssCH2AR(75)
2849(s)	2848(s)	2950	2847	30.26	75.41	νssCH2MG(98)
2239(w)	2238(s)	2341	2259	3.91	116.43	νCNNG(92)
1659(s)	1656(s)	1719	1659	258.54	16.88	νCO(84)
1478(w)	1482(w)	1530	1476	4.02	3.44	βscCH2PR(73)+βscCH2PR(10)
1463(w)	1465(w)	1525	1471	3.00	1.88	βscCH2MG(65)+βscCNH(12)
1453(m)	1455(w)	1521	1468	13.82	3.58	βscCH2MG(15)+βscCNH(41)
–	–	1504	1451	3.88	5.86	βscCH2PR(11)+βscCH2PR(72)
1449(w)	–	1500	1448	5.92	0.16	βscCH2AR(82)
–	1441(w)	1497	1445	6.71	1.66	βscCH2AR(79)
1440(m)	–	1496	1444	12.08	0.11	βscCH2AR(83)
1437(w)	1434(m)	1494	1442	6.16	8.56	βscCH2PR(84)
–	–	1489	1437	7.90	2.21	βscCNH(12)+βscCH2MG(70)
–	–	1484	1432	0.78	14.16	βscCH2AR(82)
–	–	1482	1431	0.23	14.24	βscCH2AR(86)
1406(s)	1405(w)	1423	1373	336.54	2.79	νNCAB(38)
1363(w)	–	1408	1359	58.49	0.57	βwagCH2AR(32)+βscCOH(40)
1354(s)	1353(w)	1394	1345	17.69	0.87	βwagCH2AR(33)+βscCOH(14)+τHCCC(10)
1342(w)	1342(w)	1389	1340	23.89	1.60	βwagCH2AR(39)
–	–	1388	1339	34.77	1.23	βwagCH2AR(31)+τHCCC(13)
1328(m)	–	1383	1334	6.21	1.92	βscHCCPR(51)
–	–	1376	1328	3.84	0.05	βwagCH2AR(55)+τHCCC(16)
1321(w)	1321(w)	1373	1325	6.61	2.84	βwagCH2PR(50)
–	–	1358	1310	1.81	0.46	βwagCH2PR(53)
1309(m)	1308(w)	1355	1308	14.70	3.43	βwagCH2AR(13)
–	–	1353	1305	16.58	2.43	βwagCH2AR(19)+τHCCC(12)+τHCCC(16)
1291(w)	1293(w)	1338	1291	80.98	5.02	βwagCH2MG(18)
1280(w)	1279(m)	1336	1289	41.24	2.26	βwagCH2MG(40)+βwagCH2AR(14)
–	–	1335	1288	5.20	1.39	τHCNCPR(10)+τHCCC(54)+τHCCC(14)
–	–	1315	1269	2.24	1.74	τHCCC(11)+βtwCH2(23)+τHCCC(20)
–	–	1309	1263	0.71	0.59	τHCCC(13)+βtwCH2(25)+νCC(14)
–	1264(w)	1309	1263	1.45	3.73	βtwCH2(27)
1254(m)	1255(m)	1305	1259	1.85	5.14	βtwCH2(34)
1248(m)	1248(m)	1294	1248	45.65	5.30	τHCCC(16)+νNCPR(25)+βwagCNCPR(11)
–	–	1277	1232	1.88	9.53	βHCC(15)+τHCCC(22)
–	–	1274	1229	0.63	3.76	βHCC(51)+βtwCH2(11)
1224(w)	1225(w)	1265	1221	4.07	8.81	βHCC(50)+τHCCN(14)+βtwCH2(13)
1217(w)	1216(w)	1263	1219	5.80	6.41	τHCCC(10)
1189(m)	1187(w)	1215	1173	16.60	9.42	βHCC(27)+βHOC(18)+βtwCH2(10)
1174(w)	1173(m)	1214	1171	47.33	5.35	βHCC(33)+βHCC(10)+νNCPR(11)
1165(w)	–	1199	1157	5.96	2.62	τHCCC(15)
–	–	1194	1153	11.33	9.89	βHCC(10)+βHCC(16)+βtwCH2(12)
1151(m)	1151(m)	1191	1149	48.80	4.56	νNCAN(31)
–	1135(w)	1182	1141	4.84	4.82	βHCC(10)+νNCAN(17)
1120(m)	1117(w)	1156	1115	5.99	6.21	νNCAN(19)
1102(w)	1105(w)	1146	1106	29.65	6.42	νNCAN(13)+βHOC(16)
1054(m)	1055(m)	1132	1092	7.30	1.50	τHCCC(24)+βHCC(10)
–	–	1129	1089	3.81	1.84	βHCC(25)
–	–	1127	1088	0.65	0.21	βHCC(52)+βtwCH2(21)
–	–	1126	1087	0.51	1.16	τHCCCPR(13)
1032(m)	1029(m)	1071	1033	50.94	8.12	νOCAO(19)
–	–	1052	1015	13.14	2.09	νCCAR(15)
–	–	1050	1013	1.64	1.41	βHCC(19)+νCCAR(29)+βtwCH2(17)
1007(w)	1006(w)	1047	1011	3.44	8.49	νCCAR(11)+νCCPR(17)
998(w)	–	1041	1004	17.56	1.75	νCCAR(21)+βtwCH2(15)
984(w)	985(w)	1018	982	10.67	4.45	τHCCNAB(20)+τCONCAB(10)+βrockCH2MG(10)
974(w)	973(w)	1013	977	3.16	2.41	νCCAC(15)+βrockCH2(10)
–	–	1007	971	1.37	1.77	τHCCNAB(20)+νCCAC(10)+βrockCH2(10)
964(w)	963(w)	996	961	2.08	4.34	νCCAR(13)+τHCCC(16)
–	–	983	948	1.87	1.13	νCCAR(17)
950(w)	955(m)	977	943	6.64	3.82	βCCNPR(12)+νCCPR(14)
921(w)	922(w)	961	927	3.54	3.67	νCCAR(32)+βrockCH2(19)
–	–	959	925	2.08	2.78	νCCAR(36)
–	897(w)	932	900	10.43	2.68	νCCAR(11)+νCCPR(13)+βrockCH2(11)
888(w)	889(w)	924	891	15.10	4.35	νCCPR(30)+βrockCH2(12)
882(w)	–	922	889	9.22	0.91	νCOAO(10)+νCCPR(11)+βrockCH2(10)
–	–	906	875	0.16	0.14	βHCCPR(10)+τHCCC(39)
–	–	904	872	0.04	0.26	βHCCAR(10)+τHCCC(38)
–	–	903	871	0.74	0.13	νCCAR(11)+τHCCC(39)
865(w)	865(w)	884	853	2.88	3.84	βHCCAR(10)+νCCAR(12)+τHCCC(27)
837(w)	838(m)	857	827	6.80	11.43	νCNPR(13)
812(w)	–	842	813	2.72	2.07	νCCAR(23)
796(w)	805(w)	829	800	14.67	0.41	τHCCC(12)+νCCPR(20)
775(w)	775(w)	809	781	6.71	3.70	νCCAR(10)
–	741(m)	785	757	8.52	6.85	νCCAR(22)
737(w)	–	778	751	31.95	2.24	νCCAR(26)+ γHNCC(12)
699(w)	699(m)	737	711	26.60	6.74	γHNCC(25)+βCCOAB(15)+βCCNAN(10)
–	683(w)	706	682	0.82	11.90	νCCAR(13)+βCCCAR(22)
644(w)	644(w)	658	635	0.59	1.98	βCCCAR(14)+τCCCCAR(15)
635(w)	635(w)	642	620	1.89	1.92	τHCCCPR(11)+βCCCPR(32)
603(w)	603(w)	612	591	7.34	1.12	τCONCAB(21)+βCNCPR(11)
586(w)	585(w)	594	573	5.10	0.75	βCCCPR(10)+τCONCAB(11)
551(w)	552(w)	560	540	3.26	1.13	βCCCPR(10)+τCONCAB(22)
515(w)	515(w)	552	532	2.89	4.24	νOCAO(11)+βCCCAR(14)
–	495(w)	522	504	4.22	2.88	βCNCAB(20)+βCNCNG(10)
480(w)	480(w)	494	477	3.72	1.44	βCNCAB(15)+βCNCAN(13)
463(w)	461(w)	482	465	3.12	0.64	τHCCCAR(13)+τCCCCAR(10)+τCCNCAB(14)+βCCOAO(11)
452(w)	–	467	451	2.88	0.69	τHCCCAR(21)+τCOCCAO(19)
432(w)	431(w)	458	441	1.99	0.21	βCNCAB(11)+βCNCAN(12)
422(w)	421(w)	435	420	1.46	1.35	τCCNCAN(10)+τCCOCAO(12)
404(w)	405(w)	423	408	1.37	0.92	βCCCAR(10)+τHCCCAR(17)+βCCCAR(20)
–	–	411	396	0.51	0.92	βCCCAR(31)+βCCCAR(10)
–	394(w)	409	395	0.29	1.01	βCCCAR(11)+βCCCAR(47)
–	373(w)	396	382	5.63	0.28	τCCOCAO(23)
–	346(w)	347	335	8.26	0.99	τCCCCAR(23)+βCCOAB(11)
–	307(w)	316	305	7.39	0.78	βCCOAB(10)+βCCOAO(12)+βCCNAN(17)
–	281(w)	297	286	2.40	1.35	τHCCNPR(20)+βCCNNG(24)
–	272(w)	283	274	34.88	0.80	βCCCAR(10)+τHCCCAR(12)+τHOCCAO(22)
–	–	273	264	12.72	0.60	τCCCCAR(22)
–	–	272	262	6.37	0.18	τCCCCAR(22)+βCCOAO(39)
–	236(w)	252	243	50.84	1.37	τHOCCAO(74)
–	–	233	224	3.87	0.43	τHCNCPR(14)+τHCCNNG(18)
–	197(w)	195	188	0.53	1.38	νNCAN(11)+βCCNAN(20)
–	165(w)	175	168	4.42	0.35	βCCNAN(34)
–	–	160	154	0.45	0.50	βCCNAB(31)
–	–	134	129	1.16	0.53	βCCNNG(16)+βCNCAB(18)+βCCCPR(12)
–	–	121	117	1.66	0.58	τCNCCAB(45)
–	–	74	72	3.67	1.75	τCNCCAB(15)+τCNCCAB(23)+τNCCN(10)
–	–	58	56	1.13	1.15	βCCNAN(14)+τCCCNPR(41)
–	–	40	39	2.96	0.60	βCCNAN(10)βCCNAB(14)+τCNCCPR(48)
–	–	24	24	3.53	0.19	τCNCCPR(13)+τNCCN(58)
–	–	13	13	0.39	0.20	τCCNCAN(83)

ν , stretching; ss, symmetrical; as, asymmetrical; β, bending; wag, wagging; sc, scissoring; tw, twisting; rock, rocking; γ, out of plane bending; τ, torsion; AR, adamantane ring; PR, pirrolidyne ring; AN, amine nitrogen; AB, amide group; AO, alcohol oxygen; AC, amide carbon; NG, nitrile group; MG, methylene group

The O–H stretching vibration of the hydroxyl group appears as a broad band in the FTIR spectrum, centered at 3385 cm⁻¹. In the Raman spectrum, this mode manifests as a faint, low-intensity signal near the noise threshold. The broadening of the IR band likely arises from intermolecular hydrogen bonding within the crystalline lattice. The DFT-calculated wavenumber for this mode (3673 cm⁻¹) exhibits a significant redshift compared to experimental data, a discrepancy attributable to the harmonic approximation used in simulations and the exclusion of crystal packing effects. In the literature, one can find interpretations of FTIR spectra for the core structure of vildagliptin (3-amino-1-adamantanol), where a characteristic broad band from the hydroxyl group can be observed around 3350 cm⁻¹ [59]. This band partially masks the N–H stretching vibration, which appears as a sharp peak around 3300 cm⁻¹ [60].

The COH bending vibration is observed as a broad IR band overlapping with HCCC torsional modes. In the Raman spectrum, this feature appears as a weak signal at 1354 cm⁻¹. The OHC bending vibration also contributes to a combination band at 1102 cm⁻¹ (PED: 16%). At 1055 cm⁻¹, both FTIR and Raman spectra exhibit a broad band that lacks a corresponding feature in the computational model; this band likely arises from a combination vibration incorporating a COH bending component and is notably red-shifted due to intermolecular forces in the solid phase.

HOCC torsional vibrations lie beyond the FTIR detection range but were identified via Raman spectroscopy and computational analysis at 272 cm⁻¹ (calculated: 273 cm⁻¹) and 236 cm⁻¹ (calculated: 246 cm⁻¹).

The O–C stretching vibration of the hydroxyl group is observed as intense bands at 1032 cm⁻¹ in both IR and Raman spectra. This mode also contributes to combination bands at 882 cm⁻¹ (PED 10%) and 515 cm⁻¹ (PED 11%). Bending and torsional modes involving OCC and OCCC moieties appear as components of multiple combination bands below 460 cm⁻¹.

The prominent IR and Raman band at 1659 cm⁻¹ is unambiguously assigned to the carbonyl (C = O) stretching vibration. OCC bending modes contribute to combination bands observed at 699 cm⁻¹ (PED 15%) and 346 cm⁻¹ (PED 11%). Torsional OCNC vibrations manifest as composite bands, likely corresponding to features at 984 cm⁻¹ (PED 10%), 603 cm⁻¹ (PED 21%), 586 cm⁻¹ (PED 11%), and 551 cm⁻¹ (PED 22%).

A medium-intensity, sharp IR band at 3293 cm⁻¹, accompanied by a moderately intense Raman feature, is assigned to the N–H stretching vibration of the secondary aliphatic amine group, consistent with the characteristic spectral profile of such moieties. The HNC bending vibration of the amine group is confidently identified as the medium-intensity IR/Raman band at 1453 cm⁻¹, while the HNCC out-of-plane bending modes appears as a distinct bands at 737 and 699 cm⁻¹.

The N–C stretching vibration of the amine group manifests as a broad band at 1151 cm⁻¹ and contributes to a combination mode at 1102 cm⁻¹ (PED 13%). CNC bending vibrations are observed as low-frequency combination modes at 699, 480, and 432 cm⁻¹. Torsional NCCC vibrations are tentatively attributed to features near 435, 24, and 13 cm⁻¹.

The sharp, high-intensity IR and Raman band at 2239 cm⁻¹ is assigned to the C≡N stretching vibration of the nitrile group - a feature seldom reported in organic compounds. Bending modes of this group contribute to low-frequency combination bands, tentatively identified at 495 cm⁻¹ (calculated: 521 cm⁻¹, PED 10%), 281 cm⁻¹ (PED 24%), and 129 cm⁻¹ (PED 16%). Torsional NCCH vibrations, lying beyond the instrumental detection range, are hypothesized near 224 cm⁻¹ (PED 18%).

The N-C stretching vibration of the amide group appears as an intense IR band and weak Raman feature at 1406 cm⁻¹. HCCN torsional modes correlate with a medium-intensity IR band at 984 cm⁻¹, while low-intensity CCNC torsional vibrations manifest as components of combination bands below 500 cm⁻¹. Bands at 1248 and 1174 cm⁻¹ are partially attributed to N-C stretching involving pyrrolidine ring carbons. A weak IR band at 950 cm⁻¹ is tentatively linked to the CNC bending vibration of the amide nitrogen atom within the pyrrolidine scaffold.

The C–H stretching vibrations generate overlapping medium-intensity IR bands and stronger Raman features within the 3012–2849 cm⁻¹ range. Notably, the bands at 3012 and 2994 cm⁻¹ are distinct, corresponding to CH stretching within the pyrrolidine ring, while those at 2957, 2952, 2932, and 2882 cm⁻¹ are attributed to adamantane-associated C-H bonds. A band at 2848 cm⁻¹ likely corresponds to methylene group C-H stretching.

Bending vibrations of HCH initiate near 1478 cm⁻¹, with Raman spectra displaying a composite band spanning 1478–1373 cm⁻¹, encompassing symmetric HCH bending modes of the methylene group, pyrrolidine ring, and adamantane scaffold. Overlapping bands at 1263–1280 cm⁻¹ reflect HCH wagging vibrations, predominantly manifesting as combination modes. Raman bands at 1189, 1173, and 1054 cm⁻¹ are linked to combination modes involving HCH bending contributions. In the ranges of 1269–998 cm⁻¹ and 984–882 cm⁻¹, bending vibrations of the twisting and rocking types, respectively, are observed as components of combination vibrations with a relatively low percentage of Potential Energy Distribution (PED). This is consistent with literature data obtained for similar compounds [61].

Computational modeling indicates torsional HCCC vibrations contribute to combination bands across a broad spectral range (1354–281 cm⁻¹). However, their low potential energy distribution (PED) values and weak intensities suggest minimal energetic contributions to the overall vibrational profile.

The C-C stretching vibrations are observed in both the IR and Raman spectra with low intensity, beginning at 1263 cm⁻¹ according to the computational model. However, in the experimental spectra these vibrations are assigned to a wavenumber of 1006 cm⁻¹, and at lower wavenumbers they contribute to combination bands. CCC bending vibrations appear as components of combination bands, for example at 683, 635, and 585 cm⁻¹. Additionally, CCCC twisting vibrations, which exhibit low intensity, have been detected experimentally only at 644, 461, and 346 cm⁻¹. The remaining wavenumbers attributed to these modes through computational analysis are listed in Table 2.

Hirshfeld surface and 2D fingerprint plot

To analyze the intermolecular interactions among vildagliptin atoms within the crystal lattice, a Hirshfeld surface analysis and 2D fingerprint plots were performed. Figure 4 displays the Hirshfeld surface using d_norm (normalized contact distance [62]), where the minimum contact distance (red) and the maximum contact distance (blue) are − 0.3669 and 1.6169, respectively. It is evident that the intermolecular interactions predominantly occur between nitrogen and oxygen atoms, as well as the hydrogen atom of the hydroxyl group.

Fig. 4.

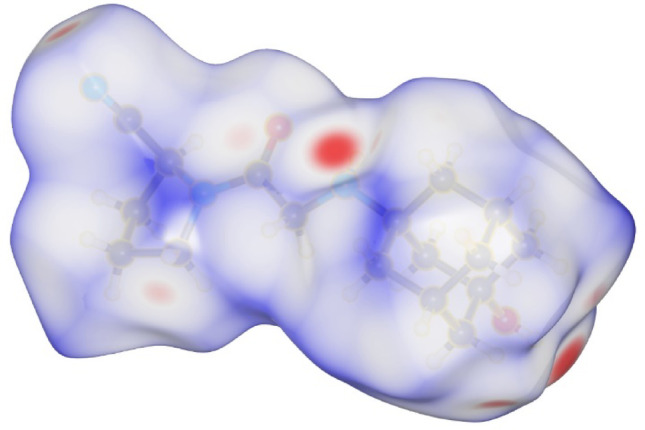
Hirshfeld surface of VILD mapped over d_norm

The 2D fingerprint histogram (Fig. 5) provides a more detailed breakdown of various intra- and intermolecular interactions along with their estimated percentage contributions. For example, interactions between the carbon atom of the nitro group and hydrogen atoms of neighboring molecules account for 4.9% of the total interactions. Interactions involving nitrogen atoms from the nitro and amino groups with hydrogen atoms comprise 17.8%, while those between oxygen atoms and hydrogen atoms account for 13.8%. The majority of the intermolecular interactions (60.8%) result from mutual interactions between hydrogen atoms. The remaining calculated parameters, such as distance to external atom, distance to internal atom, shape index, curvedness, and fragment patch, are presented in Table 3.

Fig. 5.

2D finger plot graphs representing the number of molecular interactions of VILD. A– O H interactions, B– H–H interactions, C– N–H interactions, D– C–H interactions

Table 3.

Hirshfeld surface properties of VILD

Mode	Minimum interaction	Maximum interaction
dnorm	−0.3669	1.6169
di	0.9369	2.5997
de	0.9365	2.6483
Shape index	−0.9983	0.998
Curvedness	−3.899	0.2201
Fragment patch	0	13

Molecular electrostatic potential (MEP) surface analysis

The ESP surface analysis provides a visual representation and interpretation of the charge distribution around a molecule. This technique is instrumental in predicting how the molecule may interact with ions, reactive species, or solvents by highlighting regions predisposed to electrophilic or nucleophilic attacks. It also offers insights into the binding affinity of drug molecules toward proteins and their preference for polar or nonpolar solvents. The MEP map is constructed on a molecular surface defined by a specific electron density value [63].

For this study, the electrostatic potential was calculated using a molecular model optimized at the B3LYP-D3BJ/6-311++G(2d, p) level. The map indicates the most negative potential in red (−5.456 × 10^− 2, −1.485 eV) and the most positive in blue (4.556 × 10^− 2, 1.24 eV), with the color scale progressing from red to orange, yellow, green, and blue (Fig. 6). The N6 atom of the nitrile group, due to its lone electron pair, exhibits the most negative potential. Likewise, the oxygen atoms O1 and O2, each carrying two lone pairs, display high electron density and appear in red. These regions are key contributors to the electrophilic reactivity of vildagliptin with less electronegative species.

Fig. 6.

Molecular electrostatic potential surface (MEP) of vildagliptin

Conversely, the highest positive potential is located on the outer part of the pyrrolidine ring, particularly around the C10-C19-C20 region. This area, depicted in light blue on the MEP map, is susceptible to nucleophilic attack due to the electron density being drawn toward nearby electronegative oxygen and nitrogen atoms. The adamantane ring shows a uniformly high potential, represented in green, except for the region with the attached hydroxyl group O2-H23, which creates localized areas of strong negative potential near the oxygen and strong positive potential near the hydrogen.

Nonlinear optical (NLO) properties

The exploration of non-linear optical (NLO) characteristics is a critical element in contemporary photonics and optoelectronics, driving the development of materials with specific optical functionalities. These properties arise from the non-linear response of a material’s electron density to high-intensity electromagnetic fields, diverging from the linear response described by classical optics. Density functional theory (DFT) offers a robust framework for predicting and analyzing NLO phenomena, yielding insights into the structure-property relationships essential for material design [64].

To assess the NLO potential of vildagliptin, dipole moment (µ), polarizability (α), and first hyperpolarizability (β) were computed using its vacuum-optimized geometry. The computed polarizability and hyperpolarizability of VILD were determined to be 31.8 × 10^− 24 esu and 1.16 × 10^− 30 esu, respectively, representing a considerable enhancement over urea - the prototypical NLO material (Table 4). These results suggest that the compound under investigation may be a promising candidate for further research into optically active materials.

Table 4.

Calculated values of dipole moment, polarizability and hyperpolarizability for VILD

Dipole moment		Polarizability		Hiperpolarizability
Parameter	DFT (Debye)	Parameter	DFT (esu x10− 24)	Parameter	DFT (esu x10− 30)
µ x	− 2.29	α xx	38.00	β xxx	− 0.08
µ y	5.54	α xy	− 0.12	β xxy	0.60
µ z	1.99	α yy	29.74	β xyy	− 0.11
µ	6.31	α xz	0.33	β yyy	0.53
		α yz	0.47	β xxz	− 0.62
		α zz	27.59	β xyz	0.20
		α	31.78	β yyz	0.49
				β xzz	− 0.06
				β yzz	− 0.07
				β zzz	0.12
				β tot	− 1.16

Natural bond orbital (NBO) analysis

NBO analysis offers valuable insights into the electronic structure and bonding features of molecules, detailing charge distribution, hybridization states, and donor-acceptor interactions that influence molecular stability and reactivity. By quantifying second-order perturbation energies (E⁽²⁾), this method identifies key hyperconjugative interactions and lone pair contributions, which are essential for understanding intramolecular charge transfer and non-covalent forces involved in ligand-receptor binding [65].

NBO calculations were performed on the gas-phase optimized structure using the same functional and basis set with dispersion correction. Data concerning the types of donor and acceptor orbitals, along with second-order perturbation energies exceeding 4 kcal/mol, are summarized in Table 5. High E⁽²⁾ values indicate strong conjugation between donor and acceptor components.

Table 5.

Second order perturbation theory analysis of Fock matrix in NBO for vildagliptin molecule

Type	Donor NBO(i)	ED	Type	Acceptor NBO(j)	ED	E(2) [kcal/mol]	E(j)-E(i) a.u.	F(i, j) a.u.
σ	C5-C13	1.97540	σ*	N3-C16	0.26392	4.55	0.95	0.059
σ	N6-C21	1.99547	σ*	C16-C21	0.02481	5.17	1.47	0.079
π	N6-C21	1.98348	σ*	N3-C16	0.26392	4.15	0.66	0.047
σ	C16-C21	1.98305	σ*	N6-C21	0.02481	5.73	1.67	0.087
LP	O1	1.86428	σ*	N3-C5	0.29639	25.30	0.72	0.123
LP	O1		σ*	C5-C13	0.02142	19.76	0.63	0.102
LP	O2	1.95842	σ*	C7-C9	0.01302	6.23	0.68	0.058
LP	O2		σ*	C9-C11	0.01897	5.75	0.68	0.056
LP	N3	1.69726	π*	O1-C5	0.02024	60.66	0.29	0.119
LP	N3		σ*	C10-H28	0.02142	4.93	0.66	0.055
LP	N3		σ*	C10-H29	0.03328	5.57	0.65	0.058
LP	N3		σ*	C16-C21	0.02481	6.75	0.68	0.065
LP	N4	1.90831	σ*	C13-H33	0.10773	6.10	0.66	0.057
LP	N4		σ*	C13-H34	0.26392	6.70	0.64	0.059
LP	N6	1.96999	σ*	C16-C21	0.02481	10.70	0.92	0.089

LP, lone pair

Given that the VILD molecule contains relatively few multiple bonds, no significant π→π* interactions were observed, with these interactions exhibiting stabilization energies below 5 kcal/mol. Instead, the molecule is characterized by the presence of five heteroatoms possessing lone pairs, all of which contribute notably to its stability through interactions with neighboring antibonding orbitals. The most substantial stabilization energy (60.7 kcal/mol) originates from the interaction between the lone pair on the N3 atom and the π-antibonding orbital of the O1–C5 carbonyl group.

Furthermore, strong hyperconjugative interactions were identified between the lone pair on the O1 atom and the σ-antibonding orbitals of both the N3-C5 bond in the amide group and the C5–C13 bond. An additional interaction, between the nonbonding electrons of the N6 atom and the σ-antibonding orbital of the C16-C21 bond, contributes over 10 kcal/mol to the stabilization of the molecule.

Natural population analysis (NPA)

Natural Population Analysis (NPA), a fundamental component of the NBO methodology, offers a chemically intuitive approach for quantifying atomic charge distributions in molecules. By partitioning electron density into natural atomic orbitals (NAOs), NPA assigns atomic charges that reflect localized bonding patterns, hybridization, and resonance effects, providing a coherent picture of the electronic structure that aligns with classical chemical concepts. This approach rigorously accounts for electron delocalization, including hyperconjugation and lone pair interactions, which is essential for understanding charge-transfer phenomena in bioactive compounds. Developed as an alternative to conventional Mulliken population analysis, NPA exhibits enhanced numerical stability and more accurately describes electron distribution in complex molecules [66].

In the vildagliptin molecule, the atomic partial charges show significant variation (Table 6). The most positive charge (0.7099) is found on the carbon atom C5, which forms part of the carbonyl group. Conversely, the most negative charge (−0.7530) is located on oxygen atom O2, a constituent of the alcohol group attached to the adamantane ring. This markedly negative value is attributed to the substantial electronegativity difference between oxygen and its neighboring atoms. All heteroatoms carry negative partial charges, ranging from − 0.3223 to −0.7530, suggesting that these sites are likely to undergo electrophilic attack.

Table 6.

Natural charges of vildagliptin atoms

No	Atom	Charge	No	Atom	Charge
1	O	− 0.63999	25	H	0.19511
2	O	− 0.75298	26	H	0.20564
3	N	− 0.51188	27	H	0.20101
4	N	− 0.69742	28	H	0.20325
5	C	0.70988	29	H	0.18992
6	N	− 0.32229	30	H	0.20907
7	C	− 0.39655	31	H	0.19359
8	C	− 0.22076	32	H	0.19879
9	C	0.27199	33	H	0.19826
10	C	− 0.16425	34	H	0.19166
11	C	− 0.39693	35	H	0.19580
12	C	− 0.21999	36	H	0.21051
13	C	− 0.25368	37	H	0.26284
14	C	− 0.38500	38	H	0.21276
15	C	0.14244	39	H	0.20105
16	C	− 0.11287	40	H	0.20212
17	C	− 0.37717	41	H	0.21228
18	C	− 0.41048	42	H	0.21488
19	C	− 0.39312	43	H	0.21008
20	C	− 0.36684	44	H	0.22397
21	C	0.29170	45	H	0.20663
22	C	− 0.37120	46	H	0.19760
23	H	0.45705	47	H	0.20158
24	H	0.38191

Most carbon atoms in VILD possess a negative partial charge, with the exceptions of atoms C5, C9, C15, and C21. Notably, C5 exhibits the highest positive charge (0.7099), indicating its susceptibility to nucleophilic attack. This elevated positive charge arises from its double bond with a highly electronegative oxygen atom, as well as its linkage to a nitrogen atom. The nitrogen atoms display partial charges of −0.5119 for N3, −0.6974 for N4, and − 0.3223 for N6. The higher negative charge on N4 is consistent with its single bond to carbon atoms, while N3, which is involved in an amide bond that partially attains double bond character, shows a bit lower negative charge. The lowest negative atomic charge is observed on N6, due to its triple bond with carbon C21.

For hydrogen atoms bonded to carbon, the majority of partial charges lie between 0.19 and 0.22, with the lowest value (0.1899) recorded for hydrogen H29, a member of the pyrrolidine ring. In contrast, other hydrogen atoms exhibit higher charges, such as H23 (0.4571) in the alcohol group, H37 (0.2626) located near the nitrogen atoms of the amide and nitrile groups, and H24 (0.3819) which is directly bonded to nitrogen N4.

Local reactivity descriptors

Fukui functions serve as critical descriptors for identifying the most reactive atomic sites within a molecule. By analyzing the electron density distributions of the neutral species as well as its forms with added and removed electron, it is possible to determine whether a given fragment exhibits electrophilic or nucleophilic character. These functions quantify changes in electron density induced by variations in electron count and are mathematically defined as:

1

where ρ(r) represents electron density, N denotes the total number of electrons, and v(r) corresponds to the external nuclear potential.

The function describing electron acquisition (nucleophilic reactivity), denoted as f⁺(r), is expressed as:

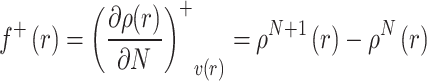2

Conversely, the function for electron donation (electrophilic reactivity), f⁻(r), is defined as:

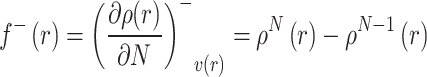3

Here, r specifies the atomic site, N is the electron count in the neutral state, while ρ^N+1​(r) and ρ^N−1​(r) represent electron densities for the species with added and removed electron, respectively [67].

A refined extension of the Fukui functions is the dual descriptor, which offers better efficiency in characterizing atomic site reactivity. This index is formulated as the difference between f⁺(r) and f⁻(r). Positive values of the dual descriptor highlight regions susceptible to nucleophilic attack, whereas negative values indicate sites prone to electrophilic interactions [68].

The Fukui functions were calculated based on natural population analysis, and the values are shown in Table 7. The analysis of the computed Fukui functions for the vildagliptin molecule suggests that a nucleophilic attack is most likely at atom C21, the carbon of the nitrile group. In contrast, markedly lower function values are observed for atom C15 (the adamantane carbon connected to the amino-group nitrogen) and for atom N3, the nitrogen of the amide group within the pyrrolidine ring. Additionally, atoms C17 and C5 exhibit positive f⁺ values.

Table 7.

Values of the Fukui indices calculated from natural population analysis

No	Atom	f+	f−	f0	dual
1	O	− 0.01509	− 0.03819	− 0.02664	0.02310
2	O	− 0.00615	− 0.02307	− 0.01461	0.01692
3	N	0.00324	− 0.07326	− 0.03501	0.07650
4	N	− 0.00043	− 0.45465	− 0.22754	0.45422
5	C	0.00169	0.02357	0.01263	− 0.02188
6	N	− 0.03594	− 0.05562	− 0.04578	0.01968
7	C	− 0.00995	0.00408	− 0.00294	− 0.01403
8	C	− 0.00496	0.00147	− 0.00175	− 0.00643
9	C	− 0.00455	− 0.00881	− 0.00668	0.00426
10	C	− 0.02684	0.01469	− 0.00608	− 0.04153
11	C	− 0.00535	0.00531	− 0.00002	− 0.01066
12	C	− 0.00848	0.00172	− 0.00338	− 0.01020
13	C	− 0.01091	0.05740	0.02325	− 0.06831
14	C	− 0.00613	0.00543	− 0.00035	− 0.01156
15	C	0.00374	0.02151	0.01263	− 0.01777
16	C	− 0.00330	0.00116	− 0.00107	− 0.00446
17	C	0.00199	0.00828	0.00514	− 0.00630
18	C	− 0.00315	− 0.02892	− 0.01604	0.02577
19	C	− 0.01960	0.00150	− 0.00905	− 0.02110
20	C	− 0.01856	0.00207	− 0.00825	− 0.02063
21	C	0.02378	0.02622	0.02500	− 0.00244
22	C	− 0.00574	0.00551	− 0.00012	− 0.01125

All carbon atoms display a propensity for electrophilic attack, except for atom C18, which is situated near an alcohol group. The highest f⁻ values are found at carbon atom C13 of the glycine fragment bonded to an amino group. Moreover, both atom C5 of the amide group and atom C21 of the nitrile group show elevated Fukui function values, while atoms C15 and C10 exhibit a somewhat reduced susceptibility to electrophilic attack.

For radical attacks, atoms C21 and C13 appear to be the most favorable sites, with lower f⁰ values calculated for atoms C5 and C15. Meanwhile, the dual descriptor highlights atom N4 (a secondary amine) as preferentially prone to nucleophilic attack, likely due to the nearby amide group - a potent electron-withdrawing system. Conversely, the carbon atom C13 bonded to N4 shows the highest tendency toward electrophilic attack.

Global reactivity

An evaluation of frontier orbitals (HOMO - Highest Occupied Molecular Orbital and LUMO - Lowest Unoccupied Molecular Orbital) together with reactivity parameters is fundamental in contemporary computational chemistry, enabling the prediction of reaction mechanisms and the assessment of molecular stability. Density functional theory (DFT) methods offer a quantitative framework for characterizing these properties. In particular, they allow the determination of parameters such as hardness (η) and chemical softness (S), which reflect a molecule’s susceptibility to structural deformation under external charge perturbations. Molecules that are more reactive in interactions driven by polarization are classified as soft, while those resisting charge-induced distortion are regarded as hard. Notably, molecular hardness is enhanced by higher electronegativity, a measure of an atom’s tendency to attract electrons, and by an increased HOMO-LUMO energy gap. Electronegativity (χ) measures an atom’s attraction to electrons, while chemical potential (µ) reflects the likelihood of an electron leaving its orbital. The electrophilicity index (ω) indicates a molecule’s tendency to accept electrons in reactions [69, 70].

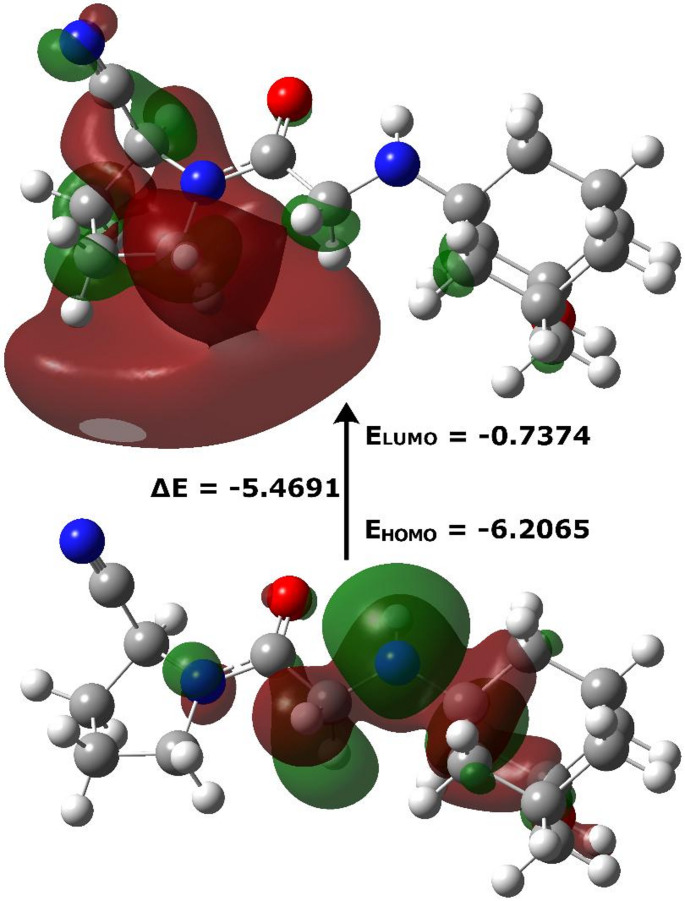
The HOMO-LUMO energy gap (ΔE = E_LUMO - E_HOMO) for the vildagliptin molecule, optimized in vacuum, was determined to be 5.4691 eV (Table 8). This value indicates moderate chemical stability, which is typical for many organic compounds. For context, compounds with significantly higher energy gaps, such as 9.848 eV [71], are generally considered more chemically stable, while those with lower gaps, for example 3.573 eV [72], tend to be more reactive. The high ionization potential (IP = 6.21 eV), representing the energy required to remove an electron from the molecule, points to a low propensity for ionization and, consequently, high chemical robustness. Although the electron affinity is relatively low (0.74 eV), suggesting that only a modest amount of energy is released upon the theoretical formation of an anion, the fact that it remains positive, together with the negative chemical potential (-3.4 eV) and a comparatively high electrophilicity index (2.2), implies a notable tendency for electron acceptance, thereby classifying the molecule as a good electrophile. This characterization is further reinforced by the electronegativity value (3.47), which reflects the molecule’s ability to attract electrons.

Table 8.

Calculated global reactivity descriptors of VILD

Descriptor	Value
HOMO [eV]	− 6.2065
LUMO [eV]	− 0.7374
IP [eV]	6.2065
EA [eV]	0.7374
χ	3.4720
η	2.7345
S	0.3657
µ	− 3.4720
ω	2.2041

Vildagliptin is characterized by a high chemical hardness (2.73) and low chemical softness (0.37), suggesting that it is more predisposed to engage in ion-forming reactions rather than in processes that lead to the formation of covalent bonds.

The molecular orbital model for the HOMO and LUMO is presented in Fig. 7. It can be observed that the electron density in the highest occupied molecular orbital is predominantly localized on the nitrogen atom of the amino group, with partial extension onto carbon atom C13 of the glycine fragment and the carbons C15 and C18 of the adamantane moiety. Conversely, the lowest unoccupied molecular orbital is primarily distributed over the pyrrolidine ring, with a lesser contribution from the nitrile group.

Fig. 7.

Frontier molecular orbitals of VILD calculated with DFT

UV-Vis spectroscopic analysis

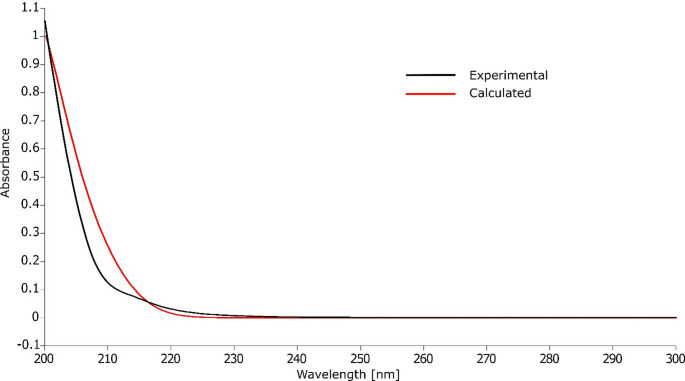
The UV-Vis spectrum of vildagliptin was acquired in methanol (Fig. 8) using a 0.001% w/v solution. Experimental results demonstrated strong alignment with computational predictions derived from time-dependent density functional theory (TD-DFT) simulations employing the CAM-B3LYP functional, 6-311++G(2d, p) basis set, and Grimme’s D3BJ dispersion correction. Geometrical optimization and spectral modeling were conducted using the integral equation formalism polarizable continuum model (IEF-PCM) to account for solvation effects in methanol.

Fig. 8.

Experimental and theoretical UV-Vis spectra of vildagliptin solution in methanol

Excitation energies and oscillator strengths, calculated via TD-DFT, were processed using GaussSum [73], enabling systematic assignment of electronic transitions to specific molecular orbital interactions with quantified percentage contributions. The first ten excited states of VILD are summarized in Table 9. For mixed-character excitations, natural transition orbital (NTO) analysis was employed to visualize dominant electron-hole pair interactions. This method diagonalizes the transition density matrix, distilling complex excitations into spatially localized charge transfer pathways, thereby clarifying the primary contributors to each transition [74].

Table 9.

Calculated absorption wavelength, oscillator and rotatory strength and major contributions to excitation

No.	Wavelength	Osc. strength	Rotatory strength	Major contributions
1	206.77	0.007	14.87	HOMO->LUMO (51%), HOMO->L+5 (14%)
2	205.77	0.0029	− 7.79	H-3->L+9 (34%), H-3->L+10 (23%), H-3->L+16 (10%)
3	197.84	0.0395	− 15.79	HOMO->L+7 (14%), HOMO->L+9 (33%), HOMO->L+10 (15%), HOMO->L+16 (10%)
4	191.05	0.0153	− 0.34	HOMO->L+2 (34%), HOMO->L+3 (20%)
5	187.59	0.0315	1.51	HOMO->L+1 (10%), HOMO->L+2 (28%), HOMO->L+3 (21%), HOMO->L+7 (10%)
6	185.23	0.0016	− 5.29	H-2->LUMO (15%), HOMO->L+1 (31%), HOMO->L+3 (11%)
7	181.51	0.005	− 9.32	H-2->LUMO (30%), H-2->L+1 (13%), HOMO->L+1 (21%)
8	180.86	0.0192	7.16	H-1->LUMO (24%), H-1->L+1 (19%), H-1->L+3 (13%)
9	176.77	0.2057	− 18.71	H-2->L+9 (31%), H-2->L+10 (15%), H-2->L+12 (14%)
10	172.80	0.0258	− 14.81	H-3->LUMO (24%), HOMO->L+7 (14%)

The vildagliptin molecule does not contain chromophores with strong light-absorbing capabilities, necessitating the input of relatively high energy to achieve electronic excitation. The primary chromophores are the lone pairs on the nitrogen and oxygen atoms, along with the π bonds in the carbonyl and nitrile groups. In the first electronic transition, electron transfer from the HOMO to the LUMO dominates, accounting for 51% of the transition, although the oscillator strength for this process is low. This is reflected in the experimental spectrum, which shows only a subtle inflection at approximately 209 nm. It is also important to note that UV-Vis spectra recorded in solution typically exhibit broadened absorption bands. This broadening arises from solute-solvent interactions (hydrogen bonds, van der Waals forces), which can perturb the energy levels of the solute molecules and lead to loss of fine spectral structure.

The hole NTO is predominantly localized near the lone pair of the amine nitrogen in VILD (Fig. 9), whereas the particle NTO is mainly associated with the π* orbital of the carbonyl group. Subsequent transitions in the computational model are closely spaced. Transitions No. 3 and No. 5, occurring at 197.84 nm and 187.59 nm respectively, display high oscillator strengths and involve the HOMO and higher-lying LUMO orbitals. In the experimental spectrum, these wavelengths correspond to a very intense peak, arising from the overlap of multiple electronic transitions.

Fig. 9.

Representation of natural transition orbitals (NTO) of the “particle” and “hole” pairs for the VILD excitations

For these transitions, the hole NTOs exhibit a distribution similar to that of the first transition, which is consistent with the dominant involvement of the HOMO. In transition No. 3, the particle NTO is primarily localized within the amide group, with a lesser contribution from the nitrile group. Conversely, the particle NTO for transition No. 5 extends over the central region of VILD, encompassing the amine and amide nitrogens as well as the carbonyl group. Transition No. 9, observed at 176.77 nm, exhibits the highest oscillator strength; however, this region falls outside the measurable range of the available instrumentation.

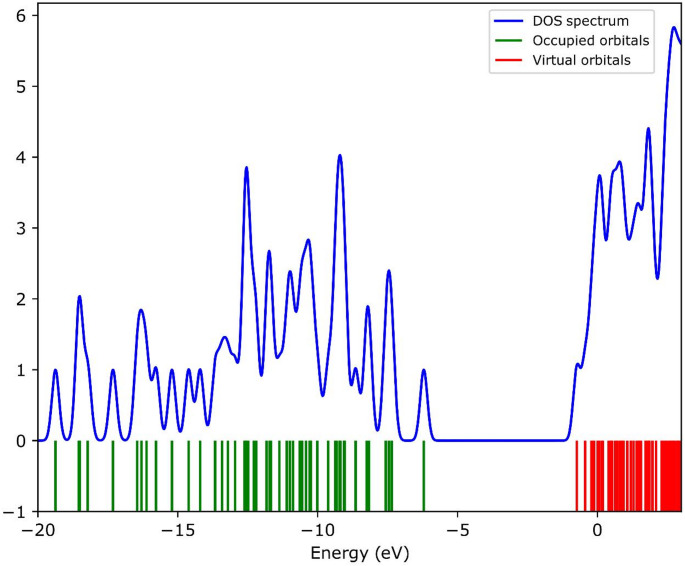
Analysis of the density of states (DOS) for molecular orbitals provides valuable insights into the energy-dependent distribution of electronic states and enables the determination of the contributions from specific orbitals to the overall electronic characteristics of the system [75]. In Fig. 10, occupied states are depicted in green while unoccupied states are shown in red. A significant energy gap is evident between the ground and excited states, and the states around 6–7 eV are observed to be very closely spaced.

Fig. 10.

Density of state spectrum of VILD

Circular dichroism analysis

Circular dichroism (CD) is a UV-Vis spectroscopic technique that elucidates the structure of compounds by measuring the differential absorption of right- and left-circularly polarized light. This method is particularly effective for molecules featuring chiral groups adjacent to their chromophores. Enhanced absorption of left-circularly polarized light results in positive Cotton effects, whereas predominance in right-circularly polarized absorption gives rise to negative bands [76]. Experimental CD spectra were obtained using the same methanolic solution (0.001% w/v) as for the UV-Vis analysis. In parallel, theoretical data were generated via time-dependent DFT (TD-DFT) on a geometry optimized in methanol using the CAM-B3LYP/6-311++G(2d, p) basis set with D3BJ dispersion corrections.

Figure 11 displays the CD spectra, where a low-intensity positive band is observed with maxima at 224 nm (experimental) and 213 nm (computational), alongside a more intense negative band with peaks at 204 nm (experimental) and 195 nm (theoretical). The ordering of the positive and negative Cotton effects is consistent across both datasets, although the theoretical model overestimates the excitation wavelength by approximately 11 nm. This shift may result from not accounting for all specific interactions between the solute and solvent molecules (the IEF-PCM approximation was used). Analysis of the rotatory strengths indicates that the positive Cotton effect arises from two overlapping electronic transitions near 206 and 205 nm, one contributing positively and the other negatively. The second prominent CD feature is attributed to transition No. 3, which exhibits a relatively high negative rotatory strength (see Table 9). Overall, the presence of distinct Cotton effects in VILD confirms that the molecular orbitals involved in the initial electronic transitions have a high electron density in the vicinity of the chiral center (carbon C16).

Fig. 11.

Experimental and theoretical circular dichroism spectra of VILD

Fluorescence analysis

A spectrofluorimetric measurement was performed on a 0.001% methanolic solution of vildagliptin, capturing the interrelation among excitation wavelength, emission wavelength, and emission intensity (3D fluorescence). Figure 12 illustrates the spectrum, where (in addition to the Rayleigh scattering line detected at a 45° angle) a region of relatively intense emission is observed upon excitation with radiation in the 200–210 nm range. The emission maximum occurs around 240 nm.

Fig. 12.

3D fluorimetric spectrum of vildagliptin solution in methanol

In contrast, the computational spectrum (TD-DFT/CAM-B3LYPD3BJ/6-311++G(2d, p)) predicts an emission maximum at 437 nm upon excitation at 206 nm, a value that is clearly overestimated. The pronounced emission intensity between 200 and 240 nm may be attributed to the small energy differences among the higher occupied orbitals. Consequently, via internal conversion, the observed emission likely results from overlapping emissions from transitions involving S5-S1 to S0.

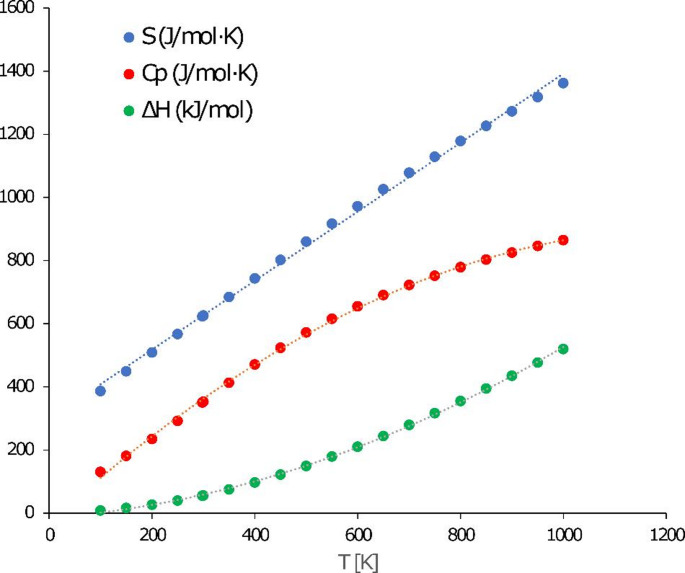
Thermodynamic properties analysis

Thermodynamic parameters of vildagliptin were derived from density functional theory (DFT) frequency calculations performed on the gas-phase optimized molecular structure. Standard thermodynamic functions - heat capacity (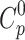), entropy (S⁰), and enthalpy (H⁰) - were computed across a temperature range of 100–1000 K at constant pressure. Vibrational frequencies were scaled by a factor of 0.965 to enhance accuracy (Table S2). The temperature-dependent data were fitted to quadratic functions Eqs. (2)–(5), achieving correlation coefficients (R²) exceeding 0.9996.

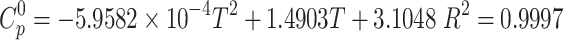4

5

6

As the temperature increases, the VILD molecule behaves as anticipated. Its enthalpy, heat capacity, and entropy all rise with temperature; entropy increases in an almost linear fashion, heat capacity shows a diminishing rate of increase at higher temperatures, and the enthalpy growth accelerates with temperature (see Fig. 13).

Fig. 13.

Entropy, enthalpy and heat capacity curves calculated for vildagliptin

Molecular Docking

Molecular docking has become a cornerstone in analyzing interactions between substances and protein structures, enabling fast and virtually cost-free preliminary testing of potential ligand-protein interactions. It allows atomic-level examination of intermolecular forces, which facilitates the exploration of new mechanisms of action or rational changes to the core structure for better ligand binding. Three proteins, commonly considered as potential targets for anticancer drugs, were selected in this study. They were analyzed using molecular docking and molecular dynamics simulations to assess the stability of the possible complexes with VILD and to determine the types of interactions preferred in protein-ligand binding.

Tyrosine kinases are enzymes that catalyze the phosphorylation of tyrosine residues within proteins, thereby initiating signaling cascades essential for cellular processes such as proliferation, differentiation, migration, metabolism, and apoptosis. Genetic alterations, including mutations or overexpression of these enzymes, have been implicated in oncogenic transformation. The EGFR, a prominent member of the tyrosine kinase family, is frequently overexpressed in various types of cancer, including non-small cell lung cancer, breast, esophageal, cervical cancer, as well as head and neck tumors [77]. Given these observations, targeting EGFR activity represents a rational and promising approach in the development of anticancer therapies [78, 79].

Under pathological conditions, the activation of EGFR leads to upregulation of VEGF expression. Subsequent binding of VEGF to its receptor, particularly VEGFR2, initiates the process of angiogenesis. VEGFR, itself a member of the tyrosine kinase receptor family, plays a pivotal role in tumor progression by mediating angiogenic pathways. Consequently, VEGFR has emerged as an attractive molecular target for anticancer drug development [79, 80].

HER2, a transmembrane receptor belonging to the tyrosine kinase family, plays a crucial role in modulating cellular proliferation and division. This protein is capable of forming both homodimers and heterodimers with other members of the EGFR family, through mechanisms that may depend on the presence or absence of specific ligands [81]. The amplification and overexpression of HER2 are key factors underlying the aggressive behavior observed in certain cancers, highlighting the urgent necessity for precision-targeted therapies. Small-molecule inhibitors targeting the tyrosine kinase activity of HER2 have been developed, providing a selective means to disrupt aberrant signaling pathways in HER2-driven tumors [82].

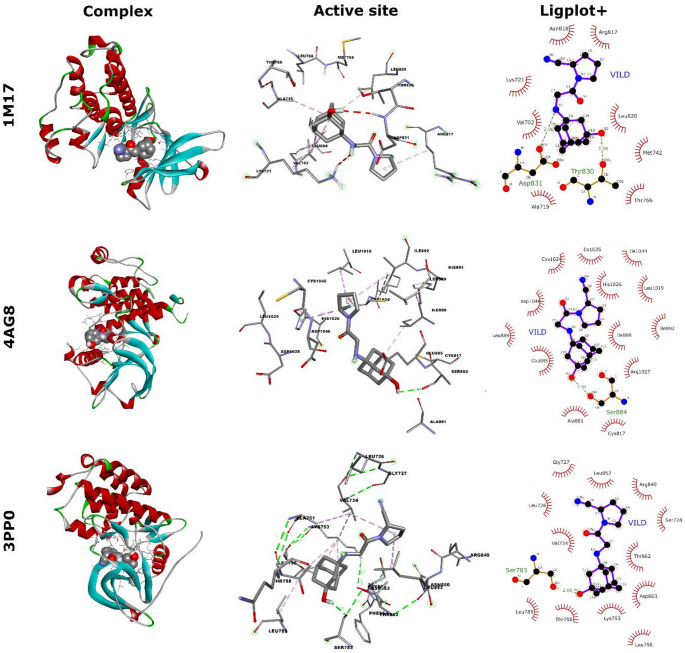
The interactions between VILD and 1M17 are predominantly hydrophobic. Amino acids located in close proximity to the ligand and participating in these interactions include Val702, Ala719, Lys721, Met742, Thr766, and Leu820, which interact with the adamantane moiety, as well as Arg817 and Asn818, which interact with the pyrrolidine ring. In addition, two hydrogen bonds can be observed: one formed between Lys720 or Asp831 (or both, as indicated by the molecular dynamics simulation) and the hydrogen atom of the amino group, and another between Thr830 and the hydrogen atom of the hydroxyl group (Fig. 14). The calculated binding energy for this complex is -7.612 kcal/mol. The amino acids in the vicinity of VILD are very similar to those identified as interacting with various anticancer ligands [79, 83–86].

Fig. 14.

Docking results of VILD and three analyzed proteins with specified, nearest amino acids interacting with the ligand

Vildagliptin binds to the tyrosine kinase inhibitor site of VEGFR2 (4AG8) at nearly the same location as ligands reported in the literature [79, 83, 87]. However, in contrast to these ligands, the interactions between VILD and 4AG8 are predominantly hydrophobic. Amino acids in close proximity to the adamantane scaffold of the ligand include Cys817, Ala881, Glu885, Ile888, and Arg1027. Leu889, Leu1019, Cys1024, His1026, Ile1025, Ile1044, and Asp1046 interact hydrophobically with the pyrrolidine ring. Only one hydrogen bond was identified in this complex, formed between the hydrogen atom of the hydroxyl group and Ser884. The binding energy determined for this complex is -6.996 kcal/mol.

In the 3PP0 complex with vildagliptin, a single hydrogen bond is observed between the hydroxyl hydrogen of VILD and Ser783. The remaining interactions are hydrophobic in nature and occur between Leu726, Gly727, Ser728, Val734, Arg849, and Leu852 and the pyrrolidine ring, as well as between Lys753, Leu785, Leu796, Thr798, Thr862, and Asp863 and the adamantane moiety. The docking algorithm estimated the binding energy for this interaction at -8.587 kcal/mol. In this case, these amino acids can also be identified as interacting with other compounds exhibiting anticancer activity [88, 89].

Molecular dynamics simulations

Molecular dynamics simulations were employed enable real-time observation of interactions between proteins and ligands, allowing for the assessment of complex stability and understanding the mechanism of interaction between the respective structures. For each of the three docked protein-vildagliptin systems 100 ns MD simulations were conducted at a temperature of 300 K. The stability of the complexes was confirmed by monitoring parameters over time, including root mean square deviation (RMSD), radius of gyration (Rg), root mean square fluctuation (RMSF) and hydrogen bond count (Fig. 15). Binding free energy was calculated using the Poisson-Boltzmann method with the gmx_MMPBSA package [90], based on van der Waals, electrostatic interactions, and solvation energy terms.

Fig. 15.

RMSD, RMSF curves, radius of gyration and a number of hydrogen bonds formed between VILD and three analyzed proteins

For the 1M17 system, the RMSD ranged between 0.15 and 0.35 nm over the course of the simulation for both the isolated protein and its ligand-bound complex. However, following ligand binding, the fluctuation amplitude decreased significantly, and the average RMSD of the complex was reduced by approximately 0.5 nm compared to the unbound protein, reaching a plateau after around 40 ns. For the last 50 ns, the average RMSD values were 0.27 ± 0.02 nm, with the slope of the curve being 0.0002 nm/ns. The RMSF values showed only minor differences between the protein and the complex, and they did not exceed 0.3 nm. A decrease in values can be observed for amino acids located in close proximity to the ligand. The radius of gyration stayed below 2.07 nm during the entire simulation, with a slightly lower value observed for the 1M17-VILD complex (for the last 50 ns, the average RMSD values were 1.98 ± 0.03 nm). The number of hydrogen bonds fluctuated between 0 and 4, averaging around 1 for most of the trajectory. During the last 50 ns of the simulation, the ligand is observed to be in contact with the amino acids Thr830 and Asp831 for most of the time (Fig. 16). For approximately half of the production simulation, VILD remains in the vicinity of the amino acids Val718, Ala719, Met742, Ala743, Ser744, Arg817, and Leu820. Notably, interaction with the gatekeeper residue Thr766 is also observed, which is consistent with the results obtained from molecular docking as well as with literature data describing ligand-binding sites in EGFR [91, 92]. The calculated binding free energy (ΔG_total) was − 5.3 kcal/mol (Fig. 17), indicating a moderate stability of the interaction between the enzyme and vildagliptin.

Fig. 16.

The occupancy plot of the amino acid residues of proteins in contact with VILD (the number of simulation frames from the last 50 ns of MD production run)

Fig. 17.

Binding energies with energy components of VILD complexes with 1M17, 4AG8 and 3PP0 proteins

Similarly, in the vildagliptin-VEGF receptor complex, minor RMSD fluctuations were observed during the simulation, stabilizing around 40 ns within the range of 0.15–0.25 nm (with an average of 0.19 ± 0.03 nm and a slope of -0.0004 nm/ns for the last 50 ns). The unbound protein exhibited slightly higher amplitude, suggesting system stabilization upon ligand binding. RMSF analysis revealed minimal differences between the complex and the unbound protein, with stabilization observed in residues interacting with the adamantane moiety and marginally elevated RMSF values for amino acids near the pyrrolidine ring. The radius of gyration for both the complex and the unbound protein remained nearly identical, fluctuating within a narrow range (2.00–2.05 nm), with marginally lower values for the complex (for the last 50 ns, the average RMSD was 2.02 ± 0.02 nm). A single hydrogen bond remained stable throughout the simulation, likely involving Ser884 or Asp1046, as suggested by the contact analysis (Fig. 16), which is consistent with literature data for other compounds interacting with the enzyme [93–95]. VILD also spends a noticeable amount of time in the vicinity of the amino acids Cys817, Glu885, Cys919, Cys1024, Ile1025, and His1026. The calculated binding free energy ΔG_total was − 5.2 kcal/mol, also indicating a moderate stability of the interaction between the receptor and vildagliptin.

The vildagliptin-3PP0 protein complex exhibited slightly reduced stability under the tested conditions. Minor variations in RMSD values were observed between the isolated protein and the 3PP0-VILD complex. Specifically, RMSD values peaked at 0.4 nm twice during the simulation (approximately 50 ns and 90 ns), but remained within 0.2–0.3 nm for the majority of the trajectory, indicating system stabilization. For the last 40 ns of the simulation, the average RMSD values were 0.26 ± 0.05 nm, with a slope of 0.0003 nm/ns. RMSF analysis revealed higher fluctuations in the complex compared to the unbound protein for residues interacting with the cyanopyrrolidine moiety, while lower fluctuations were observed for amino acids near the adamantane scaffold. Overall, fluctuations were minimal, with most residues exhibiting RMSF values in the 0.05–0.2 nm range. The radius of gyration analysis showed no significant differences between the complex and unbound protein, fluctuating within 1.97–2.07 nm for both systems. However, minor transient spikes (still below 2.07 nm) were detected in the complex (the average Rg was 2.03 ± 0.04 nm, for the last 40 ns of the simulation). Hydrogen bonding in the 3PP0-VILD complex varied between 0 and 3 throughout the simulation, with two bonds being the most frequently observed configuration. Compared to previously described kinases, VILD remains in the vicinity of several amino acids for most of the production simulation (the last 50 ns). These include, in particular, Lys753, Ser783, Leu785, Leu796, Thr798, Thr862, and Asp863, which were also identified in the docking analysis and are commonly reported in the literature as residues frequently interacting with various ligands [96–98]. The computed total binding free energies (ΔG_total) were − 23.3 kcal/mol for the 3PP0-VILD indicating a high stability of the interaction between the receptor and vildagliptin. Detailed ΔG values for the three protein systems are provided in Table 10.

Table 10.

Interaction energy components calculated with gmx_mmpbsa method

Energy component [kcal/mol]	1M17	4AG8	3PP0
van der Waals contribution	− 10.2	− 18.6	− 41.9
electrostatic contribution	− 5.6	− 27.3	− 16.7
polar contribution to the solvation free energy	11.9	43.6	39.1
non-polar contribution to the solvation free energy	− 1.4	− 2.9	− 3.9
ΔGgas	− 15.8	− 45.8	− 58.6
ΔGsolv	10.5	40.7	35.3
ΔGtotal	− 5.3	− 5.2	− 23.3

Conclusions

This study undertook a comprehensive examination of the geometry and physicochemical properties of vildagliptin (VILD) through an integrated approach combining experimental techniques (UV-Vis spectroscopy, spectrofluorimetry, FTIR/Raman spectrometry, circular dichroism spectroscopy) and computational strategies (DFT, molecular docking, molecular dynamics simulations). The computationally derived geometric model of the molecule aligns with crystallographic data reported in the literature. The accuracy of this structural framework enabled the acquisition of vibrational frequency data, which demonstrated a strong correlation with experimental results, thereby facilitating the assignment of wavenumbers to specific vibrational modes.

Hirshfeld surface analysis and molecular electrostatic potential mapping provided a visual assessment of VILD’s reactivity, while quantitative descriptors such as HOMO-LUMO energies, Fukui functions, and natural population analysis yielded quantifiable numerical values for local and global reactivity parameters. In addition, NBO analysis revealed substantial hyperconjugative interactions that contribute to the stabilization of the molecule. The combined use of UV–Vis spectrophotometry and TD-DFT computations clarified the details of the electronic transitions, indicating that relatively high energy (corresponding to wavelengths below 209 nm) is required to trigger these processes. NTO visualization further clarified the spatial characteristics of “hole” and “particle” orbitals. Moreover, both experimental and computational circular dichroism assessments provided insights into the origins of the Cotton effect observed in vildagliptin. Spectrofluorimetric studies, however, suggested that this technique may not be the most effective for detecting VILD.

Based on literature data regarding the potential anticancer activity of VILD, three proteins were selected as possible targets for vildagliptin. Molecular docking provided detailed insights into these interactions, while molecular dynamics simulations revealed that the most stable complexes are formed between VILD and targets 1M17 and 4AG8, whereas slightly less stable associations occur with 3PP0 protein. These findings collectively enhance the understanding of VILD’s molecular behavior and its interactions with biological targets, providing a foundation for further pharmacological exploration as a potential therapeutic agent in anticancer treatment.

Supplementary Information

Below is the link to the electronic supplementary material.

Author contributions

The author confirms sole responsibility for the following: study conception and design, data collection, analysis and interpretation of results, and manuscript preparation.

Funding

No funding was received to assist with the preparation of this manuscript.

Data availability

No datasets were generated or analysed during the current study.

Declarations

Conflict of interest

The author declare no competing interests.