Abstract
Coverage optimization in wireless sensor networks (WSNs) is critical due to two key challenges: (1) high deployment costs arising from redundant sensor placement to compensate for blind zones, and (2) ineffective coverage caused by uneven node distribution or environmental obstacles. Cuckoo Search (CS), as a type of Swarm Intelligence (SI) algorithm, has garnered significant attention from researchers due to its strong global search capability enabled by the Lévy flight mechanism. This makes it well-suited for solving such complex optimization problems. Based on this, this study proposes an improved Cuckoo Search algorithm with multi-strategies (ICS-MS), motivated by the ‘no free lunch’ theorem’s implication that no single optimization strategy universally dominates. This is achieved by analyzing the standard CS through Markov chain theory, which helps identify areas for enhancement after characterizing the WSN and its coverage issues. Subsequently, the strategies that constitute ICS-MS are individually explained. The evaluation of the proposed ICS-MS is carried out in two phases. First, a numerical comparison is provided, a numerical comparison is presented by contrasting the performance of ICS-MS with the standard CS and its variations employing different strategies in terms of function optimization results. Second, a series of coverage optimization experiments are conducted under various scenarios. The experimental results demonstrate that ICS-MS exhibits significant improvements in both test function optimization and WSN coverage applications. In high-dimensional optimization problems, all enhancement strategies of ICS-MS prove independently effective, showing strong robustness, faster convergence speed, and higher solution accuracy. For WSN coverage optimization, the ICS-MS algorithm outperforms comparative algorithms. At 200 iterations, it achieves an average coverage increase of 2.32-22.17% for 20-node deployments and 2.75-22.21% for 30-node deployments. At 1000 iterations, coverage improves by 1.78-21.65% for 20-node deployments and 1.23-20.99% for 30-node deployments. Additionally, the algorithm demonstrates enhanced stability, more uniform node distribution, and reduced optimization randomness. These improvements collectively elevate coverage rates while lowering deployment costs.
Keywords: Wireless sensor network, Coverage, Optimization, Cuckoo search algorithm, Markov chain
Subject terms: Computer science, Applied mathematics, Computational science
Introduction
Wireless Sensor Networks (WSNs) are self-organizing distributed systems composed of numerous micro-sensor nodes equipped with sensing and communication capabilities1. Their primary function is to detect and collect data, such as sound and temperature, within their designated coverage area, subsequently transmitting this information to a management center for statistical analysis and processing2. Due to their lightweight nodes, robust self-organizing capabilities, and low power consumption, WSNs can be deployed in almost any environment, including areas devoid of communication and power infrastructure, as well as locations that yield critical insights into the behavior, location, or composition of objects. WSNs have found extensive application in industrial domains, such as system monitoring3, disaster warning4, smart cities5, and others6–9.
The information-gathering capability of WSNs is crucial for effectively completing subsequent tasks. The reliability and accuracy of the collected data are essential for accurately and efficiently analyzing the monitored area via WSN10. When coverage is incomplete, WSNs may lose the ability to gather information from certain parts of the monitored area, thus compromising the reliability and accuracy of the data collected. Therefore, enhancing the coverage rate of WSNs is a significant approach to improving their performance11.
The coverage optimization problem in WSNs is described as an engineering constraint problem9. Although numerous traditional numerical and analytical methods have been examined, some deterministic techniques cannot provide a feasible solution due to the complexity of the issues, which are non-convex and characterized by highly nonlinear search domains coupled with exponentially growing dimensions8–14. For the WSN optimisation problem, Singh et al. pointed out that Swarm Intelligence algorithms can effectively solve such problems by virtue of their approximate search characteristics, and have now become one of the main methods for WSN coverage optimisation15. Hanh et al. proposed a WSN coverage optimisation method in the form of a genetic algorithm, which combines the Laplace crossover and arithmetic crossover operators and effectively improves network coverage in experimental validation16. Li et al. propose an improved multi-objective ant lion optimizer algorithm based on fast non-dominated sorting to successfully increase the coverage of wireless sensor networks and reduce the average distance travelled by nodes with respect to the two objectives of wireless sensor coverage and average distance travelled by nodes17. Miao et al. In to improve the convergence accuracy of the grey wolf optimization algorithm and balance its global and local search ability to solve the WSN coverage optimization problem, which effectively improves the network coverage18. Cao et al. introduced a WSN coverage optimization method based on a chaos-based improved Social Spider Optimization to curtail energy expenditure and boost WSN coverage19. The aforementioned literature discusses coverage optimization strategies for WSNs using various SI algorithms. However, there remains potential for further optimization concerning convergence speed and coverage rate.
Cuckoo Search (CS), a novel stochastic iterative algorithm with high global search capabilities and strong randomness due to its Levy flight, has recently garnered considerable attention for effectively tackling constrained, large-scale, and nonlinear engineering problems20. Braik et al. introduced an enhanced CS tailored for parameter estimation in linear and nonlinear model structures within actual wrapping processes21. Cuong-Le et al. proposed a CS augmented with a novel movement strategy, where the step size parameter is dynamically controlled by randomly choosing from among three predefined functions to enhance flexibility22. Ye et al. proposed a hybrid HS-CS by enhancing global search ability while avoiding falling into local optima to extract fuzzy production rules and have proven three theorems to reveal HS-CS as a global convergence meta-heuristic23. Although the CS has achieved fruitful results in various practical engineering domains, the ‘no free lunch’ theorem emphasizes that no method or model can be universally optimal without making prior assumptions about the nature of the optimization problem24,25.
This paper proposes a more suitable CS variant to meet the requirements of the WSN coverage optimization problem by analyzing the standard CS using a Markov chain. The key contributions of this manuscript are:
The employment of a Markov chain to analyze the standard CS and to identify the direction for enhancement. This approach is designed to address the complexities of multi-modality and high-dimensionality inherent in WSN coverage optimization.
The explicit development of an improved CS with multi-strategies (ICS-MS) for WSN coverage optimization. This design objective is to reduce the average number of iterations and to mitigate inter-dimensional interference.
The performance of the proposed ICS-MS is validated through experiments conducted under conditions involving 20 and 30 nodes, and 200 and 1000 iterations, respectively. Furthermore, the four enhancement strategies, CS-I, CS-II, CS-III, and CS-IV, are included in the comparative analysis to examine their influence. Experimental results indicate that ICS-MS significantly outperforms the standard CS in terms of mean coverage rate across various node counts and iteration numbers scenarios. Compared with other CS variants, ICS-MS demonstrates faster convergence and a more equitable node distribution, and the four enhancement strategies are each independently effective.
The remainder of the paper is structured as follows: Sect. 2 introduces the WSN coverage issue and the standard CS; Sect. 3 provides a concise theoretical analysis using a Markov chain to inform the proposed improvements and discusses the ICS-MS in detail; Sect. 4 validates the performance of ICS-MS in WSN coverage optimization; and Sect. 5 concludes the paper with a synthesis of its findings.
WSN coverage problem and standard CS
The WSN coverage problem
In the cooperative efforts of multiple sensors within a WSN, it is crucial to cover the monitoring area as extensively as possible to ensure efficient completion of tasks regarding to object perception, information acquisition, and data transmission, etc. However, practical scenarios often involve obstacles that lead to varying degrees of attenuation in wireless signals. Due to the time-varying nature of wireless signals, the perception areas of nodes within the WSN tend to be irregular. Generally, it is assumed that the monitoring area can be represented as a two-dimensional plane with the following idealized conditions to simplify the problem and maximize WSN coverage.
Assumption 1: All nodes are homogeneous and have the same perception and communication ranges.
Assumption 2: Perception and communication ranges of all nodes are circular in shape.
Assumption 3: All nodes could sense and determine the positions of other nodes within their communication radius in real-time.
Based on the above assumptions, the WSN coverage model is as follows:
The calculation of the ratio of a sensor’s coverage area to the entire coverage area represents a significant challenge, given the potential for overlap between the respective coverage areas of each sensor. In response to the aforementioned considerations, this paper proposes the use of point monitoring for the calculation of the coverage area. Consider a monitoring region in the shape of a rectangle with length L and width W, with an area of L × W. Randomly deploy n sensor nodes within the monitoring region, and let the set formed by these n nodes be denoted as  . All nodes adopt a Boolean sensing model, where the sensing radius of each node is R.
. All nodes adopt a Boolean sensing model, where the sensing radius of each node is R.
To estimate network coverage, the monitoring area is divided into N grids of equal size. Each grid’s center point serves as a monitoring node, and the collection of these nodes is denoted as 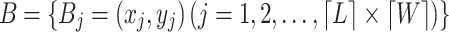 .
.
The Euclidean distance between the sensor node and the monitoring point is:
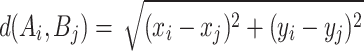 |
1 |
Given the sensing radius R of a node, if the location of the monitoring point Bj is within the circle formed by the sensor node Ai with itself as the center and a radius of R, it indicates that the monitoring point is sensed by the sensor node. The probability of the monitoring point Bj being sensed by sensor node Ai is defined by Eq. (2).
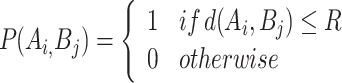 |
2 |
Each monitoring point Bj is sensed by multiple sensor nodes Ai. The definition of joint sensing probability is given by Eq. (3).
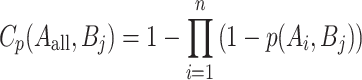 |
3 |
Among them, Aall represents all the sensor nodes within the region, covering the area as the sum of the joint perception probabilities of all monitoring points. The Coverage Rate Cr is defined as the ratio of the coverage area to the region area in Eq. (4).
 |
4 |
In to cover as much area as possible, the rectangular area is considered to have its origin at a vertex. The WSN coverage problem can be abstracted as an optimization problem, as shown in Eq. (5).
 |
5 |
The relationship between model elements is shown in the Fig. 1.
Fig. 1.

WSN coverage optimization model.
In Fig. 1, the monitoring area is divided into several symmetric grids of the same size, and the centre point of each grid is recorded as a monitoring point. If the Euclidean distance between a monitoring point and a node is less than the sensing radius R, the monitoring point is said to be sensed and is recorded as the monitored point. The coverage of the WSN can be derived by calculating the ratio of monitored points to total monitoring points. The more the monitoring area is divided into grids, the closer the calculated coverage is to the real value.
Standard CS
CS inspired by the nest parasitism of cuckoos and the Levy flight pattern of insects such as fruit flies, maps the quality of parasitised nests to the fitness of solutions in its population space, governed by three idealised rules related to the nest parasitism of cuckoos26.
Rule 1: Each bird produces only one egg at a time, and one nest is randomly chosen from all the nests for incubation.
Rule 2: In a randomly selected group of nests, the best nest location is preserved for the next generation.
Rule 3: The number of nests is fixed, and the probability of the host bird discovering a foreign egg is Pa ∈ [0,1]. If the host bird discovers a foreign egg, it will either abandon the egg or build another nest.
Due to these assumptions, the standard CS usually includes five main steps below.
Step 1: Initialisation parameters (including population size, search domain, dimension, and a maximum number of iterations), randomly initialise the position of the bird’s nest, and define the objective function.
- Step 2: Generate N nests in D-dimensional space by Eq. (6), evaluate the randomly generated nest positions, and retain information about the best nest.
where, X represents a collection of randomly generated bird nests;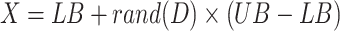
6 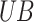 and
and 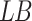 represent the upper and lower bounds of the search space;
represent the upper and lower bounds of the search space; 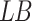 represent D-dimensional random numbers, the values in each dimension fall between 0 and 1.
represent D-dimensional random numbers, the values in each dimension fall between 0 and 1. - Step 3: The Levy flight updates the position of the bird’s nest. Assuming the position of the ith bird’s nest is
 , 1 ≤ i ≤ N, the t + 1 generation of the bird’s nest
, 1 ≤ i ≤ N, the t + 1 generation of the bird’s nest 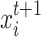 is obtained from the tth generation nest
is obtained from the tth generation nest 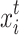 using Eq. (7).
using Eq. (7).
where,
7 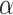 is the control parameter for step size, ⨁ represents point-to-point multiplication, and
is the control parameter for step size, ⨁ represents point-to-point multiplication, and 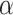 represents that the random search path follows a Levy distribution:
represents that the random search path follows a Levy distribution: , where
, where  is the random step length obtained from Levy flights. Due to the complexity of integrating the Levy distribution, Eq. (8) is commonly used to simulate Levy flight.
is the random step length obtained from Levy flights. Due to the complexity of integrating the Levy distribution, Eq. (8) is commonly used to simulate Levy flight.
where, both μ and v are random variables that follow a normal distribution: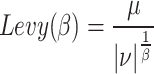
8 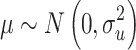 ,
, . Typically,
. Typically,  = 1, β = 1.5, and σu is calculated by Eq. (9).
= 1, β = 1.5, and σu is calculated by Eq. (9).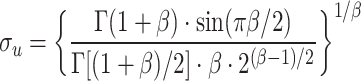
9 - Step 4: After discarding a portion of the solutions with a certain probability (discovery probability Pa), the CS regenerates the same number of new solutions using Eq. (10), evaluates the updated information of the nests, and retains the current optimal nest information.
where, r represents the scaling factor that follows a uniform distribution (0,1), and
10 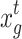 and
and 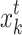 are two randomly selected bird nests in the tth generation population.
are two randomly selected bird nests in the tth generation population. Step 5: Output the current global optimal position xbest, check whether f(xbest) fulfills the termination condition. If yes, the output xbest will be used as the globally optimal solution, otherwise, move to Step 3.
Theoretical analysis of STANDARD CS by Markov chain
In this chapter, based on the proof of convergence of the standard CS in the literature27, refer to its Markov model establishment28 of the cuckoo search algorithm from the standard CS algorithm, through the analysis of the iteration process of the standard CS algorithm, with the aim of reducing the average number of iterations, to make clear that the subsequent CS algorithm improvement strategy, and to provide theoretical support for the improvement of the CS algorithm.
Markov modeling of the standard CS
Definition 1
(Nest Position State and Nest Position State Space) The nest position constitutes the state of the nest position, denoted as x, where x ∈ A, and A represents the feasible solution space. The collection of all possible states of the nest position constitutes the state space of the nest position, denoted as X = {x|x ∈ A}.
Definition 2
(Collective State of Nest Positions and Collective State Space of Nest Positions) The collective state of all nest positions in a group of nest positions is referred to as the collective state of nest positions, denoted as q = (x1, x2, … ,
xN), where xi represents the state of the position of the ith nest. The set composed of all possible states of the group of nest positions constitutes the collective state space of nest positions, denoted as 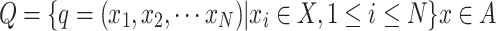 .
.
Definition 3
(State Transition of Nest Positions) For 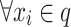 ,
,  , during the iteration of the standard CS, the state of the nest position transitions from xi to xj, denoted as xi → xj.
, during the iteration of the standard CS, the state of the nest position transitions from xi to xj, denoted as xi → xj.
Theorem 1
During one iteration of the standard CS, there is an intermediate transfer state
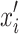 between the transfer of state xi (bird’s nest position) from transfer to xj. The transfer probability of the position state from xi to xj is
between the transfer of state xi (bird’s nest position) from transfer to xj. The transfer probability of the position state from xi to xj is 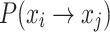 , expressed as
, expressed as  .
.
Proof
According to Eq. (7), the probability of transferring the state of the bird’s nest position from 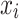 to
to  is determined.
is determined.
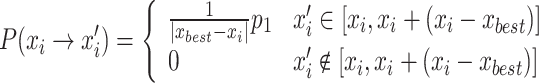 |
11 |
In Eq. (11),  denotes the optimal nest location in the current population; since
denotes the optimal nest location in the current population; since  and
and  are multi-dimensional data, the plus and minus signs indicate vector addition and subtraction, and the absolute value represents the volume of the hypercube in the super-space. P1 represents that, under the standard CS survival-of-the-fittest update mechanism, the transition occurs only when the state xi’ is better than the state xi, as shown in Eq. (12).
are multi-dimensional data, the plus and minus signs indicate vector addition and subtraction, and the absolute value represents the volume of the hypercube in the super-space. P1 represents that, under the standard CS survival-of-the-fittest update mechanism, the transition occurs only when the state xi’ is better than the state xi, as shown in Eq. (12).
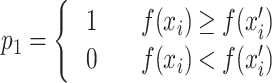 |
12 |
Starting from the Step 4 of the standard CS , it can be seen that the standard CS compares a random number r ∈ [0,1] with Pa = 0.25. If r < Pa, the nest location is randomly altered; otherwise, it remains unchanged. The probability of the nest’s state transitioning from xi’ to xj is given by Eq. (13).
 |
13 |
In Eq. (13), P2 represents the update mechanism of the standard CS’s survival of the fittest, where a transition is made only when the state xi’ is superior to the state xi, as shown in Eq. (14):
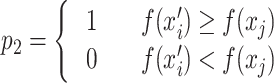 |
14 |
To summarize, the standard CS involves two transfers, 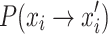 and
and 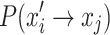 , in order to transfer the bird’s nest location state from xi to xj.
, in order to transfer the bird’s nest location state from xi to xj.  represents the probability of the location transfer via Eq. (6) in the standard CS, while
represents the probability of the location transfer via Eq. (6) in the standard CS, while 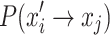 represents the probability of the location transfer resulting from being discovered by the host. Therefore, the state transfer probability of a bird’s nest location state transferring from xi to xj is
represents the probability of the location transfer resulting from being discovered by the host. Therefore, the state transfer probability of a bird’s nest location state transferring from xi to xj is 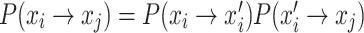 .
.
Thus, the theorem can be proven.
Definition 4
(Swarm State Transition of Nest Locations) In the iterative process of the CS algorithm, for  and
and 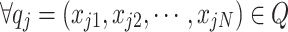 , the swarm state of the nest location transitions from qi to qj, denoted as T(qi) = qj.
, the swarm state of the nest location transitions from qi to qj, denoted as T(qi) = qj.
Theorem 2
In the CS algorithm, the transition probability of the swarm state of the nest location from qi to qj is given by Eq. (15).
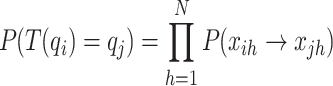 |
15 |
Proof
It must be demonstrated that the swarm state of nest locations includes all states of individual nest locations. When the swarm state of nest locations transitions from qi to qj, it signifies that all positional states of the swarm state will transition simultaneously, meaning that 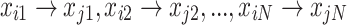 all hold true. Therefore, the probability of the swarm state transition of nest locations is:
all hold true. Therefore, the probability of the swarm state transition of nest locations is:
 |
16 |
Thus, the theorem is proven.
Theorem 3
The sequence of swarm states of nest locations in the standard CS, 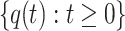 is a finite homogeneous Markov chain.
is a finite homogeneous Markov chain.
Proof
For every optimization algorithm, their search spaces are finite. Since each nest location state xi is finite, the state space X of nest locations in the standard CS is also finite. The swarm state q, which is composed of the states of N nest locations q = (x1, x2, … , xN), where N is a finite positive integer, is therefore also finite.
From Theorem 2, the transition probability  in the sequence of swarm states
in the sequence of swarm states 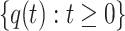 for
for 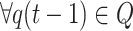 and
and 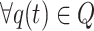 , is determined by the transition probabilities of all cuckoo nest locations
, is determined by the transition probabilities of all cuckoo nest locations 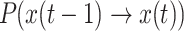 . According to Theorem 1, the cuckoo state transition probability
. According to Theorem 1, the cuckoo state transition probability  is only related to the state x at time t-1 and the extremum of the optimization problem. Therefore,
is only related to the state x at time t-1 and the extremum of the optimization problem. Therefore,  is also only related to the state at time t-1 and is independent of the time t-1. This means that in the CS algorithm, the sequence of swarm states
is also only related to the state at time t-1 and is independent of the time t-1. This means that in the CS algorithm, the sequence of swarm states  exhibits both Markovian and homogeneous properties. Given that the state space is a countable set, it constitutes a finite homogeneous Markov chain.
exhibits both Markovian and homogeneous properties. Given that the state space is a countable set, it constitutes a finite homogeneous Markov chain.
Theorem 4
The sequence of swarm states of nest locations in the standard CS,
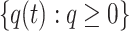 can be regarded as an absorbing Markov chain.
can be regarded as an absorbing Markov chain.
Proof
According to Definition 1, let xopt be the globally optimal nest location. From Theorem 3, we know that the sequence of swarm states 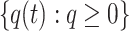 has Markovian properties. Consequently, based on the survival of the fittest population update mechanism of the CS algorithm, when a nest is at the globally optimal position, the Eq. (17) could be obtained.
has Markovian properties. Consequently, based on the survival of the fittest population update mechanism of the CS algorithm, when a nest is at the globally optimal position, the Eq. (17) could be obtained.
 |
17 |
According to the definition of an absorbing Markov chain, if the stochastic process q(t) satisfies Markovian properties and 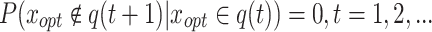 . Then the stochastic process is called an absorbing Markov chain, with xopt being the absorbing state.
. Then the stochastic process is called an absorbing Markov chain, with xopt being the absorbing state.
Thus, the theorem is proven.
Based on Theorem 4, it could construct a finite homogeneous Markov chain with 1 absorbing state and 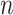 states in total for a non-specific nest within the population
states in total for a non-specific nest within the population 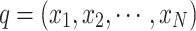 , as shown in Fig. 2.
, as shown in Fig. 2.
Fig. 2.

Absorbing Markov chain.
The n states as the set of all possible positions for the nest x, which constitutes the state space X for the nest location x. Among these states, state n is the absorbing state, and these states are arranged from left to right according to their corresponding fitness values, with the better fitness values on the left.
Referring to Fig. 2, when the nest is at state i, there are three possible transition types with their transition probabilities defined as follows:
Definition 5
(Transition to the left)  .
. 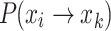 represents the probability of an individual transitioning from state i to state k, where k is a state with a worse fitness than i (i.e., k < i). Due to the survival of the fittest update mechanism,
represents the probability of an individual transitioning from state i to state k, where k is a state with a worse fitness than i (i.e., k < i). Due to the survival of the fittest update mechanism, 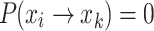 .
.
Definition 6
(State remains unchanged)  .
. 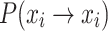 represents the probability that an individual’s state remains unchanged after one iteration in state i.
represents the probability that an individual’s state remains unchanged after one iteration in state i.
Definition 7
(Transition to the right to state j (j > i))  .
. 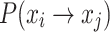 represents the probability of an individual transitioning to multiple states to the right in one iteration, moving from state i.
represents the probability of an individual transitioning to multiple states to the right in one iteration, moving from state i.
Theorem 5
The state of the nest can only remain unchanged or transition rightward, meaning the sum of these two state transition probabilities equals 1.
Proof
According to definition 5–7, the state of an individual can only be transferred in one of three cases:
 |
18 |
From Eq. (18), the total probability of an individual transitioning to the right during one iteration is:
 |
19 |
In Eq. (19), 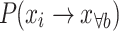 represents the probability of an individual transitioning to any state to the right,
represents the probability of an individual transitioning to any state to the right,  .
.
Since 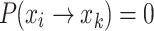 , it follows that:
, it follows that:
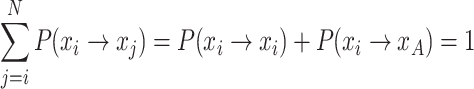 |
20 |
This means that under the standard CS update mechanism, an individual has only two possibilities: to remain at the current nest location (with a probability of  ) or to transition to a better nest location to the right (with a probability of
) or to transition to a better nest location to the right (with a probability of 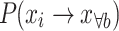 ), and the sum of these two probabilities is 1.
), and the sum of these two probabilities is 1.
Thus, the theorem is proven.
Analysis of the theoretical average number of iterations
Based on the Markov model developed for the standard CS, it can be observed that since the total number of states n is finite and constant, as the individual state increasingly approaches the absorbing state, the number of available solutions for successful updates will gradually decrease. This means that the probability of choosing a worse solution than the current one will gradually increase. However, due to the CS algorithm’s own mechanism of survival of the fittest, when a worse solution is chosen, the algorithm will discard the new solution and retain the old one. Consequently, the probability of maintaining the same state,  , will continue to increase. At the same time, according to Eq. (20), the total probability of moving rightward to a better nest position,
, will continue to increase. At the same time, according to Eq. (20), the total probability of moving rightward to a better nest position,  , will also decrease.
, will also decrease.
To specifically analyze the impact of the change in the individual’s self-transition probability 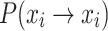 on the algorithm during the CS iteration process, we now establish the relationship between the self-transition probability
on the algorithm during the CS iteration process, we now establish the relationship between the self-transition probability  and the average number of iterations required for the algorithm to converge to the absorbing state xopt.
and the average number of iterations required for the algorithm to converge to the absorbing state xopt.
Definition 8
(Mean Iterations to Absorption) The theoretical average number of iterations required for the nest state to reach an absorbing state is denoted as 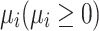 .
.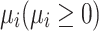 represents the iteration count required for the position state transition
represents the iteration count required for the position state transition 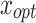 to reach absorbing state
to reach absorbing state 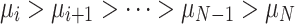 .
.
Theorem 6
Decreasing the nest’s self-transition probability
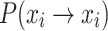 reduces the theoretical mean iterations
reduces the theoretical mean iterations
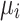 required to reach an absorbing state.
required to reach an absorbing state.
Proof
According to definition 8,  can be expressed as:
can be expressed as:
 |
21 |
Since  , it follows that:
, it follows that:
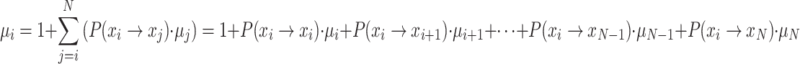 |
22 |
From Eq. (20), it can be seen that when 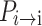 decreases,
decreases, 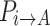 increases, and the sum of the two remains unchanged. Furthermore, since
increases, and the sum of the two remains unchanged. Furthermore, since 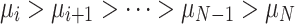 , in conjunction with Eq. (22), it can be deduced that when the individual’s self-transition probability
, in conjunction with Eq. (22), it can be deduced that when the individual’s self-transition probability  decreases, the theoretical number of iterations required to reach the absorbing state,
decreases, the theoretical number of iterations required to reach the absorbing state, 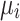 , also decreases.
, also decreases.
Thus, the theorem is proven.
Inspiring amendment directions for the standard CS
According to Theorem 6, as the CS algorithm progresses through later iterations, individuals increasingly approach the absorbing state. The self-transition probability  increases, the probability of transitioning rightward
increases, the probability of transitioning rightward 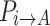 decreases, and the theoretically required iteration count
decreases, and the theoretically required iteration count 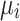 for converging to the absorbing state increases. Mapping this to the specific optimization process, it manifests as follows: as individuals move through the search space, the feasible solution space gradually shrinks with increasing iterations, making it harder to find better solutions. This leads to slower convergence or even stagnation.
for converging to the absorbing state increases. Mapping this to the specific optimization process, it manifests as follows: as individuals move through the search space, the feasible solution space gradually shrinks with increasing iterations, making it harder to find better solutions. This leads to slower convergence or even stagnation.
The reasons for this phenomenon are as follows:
Limitations of the update mechanism: The standard CS algorithm employs a survival-of-the-fittest population update mechanism, ensuring that new solutions are guaranteed to be equal to or better than the old solutions during iterations. As the iteration progresses, whenever an individual’s solution is updated, the number of potentially better solutions available to that individual decreases, thereby increasing its self-transition probability.
Insufficient search strategy: The standard CS algorithm uses a difference-search strategy involving two random solutions during its local search phase. This approach makes individual adjustments overly random. Furthermore, Since ‘r’ in Eq. (10) randomly varies between values (0,1), it restricts the direction of adjustment. Consequently, it becomes uncertain whether the quality of the new individuals produced will be superior to that of the preceding generation, thereby increasing the probability of the state remaining unchanged.
Fixed step size and discovery probability: Using fixed step size and discovery probability in the standard CS algorithm makes it difficult for the algorithm to adapt to different phases of the iteration. It cannot flexibly adjust based on the current population distribution, which also increases the possibility of the state remaining unchanged.
Proposed ICS-MS
Due to the theoretical analysis provided above, the objective of the proposed CS variant is to decrease the self-transition probability  , thereby refining the overly random search method within the local search phase. This adjustment aims to balance the global and local search capabilities of the algorithm, allowing it to migrate efficiently from one local optimal region to a superior one.
, thereby refining the overly random search method within the local search phase. This adjustment aims to balance the global and local search capabilities of the algorithm, allowing it to migrate efficiently from one local optimal region to a superior one.
Considering the high-dimensional and multi-modal nature of the WSN)coverage problem, the proposed ICS-MS algorithm employs a variety of strategies to fulfill the goal, which includes enhancements to the local search mechanism and the introduction of a phased incremental dimension update strategy.
Phased approach to dimension-by-dimension updating
When addressing multi-dimensional optimization problems through the updating of old solutions in a full-dimensional manner in the standard CS, it is common to encounter interference between dimensions. This interference can result in the oversight of the impact that changes in the values of individual dimensions have on the fitness of the solution. Therefore, replacing the full-dimensional update evaluation strategy with a dimension-by-dimension update evaluation strategy could effectively mitigate the phenomenon of inter-dimension coupling in high-dimensional optimization problems.
However, the fitness of individuals is re-evaluated each time they adopt a dimension-by-dimension update evaluation method. Although this strategy can significantly increase the likelihood of individual updates and reduce the self-transition probability  , it may primarily focus on single-dimensional searches, which is less favorable for exploring unknown areas and can lead to a substantial computational load. Therefore, a modification that combines full-dimensional and single-dimensional searches is utilized, and it is applied only during the local search phase to address the aforementioned issues. The dimension-by-dimension updating approach used in the IMC-HS encompasses two stages. In the initial 2/3 of the iterations, the full-dimensional update strategy is employed to enhance search efficiency, explore unknown areas, and pinpoint the approximate location of the optimal solution. Subsequently, the dimension-by-dimension update strategy is adopted to guide the current solution, utilizing evolved single-dimensional information for the local search, thereby yielding higher-quality solutions in the remaining stage.
, it may primarily focus on single-dimensional searches, which is less favorable for exploring unknown areas and can lead to a substantial computational load. Therefore, a modification that combines full-dimensional and single-dimensional searches is utilized, and it is applied only during the local search phase to address the aforementioned issues. The dimension-by-dimension updating approach used in the IMC-HS encompasses two stages. In the initial 2/3 of the iterations, the full-dimensional update strategy is employed to enhance search efficiency, explore unknown areas, and pinpoint the approximate location of the optimal solution. Subsequently, the dimension-by-dimension update strategy is adopted to guide the current solution, utilizing evolved single-dimensional information for the local search, thereby yielding higher-quality solutions in the remaining stage.
Adaptive discovery probability
The discovery probability Pa determines the proportion of individuals engaging in local search and maintains the balance between global and local search capabilities in the standard CS,. It further suggests that the balance between global and local search capabilities could be significantly improved if Pa had adaptive adjusting ability. Based on this finding, the IMS-CS incorporates Pa’s adaptive adjusting ability according to the following standard.
At the beginning of the iteration, there is a large discrepancy in fitness values among individuals, and higher variance results in a smaller Pa, which enhances the global search capability of the algorithm. As the iteration progresses, fitness values among individuals converge, and the decrease in variance leads to an increase in Pa, thereby increasing the probability of individuals initiating local search—a process that is beneficial for improving the convergence accuracy of the algorithm.
The updating strategy of Pa is illustrated as follows:
 |
23 |
where, Pat represents the discovery probability at the tth generation; Pa,max and Pa,min represent the minimum and maximum values of Pa, respectively; Dt is a diversity function determined by
 |
24 |
In Eq. (24), E is the variance of the fitness values of all individuals in the population, determined by Eq. (25):
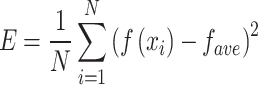 |
25 |
In Eq. (25), E and  are the fitness value of the current i-th individual and the average fitness value of all individuals, respectively.
are the fitness value of the current i-th individual and the average fitness value of all individuals, respectively.
Multi-strategy preference wandering
Individuals are updated based on the difference between two random solutions in the local search phase of the standard CS. Although this optimization method can maintain population diversity, it encounters challenges in refining the search near the solution. This is due to a large search range and limited search direction, which increases the probability of individual self-transfer.
The ICS-MS mitigates this issue by setting the scaling factor, r, as a uniformly distributed random number within the interval (− 1, 1), to realize a bidirectional search mechanism. Moreover, it considers global optimal information to guide other individuals in the population toward the optimal solution direction. This enhances the aggregation level within the population and reduces the probability of individual self-transfer. Meanwhile, a multi-strategy random preference walk strategy is employed to further prevent the rapid loss of population diversity resulting from the introduction of global optimal information (Eq. 26)
 |
26 |
where, 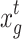 and
and  represent two randomly selected nests from the t-th generation population;
represent two randomly selected nests from the t-th generation population; 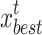 is the global optimal nest of the t-th generation; r, r1, and r2 are scaling factors that follow a uniform distribution within (− 1, 1); Pc is a random number that follows a uniform distribution within (0,1); Pb is the probability of initiating the search strategy that considers global information.
is the global optimal nest of the t-th generation; r, r1, and r2 are scaling factors that follow a uniform distribution within (− 1, 1); Pc is a random number that follows a uniform distribution within (0,1); Pb is the probability of initiating the search strategy that considers global information.
Elite opposition-based learning
Opposition-Based Learning (OBL) refers to the strategy of comparing the distance of a random point and its counterpart at the opposite position to the optimal solution, recursively halving the search interval to locate the optimal solution more quickly29. The ICS-MS selectively identifies elite individuals based on fitness and performs reverse searches on these elites to reduce the substantial computational load and enhance the algorithm’s efficiency while expanding the search space for high-quality solutions and exploring unknown regions. Additionally, during the local search phase, it provides higher-quality optimal solutions for the multi-strategy preference walk described aforementioned, guiding other individuals in the population to explore unknown areas, increasing the chances of discovering better solutions, and reducing the probability of individual self-transfer.
Let the set 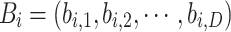 represent the elite individuals in the current cuckoo population, and their corresponding reverse solutions
represent the elite individuals in the current cuckoo population, and their corresponding reverse solutions 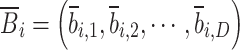 are calculated by
are calculated by
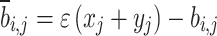 |
27 |
where, 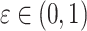 is the generalization coefficient; bi,j ∈ [xj, yj] where [xj, yj] denotes the dynamic boundary of the search space for the j-th dimension, with xj and yj being the lower and upper bounds, respectively. In the dimension-by-dimension updating strategy, the lower and upper bounds for each dimension can be calculated as xj =
min(Bi,j), yj =
max(Bi,j).
is the generalization coefficient; bi,j ∈ [xj, yj] where [xj, yj] denotes the dynamic boundary of the search space for the j-th dimension, with xj and yj being the lower and upper bounds, respectively. In the dimension-by-dimension updating strategy, the lower and upper bounds for each dimension can be calculated as xj =
min(Bi,j), yj =
max(Bi,j).
ICS-MS implementation steps
According to the aforementioned improvement strategies, ICS-MS comprises the following steps:
Step 1: Initialize parameters.
Step 2: Initialize the population and evaluate individual fitness. The initial population is randomly generated y Eq. (6).
Step 3: Update dimension-by-dimension in phases. Based on the current iteration number, if the current iteration number is less than 2/3 of the total iterations, perform full-dimensional search to update the nest; otherwise, update the nest using one-dimensional search.
Step 4: Levy flight. Update all nest positions through Eqs. (7) to (9) and greedily retain nests with better fitness.
Step 5: Elite reverse search. Select the top 1/10 individuals based on fitness, then divide the upper and lower bounds of each dimension for the elite population. Generate reversed solutions using Eq. (27) to update the current nest position information, and greedily retain nests with better fitness.
Step 6: Adaptive preference random walk. Eliminate some nests using the dynamic discovery probability Pa from Eqs. (23) to (25), and update the positions of the eliminated nests using the improved preference random walk formula (26), greedily retaining nests with better fitness.
Step 7: Termination condition. If the current iteration of the algorithm meets the termination condition, output the optimal solution; Otherwise, move to Step 3.
Analysis of the effectiveness of improvement strategies
In this section, five classical unimodal test functions and five classical multimodal test functions are selected as benchmark functions to evaluate the effectiveness of ICS-MS. Different types of optimisation problems are covered in the selection of test functions, including single peak, multi-peak, fixed dimension and non-linear. In addition, the impact of four enhancement strategies on their performance is analysed. Additionally, it analyzes the impact of four improvement strategies on its performance. A numerical comparison of the optimization results between ICS-MS and standard CS, CS-I, CS-II, CS-III, and CS-IV is conducted. CS-I is the standard CS with the staged dimensional update strategy only; CS-II is the standard CS with the adaptive discovery probability only; CS-III is the standard CS with the multi-strategy preference walk mechanism only; and CS-IV is the standard CS with the elite reverse learning strategy only. Furthermore, each algorithm is independently optimized for each test function 30 times to ensure fairness in testing and to reduce the influence of randomness during the optimization process of the algorithms. The maximum number of iterations is set to 1000 times for each run. The ten class benchmark functions selected are presented in Table 1.
Table 1.
Ten benchmark functions in the experiment.
| No. | Function | Formula | Dim | Interval | f (x*) |
|---|---|---|---|---|---|
| F1 | Sphere | 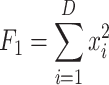 |
30, 50 | [− 5.12, 5.12] | 0 |
| F2 | Step |  |
30, 50 | [− 100, 100] | 0 |
| F3 | Schwefel 2.22 |  |
30, 50 | [− 100, 100] | 0 |
| F4 | Rosenbrock |  |
30, 50 | [− 30, 30] | 0 |
| F5 | Ackley | 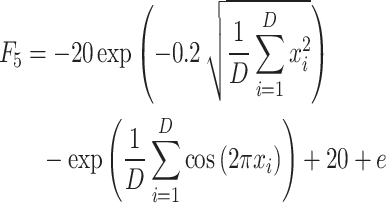 |
30, 50 | [− 32, 32] | 0 |
| F6 | Griewank |  |
30, 50 | [− 600, 600] | 0 |
| F7 | Rastrigin | 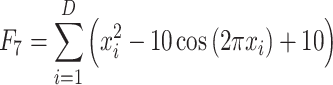 |
30, 50 | [− 600, 600] | 0 |
| F8 | Bohachevsky | 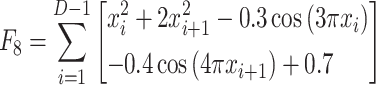 |
30, 50 | [− 100, 100] | 0 |
| F9 | Beale | 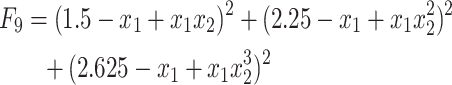 |
2 | [− 4.5, 4.5] | 0 |
| F10 | SchafferN.2 |  |
2 | [− 100, 100] | 0 |
In Table 1, F1–F4 are single peak functions, F4–F8 are multi peak functions, F9 is a fixed dimensional single peak function and F10 is a fixed dimensional multi peak function. For functions F1–F8, the optimisation test is performed in 30 and 50 dimensional space; for test functions F9 to F10, optimization benchmarks were conducted in the 2D space primarily to rigorously evaluate whether the dimension-wise update strategy could introduce adverse impacts when applied to low-dimensional functions.
Test platform and parameter settings
The experiment was conducted using Python 3.7, with PyCharm as the development tool. The development environment was equipped with an Intel(R) Core(TM) i7-10875H CPU @ 2.30 GHz, 16 GB of memory, and operating system Windows 11. The parameter settings are as shown in Table 2.
Table 2.
Initialization parameters of all algorithms.
| Algorithm | Parameters setting |
|---|---|
| CS | α0 = 0.01, Pa = 0.25 |
| CS-I | α0 = 0.01, Pa = 0.25 |
| CS-II | α0 = 0.01, Pa max = 0.4, Pa min = 0.05 |
| CS-III | α0 = 0.01, Pa = 0.25, Pb = 0.5 |
| CS-IV | α0 = 0.01, Pa = 0.25 |
| ICS-MS | α0 = 0.01, Pa max = 0.4, Pa min = 0.05, Pb = 0.5 |
Optimization test results
Figures 3 and 4 respectively represent the average convergence curves of the six algorithms for the functions F1–F8, after independently optimizing 1000 times in 30-dimensional and 50-dimensional spaces. Figure 5 shows the average convergence curves of the six algorithms for the functions F9–F10, after independently optimizing 1000 times in a 2-dimensional space.
Fig. 3.
Optimization of test functions in 30 dimension.
Fig. 4.
Optimization of test functions in 50 dimension.
Fig. 5.
Optimization of test functions in 2 dimension.
Tables 3 and 4 present the optimization results of the functions F1–F8 utilizing the six algorithms for, respectively, after 1000 iterations in both 30-dimensional and 50-dimensional spaces. Similarly, Table 5 records the optimization results for the functions F9–F10, following 1000 iterations in a 2-dimensional space.
Table 3.
Test function optimization results under 30 dimension.
| No. | Function | Indicator | CS | CS-I | CS-II | CS-III | CS-IV | ICS-MS |
|---|---|---|---|---|---|---|---|---|
| F1 | Sphere | Best | 1.88E − 02 | 1.93E − 16 | 9.47E − 03 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 1.73E − 01 | 3.27E − 15 | 1.13E − 01 | 9.09E − 02 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 5.83E − 02 | 3.20E − 15 | 3.87E − 02 | 4.05E − 02 | 0.00E + 00 | 0.00E + 00 | ||
| F2 | Step | Best | 7.78E − 02 | 7.70E − 29 | 1.13E − 03 | 2.97E − 06 | 1.17E − 06 | 0.00E + 00 |
| Mean | 7.09E − 01 | 5.84E − 15 | 4.62E − 03 | 1.40E − 05 | 3.13E − 06 | 6.86E − 33 | ||
| Std | 2.01E − 01 | 8.41E − 15 | 3.08E − 03 | 9.50E − 06 | 2.05E − 06 | 1.44E − 32 | ||
| F3 | Schwefel 2.22 | Best | 4.47E − 01 | 7.13E − 17 | 2.42E − 02 | 1.17E − 06 | 0.00E + 00 | 0.00E + 00 |
| Mean | 1.65E + 00 | 2.06E − 08 | 4.54E − 062 | 2.49E − 03 | 9.77E − 257 | 0.00E + 00 | ||
| Std | 3.46E − 01 | 2.28E − 08 | 1.69E − 02 | 1.59E − 03 | 0.00E + 00 | 0.00E + 00 | ||
| F4 | Rosenbrock | Best | 1.22E − 20 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 5.39E − 13 | 2.40E − 21 | 9.28E − 15 | 2.37E − 17 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 1.01E − 12 | 6.46E − 21 | 3.65E − 14 | 5.43E − 17 | 0.00E + 00 | 0.00E + 00 | ||
| F5 | Ackley | Best | 3.24E − 01 | 6.29E − 08 | 2.40E − 04 | 0.00E + 00 | 7.11E − 15 | 0.00E + 00 |
| Mean | 9.79E − 01 | 2.74E − 04 | 2.79E − 02 | 1.30E − 18 | 1.63E − 14 | 0.00E + 00 | ||
| Std | 3.09E − 01 | 3.07E − 04 | 1.15E − 02 | 6.48E − 18 | 5.22E − 15 | 0.00E + 00 | ||
| F6 | Griewank | Best | 4.87E − 04 | 0.00E + 00 | 1.94E − 05 | 2.48E − 12 | 0.00E + 00 | 0.00E + 00 |
| Mean | 5.91E − 03 | 1.50E − 16 | 1.98E − 04 | 8.54E − 07 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 2.41E − 03 | 2.36E − 16 | 2.78E − 04 | 1.95E − 06 | 0.00E + 00 | 0.00E + 00 | ||
| F7 | Rastrigin | Best | 1.11E + 01 | 6.06E − 11 | 1.32E + 01 | 1.30E + 01 | 0.00E + 00 | 0.00E + 00 |
| Mean | 1.47E + 01 | 1.58E + 00 | 1.68E + 01 | 1.72E + 01 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 1.89E + 00 | 3.34E + 00 | 3.89E + 00 | 6.36E + 00 | 0.00E + 00 | 0.00E + 00 | ||
| F8 | Bohachevsky | Best | 4.88E − 15 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 6.15E − 09 | 0.00E + 00 | 4.81E − 11 | 1.47E − 13 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 1.11E − 08 | 0.00E + 00 | 7.53E − 11 | 4.65E − 13 | 0.00E + 00 | 0.00E + 00 |
Table 4.
Test function optimization results under 50 dimension.
| No | Function | Indicator | CS | CS-I | CS-II | CS-III | CS-IV | ICS-MS |
|---|---|---|---|---|---|---|---|---|
| F1 | Sphere | Best | 7.14E − 02 | 6.31E − 12 | 1.09E − 01 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 5.11E − 01 | 4.28E − 11 | 5.03E − 01 | 1.47E − 02 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 1.49E − 01 | 6.63E − 11 | 1.51E − 01 | 1.36E − 02 | 0.00E + 00 | 0.00E + 00 | ||
| F2 | Step | Best | 5.73E − 01 | 4.12E − 21 | 6.41E − 02 | 2.53E − 05 | 9.82E − 06 | 0.00E + 00 |
| Mean | 2.45E + 00 | 4.10E − 11 | 3.02E + 00 | 1.42E − 02 | 1.39E − 03 | 1.82E − 30 | ||
| Std | 6.03E − 01 | 3.44E − 11 | 1.38E + 00 | 1.16E − 02 | 1.40E − 03 | 2.85E − 30 | ||
| F3 | Schwefel 2.22 | Best | 1.64E + 00 | 5.85E − 13 | 1.48E + 00 | 1.18E − 01 | 0.00E + 00 | 0.00E + 00 |
| Mean | 3.70E + 00 | 5.07E − 06 | 4.37E + 00 | 2.98E − 01 | 2.88E − 251 | 0.00E + 00 | ||
| Std | 6.12E − 01 | 3.91E − 06 | 7.05E − 01 | 1.14E − 01 | 0.00E + 00 | 0.00E + 00 | ||
| F4 | Rosenbrock | Best | 2.96E − 26 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 2.23E − 12 | 3.58E − 21 | 1.86E − 14 | 1.30E − 18 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 5.28E − 12 | 1.35E − 20 | 3.29E − 14 | 6.48E − 18 | 0.00E + 00 | 0.00E + 00 | ||
| F5 | Ackley | Best | 3.24E − 01 | 1.86E − 10 | 6.42E − 01 | 1.07E − 03 | 2.84E − 14 | 0.00E + 00 |
| Mean | 9.79E − 01 | 5.38E − 06 | 1.05E + 00 | 6.23E − 02 | 3.40E − 14 | 0.00E + 00 | ||
| Std | 3.09E − 01 | 3.97E − 06 | 2.13E − 01 | 2.76E − 02 | 5.98E − 15 | 0.00E + 00 | ||
| F6 | Griewank | Best | 5.90E − 04 | 0.00E + 00 | 1.84E − 03 | 8.82E − 05 | 0.00E + 00 | 0.00E + 00 |
| Mean | 1.40E − 02 | 1.81E − 12 | 1.11E − 02 | 4.16E − 04 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 4.73E − 03 | 2.53E − 12 | 3.49E − 03 | 3.47E − 04 | 0.00E + 00 | 0.00E + 00 | ||
| F7 | Rastrigin | Best | 2.52E + 01 | 1.28E + 00 | 1.32E + 01 | 3.00E + 01 | 0.00E + 00 | 0.00E + 00 |
| Mean | 3.40E + 01 | 4.57E + 00 | 1.68E + 01 | 3.66E + 01 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 4.95E + 00 | 6.01E + 00 | 3.89E + 00 | 5.28E + 00 | 0.00E + 00 | 0.00E + 00 | ||
| F8 | Bohachevsky | Best | 7.92E − 13 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 3.50E − 09 | 0.00E + 00 | 4.81E − 11 | 5.60E − 14 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 6.76E − 09 | 0.00E + 00 | 7.53E − 11 | 1.56E − 13 | 0.00E + 00 | 0.00E + 00 |
Table 5.
Test function optimization results under 2 dimension.
| No | Function | Indicator | CS | CS-I | CS-II | CS-III | CS-IV | ICS-MS |
|---|---|---|---|---|---|---|---|---|
| F9 | Beale | Best | 1.02E − 18 | 1.90E − 14 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 7.38E − 14 | 6.66E − 10 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 3.94E − 13 | 3.54E − 09 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | ||
| F10 | SchafferN.2 | Best | 5.18E − 11 | 7.20E − 11 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| Mean | 3.23E − 08 | 6.73E − 07 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | ||
| Std | 7.99E − 08 | 2.79E − 06 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
In these tables, “min” denotes the best value achieved by each algorithm across 30 independent optimizations, “mean” represents the average of the results from these optimizations, and “std” indicates the standard deviation of the results.
By analyzing Figs. 3, 4, 5 and Tables 3, 4, 5, the following conclusions can be drawn:
For function, F1, a continuous single-peak spherical function with a single global minimum value, both ICS-MS and CS-IV consistently converge to the optimal value, regardless of whether the search space is 30 or 50 dimensions. ICS-MS demonstrates faster convergence than CS-IV. Additionally, CS-I, CS-II, and CS-III enhance convergence accuracy compared to CS, with CS-I’s convergence speed significantly improving in the first one-third of the iterations due to its staged dimensional update strategy.
Finding the correct direction towards the global optimal solution is challenging for function F2, characterized by a step-wise value distribution and non-differentiability at step boundaries. None of the algorithms can stably converge to the global optimum. Among them, ICS-MS exhibits a superior iteration trend and optimization accuracy compared to the other five algorithms. Despite its staged dimensional update strategy, CS-I shows a trend similar to ICS-MS but still lags in optimization speed and accuracy.
For function F3, the complexity of the solution space increases with the number of dimensions. Consequently, whether the search space is 30 or 50 dimensions, CS-I, CS-II, and CS-III do not significantly outperform the standard CS. CS-IV’s reverse learning, based on the maximum and minimum values of each dimension in the current population, allows it to approach the global optimum, but its iteration trend and convergence accuracy are still not as robust as the combined strategies of ICS-MS.
For function F4, the iteration trends of CS-I, CS-II, and CS-III are similar to CS but with higher optimization accuracy, suggesting that the strategies of staged dimensional update, adaptive discovery probability, and multi-strategy preference random walk are effective. Influenced by CS-IV’s elite reverse learning, ICS-MS and CS-IV show a similar iteration trend, yet ICS-MS achieves higher optimization accuracy.
For function, F5, with multiple extrema, CS-III, guided by the current best value, exhibits a superior iteration trend compared to CS. CS-I shows a similar trend to CS in the first two-thirds of the iterations but significantly improves its optimization speed and accuracy in the last one-third of the iterations. With its four-strategy collaboration, ICS-MS successfully converges to the theoretical optimal value, while the other independent strategies and the standard CS cannot converge to the global optimum.
For functions F6 and F7, which are similar with large search spaces and numerous local minima, the CS-II and CS-III optimization strategies do not significantly improve over the standard CS. CS-IV’s elite reverse learning strategy converges stably to the global optimum in large search spaces but still has a lower convergence speed than the four strategies combined in ICS-MS.
For function F8, ICS-MS exhibits the highest convergence speed and accuracy compared to the other algorithms in 30 and 50 dimensions. From the convergence curves of CS-I, CS-II, CS-III, and CS-IV, it can be observed that the four improvement strategies are all independently effective for function F8.
For functions F9 and F10, CS-I’s staged dimensional update strategy is ineffective in low-dimensional spaces, and its convergence speed is even lower than CS. CS-II, CS-III, CS-IV, and ICS-MS can all converge to the theoretical optimal value, with ICS-MS having a superior iteration trend.
Overall, in the optimization experiments conducted on the ten test functions, the staged dimensional update strategy of CS-I exhibited good performance when confronted with high-dimensional test functions. However, this strategy compromised low-dimensional test functions’ convergence accuracy and speed. The adaptive discovery probability and multi-strategy preference walk mechanism of CS-II and CS-III primarily governed the global and local search balance. Nevertheless, their enhancements over the standard CS algorithm were relatively limited, as evidenced by the optimization results for high-dimensional functions. The elite reverse learning strategy of CS-IV, which integrates the concept of dimensional update, yielded superior results to the standard CS, CS-I, CS-II, and CS-III across most test functions. Furthermore, ICS-MS, which amalgamates the four strategies mentioned above, substantially outperformed all other compared algorithms regarding optimization accuracy and convergence speed. The standard deviation of the optimization experiments on the ten test functions also suggests that ICS-MS exhibited the highest stability.
Wilcoxon Signed-Rank Test
A one-way Wilcoxon signed-rank test with a confidence level 0.05 was employed to evaluate the impact of the four improvement strategies on ICS-MS. The final values obtained from the independent runs of the standard CS, CS-I, CS-II, CS-III, CS-IV, and ICS-MS on the functions F1–F10, each run for 30 iterations, were recorded. This was conducted to ascertain the superiority or inferiority of ICS-MS’s optimization results compared to the benchmark algorithms.
Moreover, two hypotheses are utilized to summarize the findings. On the one hand, the test’s null hypothesis (H0) posits that there is no significant difference between ICS-MS and the comparison algorithms, or the optimization results of ICS-MS are worse than those of the comparison algorithms. On the other hand, the alternative hypothesis (H1) asserts a significant difference between ICS-MS and the comparison algorithms, and the optimization results of ICS-MS are better than those of the comparison algorithms.
A test result greater than 0.05 signifies the failure to reject the null hypothesis; a result less than 0.05 indicates the acceptance of the alternative hypothesis and the rejection of the null hypothesis. The results of the signed-rank test are presented in Tables 6, 7 and 8. Tables 6 and 7 capture the signed-rank test results for the standard CS, CS-I, CS-II, CS-III, and CS-IV on functions F1-F8 at both 30 dimensions and 50 dimensions, respectively. Table 8 presents the signed-rank test results for the standard CS, CS-I, CS-II, CS-III, and CS-IV on functions F9–F10 at 2 dimensions. Significant results, those equal to or greater than 0.05, are bolded for emphasis.
Table 6.
Results of rank sum test for 30-dimensional test function.
| No | Function | CS | CS-I | CS-II | CS-III | CS-IV |
|---|---|---|---|---|---|---|
| F1 | Sphere | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 6.33E − 11 | 1.44E − 11 |
| F2 | Step | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 |
| F3 | Schwefel 2.22 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.06E − 09 |
| F4 | Rosenbrock | 1.44E − 11 | 6.33E − 11 | 4.06E − 09 | 6.33E − 11 | 5.00E − 01 |
| F5 | Ackley | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 |
| F6 | Griewank | 1.44E − 11 | 4.40E − 04 | 1.44E − 11 | 1.44E − 11 | 5.00E − 01 |
| F7 | Rastrigin | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 5.00E − 01 |
| F8 | Bohachevsky | 1.44E − 11 | 5.00E − 01 | 2.66E − 10 | 1.06E − 09 | 5.00E − 01 |
Significant values are in bold.
Table 7.
Results of rank sum test for 50-dimensional test function.
| No | Function | CS | CS-I | CS-II | CS-III | CS-IV |
|---|---|---|---|---|---|---|
| F1 | Sphere | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 6.33E − 11 | 1.44E − 11 |
| F2 | Step | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 |
| F3 | Schwefel 2.22 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 4.06E − 09 |
| F4 | Rosenbrock | 1.44E − 11 | 6.33E − 11 | 4.06E − 09 | 1.06E − 09 | 5.00E − 01 |
| F5 | Ackley | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 |
| F6 | Griewank | 1.44E − 11 | 2.66E − 10 | 1.44E − 11 | 1.44E − 11 | 5.00E − 01 |
| F7 | Rastrigin | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 1.44E − 11 | 5.00E − 01 |
| F8 | Bohachevsky | 1.44E − 11 | 5.00E − 01 | 6.33E − 11 | 4.06E − 09 | 5.00E − 01 |
Significant values are in bold.
Table 8.
Results of rank sum test for 2-dimensional test function.
| No | Function | CS | CS-I | CS-II | CS-III | CS-IV |
|---|---|---|---|---|---|---|
| F9 | Beale | 1.44E − 11 | 1.44E − 11 | 5.00E − 01 | 5.00E − 01 | 5.00E − 01 |
| F10 | SchafferN.2 | 1.44E − 11 | 1.44E − 11 | 5.00E − 01 | 5.00E − 01 | 5.00E − 01 |
According to Figs. 3, 4, 5 and Tables 3, 4, 5, 6, 7 and 8, some conclusions can be drawn below.
On both 30-dimensional and 50-dimensional test functions, the indicators for ICS-MS show significant differences when compared to the standard CS, with ICS-MS exhibiting a superior iteration trend. This indicates a marked performance disparity between ICS-MS and the standard CS. CS-I, which employs a staged dimensional update strategy, exhibits no significant difference from ICS-MS on function F8, while CS-IV, which incorporates the elite reverse learning strategy, shows no significant difference from ICS-MS on functions F4, F6, F7, and F8. This suggests the effectiveness of the staged dimensional update strategy and the elite reverse learning strategy, with the latter proving more potent. However, CS-II, which employs an adaptive discovery probability strategy, and CS-III, which utilizes a multi-strategy preference walk, display significant differences from ICS-MS across the F1-F8 test functions, making it premature to assess the efficacy of their improvements. Nevertheless, their performance is not significantly different from ICS-MS on the 2-dimensional test functions in Table 8, indicating that their enhancement strategies are effective, albeit not as effective as ICS-MS.
Each of the four improvement strategies demonstrates independent efficacy. CS-I, representing the staged dimensional update strategy, underperforms on low-dimensional test functions. CS-II and CS-III, representing the adaptive discovery probability and multi-strategy preference walk strategies, respectively, still present significant differences with ICS-MS on high-dimensional functions but are not significantly different on low-dimensional test functions. CS-IV, representing the elite reverse learning strategy, exhibits no significant difference from ICS-MS on multiple test functions and contributes most significantly to improving ICS-MS’s performance. The analysis of these four strategies also indirectly confirms the robustness and adaptability of ICS-MS, which integrates dimensional update, adaptive discovery probability, multi-strategy preference random walk, and elite reverse learning. This validates the effectiveness of the proposed ICS-MS.
WSN coverage optimization experiment design
To validate the effectiveness of the proposed ICS-MS in optimizing the coverage problem of WSNs, the coverage rate Cr (Eq. 4) is used as the fitness value. The standard CS and three classic algorithms, which include Genetic Algorithm (GA)30, Ant Colony Optimization (ACO)31, and Particle Swarm Optimization (PSO)32, are used to optimize the coverage problem of WSNs separately for a lateral comparison. At the same time, the ECS algorithm33, MACS algorithm34, WCSDE algorithm35, CSDE algorithm36, ICS-ABC-OBL algorithm37, ICS algorithm38, and ICS-MS algorithm are added to optimize the coverage problem of WSNs in the same environment separately for a vertical comparison to verify the superiority of ICS-MS algorithm over other similar algorithms and CS variants.
Swarm intelligence-based WSN coverage optimization strategy
Based on the coverage model mentioned above, each sensor node in the WSN coverage optimization problem is represented in the form of a two-dimensional vector. For the deployment of n nodes, it is represented by a 2n-dimensional individual, meaning that each individual in the algorithm represents a deployment scheme for the nodes. The WSN coverage optimization strategy is demonstrated by Fig. 6.
Fig. 6.
Coverage optimization strategy for WSN.
In this figure, the distribution and positions of n nodes are obtained through initialization; second, the best individual is obtained through optimizing the improved CS algorithm; and finally, the best individual is output. The best individual represents the optimal deployment scheme obtained after the optimization by swarm intelligence algorithms.
Testbed and parameter settings
The experiments were conducted using Python 3.7, with the development tool being PyCharm, running on an Intel(R) Core(TM) i7-10875H CPU @ 2.30 GHz with 16 GB of memory, and the operating system being Windows 11. The specific parameter settings are shown in Table 9.
Table 9.
Parameter setting of wireless sensor network coverage experiment.
| Parameters | Value |
|---|---|
| Monitoring area | 100 m × 100 m |
| Number of nodes | 20/30 |
| Node perception radius r | 12 m |
| Number of iterations T | 200/1000 |
| Number of Pixel Dots | 100 × 100 |
When the number of nodes is set to 20, and the node sensing radius r is set to 12, it represents a scenario of limited resources. In this case, the sensor network theoretically cannot achieve full coverage of the target area, and it should focus on observing its redundancy. Combined with the coverage rate, this can help judge the algorithm’s performance. When the number of nodes is set to 30, and the node sensing radius r is again set to 12, it represents abundant resources. Here, the sensor network can theoretically cover the entire target area, and one should focus on observing its coverage gaps. Combined with the coverage rate, this can help judge the performance of the algorithm optimization.
Finally, since the ideal plane of wireless sensor nodes needs to be represented by two-dimensional vectors, this paper uses 40-dimensional and 60-dimensional individuals, respectively, for the number of nodes set to 20 and 30 to represent a set of sensor deployment schemes. Therefore, setting the number of nodes to 20 and 30 can also be a good test of the algorithm’s high-dimensional optimization ability.
The number of individuals for all algorithms is set to 30 to ensure the algorithms’ normal operation and the experiment’s fairness. The relevant parameters for the remaining comparison algorithms are set, as shown in Table 10.
Table 10.
Initialization parameters of all algorithms.
| CS | α0 = 0.01, Pa = 0.25 |
| GA | Pc = 1, Pm = 0.01 |
| ACO | ρ = 1, Q = 0.1 |
| PSO | C1 = 2, C2 = 2, ω = 0.8, Vmax = 1, Vmin = -1 |
| ECS | α0 = 0.01, Pa = 0.25 |
| MACS | α0 = 0.01, Pa = 0.25 |
| WCSDE | α0 = 0.01, ω0 = 1.5, t0 = 100, F = 0.6, CR = 0.8, Pa = 0.25 |
| CSDE | α0 = 0.01, F = 0.5, CR = 0.8, Pa = 0.25 |
| ICS-ABC-OBL | α0 min = 0.01, α0 max = 0.5, Pa = 0.25 |
| ICS | α0 = 0.01, Pa = 0.25, Pb = 0.35 |
| ICS-MS | α0 = 0.01, Pa max = 0.4, Pa min = 0.4, Pb = 0.5 |
Optimization coverage results
Each algorithm was run independently for 30 iterations to ensure the fairness of the experiment. Table 11 displays the optimization results for the WSN coverage problem using various algorithms—CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, ICS, and ICS-MS—under different scenarios with node counts of 20 and 30, and iteration counts of 200 and 1000. The optimal coverage values and the mean and standard deviation of the coverage achieved are presented.
Table 11.
Comparison of coverage results.
| Algorithms | Iterations | Coverage Performance | Number of nodes 20 | Number of nodes 30 |
|---|---|---|---|---|
| CS | 200 |
Best Mean Std |
70.93% 67.12% 0.0149372 |
82.62% 80.18% 0.0170272 |
| 1000 |
Best Mean Std |
72.12% 70.41% 0.013902 |
84.80% 81.73% 0.0259844 |
|
| GA | 200 |
Best Mean Std |
75.16% 72.35% 0.0157003 |
88.60% 85.89% 0.0171310 |
| 1000 |
Best Mean Std |
77.14% 74.18% 0.0203110 |
91.63% 87.86% 0.0256515 |
|
| ACO | 200 |
Best Mean Std |
64.61% 62.07% 0.0157003 |
79.31% 76.89% 0.0138658 |
| 1000 |
Best Mean Std |
65.53% 63.42% 0.01310163 |
82.12% 78.47% 0.0181968 |
|
| PSO | 200 |
Best Mean Std |
68.26% 66.05% 0.0184519 |
80.93% 78.98% 0.0115261 |
| 1000 |
Best Mean Std |
69.31% 66.59% 0.0189453 |
81.94% 78.65% 0.017797 |
|
| ECS | 200 |
Best Mean Std |
80.44% 79.52% 0.0053903 |
94.12% 93.09% 0.0050917 |
| 1000 |
Best Mean Std |
83.50% 82.71% 0.0037609 |
96.91% 96.62% 0.0019163 |
|
| MACS | 200 |
Best Mean Std |
74.69% 73.69% 0.0098432 |
89.86% 89.01% 0.0060058 |
| 1000 |
Best Mean Std |
82.59% 81.88% 0.0034299 |
96.31% 95.80% 0.0033658 |
|
| WCSDE | 200 |
Best Mean Std |
73.98% 72.11% 0.0076542 |
87.22% 85.22% 0.0089778 |
| 1000 |
Best Mean Std |
75.42% 74.51% 0.0060133 |
89.69% 87.93% 0.0103000 |
|
| CSDE | 200 |
Best Mean Std |
83.44% 81.92% 0.0102460 |
97.30% 96.35% 0.00565842 |
| 1000 |
Best Mean Std |
84.77% 83.29% 0.0083995 |
99.00% 98.23% 0.0038888 |
|
| ICS-ABC-OBL | 200 |
Best Mean Std |
73.08% 71.76% 0.0108151 |
87.94% 86.01% 0.0124267 |
| 1000 |
Best Mean Std |
74.23% 72.31% 0.0502111 |
88.02% 86.14% 0.0104085 |
|
| ICS | 200 |
Best Mean Std |
71.82% 66.89% 0.02595667 |
84.93% 81.05% 0.0161400 |
| 1000 |
Best Mean Std |
72.44% 67.80% 0.0239626 |
83.88% 81.16% 0.0194161 |
|
| ICS-MS | 200 |
Best Mean Std |
84.83% 84.24% 0.0036245 |
99.33% 99.10% 0.0012426 |
| 1000 |
Best Mean Std |
85.63% 85.07% 0.0046045 |
99.61% 99.46% 0.0010821 |
From Table 11, it can be observed that, for 20 nodes, after 200 iterations, the average coverage rate of the ICS-MS algorithm is respectively 17.12%, 11.89%, 22.17%, 18.19%, 4.72%, 10.55%, 12.13%, 2.32%, 12.48%, and 17.35% higher than those of the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms. After 1000 iterations, the average coverage rate of the ICS-MS algorithm is respectively 14.66%, 10.89%, 21.65%, 18.48%, 2.36%, 3.19%, 10.56%, 1.78%, 12.76%, and 17.99% higher than those of the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms.
For 30 nodes, after 200 iterations, the average coverage rate of the ICS-MS algorithm is respectively 18.92%, 13.21%, 22.21%, 20.12%, 6.01%, 10.09%, 13.88%, 2.75%, 13.09%, and 18.05% higher than those of the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms. After 1000 iterations, the average coverage rate of the ICS-MS algorithm is respectively 17.73%, 11.60%, 20.99%, 20.81%, 2.84%, 3.66%, 11.53%, 1.23%, 13.32%, and 18.30% higher than those of the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms.
Additionally, the MACS algorithm shows a significant improvement in the average coverage rate after 1000 iterations compared to its average coverage rate after 200 iterations, with an increase of 8.19% for 20 nodes and 6.79% for 30 nodes. This indicates that the inertia weight added to the preference random walk phase of the MACS algorithm effectively enhances the probability of escaping local optima. However, the WCSDE algorithm’s average coverage rate after 1000 iterations remains relatively unchanged from its average coverage rate after 200 iterations, with a mere increase of 2.4% for 20 nodes and 2.71% for 30 nodes. This is due to the weight of inertia added during the Levy flight phase of the WCSDE. In the CS algorithm, the global search capability mainly relies on Levy flight, and the addition of the inertia weight forces the algorithm to search toward the zero point as the number of iterations increases. However, the optimal solution for WSN coverage optimization problems is far from the zero point and needs to be symmetrical according to the definition domain. Therefore, adding the inertia weight weakens the global search capability of the WCSDE algorithm, leading to premature stagnation.
Lastly, compared to the CS algorithm, GA, ECS, MACS, CSDE, and ICS-MS algorithms all achieve a better average coverage rate under various conditions of 20/30 sensors and 200/1000 iterations. Meanwhile, ACO, PSO, and ICS show poorer optimization effects.
In summary, the ICS-MS algorithm, under various conditions involving 20/30 nodes and 200/1000 iterations, demonstrates a higher average coverage rate and lower standard deviation compared to the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms. This indicates that the ICS-MS algorithm exhibits higher convergence precision, better stability, and reduced randomness in the optimization results when solving coverage problems in WSNs relative to the other algorithms considered.
Sensor node distribution maps
Figures 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 provide the node distribution maps for the optimization of WSN coverage problems using the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, ICS, and ICS-MS algorithms under various conditions of 20/30 nodes and 200/1000 iterations.
Fig. 7.
CS optimized node distribution.
Fig. 8.
GA optimized node distribution.
Fig. 9.
ACO optimized node distribution.
Fig. 10.
PSO optimized node distribution.
Fig. 11.
ECS optimized node distribution.
Fig. 12.
MACS optimized node distribution.
Fig. 13.
WCSDE optimized node distribution.
Fig. 14.
CSDE optimized node distribution.
Fig. 15.
ICS-ABC-OBL optimized node distribution.
Fig. 16.
ICS optimized node distribution.
Fig. 17.
ICS-MS optimized node distribution.
Figures 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 and 17 show that when the number of nodes is set to 20, the WSN cannot cover the target area theoretically. At this point, the focus is on the degree of coverage redundancy and the uniformity of node distribution. After 200 iterations, the node distributions optimized by the CS, PSO, and ACO exhibit many redundancies and overlaps. The ICS optimization results in nodes being extensively distributed at the boundaries with many coverage holes. The GA, MACS, WCSDE, and ICS-ABC-OBL result in more uniform node distributions with lower coverage redundancy, but the coverage rates still need to be improved. The ECS, CSDE, and ICS-MS produce more uniform node distributions with higher coverage rates. When the number of iterations is increased to 1000, the ICS-MS optimization of the WSN is significantly more uniform than the 200 iterations, with a significant reduction in coverage redundancy. The ICS and ICS-ABC-OBL show no significant improvement in coverage rate, and the ECS, CSDE, and ICS-MS, having approached the theoretical optimal value, also show no significant improvement. The remaining algorithms all experience a certain degree of coverage redundancy and hole reduction.
When the number of nodes is set to 30, the WSN can theoretically completely cover the target area. At this point, the focus is on the size of the coverage holes and the coverage rate. After 200 iterations, the ECS, CSDE, and ICS-MS algorithms result in more uniform node distributions, with ICS-MS already unable to observe obvious coverage holes and a better node distribution. The CS, PSO, and ICS algorithms have obvious coverage holes and poor coverage rates. When the number of iterations is increased to 1000, the WCSDE and ICS-ABC-OBL algorithms show no significant improvement, while the ECS, MACS, CSDE, and ICS-MS algorithms all result in node distributions without obvious coverage holes and higher coverage rates.
In summary, the ICS-MS algorithm, under various conditions of 20/30 sensors and 200/1000 iterations, results in node distributions that are more uniform compared to the CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms, with less coverage redundancy and holes, and a broader coverage range of the wireless network.
Coverage convergence curves
Figures 17 and 18 illustrate the coverage convergence curves for the optimization of wireless sensor network coverage under various conditions, using algorithms such as CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, ICS, and ICS-MS. These curves represent different scenarios with 20/30 nodes and iteration counts of 200/1000.
Fig. 18.
Convergence curve of coverage rate for each algorithm iteration 200 times.
Figure 18 illustrates that when the iteration count is set to 200, the primary focus is on the convergence speed of the algorithms. With 20 nodes, algorithms such as GA, ACO, PSO, WCSDE, ICS-ABC-OBL, and ICS stagnate within 75 iterations, failing to optimize further. However, the CS, ECS, MACS, CSDE, and ICS-MS algorithms are all practical in optimization within 200 iterations. Among these, the CS algorithm exhibits poor convergence accuracy, while the ICS-MS algorithm achieves the highest convergence precision. With 30 nodes, only the ECS, MACS, CSDE, and ICS-MS algorithms are effective in optimization, with the ICS-MS algorithm again achieving the highest convergence precision.
Figure 19 reveals that when the iteration count is set to 1000, the algorithm focuses on its ability to escape local optima and its sustained optimization capabilities. With 20 nodes, the GA, PSO, WCSDE, ICS-ABC-OBL, and ICS algorithms stagnate within 200 iterations with poor optimization results. However, the CS, ACO, ECS, MACS, CSDE, and ICS-MS algorithms remain effective in optimization within 1000 iterations, but the CS and ACO algorithms do not yield good optimization results. Again, the ICS-MS algorithm achieves the highest convergence precision.
Fig. 19.
Convergence curve of coverage rate for each algorithm iteration 1000 times.
Regarding algorithmic mechanisms, the ECS algorithm’s strategy of combining the ABC operator to balance its global and local search capabilities has yielded promising results, reducing the probability of the ECS algorithm falling into local optima. The MACS algorithm introduces an inertia weight during its preferred random walk phase, weakening its position and reducing the likelihood of falling into local optima, allowing the algorithm to sustain optimization. However, its convergence speed still requires improvement. The CSDE algorithm improves the algorithm’s ability to escape local optima by dividing the population into subgroups, each using the strategies of CS and DE and facilitating information exchange between the subgroups. It is evident from Figs. 18 and 19 that the ICS-MS algorithm shows a significant improvement in convergence speed during the last one-third of the iterations. This is attributed to the staggered dimensional update of ICS-MS, which ensures early convergence speed while enhancing local search capabilities in the later stages, achieving the best precision among the compared algorithms.
In summary, the ICS-MS algorithm exhibits more substantial competitiveness in terms of search accuracy, convergence speed, and stability compared to CS, GA, ACO, PSO, ECS, MACS, WCSDE, CSDE, ICS-ABC-OBL, and ICS algorithms for optimizing WSN coverage under different scenarios with 20/30 nodes and 200/1000 iteration counts.
Summary
This paper proposes an ICS-MS to achieve maximized coverage in WSNs. This method is developed by analyzing the CS algorithm’s convergence properties and the relationship between iteration count and individual self-migration probability. The objective is to reduce the individual self-migration probability and balance the algorithm’s local and global search capabilities. The ICS-MS incorporates the following enhancements:
A staged dimensional update strategy is introduced to reduce computational overhead and improve search efficiency. This strategy also mitigates inter-dimensional interference in high-dimensional optimization problems and lowers the individual self-migration probability.
An adaptive discovery probability method based on population variance enhances the algorithm’s flexibility and balances global and local search capabilities.
Elite individuals are selected and divided based on their fitness, and a reverse operation is applied to them to expand the search space and improve optimization accuracy.
A multi-strategy random preference walk is utilized, considering the global optimal value with a certain probability to guide other individuals in the population toward the current best solution. This approach enhances inter-individual information exchange.
After analyzing the effectiveness of the ICS-MS improvement strategies, they are applied to the WSN coverage optimization problem. Simulation experiments indicate that the ICS-MS outperforms the standard CS, classical group intelligence algorithms (GA, ACO, PSO), and four CS variants (MACS, DA-DOCS, WCSDE, ICS-ABC-OBL) in improving WSN coverage. It leads to a more uniform distribution of nodes and can reduce the number of nodes required and deployment costs while targeting the same coverage rate.
The improved CS algorithm proposed in this paper has demonstrated promising results in tackling the WSN coverage optimization problem. However, several potential areas for further optimization remain:
Optimization of Algorithm Time Complexity: While the current improved CS algorithm shows enhanced convergence speed and solution accuracy, the runtime performance has not been comprehensively considered, nor has its time complexity been formally calculated. Future work should focus on refining the algorithm’s strategies, streamlining them by eliminating redundant computational steps. This aims to effectively reduce the time complexity while maintaining convergence speed and accuracy, making the algorithm more suitable for applications demanding high real-time performance.
Establishment of a Multi-Objective Optimization Model: The current modeling of the WSN coverage optimization problem in this work optimizes solely for coverage rate, overlooking other critical factors such as energy consumption, communication quality, and node lifespan. This approach risks achieving high coverage at the expense of significantly reduced network longevity due to excessive energy drain. Consequently, future research should incorporate these diverse factors by extending the objective function into a multi-objective optimization model. Techniques like introducing weighting coefficients or analyzing the Pareto front can be employed to balance conflicts between optimization goals, leading to more comprehensive and rational deployment strategies.
Three-Dimensional (3D) WSN Coverage Optimization: The present study primarily addresses WSN coverage optimization in two-dimensional (2D) planes. However, in practical deployment scenarios, factors such as topographical variations and building obstructions critically impact wireless signal propagation and node sensing ranges. Consequently, simulation results derived solely from 2D models may not fully translate to effective real-world deployment. Future investigations should delve deeper into addressing the WSN coverage optimization problem specifically within three-dimensional spaces.
Acknowledgements
This research is supported by the National Natural Science Foundation of China under grant numbers 62066016 and 52268049, the Natural Science Foundation of Hunan Province of China under grant number 2024JJ7395 and 2024JJ7412, the International and Regional Cooperation Project of Hunan Province of China under grant number 2025SKX-KJ-04, the Scientific Research Project of Education Department of Hunan Province of China under Grant number 22B0549 and 24B0496.
Author contributions
S.Y.Y., contributed to conceptualization, methodology, formal analysis, and writing – original draft; C.F. C., provided supervision, project administration, and funding acquisition; K.Q.Z., developed software, performed validation, and contributed to writing – review & editing; and Y.O., handled data curation, investigation, and visualization.All authors reviewed the manuscript.
Data availability
The datasets used and analysed during the current study available from the corresponding author on reasonable request.
Declarations
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Chang-Feng Chen, Email: ccf_cise@jsu.edu.cn.
Kai-Qing Zhou, Email: kqzhou@jsu.edu.cn.
References
- 1.Javaid, S. et al. Self-powered sensors: Applications, challenges, and solutions. IEEE Sens. J.23(18), 20483–20509 (2023). [Google Scholar]
- 2.Yin, B. et al. An improved beetle antennae search algorithm and its application in coverage of wireless sensor networks. Sci. Rep.14, 29372 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Liu, X. et al. An approach for tool wear prediction using customized Densenet and GRU integrated model based on multi-sensor feature fusion. J. Intell. Manuf.34(2), 885–902 (2023). [Google Scholar]
- 4.Yin, Y. et al. A 5G-enabled and self-powered sensor data management scheme for the smart medical platform system. IEEE Sens. J.23(18), 20904–20915 (2022). [Google Scholar]
- 5.Maheshwari, A. & Chand, N. A survey on wireless sensor networks coverage problems[C]. in Proceedings of 2nd International Conference on Communication, Computing and Networking: ICCCN 2018, NITTTR Chandigarh, India, 153–164. (Springer Singapore, 2019).
- 6.Ou, Y. et al. An improved Grey Wolf Optimizer with multi-strategies coverage in wireless sensor networks. Symmetry16(3), 19 (2024). [Google Scholar]
- 7.Jin, L., Wei, L. & Li, S. Gradient-based differential neural-solution to time-dependent nonlinear optimization. IEEE Trans. Autom. Control68(1), 620–627 (2023). [Google Scholar]
- 8.Liu, M. et al. Activated gradients for deep neural networks. IEEE Trans. Neural Netw. Learn. Syst.34(4), 2156–2168 (2023). [DOI] [PubMed] [Google Scholar]
- 9.Huang, H., Jin, L. & Zeng, Z. A momentum recurrent neural network for sparse motion planning of redundant manipulators with majorization-minimization. IEEE Trans. Ind. Electron.10.1109/TIE.2025.3566731 (2025). [Google Scholar]
- 10.Jin, Z. et al. A novel coverage optimization scheme based on enhanced marine predator algorithm for urban sensing systems. IEEE Sens. J.24(5), 5486–5499 (2024). [Google Scholar]
- 11.Zhu, C. et al. A survey on coverage and connectivity issues in wireless sensor networks[J]. J. Netw. Comput. Appl.35(2), 619–632 (2012). [Google Scholar]
- 12.Qin, F., Zain, A.M., Zhou, K.Q. Harmony search algorithm and related variants: A systematic review. Swarm Evolut. Comput. 74 (2022).
- 13.Qin, F., Zain, A. M., Zhou, K. Q. & Zhuo, D. B. Hybrid weighted fuzzy production rule extraction utilizing modified harmony search and BPNN [J]. Sci. Rep.15, 11012 (2025). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Liu, J. et al. A new hybrid algorithm for three-stage gene selection based on whale optimization. Sci. Rep.13, 3783 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Singh, A., Sharma, S. & Singh, J. Nature-inspired algorithms for wireless sensor networks: A comprehensive survey[J]. Comput. Sci. Rev.39, 100342 (2021). [Google Scholar]
- 16.Hanh, N. T. et al. An efficient genetic algorithm for maximizing area coverage in wireless sensor networks[J]. Inf. Sci.488, 58–75 (2019). [Google Scholar]
- 17.Li, Y. et al. Coverage enhancement strategy for WSNs based on multiobjective ant lion optimizer[J]. IEEE Sens. J.23(12), 13762–13773 (2023). [Google Scholar]
- 18.Miao, Z. et al. Grey wolf optimizer with an enhanced hierarchy and its application to the wireless sensor network coverage optimization problem[J]. Appl. Soft Comput.96, 106602 (2020). [Google Scholar]
- 19.Cao, L. et al. A novel coverage optimization strategy for heterogeneous wireless sensor networks based on connectivity and reliability[J]. IEEE Access9, 18424–18442 (2021). [Google Scholar]
- 20.Yang, X. S. & Deb, S. Engineering optimisation by cuckoo search[J]. Int. J. Math. Model. Numer. Optimisation1(4), 330–343 (2010). [Google Scholar]
- 21.Braik, M. et al. Enhanced cuckoo search algorithm for industrial winding process modeling[J]. J. Intell. Manuf.34(4), 1911–1940 (2023). [Google Scholar]
- 22.Cuong-Le, T. et al. A novel version of Cuckoo search algorithm for solving optimization problems[J]. Expert Syst. Appl.186, 115669 (2021). [Google Scholar]
- 23.Ye, S. et al. A modified harmony search algorithm and its applications in weighted fuzzy production rule extraction[J]. Front. Inform. Technol. Electron. Eng.24(11), 1574–1590 (2023). [Google Scholar]
- 24.Wolpert, D. H. & Macready, W. G. No free lunch theorems for optimization. IEEE Trans. Evolut. Comput.1(1), 67–82 (1997). [Google Scholar]
- 25.Yang X S, Deb S. Engineering optimisation by cuckoo search[J]. arXiv preprint arXiv:1005.2908, 2010.
- 26.Yang, X.S., Deb, S. Cuckoo search via Levy flights[C]//2009 World congress on nature & biologically inspired computing (NaBIC). IEEE, 2009: 210–214.
- 27.Wang, F., He, X.S., Wang, Y., et al. (2012) Markov model and convergence analysis based on Cuckoo Search Algorithm[J]. Comput. Eng. 38(11), 180–182,185 (in Chinese).
- 28.Watterson, G. A. Markov chains with absorbing states: A genetic example[J]. Ann. Math. Stat.32(3), 716–729 (1961). [Google Scholar]
- 29.Tizhoosh, H.R. Opposition-based learning: a new scheme for machine intelligence[C] //International conference on computational intelligence for modelling, control and automation and international conference on intelligent agents, web technologies and internet commerce (CIMCA-IAWTIC’06). IEEE, 2005. 1, 695–701.
- 30.Holland, J. H. Genetic algorithms and the optimal allocation of trials. SIAM J. Comput.2(2), 88–105 (1973). [Google Scholar]
- 31.Dorigo, M., Maniezzo, V., Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics). 26(1), 29–41 (1996). [DOI] [PubMed]
- 32.Eberhart, R., Kennedy, J. A new optimizer using particle swarm theory[C]//MHS’95. Proceedings of the sixth international symposium on micro machine and human science. IEEE, 1995. 39–43.
- 33.Kamoona, A. M. & Patra, J. C. A novel enhanced cuckoo search algorithm for contrast enhancement of gray scale images. Appl. Soft Comput.85, 105749 (2019). [Google Scholar]
- 34.Zhang, Z. Z. et al. Cuckoo Algorithm for multi-stage dynamic disturbance and dynamic inertia weight. Comput. Eng. Appl.58(01), 79–88 (2022) ((in Chinese)). [Google Scholar]
- 35.Zhang, C. X. et al. An improved cuckoo search algorithm utilizing nonlinear inertia weight and differential evolution for function optimization problem[J]. IEEE Access9, 161352–161373 (2021). [Google Scholar]
- 36.Zhang, Z., Ding, S. & Jia, W. A hybrid optimization algorithm based on cuckoo search and differential evolution for solving constrained engineering problems[J]. Eng. Appl. Artif. Intell.85, 254–268 (2019). [Google Scholar]
- 37.Ye, S.Q., Wang, F.L., Ou, Y., et al. An improved cuckoo search combing artificial bee colony operator with opposition-based learning[C]//2021 China Automation Congress (CAC). IEEE, 2021. 1199–1204.
- 38.Zheng, H. Q. & Feng, W. J. An improved Cuckoo Search algorithm for constrained optimization problems [J]. Chin. J. Eng. Math.40(01), 135–146 (2023) ((in Chinese)). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and analysed during the current study available from the corresponding author on reasonable request.



















