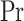Abstract
This article investigates the steady, two-dimensional electro-magneto-hydrodynamic (EMHD) flow of a micropolar dusty fluid across a linearly stretched surface, subjected to electroosmotic forces, buoyancy-driven convection, and both reversible and irreversible chemical reactions. Electrokinetic effects are modeled using the modified Helmholtz-Smoluchowski formulation. At the same time, micropolar fluid theory accounts for microstructural characteristics. The two-phase framework couples momentum, heat, and mass transport with viscous dissipation and entropy generation. The governing partial differential equations are transformed into a system of ordinary differential equations using similarity transformations and subsequently solved through the shooting method and the Runge-Kutta-Fehlberg (RKF45) technique. The model is validated against established results in limiting scenarios. Parametric analysis reveals how the electroosmotic parameter, magnetic and electric fields, and micropolar coupling govern flow behavior, entropy generation, Bejan number, skin friction, and heat transfer. Results reveal that magnetic and micropolar parameters significantly enhance entropy generation and modulate the Bejan number. Elevated electroosmotic and electric parameters promote flow acceleration, boundary-layer thinning, and suppress both microrotation and thermal gradients. This comprehensive model provides new insights into complex multiphase EMHD transport phenomena and holds potential for optimization in applications such as targeted drug delivery, thermal control in EMHD-based energy systems, and electrokinetic microfluidics.
Keywords: Micropolar fluid, Electroosmotic forces, Stretching surface, Reversible esterification process, Dusty fluid, Heat transfer
Subject terms: Engineering, Mathematics and computing
Introduction
Literature survey
Electroosmosis is the process by which fluid moves through a charged surface due to an applied electric field. The interaction between the electric field and the electric double layer (EDL) at the solid-liquid interface generates a net tangential force, causing bulk fluid to flow. This phenomenon is widely used in chemical, environmental, and microfluidic systems, where precise control over fluid motion is critical. The foundational work by Reuss1 laid the groundwork for modern electrokinetics. Recent advancements in electroosmotic microfluidics have enabled applications such as the analysis of ovarian cancer cells2, tracking cell motility in confined environments3, diagnostic platforms, and tissue ablation technologies4. Prakash et al.5 numerically analyzed EMHD ternary hybrid nanofluid flow across a permeable wedge. Latest studies in electroosmosis research are summarized in the literature6–10.
Dusty fluid flow describes the movement of a base fluid containing dispersed solid particles, often referred to as dust particles. The interaction between the fluid and suspended dust results in a two-phase system in which the fluid and particulate phases exhibit distinct properties while naturally influencing each other. Applications span across meteorology (raindrop formation), nuclear reactor cooling, paint spraying, and biomedical systems. Saffman11 first modeled dusty fluid flow using Stokes’ drag law to account for particulate resistance. Ezzat et al.12 studied such flows in porous media, while Sivaraj and Kumar13 investigated magnetized viscoelastic dusty fluid flows with radiation effects. Abbas et al.14 analyzed MHD dusty fluid flow over a permeable surface. Recent works have examined the influence of nanoparticle size15 and microchannel geometries16 in dusty MHD systems under pressure gradients and suction/injection mechanisms.
Esterification is a classic exothermic condensation process in which an alcohol interacts with a carboxylic acid, in the presence of a catalyst, to form esters. Efficient heat and mass transfer are essential for optimizing various industrial processes, including those for paints, medicines, pesticides, cosmetics, perfumery, food processing, and bioplastics. Rathod et al.17 studied esterification using a hydrophilic membrane reactor system. Khan et al.18 reviewed esterification techniques, comparing enzymatic, catalytic, and non-catalytic processes. Raju et al.19,20 explored the role of activation energy, heat generation, and MHD effects in esterification flows involving non-Newtonian fluids. Prabhakar et al.21 analyzed the esterification process by incorporating thermal radiation and bioconvection in a Casson nanofluid flow over a rotating disk.
Electrohydrodynamics (EHD) and magnetohydrodynamics (MHD) play a crucial role in optimizing heat transfer. EHD induces motion in dielectric fluids through electric fields, while MHD enhances heat transfer in conducting fluids via Lorentz forces. Both are effective in thermal regulation across various physical settings. Rana et al.22,23 explored EHD thermal instability in porous media using dielectric and viscoelastic fluids under electric and thermal effects. Gautam et al.24 highlighted EHD-driven convection in non-Newtonian nanofluids. Kumar and Singh analyzed MHD effects25 in second-grade fluid through porous media, and Shahid et al.26 investigated viscoelastic fluid flow through non-Darcy porous media. MHD impacts on hybrid nanofluid flow across stretchable wedges are investigated by Panda et al.27, with an emphasis on fluctuating magnetic fields and heat generation. Akbar et al.28 studied the influence of MHD on heat transfer in non-Newtonian fluid flow over a stretching cylinder. Hafed et al.29 studied MHD blood flow in a stenosed artery using tetra-hybrid nanofluids. In contrast, Nagy et al.30 examined radiation and viscous dissipation in MHD fourth-grade nanofluid flow through a diverging channel.
Micropolar fluid, first introduced by Eringen31, is a class of non-Newtonian fluids that account for particle microrotation and microstructure. The theory incorporates additional variables such as angular velocity and couple stress, allowing for the modeling of rotational effects, shear thinning, and internal spin. Applications include biological systems, lubricants, liquid crystals, polymeric suspensions, and microfluidic devices. Khan et al.32 investigated thermal transport in micropolar fluids with temperature-dependent transport properties. Eldabe et al.33 examined the electroosmotic flow of a non-Newtonian micropolar nanofluid in a porous medium under EMHD effects. Sharif et al.34 carried out entropy analysis of the hydromagnetic non-Newtonian micropolar trihybrid nanofluid flow between parallel disks.
To understand how internal fluid friction generates heat and impacts temperature profiles and energy efficiency during flow, viscous dissipation is examined35–37. Despite extensive research on dusty fluid dynamics, micropolar effects, and electroosmotic transport, the combined influence of these factors under electro-magneto-hydrodynamic and chemically reactive conditions remains unaddressed. Specifically, the interaction between micropolar dust-laden flows and electroosmotic forces in the presence of esterification reactions and buoyancy effects has not been explored. Furthermore, most existing models omit entropy generation analysis in the context of reversible and irreversible reactions. Table 1 outlines these research gaps.
Table 1.
Comparative analysis highlighting research gaps and the novelty of the current study.
| Authors | Micropolar | Dusty fluid | Electroosmotic | EMHD | Esterification | Entropy analysis | Buoyancy | Stretching sheet |
|---|---|---|---|---|---|---|---|---|
| Raju et al.19 | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✓ | ✓ |
| Raju et al.20 | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ | ✓ |
| Sharif et al.34 | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✗ | ✗ |
| Eldabe et al.33 | ✓ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| Hafez et al.7 | ✗ | ✗ | ✓ | ✓ | ✗ | ✗ | ✗ | ✓ |
| Hussain et al.38 | ✗ | ✓ | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ |
| Current study | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Objective and novelty of the study
This study addresses the above limitations by examining EMHD flow of a micropolar dusty fluid over a linearly stretching surface, incorporating buoyancy effects, electroosmotic forces, and esterification processes. The proposed model captures the coupled impacts of particle-phase interactions, viscous dissipation, electrokinetic forces, chemical reactivity, and microrotation. The inclusion of electric field intensity, the Helmholtz-Smoluchowski slip velocity, and two-phase coupling enables the realistic modeling of electrochemical and microfluidic systems. The stretching sheet geometry is relevant for controlling the boundary layer in engineering systems. Given the broad industrial relevance of esterification, efficient modeling of such processes is essential for applications in biofuels, polymers, solvents, and pharmaceuticals. Table 1 highlights that no previous study has integrated all the key factors addressed in the current work, thereby establishing its originality.
Research questions
This study addresses the following research questions:
How does the esterification process influence the thermal transfer characteristics in a micropolar dusty fluid under the combined effects of an electromagnetic field and electrokinetics?
What are the implications of Lorentz-force-induced body forces and viscous dissipation on entropy generation and the behavior of the Bejan number in EMHD micropolar dusty flows?
In what ways do dust particle dynamics affect heat transfer performance and entropy dynamics during esterification under buoyancy-driven convection?
How does the interplay between electroosmotic effects and EMHD forces influence the transport behavior of micropolar dusty fluids over a stretching surface?
How do reversible and irreversible chemical reactions modify the concentration boundary layers and species transport in an electro-magneto-hydrodynamic regime?
To what extent can entropy generation be suppressed through optimal tuning of key parameters in microfluidic systems?
Mathematical modeling of the problem
The present study investigates a steady, two-dimensional, incompressible electro-magneto-hydrodynamic (EMHD) flow of a micropolar fluid containing dispersed dust particles over a linearly elongating sheet, incorporating electroosmotic and buoyancy forces. The effects of viscous dissipation and mass diffusivity on the flow of dusty fluids and heat transfer are considered. The reference frame is defined with the 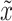 -axis parallel to the sheet and the
-axis parallel to the sheet and the 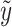 -axis normal to it. The surface stretches with velocity specified as
-axis normal to it. The surface stretches with velocity specified as 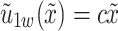 , where
, where 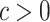 is the stretching rate. Figure 1 shows a schematic flow configuration. This study enhances heat transfer performance in heat exchangers, high-power-density systems, and microelectronic devices. The application of a homogeneous magnetic field
is the stretching rate. Figure 1 shows a schematic flow configuration. This study enhances heat transfer performance in heat exchangers, high-power-density systems, and microelectronic devices. The application of a homogeneous magnetic field 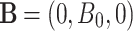 normal to the surface creates an induced electric field
normal to the surface creates an induced electric field 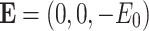 through the fluid. Ohm’s law explains electrodynamic phenomena:
through the fluid. Ohm’s law explains electrodynamic phenomena: 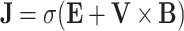 7. The dust particles are uniformly dispersed, spherical, and monodisperse. Hall and Ohmic effects are insignificant due to the weak magnetic field.
7. The dust particles are uniformly dispersed, spherical, and monodisperse. Hall and Ohmic effects are insignificant due to the weak magnetic field.
Figure 1.
Flow configuration.
Governing equations
Based on the assumptions above, the governing equations for the flow are given as follows:
Continuity equations for fluid and dust phases
The following continuity equations describe the mass conservation laws for fluid and dust phases:
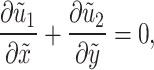 |
1 |
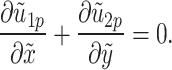 |
2 |
Momentum equations
The momentum equations, derived from Newton’s second law, govern the force balance in both dust and fluid phases33,38:
 |
3 |
 |
4 |
Based on Gauss’s law and as detailed in39,40:
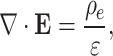 |
5 |
here, 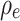 is the net charge density and
is the net charge density and 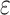 is the dielectric permittivity. The electric field is assumed conservative and may be expressed in terms of electric potential41,42:
is the dielectric permittivity. The electric field is assumed conservative and may be expressed in terms of electric potential41,42:
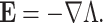 |
6 |
By combining Eqs. (5) and (6), the electrostatic body force is obtained as:
 |
7 |
The net charge density is defined using the Boltzmann distribution, expressed as:
 |
8 |
where cations 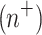 and anions
and anions 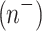 are defined as follows:
are defined as follows:
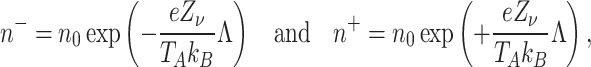 |
9 |
here, 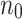 shows the bulk ion concentration,
shows the bulk ion concentration,  is the ionic valency,
is the ionic valency, 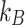 represents the Boltzmann’s constant,
represents the Boltzmann’s constant, 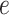 is the elementary charge, and
is the elementary charge, and 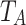 is the average temperature.
is the average temperature.
Eq. (8) may be linearized using the Debye-Hückel approximation, which holds when:
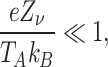 |
under this transformation, Eq. (8) reduces to:
 |
10 |
Since the flow is confined within a boundary layer, the axial variations are negligible, i.e., 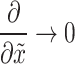 , reducing Eq. (7) to:
, reducing Eq. (7) to:
 |
11 |
where  denotes characteristic thickness of the electric double layer. In the present investigation, the electric double layer (EDL) thickness is treated as constant, consistent with the Debye-Hückel approximation, where ionic strength and temperature are approximately uniform. The chemical reactions can cause local concentration changes, this analysis is limited to weakly reacting regimes with minor alterations. This assumption maintains analytical tractability while effectively capturing electrokinetic phenomena. Introducing the following dimensionless variables:
denotes characteristic thickness of the electric double layer. In the present investigation, the electric double layer (EDL) thickness is treated as constant, consistent with the Debye-Hückel approximation, where ionic strength and temperature are approximately uniform. The chemical reactions can cause local concentration changes, this analysis is limited to weakly reacting regimes with minor alterations. This assumption maintains analytical tractability while effectively capturing electrokinetic phenomena. Introducing the following dimensionless variables:
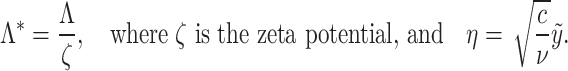 |
12 |
These substitutions convert Eq. (11) into:
 |
13 |
where 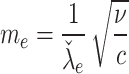 is the electroosmotic parameter. The analytical solution of Eq. (13), with boundary conditions
is the electroosmotic parameter. The analytical solution of Eq. (13), with boundary conditions 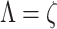 at
at 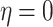 and
and 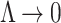 as
as  , or equivalently
, or equivalently  at
at 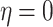 and
and 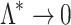 as
as 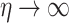 , is:
, is:
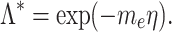 |
14 |
This expression reflects the exponential decay of electric potential within the electric double layer.
To summarize, Eq. (14) is determined under the idealized condition of an infinite domain, its utilization within the boundary layer paradigm remains valid due to the swift exponential decay of the electric potential. The expression 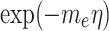 rapidly decays to negligible values beyond a few characteristic lengths, properly representing the electric field effects within the finite boundary layer thickness. Thus, the infinite-domain assumption is a mathematically sound and physically justifiable approximation that simplifies analysis while preserving model fidelity for boundary-layer-scale electrokinetic phenomena.
rapidly decays to negligible values beyond a few characteristic lengths, properly representing the electric field effects within the finite boundary layer thickness. Thus, the infinite-domain assumption is a mathematically sound and physically justifiable approximation that simplifies analysis while preserving model fidelity for boundary-layer-scale electrokinetic phenomena.
Energy equations
The energy equations for the fluid and dust phases govern each phase’s heat transmission and temperature distribution33,38,43.
 |
15 |
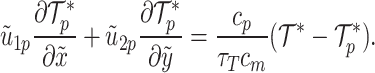 |
16 |
Concentration equations
In esterification, the solute exists in two distinct forms:
Freely diffused (unreacted) solute
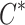 .
.Reacted solute
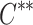 , immobilized at the reaction point.
, immobilized at the reaction point.
When the reversible reaction proceeds significantly quicker than the transport processes (diffusion and convection), a local equilibrium assumption holds. Law of mass action is written as44–46:
 |
17 |
where 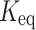 is the equilibrium constant, defined by the ratio of product and reactant concentrations. The general mass balance equation over a control volume
is the equilibrium constant, defined by the ratio of product and reactant concentrations. The general mass balance equation over a control volume 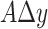 is given by19,20:
is given by19,20:
 |
18 |
The governing transport equations are written as:
Here, 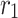 denotes the reversible reaction rate. Since
denotes the reversible reaction rate. Since 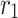 appears with opposite signs in the equations for
appears with opposite signs in the equations for  and
and 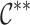 , it indicates interconversion between the two. To reduce model complexity while retaining physical fidelity, Eqs. (19) and (21) are combined to eliminate
, it indicates interconversion between the two. To reduce model complexity while retaining physical fidelity, Eqs. (19) and (21) are combined to eliminate 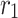 .
.
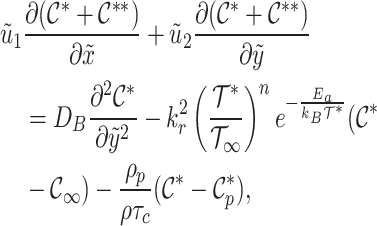 |
22 |
substituting the equilibrium condition 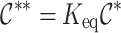 , we obtain:
, we obtain:
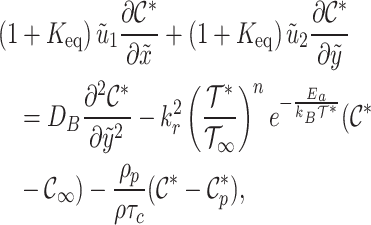 |
23 |
or, equivalently, the simplified form:
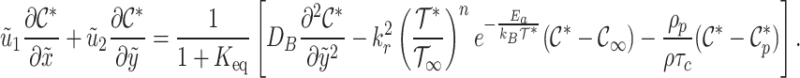 |
24 |
Although 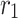 is mathematically eliminated, its physical contribution is retained through the modified convection and diffusion term scaled by
is mathematically eliminated, its physical contribution is retained through the modified convection and diffusion term scaled by 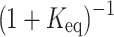 . This means
. This means
The influence of reversible reactions is integrated in the model.
The reduction of complexity does not overlook the reaction dynamics.
Accuracy is maintained as long as local equilibrium holds.
Such techniques are often used in microreactors, biochemical systems, and catalytic processes.
Micropolar equation
The following equation governs rotational behavior in micropolar fluids, particularly when microstructural effects are significant33.
 |
25 |
Here, 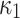 is the vortex viscosity,
is the vortex viscosity, 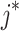 is micro inertia density, and
is micro inertia density, and  is the effective spin diffusion coefficient. This model originates from Eringen’s micropolar fluid theory31, where the term
is the effective spin diffusion coefficient. This model originates from Eringen’s micropolar fluid theory31, where the term 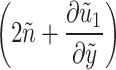 reflects the linear coupling between microrotation and velocity gradients. The micropolar framework is appropriate for modeling complex fluids, where micro-elements introduce localized spin inertia and asymmetric stress impacts. Such features are inherently absent in classical Newtonian models. This formulation is commonly used under moderate shear and magneto-hydrodynamic conditions, as examined in the current study. Although nonlinear modifications may be more appropriate under high shear rates or strong electromagnetic fields, the linear model adopted here effectively captures the essential microstructural dynamics and has been widely used in studies concerning this domain.
reflects the linear coupling between microrotation and velocity gradients. The micropolar framework is appropriate for modeling complex fluids, where micro-elements introduce localized spin inertia and asymmetric stress impacts. Such features are inherently absent in classical Newtonian models. This formulation is commonly used under moderate shear and magneto-hydrodynamic conditions, as examined in the current study. Although nonlinear modifications may be more appropriate under high shear rates or strong electromagnetic fields, the linear model adopted here effectively captures the essential microstructural dynamics and has been widely used in studies concerning this domain.
In the governing equations, the terms 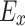 and
and 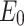 represent electroosmotic forces and electric field, respectively, while
represent electroosmotic forces and electric field, respectively, while 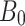 denotes the strength of the magnetic field.
denotes the strength of the magnetic field.  and
and  represent the temperature and concentration of the fluid and dust phases, respectively. Similarly,
represent the temperature and concentration of the fluid and dust phases, respectively. Similarly,  and
and 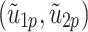 denote the velocity components of the fluid and dust phase in the
denote the velocity components of the fluid and dust phase in the  directions. The parameters
directions. The parameters 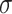 ,
, 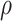 , and
, and 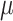 represent the fluid’s electrical conductivity, density, and dynamic viscosity, respectively, while
represent the fluid’s electrical conductivity, density, and dynamic viscosity, respectively, while  and k denote its heat capacity and thermal conductivity.
and k denote its heat capacity and thermal conductivity. 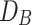 and
and 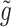 denote the Brownian diffusion coefficient and gravitational acceleration, respectively. Stokes’ drag constant, dust particle mass, thermal relaxation time, dust particle number density, and specific heat capacity are denoted by
denote the Brownian diffusion coefficient and gravitational acceleration, respectively. Stokes’ drag constant, dust particle mass, thermal relaxation time, dust particle number density, and specific heat capacity are denoted by 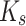 , m,
, m, 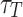 , N, and
, N, and 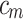 , respectively. The Arrhenius term is given by
, respectively. The Arrhenius term is given by 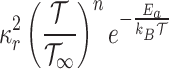 48, where
48, where 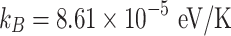 is Boltzmann constant.
is Boltzmann constant. 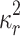 shows the chemical reaction rate, and n is the fitted rate constant. The value of n typically lies within the range
shows the chemical reaction rate, and n is the fitted rate constant. The value of n typically lies within the range 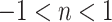 .
.
Boundary conditions
The boundary conditions regulating the two-phase micropolar dusty fluid flow are specified as follows15,33,47:
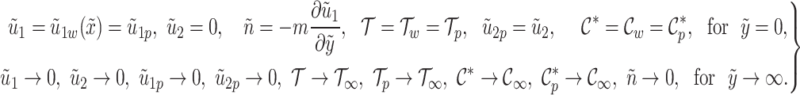 |
26 |
The boundary conditions are designed to capture realistic physical interactions occurring at both the stretching surface and in the free stream region. At the surface of sheet 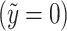 , the no-slip condition dictates the fluid adheres to the boundary, resulting in tangential velocity matching the stretching sheet velocity,
, the no-slip condition dictates the fluid adheres to the boundary, resulting in tangential velocity matching the stretching sheet velocity, 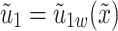 . The condition
. The condition  enforces velocity coupling between dust and fluid phases. The normal velocity components satisfy
enforces velocity coupling between dust and fluid phases. The normal velocity components satisfy  , ensuring no penetration at the boundary. The microrotation boundary condition at the sheet surface characterizes the torque balance acting on micro-elements near the boundary. The parameter m, known as the boundary interaction parameter, governs the rotational behavior of micro-elements and lies in the interval
, ensuring no penetration at the boundary. The microrotation boundary condition at the sheet surface characterizes the torque balance acting on micro-elements near the boundary. The parameter m, known as the boundary interaction parameter, governs the rotational behavior of micro-elements and lies in the interval 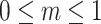 49. A value of
49. A value of 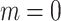 implies that the micro-elements are rigidly constrained against rotation near the wall, while
implies that the micro-elements are rigidly constrained against rotation near the wall, while  corresponds to a free-spinning condition, allowing unrestricted microrotation. The wall concentration and temperature are fixed as
corresponds to a free-spinning condition, allowing unrestricted microrotation. The wall concentration and temperature are fixed as 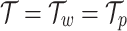 , and
, and  , respectively. These constraints represent isothermal and isoconcentration states, commonly encountered in controlled thermal and chemical processes such as coating, electroosmotic systems, and chemical vapor deposition, where boundary values are maintained externally.
, respectively. These constraints represent isothermal and isoconcentration states, commonly encountered in controlled thermal and chemical processes such as coating, electroosmotic systems, and chemical vapor deposition, where boundary values are maintained externally.
Far away from the sheet surface 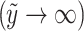 , all velocity components tend to zero, ensuring that the flow is localized near the surface and decays with distance. Similarly, concentration and temperature of both phases tend to their ambient values, i.e.,
, all velocity components tend to zero, ensuring that the flow is localized near the surface and decays with distance. Similarly, concentration and temperature of both phases tend to their ambient values, i.e.,  , reflecting thermal and solutal equilibrium with the surrounding medium. The vanishing microrotation at large
, reflecting thermal and solutal equilibrium with the surrounding medium. The vanishing microrotation at large 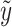 indicates that the role of microstructural effects is confined near the surface and fades in bulk fluid.
indicates that the role of microstructural effects is confined near the surface and fades in bulk fluid.
Collectively, the stated boundary conditions effectively model the essential physical constraints that describe the boundary layer flow of a micropolar dusty fluid over a stretching sheet, taking into account realistic solutal, thermal, and microrotational impacts.
Similarity transformations
The similarity transformations employed to reduce the governing multivariate partial differential equations (PDEs) into ordinary differential equations (ODEs) are given as follows33,50:
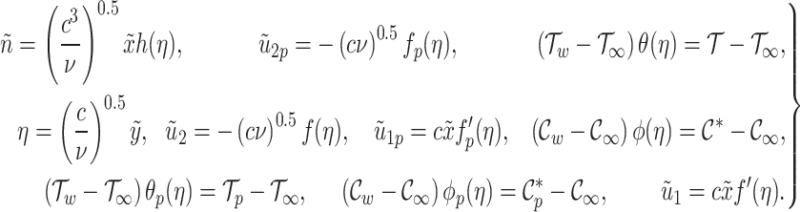 |
27 |
Dimensionless system
By applying the transformations (27), the Eqs. (1) and (2) are automatically satisfied. The remaining governing equations are transformed in the following form:
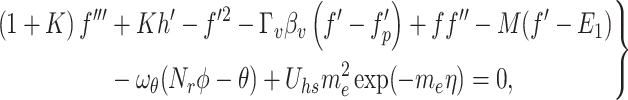 |
28 |
 |
29 |
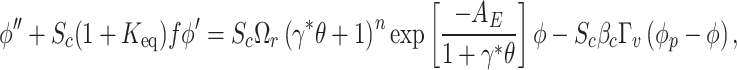 |
30 |
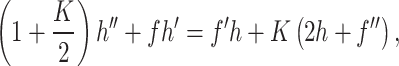 |
31 |
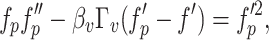 |
32 |
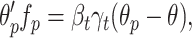 |
33 |
 |
34 |
Equations (28–34) involve the Helmholtz–Smoluchowski speed 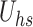 , magnetic parameter M, micropolar parameter K, temperature difference parameter
, magnetic parameter M, micropolar parameter K, temperature difference parameter 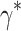 , electric parameter
, electric parameter 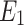 , Prandtl number Pr, buoyancy parameters (
, Prandtl number Pr, buoyancy parameters ( ,
,  ), reaction rate parameter
), reaction rate parameter 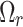 , Eckert number Ec, activation energy
, Eckert number Ec, activation energy  , Schmidt number
, Schmidt number 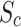 , and dusty fluid parameters
, and dusty fluid parameters 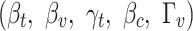 . The corresponding dimensionless parameters are defined below:
. The corresponding dimensionless parameters are defined below:
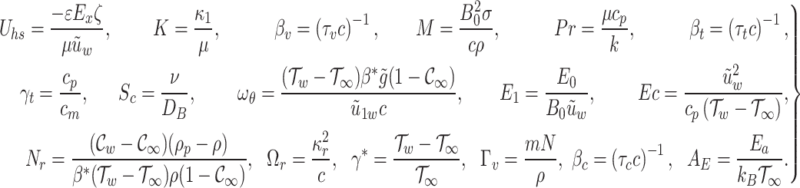 |
35 |
The boundary constraints in Eq. (26) reduce to the following simplified form:
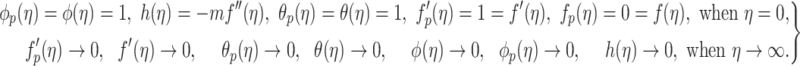 |
36 |
Esterification process
The equilibrium constant 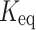 is generally determined using sophisticated thermochemical analysis, polarimetry, and spectroscopy techniques. The measurement of equilibrium concentrations was carefully investigated by Sarlo et al.51, who calculated
is generally determined using sophisticated thermochemical analysis, polarimetry, and spectroscopy techniques. The measurement of equilibrium concentrations was carefully investigated by Sarlo et al.51, who calculated 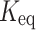 for a sequence of esterification reactions. Their study demonstrated the accuracy of these methods in describing equilibrium conditions and unveiled subtle details of reactant-product interactions. The following chemical reactions illustrate the esterification of ethanoic acid with four different alcohols catalyzed by sulfuric acid:
for a sequence of esterification reactions. Their study demonstrated the accuracy of these methods in describing equilibrium conditions and unveiled subtle details of reactant-product interactions. The following chemical reactions illustrate the esterification of ethanoic acid with four different alcohols catalyzed by sulfuric acid:
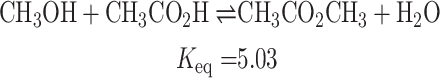 |
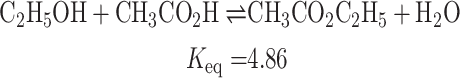 |
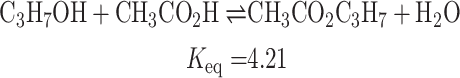 |
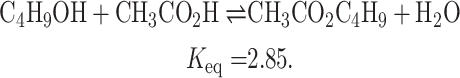 |
The equilibrium constant  is defined as:
is defined as:
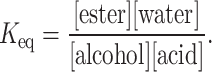 |
In this study, the equilibrium constant values are selected based on industrially validated measurements and are used to distinguish between reversible and irreversible flow scenarios. Specifically, an irreversible chemical reaction corresponds to 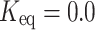 , whereas reversible reactions adopt realistic equilibrium constants such as
, whereas reversible reactions adopt realistic equilibrium constants such as 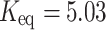 (methanol),
(methanol), 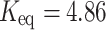 (ethanol),
(ethanol), 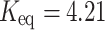 (propanol), and
(propanol), and  (butanol). These values fall within the ranges observed experimentally for esterification processes catalyzed by sulfuric acid.
(butanol). These values fall within the ranges observed experimentally for esterification processes catalyzed by sulfuric acid.
Although the current model is a theoretical study and does not correspond to a certain industrial reactor structure, the use of experimentally validated equilibrium constants ensures that the modeled conversion kinetics portray realistic chemical behavior. The chosen  values align with conversion efficiencies observed in pharmaceutical production and chemical processing, thereby enhancing the realism of the simulations. This theoretical model strikes a balance between analytical tractability and physical relevance, enabling a systematic investigation of electroosmotic flow, solutal transport coupling, and thermochemical interactions on reaction dynamics. As a result, industrial esterification applications greatly benefit from the model’s insightful explanation of how operational factors affect reaction performance.
values align with conversion efficiencies observed in pharmaceutical production and chemical processing, thereby enhancing the realism of the simulations. This theoretical model strikes a balance between analytical tractability and physical relevance, enabling a systematic investigation of electroosmotic flow, solutal transport coupling, and thermochemical interactions on reaction dynamics. As a result, industrial esterification applications greatly benefit from the model’s insightful explanation of how operational factors affect reaction performance.
Engineering quantities
The skin friction 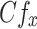 , Sherwood number
, Sherwood number 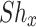 , and Nusselt number
, and Nusselt number 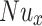 are defined as follows52,53:
are defined as follows52,53:
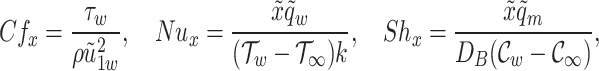 |
37 |
here, 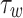 ,
, 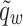 , and
, and 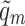 represent shear stress, surface heat flux, and surface mass flux, respectively.
represent shear stress, surface heat flux, and surface mass flux, respectively.
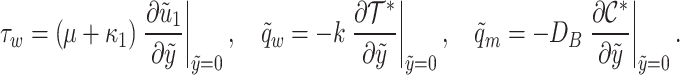 |
38 |
Applying the similarity transformations (27) and substituting the expressions in Eq. (38) into Eq. (37), we obtain the dimensionless forms:
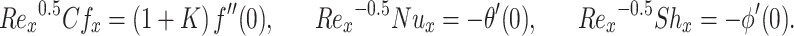 |
39 |
Here, 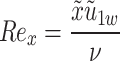 denotes the local Reynolds number.
denotes the local Reynolds number.
Entropy analysis
Reducing entropy generation is essential for thermodynamic optimization, as it is inherently linked to energy dissipation. Entropy generation is a diagnostic tool that reveals underlying defects, analogous to structural, operational, or procedural faults, which can lead to system failures. Eliminating such inefficiencies significantly improves overall system performance. Minimizing entropy generation is vital for achieving optimal thermodynamic performance across various engineering systems. The global energy crisis has highlighted the need to optimize energy generation, conversion, and utilization, encouraging the development of sustainable and effective technologies54. The expression for volumetric entropy generation rate  is given as55–57:
is given as55–57:
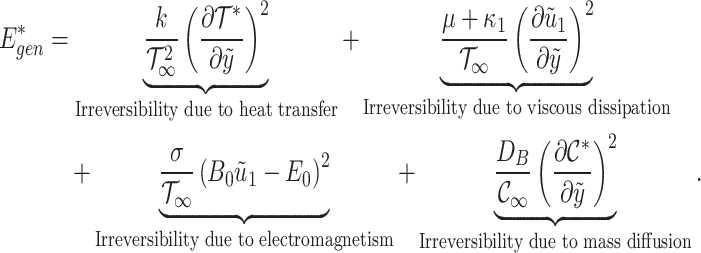 |
40 |
Eq. (40) delineates four distinct sources of entropy generation: heat transfer due to temperature gradients, viscous dissipation from fluid friction, electromagnetic effects, and irreversibility due to mass diffusion. The entropy generation number, Ns, is defined as the ratio of  to the characteristic entropy generation
to the characteristic entropy generation  , where
, where 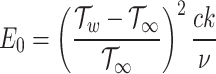 . Using the similarity variables given in (27), Eq. (40) takes the form:
. Using the similarity variables given in (27), Eq. (40) takes the form:
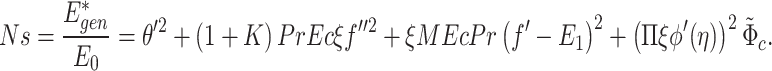 |
41 |
Here,  is the concentration diffusion parameter, while
is the concentration diffusion parameter, while 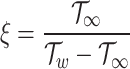 and
and 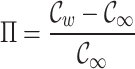 are the dimensionless temperature and concentration parameters, respectively. In engineering analysis, determining the relative importance of different entropy-generating factors such as mass and heat transfer irreversibilities within a system is often crucial. An important dimensionless parameter for this assessment is the Bejan number, mathematically defined as follows57:
are the dimensionless temperature and concentration parameters, respectively. In engineering analysis, determining the relative importance of different entropy-generating factors such as mass and heat transfer irreversibilities within a system is often crucial. An important dimensionless parameter for this assessment is the Bejan number, mathematically defined as follows57:
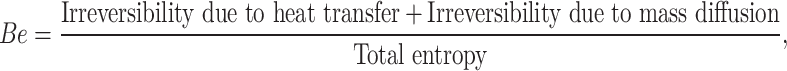 |
42 |
in dimensionless form
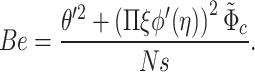 |
43 |
Numerical solution
The nonlinear nature of the obtained system of ordinary differential equations precludes an analytical solution. Hence, a robust numerical technique is needed to overcome this obstacle. In this study, the shooting method and the Runge-Kutta-Fehlberg (RKF45) technique is employed to obtain the numerical solution of Eqs. (28–34) along with conditions (36). Eqs. (28–34) are transformed into thirteen coupled first-order ordinary differential equations by introducing appropriate substitutions:
 |
The resultant system is as follows:
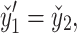 |
44 |
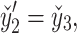 |
45 |
 |
46 |
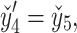 |
47 |
 |
48 |
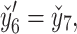 |
49 |
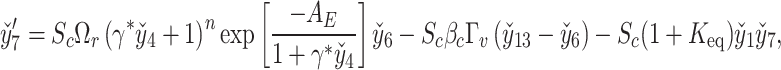 |
50 |
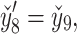 |
51 |
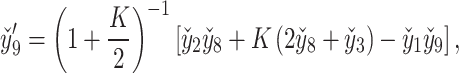 |
52 |
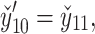 |
53 |
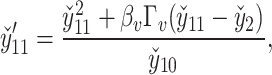 |
54 |
 |
55 |
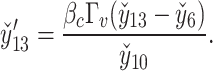 |
56 |
The transformed initial conditions are:
 |
57 |
Here, 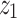 ,
,  ,
,  , and
, and 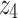 represent unknown initial slopes required to meet the asymptotic boundary conditions. The shooting method is used to guess missing initial conditions by an iterative process until the boundary conditions are satisfied. Suitable initial guesses are assumed for the missing initial conditions58. These values are iteratively updated through Newton’s approach until the residual error between successive iterations falls below the convergence threshold of
represent unknown initial slopes required to meet the asymptotic boundary conditions. The shooting method is used to guess missing initial conditions by an iterative process until the boundary conditions are satisfied. Suitable initial guesses are assumed for the missing initial conditions58. These values are iteratively updated through Newton’s approach until the residual error between successive iterations falls below the convergence threshold of 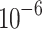 . Throughout the computations, the problem domain is chosen as
. Throughout the computations, the problem domain is chosen as  , where
, where 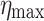 varies from 3.5 to 9.
varies from 3.5 to 9. 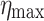 corresponds to a value beyond which there are no significant variations in results. The unknown conditions are chosen so that the known free-stream boundary conditions are approximately satisfied.
corresponds to a value beyond which there are no significant variations in results. The unknown conditions are chosen so that the known free-stream boundary conditions are approximately satisfied.
Due to the strong nonlinear coupling between momentum, thermal, concentration, and microrotation equations, a numerical stiffness arises. Initial solutions were obtained for simplified parameter regimes and then gradually extended to more complex cases. This approach guaranteed smoother convergence and numerical stability for the highly nonlinear coupled equations. Each iteration was performed with carefully tuned initial guesses, and Newton’s iterative updates were monitored to ensure convergence. The solution remained numerically stable throughout this process, and small perturbations in the guessed values did not induce significant variations in the resulting flow fields. It indicates that the system exhibits low sensitivity to guessed initial conditions within practical bounds. The numerical scheme showed convergence without erratic behavior for this nonlinear coupled system.
Results and discussion
The shooting method is used to numerically solve the nonlinear system (28–34), along with the boundary conditions (36). The influence of various controlling parameters on the flow and heat transfer is thoroughly explored. To verify the accuracy of the numerical findings, the skin friction coefficient and Nusselt number are computed and compared with published results under limiting cases. Tables 2 and 3 show that the current results are in excellent agreement with those reported in previous studies. Unless otherwise specified, the following parameter values are used in the investigation:  59
59
 ,
,  ,
,  ,
, 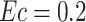 ,
, 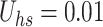 ,
, 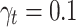 ,
, 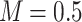 ,
, 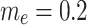 ,
, 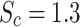 ,
, 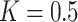 ,
, 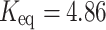 , and
, and 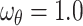 . The chosen values and their ranges are based on prior research and physical relevance. For instance, the magnetic parameter
. The chosen values and their ranges are based on prior research and physical relevance. For instance, the magnetic parameter 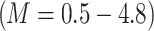 indicates weak to moderate magnetic field strengths typically observed in EMHD flows, while the micropolar parameter
indicates weak to moderate magnetic field strengths typically observed in EMHD flows, while the micropolar parameter 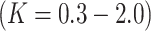 captures the transition from weak to strong microrotation impacts. The Eckert number
captures the transition from weak to strong microrotation impacts. The Eckert number 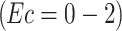 spans from negligible to significant viscous dissipation, and the electric parameter
spans from negligible to significant viscous dissipation, and the electric parameter  corresponds to moderate electroosmotic forcing. The values of
corresponds to moderate electroosmotic forcing. The values of  ,
, 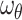 ,
, 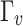 ,
,  , and
, and 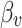 are consistent with the study of Ali et al.60, while the Schmidt number
are consistent with the study of Ali et al.60, while the Schmidt number 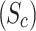 and equilibrium constant
and equilibrium constant 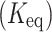 are based on studies of Raju et al.19,20. The ranges
are based on studies of Raju et al.19,20. The ranges 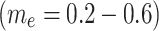 and
and 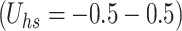 reflect realistic electrokinetic conditions encountered in charged microfluidic systems.
reflect realistic electrokinetic conditions encountered in charged microfluidic systems.
Table 2.
Comparison of skin friction coefficients for various values of M with 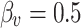 and
and 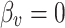 .
.
| M | 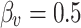 |
 |
||||||
|---|---|---|---|---|---|---|---|---|
| Ramesh et al.61 | Jalil et al.62 | Hussain et al.15 | Present Outcomes | Ramesh et al.61 | Jalil et al.62 | Hussain et al.15 | Present Outcomes | |
| 0.2 | 1.126 | 1.126114 | 1.12630 | 1.12644 | 1.095 | 1.095445 | 1.0954 | 1.09558 |
| 0.5 | 1.252 | 1.252251 | 1.25240 | 1.25289 | 1.224 | 1.224745 | 1.2247 | 1.22483 |
| 1.0 | 1.438 | 1.438101 | 1.43810 | 1.43862 | 1.414 | 1.414214 | 1.4142 | 1.41496 |
| 1.5 | 1.602 | 1.602540 | 1.60250 | 1.60283 | 1.581 | 1.581139 | 1.5885 | 1.58403 |
| 2.0 | 1.751 | 1.751609 | 1.75170 | 1.75089 | 1.732 | 1.732051 | 1.7320 | 1.73192 |
Table 3.
Comparison of Nusselt number for various values of Pr.
Figure 2a illustrates the influence of magnetic parameter M and micropolar parameter K on the velocity profiles of both dust and fluid phases. As the micropolar parameter increases, the microrotation of fluid particles is enhanced, effectively lowering the fluid’s apparent viscosity due to the presence of spin inertia. The reduction in shear resistance facilitates fluid motion, resulting in a noticeable rise in fluid velocity. The improved mobility of the carrier fluid increases the drag exerted on the suspended dust particles, thereby boosting the dust phase as well. Conversely, increasing the magnetic parameter introduces a stronger Lorentz force that acts as a resistive force opposing the flow direction. The electromagnetic retarding force suppresses the momentum of both phases, leading to a decline in their respective velocities.
Figure 2.
Influence of varying M and K on velocity and temperature profiles.
Figure 2b displays the corresponding thermal behavior. A rise in the micropolar parameter intensifies micro-rotational activity, which redistributes energy internally within the fluid without contributing effectively to bulk heat conduction. The elevated microrotation disrupts the alignment of thermal gradients, diminishing the rate of thermal energy propagation. As a result, thermal diffusion is suppressed, leading to a decrease in the temperature of both phases. In contrast, a higher magnetic parameter indirectly affects temperature by resisting velocity fields. Reduced convection weakens advective heat transfer, resulting in thicker thermal boundary layers and elevated temperatures.
Figure 3 demonstrates the effects of the electroosmotic parameter  and the Helmholtz-Smoluchowski velocity
and the Helmholtz-Smoluchowski velocity 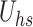 on the velocity and temperature profiles of both fluid and dust phases. As
on the velocity and temperature profiles of both fluid and dust phases. As 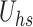 increases, the electroosmotic body force strengthens due to an intensified EDL movement. This mechanism propels the fluid forward, enhancing the velocity of the fluid phases. Owing to strong interphase drag coupling, this momentum is transferred to the dust phase, resulting in a corresponding increase in its velocity. Similarly, an increase in
increases, the electroosmotic body force strengthens due to an intensified EDL movement. This mechanism propels the fluid forward, enhancing the velocity of the fluid phases. Owing to strong interphase drag coupling, this momentum is transferred to the dust phase, resulting in a corresponding increase in its velocity. Similarly, an increase in 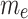 , which quantifies the strength of the applied electric field relative to viscous effects, reinforces the electroosmotic driving force. It leads to the same trend in both phases’ velocities due to increased electrokinetic propulsion. From a thermal perspective, both elevated
, which quantifies the strength of the applied electric field relative to viscous effects, reinforces the electroosmotic driving force. It leads to the same trend in both phases’ velocities due to increased electrokinetic propulsion. From a thermal perspective, both elevated 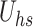 and
and 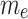 accelerate the flow, which increases convective heat transfer and reduces the residence time of fluid elements near the heated surface. This results in a thinning of the thermal boundary layer, thus reducing the temperatures of both phases.
accelerate the flow, which increases convective heat transfer and reduces the residence time of fluid elements near the heated surface. This results in a thinning of the thermal boundary layer, thus reducing the temperatures of both phases.
Figure 3.
Influence of varying 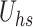 and
and 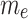 on velocity and temperature profiles.
on velocity and temperature profiles.
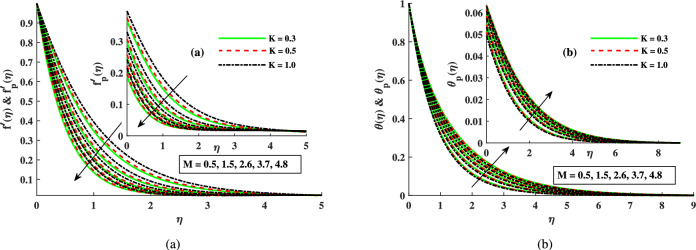
Figure 4 shows that increasing the mixed convection parameter enhances the velocities of both phases while decreasing temperatures. It is due to the combined effect of buoyancy and forced convection, which accelerates flow and improves momentum transfer. The stronger convective motion reduces thermal resistance, leading to more effective heat removal and lower temperatures. The electric parameter increases velocities in both phases owing to intensified electrokinetic forces. These forces originate from the interaction between the applied electric field and EDL, generating a slip-driven flow that accelerates the fluid. The increased fluid motion enhances interphase momentum transfer, raising the dust phase velocity as well. Since these effects primarily influence momentum transfer rather than thermal diffusion, the temperature reduction remains modest. This cooling is attributed to minor enhancements in convective transport due to accelerated flow.
Figure 4.
Influence of varying 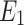 and
and 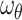 on velocity and temperature profiles.
on velocity and temperature profiles.
Figure 5 illustrates the influence of various parameters on microrotation 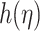 . It highlights that the magnetic parameter
. It highlights that the magnetic parameter 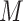 improves microrotation
improves microrotation 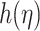 by creating Lorentz-induced torques that drive rotational motion through electromagnetic coupling with charged microstructures present in the fluid, thereby enhancing spin effects. The micropolar parameter
by creating Lorentz-induced torques that drive rotational motion through electromagnetic coupling with charged microstructures present in the fluid, thereby enhancing spin effects. The micropolar parameter 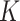 reduces rotation by inducing stronger viscous coupling stresses between the microelements and the surrounding fluid layers, which prevent angular deformation and suppress microrotation. Meanwhile,
reduces rotation by inducing stronger viscous coupling stresses between the microelements and the surrounding fluid layers, which prevent angular deformation and suppress microrotation. Meanwhile, 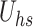 (Helmholtz-Smoluchowski slip velocity) and
(Helmholtz-Smoluchowski slip velocity) and 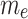 (electroosmotic parameter) reduce microrotation
(electroosmotic parameter) reduce microrotation 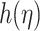 by altering the shear environment through electrohydrodynamic mechanisms, where electric body forces modify near-wall velocity gradients that generate rotational inertia in micropolar fluids. An increase in
by altering the shear environment through electrohydrodynamic mechanisms, where electric body forces modify near-wall velocity gradients that generate rotational inertia in micropolar fluids. An increase in  enhances wall slip via a stronger electroosmotic driving force, thereby diminishing the near-wall shear gradient−a primary source of spin generation in micropolar fluids. As microrotation arises from asymmetric shear stresses acting on suspended micro-elements, this reduced shear directly diminishes their angular momentum exchange, leading to suppressed microrotational effects. Simultaneously,
enhances wall slip via a stronger electroosmotic driving force, thereby diminishing the near-wall shear gradient−a primary source of spin generation in micropolar fluids. As microrotation arises from asymmetric shear stresses acting on suspended micro-elements, this reduced shear directly diminishes their angular momentum exchange, leading to suppressed microrotational effects. Simultaneously, 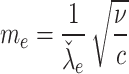 , being inversely related to the Debye length, governs the thickness of EDL. A larger
, being inversely related to the Debye length, governs the thickness of EDL. A larger 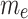 corresponds to a more compressed EDL, localizing electrokinetic forces near the wall. This compression suppresses the vorticity generation and rotational flow structures by limiting effective thickness over which electrokinetic interactions can induce shear, thus reducing rotational excitation in the boundary layer. Collectively, the combined effects of EDL confinement and elevated wall slip weaken both the source and sustenance of microrotation, yielding a reduction in
corresponds to a more compressed EDL, localizing electrokinetic forces near the wall. This compression suppresses the vorticity generation and rotational flow structures by limiting effective thickness over which electrokinetic interactions can induce shear, thus reducing rotational excitation in the boundary layer. Collectively, the combined effects of EDL confinement and elevated wall slip weaken both the source and sustenance of microrotation, yielding a reduction in  across the boundary layer.
across the boundary layer.
Figure 5.
Influence of varying M, K, 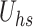 , and
, and 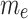 on concentration and microrotation profiles.
on concentration and microrotation profiles.
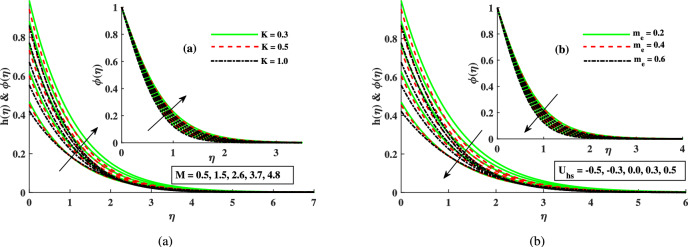
The behavior of the concentration profile  for different parameters is visually explained in Figs. 5 and 6. The concentration
for different parameters is visually explained in Figs. 5 and 6. The concentration 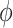 increases with the magnetic parameter
increases with the magnetic parameter 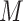 , as the Lorentz force restricts the fluid motion and facilitates solute accumulation by impeding bulk transport and allowing solute particles to linger near the surface, especially where flow deceleration occurs due to electromagnetic drag. An increased micropolar parameter
, as the Lorentz force restricts the fluid motion and facilitates solute accumulation by impeding bulk transport and allowing solute particles to linger near the surface, especially where flow deceleration occurs due to electromagnetic drag. An increased micropolar parameter 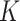 promotes rotational motion, thereby dispersing the solute and reducing accumulation. The Helmholtz-Smoluchowski velocity and electroosmotic parameter increase flow velocity, thin the concentration boundary layer, and consequently decrease
promotes rotational motion, thereby dispersing the solute and reducing accumulation. The Helmholtz-Smoluchowski velocity and electroosmotic parameter increase flow velocity, thin the concentration boundary layer, and consequently decrease  by promoting solute transport away from the surface. Figure 6 highlights that irreversible flows have a thicker concentration boundary layer than reversible flows. It suggests that mass diffusion predominates over the rate of chemical reactions in irreversible flows, resulting in a slower rate of species depletion close to the surface. Consequently, the concentration diminishes more gradually across the boundary layer. In contrast, reversible flows possess a narrower concentration boundary layer due to reaction equilibrium constraints that limit diffusive transport. The influence of Ec and
by promoting solute transport away from the surface. Figure 6 highlights that irreversible flows have a thicker concentration boundary layer than reversible flows. It suggests that mass diffusion predominates over the rate of chemical reactions in irreversible flows, resulting in a slower rate of species depletion close to the surface. Consequently, the concentration diminishes more gradually across the boundary layer. In contrast, reversible flows possess a narrower concentration boundary layer due to reaction equilibrium constraints that limit diffusive transport. The influence of Ec and  on temperature profiles of both phases is also explored in Fig. 6. By transforming kinetic energy into heat through viscous dissipation, the Eckert number enhances temperatures in both phases. This leads to an expanded thermal boundary layer and increases internal heat generation due to the improved conversion of mechanical energy into internal energy, especially in regions of high velocity gradients. The parameter
on temperature profiles of both phases is also explored in Fig. 6. By transforming kinetic energy into heat through viscous dissipation, the Eckert number enhances temperatures in both phases. This leads to an expanded thermal boundary layer and increases internal heat generation due to the improved conversion of mechanical energy into internal energy, especially in regions of high velocity gradients. The parameter  enhances inter-phase heat transmission, raising the dust phase temperature while reducing that of the fluid phase. This behavior results from enhanced heat exchange between the fluid and the dust phase, causing a reduction in fluid temperature and a corresponding increase in thermal energy in the particulate phase.
enhances inter-phase heat transmission, raising the dust phase temperature while reducing that of the fluid phase. This behavior results from enhanced heat exchange between the fluid and the dust phase, causing a reduction in fluid temperature and a corresponding increase in thermal energy in the particulate phase.
Figure 6.
Influence of varying 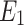 ,
, 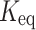 , Ec, and
, Ec, and  on concentration and temperature profiles.
on concentration and temperature profiles.
Thermal transport converts temperature gradients into enhanced molecular mobility and kinetic energy, thereby increasing microscopic disorder and resulting in entropy generation. Entropy, a measure of thermodynamic irreversibility, escalates as usable energy is dissipated into less organized forms. The relative significance of irreversibility due to mass and heat diffusion in comparison to the total entropy generated by all sources is measured by the Bejan number. Figure 7 illustrates the influence of key parameters on entropy generation and Bejan number. An increase in the magnetic parameter enhances Lorentz forces, which oppose fluid motion and convert kinetic energy into internal energy via resistive heating. It greatly increases Ns by thickening the boundary layer, increasing viscous shear, and intensifying Joule heating. The micropolar parameter accounts for microrotational effects and internal spin inertia of micro-elements; its rise amplifies local microstructural interactions, leading to more viscous dissipation and greater entropy generation. The Eckert number, which represents the ratio of kinetic to thermal energy, increases Ns through increased internal friction and thermal agitation. On the other hand, inter-phase thermal conductivity is enhanced by a greater thermal coupling value  , which promotes improved energy redistribution and lowers net entropy production.
, which promotes improved energy redistribution and lowers net entropy production.
Figure 7.
Influence of varying M, K, Ec, and 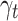 on entropy and Bejan number.
on entropy and Bejan number.
As the micropolar parameter and  increase, the Bejan number increases as well, suggesting that mass and heat diffusion irreversibility predominate over total entropy. However, it decreases as the magnetic parameter and Eckert number increase, and the entropy landscape is dominated by Joule and viscous dissipation, which are types of direct mechanical and electromagnetic deterioration. On the other hand, the Bejan number decreases as the magnetic parameter or Eckert number increases, suggesting that non-diffusive processes, such as viscous shear and electromagnetic damping, are increasingly controlling the creation of entropy. In these situations, the diffusive contributions are outweighed by the strong Joule heating and frictional dissipation, which result in irreversible energy losses. This transition represents a state in which the system’s thermodynamic deterioration is determined by direct mechanical and electromagnetic energy exchanges rather than molecular transport pathways.
increase, the Bejan number increases as well, suggesting that mass and heat diffusion irreversibility predominate over total entropy. However, it decreases as the magnetic parameter and Eckert number increase, and the entropy landscape is dominated by Joule and viscous dissipation, which are types of direct mechanical and electromagnetic deterioration. On the other hand, the Bejan number decreases as the magnetic parameter or Eckert number increases, suggesting that non-diffusive processes, such as viscous shear and electromagnetic damping, are increasingly controlling the creation of entropy. In these situations, the diffusive contributions are outweighed by the strong Joule heating and frictional dissipation, which result in irreversible energy losses. This transition represents a state in which the system’s thermodynamic deterioration is determined by direct mechanical and electromagnetic energy exchanges rather than molecular transport pathways.
Figure 8 presents the variations in skin friction coefficient and local Nusselt number. The Nusselt number reflects the surface heat transfer rate, while skin friction indicates the shear resistance at the wall. As the magnetic field strengthens, the Lorentz force near the surface increases, decelerating the fluid and acting as a resistive barrier. It weakens thermal gradients, leading to a lower Nusselt number and reduced heat transfer. A rising micropolar parameter enhances microrotational effects, prompting fluid mixing near the wall. This increases momentum diffusion, steepens temperature gradients, and thereby raises the Nusselt number. However, the skin friction becomes more negative, reflecting greater opposition to microrotation. Increasing the electroosmotic parameter 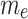 reduces the wall stress by promoting slip flow, making the skin friction coefficient more negative. This stronger electroosmotic force enhances near-wall fluid movement, improving convective transport and raising heat transfer efficiency. Figures 9 and 10 depict streamline patterns corresponding to different values of
reduces the wall stress by promoting slip flow, making the skin friction coefficient more negative. This stronger electroosmotic force enhances near-wall fluid movement, improving convective transport and raising heat transfer efficiency. Figures 9 and 10 depict streamline patterns corresponding to different values of 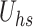 and
and  , highlighting near-wall flow behavior. Higher values of
, highlighting near-wall flow behavior. Higher values of  and
and 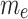 produce sharper velocity gradients and compressed streamlines near the surface.
produce sharper velocity gradients and compressed streamlines near the surface.
Figure 8.
Influence of varying M, K, and 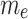 on skin friction and Nusselt number.
on skin friction and Nusselt number.
Figure 9.
Streamlines for  and
and 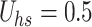 .
.
Figure 10.
Streamlines for 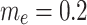 and
and  .
.
Conclusion
This work investigates the two-dimensional electro-magneto-hydrodynamic flow of a micropolar dusty fluid over a linearly stretching sheet. It particularly focuses on the influence of the esterification process, buoyancy effects, electroosmotic forces, and viscous dissipation on momentum and heat transfer. Using suitable similarity transformations, the complex multivariate partial differential equations governing the system are reduced to a set of ordinary differential equations, which are then numerically solved via the shooting method. The key findings are as follows:
An increase in the micropolar parameter enhances the velocity profiles while simultaneously reducing microrotation intensity, Nusselt number, and thermal distribution. This adjustment increases entropy generation, the Bejan number, and skin friction.
The magnetic parameter opposes fluid motion through a Lorentz force, resulting in lower velocities, Bejan number, and Nusselt number. Simultaneously, it raises temperatures, microrotation, entropy generation, and skin friction.
Higher Helmholtz-Smoluchowski velocity boosts the fluid movement and thins the thermal and solutal boundary layers.
An increase in the electroosmotic parameter further accelerates the fluid. However, this results in reduced temperature, skin friction, microrotation, and heat transfer rate due to weakened thermal gradients.
A stronger electric parameter strengthens electroosmotic motion, which increases fluid velocity. Additionally, the temperature and concentration profiles in both the fluid and dust phases decrease due to the compressed boundary layers.
Future research directions
The present study provides a theoretical investigation into electromagneto-hydrodynamic boundary layer flow in a micropolar dusty fluid, taking into account buoyancy-driven convection, chemical processes, and electroosmotic transport. While this work establishes fundamental insights, several compelling extensions could significantly improve the research’s scope and physical relevance.
A primary research direction involves sensitivity analysis and experimental validation to verify the theoretical outcomes. Another important extension is the generalization of the current two-dimensional, steady-state model to unsteady and three-dimensional flow configurations, enabling better alignment with real-world flow scenarios. Employing advanced numerical methods, such as the finite element method and the homotopy analysis method, could reduce computational errors and improve solution convergence. This model can also be extended to non-Newtonian fluids, such as Casson, Maxwell, or viscoelastic fluids, to examine microstructural effects in rheologically diverse media. The addition of thermal radiation and Joule heating would enable a more comprehensive analysis, particularly in high-temperature, electro-conductive flows. Furthermore, the inclusion of rotational reference frames may be explored to simulate flow behavior in rotating systems. Finally, future work could include nonlinear electrokinetic effects by relaxing the Helmholtz-Smoluchowski assumption, especially at high surface potential.
Acknowledgements
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/308/46.
List of symbols
Dynamic viscosity (Pa
 s)
s)
Stokes’ drag constant (N
 s/m)
s/m)
Electrical conductivity (S/m)

Specific heat of fluid (J/kg
 K)
K)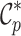
Dust phase concentration (kg/
 )
)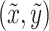
Coordinate axes (m)
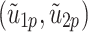
Dust phase velocity components (m/s)
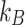
Boltzmann constant (J/K)
- M
Magnetic parameter (dimensionless)

Micro-inertia density (kg/m)
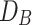
Brownian diffusion coefficient (
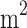 /s)
/s)
Temperature-fluid interaction parameter (dimensionless)

Fluid-particle interaction (dimensionless)

Reynolds number (dimensionless)
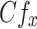
Skin friction coefficient (dimensionless)

Sherwood number (dimensionless)
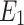
Electric parameter (dimensionless)
- m
Dust particle mass (kg)
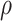
Density (kg/
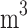 )
)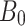
Uniform magnetic field (T)
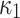
Spin (vortex) viscosity (Pa
 s)
s)- k
Thermal conductivity (W/m
 K)
K)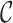
Fluid phase concentration (kg/
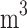 )
)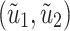
Fluid velocity components (m/s)
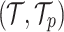
Temperatures (K)
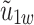
Stretching velocity of sheet (m/s)
- Pr
Prandtl number (dimensionless)

Effective spin diffusion coefficient (Pa
 s)
s)
Gravitational acceleration (m/
 )
)
Specific heat ratio (dimensionless)
- K
Micropolar parameter (dimensionless)
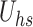
Helmholtz-Smoluchowski velocity (dimensionless)
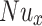
Nusselt number (dimensionless)
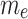
Electroosmotic parameter (dimensionless)
- Ec
Eckert number (dimensionless)

Thermal relaxation time (s)
Author contributions
A.U.A.: Supervision; Review and editing, Revision. M.H.: Formal Analysis; Writing original manuscript, Revision. B.A.: Conceptualization; Methodology, Revision. N.A.A.: Data Curation; Resources. F.G.: Investigation; Software, Revision. J.K.: Methodology; Visualization, Revision. S.N.: Validation; Investigation.
Data availability
All the data used during this study is accessible within the manuscript.
Declarations
Competing interests
The authors declare no competing interests.
Ethical approval
The authors affirm their commitment to ethical standards.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Reuss, F. F. Sur un novel effet de l’électricité galvanique. Mém. Soc. Imp. Nat. Moscou2, 327–337 (1809). [Google Scholar]
- 2.Shih, Y. C., Liao, C. R., Chung, I. C., Chang, Y. S. & Chang, P. L. Simultaneous separation of five major ribonucleic acids by capillary electrophoresis with laser-induced fluorescence in the presence of electroosmotic flow: Application to the rapid screening of 5S rRNA from ovarian cancer cells. Anal. Chim. Acta847, 73–79 (2014). [DOI] [PubMed] [Google Scholar]
- 3.Hui, T. H. et al. An electroosmotic microfluidic system to characterize cancer cell migration under confinement. J. R. Soc. Interface16, 20190062 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Waheed, S., Noreen, S. & Hussanan, A. Study of heat and mass transfer in electroosmotic flow of third order fluid through peristaltic microchannels. Appl. Sci.9, 2164 (2019). [Google Scholar]
- 5.Prakash, J., Tripathi, D. & Bég, O. A. Computation of EMHD ternary hybrid non-Newtonian nanofluid over a wedge embedded in a Darcy-Forchheimer porous medium with zeta potential and wall suction/injection effects. Int. J. Ambient Energy44, 2155–2169 (2023). [Google Scholar]
- 6.Hussain, A., Farooq, N., Ahmad, A. & Saddiqa, A. Numerical simulation of the permeable wedge-shaped geometry incorporating electroosmosis, solar radiation and heat source-sink effects. Int. Commun. Heat Mass Trans.150, 107177 (2024). [Google Scholar]
- 7.Hafez, N. M., Thabet, E. N., Khan, Z., Abd-Alla, A. M. & Elhag, S. H. Electroosmosis-modulated Darcy-Forchheimer flow of Casson nanofluid over stretching sheets in the presence of Newtonian heating. Case Stud. Therm. Eng.53, 103806 (2024). [Google Scholar]
- 8.Kumar, B. & Jangili, S. Heat transfer analysis of electroosmotic flow of couple stress fluid through a rotating circular microchannel. Int. J. Therm. Sci.208, 109359 (2025). [Google Scholar]
- 9.Kuntal, Y., Ghiya, N. & Tiwari, A. Solute dispersion in an electroosmotic flow of Carreau and Newtonian fluids through a tube: Analytical study. Eur. Phys. J. Plus140, 221 (2025). [Google Scholar]
- 10.Chowdhury, S., Pal, S. K. & Gopmandal, P. P. Dynamic electroosmotic flow and solute dispersion through a nanochannel filled with an electrolyte surrounded by a layer of a dielectric and immiscible liquid. Soft Matter21, 1085–1112 (2025). [DOI] [PubMed] [Google Scholar]
- 11.Saffman, P. G. On the stability of laminar flow of a dusty gas. J. Fluid Mech.13, 120–128 (1962). [Google Scholar]
- 12.Ezzat, M. A., El-Bary, A. A. & Morsey, M. M. Space approach to the hydro-magnetic flow of a dusty fluid through a porous medium. Comput. Math. Appl.59, 2868–2879 (2010). [Google Scholar]
- 13.Sivaraj, R. & Kumar, B. R. Unsteady MHD dusty viscoelastic fluid Couette flow in an irregular channel with varying mass diffusion. Int. J. Heat Mass Transf.55, 3076–3089 (2012). [Google Scholar]
- 14.Abbas, Z., Hasnain, J. & Sajid, M. Effects of slip on MHD flow of a dusty fluid over a stretching sheet through porous space. J. Eng. Thermophys.28, 84–102 (2019). [Google Scholar]
- 15.Hussain, M., Ali, B., Awan, A. U., Alharthi, M. & Alrashedi, Y. Role of nanoparticle radius for heat transfer optimization in MHD dusty fluid across stretching sheet. J. Therm. Anal. Calorim.149, 15179–15192 (2024). [Google Scholar]
- 16.Naz, S. Influence of injection/suction and transient pressure gradient on the Brinkman-type dusty magnetized fluid flow through a horizontal microchannel system. J. Therm. Anal. Calorim.149, 1–18 (2025). [Google Scholar]
- 17.Rathod, A. P., Wasewar, K. L. & Sonawane, S. S. Enhancement of esterification reaction by pervaporation reactor: An intensifying approach. Proc. Eng.51, 330–334 (2013). [Google Scholar]
- 18.Khan, Z. et al. Current developments in esterification reaction: A review on process and parameters. J. Ind. Eng. Chem.103, 80–101 (2021). [Google Scholar]
- 19.Raju, U., Arivukkodi, D., Alhazmi, H., Khan, I. & Omer, A. S. Heat transfer in a reversible esterification process of hydromagnetic Casson fluid with Arrhenius activation energy. Case Stud. Therm. Eng.60, 104616 (2024). [Google Scholar]
- 20.Raju, U., Rangabashyam, S., Alhazmi, H. & Khan, I. Irreversible and reversible chemical reaction impacts on convective Maxwell fluid flow over a porous media with activation energy. Case Stud. Therm. Eng.61, 104821 (2024). [Google Scholar]
- 21.Prabhakar, S., Raju, U., Santra, S. S. & Nandi, S. Bioconvective reversible (an esterification process) Casson nanofluid flow over a radiative spinning disc with microorganism. Int. J. Mod. Phys. C36, 2450171 (2025). [Google Scholar]
- 22.Rana, G. C., Chand, R. & Sharma, V. Electrohydrodynamic instability of a rotating Walters’ (model B’) fluid in a porous medium: Brinkman model. Mech. Mech. Eng.23, 138–143 (2019). [Google Scholar]
- 23.Rana, G. C., Gautam, P. K. & Saxena, H. Electrohydrodynamic thermal instability in a Walters’ (model B’) rotating nanofluid saturating a porous medium. J. Serbian Soc. Comput. Mech.13, 19–35 (2019). [Google Scholar]
- 24.Gautam, P. K., Rana, G. C. & Saxena, H. Stationary convection in the electrohydrodynamic thermal instability of Jeffrey nanofluid layer saturating a porous medium: Free-free, rigid-free, and rigid-rigid boundary conditions. J. Porous Media23, (11) (2020).
- 25.Kumar, M. & Singh, S. K. New exact solutions of a second grade MHD flow through porous media using travelling wave method. Punjab Univ. J. Math.55, 471–482 (2023). [Google Scholar]
- 26.Shahid, A. et al. Numerical spectral approach for studying activation energy behavior in viscoelastic fluid flow through non-Darcian medium. Numer. Heat Transf. Part A Appl.2024, 1–15 (2024). [Google Scholar]
-
27.Panda, S. et al. Computation of
 hybrid nanofluid flow in stretchable (shrinkable) wedge with variant magnetized force and heat generation. Eng. Sci. Technol. Int. J.58, 101839 (2024). [Google Scholar]
hybrid nanofluid flow in stretchable (shrinkable) wedge with variant magnetized force and heat generation. Eng. Sci. Technol. Int. J.58, 101839 (2024). [Google Scholar] - 28.Akbar, A. A. et al. Magnetized heat transfer visualization through computational modeling of third-grade fluid via exponentially stretching cylinder. Mod. Phys. Lett. B38, 2450334 (2024). [Google Scholar]
- 29.Hafed, Z. S., Arafa, A. A., Hussein, S. A., Ahmed, S. E. & Morsy, Z. Bioconvective blood flow of tetra composition nanofluids passing through a stenotic artery with Arrhenius energy. Numer. Heat Transf. Part B Fundam.86, 580–603 (2025). [Google Scholar]
- 30.Nagy, M., Hussein, S. A. & Mansi, A. H. Fourth-grade nanofluid model with dissipative and nonlinear radiative properties transported peristaltically via a flexible diverging duct holding a porous media under the influence of concentration and heat convection in an induced magnetic field. Numer. Heat Transf. Part A Appl.86, 4814–4840 (2025). [Google Scholar]
- 31.Eringen, A. C. Theory of micropolar fluids. J. Math. Mech.16, 1–18 (1966). [Google Scholar]
- 32.Khan, M. N., Nadeem, S. & Muhammad, N. Micropolar fluid flow with temperature-dependent transport properties. Heat Transf.49, 2375–2389 (2020). [Google Scholar]
- 33.Eldabe, N. T., Hussein, S. A., Gabr, M. E. & Zaher, A. Z. A novel mathematical model of MHD boundary layer flow of an activated micropolar nanofluid over a stretching surface under the effect of electro-osmosis forces. Mod. Phys. Lett. B37, 2350153 (2023). [Google Scholar]
- 34.Sharif, H., Habib, D. & Ali, B. Bejan number and entropy generation analysis of unsteady MHD non-Newtonian micropolar squeezed trihybrid nanofluid flow. Partial Differ. Equ. Appl. Math.10, 100703 (2024). [Google Scholar]
- 35.Hafed, Z. S., Hussein, S. A., Alenazi, A., Arafa, A. A. & Ahmed, S. E. Impacts of Arrhenius energy and viscous dissipation on variable properties of viscoelastic nanofluid flow with slip velocity. Int. J. Model. Simul.2023, 1–19 (2023). [Google Scholar]
- 36.Hussein, S. A., Ahmed, S. E., Arafa, A. A. & Elshekhipy, A. A. Temperature-dependent electrical conductivity impact on radiative and dissipative peristaltic transport of boron nitride-ethylene glycol nanofluid through asymmetric channels. ZAMM-Z. Angew. Math. Mech.104, e202300136 (2024). [Google Scholar]
- 37.Ahmed, S. E., Arafa, A. A. & Hussein, S. A. Viscous dissipation and Joule heating in case of variable electrical conductivity Carreau-Yasuda nanofluid flow in a complex wavy asymmetric channel through porous media. Mod. Phys. Lett. B38, 2450369 (2024). [Google Scholar]
- 38.Hussain, M. et al. Characterization of thermal buoyancy forces and suction on bioconvective magnetohydrodynamic dusty nanofluid flow over a stretching surface. Mod. Phys. Lett. B2025, 2550209 (2025). [Google Scholar]
- 39.Abdelsalam, S. I., Mekheimer, K. S. & Zaher, A. Z. Alterations in blood stream by electroosmotic forces of hybrid nanofluid through diseased artery: Aneurysmal/stenosed segment. Chin. J. Phys.67, 314–329 (2020). [Google Scholar]
- 40.Mekheimer, K. S., Zaher, A. Z. & Hasona, W. M. Entropy of AC electro-kinetics for blood mediated gold or copper nanoparticles as a drug agent for thermotherapy of oncology. Chin. J. Phys.65, 123–138 (2020). [Google Scholar]
- 41.Devi, J., Sharma, V., Thakur, A. & Rana, G. C. Linear stability analysis of electro-convection in dielectric Oldroydian nanofluid. Heat Transfer51(8), 7787–7804 (2022). [Google Scholar]
- 42.Sharma, V., Devi, J. & Rana, G. C. Electrohydrodynamic instability in dielectric rotating Oldroydian nanofluid layer. J. Taibah Univ. Sci.17(1), 2229087 (2023). [Google Scholar]
- 43.Wang, F. et al. MHD Williamson nanofluid flow over a slender elastic sheet of irregular thickness in the presence of bioconvection. Nanomaterials11(9), 2297 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Waage, P., & Guldberg, C. M. Studier over Affiniteten [Studies of affinities]. Forhandlinger i Videnskabs-Selskabet i Christiania, 35-45 (1864).
- 45.Waage, P. Forsøg til Bestemmelse af Lovene for Affiniteten [Experiment for the determination of the laws of affinity]. Forhandlinger i Videnskabs-Selskabet i Christiania, 92–94 (1864).
- 46.Guldberg, C. M. Foredrag om Lovene for Affiniteten, specielt Tidens Indflydelse paa de kemiske Processer [Lecture on the laws of affinity, especially the influence of time on chemical processes]. Forhandlinger i Videnskabs-Selskabet i Christiania, 111–120 (1864).
- 47.Rehman, S. U. et al. The Casson dusty nanofluid: Significance of Darcy-Forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics10(16), 2877 (2022). [Google Scholar]
- 48.Awad, F. G., Motsa, S. & Khumalo, M. Heat and mass transfer in unsteady rotating fluid flow with binary chemical reaction and activation energy. PLoS ONE9(9), e107622 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nazar, R., Amin, N., Filip, D. & Pop, I. Stagnation point flow of a micropolar fluid towards a stretching sheet. Int. J. Non-Linear Mech.39(7), 1227–1235 (2004). [Google Scholar]
- 50.Dey, D. & Chutia, B. Dusty nanofluid flow with bioconvection past a vertical stretching surface. J. King Saud Univ. Eng. Sci.34(6), 375–380 (2022). [Google Scholar]
- 51.Sarlo, E., Svoronos, P. & Kulas, P. Calculation of equilibrium constant in esterification reactions. J. Chem. Educ.67(9), 796 (1990). [Google Scholar]
- 52.Lou, Q. et al. Micropolar dusty fluid: Coriolis force effects on dynamics of MHD rotating fluid when Lorentz force is significant. Mathematics10(15), 2630 (2022). [Google Scholar]
- 53.Wang, J. et al. Computational analysis for bioconvection of microorganisms in Prandtl nanofluid Darcy-Forchheimer flow across an inclined sheet. Nanomaterials12(11), 1791 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Arikoglu, A., Ozkol, I. & Komurgoz, G. Effect of slip on entropy generation in a single rotating disk in MHD flow. Appl. Energy85(12), 1225–1236 (2008). [Google Scholar]
- 55.Sharma, B. K., Kumar, A., Gandhi, R., Bhatti, M. M. & Mishra, N. K. Entropy generation and thermal radiation analysis of EMHD Jeffrey nanofluid flow: Applications in solar energy. Nanomaterials13(3), 544 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hussain, S., Haq, F., Ghazwani, H. A., Saleem, M. & Hussain, A. Entropy optimization in bio-convective chemically reactive flow of micropolar nanomaterial with activation energy and gyrotactic microorganisms. Case Stud. Thermal Eng.55, 104131 (2024). [Google Scholar]
- 57.Das, D., Makinde, O. D. & Kairi, R. R. Analysis of entropy generation and MHD thermo-solutal convection flow of Ellis nanofluid through inclined microchannel. ZAMM-J. Appl. Math. Mech.104(10), e202300831 (2024). [Google Scholar]
- 58.Panda, S., Ontela, S., Pattnaik, P. K. & Mishra, S. R. Radiating heat effect on Powell-Eyring blood-based hybrid nanofluid over a Riga plate with thermal stratification Cattaneo-Christov heat flux model. Partial Diff. Equ. Appl. Math.11, 100769 (2024). [Google Scholar]
- 59.Panda, S. et al. Ferromagnetic effect on Casson nanofluid flow and transport phenomena across a bi-directional Riga sensor device: Darcy-Forchheimer model. Nanotechnol. Rev.13(1), 20240021 (2024). [Google Scholar]
- 60.Ali, B. et al. Significance of dust particles volume fraction to optimization of entropy in magnetohydrodynamic mixed convection flow via inclined surface. J. Mol. Liq.394, 123706 (2024). [Google Scholar]
- 61.Ramesh, G. K., Gireesha, B. J. & Bagewadi, C. S. Heat transfer in MHD dusty boundary layer flow over an inclined stretching sheet with non-uniform heat source/sink. Adv. Math. Phys.1, 657805 (2012). [Google Scholar]
- 62.Jalil, M., Asghar, S. & Yasmeen, S. An exact solution of MHD boundary layer flow of dusty fluid over a stretching surface. Math. Probl. Eng.2017, 2307469 (2017). [Google Scholar]
- 63.Wang, C. Y. Free convection on a vertical stretching surface. ZAMM-J. Appl. Math. Mech.69, 418–420 (1989). [Google Scholar]
- 64.Khan, W. A. & Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf.53, 2477–2483 (2010). [Google Scholar]
- 65.Srinivasulu, T. & Goud, B. S. Effect of inclined magnetic field on flow, heat and mass transfer of Williamson nanofluid over a stretching sheet. Case Stud. Therm. Eng.23, 100819 (2021). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All the data used during this study is accessible within the manuscript.