A fluorescent-protein spin qubit

Abstract

Quantum bits (qubits) are two-level quantum systems that support initialization, readout and coherent control¹. Optically addressable spin qubits form the foundation of an emerging generation of nanoscale sensors^2–7. The engineering of these qubits has mainly focused on solid-state systems. However, fluorescent proteins, rather than exogenous fluorescent probes, have become the gold standard for in vivo microscopy because of their genetic encodability^8,9. Although fluorescent proteins possess a metastable triplet state¹⁰, they have not been investigated as qubits. Here we realize an optically addressable spin qubit in enhanced yellow fluorescent protein. A near-infrared laser pulse enables triggered readout of the triplet state with up to 20% spin contrast. Using coherent microwave control of the enhanced-yellow-fluorescent-protein spin at liquid-nitrogen temperatures, we measure a (16 ± 2) μs coherence time under Carr–Purcell–Meiboom–Gill decoupling. We express the qubit in mammalian cells, maintaining contrast and coherent control despite the complex intracellular environment. Finally, we demonstrate optically detected magnetic resonance in bacterial cells at room temperature with contrast up to 8%. Our results introduce fluorescent proteins as a powerful qubit platform that paves the way for applications in the life sciences, such as nanoscale field sensing and spin-based imaging modalities.

An optically addressable fluorescent-protein spin qubit is realized using enhanced yellow fluorescent protein; the qubit can be coherently controlled at liquid-nitrogen temperatures and the spin detected at room temperature in cells.

Main

Qubits are the fundamental building blocks of quantum technologies. Unlike classical bits, which can exist in only two states, qubits are two-level quantum systems that can exist in a superposition of both states and can be manipulated and measured with high precision¹. In quantum sensing applications, these qubits are used as nanoscale probes whose quantum state can be initialized, coherently controlled and read out, allowing them to detect minute environmental changes with exceptional sensitivity^2–7. Optically addressable qubit sensors capable of measuring nanoscale magnetic fields^11–13, electric fields¹⁴ and temperature^15–17 have had a lasting impact on the physical sciences^3,18–21. In contrast, their adoption in the life sciences has been limited, with most applications remaining at the proof-of-concept stage. A molecule-scale genetically encodable qubit sensor could enable ultra-sensitive measurement techniques for fundamental research and medical diagnostics that are complementary to existing quantum sensing platforms^5,6.

Current quantum sensing platforms offer exceptional sensitivities but are often constrained by their size, complex surface chemistry and incompatibility with genetic techniques—limiting their use in biological measurements. Nitrogen-vacancy centres in diamond nanocrystals stand out as sensors with a certain degree of cellular delivery^22,23 and targeting^24,25 capability. However, efficient delivery and targeting with nanoparticles has remained a significant challenge. For example, quantum dots, arguably the most advanced nanoparticle-based imaging technology, struggle to efficiently label intracellular structures and processes in vivo, despite over a decade of intensive research^26,27. Optically addressable molecular spin qubits, such as polycyclic aromatic hydrocarbons^28–31, metal–organic complexes^32–34 and radical systems^35,36, offer potential advantages over solid-state systems. However, the systems examined thus far each have their own set of shortcomings, including low spin contrast, poor photon-emission rates, lack of water solubility, the requirement of a solid-state host or reactivity with ambient air, which preclude their use for most biosensing applications (an overview of different sensing platforms is given in Extended Data Fig. 1).

Extended Data Fig. 1. Comparison of different sensing platforms.

The x-axis indicates the distance between the qubit and the target molecule, and the y-axis indicates the sensor sensitivity. Circles (and star) indicate systems that have been delivered into cells. Open boxes denote systems that have not been delivered into cells. Typical state-of-the-art sensitivities for vapor cells (green)^74–76, SQUIDs (brown)^77–80, Nitrogen-vacancy centres in bulk diamond (blue boxes)^49,81–84, Nitrogen-vacancy centres in nanodiamonds (blue circle)^13,85–87, and molecular qubits in a non-aqueous host (red boxes)^33,35 are indicated. An ensemble of $773\times {10}^6$ EYFP molecules in aqueous solution (i.e., this work) is indicated by a star. The red circle indicates the projected sensitivity of a single EYFP protein. We note that in a fusion protein the relevant length scale determining the sensitivity is the separation of the EYFP protein to the target protein (i.e., the size of the EYFP protein) and not the diffraction-limited excitation volume.

Here we introduce fluorescent proteins^8,9 as optically addressable spin qubits that are 3 nm in diameter and are readily genetically encodable in a large range of target systems. Genetic encoding allows the deterministic tagging of a target with a fluorescent reporter, forming a so-called fusion protein (Fig. 1a). As a result of genetic encoding in a fusion protein, the fluorescent proteins match the expression level, nanoscopic location and real-time concentration of the protein of interest. This direct one-to-one matching of a probe to a biological target has had a profound impact on the life sciences as it allows a level of correlation that is unparalleled by synthetic molecular fluorophores or nanoparticles^8,9,37. Decades of research in biochemistry have generated a vast library of fusion proteins consisting of fluorescent proteins deterministically tagged to thousands of biological targets. Interestingly, the fluorophore of these fluorescent proteins has a metastable triplet state¹⁰ and is used in this work as an optically addressable qubit.

Fig. 1. Photophysics of EYFP proteins and OADF readout scheme.

a, Concept of EYFP-based sensing approach. Left: a fusion protein consisting of an EYFP qubit conjugated to a target protein (grey). As an illustrative example, the structure of an EYFP–glutaredoxin fusion protein is shown⁶². Genetic encoding ensures that every target protein is within a few nanometres proximity of exactly one EYFP sensor qubit. Right: to enhance sensitivity, an ensemble of fusion proteins within the optical excitation volume is probed. It is noted that, in this paper, we limit ourselves to investigating the physics of EYFP and not actual fusion proteins. b, Energy-level diagram of EYFP with OADF readout scheme. c, The natural transition orbital structure for the T1 state, calculated by ab initio calculations. d, Raw photoluminescence (PL) signals (top) and PL contrast (bottom) of OADF-based spin readout as a function of time after the onset of the 912-nm laser pulse for a π-pulse on the T_x–T_z (purple), T_y–T_z (blue) transition and the OADF signal with no microwave pulse (grey). The measurement sequence above the figure illustrates the timing of the microwave and optical pulses. The ‘detector’ channel represents the timing of the acousto-optic modulator used to gate the detector. Panel d is measured at 80 K.

Protein qubit and spin readout

Our approach uses a custom confocal microscope to optically address the metastable triplet spin state of enhanced yellow fluorescent protein (EYFP; Fig. 1b and Extended Data Fig. 2). The fluorophore of EYFP is located within its β-barrel and has a high absorption cross-section and quantum yield, and a short fluorescence lifetime. We initialize the EYFP spin with a 488-nm optical pulse, cycling the fluorophore between its ground (S0) and first-excited (S1) singlet state, which eventually undergoes intersystem crossing (ISC) to a metastable triplet (T1). The ISC rates are highly spin-projection dependent, leading to a buildup of spin polarization in the T1 state. Time-dependent density functional theory (TDDFT) calculations show that the T1 spin density is fully delocalized on the fluorophore (Fig. 1c). This metastable triplet presents challenges in its use as a spin qubit. Readout of the spin via the triplet decay is precluded by spin depolarization at most temperatures, which is fast compared with the millisecond-scale triplet lifetime^10,38. The extended triplet lifetime also limits the measurement sequence repetition rate, placing a bottleneck on the sensitivity.

Extended Data Fig. 2. Experimental setup.

488 nm and 912 nm diode lasers are gated using acousto-optic modulators (AOMs) and coupled into single-mode fibres. The fibres deliver laser light to a movable optical assembly for scanning over the sample. Dichroic mirrors overlap the excitation beams such that they are focused to the same spot by the microscope objective (60x magnification, 0.7 numerical aperture). The optical powers at the back of the objective for the 488 nm and 912 nm lasers are about 0.4 mW and 65 mW, respectively. Light collected from the sample passes through the dichroic mirrors and filters for removing the laser light, and is focused onto a single-mode fibre. The fibre acts as a pinhole, filtering out-of-focus light such that the signal is primarily from proteins illuminated with the highest laser intensities. After being gated by an AOM, the collected light is detected by a single-photon counting module or, in Extended Data Fig. 3a, a spectrometer. The sample is mounted in a custom imaging cell that holds 5 μl. It encapsulates the sample between two 500 μm thick sapphire windows, sealed by an o-ring. The sapphire substrate nearer to the cryostat window is photolithographically patterned with microwave loop structures using a lift-off process. The cryostat is evacuated to < 1 Torr and subsequently cooled following a temperature profile similar to Extended Data Fig. 4b. An external DC magnetic field is applied using a permanent magnet attached to a motorized translation stage outside of the cryostat. The microwave output of the RFSoC is fed into a series of amplifiers before being delivered to the loop structures. The microwave power before entering the cryostat was approximately 1 W.

We overcome the aforementioned challenges associated with the metastable triplet by utilizing a photophysical technique to shorten its lifetime^39,40 and enable on-demand spin readout (Fig. 1b). A 912-nm optical pulse drives the fluorophore from its triplet T1 state to a higher-lying triplet. TDDFT calculations (Methods) suggest the identity of this triplet to be the T2 state. Reverse intersystem crossing (RISC) from the triplet to the singlet manifold is accelerated in this T2 state. Following RISC, a delayed-fluorescence photon is emitted from S1. The arrival time of this delayed-fluorescence photon, in turn, encodes the T1 spin state as the RISC rates directly depend on the spin projection. Readout using this optically activated delayed-fluorescence (OADF)³⁹ scheme is approximately three orders of magnitude faster than via decay of the metastable triplet. The temporal separation of delayed from prompt fluorescence provides spin readout that is free of autofluorescence background.

We find that the OADF spectrum closely resembles the standard fluorescence spectrum at 80 K (Extended Data Fig. 3a), which indicates that the delayed-fluorescence photons are indeed emitted from the S1 to S0 transition. Furthermore, the wavelength of the intensity maxima at 80 K and room temperature are in good agreement, suggesting that the frozen protein maintains its structure in the vicinity of the fluorophore after being slowly cooled to cryogenic temperatures (Extended Data Fig. 4a,b).

Extended Data Fig. 3. Triplet state readout.

a, The EYFP initialized with a 488 nm laser pulse, then the spectra of the collected light recorded during a subsequent 912 nm laser pulse (purple), as well as the fluorescence collected during continuous illumination with the 488 nm laser (green and red). b, After initialization, the time trace of the collected light as a function of time after the onset of the 912-nm laser pulse without (grey), and with (purple) a microwave π-pulse on the T_x−T_z transition. c, The same as b, but on the T_y−T_z transition (blue). Panels b and c are measured at 80K and display similar data as Fig. 1d but over an increased time range.

Extended Data Fig. 4. Sample integrity.

a, Circular dichroism measurement taken on protein just after expression (before cooling), and after a full measurement sequence consisting of loading into the sample holder, cooling to cryogenic temperatures, and warming back up to room temperature (after cooling). b, Cooling profile of the cryostat platform. c, Bleaching lifetime of the protein versus laser power measured at the back of the objective. Panel a was measured at room temperature and c was measured at 4 K.

The addition of a microwave drive demonstrates the optical addressability of the spin state. After initialization, a microwave π-pulse induces population transfer between the spin sublevels in the T1 state. Detection of the OADF photons triggered by the 912-nm laser pulse yields a maximum spin contrast of 20% for the T_x–T_z transition and 10% for the T_y–T_z transition at 80 K (Fig. 1d and Extended Data Fig. 3b,c).

Optically detected magnetic resonance

We investigate the nature of the metastable triplet spin state through optically detected magnetic resonance (ODMR) spectroscopy. Figure 2a shows the ODMR contrast as a function of microwave frequency and external magnetic field. At zero field, we observe two characteristic resonances corresponding to the T_x–T_z and the T_y–T_z transitions. In general, for a spin-1 system, we expect a Hamiltonian of the form

$$H=ħD\left({S_z}^2-\frac{2}{3}\right)+ħE\left({S_x}^2-{S_y}^2\right)-ħ{\gamma }_{\mathrm{el}}\mathbf{S}\cdot \mathbf{B}$$ 1

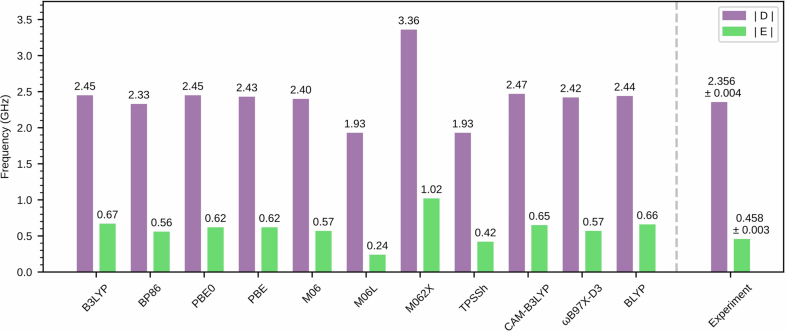
where $ħ$ denotes the reduced Planck constant, D and E are the zero-field splitting parameters, γ_el = (2π) × –28.025 GHz T⁻¹ is the gyromagnetic ratio of an electron, S is the vector of Pauli spin matrices for a spin-1 system, and B is the magnetic field. As the experiments are performed on a randomly oriented ensemble of EYFP molecules, we expect the ODMR signal to be an average over all possible molecular orientations, resulting in a powder spectrum⁴¹ (Extended Data Fig. 5). Fitting at low magnetic fields (the region where the uncertainty in the field calibration is small; Methods), we extract the zero-field splitting parameters D = (2π) × (2.356 ± 0.004) GHz and E = (2π) × (0.458 ± 0.003) GHz. These experimental values are in good agreement with computational results based on ab initio calculations with the B3LYP-optimized geometry and ωB97X-D3 functional D_DFT = (2π) × 2.42 GHz and E_DFT = (2π) × 0.57 GHz (Extended Data Fig. 6 and Supplementary Table 5). Using the fitted D and E parameters, we calculate the expected spectra of the powder-averaged transition frequencies as a function of magnetic field (Fig. 2b). The overall magnetic-field dependent broadening and asymmetric resonance profile is consistent with our model which also extrapolates well to higher fields exemplified at 34.1 mT (Fig. 2c bottom).

Fig. 2. ODMR spectroscopy of EYFP.

a, Experimental ODMR signal as a function of externally applied magnetic field. The faint resonance (indicated by the asterisk) at approximately ω = (2π) × 0.9 GHz is associated with microwave harmonics that drive the T_x–T_z and the T_y–T_z transitions. b, Simulated ODMR response based on the model from equation (1). The fit parameters (D, E, linewidth of resonance, and the T_x–T_z and the T_y–T_z amplitudes) are extracted from an ODMR measurement at low magnetic fields (Methods). The ODMR amplitude for the T_x–T_y transition is set to 0. c, Experimental (green and purple) and simulated (black) ODMR spectrum at 4.2 mT and 34.1 mT. Panels a and c are measured at 80 K.

Extended Data Fig. 5. Resonance frequencies vs. magnetic field.

Histogram of randomly oriented molecules’ resonance frequencies as a function of applied magnetic field using the Hamiltonian in eq. 1. Some molecules’ T_y−T_z and T_x−T_y transitions overlap at higher applied magnetic fields.

Extended Data Fig. 6. Calculated D and E parameters.

The calculated |D| and |E| parameters using TDDFT with B3LYP-optimized geometries and various functionals along with the experimentally measured values.

Qubit coherence

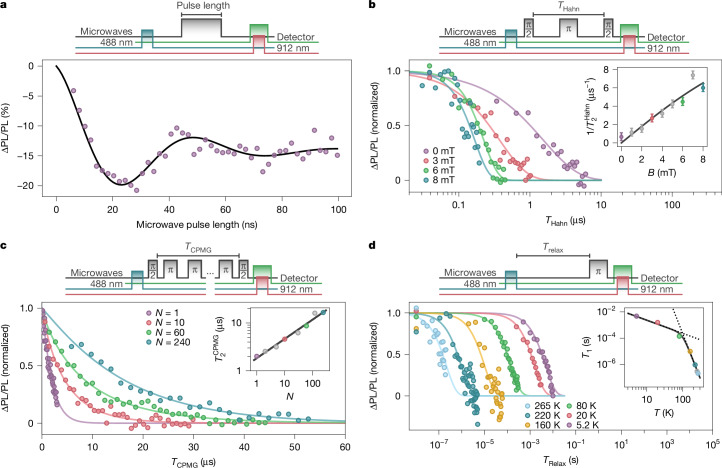
Driving the EYFP molecules with a fixed frequency that is resonant with the T_x–T_z transition results in coherent Rabi oscillations between the spin sublevels (Fig. 3a), with a spin contrast of 20%. The oscillations are highly damped, with a decay rate that increases with Rabi frequency as a result of random molecular orientations and microwave detuning (Methods and Extended Data Fig. 7).

Fig. 3. Coherent control of EYFP qubits.

a, Rabi oscillations of EYFP T_x–T_z transition driven at a frequency of (2π) × 2.815 GHz. The fit corresponds to an exponentially damped cosine (black). b, Spin coherence as a function of total evolution time (T_Hahn) under Hahn-echo decoupling for different magnetic fields, with stretched-exponential fits. Inset: the scaling of the Hahn-echo dephasing rate ($1/T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}$) as a function of external magnetic field and the corresponding theoretical model (black). c, The same as in b but under a CPMG decoupling sequence for different numbers of π-pulses (N) and no external field. Inset: $T_2^{\mathrm{CPMG}}$ scaling as a function of N and its corresponding fit (black). d, Contrast as a function of evolution time (T_relax) for different sample temperatures fit to exponential decays. Inset: the spin-lattice relaxation time (T₁) as a function of temperature fitted with 1/T₁ = AT + BT⁷, with fitted amplitudes A = 43 ± 8 K⁻¹ s⁻¹ and B = (47 ± 7) × 10⁻¹² K⁻⁷ s⁻¹. In all plots, grey data points indicate additional measurements shown in the inset but not the main plot for clarity. The fit errors in the insets of c and d are smaller than the data points and omitted. Panels a–c are measured at 80 K.

Extended Data Fig. 7. Rabi oscillation decay.

a, Simulation of the magnetic flux density and field vectors generated from an omega waveguide. The field inhomogeneity across our optical spot at the centre is negligible (< 2%). b, Experimentally observed Rabi oscillations fitted with a solid black line. The decay of the higher (lower) power Rabi oscillation is 18 ns (51 ns) and illustrated by a dashed black line. c, Simulated average population of an ensemble of randomly oriented molecules assuming a linewidth (2π) × 33 MHz. The decay of the higher (lower) power Rabi oscillation is 38 ns (77 ns) and illustrated by a dashed black line. The corresponding distributions of Rabi rates are shown in the inset. d, Damped cosine fit parameters of the simulated Rabi oscillations. We note that the powers reported in the legends of b and c are not relative to each other. Panel b is measured at 80 K.

We measure the spin coherence time ($T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}$) using a Hahn-echo sequence to refocus dephasing caused by quasi-static magnetic fields (Fig. 3b). With no applied field, the $T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}$ is (1.5 ± 0.2) μs. We find that with increasing field, $T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}$ decreases to (140 ± 30) ns at 7 mT. The scaling of $T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}$ is a consequence of the T_x–T_z resonance resembling a clock-like transition^42,43, resulting in a dephasing rate $\frac{1}{T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}}\propto {\gamma }_{\mathrm{e}\mathrm{f}\mathrm{f}}\propto \frac{\gamma B_z}{\sqrt{{\left(E/{\gamma }_{\mathrm{e}\mathrm{l}}\right)}^2+{B_z}^2}}$ proportional to the effective gyromagnetic ratio (γ_eff). This rate is in good agreement with our observations (Fig. 3b, inset), suggesting that in the vicinity of the clock transition, qubit dephasing remains primarily limited by magnetic rather than electric-field noise.

Applying a Carr–Purcell–Meiboom–Gill (CPMG) sequence improves coherence by shifting the dynamical decoupling filter function to higher frequencies⁴⁴. With 240 π-pulses, we observe a $T_2^{\mathrm{CPMG}}$ of (16 ± 2) μs at 2.7 mT (Fig. 3c), which represents a 15-fold enhancement compared with $T_2^{\mathrm{H}\mathrm{a}\mathrm{h}\mathrm{n}}$. Repeating the CPMG measurement for different numbers of π-pulses (N) yields a scaling $T_2^{\mathrm{CPMG}}\propto N^{\left(0.40\pm 0.03\right)}$ (Fig. 3c, inset), which provides insights into the magnetic noise properties and can be connected to a power spectral density S(ω) ~ ω^−2/3 that falls off at higher frequencies (ω) (ref. ⁴⁵).

We characterize the spin-lattice relaxation time and its dependence on temperature by measuring the spin contrast between the qubit initialized in T_z and T_x as a function of wait time. At 80 K, the spin polarization follows an exponential decay with a lifetime of (141 ± 5) μs (Fig. 3d). For an integer-spin system, the depolarization rate is given by 1/T₁ = AT + BT⁷, where A and B are the amplitudes of direct and Raman processes, respectively⁴¹ (Fig. 3d, inset). This model provides a good fit to our data when the amplitudes are treated as free parameters, but unambiguous identification of the exact relaxation mechanisms will require a more thorough investigation.

Operation at room temperature

At room temperature, the triplet depolarization time is shorter than the duration of a typical experiment, which hinders efficient initialization and readout. Interestingly, when the readout pulse is applied simultaneously with the microwave pulse, we observe a finite ODMR contrast in aqueous solution at room temperature—despite the fast spin relaxation (Fig. 4a and Extended Data Fig. 8). The finite contrast can be understood by considering that in the absence of an on-resonance microwave pulse, the readout laser will rapidly deplete the two shorter-lived T1 spin sublevels (T_x,y). In comparison, when an on-resonance microwave pulse is applied to the T_x–T_z or the T_y–T_z transitions, the T1 spin sublevels are mixed with each other, leading to rapid depletion of all three sublevels. We confirm the magnetic origin of the resonance by repeating the experiment in the presence of an external field (Fig. 4b).

Fig. 4. Room-temperature quantum sensing.

a, Contrast of OADF-based spin readout as a function of time after the onset of the 912-nm laser pulse for the T_x–T_z (purple) and the T_y–T_z (blue) transition. b, ODMR in aqueous solution at various magnetic fields. The red points indicate the frequencies of the field sensing experiment in c. c, DC magnetic-field sensing operating at a bias field of 36.5 mT by measuring the difference in the ODMR contrast defined as C_T = [PL_sig(ω_a) − PL_sig(ω_b)/PL_back]. The measurement is performed at the two frequencies ω_a = (2π) × 3.54 GHz and ω_b = (2π) × 3.43 GHz indicated in b. PL_sig(ω), the OADF signal at a microwave frequency (ω); PL_back, the OADF signal in the absence of a microwave drive. Panels a–c are measured at room temperature.

Extended Data Fig. 8. YZ transition at room temperature.

ODMR spectra of the T_y−T_z transition at room temperature, exhibiting a broadened linewidth with an applied magnetic field.

We demonstrate the potential of our qubit as a room-temperature DC (static) magnetic-field sensor following an approach adapted from the atomic clock community⁴⁶. Detecting subtle shifts in the ODMR spectrum by measuring at two frequency points, one above and one below the T_x–T_z resonance (Fig. 4b, right), results in a contrast difference that is a linear function of a small external magnetic field (δB; Fig. 4c). From this measurement, we can estimate a DC magnetic-field sensitivity of 2.7 mT Hz^−1/2 for the detected EYFP ensemble (see Extended Data Figs. 9 and 10 and Methods for derivation and normalization to particle number). The presence of a clock transition at zero field requires us to operate at a bias magnetic field.

Extended Data Fig. 9. Knife-edge measurements.

In order to characterize the optical beam morphology, the microscope optical assembly is positioned to focus the 488 nm laser spot on a set of optical windows outside the cryostat that mimic the measurement conditions. The power transmitted through a photolithographically-patterned metal edge in the sample plane is measured as a function of transverse displacements in X axis a and Y axis b. This measurement is repeated for various axial displacements. The power versus transverse position is fitted to an error function. The beam diameter extracted by the error function fit is then examined as a function of axial displacement (inset). A fit to a hyperbolic profile allows for the extraction of the beam waist and Rayleigh range. The beam appears to display coma or spherical aberration, as well as astigmatism. These aberrations are likely the result of errors in alignment through the cryostat window and sample coverslip.

Extended Data Fig. 10. Sensitivity estimation.

a, Residuals from Fig. 4c used to estimate the DC sensitivity at room temperature. b, CPMG sequence used for AC magnetic field sensing. c, $n_{\mathrm{\Delta },250k}$ and its fit (black). d, The residuals estimated from $n_{\mathrm{\Delta },250k}$ and its fit. e, The estimated η. Panel (c) is measured at 80 K.

Qubit sensor expressed in cells at room temperature

We highlight the potential of our genetically encodable qubit by performing spin measurements of EYFP expressed in human embryonic kidney (HEK) 293T cells at 175 K and BL21(DE3) Escherichia coli (E. coli) cells at room temperature (Methods). Fluorescence imaging of HEK cells adhered to the sapphire substrate confirms that the protein remains localized within the cells (Fig. 5a). After cooling the sample to 175 K, confocal fluorescence scans correlate well with the room-temperature wide-field images (Extended Data Fig. 11). Measuring over six bright regions containing cells, we record an ODMR signal (Fig. 5b, red). The OADF associated with these scans correlates well with the cells observed in wide-field and confocal fluorescence images. Measuring only the pixels outside of cells results in a dim background signal, indicating that the spin resonance signature originates from the bright cells rather than any extracellular EYFP. Repeating the same process, we drive Rabi oscillations in the cells (Fig. 5c). The ODMR and Rabi signals are consistent with those of the purified protein, indicating that the spin and optical interface are robust to operation within a cell. Comparing the OADF signal in HEK cells with that of purified proteins, we estimate an EYFP concentration in the HEK cells of (11 ± 7) μM, a value consistent with what would be expected from transient transfection⁴⁷. In a second experiment, we examined the feasibility of conducting ODMR measurements within living cells at room temperature. To do so, we transferred a pellet of E. coli bacteria expressing EYFP onto our sample stage (Extended Data Fig. 12). Figure 5d shows the resulting ODMR spectra of EYFP in E. coli at room temperature in the absence and presence of an external magnetic field. The high contrast observed in our measurements is enabled by the time-delayed nature of the OADF signal, which effectively suppresses autofluorescence background signals originating from the cellular environment.

Fig. 5. Coherent control in cells.

a, A wide-field fluorescence image of HEK 293T cells expressing cytosolic EYFP (blue). A loop structure for applying the microwave drive is visible. ODMR scans in b are measured in the white outlined regions, and OADF is thresholded for the brightest pixels (red). Scale bar, 100 μm. b, ODMR signal averaged over the bright pixels (red, on cells) and dark pixels (purple, off cells). Instead of contrast, the PL difference normalized to the number of pixels is shown to illustrate the size of the signal contributed by the background. c, Rabi oscillations of T_x–T_z transition driven at (2π) × 2.835 GHz measured with the same process as in b. d, ODMR spectra of EYFP measured on E. coli cells. The wide-field image in a is measured on HEK cells at room temperature. The red pixel overlay in a is measured on HEK cells at 175 K. b and c are measured at 175 K. Panel d is measured on a pellet of E. coli at room temperature.

Extended Data Fig. 11. Cell measurements.

a, Brightfield image corresponding to Fig. 5a. b, Brightfield image of loop structure scanned in Fig. 5c to measure Rabi oscillations. c, Confocal fluorescence image of a. d, OADF signal acquired during ODMR scan of selected areas in c. e, Same as Fig. 5a. f, Same as c but on the loop structure in b. g, Same as d but corresponding to f. h, Same as e but with the thresholded pixels in g. Panels a, b, e, h were taken at room temperature. Panels c, d, f, g, and the red highlighted pixels in e, h were taken at 175 K.

Extended Data Fig. 12. Mechanism of room temperature ODMR.

a, Widefield fluorescence image of E. coli expressing EYFP that was measured in Fig. 5d. The red dot marks the measurement position. b, Readout contrast as a function of time after the onset of the 912 nm readout pulse when it is applied 10 μs after the 488 nm laser pulse ends. A 100 ns microwave pulse is applied 100 ns after the onset of OADF. c, Readout contrast as a function of time after the onset of the 912 nm readout pulse when the microwave drive and readout laser have no temporal overlap. A 100 ns microwave pulse at (2π) × 2.79 GHz is applied immediately after the 488 nm pulse. A 100 ns delay between the microwave pulse and 912 nm readout pulse ensures no temporal overlap.

Discussion and outlook

Our results establish fluorescent proteins as a genetically encodable spin qubit platform. We estimate that the measured EYFP ensemble has an upper-bounded AC sensitivity of 5.11 μT Hz^−1/2 at liquid-nitrogen temperatures (see Extended Data Figs. 9 and 10 and Methods for derivation and normalization to particle number) and an upper-bounded DC sensitivity of 2.7 mT Hz^−1/2 at room temperature. For reference, a ¹⁹F spin located 5 nm away from the qubit—a practical distance for an EYFP fusion protein⁴⁸—would generate a magnetic field of approximately 18 nT at the qubit’s location. For a ¹⁹F polarization p, these parameters translate into a ¹⁹F number sensitivity of $\frac{1}{p}94\mathrm{pmol}{\mathrm{Hz}}^{-1}$ (Methods)—if an electron spin instead of a nuclear spin was detected, we would expect a $\frac{1}{p}200\mathrm{amol}{\mathrm{Hz}}^{-1}$ sensitivity. While this sensitivity falls short of state-of-the-art nitrogen-vacancy centres in bulk diamond sensors⁴⁹, the ability to utilize the large existing library of genetically encoded fusion proteins for in vitro and in vivo experiments provides significant advantages over diamond sensors.

Motivated by our findings, we speculate that EYFP-based qubit sensors may enable microscale electron paramagnetic resonance sensing. For instance, genetically fusing the sensor to target proteins could allow probing oxidation states of metalloproteins, performing double-electron–electron-resonance-style distance measurements, and investigating drug-binding mechanisms. The ability to genetically encode our sensor enables the labelling of thousands of target proteins within a cell, tissue or whole organism using existing expression libraries. At sufficiently high target protein concentrations, this approach could enable experiments at the single-cell level. With substantial improvements in sensitivity, the detection of nuclear magnetic resonance spectra may become feasible. This would offer insights into post-translational modifications, such as phosphorylation events, conformational changes of ¹⁵N-labelled proteins and protein–ligand interactions involving ¹⁹F-containing drugs. Realizing these long-term goals will require further improvements in photostability and sensitivity, as well as the development of new quantum sensing protocols.

Optical detection and control of the spin state of fluorescent proteins could also present opportunities for novel imaging modalities. For example, multiplexed detection of different fluorophores using more than their emission spectra has been demonstrated using additional degrees of freedom such as their fluorescence⁵⁰ or triplet lifetimes⁵¹. The narrow room-temperature ODMR resonances of our fluorescent-protein qubit can serve as an additional dimension for multiplexed imaging. We speculate that such an approach could potentially allow for up to 20 distinct ‘colours’—assuming a tens-of-MHz ODMR linewidth and achievable shifts in the zero-field splitting parameters (D and E) on the order of several hundred megahertz. Multiplying this with the already available palette of fluorescent proteins possessing distinct emission spectra could enable up to 100 orthogonal colours, with further colours possible through T1-lifetime-based multiplexing⁵¹. We propose that engineering fluorescent proteins with different zero-field splittings and T1 lifetimes could be achieved through modifying the protein’s primary structure in the vicinity of the fluorophore. Furthermore, taking advantage of the Zeeman shift in an external field gradient would allow for parallelized super-resolution imaging, similar to magnetic resonance imaging⁵². Realizing these imaging modalities will require advances in reducing photobleaching, improving spin-readout efficiency, engineering fluorescent proteins with tunable zero-field splitting, and/or creating well-controlled magnetic-field gradients.

Enhancements in qubit sensitivity can be achieved by improving coherence or spin readout. At liquid-nitrogen temperatures, coherence is limited by magnetic-field noise, which can be drastically reduced by substituting nearby proton spins with deuterium, resulting in expected coherence times approaching 100 μs (refs. ^53,54). Individual EYFP molecules are routinely detected in single-molecule microscopy⁵⁵. This suggests that our readout signal can be improved by several orders of magnitude (Methods). The initialization of the qubit requires an efficient population transfer from the singlet ground state to the metastable triplet state. This can be accomplished by optimizing the excitation conditions and reducing unwanted RISC caused by the initialization laser^38,56. Furthermore, OADF readout yields at most one photon per molecule. This limit can, however, be overcome by utilizing fluorescence cycling in the singlet manifold for readout, resulting in an increase in photon counts of up to 300-fold (Methods; the ultimate limit is set by the inverse of the triplet yield^38,39). Optimizing the imaging optics could further improve per-molecule collection efficiency by a factor of 810 (Methods). Collectively, these improvements would yield at least a 500-fold improvement in AC and DC sensitivity. In addition to the above approaches for increasing the readout signal, combining our system with existing single-molecule microscopy techniques could enable the detection of individual EYFP qubit sensors⁵⁷, paving the way to single-molecule spin experiments. Finally, we note that photobleaching poses the biggest limitation (Extended Data Fig. 4c). However, over the years, different strategies have been developed to address photobleaching in fluorescence microscopy. Many of these strategies can be translated to our protein qubit. This includes purging oxygen from the cell media or the addition of an oxygen scavenger as well as replenishing bleached fluorophores, in an approach similar to point accumulation for imaging in nanoscale topography⁵⁸.

Our OADF readout unlocks a large class of metastable triplet systems as spin qubits. Although EYFP is the first system we have investigated, optically activated RISC has been observed in many other fluorescent proteins and dye molecules^39,40. In fact, systems comprising a singlet ground and excited state coupled to a metastable triplet are ubiquitous among fluorescent molecules, many of which may possess the requisite photophysical parameters for their triplet state to be addressed using our spin-readout technique. The exploration of these molecules may be accelerated by the computational methods demonstrated here for predicting the optical transitions and zero-field splitting parameters.

Having demonstrated optical initialization and readout of the EYFP spin and coherence times exceeding 15 μs establishes fluorescent proteins as an optically addressable spin qubit platform. These protein-based qubits open the door to applying both quantum information science and bioengineering strategies for further development. The quantum information science and bioengineering fields have developed a diverse array of approaches to engineering complex systems. For example, the creation of highly regular structures through molecular self-assembly⁵⁹ could allow for the engineering of one-, two- and three-dimensional paramagnetic molecular arrays⁶⁰. The many-body dynamics of these spin systems could be optically read out with a fluorescent-protein qubit. Furthermore, traditional quantum engineering approaches to improving optical properties and spin coherence rely on gaining an understanding of qubit physics from first principles. Genetically encodable qubits such as EYFP can be engineered using directed evolution, a black-box optimization approach that uses high-throughput screening of protein variants. Directed evolution of fluorescent proteins has resulted in a vast array of different spectral properties and functions, which highlight their tunability and rich photophysics⁶¹. Directed evolution on our EYFP qubit could be used to optimize its optical and spin properties and even reveal unexpected insights into qubit physics. Protein-based qubits are positioned to take advantage of techniques from both quantum information sciences and bioengineering, with potentially transformative possibilities in both fields.

Methods

Protein expression and purification

In Figs. 1–4 and 5d, we measured EYFP with the mutations S2insL/S65G/V68L/S72A/T203Y/H231L of avGFP, with an additional 6x His tag on the N-terminus (the full amino acid sequence is given at the end of this section). The protein was expressed using a pET vector constructed using HiFi assembly from Addgene plasmids 78466 and 29653. The resulting vector was sequenced to confirm the inclusion of the EYFP gene. The plasmid was transformed into BL21 (DE3) E. coli for protein expression. Single colonies of the cells were picked from a kanamycin plate and incubated in 5 ml LB medium at 37 °C, 250 RPM overnight. Cultures were transferred into a 2-l flask with 500 ml LB medium and continued incubating at 37 °C. Once the optical density at 600 nm D₆₀₀ reached about 0.6, protein expression was induced with isopropyl β-D-1-thiogalactopyranoside and the temperature was lowered to 30 °C. Cells were pelleted after 16 h and lysed using 4 ml B-PER (Thermo Scientific) per gram of cells. The supernatant pre- and post-lysis appeared yellow and was loaded onto a Ni-NTA spin column (Thermo Scientific) and washed 3 times using 10 ml solution containing 50 mM sodium phosphate buffer, 500 mM NaCl and 25 mM imidazole. Elution buffer (50 mM sodium phosphate buffer, 500 mM NaCl and 250 mM imidazole) was used to elute the purified protein from the column. Buffer exchange using a 3-kDa molecular weight cut-off ultracentrifugal unit suspended the protein in the sample buffer (50 mM tris, 150 mM NaCl, 2 mM EDTA). The protein solution was concentrated, estimated to be 6 mM by measuring the optical density of the samples at 515 nm, and stored at −80 °C. When measured at cryogenic temperatures, the protein solution was mixed with 20% v/v DMSO.

The following is the amino acid sequence of the EYFP we measured from E. coli: MGSSHHHHHHENLYFQSNIMLSKGEELFTGVVPILVELDGDVNGHKFSVSGEGEGDATYGKLTLKFICTTGKLPVPWPTLVTTFGYGLQCFARYPDHMKQHDFFKSAMPEGYVQERTIFFKDDGNYKTRAEVKFEGDTLVNRIELKGIDFKEDGNILGHKLEYNYNSHNVYIMADKQKNGIKVNFKIRHNIEDGSVQLADHYQQNTPIGDGPVLLPDNHYLSYQSALSKDPNEKRDHMVLLEFVTAAGITLGMDELYKSTGSG*.

Preparation for ODMR of bacteria cells at room temperature

EYFP was expressed in E. coli as discussed above. The E. coli were pelleted, the supernatant was replaced by sample buffer (50 mM tris, 150 mM NaCl, 2 mM EDTA) and the pellet was stored at −20 °C. The sample was subsequently thawed at room temperature, loose cell debris and supernatant were discarded, and a sample of cells was scraped onto a 0.17-mm coverslip. The coverslip was placed on a printed circuit board and immediately measured using an oil immersion objective with 1.3 numerical aperture.

EYFP expression in mammalian cells

The plasmid pNWA171 encodes a second-generation chimeric antigen receptor (CAR) targeting CD19. The vector and a gene fragment encoding EYFP (Twist Bioscience) were both digested with MulI and SbfI restriction enzymes and then ligated with T4 ligase. The resulting plasmid was sequenced to confirm the inclusion of the EYFP gene and the deletion of the CAR19 gene. The plasmid was maxi-prepped, transfected with the Lenti-X 293T cell line (Takara Bio) with PEI max (Polysciences), and then cultured for 48 h for EYFP production. On the day of the experiment, a coverslip with photolithographically patterned waveguides was sterilized using 70% isopropanol, washed extensively with PBS and then incubated with 0.01% poly-l-lysine (MilliporeSigma) solution for 5 min. The residual poly-lysine solution was washed extensively with PBS. Cells were dissociated from the culture flask with trypLE (Gibco, Thermo Fisher Scientific) and then resuspended in DMEM supplemented with 10% HIFBS with a cell density of 1 × 10⁷ cells per ml. Finally, the cell suspension was incubated on the coverslip under 37 °C, 5% CO₂ for 3 h. The coverslip was gently washed with PBS, allowing only the adherent cells to remain for the experiments in Fig. 5a–c. The cells were then imaged in PBS.

The following is the amino acid sequence of the EYFP expressed in mammalian cells: MLSKGEELFTGVVPILVELDGDVNGHKFSVSGEGEGDATYGKLTLKFICTTGKLPVPWPTLVTTFGYGLQCFARYPDHMKQHDFFKSAMPEGYVQERTIFFKDDGNYKTRAEVKFEGDTLVNRIELKGIDFKEDGNILGHKLEYNYNSHNVYIMADKQKNGIKVNFKIRHNIEDGSVQLADHYQQNTPIGDGPVLLPDNHYLSYQSALSKDPNEKRDHMVLLEFVTAAGITLGMDELYK*.

Experimental methods

Experiments were performed in a closed-cycle liquid-helium cryostat with temperature control from 4 K to room temperature using a custom confocal microscope (Extended Data Fig. 2). Prolonged exposure to laser excitation results in photobleaching of the EYFP (Extended Data Fig. 4c). To counteract photobleaching, the microscope was scanned over the area within a single photolithographically patterned loop structure, except for the low temperature Rabi (Fig. 3a) and room temperature data (Figs. 4 and 5d), where it was at a fixed location. Digital signals to pulse the lasers and microwave tones for driving the spin transitions were generated using the Real Digital RFSoC 4×2 running the QICK platform⁶³ with a custom version of the software and firmware designed for optically addressable spin qubits. In Fig. 5, the wide-field fluorescence image was captured using a Leica DMi8 microscope.

Data analysis

OADF photon counts were integrated over the first approximately 300 ns following the rising edge of the 912-nm laser pulse and over multiple experiments. The contrast in Figs. 1d, 2a,c, 3a and 4a,b, and Extended Data Figs. 7b, 8, and 12b,c are defined by the following normalization C = [PL_sig(ω) − PL_back(ω)]/PL_back(ω), where PL_sig(ω) refers to the photoluminescence with microwave output switched on and PL_back(ω) refers to the photoluminescence with microwave output switched off. The contrast in Fig. 3b,c is defined as $C=\frac{\mathrm{PL}\left(\theta =-\mathrm{\pi }/2\right)-\mathrm{PL}\left(\theta =+\mathrm{\pi }/2\right)}{\mathrm{PL}\left(\theta =-\mathrm{\pi }/2\right)+\mathrm{PL}\left(\theta =+\mathrm{\pi }/2\right)}$ normalized to the fit maximum, where PL(θ) corresponds to the photoluminescence signal with the last microwave pulse having rotation angle θ. Finally, the contrast in Fig. 3d is defined as C = [PL(θ = π) − PL(θ = 0)]/PL(θ = 0). All stated errors are one standard deviation.

Sample degradation

The conformational stability of EYFP was interrogated using circular dichroism spectroscopy. The EYFP sample prepared at 100 μM in storage buffer (50 mM Tris, 150 mM NaCl and 2 mM EDTA; pH 7.4) was measured hours after purification and another sample of the same concentration was measured after cooling to 80 K in our cryostat at 5 mM concentration with 20% DMSO. Circular dichroism spectra between 180 nm and 260 nm at a scan speed of 100 nm min⁻¹ and bandwidth of 5 nm were taken using a Jasco J-1500 spectropolarimeter. Extended Data Fig. 4a shows the resulting data after averaging over three scans. The spectra show a minimum at 230 nm, indicating that the main secondary structure content of EYFP is a β-sheet configuration. No substantial differences were observed between the spectra of the two samples, suggesting that the cool-down and warm-up processes used in the experiments did not alter the structure of EYFP.

Computational methods

The orbital structures in Fig. 1c are the result of TDDFT^64,65 calculations on the negatively charged model of the EYFP fluorophore terminated with methyl groups. The geometry was optimized using the conductor-like polarizable continuum model⁶⁶ with a dielectric constant ε = 4 to mimic the protein environment. The ground-state geometry optimizations for the singlet (S0) and triplet (T1) states were performed using the Gaussian 16⁶⁷ package at B3LYP/def2-TZVP level. The ORCA 5.4.0 package⁶⁸ was used for the TDDFT calculations to compute the vertical excitation energies. Range-separated hybrid functionals CAM-B3LYP⁶⁹ and ωB97X-D3⁷⁰ were used with the B3LYP/def2-TZVP/ε = 4 optimized geometries and def2-QZVPP basis sets for the TDDFT calculations. The zero-field splitting calculations for the D and E parameters were performed at the T1 optimized geometry with a series of functionals shown in Extended Data Fig. 6. The absolute D and E parameters were calculated using spin–orbit coupling treated at the spin–orbit mean-field theory (as implemented in ORCA 5.4.0 package). The coupled-perturbed method was used for calculating the zero-field splitting tensor with DFT⁷¹.

TDDFT calculations

TDDFT calculations predict the first bright singlet–singlet excitation to occur from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO), showcasing a π → π* nature of the transition. This S0 → S1 transition corresponds to the experimental absorption at 2.54 eV. Both CAM-B3LYP and ωB97X-D3 predict an energy gap of about 3.02 eV between the S1 and S0 states. The results overestimate the experimental value, similar to an earlier report for gas-phase calculations⁷². The first bright excitation using the triplet optimized geometry occurs for T1 → T2, which also corresponds to a π → π* transition. Although this vertical excitation energy of 1.49 eV also overestimates the experimentally observed triplet–triplet absorption at 1.37 eV, it characterizes the T1 → T2 transition to involve a singly occupied molecular orbital (SOMO), where the electron is excited from SOMO-2 to SOMO-1. The oscillator strengths and transition characters for all the transitions are reported in Supplementary Tables 1–4.

Simulation of magnetic resonance spectrum

Solving for the eigenvalues of the Hamiltonian from equation (1) provides the T_x–T_z, T_y–T_z and T_x–T_y transition frequencies as a function of the magnetic field (B). Importantly the transition frequencies depend not only on the field strength but also on the molecule’s orientation relative to the magnetic field. Assuming that the EYFP molecules are randomly oriented, we sample 10,000 uniformly distributed orientations. To simulate the ODMR spectra in Fig. 2b,c, we incorporate the single-molecule ODMR linewidth (γ). The resonance for a single EYFP molecule is then modelled by a Lorentzian of the form $L\left(\omega \right)=\frac{a_{x-z}}{1+{\left(\frac{\omega -{\omega }_{x-\mathrm{z}}}{\gamma }\right)}^2}+\frac{a_{y-z}}{1+{\left(\frac{\omega -{\omega }_{y-z}}{\gamma }\right)}^2},$ where a_x−z and a_y−z denote the ODMR contrast, and ω_x–z and ω_y–z denote the transition frequencies for the T_x–T_z and the T_y–T_z transitions, respectively. It is noted that our model simplifies the fitting by only considering the T_x–T_z and T_y–T_z resonance while omitting the T_x–T_y transition, which has a reduced ODMR contrast and experimental data that overlap with a harmonic of our signal generator. We iteratively optimize the fit parameters D, E, a_x−z, a_y−z and γ by minimizing the cost function $C={\sum }_i{\left(n\left({\omega }_i\right)-L\left({\omega }_i\right)\right)}^2$, where $n\left({\omega }_i\right)$ denotes the experimentally observed ODMR spectra at the following fields: 2.1 mT, 4.5 mT, 6.1 mT, 8.2 mT and 10 mT. We find D = (2π) × (2.356 ± 0.004) GHz, E = (2π) × (0.458 ± 0.003) GHz, a_x−z = (0.17 ± 0.02), a_y−z = (0.129 ± 0.008) and γ = (2π) × (33 ± 4) MHz.

Rabi simulation

We computationally investigated the origin of the Rabi decay shown in Fig. 3a. Interestingly, we observed that the decay time increases with decreasing microwave power (Extended Data Fig. 7b) suggesting that loss in Rabi signal is not caused by dephasing. We simulated inhomogeneous broadening by sampling over a Gaussian distribution with a (2π) × 33 MHz standard deviation. The Rabi frequency depends on the molecule orientation with respect to the microwave drive field resulting in a fast decay that qualitatively captures our experimental observations (Extended Data Fig. 7c; a histogram of the Rabi frequencies is shown in the inset). In addition, the simulation captures the experimental behaviour that the decay time increases with decreasing microwave power (Extended Data Fig. 7d). We note that the inhomogeneous Rabi drive cannot be explained by spatial gradients caused by the loop geometry (Extended Data Fig. 7a).

Estimation of number of measured molecules

Knife-edge measurements of the 488-nm laser spot (Extended Data Fig. 9) estimate a beam waist w₀ = 2.81 μm (the larger between x, y) and Rayleigh range z_R = 13.18 μm. We assume a Gaussian beam with intensity $I\left(r,z\right)=I_0{\left(\frac{w_0}{w\left(z\right)}\right)}^2{\mathrm{e}}^{\frac{-2r^2}{w{\left(z\right)}^2}}$, where $w\left(z\right)=w_0\sqrt{1+{\left(\frac{z}{z_{\mathrm{R}}}\right)}^2}$ and r is the radial distance, z is the distance from focus and I₀ is the maximum intensity. We also assume that the collection and 488-nm excitation beam have the same point spread function, resulting in a confocal volume $V={\int }_{-\infty }^{\infty }{\int }_0^{2\mathrm{\pi }}{\int }_0^{\infty }{\left(\frac{1}{I_0}I\left(r,z\right)\right)}^{2}r\mathrm{d}r\mathrm{d}\varphi \mathrm{d}z=z_{\mathrm{R}}{\left(\mathrm{\pi }{w}_0\right)}^2/4$. Using this volume and a sample concentration of 5 mM, we find that the effective number of molecules in our excitation volume is 773 × 10⁶ molecules. We note that this estimate serves as an upper limit, as we collect into a single-mode fibre, but our imaging system is not diffraction limited due to poor alignment through the cryostat window and sapphire sample coverslip. With diffraction-limited imaging, we estimate that we would measure about 810-times-fewer molecules with approximately the same brightness, providing about 28-times-better sensitivity than in this work.

Sensitivity estimation

The minimum signal that can be detected when integrating for a duration T is given by S_T/σ_T = 1, where S_T denotes the signal and σ_T denotes the standard deviation of S_T. In the following, the system’s response is linear with respect to a small field (δB) such that $\frac{\mathrm{d}{S}_T/\mathrm{d}B\times \mathit{\delta }B}{{\sigma }_T}=1$. Therefore, the minimum field that can be detected is

$${\mathit{\delta }B}_{\min }\left(T\right)=\frac{{\sigma }_T}{\mathrm{d}{S}_T/\mathrm{d}B}$$ 2

where $\frac{\mathrm{d}{S}_T}{\mathrm{d}B}$ is maximized. Assuming the measurement is shot-noise limited, the sensitivity is $\eta ={\mathit{\delta }B}_{\min }\sqrt{T}$ (ref. ²).

It is noted that we report two sensitivities: first, the experimentally measured sensitivity for an ensemble of 773 × 10⁶ molecules, which has units of T Hz^−1/2. Second, we normalize the sensitivity to the total number of qubits measured in units of mol, which has units of T mol^1/2 Hz^−1/2.

DC sensitivity (293 K)

To quantify the DC field sensitivity, we measure the difference of the photoluminescence at ω_a = (2π) × 3.54 GHz and ω_b = (2π) × 3.43 GHz, and normalize the signal to the photoluminescence in the absence of microwaves (PL_back). The resulting signal measured over T = 15 min is then given by C_T = [PL_sig(ω_a) − PL_sig(ω_b)/PL_back]. The fit has a slope of dS_T/dB₀ = 5.0 T⁻¹ and the residuals (Extended Data Fig. 10a) have a standard deviation σ_T = 4.6 × 10⁻⁴ yielding a sensitivity of $\eta =\frac{{\sigma }_T}{\mathrm{d}{S}_T/\mathrm{d}B}\sqrt{T}=2.7\mathrm{m}\mathrm{T}{\mathrm{H}\mathrm{z}}^{-1/2}$. Assuming an excitation volume of 256 μm³ and an EYFP concentration of 5 mM, which translates into 773 × 10⁶ molecules, we find a room-temperature DC magnetic-field sensitivity of $2.7\frac{\mathrm{mT}}{\sqrt{\mathrm{Hz}}}\sqrt{\frac{773\times {10}^6}{6.022\times {10}^{23}\frac{1}{\mathrm{mol}}}}=98\mathrm{pT}{\mathrm{mol}}^{1/2}{\mathrm{Hz}}^{-1/2}$.

AC sensitivity (80 K)

AC sensing of small fields can be done using the CPMG sequence shown in Extended Data Fig. 10b. The signal of a single CPMG sequence is then given by $S_{\pm }=\frac{n_{\mathrm{\Delta }}}{2}\left(1\pm \sin \left(\varphi \right)\right)+\frac{n_{\mathrm{\Sigma }}}{2}$, where n_Δ denotes the difference in photon count between the T_x and T_z state, n_Σ their average, and the sign denotes the phase of the last π/2-pulse. Assuming a sinusoidal magnetic field with amplitude δB_AC, frequency T_CPMG/(2N) and in phase with the CPMG sequence, we can write the accumulated phase as $\varphi ={\gamma }_{\mathrm{eff}}\delta B_{\mathrm{AC}}{T}_{\mathrm{CPMG}}W$, with W = 2/π. The detected signal is then given by $S=S_{+}-S_{-}=n_{\mathrm{\Delta }}\sin \left(2{\gamma }_{\mathrm{eff}}\delta B_{\mathrm{AC}}{T}_{\mathrm{CPMG}}/\mathrm{\pi }\right)$ and the sensitivity by $\eta =\frac{\mathrm{\pi }}{2\left(n_{\mathrm{\Delta }}/{\mathit{\sigma }}_n\right){|\gamma }_{\mathrm{e}\mathrm{f}\mathrm{f}}|T_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}}\sqrt{2(T_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}+T_0)}$, where σ_n denotes the standard deviation of n_Δ and T₀ is the experimental overhead time. The factor $\sqrt{2}$ originates from measuring n_Δ with two CPMG sequences. To experimentally estimate the AC sensitivity of EYFP, we integrated the signal over 250,000 experiments. We fit the difference in photon counts n_Δ,250,000 = 4,541 × exp(−(T_CPMG/5.35 μs)²) as a function of T_CPMG (Extended Data Fig. 10c) and σ_n,250,000 = 288 from the corresponding residual (Extended Data Fig. 10d). We can now estimate for a single experiment that $n_{\mathrm{\Delta }}=\frac{n_{\mathrm{\Delta },\mathrm{250,000}}}{\mathrm{250,000}}$ and ${\mathit{\sigma }}_n=\frac{{\mathit{\sigma }}_{n,\mathrm{250,000}}}{\sqrt{\mathrm{250,000}}}$. Under these conditions, we find T_CPMG = 3.68 μs to be the optimal sensing duration (Extended Data Fig. 10e). Assuming an effective gyromagnetic ratio of ${\gamma }_{\mathrm{e}\mathrm{f}\mathrm{f}}=\left(2\mathrm{\pi }\right)\times -7.63\mathrm{G}\mathrm{H}\mathrm{z}{\mathrm{T}}^{-1}$ (that is, operating at B = 4.65 mT) and using T₀ = 60 μs, this results in a field sensitivity of η = 5.11 μT Hz^−1/2. Given that we measured approximately 773 × 10⁶ molecules, this translates into a sensitivity of $5.11\frac{\mathrm{\mu }\mathrm{T}}{\sqrt{\mathrm{Hz}}}\sqrt{\frac{773\times {10}^6}{6.022\times {10}^{23}\frac{1}{\mathrm{mol}}}}=183\mathrm{fT}{\mathrm{mol}}^{1/2}{\mathrm{Hz}}^{-1/2}$.

NMR sensing limit of detection

In this section, we consider a thought experiment where we calculate the sensitivity of an ensemble of N fusion proteins, each consisting of a EYFP protein conjugated to a target protein that contains a single ¹⁹F nuclear spin. This ¹⁹F nuclear spin is separated by 5 nm from the qubit and produces a local magnetic field of δB = 18 nT at the location of the fluorophore. The field strength δB is dominated by the target ¹⁹F spin in the fusion proteins, as other ¹⁹F spins are significantly farther away and do not contribute to the signal. Starting from the AC sensitivity calculation $\eta =\frac{\mathrm{\pi }}{2\left(n_{\mathrm{\Delta }}/{\mathit{\sigma }}_n\right)\left|{\gamma }_{\mathrm{e}\mathrm{f}\mathrm{f}}\right|T_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}}\sqrt{2(T_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}+T_0)}$, we derive the limit of detection for NMR spectroscopy. However, in NMR only a small fraction of nuclear spins are polarized. Using the nuclear spin polarization (p), the overall signal is reduced to $S=p{n}_{\mathrm{\Delta }}\sin \left(2{\gamma }_{\mathrm{e}\mathrm{f}\mathrm{f}}\delta B_{\mathrm{A}\mathrm{C}}{T}_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}/\mathrm{\pi }\right)$, resulting in a sensitivity of ${\eta }_p=\frac{\mathrm{\pi }}{2\left(p{n}_{\mathrm{\Delta }}/{\mathit{\sigma }}_n\right)\left|{\gamma }_{\mathrm{e}\mathrm{f}\mathrm{f}}\right|T_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}}\sqrt{2(T_{\mathrm{C}\mathrm{P}\mathrm{M}\mathrm{G}}+T_0)}=\frac{1}{p}\eta$. This results in a polarization-adjusted sensitivity of ${\eta }_p=\frac{1}{p}183\mathrm{fT}{\mathrm{mol}}^{1/2}{\mathrm{Hz}}^{-1/2}$ (see main text), allowing us to detect a magnetic field of $\mathit{\delta }B=\frac{1}{\sqrt{N}\sqrt{T}}{\eta }_p$. Solving for N we find a limit of detection of $N=\frac{1}{T}{\left({\eta }_p\frac{1}{\mathit{\delta }B}\right)}^2=\frac{1}{T}\frac{94}{p}\mathrm{pmol}{\mathrm{Hz}}^{-1}$.

Improved optical readout

We estimate the improvements that will be gained with future advances in the optical readout of EYFP. For comparison purposes, ref. ¹³ collected 0.02 photons from a single nitrogen-vacancy centre per experiment cycle. In Extended Data Fig. 10c, we measure 0.167 photons per experiment cycle from an ensemble of 773 × 10⁶ EYFP molecules, which corresponds to 2.2 × 10⁻¹⁰ photons per molecule per experiment cycle. This means that in our experiment, we collect approximately 10⁻⁸-times-fewer photons from an EYFP molecule compared with a nitrogen-vacancy centre.

OADF readout yields at most one photon per molecule per experiment cycle. This can, in principle, be improved by utilizing the cycling transition in the singlet manifold. Such a cycling could be accomplished by applying a short 912-nm pulse that transfers only the short-lived triplet states (T_x,y) into the singlet ground state but not the long-lived triplet state (T_z). The singlet population could then be probed by a subsequent 488-nm laser pulse. It is noted that this approach, relying on fluorescence cycling of the singlet state, would require an efficient triplet initialization since the population that remains in the singlet ground state after initialization would contribute a background signal to the readout.

Although we have not yet quantified the shelving efficiency, it is probably low in the current experimental configuration. Improvements in shelving efficiency translate directly into gains in signal. Let us assume an ideal scenario where we achieve 100% shelving efficiency during the 488-nm initialization laser pulse. This implies that all molecules are in the T1 state following initialization and contribute to our sensing experiment. If the shelving efficiency increases from ζ₀ to 100%, then the number of probed molecules, and thus the photon number, also increases by 1/ζ₀. The T1 triplet yield is approximately 0.003 (refs. ^39,40), so by utilizing fluorescence readout, this would yield a signal amplification of 333 due to the improved cyclicity. Improved triplet shelving efficiency also allows for a much shorter initialization laser pulse. In saturation, the EYFP should shelve in approximately 333 × 3 ns = 1 μs. The readout laser pulse can also be shortened to about 1 μs. This yields an improvement of $\frac{30\mathrm{\mu }\mathrm{s}+30\mathrm{\mu }\mathrm{s}}{1\mathrm{\mu }\mathrm{s}+1\mathrm{\mu }\mathrm{s}}=30$. Use of an oil immersion objective with a modest numerical aperture of 1.3 would yield a (1.3/0.7)² = 3.4 improvement in photon counts. As discussed in the section above, reduced aberrations would result in an 810-times improvement in signal.

Combining all of these improvements yields an enhancement of $1/{\zeta }_0\times 2.75\times {10}^7$ signal photons, which should allow us to meet or exceed the sensitivity of a single nitrogen-vacancy centre.

Room temperature ODMR mechanism

At room temperature, we observe an ODMR signal that originates from a different mechanism than at low temperatures. The 488-nm laser pulse initializes the EYFP into its triplet state and polarizes its triplet spin sublevels. This spin polarization is quickly eliminated by fast spin-lattice relaxation within 100 ns. Consequently, ODMR at room temperature is not observable using the same pulse sequence we used at 80 K where the microwave pulse is delayed from the spin readout by at least 100 ns (Extended Data Fig. 12c). Nevertheless, ODMR measurements are obtained at room temperature despite equilibration of the spin levels after the 488-nm laser pulse. As long as the EYFP persists in the triplet state, it can be re-excited to the higher-lying triplet, T2, using the 912-nm laser. Because the T_x and T_y spin sublevels undergo RISC to the singlet manifold much faster than the T_z sublevel, the 912-nm laser causes the triplet manifold to regain a spin polarization by depopulating the T_x and T_y sublevels. ODMR contrast can then be observed when a subsequent microwave drive is resonant with the T_x–T_z or T_y–T_z transitions transferring population from T_z back into T_x or T_y (Extended Data Fig. 12b).

Online content

Any methods, additional references, Nature Portfolio reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at 10.1038/s41586-025-09417-w.

Author contributions

J.S.F. and B.S.S. constructed the experimental set-up and performed the measurements. S.V. carried out the DFT calculations. Z.Z.G. expressed the EYFP in mammalian cells. J.S.F., B.S.S., S.W., B.K. and E.G.R. performed the simulations. J.S.F., B.S.S., Y.T., L.R.W., D.D.A. and P.C.M. developed the experimental design. J.S.F., B.S.S. and M.X. developed the bacterial protein expression and purification process. J.S.F., B.S.S., S.W., E.G.R., Y.T., L.R.W., D.D.A. and P.C.M. analysed the data. J.S.F., B.S.S., D.D.A. and P.C.M. wrote the paper with contributions from all co-authors. J.H., A.E.-K., L.G., D.D.A. and P.C.M. supervised the work.

Peer review

Peer review information

Nature thanks Seok-Hyun Yun and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Data availability

The data and analysis code are available via Zenodo at 10.5281/zenodo.15708665 (ref. ⁷³).

Competing interests

J.S.F., B.S.S., D.D.A. and P.C.M. are inventors on a pending patent application with the USPTO submitted by the University of Chicago that covers fluorophore-based spin qubits and associated methods.

Extended data

is available for this paper at 10.1038/s41586-025-09417-w.

Supplementary information

The online version contains supplementary material available at 10.1038/s41586-025-09417-w.