Substantial Magnetic Fields Arising from Ballistic Ring Currents in Single-Molecule Junctions

Abstract

When a small electric bias is applied to a single-molecule junction, current will flow through the molecule via a tunneling mechanism. In molecules with a cyclic or helical structure there may be circular currents, giving rise to a unidirectional magnetic field. Here, we implement the Biot–Savart law and calculate the magnetic field resulting from the ballistic current density for a selection of molecules. We find that three prerequisites are important for achieving a substantial magnetic field in a single-molecule junction. (1) The current must be high, (2) the ring current must be unidirectional within the bias window, and (3) the diameter of the ring current must be small. We identify both cyclic and linear molecules that potentially fulfill these requirements. In cyclic annulenes with bond-length alternation the current-induced magnetic field can approach the mT-range whereas archetypical cyclic molecules, such as benzene, are not suitable candidates for the generation of a substantial magnetic field. In linear carbon chains with circular currents due to their helical π-systems, the magnetic field is in the mT-range. When the bias window is gated closer to resonance, we show that the magnetic field can potentially reach the sub-tesla range. Our results provide proof-of-concept for achieving experimentally relevant current-induced magnetic fields in molecular wires at low bias.

Introduction

Over 200 years ago, it was discovered that a magnetic field appears around a wire when an electric current runs through it. Since then, electromagnetism has been generalized and now forms the scientific foundation for many of the technologies of our time, ranging from wind turbines to telecommunication. Today, state-of-the-art apparatuses, such as scanning tunneling microscopy break junctions and mechanically controllable break junctions, enable researchers to measure current passing through a single molecule trapped between two metal electrodes. − Such experiments provide both insight into the electronic nature of molecules, and form the basis for molecular electronic devices which may one day enable a new generation of functional electronics. −

An electric current that passes through a molecule via a coherent tunneling mechanism is similar to that of a macroscopic wire, in the sense that the flow of electrons will generate a magnetic field around the wire. Coherent tunneling is a ballistic transport mechanism with no charge building on the molecule during the transport process. Naturally, the magnetic field resulting from current passing through a molecular wire will often be weak due to the low bias that can be applied to molecular junctions. Such magnetic fields are potentially in the μT range, which is smaller than earth’s magnetic field at its surface (Table ). However, if suitable molecules can be identified, it may be possible to achieve substantial magnetic fields. To be experimentally relevant such magnetic fields must locally approach the tesla-range that is achieved in modern electromagnets (Table ), such as those used in nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR) spectroscopy. It is the goal of this study to identify such molecules, and provide molecular design rules for achieving this.

1. Magnetic Field Strengths.

magnet	B
earth at surface	25–65 μT
fridge magnet	1–5 mT
EPR magnet	0.1–10 T
MRI magnet	0.5–3 T
NMR magnet	1–28 T
record electromagnet	45.5 T
molecular junction	?

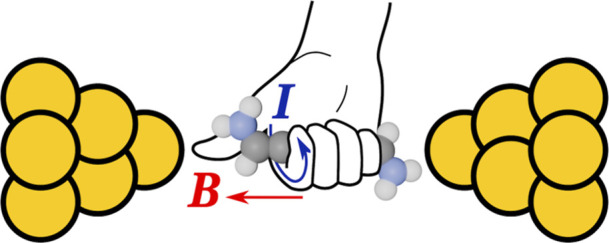
When a unidirectional electric current passes through a molecule, a circular magnetic field will form around the molecular wire in accordance with the right-hand rule. The aniline-terminated diyne in Figure a is an example of a molecule with a current density that is largely linear through the polyynic segment of the molecule. The resulting magnetic field is consequently circular around the diyne, as the right-hand rule dictates (Figure b).

1.

(a) Ballistic current density and the resulting magnetic field computed for an aniline-terminated diyne. The current density cutoff is 5% of the maximum current density; magnetic field cutoff is 20% of the maximum field strength. (b) Schematic depiction of the linear current and circular magnetic field of the diyne as predicted by the right-hand rule. (c) Schematic depiction of the circular ring current in a meta-connected benzene and the resulting enhanced unidirectional magnetic field as predicted by the right-hand rule.

If an enhanced unidirectional magnetic field is to be achieved, the molecule must behave like a coil (or solenoid). When the current moves in a circular or helical path through the molecule, the magnetic field will be enhanced in the center of the ring current in accordance with the right-hand rule (Figure c). For example, molecular systems based on benzene rings have been suggested to have strong ring currents in the molecular electronics literature. − However, studies of the magnetic fields that arise from such currents are sparse. ,− Still, studies of magnetoresistance and spin filtering effects, − such as the chirality-induced spin selectivity (CISS) effect, − suggest that magnetic fields may locally be strong.

Here, we compute the low-bias current density, and through the Biot–Savart law calculate the resulting magnetic field of cyclic and linear molecules where strong ballistic ring currents appear. We establish design rules for achieving substantial magnetic fields in single-molecule junctions, and finally discuss potential applications along with the limitations of our study.

Methods

We optimized the isolated molecules using density functional theory (DFT) at the PBE/6-311G­(d,p) level as implemented in Gaussian 09. We carried out a frequency analysis to ensure all structures were minima with no imaginary frequencies. Using these structures, we created single-molecule junctions with s-band electrodes. The electrodes consist of two dihydrogen molecules, and the amine-terminated molecule is placed between them with an N–H distance of 1.5 Å, a C–N–H bond angle of 110°. We use –NH₂ as anchoring groups for all molecules; in benzene-like molecules we use the longer acetylenamine linker to avoid steric congestion around the ring. All molecular structures are fully 3D rendered in Supporting Information Figures S11–S14.

To model electron transport via a coherent tunneling mechanism, the Landauer transmission was calculated using the nonequilibrium Green’s functions (NEGF) approach as implemented in our in-house wide-band transmission code, which is described in detail in previous work. , Transmission plots for all molecules we studied are shown in Figures S7 and S8. Computations of both the zero-bias transmission and the low-bias current density were carried out using DFT at the PBE/dzp level as implemented in ASE and GPAW. − The current was computed with a symmetric bias of 500 mV, which is opened in the middle of the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap unless otherwise noted. The total current is computed over the bias window without accounting for temperature in the Fermi function. As discussed in Supporting Information and shown in Figures S1 and S2, we expect these approximations in our code ensure a conservative estimate of the current and the resulting magnetic fields of the molecules we study. The wide-band transmission and current density code is open-access and available at https://github.com/chem-william/calc_current.

Theory

For completeness, we will give a short introduction to the calculation of current density through single molecules in the following, but refer to the literature for a full walkthrough.

The general equation for current density, J, from a wave function, ψ, in the absence of an external magnetic field is given by

$$\mathbf{J}=\frac{-e}{2m_{\mathrm{e}}}(\psi {[\mathrm{p̂}\psi ]}^{*}+{\psi }^{*}[\mathrm{p̂}\psi ])$$ 1

Here, p = iℏ∇ and is the momentum operator, ℏ is the reduced Planck constant, e is the electronic charge, m _e is mass of the electron, and ψ is the wave function of the single electron of interest.

This can be rewritten as

$$\mathbf{J}(\mathbf{r},{\mathbf{r}}^{\prime })=\frac{-e}{2m_{\mathrm{e}}}[(\mathrm{p̂}-{\mathrm{p̂}}^{\prime })\psi (\mathbf{r}){\psi }^{*}({\mathbf{r}}^{\prime })]$$ 2

By assuming steady-state conditions, we can use the following relation described by Datta

$$\psi (\mathbf{r}){\psi }^{*}({\mathbf{r}}^{\prime })=-\frac{\mathrm{i}}{2\pi }\int \mathrm{d}E{\mathbf{G}}^{<}(E;\mathbf{r},{\mathbf{r}}^{\prime })$$ 3

Here, G ^<(E; r, r′) is the lesser Green’s function. Furthermore, we transform the lesser Green’s function to a real-space representation by an orthonormal and complete atomic orbital (AO) basis ψ _i (r)­

$${\mathbf{G}}^{<}(\mathbf{r},{\mathbf{r}}^{\prime };E)=\sum _{i,j}{\psi }_i(\mathbf{r})G_{ij}^{<}(E){\psi }_j({\mathbf{r}}^{\prime })$$ 4

Inserting eqs and into eq , and rearranging, we arrive at

$$\begin{array}{l}\mathbf{J}(\mathbf{r})=\frac{e\mathrm{\hslash }}{4m_{\mathrm{e}}\pi }\sum _{i,j}\int \mathrm{d}E{G}_{ij}^{<}(E)\\ {[{\psi }_i(\mathbf{r})\mathrm{\nabla }{\psi }_j({\mathbf{r}}^{\prime })-{\psi }_j({\mathbf{r}}^{\prime })\mathrm{\nabla }{\psi }_i(\mathbf{r})]}_{r=r^{\prime }}\end{array}$$ 5

which is the current density per spin.

Under steady-state conditions, the lesser Green’s function is defined as

$${\mathbf{G}}^{<}(E)={\mathbf{G}}^{\mathrm{r}}(E){\mathbf{\Sigma }}^{<}(E){\mathbf{G}}^{\mathrm{a}}(E)$$ 6

where G ^r/a is the retarded/advanced Green’s function, and Σ ^< is the lesser self-energy.

In the limit of zero temperature, and a small bias, the lesser Green’s function can be written as

$${\mathbf{G}}^{<}=\mathrm{i}{\mathbf{G}}^{\mathrm{r}}(E){\mathbf{\Gamma }}_{\mathrm{E}}(E){\mathbf{G}}^{\mathrm{a}}(E)$$ 7

Here, G ^r/a is the retarded/advanced Green’s function and Γ _E is the spectral density of the electrode. These three components can be calculated with eqs and

$${\mathbf{G}}^{\mathrm{r}/\mathrm{a}}(E)={[E\mathbf{S}-\mathbf{H}-{\mathbf{\Sigma }}^{\mathrm{r}/\mathrm{a}}(E)]}^{-1}$$ 8

$${\mathbf{\Gamma }}_{\mathrm{E}}(E)=\mathrm{i}({\mathbf{\Sigma }}_{\mathrm{E}}^{\mathrm{r}}(E)-{\mathbf{\Sigma }}_{\mathrm{E}}^{\mathrm{a}}(E))$$ 9

The final component, the retarded/advanced self-energy of the left electrode, Σ _E (E), can be calculated as

$${\mathbf{\Sigma }}_{\mathrm{E}}^{\mathrm{r}/\mathrm{a}}(E)=\sum _a{\mathbf{V}}_{\mathrm{E}\mathrm{C}}^{†}{\mathbf{g}}_{\mathrm{E}}^{\mathrm{r}/\mathrm{a}}(E){\mathbf{V}}_{\mathrm{E}\mathrm{C}}$$ 10

where V _EC is the coupling from the electrode to the molecule (central region), and g _E = [E S _E – H _E] is the noninteracting Green’s functions of the electrodes.

J is computed in the zero-bias limit at a single energy in the middle of the bias window, and the vector field is scaled linearly with the total current. Bias windows and scaling factors are shown in Figures S7 and S8. This approach ensures that the current density scales correctly with the bias, although the variation of the current density within the bias window and the effect of polarization are not included. We refer to the Supporting Information for further discussion and benchmark of this approach (Figure S2). Conservation tests of the current density are carried out and included in Supporting Information, Figures S9 and S10. −

With all the components now in place, the resulting magnetic field from the current density can be calculated according to the Biot–Savart law

$$\mathbf{B}(\mathbf{r})=\frac{{\mu }_0}{4\pi }{\iiint }_V\frac{\mathbf{J}({\mathbf{r}}^{\prime })\times (\mathbf{r}-{\mathbf{r}}^{\prime })}{{|\mathbf{r}-{\mathbf{r}}^{\prime }|}^3}\mathrm{d}{V}^{\prime }$$ 11

Here, μ₀ is the vacuum permeability, dV′ is the volume element, r is the field point at which the contribution to the magnetic field is computed, and r′ is the source point of the contribution of the current density.

Equation calculates the magnetic field B(r) at a point r by integrating the contributions from the current density J(r′) at all other places within the molecule. Each contribution is determined by the magnitude and direction of the current at r′ and decreases with |r – r′|³ between the source point and the field point, effectively summing up the magnetic effects of all current elements throughout the molecular volume.

We have implemented eq and made it available as a Python module. It takes the current density output from our wide-band current density code , although it can, in principle, calculate the magnetic field for any arbitrary current density.

Visualization

Using Jmol, we visualize the vector fields J­(r) and B­(r) as three-dimensional arrows, where the arrow thickness is scaled proportionally with the vector magnitudes, |J⃗| and |B⃗|. We define z as the direction of transport and color the arrows based on the magnitude of one of the three vector-components relative to full magnitude. When plotting the strength of a linear (Cartesian) component, v _z , we use a yellow-purple color scale. To plot the strength of a rotating vector field, we convert the vector field to a cylindrical coordinate system and color by the azimuthal vector component using a blue-red color scale. The cylindrical vector components were calculated from the Cartesian vector components, v _x and v _y , as

$$\begin{array}{l}{\mathrm{v⃗}}_{\mathrm{r},\theta }=(v_x\times \cos \theta +v_y\times \sin \theta )\times {ê}_{\mathrm{r}}\\ +(v_y\times \cos \theta -v_x\times \sin \theta )\times {ê}_{\theta }\end{array}$$ 12

where ${ê}_{\mathrm{r}}$ and ${ê}_{\theta }$ are the cylindrical unit vectors. In Figure , as an example, the current density has a major linear component which is best visualized by coloring proportionally to the z-component of the current density, j _z . The resulting magnetic field rotates around the molecular wire and is best visualized by coloring by proportionally to the azimuthal component, b _θ. Throughout this manuscript, we primarily study ring currents, and the resulting directional magnetic fields, we will mainly color the current density based on the θ-component and the magnetic field based on a Cartesian component.

Results

To achieve strong ring currents and magnetic fields, we start by considering the right-hand rule and the Biot–Savart law (eq ). We consider the following three requirements:

• 1The ring current must be unidirectional; if both clockwise and counterclockwise ring currents exist, the magnetic field in the center of the ring will not be enhanced.
• 2To achieve the optimal enhancement, the ring diameter must be small; the magnetic field is inversely proportional to the distance from the ring current (eq ).
• 3The current density must be high in the ring current; the magnetic field is proportional to the current density in a given position (eq ).

With these three requirements in mind, we start by assessing the current density and the resulting magnetic fields of ortho-, para-, and meta-connected benzene molecules as reference systems.

Ortho- and para-linked benzenes are well-known to have fairly high single-molecule conductance (see transmission plot in Figure S1). Consequently, the current is a few nanoampere at a bias of 500 mV. Despite the small ring diameter of benzene, the magnetic field in both the ortho- and para-linked systems is weak because the ring current runs both ways around the benzene ring. In the ortho-connected case the ring current that takes the long way around the ring dominates, and a unidirectional magnetic field varying over several μT is formed inside the benzene ring. In the para-connected case the two-way ring current cancels the magnetic field inside the benzene ring.

The current of the meta-linked benzene is over 2 orders of magnitude lower than the ortho- and para-connected cases due to destructive quantum interference near the Fermi energy (transmission plot in Figure S2). A largely unidirectional ring current appears around the cyclic structure, albeit it is turbulent which is closely connected to the quantum interference effect. The ring current causes strong local enhancement of the magnetic field inside the benzene ring, which is only an order of magnitude weaker than that of ortho-linked benzene despite the much lower current. While the ideal ring current is achieved, the quantum interference effect also makes meta-linked benzene electrically insulating, and the current-induced magnetic field is insubstantial.

Cyclic Molecules

While benzene has an ideal small ring-diameter, the current-induced magnetic field is limited by two-way ring currents in the para- and ortho-linked case, and low current in the meta-linked case. Benzene is an annulene, but is a special case being a highly symmetric aromatic molecule. Tsuji et al. demonstrated that in annulenes with bond-length alternation, the current may predominantly flow the long way around the ring-structure if the injection-point into the short way in the ring is via a long (formally single) bond. In ortho-connected benzene-like molecules, it may therefore be possible to avoid the current running the short way as it does in benzene (Figure ).

2.

Current density (top row), and magnetic field (middle and bottom row) of ortho-, para-, and meta-linked benzenes. The magnetic field is plotted as a vector field (middle row) and as the point where the field is strongest (bottom row). Linkers have been removed for clarity.

Substituting two carbon atoms in benzene with a nitrogen and a boron creates a structurally analogous isoelectronic molecule. Indeed, such heterobenzenes like 1,2-azaborine (Figure ) has significant bond-length alternation. − Consequently, the double bonds are localized and we can connect the linkers and electrodes in such a way that the current through the short way around the ring is reduced. Still, in the case of the ortho-connected azaborine, the current density through the short path of the ring is too strong, and the total current is lower than ortho-linked benzene, which is also an unfortunate consequence of increased bond-length alternation. , Consequently, the magnetic field is slightly lower than that of the ortho-linked benzene.

3.

Current density (top row), and magnetic field (middle and bottom row) of cyclic molecules with bond-length alternation. The magnetic field is plotted as a vector field (middle row) and as the point where the field is strongest (bottom row). Linkers have been removed for clarity.

Benzene-like molecules with bond-length alternation have also been synthesized without heteroatoms, such as the cyclohexatriene in Figure , which is a variant of starphenylene. − Due to the peripheral antiaromatic four-membered ring moieties, there is bond-length alternation in the central benzene unit. In this cyclohexatriene there is practically no current that takes the short way, and a unidirectional ring current is thus generated (Figure ). However, the current is much lower than in the parent ortho-linked benzene due to quantum interference features in the transmission close to the Fermi energy (Figure S2), and consequently the magnetic field is still in the μT range.

Larger annulenes have bond-length alternation and were among the molecules studied by Tsuji et al. ,, While small annulenes may distort due to the proximity of their hydrogens, [18]­annulene has a stable planar structure. Even in this big ring, we can select the shortest ortho-like connection, and still the current will predominantly take the long way around the ring. Unfortunately, the ring diameter is too big to achieve strong enhancement of the magnetic field inside the ring. In combination with the relatively low current, again due to the size of the ring and the bond-length alternation, the magnetic field is in the μT range well below the background magnetic field at earth’s surface.

The dehydro[12]­annulene is a smaller ring with stronger bond-length alternation, − and higher current due to its small HOMO–LUMO gap. While the ring current is fully unidirectional, the triangular shape means the enhancement of the magnetic field is strongest in the corners of the structure. Nonetheless, due to the combination of a smaller ring diameter, high current, and unidirectional ring current, the magnetic field reaches the sub-mT range within the ring-structure. This is an example of a cyclic molecule where the current-induced magnetic field is larger than background magnetic field.

The above systems are examples of the effect that bond-length alternation and connectivity has on the path of the current through small cyclic molecules. This strategy is possible in many synthetically realistic molecules, but as we have shown there are several challenges to applying it. For example, in cyclooctatetraene derivatives, which inherently have strong bond-length alternation, , the current density is very turbulent and does not produce a clear ring currentperhaps due to the bent shape of the ring structure. We have also tested helicene molecules, where the current may follow the helical through-bond path through the molecule. In agreement with previous work, − we see that the current density is dominated by through-space contributions due to π-stacking interactions. This can potentially be avoided if the helical pitch of the molecule is larger, however, this will weaken the enhancement of the magnetic field as the current becomes less circular. The current density plots for functionalized cyclooctatetraene and helicene are included in Supporting Information (Figure S3).

Linear Carbon Wires

Cumulenes and polyynes have attracted much interest as linear carbon wires. ,− In recent work, we and others studied the ballistic current density of different types of linear carbon wires due to their helical frontier MOs. − Circular currents around the linear wire can be achieved in specific situations, ,, and we shall explore the resulting magnetic fields.

In the aniline-terminated polyyne we showed in the introduction (Figure ), the current runs linearly through the π-system when the end-groups are in parallel orientation. However, if the groups are rotated the π-system becomes helical, − , and circular current patterns appear around the linear carbon chain. , The current density and magnetic field for the polyyne with the end-groups at 60° orientation is shown in Figure . The total current is reduced due to the torsion of the end-groups, and current circulates both ways around the wire. Still these alternating ring current generates a magnetic field that is locally unidirectional, which at its strongest point in the middle of the linear carbon chain is in the μT range, similar in magnitude to the benzenes we have studied.

4.

Current density and magnetic field of aniline-terminated diyne with the end-groups rotated to 60° orientation. The magnetic field is plotted as a vector field (middle row) and as the point where the field is strongest (bottom row).

As evident by comparing Figures and , the free rotation of the end groups in polyynes are likely to disrupt any appreciable linear magnetic field. − , Other dynamic effects may affect experiments similarly. Finding ways to stabilize the twisted configurations, which emphasize helical frontier MOs and circular currents, will be important for generating strong linear magnetic fields.

The frontier MOs of cumulenes can be more helical than those of polyynes, while typically also having higher current. ,, Odd-n [n]­cumulenes, n being the number of cumulated double bonds, have coplanar end-groups and high currents. However, its frontier orbitals are not helical but regular π-orbitals. Consequently, the circular currents in [5]­cumulene are weak (Figure ), and the magnetic field is not unidirectional but runs around the molecule as in the polyyne with coplanar end-groups (Figure ). Still, this magnetic field approaches the mT range in the center of the molecule due to the relatively high current.

5.

Current density (top row), and magnetic field (middle and bottom row) of [5]- and [4]­cumulenes. Both cumulenes are also shown with end-groups rotated into 60° orientation. Note that the functionalized [5]­cumulene has near-coplanar end groups and the functionalized [4]­cumulene has near-perpendicular end groups in their ground-state structures. The magnetic field is plotted as a vector field (middle row) and as the point where the field is strongest (bottom row).

If the end-groups of the [5]­cumulene are rotated away from the coplanar orientation of the ground-state structure into 60° orientation, the total current is increased as the HOMO–LUMO gap narrows. Unidirectional ring currents appear around the wire, and the magnetic field is in the mT range and points along the carbon chain. We note that while the current is enhanced by a factor ∼5 by this manipulation of the structure, the magnetic field is increased by a factor ∼19, which underlines the effect of the ring current.

In the even-n [n]­cumulenes, the ground-state geometry has near-perpendicular end-groups as also seen in allene and the frontier MOs are helical. The conditions for achieving helical π-orbitals in functionalized cumulenes has been explored in great detail by us and others. ,,,,,,, Albeit lower than in the odd-n cumulenes due to the near-perpendicular end-groups, the total current is still fairly high in the amine-functionalized [4]­cumulene and strong unidirectional ring currents appear around the linear carbon wire (Figure ). The resulting magnetic field is enhanced at the carbon atoms where the circular current appears, and points along the carbon chain. The magnetic field approaches the mT-range at this specific point in space.

We proceed again by rotating the end-groups of the [4]­cumulene, this time from the near-perpendicular orientation of the ground-state structure to 60° orientation. This increases the total current 2-fold but the magnetic field increases somewhat less, presumably due to the circular currents being slightly weaker. A further increase of both the current and magnetic field is achieved if we rotate to 30° as shown in Figure S4, although still in the sub-mT range. For the [5]­cumulene, the current and magnetic field is smaller at 30° than at 60° (Figure S4), due to the opposite relation between torsion angle and transmission compared to the [4]­cumulene; a relation we have studied in detail in previous work.

We have previously demonstrated that the locality of the current density in [4]­cumulene at alternating carbon sites arises from the MO shapes rather than solely from the density of any particular MO. , The current density is influenced by contributions from multiple MOs at both the Fermi energy and at the MO resonances. The precise distribution of the contributions to the current density is governed by the interplay between these MOs, their gradients, and their coupling to the electrodes.

Cumulenes and polyynes are peculiar cases of the intricate relation between the electronic structure and electron transport properties of molecules. Close to the molecular wire the fine-structure of the current density controls the magnetic field which decays rapidly with distance further away from the wire in accordance with the Biot–Savart law (eq , and Figure S6). Although the direct relation between the frontier MO topology and the ballistic current density is nontrivial, the circular direction of the ring current in cumulenes, and consequently the magnetic field, can be chemically controlled due to tunability of the frontier MO helicity. ,,− Any transport effect that depends on the orientation of the current-induced magnetic effect (magnetoresistance and spin selectivity/filtering) can thus potentially be chemically controlled.

Although there are already several experimental studies exploring the single-molecule conductance of linear carbon chains, − ,− much work lies ahead to access the relevant molecular space experimentally. This is especially a challenge for the even-n cumulenes, because the stability is reduced for long carbon chains as we go from polyynes to odd-n cumulenes, to even-n cumulenes. ,

Enhancing the Current

To further increase the magnitude of the current-induced magnetic fields, higher current density in the ring currents must be achieved. Manipulating the molecular structures toward optimizing the current is one way we have explored, i.e., torsion of the end-groups of the linear carbon wires. Naturally, higher currents can be achieved by increasing the bias voltage. Here, we have chosen a symmetric bias of 500 mV to give a conservative estimate of the current. However, bias over ±1 V can often be applied experimentally. As discussed in the Supporting Information, the feasibility of using higher bias is molecule-dependent. Nonetheless, it seems realistic that total currents in the μA-range can be reached, − and in a recent report by Morris et al. covalently attached linear carbon wires sustained currents of 10–40 μA at a bias of 1.3 V. This sustained current is several orders of magnitudes higher than most currents presented here, which suggests there is much potential for achieving higher magnetic fields.

The application of a third gate electrode can be used to control the bias window. This enhances the current by avoiding antiresonance features in the transmission and by moving the bias window closer to the HOMO or LUMO resonance where the transmission approaches unity. − While the use of a gating voltage has many implications, we model it in a simplistic way. We open the bias window from the HOMO (or LUMO) resonance 500 mV in the direction toward the Fermi energy for select molecules with ring currents, which are shown in Figure . The bias-windows are visualized in the transmission plots in Figure S7 and S8 in Supporting Information.

6.

Current density (top row), and magnetic field (middle and bottom row) of meta-linked benzene, dehydro[12]­annulene, [5]­cumulene and [4]­cumulene with the bias window opened up to the HOMO resonance. The magnetic field is plotted as a vector field (middle row) and as the point where the field is strongest (bottom row).

In meta-linked benzene, the current is substantially increased as the bias window is moved away from the quantum interference feature in the HOMO–LUMO gap. The current increases into the nA-range while retaining the ring current, and the magnetic field is several mT inside the ring. When the dehydro[12]­annulene is gated toward the HOMO resonance, the increase is less significant due to the small HOMO–LUMO gap (Figure ). Nonetheless, both current and magnetic field increase by over an order of magnitude creating a magnetic field of several mT inside the ring structure. In the [5]­cumulene the circular currents have mixed directions around the wire when the molecule is gated toward the HOMO resonance. Although the current increases almost 3 orders of magnitude, the magnetic field only increases 1 order of magnitude into the mT-range like the two cyclical molecules.

Finally, we gate the [4]­cumulene toward the HOMO resonance (Figure ). As the total current increases over 2 orders of magnitudeand the unidirectional topology of the ring currents is further enhanced close to the resonancethe magnetic field increases into the sub-tesla range with a maximum field strength of 0.15 T. The magnetic field strength can thus locally reach that of EPR magnets, and potentially approaches that of NMR magnets (cf. Table ).

Whether gating is toward HOMO or LUMO also has a notable effect in some cases. When gated toward the LUMO the unidirectional ring currents in [4]­cumulene are lost (Figure S5). The magnetic field thereby becomes weaker and changes direction throughout the molecule. The circular direction of the currents is mixed (Figure S5) due to the relation to the frontier MOs that we have discussed in previous work. , Furthermore, the current is suppressed by an antiresonance near the LUMO. The other three molecules show similar or slightly less effect when gated toward the LUMO (Figure S5).

Discussion

In this study we have estimated the current-induced magnetic fields that appear due to the coherent ballistic charge transport through single-molecule junctions at low bias. We find that at low currents these magnetic fields can be in the mT-range, which is more than the background magnetic field at earth surface. Still, these are relatively weak magnetic fields. If we simulate an experiment with high current, where the voltage is increased or the bias window is gated toward resonance, the magnetic field locally comes within an order of magnitude from a tesla. While we have focused on discussing the effect of molecular design and bias, an important factor for the strength of the magnetic field is the magnitude of the current. Assuming the topology of the current density is unchanged, increasing the current through the molecule will lead to a proportional increase of the magnetic field (cf. eq ). Going forward, finding ways to design highly conductive molecules is thus essential for achieving strong magnetic fields. Some of the cumulenes we have examined here have been studied specifically for this purpose. ,

As we discussed in the Methods section and in the first section in the Supporting Information, as well as in previous studies, , our code systematically underestimates the transmission. Consequently, we are confident that we produce a conservative estimate of the current at low bias and the resulting magnetic field. The highest currents we have presented here are 1–3 μA (Figure ). While this is a high current for a molecule at low bias, it is not unrealistic to achieve currents that are an order of magnitude higher. − Most notably, Morris et al. recently presented linear polyynic carbon wires, up to 16 carbons atoms long, which are covalently bound to the Au-electrodes and achieve currents of 10–40 μA at ±1.3 V bias. Although those carbon wires differ design-wise from the ones we have studied here, should one succeed in producing such high current wires with circular current akin to those of the [4]­cumulene, the magnetic field could potentially be in the tesla-range.

To provide a proof-of-concept for generating current-induced magnetic fields, we have idealized several structural variables that will need to be studied further to experimentally realize the suggested effect. This includes the effect of anchoring groups and contact geometries, which can have major effects on the transport properties of single-molecule junctions. Furthermore, to achieve sufficiently high current at low bias, it is important to avoid destructive quantum interference near the Fermi energy as in the case of meta-linked benzene (Figure ). In [4]­cumulenes there can be interference near the Fermi energy as we have studied previously in relation to both anchoring groups and substituent effects in previous work; these effects must be actively considered in the molecular design process. , If a higher bias is applied to increase the current, the molecular structure will also change; for example in cumulenes redox chemistry can lead to torsion or bending. ,, While such distortions can be detrimental, it may also potentially be applied actively for molecular design. Finally, we underline that we have only computed the magnetic field that arises directly from the ballistic tunneling current. We have provided proof-of-concept that the induced magnetic field can be substantial and is therefore likely to be experimentally relevant; however, the response properties of the molecule are not accounted for in this study. To understand the potential experimental importance of current-induced magnetic fields in single-molecule junctions, it will be necessary to model the molecular response to the magnetic field, which is a key prospect for future computational development.

Conclusions

We have modeled the current-induced magnetic field that arises in a single-molecule junction under low bias by invoking the Biot–Savart law. Within the combined DFT-NEGF formalism we thus map the tunneling-mediated ballistic current density and magnetic field of several cyclic and linearly conjugated organic molecules where strong helical or ring currents appear. Based on the Biot–Savart law and the right-hand rule, we assume that the following three requirements must be fulfilled to achieve substantial enhancement of the magnetic field:

• 1There must be a unidirectional helical or ring current in the molecule to achieve enhancement of the magnetic field in the center of the cyclic/helical molecular unit.
• 2The ring diameter must be small in order to maximize the effect of the enhancement.
• 3The current density must be high in the ring current as the magnetic field is proportional to the current density.

We use these three rules as an instructive target for molecular design. We note that these requirements are not independent and can supplement each other; e.g., if the current is higher, the ring diameter can be bigger. We explore several types of molecules where some or all of the requirements are fulfilled.

While benzene, a typical molecule with ring currents, fails to fulfill all three requirements, we successfully propose both cyclic and linear molecules as candidates in which all three requirements are fulfilled. In annulenes it is essential to consider the bond-length alternation pattern to achieve unidirectional ring currents. As a top candidate we show that the magnetic field in a functionalized dehydro[12]­annulene is in the mT-range. We explore the circular currents in functionalized cumulenes, which are linear carbon molecules with practically no bond-length alternation, and find that the magnetic field can reach the subtesla-range if the bias window is gated toward the HOMO resonance. This high magnetic field is possible due to the small diameter of the ring currents that appear around the carbon chain. We thus identify two molecular classes where substantial magnetic fields can appear, which have remarkably different structural traits. In the cyclic molecules strong bond-length alternation is essential for directing the ring currents, while in the linear carbon wires the circular currents are strongest in the cumulenic species without bond-length alternation.

The magnetic fields we propose here are substantial in magnitude, but very local in space. These magnetic fields that arise from ballistic currents in single-molecule junctions could potentially approach the strength of the magnetic field typically used in NMR spectroscopy. The current-induced magnetic field in a single-molecule junction can thus locally reach a range where the magnetic properties of nuclei and electrons are affected to an extent where we expect it to have experimentally measurable consequences. This is subject to the time scale of the dynamics relating to the experiment, which will be left for future work to assess. Currently, no experimental setup allows for NMR or EPR spectroscopy in single-molecule junctions, but our results suggest that such measurements may produce novel insight should they become experimentally viable in the future.

The highly local nature of the current-induced magnetic fields we explore in this study, furthermore opens the question of whether it is an important effect for magnetoresistance and spin selectivity experiments, such as CISS and spin-torque experiments. − Finally, the helical movement of electrons is inherently linked to optical activity and spin–orbit coupling through transient magnetic coupling. − In the future, these fundamentally linked effects may be probed in single-molecule junctions if new experimental setups can be developed and suitable molecules can be synthesized. Such a setup may require both direct probing of the magnetic response of molecules, such as in current NMR and EPR experimental setups, and, as we have demonstrated here, a gate electrode to control the bias window in order to achieve strong ring currents at low bias.

Code to calculate the s-band approximated current density through single molecules: 10.5281/zenodo.14778214. Code to calculate the magnetic field resulting from the current density: 10.5281/zenodo.15826976.

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.5c00735.

• Benchmark of computed currents. Additional figures of current densities, magnetic fields, Landauer transmissions, and convergence plots. Visualization of structures (PDF)

• Data files containing xyz coordinate files and jmol scripts for 3D visualization of current density and magnetic fields (ZIP)

The authors declare no competing financial interest.