Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Feb 24;127(9):2022–2027. doi: 10.1021/acs.jpcb.2c07305

Machine Learning-Boosted Design of Ionic Liquids for CO2 Absorption and Experimental Verification

Nahoko Kuroki †,‡,*, Yuki Suzuki §, Daisuke Kodama §,*, Firoz Alam Chowdhury ∥, Hidetaka Yamada ∥,⊥, Hirotoshi Mori †,*
PMCID: PMC10009743  PMID: 36827525

Abstract

graphic file with name jp2c07305_0006.jpg

Efficient CO2 capture is indispensable for achieving a carbon-neutral society while maintaining a high quality of life. Since the discovery that ionic liquids (ILs; room-temperature molten salts) can absorb CO2, various solvents composed of molecular ions have been studied. However, it is challenging to observe the properties of each isolated ion component to control the function of ILs as they are mixtures of ions. Finding the optimal cation–anion combination for the CO2 absorbent from their enormous chemical space had been impossible in a practical sense. This study applied electronic structure informatics to explore ILs with high CO2 solubility from 402,114 IL candidates. The feature variables were determined by a set of cheap quantum chemistry calculations for isolated small-ion fragments, and the importance of molecular geometries and electronic states governing molecular interactions was identified via the wrapper method. As a result, it was clearly shown that the electronic states of ionic species must have essential roles in the CO2 physisorption capacity of ILs. Considering synthetic easiness for the candidates narrowed by the machine learning model, trihexyl(tetradecyl)phosphonium perfluorooctanesulfonate was synthesized. Using a magnetic suspension balance, it was experimentally confirmed that this IL has higher CO2 solubility than trihexyl(tetradecyl)phosphonium bis(trifluoromethanesulfonyl)amide, which is the previous best IL for CO2 absorption.

Introduction

Developing CO2-absorbing materials with better performance is a critical step toward achieving efficient CCUS (carbon dioxide capture, utilization, and storage), which has been proposed as a strategy to address global warming.1 While there are several types of CO2 absorbers, the intensive study of ionic liquids (ILs; room-temperature molten salts) would give basic science contributing to environmental engineering toward the development of a safe and sustainable society. ILs are highly stable (with low volatility and high heat resistance) and can be chemically designed with a wide variety of ion combinations.2−5 ILs have been applied to various gas-fixing technologies, such as temperature/pressure swing, chemical/physical absorption, and cryogenic-/membrane-based separation.6,7

A major limitation to the development of ILs for applications is the combinatorial explosion of the ion species, i.e., there are 1018 ILs in theory.2 Even when ILs are limited to physical absorption (those not causing the CO2 chemisorption), optimization of the CO2 absorption capacity is experimentally challenging. The synthesis of ILs and characterization of their physical properties are more labor intensive than for electrically neutral molecular liquids due to their high viscosities. To the best of our knowledge, [P66614][TFSA] (trihexyl(tetradecyl)phosphonium bis(trifluoromethanesulfonyl)amide) has the highest CO2 solubility per molar fraction.8 Despite the vast number of candidates, even though many previous experimental and theoretical studies have designed CO2-absorbing ILs, there has been no report of a material superior to [P66614][TFSA] in the last decade.

Machine learning has proven to be an excellent approach for overcoming such combinatorial problems if proper data sets are available. However, the synthesis and purification of ILs are typically complex, and it is difficult to consistently measure their physical properties with the same accuracy. Therefore, in the field of novel IL design, using experimental information may unintentionally bias the machine learning process. For example, the measured data of imidazolium cations are far greater than those for other cations. There have been several attempts to optimize the gas absorption properties of ILs for a narrow chemical space involving specific ionic skeletons using a machine learning approach,9−13 but a nonbiased (based on the number of ionic species) evaluation of the general chemical space has not been developed. Moreover, slight differences in the electronic states of ionic species can have critical effects on the properties of ILs. Since classical structure-based fingerprints cannot uniquely define charge delocalization, a comprehensive chemical space search by machine learning has not been achieved.

This study aimed to identify ILs with high CO2 absorption capacities with minimal experimental processes. To this end, a materials informatics approach based on quantum chemistry calculations was implemented (Figure 1). Guided by the results of a machine learning evaluation, promising IL candidates were targeted and synthesized. Their CO2 solubilities were also measured. This study focused on the simple ILs (cation–anion binary mixtures); however, it should be noted that the method has transferability to the functional design of further multicomponent systems.

Figure 1.

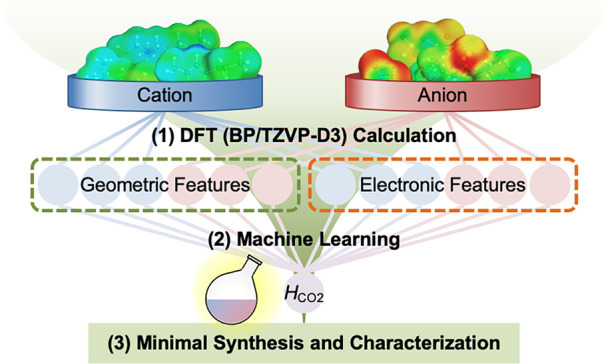
Figure 1

Open in a new tab

Proposed approach. By performing machine learning, synthesis, and precision measurement, ILs with excellent CO2 solubilities were developed in a short period.

Methods

First, a theoretical screening was performed based on quantum chemistry calculations and machine learning. 6,991 stable ion structures (6,933 cations and 58 anions; see Figure S1 and Table S1) were explored by density functional theory calculations at the BP/TZVP-D3 level of theory, which has been successfully used for organic compounds, including ILs.14−22 Using geometry optimized structures and surface-charge-density distributions (σ-profiles),23−26 the geometric and electronic features listed in Table S2 were calculated for each ion.

Then, a set of Henry’s law constant (HCO2) values at 298.15 K was evaluated by applying the COSMO-RS theory23−25 to 20,000 ILs (randomly selected from the total 402,114 candidates). It has been reported that calculated HCO2 reproduces measured values well.21,22 Half of this set was used to train a machine learning model to predict HCO2 for the other IL candidates. Using a cycle of feature selection, model creation, and performance evaluation, the essential molecular (ion) features for CO2 absorption were systematically identified (wrapper method).27 For model creation, the Gaussian process regression (GPR; kernel = ARDMatern 5/2) method28 was applied to the standardized data with the quasi-Newton optimizer and five-fold cross-validation. The performance of the created model was evaluated with 10,000 test data sets based on the coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE). These operations were repeated five times. The quantum chemistry and statistical thermodynamics calculations and machine learning were performed with the TURBOMOLE 7.0,29 COSMOtherm C30_1705,30 and MATLAB31 packages, respectively.

Guided by the electronic structure informatics results, a set of automatically recommended (i.e., minimal) experiments was performed. Three representative [P66614][A] IL candidates were investigated, where A = [PFOS]− (perfluorooctanesulfonate), [PF6]− (hexafluorophosphate), and [TFSA]−. These ILs were synthesized (see Table S3 and Figures S2) according to the literature procedures32,33 (For details, see Synthesis Section in Supporting Information). No unexpected or unusually high safety hazards were encountered. The density and viscosity under atmospheric to high-pressure conditions were measured for the ILs according to the literature procedures34−40 (For details, see Measurements Section in Supporting Information).

The CO2 solubility of an IL was measured using a magnetic suspension balance (Rubotherm GmbH), as detailed in our previous papers.39,40 The resolution and repeatability of the microbalance were 10 mg and ±30 mg, respectively. Before the measurement, the weight and volume of a blank sample basket were measured at 313.15 or 333.15 K, respectively, up to 6 MPa. The volume of the blank sample basket was determined using the buoyancy method. CO2 solubility measurements were then conducted as followings. 1 g of an IL was loaded in the sample basket, and then, the high-pressure cell was subjected to vacuum for approximately 24 h at 313.15 or 333.15 K. After evacuation, the weight of the pure IL under vacuum was recorded. A desired amount of CO2 was loaded into the high-pressure cell, and the temperature was maintained to within ±0.01 K. When the changes in weight, temperature, and pressure were less than ±0.1 mg h–1, ±0.01 K h–1, and 0.001 MPa h–1, respectively, it was assumed that the IL was saturated with CO2, and the weight was recorded. Subsequent measurements were repeated to obtain isothermal solubility data at pressures up to 6 MPa.

The amount of dissolved gas, Wg, was obtained as39,40

graphic file with name jp2c07305_m001.jpg 1

where WF and W0 are the readouts of the balance at pressure p and vacuum, respectively. ρCO2 is the CO2 density obtained using the Span–Wagner equation of state.41VIL and VB are the volumes of the IL and the sample basket (including a hook), respectively. VIL was obtained from the sample mass and specific volume of the IL at each pressure. Based on the experimental density data for the ILs, the specific volume of the IL at high pressure was calculated using the Tait equation of state.42 The volume expansion (swelling) of the IL, SW, caused by gas absorption was calculated using the Sanchez–Lacombe equation of state.43,44 The coefficients of these equations were obtained by fitting the experimental densities of the ILs (temperature: 313.15 or 333.15 K; pressure: 0.1–6 MPa).

HCO2 was evaluated for the ILs as the solubility gradients (∂p/∂xCO2) in the region of xCO2 < 0.1. Finally, the Gibbs energy (ΔabsG∞), enthalpy (ΔabsH∞), and entropy (ΔabsS∞) of CO2 absorption by the ILs were experimentally obtained using the thermodynamic relations45

graphic file with name jp2c07305_m002.jpg 2
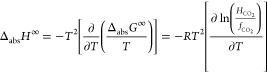graphic file with name jp2c07305_m003.jpg 3
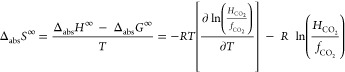graphic file with name jp2c07305_m004.jpg 4

where fCO2 is the fugacity coefficient of CO2. ΔabsH∞ and ΔabsS∞ are closely related to the solute–solvent interaction strength and the free volume of the solvent, respectively.

Results and Discussion

The correlation matrixes of cation and anion features are shown in Figures S3 and S4, respectively. These figures clearly show that the geometric and electronic structures of ions are independent of each other. Sets of the logarithm of HCO2 were normally distributed (Figures S5).

The accuracy of the machine learning procedure was confirmed by the learning curves for the test data not used for training the model and the correlation between the predicted and calculated HCO2 values. According to a wrapper cycle, the features for CO2 absorption were systematically identified. Highly accurate HCO2 predictions (R2 > 0.90, RMSE< 1.5 MPa, and MAE< 0.13 MPa) were achieved when 12 features were applied (Figure 2a). As summarized in Tables S4–S6, the wrapper method clarified that the first- and second-most important features were geometric V (volume) and electronic M2 (2nd σ-moment). This is considered reasonable because CO2 molecules are physically absorbed in polar voids surrounded by ions in the ILs. It was clearly shown that the electronic state differences of ions have essential roles in the CO2 physisorption capacity of ILs. It was also confirmed that a training data set size of 10,000 (2% of the candidates) was sufficient for obtaining an accurate model (Figure 2b). The constructed GPR model could predict HCO2 values with high accuracy (Figure S6). Other algorithms (linear, XGBoost, and random forest regression) were also tried; however, they did not exceed GPR’s performance (Figure S7).

Figure 2.

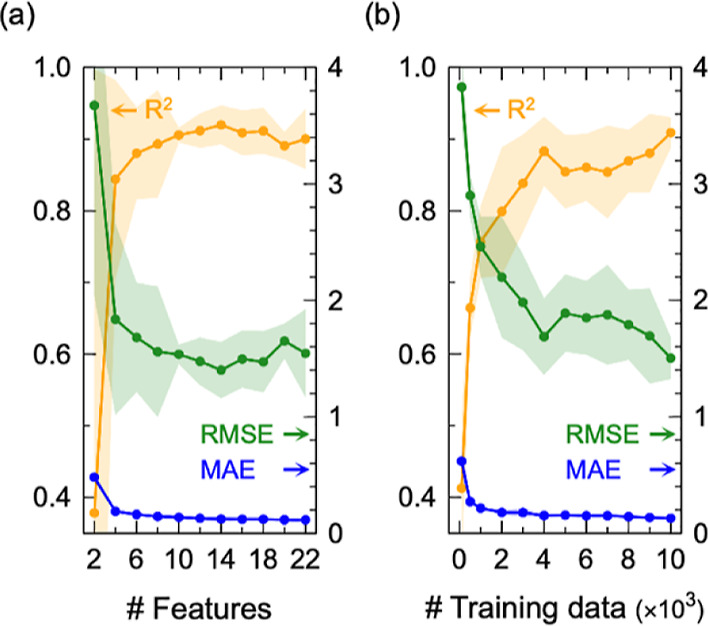
Figure 2

Open in a new tab

Learning curves for the test data not used for training the model with respect to the (a) number of features and (b) size of the training data set. For (a), the order of the features to add was determined by the wrapper method to maximize accuracy. For (b), V, M2, MW, M5, M6, and A were used for the features (see Tables S2 and S4−S6).

Then, the GPR model was applied to predict HCO2 for all 402,114 IL candidates. Using the well-trained model, superior ILs for CO2 absorption could be predicted within a minute for these candidate ILs. A set of HCO2 values regressed by the model are listed in Table S7. Considering machine learning results and synthetic possibilities (likely to yield the liquid state by a simple synthetic route), we decided to investigate two phosphonium-based ILs ([P66614][PFOS] and [P66614][PF6]) which had better predicted HCO2 values (2.78 and 2.91 MPa, respectively) than [P66614][TFSA] (3.06 MPa).

For the three ILs, the densities and the viscosities were determined to evaluate the specific volumes of the ILs (Figures S8–S10 and Tables S8-S11). Both densities and viscosities of all three ILs showed a negative correlation with increasing temperature, and high-pressure densities showed a positive correlation with increasing pressure. Here, the order of viscosity (TFSA– < PFOS– < PF6–) did not correspond with the one of density (PF6– < TFSA– < PFOS–). It has been reported that [P66614][TFSA] has lower viscosity than [P66614][PF6],46 and our results confirm this fact. These results suggest that the cation–anion electrostatic interaction of [P66614][PF6] is particularly strong. The measured densities well agreed with the calculated values fitted by the quadratic equation (average relative deviation: ARD < 0.02%). The measured viscosities correlated well with the Vogel–Fulcher–Tammann (VFT) equation (ARD < 0.46%) rather than the Arrhenius equation (ARD < 1.79%) because ILs have glass transition points. From the well-fitted high-pressure densities in the Tait equation of state (ARD < 0.01%) and the Sanchez–Lacombe equation of state (ARD < 0.14%), the volume expansions (swelling) of the ILs were obtained.

Both the mole fraction and molarity-scaled CO2 solubilities were also measured (Figure 3 and Table 1). The former does not consider the effect of molecular volume, while the latter does. Thus, the molarity-scaled CO2 solubilities are important for gas absorption process design. The solubilities proportional to pressure means that the ILs absorb CO2 by a physisorption mechanism. The CO2 solubility increased in the anion order of PF6– < TFSA– < PFOS– (with increasing fluorine atoms in the anions). The reason for the results can be considered as due to the fact that the large numbers of fluorine atoms and S=O bonds in PFOS– can develop strong interactions between the anion and CO2. From the COSMO-RS validation, it was found that PFOS– has the largest anion–CO2 contact probability (PFOS–: 0.318, TFSA–: 0.232, and PF6–: 0.151). The fact could also be explained experimentally: the absorption Gibbs energy of [P66614][PFOS] (Chart 1) was the most stable among the three ILs due to the large negative enthalpy (Table 2).

Figure 3.

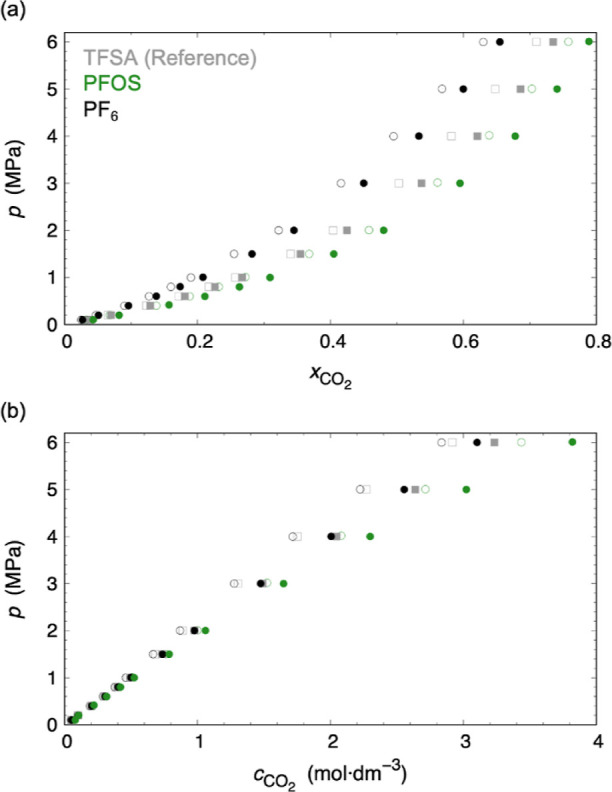
Figure 3

Open in a new tab

CO2 solubility scaled by (a) mole fraction xCO2 and (b) molarity cCO2 (mol·dm–3) in [P66614][A] (A = TFSA, PFOS, and PF6). Using the molar mass MCO2 and the mass fraction XCO2 of CO2, cCO2 was calculated by cCO2 = ρL × XCO2/MCO2. Closed and opened points are at 313.15 and 333.15 K, respectively.

Table 1. CO2 Solubility Scaled by Mole Fraction xCO2 and Molarity cCO2 (mol·dm–3) as a Function of Equilibrium Pressure p (MPa) in [P66614][A] (A = TFSA, PFOS, and PF6)a.

p xCO2 cCO2 p xCO2 cCO2 p xCO2 cCO2
T = 313.15 K
TFSA PFOS PF6
0.100 0.037 0.052 0.100 0.043 0.080 0.100 0.027 0.053
0.201 0.070 0.103 0.200 0.082 0.106 0.200 0.051 0.104
0.401 0.129 0.203 0.416 0.157 0.220 0.400 0.096 0.204
0.600 0.181 0.301 0.599 0.211 0.316 0.604 0.138 0.305
0.800 0.226 0.397 0.800 0.263 0.420 0.803 0.174 0.402
1.000 0.267 0.493 0.999 0.309 0.523 1.004 0.208 0.499
1.500 0.355 0.734 1.499 0.405 0.787 1.499 0.282 0.736
2.000 0.425 0.977 2.000 0.480 1.060 2.000 0.345 0.976
3.001 0.537 1.491 3.000 0.595 1.647 3.001 0.450 1.475
3.999 0.621 2.046 4.000 0.678 2.299 4.002 0.533 2.005
4.999 0.686 2.638 4.999 0.741 3.022 5.000 0.600 2.555
5.998 0.735 3.234 6.011 0.789 3.820 6.000 0.655 3.103
T = 333.15 K
TFSA PFOS PF6
0.101 0.035 0.050 0.100 0.033 0.066 0.100 0.025 0.049
0.201 0.065 0.099 0.199 0.068 0.101 0.200 0.047 0.099
0.400 0.123 0.199 0.400 0.138 0.213 0.399 0.090 0.191
0.600 0.172 0.295 0.600 0.188 0.305 0.600 0.127 0.290
0.800 0.217 0.386 0.802 0.232 0.412 0.800 0.160 0.377
1.000 0.257 0.473 1.010 0.272 0.510 1.000 0.190 0.460
1.500 0.340 0.682 1.500 0.368 0.762 1.499 0.255 0.666
2.000 0.404 0.888 2.006 0.458 0.999 2.000 0.322 0.869
3.000 0.503 1.304 3.014 0.561 1.523 2.999 0.416 1.276
4.000 0.582 1.753 4.018 0.639 2.081 3.998 0.495 1.716
5.000 0.648 2.271 5.007 0.703 2.714 5.004 0.568 2.224
6.000 0.710 2.917 6.004 0.758 3.436 5.997 0.630 2.836
Open in a new tab
a

Standard uncertainties are u(T) = 0.01 K and u(p) = 0.0005 MPa. Relative expanded uncertainties of Ur are u(xCO2) = 0.001 and u(cCO2) = 0.001.

Chart 1. IL [P66614][PFOS] with the Best CO2 Physisorption Capacity Achieved by Machine Learning.

Chart 1

Open in a new tab

Table 2. Henry’s Law Constants HCO2 (MPa), Gibbs Energy ΔabsG∞ (kJ·mol–1), Enthalpy ΔabsH∞ (kJ·mol–1), and Entropy ΔabsS∞ (J·mol–1·K–1) of CO2 Absorption Evaluated Experimentally for [P66614][A] (A = TFSA, PFOS, and PF6)a.

  HCO2 ΔabsG∞ ΔabsH∞ ΔabsS∞
TFSA 2.85 (3.04) 2.72 –2.62 –17.1
PFOS 2.41 (2.71) 2.29 –8.11 –33.2
PF6 4.09 (4.39) 3.67 –2.88 –20.9
Open in a new tab
a

The data outside/inside the parenthesis are at 313.15/333.15 K.

Conclusions

This study proposed an electronic structure informatics approach to predict and develop ILs with high CO2 solubility based on geometric and electronic factors of the constituent cations and anions. With a machine learning-assisted search for the best cation/anion combination, targeted organic syntheses, and precision measurements, the IL [P66614][PFOS] was experimentally proven to have a higher CO2 solubility than [P66614][TFSA]. The wrapper cycle analysis of molecular features clearly showed that the electronic features of ions have essential roles in the CO2 physisorption capacity. In other words, precisely designing electronic states of the ionic species by quantum chemistry calculation is mandatory for further tuning of the gas absorption nature. New ionic species with functional group introductions, elemental substitutions, and other modifications could also be systematically considered to accelerate research without being hindered by the enormous chemical space of ILs. The method for developing functional liquids proposed in this study can be applied to other gas-absorbing liquids, such as deep eutectic solvents (hydrogen-bonded mixed organic solvents in a broad sense) or general functional materials composed of multicomponent systems with an extension for weak intermolecular interaction. We believe our method will significantly contribute to developing a carbon-neutral society.

Data Availability Statement

All the experimental data are available in the main text or Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcb.2c07305.

  • Supporting methods including chemical space and features for machine learning, synthesis, and measurements; results including machine learning and densities and viscosities under atmospheric to high-pressure conditions; and references (PDF)

Author Contributions

N.K. and H.M. conceived the project. N.K. generated the molecular library and performed machine learning with guidance from H.M. F.A.C. and H.Y. synthesized the three ILs. Y.S. and D.K. measured the basic properties of the ILs. The manuscript was written through contributions from all authors. All authors have given their approval to the final version of the manuscript.

N.K. acknowledges support from the JST ACT-I and ACT-X projects of the Japan Science and Technology Agency (grant nos. JPMJPR16UB and JPMJAX20A9). HM acknowledges support from JSPS KAKENHI (grant no. 21H01894). DK acknowledges support from JSPS KAKENHI (grant no. 19K05130). The calculations were performed using supercomputer resources provided by the Research Center for Computational Science (RCCS) at the Okazaki Research Facilities of the National Institutes of Natural Sciences (NINS), Japan (project no. 22-IMS-C015).

The authors declare no competing financial interest.

Supplementary Material

jp2c07305_si_001.pdf (3.2MB, pdf)

References

  1. Leung D. Y. C.; Caramanna G.; Maroto-Valer M. M. An Overview of Current Status of Carbon Dioxide Capture and Storage Technologies. Renewable Sustainable Energy Rev. 2014, 39, 426–443. 10.1016/j.rser.2014.07.093. [DOI] [Google Scholar]
  2. Holbrey J. D.; Seddon K. R. Ionic Liquids. Clean Prod. Processes 1999, 1, 223–236. 10.1007/s100980050036. [DOI] [Google Scholar]
  3. Blanchard L. A.; Hancu D.; Beckman E. J.; Brennecke J. F. Green Processing Using Ionic Liquids and CO2. Nature 1999, 399, 28–29. 10.1038/19887. [DOI] [Google Scholar]
  4. Plechkova N. V.; Seddon K. R. Applications of Ionic Liquids in the Chemical Industry. Chem. Soc. Rev. 2008, 37, 123–150. 10.1039/b006677j. [DOI] [PubMed] [Google Scholar]
  5. Armand M.; Endres F.; MacFarlane D. R.; Ohno H.; Scrosati B. Ionic-liquid Materials for the Electrochemical Challenges of the Future. Nat. Mater. 2009, 8, 621–629. 10.1038/nmat2448. [DOI] [PubMed] [Google Scholar]
  6. Olajire A. A. CO2 Capture and Separation Technologies for End-of-pipe Applications–A Review. Energy 2010, 35, 2610–2628. 10.1016/j.energy.2010.02.030. [DOI] [Google Scholar]
  7. Wang M.; Lawal A.; Stephenson P.; Sidders J.; Ramshaw C. Post-combustion CO2 Capture with Chemical Absorption: A State-of-the-art Review. Chem. Eng. Res. Des. 2011, 89, 1609–1624. 10.1016/j.cherd.2010.11.005. [DOI] [Google Scholar]
  8. Carvalho P. J.; Álvarez V. H.; Marrucho I. M.; Aznar M.; Coutinho J. A. High Carbon Dioxide Solubilities in Trihexyltetradecylphosphonium-based Ionic Liquids. J. Supercrit. Fluids 2010, 52, 258–265. 10.1016/j.supflu.2010.02.002. [DOI] [Google Scholar]
  9. Yusuf F.; Olayiwola T.; Afagwu C. Application of Artificial Intelligence-based Predictive Methods in Ionic Liquid Studies: A Review. Fluid Phase Equilib. 2021, 531, 112898. 10.1016/j.fluid.2020.112898. [DOI] [Google Scholar]
  10. Wu T.; Li W.; Chen M.; Zhou Y.; Zhang Q. Y. Prediction of Henry’s Law Constants of CO2 in Imidazole Ionic Liquids Using Machine Learning Methods Based on Empirical Descriptors. Chem. Pap. 2021, 75, 1619–1628. 10.1007/s11696-020-01415-8. [DOI] [Google Scholar]
  11. Paduszyński K.; Kłębowski K.; Królikowska M. Predicting Melting Point of Ionic Liquids Using QSPR Approach: Literature Review and New Models. J. Mol. Liq. 2021, 344, 117631. 10.1016/j.molliq.2021.117631. [DOI] [Google Scholar]
  12. Valeh-e-Sheyda P.; Masouleh M. F.; Zarei-Kia P. Prediction of CO2 Solubility in Pyridinium-based Ionic Liquids Implementing New Descriptor-based Chemoinformatics Models. Fluid Phase Equilib. 2021, 546, 113136. 10.1016/j.fluid.2021.113136. [DOI] [Google Scholar]
  13. Abdi J.; Hadipoor M.; Esmaeili-Faraj S. H.; Vaferi B. A Modeling Approach for Estimating Hydrogen Sulfide Solubility in Fifteen Different Imidazole-based Ionic Liquids. Sci. Rep. 2022, 12, 4415. 10.1038/s41598-022-08304-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Masuda C.; Kuroki N. Statistical Thermodynamics Database Construction to Search for Novel Ionic Liquids with Gas Selectivity. J. Comput. Chem., Jpn. 2019, 18, 217–220. 10.2477/jccj.2019-0046. [DOI] [Google Scholar]
  15. Kuroki N.; Maruyama S.; Mori H. Theoretical Strategy for Improving CO2 Absorption of Mixed Ionic Liquids Focusing on the Anion Effect: A Comprehensive COSMO-RS Study. Ind. Eng. Chem. Res. 2020, 59, 8848–8854. 10.1021/acs.iecr.0c00488. [DOI] [Google Scholar]
  16. Becke A. D. Density-functional Exchange-energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
  17. Perdew J. P. Density-functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 33, 8822–8824. 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
  18. Perdew J. P. Erratum Density-functional Approximation for the Correlation Energy of the Inhomogeneous Electron Gas. Phys. Rev. B 1986, 34, 7406. 10.1103/physrevb.34.7406. [DOI] [PubMed] [Google Scholar]
  19. Schäfer A.; Klamt A.; Sattel D.; Lohrenz J. C. W.; Eckert F. COSMO Implementation in TURBOMOLE: Extension of an Efficient Quantum Chemical Code Towards Liquid Systems. Phys. Chem. Chem. Phys. 2000, 2, 2187–2193. 10.1039/B000184H. [DOI] [Google Scholar]
  20. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154111. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  21. Farahipour R.; Mehrkesh A.; Karunanithi A. T. A Systematic Screening Methodology Towards Exploration of Ionic Liquids for CO2 Capture Processes. Chem. Eng. Sci. 2016, 145, 126–132. 10.1016/j.ces.2015.12.015. [DOI] [Google Scholar]
  22. Sistla Y. S.; Khanna A. Validation and Prediction of the Temperature-Dependent Henry’s Constant for CO2–Ionic Liquid Systems Using the Conductor-like Screening Model for Realistic Solvation (COSMO-RS). J. Chem. Eng. Data 2011, 56, 4045–4060. 10.1021/je200486c. [DOI] [Google Scholar]
  23. Klamt A. Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena. J. Phys. Chem. 1995, 99, 2224–2235. 10.1021/j100007a062. [DOI] [Google Scholar]
  24. Klamt A.; Jonas V.; Bürger T.; Lohrenz J. C. W. Refinement and Parametrization of COSMO-RS. J. Phys. Chem. A 1998, 102, 5074–5085. 10.1021/jp980017s. [DOI] [Google Scholar]
  25. Klamt A.; Eckert F.; Hornig M. COSMO-RS. A Novel View to Physiological Solvation and Partition Questions. J. Comput.-Aided Mol. Des. 2001, 15, 355–365. 10.1023/a:1011111506388. [DOI] [PubMed] [Google Scholar]
  26. Kondor A.; Járvás G.; Kontos J.; Dallos A. Temperature Dependent Surface Tension Estimation Using COSMO-RS Sigma Moments. Chem. Eng. Res. Des. 2014, 92, 2867–2872. 10.1016/j.cherd.2014.06.021. [DOI] [Google Scholar]
  27. Urbanowicz R. J.; Meeker M.; La Cava W.; Olson R. S.; Moore J. H. Relief-based Feature Selection: Introduction and Review. J. Biomed. Inf. 2018, 85, 189–203. 10.1016/j.jbi.2018.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Williams C. K.; Rasmussen C. E.. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, 2006; Vol. 2. [Google Scholar]
  29. Ahlrichs R.; Bär M.; Häser M.; Horn H.; Kölmel C. Electronic Structure Calculations on Workstation Computers: The Program System TURBOMOLE. Chem. Phys. Lett. 1989, 162, 165–169. 10.1016/0009-2614(89)85118-8. [DOI] [Google Scholar]
  30. COSMOtherm , Version C3.0, Release 17.01; COSMOlogic GmbH & Co. KG.
  31. MATLAB ; The MathWorks Inc.: Natick, Massachusetts, 2018. 9.7.0.1190202 (R2019b).
  32. Blundell R. K.; Licence P. Quaternary Ammonium and Phosphonium Based Ionic Liquids: A Comparison of Common Anions. Phys. Chem. Chem. Phys. 2014, 16, 15278–15288. 10.1039/c4cp01901f. [DOI] [PubMed] [Google Scholar]
  33. Kang C. S. M.; Zhang X.; MacFarlane D. R. Synthesis and Physicochemical Properties of Fluorinated Ionic Liquids with High Nitrogen Gas Solubility. J. Phys. Chem. C 2018, 122, 24550–24558. 10.1021/acs.jpcc.8b07752. [DOI] [Google Scholar]
  34. Kodama D.; Kanakubo M.; Kokubo M.; Hashimoto S.; Nanjo H.; Kato M. Density, Viscosity, and Solubility of Carbon Dioxide in Glymes. Fluid Phase Equilib. 2011, 302, 103–108. 10.1016/j.fluid.2010.08.014. [DOI] [Google Scholar]
  35. Kodama D.; Sato K.; Watanabe M.; Sugawara T.; Makino T.; Kanakubo M. Density, Viscosity, and CO2 Solubility in the Ionic Liquid Mixtures of [bmim][PF6] and [bmim][TFSA] at 313.15 K. J. Chem. Eng. Data 2018, 63, 1036–1043. 10.1021/acs.jced.7b00786. [DOI] [Google Scholar]
  36. Watanabe M.; Kodama D.; Makino T.; Kanakubo M. Density, Viscosity, and Electrical Conductivity of Protic Amidium Bis(trifluoromethanesulfonyl)amide Ionic Liquids. J. Chem. Eng. Data 2016, 61, 4215–4221. 10.1021/acs.jced.6b00575. [DOI] [Google Scholar]
  37. Harris K. R.; Kanakubo M.; Kodama D.; Makino T.; Mizuguchi Y.; Watanabe M.; Watanabe T. Temperature and Density Dependence of the Transport Properties of the Ionic Liquid Triethylpentylphonium Bis(trifluoromethanesulfonyl)amide, [P222,5][Tf2N]. J. Chem. Eng. Data 2018, 63, 2015–2027. 10.1021/acs.jced.8b00011. [DOI] [Google Scholar]
  38. May E. F.; Tay W. J.; Nania M.; Aleji A.; Al-Ghafri S.; Martin Trusler J. P. Physical Apparatus Parameters and Model for Vibrating Tube Densimeters at Pressures to 140 MPa and Temperatures to 473 K. Rev. Sci. Instrum. 2014, 85, 095111. 10.1063/1.4894469. [DOI] [PubMed] [Google Scholar]
  39. Watanabe M.; Kodama D.; Makino T.; Kanakubo M. CO2 Absorption Properties of Imidazolium Based Ionic Liquids Using a Magnetic Suspension Balance. Fluid Phase Equilib. 2016, 420, 44–49. 10.1016/j.fluid.2015.12.055. [DOI] [Google Scholar]
  40. Sato Y.; Takikawa T.; Takishima S.; Masuoka H. Solubilities and Diffusion Coefficients of Carbon Dioxide in Poly(vinyl acetate) and Polystyrenen. J. Supercrit. Fluids 2001, 19, 187–198. 10.1016/s0896-8446(00)00092-9. [DOI] [Google Scholar]
  41. Span R.; Wagner W. A New Equation of State for Carbon Dioxide Covering the Fluid Region from the Triple-Point Temperature to 1100 K at Pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. 10.1063/1.555991. [DOI] [Google Scholar]
  42. Nanda V. S.; Simha R. Equation of State of Polymer Liquids and Glasses at Elevated Pressures. J. Chem. Phys. 1964, 41, 3870–3878. 10.1063/1.1725827. [DOI] [Google Scholar]
  43. Sanchez I. C.; Lacombe R. H. An Elementary Molecular Theory of Classical Fluids. Pure Fluids. J. Phys. Chem. 1976, 80, 2352–2362. 10.1021/j100562a008. [DOI] [Google Scholar]
  44. Sanchez I. C.; Lacombe R. H. Statistical Thermodynamics of Polymer Solutions. Macromolecules 1978, 11, 1145–1156. 10.1021/ma60066a017. [DOI] [Google Scholar]
  45. Jacquemin J.; Costa Gomes M. F.; Husson P.; Majer V. Solubility of Carbon Dioxide, Ethane, Methane, Oxygen, Nitrogen, Hydrogen, Argon, and Carbon Monoxide in 1-Butyl-3-methylimidazolium Tetrafluoroborate Between Temperatures 283 K and 343 K and at Pressures Close to Atmospheric. J. Chem. Thermodyn. 2006, 38, 490–502. 10.1016/j.jct.2005.07.002. [DOI] [Google Scholar]
  46. Ahosseini A.; Scurto A. M. Viscosity of Imidazolium-Based Ionic Liquids at Elevated Pressures: Cation and Anion Effects. Int. J. Thermophys. 2008, 29, 1222–1243. 10.1007/s10765-008-0497-7. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp2c07305_si_001.pdf (3.2MB, pdf)

Data Availability Statement

All the experimental data are available in the main text or Supporting Information.

Articles from The Journal of Physical Chemistry. B are provided here courtesy of American Chemical Society

RESOURCES