Contrast Variation SAXS: sample preparation protocols, experimental procedures, and data analysis

Abstract

Proteins and nucleic acids, alone and in complex are among the essential building blocks of living organisms. Obtaining a molecular level understanding of their structures, and the changes that occur as they interact, is critical for expanding our knowledge of life processes or disease progression. Here, we motivate and describe an application of solution small angle X-ray scattering (SAXS) which provides valuable information about the structures, ensembles, compositions and dynamics of protein-nucleic acid complexes in solution, in equilibrium and time-resolved studies. Contrast variation (CV-) SAXS permits the visualization of the distinct molecular constituents (protein and/or nucleic acid) within a complex. CV-SAXS can be implemented in two modes. In the simplest, the protein within the complex is effectively rendered invisible by the addition of an inert contrast agent at an appropriate concentration. Under these conditions, the structure, or structural changes of only the nucleic acid component of the complex can be studied in detail. The second mode permits observation of both components of the complex: the protein and the nucleic acid. This approach requires the acquisition of SAXS profiles on the complex at different concentrations of a contrast agent. Here, we review CV-SAXS as applied to protein-nucleic acid complexes in both modes. We provide some theoretical framework for CV-SAXS but focus primarily on providing the necessary information required to implement a successful experiment including experimental design, sample quality assessment, and data analysis.

Introduction

Protein-nucleic acid complexes play essential roles in biology. Protein interactions with DNA contribute to processes as fundamental as: packaging or remodeling chromatin, transcription, replication, recombination, damage repair, or DNA modification (Brenner & Miller, 2014). RNA-protein complexes exhibit biological activities that extend far beyond gene expression. A myriad of newly-identified RNA binding proteins have been reported; yet the structural interactions that facilitate biological activity have not yet been established for many of these complexes (Beckmann et al., 2016; Van Nostrand et al., 2020). The exploding interest in RNA underscores the need for structural characterization, alone and with partners. Finally, either DNA or RNA can be packaged by proteins into viruses, a key concern at the present time.

Traditional high-resolution structural methods such as X-ray crystallography or cryo-electron microscopy (cryo-EM) have provided exceptional insight into the interactions that stabilize complexes (Galej et al., 2016; Luger et al., 1997; Yan et al., 2015; Yusupov et al., 2001); however, the molecules are often immobilized, either through crystal contacts or by plunge freezing. Though extensive computation has been used to sequence a series of static snapshots (Frank & Ourmazd, 2016), the opportunity to measure complexes, in solution, at ambient (or higher) temperature, or in real time, during a reaction offers unique and valuable information.

Because SAXS provides structural information about biomolecules in solution at practically any temperature or buffer condition, it has often been used to complement higher resolution structural techniques (Putnam et al., 2007; Stuhrmann, 2008; Tsutakawa et al., 2007). Expansion into the wide angle (or WAXS) regime sharpens the spatial resolution of solution scattering to a few angstroms, and is being applied to study proteins, DNA and RNA (e.g. He et al., 2021; Makowski et al., 2008; Zuo et al., 2006). Solution X-ray scattering is a versatile and efficient tool to study biological systems; if the molecules are soluble, they can be measured, and their structures can be postulated, even if the biomolecular sample is not monodisperse. Specifically, for this latter case, SAXS with in-line size-exclusion chromatography (SEC-SAXS) can separate heterogeneous biomolecules by size immediately before measurement (David & Pérez, 2009; Pérez & Nishino, 2012). This technique is covered in other chapters in this volume. A true strength of SAXS is the study (measurement) of the conformational dynamics of biomolecules, either as an ensemble in equilibrium studies (Tria et al., 2015), or sequentially, through time-resolved studies which can be triggered using rapid mixing (e.g. Plumridge et al., 2018; Pollack et al., 1999) (with small or large partners) or through light (e.g. Lamb et al., 2008) or heat activation (e.g. Thompson et al., 2019).

SAXS has been most effectively applied to reveal the conformations of either protein or nucleic acid components in solution (Svergun & Koch, 2003). The signal strength scales with the electron density difference between the biomolecule and the solvent that surrounds it. The electron densities of both proteins and nucleic acids exceed that of the surrounding solvent, under typical conditions. Of particular interest to this chapter, we note that proteins and nucleic acids have different electron densities, hence they scatter with different strengths. We will show that the measured signal of a complex contains contributions that reflect the structure of each component, as well as an additional term that contains information about the relative positions of the two. It can therefore be difficult to disentangle the signals arising from individual components using conventional SAXS methods. The contrast variation method we describe circumvents this challenge. It exploits the density difference referenced above and permits the visualization of each component within a complex. Like traditional SAXS, CV-SAXS can then be used to monitor the changing structures of these distinct components as they interact.

This chapter provides essential guidelines for designing and performing CV-SAXS experiments on protein-nucleic acid complexes. We introduce the basic theory of CV-SAXS, discuss sample considerations, sample quality assessment, experimental practices and design, as well as data analysis approaches. Finally, we illustrate the types of results that can be extracted, using both DNA-protein and RNA-protein complexes as examples. Throughout the chapter, techniques used to overcome the unique challenges of CV-SAXS are extensively addressed.

Background: SAXS and CV-SAXS

The origin of any SAXS signal: electron density differences (or contrast) between molecule and background solvent

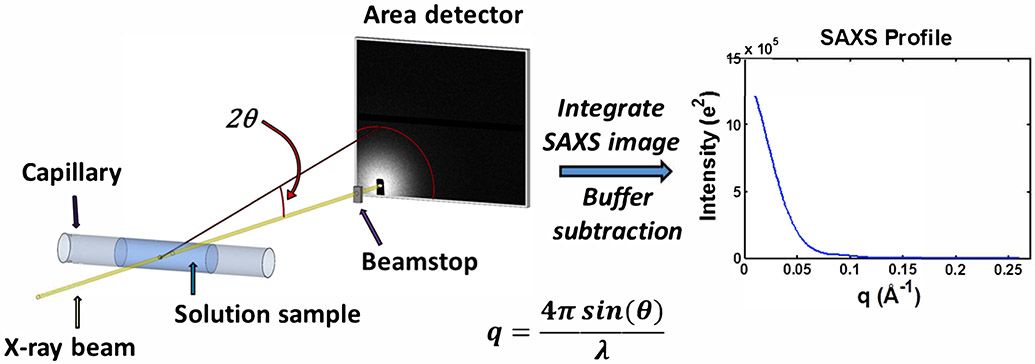
Before providing details about contrast variation SAXS, we first briefly review regular SAXS. More comprehensive reviews can be found in (Blanchet & Svergun, 2013; Jacques & Trewhella, 2010; Koch et al., 2003; Svergun & Koch, 2003) as well as other chapters in this book. It is relatively straightforward to compute the magnitude of scattering, the so-called scattering amplitude, from a single molecule in solution. This amplitude $A$ depends on the molecule’s electron density, ${\rho }_M$, its volume, $V_M$, and the arrangement of electrons within the molecule, e.g. its shape. This shape is reflected by an angle dependent form factor; the scattering decreases relative to its value in the forward or zero-angle ($\theta =0$) direction in a way that depends on the structure of the scatterer. This form factor $F$ is typically written as a function of scattering vector $q=4\pi \sin \theta ∕\lambda$, where $2\theta$ is the scattering angle and $\lambda$ is the X-ray wavelength. The geometry of a typical scattering experiment is shown in Figure 1. Experiments measure the intensity of the scattered radiation, $I(q)$, which is the product of amplitude $A$ and its complex conjugate. Because most biomolecules are dissolved in solvent with electron density ${\rho }_S$, $A$ is proportional to the electron density difference between the molecule and the background solvent, $\Delta {\rho }_M={\rho }_M\text{-}{\rho }_S$. This difference represents the excess electron density of the solute relative to the solvent and is called the contrast of the system. The scattering amplitude and intensity for a molecule of electron density ${\rho }_M$ and form factor $F(q)$ in a solvent with electron density ${\rho }_S$ can be written as:

$$\begin{gathered} A(q)=(\Delta {\rho }_M)V_{M}F(q) \\ I(q)=\Vert A(q){\Vert }^2=(\Delta {\rho }_M{)}^2{V}_M^2\langle \mid F(q){\mid }^2\rangle \end{gathered}$$ (1)

$\langle \mid F(q){\mid }^2\rangle$ represents the rotational average over many molecules in solution and is the product of $F(q)$ and its complex conjugate. It is often written as $P_M(q)$. The scattering intensity for this molecule in solution is written:

$$I(q)=(\Delta {\rho }_M{)}^2{V}_M^2{P}_M(q)$$ (2)

Figure 1.

Schematic of a typical small-angle X-ray scattering (SAXS) experiment. An X-ray beam from either a synchrotron or home/lab source is incident on a capillary containing a solution of macromolecules. The primary sample is typically a buffered solution containing protein, nucleic acid, or protein-nucleic acid complex at dilute concentrations. To avoid radiation damage from the X-ray beam, the sample is typically oscillated or flowed continuously. The scattered X-rays are imaged onto an area detector while the primary beam is either blocked or greatly attenuated by a beamstop. These images are then pooled, averaged, and azimuthally integrated to obtain SAXS profiles of intensity as a function of scattering vector, $I(0)$. For each biomolecule containing sample, a corresponding measurement of the buffer is made, and the resulting buffer profile is subtracted from the biomolecule sample profile to obtain the SAXS scattering profile from the macromolecule. SAXS intensities can be calibrated on an absolute scale.

Contrast Variation SAXS

We begin our discussion of contrast variation SAXS by modifying Equation (1) to account for scattering from a system containing two species of molecules with different electron densities, on a uniform solvent background. We are most interested in protein-nucleic acid complexes. Nucleic acids are more electron dense than proteins, because of their phosphate backbone. If component 1 represents the nucleic acid, and component 2 is the protein, the scattering amplitude of one unit of the complex can be expressed as the sum of the amplitude of each component: $A(q)=\Delta {\rho }_1{V}_1{F}_1(q)+\Delta {\rho }_2{V}_2{F}_2(q)$.

Here, ${\rho }_{\mathrm{i}}$ is the electron density of macromolecule i (= 1 or 2) and ${\rho }_s$ is the electron density of the solvent. The excess electron density of component 1 is written as $\Delta {\rho }_1={\rho }_1-{\rho }_s$. When the amplitudes are summed, and the intensity computed following the procedure outlined above, the following expression results:

$$I(q)=\Delta {\rho }_1^2{V}_1^2{P}_1(q)+\Delta {\rho }_2^2{V}_2^2{P}_2(q)+2\Delta {\rho }_1\Delta {\rho }_2{V}_1{V}_2{P}_{12}(q)$$ (3)

The first two terms of the above equation represent the scattering from the first and second molecular components, while the third term, the so-called cross-term, contains information about the relative positions of the two components. Although we discuss only the two-component case, this argument can be generalized to any number of molecular constituents.

To perform a contrast variation measurement of the type described herein, the density of the solvent, ${\rho }_S$, is increased following the addition of an inert contrast agent. The increase leads to a reduction of $\Delta {\rho }_M$ for each component. Experiments taken under multiple contrast conditions, where the contribution from the components is varied in a controlled way, can be used to separate the scattering from the components.

An extreme, but useful case arises when the electron density of the solvent, ${\rho }_s$ is increased to equal ${\rho }_2$. Under this condition, the second and third terms of Equation (3) become zero. At this so-called ‘match point’, one component of our complex has the same electron density as the solvent, and $\Delta {\rho }_2$ vanishes. Equation (3) reduces to Equation (2) where only a single species is present and its scattering detected, although at decreased contrast relative to the condition where no contrast agent is added.

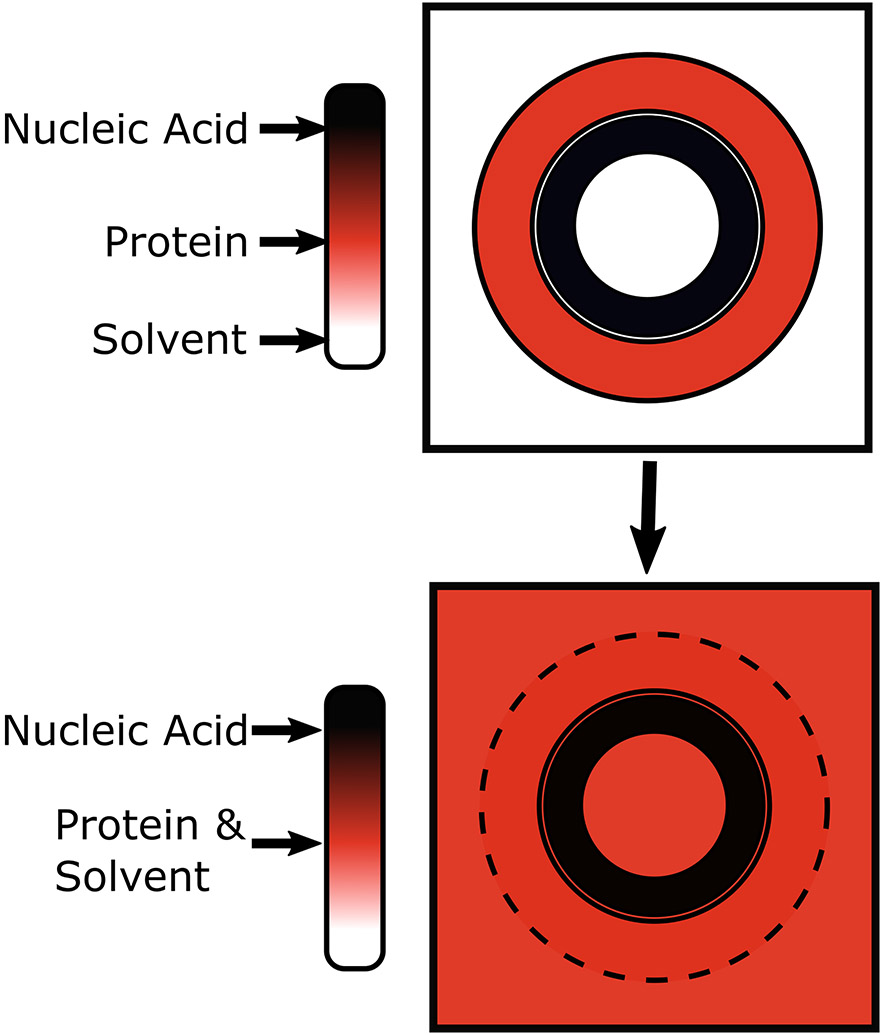
At this point, it is useful to introduce some numbers. For a DNA-protein complex in buffer, we need the electron densities of the solvent, the protein and the DNA. These densities can vary, depending on the details of the system (packing of a protein, for example); however, we quote generally accepted values (Svergun & Koch, 2003) and illustrate the method using a cartoon in Figure 2. The illustration represents a higher electron density nucleic acid surrounded by a lower electron density protein in a standard buffer (top panel) and a contrast matched buffer (bottom panel). The electron density for most buffers is close to that of water, ${\rho }_s=330{\text{e/nm}}^3$. The protein electron density is typically 420 e/nm³, and the ubiquitous phosphate atoms along each nucleic acid strand enhance the electron density of DNA to 550 e/nm³. We note that these values are quoted in the literature (Svergun & Koch, 2003). Our experience suggests that the actual contrast of nucleic acids is slightly lower. In a standard buffer (Figure 2, top panel), the excess scattering density of the protein or DNA component is easily approximated by subtracting the density of the solvent from the value quoted above. Of course, this subtraction assumes that the electron density is constant and uniform, which is not always strictly true, but it is a reasonable approximation for most proteins and nucleic acids. As the biomolecule is measured with increasing electron density in the buffer, this difference decreases. As explained in more detail later, sucrose is our contrast agent of choice to increase the electron density of the buffer. It is highly soluble in aqueous solutions and appears to be inert. When enough sucrose is added to the buffer, its electron density can reach the value quoted for the protein. The electron density difference between protein and background vanishes under this condition. In the language of Equation (3), assigning component 1 to the DNA and 2 to the protein, $\Delta {\rho }_2=0$ and any SAXS measurement tracks only the DNA conformation (Figure 2, bottom panel). CV-SAXS, in this mode, can be used to mask or ‘hide’ the protein in a protein-nucleic acid complex (Tokuda et al., 2016). Because of the solubility limit of sucrose, it is impossible to ‘match’ the density of the nucleic acid component. Thus, using sucrose, measurements can be performed up to, but not far in excess of the match point for proteins.

Figure 2.

Illustration of the principle of contrast variation SAXS. In CV-SAXS, the electron density of the solvent is increased until it matches one of the components of a multicomponent system. In this figure, the electron density is represented as color. In the top panel (no contrast agent), we model a protein-nucleic acid complex in regular aqueous solvent. In the bottom panel, the electron density of the solvent is increased (schematically shown as color change from white to red to black) by the addition of sucrose until it matches the electron density of the protein (red). Under this contrast matched condition any scattering signal that contains a contribution from the protein component blends into the background e.g. disappears. Only the scattering from the more electron dense nucleic acid is detected.

Contrast variation (CV) for biological systems is well established for small angle neutron scattering (SANS). Comprehensive reviews can be found in (Gabel, 2015; Krueger, 2017; Whitten & Trewhella, 2009) as well as in other chapters in this volume. Although CV-SAXS and CV-SANS share the same underlying principle (‘matching’ hence nulling out one component of the scattering, while leaving the other, albeit reduced), the different scattering physics for neutrons vs. X-rays creates profound differences in how the method is applied. Neutrons scatter through interactions with atomic nuclei, via nuclear forces, while X-rays scatter through interactions with electrons. Because the scattering length of the biomolecules lies between the values for H₂O or D₂O, scattering lengths that match those of biomolecules can be reached by mixing the two at the proper ratio, and a selected component can be hidden by the solvent (Krueger, 2017; Whitten & Trewhella, 2009). SANS, therefore, has the advantage that either the protein or nucleic acid can be targeted for ‘blanking’. In some cases, it has been noted that added D₂O can lead to aggregation (Krueger, 2017).

CV-SAXS derives its power from the ready availability of high intensity X-ray beams. With high intensity, synchrotron X-rays, it takes seconds to minutes to collect CV-SAXS data, in contrast to minutes to hours for CV-SANS (Krueger, 2017). The short collection times and higher signal-to-noise of CV-SAXS enables time-resolved contrast variation experiments. These measurements generally require short exposure times because measurements are made in real time, or a limited amount of biomolecules are available. In a time-resolved mode, the dynamic interaction of proteins and nucleic acids can be monitored in real time (Chen et al., 2017). As an important note, equilibrium CV-SAXS experiments can be effectively performed on the latest generation of lab sources.

Finally, although the schematic of Figure 2 focuses on measuring at the protein contrast match point, measurements can be performed at varying sucrose concentrations in the buffer, ranging from 0% to 85% w/v (weight of sucrose in grams per volume of solution in milliliters) sucrose, or 65% w/w (weight of sucrose per weight of solution) sucrose. We note the increased difficulty of working with highly viscous solutions, above 50-60% w/v sucrose. At sucrose concentrations below the match point of the protein, both protein and nucleic acid components scatter, and their contribution(s) to the overall signal vary in a readily quantifiable way. Multiple copies of equation (3) can be written to describe measurements at specific contrast levels. These simultaneous equations can be used to decompose the scattering of a complex under multiple conditions into the scattering of its constituents and of course, the cross term.

What information can be extracted from CV-SAXS Data?

Special case: analysis at the match point

For CV-SAXS data acquired at the protein match point ($\Delta {\rho }_2=0$) analysis is identical to that performed for a standard SAXS experiment. At this condition, nucleic acid conformations are revealed directly from CV-SAXS data. The analysis and modeling of SAXS data are reviewed in these references: (Da Vela & Svergun, 2020; Kikhney & Svergun, 2015; Schneidman-Duhovny et al., 2012; Weiel et al., 2019). Robust analysis packages are readily available, and provide structural information ranging from global structural parameters, such as molecular weight, largest spatial extent of the molecule or radius of gyration, or through molecular shape reconstructions. Complex stoichiometry can be determined in some conditions for both standard and CV-SAXS (see examples). Finally, dynamic structural ensembles can be created that yield scattering profiles consistent with the SAXS data (Tria et al., 2015).

Measurements at different contrast values: Zero-angle scattering and radius of gyration

Some of the best-known SAXS-derived structural parameters, radius of gyration, ${\mathrm{R}}_{\mathrm{g}}$, and the forward or zero-angle ($q=0$) scattering, $I(0)$, also provide insightful information when used in CV-SAXS studies. The radius of gyration is the second moment of the electron distribution in the molecule, it provides a measure of its size. The forward scattering is proportional to the number of excess electrons in the molecule squared (see Equation (3), and note that $P_M(q)$ is defined to be 1 at $q=0$). Both can be easily obtained using the Guinier approximation (Guinier, 1939), which models the scattering at the lowest angle as a simple Gaussian. The zero-angle scattering must be extrapolated from the fit because it is typically occluded by the large intensity of the unscattered beam (or beamstop, when used). We can compute $I(q=0)$ using the Guinier approximation (Guinier, 1939), and note that this analysis is ‘hardwired’ into many standard SAXS analysis programs, including ATSAS (Franke et al., 2017) or BioXTAS RAW (Hopkins et al., 2017). If the low $q$ data are of poor quality (for example, if there are concerns about effects of interparticle interactions (Skou et al., 2014) or access to low $q$ data is limited for technical reasons), both $I(0)$ and ${\mathrm{R}}_{\mathrm{g}}$ can be computed through a pair distance distribution function (defined below) with software such as GNOM (Svergun, 1992) or BIFT (Hansen, 2000). Here, we discuss the structural information that can be readily extracted from these parameters alone and from their dependence on contrast.

The forward intensity $I(0)$ can be used to measure the molecular weight of a macromolecule if the detector is ‘absolutely calibrated’, meaning that a standard sample like water has been used to convert the measured intensity into absolute units (Orthaber et al., 2000). The value of $I(0)$ (in absolute units of cm⁻¹) can be expressed in terms of the mass of the macromolecule, $M$ (in units of g/mol), the partial specific volume, $v$ (in units of cm³/g), the excess scattering density, $\Delta {\rho }_M$ (in units of e/cm³), the concentration of macromolecules, $c$ (in units of g/mL), Avogadro’s number, $N_A$ (6.02 x 10²³ mol⁻¹), and the classical radius of the electron, $r_o$ (2.8179 x 10⁻¹³ cm) (Feigin & Svergun, 1987; Mylonas & Svergun, 2007; Orthaber et al., 2000):

$$I(0)=\frac{cM{v}^2}{N_A}{\mathrm{r}}_{\mathrm{o}}^2\Delta {\rho }_M^2=\frac{cM{v}^2}{N_A}{r}_o^2({\rho }_M-{\rho }_S{)}^2$$ (4)

The above expression clearly shows the quadratic dependence of $I(0)$ on electron density difference and can be exploited to find the match point, the point where the molecule ‘disappears’ into the solvent background (Ibel & Stuhrmann, 1975; Inoko et al., 1992). Measurements of $I(0)$ can be performed at several different contrast agent concentrations. A linear fit of the square root of $I(0)$ vs. solvent scattering density ${\rho }_{\mathrm{s}}$ or contrast agent concentration in % sucrose can be computed. In principle, the x-intercept of the best fit line reveals the match point of the molecule (Ibel & Stuhrmann, 1975; Inoko et al., 1992; Sardet et al., 1976; Stuhrmann & Miller, 1978).

In addition, the absolute scattering at $q=0$ informs about the stoichiometry of a molecular complex, useful for determining whether the complex forms in a 1:1 ratio, for example. This information can be quite helpful in solving structures of complexes acquired by CV-SAXS; it is important to know how many copies of each molecule are present. As an example, if the protein and RNA form a complex in a 1:1 ratio, the extrapolated $I(0)$ values derived from an RNA-alone and a protein-alone can be used to estimate the $I(0)$ corresponding to the protein-RNA complex using:

$$I(0)=I_{RNA}(0)+2\sqrt{I(0{)}_{RNA}}\sqrt{I(0{)}_{protein}}+I_{protein}(0).$$ (5)

The radius of gyration, ${\mathrm{R}}_{\mathrm{g}}$ informs about the overall size of a molecule. It is easy to measure and provides ready information not only about size but more importantly, changes in molecular size that accompany dynamic molecular motions or binding. The dependence of ${\mathrm{R}}_{\mathrm{g}}$ on contrast provides guidance about molecular composition, as described by Stuhrmann and coworkers (Ibel & Stuhrmann, 1975). The measured radius of gyration follows an inverse square relationship with contrast:

$$\begin{gathered} R{g}^2=R{c}^2+\frac{\alpha }{\Delta \rho }-\frac{\beta }{\Delta {\rho }^2} \\ \alpha =\frac{1}{V}\int \rho (r)r^{2}dr \\ \beta =\frac{1}{V^2}(\int \rho (r)rdr{)}^2 \end{gathered}$$ (6)

A plot of the measured ${\mathrm{R}}_{\mathrm{g}}$ vs. the inverse of average contrast of the molecule is referred to as a Sturhmann plot. Several relevant structural parameters can be obtained by fitting the quadratic dependence on contrast in the above equation. ${\mathrm{R}}_{\mathrm{c}}$ is the radius of gyration of the same molecule, but with homogeneous density. The term $\alpha$ is the second moment of the density variations; it characterizes the distribution of phases within the particle (Stuhrmann, 2008). This term is particularly useful for complexes with a radial mass distribution i.e. viruses or apoferritin. A positive $\alpha$ indicates a higher density component on outside of the complex, whereas a negative $\alpha$ indicates higher density towards the core of the complex. The term $\beta$ relates to the square of the first moment of the density fluctuations. A non-zero $\beta$ indicates that the two phases of the complex do not share the same center of mass. For a molecule of homogeneous density, there should not be any dependence on contrast, as $\alpha$ and $\beta$ are both zero.

Structural information can be obtained from the entire SAXS profile: pair distance distribution function P(R), reconstructions, and ensemble modeling

Below we provide additional useful approaches for analyzing CV-SAXS data. Examples illustrating their application are provided in the last sections of this chapter.

Structural changes can be readily inferred by computing the pair distance distributions, P(R) from the scattering curves. P(R) reflects the sets of distances between all pairs of electrons in the macromolecule and can be derived from an inverse Fourier Transform of the scattering profile. Typically, P(R) is computed using the program GNOM (Svergun, 1992) from the ATSAS package (Franke et al., 2017) or from BIFT (Hansen, 2000). A peak in the P(R) curve often reflects a repeated length scale in a molecule, such as the radius of a sphere, or the diameter of a cylinder. This information provides an immediate assessment of repeating structures in real space (Svergun & Koch, 2003).

A single SAXS profile is often interpreted using the assumption that the system is homogeneous and monodisperse. The resulting parameters correspond to average molecular features. Under contrast matched conditions, where the entire structure has a reasonably uniform excess electron density, bead model reconstruction programs can be applied to suggest this average structure. These bead model SAXS reconstructions are typically obtained through DAMMIF (Svergun, 1999) but do not account for the differing electron densities of protein-nucleic acid complexes. Programs based on electron density reconstructions such as DENSS (Grant, 2018) might be able to overcome these limitations and assign the proper electron densities.

In many cases, structural variation is critically important for biological activity, so the data benefit from an interpretation that invites more advanced ensemble modeling approaches. It can be particularly valuable to compare data with profiles computed from simulations or models, when ensembles of conformations are present. CV-SAXS data on nucleic acids, acquired at the protein match point, are amenable to this more sophisticated approach. Typically, these approaches require an initial atomic structure which can be refined to fit the data. For instance, in the case of molecules that may have more than one conformation in solution, ensemble optimization methods (EOM) can be used to propose ensembles whose summed scattering profiles look like the data (Tria et al., 2015). Here, it is essential to computationally create a large pool of as many molecular conformations as possible. This deep structural pool is selectively refined over many cycles of a genetic algorithm. After convergence, a minimal set of structures is identified whose scattering profiles best recapitulate the data.

Reconstructions illustrate the real space positions of the components in a complex; however, obtaining them by ‘inverting’ the data is more involved for complexes than proposing structures for single component objects. Fortunately, there are packages available that exploit measurements of a contrast series to simultaneously fit two different molecular components. An algorithm available for this computation is MONSA (Svergun, 1999; Svergun & Nierhaus, 2000). The advantage of this method is that we can obtain reconstructions from both components in the assembly as well as their relative spacing.

Experimental Considerations

General Beamline details

A CV-SAXS experiment can be carried out using equipment available at most standard SAXS beamlines. Powerful lab sources can also be used for equilibrium measurements. However, the changes to the sample (either biomolecules in buffer or buffer background), especially the increased viscosity of samples prepared at high sucrose concentrations, require that attention be paid to both sample preparation and handling during the measurement. In this section, we discuss experimental requirements specific to CV-SAXS.

Buffer Subtraction

As explained in Ref. (Pollack, 2011) measuring the SAXS profile of a biomolecule requires that two sample solutions be prepared, measured, and properly subtracted. The first sample contains the molecule of interest in the selected buffer. The second sample is identical to the first but does not contain the biomolecule of interest. The scattering of this ‘buffer background’ includes the contributions from the buffer, sample cell, and any background scattering from the beamline, which should of course be reduced, but can rarely be eliminated. Assuming the sample cell thickness is identical, the scattering intensity from the two samples must be normalized to account for beam intensity variations. We use either a semi-transparent beamstop or a pin diode to record the beam intensity at the beamstop. After normalization, the biomolecule absent (buffer background) measurement is subtracted from the biomolecule present sample; the resulting profile reflects only the scattering of the biomolecular sample. This buffer subtraction is absolutely critical. It is essential to prepare a buffer background solution for each biomolecular sample, with components that as closely as possible match that of the biomolecular solution conditions. As discussed below, this simple buffer subtraction is often one of the biggest challenges of CV-SAXS experiments. Accurate buffer matching is an important step in acquiring useful data.

Contrast Agent

In an X-ray scattering contrast variation experiment, we require a simple method for increasing the electron density of the solvent relative to its intrinsic value. Historically, this has been accomplished by adding salts (Fernandez et al., 2008; Schneidman-Duhovny et al., 2013), glycerol (Bolze et al., 1996; Hickl et al., 1996; Hirai et al., 2018; Ibel & Stuhrmann, 1975) and/or sucrose (Bolze et al., 2003; Ibel & Stuhrmann, 1975; Pabit et al., 2020; San Emeterio & Pollack, 2020). Although any small molecule could be used (in theory), there are important considerations when selecting a contrast agent.

Ideally, the solubility of the contrast agent must be such that it can be added in sufficient amounts to reach the match point of at least the lower density component in the complex. Its addition should not alter the shape or properties of the molecule and it must have relatively high (reasonable) transmission of X-rays. The first requirement is obvious if we want to reach contrast levels that allow a match. The second requirement cannot be understated and is often dependent on the biological system being studied. In some cases, added contrast agents can induce aggregation (Krueger, 2017), can alter the ionic strength of the solution or induce osmotic or crowding effects in the molecule. These considerations underscore the need for control experiments, to ensure that any structural changes are not the result of the added agent. Finally, the last requirement will ensure that the remaining signal is not degraded by excessive absorption of X-rays. For water, for example, the optimal sample cell or sample capillary thickness that balances sample size against absorption is between 0.9 to 2.0 mm for typical X-ray energies (Schroer et al., 2018). If the contrast agent significantly increases the sample absorption, signal transmission at these ‘optimal’ values, computed for lower density water, may be reduced. For these reasons, a limited selection of contrast agents is available to experiments on biological molecules.

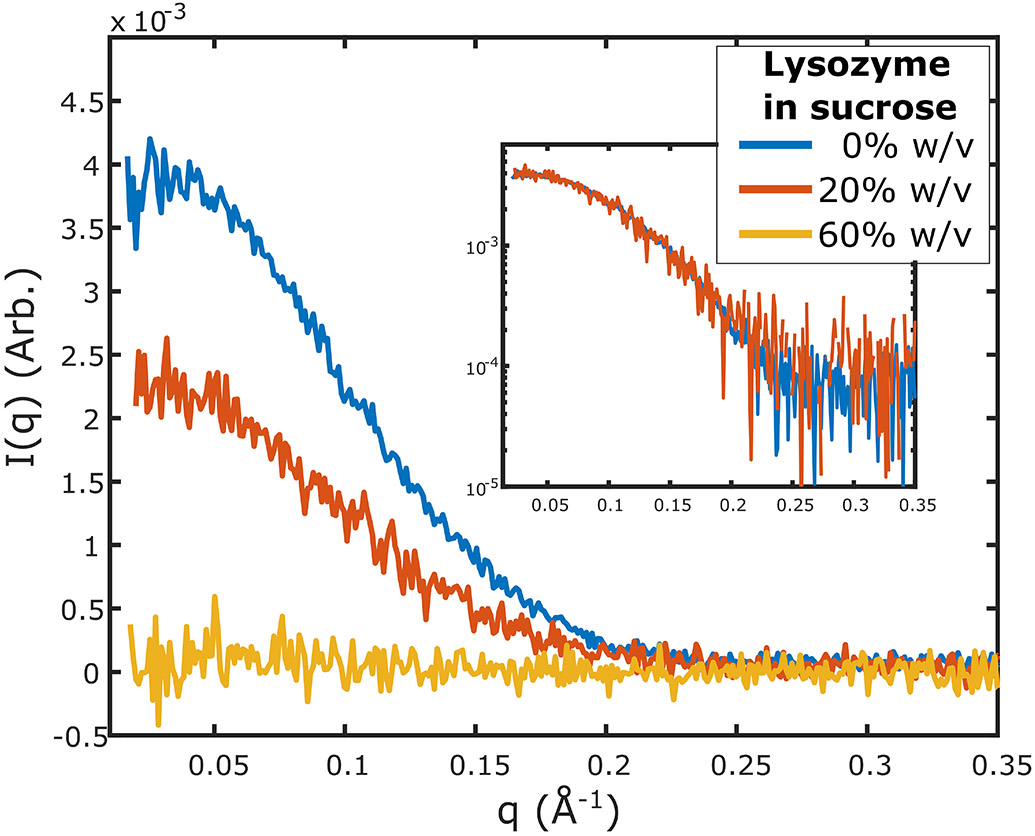
Sucrose is the most commonly used contrast agent for CV-SAXS experiments, and our contrast agent of choice. It is soluble in water up to a limit of 67% w/w sucrose (89% w/v sucrose) at room temperature. When added to buffers at a concentration of 50-65% w/v sucrose, the electron density increase is sufficient to match that of most proteins. Sucrose does not alter the conformation of many proteins (Kim et al., 2003; Lee & Timasheff, 1981), has no effect on the ion atmosphere around nucleic acids (Blose et al., 2011) and does not significantly absorb X-rays (Gabel et al., 2019). As an illustration, Figure 3 shows how increasing sucrose concentrations decrease and eventually mask the scattering of a protein sample. With added sucrose, the overall signal intensity decreases, reflecting the decrease in contrast between protein and solvent, yet the shape of the curve ideally remains unchanged, showing that the sucrose does not dramatically alter the macromolecule’s structure. When using highly concentrated sucrose containing solutions, it is important to consider their increased viscosities. For the range of concentrations needed to reach the match point of proteins, the viscosity can reach ~150 times that of water (Mathlouthi & Génotelle, 1995). The high viscosity creates several challenges in sample preparation for contrast variation experiments. We provide strategies that overcome these challenges in later sections.

Figure 3.

Scattering from lysozyme (4 mg/mL) in buffers containing different sucrose concentrations. Measurements were made on a lab source (BioXolver, Xenocs) using 10 exposures of 120 seconds each. As the contrast is varied through the addition of sucrose, the scattering intensity of lysozyme is reduced. At 20% w/v sucrose, the signal is reduced but maintains the same shape as 0% w/v sucrose. At 60% w/v sucrose the signal from lysozyme disappears below the noise threshold. Inset shows the scattering at 0% and 20% w/v sucrose scaled and superimposed to demonstrate that there are no changes in the shape of the scattering profile upon the addition of sucrose.

Several other molecules have been suggested as contrast agents for CV-SAXS studies. Due to the limitations of sucrose, Gabel et al. (Gabel et al., 2019) have proposed the use of medical contrast media, iohexol and Gd-HPDO3A as contrast agents. These molecules are more electron dense than sucrose, and can therefore more easily reach the match point of proteins, at a lower viscosity (Rickwood et al., 1982). However, they have much lower X-ray transmission than sucrose, so would require changes to the pathlength to optimize the signal. Furthermore, their compatibility with biomolecules would have to be assessed. Other possible agents include salt, which can increase electron density depending on the identity of ions chosen. However, salt can also affect the conformations, or aggregation states of highly charged biomolecules, such as RNA (Schlatterer et al., 2008). Salt also has a limited ability to increase contrast. Even when used in high (~Molar) concentrations, the solution density increases to ~ 370 e/nm³ (Stuhrmann & Miller, 1978), which is less than half of the density change required to reach the protein match point. Glycerol is also commonly used as a contrast agent. Its role as a stabilizer and cryoprotectant in protein preparations (Vagenende et al., 2009) makes it an ideal candidate for these experiments. However, pure glycerol has an electron density of 410 e/nm³ (Stuhrmann & Miller, 1978), which is still lower than that of the average value for a protein. In addition, high concentrations of glycerol can alter the hydration shell of proteins (Hirai et al., 2018; Vagenende et al., 2009). Finally, as with sucrose, glycerol containing solutions can have very high viscosity (Glycerine Producers’ Association., 1963). For all of these reasons, we recommend the use of sucrose as a contrast agent for CV-SAXS experiments.

Biomolecule considerations: molecular weight, purity, concentration

For CV-SAXS, as for most regular SAXS experiments, biomolecules must be of high purity, and monodisperse (Jacques et al., 2012; Jacques & Trewhella, 2010). In addition, the relative masses of protein and nucleic acid in a given complex are critical considerations in establishing its suitability for CV-SAXS measurements. As a general guideline, the complex should derive at least half of its overall molecular weight from nucleic acid, relative to protein. At the match point, the signal from the remaining component is reduced relative to its value in buffer alone. The noise is also increased relative to the same standard SAXS measurement due to the increased background from the added sucrose (Sedlak et al., 2017). Although possible, it would be challenging to perform a CV-SAXS experiment in which the nucleic acid component is much smaller than the protein component. Even close to the match point, the contribution of the cross term of Equation (3), could contribute significantly to, or even dominate the measured signal.

A final important concern is the biomolecule concentration. While higher biomolecule concentrations enhance the signal strength, and are especially valuable for measurements at higher sucrose concentrations where the signal is significantly reduced, interparticle interference can occur and will impact the shape of the profile at the lowest angles (Skou et al., 2014). The degree of complex formation is also dependent on the concentration of the components and must be taken into consideration, for example, one component may be present in excess or a different stoichiometry might be created. If possible, it is ideal to characterize and/or purify the complex ahead of the SAXS measurement. Note that excess protein will not contribute to the scatter if measurements are made at the contrast matched condition.

Preparing the samples: Biomolecules in buffer and its buffer background.

One of the main challenges of CV-SAXS stems from the need to ensure proper buffer matching in the presence of contrast agents. We consider buffer subtraction to be acceptable for CV-SAXS experiments when the high angle baselines match within a fraction of a percent (at most 0.5% scattering intensity difference at high $q$ when it is known that the sample does not scatter at these values). Some biomolecules, including duplex DNA and RNA, have significant scattering that extends into the wide angle regime (Zuo et al., 2006). Typically, a sucrose mismatch would appear at the largest scattering angles, e.g. $q>0.3{\mathrm{Å}}^{\text{-}1}$ or so, where the signal from the macromolecule is low and much of the scattering is derived from the buffer. One major source of measurement disagreement between the biomolecular sample and buffer sample arises if the sucrose concentration(s) in their preparation is not the same. At high $q$, even slight deviations in sucrose concentration can lead to high angle scattering of similar magnitude to that from the biomolecule. Thus, it is not possible to know if any high $q$ scattering originates from the biomolecule itself (and is interesting) or from a buffer mismatch (and is an experimental error). For this reason, special care must be taken to ensure that the sucrose concentration is consistent between biomolecule samples and their buffer background solutions. We use two strategies to prepare the sucrose samples: accurate pipetting and dialysis.

Pipetting is perhaps the most straightforward method for preparing sucrose solutions. For accurate preparation of biomolecular samples containing sucrose and their matching buffers, also in sucrose, a highly concentrated sucrose solution is prepared and mixed with each to obtain the desired final sucrose concentration. Note that mixing of buffered biomolecules and buffered sucrose solutions leads to dilution, so the biomolecules must initially be at high concentration to ensure that the proper final concentration can be reached. We present a practical method to prepare this stock sucrose solution. First, make the desired stock sucrose concentration in weight percentage (w/w). Weighing is the most precise way of combining sucrose and solvent. Then, using sucrose density tables (Anderson, 1966; Asadi, 2006; Darros-Barbosa et al., 2003), convert the weight percentage (% w/w) to volume percentage (% w/v). This allows preparation of different concentrations of biomolecules and buffers in sucrose by direct pipetting (mixing volumes). To illustrate, we describe the preparation of a 60% w/w sucrose solution at room temperature. Sucrose density tables tell us that 60% w/w sucrose is equivalent to 77.2% w/v sucrose, achieved by multiplying the weight percentage with the density, $\%(\mathrm{w}∕\mathrm{w})\times \rho =\%(\mathrm{w}∕\mathrm{v})$. In this example, 60%(w/w) x 1.286 (g/mL) = 77.2% (w/v). To prepare a 20 mL stock solution of 60% w/w sucrose in a centrifuge tube, first weigh the centrifuge tube and add the necessary amount of sucrose: 20 mL x 77.2% (w/v) = 15.44 g of sucrose. Separately prepare a 10x buffering solution containing all the necessary ions and buffering agents needed in the buffer but with no sucrose. Add the necessary amount of the 10x buffer solution (2 mL) to the sucrose powder. Then, add the necessary amount of water to reach the final weight needed to maintain the weight percentage, 15.44 g ÷ 60%(w/w) = 25.73 g final weight. For most buffers, we can approximate the amount of water that needs to be added by subtracting the sucrose and buffer weight from the final volume (25.73 g - 15.44 g – 2 g = 8.3 g ~ 8.3 mL water), however careful weighing will result in the most accurate results. Lastly, to solubilize the sucrose, place the solution on a nutator or similar device for several hours until all sucrose is fully solubilized. Gentle shaking is recommended as rapid shaking can create bubbles in the sucrose solution. If not removed (through centrifugation) these bubbles can affect the sample preparation and SAXS measurement. To enhance solubility, the solution can be heated in a water bath at temperatures near, but no higher than 60°C. Higher temperatures can break sucrose down into fructose and glucose and induce caramelization. These reactions are irreversible. The sucrose concentration can be verified with a refractometer. This stock sucrose solution can be used to prepare additional samples, by judicious mixing. We recommend mixing samples by thoroughly pipetting up and down while avoiding introduction of bubbles.

Care should be taken in pipetting, as the stock sucrose solution is highly viscous. The use of positive displacement pipettes allows more accurate pipetting when dealing with high viscosity solutions. We recommend wiping any excess sucrose solution from outside of the displacement tips to prevent sucrose concentration mismatches. Practice is recommended when learning to reproducibly pipet viscous solutions.

The pipetting method has the advantage of real time sample preparation. Samples can be adjusted, changed and improved based on examination of the acquired experimental data. However, due to the difficulty of pipetting sucrose reproducibly, buffer mismatches are common and repeated measurements, performed on independently prepared samples, are often needed to ensure consistent results.

For the pipetting method, samples containing biomolecules at the highest sucrose concentrations are made from biomolecule stock solutions (in no-sucrose buffer) that are 3-5 times more concentrated than in the final states. Unfortunately, some proteins are prone to aggregation at such high concentrations. For these biomolecules another method can be utilized: dialysis.

Using this method, samples are dialyzed into the desired sucrose-containing buffer in advance of the experiment using standard biochemical methods. This method is slower than pipetting: proper dialysis into high sucrose buffers can require 1-2 days and must be assayed beforehand to ensure that equilibrium has been reached. The dialysis time can be reduced by pre-mixing the biomolecule with sucrose to a concentration close to the target concentration. In this way the dialysis serves to ensure an exact match as opposed to a full exchange. To assay the necessary time of dialysis, several buffers can be prepared and dialyzed in the same way as the biomolecule would be. The sucrose concentration of these buffers can be then measured with a refractometer to confirm it matches the buffer it is being dialyzed into. Despite these lengthy steps, this preparation method guarantees that biomolecule containing samples will match (have the same sucrose concentration as) the buffer. Although dialysis can be difficult for small volumes (such as those used for SAXS), there are commercially available products that can facilitate this process. In our lab, we have used Slide-A-Lyzer^™ MINI (Thermo Scientific^™) and Dialysis Buttons^™ (Hampton Research). Although more reliable in the long run, this method has the disadvantage of using more biomolecules and being time intensive. It also cannot be adjusted ‘on the fly’, so conditions must be identified well in advance of the experiment. The biomolecules must also remain viable and stable in solution for days, as opposed to the minutes that elapse when prepared by pipetting.

Loading the sample at the beamline

Contrast variation experiments can be performed using any standard SAXS beamline configuration and equipment; although the vast majority of our work has employed synchrotrons, CV-SAXS experiments on static samples are possible even on commercially available lab sources (see Figure 3 for an example). In most cases, and for most setups, sample volumes between 20 and 60 microliters are used. As discussed above, each biomolecule measurement requires a matching buffer for background subtraction. We normally acquire SAXS profiles this order: buffer, biomolecule, buffer. A ‘good’ data point (from the beamline perspective) has indistinguishable pre and post buffers.

Even when all samples are carefully prepared (as described above) challenges still remain. The largest challenge to CV-SAXS data acquisition comes from the sucrose itself. Three of the major difficulties of handling sucrose at the beamline (and their resolution) are discussed here: compatibility of highly viscous sucrose with pipetting ‘robots’, radiation damage of sucrose, and proper cleaning of the sample cell between measurements to ensure a reproducible background.

Given the high viscosity of sucrose solutions, special care should be taken when loading samples. This is particularly important when beamlines employ automatic pipetting robots for sample loading (Acerbo et al., 2015; Yang et al., 2020), where a reduction in pipetting speed is recommended to ensure that the sample is withdrawn correctly. As an alternative, we frequently employ manual loading of samples. Finally, it is essential to (optically) check for the presence of bubbles in the sample plug (the sample loaded into the optically transparent sample cell that the X-rays pass through, see Figure 1, ‘solution sample’). Most beamlines have cameras that permit visualization of the liquid sample for exactly this reason.

Care must be taken to avoid radiation damage of the sucrose. Although sucrose can remediate X-ray damage of biological samples (Kuwamoto et al., 2004), a high radiation dose can induce a change in the sucrose solution itself (Wolfrom et al., 1959). This damage manifests as a change in the color and/or the appearance of bubbles in the irradiated volume. To mitigate X-ray exposure, sample plugs can be oscillated, or the sample can simply flow through the cell during the measurement (Acerbo et al., 2015; Schroer et al., 2018; Yang et al., 2020). If possible, the use of a co-flow sample cell can help by ensuring that the sample is not resting on (stuck to) the capillary wall (Kirby et al., 2016).

Finally, enhanced cleaning protocols must be implemented when dealing with sucrose solutions. We suggest starting any CV-SAXS measurement series by taking the SAXS profile of pure water in the sample cell, to get a good, ‘clean’ measure of the background. It is important to repeat this measurement at different points throughout a measurement series by loading a pure water sample, to ensure that the profiles have not deviated from the first one.

Due to the viscosity of solutions and the stickiness of sucrose, cleaning times that work for standard SAXS samples might be too short to clear the sucrose between measurements. We almost always increase the length of the ‘detergent’ step in the cleaning cycle. Failure to properly clean the sample cell can result in sample contamination and improper buffer matching. In the event that the capillary or cell gets too dirty, or sucrose has been accidentally seared on the capillary, it is important to move the X-ray beam to sample a clean part of the cell, and to restart the sequence by measuring a scattering profile of pure water.

Doing the experiment

Finding and exploiting the match point

We have employed two different CV-SAXS approaches to reveal the structures of the macromolecular constituents of a protein-nucleic acid complex. In the first, extensive experimentation is employed to identify, for each system, the sucrose concentration where the protein signal vanishes below the noise floor (the “match point”). For these measurements, data are initially acquired on a sample that contains ONLY the protein component of the complex in solution, at various sucrose concentrations, to identify the match point: the optimal sucrose concentration for subsequent measurement of the complex. Note that it is always most favorable to use the lowest possible sucrose concentration, both for ease in sample preparation, and to maximize the signal from the nucleic acid component. Subsequent measurements are taken on the complex at the sucrose concentration where the protein signal is zero.

Equation (4) guides experiment to determine the match point for a component with a given electron density. In practice, we use two different methods to find it. In the first, the protein scattering is measured in at least three distinct sucrose concentrations. For these measurements, it is important to maintain a constant protein concentration, as the signal amplitude is used to extrapolate to the match point. First, the measured scattering intensity for each profile is extrapolated to its zero angle value, $I(0)$ as described above. A plot of the square root of $I(0)$ vs. sucrose concentration is made, and fit with a line. The x-intercept of this curve yields the sucrose concentration where the intensity goes to zero. Although this method works in principle, it is important to confirm the derived value, by preparing a protein sample at the indicated sucrose concentration. In some cases, the noise floor (protein signal is smaller than the noise) appears before the predicted zero intensity.

Once this “match” condition is identified, numerous measurements should be performed (though some may have been performed in search of the match point and could be re-used, if taken using the same sample). Measurements of the protein alone, nucleic acid alone, and the complex (at appropriate concentrations) should be performed in the preferred buffer for the system, at 0% sucrose. Note, it would be ideal to have a stoichiometrically correct complex for this measurement (all the protein and nucleic acids molecules are bound together), so we recommend that additional characterization and/or purification of the complex is performed. If the concentrations are known, measurement of the molecular weight (through $I(0)$) can be used to assess the composition, though some uncertainly remains and should be considered (e.g. how to unambiguously distinguish a population of pure dimers from a population comprised of a mixture of tetramers and unbound molecules). In addition to the three contrast measurements described above, the protein, nucleic acid and complex should all be measured at the predetermined match point. Finally, two measurements should be made of the protein and nucleic acid components alone, at an intermediate value of sucrose, to test for sucrose dependent effects on the components. This protocol corresponds to a set of at least eight measurements.

The initial three, regular-contrast measurements are an essential part of a SAXS analysis and provide a benchmark for the contrast variation measurements to be performed. The second set of three verifies that the match point is indeed properly set (protein scatter should vanish) and serves as a comparison of the nucleic acid in the unbound and bound state, at the same contrast level. The additional measurement of the protein and nucleic acid at the intermediate value of contrast ensures that the sucrose does not, on its own, modify the structure(s) of the molecule.

Forgoing a comprehensive series, the match point may also be determined by trial and error. A sample is prepared and measured at a sucrose concentration that contrast matches other protein systems (based on experience or literature values). If scattering from the protein is still visible, the sucrose concentration is varied over a small range until the scattering can no longer be measured. From our experience, we find that this method can take less time than the more robust method listed above; however, samples must be prepared by pipetting and not by dialysis to ensure rapid turnaround.

Performing a contrast series to reveal the structures of all components of a complex

In a second approach, systematic measurements are performed at varying sucrose concentrations at several, preselected contrast points. For a full contrast series, scattering profiles should be acquired at around five distinct contrast values. This value is largely empirical and agrees with recommendations for contrast variation neutron experiments (Whitten et al., 2008). Ideally, measurements should be well spaced according to contrast (not grouped around the highest contrast, for example), so that significant variations can be observed and fit. All of the above described considerations should apply here (measurements should be performed on the independent components to ensure that there is no sucrose-related conformational change).

We note that these two approaches are not mutually exclusive; the contrast variation series can be used to determine the match point and provide useful information on the effect of the contrast agent on the molecules. However, we can also use the contrast series of the complex to obtain additional information of its structure. Although CV-SAXS data analysis is simplest when measuring at the match point because the signal arises exclusively from the nucleic acid component of the complex, it does not provide the full extent of information that can be derived from the series (the protein conformation in addition to the nucleic acid conformation).

Benchmarks to assess data quality and effectiveness of the method

From the above discussion it should be clear that acquisition of high quality, CV-SAXS relies on two important considerations. First, buffer subtraction must be accurate, meaning that the sucrose concentration in the buffer background sample must be as close as possible to that of the biomolecule sample, and the sample cell must remain uncontaminated between measurements. Second, as mentioned above, the contrast agent must not, by itself, alter the structure of the biomolecules.

The first consideration, accurate background subtraction can be readily assessed by a careful series of controls and some basic understanding of scattering. If, for example, the buffer background contains more sucrose than the biomolecule sample, the subtraction may yield curves that drop below zero (have negative values as an average) at high angle. This situation is unphysical and the data must be retaken. The simplest way to assess the quality of the match between buffer background and biomolecule sample is to compare the relative high to low angle data acquired from a single component sample (such as protein only) when sucrose is added, to its value taken under standard conditions (if known). For the second consideration, it is important that for each single component in the complex no change occurs in the shape of the scattering as the contrast is reduced (see Figure 3). Any differences in the shapes of the profile could indicate either a change in the biomolecule structure, a background mismatch, or possibly a large variation in the electron density of the molecule across its volume. In any case, it is important to determine the origin of any sucrose-dependent changes. These controls ensure that the buffer has the same sucrose concentration as the biomolecule samples, and that the data acquired on the complex (prepared at the same time as these samples), should be reliable. If the buffer has a different sucrose concentration, the subtractions may become unreliable. Thus, sample preparation (as described above) is critical to the success of CV-SAXS experiments.

Examples of Information extracted

In the remaining sections, we demonstrate the power of CV-SAXS through examples taken from selected studies. We first consider studies conducted on protein-RNA and protein-DNA complexes at the protein match point. The goal of the first two studies is to measure the nucleic acid (RNA or DNA) conformation(s) in a protein-nucleic acid complex. The final study illustrates the reconstruction of nucleic acid and protein complex using SAXS data acquired through a contrast series.

At the match point: First example shows primary microRNA binding to a microprocessor protein

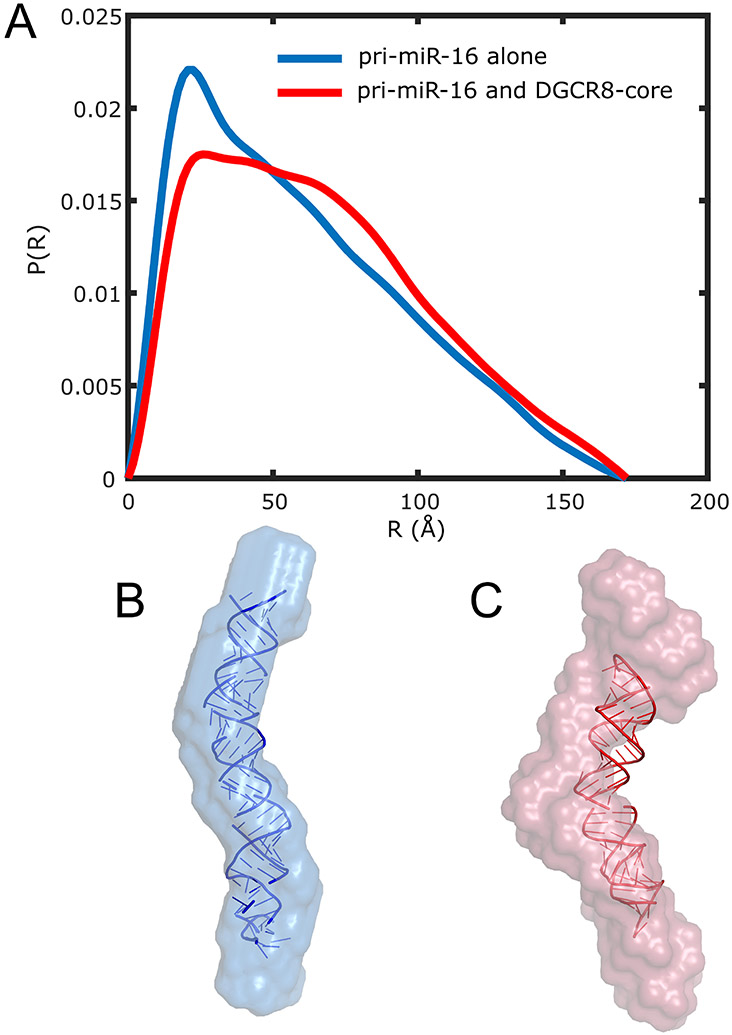
We first illustrate the application of CV-SAXS in studies of a protein-RNA complex consisting of a primary microRNA (pri-miRNA) and the DGCR8 protein (Pabit et al., 2020). The protein is part of the microprocessor complex that cleaves the primary microRNA as it matures to a functional microRNA. The goal of this work is to understand DGCR8’s role in identifying a cleavage site on the RNA. Data acquired at the 0% sucrose condition (traditional SAXS) and at the protein match point elucidate the binding stoichiometry of the complex and suggest that the protein bends the RNA once it is bound, potentially exposing the cleavage site (Pabit et al., 2020).

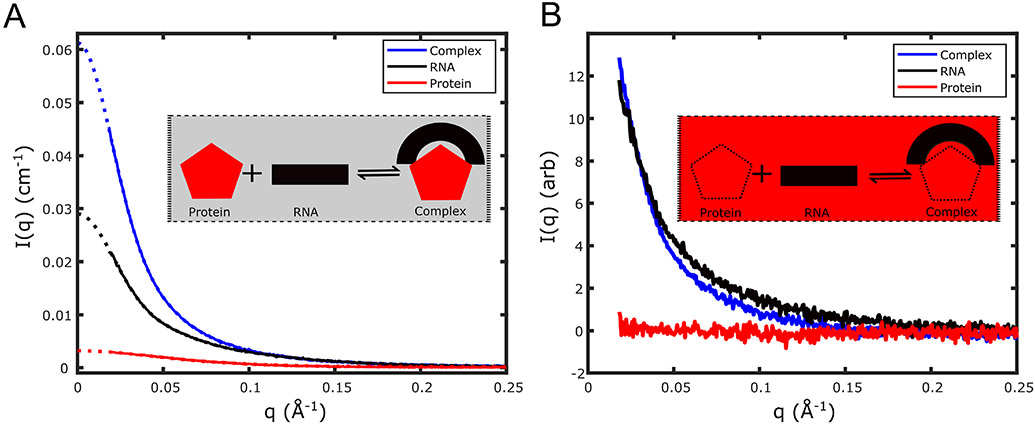
Complex stoichiometry can be inferred from I(0) and validated with CV-SAXS

Figure 4 shows scattering profiles from standard and CV-SAXS studies of the primary microRNA-DGCR8 complex (Pabit et al., 2020). We first focus on the data of Figure 4A, acquired under standard SAXS conditions (no sucrose). We extrapolate our measured curves to $I(q=0)$ using GNOM (Svergun, 1992) for each of the three samples of interest: protein alone, RNA alone and protein and RNA in complex. We then apply absolute calibration to convert these values into absolute scattering units. Plugging these values into Equation (5) (which assumes equal concentrations of the two components), we find that the stoichiometry of the protein and RNA is consistent with 1:1 binding, meaning that the zero angle scattering, $I(0)$ of the complex equals that of the sum of the contributions from the protein alone, the RNA alone and the cross term. Figure 4B shows data acquired at the sucrose match point for the DGCR8 protein. Here, the zero-angle scattering of the RNA alone is very similar to the scattering of the complex in solution at the “match” condition. The similar values of $I(0)$ obtained for the two measurements allows us to conclude that one RNA molecule is present per complex, supporting our hypothesis of 1:1 binding at 0% sucrose. For complexes where the 2 components bind in different ratios, the zero-angle scattering provides a clue to the makeup of the complex.

Figure 4.

CV-SAXS of primary microRNA and the protein DGCR8 core demonstrates that a protein can bend a rigid RNA molecule. (A) SAXS profiles, in absolute units, of DGCR8-core protein alone (red), primary microRNA (pri-miR-16) alone (black), and the complex formed (blue) by binding of pri-miR-16 RNA to the DGCR8 core are shown in buffer containing 0% sucrose. The dotted lines in the figure denote the GNOM extrapolation to extract $I(q=0)$. Comparison of the $I(0)$ value of the complex to the monomer units in absolute scale show the protein and the RNA form a 1:1 complex in the bound state. (B) SAXS profiles of protein alone (red), RNA alone (black), and complex (blue) in buffer containing 50% w/v sucrose are shown. Insets illustrate the contrast-matching method and the formation of the protein-nucleic acid complex. Under contrast matching conditions (inset of B) the molecules are in a buffer that has the same electron density as the protein (red), so the signal from the protein vanishes. Only the signal from the nucleic acid contributes to the measured SAXS curve of the complex (blue).

Radius of gyration can indicate nucleic acid conformational changes upon protein binding

In addition to stoichiometry, structural information about the components of the complex can be extracted via measurements of ${\mathrm{R}}_{\mathrm{g}}$. Specifically, when contrast matching of the protein component can be achieved, the ${\mathrm{R}}_{\mathrm{g}}$ of the contrast matched sample can be compared to that of the unbound sample, acquired at 0% sucrose. Standard analysis, performed using BioXTAS RAW (Hopkins et al., 2017; Nielsen et al., 2009), easily yields these values. Any difference between them could suggest that protein binding results in RNA structural changes.

Interpreting structural changes through distance distribution analysis and shape reconstructions

SAXS profiles provide much more information than the two parameters discussed above, ${\mathrm{R}}_{\mathrm{g}}$ and $I(0)$. A more thorough analysis involves comparing information derived from the full scattering profiles of the nucleic acid alone and in complex with the protein at the match point. For this primary microRNA and DGCR8 complex, we computed the pair distance distribution functions, P(R), from the profiles of the RNA shown in Figure 4 (in the free and bound states). These curves are shown in Figure 5A.

Figure 5.

Comparisons of pair-distance distribution functions and solution SAXS reconstructions suggest a notable bend of the pri-miR-16 upon binding the DGCR8 core. (A) P(R) of pri-miR-16 alone (blue) and pri-miR-16 bound to the DGCR8 core (red) with the protein signal blanked out by the contrast-matching agent (50% w/v sucrose) is shown. For ease of comparison, P(R) curves are normalized by dividing each curve by the area under the curve. By itself, the RNA shows a P(R) distribution characteristic of a cylindrical rod, while the P(R) of the RNA in complex with the protein implies a more bent structure. This is evident in the averaged shape envelopes from SAXS reconstructions shown in (B) for pri-miR-16 alone (blue) and (C) pri-miR-16 bound to DGCR8 core (red). The atomic model in (B) was determined from MD simulations. The atomic model in (C) was determined by imposing a bend in the model from (B) that matches the shape reconstruction.

The P(R) of the RNA alone (no sucrose, no protein partner) resembles that of a cylindrical rod with a 20 Å diameter. This length scale can simply be read off the plot, by finding the R value of the peak in the P(R) curve. The curve exhibits a featureless decay with increasing distance, R. In contrast, the P(R) of the RNA in the complex is consistent with a bent structure, suggesting that the bending is facilitated by the protein.

To convert these plots into simpler-to-visualize forms, the P(R) curves can be used to generate ab-initio models of the molecules using shape reconstruction software such as DAMMIN/DAMMIF (Franke et al., 2017; Svergun, 1999) from the ATSAS suite. These low-resolution shape reconstructions display the real space changes in the nucleic acid structure that result from protein binding. Although the reconstructions are neither unique nor high resolution, the information they convey is consistent with the changing features displayed in the P(R) plots. Figures 5B and 5C present the dummy atom reconstructions. Displaying the data in this format is often the most straightforward way to convey changes. As additional validation of these structural changes, we applied Molecular Dynamics (MD) simulations and a bending algorithm to the primary microRNA and obtained results consistent with the protein bending the RNA. Full details are reported in ref. (Pabit et al., 2020).

At the match point with changing conformations, equilibrium and time resolved studies: Second example reports studies of DNA dynamics in nucleosome core particles

For some systems, interactions with multiple partners is required for proper biological function. For example, many different proteins interact with DNA to facilitate gene expression. Within chromatin, DNA is stored in fundamental units known as nucleosome core particles (NCP). In each NCP, ~ 146 base pairs of genomic DNA is tightly wound for storage, but must also be available for ready release (Cutter & Hayes, 2015). Numerous protein partners are involved in packaging the DNA and in effecting its selective release for future processing, including histone proteins and their variants as well as other chromatin binding proteins. Fundamental biophysical studies can be used to reveal the interactions that facilitate tight storage of DNA in NCPs, but also identify ‘loose points’ that may be targeted by other protein factors for easy release. In many cases, the release of DNA from the histone core depends on both the DNA sequence as well as the specific proteins (or variants) present in the histone core. We have used CV-SAXS to study the patterns of release of different DNA sequences from the native histone core (Chen et al., 2014). Studies of DNA conformation in the presence of chromatin remodelers, such as Chd1 are also facilitated by CV-SAXS (Tokuda et al., 2018).

For some of these experiments, monovalent salt is used to weaken the electrostatic interactions that stabilize the complex. At physiological levels of salt, the DNA is fully packaged (wound around) the histone core. Once these interactions are reduced by the addition of salt, the DNA is selectively released in a sequence dependent way. When the added salt reaches 1 M concentration, the complex is fully dissociated (Chen et al., 2017). Of interest are the intermediate structures that populate this unwinding landscape.

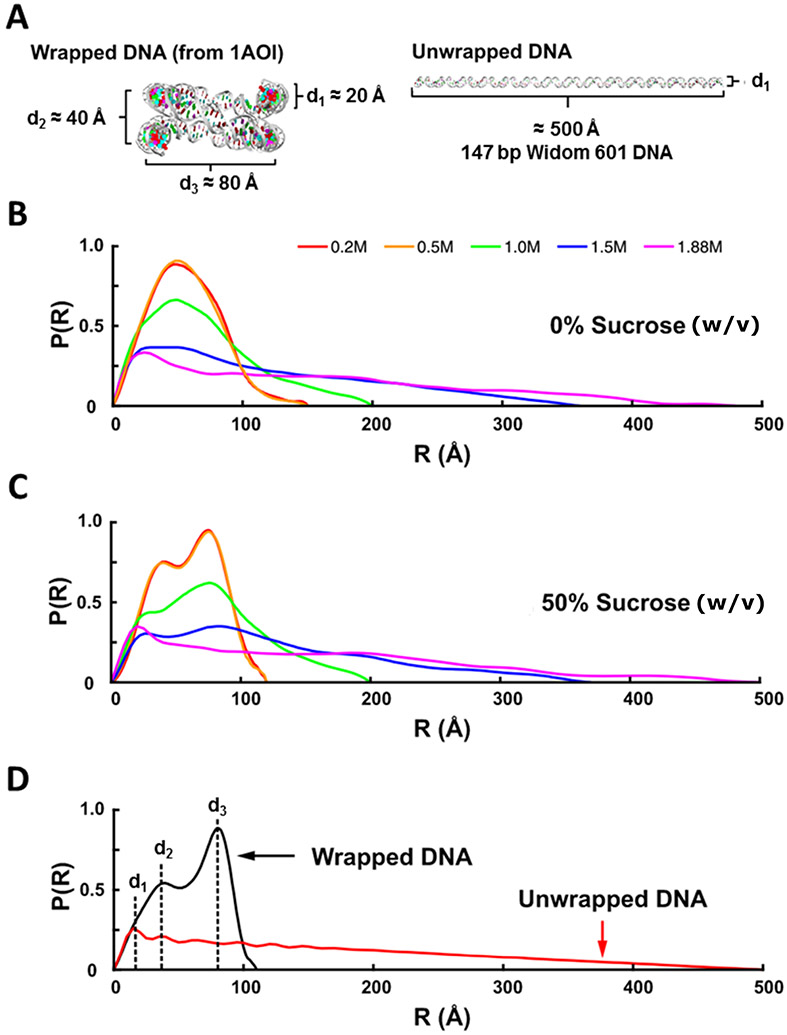
The use of CV-SAXS as a viable method for studying NCPs was first reported in 1992 by ref. (Inoko et al., 1992) using NCP from rat thymus nucleosomes. That work reported values of ${\mathrm{R}}_{\mathrm{g}}$, $I(0)$ and $\alpha$ and inspired our recent studies of the salt dependence of DNA release from the histone core (Chen et al., 2014) shown in Figure 6. This later work benefits from the use of the artificial 601 DNA (Lowary & Widom, 1998) which is tightly positioned, in conjunction with a solved NCP crystal structure (Luger et al., 1997). Knowledge of NCP structure enables application of more advanced modeling efforts (Mauney et al., 2018; Tokuda et al., 2018).

Figure 6.

Application of solution contrast variation to monitor DNA unwrapping during the salt-induced disassembly of nucleosome core particles (NCP). (A) DNA models for the expected end states of the NCP at low NaCl concentration (completely wrapped) and high NaCl concentration (completely unwrapped). (B) P(R) curves for the NCP measured in 0% sucrose and various NaCl concentrations. (C) P(R) curves for the NCP measured in 50% w/v sucrose and various NaCl concentrations. At this point, the protein is masked, and the prominent features appear in the P(R). (D) P(R) curves determined for the models in (A). Peaks in the P(R) curves can be associated with structural features as follows: ${\mathrm{d}}_1$, diameter of the duplex DNA; ${\mathrm{d}}_2$, distance between overlapping DNA ends; ${\mathrm{d}}_3$, diameter of the overall wrapped structure.

P(R) analysis provides in depth information about the changing DNA structures

Here, because the stoichiometry of the NCP is known and large shape changes are expected upon DNA release, it is difficult to interpret changes using ${\mathrm{R}}_{\mathrm{g}}$ as the sole structural metric. Instead, we use the information encoded in the entire scattering curve to facilitate analysis. Figure 6A compares the structure of 147-base pair DNA fully wrapped in an NCP (PDB ID: 1AOI) (Luger et al., 1997) to a fully extended DNA molecule. The full power of the contrast variation method is on display when comparing the evolution of the P(R) as a function of increasing salt concentration in 0% sucrose (Figure 6B) and at the match point of 50% w/v sucrose (Figure 6C). In the absence of sucrose, the peaks broaden, and the maximum extent of the complex increases with salt, but the data cannot be readily interpreted because they contain information about the proteins as well. Once the DNA dissociates, the conformations and association states of the proteins in the histone core becomes unknown. Analysis by SAXS would be very difficult under these circumstances. However, at the match point, the signal from all proteins becomes indistinguishable from the background, and the clear signal from only the DNA structure(s) is revealed. Shifting peaks can be readily interpreted using models, and from these data, the changing conformations of the DNA are readily observed. As the DNA unwraps, the pair distance distribution changes to match that of a fully extended DNA molecule as depicted in P(R) from model systems (Figure 6D).

Structural ensemble modeling provides essential information about the conformations present in equilibrium salt titrations, or as a function of added proteins (tri-nucleosomes, remodelers)

Because of the wide range of conformations populated as a function of changing salt, this system is ideally modeled using ensemble methods. At the match point, only the nucleic acid structures need to be considered. Programs and strategies used for modelling were discussed in previous sections. For these studies, we made use of EOM, ensemble optimization method (Tria et al., 2015). One of the more challenging aspects of using EOM is the need to create a pool of structures that contains all or as many as possible accessible conformations. This can be especially challenging for large molecules, such as long DNA with hundreds of base pairs. In early studies (Chen et al., 2014, 2017), we simply extended the crystal structure by releasing bits of DNA from each end. This approach, while naïve, did provide insight into conformations assumed by the DNA. More recently, we have extended coarse grain DNA models, such as cgDNA (Petkevičiūtė et al., 2014) which accounts for the mechanical properties of DNA sequences. We performed CV-SAXS experiments on long DNAs wrapped around histone cores to focus on the role of DNA sequence in release from NCPs (Mauney et al., 2018) as well as the conformations of multiple nucleosomes in tri-nucleosome chains (Mauney et al., 2021). For these cases, the CV-SAXS measurement, performed at the match point, is relatively straightforward. Because proteins are matched, we can also see the effect of added chromatin remodelers (Chd1) without observing the protein remodelers themselves, which would complicate the scattering profile (Tokuda et al., 2018).

CV-SAXS experiments can be performed in a time-resolved mode, to watch real time sequence of events

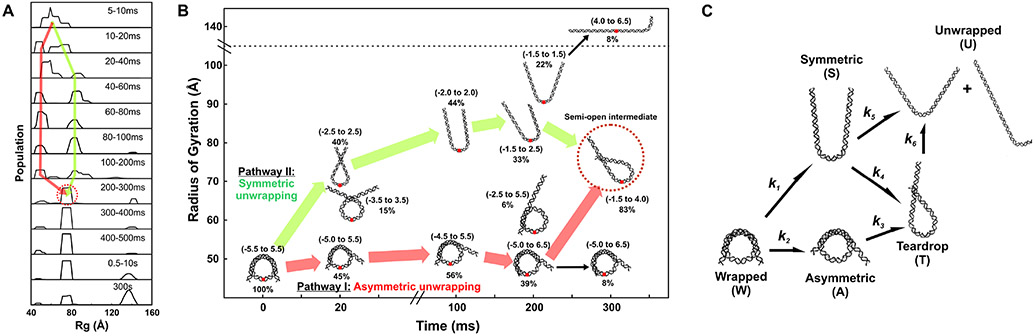
Chen et. al (Chen et al., 2014, 2017) demonstrates the coupling of CV-SAXS, time-resolved experiments using a stopped-flow mixer and EOM to investigate the real time release of DNA from the nucleosome core particles. In these studies, data acquired during a mixing experiment was described by EOM generated models. The power of this type of analysis is illustrated in Figure 7 where we see the conformational dynamics and the different structural changes DNA undergoes as it dissociates from the histone core in a time dependent manner. Of particular interest is the asymmetry of release, discussed in ref. (Chen et al., 2017).

Figure 7.

CV-SAXS applied to the time-resolved disassembly of DNA from nucleosome core particles in 50% w/v sucrose. Disassembly is triggered by the addition of 1.2 M NaCl, also in 50% w/v sucrose. Time resolved CV-SAXS data were analyzed with the ensemble optimization method (EOM) to select the DNA structures whose computed scattering profiles best recapitulate the data at different times. (A) ${\mathrm{R}}_{\mathrm{g}}$ histograms from DNA models selected by EOM that best recapitulate the SAXS data. Red and green arrows highlight two pathways through which DNA structures change before settling into a prominent peak after 300 ms (circled in red). (B) DNA models selected by EOM before (t = 0) and after mixing into 1.2 M NaCl (at t = 20 ms, 100 ms, 200 ms, and 300 ms). Green and red arrows highlight two major pathways through which DNA unwraps to form the teardrop DNA structure. Black arrows show minor pathways. Under moderate salt conditions that favor partial disassembly, the majority of structures unwrap symmetrically and asymmetrically before converging into the teardrop structure. (C) Kinetic scheme for complete disassembly with pathways inferred from prominent DNA structures selected by EOM.

Additional controls: compare with other methods (validate)

Finally, as with many biophysical experiments, CV-SAXS benefits from combination with other experimental methods. Although information about the protein composition of the histone core cannot be easily obtained from CV-SAXS due to the sheer number of components involved, the coupling to other techniques, such as single molecule Fluorescence Resonance Energy Transfer (smFRET), which selectively reports on specific protein constituents, can add significant biological understanding (Chen et al., 2017), can aid in the interpretation of data, and can validate the selection of models using the algorithms described above.

Analysis of Contrast Series: Third example to extract protein as well as RNA structure

Structure of a non-enveloped virus (or virus like particle)

For more complex systems, containing multiple molecules, specifically many copies of a given protein, a full understanding of the complex may require a determination of the protein structure in addition to the nucleic acid structure. The structure(s) of both can be obtained from a contrast series on the complex.

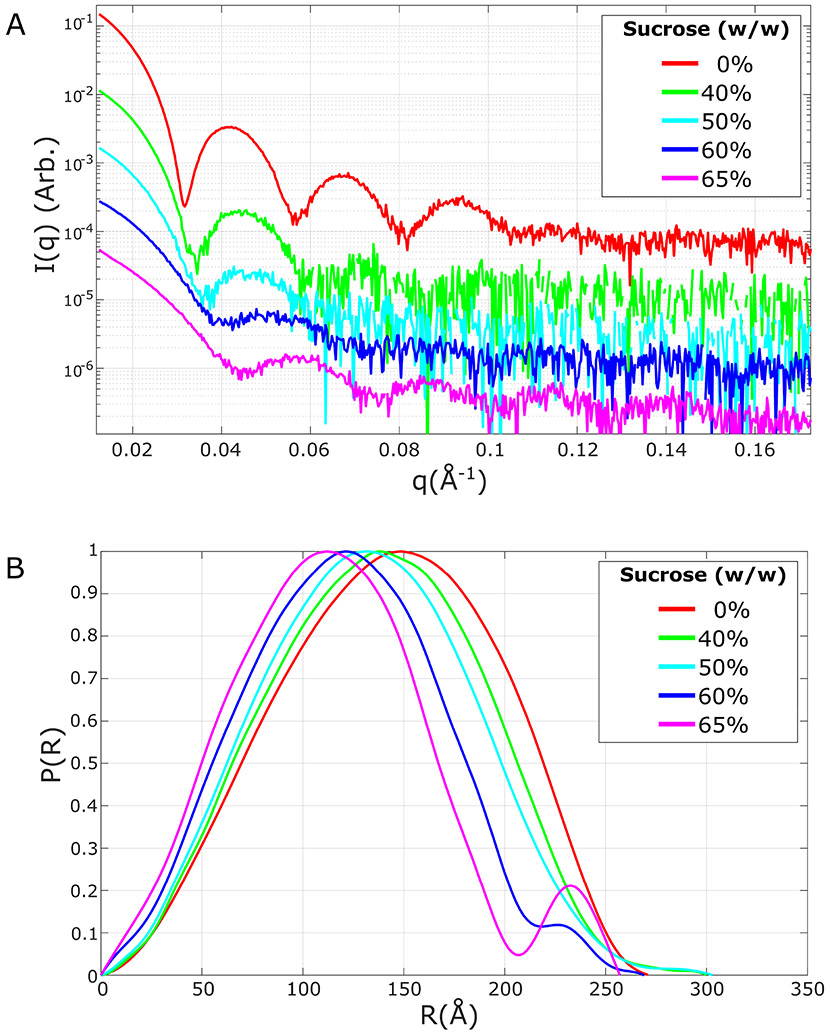
We describe recent studies on bacteriophage MS2, a non-enveloped virus or a virus that lacks a lipid membrane (San Emeterio & Pollack, 2020). Bacteriophages are large complexes, consisting of an outer protein shell (or capsid) that surrounds (encapsidates) a nucleic acid genome. For MS2, the capsid contains 180 proteins, and the single-stranded genome consists of 3569 RNA nucleotides. Scattering profiles acquired at different contrast levels (Figure 8A) can be deconvoluted to reflect the distinct contribution of protein vs. RNA constituents.

Figure 8.

CV-SAXS measurements on bacteriophage MS2 at various sucrose concentrations given in % w/w. SAXS profiles (A) are shown with an offset to aid in visualization. As the solution contrast increases, the scattering changes to reflect a higher contribution from the RNA core (relative to the protein contribution). The computed pair distance distribution functions P(R) (B) are normalized to enable comparison. As the solution contrast increases, the peak of the P(R) shifts to a lower distance. Beyond the match point (near but likely just below 60% w/w sucrose) the contribution from the protein shell reappears as the second peak in the P(R).

Analysis via P(R) - gateway for modelling

Following data acquisition at 5 different contrast values (see Figure 8), we first examine a P(R) series. As the contrast increases, and the weight of the scattering becomes dominated by the RNA core, the peak of the P(R) shifts to a lower radius. However, as is the case with all the above-described experiments, the most useful application of P(R) is the comparison between no sucrose (highest contrast) and the protein match point, where information about the relative spatial distributions of the protein and genome can be derived. These curves are shown in Figure 8B (San Emeterio & Pollack, 2020).

Here, data acquired at a series of contrasts show dramatic changes in features of the scattering profiles, such as shifting positions of minima, reflecting changing dimensions. This information can be used as input to model-building programs that specifically account for components with differing electron densities, at different contrast values. Programs such as MulCh (Whitten et al., 2008) and MONSA (Svergun, 1999; Svergun & Nierhaus, 2000) are straightforward to use.

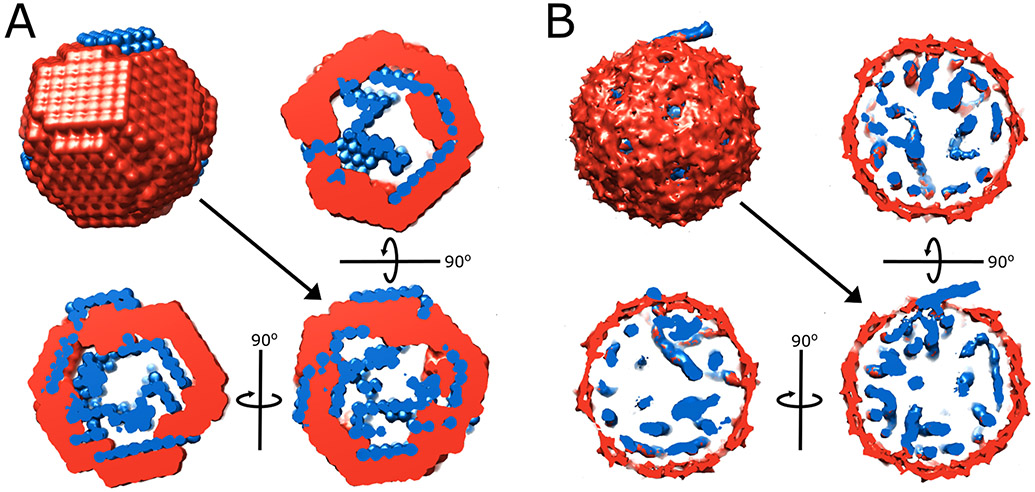
We applied MONSA to create reconstructions of the CV-SAXS series of bacteriophage MS2 (Figure 9). These model structures are pictured along with asymmetric cryo-EM reconstructions of the MS2 phage (Koning et al., 2016). The reconstruction on the left recapitulates the general location and distribution of the RNA (blue) and the protein (red) of the higher resolution cryo-EM reconstruction on the right. As with any SAXS reconstruction, the results are neither unique nor high resolution, but they provide insight into the structure of the distinct components that contribute to the overall complex.

Figure 9.

MONSA reconstructions from CV-SAXS data on bacteriophage MS2 (A) compared to the models derived from cryo-EM (EMD-3404/3403) (B). Protein is shown in red, and RNA is shown in blue. The full reconstruction and three orthogonal cross-sections are shown for each case. Although the spatial resolution obtained through SAXS is lower and the reconstruction is not unique, SAXS data are much simpler to acquire than asymmetric cryo-EM reconstructions. Similar structural features are captured by both methods, including a small, protruding piece of RNA that may reflect the position of the maturation protein.

As an alternative, it is possible to decompose the scattering of a complex into the scattering of the constituents, using a mathematical algorithm. An application for performing this calculation is contained in the Mulch (Whitten et al., 2008) software, which is available through a web server.

Conclusions and Outlook

Contrast variation SAXS is a powerful tool that can provide information about the structure(s) and dynamics of protein-nucleic acid complexes. In its simplest implementation, CV-SAXS can effectively render the protein component of the complex invisible. In this mode, the structure of the nucleic acid component can be easily determined. In another mode, a series of CV-SAXS measurements can provide information from both the protein and nucleic acid components of a complex. Perhaps the greatest strength of CV-SAXS is its ability to provide structural information on flexible systems and its utility in time-resolved experiments.

Largely motivated by the recognized importance of complexes in biological processes, measurement of the structure(s) of protein-nucleic acid complexes is now becoming routine. New tools, such as Cryo-EM expand the range of experimental tools and offer new opportunities. CV-SAXS, in conjunction with modeling, contributes by enabling measurements on complexes over a wide variety of sizes, and elucidating the dynamics of flexible molecules as they respond in real time to stimuli. CV-SAXS provides unique insight into the structure and dynamics of protein-nucleic acid complexes.

In this chapter, we have briefly provided the theoretical motivation for CV-SAXS, discussed practical considerations, experimental practices, as well as examples illustrating its application. We have outlined the procedures and pitfalls associated with CV-SAXS measurements with the aim of providing the necessary guidelines for a successful CV-SAXS experiment. Of interest is the successful demonstration of CV-SAXS measurements on laboratory sources. Future applications, especially those exploiting time-resolved measurements are anticipated to provide unique perspectives on the assembly of macromolecular complexes of biological importance. Potential targets range from complexes involved in gene expression and regulation, all the way through large multimeric complexes and viruses.