Chiral Kondo lattice in doped MoTe₂/WSe₂ bilayers

Abstract

We theoretically study the interplay between magnetism and a heavy Fermi liquid in the AB-stacked transition metal dichalcogenide bilayer system, MoTe₂/WSe₂, in the regime in which the Mo layer supports localized magnetic moments coupled by interlayer electron tunneling to a weakly correlated band of itinerant electrons in the W layer. We show that the interlayer electron transfer leads to a chiral Kondo exchange, with consequences including a strong dependence of the Kondo temperature on carrier concentration and anomalous Hall effect due to a topological hybridization gap. The theoretical model exhibits two phases, a small Fermi surface magnet and a large Fermi surface heavy Fermi liquid; at the mean-field level, the transition between them is first order. Our results provide concrete experimental predictions for ongoing experiments on MoTe₂/WSe₂ bilayer heterostructures and introduces a controlled route to observe a topological selective Mott transition.

A chiral Kondo lattice is derived leading to topological heavy fermion physics in heterobilayer transition metal dicalcogenides.

INTRODUCTION

Transition metal dichalcogenide (TMD) moiré devices created by stacking two TMD monolayers have recently emerged as a highly tunable platform to realize strongly correlated and topological states (1–21). This experimental flexibility has opened the door to control and observe phenomena that has been out of reach in conventional solid-state platforms such as a continuous Mott transition (4, 5) in a single sample. Forming heterobilayers with distinct chemical composition allows one to effectively tune the density and the interaction within an individual layer, which can open the door to synthetically realize orbital selective Mott transitions (22–26) to emulate several strongly correlated electron systems of interest.

Here, we focus on the AB-stacked MoTe₂/WSe₂ bilayer heterostructure of recent experimental (1) and theoretical (13–18) interest and show that it realizes a chiral Kondo lattice. In this system, the lattice mismatch between the two materials leads to a hexagonal moiré lattice with a moiré lattice constant of a_M ∼ 5 nm. As shown in Fig. 1A, the two sublattices of the hexagonal moiré lattice correspond to the MoTe₂ (Mo) and WSe₂ (W) layers, with the two sublattices connected by the interlayer hopping.

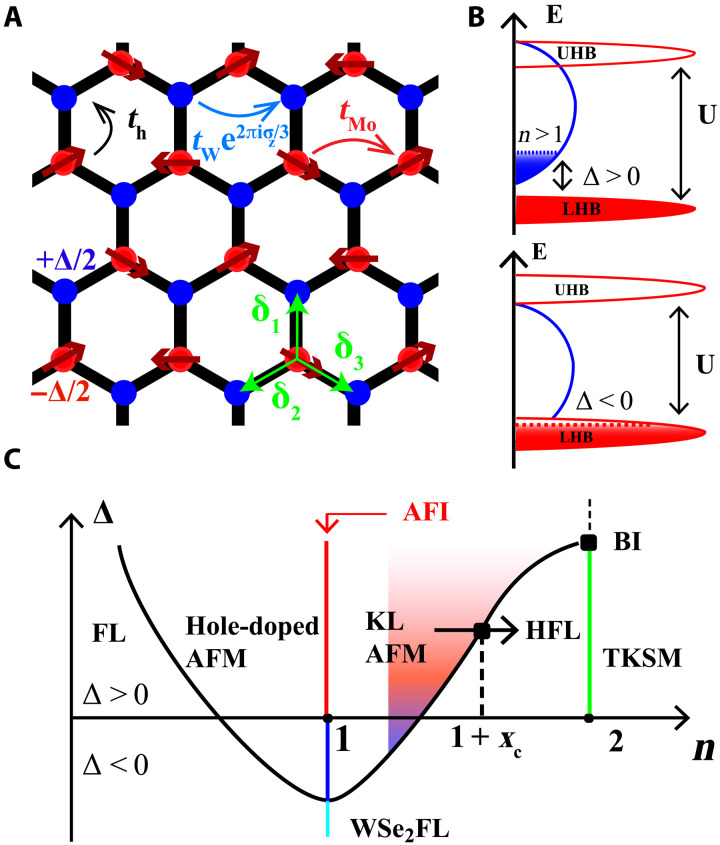
Fig. 1. Model and qualitative phase diagram.

(A) Representation of real-space structure of MoTe₂/WSe₂ bilayer showing the two triangular sublattices of the honeycomb moiré lattice. Red and blue represent the centers of the Wannier functions describing the relevant states in the bottom (Mo) and top (W) layers, respectively. The nearest neighbor vector δ_i, the Mo-W energy difference Δ, and the intralayer t_W/t_Mo and interlayer t_h hopping matrix elements are also indicated. (B) Schematic density of states for filling near n = 1 representing the Mo layer as a narrow-band strongly correlated system with lower (LHB) and upper (UHB) Hubbard bands separated by an energy gap U, while the W layer is shown as a wide-band weakly correlated system. Top: Positive Δ; showing filled Mo LHB and carriers added beyond n = 1 in the W layer. Bottom: Negative Δ; mixed valent situation with potential for simultaneous occupancy of Mo- and W-layer states at n = 1. (C) Qualitative phase diagram of the AB-stacked MoTe₂/WSe₂ bilayer as a function of hole carrier density n and displacement field Δ showing expected phases: At carrier density n = 1, as Δ is decreased, the 120° antiferromagnetic insulator (AFI) gives way to a QAH insulator and then to an FL. For n > 1, the system can be described by a Kondo lattice (KL) model. At other carrier concentrations, different metallic phases occur, including moderate mass (FL) and heavy mass (HFL) Fermi liquids, a hole-doped single-band antiiferromagnet (AFM), and a Kondo lattice AFM (KLAFM) with ordered magnetism on the Mo layer coupled to mobile carriers in the W layer. The HFL is connected to a topological Kondo semimetal (TKSM) at n = 2, which above a critical Δ becomes a band insulator (BI).

The combination of the strong spin-momentum locking of the monolayer materials and the AB stacking configuration reduces the magnitude of the interlayer tunneling to a value much smaller than the intralayer hopping of the WSe₂ moiré band (27). The small interlayer coupling means that the two layers can be discussed separately and then the effects of the interlayer coupling can be considered. The atomic physics of the monolayer materials determines that the MoTe₂ layer has a narrower moiré conduction band than does the WSe₂ layer so that the MoTe₂ layer may be regarded as strongly correlated with an upper and lower Hubbard band, while the WSe₂ layer has a wider bandwidth and a carrier concentration typically far from n = 1 and may be regarded as weakly correlated (14, 27). The resulting density of states (DOS) is sketched in Fig. 1B. The energy offset between the bands, defined here as Δ, and the total chemical potential μ can be controlled in situ by appropriate gate voltages.

Figure 1C shows a qualitative phase diagram in the plane of band offset (Δ) and total density (n = 1 + x). At large positive Δ, the MoTe₂ band is well separated from the bottom of the WSe₂ band. The first carriers added to the system go into the MoTe₂ layer, forming a correlated metal, which at n = 1 becomes a triangular-lattice Mott insulator with 120^∘ antiferromagnetic (AFM) order. At carrier concentration n = 1, decreasing Δ is predicted (14–18, 27) and observed (1, 2) to cause a transition to a quantum anomalous Hall (QAH) state, followed by a transition to a conventional metallic state. At Δ > 0, carriers in excess of the Mott concentration at half-filling (n = 1 per moiré unit cell) go into the WSe₂ band (if, as we assume, U > Δ) and are coupled to the spins of the Mott insulator via an exchange coupling $J_{\mathrm{K}}\sim t_h^2/\text{Δ}$ derived perturbatively from the interlayer hybridization t_h so that the MoTe₂/WSe₂ system can be described by an effective Kondo lattice model on the moiré scale whose study is the central topic of this paper.

Synthetic Kondo lattice models in moiré systems have been previously discussed in the context of the interplay between localized orbital and delocalized electrons in twisted bilayer (28) and trilayer graphene (29), and in relation to the orbital selective Mott transition in a two-band moiré TMD model (30). More recently, a gate-tunable Kondo interaction in trilayer TMDs has been predicted to realize heavy fermion quantum criticality (31). Here, we focus on how the combination of strong spin-orbit coupling (SOC) and the nonlocal structure of the interlayer hybridization substantially enriches the physics relative to the standard Kondo lattice/orbitally selective Mott transition picture.

Derivation of the Kondo moiré lattice model

The low-energy properties of the moiré system are described (14) by a Hubbard model on the honeycomb lattice shown in Fig. 1A. The two sublattices of the honeycomb lattice give the centers of Wannier states formed from the Mo (red) and W (blue) sites, respectively. Wannierization of band structure calculations (14) gives same-sublattice hopping parameters t_W ≃ 9 meV, t_Mo ≃ 4.5 meV, and an interlayer hopping t_h ≃ 2 meV shown as solid arrows in Fig. 1A. The monolayer Ising SOC implies that t_W has a spin-dependent complex phase factor ±2π/3 placing the W band minima at the Dirac points κ (spin up) and κ′ (spin down), respectively; for details, see (14, 27) or the Supplementary Materials (32). The local interaction U, which is taken to be the same on both layers for simplicity, is believed to be large, U/t_Mo ≫ 1 (13, 14), and, for Δ > 0, gives rise at filling n = 1 per moiré unit cell to a 120° AFM charge transfer insulator (14). At nonzero electron doping =1 + x (x > 0), the extra carriers go into the W charger-transfer band (blue shaded region of DOS in Fig. 1B) and Mo sites remain singly occupied. Because of the large bandwidth and the small doping x, we assume that the correlation effects in the W band can be, at first approximation, ignored. The hybridization term t_h induces an effective spin-exchange Kondo coupling (32–34) between the dispersive electrons in the conduction band from the W and the local moments S_r from the Mo layer. The resulting moiré Kondo lattice (spin-fermion) model reads

$$\begin{array}{c}\overline{H}={\displaystyle \sum _{\mathbf{k}\mathrm{\sigma }}}{\mathrm{\xi }}_{\mathbf{k}\mathrm{\sigma }}{c}_{\mathbf{k}\mathrm{\sigma }}^{†}{c}_{\mathbf{k}\mathrm{\sigma }}\\ +{\displaystyle \sum _{{⟨\mathbf{r},{\mathbf{r}}^{\mathrm{\prime }}⟩}_{Mo}}}{J}_H(S_{\mathbf{r}}^z{S}_{{\mathbf{r}}^{\mathrm{\prime }}}^z+\mathrm{\gamma }{S}_{\mathbf{r}}^{+}{S}_{{\mathbf{r}}^{\mathrm{\prime }}}^{-}+h.c.)+D{({\mathit{S}}_{\mathbf{r}}\times {\mathit{S}}_{{\mathbf{r}}^{\mathrm{\prime }}})}_z\\ +\frac{1}{2N}{\displaystyle \sum _{\mathbf{r}\in Mo}}{\displaystyle \sum _{\mathbf{k},\mathbf{p}}}{e}^{-i(\mathbf{k}-\mathbf{p})\cdot \mathbf{r}}{J}_{\mathbf{k},\mathbf{p}}{\mathit{S}}_{\mathbf{r}}\cdot c_{\mathbf{k}\mathrm{\sigma }}^{†}{\mathrm{\sigma }}_{\mathrm{\sigma }{\mathrm{\sigma }}^{\mathrm{\prime }}}{c}_{\mathbf{p}{\mathrm{\sigma }}^{\mathrm{\prime }}}\end{array}$$ (1)

where ${\mathrm{\xi }}_{\mathbf{k}\mathrm{\sigma }}=-2t_W{\sum }_{j=1}^3\cos (\mathbf{k}\cdot {\mathbf{a}}_i+2\mathrm{\pi }{s}_{\mathrm{\sigma }}/3)-{\mathrm{ϵ}}_F$ is the electron dispersion for the W band, ${\mathbf{a}}_1=\sqrt{3}{a}_M(1,0)$, ${\mathbf{a}}_{2,3}=\sqrt{3}{a}_M(-1/2,\pm \sqrt{3}/2)$ are the lattice vectors, where a_M = 5 nm is the moiré-lattice constant, s_↑,↓ = ± 1, and ϵ_F is the Fermi energy fixing the filling x of electrons in the conduction band ${\sum }_{\mathbf{r},\mathrm{\sigma }}⟨c_{\mathbf{r}\mathrm{\sigma }}^{†}{c}_{\mathbf{r}\mathrm{\sigma }}⟩/N=x$. The exchange J_H arises from a combination of the spin rotational invariant Heisenberg exchange in the Mo layer and virtual excitations in the W band mediated by t_h. The reduced spin rotational symmetry in the W layer induces the XXZ anisotropy γ ≠ 1/2 and also Dzyaloshinskii-Moriya D interactions (8). For simplicity, we use the Heisenberg form γ = 1/2 in Eq. 1 in our calculations, and we treat J_H as a phenomenological parameter.

In the last term of Eq. 1, $J_{\mathbf{k},\mathbf{p}}=J_K{V}_{\mathbf{k}}^{\ast }{V}_{\mathbf{p}}$, where $J_K=2t_h^2[1/\text{Δ}+1/(U_{Mo}-\text{Δ})]$ is the Kondo exchange and the hopping t_h between opposite sublattices gives the form factor $V_{\mathbf{k}}={\sum }_{j=1}^3{e}^{i{\mathbf{\text{δ}}}_j\cdot \mathbf{k}}$, where δ_j are displayed as green arrows in Fig. 1A. In proximity to the high-symmetry points κ and κ^′, centers of the spin up and down Fermi sea at low doping, respectively, the form factor takes the p-wave chiral form V_κ+k ≃ −3a_M(k_x − ik_y)/2 and due to time-reversal symmetry $V_{\mathbf{\text{κ}}\mathrm{\prime }\mathbf{+}\mathbf{k}}=V_{\mathbf{\text{κ}}\mathbf{-}\mathbf{k}}^{\ast }$. The displacement field dependence (31) and chirality will be seen to have important physics consequences.

To quantify the Kondo coupling at the Fermi energy, we introduce a Fermi surface (FS)–averaged Kondo exchange ${\overline{J}}_K$ as

$${\overline{J}}_K=\frac{J_K}{{\mathrm{\rho }}_{{\mathrm{ϵ}}_F}}\frac{3\sqrt{3}{a}_M^2}{8{\mathrm{\pi }}^2}{\oint }_{FS}d{k}_t\frac{{\mid V_{\mathbf{k}}\mid }^2}{\mid {\mathrm{\nabla }}_{\mathbf{k}}{\mathrm{ϵ}}_{\mathbf{k}\mathrm{\sigma }}\mid }\simeq \frac{x{J}_K}{4{\mathrm{\rho }}_{{\mathrm{ϵ}}_F}{t}_W}$$ (2)

where the line integral is over the conduction electron FS, k_t is the component of k along the tangent to the FS curve, and ρ_ϵF is the DOS at the Fermi energy, and in obtaining the explicit analytic form, the W band dispersion was expanded to leading (quadratic) order around its minimum.

RESULTS AND METHODS

In this section, we use the mean-field theory of Abrikosov fermions (35–37) to study the competition between the magnetic and the heavy Fermi liquid (HFL) phase. For this purpose, we factorize the local magnetic spin into charge neutral spinons ${\mathit{S}}_{\mathbf{r}}={\mathrm{\chi }}_{\mathbf{r}\mathrm{\alpha }}^{†}{\mathbf{\text{σ}}}_{\mathrm{\alpha }\mathrm{\beta }}{\mathrm{\chi }}_{\mathbf{r}\mathrm{\beta }}/2$ subject to a constraint ${\sum }_{\mathrm{\sigma }}{\mathrm{\chi }}_{\mathbf{r}\mathrm{\sigma }}^{†}{\mathrm{\chi }}_{\mathbf{r}\mathrm{\sigma }}=1$. In the following, we adopt σ for the spin degrees of freedom. In our notation, c_r is a spin-doublet (c_r↑, c_r↓)^T and the same for χ_r. We treat the Kondo interaction with an unrestricted Hartree Fock ansatz that is equally split across the hybridization order parameter Φ and magnetic order M in the Mo layer, which can induce a nonzero polarization in the W layer m. The HFL is captured by a nonvanishing amplitude of the hybridization ${\text{Φ}}_{\mathbf{r}}\equiv -{\sum }_{j=1}^3⟨c_{\mathbf{r}+{\mathbf{\text{δ}}}_j}^{†}{\mathrm{\sigma }}_0{\mathrm{\chi }}_{\mathbf{r}}⟩/2$; the magnetic order is characterized by the variational parameters M_r = (M^∥ cos Q · r, M^∥ sin Q · r, M^z) and m_r = (m^∥ cos Q · r, m^∥ sin Q · r, m^z) with Q = κ − κ^′, $M^{\parallel }={\sum }_{\mathbf{k}}[⟨{\mathrm{\chi }}_{\mathbf{k}}^{†}{\mathrm{\sigma }}_{+}{\mathrm{\chi }}_{\mathbf{k}+\mathbf{Q}}⟩+c.c.]/2N$, $M^z={\sum }_{\mathbf{k}}⟨{\mathrm{\chi }}_{\mathbf{k}}^{†}{\mathrm{\sigma }}_z{\mathrm{\chi }}_{\mathbf{k}}⟩/2N$, $m^{\parallel }={\sum }_{\mathbf{k}}[V_{\mathbf{k}}^{\ast }⟨c_{\mathbf{k}}^{†}{\mathrm{\sigma }}_{+}{c}_{\mathbf{k}+\mathbf{Q}}⟩V_{\mathbf{k}+\mathbf{Q}}+c.c.]/2N$, and $m^z={\sum }_{\mathbf{k}}{V}_{\mathbf{k}}^{\ast }⟨c_{\mathbf{k}}^{†}{\mathrm{\sigma }}_z{c}_{\mathbf{k}}⟩V_{\mathbf{k}}/2N$. To obtain the values of the variational parameters, we minimize the mean-field free energy as detailed in the Supplementary Materials (32).

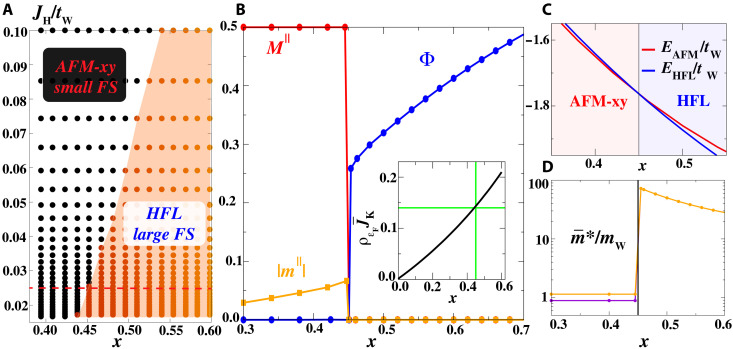
Figure 2A shows the calculated mean-field phase diagram in the plane x versus J_H/t_W. The evolution of the mean-field parameters along the line cut, red line in Fig. 2A, is displayed in Fig. 2B. In the small doping regime x < x_c, the mean-field minimum describes a magnetic solution with in-plane 120° AFM (AFM-xy). The AFM sign of J_K means that the conduction electron staggered magnetization m^∥ is directed oppositely to M, shown as the orange line in Fig. 2B. As doping x increases, ${\mathrm{\rho }}_{{\mathrm{ϵ}}_F}{\overline{J}}_K$ grows, as shown in the inset of Fig. 2B, driving a transition of the general type discussed by Doniach (38) to a nonmagnetic Kondo lattice state in which the system becomes paramagnetic M = 0 and the localized moments hybridize with the conduction electrons, giving rise to a large FS of heavy quasiparticles.

Fig. 2. Competition between HFL and magnetic order.

(A) Phase diagram in plane of WSe₂ filling x versus J_H/t_W calculated from solution of mean-field equations. Black dots (white background) indicate regions of small FS metallic phase coexisting with 120° AFM metallic order; red points (orange background) indicate regions of large FS HFL phase. (B) Line cut at J_H/t_W = 0.025 showing x dependence of the mean-field order parameters: hybridization Φ, local moment staggered magnetization M^∥, and itinerant electron staggered magnetization ∣m^∥∣. m^∥ is opposite to M^∥; we plot the absolute value of both quantities. The inset shows the effective Kondo exchange as a function of the doping x. A first-order transition happens at the critical doping x_c ≃ 0.45 corresponding to ${\mathrm{\rho }}_{{\mathrm{ϵ}}_F}{\overline{J}}_K\simeq 0.14$. (C) Energy of the two different phases as a function of x. (D) Evolution of the average quasiparticle mass as a function of x in logarithmic scale. The data are obtained setting J_K/t_W = 1 (bandwidth 9t_W).

The transition between the AFM-xy phase and the HFL is first order: Both the AFM-xy order parameter and the hybridization change discontinuously, and the computed energies cross (Fig. 2C). Across the phase transition, the topology of the FS changes from electron-like in the magnetic phase to hole-like in the HFL phase. To gain insight on the nature of the transition, it is instructive to compare the low-doping behavior ${\mathrm{\rho }}_{{\mathrm{ϵ}}_F}{\overline{J}}_K\ll 1$ of the two energy scales in the Kondo lattice model: the Kondo temperature T_K and the magnetic energy E_AFM. Expanding to close to the bottom of the conduction band, we have $T_K\simeq {\mathrm{ϵ}}_F\exp [-1/({\mathrm{\rho }}_{{\mathrm{ϵ}}_F}{\overline{J}}_K)]$, where for a quadratic dispersion the DOS is constant ${\mathrm{\rho }}_{{\mathrm{ϵ}}_F}\simeq {\mathrm{\rho }}_0=3\sqrt{3}{a}_M^2{m}_W/(4\mathrm{\pi }{h}^2)$, ϵ_F ≃ x/(2ρ₀), and $m_W={\hslash }^2/(9t_W{a}_M^2)$. On the other hand, in the magnetic state, the Kondo coupling leads to a staggered polarization of conduction electrons, which lowers the energy of the magnetic state: $E_{\mathrm{AFM}}\simeq -3J_H{M}^2/2-{\overline{J}}_K^2{\mathrm{\rho }}_{{\mathrm{ϵ}}_F}{M}^2/2$ (M = 1/2). The linear dependence of ${\overline{J}}_K$ on doping x (Eq. 2) implies that the scaling of the magnetic to paramagnetic transition is different from the standard Doniach scaling (38). Last, Fig. 2C shows the evolution of the average over the FS of the quasiparticle mass ${\overline{m}}^{\ast }$ in logarithmic scale, where m* is defined as m* = ℏ∣k_F∣/∣v_F∣, ${\overline{m}}^{\ast }={\oint }_{FS}{dk}_t{m}^{\ast }/(2\mathrm{\pi }{k}_F)$, where v_F and k_F are the Fermi velocity and momentum, respectively. The transition is signaled by a drastic change of the quasiparticle mass. We find a diminution of ${\overline{m}}^{\ast }$ increasing the doping x and a splitting of the quasiparticle mass in the magnetic regime.

Physical properties

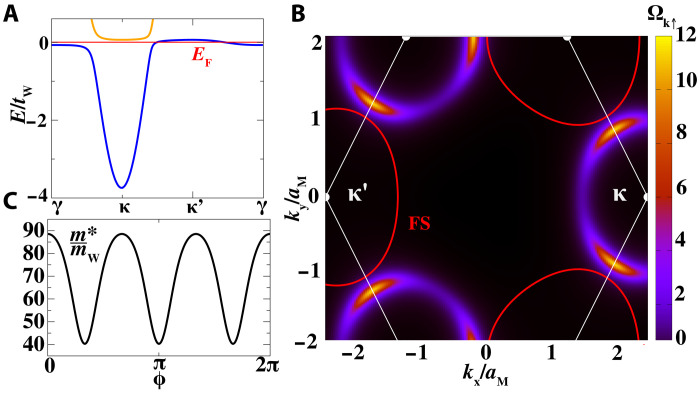
The HFL is characterized by the quasiparticle band structure in Fig. 3A. In this regime, the local moments in Mo layer participate to the total volume (39) enclosed by the FS and give rise to a large hole-like FS, which encircles the κ′(κ) point for ↑(↓) electrons in the moiré Brillouin zone, as shown by the solid red line in Fig. 3B. We also show the variation of the quasiparticle mass around the FS in Fig. 3C. In addition, we find quite unconventional properties that trace back to the form factor V_k in the Kondo coupling J_k,p. The chiral nature of V_k gives rise to a chiral hybridization order parameter whose amplitude is proportional to $⟨c_{\mathbf{\text{κ}}\mathbf{+}\mathbf{k}\uparrow }^{†}{\mathrm{\chi }}_{\mathbf{\text{κ}}\mathbf{+}\mathbf{k}\uparrow }⟩\propto \text{Φ}(k_x-i{k}_y)$ for spin up and $⟨c_{\mathbf{\text{κ}}\mathrm{\prime }\mathbf{+}\mathbf{k}\downarrow }^{†}{\mathrm{\chi }}_{\mathbf{\text{κ}}\mathrm{\prime }\mathbf{+}\mathbf{k}\downarrow }⟩\propto -\text{Φ}(k_x+i{k}_y)$ for spin down and results into the topological character of the hybridization gap. The color code in Fig. 3B shows the Berry curvature Ω_k↑ = −2 Im〈∂_kxu_k↑∣∂_kyu_k↑〉 of the lower HFL band, which is characterized by bright peaks at the position of the bare conduction electron FS. The opposite winding of spin ↑ and ↓ hybridization gap results in an opposite Berry curvature for the two-spin Ω_k↑ = −Ω_−k↓. The Berry curvature originates from the chiral interlayer hybridization between χ and c fermions. Expanding the HFL Hamiltonian around the electron pocket at κ for ↑ gives in the basis Ψ = (χ, c)

$$H_{\uparrow }(\mathbf{\text{κ}}\mathbf{+}\mathbf{k}\mathbf{)}\simeq \left(\begin{array}{cc}\mathrm{\lambda }& -{\text{Δ}}_K(k_x-i{k}_y)\\ -{\text{Δ}}_K^{\ast }(k_x+i{k}_y)& {\hslash }^2{k}^2/(2m_W)-\mathrm{\mu }\end{array}\right)$$ (3)

with Δ_K = 3J_Ka_MΦ/2 and due to time-reversal symmetry $H_{\downarrow }({\mathbf{\text{κ}}}^{\mathrm{\prime }}+\mathbf{k})=H_{\uparrow }^{\ast }(\mathbf{\text{κ}}\mathbf{-}\mathbf{k}\mathbf{)}$. The HFL is adiabatically connected to a topological compensated Kondo semimetal at total filling n = 2 with a nonquantized spin Hall effect (40). The topological gap found here is distinct from the topological Kondo gap in bulk heavy fermion systems (41, 42) such as SmB₆ (43–46), which is induced by the strong SOC and the opposite parity of d and f orbitals. In the system considered here, the orbitals of conduction electrons and local moments have identical parity character, and the topological hybridization gap originates from the nonlocal exchange involving nearest neighbor sites and the Ising SOC.

Fig. 3. Properties of the HFL.

(A) Band structure of the HFL along high-symmetry directions where the chiral Kondo coupling opens a topological hybridization gap between the upper (orange) and lower (blue) bands. The energy is measured with respect to the chemical potential. (B) Berry curvature of the lower HFL band, where the red circles denote the hole FS. The flux of Ω_k↑ in the entire Brillouin zone gives Chern number C_↑ = 1 = −C_↓. (C) Quasiparticle effective mass m*/m_W as a function of the angle ϕ on the heavy electrons FS. The calculation has been performed at x = 0.46 and J_K/t_W = 1 (bandwidth 9t_W).

In the opposite regime, at x < x_c, the ground state has a 120° AFM order with a small FS. The spin-flip scattering processes mediated by the modulation Q connecting the spin ↑ and ↓ FSs give rise to a SOC term in the conduction electron Hamiltonian. As detailed in the Supplementary Materials (32), the expansion of the Hartree-Fock Hamiltonian close to the origin of the magnetic Brillouin zone gives

$${\mathcal{H}}_c(\mathbf{k})=(\frac{{\hslash }^2{k}^2}{2m_W}-{\mathrm{ϵ}}_F){\mathrm{\sigma }}_0+\frac{9J_K{a}_M^2}{8}{\displaystyle \sum _a}{d}_a(\mathbf{k}){\mathrm{\sigma }}_a$$ (4)

where $d_z(\mathbf{k})=M^z(k_x^2+k_y^2)$, $d_x(\mathbf{k})=-M^{\parallel }(k_x^2-k_y^2)$, and d_y(k) = 2M^∥k_xk_y. The SOC splits the conduction electron FS, giving rise to two different Fermi momenta $k_F^{\pm }$. A nonzero in-plane M^∥ component in the Hamiltonian (Fig. 4) induces a 2π-Berry phase winding around the origin of the magnetic Brillouin zone. In the presence of a nonzero Zeeman field, we have a Berry curvature whose momentum space distribution depends on the value of the parameters in the Hamiltonian (Fig. 4).

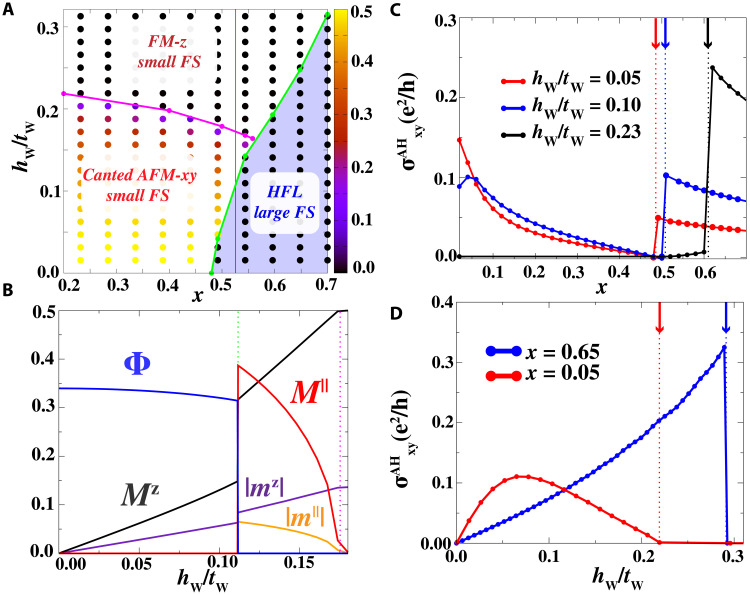
Fig. 4. Phase diagram and transport in magnetic field.

(A) Phase diagram plotted as a function of the W-layer carrier concentration x and the out-of-plane magnetic field h_W. The blue region denotes the HFL regime where the hybridization order parameter is finite. The color code before the green line shows the value of the in-plane AFM order parameter M^∥. The solid green line shows the first-order phase transition line. On the other hand, the magenta one shows the second-order transition from the canted AFM-xy to the FM-z. (B) Evolution of the variational parameter along the line cut at x = 0.52 as a function of h_W/t_W. (C) Intrinsic contribution to the anomalous Hall conductivity for three different values of the Zeeman field. The vertical dashed lines denote the critical filling where the first-order transition takes place. (D) Intrinsic AHE for different values of the filling x as a function of the Zeeman field. The vertical dashed line denotes the first-order transition between the magnetic and the HFL phase, while the solid one denotes the second-order transition from a canted AFM to the FM-z. Above this line, the AHE vanishes. The calculation has been performed at J_K/t_W = 1, J_H/t_W = 0.05 (bandwidth 9t_W).

Last, we study the evolution of the mean-field solution in an external out-of-plane magnetic field. The spin-valley locking in the AB-stacked configuration implies that the magnetic field B acts as a spin-valley Zeeman field (3) $H_z=-h_{Mo}{\sum }_{\mathbf{r}\in Mo}{\mathrm{\chi }}_{\mathbf{r}}^{†}{\mathrm{\sigma }}^z{\mathrm{\chi }}_{\mathbf{r}}/2+$ $h_W{\sum }_{\mathbf{r}\in W}{c}_{\mathbf{r}}^{†}{\mathrm{\sigma }}_z{c}_{\mathbf{r}}/2,$ where h_α = g_αμ_BB and g_α is the gyromagnetic ratio for the two different TMDs [here, we use g_Mo = g_W = 10 (3, 47)]. The phase diagram in the plane x versus B is shown in Fig. 4A. At low doping, a small magnetic field introduces an out-of-plane magnetization M^z, giving rise to a canted AFM-xy. Above the second-order transition line (magenta line in Fig. 4A), that in the limit of vanishing doping takes the value 9J_H/2, the canted AFM-xy turns into a ferromagnetic solution along z (FM-z). For larger fillings, blue region in Fig. 4A starting at x_c ≃ 0.488 in the limit h_W → 0, the small-field solution is the HFL. The line cut Fig. 4B, red line at x = 0.52 in Fig. 4A, shows the evolution of the variational parameters in magnetic field. In the HFL, a small magnetic field induces a net magnetization M^z in the localized orbital χ. On the other hand, the Kondo hybridization is slightly affected by the external field. At a critical field, displayed as a solid green line in Fig. 4A, we find a first-order transition that is accompanied by an abrupt jump in the magnetization as well as by a discontinuous change in the conduction electron FS. The state above the first-order line is a canted AFM-xy for x < 0.56 and an FM-z for x > 0.56.

Transport in magnetic field

We use a Boltzmann equation approach to describe the transport of electrons in the different regimes of the phase diagram in Fig. 4A; for details, we refer to the Supplementary Materials (32). The Hall conductivity has contribution from an ohmic part ${\mathrm{\sigma }}_{xy}^{\mathrm{Ohm}}$, which depends on the extrinsic impurity scattering rate, and also has an intrinsic geometric contribution (48, 49) ${\mathrm{\sigma }}_{xy}^{\mathrm{AH}}$ determined by the Berry curvature. In the HFL regime, the nonvanishing hybridization implies that the neutral χ-spinon also contributes to the charge transport properties (50, 51). Approximating the HFL FS shown in Fig. 3B with a circular FS with effective mass ${\overline{m}}^{\ast }$, the ohmic contribution takes the simple form ${\mathrm{\sigma }}_{xx}=e^2\mathrm{\tau }(1-x)/{\overline{m}}^{\ast }$ and ${\mathrm{\sigma }}_{xy}^{\mathrm{Ohm}}=-e^{3}B{\mathrm{\tau }}^2(1-x)/{{\overline{m}}^{\ast }}^2$. Conversely, in the magnetic regime, only the concentration x of conduction electrons contributes to the charge transport properties. Assuming a single momentum- and band-independent transport time, we find that σ_xx = e²τx/(∑_λ ‍ m_λ/2) and ${\mathrm{\sigma }}_{xy}^{\mathrm{Ohm}}=e^3{\mathrm{\tau }}^{2}Bx/(m_W{\sum }_{\mathrm{\lambda }}{m}_{\mathrm{\lambda }}/2)$ with m_λ = m_W/[1 − λJ_K∣M∣/(4t_W)] (λ = ± ). As a result, increasing the magnetic field across the first-order transition line (green line in Fig. 4, A and B), we find a drastic jump in electrical conductivities, while in the HFL we have 1 − x hole-like carriers in the AFM-xy phase a density of x electrons. We observe that the normal Hall effect has been used in HFL systems (52–54) as a proxy for the FS change.

Moreover, the AFM-xy and the HFL are characterized by different intrinsic anomalous Hall conductivity ${\mathrm{\sigma }}_{xy}^{\mathrm{AH}}$. Figure 4C shows the evolution of ${\mathrm{\sigma }}_{xy}^{\mathrm{AH}}$ along different line cuts at constant Zeeman field as a function of doping x in the phase diagram (Fig. 4A). In the AFM regime, ${\mathrm{\sigma }}_{xy}^{\mathrm{AH}}$ originates from the d_x(k) and d_y(k) terms in Eq. 4 induced by the in-plane component of the magnetic ordering, which gives rise to the anomalous Hall effect (AHE) shown in Fig. 4C. As we increase the doping, the AHE decreases because of the smaller Berry curvature flux imbalance between the two FSs with momenta $k_F^{\mathrm{\lambda }}=\sqrt{2m_{\mathrm{\lambda }}{\mathrm{ϵ}}_F/{\hslash }^2}$. The AHE is enhanced by interaction effects between conduction electrons, which favor the out-of-plane canting of the AFM spin texture. Last, above a critical density shown by the solid green line in the phase diagram (Fig. 4A), a first-order transition from the canted AFM-xy to the HFL occurs. The transition is signaled by a jump in the AHE effect, as displayed in Fig. 4C. A nonquantized jump of the AHE across the HFL transition can also originate from a chiral spin liquid state (55). In the HFL regime, the AHE originates from the chiral hybridization gap with opposite sign for spin up and down electrons, which results in a nonquantized spin Hall effect. See the Supplementary Materials (32) for details. A nonzero Zeeman field induces a flux imbalance between ↑ and ↓, which gives a finite AHE in the HFL, as shown in Fig. 4C. In Fig. 4D, we consider different concentration in the W layer, and we study the evolution as a function of h_W. We highlight that in the large field regime, we enter in the FM-z regime where the AHE vanishes, as displayed in the regions above the solid vertical lines in Fig. 4C. The transition from the HFL to the FM-z is characterized by a drastic jump in the AHE effect, which can reach values of the order of ∼e²/h depending on the flux imbalance between the two FSs. On the other hand, in the small FS regime, the AHE evolves, smoothly vanishing when the local moments are aligned to the external field.

DISCUSSION

We present a microscopic theory to explain the competition between AFM and the HFL in MoTe₂/WSe₂. A crucial finding is that the Kondo exchange is chiral, which gives rise to predictions that can be directly tested in experiments. Among them, we emphasize the topological character of the hybridization gap in the HFL regime and the Berry phase winding induced by spin-flip processes in the magnetic one. Both effects give rise to AHE, which can be measured by transport experiments in magnetic field. We show how transport measurements can clearly distinguish the various phases.

We find two different first-order transitions: either as a function of the doping x at zero magnetic field or by tuning a magnetic field (metamagnetism). The first-order character of either transition is generically robust for a finite region of fluctuation corrections to mean-field theory. However, while symmetry implies that the magnetic field–tuned transition is first order, there is no symmetry argument known to us that constrains the order of the doping-tuned transition.

Our theory for the field-tuned transition is in agreement with recent experimental observations (56) where at a critical field B_c the HFL undergoes a metamagnetic transition with a sharp jump in the carrier concentration from x − 1 to x and an abrupt variation of the quasiparticle mass at a critical magnetic field B_c. We also find that at B_c the transition between the magnetic state and the HFL is signaled by a drastic jump of the AHE. Additional experiments are needed to unveil the nature of the transition as a function of the doping at zero field.

We observe that the paramagnetic HFL solution becomes, at filling n = 2, a compensated topological Kondo semimetal with nonquantized quantum spin Hall effect. We also notice that in the magnetic regime the AHE can be further enhanced by spontaneous FM induced by accounting the on-site interaction between conduction electrons. Last, the effect of quantum fluctuations beyond the mean-field approach as well as the role of anisotropic effects in the Kondo exchange coupling are important questions for future research.

These results highlight several concrete experimental predictions relevant for current and future experimental studies in TMD bilayers. More broadly, this work provides a controlled route to realize a topological selective Mott transition.

Supplementary Materials

This PDF file includes:

Figs. S1 to S4

References