Summary:
Semi-competing risks refers to the time-to-event analysis setting where the occurrence of a non-terminal event is subject to whether a terminal event has occurred, but not vice versa. Semi-competing risks arise in a broad range of clinical contexts, including studies of preeclampsia, a condition that may arise during pregnancy and for which delivery is a terminal event. Models that acknowledge semi-competing risks enable investigation of relationships between covariates and the joint timing of the outcomes, but methods for model selection and prediction of semi-competing risks in high dimensions are lacking. Moreover, in such settings researchers commonly analyze only a single or composite outcome, losing valuable information and limiting clinical utility—in the obstetric setting, this means ignoring valuable insight into timing of delivery after preeclampsia has onset. To address this gap we propose a novel penalized estimation framework for frailty-based illness-death multi-state modeling of semi-competing risks. Our approach combines non-convex and structured fusion penalization, inducing global sparsity as well as parsimony across submodels. We perform estimation and model selection via a pathwise routine for non-convex optimization, and prove statistical error rate results in this setting. We present a simulation study investigating estimation error and model selection performance, and a comprehensive application of the method to joint risk modeling of preeclampsia and timing of delivery using pregnancy data from an electronic health record.
Keywords: multi-state model, risk prediction, semi-competing risks, structured sparsity, time-to-event analysis, variable selection
1. Introduction
Semi-competing risks refers to the time-to-event analysis setting where a non-terminal event of interest can occur before a terminal event of interest, but not vice versa (Fine et al., 2001). Semi-competing risks are ubiquitous in health research, with example non-terminal events of interest for which death is a semi-competing terminal event including hospital readmission (Lee et al., 2015) and cancer progression (Jazić et al., 2016). An example where death is not the terminal outcome is preeclampsia (PE), a pregnancy-associated hypertensive condition that complicates between 2–8% of all pregnancies and represents a leading cause of maternal and fetal/neonatal mortality and morbidity worldwide (Jeyabalan, 2013). PE can develop during the pregnancy starting at 20 weeks of gestation, but once an individual has given birth they can no longer develop PE, so PE onset and delivery form semi-competing risks. Clinically, the timing of these events is of vital importance. Once PE arises, maternal health risks increase as the pregnancy continues, while giving birth early to alleviate these risks may in turn pose risks to neonatal health and development. Therefore, we are motivated to develop risk models that identify covariates affecting risk and timing of PE while also characterizing the timing of delivery after PE has onset.
Semi-competing risks data represent a unique opportunity to learn about outcomes jointly, by (1) modeling the interplay between the events and baseline covariates, and (2) predicting the covariate-specific risk of experiencing combinations of the outcomes across time. Unfortunately, analysts commonly collapse this joint outcome, considering either the non-terminal or terminal event alone, or a composite endpoint (Jazić et al., 2016). While this enables the use of prediction methods for univariate binary or time-to-event outcomes, modeling risk for one outcome is both a lost opportunity and a severe misalignment with how health-related decisions are actually made; as the PE setting illustrates, clinical care is informed by the joint timing of PE onset and subsequent delivery, not just risk of PE.
Instead, frailty-based illness-death multi-state models (Xu et al., 2010; Lee et al., 2015) characterize the dependency of semi-competing risks and covariates, while also enabling absolute joint risk prediction across time (Putter et al., 2007). These methods comprise three cause-specific hazard submodels for: (i) the non-terminal event; (ii) the terminal event without the non-terminal event; and, (iii) the terminal event after the non-terminal event. Different covariates can affect each hazard differently, and the interplay of these submodels determines the overall covariate-outcome relationship. A person-specific random frailty shared across the submodels captures residual dependence between the two events.
Motivated by application to PE, we consider the task of developing joint risk models for semi-competing risks, specifically in high-dimensional settings such as electronic health records-based studies. Two questions framing model development emerge: (1) which covariates should be included in each submodel, and (2) can information about covariate effects be shared across submodels? To our knowledge only two published papers consider variable selection for these (and related) models, each with important limitations. Sennhenn-Reulen and Kneib (2016) propose ℓ1-penalized estimation for general multistate models, with parameter-wise penalties inducing sparsity in each submodel and a fused penalty coercing effects for a given covariate to be the same across submodels. This framework, however, does not permit a shared frailty in the model specification, focuses solely on ℓ1-penalization, and uses a Newton-type algorithm that does not scale to high dimensions. Instead, Chapple et al. (2017) propose a Bayesian spike-and-slab variable selection approach for frailty illness-death models. This framework, however, does not consider linking coefficients across submodels, and is computationally intensive even in low dimensions.
In this paper we propose a novel high-dimensional estimation framework for penalized parametric frailty-based illness-death models. A critical challenge in this setting, however, is that the likelihood-based loss function is non-convex. This renders the development of theoretical results and efficient computational tools particularly difficult. Moreover, to our knowledge no prior literature has examined theoretical properties of penalized frailty-based illness-death models. In relevant work, Loh and Wainwright (2015) prove error bounds for non-convex loss functions with non-convex penalties, but the conditions underlying their result do not directly apply to this setting. Taking into account these various issues, the contributions of this paper are threefold. First, we propose a framework for selecting sparse covariate sets for each submodel via individual non-convex penalties, while inducing parsimony via a fused penalty on effects shared across submodels. Second, we develop a proximal gradient optimization algorithm with a pathwise routine for tuning the model over a grid of regularization parameters. Finally, we prove a high-dimensional statistical error rate for the penalized frailty-based illness-death model estimator. We present a simulation study investigating estimation and model selection properties, and develop a joint risk model for PE and delivery using real pregnancy outcome data from electronic health records.
2. Penalized Illness-Death Model Framework
2.1. Illness-Death Model Specification
Let T1 and T2 denote the times to the non-terminal and terminal events, respectively. As outlined in Xu et al. (2010), the illness-death model characterizes the joint distribution of T = (T1, T2) by three hazard functions: a cause-specific hazard for the non-terminal event; a cause-specific hazard for the terminal event in the absence of the non-terminal event; and, a hazard for the terminal event conditional on T1 = t1. These three hazards can be structured as a function of covariates, denoted X, and an individual-specific random frailty, denoted γ, to add flexibility in the dependence structure between T1 and T2, as follows:
where X1, X2, and X3 are each subsets of X. Practically, in order to make progress, one must specify some form of structure regarding the dependence of each hazard on X and γ. In this paper we focus on the class of multiplicative-hazard regression models, of the form:
| (1) |
| (2) |
| (3) |
where h0g is a transition-specific baseline hazard function, g = 1, 2, 3, and is a dg-vector of transition-specific log-hazard ratio regression coefficients. For ease of notation of the hazard functions, we subsequently suppress conditionality on γ and Xg.
Within this class of models, analysts must make several choices about the structure of the specific model to be adopted. First, it must be decided how exactly the non-terminal event time T1 affects h03(t2 | t1) in submodel (3). The so-called Markov structure sets h03(t2 | t1) = h03(t2), meaning the baseline hazard is independent of t1. Alternatively, the semi-Markov structure sets h03(t2 | t1) = h03(t2 − t1), so the time scale for h3 becomes the time from the non-terminal event to the terminal event (sometimes called the sojourn time) (Putter et al., 2007; Xu et al., 2010). Semi-Markov specification also allows functions of t1 as covariates in the h3 submodel, to further capture dependence between T1 and T2. While the choice of structure changes the interpretation of h3 and β3, the proposed penalization framework and theory allow either specification. Rather than focus on one or the other, we use semi-Markov specification when writing equations to simplify notation, as well as in the simulation study. However, in our application to pregnancy data we use Markov models to facilitate interpretation of the resulting estimates on the scale of gestational age.
A second important choice concerns the form of the three baseline hazard functions. Given the overarching goals of this paper, we focus on parametric specifications with a fixed-dimensional kg-vector of unknown parameters, , for the gth baseline hazard. For example, one could adopt a form arising from some specific distribution such as the Weibull distribution: . More flexible options include the piecewise constant baseline hazard defined as , with a user-defined set of breakpoints . Web Appendix H describes other possible flexible spline-based baseline hazard specifications.
Finally, one must choose a distribution for γ, the individual-specific frailties. These terms serve to capture additional within-subject correlation between T1 and T2 beyond covariate effects, and increase flexibility beyond the assumed baseline hazard specification and Markov or semi-Markov model structure (Xu et al., 2010). In this, the frailties play a role that is analogous to that of random effects in generalized linear mixed models. As discussed in Web Appendix B, inclusion of frailties also helps to characterize variability in individualized risk predictions. While in principle one could adopt any distribution for γ, we focus on the common choice of γ ~ Gamma(e−σ, e−σ). This distribution has mean 1 and variance eσ, and uniquely yields a closed form marginal likelihood, as shown in (4). This log-variance parameter σ can be interpreted as characterizing residual variability of the outcomes beyond the specified baseline hazard and transition model structure.
2.2. The Observed Data Likelihood
Now, let C denote the right-censoring time. The observable outcome data for the ith subject is then 𝒟i = {Y1i, Δ1i, Y2i, Δ2i, Xi} where Y1i = min(Ci, T1i, T2i), Y2i = min(Ci, T2i), , and . We denote the corresponding observed outcome values as y1i, y2i, δ1i, and δ2i. Given specification of models (1), (2) and (3), let denote the k×1 vector of baseline hazard components, with k = k1 +k2 +k3, and the d × 1 vector of log-hazard ratios, with d = d1 + d2 + d3. Finally, let ψ = (β⊤, ϕ⊤, σ)⊤ denote the full set of d + k + 1 unknown parameters.
To develop the observed data likelihood, we assume independencies between: frailty and covariates, γ ╨ X; frailty and censoring time given covariates, γ ╨ C | X; and, censoring time and event times, given covariates and frailty, C ╨ T | (γ, X). Illustrating under semi-Markov specification, the ith likelihood contribution given γi is , where . Finally, integrating out the gamma-distributed frailty, the ith marginal likelihood contribution takes the closed form
| (4) |
2.3. Penalization for Sparsity and Model Parsimony
Given an i.i.d sample of size n, let denote the negative log-likelihood. Penalized likelihood estimation follows via the introduction of a penalty function Pλ(ψ), yielding a new objective function of the form Qλ(ψ) = ℓ(ψ) + Pλ(ψ).
Letting X = X1 = X2 = X3, the illness-death model’s hazards allow each Xj to potentially have three different coefficients: a cause-specific log-hazard ratio for the non-terminal event (β1j), a cause-specific log-hazard ratio for the terminal event (β2j), and a log-hazard ratio for the terminal event given the non-terminal event has occurred (β3j). We propose a structured Pλ(ψ) simultaneously targeting two properties: (i) sparsity, by identifying important non-zero covariate effects, and (ii) parsimony, by identifying relationships between the effects of each covariate across the three submodels. We propose the general form
| (5) |
The first component, regulated by λ1, induces sparsity by setting unimportant covariate effects to zero. The second component, regulated by λ2, induces parsimony by regularizing the cofficients of each covariate Xj towards being similar or shared across submodels.
For each component, one could, in principle, consider any of a wide array of well-known penalties, such as the Lasso ℓ1 penalty (Tibshirani, 1996) or non-convex penalties like smoothly-clipped absolute deviation (SCAD) (Fan and Li, 2001):
| (6) |
with ξ > 2 controlling the level of non-convexity. This penalty behaves like the Lasso near zero, but flattens out for larger values, reducing bias on truly non-zero estimates.
The motivation for this form of penalty is both clinical and statistical, and we emphasize that depending on the application, the fusion penalties between β1, β2 and/or β3 can be included or omitted from Pλ(ψ). Clinically, fusion penalties are valuable when there is subject matter knowledge indicating that covariates likely have similar effects in two or more submodels. For example, β2 and β3 both represent log-hazard ratios for the terminal event, with β2 representing cause-specific effects in the absence of the non-terminal event, and β3 representing effects conditional on the occurrence of the non-terminal event. Therefore, fusing β2 and β3 imposes a structure where covariate effects on the terminal event are similar whether or not the non-terminal event has occurred. Relatedly, β1 and β2 both represent cause-specific log-hazard ratios, for the non-terminal and terminal event respectively. Therefore, in settings where both non-terminal and terminal events represent negative health outcomes, like cancer progression and death, fusing these components induces each covariate to have similar or shared cause-specific hazard ratio estimates for the two events. In any case, well-chosen structured fusion penalties can be used to encode clinically meaningful subject matter knowledge into the estimation framework.
Statistically, fusion penalties may also be valuable when there is relatively little information on one of these submodels, and the goal is to impose structure and stabilize estimation. For example, in settings where the non-terminal event is rare relative to the terminal event, there will be more information available for estimating β2 relative to β1 or β3. Therefore, adding a fusion penalty between β2 and either β1 and/or β3 regularizes the more variable estimates of β1 and/or β3 towards the more precise estimates of β2, effectively borrowing information across submodels. As with all regularized estimation, this directly reflects a bias-variance trade off: imposing structure on covariate effects across hazards to reduce variance, or leaving effects unstructured across hazards to reduce bias.
3. Optimization
Practically, minimizing the objective function Qλ(ψ) with respect to ψ poses several interconnected challenges: the loss function ℓ is non-convex due to the marginalized random frailty; the penalty functions pλ may also be non-convex; and, the fusion penalty component does not admit standard algorithms for general fused Lasso tailored to linear regression (Tibshirani and Taylor, 2011). Finally, the combination of penalties requires tuning a two-dimensional regularization parameter λ. In this section, we propose a comprehensive optimization routine to simultaneously and efficiently handle these challenges.
3.1. Proximal Gradient Descent with a Smoothed Fusion Penalty
Proximal gradient descent iteratively minimizes objective functions like Qλ defined as the sum of a differentiable loss function and a non-differentiable penalty. When Pλ(ψ) is the standard Lasso ℓ1-penalty λ∥β∥1, the algorithm reduces to standard gradient descent with an added soft-thresholding operation. To leverage this property, we combine two techniques to recast Qλ from a loss with a complex penalty into a loss with a simple Lasso penalty.
First we decompose each pλ in (5) into the sum of a smooth concave term and a simple ℓ1 penalty term, of the form , where is a Lipschitz-smooth concave function (Zhao et al., 2018). The goal is to treat the smooth component as part of the likelihood, leaving only a simpler ℓ1 penalty. This decomposition can be done to both the parameterwise penalties and the fusion penalties , rewriting (5) as
| (7) |
where denotes the fusion ℓ1 penalty.
However, this fusion penalty still complicates optimization, so next we use Nesterov smoothing to substitute it with a smoothed, differentiable surrogate (Chen et al., 2012). Defining as a contrast matrix such that , the surrogate is
| (8) |
where and S(x) is the vector-valued projection operation onto the unit box, defined at the jth element by [S(x)]j = sign(xj)max(1, |xj|) and μ > 0 is a user-chosen smoothness parameter. Smaller μ yields a tighter approximation, with the gap between penalty and surrogate bounded by , where J is the number of pairwise fusion terms. Web Appendix G details tuning methods for μ.
Together, (7) and (8) recast the objective function Qλ(ψ) as an ℓ1-penalized objective:
| (9) |
where . Towards optimizing (9), define the vector-valued soft thresholding operation Sλ(x) at the jth element by [Sλ(x)]j = sign(xj)max(0, |xj|−λ). Then the mth step of the iterative proximal gradient algorithm is , where r(m) is an adaptive step size determined by backtracking line search (see, e.g., ‘Algorithm 3’ of Wang et al., 2014). Iterations continue until change in objective function |Qλ,μ(ψ(m))−Qλ,μ(ψ(m−1))| falls below a given threshold (e.g., 10−6 in this paper).
3.2. Tuning Regularization Parameters via Pathwise Grid Search
For non-convex penalized problems with a single regularization parameter λ, recent path-following routines apply proximal gradient descent or coordinate descent over a decreasing sequence of regularization parameters (Wang et al., 2014; Zhao et al., 2018). At each new λ, these routines initialize at the solution of the prior λ. The result is a sequence of estimates across a range of penalization levels, also called a regularization path. Under certain conditions these ‘approximate path-following’ approaches yield high-quality local solutions with attractive theoretical properties, even when the loss and/or regularizer are non-convex. Heuristically, many non-convex objective functions are locally convex in the neighborhood of well-behaved optima, and so incrementally optimizing over a sequence of small changes to λ ensures that each local solution remains in the convex neighborhood of the solution under the previous λ.
Therefore, we develop a pathwise approach to the penalized illness-death model (9) with a search routine over a two-dimensional grid of the sparsity parameter λ1 and fusion parameter λ2 (Figure 1). This routine consists of an outer loop decrementing λ1 as in standard pathwise algorithms, and an inner loop comprising a branching pathwise search over increasing λ2 values. The resulting grid search of the model space slowly grows the number of non-zero coefficient estimates as λ1 decreases in the outer loop, and then explores how the resulting non-zero coefficients fuse as λ2 increases in the inner loop. Assuming sparsity of the regression coefficients, a straightforward choice to begin the pathwise regularization grid search routine is to set β = 0, and set the remaining parameters to the unadjusted MLE estimates fit without covariates. Optimization at each point initializes from the solution at the prior relevant step.
Figure 1.
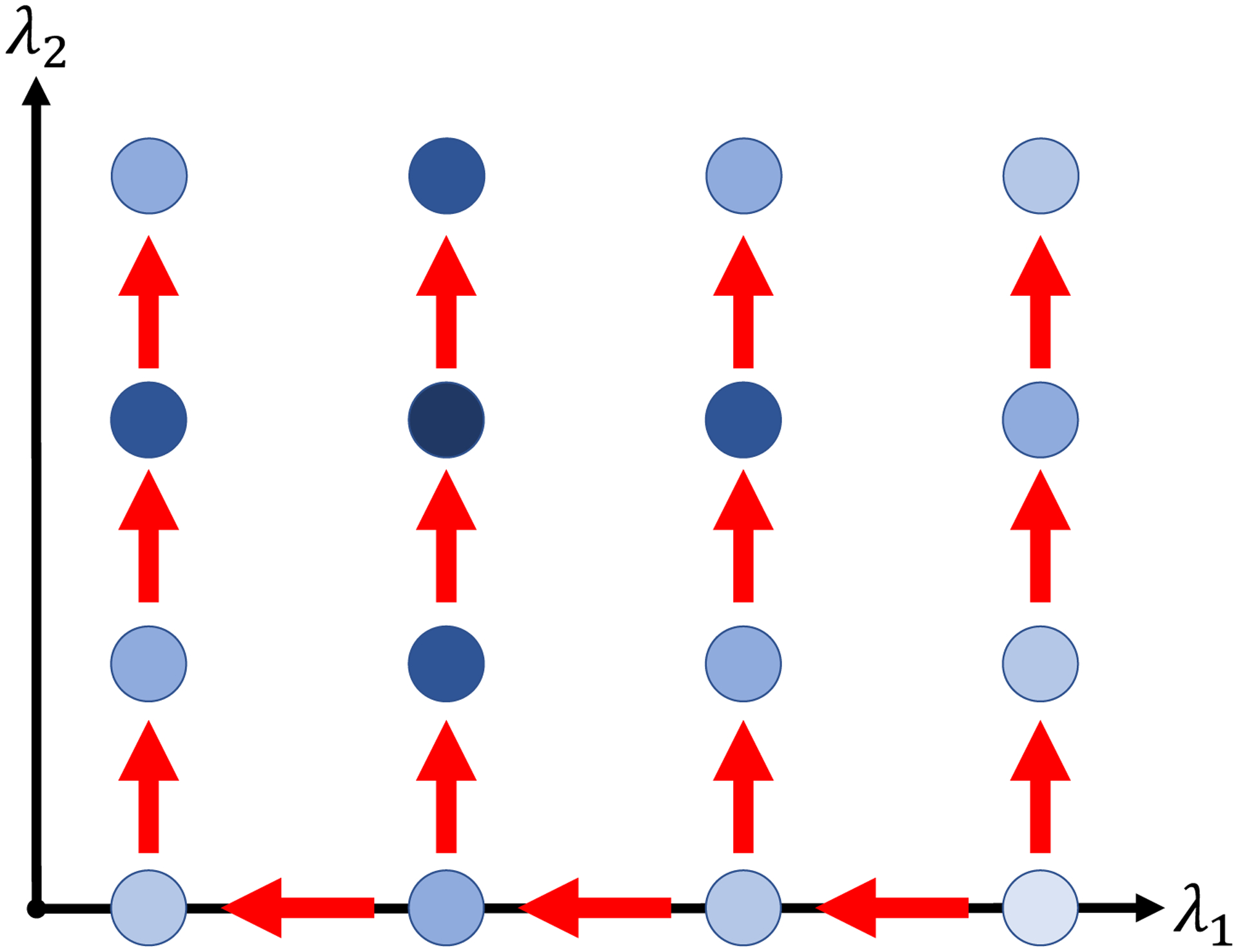
Schematic depicting path-following grid search routine over (λ1, λ2). Each dot represents a (λ1, λ2) pair for which the penalized estimator is fitted, with darker shading corresponding to better model fit metric (e.g., AIC or BIC). The arrows illustrate the path of the search routine, with optimization at each grid point starting at the solution of the previous point. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.
The grid should be as fine as computational costs allow; Wang et al. (2014) recommend that successive values of λ1 differ by no more than a factor of 0.9, and for λ2 we chose four grid points in simulations and seven for the data application. Final choice of (λ1, λ2) follows by minimizing a performance metric computed at each grid point, depicted by shading at each point in Figure 1. Metrics such as Bayesian Information Criterion (BIC) or Akaike Information Criterion (AIC) may be computed using model degrees of freedom estimated by the number of unique covariate estimates (Sennhenn-Reulen and Kneib, 2016).
4. Theoretical Results
In this section, we derive the statistical error rate for estimation of the true parameter vector ψ* in a gamma frailty illness-death model with non-convex penalty, encompassing high-dimensional settings where d > n with sparsity level denoted ∥ψ*∥0 = s. This work builds on the framework of Loh and Wainwright (2015), extended to the additional complexities of parametric gamma-frailty illness-death models. We develop a set of sufficient conditions for this setting under which we prove the statistical rate, and verify that such conditions hold with high probability under several common model specifications.
This statistical investigation focuses on the estimator
| (10) |
We note that while the general framework (5) allows a penalty on every element and pairwise difference of the regression parameter vectors β1, β2, and β3, the estimator based on (10) specifically penalizes β1 and its pairwise differences with β2 and β3. This facilitates the theoretical analysis while retaining the property that the elementwise differences between βg’s are sparse. Moreover, to accommodate the role of non-convexity the constraint ∥ψ∥1 ⩽ R1 is imposed on the parameter space over which solutions are sought (Loh and Wainwright, 2015). See Assumption 2 below and its remark for detailed discussion.
We start by listing assumptions used to derive the statistical rate of the estimator of ψ* based on (10). To unify outcome notation across all three submodels g = 1, 2, 3, let
where Ygi and Δgi are defined as in Section 2.2.
Assumption 1 (Bounded Data): There exists some administrative maximum time τY such that 0 < Y1 ⩽ Y2 ⩽ τY < ∞. Additionally, there exists some positive covariate bound τX such that τX ⩾ ∥X∥∞, where ∥X∥∞ = maxj=1, …, d|Xj|.
Assumption 1 ensures boundedness of the observed data. This assumption will invariably be satisfied in real world data applications, especially in time-to-event studies where person-time is censored and there are practical limits on covariate values.
Assumption 2 (Bounded True Parameter): There exists a R2 > 0 such that ∥ψ*∥1 ⩽ R2.
Assumption 2 characterizes the overall length of the true parameter vector in terms of ℓ1-norm. Combined with the side constraint introduced in (10) and setting R = R1 + R2, this ensures by the triangle inequality that there is an overall bound ∥ψ − ψ*∥1 ⩽ R for each iterate and all stationary points of the optimization routine.
Assumption 3 (Bounded Minimum Population Hessian Eigenvalue): There exists a ρ > 0 such that , where λmin{Σ(ψ)} is the minimum eigenvalue of , the population Hessian matrix at ψ.
Assumption 3 characterizes the positive-definiteness of the expected Hessian matrix of the loss function as a function of ψ, and guarantees curvature of the population loss function in a neighborhood around the truth.
Assumption 4 (Baseline Hazard Function Sufficient Conditions): For g, r = 1, 2, 3, j = 1, …, kg, and l = 1, …, kr, and for all {ψ : ∥ψ – ψ*∥2 ⩽ R},
H0g(t), ∂H0g(t)/∂ϕgj, and ∂2H0g(t)/(∂ϕgj∂ϕrl) are bounded functions on 0 ⩽ t ⩽ τ for any τ > 0.
is finite.
Each log-hazard second derivative factorizes into the form , where is only a function of ψ and is only a function of t. In addition, every is finite.
Assumption 4 outlines conditions regarding the baseline hazard functions in the illness-death model specification. Collectively, these conditions are imposed to control the maximum deviations of the gradient ∥∇ℓ(ψ*)∥∞, and Hessian ∥∇2ℓ(ψ) − Σ(ψ)∥max for all ψ over the ℓ2-ball ∥ψ − ψ*∥2 ⩽ R, where ∥ · ∥max is the matrix elementwise absolute maximum. Specifically, the gradient and Hessian of the empirical loss function ℓ may be unbounded, which complicates our analysis; under a Weibull specification, for example, several elements of the gradient ∇ℓ(ψ) involve the term , which diverges approaching 0. As such, Assumptions 4b and 4c are used to control the unbounded quantities, while Assumption 4a bounds remaining terms. Note, these conditions are satisfied by commonly-used baseline hazard choices; Web Appendix E contains proofs for piecewise constant and Weibull specifications. Lastly, while the conditions in Assumption 4 are presented under a semi-Markov model, analogous conditions can be expressed for a Markov model.
We now present the main theorem on the statistical rate of the estimator in (10). We take pλ to be the SCAD penalty defined in (6) to streamline the statement in terms of SCAD’s non-convexity parameter ξ, though the result holds for other penalty functions including the Lasso and minimax concave penalty (MCP) (Zhang, 2010), as described in Web Appendix C.
Theorem 1: Under Assumptions 1, 2, and 3 and sparsity level s = ∥ψ*∥0, consider a gamma frailty illness-death model satisfying Assumption 4 with SCAD penalization as in (10). Suppose the SCAD non-convexity parameter ξ satisfies 3/{4(ξ − 1)} < ρ, where ρ is the population Hessian eigenvalue bound defined in Assumption 3. Then choosing for sample size n, parameter dimensionality d, and sufficiently large constant c, any stationary point of (10) will have a statistical rate that varies with s, n, and d as
The proof of this theorem and detailed discussion are left to Web Appendix C. In particular, due to the complexities outlined in the discussion of Assumption 4, the proof relies on a weaker version of the so-called Restricted Strong Convexity condition than that of Loh and Wainwright (2015). Lastly, we note that by this result, consistency of the estimator follows in the high-dimensional regime under scaling condition s log(dn)/n → 0.
5. Simulation Studies
In this section, we present a series of simulation studies to investigate the performance of the proposed methods in terms of estimation error and selection of the covariate effects β, comparing various penalty specifications with ad hoc methods like forward selection.
5.1. Set-up and Data Generation
We consider eight simulation scenarios, each based on a true semi-Markov illness death model with gamma frailty variance eσ = 0.5. The eight scenarios arise as all combinations of two specifications for each of the baseline hazard functions, the overall covariate dimensionality and the values of the true regression parameters. The specifications under consideration are detailed in Web Table F.1, and summarized below. We repeated simulations under the given settings for three sample sizes: n = 300, 500, 1000.
The true baseline hazard specifications were piecewise constant with breakpoints at 5, 15, and 20, specified to yield particular marginal event rates for the non-terminal event. Under the ‘Low Non-Terminal Event Rate’ setting approximately 17% of subjects are observed to experience the non-terminal event, while under the ‘Moderate Non-Terminal Event Rate’ setting this number was 30%. Both specifications represent complex non-monotonic hazards not be well-approximated by Weibull parameterization, to examine the impact of such misspecification on regression parameter selection and estimation error.
We considered both low- and high-dimensional regimes under sparsity, with 25 and 350 covariates respectively, having 10 true non-zero coefficients in each submodel ranging in magnitude from 0.2 to 1. Crucially, the high-dimensional setting always has more regression parameters than observations, as d = 350 × 3 = 1050 > n. Each simulated covariate vector Xi was a centered and unit-scaled multivariate normal, with AR(0.25) serial collinearity. To assess the performance of the fusion penalty, we lastly varied the extent of shared covariate effects. Under the ‘Shared Support’ specification, the support of the non-zero effects is the same across submodels, whereas under the ‘Partially Non-Overlapping Support’ structure the supports only partially overlap.
5.2. Analyses
Under each scenario, we generated 300 simulated datasets. Each dataset was then analyzed using both Lasso and SCAD-penalized models, each with and without additional fusion ℓ1-penalties linking all three hazards. Each analysis was performed using both Weibull and piecewise constant baseline hazard specifications. For the latter, we set kg = 3 and chose breakpoints at quantiles of the data, so they also did not overlap exactly with the true data generating mechanism. In all cases, penalized models were fit over a grid comprising 21 values for λ1 in the high-dimensional setting and 29 in the low-dimensional setting, and 4 values for λ2, leading to overall regularization grids of 21×4 = 84 and 29×4 = 116 points, respectively. At each grid point, the best estimate was selected from initializations at the previous step’s solution, and 5 additional randomized starting values.
From each fitted regularization grid, two models are reported. A model without fusion was chosen that minimizes the BIC over the subset path (λ1, 0), and a model possibly with fusion was chosen which minimized BIC over the entire grid of values (λ1, λ2). Therefore, the model space with fusion encompasses the model space without fusion, so any differences between the reported estimates with and without fusion reflect improvements in the BIC due to the added fusion penalty. If fusion did not improve BIC, there would be no difference.
For comparison, we considered a forward selection procedure minimizing BIC by adding one covariate to one transition hazard at each step. Finally, we fit the ‘oracle’ MLE on the set of true non-zero coefficients, as well as the full MLE in the low-dimensional setting.
5.3. Results
To assess estimation performance, we examine ℓ2-error defined as in Table 1. Across all settings, the estimation error of the regression coefficients was insensitive to the model baseline hazard specification, with comparable results for both Weibull and piecewise constant specifications. Therefore we present results for Weibull models, with piecewise specification results given in Web Appendix F. For both n = 500 and n = 1000, the combination of SCAD and fusion penalties outperforms all comparators, particularly in the high-dimensional regime. Forward selection and the unfused SCAD-penalized estimator generally yielded the next best results. Estimators with fusion penalization also performed better in the ‘Low Non-Terminal Event Rate’ setting, likely because fusion links estimates across submodels, allowing ‘borrowing’ of information about h1 and h3 from h2 when the non-terminal event is rare. Fusion penalized estimators also performed comparably well even if the covariate supports of each submodel only partially overlapped, relative to complete overlap. However, Lasso penalized models did poorly relative to other comparators, which likely reflects elevated regularization-induced bias in the individual estimates.
Table 1.
Mean ℓ2 estimation error of , Weibull baseline hazard specification. Maximum likelihood estimates only available for low-dimensional setting.
| n = 500 | Oracle | MLE | Forward | Lasso | SCAD | Lasso + Fusion | SCAD + Fusion |
|---|---|---|---|---|---|---|---|
| Moderate Non-Terminal Event Rate | |||||||
| Shared Support | |||||||
| Low-Dimension | 0.75 | 1.34 | 1.48 | 2.06 | 1.35 | 1.49 | 0.97 |
| High-Dimension | 0.76 | — | 3.10 | 2.77 | 2.37 | 2.21 | 1.20 |
| Partially Non-Overlapping Support | |||||||
| Low-Dimension | 0.73 | 1.30 | 1.33 | 1.87 | 1.26 | 1.61 | 1.13 |
| High-Dimension | 0.74 | — | 3.47 | 2.49 | 2.34 | 2.28 | 1.45 |
| Low Non-Terminal Event Rate | |||||||
| Shared Support | |||||||
| Low-Dimension | 0.92 | 1.81 | 1.89 | 2.24 | 1.91 | 1.48 | 1.20 |
| High-Dimension | 0.88 | — | 5.13 | 2.56 | 2.23 | 2.34 | 1.28 |
| Partially Non-Overlapping Support | |||||||
| Low-Dimension | 0.80 | 1.53 | 1.55 | 2.05 | 1.50 | 1.71 | 1.27 |
| High-Dimension | 0.80 | — | 3.65 | 2.42 | 2.20 | 2.33 | 1.55 |
| n = 1000 | Oracle | MLE | Forward | Lasso | SCAD | Lasso + Fusion | SCAD + Fusion |
| Moderate Non-Terminal Event Rate | |||||||
| Shared Support | |||||||
| Low-Dimension | 0.50 | 0.82 | 0.76 | 1.53 | 0.73 | 1.39 | 0.75 |
| High-Dimension | 0.50 | — | 1.25 | 2.40 | 1.52 | 1.82 | 0.81 |
| Partially Non-Overlapping Support | |||||||
| Low-Dimension | 0.48 | 0.81 | 0.71 | 1.23 | 0.71 | 1.32 | 0.83 |
| High-Dimension | 0.49 | — | 1.18 | 2.17 | 1.20 | 1.84 | 0.97 |
| Low Non-Terminal Event Rate | |||||||
| Shared Support | |||||||
| Low-Dimension | 0.57 | 0.95 | 1.31 | 2.05 | 1.15 | 1.37 | 0.83 |
| High-Dimension | 0.58 | — | 1.86 | 2.39 | 2.10 | 1.80 | 0.90 |
| Partially Non-Overlapping Support | |||||||
| Low-Dimension | 0.52 | 0.88 | 0.85 | 1.52 | 0.84 | 1.43 | 0.96 |
| High-Dimension | 0.52 | — | 1.42 | 2.22 | 1.80 | 1.94 | 1.06 |
To assess selection performance, Table 2 reports mean sign inconsistency, which counts the estimated regression coefficients that do not have the correct sign—exclusion of true non-zero coefficients, inclusion of true zero coefficients, or estimates having the opposite sign of the true coefficient. Lower values indicate better overall model selection performance. Again performance was very similar between Weibull and piecewise constant specifications, so only Weibull results are presented in the main text. Additional simulation results, and separated results on false inclusions and exclusions are included in Web Appendix F.
Table 2.
Mean count of sign-inconsistent estimates, Weibull baseline hazard specification. Sign inconsistency counts the number of estimated regression coefficients that do not have the correct sign—exclusion of true non-zero coefficients, inclusion of true zero coefficients, or estimates having the opposite sign of the true coefficient.
| n = 500 | Oracle | Forward | Lasso | SCAD | Lasso + Fusion | SCAD + Fusion |
|---|---|---|---|---|---|---|
| Moderate Non-Terminal Event Rate | ||||||
| Shared Support | ||||||
| Low-Dimension | 0.13 | 11.51 | 15.06 | 10.28 | 11.90 | 3.45 |
| High-Dimension | 0.12 | 35.81 | 26.40 | 35.22 | 21.89 | 18.88 |
| Partially Non-Overlapping Support | ||||||
| Low-Dimension | 0.14 | 10.73 | 15.39 | 10.19 | 15.06 | 7.91 |
| High-Dimension | 0.13 | 34.56 | 27.21 | 38.52 | 23.37 | 24.35 |
| Low Non-Terminal Event Rate | ||||||
| Shared Support | ||||||
| Low-Dimension | 0.30 | 16.23 | 19.33 | 17.16 | 12.77 | 5.45 |
| High-Dimension | 0.29 | 39.50 | 26.08 | 24.94 | 23.39 | 14.42 |
| Partially Non-Overlapping Support | ||||||
| Low-Dimension | 0.24 | 12.70 | 17.11 | 12.42 | 16.33 | 9.47 |
| High-Dimension | 0.21 | 36.20 | 26.08 | 29.51 | 24.53 | 22.89 |
| n = 1000 | Oracle | Forward | Lasso | SCAD | Lasso + Fusion | SCAD + Fusion |
| Moderate Non-Terminal Event Rate | ||||||
| Shared Support | ||||||
| Low-Dimension | 0.01 | 4.03 | 13.52 | 3.99 | 8.48 | 1.51 |
| High-Dimension | 0.00 | 15.83 | 20.92 | 19.92 | 19.82 | 7.21 |
| Partially Non-Overlapping Support | ||||||
| Low-Dimension | 0.02 | 4.12 | 13.80 | 4.27 | 12.58 | 4.00 |
| High-Dimension | 0.03 | 15.57 | 19.86 | 19.30 | 21.28 | 8.44 |
| Low Non-TerminaEvent Rate | ||||||
| Shared Support | ||||||
| Low-Dimension | 0.06 | 9.70 | 16.60 | 9.01 | 8.43 | 1.86 |
| High-Dimension | 0.06 | 23.73 | 24.30 | 22.17 | 19.08 | 6.95 |
| Partially Non-Overlapping Support | ||||||
| Low-Dimension | 0.03 | 5.29 | 14.54 | 5.74 | 13.27 | 4.97 |
| High-Dimension | 0.03 | 16.96 | 21.98 | 22.18 | 21.98 | 8.72 |
For both n = 500 and n = 1000, the combination of SCAD and fusion penalties out-performed comparators, while other methods’ performances varied across sample size and setting. Fusion penalized estimators exhibited notably better selection properties in the ‘Shared Support’ setting, as fusion coerces a common block of non-zero covariates across submodels. Lasso penalized models tended to choose overly sparse models. With many of the true non-zero effects small in magnitude, regularization-induced bias may have rendered those terms indistinguishable from truly zero effects.
Lastly we summarize the results in the smallest sample setting of n = 300, which are detailed in Web Appendix F. This is a challenging setting because small samples exacerbate the non-convexity of the marginal illness-death likelihood, and when outcomes are rare some transition submodels have a small number of observed events. These complications affect small-sample empirical performance of frailty-based illness-death models even in the absence of high-dimensional covariates. For example, in the setting with 25 covariates per transition, average estimation error of the full MLE is substantially larger for n = 300 than n = 500, and more sensitive to the non-terminal event rate (see Web Table F.4). Still, in this low-dimensional regime we again observe the combination of SCAD and fusion penalties reducing estimation error relative to comparators.
However, increasing dimensionality to 350 covariates per transition while keeping n = 300 degraded performance of all methods, particularly when event rates were lowest. For example, in the ‘Low Non-Terminal Event Rate’ settings, the comparator forward selection algorithm failed for between 25 and 90 percent of simulations by adding so many covariates that optimization no longer converged. Penalized models also tended towards extremes, with SCAD-penalized models including many unnecessary covariate effects, while the Lasso models selecting few or no non-zero covariate effects. A key challenge is that likelihood-based selection criteria like BIC can be distorted in small samples by non-convexity. In certain instances, the log-likelihood can become monotonic with respect to the frailty log-variance σ, yielding artificial information criteria and leading to selected models that are either completely sparse (as with Lasso-penalized models) or completely saturated (as with SCAD-penalized and forward-selected models). These serious complications manifested only in the most difficult settings combining small samples, low-to-moderate event rates, and high dimensional covariates, but show that the challenges of very small-sample estimation with frailties is compounded by high-dimensional covariates.
6. Data Application: Preeclampsia (PE) and Delivery
The proposed methods are motivated by practical application to clinical settings where interest is in developing a risk model that jointly characterizes a non-terminal and terminal event. To this end, we consider modeling PE onset and the timing of delivery using the electronic health records of an urban, academic medical center in Boston, Massachusetts. We analyze 2127 singleton live births recorded in 2019 among individuals without pre-existing hypertension who received the majority of their prenatal care and delivered at the academic medical center. Restricting to those without hypertension targets the modeling task, as PE superimposed on chronic hypertension has distinct clinical features compared to other forms of the disease (Jeyabalan, 2013). 189 (8.9%) individuals developed PE, with median diagnosis time of 37.9 weeks (Inter-Quartile Range [IQR] 35.0–39.0). The median time to delivery was 38.0 weeks (IQR 35.4–39.3) among those who developed PE and 39.4 weeks (IQR 38.6–40.3) among those who did not. Note, because PE is only diagnosed after 20 weeks of gestation, for modeling purposes this is used as the time origin, with T1 and T2 defined as time from week 20 until PE onset and delivery, respectively.
We considered a set of 33 potential covariates, including demographics recorded at patient intake, baseline lab values annotated by the medical center with a binary indicator for abnormality, and maternal health history derived from ICD-10 diagnostic codes associated with delivery (summarized in Web Table A.1). We fit Markov illness-death models so that β2 and β3 are both interpretable on the gestational age timescale, under both Weibull and piecewise constant baseline hazards. We adopted SCAD penalties on each regression coefficient, and an ℓ1 fusion penalty between β2 and β3 to induce a shared structure between coefficients for the timing of delivery in the absence of PE and timing of delivery given the onset of PE. We specified a grid of 55 values for λ1 and seven for λ2. As above, we selected the final penalized model minimizing BIC over the entire grid of (λ1, λ2) values, while the final SCAD-only penalized model minimizes BIC over the path (λ1, 0). Again, this means that differences between the models with and without fusion reflect improvements in BIC due to the fused penalty. For comparison, we also report the unpenalized MLE.
Figure 2 compares the estimated regression coefficients between unpenalized and penalized models, for each baseline hazard specification. As in the simulation studies, there appears to be little difference in the selection properties or resulting regression estimates between models with Weibull and piecewise constant baseline hazard specifications. Across all specifications, the penalized estimates chosen by BIC are highly sparse relative to the unpenalized MLE. The inclusion of a fusion penalty linking the coefficients in h2 and h3 further improved BIC, and fused several covariate effects for the timing of delivery before PE and given PE. Specifically, parity of 1 or more (meaning a history of at least one pregnancy lasting at least 20 weeks), and in the Weibull model, the presence of leiomyomas (benign gynecological tumors), are both estimated with shared coefficients on timing of delivery with and without PE. For comparison, models chosen by AIC are provided in Web Figure A.1, which include more covariates but are still sparse relative to the full model. Finally, we find that in this application, beyond the estimated regression coefficients frailties did not play a large role in characterizing additional dependence between preeclampsia and delivery timing, as the estimated frailty variance is very close to 0 in all estimates.
Figure 2.
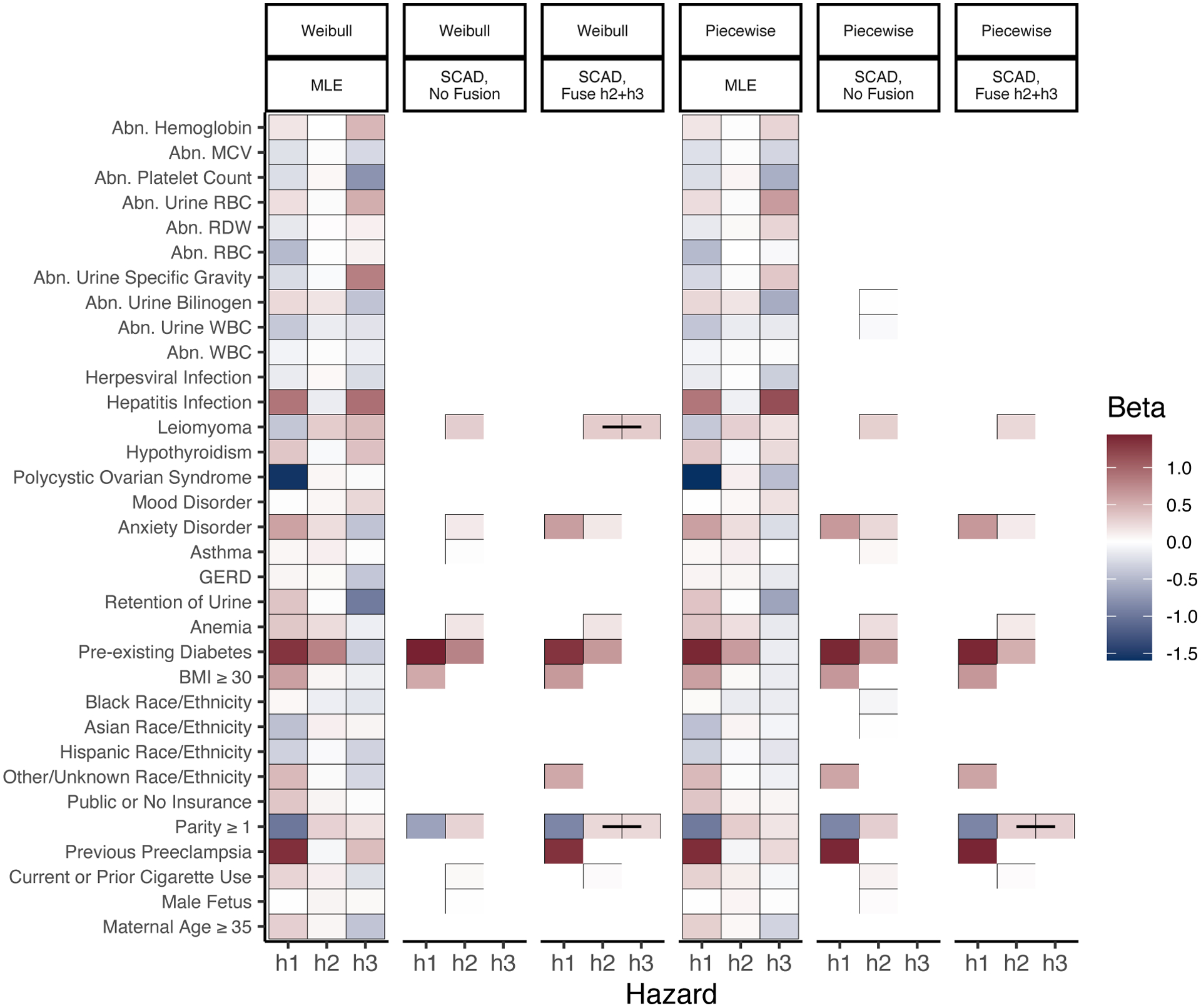
Estimated coefficients, BIC-optimal SCAD-penalized estimators with and without ℓ1 fusion between h2 and h3, and MLE under Markov specification. Fused coefficients connected with a black line. Abbreviations: abnormal (Abn), white blood cell count (WBC), red blood cell count (RBC), red cell distribution width (RDW), mean corpuscular volume (MCV), gastroesophageal reflux disease (GERD). This figure appears in color in the electronic version of this article, and any mention of color refers to that version.
These results have strong clinical significance. In every specification and across all three hazards, the selected covariates are primarily maternal health history and behaviors, rather than demographics or baseline lab measurements. Many of the variables selected for the cause-specific hazard of PE—parity of 1 or more, BMI of at least 30, and pre-existing diabetes—align with findings of recent meta-analyses of factors affecting PE risk (Giannakou et al., 2018). Further illustrating the interplay of risk factors with the outcomes, fusion penalized estimates show parity of 1 or more associated both with delayed timing of PE, and accelerated timing of delivery in the presence of PE. This correspond clinically with risk of milder late-onset PE for which delivery can occur quickly with fewer risks.
As introduced previously, care decisions for PE center two challenges: identifying those at high risk of PE, and timing delivery after PE onset to balance maternal and fetal health risks. Though our methodological focus is on regularized estimation and model selection, the resulting fitted illness-death models also generate prospective risk predictions to inform these individualized clinical care decisions (Putter et al., 2007). In Web Appendix B we present and discuss a set of four such risk profiles for sample patients using a Weibull model with fusion penalty. Specifically, from baseline the model can predict across time how likely an individual is to be in one of four categories: (i) still pregnant without PE, (ii) already delivered without PE, (iii) already delivered with PE, and (iv) still pregnant with PE. Such profiles directly address clinical needs by highlighting individuals’ overall risk of developing PE, while also characterizing the timing of PE and delivery.
7. Discussion
Frailty-based illness-death models enable investigation of the complex interplay between baseline covariates and semi-competing time-to-event outcomes. Estimates directly illustrate the relationships between risk factors and the joint outcomes via hazard ratios across three submodels, while individualized risk predictions generate an entire prospective outcome trajectory to inform nuanced clinical care decisions.
The task of modeling risk of PE and timing of delivery illustrates the value, and the potential, for penalized illness-death modeling to inform clinical practice. While analysts typically default to including the same set of covariates in all three hazards, Figure 2 illustrates that no covariate in any BIC-selected models has distinct, non-shared coefficients in all three hazards. Moreover, even in the setting of PE onset and delivery, where relatively few covariate effects appear to be shared across submodels, adding fusion regularization improved model fit metrics. We expect the impact of fusion would be even more pronounced in settings where the outcomes are more positively correlated, such as when the non-terminal event is a negative health outcome and the terminal event is death. Because frailties also tend to characterize positive correlation of the outcomes, we might also expect larger estimated frailty variance in such settings. Analysts interested in considering non-frailty models might fit regularization paths with and without the frailty, and choose a final criterion-minimizing model from amongst both frailty and non-frailty candidates.
We also note that the statistical rate result of Theorem 1 uses the specific choice of penalty given in (10), however we would expect similar theoretical performance under the similar penalty introduced in (5). The advantage of implementing the formulation as in (5) is its interpretability for the analyst, by directly distinguishing between the role of λ1 in determining the global level of sparsity of the regression parameters, and the role of λ2 in determining the level of parsimony in the sharing of effects across hazards.
Though the current work focuses on penalization of the regression parameters β, the framework also admits penalization of the baseline hazard parameters to achieve similar goals of flexibility and structure. For example, under the Markov transition specification a penalty of the form could regularize the model towards having h02(t2) = h03(t2). Xu et al. (2010) call this the ‘restricted’ illness-death model corresponding to the baseline hazard of the terminal event being equal before and after the non-terminal event. Moreover, while we presently focus on fixed-dimensional parametric baseline hazard specifications, in principle the estimation algorithms presented here extend to penalized baseline models of growing dimensionality, such as splines with number of basis functions dependent on sample size. The theoretical properties of such an estimator would be an interesting avenue of future research. Future work might also explore these methods and theory under other frailty distributions besides the closed form-inducing gamma.
Finally, establishing the statistical rate of the proposed penalized estimator also enables future development of post-selection inferential tools such as confidence intervals for selected coefficients. Most importantly, this methodology enables future work modeling semi-competing risks across a wide array of clinical domains, and leveraging data sources with high-dimensional covariates from electronic health records to genomic data.
Supplementary Material
Acknowledgments
The authors thank the Associate Editor and Reviewers for helpful comments, and thank Drs. Michele Hacker, Anna Modest, and Stefania Papatheodorou for data access at Beth Israel Deaconess Medical Center, Boston, MA and valuable discussion. This study received exemption status by institutional review boards at Beth Israel Deaconess Medical Center and Harvard TH Chan School of Public Health. HTR is supported by NIH grants T32LM012411, T32GM074897, and F31HD102159, and JL by R35CA220523 and U01CA209414. JL is supported by NSF grant 1916211.
Footnotes
Supporting Information
Web Appendices, Tables, and Figures referenced in Sections 2–7 are available with this paper at the Biometrics website on Wiley Online Library. Software for the proposed methods in R is available at https://github.com/harrisonreeder/SemiCompRisksPen.
Data Availability Statement
Data used in this paper to illustrate the proposed methods are not shared due to privacy restrictions.
References
- Chapple AG, Vannucci M, Thall PF, and Lin S (2017). Bayesian variable selection for a semi-competing risks model with three hazard functions. Computational Statistics & Data Analysis 112, 170–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Lin Q, Kim S, Carbonell JG, and Xing EP (2012). Smoothing proximal gradient method for general structured sparse regression. Annals of Applied Statistics 6, 719–752. [Google Scholar]
- Fan J and Li R (2001). Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association 96, 1348–1360. [Google Scholar]
- Fine J, Jiang H, and Chappell R (2001). On semi-competing risks data. Biometrika 88, 907–919. [Google Scholar]
- Giannakou K, Evangelou E, and Papatheodorou SI (2018). Genetic and non-genetic risk factors for pre-eclampsia: Umbrella review of systematic reviews and meta-analyses of observational studies. Ultrasound in Obstetrics & Gynecology 51, 720–730. [DOI] [PubMed] [Google Scholar]
- Jazić I, Schrag D, Sargent DJ, and Haneuse S (2016). Beyond composite endpoints analysis: semicompeting risks as an underutilized framework for cancer research. JNCI: Journal of the National Cancer Institute 108, djw163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeyabalan A (2013). Epidemiology of preeclampsia: impact of obesity. Nutrition Reviews 71, S18–S25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee KH, Haneuse S, Schrag D, and Dominici F (2015). Bayesian semiparametric analysis of semicompeting risks data: investigating hospital readmission after a pancreatic cancer diagnosis. Journal of the Royal Statistical Society: Series C (Applied Statistics) 64, 253–273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loh PL and Wainwright MJ (2015). Regularized M-estimators with nonconvexity: Statistical and algorithmic theory for local optima. Journal of Machine Learning Research 16, 559–616. [Google Scholar]
- Putter H, Fiocco M, and Geskus RB (2007). Tutorial in biostatistics: competing risks and multi-state models. Statistics in Medicine 26, 2389–2430. [DOI] [PubMed] [Google Scholar]
- Sennhenn-Reulen H and Kneib T (2016). Structured fusion lasso penalized multi-state models. Statistics in Medicine 35, 4637–4659. [DOI] [PubMed] [Google Scholar]
- Tibshirani R (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 58, 267–288. [Google Scholar]
- Tibshirani RJ and Taylor J (2011). The solution path of the generalized lasso. Annals of Statistics 39, 1335–1371. [Google Scholar]
- Wang Z, Liu H, and Zhang T (2014). Optimal computational and statistical rates of convergence for sparse nonconvex learning problems. Annals of Statistics 42, 2164–2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Kalbfleisch JD, and Tai B (2010). Statistical analysis of illness–death processes and semicompeting risks data. Biometrics 66, 716–725. [DOI] [PubMed] [Google Scholar]
- Zhang C-H (2010). Nearly unbiased variable selection under minimax concave penalty. The Annals of Statistics 38, 894–942. [Google Scholar]
- Zhao T, Liu H, and Zhang T (2018). Pathwise coordinate optimization for sparse learning: Algorithm and theory. Annals of Statistics 46, 180–218. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data used in this paper to illustrate the proposed methods are not shared due to privacy restrictions.


