Fourier optical spin splitting microscopy

Abstract

In this work, we propose a new quantitative phase imaging methodology named Fourier optical spin splitting microscopy (FOSSM). FOSSM relies on a metasurface located at the Fourier plane of a polarized microscope to separate the object image into two replicas of opposite circularly polarized states. The bias retardation between the two replicas is tuned by translating the metasurface or rotating the analyzer. Combined with a polarized camera, FOSSM can easily achieve single-shot quantitative phase gradient imaging, which greatly reduces the complexity of current phase microscope setups, paving the way for the next generation high-speed real-time multi-functional microscopy.

Label-free phase microscopy, which does not require sample staining and reduces phototoxicity, is in high demand for wide range of applications in various disciplines [1, 2]. Conventional phase imaging methods for transparent samples include phase-contrast [3] and differential interference contrast (DIC) [4]. Phase contrast microscopy produces intensity contrast dependent on object phase by generating interference between the background illumination and the scattered light from the object. DIC enhances image phase contrast by using a pair of compound birefringent prisms and crossed polarizers to separate and recombine the ordinary and extraordinary light so that a lateral shearing interferometric image of the specimen is obtained. However, these methods only provide qualitative information of the object. Recently, quantitative phase imaging (QPI) has emerged as a powerful tool for cell and tissue imaging as it provides a noninvasive way to quantitatively collect signals that reflect the intrinsic cellular structure. One QPI technique is based on DIC by taking multiple images with different bias phase retardations between the sheared ordinary and extraordinary components and extracting the encoded quantitative phase information of the object [5]. Another main category of QPI realization is based on interferometric or holographic configuration [6, 7]. The phase information is acquired by using interference of in-line geometrics in combination with temporal phase shifting, or directly from the shifted Fourier components using off-axis reference geometrics. However, these techniques usually require bulky setup, critical alignment and multiple measurements to retrieve the phase information, which limit their applications due to the complexity.

Metasurfaces composed of subwavelength-scale nanostructures can realize wavefront modulation by introducing any desired phase change [8–10]. Thanks to their flexibility in wavefront design, optical metasurface devices have been demonstrated for various functionalities, such as flat optical lenses [11–17], ultrathin holograms [18–23], nonlinear optical response design [24, 25], multiphoton quantum source [26–29], polarization engineering [30, 31], augmented reality [32], display [33] and mathematical operations [34] including spatial differentiation [35–38]. More recently, there has been some efforts in realizing phase imaging with metasurfaces [39, 40]. In 2020, Faraon’s team demonstrated a miniaturized single-shot quantitative phase gradient imaging (QPGI) technique with two cascaded transmission metasurfaces. The compact design mitigates the requirement of imaging lens but requires precise alignment of two layers of metasurface. Misalignment or fabrication error in the complex metasurface design would lower the imaging performance of the system [39]. Single-shot QPI was also realized with a metasurface simultaneously producing one focused and one defocused images for reconstruction based on transport of intensity equation. However, the resolution and the accuracy of the retrieved phase images are limited by the small size of the metasurface and the inaccurate estimation of the derivative in the transport of intensity equation. The simultaneous capturing of the two images also reduces the effective field of view (FOV) [40].

In this paper, we propose and experimentally demonstrate FOSSM, an optical microscopy technique that relies on the principle of common path interference of circularly polarized light to obtain quantitative phase information of unstained, transparent samples to reveal invisible features. a geometric phase metasurface assisted QPI method. A geometric phase metasurface placed at the Fourier plane of a polarized microscope introduces additional phase delays with different signs for the left- and right-handed circularly polarized (LCP and RCP) components of the incident light, thus forming two polarized replica images at the imaging plane with a displacement. The displacement between the two replicas is determined by the metasurface periodicity; while the bias retardation between the LCP and RCP replicas depends on the relative metasurface position or the orientation of the linear analyzer. A QPI of the object can then be extracted by measuring the resultant images with three different bias retardations spanning from 0 to $2\pi$. We first demonstrate the QPI capability of FOSSM by capturing multiple frames with varying bias retardations tuned by translating the metasurface over the space. Based on the same mechanism, we next present single shot QPGI by using a polarized camera which simultaneously captures images with various retardances. The single shot QPGI achieved by the proposed FOSSM technique paves the way for the next generation high-speed real-time multi-functional microscopy.

Consider a metasurface consisting of a periodic array of nanostructures placed at the Fourier plane of a 4f imaging system [see Fig. 1(a)], the metasurface introduce a geometric phase, defined by the orientation of nanostructures [41–43]. The metasurface has a spatially varying orientation of local optical axis $\phi (x_1,y_1)=\pi x_1/\mathrm{\Lambda }$ ($\mathrm{\Lambda }=1000\text{μm}$ is the period of designed metasurface). The subscript 0, 1, 2 and 3 of the coordinates corresponds to the input plane, the metasurface plane, the Fourier plane, and the image plane, respectively. The metasurface provides additional phases of $+2\phi$ and $-2\phi$ to the incident LCP beam and RCP beam respectively while transforming them into opposite helicities. When the metasurface is sandwiched between a pair of crossed linear polarizers, it effectively works as a sinusoidal amplitude grating with a transmittance profile of $t_{ms}(x_1,y_1)=\sin (2\pi x_1/\mathrm{\Lambda })$. With the metasurface modulating the spatial frequencies on the Fourier plane, a spatial differentiator for both amplitude and phase objects is achieved as $I_{out}(x_3,y_3)\approx {\mathrm{\Delta }}^2{\left|d{E}_{in}({\mathrm{x}}_3,{\mathrm{y}}_3)/d{x}_3\right|}^2$, where $E_{in}$ is the electric field of the input object, $\mathrm{\Delta }=\lambda f/\mathrm{\Lambda }$ is the shearing distance, and f is the focal length of the second lens [35].

FIG. 1.

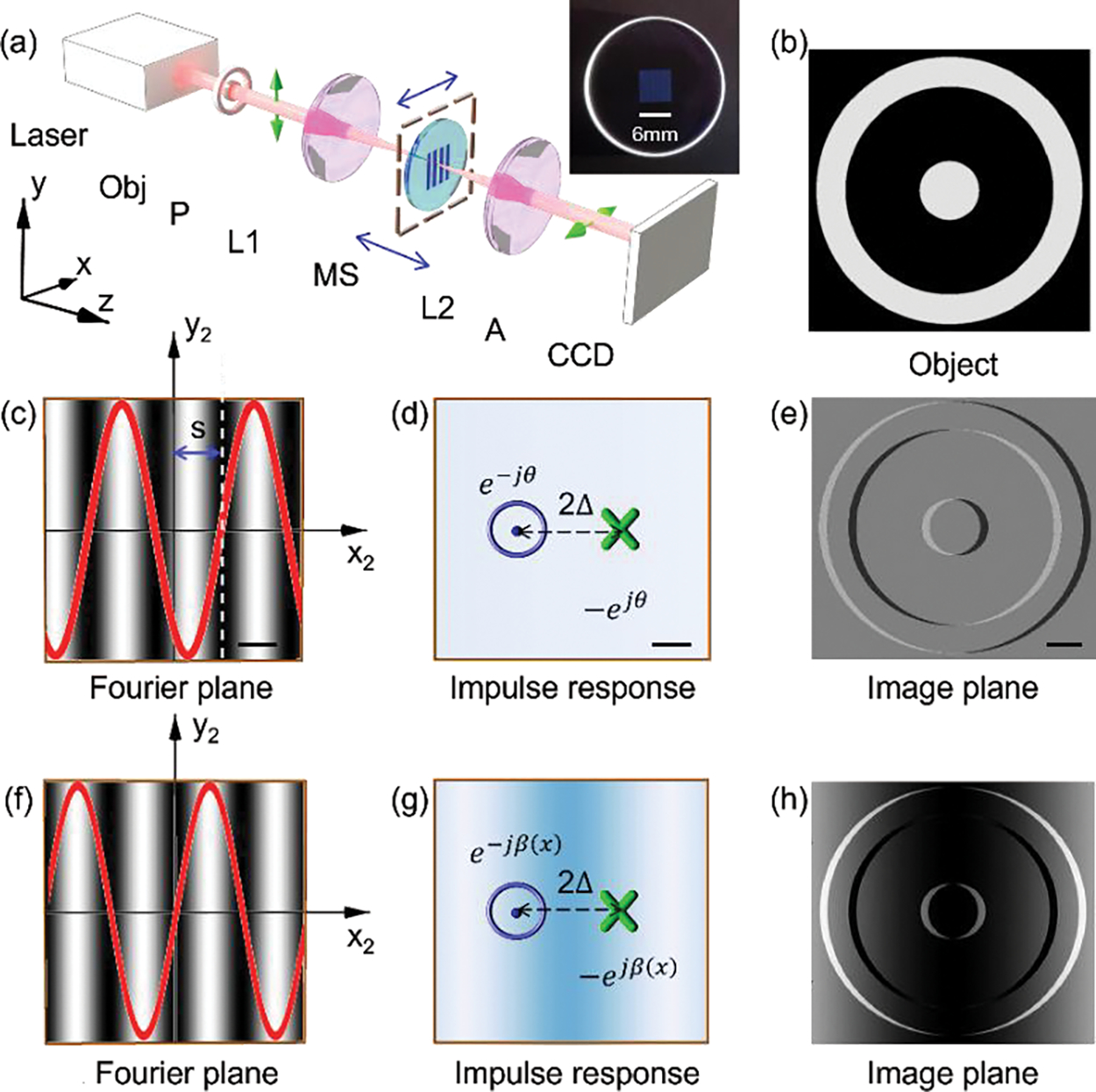
Concept of the proposed FOSSM. (a) Experiment setup. Obj, Object. P, Polarizer. L, lens. MS, metasurface. A, analyzer. Blue arrows indicate the translation direction of the metasurface. Inset, photograph of the MS. The setup is a typical 4f system composed of two lenses L1 and L2. To realize the proposed function, a MS is inserted near the Fourier plane of the 4f system, along with a pair of crossed polarizers (P and A). (b) The used phase object with unity amplitude. The photograph of the metasurface, patterned area, 6 mm*6 mm. (c-e) The concept of retardance imaging of the object with a laterally (along x direction) displaced metasurface. Scale bar in (c)-(e): 150 μm, 0.8 μm, 10 μm. (f-h) The concept of retardance imaging of the object with a longitudinally (along z direction) displaced metasurface. The fringes in (c) and (f) show the effective transmission. The red curve in (c) and (f) is the cross section of the amplitude transmittance profile of the metasurface along x direction.

A transverse shift s along x axis of the metasurface placed at the Fourier plane [Fig. 1(c)] changes the bias retardation between the LCP and RCP imaging components. The fringes in Fig. 1(c) show the effective transmission ${\left|t_{ms}({\mathrm{x}}_1-s,{\mathrm{y}}_1)\right|}^2$ of the metasurface. The red curve in Fig. 1(c) is the cross section of the amplitude transmittance profile $t_{ms}({\mathrm{x}}_1-s,{\mathrm{y}}_1)$ of the metasurface along x direction. As shown in Fig. 1(d), the corresponding impulse response of the system is therefore two Dirac-delta functions with opposite signs and conjugate bias phases $\pm \theta =\pm 2\pi s/\mathrm{\Lambda }$ brought by the transverse shift $s$ of the metasurface. The distance between the two Dirac-delta functions is $2\mathrm{\Delta }$.

A longitudinal shift $ϵ$ of the metasurface from the Fourier plane along z axis without transverse shift (s=0) [Fig. 1(f)] results in simultaneous angular and spatial shifts of the angular spectrum of the object (see Supplemental Material for details). The fringes in Fig. 1(f) show the effective transmission ${\left|t_{ms}({\mathrm{x}}_1,{\mathrm{y}}_1)\right|}^2$ of the metasurface centered along the optical axis. The red curve in Fig. 1(f) is the cross section of the amplitude transmittance profile $\left|t_{ms}({\mathrm{x}}_1,{\mathrm{y}}_1)\right|$ of the metasurface. Figure 1 (g) shows the corresponding impulse response is two Dirac-delta functions with opposite signs and spatial varying conjugate phases $\pm \beta (\mathrm{x})=\pm 2\pi \epsilon /(\mathrm{\Lambda }f)$ brought by the longitudinal shift $\epsilon$, which results in a sinusoid background.

The intensity at the image plane turns out to be the interference of the two laterally sheared images with consistent bias retardation [Fig. 1(e)] or spatially varying retardation [Fig. 1(h)]. Mathematically, the unified output electric field on image plane could be written as

$$E_{out}^{\text{'}}=\{E_{in}(x_3+\mathrm{\Delta },y_3)\exp [-j\beta ({\mathrm{x}}_3)-j\theta ]-E_{in}(x_3-\mathrm{\Delta },{\mathrm{y}}_3)\exp [j\beta (x_3)+j\theta ]\}/2$$ (1)

For a phase object $E_{in}({\mathrm{x}}_0,{\mathrm{y}}_0)=\exp [j\varphi ({\mathrm{x}}_0,{\mathrm{y}}_0)]$ with unity amplitude, the output intensity can be approximated by

$$I_{out}^{\text{'}}(x_3,y_3)\approx \frac{1}{2}\left\{1-\cos \left[2\mathrm{\Delta }\frac{d\varphi (x_3,y_3)}{d{x}_3}-2\beta (x_3)-2\theta \right]\right\}$$ (2)

QPGI can be realized by taking a series of retardance images with different bias retardation by shifting the metasurface laterally in the Fourier plane. By taking three images at $s_i=-\mathrm{\Lambda }(i-2)/6$ (i=1, 2, 3), the gradient of the phase of the object with respect to x can be calculated via the three-step phase shifting method as $G_x=d\varphi (x_3,y_3)/d{x}_3=\mathrm{atan}\left[\sqrt{3}(I_1-I_3)/(2I_2-I_1-I_3)\right]/2\mathrm{\Delta }$, where $I_i=1-cos\left(2\mathrm{\Delta }{\mathrm{G}}_{\mathrm{x}}-4\pi s_i/\mathrm{\Lambda }\right)$. The bias retardation between the two replica images can be conveniently tuned by mechanically adjusting the position of the metasurface or rotating the analyzer (see Supplemental Material for details), which allows single-shot QPGI with a polarized camera. The phase can be retrieved by 2D integration given the phase gradients with respect to x and y (see Supplemental Material for details).

If the metasurface is displaced by a distance from the Fourier plane, the presence of the spatially varying phase $\beta (x)$ leads to simultaneous edge detection and high-contrast rendition with shadow-cast pseudo 3D effects of the object within the same FOV. Quantitative phase gradient image of small objects can be retrieved in the same manner with a generalized phase stepping method by capturing three images with carefully chosen local bias retardations.

We fabricated the metasurface with structure embedded in SiO₂ substrate using laser writing method (see the inset Fig. 1(a)). High intensity laser illumination focused inside bulk SiO₂ generates highly free electron plasma, ionizing the SiO₂ structure and forming defects containing oxygen molecules, which forms elongated nanopores that create local birefringence according to the polarization of the writing laser beam. The local phase retardation between the fast and slow polarization axes of the birefringence is dependent on the writing thickness and effective refractive index along the two axes of the elongated nanopores. Therefore, by controlling the parameters of the laser writing beam, the spatially varying slow axis orientation distribution with homogeneous phase retardation provide a desired geometric phase. More fabrication information is provided in Supplemental Material.

To demonstrate the continuous tunability of the bias retardation in the retardance images using FOSSM, fixed Human embryonic kidney 293 (HEK 293) cells were imaged while translating the metasurface in the lateral direction, as shown in Fig. 2. Figure 2(a) shows the effective transmission of the metasurface at the back aperture of the microscope. It should be noted that one period of the sinusoidal transmission corresponds to half of the metasurface periodicity $\mathrm{\Lambda }$ which is 1000 μm. Figure 2(b)–2(h) correspond to the dashed lines from b to h in Fig. 2(a), which indicate the relative position of the metasurface with respect to the optical axis of the microscope. As is shown in Fig. 2(b)–2(e), the local bias retardation between the two replicates gradually reaches 0 in Fig. 2(e), of which the image contrast reaches the maximum. This is also the condition for edge imaging. As we continue shifting the metasurface, the bias retardation keeps increasing and causes reversed image contrast, as indicated in Fig. 2(e)–2(h). More calculation regarding imaging contrast in SI.

FIG. 2.

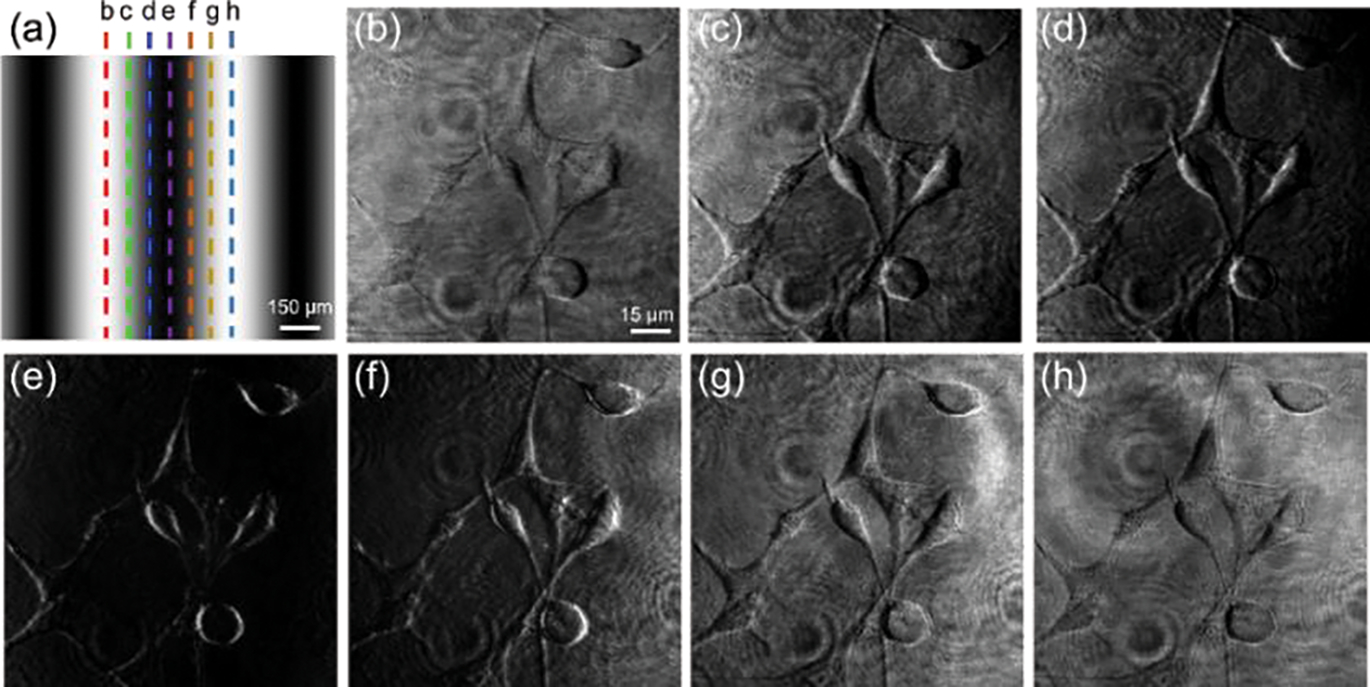
Different retardance images of Human embryonic kidney 293 cells (HEK cells) with a laterally displaced metasurface. (a) The effective transmittance of the metasurface in the Fourier plane of a polarized light microscope. The dashed lines show the relative location of the optical axis of the microscope. (b-h) Images of the HEK cells corresponding to the dashed lines in (a), respectively. The captured images transit from retardance images to edge-image (bias retardation reaches to 0) and back to retardance images with reversed contrast gradually.

Next, we demonstrate the quantitative phase imaging capability of FOSSM. NIH3T3 cells were fixed and imaged with the metasurface placed at the Fourier plane ($\epsilon =0$). Figure 3(a) and 3(c) shows three retardance images with bias retardations of −120°, 0°, 120° taken for both horizontal and vertical directions. The phase gradients [Fig. 3(b)] of the object for both directions are calculated with equation of G_x. The quantitative phase image of the object is then calculated by the 2D integration of the phase gradient images, as shown in Fig. 3(d). To verify the extracted phase, a thin polymethyl methacrylate (PMMA) film was used as a calibration sample and imaged using the same system. The extracted phase difference between regions with and without the PMMA thin film is 0.95 radian, which agrees with the phase difference predicted as: $2\pi (n_{PMMA}-n_{air})\times t_{PMMA}/\lambda$ given the film thickness $t_{\mathrm{P}\mathrm{M}\mathrm{M}\mathrm{A}}=160\text{nm}$ [Fig. 3(f)–(g)]. Here n is the refractive index. ${\mathrm{n}}_{\mathrm{P}\mathrm{M}\mathrm{M}\mathrm{A}}$ is 1.4934, n_air is 1 and $\lambda =532\text{nm}$ is the working wavelength. It should be noted that the quantitative phase imaging capability could be also achieved with the spatially varying bias retardations as we move the metasurface away from the Fourier plane of the microscope. More information about phase retrieval algorithm and all the experimental results for the case of metasurface shifted along the z direction are provided in Supplemental Material [44–48].

FIG. 3.

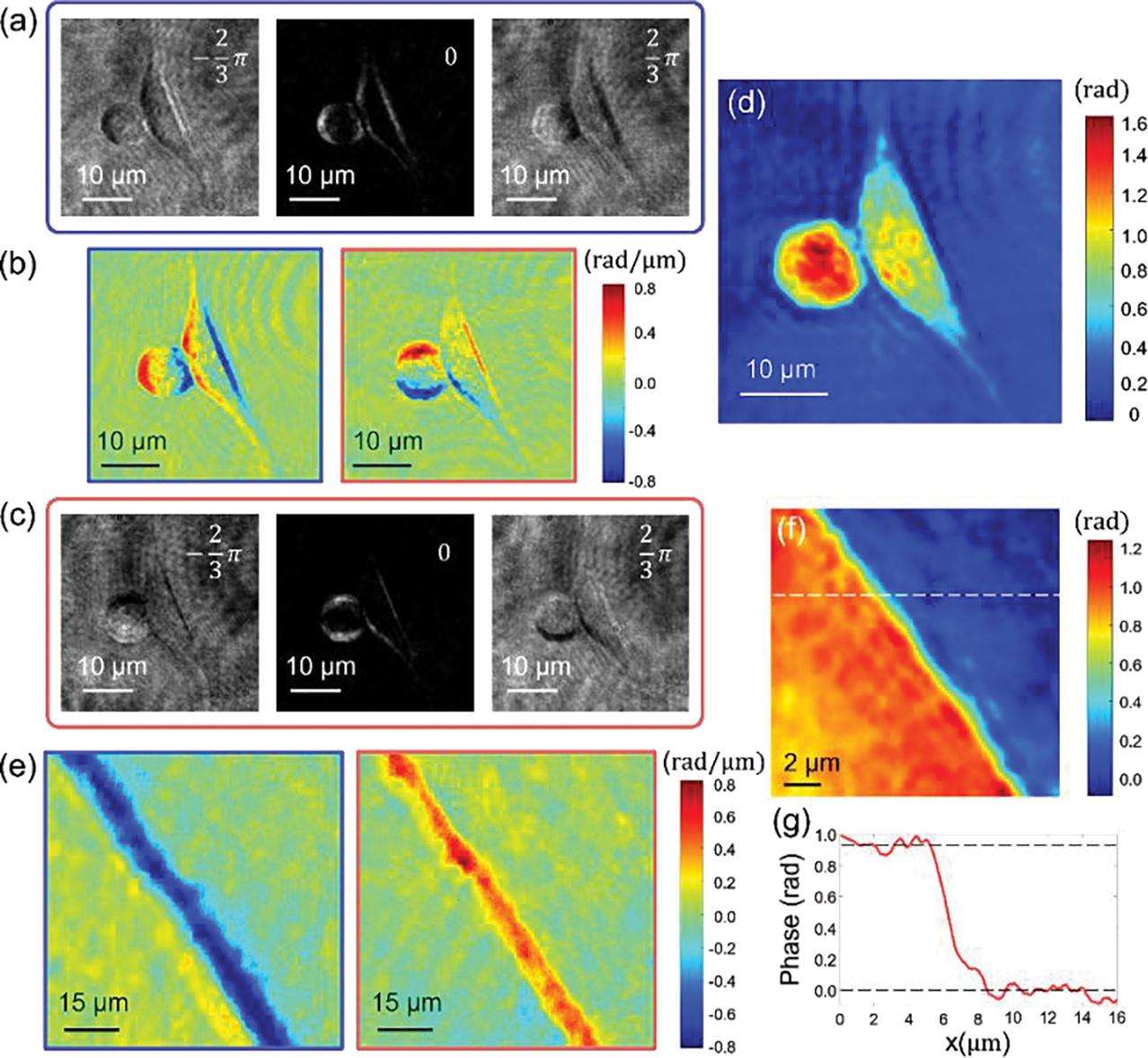
Quantitative phase imaging of NIH3T3 cells with a laterally displaced metasurface. (a) and (c) retardance images with bias retardation of −120°, 0°, 120° for vertical and horizontally orientated metasurface. Scale bar, 10 μm. (b) The phase gradient images with respect to x and y axis calculated with the three images for horizontal and vertical directions. (d) The retrieved quantitative phase image of NIH3T3 cells. (e) The phase gradient images of the calibration sample. The left region corresponds to a PMMA thin film with 160-nm-thickness. (f) The retrieved quantitative phase image of the PMMA calibration sample. (g) Cross-section along the dashed line in (f). The phase difference of the two regions matches with the expected thickness of the thin film.

The proposed FOSSM can be extended to single-shot QPGI, which is achieved by replacing the analyzer and a regular CCD with a polarized camera [Fig. 4(a)], which contains interspersed polarized pixels with 0°, 45°, 90° and 135° polarization orientation [Fig. 4 (b)]. The Jones matrix of the combination of the linear polarizer P1 along x direction, the metasurface and a micro-polarizer with orientation $a_i=(i-1)\times \pi /4$, i=1,2,3,4 can be written as

$$T_{eff}^{\prime }=\left[\begin{array}{cc}{\cos }^2{a}_i& \cos a_i\sin a_i\\ \cos a_i\sin a_i& si{n}^2{a}_i\end{array}\right]\left[\begin{array}{cc}\cos 2\phi & \sin 2\phi \\ \sin 2\phi & -\cos 2\phi \end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}\cos a_i\cos (a_i-2\phi )& 0\\ \sin a_i\cos (a_i-2\phi )& 0\end{array}\right]$$ (3)

FIG. 4.

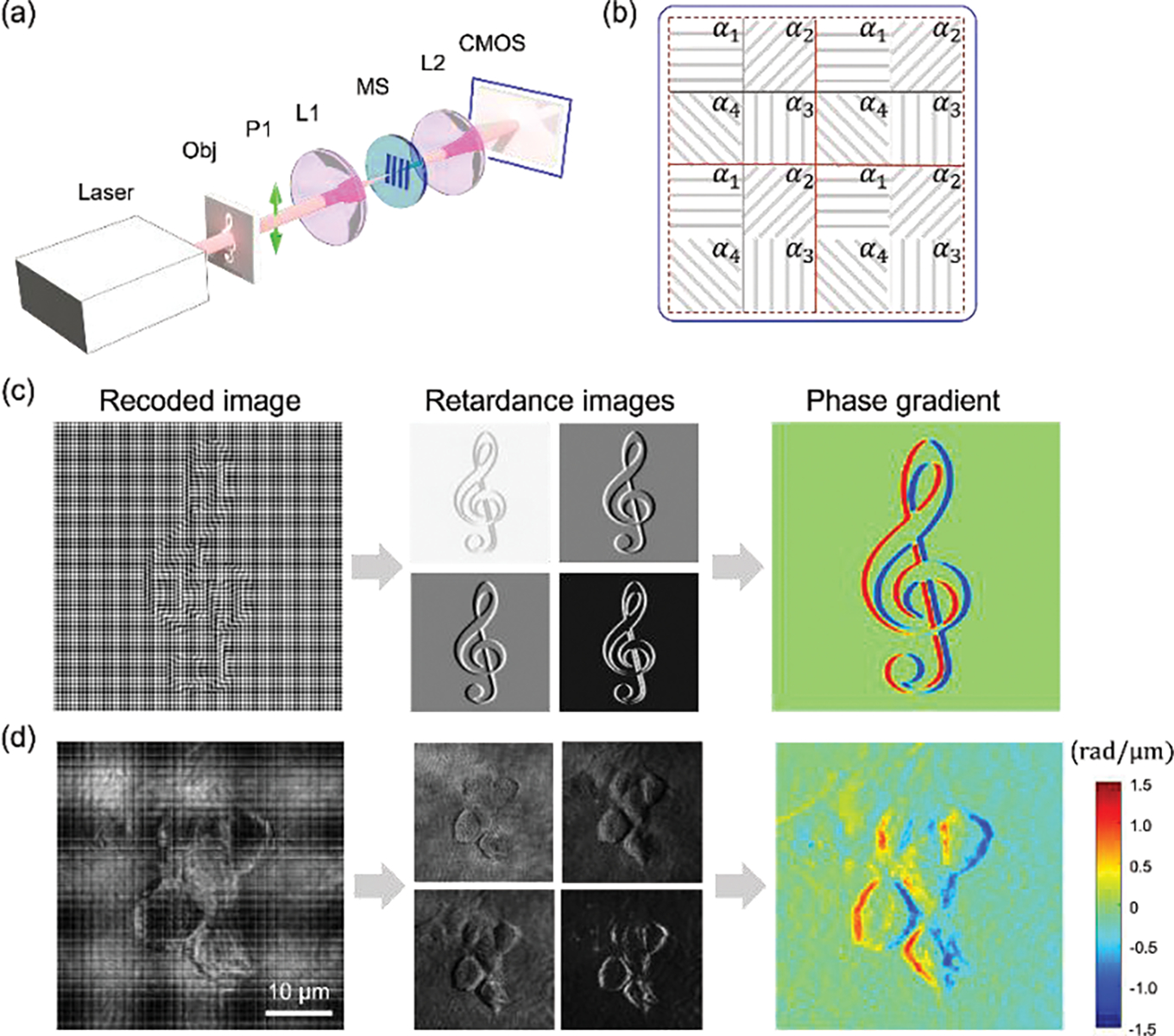
Single shot QPGI with metasurface. (a) Experiment setup. The analyzer is removed from the setup. A polarized CMOS camera is used instead of a regular CMOS camera. (b) The polarization orientation for each pixel on the camera. (c) Simulation of single shot QPGI. (d) Single shot QPGI of NIH3T3 cells.

It can be readily seen the system rotates the incident polarization by angle $a_i$ and have an effective transmittance function $t_{ms,i}(x_1,y_1)=cos(a_i-2\phi )$, which is equivalent to a sinusoidal amplitude grating with a lateral shift controlled by the relative angle of the micro-polarizer. Similar with the deviation of Eq. 2, the output image can be given asagrees with the phase difference predicted as

$$I_{out}^{\prime }(x_3,y_3,a_i)=\frac{1}{2}\left\{1-\cos \left[2\mathrm{\Delta }\frac{d\varphi (x_3,y_3)}{d{x}_3}-2a_i+\pi \right]\right\}$$ (4)

Note that Eq. 4 shares a very similar form with Eq. 2 with only a $\pi$ phase difference in the cosine term. In both cases, the tunable phase $\theta$ and $a_i$ provide the necessary bias retardation between the two images to achieve QPI. By deinterlacing one captured image by the polarized camera into four images and interpolating them [49], four retardance images with phase retardations of 0°, 90°, 180°, 270° can be obtained, which are then used to calculate the unidirectional phase gradient via the four-step phase shifting method [Fig. 4(c)]. To experimentally demonstrate single shot QPGI, we use a polarization CMOS camera (BFS-U3-51S5P-C, IMX250MZR, FLIR) to capture four sub-frames simultaneously. Figure 4(d) shows the single-shot QPGI for NIH3T3 cells. The four retardance images of different bias retardations can be clearly distinguished after rearranging the interlaced pixels from the polarization camera. The phase gradient information of the object is then retrieved.

The resolution of the proposed FOSSM method depends on the numerical aperture of the microscope and the pattern area of the metasurface. Here, the resolution is determined by the former since the fabricated sample area is much large than the size of the Fourier plane in our imaging system. Meanwhile, because FOSSM performs Fourier space modulation, the FOV of the system is only limited by the objective. The tuning of the bias retardation can not only be achieved by translating the position of the metasurface, but also by rotating the polarization orientation of the incident beam, so that there is no need for precise alignment of the metasurface in our system.

One main advantage of FOSSM over other conventional QPI techniques is that it does not require external reference beams that are generally seen in interference-based QPI setups and therefore minimizes factors that affect image interference quality, such as mechanical shocks, air turbulence, temperature fluctuations. Compared to traditional DIC or QPGI based on cascaded multiple metasurface layers, our method does not require bulky components or precise alignment process between metasurface layers. Moreover, with the metasurface displaced along the z direction, FOSSM is able to capture retardance images with spatially varying bias retardations in one FOV, while the classical DIC introduce constant bias retardation over the entire frame. The currently demonstrated FOSSM technique could be extended in several pathways in the future. Firstly, different from all the non-metasurface based QPI technologies relying on linear polarization responses of the object, FOSSM interacts with and processes the circular polarized components of the object. Most substance relevant to biological study are chiral and response differently to light helicity. We speculate that the FOSSM will provide significantly improved sensitive to light helicity, which can be used to characterize the chirality of the samples. Secondly, the current single-shot FOSSM produces 1D QPGI of the object. 2D QPGI using same methodology could be achieved with a different metasurface design [36].

In conclusion, we propose and demonstrate a multimodality microscopy, FOSSM, with the aid of a dielectric metasurface to achieve single-shot QPGI using multiple retardance images. The metasurface separates the object image into two replicas of opposite circular polarization states with varying retardations tuned by the displacement of the metasurface or rotation of the analyzer. FOSSM provides a user-friendly, cost-effective solution for ultra-fast real-time quantitative phase imaging which may lead to various applications in the fields of biological and biomedical research.