Abstract
In this work we introduce a novel medical image style transfer method, StyleMapper, that can transfer medical scans to an unseen style with access to limited training data. This is made possible by training our model on unlimited possibilities of simulated random medical imaging styles on the training set, making our work more computationally efficient when compared with other style transfer methods. Moreover, our method enables arbitrary style transfer: transferring images to styles unseen in training. This is useful for medical imaging, where images are acquired using different protocols and different scanner models, resulting in a variety of styles that data may need to be transferred between. Our model disentangles image content from style and can modify an image’s style by simply replacing the style encoding with one extracted from a single image of the target style, with no additional optimization required. This also allows the model to distinguish between different styles of images, including among those that were unseen in training. We propose a formal description of the proposed model. Experimental results on breast magnetic resonance images indicate the effectiveness of our method for style transfer. Our style transfer method allows for the alignment of medical images taken with different scanners into a single unified style dataset, allowing for the training of other downstream tasks on such a dataset for tasks such as classification, object detection and others.
Supplementary Information
The online version contains supplementary material available at 10.1007/s10278-022-00755-z.
Keywords: Style transfer, Breast MRI, Deep learning, Machine learning, Computer vision
Introduction
The same object can be depicted in an image in different styles. For example, a building can be shown in a photograph, a painting by a specific artist, or a sketch. Within the field of medical imaging, different styles manifest as data obtained by different scanner models and/or manufacturers. Deep learning, a subfield of artificial intelligence based on artificial neural networks, has demonstrated an exceptional ability of solving image analysis problems. However, such a difference in style can be detrimental to these methods because it violates their common assumption that training and testing data possess the same style [1]. Style transfer methods, such as the one introduced in this paper, were proposed to address this problem in deep learning.
Style transfer is a methodology that aims to preserve the consistency of the content of an image while changing the visual “style”. Building upon this, Arbitrary style transfer aims to transfer images to new styles unseen in training, during which the content of the image can be transferred to the new style with minimal or zero additional model optimization. Preserving content is crucial in the medical imaging field because it is very important to ensure that underlying anatomical structure is preserved throughout the transformation process, and changing it could negatively impact the accuracy of diagnosis.
This task of unseen style transfer is important to develop for use within the medical setting. As an example: consider the case of one hospital, Hospital A, having MRI data of one style, Style A (e.g., GE scanner). Now, Hospital A receives certain data from another Hospital, Hospital B, of unknown or unseen style, Style B (e.g., Siemens scanner). If Hospital A wishes to use a model trained at Hospital B on images of Style B, but on their own Style A data, even if Hospital B only provides one or two images of Style B to Hospital A, our model could be used to extract the style code of Style B, and transfer all of Hospital A’s Style A data to Style B, allowing Hospital A to use Hospital B’s model on its own data. The “One-Shot Style Transfer II: MRI Scanner Styles’’ section involves an experiment that explores this exact scenario, where our model, StyleMapper, is used to transfer images of one MRI style to another MRI style unseen in training.
At a high level, our method learns to extract informative disentangled numerical representations of style and anatomical content of images. These representations, or style and content codes, are obtained by inputting an image to a trained style encoder and content encoder. A pair of style and content codes, possibly from different images, can then be combined via a decoder to synthesize a new image that contains the encoded content, but in the style described by the style code; both the encoders and the decoder are neural networks.
We introduce our model beginning with the “The Modified Baseline Model’’ section, which introduces our method of training our model to extract style and content codes from both raw image data and images transferred to simulated styles. The simulated style images are created by applying randomly sampled image transformation functions to raw images; these transformations are well-representative of the range of many styles/scanner types seen within medical imaging. In this way, the style transfer model sees a different style at each iteration of training. Because the image transformation functions have continuously random parameters, the model can observe practically unlimited distinct styles during training, giving the style encoder more styles to learn from. This characteristic allows the model to be trained on fewer datapoints, as a single datapoint can be “reused” with a different style at each occurrence of that datapoint in training.
We proceed in the “Central Model: StyleMapper’’ section to introduce further key components of StyleMapper, including (1) the image style/content encoders and decoder, (2) the use of both raw and transformed images at each iteration of training to further encourage consistent style/content encoding and decoding operations, (3) image and style/content code reconstruction terms, and (4) a novel cross-domain reconstruction triplet loss term that is used to encourage further generalization ability of the encoders and decoders for style transfer. We note that this method of generating unlimited possible style images in training could be adapted to train many other applicable style transfer methods within the medical imaging domain.
In the “Results’’ section we explore experiments run with StyleMapper on the tasks of transferring test data to new target styles both simulated (“One-Shot Style Transfer I: Simulated Styles’’) and real (“One-Shot Style Transfer II: MRI Scanner Styles’’), all while being trained on just 528 datapoints. We then discuss the limitations of this work in the “Discussion’’ section, and conclude with the “Conclusions’’ section.
The contribution of this paper can be summarized as follows.
We introduce a new method for training arbitrary style transfer models with limited data within the medical imaging domain.
We propose a new disentangled representation learning style transfer model that uses this method, included a novel loss component.
We demonstrate arbitrary style transfer and style discrimination on breast MRIs with our method, with both real and simulated medical imaging styles.
Related Works
Style Transfer in Natural Images
Style transfer research in deep learning has often focused on transferring natural images to artistic styles. The seminal work of [2] surmounted the goal of arbitrary style transfer by leveraging the feature-extracting behavior that is intrinsic to convolutional neural networks [3]. In that work, the transfer between styles for a test image was performed by aligning the style information of the image with the information of the target style image. Later works expanded upon this idea with improvements such as greatly increased transfer speed [4], the accounting for cross-channel correlations within image feature maps [5], a closed form solution to the task [6], improved and more diverse stylization [7], and generally more robust stylization and content preservation [8, 9].
However, these models are trained on tens of thousands of content (and in some cases, style) examples, via content and style datasets such as MS-COCO [10] and WikiArt [11], respectively. This is not a problem within the aforementioned models’ original context of artistic style transfer, but if we wish to switch to the medical domain, obtaining similar quantities of usable, standardized training data can be very difficult in practice. As such, we wish to develop an arbitrary style transfer method to be used within the medical imaging domain that can be trained on the lower end of typical sizes of many medical imaging datasets: only a few hundred images.
Style Transfer in Medical Images
While a large portion of style transfer research focuses on artistic style transfer, there is still a rich literature of style transfer methods specialized for the domain of medical imaging. Following the many-to-many mapping approach of [12], works such as [13, 14] explore the adaptation of unpaired images across medical modality domains (CT and MR scans), also trained to utilize a shared content space with invertible mappings between image, style and content spaces. However, a key limitation of such methods is that they require observing the target test style in training and/or explicitly modifying the model architecture whenever an additional style is desired to be learned from and generalized to, something that StyleMapper does not require.
Other models have been built to automatically standardize different MRI image types (e.g., created by different manufacturers) without explicitly providing knowledge of the underlying scanner technology that was used to generate the image, such as [15], which used piecewise linear mapping to normalize intensities across different anatomical regions. The study in [16] approaches the task of translating between different MRI modalities using Conditional GANs ([17]) and paired data. Unlike our approach and the other aforementioned disentangled representation learning approaches, this method does not rely on the consistency of translating across image, content and style domains; instead it directly maps from one image space to another. Whereas our method forms separate estimates of style and content of test images, e.g., allowing for the interchange of styles for a fixed-content image, such style/content disentangling ability is not present in these works.
The work of [18] uses CycleGANs ([19]) to learn normalization between breast MRIs of two different manufacturers, along with the addition of a mutual information loss term and a modified discriminator to ensure the consistency of intensity, noise and anatomical structure. As compared to traditional CycleGAN applications, the modifications of this method allow for training upon unpaired data, a philosophy that we follow due to the fact that cross-domain paired (medical) data is generally more scarce than unsorted data. However, this method is different from ours in that it cannot transfer to new styles unseen in training.
Similar to our goal of transferring images to a single fixed style is the work of [1], which focuses on style transfer within the domain of 3D cardiovascular MRIs. Style transfer is performed in this work using hierarchical clustering methods to best map test images to the domain of training images, given the results of extracting features from various inner layers of a VGG-16 network. In this work, a test image is mapped to the most similar image out of the utilized training set using the Wasserstein distance, with style mapped according to a “style library” learned during training. A limitation of this is that rather than learning a fixed set/library of styles from the training set, we attempt to generalize our style encoder to be more flexible, and work on images of unseen target styles that may only be vaguely similar to those seen in training.
Materials and Methods
Dataset
For this work, we experimented with 628 breast MR (Magnetic Resonance) images taken from 628 different breast cancer patients with a GE Healthcare MRI machine, obtained from the Breast Cancer DCE-MRI dataset of [20]. All scans had field strengths of 1.5 Tesla or 3 Tesla, with manufacturer models of MR450w, SIGNA EXCITE, SIGNA HDx, and SIGNA HDxt. All images have a resolution, and were preprocessed by assigning the top 1% of pixel values in the entire dataset to a value of 255, followed by linearly scaling the remaining pixel intensities to the 0–255 range, giving the data the same “raw” style. 528 datapoints were used to produce the training set, 50 were kept as a test set, and the other 50 were used for validation. 25 similarly preprocessed images from a Siemens scanner were also used in the “One-Shot Style Transfer II: MRI Scanner Styles’’ section. We describe the details of creating our specific dataset in Appendix A.
Methods
In this section we will introduce a modified domain adaptation model [13] and its evolution to our proposed model, StyleMapper. In summary, a model that learns to disentangle the style of an image from its content is known as a disentangled representation learning (DRL) model [12]. We introduce an improved DRL model for domain adaptation that is trained on infinite possible randomized styles, with domain-independent style/content encoders and decoder that include a novel cross-domain training loss term, all towards a model that is designed to generalize to completely new styles at test time.
The Modified Baseline Model
We begin with an unsupervised Domain Adaptation, Disentangled Representation learning (DADR) model that can map between two different image domains by disentangling style and content representations within both of the domains [12, 13]. We label this model as the baseline model. In particular, given images and from different domains and , respectively, the model can learn the representation of an image within a style space and a content space (), described respectively via a style code and a content code . The authors of [12] define the content as the “underling spatial structure” of the image, and style as “the rendering of the structure”. As such, the content is assumed to be invariant to the imaging domain/scanner, while the style code describes domain-specific visual characteristics.
Diverse Styles via Image Transformation Functions
The baseline model performs well with style transfer to a set of discrete styles seen in training, but we wish to extend the work to transfer from an image of some style to an arbitrary target style that is unseen in training. This is beneficial in the medical imaging field because many styles exist that may be desired to be transferred to, some of which have limited available data. As such, we propose to train the model on both raw images and style-transferred versions of the same images, with these styles simulated via random image transformation functions that act on the raw images. In this way, the model learns to both distinguish between and extract different styles while keeping content unchanged. This not only allows for the model to adapt to a wider range of possible styles, but also allows the model to learn from fewer datapoints, because a single datapoint can be seen with a variety of distinct styles at different training iterations.
In order to generate diverse styles for our model to learn, we use seven classes of some of the most common image intensity transformations [21]: (1) the linear transformation, (2) the negative transformation, (3) the log transformation, (4) the power-law (gamma) transformation, (5) the piecewise linear transformation, and (6, 7) the Sobel X and Y operators. At each training step, one of the seven transformations is randomly selected to change a raw image to a new style. Although not very representative of the many possible artistic styles of traditional style transfer works, we believe that the simulated styles described by the application of these random transformations, which manifest as generally nonlinear changes in pixel intensities, are a good proxy for many possible styles seen in medical imaging, which do not vary nearly as drastically as artistic styles do. We provide example images of each class of transformation in Fig. 1.
Fig. 1.
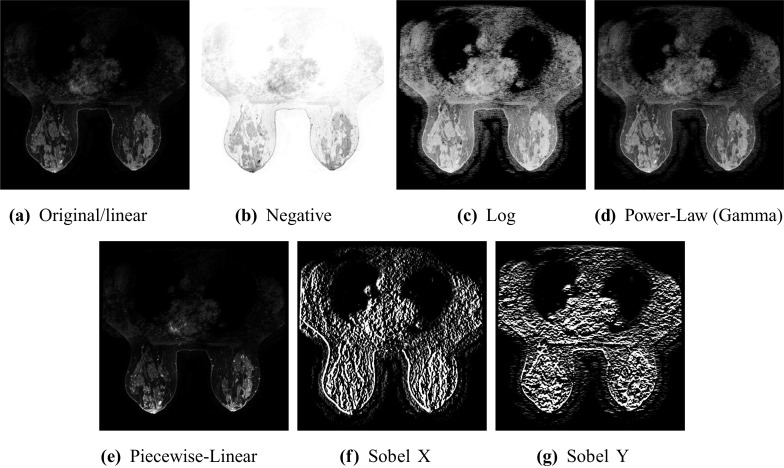
A comparison of the effects of the seven different image transformation functions that we use (“Diverse Styles via Image Transformation Functions’’ on a DCE-MRI breast scan, with randomized transfer function parameters fixed to the means of their sampling distributions
The first five of these transformations are parametrically randomized: when selected, the transformation function randomly selects its parameters from some pre-determined distribution. This allows the exact transfer function to be previously unseen at each training iteration. The two-step randomized transformation function selection allows the model to extract codes corresponding to a practically unlimited range of distinct styles during training and to boost the style encoder’s generalization ability and robustness at test time.
We provide the explicit formulae and probabilistic schema for generating the parameters of these transformation functions, as well as visual examples of them, in Appendix B. We also take this simulated style approach for our experiments so that a “ground truth” deterministic transferred image can be directly compared to the neural style transfer result.
It is important to consider that the first five transformation functions are all invertible, meaning that given an output pixel value , we can deterministically map back to its corresponding input pixel value , implying that no information is lost through these transformations. The Sobel X and Y operators, however, could introduce information loss because of the additive nature of the convolution operation. In practice, because of the high resolution of the images, we assume that such an operation will only slightly affect the overall global content of the images, and thus decide to include the Sobel operators in the pool of possible transformations. Experiments of training without the Sobel operators further confirmed this statement. We do not “randomize” the Sobel transformations during training due to the more severe nature of these transformations as compared to the first five.
Modified Baseline Model Architecture
A precursor of our final model, the modified baseline model consists of two main components: (1) content and style encoders for obtaining content and style representations, or codes, of images and (2) generators/decoders for mapping content-style code pairs back to the space of images. In this model two encoderdecoderencoder pipelines run in parallel: one for a raw image, and the other for the transformed version of the same image, where the image transformation is randomly chosen from one of the seven transformations described in the “Diverse Styles via Image Transformation Functions’’ section.
The model is trained with objectives that enforce reconstruction where applicable both in-domain and cross-domain, as well as adversarial objectives that ensure the translated images to be indistinguishable from real images in the target domain.
Central Model: StyleMapper
Using the modified baseline model of the previous section as a starting point, we created a custom style transfer model which we name StyleMapper (Fig. 2). We will next outline (1) the novel components of StyleMapper and (2) the main differences between StyleMapper and the modified baseline model, both in the architecture and in the training procedure/loss function.
Fig. 2.
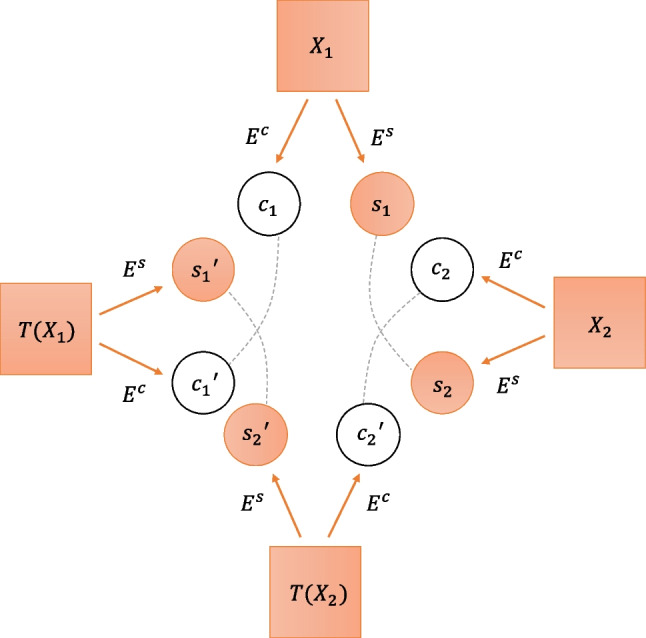
StyleMapper: Our novel architecture used for style transfer. Solid arrows indicate encoding operations, and dashed lines indicate pairs of codes that should be optimally equivalent (Eq. (3)), with the model trained to achieve as such. The decoder/generator G is not pictured, as it receives input of various combinations of all of the pictured style and content codes
General Features
Multiple Data Pairs per Training Step
As opposed to the modified baseline model, StyleMapper uses two raw images per training iteration: a pair of distinct raw data , and the results of applying the same random image transformation T to that pair, ; T is resampled for each pair at each training step. This implies that and should have the same style but different content, and should have the same content but different style for , and and should have the same style yet different content. As will be shown shortly, consistency of both content and style encoding can then be enforced through reconstruction constraints of different pairings of these four images that should have the same content or style, respectively, further encouraging the encoders and decoder to work across diverse domains.
Unifying the Encoders and Decoders
In the modified baseline model, separate content and style encoder/decoder groups are trained corresponding to each of the input images and their corresponding transformed versions. We must consider the possibility of there being inconsistencies between the members of each of these pairs of networks; to account for this, we switch to using single encoders for content and for style and a single decoder/generator G, allowing for the potential of a boost in style transfer generalizability, and a simpler model.
Most Representative Style Code
Upon inference, we introduce a fixed most representative style code s instead of a target style code (as in [13]) to map input images to the target style is defined as the style code that is closest on average to all of the style codes of that test set. Specifically, for each of the N images in the target style test set, record the style code obtained from the trained model’s style encoder. If , we then compute the most representative style code as
| 1 |
and is the mean absolute error function. In the case of , is simply the style code obtained from the single target style image. This task is labeled as few-shot style transfer. In the “One-Shot Style Transfer I: Simulated Styles’’ section, we show that is sufficient for successful style transfer, meaning that our method is compatible to one-shot learning.
Training Loss Terms
Image Reconstruction Loss
The model should be able to reconstruct an image sampled from the data distribution after encoding and decoding. To achieve this, the style and content encoders and decoder G are trained to minimize the mean absolute error/ distance between reconstructed images and original images, via the image reconstruction loss from [13] of
| 2 |
where is the distribution of data. Further image reconstruction loss terms , and for , and are then respectively defined the same.
We note that when building StyleMapper from the baseline model, we removed the discriminator because the generator can solely be trained by the image reconstruction loss, and we do not need the discriminator for any classification role. As such, the adversarial loss term of the modified baseline model ([13]) is not present for StyleMapper.
Latent Reconstruction Loss
We wish to encourage translation and reconstruction across diverse domains of style and content. One characteristic of StyleMapper that is different from the modified baseline model is that the (encodedecodeencode) progression found in the modified baseline model used for latent space reconstruction is reduced to (encodedecode), such that we no longer train for latent space consistency in this manner.
Instead, we enforce these latent embedding consistency requirements with style and content reconstruction loss terms, adapted from [13], that are defined respectively as
| 3 |
with . These constraints can be seen via the dashed lines in Fig. 2.
Cross-Domain Reconstruction Triplet Loss
We include a cross-domain reconstruction triplet loss term, to encourage content and/or style reconstruction given twelve certain combinations of the images and , as
| 4 |
where is the set of twelve triplets constructed from by the condition
| 5 |
(note that and don’t necessarily have to be different images). Given the set of four images , each one of these twelve reconstruction constraints corresponds to encouraging the decoder to create an image from a particular pair of style and content codes extracted from this set, such that the generated images match another image from the set that has the same content and style. This loss term is important for training the encoders and decoder to have flexible and generalizable performance across domains, and is written explicitly in Appendix C.
We now come to the full loss function that is minimized to train StyleMapper,
| 6 |
where , , , and are loss weight hyperparameters. We will now proceed to implementational and training details in the next section, followed by our experimental results in the “Results’’ section.
Implementational Details
Network Architecture
We build off of the MUNIT model of [12]. Content encoders consist of several strided convolutional layers to downsample the input, and several residual blocks to further process it. All convolutional layers are followed by Instance Normalization (IN) modules [22]. Style encoders include several strided convolutional layers, followed by a global average pooling layer and a fully connected (FC) layer. We do not use IN layers in the style encoder, since IN removes the original feature mean and variance that represent important style information. We provide the architecture in full layer-by-layer detail in Appendix E.
Network Training
We use the Adam optimizer [23] to train StyleMapper by minimizing the loss (Eq. (6)), with weight decay strength of 0.0001, and . Kaiming’s Method [24] was used to initialize model weights, and we trained with a learning rate of 0.0001. We used a batch size of 1 (due to memory limitations), training until no further minimization of the loss term(s) was observed (a minimum of about 10,000 iterations was needed in essentially all cases).
For the loss weights, we used values of , and . Additional hyperparameters from MUNIT are unchanged from their settings in that work. We train our models until we observe loss convergence, assisted by validation via the MAE residuals between style-transferred image results through learning style mapping (our model) and transferred image results through direct image transformations (the “ground truth” to compare to). All computations are performed with an NVIDIA QUADRO M6000 24GB GPU.
Results
One-Shot Style Transfer I: Simulated Styles
The core goal of our StyleMapper model is to be able to (1) learn a new style from an image and (2) transfer another new image to that style, while preserving the anatomical content of the image. To test this, we train StyleMapper following Eq. (6) on all image transformation functions/styles in the “Diverse Styles via Image Transformation Functions’’ section, but excluding a particular class of transformation T from the pool of possible transformations, to be used as a target style.
After training, we apply T, but with parameters fixed, to the first 25 of the test set to obtain , and then extract the content and style codes of each of these using the style encoder to obtain codes . We fix the parameters of the target style T so that the style is exactly the same for all target style images, to simulate them being collected with the same scanner. Finally, we obtain the most representative style code for the target style by applying Eq. (1) to some of these 25 style codes, to judge how many target style images the model needs to observe to compute a useful target style code. In the “Transferring to Multiple Unseen Styles with One Model’’ section, we evaluate our model’s ability to handle the more difficult case of transferring to multiple styles T not seen in training.
We evaluate the ability of the style encoder to extract the correct style code from the target style test images by taking the remaining 25 of the test set , transferring these images to the target style via to obtain , and comparing these to the “ground truth” of transformed images . In particular, the content encoder extracts content codes from the images , and the generator/decoder G takes each of these content codes with the target style code to synthesize the transferred images .
We do this comparison using the MAE between and . We also note that for better performance comparison between styles, for a given style we normalize all MAEs across the different values by dividing each MAE by .
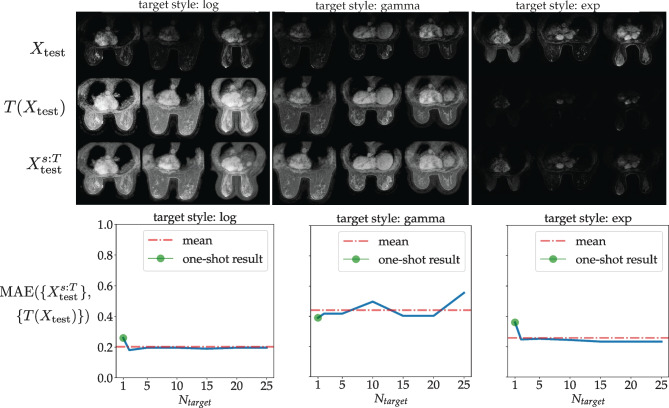
We will explore examples of this by transferring to (1) a target style that is fairly similar to those seen in training—the log transformation for a model trained on all transformations but log, and the same but for the gamma/power-law transformation—and (2) a target style that is distinct from the styles/transformation seen in training (the exponential function ). We test these on a range of to see if the most representative target style computation is dependent on the quantity of target style data seen by the style encoder.
To begin we examine a log target style, which we define via the logarithmic intensity transfer function with parameter fixed to its average value (Equation (B3) in Appendix B). Next, we perform the same experiments with a power-law target style, via the power-law transfer function with exponential parameter fixed to (Equation (B4) in Appendix B). Finally, we test a target style described by the exponential transfer function equation with , on a style encoder trained on all of the parametrically random styles of the “Diverse Styles via Image Transformation Functions’’ section. In this case, we have a style with a transfer function curve that is not as similar to any of the possible randomized transfer curves seen by the style encoder during training as in the first two examples, where the target log and power-law transformations had the possibility of being similar to certain settings of the randomized power-law and log transformations seen in training, respectively.
The qualitative and quantitative results of these experiments are shown in Fig. 3. We see that style transfer performance described by the MAE between and is mostly independent to , implying that only a single target style image is needed by the style encoder to perform style transfer. In particular, for this one-shot case, we have MAEs for the log, gamma and exp styles of 0.2595, 0.3902 and 0.3601, respectively. As explored in Appendix D, indeed the style codes extracted from different images of one same style are almost identical, implying that the most representative style code obtained from aggregating of these individual codes will be almost the same as any one of them.
Fig. 3.
One-shot style transfer with various target styles: Results. See the One-Shot Style Transfer I: Simulated Styles’’ section. Each column corresponds to a different trained model. Top row: Transferring a set of 25 MR test images (top row) to different target styles not seen in training (bottom row), with target style code obtained from a single test image of the target style. The transferred images are compared to the “ground truth” (middle row) of the images directly transformed by the target style’s corresponding transformation function T. From left to right, the target styles/transformations are the fixed log, gamma/power-law and exp transformations, as described in the “One-Shot Style Transfer I: Simulated Styles’’ section, and for each style, three random images are visualized. Bottom row: Mean absolute error (MAE) between style-transferred images and “ground truth” transformed images , indicating performance of style transfer, with respect to number of target style images used to compute the most representative target style code that is used to perform style transfer. The one-shot case of (visualized in the top row) is outlined by the green circles, which correspond to normalized MAEs between transformed (“ground truth”) and style-transferred results of 0.2595, 0.3902 and 0.3601 for the styles of log, gamma and exponential, respectively
The behavior of the style encoder over a range of styles, as well as the structure of the style codes themselves, are worth exploring. Although beyond the scope of the main body of this work, we explore both how extracted style codes differ between (1) different styles and (2) different images of the same style in Appendix D.
Transferring to Multiple Unseen Styles with One Model
Here, we perform similar experiments to the previous section, except for the more difficult case of having to transfer to multiple styles T that were unseen in training. We evaluate two scenarios where StyleMapper is trained on five (randomized) styles, and tested on three other unseen styles, which we outline in Table 1. Analogous to Fig. 3, we present qualitative and quantitative one-shot style transfer results for the two scenarios in Figs. 4 and 5.
Table 1.
Scenarios tested for transferring to multiple unseen styles with one model
| Scenario | Styles/transformations seen in training | New styles tested on (T) |
|---|---|---|
| 1 | log, gamma, piecewise linear, Sobel X and Y | negative, linear, exponential |
| 2 | linear, negative, piecewise linear, Sobel X and Y | log, gamma, exponential |
Fig. 4.
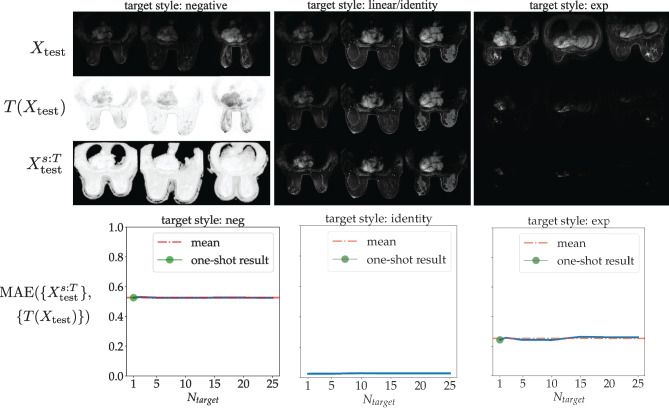
One-shot style transfer with multiple unseen target styles: Scenario 1. Similar to Fig. 3, but all for one model that did not see these styles during training. Corresponds to Scenario 1 of Table 1. The one-shot case of (visualized in the top row) is outlined by the green circles in the bottom row, which correspond to normalized MAEs between transformed (“ground truth”) and style-transferred results of 0.5256, 0.0 and 0.2426 for the styles of negative, identity and exponential, respectively. Note that the identity transformation “style” does not change an image, and serves as a proof of consistency for StyleMapper, showing that it leaves an image unchanged when it should (MAE of zero)
Fig. 5.
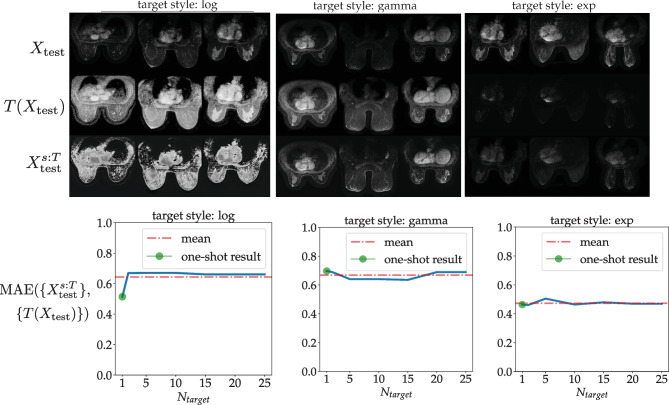
One-shot style transfer with multiple unseen target styles: Scenario 2. Similar to Fig. 3, but all for one model that did not see these styles during training. Corresponds to Scenario 2 of Table 1. The one-shot case of (visualized in the top row) is outlined by the green circles in the bottom row, which correspond to normalized MAEs between transformed (“ground truth”) and style-transferred results of 0.5140, 0.6969 and 0.4640 for the styles of log, gamma and exponential, respectively
As shown in these figures, StyleMapper was still able to perform one-shot style transfer of images to new target styles to a decent level of matching the visual characteristics of the target style. However, as evidenced by the increase in MAEs as compared to the experiments of the “One-Shot Style Transfer I: Simulated Styles’’ section (see the captions of Figs. 4 and 5), the model had more difficulty extrapolating to new styles. This is reasonable, as the model had a more limited number of classes of styles seen in training, so the required extrapolation to a new style from those seen in training is likely to be more drastic. For the (somewhat unrealistic) case of the negative target style (left column of Fig. 4), the model was still able to somewhat learn the large intensity shifts required to extrapolate to this style, despite the style being drastically different from any seen in training. Finally, we note that we test the identity transformation (no style change) as a target style (Fig. 4, middle column), as a proof of consistency that our model will not change an image’s style when no modification is required.
One-Shot Style Transfer II: MRI Scanner Styles
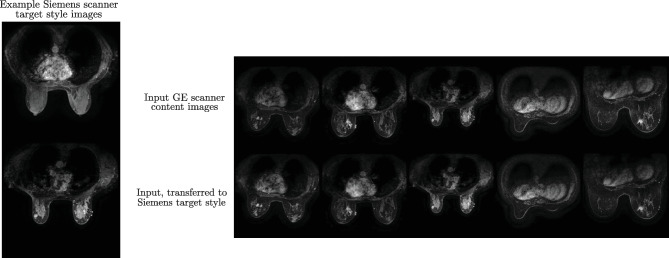
We will now explore the ability of StyleMapper to transfer images to a new medical scanner style that is unseen in training, that of Siemens MR scanners, as only GE scanner data was used to train the model.
We performed one-shot style transfer on the same set of 25 raw GE scanner images as in the previous section, with a StyleMapper trained on all of the randomized styles (“Diverse Styles via Image Transformation Functions’’), and a single Siemens scan image used to obtain the target style. Example results of this are shown in Fig. 6. Given that there is no “ground truth” to compare the transferred results to as in the previous section of simulated target styles, we believe these results to be strong given the fact that certain stylistic characteristics of Siemens scans as compared to GE scans—such as Siemens on average appearing to be slightly brighter than GE—appear in the transferred results.
Fig. 6.
MRI Style Transfer to Unseen Scanner Style. Results (right block, bottom row) of transferring GE scanner MR Images (right block, top row) to the Siemens scanner style unseen in training (left column). Note that certain regions of the GE input images will grow or dim in intensity to match the style extracted from Siemens images. Starting from the left in the right block, the first three GE input images have MRI field strengths of 3 Tesla, while the last two are 1.5 Tesla
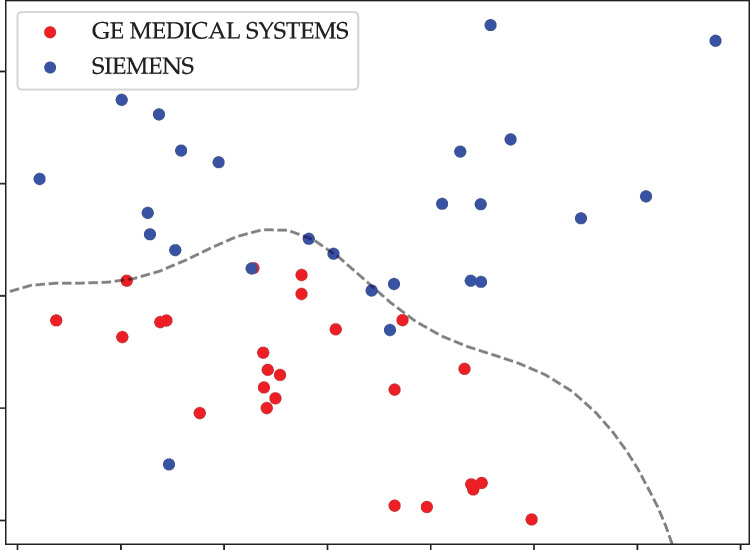
We can also use the same StyleMapper to distinguish between these two styles of GE and Siemens. To do this, we use the style encoder of StyleMapper to extract style codes from 25 GE and 25 Siemens images (all with different content). Next, we performed dimensionality reduction on these 8-dimensional style code vectors via principal component analysis (PCA) to map them to , and trained a support vector classifier (SVC) with a radial basis function kernel to discriminate between the two classes of points [25]. As shown in Fig. 7, the style encoder is able to usually discriminate successfully between the two styles via the differences in their encodings, with an SVC accuracy of .
Fig. 7.
Discriminating a realistic unseen style. Using a StyleMapper style encoder we extracted style codes of a set of unpaired MR scans of two different manufacturers, GE and Siemens, with the latter style previously unseen by the model. Pictured are these style codes embedded into , and the decision boundary learned by training a support vector classifier (SVC) on them. Classification accuracy: 88.0%. The figure recommended to be viewed in color
Ablation Study: Finite Set of Training Styles
In order to show the necessity of using parametrically randomized transformations as training styles, rather than the fixed transformations tested in Appendix D—we will attempt one of the same few-shot style transfer experiments of the “One-Shot Style Transfer I: Simulated Styles’’ section, but with a style encoder trained only on these fixed transformations. In other words, the former configuration allows for the style encoder to see a continuous range of styles in training—technically a new particular style at every iteration (excluding the Sobel transformations)—while the latter only gives the style encoder a discrete, finite set of possible styles to learn to extract style codes from, a problem that is exacerbated when only limited training data is present.
We will repeat the experiment with the same fixed-parameter log target style as in the “One-Shot Style Transfer I: Simulated Styles’’ section, but with a model trained on fixed versions of all of the other six transformations, with parameters fixed to their average values (Appendix D), except for the power-law function which is fixed the same as in the target power-law style experiment of the “One-Shot Style Transfer I: Simulated Styles’’ section. The failure of using this finite set of transformations is seen when comparing the one-shot transfer and MAE between the transformed “ground truth” and the transferred result, of 0.2778, to be compared to 0.1178 for the non-ablated case (“One-Shot Style Transfer I: Simulated Styles’’).
Just as in the compared experiment, we found the MAE here to not be improved by increasing , the number of target style images used by the style encoder to estimate the target style code used to perform transfer. We note that we observed significantly more noise on MAE values about the one-shot transfer MAE with respect to than in the other experiment, indicating that the style encoder was not nearly as consistent as for the case of it being trained on parametrically random transformations, extracting erroneous, but different codes from the target style images.
Discussion
One limitation of our work is that in order to successfully estimate the correct target style code, test target styles usually need to be at least somewhat similar to the styles seen in training; not identical, but also not completely orthogonal. Target styles that are very distant from those seen in training, that require the model to perform large amounts of extrapolation, not just interpolation, give more trouble.
We focused on training the model on simulated styles described by intensity transfer functions (besides the non-invertible Sobel X and Y transformations), in order to focus on content-preserving medical imaging styles and to facilitate training on a small dataset. Because of the content-preserving nature of these styles/transformation functions, they could potentially be useful in a training data augmentation pipeline for traditional supervised learning on medical images, to combat overfitting on a small training set. This could also be applicable to semi-supervised contrastive learning (e.g., in [26]), where it is important that augmentations used to obtain differing “views” of the same image do not change the underlying content of the image. This is because augmentations used for traditional natural image-targeted computer vision, such as blurring or rotation, may inadvertedly affect the content of medical images.
Additionally, an important future endeavor will be to explore how to train and test the model on non-medical images of more diverse styles, to see how well it can generalize to these situations, while potentially maintaining the requirement for only limited data.
Conclusions
In this work we introduced a novel medical image style transfer method, StyleMapper, that can transfer images to a new target style unseen in training while observing only a single image of this style at test time, and can be successfully trained on limited amounts of single-style data. We explored the applications of StyleMapper to both style transfer and the classification of unseen styles.
Supplementary Information
Below is the link to the electronic supplementary material.
Author Contribution
S.C. created the original idea for the project, implemented it in code, ran initial experiments, and began the paper. N.C.K. wrote the final paper, introduced additions to the model/code, and ran final experiments presented herein. J.S.D. provided essential advice for both the direction of the project and the necessary experiments to run, as well as suggesting edits to the paper. M.A.M. oversaw the project from start to finish and provided original inspiration and guidance.
Availability of Data and Materials
All data is publicly available for download; see Appendix A for details.
Code Availability
Code will be made publicly available upon publication.
Declarations
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Shixing Cao, Email: shixing.cao@duke.edu.
Nicholas Konz, Email: nicholas.konz@duke.edu.
James Duncan, Email: james.duncan@yale.edu.
Maciej A. Mazurowski, Email: maciej.mazurowski@duke.edu
References
- 1.Ma, C., Ji, Z., Gao, M.: Neural style transfer improves 3d cardiovascular mr image segmentation on inconsistent data. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 128–136 (2019). Springer
- 2.Gatys, L.A., Ecker, A.S., Bethge, M.: Image style transfer using convolutional neural networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2414–2423 (2016)
- 3.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems. 2012;25:1097–1105. [Google Scholar]
- 4.Huang, X., Belongie, S.: Arbitrary style transfer in real-time with adaptive instance normalization. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 1501–1510 (2017)
- 5.Li, Y., Fang, C., Yang, J., Wang, Z., Lu, X., Yang, M.-H.: Universal style transfer via feature transforms. arXiv preprint arXiv:1705.08086 (2017)
- 6.Lu, M., Zhao, H., Yao, A., Chen, Y., Xu, F., Zhang, L.: A closed-form solution to universal style transfer. In: Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 5952–5961 (2019)
- 7.Sheng, L., Lin, Z., Shao, J., Wang, X.: Avatar-net: Multi-scale zero-shot style transfer by feature decoration. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 8242–8250 (2018)
- 8.Deng, Y., Tang, F., Dong, W., Sun, W., Huang, F., Xu, C.: Arbitrary style transfer via multi-adaptation network. In: Proceedings of the 28th ACM International Conference on Multimedia, pp. 2719–2727 (2020)
- 9.Yao, Y., Ren, J., Xie, X., Liu, W., Liu, Y.-J., Wang, J.: Attention-aware multi-stroke style transfer. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 1467–1475 (2019)
- 10.Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P., Ramanan, D., Dollár, P., Zitnick, C.L.: Microsoft coco: Common objects in context. In: European Conference on Computer Vision, pp. 740–755 (2014). Springer
- 11.Nichol, K.: Painter by numbers, wikiart (2016)
- 12.Huang, X., Liu, M.-Y., Belongie, S., Kautz, J.: Multimodal unsupervised image-to-image translation. In: Proceedings of the European Conference on Computer Vision (ECCV), pp. 172–189 (2018)
- 13.Yang, J., Dvornek, N.C., Zhang, F., Chapiro, J., Lin, M., Duncan, J.S.: Unsupervised domain adaptation via disentangled representations: Application to cross-modality liver segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 255–263 (2019). Springer [DOI] [PMC free article] [PubMed]
- 14.Yang, J., Li, X., Pak, D., Dvornek, N.C., Chapiro, J., Lin, M., Duncan, J.S.: Cross-modality segmentation by self-supervised semantic alignment in disentangled content space. In: Domain Adaptation and Representation Transfer, and Distributed and Collaborative Learning, pp. 52–61. Springer, ??? (2020)
- 15.Zhang, J., Saha, A., Soher, B.J., Mazurowski, M.A.: Automatic deep learning-based normalization of breast dynamic contrast-enhanced magnetic resonance images. arXiv preprint arXiv:1807.02152 (2018)
- 16.Yang Q, Li N, Zhao Z, Fan X, Eric I, Chang C, Xu Y. Mri cross-modality image-to-image translation. Scientific reports. 2020;10(1):1–18. doi: 10.1038/s41598-020-60520-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mirza, M., Osindero, S.: Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014)
- 18.Modanwal, G., Vellal, A., Mazurowski, M.A.: Normalization of breast mris using cycle-consistent generative adversarial networks. arXiv preprint arXiv:1912.08061 (2019) [DOI] [PubMed]
- 19.Zhu, J.-Y., Park, T., Isola, P., Efros, A.A.: Unpaired image-to-image translation using cycle-consistent adversarial networks. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 2223–2232 (2017)
- 20.Saha A, Harowicz MR, Grimm LJ, Kim CE, Ghate SV, Walsh R, Mazurowski MA. A machine learning approach to radiogenomics of breast cancer: a study of 922 subjects and 529 dce-mri features. British journal of cancer. 2018;119(4):508–516. doi: 10.1038/s41416-018-0185-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zakhor, A.: Lecture 2. intensity transformation and spatial filtering. In: EE225B: Digital Image Processing (2014). University of California, Berkeley
- 22.Ulyanov, D., Vedaldi, A., Lempitsky, V.: Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022 (2016)
- 23.Kingma, D.P., Ba, J.: Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014)
- 24.He, K., Zhang, X., Ren, S., Sun, J.: Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 1026–1034 (2015)
- 25.Schölkopf B, Smola AJ, Williamson RC, Bartlett PL. New support vector algorithms. Neural computation. 2000;12(5):1207–1245. doi: 10.1162/089976600300015565. [DOI] [PubMed] [Google Scholar]
- 26.Chen, T., Kornblith, S., Norouzi, M., Hinton, G.: A simple framework for contrastive learning of visual representations. In: International Conference on Machine Learning, pp. 1597–1607 (2020). PMLR
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data is publicly available for download; see Appendix A for details.
Code will be made publicly available upon publication.