Significance
The question of how cooperation might evolve by natural selection, famously posed by Darwin, has since been answered many times over. Most explanations boil down to some form of population structure, either physical or social, so that cooperative partnerships arise more often than expected in a well-mixed community. Here, we report a qualitatively different mechanism that can favor cooperation, without any population structure whatsoever. The simple fact that reproduction or social contagion involves randomness can alone reverse the evolutionary outcome for cooperation and for many other social behaviors. This account of evolution shows that stochasticity during reproduction can be as strong a force as fitness, when interacting types compete in a population.
Keywords: cooperation, evolutionary game theory, demographic stochasticity, over-dispersion
Abstract
The concept of fitness is central to evolution, but it quantifies only the expected number of offspring an individual will produce. The actual number of offspring is also subject to demographic stochasticity—that is, randomness associated with birth and death processes. In nature, individuals who are more fecund tend to have greater variance in their offspring number. Here, we develop a model for the evolution of two types competing in a population of nonconstant size. The fitness of each type is determined by pairwise interactions in a prisoner’s dilemma game, and the variance in offspring number depends upon its mean. Although defectors are preferred by natural selection in classical population models, since they always have greater fitness than cooperators, we show that sufficiently large offspring variance can reverse the direction of evolution and favor cooperation. Large offspring variance produces qualitatively new dynamics for other types of social interactions, as well, which cannot arise in populations with a fixed size or with a Poisson offspring distribution.
The past decades have seen a proliferation of research using evolutionary theory to study social traits, in the fields of biology, animal behavior, and even social science (1–7). Most of this theoretical development has been based on mathematical models that assume either infinite populations (5, 6, 8–10) or finite populations of constant size (2–4). Despite these simplifying assumptions, mathematical models provide rich insights into how exogenous and intrinsic factors drive the evolutionary dynamics of social behavior. The literature contains a rich set of explanations for cooperation based on repeated interactions, the establishment of reputations, and various forms of population structure (3, 4, 7, 11–21). Several of these theoretical insights have been validated by controlled experiments on human subjects (22–29). This field of research has been so successful that the question of how cooperation can be favored by natural selection, famously posed by Darwin, is now not only resolved, but resolved in distinct ways applicable in different contexts.
But most mechanisms known to support cooperation boil down to some form of population structure, either physical or social, so that cooperative interactions occur more often than by random chance (30). Here, by contrast, we reveal a qualitatively different and pervasive mechanism that can promote cooperation by natural selection or social contagion—even in populations lacking any form of exogenous or endogenous structure. We focus on demographic stochasticity—namely, fluctuations in the abundances of types that arise from randomness in birth and death processes. We show that this realistic feature of natural populations can by itself promote social behaviors that would otherwise be suppressed in idealized populations of constant (or infinite) size.
There is precedent for the idea that demographic stochasticity alters evolutionary dynamics. Foundational work by Gillespie established that the variance in the number of offspring, not just the mean, influences the evolution of competing types (31, 32). More generally, demographic stochasticity alters the dynamics of competing types under frequency-independent selection (33–43) and also frequency-dependent selection (44–48) in populations of nonconstant size. For example, when a population of nonconstant size contains two types with the same expected number of offspring but different variances, one type is favored when the population size is small, and the other type is favored when the population size is near its carrying capacity (33–35). A few studies have shown that demographic stochasticity can even reverse the direction of natural selection, promoting a type that would otherwise be disfavored without demographic stochasticity (44–46).
Prior work on selection with demographic stochasticity has either assumed constant fitness (33–35, 42), in which one’s fitness is independent of the composition of the population, or assumed different carrying capacities for different phenotypes, e.g., producers enjoy a larger carrying capacity than nonproducers (44–46). In addition, prior studies of reproductive variance typically assume that offspring numbers follow a Poisson distribution (33–35, 44–47), so that the mean and variance in offspring number are identical. However, a Poisson-distributed offspring number is a special case, and empirical field studies have found that over-dispersion in offspring number (i.e., variance greater than mean) is commonplace across diverse taxa (49–52) and also for human social contagion (53–55). We will show that demographic stochasticity with over-dispersion produces qualitatively different outcomes than stochasticity with Poisson offspring numbers.
In this paper, we develop a general framework to study evolutionary dynamics with demographic stochasticity, which can capture both frequency-dependent fitness, arising from social interactions, as well as over-dispersion in the number of offspring, or imitators. We provide a simple analytical condition that governs the long-term outcome of competition between multiple types. Applied to pairwise social interactions involving cooperation or defection, we find that demographic stochasticity can favor cooperators provided the offspring variance is sufficiently large, even without any other mechanisms. For more general pairwise payoff structures, we show that demographic stochasticity can reverse the stability of equilibria, from coexistence to bistability and vice versa or from dominance of one type to dominance of another type. Our analysis highlights the profound effects of demographic stochasticity on the evolution of interacting types in a population.
Model
We first consider an evolving population of two types: cooperators (C) and defectors (D). Each individual interacts pairwise with each other, in which the cooperator pays a cost c to bring his opponent a benefit b (b > c), and the defector pays no cost and provides no benefit. In other words, pairwise interactions follow a simple “donation game”, which provides a minimal model for studying the evolution of cooperation (56). Following all pairwise interactions, each individual obtains an average payoff that will determine their reproductive output (or, equivalently, the number of individuals who copy their type by social contagion). In a population with x cooperators and y defectors, the cooperator’s payoff (denoted by πC) and the defector’s payoff (denoted by πD) are
| [1a] |
| [1b] |
In a classic Moran model, which is the most common description of haploid population dynamics, each birth event is followed by a death event, and so the population size remains constant. Here, we remove this constraint by decoupling the birth and death events. Births are assumed to follow a continuous-time Markov process with independent and stationary increments (SI Appendix, section 1), such that the expected number of offspring individual i produces per unit time is
| [2] |
where B is a baseline number of offspring, πi is the payoff for i′s, and the parameter s > 0 is the intensity of selection. Note that the baseline birth rate is the same for all individuals, regardless of type, and it does not depend upon payoffs from social interactions. The selection intensity s measures to what degree the payoff derived from social interactions affects the offspring number. Since the defector’s payoff πD is larger than the cooperator’s payoff πC in any population state, defectors always have a greater expected fecundity.
To fully describe the birth process, we also specify the variance in the number of offspring. We are particularly interested in cases of over-dispersion, which can be modeled in many alternative ways (50, 51), such as a quasi-Poisson model (variance proportional to mean), mixed-effects Poisson model, and negative binomial model (variance a quadratic function of mean). Here, we study a general class of Markov birth models by stipulating
| [3] |
where parameters δ1 and δ2 measure the magnitude of offspring variance Var(ξi) relative to the mean 𝔼(ξi). The parameter δ1 controls how offspring variance depends on the baseline birth rate; and δ2 controls how offspring variance depends on payoffs from social interactions. Specific choices of δ1 and δ2 produce various well-known classical models, such as a deterministic system with logistic total population size (δ1 = δ2 = 0) or a Poisson offspring distribution (δ1 = δ2 = 1). In the regime of weak selection, the number of offspring produced per unit time is overdispersed whenever δ1 > 1.
Deaths are modeled as a Poisson process, arising from two rates that are summed. First, an individual dies at constant baseline rate, D. Second, to model competition for limited resources, additional deaths occur at rate λ times the current total population size. Thus, for cooperators, the number of individuals who die within a unit of time follows a Poisson distribution with mean and variance equal to Dx + λx(x + y); and likewise for defectors with mean and variance Dy + λy(x + y). This formulation of a density-dependent death process constrains the total population size to remain finite (Fig. 1).
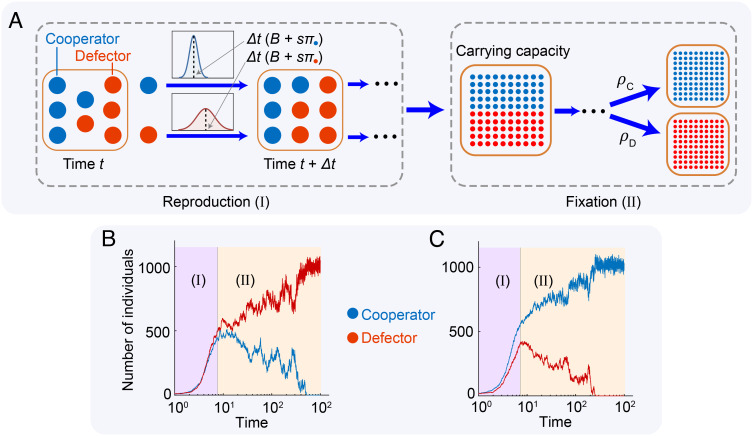
Fig. 1.
Evolutionary dynamics with demographic stochasticity. (A) Competition between cooperators (blue circle) and defectors (red circle) in a stochastic population of nonconstant size. Each individual i derives payoff πi from pairwise game-play with each other individual in the population. The number of offspring produced by an individual within time Δt has mean (B + sπi)Δt and variance (δ1B + δ2sπi)Δt, both of which are higher for defectors than for cooperators. When selection is weak (s ≪ α), the population quickly reaches carrying capacity (during time period I) while the frequency of cooperators and defectors remains unchanged from its initial value (p0 = 1/2 shown here). Thereafter (time period II), the population remains near carrying capacity (M ≈ 1,000 shown here), while the frequencies of cooperators and defectors slowly vary until either cooperators go extinct (example in panel B) or defectors go extinct (panel C). Parameters: b = 3, c = 1, s = 0.01, δ1 = δ2 = 1, x0 = y0 = 10, λ = 1 × 10−3, B = 2, D = 1.
For simplicity, we define α = B − D which describes the net population growth rate from baseline birth and death events. To avoid rapid extinction of the population, we consider the regime α > 0. For most of our analysis, we focus on the scenario where the selection is weak relative to the population growth rate (i.e., s ≪ α). When α ∼ O(1), this condition is equivalent to the classic assumption of weak selection s ≪ 1 (2, 4, 7, 13).
Results
Evolution of Cooperation with Demographic Stochasticity.
Given the class of models described above for the payoff-dependent birth process and the population size–dependent death process, the evolutionary dynamics of x and y can be approximated by a two-dimensional Itô stochastic differential equation (SI Appendix, section 1):
| [4a] |
| [4b] |
where Wt(1) and Wt(2) are independent standard Wiener processes. Although the birth process can be overdispersed in our model (when δ1 > 1), deaths follow a simple Poisson process with variance equal to mean.
To study how the relative abundance of cooperators and the total population size evolve over time, we make the coordinate transformation (p, n) = (x/(x + y),x + y). Applying Itô’s lemma to Eq. 4, neglecting diffusion terms of order O(s), and assuming δ1B ≫ δ2s (SI Appendix, section 2A), the dynamics can then be described by the equations
| [5a] |
| [5b] |
In the simple case when there is zero variance in the birth and death numbers (i.e., δ1 = δ2 = 0 for births and zero variance for deaths), the diffusion terms in the SDE above vanish, and the system reduces to an ordinary differential equation (SI Appendix, Eq. 13). This deterministic ODE provides a reference point for comparison to any stochastic system. In the deterministic system (i.e., when there is no variance in the number of births and deaths per unit time), dp is always negative and the abundance of cooperators continuously decreases until cooperators reach extinction. Thus, cooperation is never favored by natural selection in this deterministic limit.
In general, changes in the total population size depend on both the frequency of cooperators and the current population size. But for sufficiently weak selection intensity (s ≪ α), changes in the total population size n are much more rapid than changes in the cooperator frequency, p. And so, we can approximate the dynamics under weak selection by a separation of timescales, assuming that the cooperator frequency p does not change its value until the total population size n has grown logistically to its equilibrium value (α + s(b − c)p)/λ, which we denote by M (SI Appendix, section 2A for discussion of this approximation). M is called carrying capacity, and it describes the maximum number of individuals that the environment can sustain. When the net growth rate is much larger than selection intensity, α ≫ s, the carrying capacity is well-approximated by M ≈ α/λ.
For a stochastic system (δ1 ≠ 0 and δ2 ≠ 0), the trajectories of p and n are not determined by the initial conditions alone but also depend upon chance events in the birth process. We quantify the evolutionary advantage of cooperators by studying the probability of fixation—namely, the chance of eventual absorption into the full-cooperation state (p = 1). Starting from x0 cooperators and y0 defectors initially (thus p0 = x0/(x0 + y0) and n0 = x0 + y0), the fixation probability, denoted by ρ(x0, y0) or ρ(p0, n0), is the probability that at some time t defectors become extinct while cooperators still exist, that is y(t)=0 but x(t)> 0 (57). In the regime s ≪ α, the fixation probability can be approximated by separating the timescale of changes in p versus changes in n (58). This analysis is tantamount to assuming that the total population size n rapidly reaches its carrying capacity, while p remains unchanged from p0 and that subsequently p evolves in one dimension while the population size remains near the slow manifold n = M (Fig. 1 and SI Appendix, Fig. S2). Under this analysis, we can derive a simple expression for the fixation probability (SI Appendix, section 2A)
| [6] |
We performed numerical simulations, drawing sample paths from the full SDE system given by Eq. 4, to verify the accuracy of this analytic approximation for the fixation probability (Fig. 2).
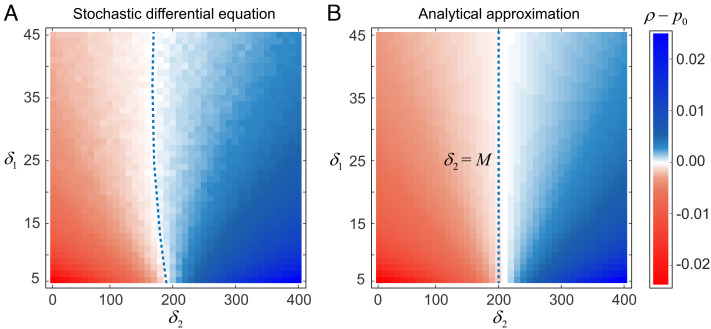
Fig. 2.
Demographic stochasticity can favor the evolution of cooperation. Colors represent the fixation probability of cooperation relative to neutral drift, ρ − p0, as a function of parameters δ2 and δ1. We say that selection favors cooperation when cooperators are more likely to fix than under neutrality (blue regions). Panel (A) shows exact solutions sampled from the stochastic differential equation (Eq. 4), whereas panel (B) shows the analytical approximation in the regime of weak selection (Eq. 6). The dashed line indicates the separation between regimes that favor cooperation (blue) or favor defection (red). Parameters: B = 2, D = 1, s = 0.005, b = 1.1, c = 1, λ = 5 × 10−3, x0 = y0 = 50.
Note that fixation probability does not depend on the initial population size, but rather on the initial frequency of cooperators. In the absence of selection (s = 0), the fixation probability equals the initial frequency of cooperators, p0. And so, we say that cooperation is favored by selection if the fixation probability exceeds p0, which will occur whenever
| [7] |
This simple condition tells us when demographic stochasticity causes selection to favor cooperators, even though selection disfavors cooperation in a population of constant (or infinite) size. In particular, demographic stochasticity can favor the fixation of cooperators when the offspring variance is sufficiently large–that is, when δ2 exceeds the carrying capacity M. What matters for the direction of selection, then, is the size of the offspring variance arising from payoffs in social interactions, relative to its mean.
We can gain some useful intuition for the forces that govern the fate of cooperators by considering the advection term in Eq. 5a. The first term in this expression, −scp(1 − p), represents the deterministic contribution to the evolution of cooperator frequency, which always opposes cooperators. However, the second term in this equation, δ2scp(1 − p)/n, arises from demographic stochasticity and it always favors cooperators. Whether or not cooperation is favored overall depends upon the balance between these two forces—the deterministic force suppressing cooperation and demographic stochasticity that favors cooperation. For δ2 < M, the deterministic disadvantage is the stronger force and so cooperators are net disfavored (recall that n rapidly reaches carrying capacity n = M before cooperators change frequency, because α ≫ s). However, if δ2 > M, the stochastic advantage matters more than the deterministic disadvantage so that cooperators are favored, which constitutes an evolutionary reversal compared to a classical model without demographic stochasticity.
Other model parameters, s, c, p0, δ1, and B, do not produce a reversal in the direction of selection for cooperation, but they nonetheless influence the fixation probability. For example, increasing δ1 or increasing the baseline birth rate B moves the fixation probability toward the neutral value, p0. Moreover, in the regime where demographic stochasticity favors cooperation, δ2 > M, the fixation probability is increased yet further when the selection intensity s is large or when the cost of cooperation c is large (Eq. 6). Both of these results contravene the classical intuition that selection and the cost of cooperation should disfavor cooperators. We have performed simulations to verify the effects of all these parameters, in comparison to the analytical approximation (SI Appendix, Fig. S1).
An Explicit Birth–Death Process.
Our model of demographic stochasticity is quite general, stipulating only a few properties of the Markov birth and death processes for competing types. We have analyzed this class of models by approximation, using a stochastic differential equation. We can construct explicit examples of discrete-state birth and death processes that satisfy our model stipulations.
Most prior studies of demographic stochasticity are based on a reproduction process with a single offspring per birth event, which naturally leads to a Poisson birth process (33–35, 44, 47, 59). The Poisson process occurs as a special case within our family of models, when δ1 = δ2 = 1. In this case, our analysis shows that demographic stochasticity alone cannot favor cooperation because δ2 < M. We will therefore consider non-Poisson birth process, in which the offspring produced per unit time is overdispersed. This is a realistic scenario for many species, especially pelagic organisms, that have heavy-tailed offspring distributions (60, 61); as well as for social contagion (53–55).
We define a birth process in discrete states and continuous time by two factors: the times of birth events and the litter size (offspring number) in each such birth event. A natural way to describe this is through a compound Poisson process (62). Specifically, for individual i with payoff πi, the times of birth events obey a Poisson process with intensity θi. In each such birth event, the number of offspring produced (litter size) is also stochastic. We consider two cases: the litter size itself follows a Poisson distribution with mean μi, or the litter size follows a negative binomial distribution with parameters qi and m (qi ∈ [0, 1] and m ∈ ℕ*). Both of these distributions have been used to model litter sizes in empirical studies (50, 52, 63).
We consider compound birth Poisson processes whose parameters (θi, μi, and qi) depend linearly on the payoff πi. For any choice of parameters δ1, δ2, and B, a corresponding compound Poisson process can be constructed (SI Appendix, section 3 and Fig. S3). We have performed Monte-Carlo simulations of these explicit population processes (discrete state, continuous time). We find good agreement (SI Appendix, Fig. S3) between the fixation probability observed in these individual-based simulations and the analytic approximation for the fixation probability that we derived from a stochastic differential equation (Eq. 6).
Intuition for the Effects of Demographic Stochasticity.
There is a simple intuition for how demographic stochasticity can favor cooperation in our class of models, even though cooperation is always disfavored in models with constant (or infinite) population size. The key insight has to do with the rapid growth of the total population size to carrying capacity, followed by slow dynamics in the frequency of cooperators near the manifold n = M. Importantly, during the slow dynamics, there are still small fluctuations that move the population off the manifold n = M, followed by a rapid return back to carrying capacity. These small fluctuations have the effect of inducing an advective force pushing the frequency of cooperators p in one direction or another.
To be more precise, we have already noted that the total population size n equilibrates much more quickly than the frequency of cooperators p (Eq. 5), in the regime we study α ≫ s. And so, given an arbitrary initial state p0 and n0, n will quickly converge to the slow manifold n = M ≈ α/λ, while p does not change from p0 (SI Appendix, Fig. S2B). After the population size reaches carrying capacity, trajectories then move along the slow manifold until one type or the other fixes (p = 0 or p = 1). We focus on the dynamics on the slow manifold, which simplifies the analysis to a one-dimensional system (58).
In the coordinate system (x, y), the slow manifold is defined by x + y = M, and the fast manifolds are lines connecting the origin to points on the slow manifold (Fig. 3A). Given any initial condition, the trajectory will rapidly approach the slow manifold along one of these lines and then subsequently move within the slow manifold. However, unlike the case of a strictly constant population size, the system with demographic stochasticity does not lie precisely on the slow manifold at all times. Small fluctuations take the system off the slow manifold briefly, and then the system rapidly returns to the slow manifold. Critically, the position where the system returns to the slow manifold, after a fluctuation, is not necessarily the same as where it started. In fact, there can be a systematic deviation in the position on the slow manifold that arises from stochastic fluctuations and rapid returns—which produces an advective force on the frequency p along the slow manifold (Fig. 3B). It is this systematic deviation, caused by demographic stochasticity, that introduces a force favoring cooperation.
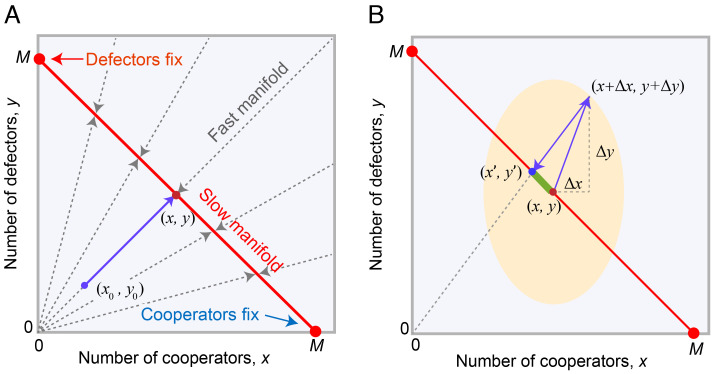
Fig. 3.
How demographic stochasticity can favor cooperation or defection. (A) We consider stochastic population dynamics that feature a separation of timescales, where the total number of individuals n = x + y changes much faster than the fraction of cooperators p = x/(x + y). Starting from x0 cooperators and y0 defectors, trajectories rapidly converge to the slow manifold (x + y = M) along the fast manifold x/y = x0/y0. (B) Stochastic fluctuations away from the slow manifold, followed by rapid return to the slow manifold, can induce an advective force on the frequency of cooperators. Stochastic fluctuations follow a two-dimensional Gaussian distribution whose variance–covariance structure is illustrated by the ellipse. For example, a fluctuation from point (x, y) to point (x + Δx, y + Δy) will rapidly return to the slow manifold at point (x′,y′), producing a deviation x′−x in the number of cooperators. The effect of these fluctuations constitutes an advective force on the frequency p of cooperators (Eq. 8). The direction of the advective force depends on the shape of the ellipse, governed by the variance of Δx and Δy. These effects of demographic noise are similar to those discussed by ref. 44, but they arise here even when both types have the same baseline birth rate and the same carrying capacity.
To understand these effects of stochasticity, we consider a population starting at point (x, y) on the slow manifold. In a short interval Δt, the population will leave the slow manifold and move to (x + Δx, y + Δy), due to stochasticity in birth and death processes; and then, it will rapidly return to the slow manifold at some point (x′,y′). The fluctuation (Δx, Δy) follows a two-dimensional Gaussian distribution with variance x(δ1B + δ2sπC + D + λn)Δt in the x-direction and variance y(δ1B + δ2sπD + D + λn)Δt in the y-direction (SI Appendix, section 1). And so, we can compute the return point and the corresponding expected change in x:
| [8] |
We conclude that if πC < πD, fluctuations from and rapid returns to carrying capacity are expected to increase the number of cooperators and decrease the number of defectors. However, if πC > πD, the cooperator frequency is expected to decrease. And when πC = πD, demographic fluctuations will not affect the direction of evolution (SI Appendix, Fig. S4).
For the donation game we have studied so far, cooperators always have a lower payoff than defectors regardless of the population state. And so, the advective force arising from demographic stochasticity always favors cooperation, regardless of p. If this force is large enough relative to the deterministic force favoring defectors, then it can produce a net advantage for cooperators. For other types of pairwise games, however, the direction of deterministic selection (πC vs πD) may depend on the current frequency p in the population, and so, the noise-induced advection may change sign along the slow manifold, producing complicated effects on long-term dynamics. We investigate these effects of demographic noise on evolutionary dynamics for general two-player games in the next section.
General Evolutionary Games with Demographic Stochasticity.
For an arbitrary two-player/two-action game, the two-dimensional system can be simplified to a one-dimensional system by separation of timescales, provided selection is sufficiently weak, s ≪ α. Suppose the game has the following payoff structure:
| [9] |
Players have two strategies, which we still generically call cooperation (C) or defection (D). When two cooperators interact, both of them receive payoff a. When a cooperator interacts with a defector, the cooperator receives b and the defector c. Mutual defection brings payoff d to both players. The average payoffs for a cooperator or defector in a population are, respectively,
| [10] |
We can describe the dynamics by a stochastic differential equation:
| [11a] |
| [11b] |
Since the population size quickly equilibrates to the carrying capacity M ≈ α/λ, we substitute n = M into Eq. 11a which yields a one-dimensional equation for the evolution of p along the slow manifold:
| [12] |
In the case of deterministic births and deaths (δ1 = δ2 = 0 and neglecting variance in the death process), this equation simplifies to the classic replicator equation (9, 10).
For general games, there may be interior equilibria of interest, instead of simply fixation of one strategy or the other. But p = 0 and p = 1 are absorbing states of the SDE system, and so all trajectories will eventually reach one of these states and then become invariant. To study the interior dynamics, therefore, in this section, we introduce rare mutations to avoid fixation on the boundary (p = 0 and p = 1). We assume that the mutation occurs only when a phenotype perishes (i.e., when the number of one phenotype reaches zero, a new mutant of this phenotype arises). Technically, this is equivalent to imposing a reflecting boundary condition on the boundary. The resulting evolution of cooperator frequency p becomes an ergodic Markov process which has a unique stationary distribution v*(p), conditioned on n > 1. The probability density at p will be proportional to the amount of time trajectories spend near p. We will study the stationary distribution from two perspectives. One perspective is to analyze the deterministic behavior on the slow manifold, which neglects stochasticity altogether in Eq. 12 and studies the equilibria of the resulting ordinary differential equation. The other, more nuanced perspective accounts for stochasticity.
When we neglect the stochastic terms, then Eq. 12 becomes an ODE with the same equilibrium points and stabilities as the classic replicator equation, provided δ2 < M. However, if δ2 > M, then the equilibrium points are the same as the classic replicator equation, but the stabilities are reversed: Equilibrium points that are classically unstable become stable and conversely. And so, the value of δ2, which determines the payoff-related component of offspring variance, can reverse the evolutionary outcome, even from a deterministic perspective.
More generally, we can classify three different types of two-player/two-action games. Dominance games (Fig. 4A) arise when one strategy is always dominant, providing higher payoff than the other strategy regardless of their frequencies in the population. Here, without loss of generality, we assume defection dominates cooperation (a < c and b < d, e.g., a prisoner’s dilemma). For dominance games, when δ2 < M, then all trajectories will converge to the full-defector state (p = 0 stable and p = 1 unstable). However, if δ2 > M, then all trajectories will converge to full-cooperator state (p = 1 stable and p = 0 unstable). Coexistence games (a < c and b > d, e.g., a snowdrift game) arise when each strategy yields a higher payoff when the other strategy is more frequent in the population (Fig. 4B). For coexistence games, if δ2 < M there is only one stable equilibrium, p* = (d − b)/(a − b − c + d), and so cooperators and defectors will stably coexist. But when δ2 > M, then p* becomes unstable and p = 0 and p = 1 are each stable—so that all trajectories converge to either the full-cooperator state or the full-defector state. Coordination games (a > c and d > b, e.g., a stag-hunt game) arise when each strategy yields a greater payoff when it is more frequent than the alternative strategy (Fig. 4C). For coordination games, when δ2 < M, there is an unstable internal equilibrium p* and stable boundaries (p = 0 and p = 1). But when δ2 > M, p* becomes stable while p = 0 and p = 1 become unstable. In summary, in a population with sufficiently large offspring variance (δ2 > M), the outcome of each type of game has the dynamical properties classically associated with the opposite type of game in a deterministic setting. In other words, demographic stochasticity effectively transforms the payoff structure of a game in the following way
| [13] |
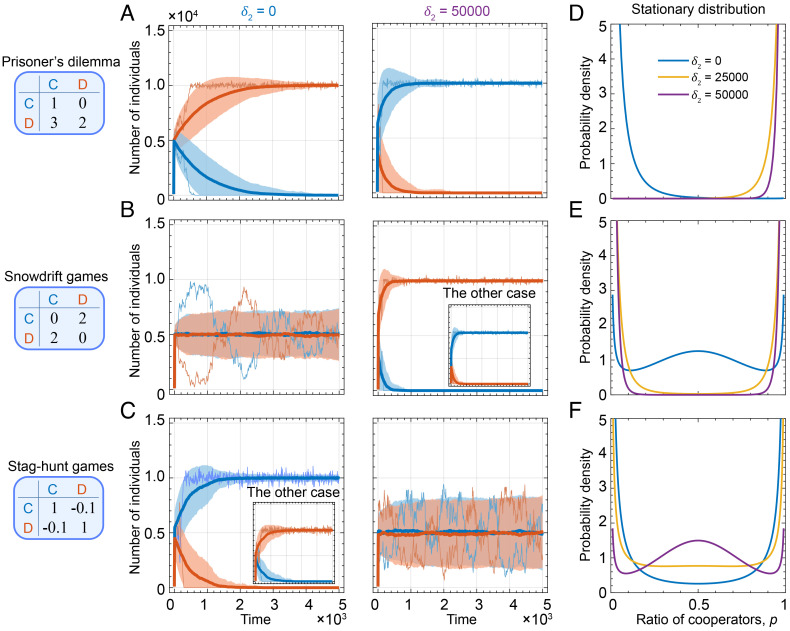
Fig. 4.
General evolutionary game dynamics with demographic stochasticity. We consider three types of representative games, such as prisoner’s dilemma (A and D), snowdrift game (B and E), and stag-hunt games (C and F). In the prisoner’s dilemma games, when demographic stochasticity is absent or does not meet δ2 > M, defectors dominate the population (see trajectories sampled in A, Left part). However, the evolutionary direction can be reversed for δ2 > M, where cooperation becomes the dominant strategy (see trajectories sampled in A, Right part). Shown in (D) is the stationary distribution of cooperators, conditioned on n > 0, for δ2 = 0, δ2 = 25, 000, and δ2 = 50, 000. Analogously, in the snowdrift game, demographic stochasticity with δ2 > M changes the equilibrium from coexistence of two strategies (B, Left part) to bistability (B, Right part), effectively transforming the snowdrift game to a stag-hunt game. And conversely, demographic stochasticity can transform the stag-hunt games into a snowdrift game, with respect to equilibria. Parameters: B = 2, D = 1, s = 10−3, δ1 = 1 (A, B, D, E), δ1 = 2.5 (C, F), λ = 10−4, x0 = y0 = 100.
We can also characterize general two-player games in terms of the stationary frequency distribution of the two strategies. We derive the stationary distribution v*(p) under reflecting boundaries in SI Appendix, section 4A. This description accounts for more details in the stochastic dynamics, and it reveals a similar, transformative effect of large offspring variance. If δ2 is sufficiently large, namely δ2 > M, then the modes of the stationary distribution can be moved from one boundary to the other boundary (dominance games, Fig. 4D), from the interior to the boundaries (coexistence games, Fig. 4E) or from the boundaries to the interior (coordination games, Fig. 4F). These results are in agreement with the ODE-based analysis above, and they show that a sufficiently large offspring variance will reverse the evolutionary dynamics in an interacting population. These dramatic effects extend to games with more than two actions, including the rock-paper-scissors game (SI Appendix, Fig. S5).
We have seen that large offspring variance can reshape the payoff structure of a game, producing dynamics classically seen in an entirely different game type. So far, we have focused on the scaling factor δ2, which governs how offspring variance grows with payoff, as opposed to δ1, which governs the baseline offspring variance. The value of δ1 can also profoundly influence evolutionary outcomes, although this cannot be seen from a deterministic perspective alone because δ1 has no effect on stabilities of equilibria. Analysis of the stationary frequency distribution shows that a large baseline variance (δ1B) can transform any game into a coordination game (SI Appendix, section 4A). An example of this result is shown in Fig. 4F, where even though δ2 = 25,000 exceeds the carrying capacity, the stationary distribution is not unimodal around an intermediate frequency. This is because the effect of δ2 here is offset by the effect of δ1. And so demographic noise, especially when offspring variance is high, can qualitatively change the evolutionary outcomes compared to predictions of traditional analysis by replicator equations for fixed or infinite population size (64).
Discussion
The question of how cooperation can be maintained is a longstanding and active area of research, spanning multiple disciplines. A large literature has produced compelling explanations for cooperation, but these typically rely on some form of population structure or repeated interactions. Here, we find that even in a well-mixed population with one-shot interactions, natural stochasticity in the offspring process can favor cooperation that would otherwise be suppressed. For other types of social interactions, as well, demographic stochasticity can reverse the direction of evolutionary trajectories and produce behavioral outcomes that contravene classical expectations.
It is intuitively easier to invade a noisy population than a stable population. And so, natural selection near carrying capacity prefers types not only with higher fecundity (greater mean offspring number) but also with lower reproductive noise (smaller offspring variance) (31, 33, 34). The reversal in the direction of selection in a stochastic population reflects this basic trade-off between offspring mean and offspring variance. A larger payoff produces higher fecundity but also greater noise in the reproduction process. Whether it is the mean or the variance in offspring number that dominates the course of evolution is determined by their relative importance, which is governed by δ2 in our model. Classical models of populations often neglect the effects of offspring variance or assume the offspring variance is small (Poisson offspring distribution); but more realistic models, we have seen, permit regimes where offspring variance is more important than fecundity.
Although demographic noise has been studied extensively in population models, the underlying mechanism for our results is qualitatively different from those explored in prior studies. Most research on demographic noise has been restricted to constant fitness for competing types (31, 33–42), which does not describe social interactions. However, Constable et al. analyzed a frequency-dependent fitness model, and they also found that demographic noise can reverse the direction of selection (44). Their model is based on the production and consumption of a public good. One phenotype produces the public good at a cost that reduces its baseline birth rate, while the other phenotype does not produce the public good. They analyze the case when “cooperators” (who produce the public good) have a larger intrinsic carrying capacity than nonproducers, and the larger carrying capacity then yields an evolutionary advantage by making producers more robust against invasion. This mechanism is thus a stochastic form of r versus K selection (65), and it occurs when births and deaths follow Poisson processes. By contrast, in our model, the evolutionary advantage of cooperators arises even though both types have the same baseline birth rate and the same carrying capacity; and it arises only when the birth process related to payoff is sufficiently overdispersed. This mechanism is thus fundamentally different from a trade-off between baseline birth rate and carrying capacity (44–46), and it is more closely related to phenomena in populations with heavy-tailed offspring distributions (61, 66–68), even though our model lacks discontinuous jumps in frequency trajectories that arise in models with constant population size. We note that selection is assumed to be weak in our analysis, with respect to mean offspring number, but that payoffs may still have substantial effects on the offspring distribution, especially when it is over-dispersed.
Aside from promoting cooperation in the prisoner’s dilemma, demographic stochasticity also transforms outcomes in other forms of social interaction. Stochasticity can effectively convert a snowdrift game into a stage-hunt game, for example, so that the stable co-existence of types expected in a deterministic or Poisson setting is transformed into bi-stability, with one type or the other winning out. Here, again, the underlying mechanism that reverses the evolutionary outcome is over-dispersion in the offspring contribution related to payoff, even when both types have the same baseline birth rate and carrying capacity.
The core insight underlying these results arises from the work of Gillespie on the evolutionary effects of fitness variance (31, 32). And yet, the mechanism by which offspring variance influences evolution, in our analysis, is qualitatively different from models of exponentially growing (31) or constant (32) population size. Our analysis incorporates explicit density dependence in the death rates, which keeps the population size bounded without imposing an (unrealistic) assumption of constant size. In this explicit setting, the effects of offspring variance on type frequencies can be understood as the combined result of stochastic fluctuations away from carrying capacity followed by rapid return along a fast manifold (Fig. 3). Moreover, our analysis pertains to frequency-dependent selection, unlike early studies on variance effects, and it reveals that stable internal equilibria (balanced polymorphism) can be converted to the dominance of one type or conversely. Finally, by constructing explicit discrete models that satisfy the stipulations of our SDE, we have shown that offspring variance can reverse the arrow of selection only when the birth process is overdispersed, whereas such reversals cannot occur for Poisson clutch sizes. All these results are qualitatively different from early studies on fitness variance (31, 32).
Our analysis has assumed a fast-growing population (α ≫ s), which rapidly reaches carrying capacity before any change in the relative frequencies of competing types. The dynamics of competition may be more complicated in a stochastic, slow-growing population, because their analysis cannot be reduced to a one-dimensional slow manifold. In this regime, fixation of one type may occur before reaching carrying capacity. We can nonetheless derive approximations for the fixation probability in this regime as well (SI Appendix, section 4B), and, in the case of the donation game, we find that cooperation will be favored by selection provided δ2 exceeds the initial population size, δ2 > n0. This condition is typically easier to satisfy than Eq. 7, and it is confirmed by both numerical simulations and Monte Carlo simulations of compound Poisson process (SI Appendix, Figs. S6 and S7). Moreover, in this regime of a slow-growing population, after either cooperators or defectors fix, the population will then tend to grow logistically to its carrying capacity; but in this case, the carrying capacity is larger for cooperators (SI Appendix, Fig. S8), which provides an additional evolutionary advantage and by increasing their chance of long-term persistence (SI Appendix, Fig. S9).
Our results highlight the strong impact of stochasticity on evolutionary outcomes for competition in populations. The demographic stochasticity we have studied arises from intrinsic properties of birth and death processes, which have size of order . As the population size grows toward infinity this form of stochasticity has little influence on evolutionary dynamics, which is consistent with the recent finding that migration in finite, group-structured populations can favor cooperators provided the population size is not too large (69). Aside from intrinsic stochasticity during reproduction, real populations may also be subject to external noise, arising from exogenous variation in environmental conditions. Unlike demographic noise, exogenous noise can be substantial even in populations of arbitrarily large size. Prior studies on environmental fluctuations, including fluctuations in selection intensity (70), carrying capacity (40, 41), and payoff structure (39), have analyzed their effects by imposing an external noise term onto an otherwise classical, deterministic and continuous system of equations. The effects of exogenous noise on discrete stochastic systems remain less explored, and they are likely to differ qualitatively from stochastic perturbations of continuous systems (71). Coupling intrinsic demographic noise with external environmental noise may produce even more complicated effects, which remains a topic for future research.
The impact of stochasticity on competing strategic types likely extends beyond the two-player games we have focused on, to include many aspects of nonhuman and human social behavior. Even if behavioral spread is caused by biased imitation, there is nonetheless variance in the number of individuals who imitate a type, as well as physical variation in population sizes of interacting social groups as individuals move between social settings. Empirical data have documented burstiness, a form of over-dispersion, in social interactions (72, 73). Likewise, in the context of behavior during an epidemic, there is evidence of super-spreading individuals that cause over-dispersion in infectiousness (55, 74), which may influence frequency-dependent competition among cocirculating variants. Extending our model and analysis to these settings remains an open topic for future research.
Materials and Methods
There are no empirical experiments associated with this study. SI Appendix provides a formal definition of our mathematical model and the derivation of its analysis by separation of timescales. The SI Appendix also presents the analysis of arbitrary two-player/two-action games, and games with more than two strategies, by deriving the stationary frequency distribution under reflecting boundaries. Finally, the SI Appendix describes the implementation of Monte Carlo simulations for associated discrete-state, continuous time processes.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We thank the anonymous referees for their constructive input. G.W. and L.W. acknowledge the support from the National Natural Science Foundation of China (NSFC 62036002) and the PKU-Baidu Fund (2020BD017). J.B.P. and Q.S. acknowledge the support from the Simons Foundation (Math+X Grant to the University of Pennsylvania), the John Templeton Foundation (grant no. 62281), and the David & Lucille Packard Foundation.
Author contributions
G.W., Q.S., L.W., and J.B.P. designed research; G.W. performed research; G.W., Q.S., L.W., and J.B.P. analyzed data; and G.W., Q.S., L.W., and J.B.P. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Contributor Information
Qi Su, Email: qisu1991@sas.upenn.edu.
Long Wang, Email: longwang@pku.edu.cn.
Joshua B. Plotkin, Email: jplotkin@sas.upenn.edu.
Data Availability Statement
All study data are included in the article and/or SI Appendix.
Supporting Information
References
- 1.Nowak M. A., Sigmund K., Evolution of indirect reciprocity by image scoring. Nature 393, 573–577 (1998). [DOI] [PubMed] [Google Scholar]
- 2.Nowak M. A., Sasaki A., Taylor C., Fudenberg D., Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Hilbe C., Šimsa Š, Chatterjee K., Nowak M. A., Evolution of cooperation in stochastic games. Nature 559, 246–249 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Ohtsuki H., Hauert C., Lieberman E., Nowak M. A., A simple rule for the evolution of cooperation on graphs and social networks. Nature 441, 502–505 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Weitz J. S., Eksin C., Paarporn K., Brown S. P., Ratcliff W. C., An oscillating tragedy of the commons in replicator dynamics with game-environment feedback. Proc. Natl. Acad. Sci. U.S.A. 113, E7518–E7525 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tilman A. R., Plotkin J. B., Akçay E., Evolutionary games with environmental feedbacks. Nat. Commun. 11, 915 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Allen B., et al. , Evolutionary dynamics on any population structure. Nature 544, 227–230 (2017). [DOI] [PubMed] [Google Scholar]
- 8.Taylor P. D., Jonker L. B., Evolutionary stable strategies and game dynamics. Math. Biosci. 40, 145–156 (1978). [Google Scholar]
- 9.Schuster P., Sigmund K., Replicator dynamics. J. Theor. Biol. 100, 533–538 (1983). [Google Scholar]
- 10.Nowak M. A., Evolutionary Dynamics: Exploring the Equations of Life (Harvard University Press, Cambridge, 2006). [Google Scholar]
- 11.Nowak M. A., May R. M., Evolutionary games and spatial chaos. Nature 359, 826–829 (1992). [Google Scholar]
- 12.Tarnita C. E., Ohtsuki H., Antal T., Fu F., Nowak M. A., Strategy selection in structured populations. J. Theor. Biol. 259, 570–581 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McAvoy A., Allen B., Fixation probabilities in evolutionary dynamics under weak selection. J. Math. Biol. 82, 14 (2021). [DOI] [PubMed] [Google Scholar]
- 14.Su Q., Allen B., Plotkin J. B., Evolution of cooperation with asymmetric social interactions. Proc. Natl. Acad. Sci. U.S.A. 119, e2113468118 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Su Q., McAvoy A., Mori Y., Plotkin J. B., Evolution of prosocial behaviours in multilayer populations. Nat. Hum. Behav. 6, 338–348 (2022). [DOI] [PubMed] [Google Scholar]
- 16.Cooney D. B., The replicator dynamics for multilevel selection in evolutionary games. J. Math. Biol. 79, 101–154 (2019). [DOI] [PubMed] [Google Scholar]
- 17.Santos F. P., Santos F. C., Pacheco J. M., Social norm complexity and past reputations in the evolution of cooperation. Nature 555, 242–245 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Nowak M. A., Sigmund K., Evolution of indirect reciprocity. Nature 437, 1291–1298 (2005). [DOI] [PubMed] [Google Scholar]
- 19.Nowak M. A., Sigmund K., A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 364, 56–58 (1993). [DOI] [PubMed] [Google Scholar]
- 20.Nowak M. A., Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stewart A. J., Plotkin J. B., From extortion to generosity, evolution in the Iterated Prisoner’s Dilemma. Proc. Natl. Acad. Sci. U.S.A. 110, 15348–15353 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gächter S., Herrmann B., Reciprocity, culture and human cooperation: Previous insights and a new cross-cultural experiment. Philos. Trans. R. Soc. B Biol. Sci. 364, 791–806 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yamauchi A., Tanimoto J., Hagishima A., An analysis of network reciprocity in Prisoner’s Dilemma games using Full Factorial Designs of Experiment. BioSystems 103, 85–92 (2011). [DOI] [PubMed] [Google Scholar]
- 24.Yoelia E., Hoffman M., Rand D. G., Nowak M. A., Powering up with indirect reciprocity in a large-scale field experiment. Proc. Natl. Acad. Sci. U.S.A. 110, 10424–10429 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Greiner B., Levati M. V., Indirect reciprocity in cyclical networks: An experimental study. J. Econ. Psychol. 26, 711–731 (2005). [Google Scholar]
- 26.Fehr E., Gintis H., Human motivation and social cooperation: Experimental and analytical foundations. Ann. Rev. Soc. 33, 43–64 (2007). [Google Scholar]
- 27.Cinyabuguma M., Page T., Putterman L., Cooperation under the threat of expulsion in a public goods experiment. J. Public Econ. 89, 1421–1435 (2005). [Google Scholar]
- 28.Casari M., Luini L., Cooperation under alternative punishment institutions: An experiment. J. Econ. Behav. Organ. 71, 273–282 (2009). [Google Scholar]
- 29.Wang Z., et al. , Onymity promotes cooperation in social dilemma experiments. Sci. Adv. 3, e1601444 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kay T., Keller L., Lehmann L., The evolution of altruism and the serial rediscovery of the role of relatedness. Proc. Natl. Acad. Sci. U.S.A. 117, 28894–28898 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gillespie J. H., Natural selection for within generation variance in offspring number. Genetics 76, 601–606 (1974). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gillespie J. H., Natural selection for within generation variance in offspring number II. Discrete haploid models. Genetics 81, 403–413 (1975). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Parsons T. L., Quince C., Fixation in haploid populations exhibiting density dependence I: The non-neutral case. Theor. Popul. Biol. 72, 121–135 (2007). [DOI] [PubMed] [Google Scholar]
- 34.Parsons T. L., Quince C., Fixation in haploid populations exhibiting density dependence II: The quasi-neutral case. Theor. Popul. Biol. 72, 468–479 (2007). [DOI] [PubMed] [Google Scholar]
- 35.Parsons T. L., Quince C., Plotkin J. B., Some consequences of demographic stochasticity in population genetics. Genetics 185, 1345–1354 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.McKane A. J., Newman T. J., Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 94, 218102 (2005). [DOI] [PubMed] [Google Scholar]
- 37.Butler T., Goldenfeld N., Robust ecological pattern formation induced by demographic noise. Phys. Rev. E 80, 030902 (2009). [DOI] [PubMed] [Google Scholar]
- 38.Hallatschek O., Hersen P., Ramanathan S., Nelson D. R., Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. U.S.A. 104, 19926–19930 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Stollmeier F., Nagler J., Unfair and anomalous evolutionary dynamics from fluctuating payoffs. Phys. Rev. Lett. 120, 58101 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Wienand K., Frey E., Mobilia M., Evolution of a fluctuating population in a randomly switching environment. Phys. Rev. Lett. 119, 158301 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Taitelbaum A., West R., Assaf M., Mobilia M., Population dynamics in a changing environment: Random versus periodic switching. Phys. Rev. Lett. 125, 048105 (2020). [DOI] [PubMed] [Google Scholar]
- 42.Chotibut T., Nelson D. R., Population genetics with fluctuating population sizes. J. Stat. Phys. 167, 777–791 (2017). [Google Scholar]
- 43.Okabe T., Yoshimura J., A new long-term measure of sustainable growth under uncertainty. Proc. Natl. Acad. Sci. Nexus 1, pgac228 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Constable G. W., Rogers T., McKane A. J., Tarnita C. E., Demographic noise can reverse the direction of deterministic selection. Proc. Natl. Acad. Sci. U.S.A. 113, E4745–E4754 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Houchmandzadeh B., Vallade M., Selection for altruism through random drift in variable size populations. BMC Evol. Biol. 12, 61 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Houchmandzadeh B., Fluctuation driven fixation of cooperative behavior. BioSystems 127, 60–66 (2015). [DOI] [PubMed] [Google Scholar]
- 47.Huang W., Hauert C., Traulsen A., Stochastic game dynamics under demographic fluctuations. Proc. Natl. Acad. Sci. U.S.A. 112, 9064–9069 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.McAvoy A., Fraiman N., Hauert C., Wakeley J., Nowak M. A., Public goods games in populations with fluctuating size. Theor. Popul. Biol. 121, 72–84 (2018). [DOI] [PubMed] [Google Scholar]
- 49.Zuur A. F., et al. , Mixed Effects Models and Extensions in Ecology with R (Springer, New York, 2009). [Google Scholar]
- 50.Lindén A., Mäntyniemi S., Using the negative binomial distribution to model overdispersion in ecological count data. Ecology 92, 1414–1421 (2011). [DOI] [PubMed] [Google Scholar]
- 51.Ver Hoef J. M., Boveng P. L., Quasi-Poisson vs. negative binomial regression: How should we model overdispersed count data? Ecology 88, 2766–2772 (2007). [DOI] [PubMed] [Google Scholar]
- 52.Richards S. A., Dealing with overdispersed count data in applied ecology. J. Appl. Ecol. 45, 218–227 (2008). [Google Scholar]
- 53.Brady W. J., Wills J. A., Jost J. T., Tucker J. A., Van Bavel J. J., Emotion shapes the diffusion of moralized content in social networks. Proc. Natl. Acad. Sci. U.S.A. 114, 7313–7318 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.J. M. Schröder, Merz E. M., Suanet B., Wiepking P., The social contagion of blood donations: Sustaining repeated prosocial behaviour. SocArXiv (2021). Accessed 9 July 2021. [Google Scholar]
- 55.Kirkegaard J. B., Sneppen K., Superspreading quantified from bursty epidemic trajectories. Sci. Rep. 11, 24124 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rapoport A., Chammah A. M., Orwant C. J., Prisoner’s Dilemma: A Study in Conflict and Cooperation (University of Michigan Press, 1965), vol. 165. [Google Scholar]
- 57.Czuppon P., Traulsen A., Fixation probabilities in populations under demographic fluctuations. J. Math. Biol. 77, 1233–1277 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Parsons T. L., Rogers T., Dimension reduction for stochastic dynamical systems forced onto a manifold by large drift: A constructive approach with examples from theoretical biology. J. Phys. A Math. Theor. 50, 415601 (2017). [Google Scholar]
- 59.Feller W., An Introduction to Probability Theory and Its Applications (Wiley, New York, 1950). [Google Scholar]
- 60.Davis H. C., Chanley P. E., Spawning and egg production of oysters and clams. Biol. Bull. 110, 117–128 (1956). [Google Scholar]
- 61.Eldon B., Wakeley J., Coalescent processes when the distribution of offspring number among individuals is highly skewed. Genetics 172, 2621–2633 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Last G., Penrose M., Lectures on the Poisson process (Cambridge University Press, London, 2017). [Google Scholar]
- 63.Sheldon B. C., Kruuk L. E., Merilä J., Natural selection and inheritance of breeding time and clutch size in the collared flycatcher. Evolution 57, 406–420 (2003). [DOI] [PubMed] [Google Scholar]
- 64.Hofbauer J., Sigmund K., Evolutionary Games and Population Dynamics (Cambridge University Press, UK, 1998). [Google Scholar]
- 65.Pianka E. R., On r- and K-selection. Am. Nat. 104, 592–597 (1970). [Google Scholar]
- 66.Schweinsberg J., A necessary and sufficient condition for the Λ-coalescent to come down from infinity. Electron. Commun. Probab. 5, 1–11 (2000). [Google Scholar]
- 67.Sargsyan O., Wakeley J., A coalescent process with simultaneous multiple mergers for approximating the gene genealogies of many marine organisms. Theor. Popul. Biol. 74, 104–114 (2008). [DOI] [PubMed] [Google Scholar]
- 68.Der R., Epstein C., Plotkin J. B., Dynamics of neutral and selected alleles when the offspring distribution is skewed. Genetics 191, 1331–1344 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Braga I., Wardil L., When stochasticity leads to cooperation. Phys. Rev. E 106, 014112 (2022). [DOI] [PubMed] [Google Scholar]
- 70.Assaf M., Mobilia M., Roberts E., Cooperation dilemma in finite populations under fluctuating environments. Phys. Rev. Lett. 111, 238101 (2013). [DOI] [PubMed] [Google Scholar]
- 71.Durrett R., Levin S., The importance of being discrete (and spatial). Theor. Popul. Biol. 46, 363–394 (1994). [Google Scholar]
- 72.Stehlé J., Barrat A., Bianconi G., Dynamical and bursty interactions in social networks. Phys. Rev. E 81, 035101 (2010). [DOI] [PubMed] [Google Scholar]
- 73.Goh K. I., Barabási A. L., Burstiness and memory in complex systems. Europhys. Lett. 81, 48002 (2008). [Google Scholar]
- 74.Tkachenko A. V., et al. , Time-dependent heterogeneity leads to transient suppression of the COVID-19 epidemic, not herd immunity. Proc. Natl. Acad. Sci. U.S.A. 118, e2015972118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All study data are included in the article and/or SI Appendix.