Identifying regulation with adversarial surrogates

Significance

The stability of living systems is maintained through multiple internal regulation and control processes. Failure of this “homeostasis” is associated with dysfunction and disease. Yet, it is difficult to identify what exactly is regulated, even given the current abundance of data from many biological systems. Internal control objectives are generally not directly measured, and identifying composite conserved quantities is a challenging computational problem. We develop an iterative two-player algorithm that receives an array of temporal measurements and outputs a highly regulated or conserved quantity. The algorithm was tested on simulated and experimental data, demonstrating excellent empirical results. We expect our data-driven approach to be broadly applicable to internally regulated systems, biological, as well as chemical and physical.

Abstract

Homeostasis, the ability to maintain a relatively constant internal environment in the face of perturbations, is a hallmark of biological systems. It is believed that this constancy is achieved through multiple internal regulation and control processes. Given observations of a system, or even a detailed model of one, it is both valuable and extremely challenging to extract the control objectives of the homeostatic mechanisms. In this work, we develop a robust data-driven method to identify these objectives, namely to understand: “what does the system care about?”. We propose an algorithm, Identifying Regulation with Adversarial Surrogates (IRAS), that receives an array of temporal measurements of the system and outputs a candidate for the control objective, expressed as a combination of observed variables. IRAS is an iterative algorithm consisting of two competing players. The first player, realized by an artificial deep neural network, aims to minimize a measure of invariance we refer to as the coefficient of regulation. The second player aims to render the task of the first player more difficult by forcing it to extract information about the temporal structure of the data, which is absent from similar “surrogate” data. We test the algorithm on four synthetic and one natural data set, demonstrating excellent empirical results. Interestingly, our approach can also be used to extract conserved quantities, e.g., energy and momentum, in purely physical systems, as we demonstrate empirically.

Living systems maintain stability against internal and external perturbations, a phenomenon known as homeostasis (1–3). This is a ubiquitous central pillar across all scales of biological organization, such as molecular circuits, physiological functions, and population dynamics. Failure of homeostatic control is associated with diseases including diabetes, autoimmunity, and obesity (3). It is therefore vital to identify the regulated variables that the system aims to maintain at a stable setpoint.

In contrast to simple human-made systems, where often a small number of known variables are under control, biological systems are characterized by multiple coupled feedback loops as well as other dynamic structures (1). In particular, they are not divided to separate “plant” and “controller” entities, as commonly characterized in control theory, but rather make up a complex network of interactions. In such a network some variables are maintained at a stable setpoint, whereas others are more flexibly modulated to maintain the former regulated variables around their setpoints. A classic example is blood glucose concentration, which is tightly regulated, while the rates of glycolysis and gluconeogenesis are flexible variables (3). Thus, in general, one may find a hierarchy of control, where some variables are more tightly controlled than others (4, 5). This biological complexity makes it challenging to identify the regulated variables that the system actively maintains at a setpoint, in contrast to those which are stabilized as a byproduct.

Experimentally, a regulated variable can be identified by performing perturbations (6). When the system is perturbed, compensatory mechanisms will adjust other variables to restore it to its setpoint by using feedback (4). However, designing such experiments requires prior knowledge about the system, which is not always at hand, and may be technically challenging or infeasible. Biological systems regulate internal variables, rather than measured variables, which are generally determined by experimental constraints. Our assumption, related to the concept of observability (7), is that a combination of the observed variables will correspond to the relevant internal variable.

In recent years, technological advancements brought about a huge number of available datasets that were not tailored to find regulated variables, but could offer the opportunity to point out possible candidates. This raises the question: can we elicit the regulated variables of a system given a set of measurements with minimal prior assumptions?

In this work, we develop an algorithm, Identifying Regulation with Adversrial Surrogates (IRAS), that aims to identify the most conserved combination of variables in a system. This combination, operationally denoted the control objective, may represent a quantity that is of high importance to the system. To this end, a quantitative measure needs to be defined, which enables comparing the degree of invariance of different combinations. Standard statistical measures, such as the variance or coefficient of variation, are not suitable due to their sensitivity to scale and bias and insensitivity to temporal aspects. We propose a new measure, the Coefficient of Regulation (CR), which captures the property of temporal invariance. Straightforward optimization of this measure does not provide the required result (for reasons explained below). Rather, we show that a combined utilization of temporal invariance, and the geometric distribution of data, can be successful in the task.

IRAS receives as input an array of temporal measurements and outputs the control objective as a combination (function) of the observed variables. At its core, it runs iteratively between two competing players; one player aims to minimize the CR, i.e., to find the combination which is most invariant in the data relative to time-shuffled data. The second player gradually pushes the time-shuffled ensemble to statistically resemble the real data, thus rendering the optimization problem more difficult for the first player. Eventually, the control objective is found when these two players converge.

To demonstrate the generality of our approach, we validate it on five examples from very different domains. First, we simulate a kinetic model of protein–protein interactions, in which the controlled variable combination is known. We show that IRAS identifies with high accuracy the control objective. Second, we analyze data from a psychophysical experiment, where human observers’ response statistics are modulated by an artificial controller. Our algorithm identifies correctly the known control circuit. Then, extending beyond the biological domain, we illustrate the generality of IRAS by considering two examples of dynamical systems with conserved quantities—a physical spring system with energy conservation and the nonlinear Lotka–Volterra predator–prey system with a particular known conserved quantity. Based on observing noisy trajectories of these systems, with different parameters, we recover both the individual parameters of each system and the explicit forms for the conserved quantities. Finally, we evaluate IRAS on a dataset of complex physical equations (8) that serves for benchmarking machine-learning algorithms and identify the correct governing equations from trajectories without prior information.

A. Problem Illustration.

We are interested in identifying empirically, from a set of measurements, a quantity which is most conserved around a setpoint. This “control objective” could represent something of high importance to the system and could thus shed light on the system’s functionality. How can we elicit a possible control objective of a system given a set of n measurements over time, Z(t) = (z₁(t),…,z_n(t))? If the control objective itself is unknown, it is likely not directly measured. However, it could be possible to describe it as a combination of the measured variables, that is maintained around a setpoint,

$$\begin{array}{c}\hfill c(t)=g(Z(t))\approx c_{\mathrm{set}}.\end{array}$$ [1]

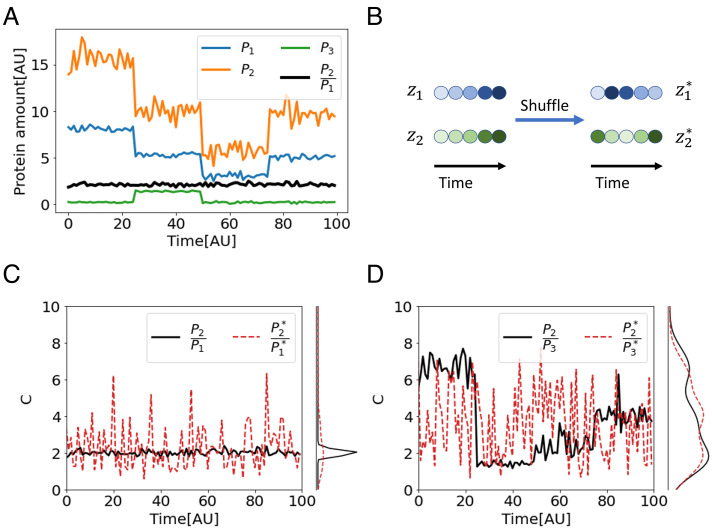
As a simple illustrative example, consider the case of three proteins whose abundance is measured across time in a single cell. Fig. 1A shows these traces along time, as the system presumably goes through various perturbations. While the amount of the three proteins, P₁(t), P₂(t), and P₃(t), varies significantly over time, the ratio $\raisebox{1ex}{$P_2(t)$}\!\left/ \!\raisebox{-1ex}{$P_1(t)$}\right.$ is maintained around a setpoint c_set​ = ​2 with small fluctuations (black line). No other instantaneous relationship between the proteins is present in the data. We thus expect the combination $g(P_1,P_2,P_3)=\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.$ to be identified as the control objective of the system.

Fig. 1.

Coefficient of Regulation (CR) as a measure of combination invariance. (A) A synthetic example of ratio control in a biological system. The amounts of three proteins, P₁, P₂, and P₃, fluctuate over time and are modulated by discontinuous perturbations (t​ = ​25, 50, 75). In the face of these perturbations, the ratio $\raisebox{1ex}{$P_2(t)$}\!\left/ \!\raisebox{-1ex}{$P_1(t)$}\right.$ is held around a setpoint c_set​ = ​2 with small fluctuations (noise with SD 0.15). (B) To calculate CR, temporal correlations between the measurements are destroyed by shuffling the time points of each measurement independently. (C) While the distribution of $\raisebox{1ex}{$P_2(t)$}\!\left/ \!\raisebox{-1ex}{$P_1(t)$}\right.$ in real data is narrow (black), the distribution of the ratio between shuffled measurements is much wider (red dashed), resulting in a small CR. (D) Since there is no correlation between P₂ and P₃, the distributions of their ratio in real and in shuffled data are of the same width, and CR = 1.

Our aim in what follows is to develop an algorithm that receives as input a set of experimental measurements, and outputs the control objective as a combination of current, and possibly previous, measurements. After defining a measure of invariance (Section 1.A), we explain why simply optimizing it is insufficient (Section 1.B) and construct IRAS, a two-player algorithm, to minimize it under iterative constraints (Section 1.C). Then, we validate the algorithm on five examples, where the control objective depends on current variables in one case (Section 2.A), extended to include also past values in a second case (Section 2.B) and then also extended to include system-specific parameter estimation in the third and fourth cases (Section 2.C). Finally, we validate the algorithm on a dataset of physics-related examples that serves for benchmarking machine-learning algorithms (Section 2.D). IRAS is data-driven and is not provided with a model of the system or with possible candidates for the control objective based on prior knowledge. Rather, it is based solely on the raw measurements. To the best of our knowledge, such an empirical approach has not been developed previously and could potentially be useful to many experimental systems.

1. Algorithm Development

A. Quantifying Invariance Around a Setpoint.

Based on our assumption that a regulated variable is held relatively constant, we first seek a measure that quantifies the invariance of a combination around a stable setpoint. We posit that the controller couples system variables (such as the levels of the two proteins above) that would otherwise be less, or even completely, decoupled. As perturbations are encountered, these variables covary, and their joint distribution

$$\begin{array}{c}\hfill Z\sim P_Z(z_1,\cdots ,z_n),\end{array}$$ [2]

defines the geometry of the manifold which the data occupy. By arbitrarily permuting each component z_i independently over time, we can create a surrogate dataset Z^* in which the correlations in the data have been eliminated—in particular, those induced by the control. The distribution of this surrogate dataset reflects only the single-variable properties:

$$\begin{array}{c}\hfill Z^{\ast }\sim P_{Z^{\ast }}(·)={\mathrm{\Pi }}_i{P}_{z_i}(z_i).\end{array}$$ [3]

Importantly, a combination c(t)​ = ​g(Z(t)) that is invariant due to the operation of the controller, would become noninvariant in the surrogate data,

$$\begin{array}{c}\hfill c^{\ast }(t)=g(Z^{\ast }(t))\ne c(t).\end{array}$$ [4]

To quantify the sensitivity of a combination to independent shuffling, we consider the ratio

$$\begin{array}{c}\hfill \frac{\sigma (c)}{\sigma (c^{\ast })}=\frac{\sigma (g(Z))}{\sigma (g(Z^{\ast }))},\end{array}$$

where σ is the standard deviation (SD) computed over time. We expect that for a regulated combination, destroying all temporal order will increase its SD considerably and decrease this ratio. Note that when the components of Z are independent, i.e., there is no relation between them, the ratio is identically 1 for any combination g.

Fig. 1B illustrates this definition: Starting from measurements Z, we create the independently shuffled ensemble Z^* where correlations between variables are destroyed. Referring to the protein example in Fig. 1A, the combination $g(P_1,P_2,P_3)=\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.$ is maintained around the setpoint, resulting in a narrow distribution over time and a small SD (Fig. 1C, black). Eliminating the temporal correlation between P₁ and P₂ by shuffling their time points results in a much wider distribution and a higher SD (Fig. 1C, dashed red). Other combinations such as $g(P_1,P_2,P_3)=\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_3$}\right.$, exhibit distributions of similar widths over the shuffled and the original data (Fig. 1D). Consequently, the SD ratio is approximately 1, indicating that this combination is not regulated by the system.

The SD ratio, that quantifies invariance in temporally ordered vs. temporally shuffled data, can be generalized to shuffles that are not completely random but obey some constraint. As shown below, this generalization will be required for developing our two-player algorithm. Specifically, given a suggested combination c​ = ​g(⋅), one may construct a weighting function ζ(⋅), that defines a biased shuffled ensemble $\tilde{Z}$. Then, we define the Coefficient of Regulation (CR) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}& \gamma =\frac{\sigma (g(Z))}{\sigma (g(\tilde{Z}))}\hfill \\ \hfill & \mathrm{where}\tilde{Z}\sim P_{\tilde{Z}}(\tilde{Z})=P_{Z^{\ast }}(\tilde{Z})\zeta (g(\tilde{Z})),\hfill \end{array}\end{array}$$ [5]

and the special case of completely random shuffles is obtained for ζ = 1.

To summarize, we defined the Coefficient of Regulation (CR) as a measure that quantifies the sensitivity of a given combination to the destruction of temporal correlations between its constituents. It is based on a surrogate data technique (9), applied here to multiple variables by shuffling each of them separately and measuring the effect on their combinations. The shuffles can be completely random or performed under some constraints. We next consider the question of how this measure can be used to identify the control objective without prior assumptions.

B. Straightforward Optimization Fails by Shuffle Artifacts.

Since low values of CR indicate invariance around a setpoint, one may expect that the combination that minimizes CR with respect to unconstrained shuffling, ζ(⋅)​ ≡ ​1 in Eq. 5, is a good candidate for the control objective of the system. If so, we would seek to find

$$\begin{array}{c}\hfill {\mathrm{argmin}}_{\mathrm{g}}\frac{\sigma (g(Z))}{\sigma (g(Z^{\ast }))}.\end{array}$$ [6]

A prohibitive pitfall of this approach can come about by unconstrained shuffling of the data to produce Z^* in Eq. 6. In fact, the CR can be brought to its minimal value of zero, if there is a property that is always satisfied by the data but is violated by the shuffles (SI Appendix, section SI3.1, (S.9) for a proof). With such a property, one can construct a combination which attains a value of zero on the data and nonzero on the shuffled data, rendering the CR zero. This solution of the simple optimization problem holds information about the geometric distribution of data points but does not necessarily identify a regulated combination.

We illustrate this for the protein example presented above, where the ratio $\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.$ is maintained around a stable setpoint. The average CR of this combination over 100 realizations is not zero but rather 0.17 ± 0.09 because of random fluctuations. Conversely, a combination with a zero CR can be constructed based on the following general property of the data: in the observed time-series, $\raisebox{1ex}{$P_2(t)$}\!\left/ \!\raisebox{-1ex}{$P_1(t)$}\right.\approx 2$ with small noise such that the data always satisfies P₂ > P₁. This constraint is not obeyed by the shuffled data: some values of P₂ are smaller than P₁ at other time points, so that some shuffled traces will have P₂^* < P₁^*. Thus, for example, the combination g(P₁, P₂, P₃)​ = ​sgn(P₂ − P₁) is 1 at each time point yielding a SD of zero for the real data, but different from zero in the shuffled data. Consequently, the CR is equal to zero. This artifact creates a potential pitfall to a simple optimization of Eq. 6.

Let us demonstrate this effect by a specific implementation, where the CR is optimized by an artificial neural network. Stretches of data similar to those presented in Fig. 1A are fed into the network, with the target of minimizing the CR. Using a nonlinear network allows to search for combinations which are not necessarily linear, such as the desired ratio or the undesired sign function in this example. The network provided as output an optimal combination g(P₁, P₂, P₃) that can be computed for any value of P₁, P₂, P₃ but, due to the nonlinearity, cannot be easily expressed as a simple analytic formula.

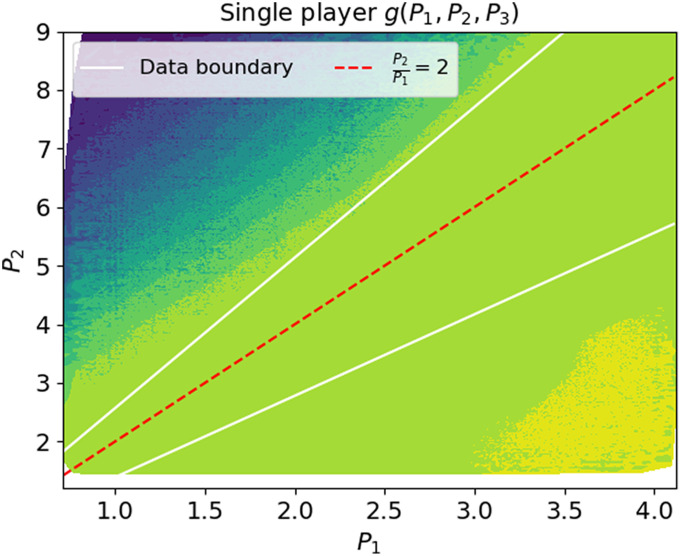
To gain intuition into the combination found by the network, we compute g(P₁, P₂, P₃) over the shuffled ensemble and plot its value as a function of P₁ and P₂. Fig. 2 depicts this value as a colormap in the (P₁, P₂) plane. Our prior knowledge of the true regulated combination in this example allows us to mark its value (red line, depicting $\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.=2$) and moreover to delineate the region where real measurements occur (two white lines). Examination of this figure reveals that the optimal combination found by the neural network is practically constant on shuffles that remain within the limits of the data (flat light green area between the white lines). Outside these limits, it obtains varying values correlated with the distance of the shuffled point from the real data.

Fig. 2.

Failure of straightforward optimization. Optimal combination values found by the single-player algorithm, a neural network which minimizes the Coefficient of Regulation with unconstrained shuffling (CR, Eq. 5, ζ(⋅)≡1). This algorithm was fed with time traces of the three proteins, with the ratio $\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.$ being the conserved combination. The network output is displayed as an arbitrary-value colormap in the (P₁, P₂) plane. Shuffles that fall within the boundaries of the data (the white lines) have a practically fixed value, while shuffles outside these boundaries attain values that are correlated with their distance from the boundaries. The found combination has a CR of almost zero (0.004 ± 0.003). However, its Pearson correlation with the ground truth conserved combination is 0.11 ± 0.08.

This suggests that the optimal combination found by the neural network identifies the region occupied by the data, presumably by constructing an indicator function as described qualitatively above. Indeed, the output combination has a CR value of nearly zero, but a very low correlation with the true regulated quantity $\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.$. We refer to this algorithm as the “single player” since it involves only a single optimization goal: a “combination player” that aims to find a combination minimizing the CR. Analyzing its failure allows us to identify a way to correct it: If we constrain the shuffles to a set that is plausible in light of the data distribution, we may prevent the optimization algorithm from constructing artifact functions that reflect structural differences between the measured and shuffled ensembles. This is analogous to the scientific process of searching for appropriate surrogate data when trying to demonstrate statistically significant effects: too strong a shuffle may show significance when it is absent (10, 11). In our case, we automate this process by introducing a second player. The goal of this “shuffle player” is to constrain the shuffled ensemble such that it better resembles the data distribution, while still destroying temporal relations. This will be called IRAS (the “two-player algorithm”) and will be described next.

C. IRAS Captures the Control Objective.

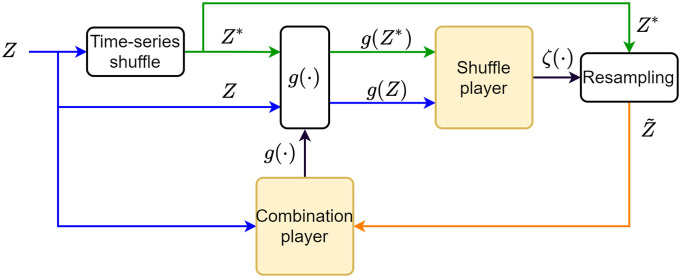
In the previous section, we reasoned that constraining the shuffled ensemble to be more similar to the real data may avoid artifacts and lead to meaningful combinations. Inspired by the concept of two competing players as implemented in the Generative Adversarial Nets algorithm (12), we developed a scheme that alternates between optimizing the CR and constraining the shuffled ensemble.

The first player, termed the combination player, is a neural network that takes a step toward minimizing the CR. In the first iteration, CR is computed with respect to the unconstrained shuffled ensemble (ζ ≡ 1), outputting the first proposed conserved combination. The shuffle player makes use of this proposed combination, g(⋅), to create a new shuffled ensemble $\tilde{Z}$, which better resembles the statistical structure of the data. Formally, this corresponds to the selection of a resampling function ζ(⋅) that minimizes the distributional distance

$$\begin{array}{c}\hfill \begin{array}{cc}& D\left(g(Z),g(\tilde{Z})\right)\hfill \\ \hfill & \mathrm{where}\tilde{Z}\sim P_{\tilde{Z}}(\tilde{Z})=P_{Z^{\ast }}(\tilde{Z})\zeta (g(\tilde{Z})).\hfill \end{array}\end{array}$$ [7]

The constraint in the second line, as well as the inputs to the shuffle player in Fig. 3, stresses the fact that this player only has access to g(⋅) for creating the new ensemble. It turns out that the shuffle player can solve Eq. 7 exactly and obtain D = 0. To see this, we note that the distribution of $g(\tilde{Z})$ is given by $P_{\tilde{Z}}(g(\tilde{Z}))=P_{Z^{\ast }}(g(\tilde{Z}))\zeta (g(\tilde{Z}))$. We obtain $P_{\tilde{Z}}(g(\tilde{Z}))=P_Z(g(\tilde{Z}))$ for the choice

$$\begin{array}{c}\hfill \zeta (g(\tilde{Z}))=\frac{P_Z(g(\tilde{Z}))}{P_{Z^{\ast }}(g(\tilde{Z}))}.\end{array}$$ [8]

Fig. 3.

IRAS Algorithm outline. The time-series data Z is shuffled to create the unconstrained shuffled time-series Z^*. The “shuffle player,” exposed only to the 1D combinations g(Z) and g(Z^*), sets the weighting function ζ(⋅) used to resample $\tilde{Z}$ from Z^*, such that the 1D distributions, P_Z(g(Z)) and $P_{\tilde{Z}}(g(\tilde{Z}))$, are identical. Then, given Z and $\tilde{Z}$, the “combination player” updates g(⋅) toward minimizing its CR. These steps continue to iterate until no further improvement is possible.

The resampling function ζ(⋅) takes into account the distribution of g(⋅) both in the original data Z and the unconstrained shuffled ensemble Z^*. A detailed description of the resampling procedure is given in SI Appendix, section SI3.2.1. At the end of this step, g has a CR of 1 with respect to the new resampled surrogate data $\tilde{Z}$ (by definition—these ensembles have the same distribution of g). The combination player then starts another round of optimization, searching for a new g based on the CR with respect to the new shuffled ensemble

$$\begin{array}{c}\hfill {\text{argmin}}_g\frac{\sigma (g(Z))}{\sigma (g(\tilde{Z}))}.\end{array}$$ [9]

In this way, the two players mutually inform each other of their current step results, and the process continues iteratively until the combination player can no longer decrease the CR. We refer to this as IRAS, the two-player algorithm (Fig. 3).

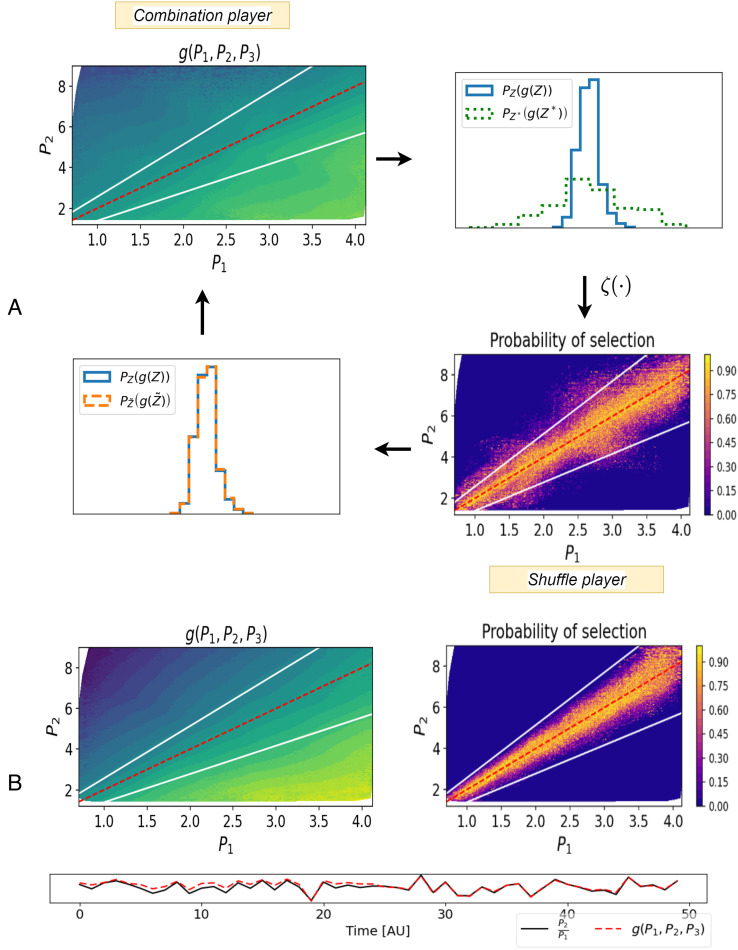
To demonstrate IRAS in action, we return to the protein example. Fig. 4A depicts the progression of steps of the two players at a stage of the iterative optimization. A colormap of the combination in the (P₁, P₂) plane, found by the combination player, is shown on the top left. This combination defines a probability distribution on the real and shuffled data (Top Right). The shuffle player constructs a new shuffled ensemble by resampling (Bottom Right); by construction, in this new shuffled ensemble, the distribution of g matches that of the data (Bottom Left). The combination player receives this updated shuffled ensemble and the next optimization step begins.

Fig. 4.

IRAS demonstration. (A) A step of the iterative algorithm (Fig. 3) is displayed. Top Left: the value of an intermediate combination g(⋅) given by the combination player, is displayed in the (P₁, P₂) plane together with the true combination (red line) and the data limits (white lines). Top Right: distriubtions of this combination over the data (P_Z(g(Z)), blue) and unconstrained shuffles (P_Z^*(g(Z^*)), dashed green). Bottom Right: The shuffle player examines these 1D distributions and resamples Z^* via the weighting function ζ(⋅) to construct the constrained shuffles $\tilde{Z}$, over which the 1D distribution of g matches the data. The resampling probability is displayed in the (P₁, P₂) plane. Bottom Left: Combination player receives this resampled shuffled ensemble, another optimization step begins and the combination player updates g(⋅). (B) Combination values (Top Left) and resample probability (Top Right) at the final iteration. The combination player has captured the control objective (the map approximates $\raisebox{1ex}{$P_2$}\!\left/ \!\raisebox{-1ex}{$P_1$}\right.$), and the shuffle player has captured the data distribution (delineated by white lines). Bottom: values of the combination along a stretch of time together with the ground-truth combination.

Gradually, the resampled shuffled ensemble approximates the distribution of the real data and a map which approximates $\raisebox{1ex}{$P_2(t)$}\!\left/ \!\raisebox{-1ex}{$P_1(t)$}\right.$ emerges as the output combination. At the final step, Fig. 4B, the combination player cannot further minimize the CR. We find that indeed IRAS converges and outputs the true conserved quantity, $\raisebox{1ex}{$P_2(t)$}\!\left/ \!\raisebox{-1ex}{$P_1(t)$}\right.$, as observed in the Bottom row of Fig. 4B^*.

2. Validation

After presenting the construction of IRAS, we seek to validate it on datasets with a known control objective or a conserved quantity. We chose three validation examples from different biological scales: a kinetic model of protein interactions, a measured dataset from a psychophysical experiment, and a model of interactions in an ecological system. Additionally, to demonstrate the efficiency of our algorithm in studying mechanical physical systems, we model a simple physical spring system where energy is conserved. Finally, we validate the algorithm on a dataset that serves for benchmarking machine-learning algorithms. Throughout the validation examples, we use a single neural network architecture whose details are listed in SI Appendix, section SI4. Code implementing IRAS on one of these validation examples is available at https://github.com/RonTeichner/IRAS.

A. A Kinetic Model of Regulatory Interactions.

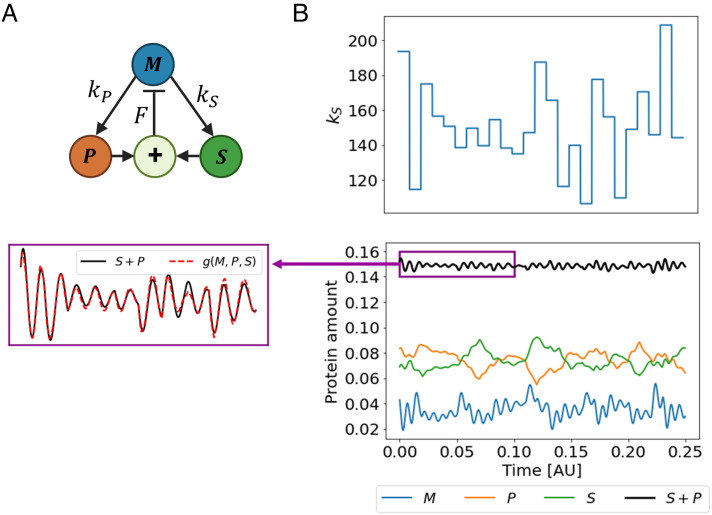
We first validate IRAS on simulated data generated from a kinetic model that describes regulatory interactions between three proteins incorporating a feedback loop. In the considered model (inspired by ref. 4), the total amount of two proteins P and S, namely P + S, is controlled by another protein M under perturbations in protein expression parameters. The model (see illustration in Fig. 5A) is described by the differential equations

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{M}& =K-F(P+S)-{\gamma }_M(t)M\hfill \\ \hfill \dot{P}& =k_P(t)M-{\gamma }_P(t)P\hfill \\ \hfill \dot{S}& =k_S(t)M-{\gamma }_S(t)S,\hfill \end{array}\end{array}$$ [10]

Fig. 5.

IRAS captures the control objective in a kinetic model. (A) An illustration of the closed loop system. Protein M induces the production of both S and P and receives a negative feedback of their sum. (B) Top: perturbations cause step-like variation in k_S over time. The duration of each step is 0.01 which is much longer than the timescale of the feedback loop $\tau =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$F$}\right.=0.0005$ (F = 2, 000). This enables the controller to track the changes in S + P. Each step was sampled from a normal distribution with a mean 150 and a SD 30. The rest of the parameters were sampled similarly: γ_P, γ_S = 70 ± 15, γ_M = 80 ± 15, k_P = 150 ± 30. Bottom Right: The trajectories of the three proteins and the combination S + P over time. The Bottom Left: a zoom-in of the combination P + S (black) within the purple box in the Right panel along with the output of the algorithm (dashed red).

where the three proteins M, P, S are linked in a feedback loop. Both P and S are positively affected by M, with their steady-state values proportional to it. The concentration M in turn is negatively affected by the sum P + S, with the strength of this negative feedback given by the rate constant F. The degradation rates γ_M, γ_P, γ_S and the production rates k_P,k_S are perturbed over time as shown in Fig. 5B, Top. Fig. 5B, Bottom Right shows the trajectories of the three proteins across time. Small changes in S or P induce swift and sharp changes in the production rate of M and maintain P + S around a stable level. This is reflected in a high negative correlation between S and P.

To gain a better insight into the stability of the combination P + S, we consider the steady state of the system for a fixed set of parameters. At steady state, the rate of change of all three proteins is zero, and P + S is given by

$$\begin{array}{c}\hfill \begin{array}{c}{P}_{\mathrm{ss}}+S_{\mathrm{ss}}=\frac{K}{F+\frac{{\gamma }_M{\gamma }_P{\gamma }_S}{k_P{\gamma }_S+k_S{\gamma }_P}},\end{array}\end{array}$$ [11]

where P_ss and S_ss are the steady states of P and S, respectively (SI Appendix, section SI6.1 for the steady states of the three proteins). If the strength of the negative feedback is large and satisfies $F\gg \frac{{\gamma }_M{\gamma }_P{\gamma }_S}{k_P{\gamma }_S+k_S{\gamma }_P}$, P_ss + S_ss will approximately remain around the same setpoint despite the perturbations. This indicates that g(M, P, S) = S + P is a possible control objective of the system under these conditions. Indeed, applying IRAS on 30 realizations of this model, we find that it outputs the control objective S + P with high accuracy; Fig. 5B, Bottom Left shows their overlap. The mean Pearson correlation between them is 0.97 ± 0.005 over the 30 realizations. We present in SI Appendix, section SI6.2 additional examples, including cases where different parameters lead to different conserved combinations, that are still captured by the algorithm. In summary, IRAS identifies correctly the control objective in a dataset generated from a kinetic model of regulatory interactions.

B. Relational Dynamics in Perception.

Human perception is inherently noisy and the source of this noise is an important issue in Psychophysics research (13–15). An experimental design was introduced to address this question, which involves a closed-loop controller that modulates the input stimulus according to the human responses, with the goal of decreasing variability and maintaining the response probability at a pre-determined setpoint (16), Fig. 6A. It was shown that this feedback loop indeed quenches the response variability.

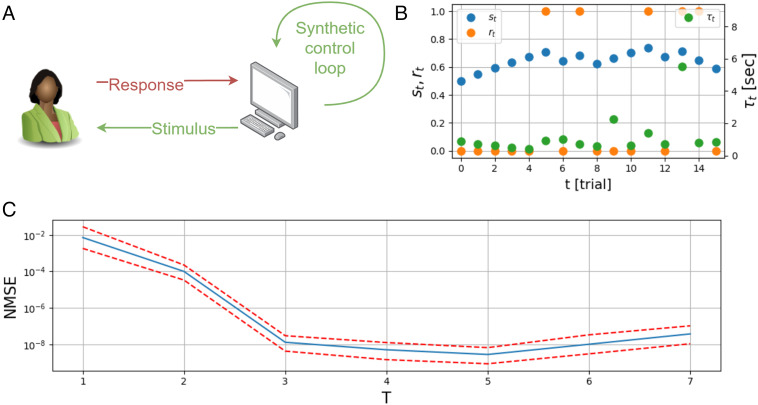
Fig. 6.

Relational dynamics in perception (A) Trial-trial variability in human sensory detection is tested. A synthetic feedback controller sets the stimulus, which is the contrast of a foreground raster displayed on the screen. Then, the user responds positively when detecting the raster or negatively when not. (B) Raw data from psychophysics experiment. A portion of the measured time-series z_t = [s_t r_t τ_t] in a human sensory detection experiment. The stimulus s_t (blue dots) is a time-series of image-contrast values, the responses r_t (orange dots) are a Boolean time-series of detection, and τ_t (green dots) is the reaction time from stimulus to response. (C) Normalized mean-square-errors of stimulus estimation values as defined in Eq. 16. Stimulus estimation is obtained from the analytical expression of the feedback loop detected. The estimation errors decrease monotonously up to T = 5 implying an effective timescale of 5 trials. Dashed red lines are the MSE of errors higher and lower than the MSE which lies on the blue line.

The data from these experiments provide a unique opportunity to apply and validate IRAS, as we have a ground truth component in the system—the engineered controller that records the human responses and determines the next stimulus. This controller is coupled to a noisy biological system, the human observer. For validating our algorithm, we feed it with the complete raw data, including both input stimuli and responses. If working correctly, IRAS should identify the synthetic controller as the most regulated combination and allow us to derive a mathematical description for the way it sets the stimulus. We emphasize that the algorithm does not have access to any internal variables of the synthetic controller.

The task in the experiment of ref. 16 consisted of sensory detection of a weak visual stimulus. In sequential trials, users were presented with a random raster of black and white pixels. A smaller foreground raster drawn from a different distribution was embedded in the background raster area. A single session was composed of multiple trials, where the foreground raster was displayed at a random location on the screen; in some of the trials, only the background was displayed. In each trial, users had to respond if they detected the foreground raster and withhold response if not. The synthetic feedback controller set the contrast of the foreground raster as a function of the previously received responses, increasing it when response probability was low and vice versa, with the objective of maintaining a fixed probability of response. The response time was also recorded in each trial, but the controller did not make any use of this information.

The experiment was performed on eight human subjects yielding a dataset that consists of three-dimensional, discrete time-series, including the stimuli, responses, and reaction times, over 450 trials for each subject. Fig. 6B depicts a portion of the three components of raw data as a function of trial number t. The three observables are the raster contrast levels (s_t​ ∈ ​ℝ, blue); corresponding binary responses (r_t​ ∈ ​{0, 1}, orange); and reaction times (τ_t​ ∈ ​ℝ, green). Our validation here will consist of feeding this data to IRAS to find the most regulated combination.

Recall that in Section 1, IRAS was presented for the case where the most regulated combination of measurements is sought among instantaneous functions c(t)​ = ​g(z(t)). The shuffle player created an ensemble where all correlations among observables measured at the same time point were eliminated. Here, we would like to derive the most regulated combination between measurements at consecutive time points. We expect that this will allow for the identification of the synthetic controller that sets the stimulus s_t as a function of past values. To this end, the shuffled data provide a random present for a given past, while preserving correlations within the same time point—and thus preventing the algorithm from detecting a combination that does not relate past and present observations. Over T + 1 consecutive observations (T > 0), we now seek the most regulated combination constructed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill c_t^{(T)}& =g_T(z_{t-T:t})\hfill \\ \hfill z_{t-T:t}& =\left[\begin{array}{cccc}{s}_{t-T}& s_{t-T+1}& \cdots & s_t\\ r_{t-T}& r_{t-T+1}& \cdots & r_t\\ {\tau }_{t-T}& {\tau }_{t-T+1}& \cdots & {\tau }_t\end{array}\right].\hfill \end{array}\end{array}$$ [12]

While the shuffle player creates surrogate data of the form

$$\begin{array}{cc}\hfill z_{t-T:t}^{\ast }& =\left[\begin{array}{cccc}{s}_{t-T}& s_{t-T+1}& \cdots & s_{j_t}\\ r_{t-T}& r_{t-T+1}& \cdots & r_{j_t}\\ {\tau }_{t-T}& {\tau }_{t-T+1}& \cdots & {\tau }_{j_t}\end{array}\right],\hfill \end{array}$$ [13]

where s_jt, r_jt, and τ_jt are the observations obtained at some random time j_t. We refer the reader to the SI Appendix, section SI3 for the complete technical details of implementing IRAS over varying time-windows of size T.

We ran the algorithm on the experimental dataset with this definition of shuffles, for different values of T. In each evaluation, the yielded combination g_T(⋅) is the output of an artificial neural network; therefore, it is effectively a black-box. In this case, we could approximate the network by a multivariate polynomial and obtain an interpretable expression while remaining close to the actual network output (Pearson correlation of 0.88 ± 3e⁻⁵ over the 8 human subjects). For T = 3, the resulting approximation is

$$\begin{array}{cc}\hfill g_3(z_{t-3:t})\approx & {\sigma }_s^{-1}(s_t-1.91s_{t-1}+0.92s_{t-2}-0.009s_{t-3})\hfill \\ \hfill & +{\sigma }_r^{-1}(8e^{-6}{r}_t+1.4r_{t-1}-1.4r_{t-2}-0.03r_{t-3})\hfill \\ \hfill & +{\sigma }_{\tau }^{-1}(2e^{-6}{\tau }_t-4e^{-6}{\tau }_{t-1}-7e^{-6}{\tau }_{t-2}\hfill \\ \hfill & -5e^{-6}{\tau }_{t-3}),\hfill \end{array}$$ [14]

where σ_s = 0.035, σ_r = 0.5, σ_τ = 0.34, are the standard deviations of the stimulus, the response, and the reaction time, respectively.

Comparing these results to our prior knowledge of the experimental system provides strong support to the validation of IRAS. We expect the synthetic controller to be identified by the algorithm, and therefore, the current stimulus will be a function of previous responses. This should translate to small coefficients for r_t and τ_t, compared to that of s_t. Furthermore, all reaction time coefficients should be negligible because they were not used by the controller. Examining the coefficients in Eq. 14 shows that these are indeed properties of the discovered combination. To examine whether this combination captures the synthetic feedback control loop, we test whether it can predict the stimulus values correctly. Removing the negligible terms in Eq. 14 and recalling that g_T(⋅)≈c_set we predict (up to a constant term),

$$\begin{array}{cc}\hfill {\sigma }_s^{-1}{\widehat{s}}_t\simeq & {\sigma }_s^{-1}(1.91s_{t-1}-0.92s_{t-2}+0.009s_{t-3})\hfill \\ \hfill & +{\sigma }_r^{-1}(-1.4r_{t-1}+1.4r_{t-2}+0.03r_{t-3}).\hfill \end{array}$$ [15]

Here, we denoted the stimulus obtained from the learned combination by ${\widehat{s}}_t$ so that it can be compared to the true stimulus value s_t, set by the controller in the experiment. The normalized mean-square prediction error

$$\begin{array}{c}\hfill \mathrm{NMSE}=\frac{\text{var}({\widehat{s}}_t-s_t)}{\text{var}(s_t)},\end{array}$$ [16]

is extremely low, approximately 10⁻⁸, testifying to a high degree of functionality of the internal synthetic feedback loop detected by IRAS.

Another important question that our methodology allows to address is the effective timescale of the feedback loop. Running the algorithm on various values of T, we estimated the mean-square prediction error Eq. 16. Fig. 6C and SI Appendix, Fig. S8 show the result as a function of T, testifying to an effective timescale of 5 trials. Because the system works in closed-loop, this timescale cannot be directly compared to the controller timescale. In summary, IRAS identifies correctly the most regulated combination, corresponding to a synthetic control feedback loop, in data obtained from a real-world experiment with a human in the loop.

C. Identifying Conservation Laws.

IRAS identifies quantities that are maintained at approximately constant values throughout the dynamics, based on the empirical criterion of CR. There can be different underlying reasons why a quantity remains fixed. For biological systems, such behavior may indicate regulation—i.e., compensation that protects some variables from external perturbations. In closed dynamical systems, constant values often represent exact conservation laws.

In the previous sections, we validated IRAS on datasets of simulated and experimental biological systems. The assumption was that different realizations of the simulation, or different experiments, were statistically similar. Specifically, we assumed that all systems share the exact same g function. More generally, different systems might share the same functional form for g, but with different system-specific parameters. In this section, we demonstrate how IRAS deals with a family of datasets that stem from systems with different parameters. As an example for this challenge, we first focus on a Hamiltonian mechanical system (17, 18). Hamiltonian mechanics describes dynamical systems through conservation laws and invariances. The Hamilton–Jacobi equations relate the state of a system to some conserved quantity, e.g., energy. In this context, specific a-priori knowledge of the system is required to identify its invariants; finding invariants in a general dynamical system, or even knowing whether or not they exist, is a difficult problem. Developing automated computational methods to find invariants from data is a challenge of much recent interest (19–24). A conservation law is a function that satisfies Eq. 1; therefore, IRAS is suitable for its identification. We note that optimizing for conservation alone can lead to trivial quantities, such as predicting a constant g(z)​ = ​c independent of z. A recent paper (25) refers to a nontrivial g(⋅) by the term useful conservation law.

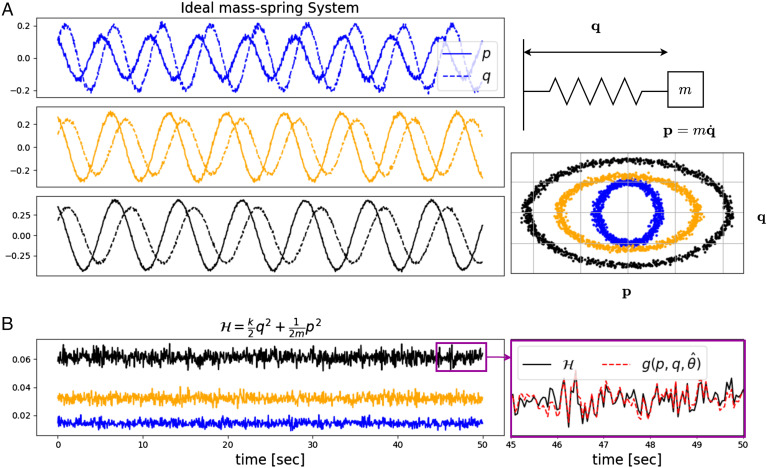
We consider the ideal frictionless mass–spring system shown in the upper right corner of Fig. 7A. This system is commonly used to test algorithms designed for the identification of conservation laws (25, 26). The system’s Hamiltonian and dynamic equations are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{H}& =\frac{k}{2}{q}^2+\frac{1}{2m}{p}^2,\hfill \\ \hfill \dot{q}& =\frac{\partial \mathcal{H}}{\partial p},\dot{p}=-\frac{\partial \mathcal{H}}{\partial q},\hfill \end{array}\end{array}$$ [17]

Fig. 7.

IRAS captures the conservation law in Hamiltonian mechanics. The dataset contains 100 different mass-spring systems. In each system, k and m were sampled uniformly between [0.5, 1.5] and the initial conditions, p₀ and q₀ between [0.15, 0.25] and [0.1, 0.2] respectively. The raw observations consist of times-series of length 1,000 of p and q corrupted by a zero-mean additive Gaussian white noise with SD 0.01. (A) Top Right: ideal mass on spring with mass m and spring constant k. Left: time traces of momentum, (p, solid lines) and coordinate, (q, dashed lines) for ideal mass–spring systems with spring and mass constants k = (0.72, 1.13, 1.05) and m = (0.59, 1.32, 1.48) in the Top, Middle, and Bottom panels, respectively. Bottom Right: same trajectories plotted in the phase plane (p, q). (B) Left: the energy as a function of time for the three systems in (A) with corresponding colors. Right: a zoom-in of the energy and output of the combination learned by IRAS in a short stretch of time.

with two parameters: the spring constant k and the mass m. The dynamic variables are q, the coordinate denoting deviation from equilibrium, and the momentum p. The most conserved instantaneous combination is the Hamiltonian, reflecting conservation of energy. We examine several systems with different parameters, such that the value of the conserved quantity differs between them but the functional form is the same. Fig. 7A shows the observed traces as a function of time (Left) and in the (p, q) phase plane (Bottom Right) for three systems. Fig. 7B, Left, shows the corresponding time-series of the Hamiltonian, namely the energy as a function of time.

The different physical systems share the same conservation law with the Hamiltonian as the invariant combination. However, the value of this combination is different in each system and depends on the parameters. Running IRAS over the pooled data from all systems, in the same setting used in the previous sections, that is, optimizing a combination c(t) = g(p(t),q(t)), leads to a low mean Pearson correlation of 0.65 ± 0.15. This low value occurs because the learned combination g() did not incorporate system-specific parameters. To address this problem, we now present an extension to IRAS that allows for identifying a regulated combination that is a function of both the measurements and of parameters that are estimated simultaneously for each system (detailed in the SI Appendix, section SI3). In the extended version, the learned instantaneous regulated combination is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill c^{(s)}(t)& =g\left(p^{(s)}(t),q^{(s)}(t),{\theta }^{(s)}\right),\hfill \\ \hfill {\theta }^{(s)}& =\mathrm{\Theta }\left(p^{(s)},q^{(s)}\right),\hfill \end{array}\end{array}$$ [18]

where superscript s is for system s ∈ {1, 2, …, 100}, and p^(s) and q^(s) are the time-series observed from system s. The set of parameters estimated for system s is θ^(s) ∈ ℝ^l with l a user-defined hyperparameter, and where Θ(⋅) is a second artificial neural-network (SI Appendix, Fig. S5 in SI Appendix, section SI3). Here, we set l = 2. Indeed, the extended IRAS captures the conservation law yielding a mean Pearson correlation of 0.95 ± 0.012 between c^(s) and ${\mathcal{H}}^{(s)}$ (averaged over all systems). Fig. 7B, Right, shows the values of ground-truth $\mathcal{H}$ together with the learned combination c along a stretch of time for a single system. The parameters estimated by Θ(⋅) match the physical quantities of spring and mass constants, exhibiting Pearson correlation of 0.88 and 0.82 with θ₁^(s) and θ₂^(s), respectively (averaged over all systems).

As a limiting case, we tested the extended algorithm, Eq. 18, in a scenario where all mass–spring systems are identical with k = 1 and m = 1. The resulting Pearson correlation between $\mathcal{H}$ and the identified combination is 0.96 ± 0.01. This testifies that the extended algorithm does not negatively affect the performance when estimating system-specific parameters is unnecessary.

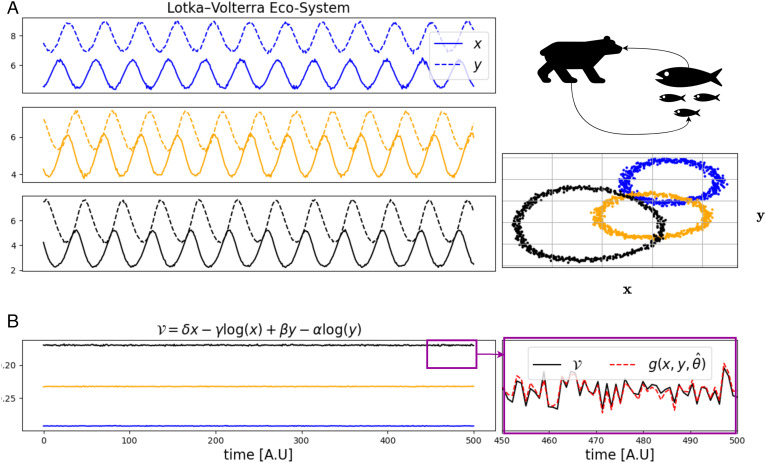
As a second example for identifying conserved quantities, we consider the Lotka–Volterra ecological system model, also known as the predator–prey equations (27),

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{x}& =\alpha x-\beta xy\hfill \\ \hfill \dot{y}& =\delta xy-\gamma y.\hfill \end{array}\end{array}$$ [19]

The model consists of a pair of first-order nonlinear differential equations in which two species interact, one as a predator and the other as prey. The densities of prey and predator are x and y, respectively, and α, β, γ, δ are positive real parameters describing the interaction of the two species. This is an autonomous system with a well-known conserved quantity given by

$$\begin{array}{c}\hfill \mathcal{V}=\delta x-\gamma log(x)+\beta y-\alpha log(y).\end{array}$$ [20]

As in the frictionless mass–spring system example, we examine 100 systems with different (α, β, γ, δ) parameters, such that the value of the conserved quantity differs between them but the functional form of $\mathcal{V}$ is the same. Fig. 8A shows three examples of trajectories from such systems, while Fig. 8B, Left demonstrates the known conserved quantity. Similarly to the previous example, the extended IRAS captures the conservation law yielding a mean Pearson correlation of 0.93 ± 0.03 between c^(s) and ${\mathcal{V}}^{(s)}$ (averaged over all systems). Fig. 8B, Right, shows the values of ground-truth $\mathcal{V}$ together with the learned combination c along a stretch of time for a single system. We note that running IRAS over the pooled data from all systems without learning system-specific parameters leads to a low mean Pearson correlation of 0.12 ± 0.11.

Fig. 8.

IRAS captures the conservation law in predator–prey dynamical systems. The dataset contains 100 systems where in each system, the parameters were sampled uniformly within a range of 0.1 about the values (α, β, γ, δ)=(0.25, 0.075, 0.15, 0.07), and the initial conditions, x₀ and y₀ within a range of 1.0 about the values (x₀, y₀)=(4.5, 7.5). The raw observations consist of times-series of length 500 of x and y corrupted by a zero-mean Gaussian white noise with SD 0.055. (A) Top Right: predator–prey illustration. Left: time traces of the numbers of predator, (x, solid lines) and prey, (y, dashed lines) for a Lotka–Volterra model with parameters α = (0.208, 0.205, 0.200), β = (0.026, 0.032, 0.034), γ = (0.106, 0.106, 0.101) and δ = (0.020, 0.021, 0.028) in the Top, Middle, and Bottom panels, respectively. Bottom Right: same trajectories plotted in the phase plane (x, y). (B) Left: the conserved quantity as a function of time for the three systems in (A) with corresponding colors. Right: zoom of the conserved quantity and output of the combination learned by IRAS in a short stretch of time.

In summary, IRAS correctly identifies a conservation law which is the most “regulated” (conserved) combination in two examples of closed dynamical systems. With the extension of estimating a user-specified number l of parameters for different systems, the algorithm can identify the relevant parameters and construct the conserved quantity as a combination of the instantaneous observations and the estimated parameters.

D. Identifying Complex Physical Equations.

To further challenge the IRAS algorithm, we evaluate it on a broad range of physics problems, taking advantage of the recently published “Feynman Symbolic Regression Database” (FSReD) (8). This was generated using equations from the seminal Feynman Lectures on Physics (28). For each physical equation, the dataset provides a table of numbers, whose rows are of the form {z₁, z₂, …, z_n, y}, where y = f(z₁, z₂, …, z_n). In symbolic regression challenges (29), the aim is to discover the correct analytic expression for the function f(⋅). Here, to validate IRAS, we denote y as the n + 1 observable, and we look for a combination g(Z) where Z = [z₁, …, z_{n + 1}]. IRAS, if working correctly, should learn the combination g(Z) = z_{n + 1} − f(z₁, z₂, …, z_n).

The dataset contains equations with between 2 and 10 observables. The table for each equation contains 10⁵ rows with the data points [z₁, …, z_n] that were sampled uniformly in [1, 5]. Out of 100 different available equations, we picked four with high numbers of observables. For example, this is the 10 observable equation for the law of force in planetary motion

$$\begin{array}{c}\hfill g(Z)=F-\frac{G{m}_1{m}_2}{{(i_2-i_1)}^2+{(j_2-j_1)}^2+{(k_2-k_1)}^2},\end{array}$$ [21]

where Z = [G, m₁, m₂, i₁, i₂, j₁, j₂, k₁, k₂, F]. As in ref. 8, we added independent Gaussian noise to z_{n + 1} (F in Eq. 21) of standard-deviation 0.1σ(z_{n + 1}). To quantify the performance of IRAS, we compute the Pearson correlation between the ground-truth physical equation and the learned g(Z), for each of the four examples. As shown in Table 1, the agreement is excellent.

Table 1.

IRAS captures physical relations

	Combination	#observables	Corr
I.9.18	$F-\frac{G{m}_1{m}_2}{{(i_2-i_1)}^2+{(j_2-j_1)}^2+{(k_2-k_1)}^2}$	10	0.91
II.36.38	$f-\frac{{\mu }_{m}B}{K_{b}T}-\frac{{\mu }_m\alpha M}{ϵc^2{K}_{b}T}$	9	0.87
I.11.19	A − x1y1 − x2y2 − x3y3	7	0.92
I.29.16	$x-\sqrt{x_1^2+x_2^2-x_1{x}_{2}cos({\theta }_1-{\theta }_2)}$	5	0.92

Observations generated in FSReD (8) for four physical equations describing the law of force in planetary motion, spontaneous magnetization, scalar product of vectors, and the interference effect (28) serve as inputs to IRAS. The observables are corrupted by noise as described in the main text. The final column lists the Pearson correlation between the known physical equation and the combination learned by IRAS. The high correlation values testify to a correct identification of the underlying physical equation.

3. Discussion

Detecting invariants in dynamic data is a technically challenging problem with many potential applications. We presented IRAS, an algorithm that receives as input raw dynamic measurements and provides combinations, or functions, of these variables that are maximally conserved across time. Such conservation can be the result of internal regulation, where some variables compensate others to protect a control objective or it can be the result of symmetry and exact conservation laws. Taking a phenomenological approach to the problem, we introduced a quantitative measure—the Coefficient of Regulation (CR)—that characterizes the sensitivity of a combination to destroying temporal order among its constituents. This measure, regardless of the mechanism underlying invariance, serves as the basis of an optimization algorithm that outputs the combination most severely affected by temporal shuffling.

While the CR is an intuitive measure and can be shown to be very small for regulated or conserved combinations, its straightforward optimization is insufficient to escape “trivial” combinations that do not provide meaningful relations between the variables (Section B). To identify meaningful combinations with small CR, some constraints on the shuffled ensemble need to be implemented, so that time-ordering is destroyed while respecting the boundaries of the data. We proposed an iterative process between two players, one minimizing the CR and the other creating successively more constrained shuffled ensembles. IRAS converges when the two players cannot further improve. The algorithm then outputs a combination of variables as a proposed conserved quantity.

We provide validation in five distinct examples taken from very different realms and which reveal three versions of IRAS. First, we validated the simplest version, which optimizes an instantaneous combination—namely a function of the dynamic measurements at the same time point. Using a kinetic model of interactions between proteins, with feedback regulating a sum of two of them, we simulated traces over time in which system parameters were randomly perturbed. The feedback in the system induced compensations that maintained the control objective at a setpoint. This objective was correctly identified by the algorithm.

Second, we analyzed data from a human-computer closed-loop visual detection experiment (16), where the computer implemented a feedback loop that clamps the human response. Here, the CR was minimized among combinations that include consecutive time points in the data, aiming to recover the target of the engineered control system. The qualitative dependence between variables was identified correctly.

Third, we investigated two dynamical systems with known conservation laws. Here, we presented a generalized version of IRAS, suitable for cases where data from many similar systems are available, each with a different parameter set. Another neural network was added which identifies the parameters simultaneously with the two-player CR optimization (SI Appendix, Fig. S5). We emphasize that also here, no prior knowledge regarding the parameters was used. We demonstrated the success of the algorithm in identifying correctly the energy constant in a collection of ideal spring systems with different masses and spring constants, in the presence of noise. Similarly, we demonstrated the correct identification of the conservation law in a predator–prey system. These results are significant in light of the difficulty to identify conserved quantities, even in a single system (26). For example, trivial constants can result when attempting to identify conserved quantities in physical systems (25).

The conserved quantity is an implicit relation between measurements, defining a constraint and thus effectively reducing the dimensionality of the data. This is somewhat reminiscent of dimensionality reduction problems. The goal, however, is quite distinct in the two scenarios. Dimensionality reduction aims to describe the maximal amount of variability in the data using as few descriptors as possible. In contrast, we aim to find a meaningful combination of the data with a minimal amount of variability. The restriction to meaningful combinations, achieved through temporal shuffling, renders the two approaches qualitatively different and not easily comparable.

Our main motivation in this work was to understand regulation in complex biological systems. Often, such systems are “reverse engineered”—for example, using system identification or other methods, to build mathematical models based on observed data (30–36). A model can then be investigated to shed light on the functionality of the system, its robustness, and other properties. However, multivariable, multiparameter models are generally hard to understand even with explicit equations. Specifically, identifying a conservation law analytically or even proving its existence is an open research problem (37–43); thus, methods for deriving the differential equations of a system leave the question of identifying the conservation law unsolved.

Instead, we propose to analyze the properties of complex biological systems bypassing the modeling stage, to provide insight directly from dynamic data. We ask the general question: “What does the system care about”? in the sense of control theory. Namely, we seek to identify, directly from data, conserved or regulated quantities that the system protects from fluctuations and perturbations. Such homeostasis is a phenomenon of central importance in many biological contexts.

Recovering the control objective in an observed system is dealt with in Inverse Optimal Control (IOC) and Inverse Reinforcement Learning (IRL) (44, 45). However, in both IOC and IRL one has access to samples of a behaving system, acting according to some policy (usually a near-optimal one). These samples consist of both the system states and the external controls that drive the state-transitions. There is a clear separation between the states and the controls. Our biologically motivated setting corresponds to observing measurements of system variables without such separation. We are not aware of any IOC or IRL methods that deal with this type of problem.

Identifying conservation laws from observed data was also addressed in ref. 31. By identifying correlations between partial derivatives of pairs of variables, the algorithm detects physically meaningful quantities. These include the conserved Hamiltonian and the nonconserved Lagrangian. No distinction in terms of invariance is made between them. IRAS, on the contrary, is designed to find the most conserved quantity in the data by optimizing a measure of invariance under the shuffle constraint. Additionally, the algorithm in ref. 31 does not scale well to high-dimensional data and does not address homeostasis in families of systems that differ in their parameters.

Being a purely data-driven analysis method, we tell the story of the system in the “language” of the observables. Thus, we are limited by them. Spurious correlations between measurements may manifest as artefactual regulated combinations. Likewise, if by some fortunate coincidence, the controlled objective of the system is one of the individual raw measurements—IRAS will discard it because it is not a combination. Both of these caveats highlight the importance of biological context in data analysis.

The presented algorithm detects the most regulated combination within the observables. Commonly, a biological system will regulate multiple different objectives via different feedback loops. Once the most regulated combination was identified, we would like to continue the analysis and discover the next regulated combinations and be able to describe a hierarchy of control objectives (5). This aim is left for future work.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix. Previously published data were used for this work (Included in references).