MOMA: a multi-task attention learning algorithm for multi-omics data interpretation and classification

Abstract

Motivation

Accurate diagnostic classification and biological interpretation are important in biology and medicine, which are data-rich sciences. Thus, integration of different data types is necessary for the high predictive accuracy of clinical phenotypes, and more comprehensive analyses for predicting the prognosis of complex diseases are required.

Results

Here, we propose a novel multi-task attention learning algorithm for multi-omics data, termed MOMA, which captures important biological processes for high diagnostic performance and interpretability. MOMA vectorizes features and modules using a geometric approach and focuses on important modules in multi-omics data via an attention mechanism. Experiments using public data on Alzheimer’s disease and cancer with various classification tasks demonstrated the superior performance of this approach. The utility of MOMA was also verified using a comparison experiment with an attention mechanism that was turned on or off and biological analysis.

Availability and implementation

The source codes are available at https://github.com/dmcb-gist/MOMA.

Supplementary information

Supplementary materials are available at Bioinformatics online.

1 Introduction

Deep neural networks (DNNs) have been developed with diverse variations for increased performance according to different goals and domains; these include convolutional neural networks based on image data, recurrent neural networks based on sequence data, generative adversarial networks based on adversarial training and auto-encoders (AE) for learning representation. However, in biology and medicine, models require not only performance and prediction accuracy but also interpretability (Hanczar et al., 2020): interpretability helps physicians make accurate decisions related to diagnosis and treatment courses, thus impacting patients’ lives. High-performance models also reveal new biological relationships, for which interpretability is indispensable.

Module detection is an essential process for interpreting the heterogeneity between samples, as genetic or transcriptional variation differs with samples, even for the same disease. A module in this context is defined as a gene set with inter-relationships between genes. Many studies, using various machine learning methods, have identified inter-relationships including canonical correlation analysis (Min et al., 2021), clustering (Fu and Medico, 2007), generalization of principal component analysis (Argelaguet et al., 2018) and non-negative matrix factorization (NMF) (Yang and Michailidis, 2016). Recently, Min et al. (2021) constructed a canonical correlation analysis-based model and identified cancer-specific and shared microRNA-gene modules using multi-omics data sets of 33 cancer types from The Cancer Genome Atlas (TCGA). However, these traditional methods miss non-linear relationships between features (Argelaguet et al., 2018). Recently, neural network-based models have been developed (Chen et al., 2018; Dwivedi et al., 2020) that overcome these shortcomings and solve the lack of interpretability. Chen et al. (2018) have used AEs to embed gene-set nodes, include genes in the gene set through the first layer, and combine the gene set with the superset through weights in the second layer. The study by Dwivedi et al. (2020) uses AE and a light-up procedure to associate genes with hidden nodes to derive disease modules. These lines of work focus on unsupervised learning; however, with the accumulation of clinical phenotypes, such as disease presence, disease stage, drug response and medical value, supervised learning with clinical phenotypes is more appropriate for broad and flexible interpretation.

With advances in high-throughput techniques, the large amount of biomedical data, including molecular and medical information, have been accumulated (Bennett et al., 2018; Chen et al., 2021; Hutter and Zenklusen, 2018; Zeng et al., 2021), which can improve our current understanding of various diseases. Integration of these data promises to improve the prognosis and predictive accuracy of clinical phenotypes and facilitate more comprehensive analyses of complex disease prognosis (Hasin et al., 2017; Subramanian et al., 2020). Existing studies have demonstrated the advantage of integrating multi-biomedical data with various approaches, including matrix factorization (Chen and Zhang, 2018; Lock et al., 2013; Zhang et al., 2011, 2012; Zhang and Zhang, 2019), networks (Huang et al., 2019a; Koh et al., 2019) and DNNs (Chaudhary et al., 2018; Huang et al., 2019b; Sharifi-Noghabi et al., 2019). For example, Zhang et al. (2011) developed an NMF-based model to integrate microRNA and mRNA expression data in ovarian cancer. Chen and Zhang (2018) proposed the NMF framework in a network manner (NetNMF) to integrate pairwise genomic data. Recently, Zhang and Zhang (2019) adopted a matrix factorization-based model to reveal common as well as specific patterns from multiple datasets.

However, the integration of multi-biomedical data is one of the major challenges. Early integration, as reported by Chaudhary et al. (2018), is an approach to concatenate multiple datasets into a single dataset. However, early integration has three main disadvantages (Rappoport and Shamir, 2018). First, the weight is focused on a dataset with many features. Second, the distribution difference between datasets is ignored. Third, the input dimension of the model is increased. Late integration models (Sharifi-Noghabi et al., 2019) overcome these problems by separately learning each dataset and then integrating them. This approach preserves the unique data distribution. However, weak signals in each dataset may be lost during the integration phase (Rappoport and Shamir, 2018). Moreover, the biological interactions between features in multiple datasets may be lost (Sharifi-Noghabi et al., 2019).

Motivated by these limitations, we propose a Multi-task Attention Learning Algorithm for Multi-omics Data (MOMA) model, a novel and flexible approach that learns complex biological knowledge from multi-biomedical data to achieve high performance and interpretability. Using a geometrical approach, genes and modules were vectorized, and the vector sum of genes included in the module was interpreted as the corresponding module vector. To the best of our knowledge, this work represents the first attempt to use gene and module vectorization in DNNs. An attention mechanism (Bahdanau et al., 2014) was also designed as a mediator to identify related modules among multiple data. The result is an intermediate integration that overcomes the limitations of early and late integration, maintains a unique distribution of each dataset, considers biological interactions, and does not increase the input dimension of the model. MOMA also improves classification performance by focusing on important modules that are highly related to each other in each dataset.

The main contributions of this article are summarized as follows:

• This work introduces a new type of module detection system based on geometric interpretation.

• This work demonstrates the application of an attention mechanism for learning with a focus on the relevant modules between multi-omics data.

• Experimental results with various public datasets and various classification tasks demonstrate that this model outperforms several strong baselines, including the top-performing systems.

• Interpretation of module detection illustrates why the proposed model works well.

• The algorithm has been validated by turning on and off the attention mechanism, which is an important part of the MOMA algorithm.

2 Our proposed MOMA model

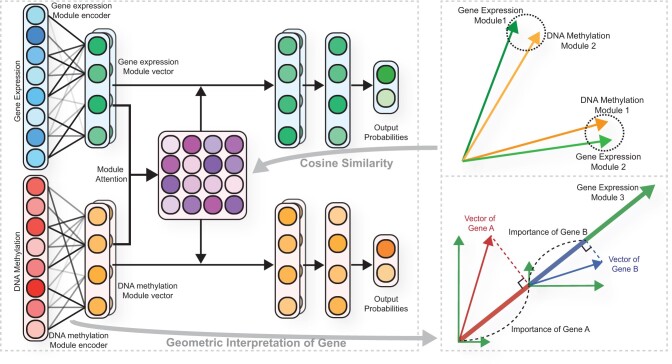
We propose the MOMA model (Fig. 1) for multi-omics module analysis and classification. Our model is composed of three stages: (i) building a module for each dataset using the module encoder, (ii) focusing on the important modules between each omics data using module attention and (iii) multi-task learning for each dataset in a fully connected layer.

Fig. 1.

Overview of the proposed MOMA algorithm for two omics datasets: gene expression and DNA methylation. Each module encoder generates module vectors for each dataset. The module encoder consists of a fully connected layer. The weights of the fully connected layer represent the association between genes and modules, and the weight vector of each gene represents weights between the gene and each module. The vector of the gene is the product of the gene input value and its weight vectors. Each module vector is generated by the sum of the vectors of all genes in that module. The inner product of a gene vector and a module vector represents the degree of gene contribution to the module vector. The gene expression and DNA methylation module vectors are fed into an attention layer that assigns higher weights to the relevant module vectors for disease prediction. The model is trained via multi-task learning

2.1 Module encoder

The module encoder consists of a fully connected layer that connects features of the omics data to each module, where each module is represented by a vector. Let weights of the fully connected layer ${\theta }_{\mathit{module}}^j$ represent the association between features and modules of the jth omics data and a weight vector corresponding to each feature and each module represent associations between them. The output nodes of the fully connected layer are normalized to unit vectors, which represent module vectors. Given a training sample $\{x^j,\hspace{0.17em}y\}$, where x^j denotes the sample under the jth omics of J omics datasets and y is the corresponding label, let $f_{\mathit{module}}^j$ denote the module encoder of jth omics data. The module vectors of jth omics data M^j are defined as follows:

$$M^j(x^j)=f_{\mathit{module}}^j\left(x^j;{\theta }_{\mathit{module}}^j\right)\in {\mathbb{R}}^{N^j\times D},$$ (1)

where θ_module denotes the weights of f_module, N^j is the number of modules of jth omics data, and D is the dimension of the module vector.

2.2 Module attention

A module attention mechanism was devised to focus on modules with high similarity between each omics data module. Cosine similarity was used to measure relevance. Let Att denote the module attention matrix between the module vectors of two omics datasets and Att_lk denote the element in row l and column k (that is the (l, k)th element of Att). Att_lk stores the relationship information with possible dependence between the lth module from one omics data and the kth module from another omics data module. The element in the attention matrix was devised as follows:

$$\begin{array}{c}At{t}_{lk}(M^i,M^j)=\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}\left(\text{cos}\hspace{0.17em}\left(M_l^i,M_k^j\right)\right)}{\hspace{0.17em}\sum _{k=1}^{N^j}\exp \left(\text{cos}\hspace{0.17em}\left(M_l^i,M_k^j\right)\right)},\hfill \\ s.t.\hspace{1em}i,j\in \{1,\dots ,J\}, i\ne j,\hfill \end{array}$$ (2)

where $M^j=M^j(x^j)$ for short and $M_l^i$ and $M_k^j$ are the lth module vector of ith omics data and the kth module vector of jth omics data. To highlight the important modules, the module vectors are multiplied by the attention matrices with the other omics data and concatenated. The updated module vector is

$$\begin{array}{c}\mathit{Att}\_M^j(x^j)=\left[{\left(\mathit{Att}(M^j,\overline{M^j})\right)}^T{M}^j\right],s.t.\overline{M^j}\in \left\{M\right|M\ne M^j\},\hfill \end{array}$$ (3)

where $M^j=M^j(x^j)$ for short. A toy example of the module attention mechanism is shown in Supplementary Figure S1.

2.3 Training

The fully connected layers are then applied, which flattens the multi-dimensional vectors and yields the final probabilities for each label. In the model, loss L is set to the cross-entropy error between the gold label and task-specific outputs:

$$\begin{array}{c}L=-\sum _{j=1}^J\sum _{c=1}^C{y}_c·\log \left(f_{fc}^j\left(\mathit{Att}\_M^j(x^j);{\theta }_{fc}^j\right)\right)\hspace{1em}\hspace{0.17em}\hfill \\ +\lambda \sum W^2, s.t.\hspace{0.17em}W\in \{{\theta }_{\mathit{module}},{\theta }_{fc}\},\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hfill \end{array}$$ (4)

where C represents the total number of classes, y_c denotes a labeling of c, $f_{fc}^j$ consists of multiple fully connected layers for jth omics data, θ_fc denotes the weights of f_fc, W denotes the weights, and an L2-norm penalty with a regularization parameter λ was used for optimization to avoid overfitting the module encoders and the multiple connected layers. The time complexity of the proposed approach is $\mathcal{O}(\mathit{IRFNJD})$, where I is the number of iterations, R is the number of samples, F is the number of features of omics data, N is the number of modules, J is the number of omics data types, and D is the dimension of the module vector. The MOMA models for two and three datasets are described in Supplementary Sections S2 and S3, respectively.

2.4 Module detection

The proposed model is an explainable model capable of not only predicting phenotypes, such as disease status, but also detecting modules containing genes related to phenotypes. The most relevant modules for a specific phenotype are identified using the module attention matrix. Each element in the module attention matrix represents the cosine similarity value between a pair of module vectors, each of which is obtained from a respective omics dataset. A pair of the modules having the largest cosine similarity paid the most attention in the training phenotype. Thus, they are selected as the most relevant modules.

From the most relevant modules identified, we next select the important features. Let $x_a^j$ be the value of feature a of jth omics data, ${\theta }_{\mathit{module}}^j(a,b)$ be the weight vector between feature a and the b-th module, and $M_b^j(x^j)$ be the bth module vector of jth omics data. Then, a feature vector of gene a is the product between $x_a^j$ and ${\theta }_{\mathit{module}}^j(a,b)$. The importance of the feature in the module is the inner product of the feature vector and the module vector, e.g. importance of feature a in module b is defined as follows:

$$\begin{array}{c}\mathit{Importance}(a,b)=\left(x_a^j\times {\theta }_{\mathit{module}}^j(a,b)\right)·M_b^j(x^j).\hfill \end{array}$$ (5)

Features with an importance greater than a predefined threshold are selected for each module.

3 Experiments

In this study, three experiments were performed: three different types of classification experiments, a turn-off and turn-on attention mechanism experiment, and a module detection experiment for the proposed MOMA validation method. TCGA datasets were used for the classification of 34 classes (33 types of cancer and normal) and for classification between the early and late stages of each cancer type. The Religious Orders Study (ROS) and Rush Memory and Aging Project (MAP) (ROSMAP) datasets were used for classification between Alzheimer’s disease (AD) and normal (NL) samples.

The classification performance of the proposed MOMA method was compared against that of eXtreme Gradient Boosting (XGBoost) and a DNN of single omics data. In a recent study (Ma et al., 2020), XGBoost displayed a remarkable performance in predicting early- and late-stage patients with kidney renal clear cell carcinoma (KIRC), kidney renal papillary cell carcinoma (KIRP), lung squamous cell carcinoma (LUSC), and head and neck squamous cell carcinoma (HNSC) in TCGA, when compared to the support vector machine, random forest, DNN, k-nearest neighbor, naive Bayes and elastic net models.

In addition, the MOMA model was compared with other multi-omics integration models based on an inductive learning approach. MOMA is an inductive learning approach, where the model is trained on a training dataset and then applied to a test dataset separated from the training dataset. Therefore, information related to the test dataset is not seen while creating the model. On the contrary, a transductive learning approach builds the model based on a training dataset and an unlabeled test dataset and then applies the model to the test dataset (Vapnik, 2000). For a fair comparison, we excluded the transductive supervised learning approach (Wang et al., 2017; Zhang et al., 2019). The compared methods include: (i) Multi-Omics gRaph cOnvolutional NETworks (MORONET) (Wang et al., 2020); (ii) Multi-Omics Factor Analysis (MOFA) (Argelaguet et al., 2018); (iii) Robust Multimodal Approach to Integrative Analysis of Multiomics Data (SMSPL) (Yang et al., 2020) and (iv) Pathway-aware multi-layered hierarchical NETwork (P-NET) (Elmarakeby et al., 2021). MORONET is a supervised multi-omics data classification model that uses graph convolutional networks incorporating patient associations for better performance. MORONET utilizes a view correlation discovery network to explore the cross-omics correlations at the label space. MOFA is a Bayesian model for unsupervised integration of multimodal data. For comparison of classification performance, we used a MOFA+SVM model that is composed of MOFA for feature extraction of multi-omics data and the SVM for classification. SMSPL is a self-paced learning model that interactively recommends high-confidence samples between multi-omics data. SMSPL demonstrates the advantage of a robust performance even in the presence of heavy noises and displays a good generalization performance. P-NET is a biologically informed neural network model and has been applied to predict the treatment-resistance state in prostate cancer patients using multi-omics datasets. It encodes different biological entities in a neural network with customized connections between consecutive layers of genes, pathways and biological processes.

In addition, for MOMA, in the attention mechanism turn-off and turn-on experiments, the ROSMAP data classification performance was compared through various parameter combinations. Module analysis was also performed to identify the effects of the multi-omics attention mechanism.

3.1 Datasets

3.1.1 ROSMAP datasets

Batch effect-normalized mRNA data, methylation data and clinical data were obtained from the ROSMAP cohort provided on the AMP-AD Knowledge Portal (https://adknowledgeportal.synapse.org/). Patients with gene expression and DNA methylation profiles were included. The clinical consensus diagnosis of cognitive status at the time of death (COGDX) scores 4 and 5 were labeled as AD, and the COGDX score 1 as NL. Quantile normalized fragments per kilobase of transcript per million mapped reads (FPKM) values of the gene expression profiles were log2-transformed. In the DNA methylation profile, β-values were measured using the Infinium HumanMethylation450 BeadChip and missing β-values were imputed using a k-nearest neighbor algorithm.

3.1.2 TCGA datasets

Batch effect-normalized mRNA data, methylation data and clinical data were obtained from the TCGA Pan-Cancer dataset provided on Xena (https://xenabrowser.net/). Patients with both gene expression and DNA methylation profiles and with available clinical information were included in the analyses. For classification of the 34 classes, ‘Primary Solid Tumor’, ‘Primary Blood-Derived Cancer Peripheral Blood’ and ‘Solid Tissue Normal’ sample types were included. For early- and late-stage classification, only primary tumors and samples with ‘pathologic stage’ information were included. Cancer types with at least 20 minor class patients were also included in experiments. The gene expression profile in this dataset has log2 transformed FPKM values. In the DNA methylation profile, CpG site levels were calculated as β-values measured using the Infinium HumanMethylation450 BeadChip.

3.2 Preprocessing

For DNA methylation data, CpGs located in promoter regions (TSS200 or TSS1500) were preprocessed into the corresponding gene. Next, all duplicated genes were averaged. For each dataset, the gene expression value and DNA methylation value were normalized to the range of 0–1. Finally, ROSMAP datasets, comprising 18 164 gene expression features and 19 353 DNA methylation features, and TCGA datasets, comprising 16 335 gene expression features and 17 016 DNA methylation features, were obtained. Table 1 shows the number of samples for each class in each experiment.

Table 1.

Summary of datasets used in this study

Cohort	Experiment	Class (Number of samples)
ROSMAP Cohort	AD and NL classification	NL (171), AD (218)
TCGA Cohort	34 classes classification	NL (394), ACC (78), BLCA (408), BRCA (777), CESC (303), CHOL (36), COAD (288), DLBC (48), ESCA (182), GBM (51), HNSC (515), KICH (65), KIRC (311), KIRP (270), LAML (170), LGG (514), LIHC (368), LUAD (452), LUSC (364), MESO (87), OV (9), PAAD (177), PCPG (178), PRAD (494), READ (94), SARC (255), SKCM (103), STAD (370), TGCT (149), THCA (501), THYM (120), UCEC (417), UCS (57), UVM (80)
	Early- and late-stage classification	ACC (46/30), BLCA (132/274), BRCA (557/208), COAD (155/121), ESCA (94/65), HNSC (98/343), KICH (45/20), KIRC (130, 179), KIRP (183/63), LIHC (255/90), LUAD (355/92), LUSC (302/59), MESO (26/61), READ (40/46), SKCM (68/30), STAD (168/192), THCA (334/165), UVM (39/40)

3.3 Experimental settings

The models were trained using nested cross-validation (CV) for unbiased performance estimates (Supplementary Fig. S2). Hyperparameters were estimated using inner CV loops nested in each outer CV loop. With an outer 5-fold CV, the classification performances were measured in terms of the accuracy (ACC), area under the receiver operating characteristic curve (AUC), F1 score, Matthews correlation coefficient (MCC) and average precision (AP), which is also known as a precision-recall AUC. Weighted AUCs, weighted F1 scores and weighted AP were used for multiclass classification.

The hyperparameters of each model were determined in the 3-fold inner CV on the training set. AUC was used as an evaluation metric. However, in the classification of 34 TCGA classes, because the AUC was ∼1, the ACC was used as an evaluation metric. For MOMA, the parameters of ‘the number of modules’ from the set {32, 64, 128}, ‘the learning rate’ from the set $\{5\times {10}^{-6},5\times {10}^{-7}\}$, ‘the weight decay’ from the set $\{{10}^{-3},{10}^{-5},{10}^{-7},0\}$, and ‘the early stopping patience’ from the set {50, 100} were optimized. The number of fully connected layers was fixed according to the number of modules. The Adam optimizer (Kingma and Ba, 2014) was used in the MOMA model. Details on the algorithm for this experiment and the list of other model hyperparameters are described in Supplementary Section S2. The grid search results for MOMA on the ROSMAP validation sets are described in Supplementary Tables S1 and S2.

3.4 Experimental results

3.4.1 Classification performance

XGBoost based on gene expression datasets, XGBoost based on DNA methylation datasets, DNN based on gene expression datasets, DNN based on DNA methylation datasets and MOMA are compared in terms of their classification performance in the ROSMAP and TCGA cohorts in Table 2 and Supplementary Table S3. An average scoring metric of 5-fold CV was reported. MOMA demonstrated the best ACC, F1 score, AUC, MCC and AP in the ROSMAP cohort. For TCGA 34 classes classification, MOMA showed the best prediction performance in ACC, F1 and MCC, whereas XGBoost showed the best performance in the AUC and AP. In the TCGA early- and late-stage classification, MOMA showed the best ACC performance in 7 of 18 datasets, the best F1 score performance in 13 of 18 datasets, the best AUC performance in 9 of 18 datasets, the best MCC performance in 12 of 18 datasets, and the best AP performance in 8 of 18 datasets. The number of datasets showing the best performance in ACC was smaller than that for the F1 score; this might be because of the imbalanced numbers of positive and negative samples. MOMA showed the best ACC performance in 5 of 7 balanced datasets and 2 of 11 imbalanced data sets (the proportion of samples of minor class patients was <35%).

Table 2.

Classification performance of XGBoost, DNN, and MOMA in ROSMAP NL and AD classifications, TCGA 34 classes classification, and TCGA early- and late-stage classification

		XGBoost				XGBoost				DNN				DNN				MOMA
		GE				DM				GE				DM				GEa				DMa
Task and datasets		ACC	F1	AUC	MCC	ACC	F1	AUC	MCC	ACC	F1	AUC	MCC	ACC	F1	AUC	MCC	ACC	F1	AUC	MCC	ACC	F1	AUC	MCC
ROSMAP NL/AD		0.686	0.723	0.757	0.363	0.596	0.664	0.632	0.168	0.653	0.740	0.764	0.284	0.589	0.581	0.616	0.180	0.737	0.740	0.812	0.488	0.720	0.753	0.807	0.432
TCGA 34 classes		0.953	0.951	0.998	0.951	0.950	0.949	0.998	0.948	0.878	0.848	0.988	0.874	0.875	0.837	0.985	0.870	0.948	0.945	0.996	0.946	0.954	0.952	0.996	0.952
TCGA early- and late-stage	ACC	0.633	0.455	0.681	0.191	0.672	0.435	0.673	0.241	0.618	0.386	0.671	0.157	0.578	0.305	0.710	0.024	0.723	0.654	0.725	0.429	0.710	0.611	0.720	0.393
	BLCA	0.756	0.832	0.772	0.410	0.685	0.785	0.688	0.221	0.675	0.806	0.636	0.000	0.699	0.800	0.712	0.223	0.705	0.771	0.736	0.352	0.663	0.716	0.747	0.335
	BRCA	0.718	0.179	0.630	0.101	0.716	0.154	0.584	0.094	0.701	0.188	0.573	0.088	0.705	0.232	0.602	0.117	0.692	0.288	0.616	0.134	0.651	0.331	0.618	0.125
	COAD	0.634	0.539	0.664	0.247	0.605	0.499	0.627	0.185	0.579	0.513	0.626	0.178	0.609	0.367	0.644	0.179	0.630	0.624	0.703	0.310	0.667	0.605	0.726	0.322
	ESCA	0.547	0.369	0.508	0.033	0.548	0.319	0.457	0.013	0.479	0.347	0.472	0.000	0.566	0.218	0.542	0.000	0.509	0.467	0.526	0.026	0.510	0.417	0.441	−0.001
	HNSC	0.780	0.874	0.607	0.131	0.605	0.499	0.627	0.185	0.778	0.875	0.542	0.000	0.778	0.875	0.501	0.000	0.728	0.832	0.631	0.079	0.648	0.727	0.643	0.196
	KICH	0.631	0.280	0.617	0.088	0.646	0.253	0.567	0.062	0.692	0.067	0.522	0.000	0.554	0.201	0.450	0.018	0.631	0.357	0.556	0.141	0.708	0.286	0.617	0.176
	KIRC	0.719	0.647	0.781	0.421	0.735	0.662	0.798	0.453	0.719	0.641	0.772	0.476	0.735	0.584	0.752	0.429	0.754	0.717	0.836	0.507	0.754	0.714	0.830	0.510
	KIRP	0.845	0.638	0.845	0.573	0.833	0.592	0.848	0.523	0.817	0.463	0.819	0.430	0.805	0.447	0.789	0.400	0.813	0.637	0.842	0.522	0.849	0.684	0.858	0.602
	LIHC	0.725	0.226	0.593	0.120	0.696	0.127	0.644	−0.004	0.733	0.088	0.547	0.034	0.733	0.236	0.665	0.134	0.699	0.366	0.680	0.188	0.730	0.314	0.688	0.190
	LUAD	0.779	0.056	0.605	0.020	0.792	0.130	0.643	0.132	0.794	0.000	0.612	0.000	0.794	0.000	0.509	0.000	0.711	0.241	0.595	0.092	0.761	0.177	0.612	0.092
	LUSC	0.834	0.029	0.564	0.020	0.831	0.084	0.460	0.085	0.703	0.057	0.567	0.000	0.837	0.000	0.533	0.057	0.698	0.190	0.506	0.023	0.695	0.224	0.500	0.044
	MESO	0.758	0.837	0.682	0.401	0.610	0.740	0.511	−0.027	0.701	0.822	0.622	0.033	0.690	0.816	0.421	−0.032	0.643	0.773	0.572	−0.064	0.609	0.719	0.607	0.019
	READ	0.571	0.624	0.519	0.138	0.536	0.560	0.582	0.063	0.523	0.620	0.605	−0.007	0.501	0.415	0.521	0.000	0.410	0.473	0.461	−0.203	0.465	0.516	0.479	−0.121
	SKCM	0.622	0.160	0.457	−0.059	0.623	0.237	0.590	0.027	.614	0.092	0.528	0.000	0.684	0.000	0.382	−0.030	0.654	0.292	0.490	0.101	0.644	0.153	0.446	0.001
	STAD	0.550	0.582	0.592	0.096	0.569	0.617	0.595	0.132	0.581	0.579	0.626	0.173	0.500	0.301	0.541	0.035	0.594	0.637	0.627	0.183	0.594	0.587	0.643	0.198
	THCA	0.719	0.460	0.718	0.307	0.731	0.487	0.732	0.343	0.705	0.350	0.694	0.262	0.735	0.434	0.708	0.322	0.687	0.595	0.761	0.378	0.727	0.618	0.769	0.418
	UVM	0.378	0.358	0.404	−0.252	0.480	0.454	0.509	−0.038	0.506	0.592	0.608	0.013	0.493	0.267	0.469	0.000	0.533	0.501	0.587	0.060	0.545	0.417	0.580	0.115

Note: The performance of the methods was evaluated for gene expression (GE) and DNA methylation (DM) datasets. Bold texts indicate the best performance in each metric, ACC, F1-score, AUC and MCC.

^aThe dataset used for the performance measurement (a task data set) is specified.

MORONET, MOFA+SVM, SMSPL, P-NET and Ensem-MOMA are compared in terms of their classification performance in the ROSMAP and TCGA cohorts in Table 3. Ensem-MOMA indicates an ensemble of the results of each MOMA task. The Ensem-MOMA model used logistic regression as a combiner. MORONET displayed a better performance than MOFA+SVM and SMSPL in TCGA 34 classes classification. Moreover, MOFA+SVM and SMSPL displayed a better performance than MORONET in a large number of binary classification tasks. These results might be attributed to the fact that MORONET is a complex multi-layered model, whereas MOFA, based on a Bayesian model, and SMSPL, based on a logistic regression model, are relatively uncomplicated. P-NET displays more strength in binary classification than in multiclass classification; this might be due to the smaller numbers of parameters in P-NET than in MORONET. Ensem-MOMA outperformed other methods in both binary classification and multiclass classification tasks. Supplementary Table S4 shows the results of the two-tailed paired t-test between other methods and MOMA for 5 CVs × 20 tasks (including ROSMAP NL/AD classification, TCGA 34 classes classification, and early- and late-stage classification of 18 cancer types). There were statistically significant differences in performance in all metrics except for ACC and an F1 score with P-NET. These results indicate that MOMA is a viable approach for improving performance in general classification tasks regardless of the datasets used.

Table 3.

Classification performance of MORONET, MOFA+SVM, SMSPL, P-NET and MOMA in ROSMAP NL and AD classification, TCGA 34 classes classification and TCGA early- and late-stage classification

		MORONET					MOFA+SVM					SMSPL					P-NET					Ensem-MOMA
Task and datasets		ACC	F1	AUC	MCC	AP	ACC	F1	AUC	MCC	AP	ACC	F1	AUCa	MCC	AP	ACC	F1	AUC	MCC	AP	ACC	F1	AUC	MCC	AP
ROSMAP NL/AD		0.612	0.647	0.648	0.222	0.661	0.663	0.699	0.769	0.320	0.826	0.689	0.732	0.678	0.368	0.757	0.663	0.708	0.777	0.313	0.843	0.732	0.750	0.815	0.466	0.861
TCGA 34 classes		0.945	0.943	0.997	0.943	0.971	0.869	0.865	0.994	0.863	0.914	0.891	0.874	0.902	0.886	0.805	0.725	0.757	0.996	0.739	0.948	0.958	0.957	0.996	0.957	0.980
TCGA early- and late-stage	ACC	0.712	0.508	0.747	0.351	0.663	0.553	0.084	0.670	−0.087	0.541	0.592	0.413	0.557	0.115	0.458	0.659	0.465	0.777	0.228	0.706	0.723	0.663	0.730	0.438	0.596
	BLCA	0.682	0.755	0.669	0.305	0.772	0.712	0.803	0.713	0.291	0.821	0.717	0.804	0.638	0.305	0.840	0.685	0.775	0.715	0.253	0.842	0.712	0.787	0.742	0.342	0.852
	BRCA	0.654	0.246	0.567	0.056	0.319	0.728	0.000	0.525	0.000	0.310	0.663	0.265	0.548	0.082	0.299	0.708	0.366	0.611	0.193	0.408	0.634	0.405	0.620	0.168	0.419
	COAD	0.623	0.580	0.633	0.244	0.568	0.649	0.575	0.681	0.279	0.615	0.645	0.613	0.645	0.292	0.584	0.656	0.605	0.738	0.302	0.700	0.641	0.660	0.713	0.335	0.665
	ESCA	0.534	0.255	0.477	−0.032	0.454	0.567	0.188	0.434	0.018	0.411	0.585	0.395	0.547	0.110	0.416	0.554	0.393	0.488	0.055	0.462	0.484	0.459	0.489	−0.007	0.467
	HNSC	0.748	0.852	0.555	0.028	0.819	0.733	0.838	0.617	0.051	0.857	0.757	0.853	0.562	0.142	0.819	0.753	0.856	0.609	0.060	0.855	0.726	0.834	0.632	0.035	0.859
	KICH	0.646	0.397	0.567	0.195	0.488	0.708	0.080	0.461	0.087	0.451	0.662	0.214	0.533	0.068	0.371	0.708	0.080	0.561	0.087	0.529	0.662	0.337	0.583	0.152	0.534
	KIRC	0.689	0.565	0.732	0.350	0.656	0.735	0.657	0.766	0.450	0.696	0.751	0.691	0.740	0.492	0.722	0.744	0.690	0.797	0.473	0.716	0.751	0.714	0.832	0.503	0.768
	KIRP	0.764	0.515	0.784	0.388	0.578	0.801	0.426	0.853	0.378	0.733	0.846	0.648	0.758	0.572	0.666	0.809	0.574	0.853	0.463	0.738	0.837	0.682	0.850	0.584	0.763
	LIHC	0.699	0.352	0.571	0.175	0.384	0.707	0.164	0.646	0.065	0.384	0.681	0.191	0.522	0.018	0.317	0.684	0.298	0.657	0.106	0.381	0.684	0.452	0.685	0.239	0.418
	LUAD	0.765	0.127	0.481	0.050	0.252	0.794	0.000	0.629	0.000	0.330	0.740	0.135	0.506	0.011	0.240	0.774	0.150	0.609	0.091	0.324	0.714	0.287	0.598	0.119	0.320
	LUSC	0.814	0.050	0.477	0.008	0.214	0.837	0.000	0.577	0.000	0.238	0.784	0.083	0.497	−0.021	0.192	0.812	0.025	0.405	−0.036	0.188	0.715	0.212	0.504	0.048	0.236
	MESO	0.608	0.715	0.584	0.004	0.790	0.690	0.816	0.481	−0.032	0.731	0.622	0.736	0.521	0.036	0.750	0.642	0.768	0.562	−0.056	0.792	0.666	0.790	0.621	0.044	0.813
	READ	0.534	0.633	0.486	0.062	0.562	0.443	0.448	0.614	−0.121	0.673	0.594	0.578	0.598	0.210	0.574	0.522	0.593	0.488	0.024	0.592	0.523	0.592	0.473	0.046	0.606
	SKCM	0.602	0.194	0.565	−0.015	0.445	0.694	0.000	0.625	0.000	0.487	0.592	0.150	0.463	−0.095	0.262	0.603	0.057	0.433	−0.138	0.335	0.644	0.260	0.456	0.070	0.391
	STAD	0.550	0.502	0.577	0.127	0.601	0.564	0.610	0.570	0.120	0.601	0.597	0.626	0.595	0.192	0.642	0.611	0.650	0.629	0.217	0.647	0.586	0.630	0.636	0.166	0.656
	THCA	0.669	0.469	0.690	0.237	0.535	0.701	0.337	0.698	0.222	0.582	0.693	0.546	0.667	0.329	0.579	0.723	0.515	0.745	0.338	0.648	0.703	0.602	0.765	0.385	0.701
	UVM	0.457	0.477	0.521	−0.072	0.572	0.544	0.603	0.387	0.087	0.503	0.533	0.492	0.536	0.076	0.514	0.563	0.453	0.531	0.140	0.620	0.596	0.561	0.577	0.205	0.628

Note: Bold texts indicate the best performance in each metric, accuracy, F1-score, AUC, MCC and AP.

^aIn SMSPL, predictor is categorical. AUC is computed by categorical values.

Supplementary Table S5 shows the computational time, number of parameters, memory usage and graphics processing unit (GPU) memory usage of XGBoost, DNN, MORONET, MOFA, SMSPL, P-NET and MOMA. In multi-omics data, DNN requires a large number of parameters and consumes a large amount of memory resources. Although MORONET, P-NET and MOMA are neural network-based models, they have relatively few parameters. MORONET reduces the number of features through feature selection, and P-NET uses a biologically informed neural network with customized connections. MOMA maintains the strength of neural networks and reduces the number of parameters through interactions between input features through the modularization of features and the attention mechanism.

To further compare the classification performance on different numbers of tasks and different data types, we performed two additional experiments. First, we experimented with three datasets from the Alzheimer's Disease Neuroimaging Initiative (ADNI), where two bioimaging datasets [magnetic resonance imaging regions of interest (ROIs) and AV45 positron emission tomography ROIs] and gene expression data were included. Supplementary Table S6 shows that the proposed model outperformed the existing models. The MOMA algorithm and experimental details are shown in Supplementary Material. Second, we applied MOMA to single-cell multi-omics data (single-cell RNA-seq and DNA-methylation datasets) to classify 2i and serum conditions of mouse embryonic stem cells (Supplementary Material). Supplementary Table S7 shows that MOMA outperformed XGBoost, MORONET, MOFA+SVM and SMSPL when the single-cell datasets were used.

3.4.2 Comparison between turning the module attention on and off

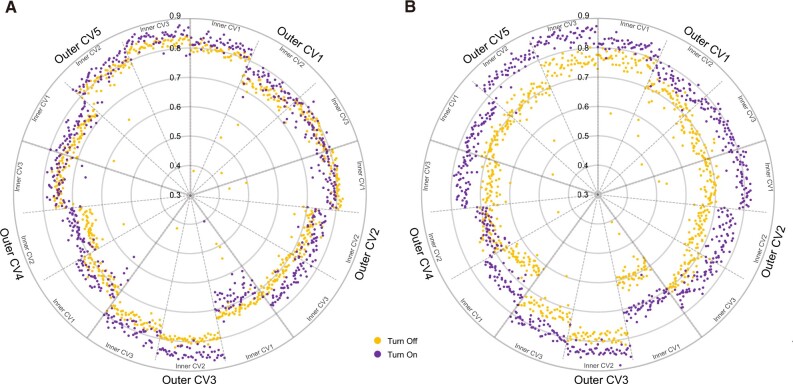
The performance of turning the module attention on and off according to various hyperparameter sets was compared through inner CV results in every outer CV. Figure 2 shows the results of each inner CV in the ROSMAP cohort; each point shows a different set of hyperparameters. Classification of AD and NL samples with gene expression and DNA methylation data showed statistically significant differences between turning the module attention on and off (p-values = $6.644E-31$ and $1.788E-222$ with two-sided paired t-tests, respectively). We also found statistically significant differences between turning the module attention on and off in the test results of 5-fold CV (P-value = $2.995E-5$ with a two-sided paired t-test). These results indicate that the module attention was helpful in learning the classification of AD and NL samples.

Fig. 2.

Comparison of turning the module attention on/off in the ROSMAP cohort. Every inner cross-validation result is reported along with the area under the receiver operating characteristic curve (AUC). Every point shows a different set of hyperparameters. (A) Results of gene expression classification. (B) Results of DNA methylation classification

To validate the generality of this experiment, the performance of turning the module attention on and off was compared in 18 cancer types of TCGA (Supplementary Figs S3–S7). In 5 of the 18 cancers, identifying related modules was not assisted by the attention mechanism. In esophageal carcinoma (ESCA) and LUSC, the attention mechanism negatively affected the identification of related modules (P-value < 0.05 with a t-test). In kidney chromophobe (KICH), rectum adenocarcinoma (READ) and skin cutaneous melanoma (SKCM), the attention mechanism had no role in identifying related modules. However, the classification performance on these data was low; thus, the attention mechanism might be difficult to use. Interestingly, there was a relationship between the classification performance and the impact of the module attention (Fig. 3). The higher the predictive performance, the more the attention mechanism helped. This result indicated that module attention was more effective for well-learned modules.

Fig. 3.

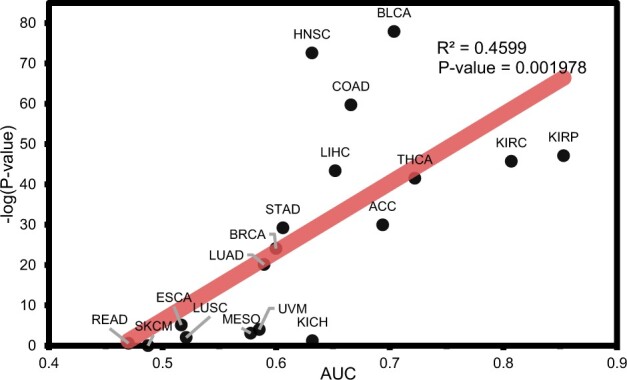
Relationship between the average area under the receiver operating characteristic curve (AUC) of inner cross-validation results in each TCGA cancer type and P-value in a paired t-test for the difference in turning the module attention on/off

3.4.3 MOMA module analysis

Figure 4 and Supplementary Figure S8 show the clustering results of the cosine similarity scores between gene expression and DNA methylation module vectors across the training and test datasets for each of the outer 5-fold CV results in the ROSMAP cohort. These results demonstrated that different module pairs of gene expression and DNA methylation were focused on while learning the AD and NL classification. Hierarchical clustering indicated that pairs that were important for each label during training were also maintained in the test.

Fig. 4.

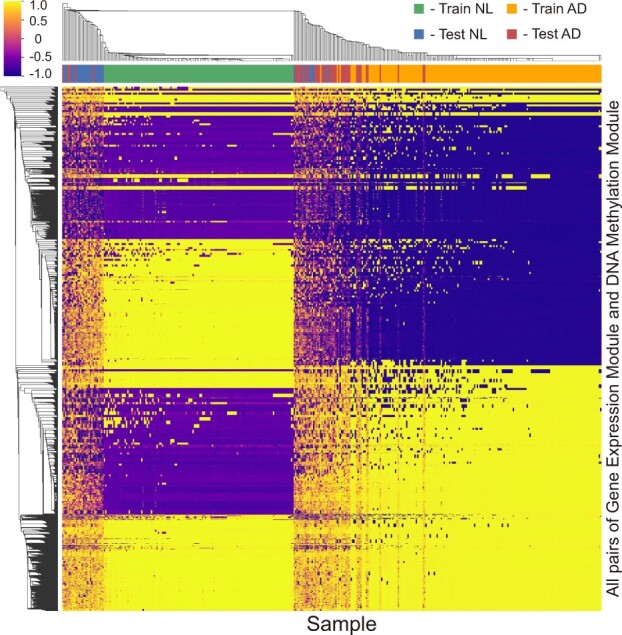
Heatmap of hierarchical clustered cosine similarity scores of the MOMA model in the ROSMAP cohort. Cosine similarity scores between the gene expression and DNA methylation modules of each sample are extracted

Next, we investigated the module attention to examine the genes contributing to the high classification performance in the ROSMAP cohort. A pair of the gene expression and DNA methylation module vectors that paid the most attention in training AD samples in each fold was selected. This pair had the largest cosine similarity score in the module attention matrix. In the selected modules, the importance of genes within each module was calculated using Equation (5) and their Z-scores were then calculated. Genes with greater than the Z-score threshold (empirically set to 99 percentile and 99.9 percentile for gene expression and DNA methylation, respectively) were selected. Pathway enrichment analysis was performed on these selected genes based on the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (Kanehisa and Goto, 2000) using Enrichr (Kuleshov et al., 2016).

Figure 5 shows the enriched KEGG pathways with P-values less than 0.05. The AD pathway was significantly enriched with q-values lesser than 0.05 in CV4 and CV5, and the AD pathway-related genes were also included in other CVs. Pathways associated with neurodegenerative disorders, including Parkinson’s disease and Huntington’s disease, were also significantly enriched (q-value < 0.05).

Fig. 5.

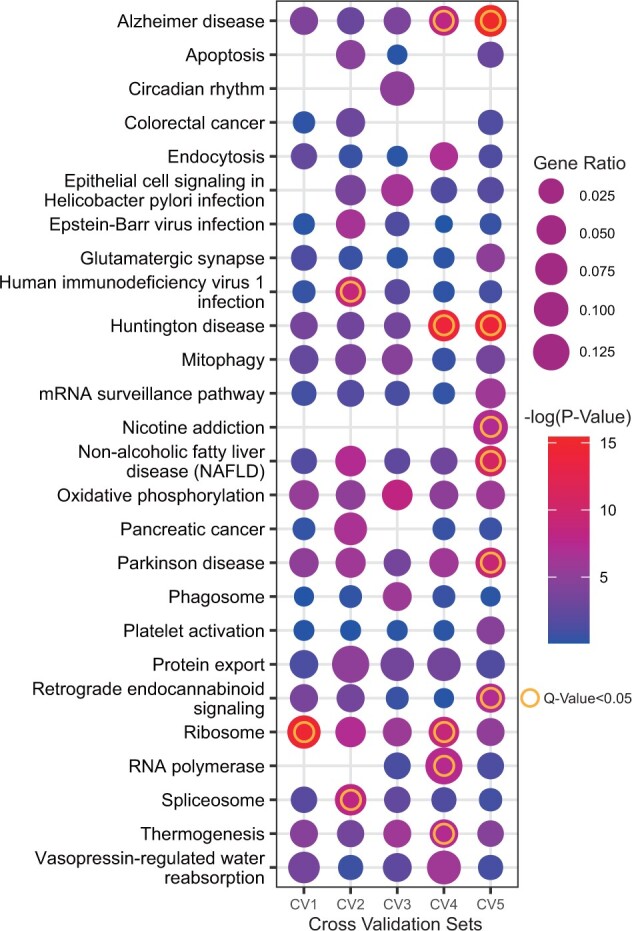
The Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway enrichment analysis of each cross-validation (CV) model. The dot size indicates the gene ratio. The dot color indicates the P-value. The ring indicates a significant pathway (q-value < 0.05)

Previous studies have revealed that AD is closely related to enriched pathways, such as apoptosis (Shimohama, 2000), circadian rhythms (Wu and Swaab, 2007), glutamatergic synapses (Rudy et al., 2015), mitophagy (Chen and Chan, 2009), oxidative phosphorylation (Manczak et al., 2004), platelet activation (Sevush et al., 1998) and ribosome (Ding et al., 2005). This observation is an interesting example of effective learning, including biological meaning, as well as module disease detection.

Module analysis results on TCGA cohort are shown in Supplementary Figures S9–S11. Supplementary Figures S9–S11 show the well-separated clustering results of the similarity score across the training and test datasets for the 34 TCGA class classification and early- and late-stage classification on KIRC and KIRP. Supplementary Figures S10–S11 show the possibility of module analysis in various classification tasks with enrichment analysis of cancer-related functions and pathways.

We additionally performed an experiment to identify cancer-specific modules using 34 TCGA cancer types. The attention matrix was calculated based on the input values using samples of each cancer type. We averaged the cosine similarity score for each module of one omics dataset to all modules of another omics dataset. Next, we identified a module having the highest average similarity score for each cancer type. Supplementary Figure S12 shows the cancer-specific modules and NL-specific modules and demonstrates that different modules tend to be enriched in different pathways.

4 Conclusions

In summary, this study used DNNs to identify biologically important mechanisms from multi-biomedical data, outperforming the classification of disease-related phenotypes and module analysis. A MOMA interpretable supervised learning model was proposed. Using a geometric approach, a module encoder layer and module attention mechanism were designed that capture important related modules from multi-omics data. In the AD and NL classification tasks, 34 cancer type classification tasks, and early- and late-stage classification tasks, the proposed method outperformed the XGBoost and DNN models for each single dataset. The proposed model also outperformed the recent multi-omics integration models when compared. Furthermore, through internal comparison with turning the module attention on and off, the effectiveness of the module attention mechanism in MOMA was demonstrated. Through module analysis, it was demonstrated that modules enriched in disease-related biological pathways were focused on by the module attention mechanism.

However, some limitations remain, which should be addressed to further improve the performance of the model. The model involves simple multi-task learning with uniform loss weights. This may cause an optimization conflict for each task or unbalanced learning for each task. As in the inner CV1 of outer CV3 in Figure 2, negative transfer occurs. Although the performance improved on average over all tasks, the performance of the model that turned the attention mechanism off was worse than that of the model that turned the attention mechanism on for the gene expression classification task. Recently, multi-task learning with uncertainty (Kendall et al., 2018) has been shown to alleviate unbalanced learning for each task. Therefore, multi-task learning optimization has the potential to improve performance. In future studies, we plan to use various formats, such as learning each gene encoder as a common parameter with soft-parameter sharing and learning with an adaptive sharing approach (Sun et al., 2019), which learns what to share for efficient multi-task learning. Another direction for improving performance is to consider training on a single output as well. In this study, our model had multiple outputs for prediction, the number of which was equal to the number of input datasets. Ensemble running was then performed with these outputs. We expect that the end-to-end training on one output together with multimodal learning may further improve the performance of the model. Furthermore, a bootstrapping technique (Li et al., 2019) and an accurate estimation of the density of models (Liu et al., 2021) can be incorporated to overcome the instability of models and improve performances of the model.