Integrative Analysis of Multi-modal Correlated Imaging-Genomics Data in Glioblastoma

Abstract

We propose a method to integrate high-dimensional genomics datasets across multiple platforms with multiple imaging outcomes. This new statistical framework uses a hierarchical model to integrate biological relationships across platforms to identify genes that associate with multiple correlated imaging outcomes. Our two-stage hierarchical model uses the information shared across the platforms and thus increasing the predictive power to identify the relevant genes. We assess the performance of our proposed method through simulation and apply to data obtained from the Cancer Genome Atlas Glioblastoma Multiforme dataset. Our proposed method discovers multiple copy number and microRNA regulated genes that are related to patients’ imaging outcomes in glioblastoma.

I. Introduction

Glioblastoma Multiforme (GBM) is the most lethal brain tumor with a patient survival rate of 15 months [1]. GBM develops for the most part in the cerebral hemisphere. If GBM is operable, then surgery is performed, followed by radiation therapy or a combination of radiation therapy and chemotherapy. Otherwise, radiation or radation/chemotherapy are administered. Radiological characterization/phenotyping has been carried out to identify survival-associated phenotypes. Typically, such studies have focused on single phenotypes such as T₁ or flair separately. In this study, we report analyses of combinatorial phenotypes that stratify survival in a subset of patients from the TCGA-GBM collection. Furthermore, we investigated molecular differences using messenger RNA (mRNA), microRNA (miRNA) expression and copy number alteration.

Cancer is a disease of the genome. Many profiling technologies have been developed and used to profile the cancer genome. Characterize the biology of cancer more comprehensibly the Cancer Genome Atlas (TCGA) created a project in 2006 to understand the molecular basis of cancer through genomic profiling. TCGA profiled genomic data using multiple platforms on more than 20 cancer types, and GBM was the first brain tumor to be selected because of its poor prognosis [2]. Thus, by combining all these various types of data, one can provide a unified view of the different molecular processes across the whole genome, which enables us to understand the gene functions across platforms. In addition, integrating all these various types of data in one statistical model will increase the statistical power to identify clinical relevant genes and/or better predict relevant patient-level clinical outcomes. Jennings [3] et al. proposed a general integrative Bayesian analysis of genomics data (iBAG) framework that models the biological relationships between several platforms to a single clinical outcome. This approach involves a global gene search, and uses variable selection via the Bayesian lasso-based shrinkage prior to deal with the high dimensionality of the data.

In this paper, we introduce a multivariate integrative analysis of high-dimensional genomic data with correlated imaging outcomes. This model uses a hierarchal approach to model biological relationships among and between different platforms and subsequently uses this information to the find associations with imaging outcomes. In this paper, we focus on aberrations of the RTK/PI3K, p53, and an RB cell signaling pathway which is known to be important pathways in cancer. We integrate mRNA expression, miRNA expression and copy number alteration to predict a combinatorial phenotype that stratifies survival for GBM patients. The two imaging phenotypes of interest in this paper are the volume of tumor T₁ and T₁ : flair ratio, where T₁ is the post contrast MRI image and flair is the hypertense volume. We also conduct simulation studies that show high sensitivity and specificity of our approach in gene selection.

The outline of this paper is as follows. In Section 2, we describe our multivariate integrative analysis model construction. In Section 3, we describe the implementation of our model and a bootstrap lasso stability variable selection method to identify important predictors of imaging outcome(s). In Section 4 we present our simulation studies and Section 5 summarizes the application to TCGA-GBM data. Section 6 contains conclusions and discussions.

II. A Multivariate Integrative Analysis of Multiplatform Genomic Data

We construct a multivariate integrative analysis model that uses a two-level hierarchical approach to integrate multiplatform genomic data and evaluates the relationships to the imaging outcome(s) of interest. The first-level is the genomic model that assesses the biological relationship between and among the platforms, miRNA, mRNA and copy number in this case, and directly infers the effects of miRNA and copy number on mRNA expression. We the subsequently use this information in our second stage imaging model to asses and detect which genes affect the imaging outcome(s).

Each patient datum in our analysis consists of multiple imaging outcomes (e.g. T₁, flair and ratio), mRNA expression, miRNA binding sites, genes copy number expression and “other” prognostic clinical factors (e.g. age, Karnofsky score). In the subsections below, we describe the constructions of the genomic and imaging models.

A. Genomic Model

Suppose n is the number of patients, j indicates the type of the genome platform and p_j is the number of genes measured on platform j. The genomic model for each gene can be expressed as:

$${\mathrm{X}}_{\mathit{mRN}{A}_g}={\mathrm{X}}_{\mathit{mRN}{A}_g}{\beta }_{1_g}+{\mathrm{X}}_{C{N}_g}{\beta }_{2_g}+{\mathrm{O}}_g,$$

where the terms in the genomic model can be described as follows:

• ${\mathrm{X}}_{\mathit{mRN}{A}_g}$ is the mRNA gene expression for gth gene denoted by gene_g and is of dimension n×1, g = 1, …, G

• ${\mathrm{X}}_{\mathit{mRN}{A}_g}$ are the miRNAs binding sites on the complete sequence (promoter, five prime untranslated region (5′UTR), coding region (CDS) and three prime untranslated region (3′ UTR)) to gene_g and is of dimension $n\times p_{j_g}$. In the miRNA data, we have multiple miRNA targets bind to any given gene. We use miRWalk [4], a comprehensive human database, that enables us to map miRNA-validated targets to the associated genes.

• ${\mathrm{X}}_{C{N}_g}$ is the expression of gene_g that is attributed to changes in copy number and of dimension n × 1

• O_g represents the “other” (residual) part of the gene_g expression unexplained by miRNA and CN and could be attributed to “other” biological mechanisms and is of dimension n × 1

In essence, the genomic component models the multiple miRNA validated targets and copy number jointly on the mRNA expression. Thus, for any given gene, our genomic model regresses (independently) each gene’s mRNA expression on the miRNA validated targets sites and copy number alterations – resulting in estimation of specific platform specific components in the above equation. We then subsequently use the estimated copy number, miRNA and residual components in our second level of the hierarchicy – the imaging model.

B. Imaging Model

Our imaging model relates the gene expression effects from the genomic model on the imaging outcome(s). We include the estimated effects from the genomic model as factors on the imaging model to find which genes’ expression, copy number and/or miRNA influence the imaging outcome(s) across multiple genes and can be written as:

$$\mathbf{Y}=\mathbf{C}{\gamma }^C+\mathbf{miR}{\gamma }^{\mathit{miR}}+\mathbf{C}\mathbf{N}{\gamma }^{CN}+\mathbf{R}{\gamma }^R+\epsilon$$

where the terms of the imaging model have the following representations and interpretations:

• Y is a n × k matrix, where k is the number of imaging outcome(s)

• miR =X_miRNAβ is a n × G matrix where the columns are the number of genes with miRNA expression.

• CN= X_CNβ is a n × G matrix where the columns are the number of genes with copy number profiling.

• R= X_mRNA−(miR+CN) is a n × G matrix where the columns are the number of genes for the “other” genomic profiles.

• C is a n × L matrix, were the columns are the number non-genomic clinical variables (e.g age, demographics)

• γ^miR are the expression effects through miRNA

• γ^CN are the expression effects through copy number

• γ^R are the expression effects through “other” biological mechanism

• γ^C are the clinical effects

The number of estimated miRNA-validated gene targets and the copy number from our genomic model could be very large (on the order of thousands) compared to the number of patients (on the scale of hundreds). The vast majority of the genes have no substantial influence on the imaging outcome(s); we are require, to perform some variable selection and/or sparse regularization to effectively identified which variables are significant/important.

III. Implementation

The implementation of our hierarchical model and the variable selection methods are described in this section. To conduct the estimation and the subsequent inference we first apply a Yeo-Johnson transformation [5] to satisfy the normality assumptions. Subsequently we use a covariance decomposition based projection approach to decorrelate the imaging outcomes and use a L1 (Lasso [6]) penalty for variable selection and shrinkage for a fast and scalable implementation of our approach.

Briefly, assuming the imaging features follow a multivariate normal distribution Y ∼ Normal(Xγ, Σ) where X is now stacked X = {miR, CN, R} and γ = {γ^miR, γ^CN, γ^O, γ^C}. To decorrelate the imaging outcomes we carry out the following steps. First we estimate the covariance matrix Σ using the empirical covariance matrix $\widehat{\sum }={\mathbf{Y}}^T\mathbf{Y}/n$. Next, we decompose the estimated covariance matrix using singular value decomposition (SVD) as $\widehat{\sum }=\mathbf{P}\mathbf{\Lambda }{\mathbf{P}}^T$ and subsequently define a “projection” matrix $\mathbf{\Phi }=\mathbf{P}{\mathbf{\Lambda }}^{-\frac{1}{2}}$. Now define Y* = YΦ as the projections of Y on Φ, which now represent the decorrelated (“whitened”) imaging outcomes, and now can be treated as independent random variables which enables fast fitting out our algorithms. Thus, Y* follows a Normal(X_γ*, I_n) were γ = γΦ. After the whitening procedure is perform, we use a L1 (Lasso) penalization for variable selection and shrinkage for each of the imaging outcomes Y*. Thus, the lasso penalization for each of the imaging outcomes i is:

$${\widehat{\gamma }}_{i_{\lambda }}^{\ast }=\mathit{argmin}\{{\Vert y_i^{\ast }-X{\gamma }_i^{\ast }\Vert }_2^2+\lambda {\Vert {\gamma }_i^{\ast }\Vert }_1\}$$

where $\lambda \in {\mathrm{\Re }}^{+}$ is the regularization parameter, ${\gamma }_i^{\ast }=\{{\gamma }_i^{C\ast },{\gamma }_i^{\mathit{miR}\ast }{\gamma }_i^{CN\ast },{\gamma }^{R\ast }\}$ and λ is selected to be min(λ) that achieves 80% of the deviance/MSE. For interpretation we transform back (“un-whiten”) the coefficients to the original scale by multiplying γ by Φ⁻¹

We expect the solution to be very sparse, since most of the genes will have no substantial contribution on the imaging outcome(s). To find the relative importance of each gene on the imaging outcome(s), we perform the bootstrap-based stability selection [7] procedure as described below:

Bootstrap Lasso Stability Selection

1. We pair (y_j1, …, y_jk, ${\mathbf{x}}_j^T$) where j = 1, …n and $x_j^T=\{x_{j1},\dots ,x_{jl}\}$.

2. for b = 1, …, B, resample the $\{y_{1j},\dots ,y_{kj},x_j^T\}$

   1. Decorrelate the k imaging outcomes

   2. for i = 1, …, k

   3. ${\widehat{\mathrm{\Gamma }}}_{i_{\lambda }}^{\ast (b)}=\mathit{argmin}\{{\Vert y_i^{\ast (b)}-X^{(b)}\mathrm{\Gamma }\ast \Vert }_2^2+\widehat{\lambda }{\Vert \mathrm{\Gamma }\ast \Vert }_1\},$ λ = min(λ ≥ Deviance_0.80) and i = 1, …, k

   4. “Un-whiten” ${\widehat{\mathrm{\Gamma }}}_{\lambda }^{\ast (b)}=\{{\widehat{\mathrm{\Gamma }}}_{1_{\lambda }}^{\ast (b)},\dots ,{\widehat{\mathrm{\Gamma }}}_{k_{\lambda }}^{\ast (b)}\}\Rightarrow {\mathbf{\Gamma }}^{(b)}$

3. repeat

Given the coefficients effect estimates for the B bootstrap samples, we determine the variable gene importance. We do this by first defining a practically minimum effect size δ (δ = 0.01, our analysis). Note that for any bootstrap sample b, ${\gamma }_{i,l}^{(b)}$, is considered not important if it does not exceed the δ cut-off. Then, we compute a gene marker l importance “probability”, $P(y_i,x_l)={\displaystyle {\sum }_{b=1}^B\mathbf{I}(|{\gamma }_{i,l}^{(b)}|\ge \delta )}$ for each i imaging outcome. Finally, we select the gene markers for each of imaging outcomes as important if the $P(y_i,x_l)={\displaystyle {\sum }_{b=1}^B\mathbf{I}(|{\gamma }_{i,l}^{(b)}|\ge \delta )}\ge 0.5$, ∀i,l.

Once the relevant genes are identified, we estimate the gene effects, by regressing the imaging outcome(s) on the relevant genes to learn which genes have a positive effect on the imaging imaging(s) and vice-versa.

IV. Simulations

In this section, we assess the performance of our models in terms of accuracy (sensitivity and specificity) of detecting associated genes. To better illustrate the basics features of our imaging model, we generate data with two distinct outcome variables based on our real data. We set n = 100, X ~ Normal(0, 1) and Y∼ Normal(Xγ, Σ). The correlation for the two imaging outcomes is set to ρ = −0.5. This correlation was chosen to mimic the correlation of the TCGA data imaging outcome(s). We simulated data for p = (100, 250) predictors for γ₁ and γ₂, were 90% of γ₁ and γ₂ are set to 0, and the other 10% of Γ₁ and γ₂ are sample from Normal(4, 1) with probability 0.5 or from a Normal(−4, 1) with a probability 0.5. We allowed 5% both γ₁ and γ₂ to have an effect on the outcomes. For example, the regression coefficients for the first and second response could be:

$$\begin{array}{l}{\gamma }_1=(\stackrel{10\mathrm{\%}}{\overbrace{1,1,\dots ,\stackrel{5\mathrm{\%}}{\overbrace{1,1,\dots ,1}}}},\stackrel{90\mathrm{\%}}{\overbrace{0,0,0,0,0,0,0,0,0,\dots ,0}})\\ {\gamma }_2=(\stackrel{5\mathrm{\%}}{\overbrace{0,0,\dots ,0}},\stackrel{10\mathrm{\%}}{\overbrace{1,1,1,\dots ,1,1,1,1}},\stackrel{85\mathrm{\%}}{\overbrace{0,0,0,\dots ,0}})\end{array}$$

Now we apply our method to estimate the coefficients for our imaging model and evaluate the number of genes identified, the number of true positive rate and true negative rate which are shown in Table 1. Our simulation suggests that our method is very effective in selecting true positive and true negative genes. Our method mean γ₁ and γ₂ sensitivity is about 98% and mean specificity is about 92% for 200 parameters (100 each). The mean specificity and sensitivity for 500 parameters (250 each) is about 86% and is 82% respectively – thus demonstrating good performance in relevant gene selection.

Table I.

Simulations: sensitivity and specificity for various sample sizes and regression parameters.

		Sensitivity		Specificity
# Parameters		γ 1	γ 2	γ 1	γ 2
200	mean	0.986	0.987	0.926	0.927
	stdev	0.0377	0.0368	0.0171	0.0171
500	mean	0.861	0.858	0.823	0.822
	stdev	0.07012	0.0719	0.0172	0.0284

V. Integrative analysis of GBM data

Radiological characterization/phenotyping was been done to identify survival-associated phenotypes on 83 TCGA-GBM patients. The two radiological characterization are T₁ and ratio. The T₁ feature represent the volume contrast enhancing region of the tumor as seen as a T₁-weighted post contrast MRI image. The ratio refers to the ratio of the T₁ post contrast image to the volume T₂-flair image. In our integrative analysis we use 83 matched tumor samples that have been assayed by expression, microRNA and copy number platforms.

A. Description of data

We focus on 49 genes of the RTK/PI3K, p53, and RB cell signaling pathways which is known to be an important pathway in cancer [8]. The level 3 processed data was downloaded from TCGA data portal by MD Anderson. The Karnofsky score (KPS) was downloaded from cBioPortal for Cancer Genomics [9] which resulted in the following data matrices:

• Radiological features (83×2) : T₁ is the volume enhancing region, ratio of the T₁ and flair hypertense volume

• Pathway-mRNA (83×49) contains the mRNA expression level for genes and patients.

• Pathway-CopyNumber (83 × 49) contains the genes log copy numnber and the patients

• Pathway-microRNA (83 × 534) contains the miRNA target sites and the patients

We removed six patients from our analysis. One TCGA patient is missing from the mRNA platform, another one is missing from the copy number platform, three more are missing from microRNA platform, and one more for being an outlier (TCGA-08-0352 flair=2.73E+05 T1=286 ratio=953.1). Thirteen KPS values were imputed. Therefore, at the end, we kept 77 patients for each platform. After performing a multivariate Yeo-Johnson transformation ( $T_1^{0.29}$ and ratio^0.1), we apply our method to estimate the effects of our integrative model.

B. Results

The results indicate that 28 genes are significant from the 49 genes aberrations of the RTK/PI3K, p53, and RB cell signaling pathways. In figure 1 and 2, we show the gene relative importance “probability” for the 49 genes group by copy number, miRNA and “other”. We consider a gene to be significant if the relative importance “probability” is greater than the cut-off 0.5, otherwise, it is classified as not significant. The genes with higher relative importance “probability” are blue in the heatmap and those that are not significant are gray. Few genes barely meet the cut-off, for example, the PDGFRB for the “other” biological mechanism importance “probability” is 0.51 for T₁ and .502 for ratio. We found 28 genes to be significant, 12 genes attributed through copy number (FGFR1, CDKN2B, CDKN2C, PIK3R1, CCND1, HRAS, PDGFRA, AKT3, CDK6, PIK3CD, MDM2 and AKT1), 2 genes attributed through miRNA (CCND2 and PDPK1) and 15 genes attributed through the “other” (MDM4, AKT2, ERBB2, PIK3CG, PDGFRA, ARAF, PIK3C2G, PIK3R1, PIK3CB, CBL, CDKN2C, TP53, MDM2, IRS1 and PDGFRB) biological mechanism in both T₁ and ratio. Only four genes CDKN2C, PIK3R1, PDGFRA and MDM2 were classified to be significant for both copy number and the “other” (e.g. methylation, transcriptional) mechanism.

Fig. 1.

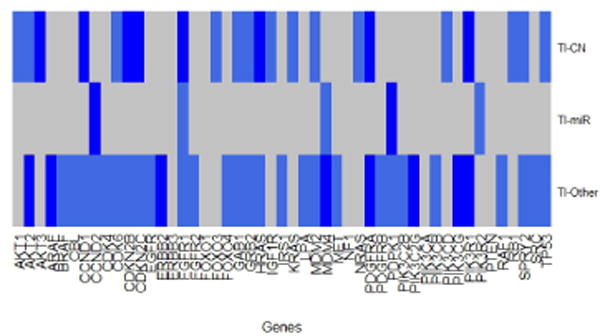
T₁ significant importance “probability” heatmap plot. A gene is consider significant if the “probability” of being chosen is greater than 0.5. The gray shaded markers are the genes that are not significant and the blue shaded markers are the significant genes.

Fig. 2.

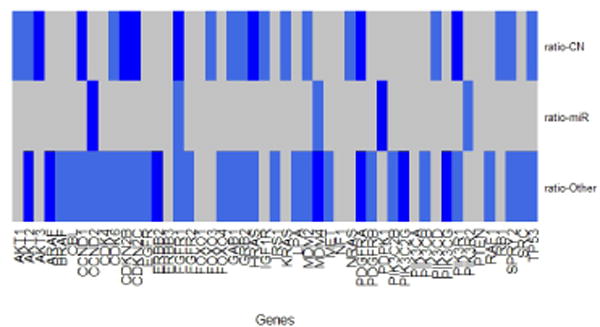
ratio significant importance “probability” heatmap plot. A gene is considered significant if the “probability” of being chosen is greater than 0.5. The gray shaded markers are the genes that are not significant and the blue shaded markers are the significant genes.

After selecting the importance genes, we regress the two radiological phenotypes (T₁,ratio) on the estimated pieces for those relevant genes from the genomic model and the two clinical predictors (KPS, Age). In figure 3, we show that eight genes to be significant for the T₁ image outcome and eleven genes to be significant for the ratio image outcome. Six out of the eight significant genes from the T₁ image outcome have a negative effect (smaller tumor) and two have a positive effect (larger tumor) on T₁. Four out of the eleven significant genes from the ratio image outcome have a negative effect (greater infiltration) and seven have a positive effect (smaller infiltration) on ratio. We found that copy number attribute gene FGFR1 has antagonistic gene effect on the imaging T₁ and ratio outcomes.

Fig. 3.

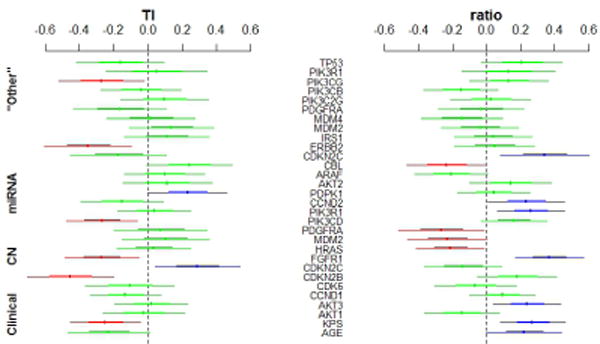
The direction of the important gene effects for the T₁ and ratio outcomes. Red: significant negative effect on T₁ (smaller tumor) and on ratio (greater infiltration); Blue: significant positive effect on T₁(lager tumor) and on ratio (less infiltration) ; Green: not significant

VI. Conclusion

In this paper, we have introduced an innovative multivariate integrative model that integrates genomic data from various platforms with multiple imaging outcome(s). Our model uses a two level hierarchical approach to integrate biological relationships, and then uses this information to identify the significant genes that influence the imaging outcome(s). Our simulation shows that our model identifies true positive and true negative genes very effectively. We apply this model to integrate copy number, micorRNA and “other” expression from TCGA-GBM data. Our model helps us identify relevant genes effects from copy number, microRNA and “other” biological mechanisms influence the imaging outcome(s). In summary, the advantages from our model are to (i) identify genes effects that influence a disease, (ii) integrate a number of multiple platforms into one statistical model, (iii) model biological relationships among and between different platforms to the imaging outcome(s), (iv) handle high-dimensional data effectively and (v) relates effectively multiple correlated imaging outcome(s) to predictors from different genomic platforms. In the future, we plan to investigate non-linear extensions of our model which might be more biologically relevant in some instances. Another avenue of research might be to include a multiple pathways into our model to further explore the effects on imaging outcomes.