Abstract
Target trial emulation (TTE) applies the principles of randomized controlled trials to the causal analysis of observational data sets. One challenge that is rarely considered in TTE is the sources of bias that may arise if the variables involved in the definition of eligibility for the trial are missing. We highlight patterns of bias that might arise when estimating the causal effect of a point exposure when restricting the target trial to individuals with complete eligibility data. Simulations consider realistic scenarios where the variables affecting eligibility modify the causal effect of the exposure and are missing at random or missing not at random. We discuss means to address these patterns of bias, namely: 1) controlling for the collider bias induced by the missing data on eligibility, and 2) imputing the missing values of the eligibility variables prior to selection into the target trial. Results are compared with the results when TTE is performed ignoring the impact of missing eligibility. A study of palivizumab, a monoclonal antibody recommended for the prevention of respiratory hospital admissions due to respiratory syncytial virus in high-risk infants, is used for illustration.
Keywords: average causal effect, eligibility, missing data, multiple imputation, target trial emulation
Abbreviations
- ACE
average causal effect
- CI
confidence interval
- HTI
Hospital Treatment Insights database
- MAR
missing at random
- MCAR
missing completely at random
- MI
multiple imputation
- MNAR
missing not at random
- RCT
randomized controlled trial
- RSV
respiratory syncytial virus
- TT
target trial
Randomized controlled trials (RCTs) are commonly used for estimating causal effects of point interventions. However, in many epidemiologic settings, an RCT may be infeasible or ethically nonviable. Hence, observational data are also used to compare effectiveness, with various strategies adopted to address the lack of randomization and indication bias, for example, by controlling for measured confounders. Analysis of observational data suffers from various additional sources of bias, such as selection bias, indication bias, and immortal time bias (1).
Target trial emulation aims to avoid some of these biases by adopting the design principles of RCTs. Individuals in an observational database, such as administrative health records, are selected according to a set of eligibility criteria that mirror those that would be used in an RCT (2). However, data on variables that determine eligibility are often incomplete, and as such not all participants of the target trial (TT) are identifiable from the observational database. It is typically advised to consider a different target trial with more complete eligibility criteria (1) or to exclude or censor individuals with missing data (3, 4). Missing data is often a source of bias when those excluded are systematically different from the observed (i.e., if data are missing at random (MAR) or missing not at random (MNAR)) (5, 6). Although identified as a potential limitation, there is little work investigating the extent to which missing eligible data can impact the analysis of a target trial.
One solution is to impute missing eligibility prior to selection into a target trial. However, we could find only one precedent of imputation of eligibility criteria prior to the creation of a target trial in (7). More generally, multiple imputation (MI) of exclusion criteria in observational studies has been considered in a recent work (8) for validating error-prone confounders, but it remains an infrequently studied topic. We intend to bring attention to work of this kind to the context to target trial emulation.
In this paper we investigate biases in the average causal effect (ACE) of a point exposure, in a target trial with missing eligibility data. Our simulations consider realistic scenarios where the eligibility variables modify the true causal effect. We consider two strategies of analysis: 1) conditioning on variables that drive missingness eligibility, and 2) recovering the missing eligibility data via MI. A study of palivizumab, a monoclonal antibody for prevention of symptoms of severe respiratory syncytial virus (RSV) infection in high-risk infants, based on administrative hospital and pharmacy dispensing data is used to illustrate these alternative approaches.
METHODS
Setup
Consider the setting with a binary treatment 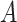 , end of study outcome
, end of study outcome 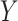 , and confounding variables
, and confounding variables 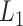 and
and 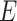 , where the latter determines eligibility. Suppose
, where the latter determines eligibility. Suppose 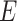 has informative missingness, with
has informative missingness, with 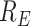 being an indicator of completeness (1 = complete, 0 = missing). Missingness in
being an indicator of completeness (1 = complete, 0 = missing). Missingness in 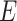 may be MAR, driven by variables that are not necessarily confounders, which we denote
may be MAR, driven by variables that are not necessarily confounders, which we denote 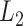 and
and 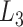 , or MNAR, if also driven by
, or MNAR, if also driven by 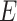 itself (9) (Figure 1). This is a typical setting, whereby
itself (9) (Figure 1). This is a typical setting, whereby 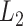 and
and 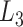 are separate causes of respectively
are separate causes of respectively 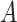 and
and 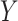 .
.
Figure 1.
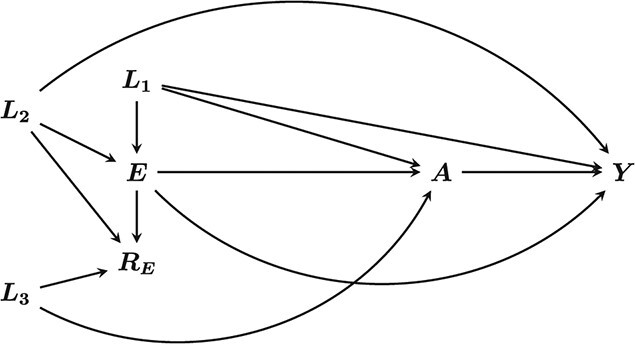
Directed acyclic graph of the assumed relationships between exposure, outcome, confounders, and data missingness indicator. A and Y are the exposure and outcome respectively. 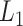 are confounders of the association between A and Y, with E the variable that determined eligibility for the target trial.
are confounders of the association between A and Y, with E the variable that determined eligibility for the target trial. 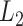 and
and 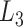 are drivers of missing data in
are drivers of missing data in 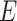 .
.
We emulate a TT where eligibility is defined by 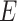 being greater than or equal to some value
being greater than or equal to some value 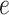 . In practice
. In practice 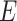 may represent a set of variables, which determine an eligibility indicator variable
may represent a set of variables, which determine an eligibility indicator variable 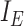 . The mechanism for inclusion is shown in Figure 2, represented by the box (indicating conditioning) surrounding
. The mechanism for inclusion is shown in Figure 2, represented by the box (indicating conditioning) surrounding 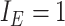 . It also shows the selection mechanism induced by restricting the TT to individuals with complete
. It also shows the selection mechanism induced by restricting the TT to individuals with complete 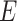 , indicated by the box around
, indicated by the box around 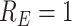 . We distinguish between:
. We distinguish between:
Figure 2.
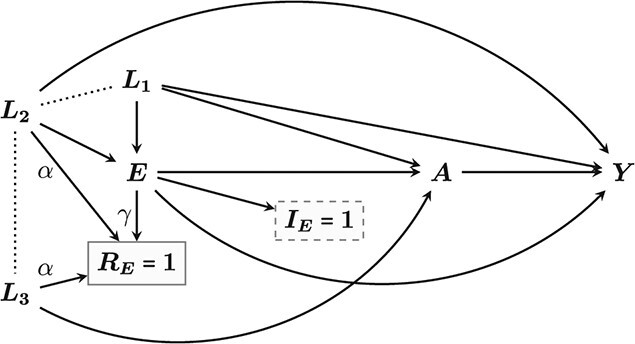
Directed acyclic graph of the assumed relationships between exposure (A), outcome (Y), and confounders (L), and the eligibility processes represented by the indicator 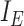 plus the missing mechanism in
plus the missing mechanism in 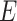 represented by
represented by 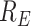 . The solid and dashed boxes around these main indicators represent conditioning and the dotted lines represent spurious associations caused by this conditioning.
. The solid and dashed boxes around these main indicators represent conditioning and the dotted lines represent spurious associations caused by this conditioning.
The source population, from which the TTs are derived
The full eligibility TT (
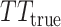 ), containing all those who are eligible
), containing all those who are eligible 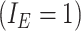
The complete eligibility TT (
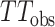 ), containing those who are complete and eligible, (
), containing those who are complete and eligible, (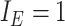 and
and 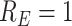 )
)
Our target estimand is the ACE of 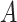 on
on 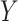 in
in 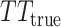 , defined as,
, defined as,
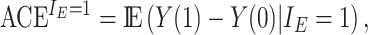 |
(1) |
where 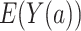 is the average value of
is the average value of 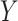 , if the exposure
, if the exposure 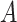 were set to take the value of a, for a = 0,1 in the whole population. In reality,
were set to take the value of a, for a = 0,1 in the whole population. In reality, 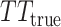 is not known, and thus
is not known, and thus 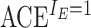 is approximated by the equivalent estimand from
is approximated by the equivalent estimand from 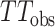 ,
,
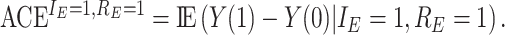 |
(2) |
The ACE of a point exposure can be identified by invoking assumptions of no interference, counterfactual consistency, and conditional exchangeability (i.e., no unmeasured confounding) (2).
Sources of bias
If we attempt to estimate 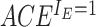 from an estimate of
from an estimate of 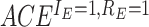 we would be prone to 2 sources of bias: collider bias and selection bias.
we would be prone to 2 sources of bias: collider bias and selection bias.
Collider bias.
The confounders 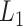 and
and 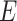 are common causes of exposure and outcome which need to be controlled for, while
are common causes of exposure and outcome which need to be controlled for, while 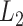 and
and 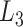 , the drivers of missingness, are not. However, when we condition on
, the drivers of missingness, are not. However, when we condition on 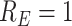 , we create a spurious association between
, we create a spurious association between  and
and  , which confounds the causal effect of
, which confounds the causal effect of 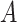 on
on 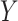 via
via 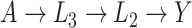 (Figure 2). This is a type of collider bias known as Berkson’s bias (10, 11), which must be removed by conditioning on either
(Figure 2). This is a type of collider bias known as Berkson’s bias (10, 11), which must be removed by conditioning on either 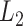 or
or 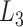 .
.
Selection bias.
When 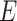 has informative missing data, the missing eligible (
has informative missing data, the missing eligible (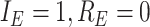 ) contain information about
) contain information about 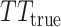 that cannot be recovered by
that cannot be recovered by 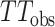 . This can result in selection bias when conducting an analysis on
. This can result in selection bias when conducting an analysis on 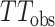 if, for any reason, the causal effect of
if, for any reason, the causal effect of 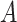 on
on 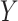 is different in the missing eligible, compared with the complete eligible.
is different in the missing eligible, compared with the complete eligible.
By controlling for 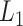 ,
, 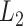 , and
, and 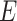 we identify the causal effect,
we identify the causal effect,
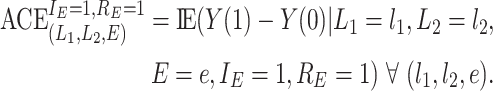 |
(3) |
To find 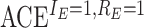 we marginalize (average)
we marginalize (average) 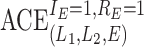 over the distribution of
over the distribution of 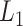 ,
, 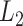 and
and 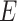 in
in 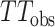 .
.
If the effect of 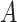 on
on 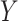 is modified by these confounders, then the value of
is modified by these confounders, then the value of 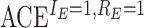 depends on the distribution of that confounder in
depends on the distribution of that confounder in 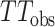 .
.
Hence, since we cannot recover the distribution of the confounders in 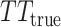 ,
, 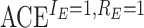 , obtained from
, obtained from 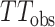 , is a biased approximation of
, is a biased approximation of 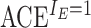 . In other words, the distribution of the confounders in
. In other words, the distribution of the confounders in 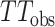 , does not match that in
, does not match that in 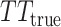 .
.
Suppose 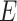 was a score capturing standards of hospital care. We might expect a treatment
was a score capturing standards of hospital care. We might expect a treatment 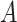 to be more effective on the outcome at higher standards of care. Now if hospitals of a low standard are more likely to have a missing score, then we would overrepresent eligible hospitals of higher standards in
to be more effective on the outcome at higher standards of care. Now if hospitals of a low standard are more likely to have a missing score, then we would overrepresent eligible hospitals of higher standards in 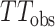 , and lead to a biased ACE.
, and lead to a biased ACE.
Dealing with this bias requires recreating the joint distribution of exposure, outcome, and confounders of 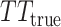 , for example, using multiple imputation (12–14).
, for example, using multiple imputation (12–14).
This bias has been discussed in the wider setting of “data-fusion” of multiple data sources (15), with identification of targeted causal effects involving knowledge of the distribution of the confounders in the “fused” population, as we discuss above. This type of bias has been referred to as an issue of “transportability” (15) or external validity to a different population (16). Our setting is created by missing information that precludes the identification of the target population. This could be viewed as an issue of internal validity of 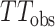 itself, or of its external validity to
itself, or of its external validity to 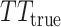 . The issue also has an impact on the generalizability of results to other populations.
. The issue also has an impact on the generalizability of results to other populations.
Strategies
We indicate possible strategies to address the above biases in the estimation of 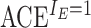 .
.
Strategy 1: ignoring missing eligibility.
In the setting of Figure 2, we fit an outcome regression model for 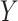 on
on 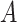 , controlling for
, controlling for 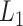 and
and 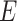 in the model, and then estimate
in the model, and then estimate 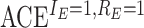 by marginalizing over their distribution in
by marginalizing over their distribution in 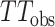 , as described in Aolin et al. (17).
, as described in Aolin et al. (17).
Strategy 2: dealing with collider bias.
With this approach we fit an outcome regression model for 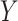 on
on 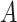 , controlling for
, controlling for 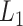 ,
, 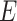 , and either
, and either 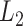 or
or 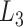 in order to block the path opened by conditioning on
in order to block the path opened by conditioning on 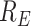 , and then estimate
, and then estimate 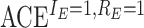 as in strategy 1.
as in strategy 1.
If the estimand of interest is 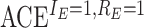 , then this strategy is sufficient to remove bias induced by missing eligibility data.
, then this strategy is sufficient to remove bias induced by missing eligibility data.
Strategy 3: dealing with collider and selection bias.
We specify an imputation model to predict the missing eligibility data in the source population. We impute 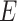 in multiple copies of the source population and, from each, construct an imputed copy of
in multiple copies of the source population and, from each, construct an imputed copy of 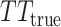 using imputed eligibility criteria. We then control for
using imputed eligibility criteria. We then control for 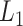 and
and 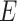 as in strategy 1 to estimate
as in strategy 1 to estimate 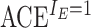 in each of the copies, which are pooled using Rubin’s Rules (9).
in each of the copies, which are pooled using Rubin’s Rules (9).
Implementation.
The imputation step is as follows:
Specify an imputation model for the missing mechanism of
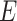 .
.Generate
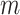 copies of the source population and impute
copies of the source population and impute 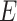 in each copy based on the imputation model.
in each copy based on the imputation model.Apply the eligibility criteria to each imputed data set to obtain
 emulated versions of
emulated versions of 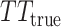 .
.Estimate
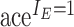 in each imputed
in each imputed 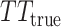 , controlling for
, controlling for 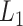 and
and 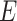 to obtain
to obtain 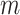 estimates of the causal effect of
estimates of the causal effect of  on
on 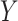 ,
, 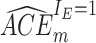 .
.- Obtain Rubin’s pooled estimate of the target causal effect by taking the average over the
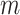 imputed sets:
imputed sets: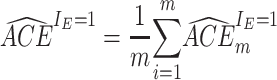
To capture any suspected treatment effect heterogeneity, imputations are carried out separately for each value of 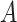 . Note that this technique requires
. Note that this technique requires 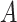 be fully observed (18).
be fully observed (18).
Giganti and Shepherd (8) highlight that excluding data relevant to inclusion in a study after MI leads to biased estimates of Rubin’s pooled estimate of the variance because of incongeniality between the imputation and outcome model. We hence consider confidence intervals using a percentile-based bootstrap.
Combining bootstrap and imputations.
We combine bootstrapping with MI using the “Boot-MI” methodology (19). This consists of the following steps:
Obtain
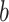 bootstrap samples of the source population.
bootstrap samples of the source population.Apply steps 1–5 of the MI procedure above for each of the
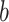 data sets, and obtain
data sets, and obtain 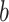 estimates of
estimates of 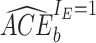 .
.A percentile-based bootstrapped confidence interval (CI) is then derived as the
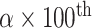 and
and 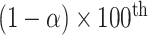 percentiles of the ordered bootstrapped estimates.
percentiles of the ordered bootstrapped estimates.
We used single imputation 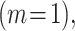 which has been shown to have good statistical properties (20), and reduce computational burden (19, 20), nested within b = 1,000 bootstraps, which is at or above the typically recommended number (21).
which has been shown to have good statistical properties (20), and reduce computational burden (19, 20), nested within b = 1,000 bootstraps, which is at or above the typically recommended number (21).
Sensitivity analyses.
Imputation models for 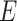 that allow for different mean values depending on
that allow for different mean values depending on 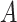 could be used,
could be used,
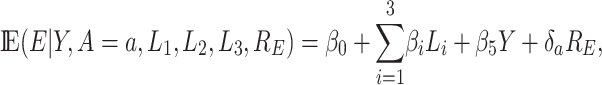 |
for a = 0,1.We use fully conditional specification (or multiple imputation by chained equations) using the “mice” package in R (R Foundation for Statistical Computing, Vienna, Austria) (13, 22) to impute the data. The parameters 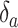 are MNAR sensitivity parameters. If MNAR is suspected, setting
are MNAR sensitivity parameters. If MNAR is suspected, setting 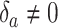 shifts the imputed values of
shifts the imputed values of 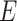 (separately for each
(separately for each 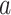 ) by an amount that accounts for the effect of
) by an amount that accounts for the effect of 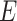 on its own missingness (23, 24). In practice, sensible ranges for
on its own missingness (23, 24). In practice, sensible ranges for 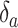 are chosen, with the data imputed over these ranges.
are chosen, with the data imputed over these ranges.
SIMULATIONS
We investigate strategies 1–3 by simulating data according to the structure of Figure 2. Specifically:
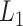 ,
, 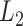 , and
, and 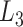 are independent
are independent 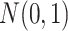 .
.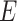 is a normal variable dependent on
is a normal variable dependent on 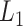 and
and 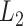 :
:
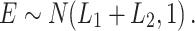
Eligibility is defined as
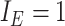 if
if 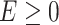 ;
; 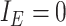 otherwise. Hence, around 50% of the population is eligible.
otherwise. Hence, around 50% of the population is eligible.- The missing mechanism of
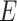 is expressed as a linear function of
is expressed as a linear function of 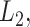
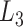 , and
, and 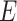 :
:
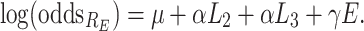
- The exposure
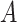 is a binary variable, and generated in terms of the log-odds of exposure, expressed as a linear function of
is a binary variable, and generated in terms of the log-odds of exposure, expressed as a linear function of 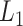
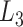 , and
, and 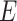 :
:
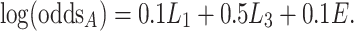
Around 54% of individuals in the source population are exposed.
- The outcome
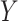 is a normal variable that depends on exposure
is a normal variable that depends on exposure 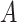 , eligibility
, eligibility 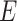 , their interaction, and also on
, their interaction, and also on 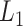 and
and 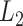 , with
, with 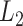 exercising a stronger impact than
exercising a stronger impact than 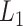 :
:
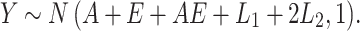
The source population is of size 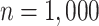 . We investigated strategies 1–3 at different values of
. We investigated strategies 1–3 at different values of 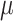 ,
, 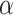 , and
, and 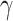 , the parameters affecting
, the parameters affecting 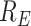 . Specifically,
. Specifically, 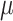 drives the percentage of missing completely at random (MCAR) missingness.
drives the percentage of missing completely at random (MCAR) missingness. 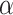 drives the strength of the MAR assumption, and the spurious association between
drives the strength of the MAR assumption, and the spurious association between 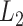 and
and 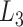 , and
, and 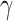 drives the strength of the MNAR mechanism, with positive values leading to a higher probability of larger values of
drives the strength of the MNAR mechanism, with positive values leading to a higher probability of larger values of 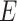 being observed.
being observed.
The parameter 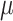 was set at 0 and 1.5, leading to severe (50%) and moderate (18%) MCAR missingness.
was set at 0 and 1.5, leading to severe (50%) and moderate (18%) MCAR missingness. 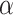 and
and 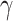 were set to range from 0 (no association) up to
were set to range from 0 (no association) up to 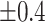 . For each combination we carried out
. For each combination we carried out 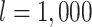 simulations for each of these scenarios using
simulations for each of these scenarios using 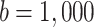 bootstraps, reporting for each the average bias in the estimation
bootstraps, reporting for each the average bias in the estimation 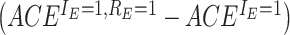 , its Monte Carlo error (MCE), root mean squared error (RMSE), and 95% coverage (25).
, its Monte Carlo error (MCE), root mean squared error (RMSE), and 95% coverage (25).
RESULTS
Observed and true target trial comparisons
Table 1 describes the characteristics of a set of single large simulations of 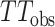 for different values of
for different values of 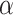 ,
, 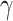 , and
, and 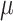 . We set
. We set 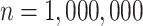 to minimize random variation. The 3 missingness scenarios are MCAR (
to minimize random variation. The 3 missingness scenarios are MCAR (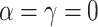 ), MAR (
), MAR (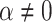 and
and 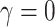 ), and MNAR (
), and MNAR (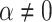 and
and 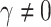 ). The scenario when
). The scenario when 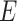 is not missing (
is not missing (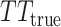 ) is included for comparison.
) is included for comparison.
Table 1.
Summary Statistics of Simulated Variables in the Observed Target Trial for n = 1,000,000 for Selected Values of 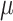 ,
, 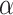 , and
, and 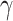
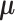
|
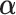
|
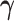
|
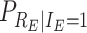 a
a
|
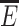
|
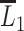
|
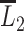
|
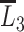
|
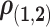 b
b
|
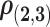
|
|---|---|---|---|---|---|---|---|---|---|
| No Missingness | |||||||||
| 0 | 0 | 0 | 1.00 | 1.38 | 0.46 | 0.46 | 0.0 | −0.27 | 0.0 |
| MCAR | |||||||||
| 1.5 | 0 | 0 | 0.82 | 1.38 | 0.46 | 0.46 | 0.0 | −0.27 | 0.0 |
| 0 | 0 | 0 | 0.50 | 1.38 | 0.46 | 0.46 | 0.0 | −0.27 | 0.0 |
| MAR | |||||||||
| 1.5 | 0.4 | 0 | 0.83 | 1.40 | 0.45 | 0.51 | 0.07 | −0.27 | −0.02 |
| 1.5 | 0.2 | 0 | 0.83 | 1.39 | 0.45 | 0.49 | 0.04 | −0.27 | −0.01 |
| 1.5 | −0.2 | 0 | 0.80 | 1.37 | 0.47 | 0.43 | −0.04 | −0.27 | −0.01 |
| 1.5 | −0.4 | 0 | 0.78 | 1.35 | 0.48 | 0.39 | −0.08 | −0.27 | −0.02 |
| 0 | 0.4 | 0 | 0.54 | 1.44 | 0.42 | 0.60 | 0.17 | −0.25 | −0.03 |
| 0 | 0.2 | 0 | 0.52 | 1.41 | 0.44 | 0.53 | 0.09 | −0.26 | −0.01 |
| 0 | −0.2 | 0 | 0.48 | 1.34 | 0.48 | 0.38 | −0.10 | −0.28 | −0.01 |
| 0 | −0.4 | 0 | 0.46 | 1.31 | 0.50 | 0.30 | −0.20 | −0.28 | −0.03 |
| MNAR | |||||||||
| 1.5 | 0.4 | 0.4 | 0.88 | 1.43 | 0.46 | 0.51 | 0.05 | −0.26 | −0.02 |
| 1.5 | 0.2 | 0.2 | 0.86 | 1.42 | 0.46 | 0.49 | 0.03 | −0.26 | −0.01 |
| 1.5 | −0.2 | −0.2 | 0.75 | 1.31 | 0.45 | 0.40 | −0.05 | −0.29 | −0.01 |
| 1.5 | −0.4 | −0.4 | 0.67 | 1.20 | 0.44 | 0.32 | −0.12 | −0.31 | −0.04 |
| 1.5 | 0 | −0.4 | 0.71 | 1.25 | 0.42 | 0.42 | 0.00 | −0.30 | 0.00 |
| 1.5 | 0.4 | −0.4 | 0.42 | 1.23 | 0.34 | 0.55 | 0.22 | −0.29 | −0.02 |
| 1.5 | −0.4 | 0.4 | 0.58 | 1.49 | 0.55 | 0.39 | −0.16 | −0.24 | −0.02 |
| 1.5 | 0.2 | −0.2 | 0.46 | 1.31 | 0.40 | 0.50 | 0.11 | −0.28 | −0.01 |
| 1.5 | −0.2 | 0.2 | 0.55 | 1.45 | 0.51 | 0.42 | −0.09 | −0.26 | −0.00 |
| 0 | 0.4 | −0.4 | 0.74 | 1.31 | 0.40 | 0.50 | 0.10 | −0.28 | −0.01 |
| 0 | −0.4 | 0.4 | 0.85 | 1.42 | 0.49 | 0.43 | −0.06 | −0.26 | 0.00 |
| 0 | 0.2 | −0.2 | 0.78 | 1.35 | 0.44 | 0.48 | 0.04 | −0.27 | 0.00 |
| 0 | −0.2 | 0.2 | 0.84 | 1.40 | 0.48 | 0.44 | −0.03 | −0.26 | 0.00 |
| 0 | 0.4 | 0.4 | 0.66 | 1.54 | 0.48 | 0.60 | 0.13 | −0.25 | −0.04 |
| 0 | 0.2 | 0.2 | 0.59 | 1.49 | 0.47 | 0.55 | 0.08 | −0.25 | −0.01 |
| 0 | −0.2 | −0.2 | 0.41 | 1.22 | 0.45 | 0.33 | −0.11 | −0.31 | −0.01 |
| 0 | −0.4 | −0.4 | 0.34 | 1.07 | 0.44 | 0.19 | −0.24 | −0.34 | −0.04 |
| 0 | 0 | −0.4 | 0.37 | 1.13 | 0.38 | 0.38 | 0.00 | −0.32 | 0.00 |
Abbreviations: MAR, missing at random; MCAR, missing completely at random; MNAR, missing not at random.
a Note that 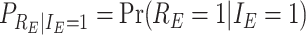 is a measure of the number of missing eligible participants.
is a measure of the number of missing eligible participants.
b
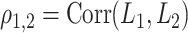 ;
; 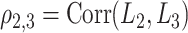 .
.
When the mechanism is MCAR, the means and correlations of relevant variables are not affected. When the mechanism is MAR, they depart from those found in 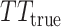 : When
: When 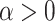 , individuals in
, individuals in 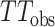 have larger mean values for
have larger mean values for 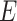 ,
, 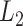 , and
, and 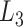 than in
than in 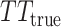 . This is because
. This is because 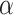 leads to individuals with larger values for
leads to individuals with larger values for 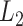 and
and 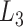 being more likely to be observed, shifting upward their distributions, and by extension, the distribution of
being more likely to be observed, shifting upward their distributions, and by extension, the distribution of 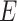 . When
. When 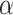 is negative, the opposite is true. These biases are more noticeable at
is negative, the opposite is true. These biases are more noticeable at 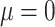 due to the greater proportion of missing individuals.
due to the greater proportion of missing individuals.
Under MNAR, setting 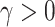 makes higher values of
makes higher values of 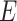 more likely to be observed in
more likely to be observed in 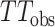 , with the opposite occurring when
, with the opposite occurring when 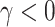 , leading to shifts in the distributions for
, leading to shifts in the distributions for 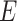 ,
, 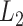 , and
, and 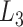 similar to what occurs with
similar to what occurs with 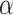 .
.
The combined impact of 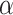 and
and 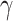 varies. When both are of the same sign, their impacts compound and strengthen the corresponding shifts in distribution. When they are of opposite sign, their impacts partially offset one another.
varies. When both are of the same sign, their impacts compound and strengthen the corresponding shifts in distribution. When they are of opposite sign, their impacts partially offset one another.
The shifts in distribution for 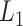 are complicated, shifted downward when
are complicated, shifted downward when 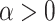 but shifted upward when
but shifted upward when 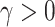 . This is due to a complicated relationship between the spurious negative
. This is due to a complicated relationship between the spurious negative  association (caused by conditioning on
association (caused by conditioning on 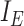 ), driving a downward shift in
), driving a downward shift in 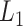 with higher values of
with higher values of 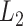 , and the positive
, and the positive 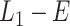 association, driving an upward shift with higher values of
association, driving an upward shift with higher values of 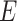 .
.
Strategies
For strategies 1 and 2, bias in estimation of ACE increased with higher values of α and γ, and was worse when μ = 0 (Tables 2 and 3). This is due to having to average over the distribution of the confounders to estimate 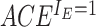 . The size and direction of this bias is nearly identical to the shift in the distribution of
. The size and direction of this bias is nearly identical to the shift in the distribution of 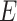 observed in Table 1. This is because effect modification by
observed in Table 1. This is because effect modification by 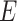 has effect size equal to 1.
has effect size equal to 1.
Table 2.
Results of Applying the 3 Strategies to Data Generated Under Different Scenarios, With 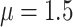 and
and 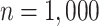
| Strategy |
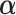 a
a
|
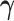
|
Bias | Coverage | RMSE | MCE |
|---|---|---|---|---|---|---|
| No Missingness | ||||||
| 1 | 0 | 0 | 0.00 | 95.0 | 0.00 | 0.01 |
| MCAR | ||||||
| 1 | 0 | 0 | 0.01 | 94.4 | 0.17 | 0.01 |
| 2 | 0.01 | 93.9 | 0.1 | 0.00 | ||
| 3 | −0.01 | 95.4 | 0.17 | 0.01 | ||
| MAR | ||||||
| 1 | −0.4 | 0 | −0.04 | 94.8 | 0.20 | 0.01 |
| 2 | −0.03 | 93.4 | 0.14 | 0.00 | ||
| 3 | 0.00 | 95.9 | 0.17 | 0.01 | ||
| 1 | 0.4 | 0 | 0.02 | 94.2 | 0.17 | 0.01 |
| 2 | 0.03 | 93.1 | 0.10 | 0.00 | ||
| 3 | −0.01 | 95.3 | 0.17 | 0.01 | ||
| MNAR | ||||||
| 1 | 0.4 | 0.4 | 0.05 | 93.9 | 0.17 | 0.01 |
| 2 | 0.06 | 91.6 | 0.14 | 0.00 | ||
| 3 | −0.01 | 95.2 | 0.05 | 0.01 | ||
| 1 | 0.2 | 0.2 | 0.04 | 94.6 | 0.17 | 0.01 |
| 2 | 0.04 | 92.2 | 0.10 | 0.00 | ||
| 3 | −0.01 | 95.4 | 0.17 | 0.01 | ||
| 1 | −0.2 | −0.2 | −0.07 | 93.1 | 0.20 | 0.01 |
| 2 | −0.07 | 89.9 | 0.14 | 0.00 | ||
| 3 | 0.01 | 95.7 | 0.05 | 0.01 | ||
| 1 | −0.4 | −0.4 | −0.19 | 82.4 | 0.26 | 0.01 |
| 2 | −0.17 | 70.4 | 0.22 | 0.00 | ||
| 3 | 0.00 | 96.9 | 0.20 | 0.01 | ||
Abbreviations: MAR, missing at random; MCAR, missing completely at random; MCE, Monte Carlo error; MNAR, missing not at random; RMSE, root mean square error; 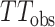 , target trial emulated from observed data; TTtrue, the full eligibility target trial, containing all those who are eligible.
, target trial emulated from observed data; TTtrue, the full eligibility target trial, containing all those who are eligible.
a Average size of 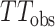 for the 7 settings of
for the 7 settings of 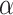 and
and 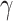 are n = 410, 387, 415, 442, 430, 374, and 332 respectively. Average size of
are n = 410, 387, 415, 442, 430, 374, and 332 respectively. Average size of 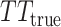 is 500. Note that the average causal effect
is 500. Note that the average causal effect 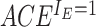 was calculated from a single simulation with
was calculated from a single simulation with 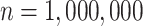 and was estimated at 2.386.
and was estimated at 2.386.
Table 3.
Results of Applying the 3 Strategies to Data Generated Under Different Scenarios, With 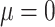 and
and 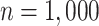
| Strategy |
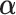 a
a
|
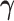
|
Bias | Coverage | RMSE | MCE |
|---|---|---|---|---|---|---|
| No Missingness | ||||||
| 1 | 0 | 0 | 0.00 | 95.0 | 0.00 | 0.01 |
| MCAR | ||||||
| 1 | 0 | 0 | 0.01 | 95.0 | 0.24 | 0.01 |
| 2 | 0.01 | 94.6 | 0.14 | 0.00 | ||
| 3 | 0.00 | 97.9 | 0.22 | 0.01 | ||
| MAR | ||||||
| 1 | −0.4 | 0 | −0.09 | 93.2 | 0.26 | 0.01 |
| 2 | −0.07 | 91.7 | 0.17 | 0.00 | ||
| 3 | −0.01 | 97.9 | 0.24 | 0.01 | ||
| 1 | 0.4 | 0 | 0.05 | 94.3 | 0.22 | 0.01 |
| 2 | 0.07 | 92.8 | 0.14 | 0.00 | ||
| 3 | 0.00 | 97.6 | 0.22 | 0.01 | ||
| MNAR | ||||||
| 1 | 0.4 | 0.4 | 0.16 | 86.3 | 0.26 | 0.01 |
| 2 | 0.17 | 73.0 | 0.22 | 0.00 | ||
| 3 | −0.00 | 97.3 | 0.20 | 0.01 | ||
| 1 | 0.2 | 0.2 | 0.12 | 90.4 | 0.24 | 0.01 |
| 2 | 0.12 | 85.3 | 0.17 | 0.00 | ||
| 3 | 0.00 | 97.6 | 0.22 | 0.01 | ||
| 1 | −0.2 | −0.2 | −0.17 | 90.0 | 0.30 | 0.01 |
| 2 | −0.15 | 83.3 | 0.22 | 0.00 | ||
| 3 | 0.00 | 98.2 | 0.07 | 0.01 | ||
| 1 | −0.4 | −0.4 | −0.33 | 75.3 | 0.42 | 0.01 |
| 2 | −0.31 | 53.4 | 0.34 | 0.01 | ||
| 3 | 0.01 | 98.7 | 0.17 | 0.01 | ||
Abbreviations: MAR, missing at random; MCAR, missing completely at random; MCE, Monte Carlo error; MNAR, missing not at random; RMSE, root mean square error; 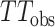 , target trial emulated from observed data; TTtrue, the full eligibility target trial, containing all those who are eligible.
, target trial emulated from observed data; TTtrue, the full eligibility target trial, containing all those who are eligible.
a Average size of 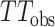 for the 7 settings of
for the 7 settings of 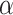 and
and 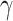 are n = 250, 228, 271, 328, 294, 206, and 172 respectively. Average size of
are n = 250, 228, 271, 328, 294, 206, and 172 respectively. Average size of 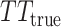 is 500. Note that the average causal effect
is 500. Note that the average causal effect 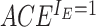 was calculated from a single simulation with
was calculated from a single simulation with 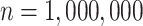 and was estimated at 2.386.
and was estimated at 2.386.
The impact of collider bias induced by 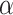 is negligible, as shown by the small differences in bias for strategies 1 and 2. The root mean squared error is smaller for strategy 2 but has more undercoverage, possibly because it involves averaging
is negligible, as shown by the small differences in bias for strategies 1 and 2. The root mean squared error is smaller for strategy 2 but has more undercoverage, possibly because it involves averaging 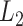 , which also has a shifted distribution.
, which also has a shifted distribution.
Table 1 implies that had 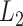 been the effect modifier rather than
been the effect modifier rather than 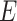 , strategies 1 and 2 would have shown more bias under the MAR assumption. This is investigated in Web Appendix 1 and Web Table 1 (available at https://doi.org/10.1093/aje/kwac202; additional supporting information can be found in Web Tables 2–4).
, strategies 1 and 2 would have shown more bias under the MAR assumption. This is investigated in Web Appendix 1 and Web Table 1 (available at https://doi.org/10.1093/aje/kwac202; additional supporting information can be found in Web Tables 2–4).
Strategy 3 shows unbiased estimates (within Monte Carlo error) in all cases, indicating a successful recovery of the causal effect in 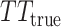 . The CIs, however, display overcoverage, particularly when a large fraction of the eligible are missing.
. The CIs, however, display overcoverage, particularly when a large fraction of the eligible are missing.
Selection bias appears to increase under the following conditions:
Larger numbers of missing eligible individuals
Larger values of
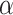 and
and 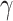 , the drivers of missingness
, the drivers of missingnessA stronger effect modification of the causal effect of
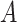 on
on 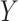 by
by 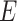 (or any variables related to
(or any variables related to 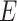 )
)
With fewer eligible participants lost to missingness, there is less missing data to drive a differentiation in the distributions of 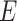 in
in 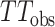 and
and 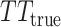 , which is why bias decreased when
, which is why bias decreased when 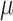 was larger, and the number of missing eligible participants decreased. None of these features are likely to be known in advance.
was larger, and the number of missing eligible participants decreased. None of these features are likely to be known in advance.
When 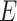 was MNAR, imputation was carried out with the correct values of the sensitivity parameters
was MNAR, imputation was carried out with the correct values of the sensitivity parameters 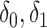 . This was to demonstrate that, all other biases (including a misspecified imputation model) accounted for, strategy 3 can eliminate the biases described above in Sources of Bias when
. This was to demonstrate that, all other biases (including a misspecified imputation model) accounted for, strategy 3 can eliminate the biases described above in Sources of Bias when 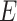 is MNAR. This is unlikely to be possible in reality; hence, in Web Appendix 2 we repeat specific MNAR simulations of Table 3 assuming a MAR imputation model
is MNAR. This is unlikely to be possible in reality; hence, in Web Appendix 2 we repeat specific MNAR simulations of Table 3 assuming a MAR imputation model 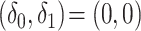 , which shows notable bias. This highlights that, in practice, MNAR imputation is an exploratory technique, and careful considerations must be made to choose informative values of ranges for
, which shows notable bias. This highlights that, in practice, MNAR imputation is an exploratory technique, and careful considerations must be made to choose informative values of ranges for 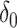 and
and 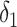 to investigate (23, 24). A realistic application of strategy 3 is shown in the case study.
to investigate (23, 24). A realistic application of strategy 3 is shown in the case study.
In summary, strategy 3 is necessary in the case that missing data are noticeably MAR or MNAR. If that is not the case, a user may prefer the simpler strategies 1 and 2. Strategy 2 is the most precise, if this is preferred by the user, but one must account for the possibility of undercoverage if a CI is sought.
CASE STUDY: EFFECT OF PALIVIZUMAB ON INFANT HOSPITAL ADMISSION
RSV is a major cause of acute lower respiratory tract infection in infants, with RSV bronchiolitis responsible for 40,000 hospital admissions annually in England (26). Palivizumab is licensed for passive immunization to prevent RSV in premature infants with congenital heart disease or chronic lung disease. Due to its high cost, palivizumab is typically recommended to more select groups of high-risk infants than those in clinical trials, with limited data on real-world effectiveness (27). Hence, analysis by a selective emulated trial is of interest.
An observational cohort of infants potentially eligible for palivizumab treatment in England has been developed (27), using the Hospital Treatment Insights database (HTI), which links pharmacy dispensing records from 43 acute hospitals in England, and hospital records from Hospital Episode Statistics (HES). This cohort details infants born between January 1, 2010, and December 31, 2016, with follow-up data on palivizumab prescriptions and hospital admission up to their first year of life. HTI is maintained by IQVIA (https://www.iqvia.com/).
This cohort identifies a source population of 8,294 high-risk infants, defined as having congenital heart disease or chronic lung disease, under care of an HTI-reporting hospital, alive at the start of their first RSV season (October 1 to March 31), with a full linked hospital admission history. This is shown in the cohort flow charts of Figures 3 and 4.
Figure 3.
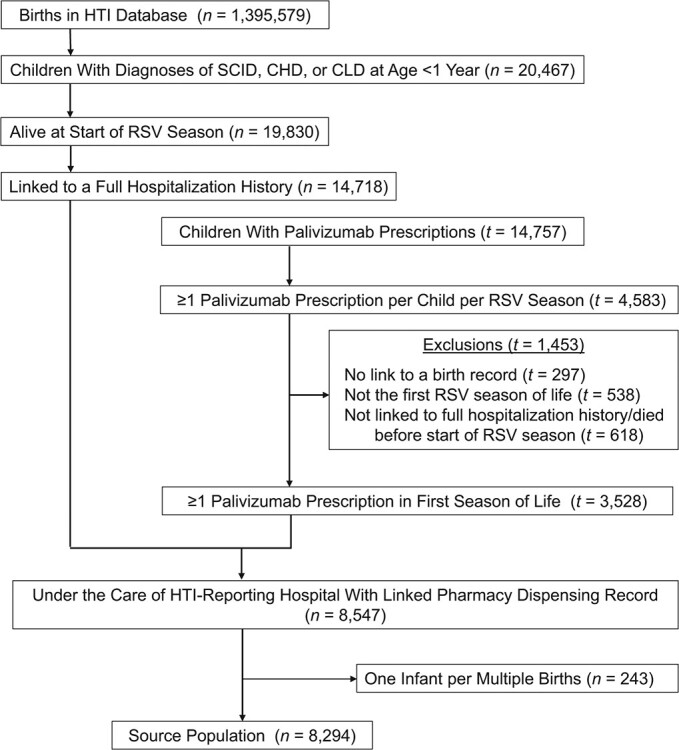
Derivation of the source population for the IQVIA (https://www.iqvia.com/) cohort; infants born in England between January 1, 2010, and December 31, 2016, with linked Hospital Episodes Statistics and prescription data. Note that the palivizumab prescriptions database contains a separate but overlapping population from those in the Hospital Treatment Insights database (HTI). Thus, this population is denoted by  until linked to individuals in the HTI population (
until linked to individuals in the HTI population ( ). CHD, congenital heart disease; CLD, chronic lung disease; RSV, respiratory syncytial virus; SCID, severe combined immunodeficiency.
). CHD, congenital heart disease; CLD, chronic lung disease; RSV, respiratory syncytial virus; SCID, severe combined immunodeficiency.
Figure 4.
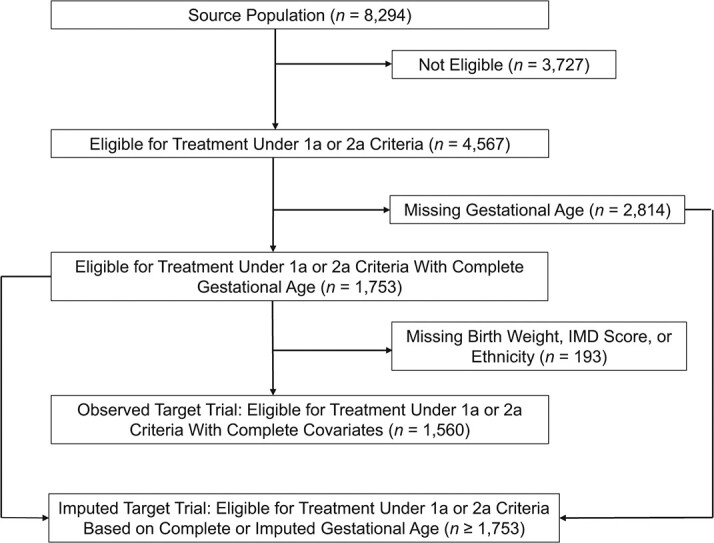
Derivation of the complete records target trial and of the imputed target trials of palivizumab treatment; infants born in England between January 1, 2010, and December 31, 2016, with linked Hospital Episodes Statistics and prescription data who were eligible to receive treatment under 1a and 2a criteria. Note that the exact size of the imputed target trial is unknown, and depends on the imputed data, but must be at least of size 1,753 (those with complete eligible data who qualify).
Infants in the source population were considered eligible for the TT if they had a diagnosis of congenital heart disease or chronic lung disease and met additional eligibility criteria based on gestational age and chronological age at start of RSV season and, specifically, those who met 1a or 2a criteria for recommendation of treatment by palivizumab in Chapter 27a in the Green Book (28) (Web Table 3). Gestational age, however, is missing for 2,814 (34%) infants in the source population. As a result, the eligibility of many children cannot be identified.
Target trial emulation
The emulated target trial protocol is detailed in Web Appendix 3 and Web Table 2. We define 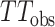 to include all eligible individuals with complete eligibility data on gestational age, birth weight, Index of Multiple Deprivation score, and ethnicity. This led to a trial of 1,560 infants. We also aimed to recover
to include all eligible individuals with complete eligibility data on gestational age, birth weight, Index of Multiple Deprivation score, and ethnicity. This led to a trial of 1,560 infants. We also aimed to recover 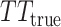 by imputing missing gestational age in the high-risk cohort. This corresponds to using strategies 2 and 3, respectively.
by imputing missing gestational age in the high-risk cohort. This corresponds to using strategies 2 and 3, respectively.
We are interested in the effect of any palivizumab prescription on RSV-related hospital admission in infants during their first RSV season of life. A full course of treatment by palivizumab requires up to 5 monthly doses during RSV season. As we could not determine adherence to treatment from the HTI data, we define a simplified exposure as a binary indicator of having been prescribed at least 1 dose of palivizumab in their first RSV season of life. Infants are identified in the first month of life for treatment, and it is typically administered in outpatient clinics, not when hospitalized for RSV. Our outcome is a binary indicator of having been hospitalized for an RSV-related condition during their first RSV season of life.
Our target estimand is the ACE of palivizumab prescription on RSV-related hospital admission in  , expressed as the average difference in absolute risk of hospital admission (the intent to treat (ITT) effect).
, expressed as the average difference in absolute risk of hospital admission (the intent to treat (ITT) effect).
To balance the confounders in the treated and untreated, we fitted a model for the propensity of receiving palivizumab, including gestational age, age at start of RSV season, Index of Multiple Deprivation quintiles, sex, ethnicity, year of birth, diagnosis of congenital heart disease or chronic lung disease (or both), and other comorbidities. The resultant propensity scores showed reasonable overlap in the treated and untreated (Web Figure 1). Mean differences between treated and untreated, adjusted for inverse probability of weighting by propensity score, were within 0.1, indicating good confounder balance.
We fitted 2 different outcome models, a logistic regression model of hospital admission against treatment with inverse probability weight of being treated (IPTW), corresponding to a marginal structural model (MSM) (29), and a second where we controlled for the propensity score and all confounders directly in the outcome model, similar to those in 2-stage g-estimation of structural nested mean models (SNMMs) (30). The ACE is calculated by estimating potential outcomes via the “data stacking” method of (17).
Continuous gestational age is imputed in the treated and untreated arms separately (to account for any interaction between gestational age and palivizumab) using a MNAR imputation model that includes all the variables of the propensity score model, plus the outcome and birth weight. Birth weight is not included in the outcome model due to collinearity with gestational age. There are thus 2 sensitivity parameters: 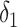 for exposed and
for exposed and 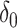 for unexposed. We assert that infants with missing gestational age may have higher mortality, implying a shorter gestation (31). Hence we performed the analysis setting
for unexposed. We assert that infants with missing gestational age may have higher mortality, implying a shorter gestation (31). Hence we performed the analysis setting 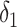 and
and 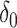 to either 0 (MAR), or −4 (MNAR).
to either 0 (MAR), or −4 (MNAR).
Based on recommendations in Tompsett et al. (23), rather than compare the ACE directly with  and
and 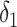 , which are difficult to interpret physically, we estimated from the imputed data the mean gestational age in treated and untreated infants to contrast against the results.
, which are difficult to interpret physically, we estimated from the imputed data the mean gestational age in treated and untreated infants to contrast against the results.
Missing birth weight, Index of Multiple Deprivation score, and ethnicity were imputed alongside gestational age using MICE. We report the results in Tables 4 and 5 below.
Table 4.
Estimate of the Average Causal Effect for the Palivizumab Case Study Obtained Using Strategies 2 and 3, Using an Outcome Model Controlled for Confounders and Propensity Score
| Sensitivity Parameters | Trial Size |
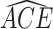 a
a
|
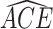 , %
, %
|
95% CI | Mean Gestational Age, Treated | Mean Gestational Age, Untreated |
|---|---|---|---|---|---|---|
| ||||||
| N/A | 1,560 | −0.003 | −0.3% | −0.05, 0.05 | 26.5 | 27.2 |
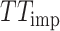
| ||||||
| (0,0) | 2,643 | −0.002 | −0.2% | −0.04, 0.04 | 26.9 | 27.7 |
| (−4,0) | 3,659 | −0.010 | −1.0% | −0.04, 0.03 | 26.9 | 25.5 |
| (0,−4) | 2,985 | 0.013 | 1.3% | −0.03, 0.05 | 24.2 | 27.7 |
| (−4,-4) | 3,964 | 0.006 | 0.6% | −0.02, 0.04 | 24.2 | 25.5 |
Abbreviations: ACE, average causal effect; CI, confidence interval; N/A, not applicable; 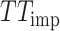 , target trial emulated from observed and imputed data;
, target trial emulated from observed and imputed data; 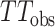 , target trial emulated from observed data.
, target trial emulated from observed data.
a The ACE is expressed as a risk difference both in absolute value and in percentage risk difference The sensitivity parameters are listed in order 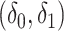 . With sensitivity parameter
. With sensitivity parameter 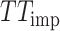 (0,0), the data are assumed missing at random. In all other cases for
(0,0), the data are assumed missing at random. In all other cases for 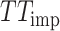 it is assumed missing not at random. This is not applicable for
it is assumed missing not at random. This is not applicable for 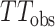 , which has complete data.
, which has complete data.
Table 5.
Estimated Average Causal Effect for the Palivizumab Case Study Obtained Using Strategies 2 and 3, Using an Inverse Probability Weighted Outcome Model
| Sensitivity Parameter | Trial Size |
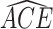 a
a
|
 , %
, %
|
95% CI | Mean Gestational Age, Treated | Mean Gestational Age, Untreated |
|---|---|---|---|---|---|---|
| ||||||
| N/A | 1,560 | −0.010 | −1.0% | −0.06,0.04 | 26.5 | 27.2 |
| ||||||
| (0,0) | 2,643 | −0.001 | −0.1% | −0.04,0.04 | 26.9 | 27.7 |
| (−4,0) | 3,659 | −0.031 | −3.1% | −0.08,0.01 | 26.9 | 25.5 |
| (0,−4) | 2,985 | 0.023 | 2.3% | −0.03,0.07 | 24.2 | 27.7 |
| (−4,-4) | 3,964 | 0.011 | (1.1%) | −0.03,0.05 | 24.2 | 25.5 |
Abbreviations: ACE, average causal effect of treatment; CI, confidence interval; N/A, not applicable;  , target trial emulated from observed and imputed data;
, target trial emulated from observed and imputed data; 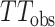 , target trial emulated from observed data.
, target trial emulated from observed data.
a The ACE is expressed as a risk difference both in absolute value and in percentage risk difference The sensitivity parameters are listed in order 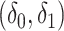 . With sensitivity parameter
. With sensitivity parameter 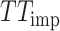 (0,0), the data are assumed missing at random. In all other cases for
(0,0), the data are assumed missing at random. In all other cases for 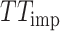 it is assumed missing not at random. This is not applicable for
it is assumed missing not at random. This is not applicable for 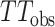 , which has complete data.
, which has complete data.
Results
Analysis of 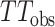 suggests that treatment by at least 1 dose of palivizumab has little effect on the risk of being hospitalized, indicated by an ACE of
suggests that treatment by at least 1 dose of palivizumab has little effect on the risk of being hospitalized, indicated by an ACE of 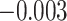 using a propensity score–conditioned outcome model, and
using a propensity score–conditioned outcome model, and 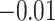 under inverse probability weighting (a 0.3% or 1.0% lower risk of hospital admission). When imputing the TT under MAR we observed a 0.1% and 0.2% lower risk of hospital admission, respectively. Under MNAR there is a more noted effect of palivizumab, ranging from −1.0% to 1.3% using an outcome model controlled for the propensity score, and −3.1% to 2.3% using inverse probability weighting.
under inverse probability weighting (a 0.3% or 1.0% lower risk of hospital admission). When imputing the TT under MAR we observed a 0.1% and 0.2% lower risk of hospital admission, respectively. Under MNAR there is a more noted effect of palivizumab, ranging from −1.0% to 1.3% using an outcome model controlled for the propensity score, and −3.1% to 2.3% using inverse probability weighting.
The imputation model implies a high number of missing eligible participants, with over 1,000 more individuals under the MAR imputed trial, and up to nearly 2,500 more under MNAR.
When 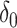 was set to
was set to 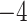 , this led to a reduction in average gestational age in the untreated by 2.2 weeks. In this case there was stronger reduction in risk of hospital admission when treated. When
, this led to a reduction in average gestational age in the untreated by 2.2 weeks. In this case there was stronger reduction in risk of hospital admission when treated. When 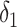 was set to
was set to 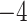 , the average gestational age in the treated was reduced by 2.7 weeks and there was an increasing risk of hospital admission under treatment.
, the average gestational age in the treated was reduced by 2.7 weeks and there was an increasing risk of hospital admission under treatment.
No estimate was found to be significant based on a 95% CI. Despite there being a clear change in the distribution of gestational age under MNAR conditions, and a large number of missing eligible, there is only weak evidence of selection bias in this study. This implies that gestational age only weakly modifies the effect of palivizumab on hospital admission.
The implication is that receiving at least 1 dose of palivizumab appears to have little effect on hospital admission, and the results are robust to changes in the missing data assumption.
DISCUSSION
In this paper we bring to light notable sources of bias in target trial emulation, emanating from ignoring missing eligible data. We explored one means to analyze a TT combined with multiple imputation of eligibility criteria prior to selection. We demonstrated via simulation that an imputed TT can eliminate sources of selection and collider bias, improve the sample size of a TT, and allow users to investigate sensitivity to changes in the assumptions of the missing eligible data on effect size.
An imputed TT of the effect of receiving at least 1 dose of palivizumab on RSV-related hospital admission indicated that a significant number of infants with missing gestational age were eligible, although any selection bias in this case was small.
We identified characteristics of the data that determine the size of selection bias, namely the strength of the MAR or MNAR mechanism, the number of missing eligible individuals and the size of the effect modification. None of these characteristics can be calculated from the source population but could be inferred using external linked data sets. This selection bias can occur if any variable related to eligibility is an effect modifier. We showed in Web Appendix 1 that when 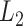 was the effect modifier, strong selection bias was identified when
was the effect modifier, strong selection bias was identified when 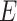 was MAR.
was MAR.
A limitation of this method is the tendency of CIs to overcover. The Boot-MI method (19) is computationally intensive, and thus one should expect an analysis to take several hours even with cluster computing methods. Hence we constructed CIs using a percentile bootstrap with just single imputation. However, single imputation lends itself to overcoverage (19). In Web Appendix 2, we applied strategy 3 using MI with 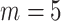 , which demonstrates improved coverage. One alternative would be to investigate the corrected Rubin’s pooled variance of
, which demonstrates improved coverage. One alternative would be to investigate the corrected Rubin’s pooled variance of 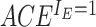 suggested in Giganti and Shepherd (8). However, obtaining accurate confidence interval estimates in this way for the ACE using MI requires complex methods (32–34).
suggested in Giganti and Shepherd (8). However, obtaining accurate confidence interval estimates in this way for the ACE using MI requires complex methods (32–34).
Instead of MI, we could consider using inverse probability weighting to address the bias caused by missingness in E (35). We investigated this method in Web Appendix 2 and found that it did not correct the bias. Another possible alternative is to utilize the work in Bareinboim and Pearl (15), by inferring or presuming the distribution of the confounders in 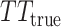 and standardizing the conditional ACE estimated in
and standardizing the conditional ACE estimated in 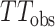 , but it would be a considerable challenge.
, but it would be a considerable challenge.
It is also worth noting that using strategy 2, and targeting the causal effect in those with complete records, may be a pragmatic choice if the expected selection bias is limited and the source population is cumbersome.
Data on palivizumab prescriptions and adherence were limited, and this had an impact on the quality of conclusions that could be made. Clinical colleagues reassure us that children hospitalized with RSV would not be issued palivizumab, protecting from reverse causation. However, other issues, such as confounding by indication, cannot be discounted. Limitations of the diagnostic data also meant a slight inflation of our definition of the eligible population because some of the diagnoses may include less severe diseases than those listed in the Green Book (28).
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Population Policy and Practice Department, UCL Great Ormond Street Institute of Child Health, University College London, London, United Kingdom (Daniel Tompsett, Ania Zylbersztejn, Pia Hardelid, Bianca De Stavola).
A Medical Research Council (MRC) Methodology Grant (number MR/R025215/1) supported D.T. and B.D., and a Wellcome Trust Seed Award in Science (number 207673/Z/17/Z) supported A.Z. and P.H.
The Hospital Treatment Insights database (HTI) is maintained by IQVIA (https://www.iqvia.com/), Copyright 2019, re-used with the permission of The Health and Social Care Information Centre. All rights reserved. Copyright 2021, re-used with the permission of IQVIA. All rights reserved. The authors do not have permission to share patient-level HTI data. Qualified researchers can request access to the data from IQVIA (contact Tanith Hjelmbjerg, tanith.hjelmbjerg@iqvia.com).
We would like to thank Hassy Dattani and Tanith Hjelmbjerg for their help with accessing the Hospital Treatment Insights database. This work uses data provided by patients and collected by the National Health Service as part of their care and support.
Conflict of interest: none declared.
REFERENCES
- 1. Hernán MA, Robins JM. Using big data to emulate a target trial when a randomized trial is not available. Am J Epidemiol. 2016;183(8):758–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Hernán MA. Causal Inference: What If? Boca Raton, FL: Chapman and Hall CRC; 2020. [Google Scholar]
- 3. Kutcher SA, Brophy JM, Banack HR, et al. Emulating a randomised controlled trial with observational data: an introduction to the target trial framework. Can J Cardiol. 2021;37(9):1365–1377. [DOI] [PubMed] [Google Scholar]
- 4. Maringe C, Benitez Majano S, Exarchakou A, et al. Reflection on modern methods: trial emulation in the presence of immortal-time bias. Assessing the benefit of major surgery for elderly lung cancer patients using observational data. Int J Epidemiol. 2020;49(5):1719–1729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Roderick L, Rubin D. Statistical Analysis With Missing Data. 3rd ed. Hoboken, NJ: Wiley; 2019. [Google Scholar]
- 6. White IR, Eleftheria K, Thompson SG. Allowing for missing outcome data and incomplete uptake of randomised interventions, with application to an internet-based alcohol trial. Stat Med. 2011;30(27):3192–3207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Hong JL, Johnsson Funk M, LoCasale R, et al. Generalizing randomized clinical trial results: implementation and challenges related to missing data in the target population. Am J Epidemiol. 2017;187(4):817–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Giganti MJ, Shepherd BE. Multiple-imputation variance estimation in studies with missing or misclassified inclusion criteria. Am J Epidemiol. 2020;189(12):1628–1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Rubin DB. Inference and missing data. Biometrika. 1976;63(3):581–592. [Google Scholar]
- 10. Snoep JD, Morabia A, Hernandez-Diaz S, et al. Commentary: a structural approach to Berksons fallacy and a guide to a history of opinions about it. Int J Epidemiol. 2014;43(2):515–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Westreich D, Daniel RM. Commentary: Berkson’s fallacy and missing data. Int J Epidemiol. 2014;43(2):524–526. [DOI] [PubMed] [Google Scholar]
- 12. Choi J, Dekkers OM, Cessie S. A comparison of different methods to handle missing data in the context of propensity score analysis. Eur J Epidemiol. 2019;34(1):23–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Buuren S, Groothuis-Oudshoorn K. mice: multivariate imputation by chained equations in R. J Stat Softw. 2011;45:1–67. [Google Scholar]
- 14. White IR, Royston P, Wood AM. Multiple imputation using chained equations: issues and guidance for practice. Stat Med. 2011;30(4):377–399. [DOI] [PubMed] [Google Scholar]
- 15. Bareinboim E, Pearl J. Causal inference and the data-fusion problem. Proc Natl Acad Sci. 2016;113(27):7345–7352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Dekkers OM, Elm E, Algra A, et al. How to assess the external validity of therapeutic trials: a conceptual approach. Int J Epidemiol. 2009;39(1):89–94. [DOI] [PubMed] [Google Scholar]
- 17. Aolin W, Roch N, Onyebuchi A. G-computation of average treatment effects on the treated and the untreated. BMC Med Res Methodol. 2017;17(1):3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Tilling K, Williamson EJ, Spratt M, et al. Appropriate inclusion of interactions was needed to avoid bias in multiple imputation. J Clin Epidemiol. 2016;80:107–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Schomaker M, Heumann C. Bootstrap inference when using multiple imputation. Stat Med. 2018;37(14):2252–2266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Jaap B, van BuurenS, Cessie S, et al. Combining multiple imputation and bootstrap in the analysis of cost effectiveness trial data. Stat Med. 2019;38(2):210–220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Pattengale ND, Alipour M, Bininda-Emonds ORP, et al. How many bootstrap replicates are necessary? J Comput Biol. 2010;17(3):337–354. [DOI] [PubMed] [Google Scholar]
- 22. R Core Team . R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical ComputingVienna; 2019. [Google Scholar]
- 23. Tompsett DM, Leacy F, Moreno-Betancour M, et al. On the use of the not at random fully conditional specification (NARFCS) procedure in practice. Stat Med. 2018;37(15):2338–2353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Tompsett D, Sutton S, Seaman SR, et al. A general method for elicitation, imputation, and sensitivity analysis for incomplete repeated binary data. Stat Med. 2020;39(22):2921–2935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Morris TP, White IR, Crowther MJ. Using simulation studies to evaluate statistical methods. Stat Med. 2019;38(11):2074–2102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. National Health Service . RSV hospitalisaions data. https://digital.nhs.uk/data-and-information/publications/statistical/hospital-admitted-patient-care-activity/2017-18. Accessed December 2, 2019.
- 27. Zylbersztejn A, Almossawi O, Gudka N. et al., Access to palivizumab among children at high risk of respiratory syncytial virus complications in English hospital. Br J Clin Pharmacol. 2022;88(3):1246–1257. [DOI] [PubMed] [Google Scholar]
- 28. Department of Health . Respiratory Synctial Virus, Chapter 27a. Green Book: Immunisation Against Infectious Disease. London, UK: The Stationary Office September 2015. https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/458469/Green_Book_Chapter_27a_v2_0W.PDF. Accessed July 1, 2021. [Google Scholar]
- 29. Robins J, Hernán MA, Brumback B. Marginal structural models and causal inference in epidemiology. Epidemiology. 2000;11(5):550–560. [DOI] [PubMed] [Google Scholar]
- 30. Vansteelandt S, Sjölander A. Revisiting g-estimation of the effect of a time-varying exposure subject to time-varying confounding. Epidemiol Methods. 2016;5:37–56. [Google Scholar]
- 31. Zylbersztejn A, Gilbert R, Hjern A, et al. Child mortality in England compared with Sweden: a birth cohort study. Lancet. 2018;391(10134):2008–2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Yang S, Zhang Y, Liu GF, et al. SMIM: a unified framework of survival sensitivity analysis using multiple imputation and martingale [published online ahead of print August 27, 2021]. Biometrics. 2021. ( 10.1111/biom.13555). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Taylor T, Zhou XH. Multiple imputation methods for treatment noncompliance and nonresponse in randomized clinical trials. Biometrics. 2009;65(1):88–95. [DOI] [PubMed] [Google Scholar]
- 34. Corder N, Yang S. Estimating average treatment effects utilizing fractional imputation when confounders are subject to Missingness. J Causal Inference. 2020;8:249–271. [Google Scholar]
- 35. Seaman SR, White IR. Review of inverse probability weighting for dealing with missing data. Stat Methods Med Res. 2013;22(3):278–295. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


