Significance
Our study shows how in Hydra, with one of the simplest nervous systems, behavior arises from a combination of neural and muscle excitation dynamics, transformed by body mechanics. This work demonstrates the feasibility of developing a complete account of the neural control of behavior, from neuronal activation to muscle and body biomechanics, in a model system.
Keywords: Hydra, biomechanical model, neural activity, muscle activity, behaviors
Abstract
How does neural activity drive muscles to produce behavior? The recent development of genetic lines in Hydra that allow complete calcium imaging of both neuronal and muscle activity, as well as systematic machine learning quantification of behaviors, makes this small cnidarian an ideal model system to understand and model the complete transformation from neural firing to body movements. To achieve this, we have built a neuromechanical model of Hydra’s fluid-filled hydrostatic skeleton, showing how drive by neuronal activity activates distinct patterns of muscle activity and body column biomechanics. Our model is based on experimental measurements of neuronal and muscle activity and assumes gap junctional coupling among muscle cells and calcium-dependent force generation by muscles. With these assumptions, we can robustly reproduce a basic set of Hydra’s behaviors. We can further explain puzzling experimental observations, including the dual timescale kinetics observed in muscle activation and the engagement of ectodermal and endodermal muscles in different behaviors. This work delineates the spatiotemporal control space of Hydra movement and can serve as a template for future efforts to systematically decipher the transformations in the neural basis of behavior.
To generate behaviors, neural activity is transformed through the biomechanics of the body. There have been exciting developments of predictive models that incorporate musculoskeletal dynamics in an array of vertebrate and invertebrate animals (1–5), including humans (6, 7). Neuromechanical approaches have been taken to describe the movements of C. elegans (8–13), larval Drosophila (14–16), and leech (17, 18), which all act as muscular hydrostats. In cnidarians, a 2D model of the medusa form of jellyfish Aurelia aurita neuronal network and muscles simulates swimming and turning behaviors (19). In octopus, Yekutieli et al. have simulated the biomechanics and control of reaching movements (20, 21). However, generally, these models are limited in their completeness by the inability to observe the system in its entirety, with simultaneous spatiotemporal patterns of neural activity, muscular activation, and whole animal behavior.
Small model systems pose the opportunity to develop relatively complete models of the transformations from neural activity to behavior, taking into account not only the biomechanics of the body but also the biophysics of muscle activation. As an active medium, muscle tissue has its own dynamics that can contribute significantly to this transformation. The small freshwater cnidarian Hydra offers a unique inroad into this problem. Along with Hydra’s simple body structure, recently developed genetic lines now allow the direct imaging of calcium-based activity in both neurons (22, 23) and muscle cells (24, 25) during behavior. This system thus presents an opportunity to account for the transformation from neural firing to behavior by modeling both body and active muscle dynamics, which determine how neural activation mediates behavioral outputs.
Anatomy and Behaviors of Hydra.
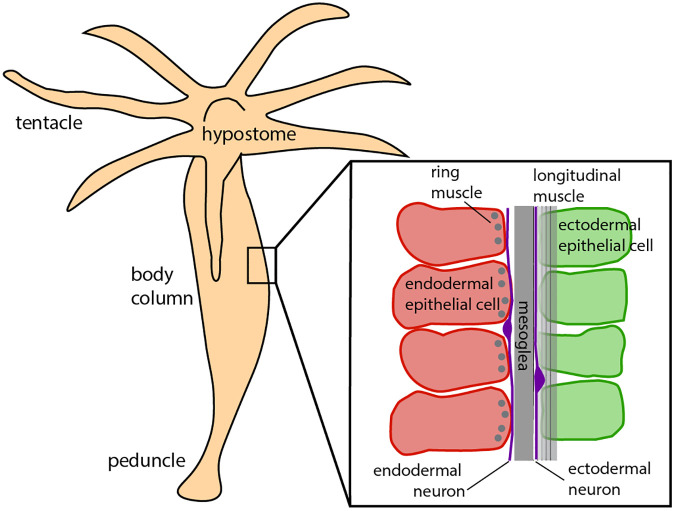
Hydra’s anatomy is that of a fluid-filled body column consisting of two body layers, the ectodermal and endodermal epithelia, separated and supported by an acellular gelatinous layer, the mesoglea (Fig. 1) (26–28). The epithelial layers consist of a sheet of epitheliomuscular cells, innervated by separate nerve nets (22). The ectodermal and endodermal epitheliomuscular cells respectively display longitudinal and circumferential processes called myonemes, producing contractions oriented in corresponding directions (26). These layers, together with the enclosed fluid, form a hydrostatic skeleton in which the force of muscle contraction is transmitted throughout the body column by internal pressure (29).
Fig. 1.
Simplified Hydra anatomy, adapted from ref. (28).
Movement in Hydra is controlled by a diffuse nerve net. Early cnidarians are believed to have acquired one of the first nervous systems (30, 31). Their descendant Hydra’s uncoupled ectodermal and endodermal nerve nets (32) lack a centralized “brain” or ganglia, yet their firing activity underlies a rich repertoire of behaviors. These include contraction bursts, active elongation, nodding, bending, and two forms of locomotion (24, 33–37). However, how neural activity drives behavior is not understood. Early extracellular recordings identified several distinct electrical events in Hydra: contraction bursts (CB), rhythmic potentials (RP), and prelocomotion bursts (PLB) (35, 36, 38, 39). Recent work has clearly identified three separate functional nerve subnetworks responsible for these electrical events (22). However, only one of these, the contraction burst (CB) network, is directly correlated with a motor output, namely whole-body contraction (22). What causes the CB nerve net to fire is still not known, although its frequency is influenced by environmental conditions including osmolarity (25, 40–47) and temperature (48), as well as microbes (49, 50). Aside from the CB, the precise association of neural activity with behavior has not yet been mapped out.
Neural Control of Behavior in Hydra.
At what length scale and with what precision does the firing of nerve cells influence movement? These factors depend on how activation is conveyed through muscles and how the resulting network of muscular contractions interacts with the biomechanics of the body. Due to gap junctional coupling (51, 52), the epitheliomuscular network is able to propagate excitation (35, 53–55) even when Hydra’s nerve cells have been removed (56, 57). Several studies have suggested that contraction pulses can be conducted by the epithelium in Hydra (53, 54, 58–60); conduction in nerve-free epithelia has also been demonstrated in other hydrozoans such as Siphonophores, Sarsia, and Euphysa (61, 62). By imaging calcium signals in the endodermal and ectodermal epithelial layers, Szymanski and Yuste (24) reported two distinct forms of muscle layer activation: a rapid global activation that drives whole-body contraction, and slow waves of local activation, including body column waves, that initiate anywhere in the body column, and bending waves, initiating in a region of the peduncle and that correlate with bending.
Furthermore, as noted, Hydra has a fluid hydrostatic skeleton, and its endodermal and ectodermal muscle fibers are oriented in orthogonal directions. One would expect, therefore, that contraction is effected by activating the longitudinal ectodermal layer, while extension is due to activation of the circumferentially oriented endodermal muscles. However, Szymanski and Yuste (24) showed, counterintuitively, that the two muscle layers activate together during contraction bursts, despite the fact that the CB neural network is localized to the ectoderm, and that this activation would presumably cause the muscle layers to act against one another during contraction. How can we account for the generation and transformation of this activation pattern into the observed behavior? All of these observations suggest that the dynamics of the muscle layer itself form an important and nontrivial component of the transformation from nerve firing to behavior.
Here, we construct a model of Hydra that includes sufficient biophysical and biomechanical detail to simulate the complete transformation from measured neural activity to muscle activity to behavior. We aimed to address the following specific questions: i) What are the mechanisms that support the observed dual time scales of muscle activation, and how does Hydra use these different dynamics in behavior? ii) During contraction bursts, although only neurons in the ectodermal nerve net fire (22), both muscle layers are activated (24), and thus work against one another. What explains this dual-layer activation, and how can body contraction be achieved with opposing muscle drive? iii) Can we quantitatively reproduce basic behaviors (37), including contraction, elongation, and bending?
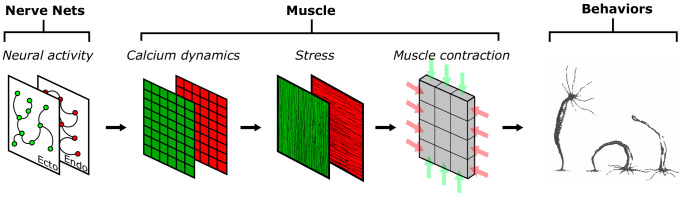
To answer these questions, we implemented a multilayered model (Fig. 2) to transform neural activity to movement. Our models are constrained both by observations from calcium imaging and by the use of physiologically plausible mechanisms consistent with a recently developed RNAseq database for Hydra (63). To model calcium dynamics in the epitheliomuscular cell network, we postulate the coexistence of a fast cellular electrically mediated pathway and a slow IP3-driven pathway. We assume that these activation signals are transmitted through the epithelial layers by gap junctions (64–67). These two mechanisms permit the coexistence of the fast electrically driven contractions as well as slow waves responsible for bending; the model predicts that these dynamics are triggered by distinct signals. We show that an intermediate level of gap junctional coupling between the ectodermal and the endodermal epithelium can share contraction activation between the two muscle layers but isolate slow wave activity to the ectoderm, consistent with observation. We next convert calcium dynamics to force generation. In order to account for Hydra’s movement dynamics, it was necessary to hypothesize that the relationship between calcium and force has more persistent dynamics in the endoderm than in the ectoderm, leading to slower relaxation times for endodermal muscles. Finally, we convert the simulated epithelial calcium dynamics to strain, which provides an active force input into a biomechanical model of the fluid-filled hydrostat. While previous hydrostatic models generally model the body by actuating longitudinal segments (68), here all forces are applied in the fluid-enclosing shell. We use this model to show that the simulated muscle activation, when driven by neural activity inferred from calcium imaging, can account quantitatively for the measured behaviors of contraction, elongation, and bending.
Fig. 2.
Framework of our project. Neural activity patterns trigger calcium dynamics in the muscle layers, which are transformed into contractile forces in the longitudinal (ectoderm; green) and circumferential (endoderm; red) directions, here indicated by the direction of fibers in the muscle layers. This provides the active force to drive a viscoelastic biomechanical model of the Hydra body column, simulating behaviors.
Results
Slow and Fast Intracellular Calcium Pathways Explain Two Timescale Dynamics.
We first show how the muscle system can exhibit two activation patterns with distinct timescales. The mechanisms of muscle activation are rooted in the biophysics of the single muscle cells and their interactions; thus, we begin by modeling the intracellular dynamics of a single Hydra muscle cell.
Muscle contraction is controlled by calcium dynamics, where calcium elevation has two possible sources: i) IP3-induced Ca2+ release from the endoplasmic reticulum/sarcoplasmic reticulum (ER/SR) calcium store and ii) Ca2+ influx from the extracellular space through L-type/T-type calcium channels (69–72). We will refer to these two calcium signaling pathways as the “slow” and “fast” pathways respectively, based on their typical time scales. Both IP3-related calcium release (73) and electrical excitability (74) are observed in epitheliomuscular cells, and the genes of the relevant proteins including the IP3 receptor, L-type/T-type calcium channels, PMCA, SERCA, etc., are present in Hydra’s genome (Materials and Methods, for details).
Models of smooth muscle frequently treat only one of these pathways. Some models of calcium signaling consider only the slow pathway, ignoring membrane ion channels (75–78), while others consider only the fast pathway, neglecting the dynamics of the internal calcium stores; examples include models for uterine smooth muscle (79–83), gastric smooth muscle (84), urinary bladder smooth muscle (85), and pancreatic β-cells (86). While some models integrate both pathways by incorporating both influx through ion channels and Ca2+ release from stores (64, 67, 87, 88), modeling the two pathways separately and simulating calcium dynamics at different time scales is rare (89, 90). However, since calcium imaging in Hydra clearly reveals dynamics with different time scales short-lasting and fast-propagated calcium transients in CB; long-lasting, slow calcium waves in bending and nodding (24), we incorporate the necessary components for both slow and fast pathways in our model for Hydra epitheliomuscular cells.
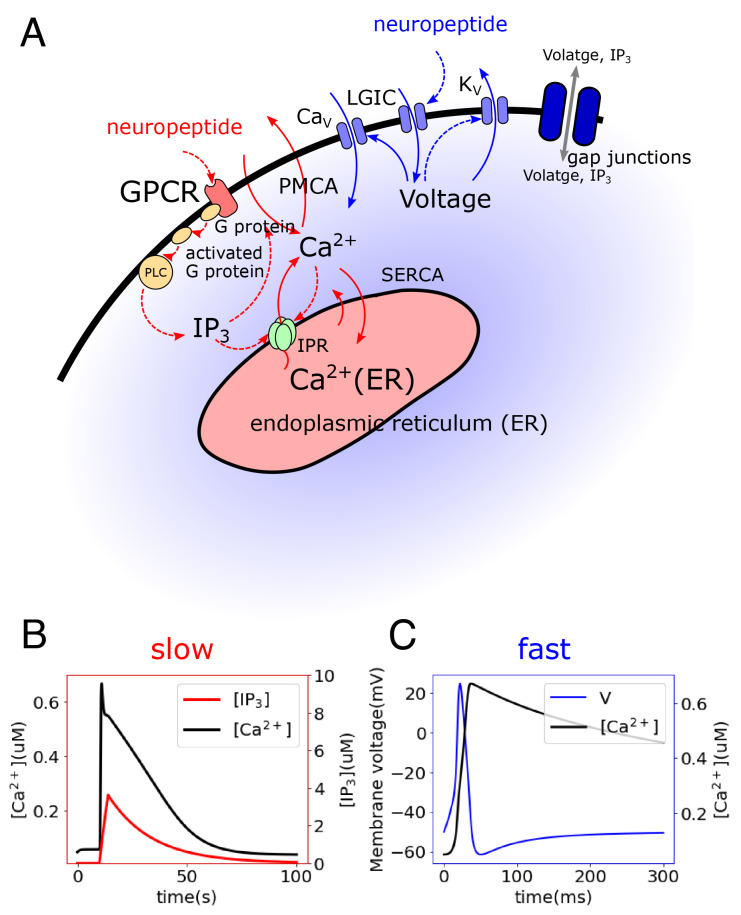
Neurons are believed to connect to and stimulate muscles via neuropeptides. While electron microscopy (EM) observations have shown evidence of dense core vesicles in Hydra tissue (51), these are not associated with the postsynaptic structure typical of synapses. The neuropeptides Hydra-RFamide and Hydra-KVamide (expressed in the peduncle region) may play roles in neuromuscular transmission (92–94). The neuropeptide Hym-176C can induce ectodermal contraction and is selectively expressed in ectodermal peduncle neurons (50, 63, 93, 95). Nonselective cation channels HyNaCs were identified in epitheliomuscular cells, which are directly activated by Hydra-RFamides I and II and can depolarize the cellular membrane potential (92, 96). These findings indicate that neural control may be achieved by the binding of these neuropeptides by receptors in muscle cells. In our model, we propose that two different types of neuropeptides trigger the fast and slow pathways, enabling differential control of distinct spatiotemporal dynamics in the muscle layers, potentially by distinct neurons (30) (Fig. 3A).
Fig. 3.
Modeled single-cell dynamics. (A) Intracellular calcium signaling model including two pathways: (i) In the slow pathway (red), neuropeptides bind a G protein-coupled receptor (GPCR) and activate a G protein, which activates phospholipase C (PLC) and hydrolyzes phosphatidylinositol bisphosphate (PIP2) into inositol 1,4,5-trisphosphate (IP3), which plays a role of the second messenger for calcium signaling. IP3 can bind to IP3 receptors (IPR) on the endoplasmic reticulum (ER) membrane and thus cause the release of Ca2+ from the ER. Ca2+ is extruded to the extracellular space through plasma membrane Ca2+ ATPase (PMCA) and is recycled to the ER through sarco/endoplasmic reticulum Ca2+-ATPase (SERCA) (30, 91). (ii) The fast pathway (blue) is initiated by the binding of neuropeptides on ionotropic receptors, which activate ligand-gated ion channels (LGIC) and depolarize the cellular membrane (92). The elevated membrane potential activates calcium channels (L-type/T-type), triggering a large influx of Ca2+ from the extracellular space and invoking further depolarization. Meanwhile, the high membrane potential inactivates calcium channels and activates potassium channels, resulting in membrane repolarization (71). (B) Simulated slow dynamics showing change of Ca2+ and IP3 concentrations. (C) Simulated fast dynamics showing change of membrane potential and Ca2+ concentration.
The simulated slow and fast dynamics are shown in Fig. 3 B and C, respectively. With reasonable choices of parameters, the timescale of the calcium dynamics triggered in the slow pathway is much larger than that in the fast pathway, consistent with the observations from calcium imaging. Sensitivity analysis of the parameters on the single cellular dynamics is included in SI Appendix, Figs. S1 and S2. Ca2+ fluxes, and ion current traces are shown in SI Appendix, Fig. S3.
Muscle Activation Patterns Can Be Simulated by Dual-Function Coupling through Intercellular Gap Junctions.
We next extend the single-cell model to a multicellular model by incorporating intercellular communication. We construct a muscle sheet composed of 60 × 30 30 μm × 30 μm cells, as measured in an example small Hydra (SI Appendix, Fig. S4), with each cell modeled as described above. While cell shape varies during contraction, for modeling simplicity, we neglect this deformation. Neighboring cells are taken to be electrically coupled, which we assume here to be via gap junctions. Gap junctions have been observed in EM studies (32) both between cells in the same layer and also penetrating the mesoglea to connect the ectoderm and endoderm (32, 52, 97). Further, single-cell RNA sequence analysis in Hydra shows multiple innexin types in both epithelial cells and neurons (63).
Junctions between cells, including gap junctions, propagate signals by i) allowing the diffusion of Ca2+ as well as second messengers like IP3 and ii) conducting electrical signals (55, 98, 99). We hypothesize that the two different observed forms of wave propagation in Hydra (slow waves and fast calcium synchronization) both occur through different epithelial activation patterns. In other systems, the propagation of IP3, but not Ca2+ which is generally so heavily buffered that its effective intercellular diffusion is negligible (64, 65, 91, 100), through junctional coupling is believed to be the primary trigger of slow intercellular calcium waves (ICW) (65, 101–105), whose propagation timescale is thus driven by diffusion. The fast wave of calcium synchronization has generally been modeled through electrical conduction by gap junctions (87, 106, 107). Given the prevalence of gap junctional innexin genes in theHydra genome (63), we will for simplicity here assume that muscle cells are coupled gap junctionally.
Based on this setting, we simulate several different muscle activation patterns, by assuming the necessary neural stimulation for each pattern and applying it to trigger specific muscle cells directly:
Body-column wave.
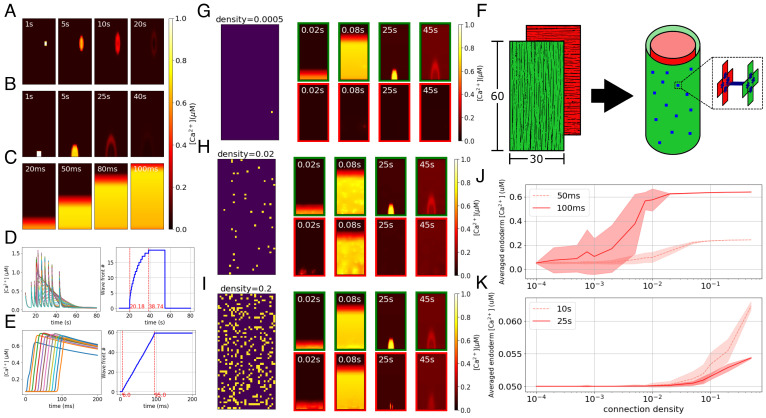
We hypothesize that the body-column waves are initiated at neuromuscular junctions at which neurons release a neuropeptide that locally triggers the slow pathway in muscle cells randomly located in the body column. To simulate these waves, we randomly select a small (2 × 2) region of cells in the sheet and stimulate their slow pathways. The elevated IP3 in the stimulated cells diffuses to the neighboring cells and triggers the slow dynamics there, resulting in slow calcium waves propagating through the corresponding local domains. The example results of the simulation are shown in Fig. 4A.
Fig. 4.
Modeled multicellular calcium dynamics. (A–C) Simulation of calcium dynamics in a muscle sheet: (A) the body column wave, (B) the bending wave, and (C) the fast wave. (D and E) [Ca2+]i traces (Left panels, each trace corresponds to a cell) and indices of wavefronts (Right panels, increasing from the Bottom to the Top) along the center longitudinal line of the muscle sheet: (D) bending wave simulated as occurring simultaneously with a late stage of contraction bursts, which is commonly observed in experiments (24); (E) fast wave. (F) Layout of the body column model. Green and red represent the ectodermal and endodermal layers respectively, in which the myonemes are aligned in longitudinal and circumferential directions respectively, as represented by the fiber directions. Blue dots represent cross-layer gap junctions. (G–I) Connectivity patterns and calcium patterns of ectoderm (green border) and endoderm (red border) in simulations with different connectivity ratios, where the ratios are separately 20% (G), 2% (H), and 0.05% (I). In connectivity patterns, each bright spot represents a gap junctional connection at that position. (J and K) Diagrams show cross-layer propagation for different connection densities of cross-layer gap junctions. We simulate 20 epochs for each density; we take snapshots at 50 ms and 100 ms after triggering only the fast pathway (J) and 10 s and 25 s after triggering only the slow pathway (K) and then average the [Ca2+]i of the whole endoderm, plotting the mean and SD of the 20 epochs for each density at these time points.
Bending wave.
A second type of slow wave initiates at the peduncle and slowly propagates in the oral direction through the ectoderm (24). This asymmetrical calcium activity in the ectoderm is believed to cause bending. To simulate the bending wave, we stimulate the slow pathway in a 4 × 4 cell-patch located in the peduncle of the ectoderm sheet of our model; propagation is due as above to gap junctional IP3 diffusion (Fig. 4B). To obtain a wave as observed in data, it is necessary to assume that gap junctional coupling is anisotropic, larger longitudinally than circumferentially (Discussion).
Fast wave (contraction pulse).
Hydra’s contraction burst (CB) is driven by the firing of a unique subnetwork of the ectodermal nerve net (22) that is distributed across the body but particularly concentrated in a ring in the peduncle. Each contraction pulse causes a global calcium synchronization activating all muscle cells in both ectoderm and endoderm. Measurements in ref. (24) showed that the contraction pulses initiate in the peduncular epithelium and propagate to the rest of the body column. Here, we assume these neurons to be the primary source of activation although, as we show later, the distribution of these neurons is not critical to the dynamics. We initiate the fast wave by simulating inputs from a ring of neurons in the peduncle onto the connected muscle cells: We stimulate the fast pathway dynamics in the bottom row (1 × 30) of the ectodermal sheet. Elevated membrane potentials propagate rapidly to the remainder of the cells via their electrical coupling, giving global calcium synchronization, as shown in Fig. 4C.
To quantitatively compare the speed of the simulated waves with experimental data, we identified the wavefront of the bending wave in our model as shown in Fig. 4D, from which the average propagation speed can be calculated as around 0.9 cells/s. The length of our biomechanical model is in the range of 0.6 mm (fully contracted) to 1.7 mm (elongated), based on which the length of each cell can be calculated as 9.8 μm (contracted) to 28.8 μm (elongated), so the propagation speed is in the range of 9 μm/s to 26.5 μm/s. In ref. (24), the propagation speed of the bending wave was calibrated as 13 ± 0.7 μm/s, which falls in the range of the simulation. The speed of the fast wavefront is computed as shown in Fig. 4E, giving 0.7 cells/ms or 6 mm/s when the model is in the contracted state. This is of the same order as the propagation speed measured from calcium imaging (4.6 to 5 mm/s) in ref. (24). The dependence of these speeds on choices of parameters such as stimulation strength, gap junctional coupling coefficients, and some intracellular parameters is explored in SI Appendix, (Figs. S5–S7).
Sparse Cross-Layer Gap Junctions Can Explain Synchronous Fast Wave and Isolated Slow Wave Between Ectoderm and Endoderm.
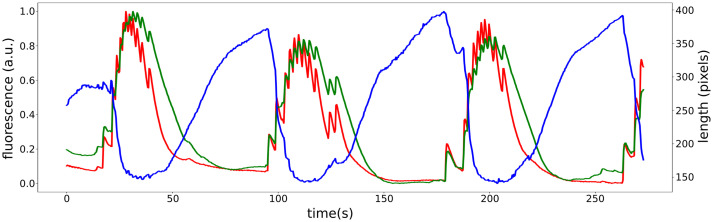
During a contraction burst, neuronal activity is confined to the ectoderm, indicating that CB neurons are localized to the ectoderm (22), while both the ectoderm and the endoderm show an almost-synchronous fast wave of epitheliomuscular calcium (Fig. 5); in contrast, body column waves and bending waves are observed only in the ectoderm (24).
Fig. 5.
Recorded fluorescence from calcium imaging showing simultaneous activation of ectoderm (green) and endoderm (red) during contractions, shown by computing the corresponding time-varying length (blue) of Hydra.
We propose that the synchronization of fast waves in the two layers is due to electrical coupling through cross-layer gap junctions which have been observed to penetrate the mesoglea: When cells in the ectoderm are electrically activated, the action potential can propagate through the gap junction and trigger activity in the endodermal epithelium. Cross-layer gap junctions should then also allow a flow of IP3. However, there is no evidence that slow waves in ectoderm propagate to the endoderm (24). How can we resolve this? One possibility is that the epitheliomuscular cells of the endoderm do not have the slow activation pathway. Another possibility is that the biophysics of calcium activation is the same, but the physical properties of coupling can lead to this differential filtering.
We test the idea that physical coupling can explain these findings, ie., that the ability of global fast waves to cross between the muscle layers while local slow waves are blocked is due simply to the density of cross-layer coupling (Fig. 4F). By varying the connectivity ratio (density) of the cross-layer gap junctions in our model, we indeed found that when the connectivity ratio is high, both fast and slow waves can propagate between the two layers; when the ratio is low, neither of the two waves propagates; and there is an intermediate range in which only the fast wave crosses the layer (Fig. 4G–I).
To further probe the effect of cross-layer gap junction density on the propagation of transmesoglea calcium waves, we quantitatively analyzed the relationship between the averaged calcium concentration of the endodermal muscle sheet and the connection density, after stimulating the ectodermal muscle cells’ fast (Fig. 4J) and slow (Fig. 4K) pathway. As shown, for both slow and fast waves, a higher connection density of cross-layer gap junctions allows stronger calcium wave propagation from the stimulated ectoderm to the endoderm. When the connection density is very low or very high, the SD is small. In intermediate ranges, there is considerable variability, depending on the specific placement of cross-layer connections. Overall, for an intermediate range of connection densities, only fast waves can cross layers, and slow waves are limited to the directly stimulated ectodermal layer.
As noted, while it is also possible that the endodermal epithelial cells lack mechanisms supporting the slow dynamics of the ectoderm, we will for simplicity use the same single-cell model for all epithelial cells along with this proposed mechanism for sharing of muscle activation in subsequent simulations.
Transforming Calcium Dynamics to Muscle Contraction.
Given the modeled calcium dynamics and activation patterns of the whole-body muscle system, we next compute how they generate contraction.
Calcium to force.
In smooth muscle, a rise of intracellular calcium concentration [Ca2+]i leads to a rise of calmodulin, leading to increased activation of MLCK (myosin light-chain kinase), phosphorylation of myosin, and thus contraction (91). The Hai–Murphy model of smooth muscle (108) uses four states of the cross-bridge to simulate the force-production process, where Ca2+ plays a role in MLCK activation. The Hai–Murphy model includes the “latch-state” of the cross-bridge, which allows the maintenance of steady-state stress of muscle even if the Ca2+ concentration has decreased. Modified Hai–Murphy models have been used to simulate contractions in arteriole (109) and uterine (82, 110) smooth muscle. In our work, we applied a modified version of the Hai–Murphy model, following (82) and (110), to transform [Ca2+]i into active stress.
Force to contraction.
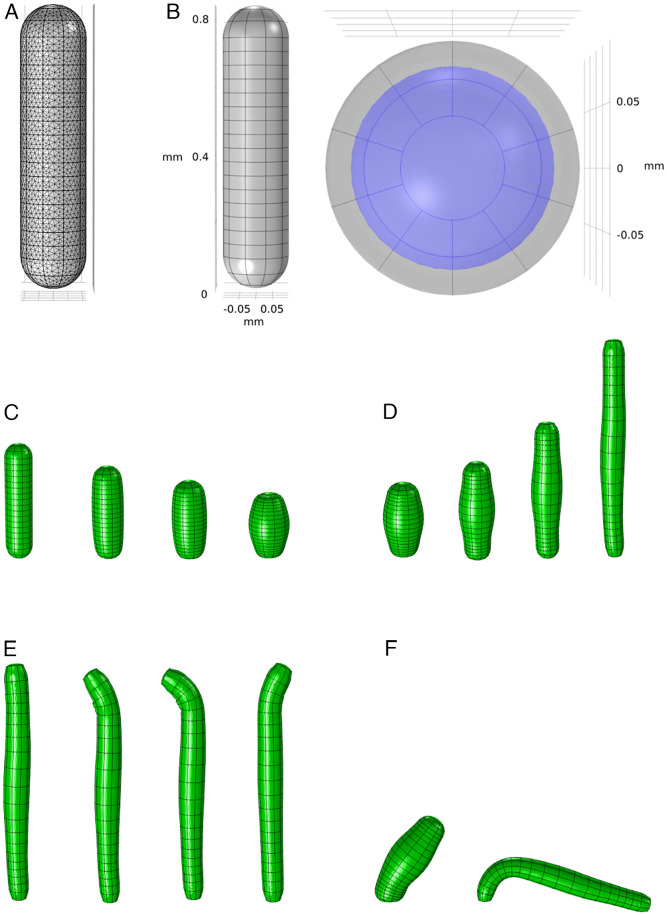
To further convert the stress into Hydra movement, as our final step, we need to construct a model of the hydrostatic skeleton of Hydra that can simulate the biomechanics of the body, driven by the transformed stress. We construct our model using COMSOL Multiphysics® 5.3a. We approximate the anatomy of Hydra with a simplified biomechanical model that contains two domains: the body shell and the enclosed fluid. The body shell, which represents the combination of the ectoderm and endoderm layers and the mesoglea, is composed of a half-spherical shell at the hypostome and a half-spherical shell at the peduncle, connected by a uniform body column cylinder shell. COMSOL automatically generates a physics-controlled mesh by dividing the model into small finite elements for simulation (Fig. 6A). The body shell and enclosed fluid together form a hydrostatic skeleton. In order to manipulate the biomechanical model at high resolution, we divide the body shell into 10 (radial) by 20 (longitudinal) domains (Fig. 6B).
Fig. 6.
Biomechanical model and simulated behaviors. (A) Finite element mesh of the biomechanical model generated by COMSOL. (B) Geometry of the biomechanical model from a side view (Left) and Top view (Right). Gray represents the muscle shell domain, while the enclosed fluid is shown as purple. (C–F) Different behaviors simulated by the model: (C) contraction, (D) elongation, (E) nodding, and (F) bending.
While the COMSOL architecture as described handles the passive biomechanical properties, we apply time-varying active stresses generated by the output of the calcium signaling models; the ectodermal model drives longitudinal external stresses, while the endodermal output drives stress in the circular direction. We obtain the active stress from the calcium signaling model as described above and average the stress of neighboring 9 cells, coarse-graining the original 30 × 60 matrix to fit the 10 × 20 dimensions of the biomechanical model.
Phasic ectoderm and tonic endoderm muscle types simulate the interplay of contraction and elongation.
Calcium measurements in the ectoderm and endoderm pose two major questions. How does the observed coactivation of the opposing ectodermal and endodermal contracting forces result in a total effect of longitudinal contraction of Hydra, instead of opposing each other? Further, why do we see no calcium signal in the endoderm during elongation between contractions (Fig. 5)? Indeed, when we directly apply the transformed stress from calcium dynamics to the biomechanical model, the predicted stresses act in opposition, preventing normal contraction (Movie S2).
As a potential resolution to this conundrum, we propose that ectoderm and endoderm may exhibit different Ca-stress relationships. Different muscle properties can be accounted for within the Hai–Murphy formulation, which can account either for fast-acting phasic behavior as for “fast” myosin isoforms or tonic contraction via the latch-bridge mechanism, as for “slow” isoforms (111). By assuming that the ectoderm is phasic and endoderm is tonic, and under the hypothesis that ectoderm can generate a larger maximum stress than that of endoderm inspired by the observations that the myonemes in ectoderm are longer than those in endoderm (26), we can successfully simulate the interplay of contraction and elongation. When CB neurons fire, both layers are activated, and the ectoderm initially dominates, driving a longitudinal contraction. When CB firing ceases and [Ca2+]i drops in both layers, the hypothesized slow dynamics of the endoderm allow it to maintain the stress longer without ongoing neuronal stimulation, thus dominating during Hydra’s elongation phase.
Integration: Simulating the Transformation from Neural Activity to Behaviors.
With the bottom–up pipeline described above, we can now simulate the observed behaviors of Hydra, using different spatiotemporal neural firing patterns to drive muscle activation.
Fig. 6C–F shows the model simulation of several typical behaviors of Hydra. We simulate contraction and elongation as described above. We simulate bending by stimulating the slow pathways of a small localized group of ectodermal cells at the peduncle, which triggers the bending wave as shown in Fig. 4B, generating local contraction which causes Hydra to bend toward the stimulated side. This demonstrates that activation of the slow and fast pathways can coexist without interfering with each other, as the contraction event in the fast pathway does not saturate the calcium dynamics. For nodding, a separate nerve net, called the subtentacular network (22), is found to be correlated with nodding behavior. Here, we assume that this network simply stimulates the slow pathways of a small set of ectodermal cells in the subhypostomal region. This is similar to bending behavior but with an opposite location. Our model is thus able to generate a “bending” of the hypostome toward the stimulated side.
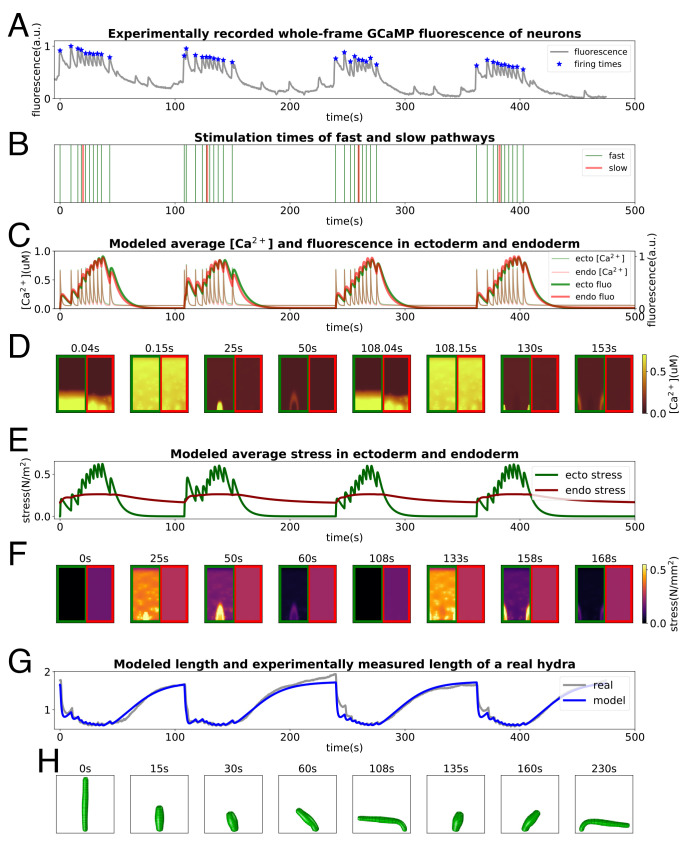
Next, we attempt to reproduce naturalistic behavioral sequences of Hydra. Left undisturbed, Hydra undergoes repeated cycles of contraction and elongation, combined with bending. From videos of the neuronal GCaMP Hydra, we extract behavior, characterized by the animal’s skeletonized body length (Materials and Methods). We use the integrated GCaMP fluorescence trace to infer the firing times of the CB neurons (Fig. 7A) and additionally include sparse triggering times for the bending waves (Fig. 7B). With this stimulation, we compute the calcium dynamics underlying fast and slow bending waves in the epithelial sheets (Fig. 7 C and D); the simulated fluorescence traces match the observed curves in Fig. 5. After encoding the calcium concentration into stress (Fig. 7 E and F)), we use it to drive the biomechanical model, successfully exhibiting a series of behaviors that mimic the real Hydra (Fig. 7H). The simulated length changes show very good quantitative agreement with the dynamics of contraction and elongation of the animal (Fig. 7G). An animation of the entire simulation pipeline is provided in Movie S1 as well as an additional example with a different neural drive (SI Appendix, Fig. S8).
Fig. 7.
Pipeline of the simulation from neural activity to behaviors. (A and B) NGCaMP fluorescence trace: stars mark estimated times of neural firing (A) and consequently stimulation times for the model (B). (C and D) Averaged [Ca2+]i and fluorescence intensities in ectoderm and endoderm (C) and [Ca2+]i patterns of some moments (D). (E–F) Averaged active stress in ectoderm and endoderm (E) and stress patterns of some moments (F). (G and H) Comparison between length evolution of the model and from a Hydra (G) recording and some stills of the final simulated behaviors from the model (H).
The fits capture well the form of the “impulse response” of the length to the neural inputs as well as the total elongation. This fit is achieved by an appropriate setting of the parameters of the Hai–Murphy model, as shown in SI Appendix, Fig. S9 A–C, governing the offset in timescales of force generation of the ectoderm and endoderm. It is also quite sensitive to the relaxation time constant of the muscle, SI Appendix, Fig. S9D, serving as a prediction for future experiments.
Discussion
In this work, we have succeeded in implementing a model framework that predicts behaviors from neural firing patterns. Here, we review the assumptions, required mechanisms, and limitations of our model. We began with a biophysical model for single muscle cell dynamics that is grounded in known molecular mechanisms; we then linked muscle cells into a network via gap junctional coupling, which successfully simulated multiple-timescale calcium activation dynamics observed in GCaMP imaging experiments in Hydra. Such multiple-timescale calcium signaling has also been observed in arterial smooth muscles (90). We then used this model to generate active stress to drive a passive biomechanical model of the body. This model successfully simulated Hydra behaviors including contraction bursts, bending, and elongation. These two components together form a model that can exhibit different behaviors with given neuronal stimulation and can thus serve as a testbed for reverse-engineering the neural activity that underlies more complex Hydra behaviors.
In order to match observed activity and behavior, we raised and addressed a series of questions. We accounted for the two distinct time scales of calcium patterns in imaging experiments by assuming that there are two different calcium pathways (ionotropic and metabotropic) in each single muscle cell and then captured the different propagation speeds through the dual functions (electrical coupling and chemical diffusion) of gap junctions. By assuming sparsely distributed cross-layer gap junctions between ectoderm and endoderm, we succeeded in producing synchronized fast waves in the two layers along with the isolation of slow waves to the ectoderm. To explain how Hydra can longitudinally contract although the two counteraligned muscle layers are simultaneously activated, we postulated that muscles of ectoderm and endoderm have different properties (phasic and tonic). This further explains how Hydra can elongate with no apparent endodermal calcium activation (Fig. 5). Putting these factors together, we successfully simulated cycles of contraction, elongation, and bending.
Despite this success, there are many details and limitations that need to be explored further. For instance, how and which groups of neurons generate activity patterns and transmit these distinct inputs to the muscle is still unclear. We have considered a simplified structure of Hydra and neglected the effects of the surrounding water, whose viscosity and buoyancy may influence natural behavior (112–114). Furthermore, our model assumes only feedforward transformations from neural activity to behaviors although it is likely important to understand how behavior influences neural firing through mechanosensation and other forms of sensory feedback.
Electrical Signaling in Nerve Net and Muscle.
Our model addresses the question of whether electrical activity during contraction bursts is transmitted through the nerve net or the muscle layer. We propose that hypostomal neurons play a role in integrating information from the environment: Following a decision to fire, the signal is propagated through the sparsely distributed CB nerve subnet to the peduncle ring of motor neurons, which acts as the primary drive of contraction. This architecture is supported by the observed propagation of fast calcium activation from the peduncle toward the oral side (24), the expression of Hym-176C in the peduncle (93), and the previous observation that nerve-free Hydra epithelia are capable of electrical conduction (56).
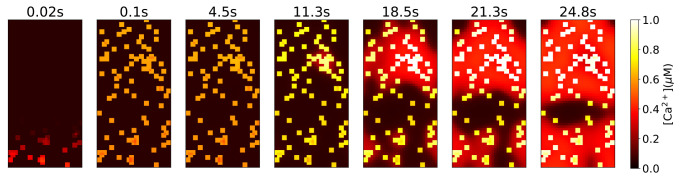
However, the success of our model supports the proposal that during contraction, synchronous drive from the nerve net is supplemented by the electrical coupling property of muscle cells themselves. The CB neurons are sparsely distributed in the body column; it is unlikely that the CB neurons directly innervate all muscle cells although it is possible that each neuron drives a small group of them. We simulate the case that muscles are electrically isolated, and small groups receive input from an electrical wave purely in the nerve net; this leads to slowly growing nodes of excitation via the slow chemical diffusion of IP3 (Fig. 8). Thus, we believe that electrical coupling of muscle cells contributes to the rapid synchronization of calcium activity in the epithelium (115). The distributed network of CB neurons likely serves to integrate and generate the contraction activity and may contribute to the robustness of contraction.
Fig. 8.
Modeled calcium activation pattern under sequential stimulation of the fast pathways of randomly chosen 2 × 2 groups of muscle cells in the body column with no gap junctional electrical conductance between muscle cells.
We also demonstrated that sparse electrical coupling between the muscle layers is a mechanism that can account for the coactivation of longitudinal and circumferential contraction during contraction bursts. We note that it is also possible that the internal muscle layer is triggered to contract through mechanosensation in the interior, caused by the contraction of the outer layer. While it is counterintuitive for these muscles to activate together, this may have a functional role; as suggested in ref. (24), the resulting stresses on the body may serve to squeeze absorbed water out of the body walls.
Hydra has two additional known synchronously firing networks, the “rhythmic potentials” RP1 and RP2. We have found no correlation of RP firing with instantaneous length changes; thus, it is unlikely that the RP networks directly control muscle contraction. However, it has been suggested that “radial contraction” behavior is related to RP2 (22). The ectodermal RP1 nerve net may inhibit CB neurons, therefore suppressing contraction bursts, as its frequency is inversely proportional to contraction bursts (22, 38, 116). Previous studies have proposed a mutual postinhibitory rebound relationship between CB and RP neurons (117, 118), but the mechanism governing CB and RP interaction has not yet been identified.
Feedback from Behavior and the Environment.
Our model simulates the transformation from neural activity to behaviors as a purely feedforward control pipeline, but there are several ways in which feedback may play a role.
We have not modeled direct feedback from the body to generation of neural activity. Many previous studies have postulated that contraction bursts play a role in osmoregulation (25, 40, 42, 43, 45, 119). EM studies show that intercellular vacuoles in Hydra tissue may contribute to hyposmotic fluid formation, so that contraction bursts may regulate the osmotic pressure by periodically squeezing the fluid from vacuoles to the enteron (44). Based on these observations, it is reasonable to assume that periodic neural activity is mediated by osmotic pressure through mechanosensation (115).
A further source of potential feedback that we have neglected is that between the state of the animal’s body and the modeled dynamics. First, diffusion dynamics may be affected. In the model, we assumed that the speed of IP3 diffusion is faster in the longitudinal direction than in the circular direction, in order to account for the different propagation speeds of bending waves in longitudinal and circular directions, in units of cells per second. While it is possible that the density of longitudinally oriented gap junctions may be larger than that of circularly oriented ones, it is also possible that the propagation speeds in the two directions are the same, but since bending waves are usually initiated when Hydra is contracted and cells are squeezed longitudinally, the diffusive wave may travel through more cells longitudinally than circumferentially. In order to incorporate this, one would need to compute the speed of IP3 diffusion as a function of the local cell shape. Second, we have not incorporated a model of water absorption, thus neglecting the possible biomechanical influence of changes in tissue thickness and stiffness due to variable turgidity.
Implementing feedback between calcium activation in the muscle layer and the biomechanical model would be very complex within COMSOL and require considerable engineering effort. In general, however, accounting for any of these effects is possible by extending the framework of our model.
Body Plan Simplicity.
Our biomechanical model simplifies Hydra to a hollow cylinder with two spherical ends. However, Hydra’s body column deviates from cylindrical, slimming toward the peduncle. Furthermore, cells across the body are heterogeneous in size and shape. Recent work indicates that there is variation in Young’s modulus of the body column and suggests that this can affect somersaulting behavior (112). Future work could explore more precisely how the body wall mechanics influence the transformation of neural signals and muscle forces into behavior. Further, we do not attempt to model the tentacles, whose sensory input likely contributes significantly to Hydra’s movement and whose adhesion to surfaces frequently affects body movement. Modeling such details will be necessary to obtain detailed quantitative agreement between the model and additional aspects of behavior, including the effects of water, that are present in fully natural 3D behaviors.
Model Fitting and Parameter Selection.
Overall, our model succeeds in qualitatively reproducing observed wavefronts and dynamics of calcium activation and transforming this into observed behaviors, showing good quantitative match to body extension data. While we began with generic formulations of biomechanics and muscle dynamics, we incorporated minimal additional mechanisms that account for the set of observations we aimed to describe. While the result is a fairly complex model, we have constructed it according to the following principles:
-
1.
Biological plausibility: We have included only parameters for key mechanisms that plausibly exist in Hydra, determined through Hydra gene expression; further, the values of those parameters should be in a physiological reasonable range, determined from related experimental papers and in comparison with other biophysical models, or from direct measurements on Hydra.
-
2.
Simplicity: We have included only a minimal set of mechanisms that account for the observed dynamics.
-
3.
Robustness: We avoid selecting parameter values at singular or exotic points and have confirmed that a reasonable range of perturbation of the value does not dramatically change the simulation results.
-
4.
Significance: We focused on a subset of parameters that play important roles in wave propagation speed and range (SI Appendix, Figs. S5–S6) and length change (SI Appendix, Fig. S9). We include all parameters involved in important dynamics but have focused attention on those that dominate the macroscopic dynamics and behaviors.
Given this general philosophy, we have built our model using the following parameters, ordered by decreasing significance for the focus of our work:
-
1.
Parameters that strongly influence match with recorded behavior through the mechanics of the muscle layers:
-
(a)
Geometrical parameters, e.g., Hydra’s length, width, thickness, etc: These parameters are given reasonable values following the literature (24, 27) and through direct measurement (SI Appendix, Fig. S4).
-
(b)
Hai–Murphy model parameters: We apply the Hai–Murphy model as a classic model of the transformation from calcium concentration to stress. However, to date, no experiments have directly measured this transformation in Hydra. Therefore, the choice of these parameters is an assumption and introduces one of our most important hypotheses—the proposal of phasic and tonic properties for the ectodermal and endodermal muscle layers. The parameter values we adopt in the model serve primarily to differentiate the two layers. We show the effects of variation of these critical parameters on the simulated behavior (SI Appendix, Fig. S9 A–C).
-
(c)
Biomechanical parameters describing the material properties of muscle: Some of these have already been calibrated in experiments (27) (including Lamé parameters and bulk modulus of Hydra’s shell), while others are tuned to lie in a reasonable range to fit experimental data, in particular, the relaxation time of muscle (SI Appendix, Fig. S9D).
-
(a)
-
2.
Parameters that determine macroscopic calcium dynamics (wave propagation speeds/range):
-
(a)
Stimulation strengths (vPLCβ, slow pathway, and Istim, fast pathway). Through parameter sweeping (SI Appendix, Fig. S5), we selected values that trigger an effective calcium dynamics and wave propagation.
-
(b)
Gap junctional coupling coefficients (gc and gIP3). It is intuitive that these parameters play an important role in determining wave propagation as we assume that both slow and fast waves propagate through the muscle sheet through gap junctions. We tested the effects of parameter values and inhomogeneity on wave propagation (SI Appendix, Fig. S6), selecting values that fit the imaging data.
-
(a)
-
3.
Parameters of single-cell dynamics: Perturbation of these values subtly affects simulation results (SI Appendix, Fig. S1). Parameters of the voltage-dependent channels can influence details of the electrical current and corresponding Ca waveforms, but due to the rapid spread of activation across the entire body through electrical coupling, these variations have little to no influence on behavior. The most significant effect of these parameters is to establish single-cell excitability, influencing how neural firing drives muscle activation. We have set these parameters in a range that avoids spontaneous muscle activity, consistent with experiments, and in which neural inputs drive a rapid (20-ms delay) response. A quite wide range of parameters is consistent with this behavior (SI Appendix, Fig. S1). Furthermore, the specific timescale of delay is an unmeasured property as one cannot yet simultaneously image both neural and muscle calcium activity, so it is possible that a different set of parameters may ultimately provide a better fit. In either case, these settings have no significant effect on behavior. Other parameters that affect the [Ca2+]i/membrane potential curve shapes have been discussed above and results are shown in SI Appendix, Fig. S2.
In bridging from neural firing to behavior, our model incorporates sufficient biological realism, including the most significant biomechanical factors, to account for recorded calcium activity in muscles and to successfully reproduce a basic suite of behaviors. Our model stands as an important step toward a complete account of the neural basis of behavior in this model organism and will serve as a starting point for further work to capture the full richness of Hydra’s natural behavior.
Materials and Methods
Single-Cell Model.
The differential equations that describe the calcium dynamics in a single cell are shown in Eq. 1,
| [1a] |
| [1b] |
| [1c] |
| [1d] |
where C is the cytosolic Ca2+ concentration; S is the ER Ca2+ concentration; P is the cytosolic IP3 concentration; and V is the membrane potential. Detailed expressions of terms and equilibrium conditions are included in SI Appendix; the corresponding parameters can be found in SI Appendix, Table S1.
Triggering of the slow pathway is simulated by elevating vPLCβ from 0.002 to 1 μM/s for 4 s; triggering of the fast pathway is simulated by a 10-ms current Istim. Though the dynamics of both fast and slow pathways are formulated with the same set of equations, one does not interfere with the other when activated—when only the fast pathway is on, the elevated [Ca2+]i cannot activate IPR alone with a low [IP3]i; when only the slow pathway is on, since the dynamics is in the inner cytosol (65, 91), the membrane potential remains subthreshold and the voltage-gated channels remain inactivated (64). Both slow and fast pathways are active during the initiation of bending during contraction bursts, but, as shown in the simulation results, they simply overlap one another, giving a natural activation pattern and motion.
The sensitivity analysis showing how parameters affect the single cellular dynamics is included in SI Appendix, Text and Fig. S1, showing the sensitivity analysis of parameters involved in the slow pathway; SI Appendix, Fig. S2 shows a phase diagram of how gCa and gK together affect the lag time of action potential after the stimulation.
Multicellular Model.
Each cell is treated as a compartment. To model the role of gap junctions in propagating electrical signals and diffusing IP3, neighboring cells within a layer and the cells at the same location in the endoderm and ectoderm are connected by coupling terms Vcoupling = ∑k ∈ neighborsgc(Vk − V) and Pcoupling = ∑k ∈ neighborsgIP3(Pk − P) (incorporated in Eq. 1). While all neighboring cells within a layer are coupled, cells with the same indices in the two layers are connected probabilistically, with a defined connection density as the ratio. The sensitivity analysis showing how parameters affect the wave propagation is included in SI Appendix, Text and Fig. S5, showing the effects of stimulation strength; SI Appendix, Fig. S6 shows the effects of coupling coefficients and SI Appendix, Fig. S7 shows the effects of some intracellular parameters.
Force Generation.
We apply the Hai–Murphy model (108) to transform calcium concentration to force, described by Eq. 2,
| [2a] |
| [2b] |
| [2c] |
| [2d] |
where M, Mp, AMp, and AM represent the ratios of four possible states of the myoneme, respectively unattached and unphosphorylated (M), unattached and phosphorylated (Mp), attached and phosphorylated (AMp), as well as attached and unphosphorylated (AM). The final active stress is Fa = KF(AMp + AM).
The proposed difference between ectoderm and endoderm is reflected by different parameters of the Hai–Murphy model, primarily represented by the difference of k7, which is the detachment rate of the “latch-bridge” state of myoneme: Its value for endoderm (tonic muscle) is set to be much larger than that for ectoderm (phasic muscle), allowing the endoderm to maintain the contraction for a longer time than the ectoderm; also, k1 of the endoderm is more sensitive to calcium concentration than that of the ectoderm, so endoderm activates more readily.
The values of these parameters can be found in SI Appendix, Table S2. The match between the length change of the model and Hydra data in Fig. 7G is primarily achieved by tuning these Hai–Murphy model parameters.
Biomechanics.
We build our biomechanical model on COMSOL Multiphysics® 5.3a, based on the finite-element method. To define the passive properties of Hydra body, we define the body shell of our model as an incompressible hyperelastic material which follows a Neo-Hookean model (120). Hyperelastic materials exhibit a nonlinear stress–strain behavior and can respond elastically under very large strains (121). Muscle tissues are often well described (122–124) and modeled (125–127) using hyperelastic properties. The passive biomechanical properties were mostly modeled based on Hill’s three-element model (128). Since biological soft tissues have hyperplasticity or viscoelasticity (129), we use hyperelastic material parameters to model the Hydra muscle shell and further incorporated viscoelasticity by including a Kelvin–Voigt model into the body shell material. For the enclosed fluid, we use the COMSOL simulation environment’s preset material “Water,” with a moving mesh. The elastic modulus and viscosity are set based on previous experimental measurements (27). The interaction between the body shell and enclosed fluid is simulated by the Fluid-Structure Interaction (FSI) module of COMSOL.
To integrate the biophysical Ca model with the COMSOL-based biomechanical model, we use the LiveLinkTMfor MATLAB® extension of COMSOL: We save the Python simulation results of stress into .csv files and then use MATLAB to load them and call API of the LiveLink to apply the resulting stress to the biomechanical model built on COMSOL; finally, we run the biomechanical simulation on COMSOL.
The parameters used in the COMSOL model are shown in SI Appendix, Table S3. Our biomechanical settings (represented by Lamé parameters) assume a 10 kPa elastic modulus and 20 μm shell thickness, which are consistent with Kücken et al. (46)’s 11 kPa and 20 μm, and do not conflict with the parameters (4.94 kPa ectodermal, 4.39 kPa endodermal, in the absence of mesoglea) measured by Carter et al. (27). For simplicity, we treat the muscle shell as incompressible, without taking its inner vacuoles and water excretion (44) into specific consideration; thus, we set Poisson’s ratio as 0.499 (not 0.5 for numerical simulation restriction), rather than 0.25 as in Kücken et al. (46).
Configurations for the COMSOL solver are shown in Table S4. Sensitivity analysis showing how some pivotal parameters affect the length change of the biomechanical model during the simulation is shown in SI Appendix, Fig. S9.
Model Constraints: Gene-Expression Database.
To validate choices of biophysical mechanisms including channels, receptors, and pumps, we queried gene expression databases for proposed components. We identified candidate genes by FASTA using the https://www.ncbi.nlm.nih.gov/protein/ and then used BLAST (130) to search for these genes in the databases Hydra 2.0 genome, Augustus Gene Models and Juliano aepLRv2. The Broad Hydra Single-Cell Portal (63) further allowed us to identify body regions with corresponding gene expression. We limited ourselves to mechanisms that were consistent with these databases.
Fluorescence Encoding.
We adopt a modified SBM model from ref. (131) to simulate fluorescence traces from [Ca2+]i, in which GCaMP6s has five different binding states depending on how many Ca2+ ions are binding, and the fluorescence can be produced by all binding states to different extents. Since fluorescence encoding is independent of our neuromechanical modeling and we lack single-cellular-level accurate data with which to fit the model, we roughly tuned the parameters to produce qualitatively reasonable traces for comparison.
Hydra Cultures and Imaging.
All Hydra lines were maintained at 18℃ and fed newly hatched Artemia nauplii two to three times per week. Hydra expressing the calcium indicator GCaMP6 in the ectoderm of the animal were used for imaging experiments. We used a modified imaging preparation from ref. (22). All imaging took place under a ZEISS Axio Zoom.V16 equipped with a Zeiss AxioCam 506 monochrome camera for fluorescent imaging, a PlanNeoFluar Z 2.3X objective lens, and a GFP fluorescent filter set. The imaging arena consisted of a microscope slide, 50- to 100-μm spacer, and a coverslip. The use of the spacer allowed us to keep the animals in focus by preventing motion in the z direction while still allowing free motion in the x and y directions. Animals were recorded in the arena for 30 to 60 min at a sampling rate of 4 to 10 frames per second.
Video Analysis.
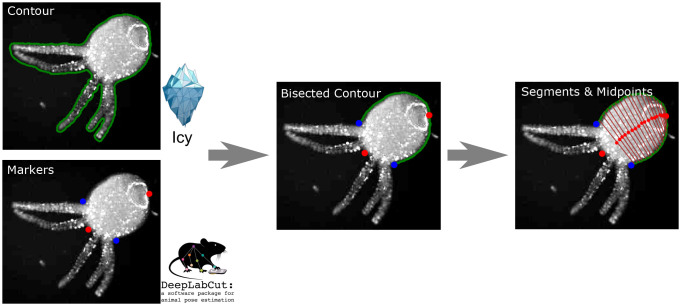
We used image analysis to estimate integrated fluorescence in the neuronal and muscle GCAMP lines in contrast to single neuron tracking (132) as well as to accurately characterize Hydra’s body configuration. Acquired movies were processed using a combination of ImageJ (133), the Icy Imaging software suite (134), DeepLabCut (135), and custom scripts (136), with a pipeline shown in Fig. 9. ImageJ was used to adjust the contrast from background noise, which is essential to accurately extract contours of the Hydra. Noise was reduced using median filtering (Despeckle plugin). Icy Imaging was then used to extract the contours of individual frames using the Active Contours plugin. We can then integrate fluorescence signals within the contour. We then used DeepLabCut to track 4 reasonably well-identified body locations: the center of the hypostome, the center of the peduncle, and the points of intersection of the leftmost and rightmost tentacles with the body column (the “armpits”). The tracked “armpits” from DeepLabCut were used to exclude the tentacles from the Icy contour. We then used the peduncle to bisect the contour and proportionally segment the two contour halves. Connecting the midpoints of the segmentation points allowed us to extract the curved midline of the Hydra body in each frame.
Fig. 9.
Pipeline of the video analysis.
Model Reduction.
While all of the parameters included in our model are based on previous work and lie within physiological ranges, such a biophysical-level model inevitably includes many parameters. Therefore, we explored reducing the dimensionality of our model by fitting Green’s functions, which can represent spatiotemporal patterns as an impulse response to neural input. This had some success in capturing qualitative aspects of the responses, but as a linear method, it cannot capture nonlinear interactions between activations. Details of this analysis are shown in SI Appendix, Text, Figs. S10–S11 and Table S5.
Supplementary Material
Appendix 01 (PDF)
Simulation results from neural activity to muscle dynamics to behaviors.
Simulation results from directly applying the transformed stress on the biomechanical model without distinguishing phasic/tonic muscle types.
Acknowledgments
This project is supported by NSF CRCNS 1822550, NSF 2203119, and a Simons Collaboration for the Global Brain grant to A.L.F. R.Y. was supported by the Burroughs Wellcome Fund 2018 Collaborative Research Travel Grant and the Vannevar Bush Faculty Award (ONR N000142012828). MBL research was supported in part by competitive fellowship funds from the H. Keffer Hartline, Edward F. MacNichol, Jr. Fellowship Fund, The E. E. Just Endowed Research Fellowship Fund, Lucy B. Lemann Fellowship Fund, Frank R. Lillie Fellowship Fund, the Fries Trust Research Award, Hartline MacNichol Research Award, L. & A. Colvin Summer Research Fellowship, and John M. Arnold Fellowship Research Award of the Marine Biological Laboratory in Woods Hole, MA. M.M.B., A.L.F. and J.S. were supported by the University of Washington’s Royalty Research Fund. M.R. and T.L.D. were supported in part by the University of Washington Center for Translational Muscle Research (1 P30 AR074990). We thank Rob Steele, Celina Juliano, and Jacob Robinson for valuable discussions. We thank the MBL Whitman Center for supporting the Hydra lab in the summers of 2017, 2018, and 2019. Portions of the paper were developed from the thesis of H.W.
Author contributions
A.L.F. designed research; H.W. and J.S. performed research; H.W., J.S., J.R.S., R.Y., and M.M.B. contributed new reagents/analytic tools; H.W., J.S., and S.S. analyzed data; and H.W., J.S., R.Y., T.L.D., M.R., M.M.B., and A.L.F. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
Code, imaging data, and simulation data have been deposited in https://github.com/hengjiwang/hydramuscle (N/A).
Supporting Information
References
- 1.Daniel T. L., Invertebrate swimming: Integrating internal and external mechanics. Symposia Soc. Exp. Biol. 49, 6189 (1995). [PubMed] [Google Scholar]
- 2.Rajagopal A., et al. , Full-body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans. Biomed. Eng. 63, 2068–2079 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Delp S. L., Loan J. P., A computational framework for simulating and analyzing human and animal movement. Comput. Sci. Eng. 2, 46–55 (2000). [Google Scholar]
- 4.L. H. Ting, H. J. Chiel, “Muscle, biomechanics, and implications for neural control” in Neurobiology of Motor Control: Fundamental Concepts and New Directions (John Wiley& Sons, Inc., 2017), pp. 365–416.
- 5.B. Weissbourd et al., Functional modules within a distributed neural network control feeding in a model medusa (SSRN, 2021).
- 6.De Groote F., Falisse A., Perspective on musculoskeletal modelling and predictive simulations of human movement to assess the neuromechanics of gait. Proc. R. Soc. B 288, 20202432 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ren L., Jones R. K., Howard D., Predictive modelling of human walking over a complete gait cycle. J. Biomech. 40, 1567–1574 (2007). [DOI] [PubMed] [Google Scholar]
- 8.Sakamoto K., Soh Z., Suzuki M., Iino Y., Tsuji T., Forward and backward locomotion patterns in C. elegans generated by a connectome-based model simulation. Sci. Rep. 11, 1–13 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Olivares E., Izquierdo E. J., Beer R. D., A neuromechanical model of multiple network rhythmic pattern generators for forward locomotion in C. elegans. Front. Comput. Neurosci. 15, 10 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Izquierdo E. J., Beer R. D., From head to tail: A neuromechanical model of forward locomotion in Caenorhabditis elegans. Philos. Trans. Royal Soc. B: Biol. Sci. 373, 20170374 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.P. Gleeson, D. Lung, R. Grosu, R. Hasani, S. D. Larson, c302: A multiscale framework for modelling the nervous system of Caenorhabditis elegans. Philos. Trans. Royal Soc. B: Biol. Sci. 373, 20170379 (2018). [DOI] [PMC free article] [PubMed]
- 12.J. Kim, J. A. Santos, M. J. Alkema, E. Shlizerman, Whole integration of neural connectomics, dynamics and bio-mechanics for identification of behavioral sensorimotor pathways in Caenorhabditis elegans. bioRxiv [Preprint] (2019). https://www.biorxiv.org/content/10.1101/724328v1 (Accessed 3 August 2019).
- 13.J. Kim, E. Shlizerman, Deep reinforcement learning for neural control. arXiv [Preprint] (2020) http://arxiv.org/abs/2006.07352 (Accessed 11 June 2020).
- 14.Loveless J., Lagogiannis K., Webb B., Modelling the mechanics of exploration in larval drosophila. PLoS Comput. Biol. 15, e1006635. (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.P. Sakagiannis, A.-M. Jürgensen, M. P. Nawrot, A realistic locomotory model of Drosophila larva for behavioral simulations. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.07.07.451470v1 (Accessed 7 July 2021).
- 16.Zarin A. A., Mark B., Cardona A., Litwin-Kumar A., Doe C. Q., A multilayer circuit architecture for the generation of distinct locomotor behaviors in drosophila. Elife 8, e51781. (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. M. Wadepuhl, W.-J. Beyn, Computer simulation of the hydrostatic skeleton. The physical equivalent, mathematics and application to worm-like forms. J. Theoret. Biol. 136, 379–402 (1989). [DOI] [PubMed]
- 18.Skierczynski B. A., Wilson R. J. A., Kristan W. B. Jr., Skalak R., A model of the hydrostatic skeleton of the leech. J. Theor. Biol. 181, 329–342 (1996). [DOI] [PubMed] [Google Scholar]
- 19.Pallasdies F., Goedeke S., Braun W., Memmesheimer R.-M., From single neurons to behavior in the jellyfish Aurelia aurita. Elife 8, e50084 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Y. Yekutieli, R. Sagiv-Zohar, R. Aharonov, Y. Engel, B. Hochner, T. Flash, Dynamic model of the octopus arm. I. Biomechanics of the octopus reaching movement. J. Neurophysiol. 94, 1443–1458 (2005). [DOI] [PubMed]
- 21. Y. Yekutieli, R. Sagiv-Zohar, B. Hochner, T. Flash, Dynamic model of the octopus arm. II. Control of reaching movements. J. Neurophysiol. 94, 1459–1468 (2005). [DOI] [PubMed]
- 22.Dupre C., Yuste R., Non-overlapping neural networks in hydra vulgaris. Curr. Biol. 27, 1085–1097 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Badhiwala K. N., Gonzales D. L., Vercosa D. G., Avants B. W., Robinson J. T., Microfluidics for electrophysiology, imaging, and behavioral analysis of hydra. Lab Chip 18, 2523–2539 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Szymanski J. R., Yuste R., Mapping the whole-body muscle activity of hydra vulgaris. Curr. Biol. 29, 1807–1817 (2019). [DOI] [PubMed] [Google Scholar]
- 25. W. Yamamoto, R. Yuste, Whole-body imaging of neural and muscle activity during behavior in hydra vulgaris: Effect of osmolarity on contraction bursts. Eneuro 7 (2020). [DOI] [PMC free article] [PubMed]
- 26.Leclère L., Röttinger E., Diversity of cnidarian muscles: Function, anatomy, development and regeneration. Front. Cell Dev. Biol. 4, 157 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Carter J. A., Hyland C., Steele R. E., Collins E.-M.S., Dynamics of mouth opening in hydra. Biophys. J. 110, 1191–1201 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Technau U., Steele R. E., Evolutionary crossroads in developmental biology: Cnidaria. Development 138, 1447–1458 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kier W. M., The diversity of hydrostatic skeletons. J. Exp. Biol. 215, 1247–1257 (2012). [DOI] [PubMed] [Google Scholar]
- 30.Fujisawa T., Hayakawa E., Peptide signaling in hydra. Int. J. Dev. Biol. 56, 543–550 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Klimovich A. V., Bosch T. C. G., Rethinking the role of the nervous system: lessons from the hydra holobiont. BioEssays 40, 1800060 (2018). [DOI] [PubMed] [Google Scholar]
- 32.Takaku Y., et al. , Innexin gap junctions in nerve cells coordinate spontaneous contractile behavior in hydra polyps. Sci. Rep. 4, 3573 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.A. Trembley, Mémoires pour servir à l’histoire d’un genre de polypes d’eau douce, à bras en forme de cornes (Chez Jean& Herman Verbeek, 1744), vol. 1.
- 34.Rushforth N. B., Burnett A. L., Maynard R., Behavior in hydra: Contraction responses of hydra pirardi to mechanical and light stimuli. Science 139, 760–761 (1963). [Google Scholar]
- 35. L. M. Passano, C. B. McCullough, Co-ordinating systems and behaviour in hydra: I. Pacemaker system of the periodic contractions. J. Exp. Biol. 41, 643–664 (1964).
- 36. L. M. Passano, C. B. McCullough, Co-ordinating systems and behaviour in hydra II. The rhythmic potential system. J. Exp. Biol. 42, 205–231 (1965). [DOI] [PubMed]
- 37.Han S., Taralova E., Dupre C., Yuste R., Comprehensive machine learning analysis of hydra behavior reveals a stable basal behavioral repertoire. Elife 7, e32605. (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Passano L. M., McCullough C. B., The light response and the rhythmic potentials of hydra. Proc. Natl. Acad. Sci. U.S.A. 48, 1376 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Passano L. M., McCullough C. B., Pacemaker hierarchies controlling the behaviour of hydras. Nature 199, 1174–1175 (1963). [DOI] [PubMed] [Google Scholar]
- 40.Lilly S. J., Osmoregulation and ionic regulation in hydra. J. Exp. Biol. 32, 423–439 (1955). [Google Scholar]
- 41.Macklin M., Josephson R. K., The ionic requirements of transepithelial potentials in hydra. Biol. Bull. 141, 299–318 (1971). [Google Scholar]
- 42.Macklin M., Roma T., Drake K., Water excretion by hydra. Science 179, 194–195 (1973). [DOI] [PubMed] [Google Scholar]
- 43.Benos D. J., Prusch R. D., Osmoregulation in fresh-waterhydra. Comp. Biochem. Physiol. A Physiol. 43, 165–171 (1972). [Google Scholar]
- 44.Benos D. J., Kirk R. G., Barba W. P., Goldner M. M., Hyposmotic fluid formation in hydra. Tissue Cell 9, 11–22 (1977). [DOI] [PubMed] [Google Scholar]
- 45.Wanek N., Marcum B. A., Lee H.-T., Chow M., Campbell R. D., Effect of hydrostatic pressure on morphogenesis in nerve-free hydra. J. Exp. Zool. 211, 275–280 (1980). [Google Scholar]
- 46.Kücken M., Soriano J., Pullarkat P. A., Ott A., Nicola E. M., An osmoregulatory basis for shape oscillations in regenerating hydra. Biophys. J. 95, 978–985 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang R., et al. , Mouth function determines the shape oscillation pattern in regenerating hydra tissue spheres. Biophys. J. 117, 1145–1155 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tzouanas C. N., Kim S., Badhiwala K. N., Avants B. W., Robinson J. T., Hydra vulgaris shows stable responses to thermal stimulation despite large changes in the number of neurons. Iscience 24, 102490. (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Murillo-Rincon A. P., et al. , Spontaneous body contractions are modulated by the microbiome of hydra. Sci. Rep. 7, 1–9 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Klimovich A., et al. , Prototypical pacemaker neurons interact with the resident microbiota. Proc. Natl. Acad. Sci. U.S.A. 117, 17854–17863 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Westfall J. A., Ultrastructural evidence for a granule-containing sensory-motor-interneuron in hydra littoralis. J. Ultrastruct. Res. 42, 268–282 (1973). [DOI] [PubMed] [Google Scholar]
- 52.Hand A. R., Gobel S., The structural organization of the septate and gap junctions of hydra. J. Cell Biol. 52, 397–408 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Josephson R. K., Conduction and contraction in the column of hydra. J. Exp. Biol. 47, 179–190 (1967). [Google Scholar]
- 54.Josephson R. K., Macklin M., Electrical properties of the body wall of hydra. J. Gen. Physiol. 53, 638–665 (1969). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Its properties and functions , P. Av Anderson, Epithelial conduction. Prog. Neurobiol. 15, 161–203 (1980). [DOI] [PubMed] [Google Scholar]
- 56.Campbell R. D., Josephson R. K., Schwab W. E., Rushforth N. B., Excitability of nerve-free hydra. Nature 262, 388–390 (1976). [DOI] [PubMed] [Google Scholar]
- 57.Lepault J., McDowall A. W., Grimmelikhuijzen C. J. P., Intercellular junctions in nerve-free hydra. Cell Tissue Res. 209, 217–224 (1980). [DOI] [PubMed] [Google Scholar]
- 58.G. Kass-Simon, Multiple excitation sites and straight-line conduction in contraction burst system of hydra. Am. Zool. 10, 505 (1970).
- 59.Kass-Simon G., Longitudinal conduction of contraction burst pulses from hypostomal excitation loci inhydra attenuata. J. Comp. Physiol. 80, 29–49 (1972). [Google Scholar]
- 60.Rushforth N. B., Behavioral and electrophysiological studies of hydra. I. Analysis of contraction pulse patterns. Biol. Bull. 140, 255–273 (1971). [DOI] [PubMed] [Google Scholar]
- 61.Mackie G. O., Conduction in the nerve-free epithelia of siphonophores. Am. Zool. 5, 439–453 (1965). [DOI] [PubMed] [Google Scholar]
- 62.Mackie G. O., Passano L. M., Epithelial conduction in hydromedusae. J. Gen. Physiol. 52, 600–621 (1968). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. S. Siebert, J. A. Farrell, J. F. Cazet, Y. Abeykoon, A. S. Primack, C. E. Schnitzler, C. E. Juliano, Stem cell differentiation trajectories in hydra resolved at single-cell resolution. Science 365, eaav9314 (2019). [DOI] [PMC free article] [PubMed]
- 64.M. Koenigsberger, R. Sauser, M. Lamboley, J.-L. Bény, J.-J. Meister, Ca2+ dynamics in a population of smooth muscle cells: Modeling the recruitment and synchronization. Biophys. J. 87, 92–104 (2004). [DOI] [PMC free article] [PubMed]
- 65.Höfer T., Venance L., Giaume C., Control and plasticity of intercellular calcium waves in astrocytes: A modeling approach. J. Neurosci. 22, 4850–4859 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Loppini A., Braun M., Filippi S., Pedersen M. G., Mathematical modeling of gap junction coupling and electrical activity in human β-cells. Phys. Biol. 12, 066002. (2015). [DOI] [PubMed] [Google Scholar]
- 67.Md. A. Ahmed, S. Venugopal, R. Jung, Engaging biological oscillators through second messenger pathways permits emergence of a robust gastric slow-wave during peristalsis. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.06.19.449120v1 (Accessed 19 June 2021). [DOI] [PMC free article] [PubMed]
- 68.Hemingway E. G., M ÓReilly O., Continuous models for peristaltic locomotion with application to worms and soft robots. Biomech. Modeling Mechanobiol. 20, 5–30 (2021). [DOI] [PubMed] [Google Scholar]
- 69.Horowitz A., Menice C. B., Laporte R., Morgan K. G., Mechanisms of smooth muscle contraction. Physiol. Rev. 76, 967–1003 (1996). [DOI] [PubMed] [Google Scholar]
- 70.Berridge M. J., Smooth muscle cell calcium activation mechanisms. J. Physiol. 586, 5047–5061 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Hill-Eubanks D. C., Werner M. E., Heppner T. J., Nelson M. T., Calcium signaling in smooth muscle. Cold Spring Harb. Perspect. Biol. 3, a004549 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Kuo I. Y., Ehrlich B. E., Signaling in muscle contraction. Cold Spring Harb. Perspect. Biol. 7, a006023 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Johnson C. J., Razy-Krajka F., Stolfi A., Expression of smooth muscle-like effectors and core cardiomyocyte regulators in the contractile papillae of ciona. EvoDevo 11, 1–18 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Holman M. A., Anderson P. A. V., Voltage-activated ionic currents in myoepithelial cells isolated from the sea anemone calliactis tricolor. J. Exp. Biol. 161, 333–346 (1991). [Google Scholar]
- 75.G. W. De Young, J. Keizer, A single-pool inositol 1, 4, 5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. U.S.A. 89, 9895–9899 (1992). [DOI] [PMC free article] [PubMed]
- 76.Y.-X. Li, J. Rinzel, Equations for insp3 receptor-mediated [Ca2+] i oscillations derived from a detailed kinetic model: A Hodgkin-Huxley like formalism. J. Theor. Biol. 166, 461–473 (1994). [DOI] [PubMed]
- 77.Schuster S., Marhl M., Höfer T., Modelling of simple and complex calcium oscillations: From single-cell responses to intercellular signalling. Eur. J. Biochem. 269, 1333–1355 (2002). [DOI] [PubMed] [Google Scholar]
- 78.Handy G., Taheri M., White J. A., Borisyuk A., Mathematical investigation of IP 3-dependent calcium dynamics in astrocytes. J. Comput. Neurosci. 42, 257–273 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Rihana S., Terrien J., Germain G., Marque C., Mathematical modeling of electrical activity of uterine muscle cells. Med. Biol. Eng. Comput. 47, 665–675 (2009). [DOI] [PubMed] [Google Scholar]
- 80. W.-C. Tong, C. Y. Choi, S. Karche, A. V. Holden, H. Zhang, M. J. Taggart, A computational model of the ionic currents, Ca2+ dynamics and action potentials underlying contraction of isolated uterine smooth muscle. PloS One 6 (2011). [DOI] [PMC free article] [PubMed]
- 81.Cochran A. L., Gao Y., A model and simulation of uterine contractions. Math. Mech. Solids 20, 540–564 (2015). [Google Scholar]
- 82.Yochum M., Laforêt J., Marque C., An electro-mechanical multiscale model of uterine pregnancy contraction. Comput. Biol. Med. 77, 182–194 (2016). [DOI] [PubMed] [Google Scholar]
- 83.Testrow C. P., Holden A. V., Shmygol A., Zhang H., A computational model of excitation and contraction in uterine myocytes from the pregnant rat. Sci. Rep. 8, 1–14 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Corrias A., Buist M. L., A quantitative model of gastric smooth muscle cellular activation. Ann. Biomed. Eng. 35, 1595–1607 (2007). [DOI] [PubMed] [Google Scholar]
- 85. C. Mahapatra, K. L Brain, R. Manchanda, A biophysically constrained computational model of the action potential of mouse urinary bladder smooth muscle. PloS One 13 (2018). [DOI] [PMC free article] [PubMed]
- 86.L. E. Fridlyand, D. A. Jacobson, A. Kuznetsov, L. H. Philipson, A model of action potentials and fast Ca2+ dynamics in pancreatic β-cells. Biophys. J. 96, 3126–3139 (2009). [DOI] [PMC free article] [PubMed]
- 87.M. S. Imtiaz, C. P. Katnik, D. W. Smith, D. F. van Helden, Role of voltage-dependent modulation of store Ca2+ release in synchronization of Ca2+ oscillations. Biophys. J. 90, 1–23 (2006). [DOI] [PMC free article] [PubMed]
- 88.Kusters J. M. A. M., et al. , Stabilizing role of calcium store-dependent plasma membrane calcium channels in action-potential firing and intracellular calcium oscillations. Biophys. J. 89, 3741–3756 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Fletcher P. A., Li Y.-X., An integrated model of electrical spiking, bursting, and calcium oscillations in GnRH neurons. Biophys. J. 96, 4514–4524 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.N. Halidi, F.-X. Boittin, J.-L. Bény, J.-J. Meister, Propagation of fast and slow intercellular Ca2+ waves in primary cultured arterial smooth muscle cells. Cell Calcium 50, 459–467 (2011). [DOI] [PubMed]
- 91. G. Dupont, M. Falcke, V. Kirk, J. Sneyd, Models of Calcium Signalling (Springer, 2016), vol. 43.
- 92.Gründer S., Assmann M., Peptide-gated ion channels and the simple nervous system of hydra. J. Exp. Biol. 218, 551–561 (2015). [DOI] [PubMed] [Google Scholar]
- 93.Yum S., et al. , A novel neuropeptide, Hym-176, induces contraction of the ectodermal muscle in hydra. Biochem. Biophys. Res. Commun. 248, 584–590 (1998). [DOI] [PubMed] [Google Scholar]
- 94.Evidence for colocalization , G. Nørgaard Hansen, M. Williamson, C. J. P. Grimmelikhuijzen, Two-color double-labeling in situ hybridization of whole-mount hydra using RNA probes for five different hydra neuropeptide preprohormones. Cell Tissue Res. 301, 245–253 (2000). [DOI] [PubMed] [Google Scholar]
- 95.Noro Y., et al. , Regionalized nervous system in hydra and the mechanism of its development. Gene Expr. Patterns 31, 42–59 (2019). [DOI] [PubMed] [Google Scholar]
- 96.Dürrnagel S., Falkenburger B. H., Gründer S., High Ca2+ permeability of a peptide-gated DEG/ENaC from hydra J. Gen. Physiol. 140, 391–402 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Wood R. L., Kuda A. M., Formation of junctions in regeneratin hydra: Gap junctions. J. Ultrastruct. Res. 73, 350–360 (1980). [DOI] [PubMed] [Google Scholar]
- 98.Huizinga J. D., Liu L. W. C., Blennerhassett M. G., Thuneberg L., Molleman A., Intercellular communication in smooth muscle. Experientia 48, 932–941 (1992). [DOI] [PubMed] [Google Scholar]
- 99.Christ G. J., Spray D. C., El-Sabban M., Moore L. K., Brink P. R., Gap junctions in vascular tissues: evaluating the role of intercellular communication in the modulation of vasomotor tone. Circ. Res. 79, 631–646 (1996). [DOI] [PubMed] [Google Scholar]
- 100.M. S. Jafri, J. Keizer, Diffusion of inositol 1, 4, 5-trisphosphate but not ca2+ is necessary for a class of inositol 1, 4, 5-trisphosphate-induced Ca2+ waves. Proc. Natl. Acad. Sci. U.S.A. 91, 9485–9489 (1994). [DOI] [PMC free article] [PubMed]
- 101.L. Leybaert, M. J. Sanderson, Intercellular Ca2+ waves: Mechanisms and function. Physiol. Rev. 92, 1359–1392 (2012). [DOI] [PMC free article] [PubMed]
- 102.Sneyd J., Wetton B. T., Charles A. C., Sanderson M. J., Intercellular calcium waves mediated by diffusion of inositol trisphosphate: A two-dimensional model. Am. J. Physiol. Cell Physiol. 268, C1537–C1545 (1995). [DOI] [PubMed] [Google Scholar]
- 103.Dupont G., et al. , Mechanism of receptor-oriented intercellular calcium wave propagation in hepatocytes. FASEB J. 14, 279–289 (2000). [DOI] [PubMed] [Google Scholar]
- 104.T. Höfer, A. Politi, R. Heinrich, Intercellular Ca2+ wave propagation through gap-junctional ca2+ diffusion: A theoretical study. Biophys. J . 80, 75–87 (2001). [DOI] [PMC free article] [PubMed]
- 105.M. Goldberg, M. De Pittà, V. Volman, H. Berry, E. Ben-Jacob, Nonlinear gap junctions enable long-distance propagation of pulsating calcium waves in astrocyte networks. PLoS Comput. Biol. 6, e1000909 (2010). [DOI] [PMC free article] [PubMed]
- 106.Kusters J. M. A. M., van Meerwijk W. P. M., Ypey D. L., Theuvenet A. P. R., Gielen C. C. A. M., Fast calcium wave propagation mediated by electrically conducted excitation and boosted by CICR. Am. J. Physiol. Cell Physiol. 294, C917–C930 (2008). [DOI] [PubMed] [Google Scholar]
- 107.Koenigsberger M., Seppey D., Bény J.-L., Meister J.-J., Mechanisms of propagation of intercellular calcium waves in arterial smooth muscle cells. Biophys. J. 99, 333–343 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.C.-M. Hai, R. A. Murphy, Cross-bridge phosphorylation and regulation of latch state in smooth muscle. Am. J. Physiol.-Cell Physiol. 254, C99–C106 (1988). [DOI] [PubMed]
- 109.Wang I., et al. , A mathematical model of airway and pulmonary arteriole smooth muscle. Biophys. J. 94, 2053–2064 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Maggio C. D., Jennings S. R., Robichaux J. L., Stapor P. C., Hyman J. M., A modified hai-murphy model of uterine smooth muscle contraction. Bull. Math. Biol. 74, 143–158 (2012). [DOI] [PubMed] [Google Scholar]
- 111.S. Han, J. E. Speich, T. J. Eddinger, K. M. Berg, A. S. Miner, C. Call, P. H. Ratz, Evidence for absence of latch-bridge formation in muscular saphenous arteries. Am. J. Physiol.-Heart Circ. Physiol. 291, H138–H146 (2006). [DOI] [PubMed]
- 112.Naik S., et al. , Differential tissue stiffness of body column facilitates locomotion of hydra on solid substrates. J. Exp. Biol. 223, jeb232702 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.W. M. Megill, “The biomechanics of jellyfish swimming.” PhD thesis, University of British Columbia, BC, Canada (2002).
- 114. D. Rudolf, D. Mould, “An interactive fluid model of jellyfish for animation” in International Conference on Computer Vision, Imaging and Computer Graphics (Springer, 2009), pp. 59–72.
- 115.Badhiwala K. N., Primack A. S., Juliano C., Robinson J. T., Multiple neuronal networks coordinate hydra mechanosensory behavior. Elife 10, e64108 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.McCullough C. B., Pacemaker interaction in hydra. Am. Zool. 5, 499–504 (1965). [DOI] [PubMed] [Google Scholar]
- 117.Taddei-Ferretti C., Chillemi S., Modulation of hydra attentuata rhythmic activity. Biol. Cybern. 56, 225–235 (1987). [PubMed] [Google Scholar]
- 118. C. Taddei-Ferretti, C. Musio, “The neural net of hydra and the modulation of its periodic activity” in International Work-Conference on Artificial Neural Networks (Springer, 1999), pp. 123–137.
- 119.Benos D. J., Prusch R. D., Osmoregulation in hydra: Column contraction as a function of external osmolality. Comp. Biochem. Physiol. Part A: Physiol. 44, 1397–1400 (1973). [Google Scholar]
- 120. R. S. l. Rivlin, Large elastic deformations of isotropic materials. I. Fundamental concepts. Philos. Trans. Royal Soc. London. Series A Math. Phys. Sci. 240, 459–490 (1948).
- 121. A. F. Bower, Applied Mechanics of Solids (CRC Press, 2009).
- 122. Laure-Lise. Gras, David Mitton, Philippe Viot, Sébastien. Laporte, Hyper-elastic properties of the human sternocleidomastoideus muscle in tension. J. Mech. Behav. Biomed. Mater. 15, 131–140 (2012). [DOI] [PubMed]
- 123.Sarma P. A., Pidaparti R. M., Moulik P. N., Meiss R. A., Non-linear material models for tracheal smooth muscle tissue. Bio-Med. Mater. Eng. 13, 235–245 (2003). [PubMed] [Google Scholar]
- 124. Grégory. Chagnon, Marie Rebouah, Denis Favier, Hyperelastic energy densities for soft biological tissues: A review. J. Elast. 120, 129–160 (2015).
- 125.M. Ansari, S. K. Lee, C. D. Cho, et al., “Hyperelastic muscle simulation” in Key Engineering Materials (Trans Tech Publ, 2007), vol. 345, pp. 1241–1244.
- 126.Gras L. L., et al. , Modelling of human muscle behaviour with a hyper-elastic constitutive law. Comput. Methods Biomech. Biomed. Engin. 13, 63–64 (2010). [Google Scholar]
- 127.Tang C. Y., Zhang G., Tsui C. P., A 3D skeletal muscle model coupled with active contraction of muscle fibres and hyperelastic behaviour. J. Biomech. 42, 865–872 (2009). [DOI] [PubMed] [Google Scholar]
- 128. A. V. Hill, The heat of shortening and the dynamic constants of muscle. Proc. Royal Soc. London. Ser. B-Biol. Sci. 126, 136–195 (1938).
- 129.Martinek Johannes, Stickler Yvonne, Reichel Martin, Mayr Winfried, Rattay Frank, A novel approach to simulate Hodgkin-Huxley-like excitation with comsol multiphysics. Artif. Organs 32, 614–619 (2008). [DOI] [PubMed] [Google Scholar]
- 130.Altschul S. F., Gish W., Miller W., Myers E. W., Lipman D. J., Basic local alignment search tool. J. Mol. Biol. 215, 403–410 (1990). [DOI] [PubMed] [Google Scholar]
- 131.D. S. Greenberg et al., Accurate action potential inference from a calcium sensor protein through biophysical modeling. bioRxiv [Preprint] (2018). https://www.biorxiv.org/content/10.1101/479055v1 (Accessed 10 May 2019).
- 132.Lagache T., Hanson A., Fairhall A., Yuste R., Robust single neuron tracking of calcium imaging in behaving hydra. PLoS Comput. Biol. 17, e1009432 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Schneider C. A., Rasband W. S., Eliceiri K. W., Nih image to imagej: 25 years of image analysis. Nat. Methods 9, 671–675 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.De Chaumont Fabrice, et al. , Icy: An open bioimage informatics platform for extended reproducible research. Nat. Methods 9, 690–696 (2012). [DOI] [PubMed] [Google Scholar]
- 135.Mathis A., et al. , Deeplabcut: markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 21, 1281–1289 (2018). [DOI] [PubMed] [Google Scholar]
- 136.H. Wang, “Modeling Hydra from neuron to muscle to behavior,” PhD thesis, University of Washington, Seattle, WA (2022).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Simulation results from neural activity to muscle dynamics to behaviors.
Simulation results from directly applying the transformed stress on the biomechanical model without distinguishing phasic/tonic muscle types.
Data Availability Statement
Code, imaging data, and simulation data have been deposited in https://github.com/hengjiwang/hydramuscle (N/A).