Quest for the Most Aromatic Pathway in Charged Expanded Porphyrins

Abstract

Despite the central role of aromaticity in the chemistry of expanded porphyrins, the evaluation of aromaticity remains difficult for these extended macrocycles. The presence of multiple conjugation pathways and different planar and nonplanar π‐conjugation topologies makes the quantification of global and local aromaticity even more challenging. In neutral expanded porphyrins, the predominance of the aromatic conjugation pathway passing through the imine‐type nitrogens and circumventing the amino NH groups is established. However, for charged macrocycles, the question about the main conjugation circuit remains open. Accordingly, different conjugation pathways in a set of neutral, anionic, and cationic expanded porphyrins were investigated by means of several aromaticity indices rooted in the structural, magnetic, and electronic criteria. Overall, our results reveal the predominance of the conjugation pathway that passes through all nitrogen atoms to describe the aromaticity of deprotonated expanded porphyrins, while the outer pathway through the perimeter carbon atoms becomes the most aromatic in protonated macrocycles. In nonplanar and charged macrocycles, a discrepancy between electronic and magnetic descriptors is observed. Nevertheless, our work demonstrates AV_min remains the best tool to determine the main conjugation pathway of expanded porphyrins.

Choosing the right path: We show that the search for the most aromatic pathway in charged expanded porphyrins is a more puzzling quest than for their neutral analogue structures. Among the most popular aromatic indices, AV_min turns out to be the most useful tool for seeking the most aromatic path.

Introduction

Due to their versatile topology and tunable photophysical properties, expanded porphyrins are excellent candidates to develop molecular switches, near‐infrared dyes, chemical sensors, and nonlinear optical materials.[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ ] An attractive feature of these extended macrocycles is their enhanced conformational and electronic flexibility with respect to the regular porphyrins, which allow them to interconvert between different π‐conjugation topologies (Hückel, Möbius, and twisted‐Hückel), each with distinct optoelectronic properties and aromaticity.[ ¹ , ¹¹ , ¹² , ¹³ ] Such a change of topology can be triggered by different external stimuli, including solvent, temperature, variations in pH, and even mechanical forces.[ ¹⁴ , ¹⁵ , ¹⁶ , ¹⁷ ] Among the toolbox of stimuli to induce Hückel‐Möbius interconversions, protonation and deprotonation of the macrocycles are considered to be easy and efficient for fine‐tuning the conformational preferences and aromaticity of expanded porphyrins. ^[11]

The NH protons in expanded porphyrins significantly affect the determination of their molecular structures. In neutral conditions, the arrangement of intramolecular hydrogen bonds constitutes one of the main factors governing the relative energies of the different conformations.[ ¹⁸ , ¹⁹ ] However, intramolecular hydrogen bonding becomes ineffective in acidic conditions, so the molecular conformations of expanded porphyrins drastically change upon protonation. For example, meso‐substituted [32]heptaphyrin(1.1.1.1.1.1.1) and [36]octaphyrin(1.1.1.1.1.1.1.1) adopt a twisted‐Hückel conformation in neutral conditions due to its more effective hydrogen bonding.[ ¹⁴ , ²⁰ ] Protonation induces conformational changes to the Möbius topology in both macrocycles probably driven by the gain of aromatic stabilization.[ ¹⁴ , ²¹ ] The protonation‐induced conformational changes from twisted‐Hückel to Möbius structures is coupled to important variations in the absorption spectra, two‐photon absorption cross‐sections, excited‐state dynamics, and ¹H NMR spectra. Accordingly, protonation emerges as an effective means to realize Möbius aromatic expanded porphyrins by disrupting intramolecular hydrogen bonding. ^[22]

Similarly, recent works have shown that deprotonation is one of the most effective methods for controlling the conformation and aromaticity of expanded porphyrins since the elimination of pyrrolic protons also breaks the hydrogen bonds in their inner cavity.[ ²³ , ²⁴ , ²⁵ ] For instance, upon treatment with tetrabutylammonium fluoride, [32]heptaphyrin and [36]octaphyrin undergo a conformational change to Möbius aromatic species.[ ²⁴ , ²⁵ ] In the case of the [26]hexaphyrin, deprotonation of the inner NH groups induces further structural planarization, which leads to a change in the main conjugated π‐electronic circuit and enhance aromaticity. ^[23] The local aromaticity of different macrocyclic pathways was assessed using the harmonic oscillator model of aromaticity (HOMA) index widely used to estimate the geometrical aspects of aromaticity by comparison to reference optimal distances in archetypal aromatic systems.[ ²³ , ²⁶ ] However, extensive research has shown that the index HOMA should be applied with caution to assess the global and local aromaticity of expanded porphyrins. ^[27] Although aromatic macrocycles are usually characterized by larger HOMA values, the differences between aromatic and antiaromatic counterparts are rather small and the HOMA index behaves qualitatively different for aromatic and antiaromatic species.[ ²⁷ , ²⁸ , ²⁹ , ³⁰ ] In addition, the HOMA index of different pathways in hexaphyrins is rather unsystematic, which makes difficult the assessment of the main conjugation pathway according to the structural criterion. ^[31]

In our long‐standing effort to characterize Hückel and Möbius aromaticity,[ ³ , ⁴ , ¹⁹ , ²⁷ , ²⁸ , ³² , ³³ , ³⁴ , ³⁵ , ³⁶ ] we report herein an exhaustive investigation of the global and local aromaticity of a set of expanded porphyrins with varying ring size and protonation states (Figure 1). Aromaticity is a theoretical concept of enormous practical importance in porphyrinoids since it dictates their optoelectronic, photophysical, and transport properties.[ ¹⁰ , ³⁴ , ³⁷ ] However, the quantification of aromaticity in these extended systems is challenging. On one side, most of the aromaticity descriptors have been developed for planar Hückel monocycles, while expanded porphyrins adopt planar and non‐planar structures as well as sustain multiple conjugation pathways. On the other side, there is an intricate local versus macrocyclic ring currents interplay, resulting in large discrepancies between energetic and magnetic descriptors. ^[38] An additional problem in the evaluation of aromaticity concerns the delocalization error, which is directly connected to the amount of exact exchange used in density functional approximations. ^[39] The delocalization error changes the magnitude of both global and local descriptors, although in some cases the aromaticity trends remain.[ ²⁷ , ⁴⁰ , ⁴¹ , ⁴² ] In other cases, the description of the system changes completely.[ ⁴³ , ⁴⁴ , ⁴⁵ ] Due to the lack of a universal aromaticity descriptor, we strongly recommend a multidimensional approach to quantify aromaticity in expanded porphyrins based on different criteria.[ ⁴⁶ , ⁴⁷ , ⁴⁸ , ⁴⁹ , ⁵⁰ , ⁵¹ ] In this regard, we recently proposed a set of global and local descriptors based on the energetic, magnetic, structural, reactivity, and electronic criteria.[ ²⁹ , ⁵² ] Statistical analysis revealed that the magnetic indices together with the reactivity descriptors are the best to assess the global aromaticity in Hückel and Möbius porphyrinoids.[ ²⁸ , ⁵³ ] However, these global indices cannot be applied to identify the main conjugation pathway, hence some of the present authors introduced new electron delocalization indices to assess the aromaticity of different pathways in large macrocycles.[ ²⁷ , ⁵² , ⁵⁴ ]

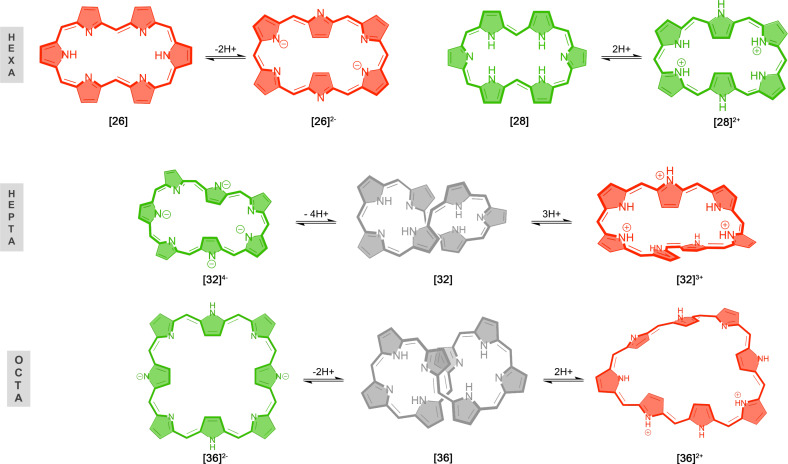
Figure 1.

Representative molecular structures of [26]‐ and [28]hexaphyrins, [32]heptaphyrin, and [36]octaphyrin in neutral, protonated, and deprotonated states. Aromatic, antiaromatic, and nonaromatic macrocycles are colored red, green, and gray, respectively.

In preliminary works,[ ²⁷ , ⁴⁰ ] we have investigated the conjugated pathways in neutral porphyrinoid compounds using several aromaticity descriptors, including BLA, BOA, FLU, and HOMA, as well as the recently introduced AV1245 and AV_min indices.[ ⁵² , ⁵⁴ ] Our results evince the difficulty of finding the most aromatic pathway for large porphyrinoids, resulting in important discrepancies between the structural and electronic descriptors. Some of the local indices are based on average values and, therefore, conceal disconnected fragments that are responsible for the loss of aromaticity. AV_min does not suffer from this drawback and it is actually the only index capable of recognizing the annulene pathway as the most aromatic one in the nine studied neutral macrocycles. In addition, AV_min can be used to identify highly dispersive bands in conjugated polymers. ^[54] Similarly, Aihara et al. have shown that the bridged annulene model can be justified well in terms of the circuit resonance energies in neutral porphyrinoids.[ ⁵⁵ , ⁵⁶ , ⁵⁷ ]

In porphyrinoid chemistry, the annulene[ ⁵⁸ , ⁵⁹ ] and perimeter[ ⁶⁰ , ⁶¹ , ⁶² , ⁶³ , ⁶⁴ ] models have been guiding principles to rationalize aromaticity, UV‐visible absorption, emission, and magnetic circular dichroism. According to the annulene model, the ring of a porphyrinoid is treated as a bridged heteroannulene; hence, aromaticity can be qualitatively predicted by applying the Hückel and Möbius aromaticity rules to the annulene substructure. The atoms through which the heteroannulene model passes are given as the annulene‐type conjugation pathway (CP), which passes through the imine‐type nitrogens but circumvents the amino NH groups in the case of all‐pyrrole expanded porphyrins. ^[65] While the predominance of the annulene‐like path is well established for neutral porphyrinoids, the question about the main conjugation pathway remains open for charged macrocycles.

For these reasons, we report herein a theoretical investigation on the aromaticity of a set of expanded porphyrins, including neutral, protonated, and deprotonated macrocycles. These synthetically feasible macrocycles were carefully selected from our previous research on the conformational preferences interconversion pathways and aromaticity of neutral expanded porphyrins with varying ring size and oxidation state.[ ²⁸ , ³⁵ , ⁶⁶ ] In addition, extensive experimental data on the protonation and deprotonation of hexaphyrins, heptaphyrins, and octaphyrins is currently available, which can be used to test our computational findings and select the most plausible cationic and anionic conformation for each macrocycle.[ ¹⁴ , ²⁰ , ²¹ , ²³ , ²⁴ , ²⁵ ] By controlling the amount of acid/base, protonation, and deprotonation of meso‐aryl‐substituted heptaphyrins led to the formation of distinct cationic and anionic species, respectively. In our study, we focus on the full protonation and deprotonation of hexaphyrin and heptaphyrin macrocycles, in which the intramolecular hydrogen bonding network is completely disrupted. In the case of [36]octaphyrin, the dicationic and dianionic species were selected based on the experimental assignment of the protonated and deprotonated structures.[ ¹⁴ , ²⁵ ] First, we have investigated the structural changes induced by (de)protonation in hexa‐, hepta‐, and octaphyrin compounds. Second, structure‐aromaticity relationships in neutral and charged macrocycles have been established by means of global descriptors rooted in the magnetic and reactivity criteria. Third, three main conjugation pathways have been evaluated using six local descriptors belonging to the structural and electronic criteria. Importantly, while the annulene pathway corresponds to the most conjugated circuit in neutral expanded porphyrins, the inner and outer pathways become the most favored circuit in deprotonated and protonated macrocycles, respectively. We have named the one that passes through all N atoms in all five‐membered rings (5MRs) the “inner pathway” and refer to the one that goes through all C−C bonds in all 5MRs for neutral and (de)protonated systems as the “outer pathway”. Finally, the main conjugation pathway upon (de)protonation is thoroughly studied using the gauge‐including magnetically induced currents (GIMIC).[ ⁶⁷ , ⁶⁸ , ⁶⁹ ]

Methodology

In this section, we will briefly describe how to compute some global and local measures of aromaticity for expanded porphyrins. Global aromaticity measures encompass the nucleus‐independent chemical shift (NICS),[ ⁶⁹ , ⁷⁰ ] the aromatic stabilization energies (ASE),[ ⁷¹ , ⁷² , ⁷³ ] the magnetic susceptibility exaltation (Λ), ^[74] and the relative hardness (Δη). ^[75] Both relative hardness and magnetic susceptibility exaltation can be computed using the isomerization method that relies on the comparison of the hardness and magnetic susceptibility of a methyl derivative of the π‐conjugated system and its nonaromatic methylene homologue (Figure S1 in the Supporting Information).[ ⁷¹ , ⁷² , ⁷³ ]

As the majority of the global measures of aromaticity cannot identify the most conjugated pathway, we also apply several local measures of aromaticity to compare the aromaticity of different pathways. To measure the electronic delocalization of a molecule and its aromaticity, we employ the quantum theory of atoms‐in‐molecules (QTAIM).[ ⁷⁶ , ⁷⁷ ] In addition, we use the delocalization index (DI) that corresponds to the following equation [Eq. 1],[ ⁷⁶ , ⁷⁷ , ⁷⁸ ]

$${\displaystyle \delta \left(A,B\right)=2{\int }_A{\int }_{B}d{\mathrm{r}}_{1}d{\sigma }_{1}d{\mathrm{r}}_{2}d{\sigma }_2{\rho }_{xc}\left({\mathrm{r}}_1{\sigma }_1,{\mathrm{r}}_2{\sigma }_2\right)}$$ (1)

where A and B are atoms, and ρ_xc is the exchange‐correlation density. ^[79] Hereafter, we will represent the ring structure consisting of n atoms by the string $𝒜=\left\{A_1,A_2,...,A_n\right\}$ , whose elements are ordered according to the ring's connectivity. As a structural index of aromaticity, the bond‐length alternation (BLA) compares the average bond length of subsequent bonds in a cycle. BLA evaluates the bond length equalization of an aromatic circuit without relying on a reference value [Eq. 2],

$${\displaystyle BLA\left(𝒜\right)=\frac{1}{n_1}\sum _{i=1}^{n_1}{R}_{{\mathrm{A}}_{2i-1},{\mathrm{A}}_{2i}}-\frac{1}{n_2}\sum _{i=1}^{n_2}{R}_{{\mathrm{A}}_{2i},{\mathrm{A}}_{2i+1}},}$$ (2)

where n ₁=$⌊\left(n+1\right)/2⌋$ and n ₂=$⌊\left(n\right)/2⌋$ , $⌊x⌋$ stands for the floor function of x. As Eq. (2) is not well defined for rings with an odd number of members, Matito et al. recently proposed an alternative definition for BLA ^[40] [Eq. 3],

$${\displaystyle BLA{}^{\text{'}}\left(𝒜\right)=\frac{1}{2n}\sum _{i=1}^n|R_{{\mathrm{A}}_i,{\mathrm{A}}_{i+1}}-R_{{\mathrm{A}}_{i+1},{\mathrm{A}}_{i+2}}|.}$$ (3)

As bond‐length alternation does not always reflect electronic delocalization, ^[80] bond order alternation (BOA) is often computed using the delocalization index instead of the bond distances [Eq. 4]. ^[78]

$${\displaystyle BOA\left(𝒜\right)=\frac{1}{n_1}\sum _{i=1}^{n_1}\delta \left({\mathrm{A}}_{2i-1},{\mathrm{A}}_{2i}\right)-\frac{1}{n_2}\sum _{i=1}^{n_2}\delta \left({\mathrm{A}}_{2i},{\mathrm{A}}_{2i+1}\right),}$$ (4)

where $\delta \left(A,B\right)$ corresponds to the bond order. By analogy to Eq. (3), one can construct $BOA{}^{\text{'}}\left(𝒜\right)$ . Another structural descriptor is the harmonic oscillator model of aromaticity [Eq. 5],[ ⁸¹ , ⁸² ]

$${\displaystyle HOMA\left(𝒜\right)=1-\frac{\alpha }{n}\sum _{i=1}^n{(R_{opt}-R_i)}^2,}$$ (5)

where α denotes an empirical constant fixed for each type of bond and n is the number of bonds taken into account in the summation. R_i corresponds to the running bond length along the selected conjugation pathway. Ideally, HOMA is equal to 0 for nonaromatic systems, while HOMA=1 for fully aromatic ones with all bonds equal to the optimal value (R_opt ). It is important to note that the structural index HOMA should be applied with caution to assess the aromaticity of expanded porphyrins.[ ²⁷ , ³⁰ , ³¹ , ³⁴ ] Although aromatic macrocycles are characterized by larger HOMA values than antiaromatic counterparts, the differences between aromatic and antiaromatic counterparts are rather small. An electronic index equivalent to HOMA can be defined, namely the aromatic fluctuation index (FLU). FLU is built on the delocalization index in a ring and uses reference data. ^[83] This quantity is close to zero for aromatic macrocycles and departs from zero for antiaromatic and nonaromatic molecules [Eq. 6],

$${\displaystyle FLU\left(𝒜\right)=\frac{1}{n}\sum _{i=1}^n{\left[{\left(\frac{\delta \left(A_i\right)}{\delta \left(A_{i-1}\right)}\right)}^{\alpha }\left(\frac{\delta \left(A_i,A_{i-1}\right)-{\delta }_{ref}\left(A_i,A_{i-1}\right)}{{\delta }_{ref}\left(A_i,A_{i-1}\right)}\right)\right]}^2,}$$ (6)

α being a function guaranteeing that the first term in Eq. (6) is larger or equal to 1 and ${\delta }_{ref}\left(A,B\right)$ denoting the DI associated with a reference aromatic system which possesses the bond A−B. Benzene and pyridine are the reference aromatic systems for C−C and C−N bonds, respectively.

Currently, multicenter electron delocalization indices are considered the most reliable measure of aromaticity.[ ⁴⁶ , ⁸⁴ , ⁸⁵ ] Nevertheless, multicenter indices cannot be applied to extended systems due to their prohibited computational cost and large numerical errors for large ring systems (n>12). Accordingly, Matito recently developed the AV1245 index for large macrocycles. ^[52] AV1245 index evaluates the average delocalization along the ring and corresponds to the average value of the four‐atom multicenter index (MCI) index between relative positions 1–2 and 4–5 built from each five‐atom fragment along the perimeter of the ring.[ ⁵² , ⁵⁴ ] Moreover, the minimal absolute value of the aforementioned four‐atom MCI values along the ring, AV_min, provides a better electronic descriptor of aromaticity because it does not rely on average values. ^[27] Aromatic molecules are typically characterized by larger AV1245 and AV_min values than antiaromatic and nonaromatic counterparts; however, the difference between aromatic and antiaromatic macrocycles becomes smaller as the size of the macrocycle increases.

The magnetic criterion for assessing aromaticity is founded on the notion that aromatic/antiaromatic molecules sustain a diatropic (clockwise)/paratropic (counterclockwise) ring current in response to an external magnetic field perpendicular to the molecular ring.[ ⁸⁶ , ⁸⁷ , ⁸⁸ , ⁸⁹ ] Therefore, the magnetic behavior can be analyzed by manifestations of this ring current, that is, induced magnetic fields or by directly evaluating the magnetically induced current density. Commonly, the presence of induced ring currents and their intensities are also rationalized from NICS computations, which Schleyer and coworkers defined as the negative of the absolute magnetic shielding, further suggesting to compute it at the molecular center, at 1 Å above/below the molecular plane ^[90] or even better to employ the out‐of‐plane component of the NICS tensor,[ ⁹¹ , ⁹² ] which was shown to better correlate with ring current analysis. ^[92] The anisotropy induced current density (AICD) ^[93] is also employed to assess the aromaticity of molecules. AICD plots represent the density and the direction of induced ring current when an external magnetic field is applied perpendicularly to the π‐system.[ ³⁰ , ⁹³ ] The direction of the current density vectors plotted on AICD isosurfaces enables to distinguish aromatic from antiaromatic macrocycles.

An additional way to obtain the magnetic induced current density is the gauge‐including magnetically induced current.[ ⁶⁷ , ⁶⁸ , ⁶⁹ ] The GIMIC method[ ⁶⁷ , ⁶⁸ , ⁶⁹ ] relies on the selection of a gauge origin to ensure the gauge independence of the current density. The GIMIC method assumes that NMR shieldings are equivalent in each point in space when using the analytic gradient and Biot‐Savart NMR shielding expressions.

Results and Discussion

Conformational and topological switches induced by (de)protonation

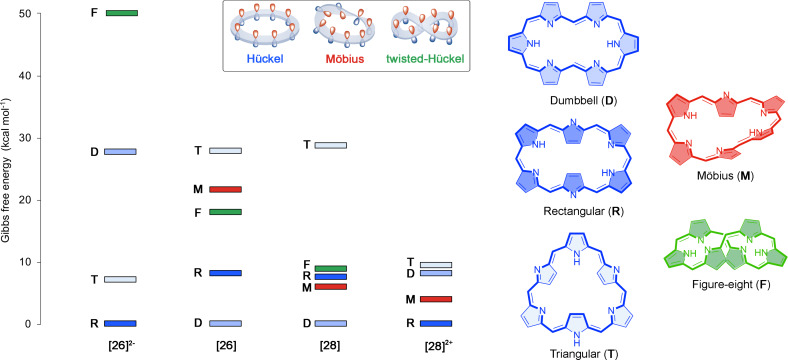
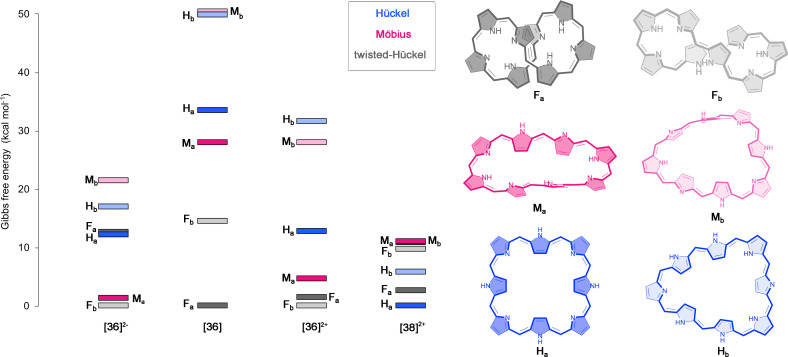
Since protonation and deprotonation reactions induce conformational changes in several expanded porphyrins,[ ¹⁴ , ²⁰ , ²² , ²⁴ ] we have investigated them as potential chemical stimulus to trigger conformational and/or aromaticity switches in hexa‐, hepta‐, and octaphyrins. The relative Gibbs free energy are collected in Table 1 and summarized in Figures 2 and 3 (see also Figure S2 for the predominant conformation of each state with its corresponding label). The labelling of each structure denotes the oxidation state followed by the symbol associated to the conformation and the charge of the macrocycle. As such, 26R²⁻ stands for a deprotonated dianion [26]hexaphyrin displaying a rectangular conformation. In the case of octaphyrin macrocycles, the additional subindices a and b are used to distinguish the two conformations considered for each topology (see below). In addition, for certain macrocycles, several oxidation states have been considered to assess the influence of the number of π‐electrons on the conformational preferences of expanded porphyrins. In this regard, expanded porphyrins provide congeneric macrocycles with [4n+2] and [4n] π‐electrons that can be easily interconverted by two‐electron redox reactions. Accordingly, they are recognized as the test bed to unravel the relationship between molecular properties and (anti)aromaticity.[ ¹ , ¹¹ ] Figures 2, 3, and S2 illustrate the evolution of the relative Gibbs free energies with the variation of global charge and oxidation state.

Table 1.

Relative Gibbs free energies [kcal ⋅ mol⁻¹] of the selected conformations of unsubstituted hexa‐, hepta‐, and octaphyrins with distinct global charge and oxidation states.^[a]

	[26]2−	[26]	[28]	[28]2+		[32]4−	[32]	[32]3+		[36]2−	[36]	[36]2+	[38]2+
R	0.0	8.1	7.6	0.0	H	0.0	29.8	0.8	H a	12.2	33.4	13.7	0.0
D	27.7	0.0	0.0	8.1	M	24.2	11.9	0.0	H b	17.0	49.8	31.6	5.8
T	7.1	27.8	28.7	9.5	F	[b]	0.0	7.5	M a	1.2	27.9	4.6	10.9
M	[b]	21.5	5.9	3.8	–	–	–	–	M b	21.4	49.7	27.9	11.0
F	50.3	17.9	8.8	[b]	–	–	–	–	F a	12.6	0.0	1.5	2.3
–	–	–	–	–	–	–	–	–	F b	0.0	14.5	0.0	9.7

^[a] Gibbs free energies at the M06‐2X/6‐311+G(d,p)//CAM‐B3LYP/6‐311G(d,p) level of theory. ^[b] The optimization of 28F²⁺ , 26M²⁻ , and 32F⁴⁻ did not lead to minimum geometry compatible with these conformations; instead it led to untwisted geometries.

Figure 2.

Evolution of the relative Gibbs free energy [kcal ⋅ mol⁻¹] for the different conformations of [26]‐ and [28] hexaphyrins with different protonation states. The selected conformations for neutral [26]hexaphyrin are also displayed.

Figure 3.

Evolution of the relative Gibbs free energy [kcal ⋅ mol⁻¹] for the different conformations of [36]‐ and [38]octaphyrins with different protonation states. The selected conformations for neutral [36]octaphyrin are also displayed.

It is important to stress that the relative Gibbs free energies for the different conformations are computed without meso‐substituents or counterions, which can largely affect the conformational preferences of the investigated macrocycles in the neutral and (de)protonated states. An exhaustive investigation of the effect of meso‐substitution on the conformations of neutral and protonated expanded porphyrins can be found in our previous studies on hexa‐, ^[35] hepta‐, ^[19] and octaphyrins. ^[28] Furthermore, the preferred conformation of such flexible macrocycles can be thermodynamically or kinetically controlled, ^[35] but this study only considers thermodynamic aspects.

First, we investigated the structural changes induced by protonation and deprotonation in [26]‐ and [28]hexaphyrins. Based on our previous studies,[ ²⁹ , ⁶⁶ ] five main conformations have been selected in our study: dumbbell (D), rectangular (R), twisted‐Hückel (F), triangular (T), and Möbius (M) conformers. According to Table 1, both deprotonation and protonation induce conformational switches in unsubstituted [26]‐ and [28]hexaphyrins. The Hückel conformation R is predominant in the dianionic [26] and diprotonated [28]hexaphyrins ([26]²⁻ and [28]²⁺ ), whereas the dumbbell conformation (D) corresponds to the global minimum in neutral hexaphyrins ([26] and [28]). Besides the dumbbell conformation, rectangular and Möbius structures can coexist in dynamic equilibrium for the neutral [28]hexaphyrin and the conformational equilibrium can be shifted by means of meso‐substituents or external conditions.[ ¹⁷ , ³⁵ , ⁹⁴ ] Herein, the stability of neutral unsubstituted [26]‐ and [28]hexaphyrins is mainly governed by the number of hydrogen bonds, followed by the macrocyclic strain and aromaticity (for the sake of simplicity, the role of meso‐substituents has not been considered in this work). As reported in previous studies in hexaphyrins, one hydrogen bond provides a stabilization of about 10 kcal⋅mol⁻¹.[ ¹⁸ , ²⁹ ] In unsubstituted macrocycles with the same number of hydrogen bonds such as 26D and 26F the conformational energy is related to the strength of the hydrogen bond and the ring strain, as well as aromaticity. Ring strain is quantified by means of the average dihedral angles between the neighboring pyrrole rings (Φ _p , see Tables S1‐2). In principle, conformations with small values of Φ _p should be favorable. For instance, 26F (Φ _p =33.4°) is characterized by a significantly larger ring strain than 26D (Φ _p =3.1°), owing to the presence of two half‐twists in the π‐system of 26F.

By contrast, protonation and deprotonation processes cut off intramolecular hydrogen bonds between aminic and iminic pyrroles. Thus, both [26]²⁻ and [28]²⁺ macrocycles are not stabilized by any intramolecular hydrogen bond (N _H =0). In these macrocycles, the relative stabilities are mainly dictated by the macrocyclic ring strain. The predominance of 26R²⁻ and 28R²⁺ is in agreement with experimental findings.[ ²¹ , ²³ ] Experimental studies reported that the protonation of [28]hexaphyrins induces distinct conformational switches depending on the protonation state and the acid agent. ^[21] For instance, our results support that the triangular conformation becomes highly stabilized upon diprotonation of the [28]hexaphyrin with a reduction in the relative energy of about 19.2 kcal⋅mol⁻¹. Nevertheless, the most stable conformation of [28]²⁺ corresponds to the rectangular one. The discrepancy between the computed unsubstituted and experimental structures of [28]²⁺ (28R²⁺ vs 28T²⁺ ) is connected to the meso‐substituents, since the presence of six pentafluorophenyl groups affects significantly the relative energies due to additional noncovalent interactions or steric clashes, as we have previously observed for several expanded porphyrins.[ ¹⁹ , ²¹ , ²⁸ , ³⁵ ]

Regarding [32]heptaphyrins, we have included the Hückel (H), Möbius (M), and twisted‐Hückel (F) conformations in the neutral ([32]), anionic ([32]⁴⁻ ), and cationic ([32]³⁺ ) states (Figure S2). In agreement with experimental and conformational studies,[ ¹⁹ , ²⁰ ] the twisted‐Hückel conformation, 32F, corresponds to the global minimum for neutral [32]heptaphyrins due to its more effective hydrogen bonding. The computed relative energies indicate that both protonation and deprotonation trigger a topological switch, in line with the experimental observations.[ ²⁰ , ²⁴ ] Triprotonated [32]heptaphyrins adopt a Möbius topology, though the relative energy difference between 32M³⁺ and 32H³⁺ is rather small. As the relative energy of 32M⁴⁻ lies 24 kcal⋅mol⁻¹ above 32H⁴⁻ , the fully deprotonated [32]heptaphyrin prefers the Hückel topology.

In the case of octaphyrins, six conformations with Hückel, Möbius, and twisted‐Hückel topologies were considered (Figure 3), which were selected based on our extensive conformational study on neutral and protonated octaphyrins. ^[28] As it can be inferred from Table 1, deprotonation and protonation of octaphyrins result in conformational changes. In neutral [36]octaphyrins, the global minimum corresponds to 36F _a owing to its more effective intramolecular hydrogen‐bonding interactions, $\pi -\pi$ stacking of the central pyrrole rings and reduced ring strain (Φ _p =15.4°). ^[28] Upon protonation, an alternative twisted‐Hückel conformation ${\mathbf{36}\mathbf{F}}_b^{2+}$ becomes the lowest‐energy minimum, although the Möbius topologies $({\mathbf{36}\mathbf{M}}_a^{2+}$ and ${\mathbf{36}\mathbf{M}}_b^{2+})$ become greatly stabilized. Despite ${\mathbf{36}\mathbf{M}}_a^{2-}$ and ${\mathbf{36}\mathbf{H}}_a^{2-}$ are both stabilized upon deprotonation, the twisted‐Hückel conformation $({\mathbf{36}\mathbf{F}}_b^{2-})$ is also predominant in unsubstituted deprotonated dianionic macrocycles. In comparison to its neutral counterpart, the relative Gibbs free energy of 36M _a and 36M _b becomes reduced by more than 20 kcal⋅mol⁻¹, indicating a huge stabilization of the Möbius topologies upon protonation.[ ¹⁴ , ⁹⁵ ] Basic conditions trigger the topological switch from 36F _a to a Möbius or to a squared Hückel anionic conformations, depending on the amount of tetrabutylammonium fluoride. ^[25] The combination of protonation and reduction results in the predominance of the Hückel conformation ${\mathbf{38}\mathbf{H}}_a^{2+}$ . Since no intramolecular hydrogen bonds are possible in the diprotonated [38]octaphyrin, the enhanced stability of the Hückel topologies is mainly ascribed to the reduction of the ring strain (lowest Φ _p value, see Table 2) and the gain of Hückel aromatic stabilization energy due to the presence of [4n+2] π‐electrons. ^[14] In general, relative energies predict conformational preferences that are in agreement with experimental results.[ ¹⁴ , ²⁰ , ²¹ , ²⁴ , ²⁵ ] Our results demonstrate that protonation and deprotonation are excellent chemical triggers to induce conformational switches in hexa‐, hepta‐, and octaphyrin macrocycles.

Table 2.

Reactivity and magnetic indices of aromaticity of selected unsubstituted expanded porphyrins in neutral, anionic, and cationic states. A, NA, and AA stand for aromatic, nonaromatic, and antiaromatic, respectively.

π e	Δη	$\Delta E_{HL}$	Λ	NICS(0)	NICS zz (1)	AICD
26R	−1.8[a]	3.78	−153.6	−8.7	−11.7	A
26R2−	3.9	3.44	−249.6	−10.1	−23.1	A
26F2−	[b]	3.12	[b]	−12.8	−27.5	A
28R	−11.5	3.09	241.1	9.8	23.1	AA
28R2+	−8.5	3.14	272.4	8.5	33.4	AA
28M	5.3	3.85	−90.0	−7.5	−6.1	A
28M2+	7.1	3.90	−111.1	−5.9	−5.4	A
32H	−2.8	3.38	84.6	4.0	16.1	AA
32H4−	−8.1	2.60	375.3	13.4	40.4	AA
32M	4.1	3.72	−51.1	−5.4	−5.8	A
32M4−	−4.4[a]	3.00	−198.3	−5.8	−13.1	A
32M3+	2.1	3.51	−151.5	−5.3	−8.4	A
32F	−9.2	3.23	40.8	0.3	−3.8	NA
32F3+	−7.4	3.16	87.0	1.2	10.3	NA
36H a	−9.0	3.09	191.2	4.4	14.3	AA
36H b	−7.7	3.43	90.2	9.8	8.7	AA
36H ${}_a^{2-}$	−3.4	2.95	231.6	4.9	16.2	AA
36M b	0.9[a]	3.76	−53.1	−1.2	−4.5	A
36M ${}_b^{2+}$	12.9	3.43	−77.2	−1.5	−3.9	A
36F a	−7.8	3.27	8.7	−3.8	0.4	NA
38H ${}_b^{2+}$	5.3	3.23	−190.8	−3.3	−6.3	A

^[a] Due to a highly distorted methylene derivative, 26R, 32M⁴⁻ , and 36M _b exhibit negative or reduced Δη values. ^[b] The methylene isomer untwists the conformation 26F²⁻ during the optimization, precluding the evaluation of Δη and Λ. ^[c] NICS‐based index in ppm, $\Delta \eta$ in kcal ⋅ mol⁻¹, $\Delta E_{HL}$ in eV, Λ in ppm ⋅ cgs.

Global aromaticity of neutral and charged expanded porphyrins

Since the quantification of aromaticity in expanded porphyrins is not trivial due to the existence of multiple conjugation pathways and numerous π‐conjugation topologies, it is advisable to use several descriptors of aromaticity rooted on different criteria to quantify the global aromaticity of expanded porphyrins. The structure‐aromaticity relationships in neutral, protonated, and deprotonated expanded porphyrins have been first established by means of global aromaticity descriptors belonging to the magnetic and reactivity criteria (Table 2). As magnetic descriptors, we employed the magnetic susceptibility exaltation (Λ) and NICS‐based indices [NICS(0) and NICS _zz (1)] together with the AICD plots to visualize the macrocyclic induced ring currents. As reactivity criteria, the relative hardness (Δη) and the HOMO‐LUMO energy gap were computed. Generally, larger gaps $(\Delta E_{HL})$ are found for aromatic macrocycles than for the antiaromatic counterparts.[ ¹¹ , ⁹⁶ , ⁹⁷ ]

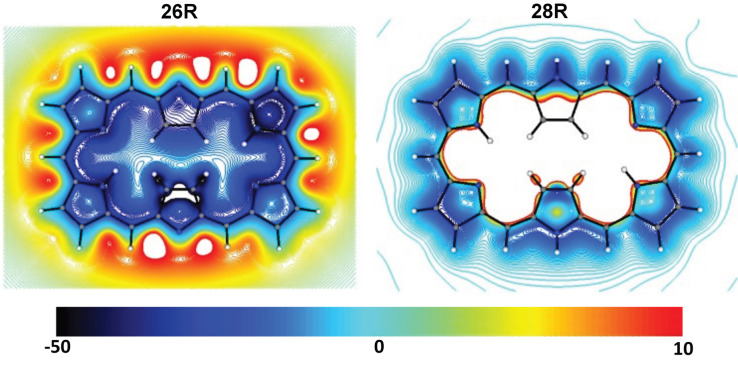
Some neutral expanded porphyrins such as 26R and the Möbius conformers (28M, 32M, and 36M _b ) are aromatic with positive Δη (or small negative values) and diatropic ring currents (negative Λ and NICS based indices). By contrast, the Hückel macrocycles with [4n] π‐electrons (28R, 32H, 36H _a , and 36H _b ) are antiaromatic with paratropic ring currents and negative Δη. In addition, the antiaromatic macrocycles exhibit reduced HOMO‐LUMO gap $(\Delta E_{HL})$ in comparison to the aromatic counterparts. As revealed by their reduced Λ and NICS values, the conformers 32F and 36F present a very weak paratropicity and can be labelled as nonaromatic (Table 2). Some aromatic Möbius topologies are characterized by negative NICS _zz (1) with a reduced magnitude. It is noteworthy that the magnitude of NICS${}_{zz}\left(1\right)$ is more variable in the xy‐plane 1 Å above the molecular plane of a Möbius topology than in a Hückel topology as can be inferred from the two‐dimensional plots of 28R and 28M (Figures 4 and S3).

Figure 4.

2D‐NICS _zz (1) plots (in ppm) of the magnetic shielding of 26R and 28R in the xy‐plane situated 1 Å above the molecular plane.

To visualize the induced ring currents, AICD plots of the neutral macrocycles were evaluated (Figures 5 and S6). Aromatic expanded porphyrins (26R, 28M, and 32M) are characterized by clockwise current density vectors indicative for diatropic ring currents. By contrast, the antiaromatic 28R exhibits counterclockwise current density vectors, which corresponds to paratropic ring currents. However, the global tropicity of the ring currents is difficult to assess in the twisted‐Hückel conformations 32F and 36F _a because the induced current density vectors displayed little global current directionality (Figure S4). Overall, the global aromaticity indices are able to grasp the reversal of aromaticity in redox interconversions involving compounds with a similar topology (26R to 28R) and a Hückel‐Möbius topology change (28R to 28M).

Figure 5.

AICD plots of selected neutral, protonated, and deprotonated expanded porphyrins (isovalue of 0.06 au). The large arrows denote the direction of the induced ring current: clockwise for diatropic ring currents and anticlockwise for paratropic ring currents. For the Möbius topologies, the direction of the arrows is more difficult to assess due to the non‐planar geometry.

In opposition to redox reactions, protonation of the macrocycle does not reverse the sign of the global aromaticity descriptors of the conformations with respect to the neutral state (Table 2). Thus, for [4n] π‐macrocycles, protonated Möbius topologies (28M²⁺ , 32M³⁺ , and 36M ${}_b^{2+}$ ) display an aromatic behaviour whereas protonated Hückel topologies (28R²⁺ and 32F³⁺ ) are antiaromatic. Interestingly, protonation of the macrocycles enhances their magnetic properties while reducing the energy gap in both aromatic and antiaromatic expanded porphyrins. The strength of the induced ring current is enhanced in protonated macrocycles with respect to their neutral homologues, in agreement with the enhancement of aromaticity observed experimentally in the ¹H NMR spectra of protonated expanded porphyrins. ^[22] For instance, while the Λ and NICS _zz (1) indices of 28R are 241 ppm⋅cgs and 23 ppm, respectively, those of the diprotonated form 28R²⁺ become 272 ppm⋅cgs and 33 ppm. The increased density of AICD plots of cationic macrocycles further supports the enhancement of (anti)aromaticity upon protonation (Figure 5).

As in protonated species, structure‐aromaticity relationships are conserved upon deprotonation. For instance, 26R²⁻ , 26F²⁻ , and 32M⁴⁻ are aromatic whereas 32H⁴⁻ and ${\mathbf{36}\mathbf{H}}_a^{2-}$ display an antiaromatic behaviour. Similar to the cationic macrocycles, the magnetic descriptors of the deprotonated species indicate an increase of the aromatic and antiaromatic character upon deprotonation. In comparison to the neutral 26R, 26R²⁻ presents more negative NICS _zz (1) and Λ values. Accordingly, the strength of the induced ring current increases from the neutral to the deprotonated species, in agreement with the spectroscopic observations of anionic expanded porphyrins.[ ²³ , ²⁴ , ²⁵ ] Similarly, the density of the induced ring current is significantly larger in the AICD plots of the anionic macrocycles relative to the neutral counterparts. However, anionic macrocycles are characterized by decreased ΔE _HL in both aromatic and antiaromatic molecules.

Even though the selected indices of aromaticity can distinguish aromatic from antiaromatic macrocycles, only magnetic indices of aromaticity (Λ and NICS) are highly correlated to each other for all the considered macrocycles (Table S4). By contrast, the relative hardness and magnetic descriptors do not show a quantitative linear correlation between them. This is not totally unexpected taking into account that magnetic indices are based on a response property that occurs only in the presence of an external magnetic field, whereas structural, electronic, and energetic criteria measure intrinsic ground‐state properties. ^[98] However, there are some important qualitative trends between these two groups of aromaticity indices. For instance, all the molecules with positive Λ, NICS(0), or NICS${}_{zz}\left(1\right)$ display negative relative hardness (Table 2). Similarly, all the molecules with positive relative hardness display negative Λ, NICS(0), and NICS${}_{zz}\left(1\right)$ values. In fact, only two molecules out of 20 data points (26R and 32M ⁴⁻) are an exception to the rule that the sign of the relative hardness is the opposite sign of Λ or NICS${}_{zz}\left(1\right)$ . In this sense, and despite the lack of a quantitative relationship between the relative hardness and the magnetic indices, in most cases, it is remarkable that we can use the reactivity descriptor to anticipate whether a molecule would be globally aromatic or antiaromatic according to magnetic criteria.

Magnetically induced currents in neutral and charged expanded porphyrins

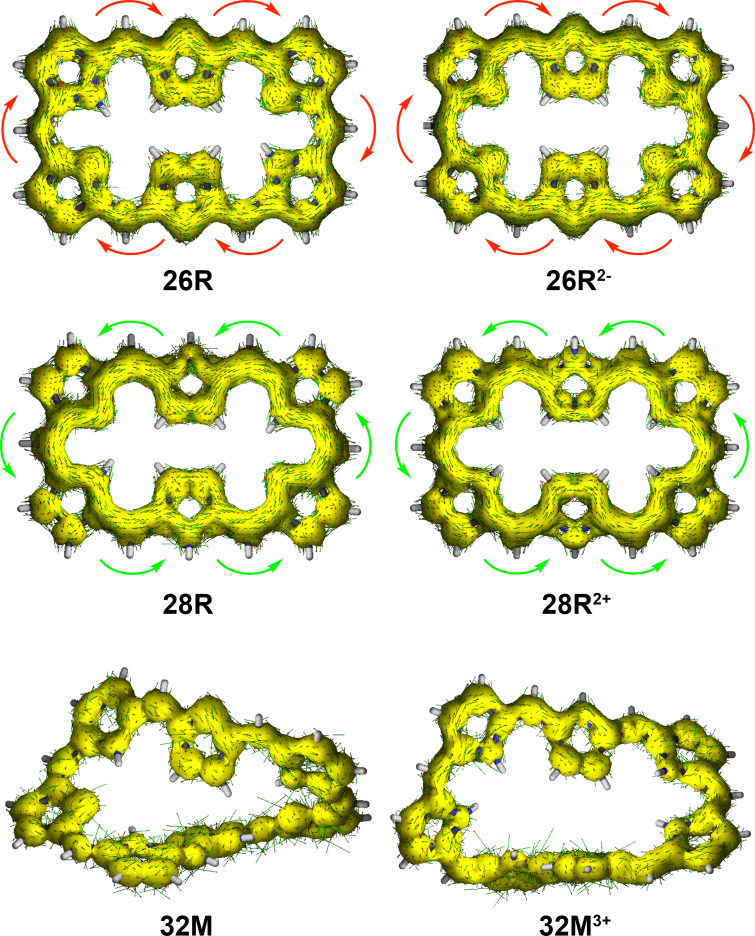
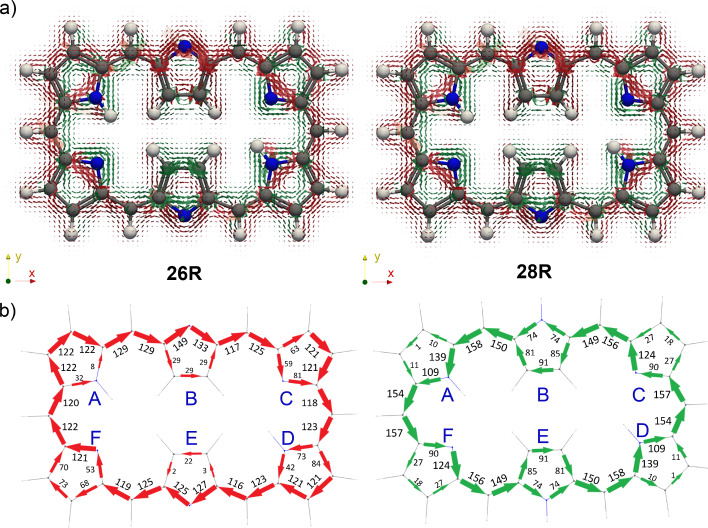
An alternative approach to assess the main aromatic pathways and the degree of aromaticity of expanded porphyrins is the gauge‐including magnetically induced current approach.[ ⁶⁸ , ⁶⁹ ] The GIMIC method has been successfully applied to rationalize the local and macrocyclic (anti)aromaticity of porphyrinoids according to the magnetic criterion.[ ⁹⁹ , ¹⁰⁰ , ¹⁰¹ , ¹⁰² ] The visualization of the current density plots using a vector representation in neutral hexaphyrins clearly shows that 26R sustains a net diatropic ring current along the macrocyclic ring (colored in red), while the macrocyclic ring current is clearly paratropic (colored in green) in 28R, in full agreement with the Hückel rule and the global aromaticity descriptors (Figure 6a).

Figure 6.

a) Visualization of the current density plots using a vector representation in neutral hexaphyrins. The external magnetic field is parallel to the symmetry z‐axis and pointing toward the viewer. b) Percentage ratios with respect to the net bond current strength in pyrrole (11.8 nA ⋅ T⁻¹).

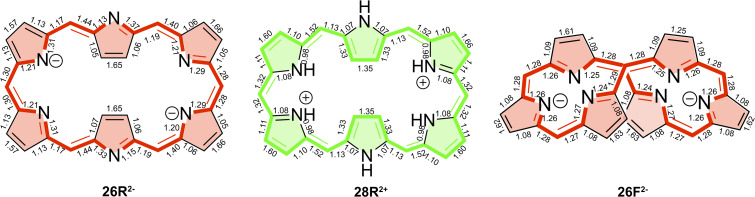
In this work, two different pathways through the individual five‐membered rings of the macrocycle are defined. The inner (outer) pathway goes through the C−N−C (C−C) bonds of the five‐membered ring subunit (Figure 9). A more detailed picture on the routes and strengths of the magnetically induced currents can be obtained by numerically integrating the current strength for the different covalent bonds in each macrocycle. ^[69] Figure 6b collects the percentage ratios with respect to the net bond current strength in pyrrole (11.8 nA⋅T⁻¹). Interestingly, the pathway with the largest integrated induced current values mostly corresponds to the annulene pathway. For the 26R, we observe that the outer route via the C=C bond is preferred in the pyrrole rings A and D, while the inner route via the C−N−C moiety dominates at the imine‐type subunits B and E. At the imine rings C and F, the current is almost equally split. In addition, the bond current strengths support that the contribution from the macrocyclic ring current to the global aromaticity of 26R is more important than the local contribution from the individual pyrrole subunits. Upon reduction of the macrocycle to 28R, there is a significant change in the current pathways. While the inner route via the C−N−C bonds becomes strongly favored at the rings A, C, D, and F, the ring current is split at the central pyrroles B and E, though with a slight preference for the outer route via the C=C bond. The GIMIC of 28R reveals a larger contribution from the central NH pyrrolic circuits than in 26R, although the macrocyclic paratropic ring current still prevails.

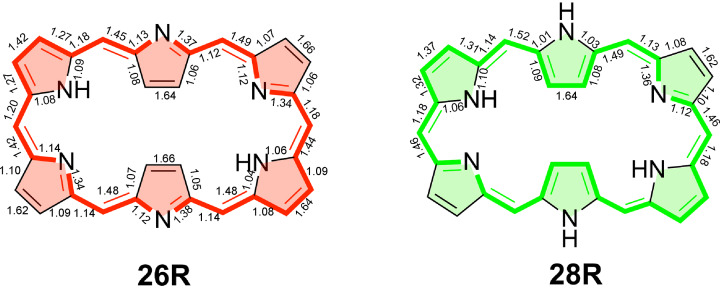
Figure 9.

Delocalization indices (DIs) for 26R and 28R macrocycles computed at the CAM‐B3LYP/6‐311+G(d,p) level of theory. The annulene‐type conjugation pathway is depicted with bold bonds. Note that the 28R structure exhibits C_i symmetry.

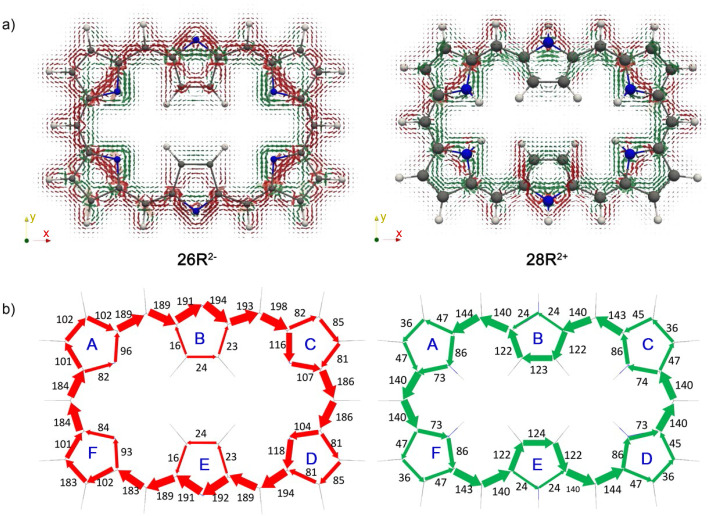
The GIMIC plots of the charged hexaphyrins 26R²⁻ and 28R²⁺ illustrate major variations in the current pathways triggered by (de)protonation of the macrocycles. In comparison to neutral homologues, there is an increase of the global (anti)aromaticity in both 26R²⁻ and 28R²⁺ , as indicated by the enhanced current density along the charged macrocycles (Figure 7a). Nevertheless, the global (anti)aromaticity of [26]‐ and [28]hexaphyrins remains unaltered upon (de)protonation. Thus, while 26R²⁻ exhibits a clear diatropic macrocyclic ring current, the macrocyclic ring current is distinctly paratropic in 28R²⁺ . According to the current density vector plots, the inner pathway via the C−N−C moieties is dominant in the deprotonated 26R²⁻ .

Figure 7.

a) Visualization of the current density plots using a vector representation in charged hexaphyrins. The external magnetic field is parallel to the symmetry z‐axis and pointing toward the viewer. b) Percentage ratios with respect to the net bond current strength in pyrrole (11.8 nA ⋅ T⁻¹).

The integration of the current density for each bond confirms that the main pathway goes mostly through the inner circuit for the deprotonated 26R²⁻ . At pyrroles A and F, similar current strengths are computed for the C−N−C and C=C moieties, indicating that the current flow is almost equally split. Regarding the diprotonated 28R²⁺ , the values of the integrated current suggest that the predominant pathway goes through the outer C=C bonds at the central pyrrolic subunits B and E and the inner C−N−C route in pyrroles A, C, D, and F. To get a more general view on the ring current of expanded porphyrins, we compute the GIMIC plots of additional charged molecules (28M²⁺ , 32H⁴⁻ 32M³⁺ , ${\mathbf{36}\mathbf{H}}_a^{2-}$ , and ${\mathbf{36}\mathbf{M}}_b^{2+}$ ) and their neutral counterparts (Figures S6–S10). Surprisingly, the integration of the current density reveals that the annulene pathway is not the preferred pathway for the neutral systems except for 36H _a . This discrepancy might be related to the non‐planarity of the considered molecules. As in 26R²⁻ , the current flows preferentially through the inner and semi‐outer pathway in 32H⁴⁻ and ${\mathbf{36}\mathbf{H}}_a^{2-}$ , respectively. Likewise, the determination of the preferred circuit is more problematic in cationic species since the current flow splits in nearly equal parts in some pyrrolic rings.

Identification of the most conjugated pathway

All the magnetic and reactivity indices described above were used to characterize the global aromaticity of the macrocycles and its evolution upon (de)protonation. However, expanded porphyrins contain multiple π‐conjugation pathways and, as such, one of the main issues to describe their aromaticity concerns the selection of the main macrocyclic conjugation pathway. Accordingly, we have applied different electronic and structural local indices in order to identify the main conjugation pathway in neutral, protonated, and deprotonated expanded porphyrins. In total, we have computed six local aromaticity indices (FLU, BOA, HOMA, BLA, AV1245, and AV_min) for three different conjugation pathways in neutral, cationic, and anionic hexaphyrins (Table 3). As shown in Figure 8, the first pathway corresponds to the annulene circuit, which passes through the imine groups and circumvents the amine NH groups in all‐pyrrole expanded porphyrins. The other two conjugated pathways correspond to the inner circuit, which goes through all the C−N−C bonds involving all imine and amine groups in the macrocycle, and the outer path that passes through the C−C bonds (Figure 8).

Table 3.

Aromaticity indices for the annulene, inner, and outer pathways of [26]‐ and [28] hexaphyrins, calculated at the CAM‐B3LYP/6‐311+G(d,p) level of theory. The most aromatic pathway according to each aromaticity probe is boldfaced.

System	π e−	Pathway	FLU	BOA	HOMA	BLA	AV1245	AVmin
26R	26	Annulene	0.019	0.278	0.716	0.065	1.56	0.60
26R2−	26	Annulene	0.017	0.218	0.659	0.057	1.58	0.38
28R	28	Annulene	0.021	0.300	0.620	0.067	1.31	0.42
28R2+	28	Annulene	0.020	0.264	0.682	0.051	1.07	0.16
26R	24	Inner	0.017	0.250	0.785	0.057	1.05	0.12
26R2−	24	Inner	0.009	0.142	0.888	0.045	1.73	1.23
28R	24	Inner	0.020	0.251	0.719	0.054	0.07	0.03
28R2+	24	Inner	0.020	0.219	0.735	0.043	−0.07	0.05
26R	30	Outer	0.031	0.351	0.346	0.078	1.02	0.01
26R2−	30	Outer	0.031	0.334	0.286	0.077	1.13	0.01
28R	30	Outer	0.026	0.324	0.487	0.069	1.45	0.08
28R2+	30	Outer	0.022	0.295	0.604	0.063	1.59	0.20

Figure 8.

Evolution of AV1245/AV_min values along three π‐conjugation pathways upon the (de)protonation of [26]‐ and [28]hexaphyrins. The pyrrolic subunits are colored in red when the macrocyclic pathway goes via the C−N−C bonds and in blue when the circuit passes via the C−C bonds.

Table 3 collects the electronic (FLU, BOA, AV1245, and AV_min) and structural (HOMA and BLA) indices of aromaticity along the annulene, inner, and outer pathways of neutral and charged hexaphyrins. The electronic and structural indices of aromaticity of the other considered macrocycles can be found in the supporting information (Tables S5–S12). The FLU, BOA, and BLA are close to zero in fully aromatic systems in which the bond‐order and bond‐length alternation is minimal, while they take larger values in nonaromatic and antiaromatic systems. By contrast, the larger the HOMA, AV1245, and AV_min values, the larger the degree of π‐electron delocalization and, thus, the greater the aromaticity. In line with our previous study, ^[27] discrepancies between the different electronic and structural indices are observed regarding the most conjugated pathway in neutral macrocycles. While the delocalization of the annulene pathway is significantly larger than the inner and outer circuit according to AV_min and AV1245, the indices BOA, FLU, BLA, and HOMA identify the inner circuit as the most delocalized one. However, the reduced values of BOA and FLU need to be taken with caution since they are due to the compensation of deviations between odd and even bonds. ^[27] Indeed, when the delocalization indices (DIs) for all the bonds are examined in the neutral hexaphyrins, the DIs with largest values follow the annulene pathway (Figure 9). In the case of HOMA and FLU, these indices rely on reference values and they measure the degree of similarity with respect to structural and electronic patterns, respectively, found in archetypal aromatic molecules. ^[103] Among all electronic and structural indices, AV_min is actually the only index capable of identifying the annulene pathway as the most aromatic one in all considered neutral macrocycles.

For neutral macrocycles, the electronic indices AV1245 and AV_min along the annulene pathway are larger for the aromatic macrocycles than for the antiaromatic counterparts (e. g., 26R >28R). Overall, the magnetic and electronic indices agree on the annulene pathway being the most conjugated one in neutral hexaphyrins. Nevertheless, unlike in the case of small annulenes, ^[40] we observe small differences in the electronic indices among aromatic, nonaromatic, and antiaromatic porphyrinoids. Furthermore, the differences in AV1245 and AV_min become attenuated as the size of the macrocycle increases. For instance, no noticeable differences are observed between the formally aromatic 36M _b and antiaromatic 36H _a and 36H _b (Tables S5–S10). These results suggest the aromaticity of extended porphyrinoids decreases with the size of macrocycle, in line with the results recently obtained for large annulenes. ^[40] Additionally, the AV1245 and AV_min differences between aromatic and antiaromatic expanded porphyrins are more subtle than one could initially expect. Hence, from an electron delocalization perspective, most of these systems should be considered nonaromatic.

Regarding protonated macrocycles, the predominant conjugation pathway is the outer pathway according to AV1245 and AV_min. Charged macrocycles exhibit an enhanced difference between the C−N−C and the C=C routes at the pyrrolic subunits with respect to neutral macrocycles. In agreement with AV1245 and AV_min, the DIs indicate the predominance of the outer pathway over the annulene pathway in cationic macrocycles (Figure 10). In comparison to the annulene circuit in their neutral homologues, the outer circuit of cationic expanded porphyrins is characterized by larger AV1245 and increased AV_min values. The individual paths behave differently upon protonation: the delocalization of annulene pathway is significantly reduced, the inner pathway is unaffected and the outer pathway increases its aromaticity. As a result, the protonation changes the most aromatic pathway from the annulene one to the outer pathway in most cases (32F³⁺ and 36M ${}_b^{2+}$ being exceptions) and its aromaticity is importantly reduced in all cases – as indicated by AV_min. These results are in agreement with the concomitant decrease of the C−N delocalization indices for the protonated five‐membered rings (compare Figures 9 and 10). Nevertheless, the predominant outer pathway in diprotonated hexaphyrins can be justified in terms of the annulene model assuming that the canonical structures with the positive charge located at the perimeter carbon atoms make a major contribution. ^[58]

Figure 10.

Delocalization indices (Dis) for 26R²⁻ , 28R²⁺ , and 26F²⁻ macrocycles computed at the CAM‐B3LYP/6‐311+G(d,p) level of theory. The conjugation pathway with the largest DIs is depicted with bold bonds. The main circuit corresponds to the inner pathway in 26R²⁻ and 26F²⁻ , and the outer one in 28R²⁺ .

As can be inferred from AV1245 and AV_min values, the inner circuit is predominant in anionic species, that is, it is characterized by significantly larger delocalization than other pathways (the only exception being 36H ${}_a^{2-}$ ). The inner circuit of anionic expanded porphyrins corresponds to the pathway with the largest DIs (Figure 10). Thus, in anionic species, the main circuit takes the inner route of the pyrrolic subunits via the C−N−C moieties (as shown by ring current plots). The different canonical structures of 26R²⁻ seem to emphasize the dominant role of the inner pathway in deprotonated hexaphyrins as compared to the neutral ones. ^[104] In comparison to the annulene pathway in neutral species, the inner pathway of anionic species is characterized by larger AV1245 and AV_min values, which together with the results of the previous section, supports an enhancement of the π‐electron delocalization both globally and locally. This is particularly relevant for 26R²⁻ and 26F²⁻ (Figure 10), which display the two largest AV_min values of all the systems studied in this work (1.23 and 1.54, respectively). In fact, the value of AV_min is similar or larger than the annulene pathways of porphine (1.28), ^[27] which presents a significantly shorter circuit. HOMA and FLU values also suggest that 26R²⁻ and 26F²⁻ might be two of the most aromatic expanded porphyrins. The strong diatropic ring current in both anionic hexaphyrins is further supported by the integrated bond current strengths (Figures 8 and S7). It is worth highlighting that there is also experimental evidence supporting the enhanced aromaticity of 26R²⁻ . ^[23]

Finally, we focus on the effect of (de)protonation on the electronic delocalization of the different pathways. Regarding the inner pathway, protonation of the macrocycle does not induce any notable variation in the degree of π‐electron delocalization (Table S6), while deprotonation enhances the delocalization with respect to its neutral homologues (Table S9). By contrast, protonation of expanded porphyrins results in larger electronic delocalization of the outer circuit in comparison to the neutral ones, the only exception being ${\mathbf{36}\mathbf{M}}_b^{2+}$ (Table S7). Similarly to the effect of the protonation on the inner circuit, in most cases, the electronic delocalization of the outer circuit barely changes upon deprotonation (Table S10). Interestingly, the increase of AV_min and AV1245 values of the inner circuit upon deprotonation is far more important than the one triggered by protonation for the outer circuit. This difference is corroborated by the variation of magnetic indices of aromaticity that also change more significantly upon deprotonation than protonation. The main pathway in the diprotonated 28R²⁺ cannot be clearly assessed. For the diprotonated macrocycle, the magnetic and electronic indices do not agree with each other regarding the dominant conjugation pathway in 28R²⁺ since the outer pathway is clearly dominant according to the electronic indices AV1245 and AV_min as well as the delocalization indices. In this sense, the main current‐density pathways and the most delocalized one do not coincide in this molecule. Similar discrepancies have been previously documented in the literature. ^[48] As 36H ${}_a^{2-}$ and 36M ${}_b^{2+}$ are partially deprotonated and protonated respectively, the main pathway is more difficult to define than in fully protonated and deprotonated systems. However, a closer inspection of all potential CPs in 36H ${}_a^{2-}$ reveals the existence of other conjugation pathways characterized by AV_min=0.54 (Table S11). The most aromatic circuits include the unchanged annulene pathway with 36 π‐electrons, the semi‐inner pathway with 34 π‐electrons, and one pathway with 35 π‐electrons (Figure S16). Regarding 36M ${}_b^{2+}$ , the most aromatic circuit corresponds to a pathway with 35 π‐electrons and is characterized by AV_min=0.15. Nevertheless, the difference in AV_min between the most aromatic pathways in 36M ${}_b^{2+}$ is small. This feature is present in charged hexaphyrins and heptaphyrins (Figure S17). These results show that the largest charged expanded porphyrins do not present a clear main conjugation pathway.

Conclusions

In this work, we have investigated the evolution of the conformational preferences and aromaticity of a set of expanded porphyrins upon protonation and deprotonation of the macrocycle. The quantification of the aromaticity was based on several global and local descriptors rooted in different criteria, namely magnetic, structural, electronic, and reactivity indices. Local descriptors were used to assess the main conjugation pathway in both neutral and charged macrocycles in order to assess the main conjugation pathway in cationic and anionic macrocycles.

Protonation and deprotonation are shown to be effective external stimuli to trigger conformational switches in hexaphyrins as well as Hückel‐to‐Möbius topological transformations in heptaphyrins and octaphyrins. Due to the partial or full suppression of intramolecular hydrogen bonds, distinct conformations are stabilized upon (de)protonation. Overall, the majority of the global aromaticity descriptors are able to distinguish aromatic from antiaromatic systems regardless of the charge of the macrocycle. Unlike redox reactions, (de)protonation reactions do not reverse the global aromaticity of expanded porphyrins, but the strength of the induced ring current increases from the neutral to the charged species according to the magnetic descriptors.

The local aromaticity of the inner, outer, and annulene circuits was also investigated by means of AV_min and magnetic induced currents. The ring current strength, the delocalization indices of the different covalent bonds and AV_min support the predominance of the annulene and inner pathways in neutral and deprotonated hexaphyrins, respectively. Indeed, for planar molecules, all the indices suggest that the annulene pathway is the most aromatic one in neutral expanded porphyrins. However, the nonplanarity of some expanded porphyrins hinders the magnetic ring current analysis, which suggests that for some nonplanar neutral expanded porphyrins the most conjugated circuit does not match the annulene pathway. Likewise, some discrepancies between GIMIC plots and AV_min arise for a few nonplanar charged expanded porphyrins. The delocalization indices and electronic indices clearly point out the prevalence of the outer pathway in protonated expanded porphyrins. Interestingly, all aromaticity probes, including the magnetic ring currents, coincide on finding the inner pathway of 26R²⁻ one of the most aromatic circuits in this collection of expanded porphryins, in agreement with the experimental evidence. ^[23] Additionally, the inner pathway of 26F²⁻ is the most aromatic circuit we have found thus far in an expanded porphyrin; it is actually more aromatic than the annulene pathway of porphine ^[27] – which is a much shorter conjugated circuit. Although this molecule's conformation presents a much higher energy than that of 26R²⁻ , its prominent aromatic character holds the promise to be relevant under appropriate conditions. Except for 26R²⁻ and 26F²⁻ , the other charged aromatic and antiaromatic molecules present conjugated circuits with rather modest values of AV_min and are difficult to characterize from ring current plots. The latter suggests that the largest charged expanded porphyrins do not present a clear main conjugation pathway.

We believe that this work puts forward the utility of AV_min as a tool to identify the most delocalization pathway in large macrocycles.

Computational Details

All structures were optimized and characterized using harmonic vibrational frequency calculations employing the CAM‐B3LYP functional ^[105] together with the Pople basis set 6–311G(d,p). ^[106] The functional CAM‐B3LYP was selected because of the influence of delocalization error in several properties of expanded porphyrins.[ ²⁷ , ⁴³ , ⁶⁶ , ¹⁰⁷ ] Indeed, the numerical value of aromaticity descriptors is heavily influenced by the percentage of HF exchange present in DFT functionals.[ ²⁷ , ⁴⁰ , ⁴⁴ , ⁴⁵ ] Single‐point calculations were conducted at the M06‐2X/6‐311+G(d,p) level of theory. Recent benchmarks on the conformational energies of expanded porphyrins have shown that M06‐2X provides errors close to chemical accuracy relative to the golden‐standard canonical CCSD(T) calculations.[ ⁴³ , ⁶⁶ , ¹⁰⁷ , ¹⁰⁸ ] In addition, M06‐2X and CAM‐B3LYP offer similar performances in systems influenced by the electron delocalization errors.[ ²⁷ , ⁴⁰ , ⁴⁴ , ⁴⁵ , ¹⁰⁹ , ¹¹⁰ ] The influence of dispersion corrections and diffuse functions on the relative Gibbs free energies of several neutral and charged expanded porphyrins was also investigated (Table S3), showing a little dependence.

All DFT calculations were performed using Gaussian 16 software package. ^[111] In order to understand the conformational preferences of expanded porphyrins, torsional descriptors, such as Π and Φ _p , and hydrogen index (N _H ) were computed. ^[32] The torsional strain descriptor (Φ _p ) denotes the average dihedral angle between neighboring pyrrole rings, while the extent of the effective overlap of neighboring π‐orbitals was quantified through the torsional π‐conjugation index (Π). ^[65]

Electronic indices of aromaticity (FLU, ^[83] BOA, ^[40] AV1245, ^[52] and AV_min ^54]) and geometrical ones (HOMA ^[81] and BLA ^[40] ) were calculated with the ESI‐3D program[ ⁷⁸ , ⁸³ , ¹¹² ] using a QTAIM atomic partition performed by AIMAll and the CAM‐B3LYP/6‐311+G(d,p) level of theory. ^[113] The ESI‐3D code is available upon request (ematito@gmail.com). Magnetic susceptibilities were calculated using the CSGT method ^[114] at the CAM‐B3LYP/6‐311+G(d,p) level of theory, while GIAO method ^[115] was applied to obtain NICS.[ ⁶⁹ , ¹¹⁶ ] NICS values were computed at the centroid of the macrocycle considering the heavy atoms [NICS(0)], and 1 Å above and below the molecular plane [NICS _zz (1)]. For nonplanar structures, the reference plane was found by least‐squares fitting considering all of the coordinates of the heavy atoms of the macrocycles. ^[117] However, for twisted‐Hückel topologies, the molecule was oriented in such a way that the 2D projection exhibits the largest macrocyclic area, leading to the topology of a ring (Figure S4). The external magnetic field was applied to such projection. To build 2D‐NICS _zz (1) maps, we used NICSall, a simple program interfaced with Gaussian ^[111] which is used to extract information in different formats for aromaticity analysis. ^[118] The NICS plots were performed with the VisIt 2.13.0 program. ^[119]

Current densities were computed with the GIMIC program[ ⁶⁸ , ¹²⁰ ] at the CAM‐B3LYP/6‐311+G(d,p) level of theory, using the gauge including the atomic orbital (GIAO) method. ^[115] In the calculations, the magnetic field is directed along the z‐axis, that is, perpendicular to the molecular plane. The unit for current susceptibility is nA⋅T⁻¹ and the results are independent of the magnitude of the magnetic field. Current pathways are visualized using Paraview.[ ¹²¹ , ¹²² ] Ring current strengths (RCS), a measure of the net current intensity around the molecular ring, were obtained after considering different integration planes. The integration planes correspond to cutoff planes perpendicular to the bonds. The two‐dimensional Gauss‐Lobatto algorithm ^[120] was used to integrate the current passing through an integration plane. Note that negative (diatropic) and positive (paratropic) NICS at the center of the molecules are associated with aromaticity and antiaromaticity. In contrast, for RCS, a positive (diatropic) and negative (paratropic) sign corresponds to aromatic and antiaromatic molecules, respectively. For both NICS and RCS values close to zero suggest nonaromatic behavior. ^[69] A complementary and commonly used method to analyze aromaticity, according to magnetic criteria, is through the visualization of the current density vector on the AICD scalar field (anisotropy of the induced current density isosurface). AICD represents the density of delocalized electrons. The current density vectors (green arrows on the AICD isosurface) indicate a diatropic or paratropic ring current depending on the clockwise or counterclockwise direction, respectively.[ ³⁰ , ⁹³ , ¹²³ ]

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Casademont-Reig I., Woller T., García V., Contreras-García J., Tiznado W., Torrent-Sucarrat M., Matito E., Alonso M., Chem. Eur. J. 2023, 29, e202202264.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.