Summary
Cancer is a heterogeneous disease. Finite mixture of regression (FMR)—as an important heterogeneity analysis technique when an outcome variable is present—has been extensively employed in cancer research, revealing important differences in the associations between a cancer outcome/phenotype and covariates. Cancer FMR analysis has been based on clinical, demographic, and omics variables. A relatively recent and alternative source of data comes from histopathological images. Histopathological images have been long used for cancer diagnosis and staging. Recently, it has been shown that high-dimensional histopathological image features, which are extracted using automated digital image processing pipelines, are effective for modeling cancer outcomes/phenotypes. Histopathological imaging–environment interaction analysis has been further developed to expand the scope of cancer modeling and histopathological imaging-based analysis. Motivated by the significance of cancer FMR analysis and a still strong demand for more effective methods, in this article, we take the natural next step and conduct cancer FMR analysis based on models that incorporate low-dimensional clinical/demographic/environmental variables, high-dimensional imaging features, as well as their interactions. Complementary to many of the existing studies, we develop a Bayesian approach for accommodating high dimensionality, screening out noises, identifying signals, and respecting the “main effects, interactions” variable selection hierarchy. An effective computational algorithm is developed, and simulation shows advantageous performance of the proposed approach. The analysis of The Cancer Genome Atlas data on lung squamous cell cancer leads to interesting findings different from the alternative approaches.
Keywords: Bayesian, Cancer, Finite mixture of regression, Histopathological imaging–environment interaction
1. Introduction
Cancer is a highly heterogeneous disease. Patients with different subtypes of the same cancer or even with the same subtype can have different biomarkers, prognosis, and response to treatment patterns. Quantifying heterogeneity can assist better understanding cancer biology and delivering tailored treatment (Burrell and others, 2013; Baliu-Piqué and others, 2020). Most cancer heterogeneity analysis can be classified as unsupervised and supervised, both of which have led to important findings and complement but cannot replace each other. In this study, we conduct supervised heterogeneity analysis, where a response variable is present, subjects form subgroups, and different subgroups have different relationships between the response and covariates. Supervised analysis, in many cases, is “closer” to clinical practice. In supervised heterogeneity analysis, early studies have mostly analyzed low-dimensional clinical/demographic/environmental variables. The development of sequencing techniques has led to quite a few heterogeneity analyses based on high-dimensional omics variables, such as gene expressions and DNA mutations (Burrell and others, 2013; Kim and DeBerardinis, 2019; Morrison and others, 2014).
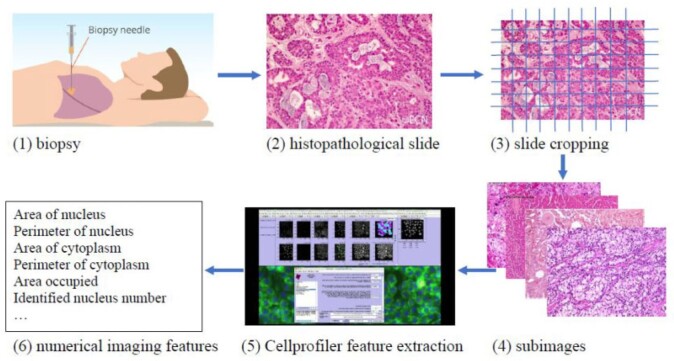
In cancer modeling, an alternative source of data comes from histopathological images—a “byproduct” of biopsy, which is ordered for most patients suspected of cancer. Brief information on extracting histopathological imaging features is provided in Figure 1 and described in detail in Section 4. Compared to omics data, histopathological imaging data enjoy much broader availability and higher cost-effectiveness. It contains rich information on tumors micro properties and the surrounding microenvironment. Here, it is noted that histopathological imaging data differ significantly from radiological image data. Radiological imaging data, such as those generated by computed tomography and magnetic resonance imaging, inform tumors macro properties such as location, density, and shape. Histopathological images have been traditionally used for definitive diagnosis and staging this is realized by pathologists examining such images under microscopes. Usually, only a small number of imaging features can be analyzed in such effort. More recently, automated digital image processing pipelines/software have been developed, which can extract high-dimensional features in a fast and objective way. A series of studies have shown that such features provide an alternative and effective way for modeling cancer outcomes (Echle and others, 2020; Chen and others, 2020a,b). In a recent study (Xu and others, 2019), inspired by gene–environment interaction analysis, histopathological imaging–environment interaction analysis is developed and shown to have sensible biological implications and satisfactory numerical performance. Our literature review suggests that most histopathological image-based analyses, including the interaction analysis, assume homogeneity. There are only a few supervised heterogeneity analysis. However, some studies, such as Belhomme and others (2015) and Luo and others (2017), are limited to main effects only (without interactions) and, quite often, low-dimensional features. He and others (2020) analyzes the main effects of high-dimensional imaging features using the penalized fusion technique and resorts to model averaging to achieve computational feasibility. In this study, we will take the natural next step and conduct supervised cancer heterogeneity analysis based on models that incorporate histopathological imaging–environment interactions. This strategy has been motivated by the significance of cancer heterogeneity analysis, still strong demand for more effective methods and analysis, unique advantages of histopathological imaging data, the promising performance of histopathological imaging–environment interaction analysis under homogeneity, and lack of heterogeneity analysis incorporating such interactions.
Fig. 1.
Pipeline for extracting imaging features.
Literature on supervised heterogeneity analysis is vast. For comprehensive discussions, we refer to, for example, Schlattmann (2009). Among the existing techniques, finite mixture of regression (FMR) (McLachlan and Peel, 2000) has been a popular choice. Under FMR, it is assumed that subjects form subgroups, and different subgroups have different regression models for the response variable. For estimation, both frequentist and Bayesian techniques have been developed (Frühwirth-Schnatter and others, 2018). When the number of variables is large, additional developments are needed to accommodate high dimensionality, screen out noises, and achieve unique and reliable estimation. Under the frequentist framework, this is often achieved using regularization, in particular penalization (Khalili and Chen, 2007; Städler and others, 2010). There have been equally successful developments under the Bayesian paradigm. For example, Gupta and Ibrahim (2007) and Lee and others (2016) propose FMR models that can identify covariates relevant for each subgroup. To determine the number of subgroups, Gupta and Ibrahim (2007) formulate a model comparison problem and compare the Bayes Factors for different subgroup numbers, and Lee and others (2016) adopt criteria such as the Akaike Information Criterion and Bayesian Information Criterion. From a Bayesian perspective, a fully Bayesian approach that treats the number of subgroups as a random variable may be preferable. A representative example is Liu and others (2015), which identifies subgroup-specific covariate effects with an unknown number of subgroups. Despite great successes, the aforementioned and other methods in the literature are not directly applicable to the proposed analysis that involves interactions. In particular, interaction analysis is uniquely challenged by the “main effects, interactions” hierarchy, which postulates that if an interaction term is identified as important, then the corresponding main effect(s) should be automatically identified (Bien and others, 2013). In the context of imaging–environment interaction analysis, this hierarchy amounts to a constraint on the interaction term and corresponding main imaging effect (Xu and others, 2019). With this hierarchy, “ordinary” high-dimensional techniques are not sufficient. Under the frequentist framework, for example, composite penalization and sparse group penalization have been developed to respect the hierarchy. One explanatory development under the Bayesian framework introduces a hierarchical prior that imposes a constraint to respect the hierarchy (Kim and others, 2018). Here, we note that this and other Bayesian developments are limited to the homogeneity case and not directly applicable to heterogeneity analysis.
The goal of this study is to develop an effective Bayesian FMR approach for supervised cancer heterogeneity analysis based on models that incorporate histopathological imaging–environment interactions. This study complements and advances from the existing literature in multiple important aspects. First, it conducts heterogeneity analysis based on imaging data, which complements the existing studies that are based on clinical, demographic, environmental, and omics variables. It may be particularly advantageous over the omics-based studies because of broader data availability and cost-effectiveness. It also advances from the existing image-based heterogeneity analysis by incorporating interactions, and from the imaging–environment interaction analysis by accommodating sample heterogeneity. Second, it tackles considerable technical challenges. More specifically, it advances from the existing Bayesian heterogeneity analysis by respecting the “main effects, interactions” hierarchy, and from the existing Bayesian interaction analysis by accommodating heterogeneity with an unknown number of subgroups. This is achieved by incorporating priors that respect the hierarchy on the subgroup-specific parameters and adopting a mixture model with a prior on the number of subgroups. It provides a competitive alternative to the penalization and other techniques. Third, this study provides a useful alternative for extracting information from The Cancer Genome Atlas (TCGA) and other cancer data, especially for lung cancer. With these advancements, it is warranted beyond the existing literature.
2. Methods
2.1. Model
Consider 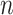 independent subjects. For the
independent subjects. For the 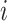 th subject, let
th subject, let 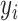 denote the response variable,
denote the response variable, 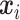 and
and 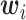 denote the
denote the 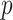 -dimensional vector of imaging (I) features and
-dimensional vector of imaging (I) features and 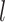 -dimensional vector of environmental (E) variables, respectively. As in Xu and others (2019) and quite a few other studies, we take a loose definition and also include demographic, clinical, and some other low-dimensional variables in
-dimensional vector of environmental (E) variables, respectively. As in Xu and others (2019) and quite a few other studies, we take a loose definition and also include demographic, clinical, and some other low-dimensional variables in 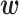 . To accommodate I–E interactions, we further denote
. To accommodate I–E interactions, we further denote  for
for  and
and 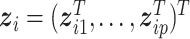 for
for 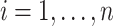 . Let
. Let 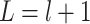 . We note that
. We note that 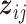 is a
is a 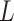 -dimensional vector that contains the main effect and all interaction terms related to the
-dimensional vector that contains the main effect and all interaction terms related to the 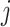 th imaging feature. As such, quantifying the effects of the
th imaging feature. As such, quantifying the effects of the 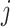 th imaging feature amounts to a two-step procedure: determining whether
th imaging feature amounts to a two-step procedure: determining whether 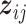 has an impact on the response variable at all, and, if yes, determining which components have an impact.
has an impact on the response variable at all, and, if yes, determining which components have an impact.
We consider a continuous response, make the Gaussian distribution assumption, and use linear regression to model its associations with covariates. Assume that there are 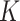 sample subgroups. Let
sample subgroups. Let 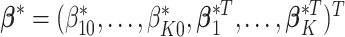 denote the vector that contains all the subgroup-specific parameters. Here, for the
denote the vector that contains all the subgroup-specific parameters. Here, for the 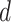 th subgroup,
th subgroup, 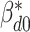 is the intercept.
is the intercept. 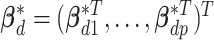 is the vector of regression coefficients associated with all imaging features, where
is the vector of regression coefficients associated with all imaging features, where 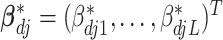 represents the main effect and interactions of the
represents the main effect and interactions of the 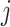 th imaging features.
th imaging features.
To facilitate estimation, we introduce a latent subgroup membership for each subject. Let 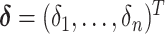 denote the vector of latent subgroup memberships for the
denote the vector of latent subgroup memberships for the 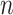 subjects. Its components take values in
subjects. Its components take values in 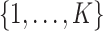 . Let
. Let 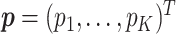 denote the vector of the unknown subgroup proportions. The proposed model is:
denote the vector of the unknown subgroup proportions. The proposed model is:
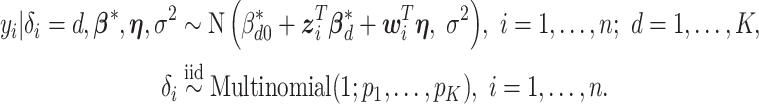 |
(2.1) |
In Bayesian mixture modeling, priors are assigned to the latent subgroup memberships and subgroup-specific parameters. Further, we take a fully Bayesian approach, assign a prior on 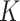 , and flexibly drop the assumption of a known
, and flexibly drop the assumption of a known 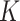 . Such a mixture model has been referred to as a Mixture of Finite Mixture. Prior specifications for the above model are described in the next subsection. Here, we note that certain individual components of the model and prior specifications have roots in the existing literature. However, their combination to address supervised heterogeneity analysis built on high-dimensional interaction models is new and innovative.
. Such a mixture model has been referred to as a Mixture of Finite Mixture. Prior specifications for the above model are described in the next subsection. Here, we note that certain individual components of the model and prior specifications have roots in the existing literature. However, their combination to address supervised heterogeneity analysis built on high-dimensional interaction models is new and innovative.
2.2. Prior specifications
We first define the prior for the subgroup-specific parameter 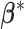 . Recall that
. Recall that 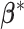 contains the subgroup-specific intercepts and regression coefficients associated with the imaging features. For the subgroup-specific intercepts
contains the subgroup-specific intercepts and regression coefficients associated with the imaging features. For the subgroup-specific intercepts 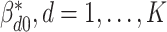 , we assume the
, we assume the 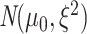 prior. For the coefficients associated with the imaging features, we introduce sparsity to accommodate high dimensionality and distinguish between signals and noises. High-dimensional imaging features extracted using digital processing software also describe properties not related to cancer, making it necessary to conduct variable selection. This is also true for I–E interaction analysis (Xu and others, 2019). In our analysis, further complication is introduced by heterogeneity. Specifically, different subject subgroups may have different subsets of important variables associated with the response. To address these challenges, we impose spike and slab priors, which have been popular in the Bayesian variable selection literature, to the subgroup-specific parameters. Specifically, to allow for both imaging feature-level and within-imaging-feature-level sparsity, we first follow Xu and Ghosh (2015) and take a reparameterization:
prior. For the coefficients associated with the imaging features, we introduce sparsity to accommodate high dimensionality and distinguish between signals and noises. High-dimensional imaging features extracted using digital processing software also describe properties not related to cancer, making it necessary to conduct variable selection. This is also true for I–E interaction analysis (Xu and others, 2019). In our analysis, further complication is introduced by heterogeneity. Specifically, different subject subgroups may have different subsets of important variables associated with the response. To address these challenges, we impose spike and slab priors, which have been popular in the Bayesian variable selection literature, to the subgroup-specific parameters. Specifically, to allow for both imaging feature-level and within-imaging-feature-level sparsity, we first follow Xu and Ghosh (2015) and take a reparameterization:
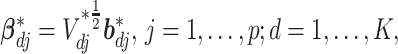 |
where 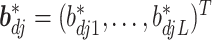 and
and 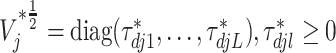 for
for 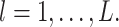
To achieve feature-level sparsity, we impose the multivariate spike and slab prior on each 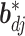 :
:
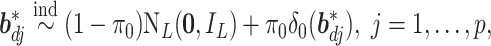 |
(2.2) |
where 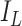 is the identity matrix, and
is the identity matrix, and 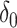 denotes the point mass at 0. This spike and slab prior, which is a mixture of a Normal distribution (slab part) and a point mass at
denotes the point mass at 0. This spike and slab prior, which is a mixture of a Normal distribution (slab part) and a point mass at 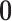 (spike part) with weights
(spike part) with weights 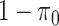 and
and 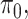 respectively, assigns a nonzero probability to the coefficients being exactly zero. If
respectively, assigns a nonzero probability to the coefficients being exactly zero. If 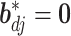 , then all elements of
, then all elements of 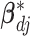 are zero, suggesting that the
are zero, suggesting that the 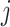 th imaging feature has no main effect or any interaction effect on the response in the
th imaging feature has no main effect or any interaction effect on the response in the 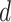 th subgroup.
th subgroup.
To induce within-feature-level sparsity, we further impose the spike and slab prior on each 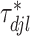 except for
except for 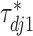 :
:
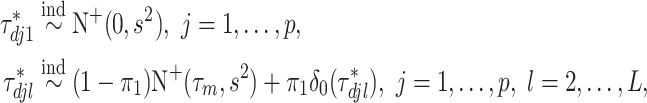 |
(2.3) |
where 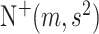 denotes the truncated normal distribution whose probability density function is proportional to that of N
denotes the truncated normal distribution whose probability density function is proportional to that of N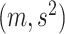 but truncated to be positive and then normalized. In our modeling, each
but truncated to be positive and then normalized. In our modeling, each 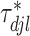 determines the magnitude of a regression coefficient for an effect associated with the
determines the magnitude of a regression coefficient for an effect associated with the 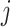 th imaging feature. When
th imaging feature. When 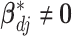 , the above prior specification ensures that
, the above prior specification ensures that 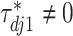 . That is, the main effect is selected. For
. That is, the main effect is selected. For 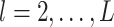 , the spike and slab priors determine whether the individual I–E interactions have nonzero effects. It is noted that if at least one interaction is nonzero, then
, the spike and slab priors determine whether the individual I–E interactions have nonzero effects. It is noted that if at least one interaction is nonzero, then 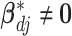 , leading to the nonzero main effect. This ensures that the “main effects, interactions” hierarchy is respected.
, leading to the nonzero main effect. This ensures that the “main effects, interactions” hierarchy is respected.
The feature-level sparsity and within-feature-level sparsity are controlled by the prior inclusion probabilities, 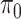 and
and 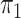 in (2.2) and (2.3), respectively. Fixing the values of these hyperparameters leads to more informative priors and poorer multiplicity control for a higher number of spurious covariates (Scott and Berger, 2010). This multiplicity problem can be handled by fully Bayesian models that assign hyperpriors to
in (2.2) and (2.3), respectively. Fixing the values of these hyperparameters leads to more informative priors and poorer multiplicity control for a higher number of spurious covariates (Scott and Berger, 2010). This multiplicity problem can be handled by fully Bayesian models that assign hyperpriors to 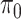 and
and 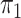 . Extending the idea of Ley and Steel (2009), we adopt conjugate beta hyperpriors
. Extending the idea of Ley and Steel (2009), we adopt conjugate beta hyperpriors 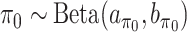 and
and 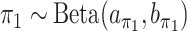 . As for the choice of hyperparameters
. As for the choice of hyperparameters 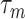 and
and 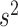 (which determine the prior of the magnitude of nonzero coefficients
(which determine the prior of the magnitude of nonzero coefficients 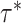 ’s), we resort to the theoretical conditions derived in Narisetty and He (2014, Section 2.1) for standard Bayesian variable selection models with spike and slab priors for a rough guideline. Briefly, the larger the number of covariates is relative to the size of each subgroup, and the more severe the multicollinearity of the design matrix, the larger the values of
’s), we resort to the theoretical conditions derived in Narisetty and He (2014, Section 2.1) for standard Bayesian variable selection models with spike and slab priors for a rough guideline. Briefly, the larger the number of covariates is relative to the size of each subgroup, and the more severe the multicollinearity of the design matrix, the larger the values of 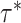 ’s need to be to achieve variable selection consistency. Since the theoretical result bears no direct implication for the choice of these values in practice, the
’s need to be to achieve variable selection consistency. Since the theoretical result bears no direct implication for the choice of these values in practice, the 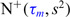 prior is assigned to give a significant probability to large values of
prior is assigned to give a significant probability to large values of 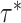 ’s, allowing their posterior values to be informed by the observed data. For most setups with moderate correlations among covariates, setting
’s, allowing their posterior values to be informed by the observed data. For most setups with moderate correlations among covariates, setting 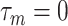 and a vague prior on
and a vague prior on 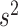 suffices. For setups with a large
suffices. For setups with a large 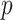 (relative to
(relative to 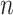 ) and highly correlated covariates, setting the mode of the slab part of the prior,
) and highly correlated covariates, setting the mode of the slab part of the prior, 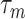 , away from the spike at zero helps identify more useful covariates. Following Xu and Ghosh (2015), a conjugate prior is assigned on
, away from the spike at zero helps identify more useful covariates. Following Xu and Ghosh (2015), a conjugate prior is assigned on 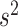 :
: 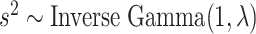 . Instead of estimating
. Instead of estimating 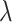 using empirical Bayesian methods, we take the full Bayesian approach and assign
using empirical Bayesian methods, we take the full Bayesian approach and assign 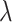 a prior,
a prior, 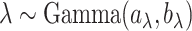 , where
, where 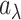 and
and 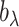 are the shape and scale parameters, respectively. More discussions on prior choice and consistency are in Supplementary material available at Biostatistics online.
are the shape and scale parameters, respectively. More discussions on prior choice and consistency are in Supplementary material available at Biostatistics online.
Given 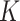 , we assign the prior
, we assign the prior 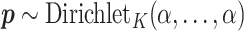 to the subgroup proportions, where
to the subgroup proportions, where 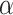 is a constant independent of
is a constant independent of 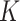 . This is the prior adopted in Miller and Harrison (2018). On one hand, imposing the same precision
. This is the prior adopted in Miller and Harrison (2018). On one hand, imposing the same precision 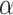 across different values of
across different values of 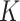 is a restriction in terms of modeling. But this can be critical to efficient computing in Section 2.3, as
is a restriction in terms of modeling. But this can be critical to efficient computing in Section 2.3, as 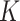 and
and 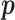 can then be marginalized out to avoid the transdimensional computing problems caused by the varying dimension of group-specific parameters for different values of
can then be marginalized out to avoid the transdimensional computing problems caused by the varying dimension of group-specific parameters for different values of 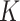 . On the other hand, given
. On the other hand, given 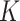 , it is not as big a restriction to set all
, it is not as big a restriction to set all 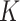 parameters in the Dirichlet distribution to be
parameters in the Dirichlet distribution to be 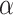 . This is because the prior on
. This is because the prior on 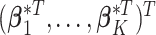 is symmetric, and hence the distribution of
is symmetric, and hence the distribution of 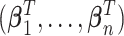 under any asymmetric distribution on
under any asymmetric distribution on  will be the same as if this asymmetric distribution is replaced by a symmetric version of it where the entries of
will be the same as if this asymmetric distribution is replaced by a symmetric version of it where the entries of 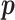 are randomly permuted. For the number of subgroups
are randomly permuted. For the number of subgroups 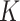 , we assume a Geometric distribution
, we assume a Geometric distribution 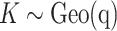 where
where 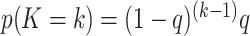 , for
, for 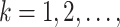 with some
with some 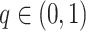 .
.
For the remaining parameters, we assign 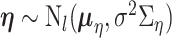 and
and 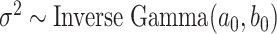 , where
, where 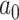 and
and 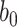 are the shape and scale parameters, respectively. In practice, E variables are usually low-dimensional, manually selected, and important, and hence will not be subject to variable selection. In the above formulation, it is assumed that
are the shape and scale parameters, respectively. In practice, E variables are usually low-dimensional, manually selected, and important, and hence will not be subject to variable selection. In the above formulation, it is assumed that 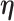 is the same across subgroups. In our data analysis, all the samples have the same cancer type. That is, based on the demographic, clinical, and environmental variables, these samples have been concluded as sufficiently alike. As such, the goal is to see if more subtle data structures can be identified with the introduction of imaging features and their interactions with E variables. If needed, it is straightforward to design subgroup-specific
is the same across subgroups. In our data analysis, all the samples have the same cancer type. That is, based on the demographic, clinical, and environmental variables, these samples have been concluded as sufficiently alike. As such, the goal is to see if more subtle data structures can be identified with the introduction of imaging features and their interactions with E variables. If needed, it is straightforward to design subgroup-specific 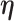 .
.
Although this study emphasizes methodological development and applications, to provide a strong statistical basis, in Supplementary material available at Biostatistics online, we provide heuristic justifications on identifiability and consistency of the proposed model. Accordingly, we have incorporated such considerations when specifying priors in our numerical studies.
2.3. Computation
We develop Markov chain Monte Carlo (MCMC) algorithms to estimate the posterior distribution. Recall that 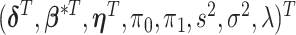 is the vector of the latent subgroup memberships and parameters for the proposed model. Here, the vector of the latent subgroup memberships
is the vector of the latent subgroup memberships and parameters for the proposed model. Here, the vector of the latent subgroup memberships 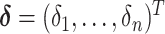 induces a partition
induces a partition 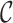 of
of 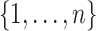 . The goal is to develop a MCMC algorithm to explore the joint distribution over the space of
. The goal is to develop a MCMC algorithm to explore the joint distribution over the space of 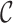 and the space of the other parameters. The joint distribution to be sampled from can be summarized as:
and the space of the other parameters. The joint distribution to be sampled from can be summarized as:
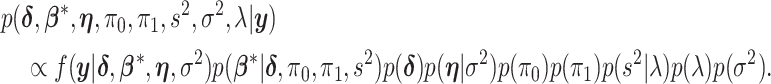 |
We develop a Metropolis-within-Gibbs sampler that updates the vector of subgroup memberships and subgroup-specific parameters, followed by the parameters that are not subgroup-specific.
To update the subgroup memberships, we adopt the strategy of introducing auxiliary variables (Miller and Harrison, 2018). Additional discussions are provided in Supplementary material available at Biostatistics online. Let 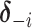 denote
denote 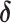 with its
with its 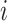 th component removed, and
th component removed, and 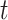 denote the number of unique values in
denote the number of unique values in 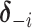 . Let
. Let 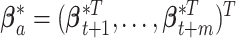 denote a set of
denote a set of 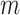 auxiliary variables that are identically and independently distributed from the prior specified in the previous subsection. Following Miller and Harrison (2018), the prior for
auxiliary variables that are identically and independently distributed from the prior specified in the previous subsection. Following Miller and Harrison (2018), the prior for  in (2.1) implies:
in (2.1) implies:
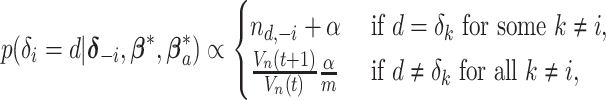 |
where 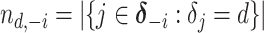 denotes the size of the
denotes the size of the 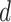 th subgroup without the
th subgroup without the 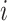 th sample,
th sample, 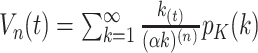 ,
, 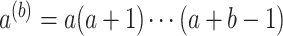 , and
, and 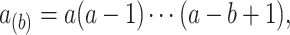 with
with 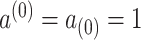 by convention. Then the full conditional distribution for
by convention. Then the full conditional distribution for 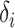 (conditional on the rest of the parameters) is:
(conditional on the rest of the parameters) is:
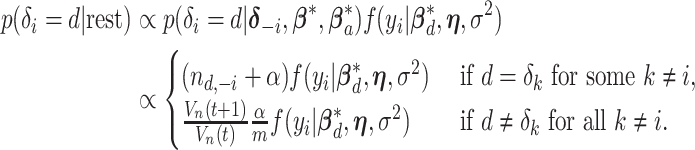 |
The subgroup-specific parameters are updated separately for each subgroup. To update the coefficients associated with the 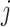 th (
th (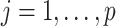 ) imaging feature for the
) imaging feature for the 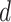 th (
th (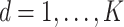 ) subgroup, we first conduct the feature-level update, followed by the within-feature-level update. For the feature-level update, let
) subgroup, we first conduct the feature-level update, followed by the within-feature-level update. For the feature-level update, let 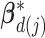 denote
denote 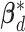 with its
with its 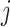 th component removed, and
th component removed, and 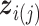 denote
denote 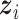 with its
with its 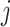 th component removed. Conditional on the rest of the parameters,
th component removed. Conditional on the rest of the parameters, 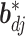 has a multivariate spike and slab distribution:
has a multivariate spike and slab distribution:
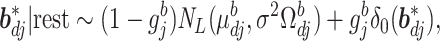 |
where 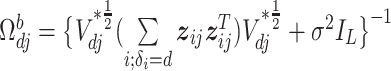 and
and 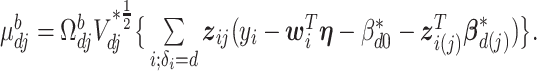 In the above,
In the above, 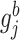 represents the full conditional posterior probability of
represents the full conditional posterior probability of 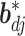 being equal to 0, which can be shown as:
being equal to 0, which can be shown as:
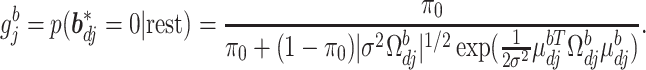 |
For the within-feature-level update, let 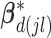 denote
denote 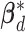 with the
with the 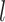 th element of the
th element of the 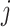 th imaging variable group removed, and
th imaging variable group removed, and 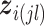 denote
denote 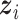 with the
with the 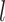 th element of the
th element of the 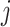 th imaging variable group removed. The conditional distribution of
th imaging variable group removed. The conditional distribution of 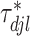 for
for 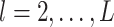 is a spike and slab distribution, while that of
is a spike and slab distribution, while that of 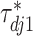 is just the slab part of the mixture distribution. That is,
is just the slab part of the mixture distribution. That is,
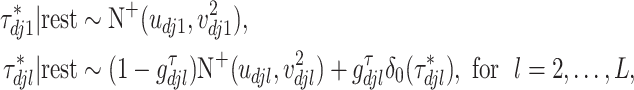 |
where for 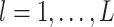 ,
, 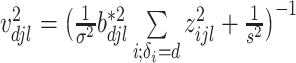 ,
, 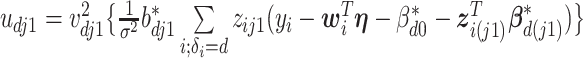 , and for
, and for 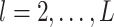 ,
, 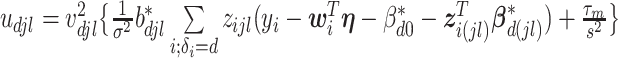 . The weight
. The weight 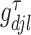 is the full conditional posterior probability of
is the full conditional posterior probability of 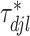 being equal to zero, that is,
being equal to zero, that is,
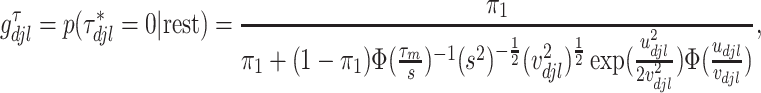 |
where 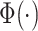 denotes the cumulative distribution function of the standard normal distribution.
denotes the cumulative distribution function of the standard normal distribution.
The full conditional distribution of the subgroup-specific intercept 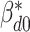 is given by:
is given by:
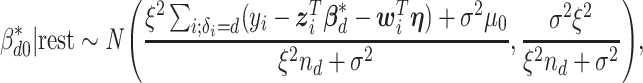 |
where 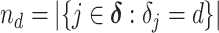 denotes the size of the
denotes the size of the  th subgroup.
th subgroup.
We next update the parameters that are not subgroup-specific. The full conditional distribution of 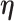 is:
is:
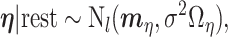 |
where 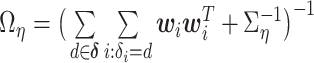 and
and 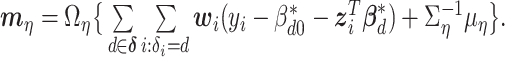
The posteriors of 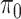 and
and 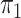 conditional on all the other parameters are:
conditional on all the other parameters are:
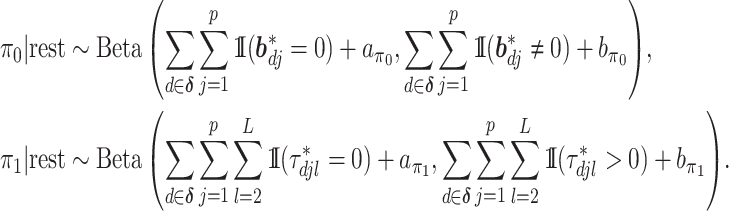 |
The conditional distribution of 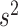 is given by
is given by
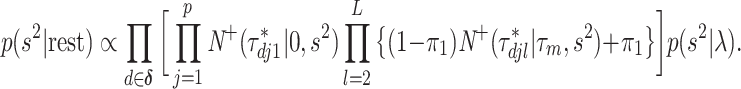 |
Since this is not a standard distribution, we resort to the random-walk Metropolis update with a Gaussian proposal distribution.
Lastly, the posterior distributions of 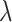 and
and 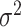 are Gamma and Inverse Gamma, respectively:
are Gamma and Inverse Gamma, respectively:
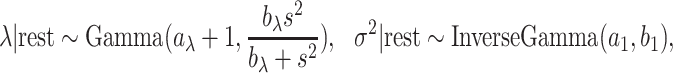 |
where 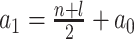 and
and 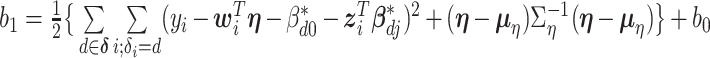 .
.
2.4. Inference based on MCMC samples
It is well known that mixture models are not identifiable, due to the label-switching problem caused by the symmetry of parameters in the likelihood. Some inference goals are label-invariant and not affected by this problem. An example is the (marginal) posterior distribution of the number of subgroups, where its mode 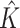 is the commonly used point estimate of
is the commonly used point estimate of 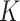 .
.
Some other inference, like that for the group-specific estimate of the coefficient of a covariate, cannot be directly obtained from its marginal posterior, as every subgroup has exactly the same marginal posterior due to symmetry. This is why for Bayesian mixture models computed with MCMC, there is a rich literature on the postprocessing procedures. See Supplementary material available at Biostatistics online for more discussions on the nonidentifiability issue and, for example, Papastamoulis (2016) for a list of MCMC postprocessing algorithms. Our data analysis adopts Algorithm 5 of the aforementioned paper for postprocessing, which is proposed in Papastamoulis and Iliopoulos (2010) and Rodríguez and Walker (2014) and implemented using the R package  .
.
Sometimes, it is of interest to obtain a point estimate of the subgrouping configuration. One solution is to assign each subject to the subgroup that it belongs to with the highest posterior probability. Given the relabeled MCMC samples, this is simply estimated by the subgroup that the subject belongs to the most often. For other alternatives that are based on decision theory, see for example, Wade and Ghahramani (2018).
Recall that one prominent feature of our model is that different variables may be selected for different subgroups. Within a subgroup, we can simply follow the standard approaches in the literature for Bayesian regression models with spike and slab priors. Specifically, in simulation, we consider the median probability model (MPM) that retains all covariates with marginal posterior inclusion probabilities (PIP) greater than 0.5. The MPM is known to have optimal prediction performance in certain setups, for example, when the design matrix is orthogonal (Barbieri and Berger, 2004). However, it tends to select too few covariates in practice (Dey and others, 2008). One remedy is to choose a lower threshold, which is recommended in Narisetty and He (2014, Section. 2.2) and adopted in our real data analysis.
Finally, for inference of the group-specific coefficients in 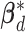 from the
from the 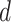 th subgroup, key quantities that measure the importance of the coefficients are their chances of being nonzero, which are the PIPs. In addition, one can inspect the marginal posterior densities of the coefficients and report summary statistics such as the posterior medians.
th subgroup, key quantities that measure the importance of the coefficients are their chances of being nonzero, which are the PIPs. In addition, one can inspect the marginal posterior densities of the coefficients and report summary statistics such as the posterior medians.
3. Simulation
We gauge the performance of the proposed approach and benchmark against alternatives using simulation. In what follows, we set the sample size 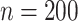 and number of subgroups
and number of subgroups 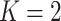 . Response variables are independently generated from model (2.1) with
. Response variables are independently generated from model (2.1) with 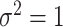 . For the E variables, we set the number of variables
. For the E variables, we set the number of variables 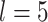 and consider both continuous and discrete types. More specifically, for the continuous E variables, we generate
and consider both continuous and discrete types. More specifically, for the continuous E variables, we generate 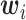 ’s from a multivariate normal distribution with mean vector zero and covariance matrix that has an auto-regressive correlation structure with
’s from a multivariate normal distribution with mean vector zero and covariance matrix that has an auto-regressive correlation structure with 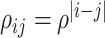 and
and 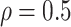 . For the discrete E variables, we first generate continuously distributed variables in the same way as above and then dichotomize at 0. The coefficients for all of the main E effects are generated from Uniform(0.8, 1.2). For the I variables, we generate
. For the discrete E variables, we first generate continuously distributed variables in the same way as above and then dichotomize at 0. The coefficients for all of the main E effects are generated from Uniform(0.8, 1.2). For the I variables, we generate 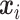 ’s from a multivariate normal distribution of dimension
’s from a multivariate normal distribution of dimension 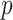 with marginal means one and two different covariance structures. The first is the block-diagonal structure, reflecting that correlations are “local”, where each block of size
with marginal means one and two different covariance structures. The first is the block-diagonal structure, reflecting that correlations are “local”, where each block of size 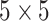 has an auto-regressive structure with
has an auto-regressive structure with 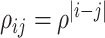 and
and 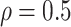 . The second is the banded correlation structure with
. The second is the banded correlation structure with 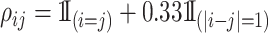 . For the subgroup-specific regression coefficients associated with the I variables,
. For the subgroup-specific regression coefficients associated with the I variables, 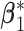 and
and 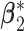 , in each subgroup, five of the main I effects and ten of the I–E interactions are set to be nonzero, and the rest are zero. The “main effects, interactions” hierarchy is satisfied. For each combination of the specifications on E variables (continuous, discrete) and covariance matrix of I features (block-diagonal, banded), we further consider the following four scenarios. [Scenario 1] The dimension of imaging features
, in each subgroup, five of the main I effects and ten of the I–E interactions are set to be nonzero, and the rest are zero. The “main effects, interactions” hierarchy is satisfied. For each combination of the specifications on E variables (continuous, discrete) and covariance matrix of I features (block-diagonal, banded), we further consider the following four scenarios. [Scenario 1] The dimension of imaging features 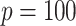 . The nonzero components of
. The nonzero components of 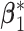 and
and 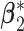 are independently generated from Uniform(
are independently generated from Uniform(  1.2,
1.2,  0.8) and Uniform(0.8, 1.2), respectively. The subgroup memberships are generated from
0.8) and Uniform(0.8, 1.2), respectively. The subgroup memberships are generated from 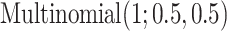 . [Scenario 2] Similar to the above, except that the nonzero components are generated from Uniform(
. [Scenario 2] Similar to the above, except that the nonzero components are generated from Uniform( 0.8,
0.8,  0.5) and Uniform(0.5, 0.8), respectively, representing weaker signals. [Scenario 3] Similar to Scenario 1, except that the subgroup memberships are generated from
0.5) and Uniform(0.5, 0.8), respectively, representing weaker signals. [Scenario 3] Similar to Scenario 1, except that the subgroup memberships are generated from 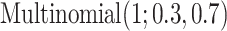 . That is, the subgroups are imbalanced. [Scenario 4] Similar to Scenario 1, except that the I variables have a higher dimension with
. That is, the subgroups are imbalanced. [Scenario 4] Similar to Scenario 1, except that the I variables have a higher dimension with 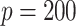 . Here, we note that the dimensions of covariates, especially
. Here, we note that the dimensions of covariates, especially 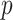 , have been chosen to be comparable to the data analyzed in the next section, and that, in principle, the proposed approach can be applied to settings with higher dimensions.
, have been chosen to be comparable to the data analyzed in the next section, and that, in principle, the proposed approach can be applied to settings with higher dimensions.
To implement the proposed method, we adopt 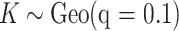 ,
, 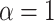 , and
, and 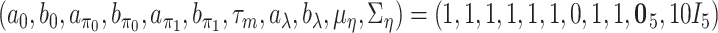 for the prior distributions. For the number of auxiliary variables
for the prior distributions. For the number of auxiliary variables 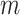 in updating the subject subgroup memberships, we set
in updating the subject subgroup memberships, we set 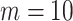 . Computation is carried out by running the proposed sampler for 20 000 iterations, with the first half discarded as burn-in, and all inferences are based on the remaining MCMC samples. To initialize each Markov chain, all samples are assigned to the same subgroup, and the values of all the other parameters are randomly drawn from their priors. With multiple MCMC runs, we inspect the trace plots, compare across runs, and do not observe obvious signs of lack of convergence (sample plots are provided in Figures S.4 and S.5 of Supplementary material available at Biostatistics online). Further, for the label-invariant variables, Gelman and Rubins potential scale reduction factor (PSRF; Gelman and Rubin, 1992) is used for assessing convergence. The PSRF values are all below 1.1, indicating satisfactory convergence.
. Computation is carried out by running the proposed sampler for 20 000 iterations, with the first half discarded as burn-in, and all inferences are based on the remaining MCMC samples. To initialize each Markov chain, all samples are assigned to the same subgroup, and the values of all the other parameters are randomly drawn from their priors. With multiple MCMC runs, we inspect the trace plots, compare across runs, and do not observe obvious signs of lack of convergence (sample plots are provided in Figures S.4 and S.5 of Supplementary material available at Biostatistics online). Further, for the label-invariant variables, Gelman and Rubins potential scale reduction factor (PSRF; Gelman and Rubin, 1992) is used for assessing convergence. The PSRF values are all below 1.1, indicating satisfactory convergence.
With the high dimensionality, complex data structure especially with the “main effects, interactions” hierarchy, and subgrouping structure, computation of the proposed method is inevitably more expensive than that in some existing studies. For one simulated dataset under Scenario 1, computation takes about 1.5 h on a desktop with standard configurations.
For comparison, we consider the following alternatives: (i) The Bayesian Sparse Group Selection with Spike and Slab Prior (BSGSS), which is developed in Xu and Ghosh (2015) and assumes homogeneity. With this benchmark approach, we can “re-establish” the importance of accounting for heterogeneity. (ii) The FMR Lasso (denoted as FMRLasso), which is developed in Städler and others (2010). This is one of the most popular heterogeneity analysis approaches for high-dimensional data. It assumes the FMR model and adopts Lasso for variable selection. It treats main effects and interactions in the same manner and may violate the variable selection hierarchy. Comparing with this approach can provide a benchmark for the proposed Bayesian estimation and also “re-establish” the importance of respecting the hierarchy. (iii) The FMR based on the Imputation-conditional consistency algorithm (denoted as ICC), which is developed in Li and others (2019). Under the FMR modeling, this approach conducts estimation using ICC, which is a general technique for handling missing data in high-dimensional settings. Conditioning on the assigned subgroup membership, the minimax concave penalty is applied for accommodating high dimensionality and conducting variable selection. It is noted that some alternative penalties (e.g., smoothly clipped absolute deviation) are expected to lead to similar performance. For the finite mixture models, it remains challenging to determine the number of subject subgroups. Here, we set their number of subgroups at the true 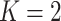 and note that this may generate favorable performance for the two FMR alternatives and is not feasible in real data analysis. The FMRLasso and ICC generate point estimates of the subgrouping configuration and subgroup-specific parameters
and note that this may generate favorable performance for the two FMR alternatives and is not feasible in real data analysis. The FMRLasso and ICC generate point estimates of the subgrouping configuration and subgroup-specific parameters 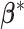 . We acknowledge that there are other potentially applicable alternatives. The above three may be the most relevant and can be readily realized.
. We acknowledge that there are other potentially applicable alternatives. The above three may be the most relevant and can be readily realized.
To gain more insight into the working characteristics of the proposed approach, in Figures S.1–S.3 of the Supplementary material available at Biostatistics online, for one representative simulation replicate, we present the true model parameters as well as estimation and variable selection performance of the proposed approach. Satisfactory performance is clearly observed. Specifically, the inclusion probabilities for the zero coefficients are very small, in particular, smaller than those for the nonzero coefficients, which leads to accurate variable selection. It is also observed that the colors of the estimates are close to those of the true values. Then, based on 100 simulation replicates, to more objectively evaluate the accuracy of estimating 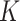 , we report the mean and standard deviation (sd) of
, we report the mean and standard deviation (sd) of 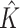 for the proposed method. To evaluate the accuracy of subgrouping, we report the mean (sd) of the Adjusted Rand Index (ARI; Hubert and Arabie, 1985) for the proposed method, FMRLasso, and ICC. ARI yields a maximal value of 1 if the estimated and true subgroupings perfectly match, and can be negative if the two subgroupings are “less similar” than what is expected under random assignments. A higher ARI value indicates higher subgrouping similarity. In our evaluation, we compare the estimated subgrouping against the true. The proposed and alternative approaches all conduct variable selection. We evaluate variable selection accuracy using the true positive (TP) and false positive (FP) rates. Summary statistics are provided in Table 1 and Table S.1 of the Supplementary material available at Biostatistics online.
for the proposed method. To evaluate the accuracy of subgrouping, we report the mean (sd) of the Adjusted Rand Index (ARI; Hubert and Arabie, 1985) for the proposed method, FMRLasso, and ICC. ARI yields a maximal value of 1 if the estimated and true subgroupings perfectly match, and can be negative if the two subgroupings are “less similar” than what is expected under random assignments. A higher ARI value indicates higher subgrouping similarity. In our evaluation, we compare the estimated subgrouping against the true. The proposed and alternative approaches all conduct variable selection. We evaluate variable selection accuracy using the true positive (TP) and false positive (FP) rates. Summary statistics are provided in Table 1 and Table S.1 of the Supplementary material available at Biostatistics online.
Table 1.
Simulation results for Scenarios 1 and 2, mean (sd) based on 100 replicates
| Subgroup | Scenario 1 | Scenario 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Proposed | FMRLasso | ICC | BSGSS | Proposed | FMRLasso | ICC | BSGSS | ||
| Continuous E variables, a block-diagonal covariance matrix for I features | |||||||||
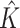
|
2.000 (0.00) | 2.000 (0.00) | |||||||
| ARI | 0.820 (0.05) | 0.685 (0.08) | 0.637 (0.17) | 0.722 (0.06) | 0.591 (0.08) | 0.561 (0.13) | |||
| Main I effects | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.906 (0.19) | 0.524 (0.33) | 0.926 (0.11) | 1.000 (0.00) | 0.768 (0.25) | 0.422 (0.28) | 0.908 (0.14) |
| 2 | 1.000 (0.00) | 0.908 (0.16) | 0.482 (0.33) | 1.000 (0.00) | 0.760 (0.23) | 0.292 (0.27) | |||
| FPR | 1 | 0.000 (0.00) | 0.021 (0.02) | 0.001 (0.00) | 0.780 (0.06) | 0.002 (0.01) | 0.016 (0.02) | 0.003 (0.01) | 0.679 (0.07) |
| 2 | 0.001 (0.00) | 0.011 (0.02) | 0.001 (0.00) | 0.003 (0.01) | 0.009 (0.01) | 0.001 (0.00) | |||
| I–E interactions | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.924 (0.16) | 0.691 (0.23) | 0.926 (0.11) | 0.998 (0.01) | 0.823 (0.14) | 0.543 (0.18) | 0.908 (0.14) |
| 2 | 1.000 (0.00) | 0.936 (0.11) | 0.714 (0.23) | 0.999 (0.01) | 0.873 (0.14) | 0.539 (0.18) | |||
| FPR | 1 | 0.006 (0.01) | 0.053 (0.02) | 0.020 (0.01) | 0.784 (0.06) | 0.022 (0.01) | 0.052 (0.01) | 0.025 (0.01) | 0.704 (0.07) |
| 2 | 0.006 (0.01) | 0.076 (0.02) | 0.020 (0.01) | 0.022 (0.01) | 0.079 (0.01) | 0.024 (0.01) | |||
| Discrete E variables, a block-diagonal covariance matrix for I features | |||||||||
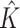
|
2.000 (0.00) | 2.000 (0.00) | |||||||
| ARI | 0.816 (0.06) | 0.700 (0.10) | 0.638 (0.25) | 0.721 (0.06) | 0.618 (0.07) | 0.582 (0.16) | |||
| Main I effects | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.932 (0.15) | 0.636 (0.36) | 0.934 (0.011) | 0.998 (0.02) | 0.802(0.21) | 0.496 (0.29) | 0.912 (0.13) |
| 2 | 1.000 (0.00) | 0.886 (0.18) | 0.548 (0.34) | 1.000 (0.00) | 0.736(0.20) | 0.372 (0.27) | |||
| FPR | 1 | 0.001 (0.00) | 0.020 (0.03) | 0.003 (0.01) | 0.811 (0.06) | 0.003 (0.00) | 0.017(0.02) | 0.001 (0.01) | 0.716 (0.08) |
| 2 | 0.001 (0.00) | 0.009 (0.01) | 0.002 (0.00) | 0.002 (0.00) | 0.010(0.02) | 0.003 (0.06) | |||
| I–E interactions | |||||||||
| TPR | 1 | 0.999 (0.01) | 0.948 (0.12) | 0.701 (0.32) | 0.934 (0.11) | 0.997 (0.02) | 0.855 (0.13) | 0.566 (0.20) | 0.912 (0.13) |
| 2 | 1.000 (0.00) | 0.948 (0.12) | 0.720 (0.30) | 1.000 (0.00) | 0.892 (0.12) | 0.586 (0.20) | |||
| FPR | 1 | 0.027 (0.01) | 0.039 (0.02) | 0.019 (0.01) | 0.815(0.06) | 0.031 (0.00) | 0.038 (0.01) | 0.022 (0.01) | 0.722 (0.08) |
| 2 | 0.026 (0.01) | 0.063 (0.02) | 0.020 (0.01) | 0.031 (0.00) | 0.065 (0.01) | 0.022 (0.01) | |||
| Continuous E variables, a banded covariance matrix for I features | |||||||||
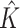
|
2.000 (0.00) | 2.000 (0.00) | |||||||
| ARI | 0.816 (0.05) | 0.688 (0.08) | 0.657 (0.15) | 0.730 (0.06) | 0.586 (0.11) | 0.557(0.17) | |||
| Main I effects | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.932 (0.17) | 0.510 (0.29) | 0.932 (0.11) | 0.996 (0.04) | 0.742 (0.25) | 0.398 (0.26) | 0.864 (0.15) |
| 2 | 1.000 (0.00) | 0.890 (0.15) | 0.490 (0.30) | 1.000 (0.00) | 0.722 (0.25) | 0.316 (0.25) | |||
| FPR | 1 | 0.001 (0.00) | 0.023 (0.03) | 0.001 (0.01) | 0.761 (0.07) | 0.002 (0.01) | 0.025 (0.03) | 0.003 (0.01) | 0.669 (0.073) |
| 2 | 0.001 (0.00) | 0.011 (0.02) | 0.001 (0.00) | 0.002 (0.00) | 0.013 (0.02) | 0.002 (0.01) | |||
| I–E interactions | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.929 (0.12) | 0.688 (0.22) | 0.932 (0.11) | 0.985 (0.05) | 0.797 (0.19) | 0.528 (0.19) | 0.864 (0.05) |
| 2 | 0.999 (0.01) | 0.941 (0.09) | 0.708 (0.22) | 0.990 (0.04) | 0.848 (0.17) | 0.543 (0.22) | |||
| FPR | 1 | 0.006 (0.01) | 0.054 (0.01) | 0.021 (0.01) | 0.766 (0.06) | 0.019 (0.01) | 0.056 (0.02) | 0.024 (0.01) | 0.675 (0.07) |
| 2 | 0.007 (0.01) | 0.076 (0.01) | 0.019 (0.01) | 0.020 (0.01) | 0.081 (0.01) | 0.024 (0.01) | |||
| Discrete E variables, a banded covariance matrix for I features | |||||||||
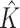
|
2.000 (0.00) | 2.000 (0.00) | |||||||
| ARI | 0.811 (0.06) | 0.699 (0.07) | 0.661 (0.20) | 0.714 (0.06) | 0.610 (0.06) | 0.563 (0.18) | |||
| Main I effects | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.948 (0.13) | 0.674 (0.31) | 0.932 (0.11) | 1.000 (0.00) | 0.832 (0.19) | 0.496(0.29) | 0.876(0.14) |
| 2 | 1.000 (0.00) | 0.898 (0.15) | 0.546 (0.30) | 1.000 (0.00) | 0.712 (0.21) | 0.314(0.27) | |||
| FPR | 1 | 0.001 (0.00) | 0.019 (0.02) | 0.002 (0.00) | 0.779 (0.06) | 0.002 (0.01) | 0.024 (0.03) | 0.003(0.01) | 0.689(0.08) |
| 2 | 0.002 (0.01) | 0.010 (0.01) | 0.002 (0.01) | 0.001 (0.00) | 0.012 (0.02) | 0.003(0.01) | |||
| I–E interactions | |||||||||
| TPR | 1 | 1.000 (0.00) | 0.949 (0.09) | 0.726 (0.26) | 0.932 (0.11) | 1.000 (0.00) | 0.852 (0.13) | 0.550(0.21) | 0.876(0.14) |
| 2 | 1.000 (0.00) | 0.961 (0.08) | 0.743 (0.24) | 1.000 (0.00) | 0.903 (0.09) | 0.562(0.22) | |||
| FPR | 1 | 0.027 (0.01) | 0.037 (0.01) | 0.019 (0.01) | 0.784 (0.06) | 0.031 (0.00) | 0.039 (0.02) | 0.023(0.01) | 0.695(0.07) |
| 2 | 0.027 (0.01) | 0.062 (0.01) | 0.018 (0.01) | 0.031 (0.00) | 0.067 (0.01) | 0.023(0.01) | |||
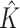 , estimated number of subgroups; ARI, adjusted rand index; TPR, true positive rate; FPR, false positive rate.
, estimated number of subgroups; ARI, adjusted rand index; TPR, true positive rate; FPR, false positive rate.
Across the whole spectrum of simulation, the proposed approach is observed to have competitive performance. For all simulation settings, it can almost perfectly identify 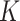 , which is often challenging in FMR and other heterogeneity analysis. It has superior subgrouping performance. Consider for example setup 1 and Scenario 1 (the upper-left corner of Table 1). The proposed approach has a mean Accuracy of 0.820, compared to 0.685 (FMRLasso) and 0.637 (ICC). It also has satisfactory variable selection performance. For the above particular setting, it is able to identify all TPs with almost no FPs for both subject subgroups. In comparison, FMRLasso has TP rates of 0.906 and 0.908 and FP rates of 0.021 and 0.011. Its lack of accuracy is at least partially attributable to the potential violation of the variable selection hierarchy. ICC has inferior performance with TP rates of 0.524 and 0.482. BSGSS has a TP rate of 0.926, however, an unsatisfactory FP rate of 0.780, which is caused by failing to account for heterogeneity. With partially dichotomized variables, the performance of the proposed approach may slightly deteriorate, which is as expected. We have also experimented with a few other simulation settings and made similar observations.
, which is often challenging in FMR and other heterogeneity analysis. It has superior subgrouping performance. Consider for example setup 1 and Scenario 1 (the upper-left corner of Table 1). The proposed approach has a mean Accuracy of 0.820, compared to 0.685 (FMRLasso) and 0.637 (ICC). It also has satisfactory variable selection performance. For the above particular setting, it is able to identify all TPs with almost no FPs for both subject subgroups. In comparison, FMRLasso has TP rates of 0.906 and 0.908 and FP rates of 0.021 and 0.011. Its lack of accuracy is at least partially attributable to the potential violation of the variable selection hierarchy. ICC has inferior performance with TP rates of 0.524 and 0.482. BSGSS has a TP rate of 0.926, however, an unsatisfactory FP rate of 0.780, which is caused by failing to account for heterogeneity. With partially dichotomized variables, the performance of the proposed approach may slightly deteriorate, which is as expected. We have also experimented with a few other simulation settings and made similar observations.
4. Data analysis
We analyze TCGA data on lung squamous cell cancer (LUSC), a major subtype of nonsmall-cell lung cancer. For lung cancer, heterogeneity analysis, both supervised and unsupervised, has been extensively conducted. Such analysis can assist more accurately classifying disease and delivering more customized treatment. As referred to in Section 1, some of such analysis have been based on histopathological imaging data. Here, we further advance such analysis to incorporate I–E interactions. Data are downloaded from the TCGA data portal (https://portal.gdc.cancer.gov/). The response variable of interest is FEV1 (forced expiratory volume in one second), which is a measure of the amount of air exhaled forcefully in 1 s. It is an important biomarker for lung capacity and has been associated with prognosis and other lung cancer outcomes. The histogram in Figure S.6 of the Supplementary material available at Biostatistics online shows that there may be two “peaks” around FEV1 = 65 and 77, respectively, suggesting that it may be sensible to assume a mixture distribution and examine heterogeneity. For E variables, we consider age, sex, smoking, and cancer stage, all of which have been associated with lung cancer outcomes and biomarkers. As such, variable selection is not of interest for these variables. Here we note that we have taken a “looser” definition of E variables, and that interaction analysis incorporating clinical and demographic variables has been strongly advocated in recent studies. In particular, these variables have been considered in the I–E interaction analysis under homogeneity (Xu and others, 2019). The imaging feature extraction pipeline is briefly sketched in Figure 1. Briefly, a histopathological slide (panel 2) obtained from biopsy is chopped into subimages (panel 3). Then 20 subimages are randomly selected (panel 4). These subimages are fed into Cellprofiler (https://cellprofiler.org/), a publicly available digital image processing software, for feature extraction (panel 5). Feature values are averaged over these 20 subimages, and irrelevant features (for example, time) are removed, leading to the final set of imaging features for analysis (panel 6). After removing subjects with missing response and E variable values, the final analyzed data contains 139 imaging features and the aforementioned four E variables on 164 subjects.
When implementing the proposed approach, we set 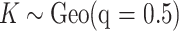 . As such, the prior encourages a relatively small number of subgroups by assigning
. As such, the prior encourages a relatively small number of subgroups by assigning 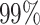 probability to
probability to 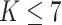 , which is appropriate considering the limited sample size. We have tried other values of
, which is appropriate considering the limited sample size. We have tried other values of 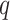 , which lead to rather similar results. For
, which lead to rather similar results. For 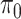 and
and 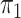 , we assign the
, we assign the 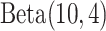 and
and 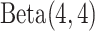 priors, respectively, under which about 70% of the imaging features are noises, and 50% of the E variables interact with the imaging features. Such numbers may be higher than in the published literature, allowing for “sufficient room” for discovery. The rest of the hyperparameter values are set as
priors, respectively, under which about 70% of the imaging features are noises, and 50% of the E variables interact with the imaging features. Such numbers may be higher than in the published literature, allowing for “sufficient room” for discovery. The rest of the hyperparameter values are set as 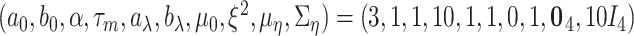 , either to reflect vague beliefs on the prior distributions or to make the computation stable. We perform four independent MCMC runs, with 10 000 iterations for burn-in and 40 000 iterations after the burn-in. Every other iterations are collected to reduce storage cost. The four runs are carefully examined, and satisfactory convergence is observed. As a testament, in Figure S.8 of the Supplementary material available at Biostatistics online, for the estimated marginal inclusion probabilities (upper triangle) and estimates of the subgroup-specific regression coefficients (lower triangle), we show the pairwise comparisons between the four chains. The final results are based on pooling the outputs of the four runs.
, either to reflect vague beliefs on the prior distributions or to make the computation stable. We perform four independent MCMC runs, with 10 000 iterations for burn-in and 40 000 iterations after the burn-in. Every other iterations are collected to reduce storage cost. The four runs are carefully examined, and satisfactory convergence is observed. As a testament, in Figure S.8 of the Supplementary material available at Biostatistics online, for the estimated marginal inclusion probabilities (upper triangle) and estimates of the subgroup-specific regression coefficients (lower triangle), we show the pairwise comparisons between the four chains. The final results are based on pooling the outputs of the four runs.
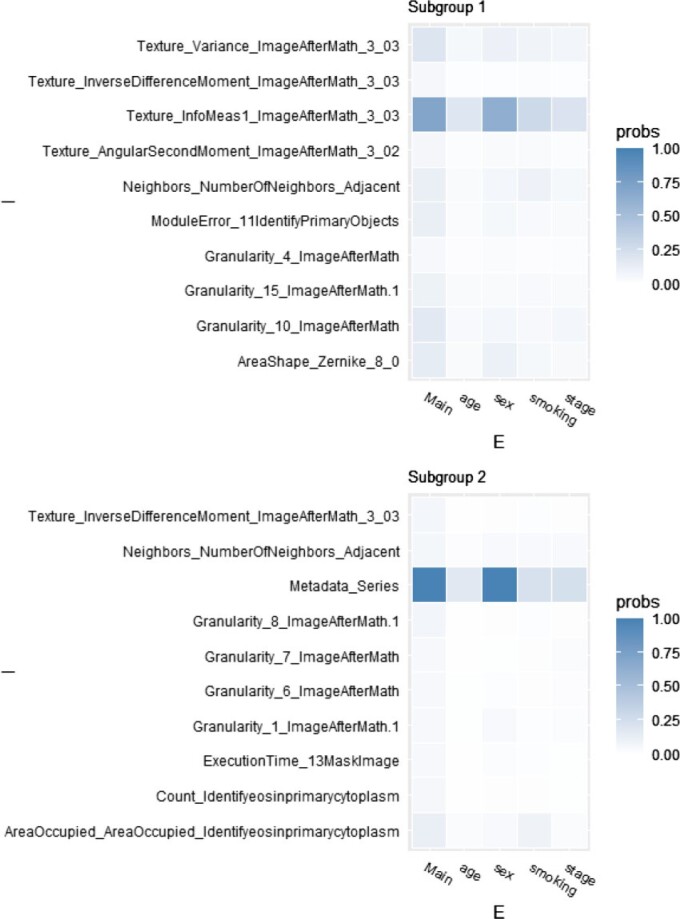
The posterior distribution of the number of subgroups and its trace plot are shown in Figure S.7 of the Supplementary material available at Biostatistics online, which suggests that there are most likely two subgroups. Conditioning on 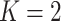 , the MCMC draws are postprocessed to address label-switching (Papastamoulis, 2016, Algorithm 5). The two subgroups have respective sizes of 36 and 128 on average. In Figure 2 and Table 2, for each of the two subgroups, we present the ten most important main effects and their interactions, where importance is measured by PIP. We note that Figure 2 shows that most of the PIPs are considerably smaller than those observed in simulation, which is expected as a result of significantly weaker signals and more complicated correlation structures. Table 2 shows that the “main effects, interactions” hierarchy is respected, and that the two subgroups are significantly different in which set of covariates are the most influential for the response. More details are in Figure S.9 of the Supplementary material available at Biostatistics online, which shows the approximate posterior distribution of
, the MCMC draws are postprocessed to address label-switching (Papastamoulis, 2016, Algorithm 5). The two subgroups have respective sizes of 36 and 128 on average. In Figure 2 and Table 2, for each of the two subgroups, we present the ten most important main effects and their interactions, where importance is measured by PIP. We note that Figure 2 shows that most of the PIPs are considerably smaller than those observed in simulation, which is expected as a result of significantly weaker signals and more complicated correlation structures. Table 2 shows that the “main effects, interactions” hierarchy is respected, and that the two subgroups are significantly different in which set of covariates are the most influential for the response. More details are in Figure S.9 of the Supplementary material available at Biostatistics online, which shows the approximate posterior distribution of 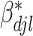 with the highest inclusion probabilities for subgroups 1 and 2.
with the highest inclusion probabilities for subgroups 1 and 2.
Fig. 2.
Data analysis, PIPs for the top ten imaging features for the two subgroups separately.
Table 2.
Data analysis, top ten imaging features (for each subgroup), and their estimated main effects and interactions
| Image feature | Main effect | Interaction with | |||
|---|---|---|---|---|---|
| age | sex | smoking | stage | ||
| Subgroup 1 | |||||
| Texture_Variance_ImageAfterMath_3_03 | 37.751 | –22.214 | |||
| Texture_InverseDifferenceMoment_ImageAfterMath_3_03 | 6.016 | ||||
| Texture_InfoMeas1_ImageAfterMath_3_03 | 34.927 | –2.519 | –34.746 | 9.512 | 1.343 |
| Texture_AngularSecondMoment_ImageAfterMath_3_02 | –3.738 | ||||
| Neighbors_NumberOfNeighbors_Adjacent | –8.971 | ||||
| ModuleError_11IdentifyPrimaryObjects | 15.694 | ||||
| Granularity_4_ImageAfterMath | 1.488 | ||||
| Granularity_15_ImageAfterMath.1 | –103.689 | ||||
| Granularity_10_ImageAfterMath | –12.48 | ||||
| AreaShape_Zernike_8_0 | 22.888 | –30.9 | |||
| Subgroup 2 | |||||
| Texture_InverseDifferenceMoment_ImageAfterMath_3_03 | 3.995 | ||||
| Neighbors_NumberOfNeighbors_Adjacent | –0.958 | ||||
| Metadata_Series | –100.833 | 1.262 | 100.984 | 1.417 | 0.111 |
| Granularity_8_ImageAfterMath.1 | 5.579 | ||||
| Granularity_7_ImageAfterMath | –1.818 | ||||
| Granularity_6_ImageAfterMath | –9.533 | ||||
| Granularity_1_ImageAfterMath.1 | 6.934 | ||||
| ExecutionTime_13MaskImage | –11.893 | ||||
| Count_Identifyeosinprimarycytoplasm | –4.64 | ||||
| AreaOccupied_AreaOccupied_Identifyeosinprimarycytoplasm | 0.84 | 9.394 | |||
Unlike in simulation, we do not know the true data generating model, and hence cannot directly evaluate subgrouping and variable selection performance. In addition, as discussed in Xu and others (2019) and references therein, high-dimensional imaging features extracted using digital image processing software do not have simple biological interpretations, making it impossible to “verify” the findings based on the selected variables. To fill this gap, we conduct a small real data-based simulation. In particular, the estimated subgrouping structures, top three imaging features for each subgroup, and their estimated main and interaction effects obtained above are taken as the true. Random errors are generated from a normal distribution as in simulation, and the response values are computed from the linear regression models. With 100 replicates, for subgrouping accuracy, the mean (sd) values are 0.793 (0.08). For the main I effects, the mean (sd) TP values are 0.927 (0.14) and 0.997 (0.03), and the mean (sd) FP values are 0.021 (0.01) and 0.006 (0.01). For the I–E interactions, the mean (sd) TP values are 0.993 (0.04) and 0.960 (0.10), and the mean (sd) FP values are 0.004 (0.00) and 0.008 (0.00). These results suggest that the subgrouping and identification findings in the above data analysis are reasonably credible.
Data are also analyzed using the alternatives, which lead to significantly different subgrouping, selection, and estimation results. As it is impossible to determine which set of results is more sensible, we conduct an indirect evaluation. Specifically, one subject is removed and form the testing data. The rest of the subjects form the training data and are analyzed using the proposed and alternative methods. The training data estimation is used for predicting the testing data. The “removal, estimation, and prediction” process is repeated across all the subjects. We note that it is not entirely clear which subgroup the removed subject belongs to and hence which model should be used. We use the subgroup/model that most of its subgroup members in the whole-data analysis belong to. The average squared roots of prediction MSE (mean squared error) values are 18.36 (proposed), 20.44 (FMRLasso), and 19.33 (ICC), which provides some support to the superiority of the proposed analysis.
5. Discussion
In this study, we have significantly expanded the scope of supervised cancer heterogeneity analysis by developing a Bayesian FMR approach that incorporates histopathological imaging features and, more importantly, their interactions with E variables. This study has also provided an alternative way for analyzing cancer studies and histopathological imaging data. As described above, the proposed approach also has multiple technical innovations, such as respecting the “main effects, interactions” hierarchy in Bayesian analysis and not specifying the number of subgroups. Simulation has shown its advantageous performance over the close competitors. In the analysis TCGA LUSC data, this study is the first to identify two subgroups based on imaging data. The data-based simulation and prediction evaluation can provide solid support to the credibility of our findings.
This study can be potentially extended in multiple ways. First, under the current model assumptions, the mixture probabilities do not depend on covariates. There are multiple ways to relax this assumption. One is to specify a mixture of joint distributions of the response and covariates, and then the probabilities of a subject belonging to different subgroups will vary with the value of its covariates. Another possibility is to directly model the mixture probabilities, say, using logistic regression based on a subset of covariates. These extensions demand additional model assumptions and may incur higher computational cost. Further, it is of interest to consider alternative data types and models. With complex data structures and analysis objectives, computation is more expensive than in some existing studies and may further increase for larger data. It is of interest to develop more efficient computation. The adopted priors are the most popular in existing literature and also computationally simpler. Yet, it may be of interest to consider alternative priors. Comparing with additional alternatives in data analysis can help further establish the superiority of the proposed approach. Finally, weaker signals have been observed in data analysis, and only internal prediction evaluation has been conducted. Conducting experimental validation, although significant, is beyond our scope. It is of interest to search for powerful data to generate more definitive findings and conduct external prediction evaluation.
Supplementary Material
Acknowledgments
We thank the editors and reviewers for their careful review and insightful comments.
Conflict of Interest: None declared.
Contributor Information
Yunju Im, Department of Biostatistics, Yale School of Public Health, 60 College ST, New Haven, CT, USA.
Yuan Huang, Department of Biostatistics, Yale School of Public Health, 60 College ST, New Haven, CT, USA.
Aixin Tan, Department of Statistics and Actuarial Science, University of Iowa, 259 Schaeffer Hall, Iowa City, IA, USA.
Shuangge Ma, Department of Biostatistics, Yale School of Public Health, 60 College ST, New Haven, CT, USA.
6. Software
Software written in Julia, together with a brief readme file, is available at github.com/shuanggema/BHA-hdInt.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Funding
NSF (1916251) and NIH (CA204120).
References
- Baliu-Piqué, M., Pandiella, A. and Ocana, A. (2020). Breast cancer heterogeneity and response to novel therapeutics. Cancers 12, 3271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbieri, M. M. and Berger, J. O. (2004). Optimal predictive model selection. The Annals of Statistics 32, 870–897. [Google Scholar]
- Belhomme, P., Toralba, S., Plancoulaine, B., Oger, M., Gurcan, M. N. and Bor-Angelier, C. (2015). Heterogeneity assessment of histological tissue sections in whole slide images. Computerized Medical Imaging and Graphics 42, 51–55. [DOI] [PubMed] [Google Scholar]
- Bien, J., Taylor, J. and Tibshirani, R. (2013). A lasso for hierarchical interactions. Annals of Statistics 41, 1111–1141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrell, R. A., McGranahan, N., Bartek, J. and Swanton, C. (2013). The causes and consequences of genetic heterogeneity in cancer evolution. Nature 501, 338–345. [DOI] [PubMed] [Google Scholar]
- Chen, M., Zhang, B., Topatana, W., Cao, J., Zhu, H., Juengpanich, S., Mao, Q., Yu, H. and Cai, X. (2020a). Classification and mutation prediction based on histopathology H&E images in liver cancer using deep learning. NPJ Precision Oncology 4, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, S., Zhang, N., Jiang, L., Gao, F., Shao, J., Wang, Tao,Zhang, E., Yu, H., Wang, X. and Zheng, J. (2020b). Clinical use of a machine learning histopathological image signature in diagnosis and survival prediction of clear cell renal cell carcinoma. International Journal of Cancer 148, 780–790. [DOI] [PubMed] [Google Scholar]
- Dey, T., Ishwaran, H. and Rao, J. S. (2008). An in-depth look at highest posterior model selection. Econometric Theory, 377–403. [Google Scholar]
- Echle, A., Rindtorff, N. T., Brinker, T. J., Luedde, T., Pearson, A. T. and Kather, J. N. (2020). Deep learning in cancer pathology: a new generation of clinical biomarkers. British Journal of Cancer, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frühwirth-Schnatter, S., Celeux, G. and Robert, C. P. (2018). Handbook of Mixture Analysis, Chapman ’ Hall/CRC Handbooks of Modern Statistical Methods. CRC Press. [Google Scholar]
- Gelman, A. and Rubin, D. B. (1992). Inference from iterative simulation using multiple sequences. Statistical Science 7, 457–511. [Google Scholar]
- Gupta, M. and Ibrahim, J. G. (2007). Variable selection in regression mixture modeling for the discovery of gene regulatory networks. Journal of the American Statistical Association 102, 867–880. [Google Scholar]
- He, B., Zhong, T., Huang, J., Liu, Y., Zhang, Q. and Ma, S. (2020). Histopathological imaging-based cancer heterogeneity analysis via penalized fusion with model averaging. Biometrics, doi: 10.1111/biom.13357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert, L. and Arabie, P. (1985). Comparing partitions. Journal of Classification 2, 193–218. [Google Scholar]
- Khalili, A. and Chen, J. (2007). Variable selection in finite mixture of regression models. Journal of the American Statistical Association 102, 1025–1038. [Google Scholar]
- Kim, J. and DeBerardinis, R. J. (2019). Mechanisms and implications of metabolic heterogeneity in cancer. Cell Metabolism 30, 434–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim, J., Lim, J., Kim, Y. and Jang, W. (2018). Bayesian variable selection with strong heredity constraints. Journal of the Korean Statistical Society 47, 314–329. [Google Scholar]
- Lee, K.-J., Chen, R.-B. and Wu, Y. N. (2016). Bayesian variable selection for finite mixture model of linear regressions. Computational Statistics and Data Analysis 95, 1–16. [Google Scholar]
- Ley, E. and Steel, M. F. J. (2009). On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. Journal of Applied Econometrics 24, 651–674. [Google Scholar]
- Li, Q., Shi, R. and Liang, F. (2019). Drug sensitivity prediction with high-dimensional mixture regression. PLoS One 14, 1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, W., Zhang, B., Zhang, Z., Tao, J. and Branscum, A. J. (2015). Model selection in finite mixture of regression models: a Bayesian approach with innovative weighted g priors and reversible jump Markov chain Monte Carlo implementation. Journal of Statistical Computation and Simulation 85, 2456–2478. [Google Scholar]
- Luo, X., Zang, X., Yang, L., Huang, J., Liang, F., Rodriguez-Canales, J., Wistuba, I. I., Gazdar, A., Xie, Y. and Xiao, G. (2017). Comprehensive computational pathological image analysis predicts lung cancer prognosis. Journal of Thoracic Oncology 12, 501–509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan, G. J. and Peel, D. (2000). Finite Mixture Models. Wiley-Interscience. [Google Scholar]
- Miller, J. W. and Harrison, M. T. (2018). Mixture models with a prior on the number of components. Journal of the American Statistical Association 113, 340–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison, C. D., Liu, P., Woloszynska-Read, A., Zhang, J., Luo, W., Qin, M., Bshara, W., Conroy, J. M., Sabatini, L., Vedell, P.. and others. (2014). Whole-genome sequencing identifies genomic heterogeneity at a nucleotide and chromosomal level in bladder cancer. Proceedings of the National Academy of Sciences United States of America 111, E672–E681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narisetty, N. N. and He, X. (2014). Bayesian variable selection with shrinking and diffusing priors. Annals of Statistics 42, 789–817. [Google Scholar]
- Papastamoulis, P. (2016). label.switching: an r package for dealing with the label switching problem in MCMC outputs. Journal of Statistical Software 69, 1–24. [Google Scholar]
- Papastamoulis, P. and Iliopoulos, G. (2010). An artificial allocations based solution to the label switching problem in Bayesian analysis of mixtures of distributions. Journal of Computational and Graphical Statistics 19, 313–331. [Google Scholar]
- Rodríguez, C. E. and Walker, S. G. (2014). Label switching in Bayesian mixture models: deterministic relabeling strategies. Journal of Computational and Graphical Statistics 23, 25–45. [Google Scholar]
- Schlattmann, P. (2009). Medical Applications of Finite Mixture Models. Statistics for Biology and Health. Berlin Heidelberg: Springer. [Google Scholar]
- Scott, J. G. and Berger, J. O. (2010). Bayes and empirical-Bayes multiplicity adjustment in the variable-selection problem. The Annals of Statistics, 2587–2619. [Google Scholar]
-
Städler, N., Bühlmann, P. and van de Geer, S. (2010).
 -penalization for mixture regression models. Test 19, 209–256. [Google Scholar]
-penalization for mixture regression models. Test 19, 209–256. [Google Scholar] - Wade, S. and Ghahramani, Z. (2018). Bayesian cluster analysis: point estimation and credible balls (with Discussion). Bayesian Analysis 13, 559–626. [Google Scholar]
- Xu, X. and Ghosh, M. (2015). Bayesian variable selection and estimation for group lasso. Bayesian Analysis 10, 909–936. [Google Scholar]
- Xu, Y., Zhong, T., Wu, M. and Ma, S. (2019). Histopathological imaging-environment interactions in cancer modeling. Cancers (Basel) 11, 579. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.