High-throughput cryo-ET structural pattern mining by unsupervised deep iterative subtomogram clustering

Significance

Automatic detection of macromolecular complexes is an open and challenging problem in cellular cryoelectron tomography. Existing computational methods rely on known structural templates or manually labeled training datasets. This paper presents an unsupervised framework with application to large-scale datasets, facilitating the efficient detection and objective interpretation of cellular structures and their spatial organizations in situ.

Abstract

Cryoelectron tomography directly visualizes heterogeneous macromolecular structures in their native and complex cellular environments. However, existing computer-assisted structure sorting approaches are low throughput or inherently limited due to their dependency on available templates and manual labels. Here, we introduce a high-throughput template-and-label-free deep learning approach, Deep Iterative Subtomogram Clustering Approach (DISCA), that automatically detects subsets of homogeneous structures by learning and modeling 3D structural features and their distributions. Evaluation on five experimental cryo-ET datasets shows that an unsupervised deep learning based method can detect diverse structures with a wide range of molecular sizes. This unsupervised detection paves the way for systematic unbiased recognition of macromolecular complexes in situ.

In recent years, cryoelectron tomography (cryo-ET) has made it possible to image densities of different molecules and their spatial distributions inside intact cells or viruses in a near-native, “frozen-hydrated” state to a resolution of a few nanometers in three dimensions (1, 2). This molecular-resolution visualization of how macromolecular complexes work together inside cells has allowed researchers to obtain mechanistic insights into particular cellular processes and distinguish competing models from one another (3). However, a major challenge remains to precisely and comprehensively identify densities of different molecules in complex cellular tomograms. A popular method to perform this task is “template matching” (4), which uses available structures obtained in vitro from X-ray crystallography or single-particle cryoelectron microscopy as template references to search for similar shapes in the tomograms. While useful, its dependency on available structural templates may introduce reference-dependent bias (5). An alternative popular practice is to manually pick target structures and then average them to obtain the initial template, which is also biased by subjective preferences (6). More importantly, as evidenced by genome sequencing and mass spectrometry, there may exist a large number of proteins with unknown structure and functions (7–10). Macromolecular complexes that lack available structural information cannot be identified in cryo-ET cellular tomograms using existing structural templates.

With that in mind, we and others have previously proposed a structural pattern mining approach (11, 12), as an important step toward template-free visual proteomics (13). This approach consists of 1) template-free particle-picking steps that detect potential structures in a tomogram and 2) recognition steps that classify each particle as a particular type of structure. However, the throughput of these methods is limited because they involve a tremendous number of geometric transformation operations for subtomogram averaging, classification, and refinement. Additional membrane segmentation preprocessing procedure may also be required (11). With the recent advance of cryo-ET data collection methods (14, 15), large numbers of tomograms can now be produced daily (more than 100 tomograms of size ∼4, 000 × 6, 000 × 1, 000 voxels, containing up to a million particles in total), allowing the effective imaging of many samples with different treatments and experimental controls for comparative analyses. The computationally expensive structural pattern mining approaches are impractical for handling such large-scale datasets. A better high-throughput analysis method is therefore needed to allow systematic and comprehensive investigation of the fast-growing size of in situ cryo-ET data.

Recently, deep learning methods have been gaining momentum both for cryo-EM particle picking (16), image enhancement (17–19), structural variability reconstruction (20, 21), and protein structure modeling (22–24) as well as for cryo-ET image segmentation (21, 25), classification (26, 27), and denoising (28, 29). By automatically learning better heuristics from accumulating data, their accuracy can improve over time, and they have been shown to perform more efficiently and accurately than the aforementioned traditional geometric approaches (30, 31). Due to their significantly faster recognition speed, they also promise better scalability to large-scale datasets with a large number of classes encompassing heterogeneous structures. However, existing deep learning-based cryo-ET subtomogram classification methods are based on supervised learning (32). Supervised methods pose an additional major challenge: creating valid training data. In these supervised deep learning methods, training a neural network requires a substantial amount of prelabeled data. For cryo-ET, training data have conventionally been produced either by using template matching as mentioned above or via laborious manual labeling of target structural patterns in tomograms (33). Both unavoidably produce biases by reference or subjective preference that limit the analysis. Unfortunately, this difficulty cannot be circumvented by using an annotated tomogram database consisting of multiple independent sources as a less-biased universal training set. This difficulty is because training from separated cryo-ET data sources, collected under different imaging conditions, was shown to result in lower recognition accuracy due to the variable image intensity distribution among data sources (34, 35). Moreover, these supervised methods remain unable to discover structures that are not annotated in the training dataset, posing a similar limitation to template matching. Therefore, a more natural and effective approach could be training the neural network in an unbiased template-and-label-free way by using comprehensive intrinsic structural features in the data themselves.

In light of this, we introduce a high-throughput unsupervised learning approach, DISCA (Deep Iterative Subtomogram Clustering Approach). DISCA automatically detects structurally homogeneous particle subsets in large-scale cryo-ET datasets by learning 3D structural features extracted by a Convolutional Neural Network (CNN) and statistically modeling the feature distributions (Fig. 1). Given a dataset of reconstructed 3D tomograms, as a preprocessing step, we first use template-free particle picking to detect potential structures and extract them as subtomograms. This preprocessing step is done automatically with no manual selection involved. The extracted subtomograms contain heterogeneous structures. We then use DISCA to sort the subtomograms into relatively homogeneous structural subsets. Specifically, we formulate a generalized expectation–maximization (EM) framework that iteratively clusters subtomograms based on their extracted CNN features and optimizes the CNN through unsupervised training. Finally, as postprocessing steps done outside our framework, the sorted subsets are aligned, averaged, and reembedded to the original tomogram space to visualize the recovered structures and their spatial distributions.

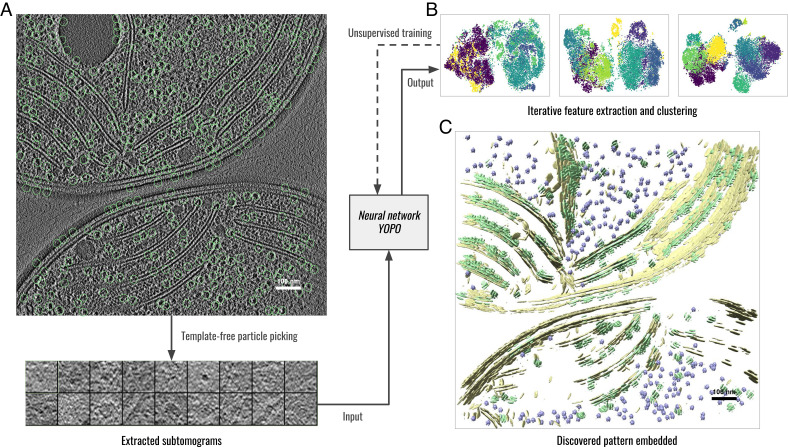
Fig. 1.

Workflow of DISCA exemplified on a Synechocystis cell (36). (A) 2D slice view of the template-free particle picking on the raw tomogram. (B) Unsupervised training of the YOPO neural network by iteratively clustering extracted features, each dot denotes the feature vector of a subtomogram in the feature space dimensionality reduced by t-SNE (37). The color of each dot denotes its cluster assignment. From Left (initial iteration) to Right (final iteration), feature vectors of different clusters became more and more separated. (C) Structural patterns detected by DISCA reembedded to the original tomogram space. Structures of the same color belong to the same detected structural class.

Results

The DISCA Computational Framework.

DISCA is mainly inspired by unsupervised image clustering methods recently proposed in the computer vision domain (38, 39). These methods integrate deep neural networks with feature clustering algorithms and self-supervised strategies to learn discriminative feature representation of images from large-scale 2D image datasets without the need for prespecified image labels. Similarly, we incorporated a feature clustering algorithm and self-supervision into DISCA. Furthermore, considering the specific properties of cryo-ET data, such as the low SNR and unknown cluster number, we designed a neural network architecture and training strategies to improve the structure-sorting performance on cryo-ET data. In supervised learning, a CNN is trained to maximize the expected prediction performance on a set of labeled training data. As we aim to learn only from unlabeled data, we develop a strategy to iteratively estimate both the number of structurally homogeneous subsets and the structural class labels of input subtomograms. The proposed iterative dynamic labeling strategy updates two models in an alternating fashion via a generalized expectation–maximization (EM) algorithm (40). Fig. 2 illustrates the YOPO (You Only Pool Once) model for feature extraction and the Gaussian distributions for the statistical modeling of structurally homogeneous subsets in the feature space ℝ^P. In the E-step, the number of structurally homogeneous subsets and the labels are estimated given the current learned features. In the M-step, YOPO parameters are updated by backpropagation training to minimize the loss function of computing the labels estimated from the E-step. We show the workflow of DISCA in SI Appendix, Fig. S1. In detail, YOPO is randomly initialized to extract feature vectors x_n ∈ ℝ^P from input subtomograms s_n ∈ S. Then, the feature vectors are fitted in the feature space by the mixed multivariate Gaussian distributions across a set of candidate K number of structurally homogeneous subsets. Only the mixture distribution with the lowest Bayesian information criterion is kept. We stabilize the optimization of the statistical model fitting by inheriting the parameters from the previous iteration. In each iteration after the first one, the parameter priors of the Gaussian mixture model, including the prior weights, means, and covariance matrix of each cluster, are initialized by the clustering solution from the previous iteration. Moreover, because errors can accumulate when initializing the statistical model fitting using parameters from the previous iteration, to avoid getting stuck at a local optimum, a de novo model fitting with randomly initialized parameters was also performed in each iteration, and its parameters were adopted if this model increased the likelihood function of the statistical model. The underlying idea of this design is similar to the Epsilon-greedy algorithm (41) in reinforcement learning in which the best solution from the previous observation is chosen with a probability of being replaced by a new solution. In our design, in each iteration, two clustering solutions are calculated: 1) fine-tuning the clustering solution from the previous iteration by inheriting the clustering model parameters and 2) running the clustering algorithm from scratch with randomly initialized parameters. The second solution will be chosen only if it improves the statistical likelihood of the model over the first solution. Otherwise, the first solution will be chosen. Using this strategy, a local optimum from the first clustering solution will be avoided. Then, the current estimated label of a subtomogram is given by a hard cluster assignment that corresponds to the component multivariate Gaussian distribution with the highest probability. In the next iteration, the current estimated labels are used for training YOPO by minimizing the categorical hinge loss function to learn better feature representations. After YOPO training, the mixture distributions are updated on the newly extracted feature vectors. This process continues iteratively until the stopping criteria (SI Appendix), consistency of labels or maximum number of iterations, have been met.

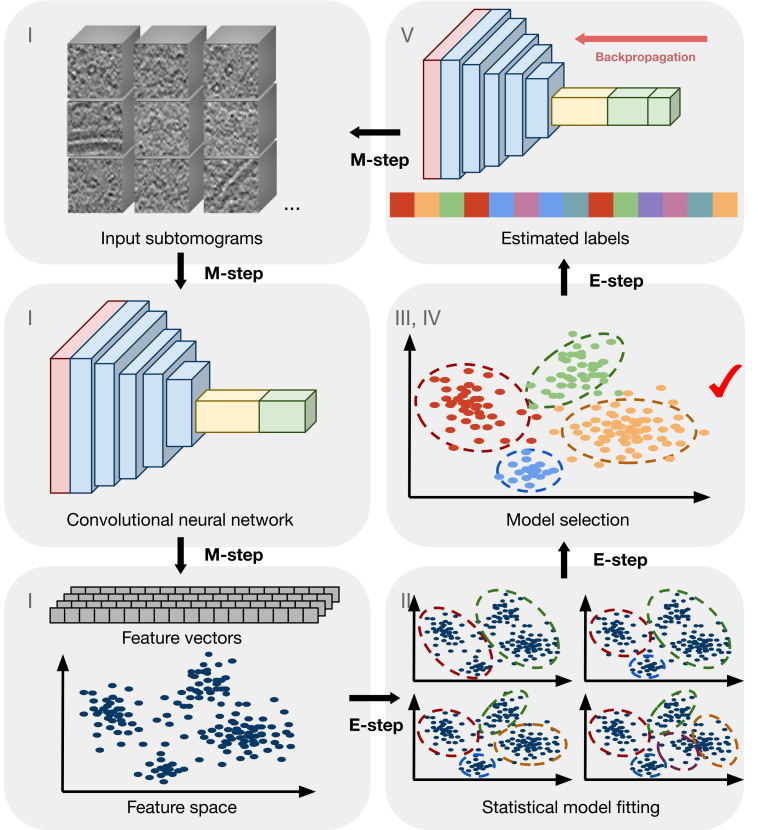
Fig. 2.

Conceptual explanation of DISCA. The numbers correspond to key steps in SI Appendix, Fig. S1. The input is a set of subtomograms extracted from tomograms using template-free picking methods. CNN features extracted (step I) from subtomograms are statistically modeled (step II) to estimate the cluster labels (steps II and IV). The CNN is in turn trained (step V) using the current estimated labels in order to learn better features iteratively.

Neural network architecture design.

We now describe the architecture design of YOPO and how we achieve rotation and translation-invariant feature extraction. A tomogram is a grayscale 3D volume of very large size (e.g., 4, 000 × 6, 000 × 1, 000 voxels). Even binned 4 times across each axis, a tomogram is still large (e.g., 1, 000 × 1, 500 × 250 voxels). Feeding such a large 3D volume into a CNN will inevitably exceed the memory of the system. One previous CNN method (33) dealt with this problem by slicing the tomogram into 2D images along the z-axis for cost-effective processing. However, taking 2D slices resulted in losing relevant structural information in 3D. In contrast, our objective is to cluster the heterogeneous densities of molecules (the majority being macromolecular complexes) enclosed in subtomograms into structurally homogeneous subsets. Because subtomograms extracted from binned tomograms are significantly smaller (e.g. 24³ voxels) than tomograms (42), they can be efficiently processed by 3D CNN without information loss.

Convolutional neural networks (CNNs) have been shown to outperform traditional hand-crafted feature extraction methods for the task of extracting discriminative features from images for various biomedical image analysis tasks (43, 44). In order to leverage the superior performance of CNNs, we designed a CNN named YOPO (SI Appendix, Fig. S2) specifically for subtomogram data that considers its distinct characteristics: 1) The structural details are essential to determine the identity of a macromolecule enclosed in a subtomogram; 2) the enclosed macromolecule is of random orientation and displacement; and 3) the signal-to-noise ratio (SNR) is extremely low. Because of the robust architecture design, YOPO achieves properties including structural detail preservation, transformation invariance, and robustness to noise. Such properties were also described as desired in traditional subtomogram classification methods (45).

Structural detail preservation: The standard pooling operation (max-pooling or average pooling) in CNN feature extraction is a problem for processing small 3D subvolumes. Indeed, even pooling by the smallest factor, 2, will dramatically reduce the subvolume size (for example, 24³ to 12³) and result in losing 87.5% of the information capacity. As structural details predominantly determine a macromolecular complex’s identity, the standard pooling operation may not be ideal for extracting features that preserve detailed structural information. In the Classification in Cryo-Electron Tomograms SHape REtrieval Contest (SHREC) 2020 (30) and 2021 (46), most of the participating semantic segmentation neural networks employ a U-Net-like architecture. Similarly, in a U-Net architecture, the low-level feature maps in the contracting path are concatenated to the expansive path as a way to preserve high-resolution structural details. Therefore, as an alternative to conventional neural network architectures in processing cryo-ET data, we equipped YOPO with a sequence of convolutional layers without any pooling operations in between for processing an input subtomogram into feature maps with both low-level and high-level structural information. Following the convolutional layers, rather than using the basic step of flattening the 3D feature maps into a 1D feature vector, we incorporated a global max-pooling layer to keep only the maximum of each of the feature maps. The global max-pooling operation also achieved translation invariance. As proved later, YOPO will output the same feature values for a subtomogram and its displaced copy because of the translation invariance.

Robustness to noise: Another challenge is the extremely low SNR of cryo-ET data. Often, raw tomograms are so noisy that even human eyes barely recognize the structure. While the convolutional layers in YOPO perform filter-like operations, we further boosted YOPO’s robustness to noise. We use a dropout strategy by adding a dropout layer after the input layer to corrupt the input subtomograms. This is inspired by denoising autoencoders (47) to regularize the network and reduce the variance of model prediction from noisy samples. Here, we use a Gaussian dropout layer, which randomly silences 50% of the nodes and injects multiplicative 1-centered Gaussian noise with standard deviation 1 during training. The Gaussian dropout layer has similar regularization performance as the conventional dropout layer, but it exhibits faster convergence properties (48). By randomly silencing a subset of nodes and injecting Gaussian noise, the Gaussian dropout layer can be viewed as a computationally efficient way to approximate multiple CNNs with slightly different parameters during CNN training. When multiple CNN models are aggregated by inactivating the Gaussian dropout layer during the prediction, the output variance is reduced, thus achieving robustness to noise. Finally, we added one fully connected layer after the global max-pooling layer to output the feature vectors of length 1024. In order to train YOPO, we equipped the final classification layer with softmax activation to output class labels. The Gaussian dropout layer, self-supervision for rotation invariance, and label smoothing described below have all been shown theoretically and empirically to be effective in preventing overfitting to increase the optimization robustness (49).

As a feature extraction model, YOPO preserves detailed structural information and extracts rotation- (through self-supervised training) and translation-invariant (through architecture design) features from subtomogram data. The translation invariance of YOPO is independent of the input data or the network weights. Such translation invariance usually cannot be achieved by standard CNN architecture designs. As independently evaluated by the SHape REtrieval Contest (SHREC) 2020 (30) in a supervised learning task, YOPO achieved the third-best accuracy and outperformed the template-matching baselines. Most importantly, YOPO requires only localized coordinates of target macromolecules for training, in which, a whole subtomogram only needs a single label. In comparison, all the other participating methods require labeled segmentation maps for training, in which every voxel needs to be labeled. The segmentation maps (dense labels) for an experimental cryo-ET dataset are extremely time-consuming to prepare as every single voxel of part of a tomogram needs to be labeled by experts. Therefore, YOPO was deemed “significantly more accessible for cryo-ET researchers” given that a minimal amount of training supervision was needed (30). We note that, in DISCA, the training of YOPO is fully unsupervised and further automated to be free from all external domain knowledge, including existing structural templates, manual labeling, or manual selection of densities in the tomograms.

Validation of the Feature Learning and Modeling Ability.

The design of DISCA enables transformation-invariant feature extraction, automatic estimation of the number of clusters, and progressively improved performance with larger sample sizes. To validate DISCA’s ability to learn to extract and model 3D transformation-invariant features, we conducted several experiments on realistically simulated datasets of various imaging parameters. These simulated datasets have prespecified ground truth labels to quantitatively assess the performance of DISCA and existing methods.

To test the accuracy of DISCA in simultaneously estimating the number of clusters K and structural class labels, we simulated subtomogram datasets of various SNR and tilt-angle ranges (examples shown in SI Appendix, Figs. S3 and S4 for each dataset). We used a standard subtomogram simulation procedure (50, 51) and took into account the tomographic reconstruction process with missing wedges and a contrast transfer function. The simulated imaging condition is similar to real experimental settings (52) with voltage 300 KeV, defocus −5 μm, and spherical aberration 2.7 mm. We chose five representative macromolecular structures (molecular weights range from 0.3 to 2.3 MDa): RNA polymerase (PDB ID: 1I6V), rotary motor in ATP synthase (1QO1), proteasome (3DY4), ribosome (4V4A), and spliceosome (5LQW). Experimental cryo-ET data typically have an SNR below 0.1 (53) and a tilt-angle range around −60° to 60°. For each macromolecular structure, we simulated 400 subtomograms with random orientations and displacements at each SNR (0.1, 0.03, 0.01, 0.003, and 0.001) and tilt-angle range (±60° and ±40°) to demonstrate the robustness of DISCA to the image noise and the missing wedge effect.

We performed DISCA on each of the simulated datasets. We evaluated the results by three criteria: 1) the estimated K with candidate K ranging from 2 to 20; 2) the homogeneity score (54) measuring how homogeneous each cluster is according to the ground truth labels. We note that the homogeneity score does not require an equal number of clusters to the ground truth; 3) the prediction accuracy measuring the percentage of correctly labeled subtomograms. The prediction accuracy can be calculated only when K is estimated correctly. The results from Table 1 show that DISCA correctly estimated the true K for eight of the ten datasets except at SNR 0.003 and 0.001 of tilt-angle range ±40°. As expected, the homogeneity scores gradually decreased with lower SNR and smaller tilt-angle ranges. However, in all settings, we achieved good results with homogeneity scores higher than 0.8, which means that the resulting clusters are generally homogeneous. We have conducted the experiments using randomly initialized models multiple times. The results were similar with ±5% margin, which ensured the reproducibility of our method.

Table 1.

Performance of three methods on simulated datasets

	Simulated ±60°					Simulated ±40°
Dataset	SNR 0.1	0.03	0.01	0.003	0.001	SNR 0.1	0.03	0.01	0.003	0.001
	-	-	-	-	-	-	-	-	-	-
Template matching	0.7013	0.4709	0.1496	0.0136	0.0032	0.5543	0.3336	0.0655	0.0062	0.0012
	83.95%	69.75%	45.35%	25.25%	20.95%	76.25%	61.15%	36.60%	23.80%	21.20%
	K = 5	K = 4	K = 5	K = 5	K = 3	K = 6	K = 5	K = 3	K = 3	K = 3
Autoencoder	0.3843	0.4539	0.3613	0.4915	0.3881	0.5227	0.3470	0.3735	0.3878	0.3874
	56.75%	-	53.45%	64.80%	-	-	53.35%	-	-	-
	K = 5	K = 5	K = 5	K = 5	K = 5	K = 5	K = 5	K = 5	K = 6	K = 6
DISCA	0.9878	0.9373	0.8746	0.8712	0.8719	0.9568	0.8020	0.8344	0.8366	0.8323
	99.70%	97.80%	94.80%	94.25%	94.50%	98.70%	90.35%	91.80%	-	-

In each cell, the first row denotes the estimated K for unsupervised methods. The second row denotes the homogeneity score compared to the ground truth. The third row denotes prediction accuracy.

We additionally performed template matching and autoencoder clustering for comparison. As we directly simulated the subtomograms, we used a subtomogram alignment method (55) implemented in AITom (56) to align each candidate template to each simulated subtomogram. The template with the highest alignment score was chosen. For template matching, even though we incorporated prior domain knowledge of known structural templates and thus K, the results are still worse than DISCA because template matching is not robust to noise. Under SNR lower than 0.01, template matching failed with accuracy close to random guess (20%). We previously proposed an unsupervised deep learning model to cryo-ET data (57), a convolutional autoencoder that coarsely groups and filters raw subtomograms. In that paper, we proposed a pose normalization step to normalize the orientation and displacement of the structure inside a subtomogram for better structural grouping. Compared with DISCA, the convolutional autoencoder can perform only coarse grouping with a homogeneity score lower than 0.55. This is mainly because DISCA is a significantly more sophisticated method that involves iterative feature learning and modeling in order to recognize the fine structure differences between different types of macromolecules.

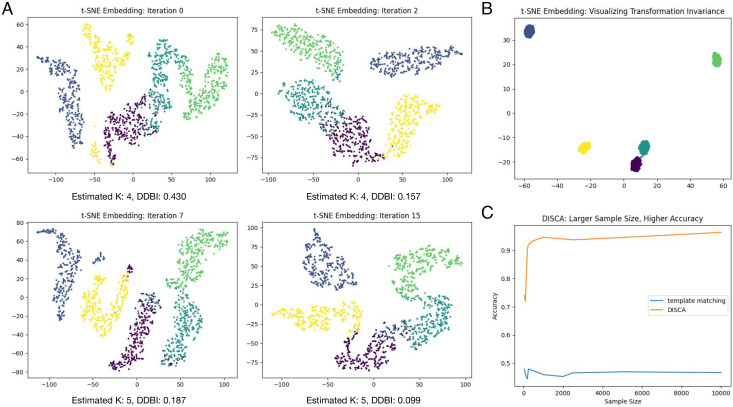
We further conducted several experiments and demonstrations using simulated dataset SNR 0.01 and tilt-angle range ±60°, which is closest to the image condition of experimental datasets as measured on the Synechocystis cell (36) and Rattus neuron (52) tomograms. In Fig. 3, K was estimated at 4 for early iterations, where some clusters were not separated well. Extracted features gradually separated out through the iterative learning process. Here, we provided a summary index, distortion-based Davies–Bouldin index (DDBI), modified from the Davies–Bouldin index (58), as an indicator measuring the cluster tightness relative to cluster separation. Rather than using Euclidean distance in the feature space, we used a distorted measure of the distance which takes each cluster’s covariance into account. The lowest DDBI is achieved at iteration 15, which was kept as the final result.

Fig. 3.

Validation on the SNR 0.01 and ±60° simulated dataset. (A) T-SNE (59) embedding of extracted features in different iterations. Each dot denotes one sample with its color indicating its structural class. (B) T-SNE embedding of extracted features from randomly transformed subtomogram copies (5 subtomograms per class and 200 copies per subtomogram; the rotation for each copy is done in the angular range of ±180° along each axis). Each dot denotes one copy with its color indicating its structural class. (C) Accuracy of template matching and DISCA with respect to different sample sizes.

To verify that the trained YOPO model extracts 3D features that are transformation-invariant to a large extent, we simulated five subtomograms for each of the five structural classes and then generated 200 randomly rotated and translated new copies for each subtomograms. The extracted features are visualized in Fig. 3B. We can see that features extracted from transformed copies are very similar to each other as compared to transformed copies of subtomograms of other classes.

To demonstrate the learning ability of DISCA with respect to different sample sizes, we conducted experiments varying input subtomogram numbers from 50 (10 subtomograms of each structural class) to 10,000 (2,000 subtomograms of each structural class). The results are shown Fig. 3C. The accuracy of DISCA improves progressively with larger sample sizes. The accuracy of template matching stays the same because it does not involve a learning process.

Unsupervised Structural Pattern Mining.

Currently, many popular subtomogram averaging software applications (60–64) have been developed that refine the averages to high resolution. However, these tools require relatively structurally homogeneous particle inputs. The main objective of DISCA is to efficiently sort representative structures into relatively structurally homogeneous subsets in large-scale datasets to complement these tools. Therefore, DISCA aims to recognize representative structures in a high-throughput way rather than to improve the subtomogram average resolution. We tested DISCA on five experimental cryo-ET datasets from distinct cell types: Rattus neuron (52), Synechocystis (36), Cercopithecus aethiops kidney (57), Mycoplasma pneumoniae (65), and Murinae embryonic fibroblast (66). Three of the datasets were obtained from the public repository EMDB (67) and ETDB (66). Unlike simulated data of which the ground truth clustering labels can be prespecified according to the structures enclosed, the clustering ground truth of subtomograms extracted from experimental cellular tomograms is not known in most experiments. There are two major commonly accepted ways to validate cryo-ET structure detection results. One is to align and average each detected structure subsets to recover the structures and compare them with existing known structures. The other is to compare with structural biologists–manual annotations. For all the five experimental datasets, we have done subtomogram averaging and calculated the gold-standard Fourier shell correlation resolution. Three of the experimental datasets (36, 52, 65) have available human experts’ annotations, which require a heavy amount of manual selection and annotation. The Cercopithecus aethiops kidney dataset has automated annotation from our previous coarse representation learning method (57). We have compared the automated annotation results of DISCA on these annotated datasets in order to validate their results. The YOPO neural networks on the experimental datasets were all randomly initialized without any pretraining process to demonstrate the robustness and generalization ability of DISCA.

As shown below, DISCA detected diverse representative structural patterns, including macromolecular complexes: ribosome, TRiC, capped proteasome, phycobilisome array, and other cellular structures: thylakoid membrane, mitochondrial membrane, and calcium phosphate precipitates. The macromolecular complexes that were detected have a wide range of sizes from 1.2 MDa to 4.5 MDa in molecular weights. The original manuscripts describing these datasets used manual density selection, template matching, and subtomogram classification to recover the structures. Our unsupervised structural pattern mining results from DISCA not only covered the previously identified spatial localization of various macromolecules well but also validated their results in a highly automatic and unbiased way. Subtomogram alignment and averaging following DISCA resulted in maps with 14 to 38 Å resolution range, confirming that template-and-label-free approaches are suited for in situ structural analyses. We describe the detailed results of these datasets in the following paragraphs.

First, we quantitatively assessed the accuracy of DISCA on the Mycoplasma pneumoniae dataset. For this dataset of 65 tomograms, obtaining the clean ribosome particles for comparison required 2 mo of time and heavy computation for traditional 3D template matching, manual curation, and computational sorting multiple times. The template was obtained by classifying and averaging some manually picked ribosomes. Then, template matching was performed on tomograms low-pass-filtered to 60 Å resolution, and the top 400 hits on each tomogram were selected, resulting in 26,000 total candidate ribosomes. We manually filtered out obvious false positives, such as ones on or outside of the bacterial cellular membrane, and checked the rest of them. A total of 18,987 true positives were left. Although no picking methods can guarantee 100% accuracy for experimental data, here we denote the precision of the “template matching & manual curation” approach as 100% because ribosomes are relatively easy to be identified by human eyes and they have been manually checked. This follows the common practice of manual detection of target structures in cryo-ET (25). Nevertheless, this template matching and manual curation approach still has missing ribosomes as false negatives, as evidenced by some true ribosomes uniquely detected by DISCA. As shown below, there are about 20% unique true ribosomes detected by DISCA that were missing from template matching detection. Therefore, we use the total number of true ribosomes detected by both approaches, 23,592, to calculate the metrics in Table 2. In addition, we would like to note that it is common that experts estimate that their miss rate is between 10 and 20% on detecting ribosomes by template matching. This estimation is consistent with our experimental results.

Table 2.

Quantitative comparison of ribosome detection by two approaches on the Mycoplasma pneumoniae dataset

	DISCA	Raw template matching	Template matching & manual curation
Total picked	22,875	26,000	18,987
Unique	6,768	–	2,843
True in unique	4,645	–	2,843
True positives	20,749	18,987	18,987
False negatives	2,843	4,605	4,605
Precision	90.7%	73.0%	100%
Recall	87.9%	80.5%	80.5%
F1 score	0.893	0.766	0.892

We compared the template matching and manual curation results as well as the raw template-matching results with the results from DISCA. In summary, DISCA achieved a high F1 score of 0.893 (Table 2). Furthermore, DISCA detected about 20% of the ribosomes missed by the template matching and manual curation approach and detected more true ribosomes overall. Fig. 4 compares an example raw tomogram slice and the corresponding reembedding annotations of the detected patterns. The voxel size of this tomogram is 6.802 Å, and the resolution measured on the ribosome average is 14.17 Å. For comparison, we applied template matching, manual curation, subtomogram averaging, and classification by Relion (60) to recover the ribosome structure, which is referred to hereafter as the template-matching approach. We consider two detections as overlapping if their Euclidean distance is smaller than 8 nm. Under this criterion, 96.9% of the 18,987 ribosomes detected by template matching are included in the 198,715 subtomograms extracted by template-free particle picking.

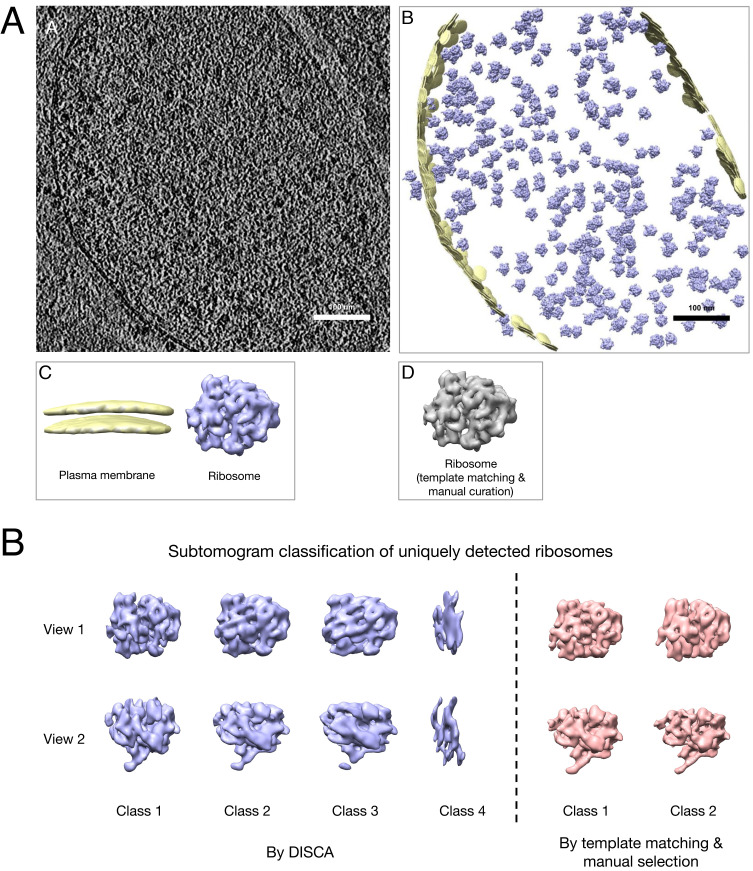
Fig. 4.

(A) Example unsupervised annotation on a Mycoplasma pneumoniae cell tomogram (65): a slice of the original tomogram; b detected patterns reembedded to the original tomogram space; c isosurface visualization of detected patterns identified (generated from subtomogram averaging); d isosurface visualization of the ribosome structure using the template-matching approach. (B) Relion subtomogram classification of uniquely detected ribosomes by the two approaches.

DISCA clustered the 198,715 total extracted subtomograms into ten clusters where one cluster corresponds to ribosome structures and one cluster corresponds to membrane structures. Among those 18,987 ribosomes detected by the template-matching approach, 85.0% of them overlap the ribosome cluster. On the other hand, 70.4% of the 22,875 ribosomes detected by DISCA overlap with the template-matching results. As shown in Fig. 4A , c and d), the template-and-label-free result from DISCA resembles the template-matching result, with a correlation coefficient of 0.995.

We further investigate the 6,768 ribosomes uniquely detected by DISCA. To assess how many of them are truly ribosomes, we used the Relion subtomogram classification function to classify them into 4 classes. As shown in Fig. 4B, classes 1, 2, and 3 clearly correspond to the ribosome structure, whereas class 4 cannot be identified. Therefore, the 4,645 subtomograms in class 1, 2, and 3 are likely to be true positives missed by the template-matching approach. For comparison, there are 2,843 ribosomes uniquely detected by the template-matching approach. Since this number is about half of the 6,768 ribosomes uniquely detected by DISCA, we classified them into 2 classes using the same Relion procedure. The results shown in Fig. 4B confirmed that they are truly ribosomes. Therefore, we empirically determined that DISCA has a false-positive rate of 9.3% and a false-negative rate of 12.1% (3.1% due to the particle-picking preprocessing step). Moreover, DISCA detected about 20% of ribosomes missed by the template-matching approach. There are 23,592 true ribosomes detected by DISCA and template matching in total, which corresponds to our estimated number of all ribosomes in these 65 Mycoplasma pneumoniae cellular tomograms. Overall, DISCA detected more true ribosomes than template matching (20,749 vs. 18,987). We note that here we used Relion for averaging the subtomograms into multiple classes only for validation purposes. The subtomogram averaging results shown in all figures correspond to averaging each cluster into only one class using Relion 3.0. Fig. 4B is the only exception in which we needed to perform subtomogram classification and averaging by Relion to inspect the ribosomes uniquely detected by DISCA.

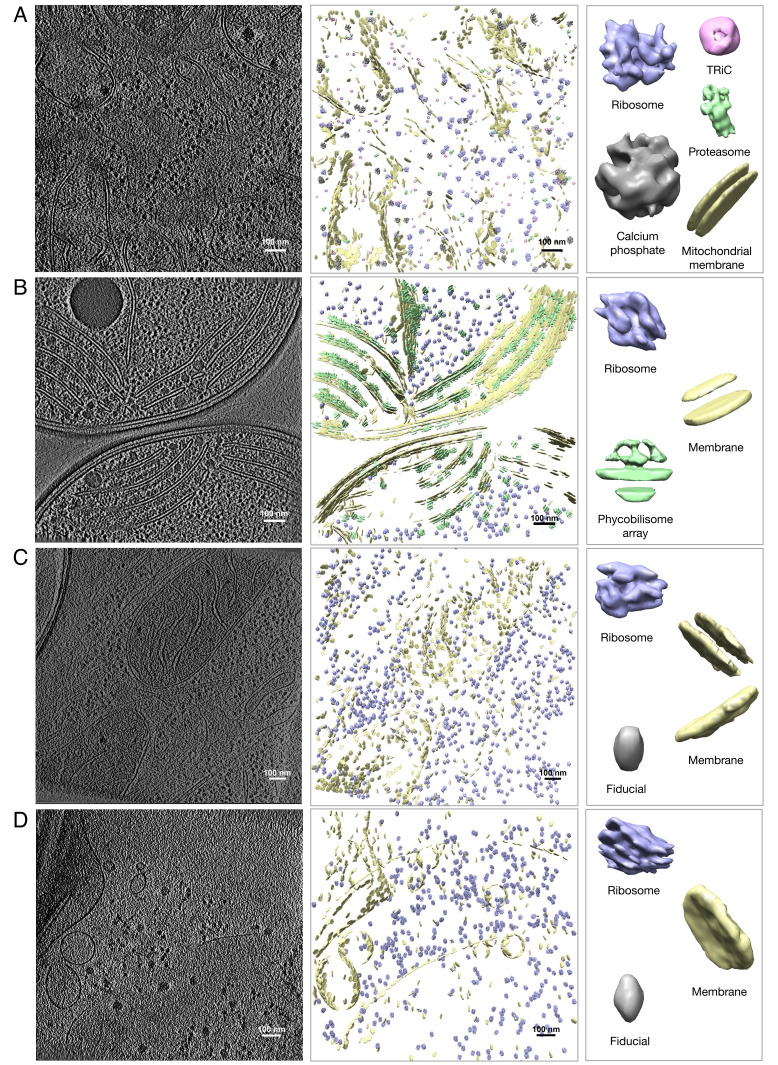
Then, we visualize the unsupervised structural pattern mining example results on the other four datasets in Fig. 5. Overall, the results obtained from DISCA validated the results reported in the original articles of these datasets: 1) On the Rattus neuron tomograms, based on their prior knowledge, the authors applied manual subtomogram picking, subtomogram classification and averaging, and iterative template matching to recover three macromolecular complexes: ribosome, proteasome, and TRiC (figure 2 in ref. 52). DISCA produced similar macromolecular complexes detection results (Fig. 5A) as well as detection of obvious subcellular structural patterns, including mitochondrial membrane and calcium phosphate precipitate. We obtained the template matching with selection by Relion classification results on three tomograms of this dataset from the authors (52) and performed a quantitative comparison (Table 3; cluster size: the number of subtomograms in the corresponding DISCA cluster; overlap: the number of overlapping subtomograms with template matching detection; template matching: the number of detected particles by template matching; the F1 score is calculated based on the overlapping results by the two approaches). Similar to the Mycoplasma pneumoniae dataset, the result on ribosome detection is promising (∼0.85 F1 score). The results on proteasome and TRiC detection are not as good but satisfactory (∼0.5 F1 score). The potential reason is that detecting smaller macromolecules is still very challenging for both template matching and DISCA. 2) On the Synechocystis cell tomograms, the authors applied manual picking and several rounds of subtomogram averaging and template matching to detect and annotate the membrane-associated phycobilisome array and ribosome structures. We note that the subtomogram averages in the original article were produced from 20 tomograms, whereas we have only two publicly available tomograms with no expert annotation to quantitatively compare with. The subtomogram averaging on the sorting results of DISCA is not ideal, but the automated annotation results of DISCA (Fig. 5B) are similar to the annotation results in the original article (figure 1 in ref. 36). 3) On the Cercopithecus aethiops kidney cell tomograms, the authors reported coarse discovery of globular and surface patterns using an autoencoder clustering model. However, the ribosome-like globular pattern is of very low resolution, which is probably due to the impurity of the resulting clusters. DISCA showed notable improvement of ribosome-like globular pattern and membrane pattern (Fig. 5D) on this dataset as compared to Fig. 5 and SI Appendix, Fig. S5 of the original article of this dataset (57). 4) The Murinae embryonic fibroblast tomograms are obtained from ETDB (66), but there is no existing research publication on this dataset. We detected biologically meaningful structural patterns including single and double membranes and ribosomes (Fig. 5C) on this dataset. For all the macromolecular structures, we plot the gold-standard Fourier shell correlation (FSC) curve of the subtomogram averages and visual comparison with existing solved structures from the Protein Databank in (SI Appendix, Figs. S9–S16).

Fig. 5.

Comparison of example raw tomogram slice and corresponding reembedding annotation of patterns detected from a set of (A) seven Rattus neuron tomograms (52). The identified clusters consist of 12,229 subtomograms from 38,292 total extracted subtomograms. The voxel size of this tomogram is 13.68 Å, and resolution measured on the ribosome pattern (averaged from 3,708 subtomograms) is 27.36 Å; (B) two Synechocystis cell tomograms (36). The identified clusters consist of 4,804 subtomograms from 12,912 total extracted subtomograms of voxel size 13.68 Å; (C) twenty Murinae embryonic fibroblast tomograms obtained from ETDB (66). The identified clusters consist of 11,471 subtomograms from 54,684 total extracted subtomograms. The voxel size of this tomogram is 15.48 Å, and resolution measured on the ribosome pattern is 33.77 Å (averaged from 2,459 subtomograms); (D) two Cercopithecus aethiops kidney cell tomograms (57). We note that since the Synechocystis cell and Cercopithecus aethiops kidney cell datasets are small datasets with only two tomograms, the ribosome pattern is not as ideal as other datasets.

Table 3.

Quantitative comparison of the three macromolecular complexes detection on the Rattus neuron dataset

	Cluster size	Overlap	Template matching	F1
Ribosome	1,127	884	1,015 (968)	0.845 (0.864)
Proteasome	77	40	98 (81)	0.462 (0.512)
TRiC	188	75	143 (117)	0.453 (0.492)

Numbers in parentheses denote quantity and statistic with respect to particles picked by the DoG methods.

We note that the preprocessing step difference of Gaussians (a variant of the Laplacian of Gaussian) is a conventionally used particle-picking method in cryo-ET. Because structures in cryo-ET data are very complex with very low SNR, DoG picks all possible particles, which tends to have many false positives such as pure noises. That is the rationale behind the proposed framework, to efficiently sort the large number of heterogeneous particles into relatively homogeneous subsets. In our experiments, we defined the recognition of a structure to be 1) with averaging resolution better than 40 Å, and 2) the average can be visually identified as a certain type of structure. Based on the averages we show that met these two criteria, about 30% of particles can be recognized.

In terms of time cost, DISCA is a very efficient method for processing a large amount of data both theoretically (overall time complexity O(N), where N is the number of samples, SI Appendix) and practically: On the Mycoplasma pneumoniae cell dataset of 65 tomograms, DISCA took less than a day to sort 198,715 template-free picked subtomograms (binned to 24³ voxels of 13.33 Å spacing). With trained DISCA models, the prediction of new data is very fast and can process millions of such sized subtomograms in less than an hour. Moreover, since the resulting clusters sorted by DISCA consist of relatively homogeneous structures, the postprocessing subtomogram averaging step also becomes more efficient. This is because we only need to average each cluster into a single map instead of performing subtomogram classification and averaging into multiple class averages. On the Mycoplasma pneumoniae cell dataset, the subtomogram averaging took only 1 d to finish.

Discussion

We describe a high-throughput unsupervised structural pattern mining framework for cryo-ET data. DISCA can efficiently produce meaningful structures from large-scale datasets that encompass very heterogeneous structures without any prior knowledge, which constitutes a major step for unsupervised structure determination in situ. The noteworthy missing wedge effect in cryo-ET is addressed by the robust network architecture design and the self-supervision step in DISCA, which is discussed in detail in Methods section. We demonstrate the performance of DISCA on five cryo-ET datasets of different cell types. We find that the structures detected by DISCA were similar to previously reported ones recovered with highly intensive computational and manual processing.

A major limitation of DISCA comes from its operation on picked subtomograms. Ideally, subtomograms at every voxel should be analyzed. However, this requires the processing of billions of particles which is computationally infeasible. Although the particle-picking step introduces some false positives and negatives, we deem that its trade-off for efficiency is acceptable. Moreover, the vast majority of particles at every single voxel contain background noise or structures that are too small to unambiguously identify in cellular cryotomograms. Including them in the sorting process will bias the model toward distinguishing structures from the background instead of the difference between structures. As different macromolecular structures have different sizes, in our experiments, we used a fixed subtomogram box size that could enclose most macromolecular structures. To avoid the issue of structures being clipped, we note that it is possible to 1) extract larger-sized subtomograms for DISCA or 2) use the same subtomogram size for DISCA and extract larger-sized subtomograms for postprocessing averaging.

Another limitation of subtomogram operation is the analysis of large continuous structures such as membranes. The embedding of subtomogram averages will appear broken into small pieces as in Fig. 5. Since the DISCA detection of membrane subtomograms is sufficiently accurate, this limitation can be easily addressed by performing membrane segmentation on the subtomograms rather than averaging them, which will produce a realistic continuous annotation of the membrane structure such as the one in SI Appendix, Fig. S8.

A major concern with unsupervised methods is their training stability. From our experience, the training in DISCA is generally stable due to the initializers used: Orthogonal kernel initializer and zero bias initializer were used for YOPO. The training stability ensures the reproducibility of DISCA. In practice, to obtain the optimal sorting performance, the users could either run DISCA multiple times and keep the results with the lowest DDBI metric or keep a DISCA model successfully pretrained on existing datasets and fine-tune on new datasets.

In terms of methodological parsimony, DISCA requires no manual intervention or selection of existing structural templates for matching. The template-and-label-free nature of DISCA offers maximal automation and objectivity. Overall, the performance demonstrates that DISCA is a reasonable alternative for cryo-ET structure discovery when manual annotation or prior knowledge of a dataset is lacking, as well as a robust tool to validate existing template-based results. By quickly detecting representative homogeneous structural subsets in a cryo-ET dataset, DISCA can also serve as a preprocessing step to complement the standard template matching and subtomogram average pipeline. Although DISCA automatically detects abundant and representative cryo-ET particles, researchers are sometimes interested in rare macromolecules or certain types of target proteins. The ability of DISCA in detecting relatively rare structures has been quantitatively demonstrated on the TRiC and proteasome structures in Table 3. Additionally, the users could 1) combine DISCA and template matching to search for certain target proteins or 2) extend DISCA to multistages in which abundant particles are first detected and excluded and apply DISCA again to sort the remaining particles. In conclusion, DISCA shows the promise of high-throughput cryo-ET structural pattern mining for discovering abundant and representative structures systematically. The proposed framework will allow researchers to fully leverage state-of-the-art cryo-ET imaging infrastructure and workflows.

Materials and Methods

Rotation and Translation-Invariant Feature Extraction.

One important characteristic of subtomogram data is that the structure enclosed is randomly oriented and exhibits small random displacement. To cluster multiple copies of the same structure in different orientations and displacements together into the same subset, YOPO must be able to extract features invariant to both translation and rotation.

The rotation invariance was achieved by self-supervised learning for enforcing a CNN to be invariant to certain geometric transformations of the input and improving its generalization ability. In each iteration, alongside the original input subtomogram, a randomly rotated copy of the subtomogram is also fed into YOPO for training. The label of the randomly rotated copy stays the same. By doing so, the rotation invariance of YOPO is enforced by backpropagating the loss gradient. Although having a full range of exhaustive sampling of rotation angles for data augmentation would force the network to learn the highest level of rotational invariance, there is a trade-off with the amount of computation. We do not have a preset range of rotation angles used. Instead, a 3D rotation is randomly sampled from all possible 3D rotation angles. Then, in each iteration, the randomly sampled 3D rotation is applied for each subtomogram input to generate a rotated copy. Our current design already achieves a satisfactory level of rotational invariance as demonstrated in our experiments in Fig. 3B. In addition, because an input subtomogram is a 3D cubic volume, there will be empty regions in the corner of rotated subtomogram copies with sharp edges along the border of the empty regions. These artifacts, creating features with no structural meaning, will negatively affect the training of the neural network. During the self-supervision step, the empty region of the rotated subtomogram is filled with Gaussian white noise to avoid sharp edge artifacts. The Gaussian white noise has a mean zero and SD one, same as the normalized image intensity distribution of the input subtomogram data.

The translation invariance is already achieved in the architecture design of YOPO by the global max-pooling layer. The convolution operations y_c are translation equivariant: The extracted feature maps of an input subtomogram s_n translated by t_θ will be the same as translating the extracted feature maps from the original subtomogram by t_θ: y_c(t_θ(s_n)) = t_θ(y_c(s_n)). Then, because the global max-pooling layer y_g computes the global maximum from a feature map, which is translation-invariant, the output from the global max-pooling layer is translation-invariant to the input subtomograms: y_g(t_θ(s_n)) = y_g(s_n). Denoting YOPO feature extraction from a subtomogram as y(s_n)=y_f ° y_g ° y_c(s_n), where y_c denotes the sequence of convolutional layers, y_g the global max-pooling layer, and y_f the fully connected layer, we have:

$$\begin{array}{cc}y(t_{\theta }(s_n))& =y_f\circ y_g\circ y_c(t_{\theta }(s_n))=y_f\circ y_g(t_{\theta }(y_c(s_n)))\\ & =y_f\circ y_g(y_c(s_n))=y(s_n).\end{array}$$ [1]

As a result, the final extracted feature vectors are translation-invariant to the input subtomograms. This property, y(t_θ(s_n)) = y(s_n), holds for all input data s_n and all network weights of y. In other words, this translation invariance is independent of the network weights and input data.

Transformation invariance is desired because if the feature vector changes when the orientation and displacement of a subtomogram structure change, it is not easy to cluster the same type of structures together. For neighbor structures in a subtomogram, first, due to the small size of a subtomogram, it is likely that only a small part of a neighbor structure exists in a subtomogram. Therefore, their influence on the extracted feature vectors is limited. Second, in the data augmentation self-supervision step, the subtomogram is randomly rotated, which helps to ignore the influence of neighbor structures located at the corner of the subtomogram.

When designing YOPO, we have tested alternative architectures such as 3D InceptionNet and ResNet as feature extractors and incorporated other layers including max-pooling, average pooling, global average pooling, flatten, and conventional dropout layers into the network design. The final YOPO design was based on empirically comparing alternative architectures.

Statistical Modeling of Structurally Homogeneous Subsets in Feature Space.

Recent works (68, 69) have shown that second-order statistics in CNNs—for instance, the covariance between features—are vital for differentiating between different visual patterns. Accordingly, simple clustering algorithms such as K-means or hierarchical clustering which do not consider second-order statistics are not suitable. Another notable class of clustering algorithm is density-based clustering such as DBSCAN (70). DBSCAN has the advantage of automatically determining the number of clusters and filtering out noisy samples. However, it has two disadvantages for our task: 1) Same as K-means, it does not consider second-order statistics; and 2) it needs to calculate pair-wise distances between all samples, resulting in time complexity of O(nlog n), which is not scalable to large-scale datasets.

To fully capture the feature covariance information, after extracting the translation and rotation invariant features from the input subtomograms by YOPO, we model the learned feature vectors for each representative structural pattern as a multivariate Gaussian distribution in the feature space.

In greater detail, given a set of N subtomograms s_n ∈ S extracted from a dataset of tomograms V, the YOPO network y extracts feature vectors x_n = y(s_n), x_n ∈ ℝ^P from each subtomogram, where P is the dimensionality of the feature space. We model the distribution of the data point x_n as a mixture of K multivariate Gaussian distributions. The mixture distribution’s probability density f_g is defined as:

$$\begin{array}{c}{f}_g(x_n;\varphi ,\mu ,\text{Σ},K)={\displaystyle \sum _{k=1}^K{\varphi }_{k}g(x_n;{\mu }_k,{\text{Σ}}_k)}.\end{array}$$ [2]

In Eq. 2, ϕ_k is the prior probability of sampling x_n from the kth component. The prior probability for each component is initialized randomly and optimized along with other model parameters. The kth component is a multivariate Gaussian distribution g with mean μ_k and covariance matrix Σ_k. Hence, the posterior probability of sampling x_n from the k^th component is ${\rho }_k(x_n)=\frac{{\varphi }_{k}g(x_n;{\mu }_k,{\mathrm{\Sigma }}_k)}{{\sum }_{i=1}^K{\varphi }_{i}g(x_n;{\mu }_i,{\mathrm{\Sigma }}_i)}$. Solving the model in Eq. 2 provides the probability ρ_k(x_n) of feature vector x_n being sampled from each component distribution g(x_n; μ_k, Σ_k). g(x_n; μ_k, Σ_k) has its own covariance matrix Σ_k to distinguish between different structural patterns. The component $\widehat{k}=\underset{k\in 1,\dots ,K}{\text{arg}\text{max}}{\rho }_k(x_n)$ is the highest posterior probability among all components. $\widehat{k}$ will be used as the class label for subtomogram s_n in the clustering solution.

Iterative Dynamic Labeling.

A potential issue is that, unlike in supervised learning, where training data labels are fixed, the YOPO training data labels are dynamic. In other words, there will inevitably be mislabeled data when training YOPO, especially in the early iterations. To address this issue, we adapt the label smoothing regularization technique (71) to make the YOPO training less prone to mislabeled data. The smoothed one-hot encoding of training labels is $l_{\mathit{ls}}=(1-\alpha )\ast l_{\mathit{hot}}+\frac{\alpha }{K}$, where K is the number of clusters, l_hot is the original one-hot encoding of training labels, and α is the smoothing factor. The larger the label smoothing factor α, the less certain the model prediction.

Moreover, the estimated K is also dynamic in different iterations. We need to enable YOPO to output different class numbers during the training. When the estimated K differs from the previous iteration, we replace the last layer, the classification layer, with a new one with the current estimated K number of nodes. Because the new classification layer has randomized initial weights, we train its weights with the fixed current extracted features as input to reach consistency between its prediction and current estimated labels.

Further details and discussion of distortion-based Davies–Bouldin index (DDBI), automatic estimation of the number of structurally homogeneous subsets, matching clustering solutions, missing wedge effect, and time cost and complexity analysis can be found in SI Appendix.

Implementation Details.

The implementation details, including those of the preprocessing particle-picking step and the postprocessing subtomogram averaging and embedding alignment steps, are described in SI Appendix.

Data Source.

The Rattus neuron dataset is obtained from ref. 52. The Synechocystis dataset is obtained from EMDB (67) EMD-4603 and EMD-4604 (36). The Cercopithecus aethiops kidney dataset is obtained from ref. 57. The Murinae embryonic fibroblast is obtained from ETDB (66) with the MefB cell line from O. Loson in Chan Lab. The Mycoplasma pneumoniae dataset was acquired as described previously (65). Tomograms were reconstructed and denoised using Warp (72). The original tilt-series data is available via EMPIAR-10499. The Rattus neuron, Synechocystis, and Mycoplasma pneumoniae datasets were collected with Volta phase plates.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

To directly benefit the cryo-ET research community, all the code is available in our open-source cryo-ET data analysis software AITom (56). User-friendly tutorials is provided on how to apply our models to users’ own datasets. Currently, we have disseminated most of our existing published algorithms into AITom. There are more than 20 tutorials provided in AITom for different cryo-ET analysis tasks with more than 30,000 lines of codes mainly written in Python and C++. AITom is also being integrated with the software Scipion (73) as a plugin. The subtomogram average of macromolecular complexes from the Rattus neuron dataset and the Mycoplasma pneumoniae dataset have been deposited in the EM Data Bank with accession numbers EMD-40043, EMD-40087, EMD-40089, and EMD-40090. The raw datasets can be obtained according to Data source. The trained models, demo data, and other generated data are available in AITom (56). All study data are included in the article and/or SI Appendix.